LOQUAT: an open-source GPU-accelerated SPH solver for geotechnical modeling

Abstract

Smoothed particle hydrodynamics (SPH) is a meshless method gaining popularity recently in geotechnical modeling. It is suitable to solve problems involving large deformation, free-surface, cracking and fragmentation. To promote the research and application of SPH in geotechnical engineering, we present LOQUAT, an open-source three-dimensional GPU accelerated SPH solver. LOQUAT employs the standard SPH formulations for solids with two geomechnical constitutive models which are the Drucker–Prager model and a hypoplastic model. Three stabilization techniques, namely, artificial viscosity, artificial pressure and stress regularization are included. A generalized boundary particle method is presented to model static and moving boundaries with arbitrary geometry. LOQUAT employs GPU acceleration technique to greatly increase the computational efficiency. Numerical examples show that the solver is convergent, stable and highly efficient. With a mainstream GPU, it can simulate large scale problems with tens of millions of particles, and easily performs more than one thousand times faster than serial CPU code.

1 Introduction

Numerical analysis plays a crucial role in modern geotechnical engineering. After approximately five decades of development, numerical analysis in geotechnical engineering has reached a certain degree of maturity. Various numerical methods were adopted in geotechnical modeling. Among them, grid-based methods such as finite element method (FEM), finite difference method (FDM) and finite volume method (FVM) are well-established and successfully employed in various applications [64, 89]. Grid-based methods use mesh for the spatial discretization. Most of the advantages and disadvantages of grid-based methods come with the utilization of mesh. For instance, grid-based methods are generally considered more robust and efficient compared to meshless methods, and can be employed to a wide range of applications. Moreover, they have more solid mathematical theory on convergence and stability. One the other hand, grid-based methods have difficulties in modeling problems involving, among others, large deformation, free-surface, moving boundary, cracking and fragmentation. All of these problems have in common changing or discontinuous computational domains due to deforming, cracking and separating of material; thus, grid-based methods need additional efforts such as remeshing or interface tracking to handle these problems.

In recent years, Lagrangian particle-based meshless methods are developed and become more and more popular. These methods have advantages in modeling problems difficult for mesh-based methods because they completely or partly avoid the use of mesh. Popular methods include, for instance, smoothed particle hydrodynamics (SPH) [41, 47, 50], material point method (MPM) [4, 5, 80] and particle finite element method (PFEM) [56, 57]. Among these methods, SPH is well-established and has a long application history in astrophysics [70], fluid dynamics [23, 68, 73, 84] and solid mechanics [26, 39, 40]. SPH is also employed to geotechnical modeling in recent years. Reported applications include large deformation [7, 10, 59], granular flow [14, 16, 45, 54, 60, 72], soil-structure interaction [8, 12, 63, 76], landslide and debris flow [13, 36, 44, 58], fluid-soil mixture dynamics [7, 9, 35, 37, 43, 53, 77, 78, 86], cracking [6, 18, 85, 87] and underground explosion [15]. It is shown that SPH is able to solve the aforementioned problems which are otherwise difficult for grid-based methods. Therefore, SPH is promising and has the potential to be employed to a wider range of academic and engineering geotechnical applications.

Although SPH has a long application history in astrophysics, fluid dynamics and solid mechanics, its employment in geotechnics is relatively new. Maeda et al. [43] and Naili et al. [53] are among the first to use SPH to model real geotechnical problems such as seepage failure and sand liquefaction. Later, Bui et al. [10] developed a complete SPH framework for large deformation analysis in geomaterials. In their work, the hypoelastic treatment of large deformation is employed. Constitutive models based on infinitesimal strain assumption are augmented with objective stress rate to model large deformation. Following the SPH framework in [10], many researchers developed new formulations, numerical algorithms and implemented various constitutive models. Notable progresses of SPH research in geotechnical modeling include, among others, the soil-structure frictional contact [76], employment of new constitutive models [7, 59, 60], extension to simulate multiphase water-soil coupling problems [7, 9, 35, 37, 77, 86], new cracking treatment method [6, 85] and the latest development of multiplicative elastoplasticity for SPH [54]. Despite these achievements, it is generally observed that in the past ten years there lacks groundbreaking progresses in SPH theories and applications in geotechnical engineering since Bui et al. [10]. The well-known numerical instabilities such as tensile instability and hourglass mode are still not completely avoided. Among many researchers and engineers, SPH is still a quite unfamiliar approach. This somewhat awkward situation can only be improved if more researchers and engineers start working on and with SPH.

Yet there are several facts discouraging new users to try SPH. SPH is a meshless method, where the approximation of field quantities is based on the particles in the support domain. Usually, the number of particles in interaction is much larger than that in the grid-based methods, especially in three-dimensional cases, where dozens to hundreds of interacting particles can be used [20, 88]. The huge number of interacting particles greatly increase the computational cost. Moreover, explicit time integration methods are used in SPH, where the time step is governed by the Courant–Friedrichs–Lewy (CFL) condition. Small time steps are resulted from the CFL condition due to the large value of the speed of sound. Therefore, the numerical efficiency of SPH is lower than grid-based methods. To the best of the authors’ knowledge, there are no SPH applications in real-scale three-dimensional geotechnical problems. The main reason is that the computational time is prohibitive if a serial SPH computing is used. To this end, acceleration techniques such as multi-thread CPU computing and GPU acceleration are necessary for SPH to achieve reasonable computational time.

Another obstacle for new SPH users is the lack of resources. In recent years, several SPH open-source codes were released, e.g. GADGET [69, 71] and GIZMO [31, 32] for astrophysical modeling, SPHysics [24, 25] and DualSPHyiscs [17, 21] for fluid dynamics, and GPUSPH [28] for lava flow modeling. These open-source codes are designed for applications in which both the dominant physics and the material behaviors are far different from geotechnical problems. Therefore, considerable modifications of the codes are needed before they can be employed in geotechnical modeling. The SPH method is also included in commercial software LS-DYNA and ABAQUS; however, SPH module in these software focuses on fluid dynamics and impact simulation, which cannot be directly used in geotechnical simulations. Till now there is no open-source or commercial SPH solver designed for geotechnical applications.

Consequently, it is beneficial for the geotechnical researchers and engineers who have already been working with SPH, as well as the new users who want to start using SPH, to have an efficient open-source SPH solver designed for geotechnical modeling. To this end, in this work, we present LOQUAT, an open-source, GPU-accelerated SPH solver for geotechnical modeling. LOQUAT is developed using C++ and CUDA with object-oriented design. It is designed for three-dimensional large scale simulations with up to tens of millions of particles using single NVIDIA GPU device. LOQUAT solves the partial differential equations by means of SPH discretization and explicit time integration. Two geomechnical constitutive models, namely, the Drucker–Prager model [22] and the hypoplastic model of Wang and Wu [75, 83] are included to capture the mechanical responses of geomaterials. A general boundary condition able to model fixed and moving boundaries with arbitrary geometry is proposed and implemented in LOQUAT. With the current implementation, LOQUAT can be used to simulate a wide range of geotechnical problems involving large deformation, free-surface and moving boundary. For instance, the two-dimensional version of the solver has already been recently applied to simulate granular flow [59, 60], slope stability [59], seepage and flow-porous media interaction [61, 62], and soil-structure interaction [63].

The main purpose of developing and releasing LOQUAT is to promote the research and use of SPH in geotechnical engineering. With this in mind, we try to keep the code as simple and readable as possible. Complex optimization techniques are not considered in the current version. Along with the solver kernel, input files for several numerical examples are also provided. The output files of LOQUAT is in .vtu format which can be visualized using the widely-used open-source visualization software ParaView [3]. The LOQUAT solver and the related documentation and test cases can be found at https://github.com/ChongPengGeotech/LOQUAT/.

In the remaining part of the paper, firstly, the theories of SPH, the implemented constitutive models and the stabilization techniques are detailed. Afterwards, the GPU acceleration, the structure of the code and brief documentation are described. Finally, several numerical examples are presented, where we demonstrate the accuracy, efficiency and stability of the solver.

2 SPH for geotechnical modeling

2.1 Governing equations

SPH is a Lagrangian particle-based methods. Therefore, in SPH the governing equations of geotechnical problems are written in the following Lagrangian form

$$\begin{aligned} \dfrac{\mathrm {d}\rho }{\mathrm {d}t}= & {} -\rho \nabla \cdot \varvec{v} \end{aligned}$$

(1)

$$\begin{aligned} \dfrac{\mathrm {d}\varvec{v}}{\mathrm {d}t}= & {} \dfrac{1}{\rho }\nabla \cdot \varvec{\sigma }+ \varvec{g} \end{aligned}$$

(2)

where $\rho$ is the density; $\varvec{v}$ denotes the velocity, $\varvec{\sigma }$ is the Cauchy stress tensor and $\varvec{g}$ is the acceleration induced by body force, e.g. gravity in most geotechnical problems. $\mathrm {d}(\cdot )/\mathrm {d}t$ represents the material time derivative and $\nabla$ is the gradient operator. In this work, pore pressure is not considered, which means the material is either dry or can be modeled using total stress. In many simulations, the Eq. (1), i.e. the continuity equation can be removed from the simulation, because Lagrangian particles are used so the mass conservation is always satisfied [10, 59]. Eq. (1) is only needed when equation of state (EOS) based constitutive models are used [39].

2.2 SPH discretization of governing equations

In SPH, the computational domain is partitioned using particles which carry field variables and move with the material. The governing equations can be solved by tracking the motions of the particles and changes of the carried variables. To do this, one has to discretize the governing equations using the SPH interpolations.

A field function can be approximated using the following integral interpolation

$$\begin{aligned} \langle\;f(\varvec{x})\rangle; = \int _\Omega f(\varvec{x}') W(\varvec{x} - \varvec{x}', h)\mathrm {d}\varvec{x}' \end{aligned}$$

(3)

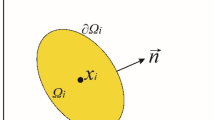
where $\langle\;\cdot \rangle\;$ represents the approximated value, $\Omega$ is the influence domain of the kernel function $W(\varvec{x} - \varvec{x}', h)$, abbreviated as W hereafter. W depends on the distance $\left||\varvec{x} - \varvec{x}'\right||$ and the parameter h, i.e. the smoothing length. In this work, the radius of the spherical support domain of W is 2h. The kernel function W has to satisfy certain requirements such as normalization condition, delta function property and compact support condition [46]. Common choices of kernel functions include the Gaussian kernel [51], the cubic spine kernel [67] and the Wendland kernels [79]. In LOQUAT, only the C2 Wendland kernel is employed because of the benefit of preventing particle clumping [20, 66].

Similarly, the spatial derivatives of the field function can be approximated through [59]

$$\begin{aligned} \langle\;\nabla f(\varvec{x})\rangle; = -\int _\Omega f(\varvec{x}') \nabla _{\varvec{x}'}W\mathrm {d}\varvec{x}' \end{aligned}$$

(4)

where $\nabla _{\varvec{x}'}$ indicates that the derivatives are evaluated at $\varvec{x}'$. The above equation is only valid when the support domain has no intersection with the boundary of the computational domain. However, this condition is generally not fulfilled for areas near the boundary. Therefore, SPH needs special treatment at boundaries to circumvent the so-called boundary deficiency. The treatment of boundary condition will be introduced in Sect. 2.4.

In SPH, the continuous forms of integral interpolation Eqs. (3) and (4) are rewritten as the summation of contributions of all the particles in the support domain

$$\begin{aligned} f(\varvec{x}_i)= & {} \sum f(\varvec{x}_j) W_{ij} \dfrac{m_j}{\rho _j} \end{aligned}$$

(5)

$$\begin{aligned} \nabla f(\varvec{x}_i)= & {} \sum f(\varvec{x}_j) \nabla _i W_{ij}\dfrac{m_j}{\rho _j} \end{aligned}$$

(6)

where the bracket $\langle\;\cdot \rangle\;$ is dropped for convenience. $\varvec{x}_i$ is the particle where the field function is approximated, and $\varvec{x}_j$ is the particle in the support domain. $\nabla _iW_{ij}$ is the short form of $\nabla _{\varvec{x}_i}W(\varvec{x}_i - \varvec{x}_j,h)$. Note that $\nabla _iW_{ij} = -\nabla _jW_{ij}$ due to the symmetry of the kernel function. $m_j$ is the mass of particle j and $m_j/\rho _j$ denotes the volume of the particle.

With the discrete forms of SPH interpolations Eq. (5) and (6), the governing equations can be rewritten as

$$\begin{aligned} \dfrac{\mathrm {d}\rho _i}{\mathrm {d}t} = \sum m_j (\varvec{v}_i - \varvec{v}_j) \cdot \nabla _iW_{ij} \end{aligned}$$

(7)

$$\begin{aligned} \dfrac{\mathrm {d}\varvec{v}_i}{\mathrm {d}t} = \sum m_j\left( \dfrac{\varvec{\sigma }_i}{\rho _i^2} + \dfrac{\varvec{\sigma }_j}{\rho _j^2}\right) \nabla _iW_{ij} + \varvec{g}_i \end{aligned}$$

(8)

The above formulations conserve the linear and angular momentum and are commonly employed, athough there are different discretization forms of the governing equations in the literature [39, 76].

2.3 Stabilization techniques

In SPH, a dissipative term is usually added into the momentum equation to stabilize the numerical simulation and prevent large unphysical oscillations. The reason is that SPH is a dynamic method, where shock waves are always present, especially in problems with abrupt loading and change of boundary condition. If the shock waves are not damped out to make sure their wave lengths are larger than the characteristic length h, spurious mode and strong instability can occur. A common dissipative term is the artificial viscosity [48]

$$\begin{aligned} \Pi _{ij}= \left\{\begin{array}{ll} \dfrac{\alpha c_s h}{{\bar{\rho }}_{ij}} \dfrac{\varvec{v}_{ij}\cdot \varvec{r}_{ij}}{r_{ij}^2 + 0.01h^2},&\quad \text {if}\,\varvec{v}_{ij}\cdot \varvec{r}_{ij}<0\\ 0,&\quad \text {otherwise} \end{array} \right. \end{aligned}$$

(9)

where $\varvec{v}_{ij} = \varvec{v}_i - \varvec{v}_j$, $\varvec{r}_{ij} = \varvec{r}_i - \varvec{r}_j$, and $r=\left\|\varvec{r}_{ij}\right\|$ is the distance between particle i and j. ${\bar{\rho }}_{ij} = (\rho _i + \rho _j)/2$ is the average density. $c_s$ denotes the speed of sound which will be introduced in Sect. 2.5. $\alpha$ is a constant determining the magnitude of the artificial viscosity.

It is well-known that the SPH method suffers from the so-called tensile instability, i.e. when material is in tensile state, the particles tend to form small clumps which eventually lead to unphysical fractures. In geotechnical modeling, Bui et al. [10] demonstrated that for non-cohesive geomaterials the tensile instability is negligible. However, if the modeled material is with cohesion, the tensile instability develops and has to be removed using additional numerical treatments. One common technique to alleviate the tensile instability is the artificial stress method, which adds a short ranged repulsive force when the material is in tensile state. The additional stress term in the artificial stress method has the following form

$$\begin{aligned} \varvec{S}_{ij} = f_{ij}^n (\varvec{R}_i + \varvec{R}_j) \end{aligned}$$

(10)

where $f_{ij} = W_{ij} / W(\Delta p)$ and $\Delta p$ is the initial particle spacing, the exponential factor n is taken as $n = W(0) / W(\Delta p)$. The term $\varvec{R}_i$ is usually obtained by first rotating the original stress tensor $\varvec{\sigma }_i$ to a pure principal stress state, then multiplying a factor if the principal stress is in tension and finally rotating back to the original direction [10, 26]. This approach is not only computationally expensive but also very difficult to perform in three-dimensional condition. In LOQUAT, an alternative approach is employed, where

$$\begin{aligned} S_{ij} = f_{ij}^n (R_i + R_j) \end{aligned}$$

(11)

where the term $R_i$ is obtained using

$$\begin{aligned} R_i= \left\{ \begin{aligned} \dfrac{\epsilon \vert p_i\vert }{\rho _i^2},\quad \text {if}\,p_i < 0\\ 0,\quad\text {otherwise} \end{aligned} \right. \end{aligned}$$

(12)

where $p = -(\sigma _{xx}+\sigma _{yy}+\sigma _{zz})/3$ is the isotropic hydrostatic pressure. $\epsilon$ is a constant controlling the magnitude of the artificial stress, usually taken as 0.2 in geotechnical modeling. $R_j$ can be computed in a similar way. This approach is very much like the original artificial stress method proposed in [49]. It is more convenient to implement in three-dimensional simulations.

With the artificial viscosity and artificial stress, the SPH momentum equation (8) is rewritten as

$$\begin{aligned} \dfrac{\mathrm {d}\varvec{v}_i}{\mathrm {d}t} = \sum m_j\left[ \dfrac{\varvec{\sigma }_i}{\rho _i^2} + \dfrac{\varvec{\sigma }_j}{\rho _j^2} + (\Pi _{ij} - S_{ij})\varvec{I}\right] \nabla _iW_{ij} + \varvec{g}_i \end{aligned}$$

(13)

where $\varvec{I}$ is an identity matrix.

SPH also has the so-called short-length-scale-noise resulting in stress fluctuations in areas with large deformation [55, 60]. Stress regularization can be applied to improve the stress results, just like the Shepard filter in SPH for fluid dynamics [55]. The stress is re-initialized after a certain number of computational steps. The new stress can be written as

$$\begin{aligned} \varvec{\sigma }_i^{new} = \dfrac{\sum \varvec{\sigma }_j W_{ij}}{\sum W_{ij}} \end{aligned}$$

(14)

The normalized SPH interpolation has linear consistency; thus, it can reproduce the linear variation of stress fields.

Among the aforementioned stabilization techniques, the artificial viscosity is suggested to be always activated. The artificial stress has to be used when simulating cohesive geomaterials. The stress regularization needs to be applied in caution, as its performance has not been thoroughly investigated.

2.4 Boundary conditions

Because SPH is a Lagrangian particle based method, the implementation of boundary condition is more difficult than in grid-based methods. The boundary treatments of SPH need to fulfill two requirements, the first is to prevent particle penetration, the second is to correct the SPH interpolation in incomplete support domains due to the intersection with the boundary. In LOQUAT the non-slip rigid wall boundary is implemented using the boundary particle method.

In the boundary particle method, the solid boundary is represented by certain layers of SPH particles. The width of the boundary zone is determined in such a way that any material particles near the boundary can have full support domain. These boundary particles are either fixed in position or moved according to prescribed velocities. The boundary particles participate in SPH computations like normal material particles. However, the field variables on the boundary particles are not computed by evolving the governing equations, but extrapolated from the material domain. Before each computation of particle interaction, the stresses on boundary particles are interpolated as

$$\begin{aligned} \varvec{\sigma }_b = \dfrac{\sum \varvec{\sigma }_m W_{bm}}{\sum W_{bm}} \end{aligned}$$

(15)

where the subscripts b and m denotes boundary and material particles, respectively. Furthermore, the stresses at boundary particles have to be corrected according to the body force to correctly approximate the stress gradient caused by the body force [1]

$$\begin{aligned} \sigma _b^{ll} = \dfrac{\sum \sigma _m^{ll}W_{bm} - g_b^l \sum \rho _m r_{bm}^l W_{bm}}{\sum W_{bm}} \end{aligned}$$

(16)

where $l = x, y, z$ is the direction of the spatial coordinates. Note that in the above equation the Einstein summation convention is not applied. It is observed that only the diagonal components of the stress tensor are subjected to the body force correction.

The proposed boundary treatment method has the benefit of being able to model fixed and moving boundaries with arbitrary geometry. However, it can not accurately simulate free-slip or frictional boundary conditions. The free-slip behavior can be roughly modeled by neglecting the effect of shear stress. However, this treatment is highly approximate. The accurate modeling of free-slip and frictional boundary conditions needs to consider the realistic contact between the material and boundary [63, 76].

2.5 Time integration

In the SPH method, the system of equations consists of Eqs. (7) and (13), which can be solved numerically using explicit integration methods, e.g. the Predictor-Corrector method [48], the leap-frog method [10] and the Verlet method [1]. In LOQUAT the original form of Predictor-Corrector scheme is adopted. Let X denote a variable (position, density, velocity, stress or strain) to be integrated and $F=\mathrm {d}X/\mathrm {d}t$ is the rate of change. With $\Delta t$ the time step, the predictor predicts the variable at half time step as

$$\begin{aligned} X^{t+\Delta t/2} = X^{t} + F^{t}\Delta t /2 \end{aligned}$$

(17)

where the superscript t is the time at the beginning of the computational step. The rate of change $F^t$ is evaluated using the variables at time instance t. In the corrective step, the value of X at the end of the computational step is obtained using

$$\begin{aligned} X^{t+\Delta t} = X^{t} + F^{t+\Delta t/2}\Delta t \end{aligned}$$

(18)

Note that the change of rate $F^{t+\Delta t/2}$ is computed based on the variables at time instance $t+\Delta t/2$, which is obtained in the predictive step. It should be pointed out that the integration of stress should follow the constitutive model.

The time step of the Predictor-Corrector scheme is controlled by the CFL condition [23]:

$$\begin{aligned} \Delta t = \chi \min {\left( \sqrt{\dfrac{h}{\max {\left||\varvec{a}_i\right||}}},\dfrac{h}{c_s}\right) } \end{aligned}$$

(19)

where $\varvec{a}_i = \mathrm {d}\varvec{v}_i/\mathrm {d}t$ is the particle acceleration, $\chi$ is the CFL coefficient usually in the range of 0.05–0.2, $c_s$ is the speed of sound, which depends on the stiffness of the simulated material.

3 Constitutive models

The governing equations (7) and (13) should be closed by equations describing geometerial behaviors. In LOQUAT, two constitutive models are included, i.e. the elastoplastic Drucker–Prager model [22] and the hypoplastic model from Wang and Wu [75, 83]. These constitutive models are developed based on the small deformation and infinitesimal strain assumptions, whereas SPH modeling of geotechnical problems often has to simulate large deformation. As a result, additional treatments should be considered.

3.1 Hypoelastic approach for large deformation analysis

In computational geomechanics, there are two approaches for finite strain and large deformation analysis. One is to employ constitutive models based on hyperelasto-plasticity, employing the multiplicative decomposition of the deformation gradient [19, 54]. The other approach is the hypoelastic-based method which employs objective (frame invariant) stress rates to provide finite strain and large deformation extension to already existing infinitesimal models [19]. The hypoelastic approach is simple in formulation and implementation; thus, most of the existing SPH numerical simulations employ it. Furthermore, the conventional SPH method (compared to total-Lagrangian SPH method) is based on the Eulerian kernel, which means that the computation is always based on the current configuration; therefore, employing the hypoelastic approach is natural and does not require modifying the SPH formulation. However, two conditions should hold to ensure the accuracy of the modeling using hypoelastic approach: (1) the elastic strain should be small compared to the plastic strain; (2) the time step should be small enough to keep the objectivity [38]. These two conditions are naturally satisfied in most SPH geotechnical modelings.

In LOQUAT, the Jaumann stress rate is adopted, which reads

$$\begin{aligned} \mathring{\varvec{\sigma }} = \dot{\varvec{\sigma }} + \varvec{\sigma }\cdot \varvec{\omega }- \varvec{\omega }\cdot \varvec{\sigma }= \varvec{H}(\dot{\varvec{\varepsilon }}, \varvec{\sigma }, ...) \end{aligned}$$

(20)

where $\mathring{\varvec{\sigma }}$ is the Jaumann stress rate, $\dot{\varvec{\sigma }}$ is the rate of Cauchy stress. $\varvec{\omega }$ denotes the spin tensor, and $\dot{\varvec{\varepsilon }}$ is the strain rate tensor. $\varvec{\omega }$ and $\dot{\varvec{\varepsilon }}$ are defined as $\varvec{\omega }= (\varvec{L} - \varvec{L}^{\mathrm {T}})/2$ and $\dot{\varvec{\varepsilon }}= (\varvec{L} + \varvec{L}^{\mathrm {T}})/2$, where $\varvec{L} = \partial \varvec{v} / \partial \varvec{x}$ is the velocity gradient. In the SPH context, the velocity gradient at a particle is obtained as

$$\begin{aligned} \varvec{L}_i = \sum (\varvec{v}_j - \varvec{v}_i)\otimes \nabla _iW_{ij}\dfrac{m_j}{\rho _j} \end{aligned}$$

(21)

In Eq. (20), $\varvec{H}$ denotes the rate form infinitesimal constitutive model which depends on strain rate, Cauchy stress and possibly other internal variables. Finally, the rate of Cauchy stress is written as

$$\begin{aligned} \dot{\varvec{\sigma }} = \varvec{\omega }\cdot \varvec{\sigma }- \varvec{\sigma }\cdot \varvec{\omega }+ \varvec{H}(\dot{\varvec{\varepsilon }}, \varvec{\sigma }, ...) \end{aligned}$$

(22)

Integrating the above equation we can obtain the stress in large deformation analysis.

3.2 Drucker–Parger model

The Drucker–Prager (DP) model is a commonly-used constitutive model in geomechanics. It is a elasto-perfectly plastic model with a smooth yield surface

$$\begin{aligned} f^s = \sqrt{J_2} - k_{\phi }p - k_c \end{aligned}$$

(23)

where $p = - (\sigma _{xx}+\sigma _{yy}+\sigma _{zz})/3$ is the isotropic hydrostatic pressure; $J_2=\varvec{s}:\varvec{s}/2$ is the second invariant of the deviatoric stress tensor defined as $\varvec{s} = \varvec{\sigma }- p\varvec{I}$. $k_{\phi }$ and $k_c$ are constitutive parameters related to parameters from the Mohr-Coulomb model

$$\begin{aligned} k_{\phi } = \dfrac{3\tan \phi }{\sqrt{9+12\tan ^2\phi }},~~k_c = \dfrac{3c}{\sqrt{9+12\tan ^2\phi }}, \end{aligned}$$

(24)

where $\phi$ and c are the fiction angle and cohesion, respectively.

Under the non-associated plastic flow assumption, the plastic potential function is written as

$$\begin{aligned} g^s = \sqrt{J_2} - k_{\psi }p \end{aligned}$$

(25)

Similarly, $k_{\psi }$ is defined as

$$\begin{aligned} k_{\psi } = \dfrac{3\tan \psi }{\sqrt{9+12\tan ^2\psi }} \end{aligned}$$

(26)

where $\psi$ is the dilatancy angle.

At each computational step, an elasto-predicted stress $\varvec{\sigma }^*$ is first obtained using linear elastic relation. Taking the corrective step as an example, we have

$$\begin{aligned} \varvec{\sigma }^* = \varvec{\sigma }^t + (\varvec{\omega }\cdot \varvec{\sigma }^t - \varvec{\sigma }^t\cdot \varvec{\omega }+ 2G\dot{\varvec{e}} + K\varepsilon _v\varvec{I})\Delta t \end{aligned}$$

(27)

where $\varepsilon _v = (\dot{\varvec{\varepsilon }}_{xx}+\dot{\varvec{\varepsilon }}_{yy}+\dot{\varvec{\varepsilon }}_{zz})/3$, and $\dot{\varvec{e}}= \dot{\varvec{\varepsilon }} - \varepsilon _v\varvec{I}$ is the deviatoric part of the strain rate tensor. K and G are the elastic bulk modulus and shear modulus, respectively.

If the predicted stress $\varvec{\sigma }^*$ is outside of the yield surface, plastic failure occurs. The corresponding plastic strain increment is computed based on the plastic flow rule

$$\begin{aligned} \Delta \varvec{\varepsilon }^p = \Delta \lambda ^s\dfrac{\partial g^s}{\partial \varvec{\sigma }} \end{aligned}$$

(28)

In the DP model, the increment of the plastic multiplier $\Delta \lambda ^s$ reads

$$\begin{aligned} \Delta \lambda ^s=\dfrac{f^s(\varvec{\sigma }^*)}{G+K k_{\phi } k_{\psi }} \end{aligned}$$

(29)

Finally, the corrected stress is obtained as

$$\begin{aligned} \varvec{s}^{t+\Delta t} = \dfrac{\sqrt{J_2^*} - G\Delta \lambda ^s}{\sqrt{J_2^*}}\varvec{s}^*,~~p^{t+\Delta t} = p^* + K k_{\psi }\Delta \lambda ^s,~~\varvec{\sigma }^{t+\Delta t} = \varvec{s}^{t+\Delta t} - p^{t+\Delta t}\varvec{I} \end{aligned}$$

(30)

where $\varvec{s}^*$, $J_2^*$ and $p^*$ are the corresponding variables of the predicted stress tensor $\varvec{\sigma }^*$.

3.3 Hypoplastic constitutive model

In LOQUAT, the hypoplastic constitutive model of Wang and Wu [75, 83] is also included. This model has the following rate form

$$\begin{aligned} \dot{\varvec{\sigma }} = \varvec{\omega }\cdot \varvec{\sigma }- \varvec{\sigma }\cdot \varvec{\omega }+ c_1 (\mathrm {tr}\varvec{\sigma })\dot{\varvec{\varepsilon }} + c_2(\mathrm {tr}\dot{\varvec{\varepsilon }})\varvec{\sigma }+ c_3\dfrac{\mathrm {tr}(\varvec{\sigma }\dot{\varvec{\varepsilon }})}{\mathrm {tr}\varvec{\sigma }}\varvec{\sigma }+ c_4(\varvec{\sigma }+ \varvec{s})\left||\dot{\varvec{\varepsilon }}\right|| \end{aligned}$$

(31)

where $\left||\dot{\varvec{\varepsilon }}\right||=\sqrt{\dot{\varvec{\varepsilon }}:\dot{\varvec{\varepsilon }}}$ is the Euclidean norm of the strain rate tenor, $\varvec{s}$ is the deviatoric stress tensor. $c_1$–$c_4$ are the four constitutive parameters that can be related to the conventional geomaterial parameters such as Young’s modulus, Poisson’s ratio, friction angle and dilatancy angle [81,82,83]. In the above equation, the first two terms are from the Jaumann stress rate to keep the rotation objectivity. The terms associated with parameters $c_1$ to $c_3$ are linear part of the model. It can be observed that constitutive equation is homogeneous of the first degree in stress, which means the predicted behaviors, e.g. stiffness and shear strength depend on the stress level, which is realistic for geomaterials. The last term in the model is the nonlinear term. The hypoplastic model does not split the strain into elastic and plastic parts. The nonlinear property of geomaterials is automatically accounted for using the model. For details of the implementation of this model in SPH, the readers please refer to [59, 60]. The Cauchy stress rate is computed from the hypoplastic model directly. Therefore, no plastic correction of the final stress is required.

The hypoplastic model Eq. (31) is mainly used for granular soils. But it can also be extended to model geomaterials with moderate cohesion by simply replacing the Cauchy stress $\varvec{\sigma }$ with a translated stress [59, 75]

$$\begin{aligned} \varvec{\eta }= \varvec{\sigma }- c\varvec{I} \end{aligned}$$

(32)

where c is the cohesion. With the translated stress, the hypoplastic model is rewritten as

$$\begin{aligned} \dot{\varvec{\eta }} = \varvec{\omega }\cdot \varvec{\eta }- \varvec{\eta }\cdot \varvec{\omega }+ c_1 (\mathrm {tr}\varvec{\eta })\dot{\varvec{\varepsilon }} + c_2(\mathrm {tr}\dot{\varvec{\varepsilon }})\varvec{\eta }+ c_3\dfrac{\mathrm {tr}(\varvec{\eta }\dot{\varvec{\varepsilon }})}{\mathrm {tr}\varvec{\eta }}\varvec{\eta }+ c_4(\varvec{\eta }+ \varvec{s}_{\eta })\left||\dot{\varvec{\varepsilon }}\right|| \end{aligned}$$

(33)

where $\varvec{s}_{\eta }$ is the deviatoric part of the translated stress.

4 GPU acceleration and numerical implementation

4.1 GPU acceleration for SPH

SPH suffers from low efficiency in serial computation because of the high computational cost. However, SPH is very attractive for parallel computing due to its embarrassingly parallel nature. Therefore, parallel computation has been used in SPH for a long time, mostly using multi-core CPUs or CPU clusters in early time [52, 74]. Recently, the high-performance computing of SPH mainly focuses on GPUs [17, 21, 28], which are superior in terms of price and energy consumption compared to traditional CPUs. The modern GPUs have hundreds or even thousands of processing cores which can execute computing kernels concurrently. A computing kernel can be viewed as a function, the same version of the function runs on all the GPU cores and shares the same global memory. Therefore, the computations of a large number of SPH particles can be distributed over many threads in a massively parallel fashion.

We implemented LOQUAT based on the Compute Unified Device Architecture (CUDA), a toolkit developed by NVIDIA to allow using their graphic cards as high-performance computing devices. The solver has a CPU part and a GPU part, as shown in Fig. 1. The CPU part works as a process controller. It is used for loading and saving data, initializing the settings of simulation, and linking the GPU computing kernels to finish computations in a designed order. The GPU part executes all the actual computations including neighbor search, boundary extrapolation, particle interaction and time integration. As memory bandwidth is a bottleneck in GPU computing, we reduce memory transfer, especially transfer between GPU and CPU as much as possible. All the data is stored in the GPU memory, with only one transfer of data from CPU to GPU at the beginning and some occasional transfers from GPU to CPU for saving results.

The neighbor search consists of several computational operations on GPU and will be detailed in Sect. 4.2. The remaining three computations, i.e. boundary extrapolation, particle interaction and time integration are performed using four computing kernels: AdamiBoundary_cuk, ParticleInteraction_cuk, Predictor_cuk and Corrector_cuk. During simulation, each computing kernel is run by a large number of GPU cores simultaneously; thus, high numerical efficiency can be achieved. Note that the computing kernels for stress integration, i.e. MatModDP_cuk and MatModHypo_cuk are called by the computing kernels for time integration.

Fig. 1

Flowchart of the simulation process in LOQUAT

4.2 Neighbor search

The basic and most time consuming operation in SPH is to compute the particle interaction. In three dimensions, the support domain of the SPH kernel function is a sphere with a radius of 2h. Only particles with distance less than 2h have interactions with the centering particle. Therefore, the computation of particle interaction needs to first identify the particles within the support domain for each particle. A naive method is to loop over all the total N particles to compute the distances and store the interacting particles. However, this method is prohibitively expensive in terms of both computational time and memory consumption; thus nobody really uses this method in code aiming to simulate large-scale problems.

Fig. 2

Sketch of the virtual search grid: a virtual search grid and support domain in two-dimensions; b virtual search grid in three-dimensions

Hence, most SPH solvers perform the neighbor search based on search algorithms such as linked-list [30] and tree [29]. Not all of these methods are suitable for GPU computing. In LOQUAT, we adopt a modified version of the linked-list method described in [27], which is used by most of the GPU-based SPH simulations [17, 21, 28]. Here we briefly describe the search algorithm.

The modified linked-list search algorithm is based on a virtual search grid which occupies the whole computational domain, as shown in Fig. 2. The grid consists of cubic cells with an edge length of 2h. With the virtual grid, a particle only needs to search possible interaction particles in its own cell and the immediately surrounding cells, because all particles outside of these cells have distances larger than 2h; thus are outside its support domain. The goal of the search algorithm is, for each cell, to search and store all the particles inside it. With this information, the particle interaction can be simply performed using the algorithm described in Algorithm 1. Note that when computing particle interaction the actual interacting particles need to be determined based on the distance. With the employed virtual search grid, the number of operations reduces from $O(N^2)$ to O(MN), where N is the total particle number and M is the particle number in all the surrounding cells, which is far less than N.

Fig. 3

A simple example to show the work flow of the modified linked-list search algorithm

The modified linked-list search algorithm is optimized to use GPU acceleration and save memory. Its main concept is shown in Fig. 3. First, all the cells in the virtual search grid is given an index following a predefined order. Then, an array part_cel is created to store the index of the cell in which a particle resides. For example, part_cel[i] stores the index of the cell containing particle i. Afterwards, all the particles, including the associated variables, are sorted according to their cell index. This sorting is to ensure that all particles in one cell locate in the same piece of memory. Therefore, we do not need to store all the particle index for each cell. Instead, we only compute the index of the beginning and ending particles in the cell, which are stored in cell_beg and cell_end, respectively. This approach does not only save much memory, but also speeds up the memory access because it ensures that the data from the memory is accessed sequentially. The whole neighbor search algorithm is performed using four CUDA computing kernels: GetParticleCellIndex_cuk, SortParticleByCellIndex, FindBegEndInCell_cuk and SortArray_cuk. An auxiliary array part_idx is used to save the old indexes of particles before sorting. This auxiliary array is important in reordering the variables carried by particles. All the computing kernels are developed by the authors except the sorting, for which we use the highly-efficient CUDA library CUB [34].

4.3 Optimization strategies

Although GPU devices have high computational power, proper design of the GPU algorithm is also very important for achieving high efficiency. Principally, there are three basic strategies for optimization: (1) achieve high occupation of GPU devices; (2) optimize memory usage and transfer; (3) optimize instruction usage. Following these principals, the following optimization strategies are employed in LOQUAT.

First, particles are properly grouped in memoey to avoid code branching and warp divergence. In SPH, soil and boundary particles have different computations. If particles of different types are put in the same kernel, code branching and warp diveregnce is inevitable, leading to low occupancy of the device. In LOQUAT, soil and boundary particles are grouped in memory sequentially. This can ensure that in one kernel only the comoutation of one type of particles is performed. Consequently, each thread has the same code flows and similar computational loads.

Second, the optimal block size of each kernel is chosen automatically using the CUDA configurator API cudaOccupancyPotentialBlockSize. This API returns the optimal block size for a kernel based on the usage of registers and constant memory in the considered kernel, the properties of the device, and the number of particles computed using the kernel. With this API, there is no need to tune the block size for given computing kernels.

Third, the memory transfer between CPU and GPU is minimized by storing all the data in GPU memory. Consequently, there is no memory transfer between CPU and GPU in the whole computation except simulation initialization and results saving.

Fourth, only single-precision float numbers are used in LOQUAT. GPUs can process single-precision float numbers and the corresponding operations much faster than double-precision ones. Furthermore, to speed-up the memory access, all particle variables are stored in GPU using the built-in type float4, which fulfills the size and alignment requirement of GPU devices.

5 Brief solver documentation

5.1 Overview of the solver

The LOQUAT solver consists of a series of C++ and CUDA source files. It also uses two open-source libraries in the form of source codes, i.e. CUB for particle sorting using GPU and TINYXML2 [33] for parsing XML file using CPU. All the sources files developed by the authors and their functionality are listed in Table 1. In LOQUAT, the CUDA computing kernels performs most of the computational work in parallel. Table 2 lists all the computing kernels and their functionality. Note that CUDA computing kernels can be called by both host (CPU) and device (GPU). If a computing kernel is called by device, it means that it is called by another computing kernel, not by the CPU code.

Table 1 The source files and their functionality

Table 2 The CUDA computing kernels and their functionality

The users need to give controlling parameters to run simulations. The controlling parameters include SPH parameters (e.g. particle size, smoothing length/particle size), material constants (e.g. density, constitutive parameters), boundary conditions such as body force and other parameters related to the simulation (e.g. maximal simulation time, CFL number). Other derived parameters important for the simulation, e.g. mass of particle and normalization coefficient of SPH kernel, can be computed from the controlling parameters. All the parameters are stored in a data type Parameters. These parameters are transferred to the constant memory of the GPU device to ensure faster access speed and reduce branching in the GPU computing kernels.

Six kinds of field variables are the primary variables that should be given to initialize the simulation and saved in the results files, i.e. position, velocity, particle type, equivalent plastic strain, stress and strain. The particle type is used to separate different groups of particle. There are other auxiliary variables necessary for the simulation. For instance, we need to store the results of acceleration and velocity gradient obtained from the particle interaction. However, these variables are only used in the simulation and are not saved in results files.

5.2 Input and output format

The LOQUAT solver is designed in such a way that output files can be used as input files for subsequent simulations. To this end, the input files consist of two files, one XML file with all controlling parameters, and one plane data file (DAT) with all the field variables. For each time of output, the solver also saves a XML file and a DAT file, containing all the information needed to restart the simulation.

The LOQUAT solver also provides an option to save results as VTU files, which can be visualized using the widely-used free visualization tool ParaView. The conversion between DAT and VTU file formats would be very easy by writing a small program. However, the current version of LOQUAT solver does not provide this functionality.

5.3 Compilation and execution

The solver is compiled by using the provided Makefile. To compile the solver, a C++ compiler and the NVIDIA CUDA compiler NVCC need to be installed. Furthermore, the solver uses several libraries from the BOOST package, so BOOST needs to be installed. We have tested the compilation on operation systems Ubuntu (versions 14.04 LTS and 16.04 LTS) and CentOS 6.0, CUDA versions from 7.0 to 9.2, and BOOST library versions from 1.62 to 1.68. The compilation generates an executable named LOQUAT.

To run the simulation, the user has to prepare two input files name-of-project.xml and name-of-project.dat. These files can be either generated by the user or from previous simulations. The simulation can be started using the command line

./LOQUAT name-of-project i

i is an optional input parameter, which allows the user choose which GPU device should be used to perform the simulation. If it is not given, the solver runs on the first GPU device. The solver creates a folder with the same name as the project name and saves all the results files there. There are several project examples delivered along with the solver to help the users to get familiar with it.

6 Performance of the solver

The performance of the solver is checked using a Nvidia GTX 1080Ti graphic card installed on a desktop computer. The card has 11 GB memory and 3584 CUDA cores, each with a core clock of 1556 MHz.

The axisymmetric collapse of dry granular materials on flat surface was experimentally studied by Lube et al [42]. It is widely-used as a benchmark for numerical methods including SPH. In this section, a series of simulations are performed with varying particle size and computational parameters to demonstrate the accuracy, convergence, efficiency and memory usage of LOQUAT. Based on the experiments, Lube et al proposed the following empirical relation linking the final runout $r_\infty$ and the initial configuration

$$\begin{aligned} \dfrac{r_\infty }{r_0}= \left\{ \begin{aligned} 1+1.24a,&~~~~a<1.7\\ 1+1.6^{0.5},&~~~~a\ge 1.7 \end{aligned} \right. \end{aligned}$$

(34)

where $r_0$ is the initial radius of the column, $a=h_0/r_0$ is the aspect ratio with $h_0$ the initial height.

All the simulation focus on a single configuration of the experiment with an aspect ratio of $a = 0.5$. The initial radius and height of the granular column are $r_0 = 0.2$ m and $h_0=0.1$ m, respectively. According to the empirical relation, the finial runout in this case is $r_\infty =0.324$ m, which is used as the experimental reference value. In all the simulations, the Druckre-Prager model is employed. Although Lube et al concluded that the final runout is independent of frictional angle, many studies reported that a frictional angle of $\phi =37^{\circ }$ gives more accurate results, a lower frictional angle leads to overestimated runout distance [54, 59, 72]. Therefore, we choose to use $\phi =37^{\circ }$ in the simulations. The dilatancy angle $\psi$ is taken as zero. The coefficient for artificial viscosity is chosen as $\alpha =0.25$. The simulated physical time is one second.

Simulations with different resolutions and support domain size are performed. The radius of the support domain is 2h, where $h=\kappa \Delta p$, $\Delta p$ is the particle size and $\kappa$ is the parameter controlling the size of the support domain. Table 3 summaries the configurations for the simulations. In total 45 simulations are carried out, the number of particles in the simulations range from 23,772 to upto 15.7 millions. The 45 simulations are with five different particle sizes. To investigate the convergence behaviors, except $\Delta p = 1$ mm, for each particle size eleven simulations are carried out with varying $\kappa$ from 1.1 to 2.1. For brevity, some results are not shown in Table 3, but will be discussed in the remainning part of this section. The simulation with the finest resolution $\Delta p = 1$ mm has an unusually large support domain of $\kappa =2.8$, resulting in a huge number of particles of around 15.7 million. The results from this simulation serve as the numerical reference solution.

Table 3 Summary of the simulations for the sand column collapse test with aspect ratio $a=0.5$. FPS: frame per second, which is the number of computational steps the solver can execute in one second

6.1 Accuracy and convergence

The theoretical analysis of accuracy and convergence of SPH is more complex than traditional methods, because SPH has two processes of approximation: the continuous SPH integral interpolation and the discrete particle approximation. The convergence of the continuous integral integration requires $h\rightarrow 0$, which is natural as h denotes the numerical resolution of SPH. On the other hand, the discrete particle approximation is more accurate when there are more particles in the support domain, which means that its convergence requires $\kappa =h/\Delta p\rightarrow \infty$ [88]. Therefore, the SPH method converges when $h\rightarrow 0$ and $\kappa \rightarrow \infty$. Obviously, it is very difficult to satisfy these two conditions at the same time, as it leads to prohibitively large number of particles. Therefore, in most SPH simulations, convergence analysis is performed with fixed $\kappa$ and varying smoothing length h, i.e., h and $\Delta p$ change proportionally. The common range of $\kappa$ is from 1.2 to 1.6. This practice is sufficient in most numerical modeling, but not enough for fully investigating the behaviors of the method and our LOQUAT solver. To this end, we performed simulations of different resolutions with a wide range of $\kappa$.

Fig. 4

The runout results for all the simulations

The results of the final runout from all the simulations are shown in Fig. 4. Generally, for a particular resolution, a larger support domain (larger $\kappa$) gives rise to a smaller runout. SPH is a continuous numerical method, where a larger support domain results in more accurate particle approximation hence better results in numerical simulation. However, as it can be observed in Fig. 4, the runouts reach stable values in simulations with $\Delta p = 10$, 7.5, and 5 mm if $\kappa$ are larger than certain values. This change of trend happens at $\kappa = 1.4$, 1.5 and 1.8 for the three resolutions. For $\Delta p = 3$ mm, the final runout decreases monotonically with increasing $\kappa$. The observed phenomenon can be explained by checking the sources of errors. As aforementioned, the approximation error of SPH consists of a integral interpolation error related to h, and a discrete particle approximation error linked to $\kappa$. In simulations with a fixed h, increasing $\kappa$ only reduces the particle approximation error, while the integral interpolation error is unchanged. Therefore, it can be observed that in simulations with $h = 10$, 7.5 and 5 mm, when $\kappa$ is respectively larger than 1.4, 1.5 and 1.8, further increasing $\kappa$ can not give more accurate results, as the numerical error is already dominated by the integral interpolation error, which only depends on h. For $\Delta p= 3$ mm, even $\kappa =2.1$ cannot fully eliminate the particle approximation error. But the effect of increasing $\kappa$ is close to “saturated”, as the curve show clear trend of converging.

The results show that in SPH simulation the resolution (h) and support domain size ($\kappa$) have to be carefully chosen. Only reducing h or increasing $\kappa$ does not necessarily result in more accurate results. These two parameters need to be consistent to make sure that both the integral interpolation and particle approximation errors are minimized simultaneously.

From the above observation and analysis, we can tell that the simulations with $h=1$ mm and $\kappa =2.8$ give more accurate results than all the other simulations; therefore, it is used as the numerical reference case. It can be seen that the SPH method converges to this reference solution with decreasing h and increasing $\kappa$. However, the numerical reference value of the final runout is 0.3412 m, larger than that obtained in the experiments. This means that our numerical simulations do not converges to the experimental data. This discrepancy may be due to many reasons such as numerical formulations, implementation and the constitutive model. However, we believe that the most dominant reason of this discrepancy is that the quasi-static Drucker–Prager model is not sufficient for the dynamic process of granular collapse. In the Drucker–Prager model, the mechanism of energy dissipation is friction; however, in dynamic process of granular collapse, particle collision plays a significant role, it has big impact on the energy dissipation and the mechanical behavior of the material. Therefore, the Drucker–Prager model naturally overestimates the final runout. This overestimation was also noticed in other studies [54, 72], the reasons are, however, not discussed there. Consequently, for granular collapse modeling, constitutive models considering both the quasi-static and dynamic regimes should be more appropriate [2, 60, 65].

Fig. 5

The rate of convergence of the sand collapse simulation

It is worth noting that some of our simulations give runout values quite close to the experimental one. e.g. when $\Delta p = 10$ mm and $\kappa =1.1$, or when $\Delta p=7.5$ mm and $\kappa =1.3$, as observed in Fig. 4. However, this agreement is purely coincidence, because the numerical results are very different from the converged solution and are inaccurate. Probably this type of agreement is also obtained in other studies, and it may happen that the corresponding results are considered as accurate solutions. This misinterpretation can lead to questionable conclusion, e.g. neglecting of the incapability of the constitutive model.

Using the numerical reference solution $r_\infty ^r$, we can obtain the convergence rate of the simulations. The error is defined as $e_r = \vert r_\infty ^r - r_\infty \vert / \vert r_\infty ^r\vert$. Note that only results from simulations with $\kappa \ge 1.8$ are used in the convergence analysis. For other values of $\kappa$, the numerical results from four resolutions are on both the upper and lower sides of the numerical reference solution, which complicates the analysis and interpretation. The results of the convergence analysis are given in Fig. 5. The rate of convergence is 1.482, between linear and quadratic convergence. This is not surprising as the SPH scheme does not have the first-order consistency.

Fig. 6

The final profile of the simulation of $\Delta p=1$ mm and $\kappa =2.8$ with a total particle number of 15.7 million: a equivalent plastic strain; b vertical stress

In all the simulations, the collapse process and the final profile of the sand body are similar, and are well-collaborated with experiments and other numerical studies [16, 42, 54, 72]. The final profiles of the simulation with the finest resolution of $\Delta p = 1$ mm and $\kappa =2.8$ are shown in Fig. 6. It is observed that the sand column collapses axisymmetrically. A undisturbed region with the initial height can be clearly observed. The final profile shows good agreement with the experiments.

6.2 Efficiency

The efficiency of the simulation is measured using the frame per second (FPS), which is the number of computational steps executed in one second of wall-clock time. The FPS does only depend on total particle number, particle distribution, particle size $\Delta p$ and $\kappa$, not affected by material parameters or the time step; thus, it is a proper measurement. The FPS and total simulation time for all the 45 simulations are listed in Table 3. The FPS and total simulation time of all the simulations except the finest one are also shown in Figs. 7 and 8. Note that the results of FPS and simulation time do not consider the time used for saving output files.

Fig. 7

The FPS results from the 44 simulations

From Fig. 7, it is observed that the simulation is very fast using LOQUAT. Several hundreds of computational steps can be executed in one second of wall-clock time if the particle number is less than half a million. The FPS decreases with decreasing particle size, it also decreases if a higher $\kappa$ is employed. This is expectable because larger number of particles and bigger support domain lead to higher computational cost in one step. For a certain particle size, the FPS drops linearly with growing $\kappa$. For instance, in the simulations of four particle sizes (10–3 mm), the FPS at $\kappa =2.1$ is only 36%, 33%, 30% and 25% of that at $\kappa =1.1$, indicating a fast grow in the computational cost in one step. However, this does not mean that the total simulation will be respectively 2.8, 3.0, 3.4 and 4.0 times longer. A larger $\kappa$ gives rise to a larger smoothing length h, hence a bigger time step $\Delta t$. As a result, for the four resolutions, the simulation time is respectively 1.47, 1.58, 1.77 and 2.14 times longer for the simulations with the largest support domain compared to those with the smallest support domain. Therefore, contrary to the common belief, using high values of $\kappa$ does not slow down the simulation much. Considering the additional gain on accuracy, large values of $\kappa$ are always recommended.

Fig. 8

The simulation time used for the simulations

As shown in Table 3 and Fig. 8, one second of simulation can be finished in around half an hour even with 712,542 particles and very large $\kappa$. The finest simulation with 15,666,190 particles and extremely large $\kappa$ can be finished in around two days. It is demonstrated that with the GPU acceleration, LOQUAT is very efficient, and can be used in large scale three-dimensional geotechnical simulation.

To further check the acceleration of LOQUAT, we carry out simulations of 8 different resolutions with fixed $\kappa = 2.1$. The particle resolutions are $\Delta p= 0.01$, 0.0075, 0.005, 0.003, 0.002, 0.0015, and 0.001 m, resulting in numbers of particle ranging from 37,116 to 14,619,748. Both GPU-accelerated LOQUAT and a single-core CPU code are used for the simulations. The implementation of the single-core CPU code follows the same algorithms described in Sect. 4 without any parallelization. The CPU simulations are performed using an Intel Core i7-7700k CPU, which has a core clock of 4.2 GHz. Because the single-core CPU code is very slow in three-dimensional simulations with large number of particles, we only execute the first 100 computational steps and compute the FPS based on the measured time. Time used for input and output are not considered. Once obtaining the FPS of GPU and CPU simulations, the speed-up is computed as

$$\begin{aligned} s_u = \dfrac{\mathrm {FPS~in~GPU~simulation}}{\mathrm {FPS~in~CPU~simulation}} \end{aligned}$$

(35)

All the parameters are the same in the GPU and CPU simulations.

The speed-up of LOQUAT is shown in Fig. 9. Hundreds to more than one thousand times of speed-up can be achieved with LOQUAT. The speed-up increases as more particles are used in the simulations, growing rapidly when the particle number is less than one million. The speed-up converges to around 1600 when the simulation scale is large enough. Traditionally, this high order of speed-up can only be realized using super-computer. However, with LOQUAT, a desktop with a mainstream graphic card is the only required hardware.

Fig. 9

The speed-up of the GPU simulations over the single-core CPU simulations

6.3 GPU memory usage

Memory usage is always an important concern in GPU acceleration, because the GPU memory is not easily extendable as conventional memory. We plot the GPU memory usage in all the simulations except the finest one in Fig. 10. It is found that the memory usage and the particle number have the following relation

$$\begin{aligned} M_g= 0.000325N + 159 \end{aligned}$$

(36)

where $M_g$ is the GPU memory usage, its unit is MB. With this relation, we predict that the finest simulation uses 4858.86 MB of GPU memory, which is quite close to the actual memory consumption (4905.02 MB). This indicates that the relation is applicable regardless of the simulation scale.

Fig. 10

The relation between GPU memory usage and total particle number

Recent mainstream graphic cards usually have 3–11 GB of GPU memory on board. As a result, LOQUAT can easily handle problems of dozens of millions of particles, making large scale three-dimensional simulation an easy task. It should be pointed out that in the current implementation, the Predictor-Corrector time integrator uses a lot of memory. If a time integrator requiring less memory is employed, even more particles can be simulated.

7 Applications

In this section, LOQUAT is employed to analysis the safety factor and the failure process of a exemplary slope. The geometry of the slope is shown in Fig. 11. Because LOQUAT is a three-dimensional solver, the slope is modeled as a 3D object with a thickness of 1.0 m. The particle motion in the y direction is restricted to mimic a plain strain condition. The material parameters of the slope are: Young’s modulus $E=30.0$ MPa, Poisson ratio $\nu =0.2$, friction angle $\phi =30.0^\circ$, dilatancy angle $\psi =0^\circ$, cohesion $c=5.0$ kPa and density $\rho =1850.0$ kg/m$^3$. Both the Drucker–Prager and hypoplastic models are used in the simulation. The hypoplastic constitutive parameters are obtained from the Drucker–Prager parameters following the procedure introduced in [81, 82].

Fig. 11

Geometry and boundary conditions of the exemplary slope

The slope with the original strength parameters is stable. A strength reduction method is used to evaluate the safety of the slope. The two strength parameters, i.e., friction angle $\phi$ and cohesion c are reduced by a factor of f. The safety factor $f_s$ is obtained by gradually increasing the reduction factor f until a convergence solution cannot be achieved in a specific time (0.5 s in this work). During this specific time, if the time-maximum displacement curve remains convex, the simulation is considered convergence; otherwise, a concave curve represents an divergence simulation [11, 59].

Fig. 12

The maximum displacement-time relation under different reduction factor with the Drucker–Prager model

Fig. 13

The maximum displacement-time relation under different reduction factor with the hypoplastic model

All the simulations with the Drucker–Prager and the hypoplastic models employ the same numerical model. The particle size in the model is $\Delta p = 0.1$ m and the smoothing length is $h=1.5\Delta p$, leading to a total particle number of 60,624. The slope material is cohesive; therefore, artificial stress is applied with $\epsilon =0.2$. Each simulation consists of two stages. The first stage is to obtain the initial stresses, in which the original unreduced strength parameters are used. A numerical damping scheme described in [9] is used to damp out the oscillation induced by the sudden imposition of the gravity. After an equilibrium state is reached, the stresses in the slope are kept unchanged but the strains and displacements are reset to zero. At the beginning of the second stage, the strength parameters are reduced according to the reduction factor f. Then the slope deforms under the gravity without numerical damping. The total physical time for the simulations is 6 s, including 0.5 s for obtaining the initial state and 5.5 s for slope failure computation.

Figures 12 and 13 show the results of the strength reduction analysis using the Drucker–Prager model and the hypoplastic model. The change of the maximum displacement in the first 0.5 s of the failure stage under different reduction factors are plotted. Three reduction factors are employed, i.e., $f=1.6$, 1.7 and 1.8. For the stability analysis using the Drucker–Prager model, The curves for reduction factor 1.6 and 1.7 are in convex shapes, indicating converged solutions according to the failure definition. The simulation with $f=1.8$ shows a concave shape in the displacement-time curve, which means that the simulation is divergent and the slope is unstable. Therefore, the safety factor should be between 1.7 and 1.8 according. On the other hand, from Fig. 13 it is observed that the simulations using the hypoplastic model show that the reduction factor 1.6 gives rise to converged solution, while 1.7 and 1.8 lead to failure. Therefore, the safety factor obtained using the hypoplastic model is between 1.6 and 1.7, lower than that obtained using the Drucker–Prager model. This discrepancy is also observed in [59], where the safety factor obtained from the hypoplastic model is lower.

Fig. 14

The displacements under reduction factor 1.8 (in meters): a Drucker–Prager model, b hypoplastic model

The final displacements of the slope under reduction factor 1.8 are shown in Fig. 14. Complete shear bands develop from the toe to the crest of the slope in both the simulations. Displacements concentrate in the sliding body above the shear bands. The simulation using the Drucker–Prager model gives a sliding surface deeper than that from the simulation using the hypoplastic model. This observation is well agreed with the findings in [59]. It should be pointed out that SPH is a continuum-based approach, and both the two constitutive models do not have any regularization regarding internal length of the material. Therefore, the SPH simulations suffer from the same mesh-dependency commonly found in FEM analysis. This means that the results of safety factor, the location and width of shear band are affected by the SPH numerical resolution, i.e., smoothing length h. The accurate modeling of strain localization is a hot topic in FEM, we believe that many approaches applicable in FEM can also be employed in SPH to overcome the mesh-dependency. However, this is beyond the scope of this work.

The physical time and the numerical model are the same for all the simulations using different constitutive models and reduction factors. As a result, the efficiency performance of LOQUAT in all the simulations are identical. For the 6 s physical time simulations with around one million particles, the used wall-clock time is around 100 s using the same GTX 1080Ti graphic card. The average FPS is 402, which means in one second of wall-clock time 402 computational steps can be executed.

8 Summary and future work

We present LOQUAT, an open-source 3D SPH solver for geotechnical modeling hoping to encourage the study and usage of SPH in geotechnical engineering. The solver uses standard SPH formulation with three stabilization options: artificial viscosity, artificial stress and stress normalization. Two soil constitutive models, i.e. the Drucker–Prager and the hypoplastic model from [75] are included in the solver. A convenient generalized boundary condition is present, which can handle static and moving solid boundaries with arbitrary geometry.

The performance of the presented solver is demonstrated using a series of numerical examples. The accuracy, convergence, efficiency and memory consumption of the solver are discussed. Specifically, LOQUAT can easily achieve more that one thousand times of speed-up compared with SPH code running on single CPU core, and is able to perform large-scale simulations with dozens of million of particles using modern GPU devices.

Future development of LOQUAT will include total-Lagrangian and updated-Lagrangian formulations, more sophisticated constitutive models, inconsistency treatment and soil-fluid interaction.