1 Introduction

Quantum teleportation is a solution for transmitting unknown quantum states over a distance without moving them physically. The idea of quantum teleportation was proposed first by Benett et al. [1]. This protocol uses EPR pairs as a quantum channel. In 1997, the first prosperous experimental demonstration of quantum teleportation was proposed by Bouwmeester [2] based on Benett et al. protocol. Karlsson and Bourennane [3] introduced a quantum teleportation protocol using the three-particle entanglements. Braunstein et al. [4] presented the first quantum teleportation of dynamical variable states with continuous spectra.

The other types of teleportation like quantum controlled teleportation (QCT), bidirectional quantum teleportation (BQT) and bidirectional quantum controlled teleportation (BQCT) were presented afterward. A multiparty-controlled teleportation of multiqubit quantum information via entanglement was presented by Yang et al. [5]. Deng et al. [6] proposed a symmetric multiparty-controlled teleportation of an arbitrary two-particle entanglement in 2005. A theoretical scheme for bidirectional swapping quantum controlled teleportation was presented based on five-qubit states in [7]. In a bidirectional quantum teleportation scheme, Alice and Bob can simultaneously send an unknown quantum state to each other.

Suppose Alice and Bob can transmit a quantum state to each other through a BQT channel. So Bob can teleport a quantum state \({\left| {\Psi }\right\rangle }\) to Alice, and then Alice applies a unitary operator U on \({\left| {\Psi }\right\rangle }\) and teleports back the state \({\left| {\Phi }\right\rangle }=U{\left| {\Psi }\right\rangle }\) to Bob. Hence, bidirectional quantum teleportation can be used to implement a quantum remote control or a nonlocal quantum gate [8, 9]. The bidirectional state teleportation is an essential part of protocol design in cryptographic applications such as quantum key distribution (QKD) and quantum secret sharing (QSS). Although the explanation of quantum cryptography is out of the scope of our work, it is worth mentioning that bidirectional quantum teleportation can play a key role to improve the security and efficiency of the quantum cryptographic systems [9]. Just to mention a few, Deng and Long proposed a practical bidirectional QKD scheme which was based on a secure quantum direct communication protocol using perfect single-photon sources. However, the proposed bidirectional protocol as opposed to the direct quantum protocol does not require the exchange of the measuring-basis information and it saves a lot of on-site classical information storage and reduces the classical communication cost. Moreover, as the protocol takes advantage of bidirectional teleportation, it is secure even when the single photons are replaced by faint laser pulses that do not contain more than two single photons [10]. These authors also proposed a quantum secret sharing (QSS) protocol for creating a private multiparty key based on the bidirectional QKD [11]. In that regard, several works in the past years have been published aiming at improving the bidirectional quantum teleportation protocols [12,13,14,15]. As a result, although creating multiparticle entanglement channel is difficult, we can design more secure and robust quantum communication protocols instead.

Imagine the situation that a speaker inquires a question of a listener through a quantum channel. Once the listener replies to the speaker, the bidirectional communication (quantum dialogue) is accomplished. Bidirectional teleportation can be utilized in a quantum dialogue scheme [16, 17], in which Alice and Bob send secret messages to each other simultaneously.

Long et al. [18] reported a scheme for multiparty-controlled teleportation of an arbitrary high-dimensional GHZ-class state with a d-dimensional \((N+2)\)-particle GHZ state. Li et al. [19] presented a scheme for bidirectional controlled teleportation making use of a five-qubit composite GHZ-Bell state as quantum channel in 2013. Fu et al. used a criterion to judge whether a four-qubit quantum state can be regarded as a quantum channel or not in a bidirectional teleportation. This criterion was based on tensor representation and Bell-basis measurement [20]. Wang et al. [21] put forward a bidirectional quantum controlled teleportation of a qubit state via partially entangled GHZ-type states. Hassanpour et al. [22] proposed a BQCT based on entanglement swapping of initial Bell state in which two users can teleport an unknown single-qubit state to each other under the permission of the supervisor. They also put forward a bidirectional teleportation of a pure EPR state by using GHZ states [23]. Chen et al. [24] proposed another BQCT scheme by using a genuine six-qubit entangled state which was deterministic. Zhang et al. [13] proposed a bidirectional and asymmetric quantum controlled teleportation protocol via maximally eight-qubit entangled state. Li et al. [25] proposed a bidirectional controlled teleportation by using nine-qubit entangled state in noisy environments. They analytically derived the fidelities of the BQCT process and showed that the fidelities in the amplitude-damping and the phase-damping noisy channels merely depend on the amplitude parameter of the initial state and the decoherence noisy rate. Moreover, a new scheme for asymmetric bidirectional controlled teleportation by using a six-qubit cluster state as quantum channel was proposed in 2016 [26]. Recently, we proposed a bidirectional quantum teleportation of two-qubit states using an eight-qubit entangled state without any controller [27].

In the recent years, teleportation protocols were developed and demonstrated to convey more qubits using lower photon resources. Zhang et al. [28] proposed a scheme for teleporting an arbitrary n-qubit quantum state between two remote parties with the control of agents in a network. Bidirectional and asymmetric quantum controlled teleportation via a maximally entangled eight-qubit state was presented in [13]. Verma et al. developed a protocol for teleporting an arbitrary n-qubit state from Alice to Bob using 2n-qubit entangled states. They also presented an n-qubit quantum controlled teleportation [29].

Several experiments have been proposed for realizing quantum teleportation. Boschi et al. [30] proposed a quantum optic experimental implementation of teleportation of unknown pure quantum states using both classical and EPR channels. Ursin et al. [31] presented a quantum teleportation over a distance of 600 m across the River Danube in Vienna using linear optics. Yin et al. [32] reported quantum teleportation of independent qubits over a 97-km one-link free-space channel with multiphoton entanglement. The high-frequency and high-accuracy acquiring, pointing and tracking techniques developed in their experiment could be directly used for future satellite-based quantum communication and large-scale tests of quantum foundations. Ma et al. [33] reported an experimental quantum teleportation using an active feed-forward system in real time. This experiment uses two free-space optical links, both quantum and classical, over 143 km. Sun et al. [34] developed an experimental teleportation of quantum states over a 30-km optical fiber network with the input single photon state and the EPR state prepared independently. It is regarded as a critical step toward the realization of quantum Internet in the future. Kiktenko et al. [35] presented a bidirectional modification of the standard one-qubit teleportation protocol where both Alice and Bob transferred noisy versions of their qubit states to each other by using single Bell state and auxiliary qubits. The suggested scheme for bidirectional teleportation could be realized by using current experimental tools.

This work extends the study in [27] in a way that the users can teleport an arbitrary number of qubits, let’s say n, to each other simultaneously. A channel with 4n qubits is exploited for the teleportation of two n qubit states.

The proposed circuit including the initial qubits, channel qubits and operators may change during an interaction with environment and lose their coherence. Bennett et al. [1] noted that less entanglement in a quantum channel entails less fidelity of teleportation and/or the range of states that can be accurately teleported. Popescu [36] investigated the relation among teleportation, Bell’s inequalities and nonlocality. Horodecki et al. [37] proved that the optimal fidelity of the teleportation is related to the maximal singlet fraction of the quantum channel. Oh et al. [38] also investigated the direct relation between quantum teleportation fidelity and the degree of entanglement. They calculate the fidelity for a simple quantum teleportation system when each part is affected by the noise. Furthermore, Jung et al. [39] compared the fidelity of mentioned simple quantum teleportation system for two different input states GHZ and W when the channel is noisy. All of these references demonstrate that there is a relationship between the degree of entanglement at the quantum channel and the quantum teleportation fidelity [38]. In Sect. 4, we calculate the fidelity function for one- and two-qubit bidirectional teleportation in our quantum teleportation system when the input and channel qubits are affected by X and Z noises. The rest of the paper is organized as follows. In Sect. 2, the proposed bidirectional quantum teleportation protocol is described. Comparison results are presented in Sect. 3. In Sect. 4, we investigate the noise and the fidelity of the proposed protocol for some special cases. Finally, Sect. 5 concludes the paper.

2 The proposed protocol

The principal goal of the proposed protocol is the teleportation of arbitrary 2n qubits between Alice and Bob simultaneously. The states of Alice’s and Bob’s qubits are given in Eqs. 1 and 2, respectively:

$$\begin{aligned}&{\left| {\Phi }\right\rangle }_{A_1A_2\ldots A_n}=\sum _{i\,=\,0}^{2^n-1}\alpha _i {\left| {i}\right\rangle }, \end{aligned}$$
(1)
$$\begin{aligned}&{\left| {\Phi }\right\rangle }_{B_1B_2\ldots B_n}= \sum _{j\,=\,0}^{2^n-1}\beta _j {\left| {j}\right\rangle }, \end{aligned}$$
(2)

where \(\sum _{i\,=\,1}^{n}|\alpha _i|^2=\sum _{i\,=\,1}^{n}|\beta _i|^2=1,\) and i and j are decimal values of \((i_1,\ldots ,i_n)_2\) and \((j_1,\ldots ,j_n)_2\), respectively. The quantum channel of the proposed protocol is given in Eq. 3:

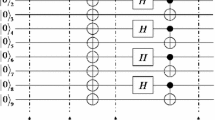
$$\begin{aligned} {\left| {G}\right\rangle }_{a_1\ldots a_nb_1\ldots b_nb_{n+1}\ldots b_{2n}a_{n+1}\ldots a_{2n}}=\frac{1}{2^{2n}}\sum _{l,k\,=\,0}^{2^n-1} {\left| {l}\right\rangle }{\left| {k}\right\rangle }{\left| {l}\right\rangle }{\left| {k}\right\rangle }. \end{aligned}$$
(3)

Figure 1 shows the circuit which produces the state \({\left| {G}\right\rangle }\). Alice (Bob) receives the qubits \(a_1\ldots a_{2n} (b_1\ldots b_{2n})\) from \({\left| {G}\right\rangle }\). The state of the whole 6n-qubit quantum system is given in Eq. 4:

$$\begin{aligned} {\left| {\Phi }\right\rangle }_{a_1\ldots a_nb_1\ldots b_nb_{n+1}\ldots b_{2n}a_{n+1}\ldots a_{2n}A_1\ldots A_nB_1\ldots B_n}={\left| {G}\right\rangle } \otimes {\left| {\Phi }\right\rangle }_{A_1\ldots A_n} \otimes {\left| {\Phi }\right\rangle }_{B_1\ldots B_n}. \end{aligned}$$
(4)

We explain the proposed protocol in five steps as follows:

Fig. 1
figure 1

Architecture of the proposed 4n-channel

Full size image
Table 1 Measurement results of Step 2 and the corresponding applied operators in Step 3
Full size table
Step 1 :

Alice (Bob) performs CNOT operators where \(A_1A_2\ldots A_n (B_1B_2\ldots B_n)\) are the control qubits and \(a_1a_2\ldots a_{n} (b_1b_2\ldots b_{n})\) are the target qubits, respectively. The state of the whole system after performing CNOT operators is given in Eq. 5:

$$\begin{aligned}&{\left| {\Phi }\right\rangle }_{A_1\ldots A_nB_1\ldots B_na_1\ldots a_nb_1\ldots b_nb_{n+1}\ldots b_{2n}a_{n+1}\ldots a_{2n}}\nonumber \\&\quad =\frac{1}{2^{2n}}\sum _{i,j,k,l\,=\,0}^{2^n-1} \alpha _i \beta _j {\left| {i}\right\rangle } {\left| {j}\right\rangle }{\left| {l \oplus i}\right\rangle }{\left| {k \oplus j}\right\rangle }{\left| {l}\right\rangle }{\left| {k}\right\rangle }. \end{aligned}$$
(5)
Step 2 :

In this step, Alice and Bob measure qubits \(a_1a_2\ldots a_n\) and \(b_1b_2\ldots b_n\) in Z basis, respectively. The results of this step are shown in Table 1.

Step 3 :

Alice and Bob apply X and I operators as shown in the fourth and fifth columns of Table 1, respectively. All states result in Eq. 6 as follows:

$$\begin{aligned} {\left| {\phi }\right\rangle }_{A_1\ldots A_nB_1\ldots B_nb_{n+1}\ldots b_{2n}a_{n+1}\ldots a_{2n}}= \frac{1}{2^{2n}} \sum _{i,j\,=\,0}^{2^n-1} \alpha _i \beta _j {\left| {i}\right\rangle } {\left| {j}\right\rangle }{\left| {i}\right\rangle } {\left| {j}\right\rangle }. \end{aligned}$$
(6)
Step 4 :

Alice and Bob perform X-basis measurement on \(A_1 A_2\ldots A_n\) and \(B_1 B_2\ldots B_n\), respectively. The measurement results and the corresponding states after the measurements are shown in Table 2.

Step 5 :

The last step of the proposed method focuses on correcting the collapsed states by applying Z operators as detailed in Table 2. After applying the mentioned Z operators, the state of whole system is as follows:

$$\begin{aligned} {\left| {\phi }\right\rangle }_{b_{n+1}\ldots b_{2n}a_{n+1}\ldots a_{2n}}=\sum _{i,j\,=\,0}^{2^n-1}\alpha _i \beta _j {\left| {i}\right\rangle } {\left| {j}\right\rangle }. \end{aligned}$$
(7)

Alice’s and Bob’s final states are shown in Eqs. 8 and 9, respectively.

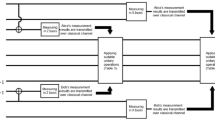
$$\begin{aligned} {\left| {\Phi }\right\rangle }_{a_{n+1}\ldots a_{2n}}= & {} \sum \limits _{i\,=\,0}^{2^n-1}\beta _i{\left| {i}\right\rangle }, \end{aligned}$$
(8)
$$\begin{aligned} {\left| {\Phi }\right\rangle }_{b_{n+1}\ldots b_{2n}}= & {} \sum \limits _{i\,=\,0}^{2^n-1}\alpha _i {\left| {i}\right\rangle }. \end{aligned}$$
(9)

Figure 2 illustrates the Alice’s steps described in the proposed bidirectional quantum teleportation protocol.

Table 2 Measurement results of Step 4 and the corresponding applied operators in Step 5
Full size table
Fig. 2
figure 2

Architecture of the proposed protocol on Alice’s side

Full size image

3 Comparison results

In this study, a new bidirectional teleportation protocol was presented in which an arbitrary number of qubits can be transmitted simultaneously. Utilizing single-particle measurement instead of Bell-state or GHZ-state measurements facilitates the realization of this protocol. Table 3 summarizes and compares the BQT and BQCT protocols.

Table 3 Comparison of QT protocols
Full size table

4 Noise analysis

Let’s consider our quantum teleportation system through the noisy channels shown by the dashed boxes in Fig. 3. We consider five different noisy channels \(N_1, N_2, N_3, N_4\) and \(N_5\) in the proposed protocol. In case \(N_1\), our unknown input state loses its coherence before it is teleported. In case \(N_2\), the entangled qubits make quantum channel noisy while being shared and kept by Alice and Bob. In cases \(N_3, N_4\) and \(N_5\), when Alice and Bob perform the operations, the impact of noise may become notable [38]. In this section, we investigate the effect of noise on input qubits (\(N_1\)) and channel qubits (\(N_2\)), for some small case \(n=1\) and \(n=2\), considering the evolution of a noisy system through a Markov evolution model. Hence, in our open quantum system after tracing out the environment degree of freedom, the dynamics of the density matrix of all our input and channel qubits can be described by a master equation in the Lindblad form [38, 42, 43]

$$\begin{aligned} \frac{\ \partial \rho }{\partial t}=-\,\frac{i}{\hslash }\left[ H_s,\rho \right] +\sum _{i,\alpha }\left( \ L_{i,\alpha }\ \rho \ \ {L_{i,\alpha }}^{\dagger }-\frac{1}{2}\left\{ {L_{i,\alpha }}^{\dagger }L_{i,\alpha },\rho \right\} \right) \end{aligned}$$
(10)

where the Lindblad operator \(L_{i,\ \alpha }=\sqrt{{\kappa }_{i,\ \alpha }}{\sigma }^i_{\alpha }\) acts on the ith qubits and describes the decoherence and \(\alpha = X, Y, Z\) stands for Pauli operations. In this relation, \(\kappa _{i,\alpha }\) is regarded as the strength of the decoherence rates. In other words, the decoherence time is approximately equal to \(1/\kappa _{i,\alpha }\). Also in this equation, \(H_{s}\) is the Hamiltonian of a qubit system as expressed below:

$$\begin{aligned} H_s\left( t\right) =-\,\frac{1}{2}\sum ^N_{i\,=\,1}{\mathbf{{B} }^{\left( i\right) }.{\varvec{{\sigma }}}^{\left( i\right) }}-\sum _{i\ne j}{J_{ij}\left( t\right) {\sigma }^{\left( i\right) }_+{\sigma }^{\left( j\right) }_-} \end{aligned}$$
(11)
Fig. 3
figure 3

All parts which can be affected by noise in our quantum teleportation system

Full size image

In solid-state qubits, various types of couplings between qubits i and j are possible such as XY coupling given here, the Heisenberg coupling and the Ising coupling \(J_{ij}{\sigma _{z}}^{(i)}{\sigma _{z}}^{(j)}\) in NMR. The various quantum gates in our quantum teleportation system which exists in \(N_3\), \(N_4\) and \(N_5\) noisy channel could be implemented by a sequence of pulses, i.e., by turning on and off \(\mathbf{{B} }^{\left( i\right) }\left( t\right) \) and \(J_{ij}\left( t\right) \) [38, 44]. It is very useful to describe our quantum teleportation system in terms of density operators. For convenience in the computation of the unitary operator for our teleportation system, we assume that for any initial states of input qubits, the results of the measurements in our teleportation protocol are pre-known. Since the effect of the noise on the system is independent of the measurement results, the obtained results for noise are valid for all measurement results. Therefore, the teleportation unitary operator can be specified in terms of CNOT, X and I operators. Hence, we can describe our teleportation system as follows:

$$\begin{aligned} {\rho }_{\mathrm{out}}= \ {\mathrm{Tr}}_{\hat{(a_{n+1}\dots a_{2n})} or \hat{(b_{n+1}\dots b_{2n})}}\ [ \ U_{\mathrm{tel}}\ ({\rho }_{\mathrm{in}}\ \otimes \ {\rho }_{\mathrm{en}})\ {U_{\mathrm{tel}}}^{\dagger }\ ] \end{aligned}$$
(12)

where

$$\begin{aligned} {\rho }_{\mathrm{in}}= & {} {\left| {\Phi }\right\rangle }_{A_1\dots A_n}{\left\langle {\Phi }\right| }\ \otimes \ {\left| {\Phi }\right\rangle }_{B_1\dots B_n}{\left\langle {\Phi }\right| } \end{aligned}$$
(13)
$$\begin{aligned} {\rho }_{\mathrm{en}}= & {} {\left| {G}\right\rangle }_{a_1\ldots a_nb_1\ldots b_nb_{n+1}\ldots b_{2n}a_{n+1}\ldots a_{2n}}{\left\langle {G}\right| } \end{aligned}$$
(14)

\({\mathrm{Tr}}_{\hat{(a_{n+1}\dots a_{2n})}}\) means partial trace over every qubits except \((a_{n+1}\dots a_{2n})\) and \({U_{\mathrm{tel}}}\) is the unitary operator which is implemented by our teleportation circuit. So, for investigating the noise effect on each channel \(N_1\) or \(N_2\) with density matrix \(\rho \), we analytically solve Lindblad equation for \(\rho \) and obtain the noisy density matrix \({\varepsilon } (\rho )\) which is a function of the state of our considered channel, \(\kappa \), t, which is time, and the type of noise acting on the qubits. Therefore, our noisy teleported qubits can be calculated as \({\varepsilon } ({\rho }_{\mathrm{out}})\) making use of Eq. 12. Now, we can quantify the properties of our quantum teleportation through noisy channels by computing fidelity between \(\rho \) and \({\varepsilon } ({\rho }_{\mathrm{out}})\) which measures the overlap between these two states as follows:

$$\begin{aligned} \mathrm{Fidelity}={\left\langle {\Phi }\right| }_{A_1\dots A_n(or B_1\dots B_n)}{\varepsilon } ({\rho }_{\mathrm{out}}){\left| {\Phi }\right\rangle }_{A_1\dots A_n(or B_1\dots B_n)} \end{aligned}$$
(15)

The fidelity depends on the initial state, \(\kappa \), t and also the type of the noise acting on the qubits. It is worth mentioning when t is small, implying that noise has a small duration, our average fidelity is close to one. For \(\kappa t = 0\), which means the noise has not affected the system, the fidelity becomes one.

In order to measure the noise on input \((N_1)\) and teleportation channel qubits \((N_2)\), we should consider the value of Hamiltonian for \(t=0\). In this case, the value of \(H_s\) is zero in Eq. 10. Moreover, for both cases \(N_1\) and \(N_2\), for \(n=1\) and \(n=2\), we get the following expression as aforementioned in Eq. 15:

$$\begin{aligned} \mathrm{Fidelity}={\left\langle {\Phi }\right| }_{A_1A_2\dots A_n}\ {{\mathrm{Tr}}}_{a_{n+1}\dots a_{2n}}({\varepsilon (\rho }_{\mathrm{out}})){\left| {\Phi }\right\rangle }_{A_1A_2\dots A_n} \end{aligned}$$
(16)

Equation 16 finds the fidelity of input qubits \(A_1A_2\dots A_n\) and the teleported state to the output qubits \(b_{n+1}b_{n+2}\dots b_{2n}\). This is the fidelity for the case that Alice sends her qubits and Bob receives them which is of course identical for the opposite teleportation direction due to the symmetry of the system for Alice and Bob.

After calculation of the fidelity, we calculate the average fidelity for all input qubit states. Note that when the noise acts on input qubits for each case of n, the average fidelities for Z noise and X noise are equal. This can be proved as follows:

Suppose the initial state of the system which is affected by the noise is \(\rho = {\left| {\psi }\right\rangle }{\left\langle {\psi }\right| }\) and \({\varepsilon }^{X}_{\kappa , t} (\rho )\) is the X noise function which evolves the initial state in terms of \(\kappa \) and t. Then, we can write the evolution function for Z noise as \({\varepsilon }^{Z}_{\kappa , t} (\rho ) = H\ {\varepsilon }^{X}_{\kappa , t} (H\ \rho \ {H}^{\dagger }) \ {H}^{\dagger }\), where H is the Hadamard gate. Therefore, the average fidelity of \({\varepsilon }^{Z}_{\kappa , t} (\rho )\) is as follows:

$$\begin{aligned} \begin{aligned} \int _{\mathrm{for\,all} \,{\left| {\psi }\right\rangle }}{{\left\langle {\psi }\right| }\ {\varepsilon }^{Z}_{\kappa , t} ({\left| {\psi }\right\rangle }{\left\langle {\psi }\right| }) \ {\left| {\psi }\right\rangle }} = \int _{\mathrm{for\,all}\, {\left| {\psi }\right\rangle }}{{\left\langle {\psi }\right| }\ H\ {\varepsilon }^{X}_{\kappa , t} (H\ {\left| {\psi }\right\rangle }{\left\langle {\psi }\right| }\ {H}^{\dagger }) \ {H}^{\dagger } \ {\left| {\psi }\right\rangle }} \end{aligned} \end{aligned}$$
(17)

and if we get \(H {\left| {\psi }\right\rangle } = {\left| {{\psi }^{\prime }}\right\rangle }\), then the above integral is simplified to the following expression:

$$\begin{aligned} \begin{aligned} = \int _{\mathrm{for\,all}\, {\left| {{\psi }^{\prime }}\right\rangle }}{{\left\langle {{\psi }^{\prime }}\right| }\ {\varepsilon }^{X}_{\kappa , t} ({\left| {{\psi }^{\prime }}\right\rangle }{\left\langle {{\psi }^{\prime }}\right| }) \ {\left| {{\psi }^{\prime }}\right\rangle }} \end{aligned} \end{aligned}$$
(18)

which equals with the average fidelity of the noise function \({\varepsilon }^{X}_{\kappa , t} (\rho )\).

Now, we investigate the noise for the case of \(n=1\). An arbitrary state can be represented as a vector in a Bloch sphere:

$$\begin{aligned} {\left| {\Phi }\right\rangle }={\mathrm {cos} \left( \frac{\theta }{2}\right) \ }\ e^{\frac{i\varphi }{2}}{\left| {0}\right\rangle }\ +\ {\mathrm {sin} \left( \frac{\theta }{2}\right) \ }\ e^{\frac{-i\varphi }{2}}{\left| {1}\right\rangle } \end{aligned}$$
(19)

where \(\theta \) is the polar and \(\phi \) is the azimuthal angle. Now, the density matrix of the input qubits and that of the teleportation channel qubits are defined, respectively, as follows:

$$\begin{aligned} {\rho }_{\mathrm{in}}= & {} {\left| {\Phi }\right\rangle }_{A_1}{\left\langle {\Phi }\right| }\otimes {\left| {\Phi }\right\rangle }_{B_1}{\left\langle {\Phi }\right| }\ \end{aligned}$$
(20)
$$\begin{aligned} {\rho }_{\mathrm{en}}= & {} {\left| {G}\right\rangle }_{a_1b_1b_2a_2}{\left\langle {G}\right| }\ \end{aligned}$$
(21)

By solving the Lindblad equation for the noise of type Z and X and for \(\rho _{\mathrm{in}}\), and \(\rho _{\mathrm{en}}\), the values of \({\varepsilon }(\rho _{\mathrm{in}})\), and \({\varepsilon }(\rho _{\mathrm{en}})\) are, respectively, calculated. Then, using Eq. 12 for each of them, the value of \({\varepsilon }(\rho _{\mathrm{out}})\) is calculated. (In the case that input qubits are noisy, simply we have \({\varepsilon }(\rho _{\mathrm{in}}) = {\varepsilon }(\rho _{\mathrm{out}})\).) Finally, the value of the fidelity is obtained making use of Eq. 16. Additionally, for case \(n=1\), the average of the fidelity can be calculated as follows:

$$\begin{aligned} {\mathrm{Fidelity}}_{{\mathrm{av}}}=\frac{1}{4\pi }\int ^{\pi }_0{\mathrm{d}\theta }\int ^{2\pi }_0{\mathrm{d}\phi \ {\mathrm{Fidelity}}\ \times \ \mathrm {sin}\mathrm {}(\theta )} \end{aligned}$$
(22)

Fidelity of Z noise on input qubits (\(N_1\)), as shown in Fig. 4, is as follows:

$$\begin{aligned} \begin{aligned} {\mathrm{Fidelity}}\left( {\theta }_{A_1},\ {\phi }_{A_1},\ \kappa ,\ t\right) = \frac{1}{4} \left[ 3 +\cos (2{\theta }_{A_1})\ +\ 2{e}^{-2\kappa t}\ {\sin }^{2}({\theta }_{A_1}) \right] \end{aligned} \end{aligned}$$
(23)

Fidelity of X noise on input qubits (\(N_1\)), as shown in Fig. 5, is as follows:

$$\begin{aligned}&{\mathrm{Fidelity}}\left( {\theta }_{A_1},\ {\phi }_{A_1},\ \kappa ,\ t\right) \nonumber \\&\quad = 1 +\ \frac{1}{8}({e}^{-2\kappa t} -\ 1) \left[ 3 -\cos (2{\phi }_{A_1})\ +\ 2{\cos }^{2}({\phi }_{A_1})\cdot \cos (2{\theta }_{A_1}) \right] \end{aligned}$$
(24)
Fig. 4
figure 4

Fidelity of Z noise. Minimum of a is 0.68, and minimum of b is 0.52. Maximum for both case is 1. On input qubits (\(N_1\)): a \(\kappa t=0.5\), b \(\kappa t=1.5\). On channel qubits (\(N_2\)): a \(\kappa t=0.25\), b \(\kappa t=0.75\)

Full size image
Fig. 5
figure 5

Fidelity of X noise. Minimum of a is 0.68 and minimum of b is 0.52. Maximum for both cases is 1. On input qubits (\(N_1\)): a \(\kappa t=0.5\), b \(\kappa t=1.5\). On channel qubits (\(N_2\)): a \(\kappa t=0.25\), b \(\kappa t=0.75\)

Full size image
Fig. 6
figure 6

Average fidelity. a \(n=1\), for input qubits (\(N_1\)). b \(n=1\), for channel qubits (\(N_2\)). c \(n=2\), for input qubits (\(N_1\)). d \(n=2\), for channel qubits (\(N_2\))

Full size image

As we previously explained, the average fidelity for Z noise and that for X noise are equal. The average fidelity for the noisy input case, as shown in Fig. 6a, is as follows:

$$\begin{aligned} {{\mathrm{Fidelity}}}_{{\mathrm{av}}}=\frac{1}{3}({e}^{-2\kappa t}+2) \end{aligned}$$
(25)

Fidelity of Z noise on teleportation channel qubits (\(N_2\)) is:

$$\begin{aligned} \begin{aligned} {\mathrm{Fidelity}}\left( {\theta }_{A_1},\ {\phi }_{A_1},\ \kappa ,\ t\right) = \frac{1}{4} \left[ 3 +\cos (2{\theta }_{A_1})\ +\ 2{e}^{-4\kappa t}\ {\sin }^{2}({\theta }_{A_1}) \right] \end{aligned} \end{aligned}$$
(26)

Fidelity of X noise on the teleportation channel qubits (\(N_2\)) is as follows:

$$\begin{aligned} \begin{aligned}&{\mathrm{Fidelity}}\left( {\theta }_{A_1},\ {\phi }_{A_1},\ \kappa ,\ t\right) \\&\quad = 1 +\ \frac{1}{8}({e}^{-4\kappa t} -\ 1) \left[ 3 -\cos (2{\phi }_{A_1})\ +\ 2{\cos }^{2}({\phi }_{A_1})\cdot \cos (2{\theta }_{A_1}) \right] \end{aligned} \end{aligned}$$
(27)

The average fidelity for the noisy channel case, as shown in Fig. 6b, is as follows:

$$\begin{aligned} {{\mathrm{Fidelity}}}_{{\mathrm{av}}}=\frac{1}{3}({e}^{-4\kappa t}+2) \end{aligned}$$
(28)

Now, we investigate the noise for the case of \(n=2\) and calculate fidelity for Z noise on input qubits and channel qubits. In this case, since \({\left| {\Phi }\right\rangle }_{A_1A_2}\) and \({\left| {\Phi }\right\rangle }_{B_1B_2}\) are not necessarily separable, we cannot represent them on Bloch sphere. So, we write \(\rho _{\mathrm{in}}\) as

$$\begin{aligned} {\rho }_{\mathrm{in}}={\left| {\phi }\right\rangle }_{A_1A_2}{\left\langle {\phi }\right| }\ \otimes \ {\left| {\phi }\right\rangle }_{B_1B_2}{\left\langle {\phi }\right| }\ \end{aligned}$$
(29)

where

$$\begin{aligned} \begin{aligned} {\left| {\phi }\right\rangle }_{A_1A_2}&={\alpha }_{1}{\left| {00}\right\rangle }+{\alpha }_{2}{\left| {01}\right\rangle }+{\alpha }_{3}{\left| {10}\right\rangle }+{\alpha }_{4}{\left| {11}\right\rangle }\\ {\left| {\phi }\right\rangle }_{B_1B_2}&={\beta }_{1}{\left| {00}\right\rangle }+{\beta }_{2}{\left| {01}\right\rangle }+{\beta }_{3}{\left| {10}\right\rangle }+{\beta }_{4}{\left| {11}\right\rangle } \end{aligned} \end{aligned}$$
(30)

where \({\alpha }_{1}\) and \({\beta }_{1}\) are real numbers.

Also we have:

$$\begin{aligned} {\rho }_{\mathrm{en}}={\left| {G}\right\rangle }_{a_1a_2b_1b_2b_3b_4a_3a_4}{\left\langle {G}\right| } \end{aligned}$$
(31)

Finally for each case, after solving Eq. 10 and using Eq. 12, \({\varepsilon }(\rho _{\mathrm{out}})\) is obtained as a function of \(\alpha _{1}\dots \alpha _{4}, \beta _{1}\dots \beta _{4}\), \(\kappa \) and t coefficients. Like before, we find the fidelity from Eq. 16. Therefore, our fidelity function is in terms of \(\alpha _{1}\dots \alpha _{4}\), \(\kappa \) and t.

Fidelity of Z noise on input qubits (\(N_1\)) is:

$$\begin{aligned} \begin{aligned}&{\mathrm{Fidelity}}\left( {\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,\ \kappa ,\ t\right) \\&\quad = {{\alpha }_1}^ 4\ +\ 2{e}^{-2\kappa t}{{\alpha }_1}^2{{\alpha }_2}^2\ +\ 2{e}^{-2\kappa t}{{\alpha }_1}^2{{\alpha }_3}^2\ +\ 2{e}^{-4\kappa t}{{\alpha }_1}^2{{\alpha }_4}^2\\&\qquad +\ {{\alpha }_2}^4\ + \ 2{e}^{-4\kappa t}{{\alpha }_2}^2{{\alpha }_3}^2\ +\ 2{e}^{-2\kappa t}{{\alpha }_2}^2{{\alpha }_4}^2\\&\qquad +\ {{\alpha }_3}^4\ + \ 2{e}^{-2\kappa t}{{\alpha }_3}^2{{\alpha }_4}^2+\ {{\alpha }_4}^4\ \ \ \end{aligned} \end{aligned}$$
(32)

Fidelity of Z noise on teleportation channel qubits (\(N_2\)) is:

$$\begin{aligned} \begin{aligned}&{\mathrm{Fidelity}}\left( {\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,\ \kappa ,\ t\right) \\&\quad = {{\alpha }_1}^4\ +\ 2{e}^{-4\kappa t}{{\alpha }_1}^2{{\alpha }_2}^2\ +\ 2{e}^{-4\kappa t}{{\alpha }_1}^2{{\alpha }_3}^2\ +\ 2{e}^{-8\kappa t}{{\alpha }_1}^2{{\alpha }_4}^2\\&\qquad +\ {{\alpha }_2}^4\ +\ 2{e}^{-8\kappa t}{{\alpha }_2}^2{{\alpha }_3}^2\ +\ 2{e}^{-4\kappa t}{{\alpha }_2}^2{{\alpha }_4}^2\\&\qquad +\ {{\alpha }_3}^4\ +\ 2{e}^{-4\kappa t}{{\alpha }_3}^2{{\alpha }_4}^2+\ {{\alpha }_4}^4\ \ \ \end{aligned} \end{aligned}$$
(33)

Now we calculate the average fidelity for these two cases by the following relation [45,46,47]:

$$\begin{aligned} {{\mathrm{Fidelity}}}_{{\mathrm{av}}}= & {} \frac{1}{64{\pi }^{3}} \int ^{2\pi }_0{\int ^{2\pi }_0{\int ^{2\pi }_0{\mathrm{d}\angle ({\alpha }_2)\cdot \mathrm{d}\angle ({\alpha }_3)\cdot \mathrm{d}\angle ({\alpha }_4)}}}\nonumber \\&\times \int ^{\pi }_0{\int ^{\pi }_0{\int ^{\pi }_0{{\mathrm{Fidelity}}\times \sin ({\alpha })\sin ({\beta })\sin ({\delta })\cdot \mathrm{d}{\alpha }\ \mathrm{d}{\beta }\ \mathrm{d}{\delta }}}} \end{aligned}$$
(34)

Assuming that:

\(\left| {\alpha }_1 \right| = \cos (\frac{\alpha }{2}) \cos (\frac{\beta }{2})\), \(\left| {\alpha }_2 \right| = \cos (\frac{\alpha }{2}) \sin (\frac{\beta }{2})\), \(\left| {\alpha }_3 \right| = \sin (\frac{\alpha }{2}) \cos (\frac{\delta }{2})\), \(\left| {\alpha }_4 \right| = \sin (\frac{\alpha }{2}) \sin (\frac{\delta }{2})\) and \({\alpha },\ {\beta }, \ {\delta }\ \in \left[ 0,\ \pi \right] \).

Using the above relation, the average fidelity of Z and X noises on input qubits (\(N_1\)) with \(n=2\), as shown in Fig. 6c, is:

$$\begin{aligned} {{\mathrm{Fidelity}}}_{{\mathrm{av}}}=\frac{4}{9} +\ \frac{7}{18} {e}^{-2\kappa t} +\ \frac{1}{6} {e}^{-4\kappa t} \end{aligned}$$
(35)

And the average fidelity of Z and X noises on channel qubits (\(N_2\)) with \(n=2\), as shown in Fig. 6d, is:

$$\begin{aligned} {{\mathrm{Fidelity}}}_{{\mathrm{av}}}=\frac{4}{9} +\ \frac{7}{18} {e}^{-4\kappa t} +\ \frac{1}{6} {e}^{-8\kappa t} \end{aligned}$$
(36)

Bennet et al. [1] have argued that the imperfect quantum channel reduces the range of the state \({\left| {\psi }\right\rangle }\) that is accurately teleported. As shown in Figs. 4 and 5, when channel qubits get noisy, the fidelity of the teleportation may decrease. It is noteworthy that noise Z and noise X do not decrease the fidelity for eigenvectors of operators \({\sigma }_{z}\) and \({\sigma }_{x}\), respectively. So Fig. 4, which presents the effects of the noise Z, for \(\theta \ =\ 0,\pi \) has the value 1 for any \(\kappa \) and t, since these values for \(\theta \) indicate the eigenvectors of \({\sigma }_{z}\). Similarly, Fig. 5, which presents the effects of the noise X, for \(\theta \ = \pi / 2\) and \(\phi \ =\ 0,\pi ,2\pi \), has the value 1 for any \(\kappa \) and t, since these values for \(\theta \) and \(\phi \) indicate the eigenvectors of \({\sigma }_{x}\). It turns out through these figures that as much as our input qubits state is closer to the mentioned eigenvectors, noise will have less impact on them. Furthermore, as much as the time duration of noise exposure on our qubits is longer or the strength of decoherence rates of the system is bigger, noise may be more effective. The minimum value of the fidelity as noted in Figs. 4 and 5 is 0.68 in case (a), whereas 0.52 in case (b) which has a bigger \(\kappa t\) compared to the case (a). From Fig. 6, we can explicitly see that the larger n leads to a more effective noise. As shown in this figure, for \(\kappa t\) being roughly more than 2, the average fidelity tends to 0.66 and 0.44, for \(n=1\) and \(n=2\), respectively.

5 Conclusion

In this paper, a simultaneous bidirectional quantum teleportation protocol was presented in which 2n arbitrary qubits can be teleported using other 2n quantum states as a channel. Further improvements can be achieved by sketching the experimental setup and developing the scheme in its practical implementations. Moreover, the protocol can be developed such that a controller can direct this bidirectional teleportation. In addition, we discussed about noise that may affect on our teleportation system for some small n, which can be inspirational for the greater ones. We saw that for \(n=1\), our system treats like the traditional unilateral one-qubit teleportation system in [38]. Moreover, we showed that the bigger the n is selected, the more effective the noise is observed.