1 Introduction

It is well known that quantum entanglement as an important quantum resource has many practical applications in quantum information processing. In 1993 Bennett et al. [1] first creatively invented quantum state teleportation (QST). It can be used for teleporting an arbitrary unknown quantum state in a qubit to a distant qubit with a shared entanglement. After Bennett et al’s pioneering work, much attention was focused on QST in both theoretical and experimental aspects [2–5]. In 1999 Hillery et al. [6] generalized classical secret sharing to quantum scenario and presented quantum state sharing (QSS). QSS is in essence the generalization of QST to some extent, for the receiver number has been enlarged from single party (in QST) to multiparty (in QSS). QSS has many potential applications in the future lives, hence it has caught much attention [7–15] after its emergence. Similar to QST, in 2011 Huelga et al. [16] first introduced quantum operation teleportation (QOT). As a useful form of quantum remote control, recently QOT has attracted many interests [17–22] too. Inspired by the generalization of QST to QSS, in 2011 Zhang and Cheungl [23] definitely put forward quantum operation sharing (QOS). The basic idea of QOS in a simplest case is that, with shared entanglement and local operations and classical communications (LOCC) the initial performer of a single-qubit operation can assure the operation be finally performed on a remote target qubit in a agent’s site if and only if both agents cooperate. If both sharers are regarded as one, QOS is reduced to QOT. Very recently, QOS starts to attract some attention [24–26].

Multi-particle entangled states as shared resources play crucial roles in quantum information processing. So far, many entangled states such as Bell states, GHZ states, cluster states and genuine states have been explored as quantum channels to fulfill various quantum tasks in different quantum scenarios. W states as a kind of entangled states were first presented by Dur et al. [27] in 2000. They own some inherent advantages (e.g., their robustness) and have already been utilized to deal different quantum tasks, too. For instance, in 2002 Shi and Tomita [28] showed that W states can be used as shared entanglement to realize probabilistic teleportation; In 2006, Cao et al. [29] proposed to realize quantum secure direct communication with a series of four-qubit W states; In 2009 Yang and Liu [30] suggested to accomplish QST or QSS with a class of three-qubit W states; and so on [31–34]. Consequently, it is well admitted that W states are a kind of useful entanglement resource of quantum information processing in the intending quantum network.

In this paper we consider the issue of QOS with W states. We take two different W states, namely, symmetric and asymmetric tripartite W states, as shared entanglements respectively to fulfill QOS. We try to reveal the differences of two QOS procedures with respect to quantum resource consumption, operation complexity, classical resource consumption, success probability and efficiency.

The rest of this paper is organized as follows. In Sect. 2, we will present two three-party QOS schemes with symmetric and asymmetric W states, respectively. In Sect. 3, we show their important features including security, symmetry and probability, and compare the two schemes from the five aspects: the consume of quantum resource, the difficulty or intensity of necessary operations, the consume of classical resource, the success probability and the intrinsic efficiency of the schemes. At last we will give a concise summary in Sect. 4.

2 Two QOS schemes with symmetric and asymmetric W states

In this section let us amply depict our two QOS schemes with symmetric and asymmetric W states, respectively. In either scheme there are three legitimate users, say, Alice, Bob and Charlie. Alice is the initial performer of the concerned operation \(U\), and Bob and Charlie are the two remote sharers of Alice. Alice wants to perform \(U\) on a state \(|\Psi \rangle \) (named target state later) in a remote qubit in one agent’s site with quantum and classical channels. The state \(U|\Psi \rangle \) is referred to as the conceivable state hereafter. As for \(U\), Alice may actually not hear of it before, either. She wants to fulfill the task of the remote operation with her agents’ assistance. However, she does not trust either agent completely but their entity. Specifically, she should assure that the operation can not be successfully executed on the qubit by either agent solely but conclusively achieved via the mutual collaboration of her two agents. Without loss of generality, at the beginning we suppose the target state is in the sharer Bob’s qubit \(b^{\prime }\) and reads

$$\begin{aligned} |\Psi \rangle _{b^{\prime }}=\alpha |0\rangle _{b^{\prime }}+\beta |1\rangle _{b^{\prime }}, \end{aligned}$$
(1)

where \(\alpha \) and \(\beta \) are arbitrarily complex and satisfy \(|\alpha |^2+|\beta |^2=1\).

2.1 Scheme with symmetric W states

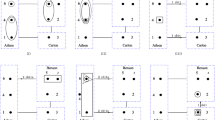
Now let us present our QOS scheme with symmetric W states. The schematic demonstration is illustrated in Fig. 1. The scheme is detailedly depicted as follows.

Fig. 1
figure 1

Illustration of the three-party QOS scheme with two symmetric W states. Dotted rectangle and trapeziums are participants’ locations. Solid lines among rectangles stand for classical channels. Solid dots denote qubits. Dash lines linking qubits are quantum channels. Solid ellipses represent Bell-state measurements. The solid square illustrates the single-qubit measurement. The circle illustrates unitary operation and the gray solid circle labels the unitary operation \(U\), respectively. In (a) Bob can reconstruct the state \(U|\Psi \rangle \), in (b) Charlie can. See text for more details

Full size image

To start with, assume two symmetric W states shared by Alice with Bob and Charlie are

$$\begin{aligned} |W_s\rangle _{{a_1}{b_1}{c_1}} = \frac{1}{\sqrt{3}}(|001\rangle _{{a_1}{b_1}{c_1}} +|010\rangle _{{a_1}{b_1}{c_1}}+|100\rangle _{{a_1}{b_1}{c_1}}) \end{aligned}$$
(2)
$$\begin{aligned} |W_s\rangle _{abc} = \frac{1}{\sqrt{3}}(|001\rangle _{abc}+|010\rangle _{abc}+|100\rangle _{abc}), \end{aligned}$$
(3)

where the qubit pair \((a_1,a)\) is in Alice’s site, the pair \((b_1,b)\) in Bob’s position, and the pair \((c_1,c)\) in Charlie’s location.

First, Bob carries out Bell-state measurements on his qubit pair \((b^{\prime },b_{1})\) and announces publicly the outcome (two classical bits) to Alice and Charlie via classical channels. Complementarily, throughout this paper the four Bell states are written as

$$\begin{aligned} |\psi ^{\pm }\rangle =(|00\rangle \pm |11\rangle )/\sqrt{2}, \ \ \ |\varphi ^{\pm }\rangle =(|01\rangle \pm |10\rangle )/\sqrt{2}, \end{aligned}$$
(4)

and the correspondence relations between them and two-classical-bit messages are:

$$\begin{aligned} |\psi ^{+}\rangle \Leftrightarrow 00, \ \ |\psi ^{-}\rangle \Leftrightarrow 11, \ \ |\phi ^{+}\rangle \Leftrightarrow 01, \ \ |\phi ^{-}\rangle \Leftrightarrow 10. \end{aligned}$$
(5)

It is known that the state of the composite system consisting of the channel qubits \( (a_1,b_1,c_1)\) and the initial target qubit \(b^{\prime }\) is

$$\begin{aligned}&|\Theta \rangle _{b^{\prime }{a_1}{b_1}{c_1}} = |\Psi \rangle _{b^{\prime }}|W_s\rangle _{{a_1}{b_1}{c_1}} = \frac{1}{\sqrt{3}}(\alpha |0\rangle _{b^{\prime }}+\beta |1\rangle _{b^{\prime }}) (|001\rangle _{{a_1}{b_1}{c_1}}\nonumber \\&\qquad \qquad \qquad \quad +|010\rangle _{{a_1}{b_1}{c_1}}+|100\rangle _{{a_1}{b_1}{c_1}}). \end{aligned}$$
(6)

Note that this state can be rewritten as

$$\begin{aligned} |\Theta \rangle _{b^{\prime }{a_1}{b_1}{c_1}}&= \frac{1}{\sqrt{6}}[|\psi ^{+}\rangle _{b^{\prime }b_{1}} (\sigma _{a_1}^{x}|\Psi \rangle _{a_1}|0\rangle _{c_1}+\alpha |0\rangle _{a_1}|1\rangle _{c_1})\nonumber \\&+\, |\psi ^{-}\rangle _{b^{\prime }b_{1}} (\sigma _{a_1}^{y}|\Psi \rangle _{a_1}|0\rangle _{c_1} + \alpha |0\rangle _{a_1}|1\rangle _{c_1}) \nonumber \\&+\,|\varphi ^{+}\rangle _{b^{\prime }b_{1}} (|\Psi \rangle _{a_1}|0\rangle _{c_1} + \beta |0\rangle _{a_1}|1\rangle _{c_1})+|\varphi ^{-}\rangle _{b^{\prime }b_{1}} ( \sigma _{a_1}^{z}|\Psi \rangle _{a_1}|0\rangle _{c_1} \nonumber \\&-\,\beta |0\rangle _{a_1}|1\rangle _{c_1})], \end{aligned}$$
(7)

where \(\sigma ^{x}=|0\rangle \langle 1|+|1\rangle \langle 0|\), \(\sigma ^{y}=|0\rangle \langle 1|-|1\rangle \langle 0|\), \(\sigma ^{z}=|0\rangle \langle 0|-|1\rangle \langle 1|\), and they and the identity operator \(I=|0\rangle \langle 0|+|1\rangle \langle 1|\) are uniformly called as Pauli operators later. Naturally, Bob’s measurements lead to the following collapses:

$$\begin{aligned} \left\{ \begin{array}{*{20}{l}} |\psi ^{+}\rangle _{b^{\prime }b_{1}} \Longrightarrow |C_1\rangle _{a_1c_1}=\sigma _{a_1}^{x}|\Psi \rangle _{a_1}|0\rangle _{c_1} + \alpha |0\rangle _{a_1}|1\rangle _{c_1}, \\ |\psi ^{-}\rangle _{b^{\prime }b_{1}} \Longrightarrow |C_2\rangle _{a_1c_1}=\sigma _{a_1}^{y}|\Psi \rangle _{a_1}|0\rangle _{c_1} + \alpha |0\rangle _{a_1}|1\rangle _{c_1}, \\ |\varphi ^{+}\rangle _{b^{\prime }b_{1}} \Longrightarrow |C_3\rangle _{a_1c_1}=|\Psi \rangle _{a_1}|0\rangle _{c_1} + \beta |0\rangle _{a_1}|1\rangle _{c_1}, \\ |\varphi ^{-}\rangle _{b^{\prime }b_{1}} \Longrightarrow |C_4\rangle _{a_1c_1}=\sigma _{a_1}^{z}|\Psi \rangle _{a_1}|0\rangle _{c_1} - \beta |0\rangle _{a_1}|1\rangle _{c_1}. \end{array} \right. \end{aligned}$$
(8)

Different outcomes appear with different probabilities, which can be easily worked out. As for \(|\psi ^{+}\rangle _{b^{\prime }b_1}\), its occurrence probability is \((1+|\alpha |^2)/6\). Analogously, the probabilities corresponding to other outcomes \(|\psi ^{-}\rangle _{b^{\prime }b_1}\), \(|\varphi ^{+}\rangle _{b^{\prime }b_1}\) and \(|\varphi ^{-}\rangle _{b^{\prime }b_1}\) are \((1+|\alpha |^2)/6\), \((1+|\beta |^2)/6\) and \((1+|\beta |^2)/6\), respectively.

Afterwards, Charlie measures his qubit \(c\) with the computational bases \(\{|0\rangle , |1\rangle \}\). From the collapsed states \(|C_i\rangle _{a_1c_1} (i=1,2,3,4)\), Charlie may measure \(|0\rangle _{c_1}\) with probabilities \(1/(1+|\alpha |^2)\), \(1/(1+|\alpha |^2)\), \(1/(1+|\beta |^2)\) and \(1/(1+|\beta |^2)\), respectively. If the measurement result is \(|0\rangle \), then he notifies Alice of his measurement result through the classical channel linking them. Surely, Charlie may measure \(|1\rangle \) and the occurrence probability is \(1/3\), which can be easily seen soon later. In this case, Charlie does nothing.

Once receiving Charlie’s information, Alice then executes an appropriate Pauli operation to convert the state in qubit \(a_1\) to \(|\Psi \rangle \). To be specific, if Bob measures \(|\psi ^{+}\rangle _{b^{\prime }b_{1}}\), \(|\psi ^{-}\rangle _{b^{\prime }b_{1}}\), \(|\varphi ^{+}\rangle _{b^{\prime }b_{1}}\), or \(|\varphi ^{-}\rangle _{b^{\prime }b_{1}}\), Alice decides to perform \(\sigma ^{x}\), \(\sigma ^{y}\), \(I\) or \(\sigma ^{z}\) on her qubit \(a_1\). Such operation will reconstruct the state \(|\Psi \rangle \) in qubit \(a_1\). The total probability Alice can reconstruct the state \(|\Psi \rangle \) in qubit \(a_1\) is

$$\begin{aligned} P_1=2\times \frac{1}{1+|\alpha |^{2}}\times \frac{1+|\alpha |^{2}}{6} + 2 \times \frac{1}{1+|\beta |^{2}}\times \frac{1+|\beta |^{2}}{6}=\frac{2}{3}. \end{aligned}$$
(9)

Incidentally, one can see that the total probability of measuring \(|1\rangle \) is \(1/3\), as we mentioned just. If Alice does not receive any information from Charlie, she then does nothing, either. This means the fulfillment of the whole sharing task has already been aborted at the moment.

After her reconstruction of the state \(|\Psi \rangle \) in qubit \(a_1\), Alice performs the concerned unitary operation \(U\) on her qubit \(a_1\), i.e.,

$$\begin{aligned} (U|\Psi \rangle )_{a_1}=\alpha ^{\prime }|0\rangle _{a_1}+\beta ^{\prime }|1\rangle _{a_1}. \end{aligned}$$
(10)

This indicates the concerned operation \(U\) has been performed on the target state \(|\Psi \rangle \) at this stage. However, the qubit inhabiting the conceivable state \(U |\Psi \rangle \) is \(a_1\) and in Alice’s location.

Subsequently, Alice measures her qubit pair \((a_1,a)\) with Bell-state measuring bases and publishes the measurement results. Note that the total joint state of the four qubits \((a_1, a, b,c)\) before measurements can be written as

$$\begin{aligned} |\Pi \rangle _{a_1abc}&= (U|\Psi \rangle _{a_1})|W_s\rangle _{abc} \nonumber \\&= \frac{1}{\sqrt{6}}[|\psi ^{+}\rangle _{a_1a}(\alpha ^{\prime }|01\rangle +\alpha ^{\prime }|10\rangle +\beta ^{\prime }|00\rangle )_{bc}\nonumber \\&+\,|\psi ^{-}\rangle _{a_1a}(\alpha ^{\prime }|01\rangle +\alpha ^{\prime }|10\rangle -\beta ^{\prime }|00\rangle )_{bc} \nonumber \\&+\,|\varphi ^{+}\rangle _{a_1a}(\beta ^{\prime }|01\rangle +\beta ^{\prime }|10\rangle +\alpha ^{\prime }|00\rangle )_{bc} +|\varphi ^{-}\rangle _{a_1a}(-\beta ^{\prime }|01\rangle -\beta ^{\prime }|10\rangle \nonumber \\&+\,\alpha ^{\prime }|00\rangle )_{bc}]. \end{aligned}$$
(11)

Therefore, one is readily to see that Alice’e measurements induce the following collapses:

$$\begin{aligned} \left\{ \begin{array}{*{20}{l}} |\psi ^+\rangle _{a_1a} \Longrightarrow \alpha ^{\prime }|01\rangle _{bc}+\alpha ^{\prime }|10\rangle _{bc}+\beta ^{\prime }|00\rangle _{bc}, \\ |\psi ^-\rangle _{a_1a} \Longrightarrow \alpha ^{\prime }|01\rangle _{bc}+\alpha ^{\prime }|10\rangle _{bc}-\beta ^{\prime }|00\rangle _{bc}, \\ |\varphi ^+\rangle _{a_1a} \Longrightarrow \beta ^{\prime }|01\rangle _{bc}+\beta ^{\prime }|10\rangle _{bc}+\alpha ^{\prime }|00\rangle _{bc}, \\ |\varphi ^-\rangle _{a_1a} \Longrightarrow -\beta ^{\prime }|01\rangle _{bc}-\beta ^{\prime }|10\rangle _{bc}+\alpha ^{\prime }|00\rangle _{bc}. \end{array} \right. \end{aligned}$$
(12)

It is obvious that different outcomes \(|\psi ^+\rangle _{a_1a}\), \(|\psi ^-\rangle _{a_1a}\), \(|\varphi ^+\rangle _{a_1a}\) and \(|\varphi ^-\rangle _{a_1a}\) may occur. Their occurrence probabilities are \([1+|\alpha ^{\prime }|^2]/6\), \([1+|\alpha ^{\prime }|^2]/6\), \([1+|\beta ^{\prime }|^2]/6\) and \([1+|\beta ^{\prime }|^2]/6\), respectively.

If Bob and Charlie collaborate and decide Bob to conclusively reconstruct the conceivable state, then they can do as follows. Charlie measures his qubit \(c\) with the computational bases. If \(|0\rangle \) is measured, then he tells Bob his measurement result through their classical communication. Otherwise, he does nothing. In the latter case, the sharing of the unitary operation has already failed at this stage. Easily one can rewrite the right hand of Eq. (12) as

$$\begin{aligned} \left\{ \begin{array}{*{20}{l}} \alpha ^{\prime }|01\rangle _{bc}+\alpha ^{\prime }|10\rangle _{bc}+\beta ^{\prime }|00\rangle _{bc} = \sigma ^x_b(U|\Psi \rangle )_b|0\rangle _c + \alpha ^{\prime }|0\rangle _b|1\rangle _c, \\ \alpha ^{\prime }|01\rangle _{bc}+\alpha ^{\prime }|10\rangle _{bc}-\beta ^{\prime }|00\rangle _{bc} = \sigma ^y_b(U|\Psi \rangle )_b|0\rangle _c + \alpha ^{\prime }|0\rangle _b|1\rangle _c, \\ \beta ^{\prime }|01\rangle _{bc}+\beta ^{\prime }|10\rangle _{bc}+\alpha ^{\prime }|00\rangle _{bc} = (U|\Psi \rangle )_b|0\rangle _c + \beta ^{\prime }|0\rangle _b|1\rangle _c, \\ -\beta ^{\prime }|01\rangle _{bc}-\beta ^{\prime }|10\rangle _{bc}+\alpha ^{\prime }|00\rangle _{bc} = \sigma ^z_b(U|\Psi \rangle )_b|0\rangle _c - \beta ^{\prime }|0\rangle _b|1\rangle _c. \end{array} \right. \end{aligned}$$
(13)

According to the re-expressions, one is readily to see that, the state in qubit \(b\) collapses to

$$\begin{aligned} \sigma ^x_b(U|\Psi \rangle )_b, \ \ \ \sigma ^y_b(U|\Psi \rangle )_b, \ \ \ (U|\Psi \rangle )_b, \ \ \ \sigma ^z_b(U|\Psi \rangle )_b, \end{aligned}$$
(14)

if Charlie measures \(|0\rangle _{c}\). The occurrence probabilities of the collapsed states are in turn \(1/(1+|\alpha ^{\prime }|^2)\), \(1/(1+|\alpha ^{\prime }|^2)\), \(1/(1+|\beta ^{\prime }|^2)\) and \(1/(1+|\beta ^{\prime }|^2)\), respectively. In total the probability with which Charlie measures \(|0\rangle _{c}\) is \(P_2=2/3\).

Upon receiving Charlie’s notice, Bob can execute a proper Pauli operation to convert the state in qubit \(b\) to the conceivable state \(U|\Psi \rangle \). Alternatively, he carries out a specific inverse operation in formula (14). Concretely, \((\sigma ^x_b)^{-1}\sigma ^x_b(U|\Psi \rangle )_b=(U|\Psi \rangle )_b\), \((\sigma ^y_b)^{-1}\sigma ^y_b(U|\Psi \rangle )_b=(U|\Psi \rangle )_b\), \((U|\Psi \rangle )_b=(U|\Psi \rangle )_b\) and \((\sigma ^z_b)^{-1}\sigma ^z_b(U|\Psi \rangle )_b=(U|\Psi \rangle )_b\). By far, the operation sharing has been achieved, i.e., the concerned operation \(U\) initially in Alice’s hand has been performed on the target state \(|\Psi \rangle \) in the remote agent Bob’s qubit \(b\). Integrated all the above mentioned, the total success probability is \(P=P_1\times P_2=4/9\).

At the beginning of sharers’ collaboration, if they decide Charlie to finally restore the conceivable state, then they can fulfill the sharing in the almost same way as that Bob is chosen to finally achieve the reconstruction. The only difference [cf. Fig. 1a, b] is that Bob and Charlie should exchange their performances. Concisely speaking, Bob measures his qubit \(b\) with the computational bases. If he measures \(|0\rangle \), then he notifies Charlie his measurement result via their classical communication. Otherwise, he does nothing. Once Charlie receives Bob’s message, Charlie implements a peculiar inverse operation to recover the conceivable state \((U|\Psi \rangle )_c\). As can be easily seen from the following re-expressions:

$$\begin{aligned} \left\{ \begin{array}{*{20}{l}} \alpha ^{\prime }|01\rangle _{bc}+\alpha ^{\prime }|10\rangle _{bc}+\beta ^{\prime }|00\rangle _{bc} = |0\rangle _b\sigma ^x_c(U|\Psi \rangle )_c + \alpha ^{\prime }|1\rangle _b|0\rangle _c, \\ \alpha ^{\prime }|01\rangle _{bc}+\alpha ^{\prime }|10\rangle _{bc}-\beta ^{\prime }|00\rangle _{bc} = |0\rangle _b\sigma ^y_c(U|\Psi \rangle )_c + \alpha ^{\prime }|1\rangle _b|0\rangle _c, \\ \beta ^{\prime }|01\rangle _{bc}+\beta ^{\prime }|10\rangle _{bc}+\alpha ^{\prime }|00\rangle _{bc} = |0\rangle _b(U|\Psi \rangle )_c + \beta ^{\prime }|1\rangle _b|0\rangle _c, \\ -\beta ^{\prime }|01\rangle _{bc}-\beta ^{\prime }|10\rangle _{bc}+\alpha ^{\prime }|00\rangle _{bc} = |0\rangle _b\sigma ^z_c(U|\Psi \rangle )_c - \beta ^{\prime }|1\rangle _b|0\rangle _c. \end{array} \right. \end{aligned}$$
(15)

2.2 Scheme with asymmetric W states

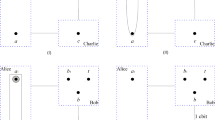
Now let us move to propose our second QOS scheme with two asymmetric W states. The schematic demonstration is illustrated in Fig. 2. The scheme is amply depicted as follow.

Fig. 2
figure 2

Illustration of the three-party QOS scheme with two asymmetric W states. The same as Fig. 1 except that solid rectangle and dot solid rectangle represent sharers’ two kinds of joint unitary operations. See text for more details

Full size image

Different from the first scheme, two asymmetric three-qubit W states instead of the symmetric ones are employed as shared entanglements in this scheme. Alice owns the qubit pair \((a_1, a)\), Bob the pair \((b_1, b)\) and Charlie the pair \((c_1, c)\), respectively. The state in these three pairs forms a product state of two asymmetric W states, i.e.,

$$\begin{aligned} |\mathcal{W}\rangle _{a_1b_1c_1abc} = |W_{as}\rangle _{a_1b_1c_1} \otimes |W_{as}\rangle _{abc}, \end{aligned}$$
(16)

where

$$\begin{aligned} |W_{as}\rangle = \frac{1}{\sqrt{2n+2}}(|001\rangle +\sqrt{n}e^{i\gamma }|010\rangle +\sqrt{n+1}e^{i\delta }|100\rangle ). \end{aligned}$$
(17)

At the beginning, Bob and Charlie collaborate to perform a collective unitary operation \(V\) on their qubit pair (\(b_1\), \(c_1\)). Here the unitary operator \(V\) under the ordering bases \(\{|00\rangle , |01\rangle , |10\rangle , |11\rangle \}\) takes the following form

$$\begin{aligned} V= \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} e^{-i\delta }&0&0&0 \\ 0&-\sqrt{\frac{n}{n+1}}&\sqrt{\frac{1}{n+1}}&0 \\ 0&\sqrt{\frac{1}{n+1}}e^{-i\gamma }&\sqrt{\frac{n}{n+1}}e^{-i\gamma }&0 \\ 0&0&0&e^{-i\delta } \end{array} \right). \end{aligned}$$
(18)

Their performance converts the state \(|W_{as}\rangle _{a_1b_1c_1}\) to

$$\begin{aligned} |\mathcal{B}^{\prime }\rangle _{a_1b_1c_1} = |\varphi ^+\rangle _{a_1b_1}|0\rangle _{c_1}. \end{aligned}$$
(19)

Obviously, the W state in the triplet \((a_1,b_1,c_1)\) has been transformed into a bipartite product state of qubit \(c_1\) and the qubit pair \((a_1,b_1)\).

Afterwards, Bob measures his qubit pair \((b^{\prime },b_1)\) with Bell-state measuring bases and publishes the measurement result. Note that before his measurements the state in the qubit triplet \((b^{\prime },a_1, b_1)\) is \(|\Psi \rangle _{b^{\prime }}|\varphi ^+\rangle _{a_1b_1}\) and it can be rewritten as

$$\begin{aligned} |\mathcal{Q}\rangle _{b^{\prime }a_1b_1}&= \frac{1}{2} [|\psi ^{+}\rangle _{b^{\prime }b_1}(\sigma ^x_{a_1})^\dagger |\Psi \rangle _{a_1} + |\psi ^{-}\rangle _{b^{\prime }b_1} (\sigma ^y_{a_1})^\dagger |\Psi \rangle _{a_1} \nonumber \\&+\,|\varphi ^{+}\rangle _{b^{\prime }b_1} |\Psi \rangle _{a_1}+|\varphi ^{-}\rangle _{b^{\prime }b_1} (\sigma ^z_{a_1})^\dagger |\Psi \rangle _{a_1}]. \end{aligned}$$
(20)

From the reexpression it is easy to see that Bob’s measurements may induce the following collapses

$$\begin{aligned}&|\psi ^{+}\rangle _{b^{\prime }b_{1}} \rightarrow \sigma ^x_{a_1}|\Psi \rangle _{a_1}, \ |\psi ^{-}\rangle _{b^{\prime }b_{1}} \rightarrow \sigma ^y_{a_1}|\Psi \rangle _{a_1}, \ |\varphi ^{+}\rangle _{b^{\prime }b_{1}} \rightarrow |\Psi \rangle _{a_1}, \nonumber \\&\quad \ |\varphi ^{-}\rangle _{b^{\prime }b_{1}}\rightarrow \sigma ^z_{a_1}|\Psi \rangle _{a_1}. \end{aligned}$$
(21)

In order to restore the target state in qubit \(a_1\), Alice carries out a specific inverse operation on her qubit \(a_1\) in terms of Bob’s classical information on the outcome, as can be easily seen from the formulae (20)–(21). Subsequently, Alice operates her qubit \(a_1\) with \(U\), i.e., \((U |\Psi \rangle )_{a_1}=\alpha ^{\prime }|0\rangle _{a_1}+\beta ^{\prime }|1\rangle _{a_1}\). Note that at this moment, the conceivable state \(U|\Psi \rangle \) has been obtained and has inhabited the qubit \(a_1\). After the operation, Alice measures her qubit pair \((a_1, a)\) with Bell-state bases and announces publicly the measurement result via a classical channel. Alice’s measurements induce the following collapses:

$$\begin{aligned} \left\{ \begin{array}{*{20}{l}} |\psi ^+\rangle _{a_1a} \Longrightarrow \alpha ^{\prime }|01\rangle _{bc}+\alpha ^{\prime }\sqrt{n}e^{i\gamma }|10\rangle _{bc}+\beta ^{\prime }\sqrt{n+1}e^{i\delta }|00\rangle _{bc}, \\ |\psi ^-\rangle _{a_1a} \Longrightarrow \alpha ^{\prime }|01\rangle _{bc}+\alpha ^{\prime }\sqrt{n}e^{i\gamma }|10\rangle _{bc}-\beta ^{\prime }\sqrt{n+1}e^{i\delta }|00\rangle _{bc}, \\ |\varphi ^+\rangle _{a_1a} \Longrightarrow \alpha ^{\prime }\sqrt{n+1}e^{i\delta }|00\rangle _{bc}+\beta ^{\prime }|01\rangle _{bc}+\beta ^{\prime }\sqrt{n}e^{i\gamma }|10\rangle _{bc}, \\ |\varphi ^-\rangle _{a_1a} \Longrightarrow \alpha ^{\prime }\sqrt{n+1}e^{i\delta }|00\rangle _{bc}-\beta ^{\prime }|01\rangle _{bc}-\beta ^{\prime }\sqrt{n}e^{i\gamma }|10\rangle _{bc}. \end{array} \right. \end{aligned}$$
(22)

On one hand, if Bob and Charlie agree to recover the conceivable state \(U|\Psi \rangle \) in Bob’s qubit \(b\), then they jointly perform a collective unitary operation \(V\) on their qubit pair \((b, c)\). Corresponding to the four collapsed states described in Eq. (22), their performance further transforms the state of qubit \(b\) into \(\sigma ^x_b(U|\Psi \rangle )_b\), \(\sigma ^y_b(U|\Psi \rangle )_b\), \((U|\Psi \rangle )_b\) or \(\sigma ^z_b(U|\Psi \rangle )_b\). It is obvious that Bob only needs to apply a unitary operation (i.e., \(\{\sigma _x\), \(\sigma _y\), \(I\) or \(\sigma _z\})\) to reconstruct the conceivable state. The fulfillment of this process means that the quantum task of operation sharing has already been achieved.

On the other hand, if both agents decide to recover the conceivable state \(U|\Psi \rangle \) in qubit \(c\), they need to perform a collective unitary operation \(V^{\prime }\) on their qubit pair \((b,c)\), where \(V^{\prime }\) takes the following form

$$\begin{aligned} V^{\prime }= \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} e^{-i\delta }&0&0&0 \\ 0&\sqrt{\frac{1}{n+1}}e^{-i\gamma }&\sqrt{\frac{n}{n+1}}e^{-i\gamma }&0 \\ 0&-\sqrt{\frac{n}{n+1}}&\sqrt{\frac{1}{n+1}}&0 \\ 0&0&0&e^{-i\delta } \end{array} \right). \end{aligned}$$
(23)

Note that \(V^{\prime }\) is different from \(V\) [cf. Eqs. (18) and (23)]. Hence the resultant scheme is accordingly different. See Fig. 2a and b for illustration. After the operation, the state in qubit \(c\) is transformed into one of that four states \(\sigma ^x_c(U|\Psi \rangle )_c\), \(\sigma ^y_c(U|\Psi \rangle )_c\), \((U|\Psi \rangle )_c\) and \(\sigma ^z_c(U|\Psi \rangle )_c\). In this case, it is easy to see that Charlie need apply an appropriate unitary operation (namely, \(\sigma _{x}, \sigma _{y}, I, \sigma _{z}\) in turn) to rebuilt the conceivable state \(U|\Psi \rangle \).

3 Discussions and comparisons

Now let us turn to some brief discussions on our schemes. As sharing schemes, their securities should be assured. In both schemes we have assumed in advance that quantum channels are assumed secure. It is the precondition of our schemes. As a matter of fact, the present quantum channels are very similar to those in Refs. [35–37] to some extent. Whether they are disturbed during the qubit distribution can be easily checked by using the mature sampling technique. In this case, any outsider’s perturbation can be detected. Moreover, there have been some other strategies [38–40] for preventing any insider’s cheating, which are applicable for our schemes, too. For simplicity, here we do not repeat them anymore.

As we have mentioned before, in both of our schemes the concerned operation \(U\) can be finally performed on the target state \(|\Psi \rangle \) via both agents’s cooperations. In particular, the conceivable state can be conclusively reconstructed in either agent’s qubit. This means that both schemes are symmetric as far as the sharers are concerned. In other words, either agent can be chosen as the last implementer to fulfill the final reconstruction. This is first feature of both schemes. In addition, such symmetry actually reflects the uncertainty of choosing the last implementer and therefore can enhance the securities of both schemes to some extent.

It is easy to see that the first scheme is probabilistic while the second is deterministic. The essential reason lies in the different inherent entanglements in the two quantum channels employed respectively. In the first scheme, two symmetric W states are utilized. Either of them can only be written as \(|W\rangle = [|1\rangle |00\rangle +|0\rangle (|10\rangle +|01\rangle )]/\sqrt{3}\). Obviously, by measuring the first one with computation bases, the state in the latter two qubits can be probabilistically converted into a maximally entangled state, which is responsible for the achievement of the sharing. In contrast, in the second scheme two asymmetric W states are used. Either asymmetric W state can be deterministically transformed into a product of a Bell-state and a single-qubit state. As a consequence, the sharing can be achieved with unit probability.

Now let us make some comparisons among our two schemes and the ZC scheme [23], which are all applicable for sharing arbitrary single-qubit unitary operation. Comparisons are carried out from the five aspects, namely, the quantum resource consumption, the necessary-operation complexity including operation difficulty and intensity, the classical resource consumption and the success probability as well as the intrinsic efficiency. They are summarized in Table 1.

Table 1 Comparisons between our two schemes and the ZC scheme
Full size table

From the table, one can see that, the quantum resource consumptions in our two schemes are equal. As for their operation complexities, they are almost same except that the two-qubit joint operation in the S2 scheme is a little difficult than the single-qubit operation in the S1 scheme. Except for this, the S2 scheme is overall better than the S1 scheme. In particular, the classical resource consumption in the S2 scheme is less than that in the S1 scheme, the success probability and efficiency in the S2 scheme are bigger than those in the S1 scheme. In all, the S2 scheme is more optimal and economic.

Comparing the S2 scheme with the ZC scheme, one is readily to see the following three differences: (1) the quantum resource consumption in the ZC scheme is less than that in the S2 scheme; (2) the operation complexity is somewhat degraded in the ZC scheme; (3) the only advantage in the S2 scheme is its less classical resource consumption. Nonetheless, the success probability and efficiency of both schemes are same. In this sense, one can take the S2 scheme as the powerful candidate of the ZC scheme.

At last, it’s worthy pointing out that if both sharers (also the two agents) are regarded as one receiver, then our present QOS schemes are reduced to the corresponding QOT schemes. In this sense, our present schemes are viewed as more general ones as far as the receiver is concerned.

4 Summary

To summarize, in this paper we have presented two symmetric QOS schemes for remotely sharing a single-qubit operation on a qubit in either sharer’s site by using two symmetric and asymmetric W states as quantum channels, respectively. We have compared their quantum and classical resource consumptions, operation complexities, success probabilities and efficiencies. It is found that the second scheme is much better than the first one, particularly in the aspect of success probability. Moreover, the second scheme is also compared with the similar ZC scheme. We think that it can be regarded as a candidate of the ZC scheme.