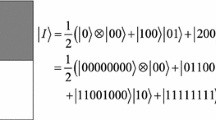Quantum multidimensional color images similarity comparison

Abstract

Based on the representation of quantum multidimensional color image, a complete scheme of solving the similarity of two quantum multidimensional color images is studied in depth. The two cases, the color image with segmentation information and without segmentation information, are considered, respectively. First, two images are connected together to form a new “link-state” according to the specific generation circuit. Then, through the Hadamard transformation on the link-state and repeated observations, the similarity value of the two quantum multidimensional color images is obtained. The simulation experiments, especially the two satellite images with a short interval and the two 3/4-color-alike color images with corresponding segmentation information, also show a wonderful performance, which drives the explorations on the multiple quantum color images processing.

1 Introduction

As a powerful tool, the image processing technique has penetrated into all aspects of daily life. Moreover, with different kinds of color images emerging at an increasing rate, color image processing is becoming crucial. Beyond that, the processing of multidimensional color image is also progressively developing. Among these processing means, an inescapable aspect is the similarity comparison between two color images. In general, in the classical computation, the evaluation of images’ similarity is often calculated by extracting two color images’ features like color, texture, structure, and stuff, which plays a vital role in pattern recognition, image retrieval, or classification. An engaging example is the satellite cloud image analysis. These images come from different time with a mini interval, and it is a very necessity to assess the similarity of these satellite images and observe their slight changes so as to make further analysis.

Of late, quantum information science [1] has shown a strong vitality, in both computation and information processing. It is primarily derived from the weirder quantum mechanics. Many special concepts in quantum mechanics, such as the superposition and coherence properties, have been successfully connected and applied in classical information processing [2, 3]. Accompanied by the fast development of quantum information, research findings on quantum image have proliferated although it is in its infancy. Capturing gray information and its position in the image, a flexible representation of quantum images [4] was explored. Soon afterward, many image processing methods had been proposed, such as the fast geometric transformations on quantum image [5, 6], the quantum cryptography algorithm based on image information security [7–11], quantum digital image processing algorithms [12, 13], and quantum image searching based on probability distributions [14, 15]. Additionally, another novel approach is a framework for representing and producing movies on quantum computers [16], it opens the door toward manipulating quantum circuits, and the recent novel quantum representation for quantum image including polar coordinate image [17, 18] applies quantum mechanics to create a new perspective in image processing, and so on.

All these studies greatly enriched the quantum image processing [19–21] technology. But these researches’ attention stays largely on gray image, and the number of researches on color image is still small. Thereamong, for quantum color image representation [22], the multidimensional color image representation, storage, and retrieval [23] is a significant contribution. It only uses a ($n+1$)-qubit normal arbitrary quantum superposition state (NAQSS) to represent a multidimensional color image (also contains segmentation information), which realizes the quantum color image’ representation and storage [24, 25] at the least cost.

In this article, the NAQSS idea, applying the amplitude of a quantum state to store the multidimensional color information, is used and improved. Moreover, based on the concept of content-based image retrieval, the two cases, image with segmentation information and without segmentation information, are discussed, respectively. In addition, in order to realize the multiple color images operation, the circuit implement scheme for connecting two quantum multidimensional color images is designed, which only needs adding 1 qubit and some operations on the basic of quantum circuit generation of NAQSS. Then, based on the relevant work like the Iliyasu’ gray scale image similarity assessing [26], through Hadamard transformation and measurement, the similarity value of the two quantum multidimensional images in the two different cases can be solved.

The paper is organized as follows: In Sect. 2, the basic concept of quantum mechanics is introduced briefly. In Sect. 3, a multidimensional color image representation is expounded in detail. Afterward, in Sect. 4, the whole workflow and realization for quantum multidimensional color image similarity comparison are stated. In Sect. 5, experimental simulation and similarity analysis are presented. Finally, in Sect. 6, we give a brief conclusion.

2 The basic concept of quantum mechanics

Just like complex is real’s extension and perfection, quantum information processing technology is also the expansion and perfection for classical information processing.

Quantum information is that information microscopic particles express. These quantum particles characterize a great deal of outstanding properties, such as superposition and entanglement. Quantum information processing is incomparable in information storage, computation, and many other aspects compared with classical information processing. For example, the famous Shor’s integer factoring algorithm [27] only needs a short polynomial time to accomplish.

2.1 Single quantum bit

In binary quantum computer, information unit is called quantum bit (qubit). Qubit as the basic information storage unit of quantum computer, unlike tossing a coin whose result is either 0 or 1, can indicate not only 0 state but also 1 state. That is to say, the qubit is in the superposition state. One qubit is expressed as follows:

$$\begin{aligned} |\varphi \rangle =\alpha |0 \rangle +\beta |1\rangle \end{aligned}$$

(1)

In the formula (1), both $\alpha$ and $\beta$ are the complex number, and they are all called the probability amplitude. Particularly, the two amplitudes must meet the condition:

$$\begin{aligned} |\alpha |^{2}+|\beta |^{2}=1 \end{aligned}$$

(2)

2.2 Multiple quantum superposition

Quantum parallel calculation, derived from the quantum linear superposition property, is an important branch of quantum information. The quantum linear superposition property can greatly improve the computing and processing ability than classical.

From the single qubit form, the double quantum bits will have four states $|00\rangle ,|01\rangle , 10\rangle ,|11\rangle$. Then, the double quantum bits are described as $|\varphi \rangle =\alpha _{00} |00\rangle +\alpha _{01} |01\rangle +\alpha _{10}|10\rangle +\alpha _{11} |11\rangle$, likewise, where the four probability amplitudes satisfy $|\alpha _{00} |^{2}+|\alpha _{01} |^{2}+|\alpha _{10} |^{2}+|\alpha _{11} |^{2}=1$.

Accordingly, the linear superposition state of multiple qubits can be easily derived, that is,

$$\begin{aligned} |\phi \rangle =c_1 |\phi _1 \rangle +c_2 |\phi _2 \rangle +c_3 |\phi _3\rangle +\cdot \cdot \cdot +c_\mathrm{n} |\phi _n \rangle = \sum _{i=1}^n {c_i |\phi _i \rangle } \end{aligned}$$

(3)

There are still the requirement $\sum \nolimits _i {|c_i |^{2}=1},\, |\varphi _\mathrm{i} \rangle$ stands for multiple qubits states like $|00101 \ldots 01\rangle ,\,|11000 \ldots 00\rangle$, or $|11111 \ldots 11\rangle$, which is one of quantum superposed state, and they are variable at any time. Thus, from (3), we can learn that a N-qubit can store $2^{N}$ data. Relative to conventional information storage, quantum storage capacity increases exponentially.

2.3 Quantum logic gate

Changing from one quantum state to another quantum state, it cannot do without the most basic operation of the quantum logic gate (Quantum gate) [28]. Quantum gate can process the quantum state for a series of unitary evolution. The only requirement is the unitary property, i.e., $H^{\dagger }H=I$, I is unit matrix, $H^{\dagger }$ is the conjugate transpose of $H$ matrix.

Commonly, the quantum gate is described as a matrix. The most significant single quantum gate is the Hadamard gate (H gate). It transforms $|0\rangle$ into the superposed state $\frac{1}{\sqrt{2}}(|0\rangle +|1\rangle )$, transforms $|1\rangle$ into the superposed state $\frac{1}{\sqrt{2}}(|0\rangle -|1\rangle )$. As the Bloch sphere in Fig. 1 illustrated, $H|0\rangle$ is equivalent to the clockwise $45^{\circ }$ rotation for $|0\rangle$, and $H|1\rangle$ is equivalent to the counterclockwise $135^{\circ }$ rotation for $|1\rangle$.

Fig. 1

$H$ gate and its function

In general, in quantum image processing, $H$ gate is often used to generate multiple quantum superposition state, such as

$$\begin{aligned}&(H\otimes H\otimes \cdot \cdot \cdot \otimes H)|00\cdot \cdot \cdot 0\rangle \nonumber \\&\quad =\frac{1}{\sqrt{2^{n}}}[(|0\rangle +|1\rangle )\otimes (|0\rangle +|1\rangle )\otimes \cdot \cdot \cdot \otimes (|0\rangle +|1\rangle )] \nonumber \\&\quad =\frac{1}{\sqrt{2^{n}}}\sum _{x=0}^{2^{n}-1} {|x\rangle } \end{aligned}$$

(4)

$\otimes$ is the tensor product, and it combines several vector space together to form a larger vector space. The tensor product has some operation nature as follows,

$$\begin{aligned} v\otimes (w1+w2)&= v \otimes w1+v\otimes w2 \end{aligned}$$

(5)

$$\begin{aligned} (v1+v2)\otimes w&= v1 \otimes w+v2\otimes w \end{aligned}$$

(6)

$$\begin{aligned} cv\otimes w&= v\otimes cw=c(v\otimes w) \end{aligned}$$

(7)

Meanwhile, the frequently used double quantum gate is the controlled NOT gate (CNOT gate). Its function is: if the control quantum bit is 1, the target quantum bit content will be inverted. The notation of CNOT gate is shown in Fig. 2.

Fig. 2

Controlled NOT gate

2.4 Quantum measurement

As a basic hypothesis of quantum mechanics, quantum measurement [29, 30] combines the classical world with quantum world and plays an irreplaceable important role in quantum information science.

Usually, quantum measurement is described by a set of measurement operators $\{M_{m}\}$. The measurement operator satisfies the completeness relation:

$$\begin{aligned} \sum _\mathrm{m} {M_m^{\dagger }M_m}=I. \end{aligned}$$

(8)

The operator performs on the measured system state space, and $m$ describes the measurement results that may be obtained in experiments. Before the measurement, the quantum state of the system is $|\varphi \rangle$, and the likelihood of m occurrence is

$$\begin{aligned} p(m)=\langle \varphi |M_m ^{\dagger }M_m |\varphi \rangle \end{aligned}$$

(9)

Then, after the measurement, the system state soon becomes $\frac{M_m |\varphi \rangle }{\sqrt{\langle \varphi |M_m ^{\dagger }M_m |\varphi \rangle }}$.

Usually, we always need to measure the quantum state for obtaining expected results. Suppose that there are two measurement operators $M_0=|0\rangle \langle 0|$ and $M_1 =|1\rangle \langle 1|$, noticing $M_0^{2}=M_0,M_1 ^{2}=M_1$ and a completeness relation $I=M_0^{\dagger }M_0+M_1 ^{\dagger }M_1 =M_0 +M_1$, then, if the measured quantum state is $a|0\rangle +b|1\rangle$, the state after measurement is

$$\begin{aligned} \frac{M_0 |\varphi \rangle }{|a|}=\frac{a}{|a|}|0 \rangle ,\frac{M_1 |\varphi \rangle }{|b|} = \frac{b}{|b|}|1\rangle \end{aligned}$$

(10)

Furthermore, in quantum mechanics, the most critical point is the quantum collapse after a measurement. So we have to prepare so many quantum states repeatedly to measure for extracting the information we need from the statistical features of measure results.

3 A representation of quantum multidimensional color images

Since the amplitude of quantum state can be used to store information, this property can make quantum information representation and storage capacity greatly improved. Therefore, our theoretical approach is also based on the excellent property.

According to a ($n+1$)-qubit normal arbitrary quantum superposition state (NAQSS), it can describe a multidimensional color image (also contains segmentation information), and its expression is as follows:

$$\begin{aligned} |\psi \rangle =\sum _{i=0}^{2^{n}-1} {\theta _i |v_1 \rangle } |v_2 \rangle \cdot \cdot \cdot |v_k \rangle |p_i \rangle \end{aligned}$$

(11)

In this representation, $|i\rangle =|v_1 \rangle |v_2 \rangle \cdot \cdot \cdot |v_k \rangle$ is a coordinate in the $k$-dimensional space $V$. $|p_i \rangle$ is used to store the additional information (here, it denotes the number of partition sub-images). $|p_i \rangle =\cos \gamma _i |0\rangle +\sin \gamma _i |1\rangle$, angle $\gamma _i$ corresponding to an integer i, and there is the relationship between them: $\gamma _i =\frac{i\pi }{2(m-1)},\,i\in \{0,1,\ldots ,m-1\}$ and if $m=1,\,\gamma _i=0$. Here, “$m$” is the number of partition sub-images (or segmentation-sub-images) which belongs to a certain image. Thus, the number of partition sub-images of a quantum color image will be stored in a qubit. On the other hand, $\theta$ prescribes the color information. At first, the R, G, B are transformed into $\varphi$, and then, $\varphi$ is transformed into $\theta$ by normalization. Table 1 and Fig. 3 explain this origin simply.

Fig. 3

The relation between color and angle $\theta$ (Color figure online)

Table 1 The calculation of $R$, $G$, $B$ value and $\varphi$ (Color figure online)

Besides, if the number of partition sub-images is small, for the convenience of illustration, we can also use several qubits to store the partition number information.

Therefore, this quantum image representation using only $n+1$ qubits can store $2^{n}$ pixels of the multitarget (partition sub-images or segmentation-sub-images) color image in multidimensional space.

In order to make a reference, the simplified version of NAQSS $(\hbox {NAQSS}_\mathrm{sv})$ is devised properly. It leaves the last qubit out, i.e., the partition information. So the image it stands for becomes the quantum multidimensional color image without any partition information.

Simply speaking, the $\hbox {NAQSS}_\mathrm{sv}$ is illustrated in Fig. 4, and only four qubits can stand for color and position information of an three-dimensional (3D) image which contains sixteen pixels. This representation is absolutely beyond classical power.

Fig. 4

The $\hbox {NAQSS}_\mathrm{sv}$ representation of 3D color images (Color figure online)

For color images with segmentation information, as is shown in Fig. 5, one two-dimensional (2D) multitarget color image with the size $8\times 8$ can be stored in NAQSS. From the Fig. 5, we can easily see that the quantum color image representation needs only 7 qubits, 6 qubits code the space location, and 1 qubit codes partition sub-image number. This representation can totally define $2^{6}=64$ different colors.

Fig. 5

A 2D color image with segmentation information (Color figure online)

So the representation for quantum state of the multiple color image with segmentation information in Fig. 5 is

$$\begin{aligned} |\varphi \rangle&= \sum _{i=0}^{63} \theta _i |i\rangle |p_i \rangle = \theta _0 |000000\rangle |1\rangle +\theta _1 |000001\rangle |1\rangle \nonumber \\&+\theta _2 |000010\rangle |2\rangle +\theta _3 |000011\rangle |2\rangle \cdot \cdot \cdot \theta _{63} |111111\rangle |16\rangle \end{aligned}$$

(12)

4 Similarity comparison work

As we all know, two quantum color images’ representation needs two states like (11). Apparently, it is impossible to compare and identify the two unknown pure states directly in the quantum computation theory.

So, according to the NAQSS and its circuit generation, combined with the gray image similarity assessing based on FRQI, we design the scheme and specific implement work based on the novel content-based image processing concepts. The two cases are discussed in the paper:

One is using the NAQSS form directly including segmentation information, i.e., the target label. It is a representation of content-based image, which lays a good foundation for subsequent image processing like color image segmentation, classification, and retrieval.

Another, for the purpose of finding the color difference more rapidly and lowering the cost of qubits, we only use $\hbox {NAQSS}_\mathrm{sv,}$, i.e., leaving the segmentation label out.

Then, the color images to be compared in the two different cases are all go through the following steps:

• (1) Produce the link-state

• (2) $H$ gate transformation

• (3) Measurement

Thus, through the specific circuit implementation we give and the whole three steps about two different cases, the similarity value for multidimensional color images can be computed and used in the further region-based image retrieval, etc.

Following that, we will go into details of the complete implementation scheme.

4.1 Produce the link-state

4.1.1 Connect two images with segmentation information

To begin with, there are $2^\mathrm{m}$ quantum color images with $2^\mathrm{n}$ pixels to be compared. “m” is the number of qubits coding required $2^\mathrm{m}$ images. And each image is called a sub-image. Here, on a separate note, the shape (or the size) of the images being compared cannot be always the same. But their total pixels number should be same. That is to say, see the Fig. 4, the 3D image can be $4\times 2\times 2$ and can also be $2\times 2\times 4$ or $2\times 4\times 2$. But the content or color of these images may be different. While in reality, the same size image comparison is more common or meaningful. So the entire scheme for image with same size is certainly more effective.

In this case, the consistent label of image segmentation information is required (coding sequence and direction of label should match in the two images). Here, the first and foremost priority is to connect the $2^\mathrm{m}$ sub-images together to form a new quantum “Link-state” $|C(m,n)\rangle$, i.e.,

$$\begin{aligned} |C(m,n)\rangle =\frac{1}{\sqrt{2^{m}}}\sum _{k=0}^{2^{m}-1} {|\varphi _k \rangle \otimes |k\rangle } \end{aligned}$$

(13)

In (13), $|\varphi _k \rangle =\sum _{i=0}^{2^\mathrm{n}-1} {\theta _{k,i} |i\rangle |p_\mathrm{i} \rangle }$ is used to store a single sub-image [see (11)]. “k” stands for the position number of each sub-image in the linked image. “n” denotes that the total number of pixels of each sub-image to be compared is all $2^{n}$. Generally, as long as we compare the two images, then the similarity of multiple images will be cognitive, i.e., just to acquire the $|C(1,n)\rangle$.

In fact, the statement “Link” is only for the convenience of understanding, and it is practically a new quantum state we prepare. Figure 6 shows the two color images with 4 segmentation labels. And the designed circuit or storage realization of connecting the two images with segmentation information can be seen in Fig. 7.

Fig. 6

Two images with segmentation information

Fig. 7

Circuit for connecting the above two images

In the Fig. 6, there are two 2D color images with segmentation label, $m=1$, $n=2$ (because the total pixels are $2^{2}=4$). Assume that each pixel is a sub-partition-image, because there are only 4 sub-partition-images, and in order to show convenient, we use 2 qubits to store the sub-partition-images information.

The link-state of the two images in Fig. 6 is expressed as follows,

$$\begin{aligned}&|C(1,2) \rangle =\frac{1}{\sqrt{2}}\sum _{k=0}^{2^{1}-1} |\varphi _k \rangle \otimes |k\rangle = \frac{1}{\sqrt{2}}(|\varphi _0 \rangle \otimes |0\rangle +|\varphi _1 \rangle \otimes |1\rangle ) \nonumber \\&\quad = \frac{\theta _{0,0} }{\sqrt{2}}|00\rangle |00\rangle |0\rangle +\frac{\theta _{0,1} }{\sqrt{2}}|01\rangle |01\rangle |0\rangle +\frac{\theta _{0,2} }{\sqrt{2}}|10\rangle |10\rangle |0\rangle \nonumber \\&\qquad + \frac{\theta _{0,3} }{\sqrt{2}}|11\rangle |11\rangle |0\rangle +\frac{\theta _{1,0} }{\sqrt{2}}|00\rangle |00\rangle |1\rangle +\frac{\theta _{1,1} }{\sqrt{2}}|01\rangle |01\rangle |1\rangle \nonumber \\&\qquad + \frac{\theta _{1,2} }{\sqrt{2}}|10\rangle |10\rangle |1\rangle +\frac{\theta _{1,3} }{\sqrt{2}}|11\rangle |11\rangle |1\rangle \end{aligned}$$

(14)

Clearly, the color value before link operation is $\theta _0 ,\theta _1,\theta _2 ,\theta _3$. But after link operation, it becomes $\frac{\theta _{0,0} }{\sqrt{2}},\;\frac{\theta _{0,1} }{\sqrt{2}},\;\frac{\theta _{0,2} }{\sqrt{2}},\;\frac{\theta _{0,3} }{\sqrt{2}}$, respectively. These changes are mainly because of the quantum state regeneration and color normalization thereof.

Based on the mentioned above and referring to the quantum circuit realization of NAQSS (the concrete quantum circuit realization of NAQSS is denoted as the “NAQSS” block in Fig. 7), the link-state generation for the two images in Fig. 6 is given. The first step is to prepare 4+1 qubits and to set all of them to $|0\rangle$. Four qubits are used to produce the image $|\phi _0 \rangle$ by the NAQSS1 circuit block, and the one qubit left is used to carry on the H gate transformation. Then, through two CNOT gates and the NAQSS2 circuit block, the image $|\phi _1 \rangle$ is also produced. Thus, the link-state $|C(1,2)\rangle$ is generated.

4.2 Connect two images without segmentation information

In the second case, $\hbox {|p}_i \rangle$ will be no longer used. The two color images are denoted as $|\phi _0 \rangle _\mathrm{sv}$ and $|\phi _1\rangle _\mathrm{sv}$. Their corresponding circuit realization is referred to as $\hbox {NAQSS}_\mathrm{sv}$1 block and $\hbox {NAQSS}_\mathrm{sv}$2 block, respectively. The specific quantum circuit diagram turns into Fig. 8, and $|C(1,2)\rangle$ is

$$\begin{aligned}&|C(1,2)\rangle =\frac{\theta _{0,0} }{\sqrt{2}}|00\rangle |0\rangle +\frac{\theta _{0,1} }{\sqrt{2}}|01\rangle |0\rangle +\frac{\theta _{0,2} }{\sqrt{2}}|10\rangle |0\rangle + \frac{\theta _{0,3} }{\sqrt{2}}|11\rangle |0\rangle \nonumber \\&\quad +\frac{\theta _{1,0}}{\sqrt{2}}|00\rangle |1\rangle +\frac{\theta _{1,1} }{\sqrt{2}}|01\rangle |1\rangle +\;\frac{\theta _{1,2} }{\sqrt{2}}|10\rangle |1\rangle +\frac{\theta _{1,3} }{\sqrt{2}}|11\rangle |1\rangle \end{aligned}$$

(15)

Fig. 8

Circuit for connecting two images without segmentation information

This representation and its circuit only contain the position $|i\rangle$, the color $\theta$ of each image and its number in the link image.

Connecting the two color images makes a better preparation for the subsequent operation.

4.3 $H$ gate transformation

As we all know, the color difference determines the image similarity to a certain extent. The accurate color difference can determine whether there is a color degradation of the same image or judge whether it is the same image, and stuff. Consequently, we need to manage to find the color difference.

Following the link-state generation, in order to identify whether the two images are similar, an effective operation is needed. Here, Hadamard transform is performed on the linked state:

$$\begin{aligned}&H(|C(1,n)\rangle )=H\left( \frac{1}{\sqrt{2}}\sum _{k=0}^{2^{1}-1} {|\varphi _k \rangle \otimes |k\rangle }\right) \nonumber \\&\quad =\frac{1}{\sqrt{2}}[(\theta _{0,0} |0\rangle |p_0 \rangle +\theta _{0,1} |1\rangle |p_1 \rangle +\cdots \theta _{0,2^{n}-1} |2^{n}-1\rangle |p_{2^{n}-1} \rangle )\otimes \frac{1}{\sqrt{2}}(|0\rangle \nonumber \\&\qquad +\, |1\rangle )+(\theta _{1,0} |0\rangle |p_0 \rangle +\cdots \theta _{1,2^{n}-1} |2^{n}-1\rangle |p_{2^{n}-1} \rangle )\otimes \frac{1}{\sqrt{2}}(|0\rangle -|1\rangle )] \nonumber \\&\quad =\frac{1}{2}[(\theta _{0,0} |0\rangle |p_0 \rangle |0\rangle +\cdots \theta _{0,2^{n}-1} |2^{n}-1\rangle |p_{2^{n}-1} \rangle |0\rangle ) \nonumber \\&\qquad +\, (\theta _{0,0} |0\rangle |p_0 \rangle |1\rangle +\cdots \theta _{0,2^{n}-1} |2^{n}-1\rangle |p_{2^{n}-1} \rangle |1\rangle )\nonumber \\&\qquad +\, (\theta _{1,0} |0\rangle |p_0 \rangle |0\rangle +\cdots \theta _{1,2^{n}-1} |2^{n}-1\rangle |p_{2^{n}-1} \rangle |0\rangle ) \nonumber \\&\qquad -\, (\theta _{1,0} |0\rangle |p_0 \rangle |1\rangle +\cdots \theta _{1,2^{n}-1} |2^{n}-1\rangle |p_{2^{n}-1} \rangle |1\rangle )] \nonumber \\&\quad =\frac{1}{2}[(\theta _{0,0} +\theta _{1,0} )|0\rangle |p_0 \rangle |0\rangle +(\theta _{0,1} +\theta _{1,1} )|1\rangle |p_1 \rangle |0\rangle \nonumber \\&\qquad + \cdots (\theta _{0,2^{n}-1} +\theta _{1,2^{n}-1} )|2^{n}-1\rangle |p_{2^{n}-1} \rangle |0\rangle )+(\theta _{0,0} -\theta _{1,0} )|0\rangle |p_0 \rangle |1\rangle \nonumber \\&\qquad +\, (\theta _{0,1} -\theta _{1,1} )|1\rangle |p_1 \rangle |1\rangle +\cdots (\theta _{0,2^{n}-1} -\theta _{1,2^{n}-1} )|2^{n}-1\rangle |p_{2^{n}-1} \rangle |1\rangle )] \end{aligned}$$

(16)

Similarly, in the second case,

$$\begin{aligned}&H(|C(1,n)\rangle )= H\left[ \frac{1}{\sqrt{2}}\sum _{k=0}^1 {\left( \sum _{i=0}^{2^{1}-1} {\theta _{k,i} |i\rangle }\right) \otimes |k\rangle } \right] \nonumber \\&\quad =\frac{1}{\sqrt{2}}[(\theta _{0,0} |0\rangle +\theta _{0,1} |1\rangle \cdots \theta _{0,2^{n}-1} |2^{n}-1\rangle )\otimes H(|0\rangle ) \nonumber \\&\qquad +\, (\theta _{1,0} |0\rangle +\theta _{1,1} |1\rangle \cdots \theta _{1,2^{n}-1} |2^{n}-1\rangle )\otimes H(|1\rangle )] \nonumber \\&\quad =\frac{1}{\sqrt{2}}[(\theta _{0,0} |0\rangle +\theta _{0,1} |1\rangle \cdots \theta _{0,2^{n}-1} |2^{n}-1\rangle )\otimes \frac{1}{\sqrt{2}}(|0\rangle +|1\rangle ) \nonumber \\&\qquad +\, (\theta _{1,0} |0\rangle +\theta _{1,1} |1\rangle \cdots \theta _{1,2^{n}-1} |2^{n}-1\rangle )\otimes \frac{1}{\sqrt{2}}(|0\rangle -|1\rangle )] \nonumber \\&\quad =\frac{1}{2}[(\theta _{0,0} +\theta _{1,0} )|0\rangle |0\rangle +(\theta _{0,1} +\theta _{1,1} )|1\rangle |0\rangle +\cdots (\theta _{0,2^{n}-1} +\theta _{1,2^{n}-1} )|2^{n}-1\rangle |0\rangle \nonumber \\&\qquad +\, (\theta _{0,0} -\theta _{1,0} )|0\rangle |1\rangle +(\theta _{0,1} -\theta _{1,1} )|1\rangle |1\rangle +\cdots (\theta _{0,2^{n}-1} -\theta _{1,2^{n}-1} )|2^{n}-1\rangle |1\rangle ]\nonumber \\ \end{aligned}$$

(17)

For Fig.6, the result after $H$ gate transformation becomes:

$$\begin{aligned}&H(|C(1,2)\rangle )=H(\frac{1}{\sqrt{2}}(|\varphi _0 \rangle \otimes |0\rangle +|\varphi _1 \rangle \otimes |1\rangle )) \nonumber \\&\quad =\frac{1}{2}[(|\varphi _0 \rangle +|\varphi _1 \rangle )\otimes |0\rangle +(|\varphi _0 \rangle -|\varphi _1 \rangle )\otimes |1\rangle ] \nonumber \\&\quad =\frac{1}{2}[(\theta _{0,0} +\theta _{1,0} )|00\rangle |00\rangle |0\rangle +(\theta _{0,1} +\theta _{1,1} )|01\rangle |01\rangle |0\rangle \nonumber \\&\qquad +\, (\theta _{0,2} +\theta _{1,2} )|10\rangle |10\rangle |0\rangle + (\theta _{0,3} +\theta _{1,3} )|11\rangle |11\rangle |0\rangle \nonumber \\&\qquad +\, (\theta _{0,0} -\theta _{1,0} )|00\rangle |00\rangle |1\rangle +(\theta _{0,1} -\theta _{1,1} )|01\rangle |01\rangle |1\rangle \nonumber \\&\qquad +\, (\theta _{0,2} -\theta _{1,2} )|10\rangle |10\rangle |1\rangle + (\theta _{0,3} -\theta _{1,3} )|11\rangle |11\rangle |1\rangle ] \end{aligned}$$

(18)

4.4 Measurement

See from (18), the qubit carried the color difference information is in the qubits string whose last qubit is $|1\rangle$. Therefore, in order to obtain the similarity value, the measurement work is indispensable. Due to the collapse of a single measurement, a large quantity of quantum states preparation is necessary. Then, by repeated measurements, refer to (16) and (17), the probability of get 1 or 0 state is as follows:

$$\begin{aligned} \hbox {pr}(|0\rangle )&= \frac{1}{4}\left[ (\theta _{0,0} \!+\!\theta _{1,0} )^{2}\!+\!(\theta _{0,1} \!+\!\theta _{1,1} )^{2}\!+\!(\theta _{0,2} \!+\!\theta _{1,2} )^{2}\!+\!\cdots (\theta _{0,2^{n}-1} \!+\!\theta _{1,2^{n}-1} )^{2}\right] \nonumber \\&= \frac{1}{4}\sum _{i=0}^{2^{n}-1} {(\theta _{0,i} +\theta _{1,i} )^{2}}\end{aligned}$$

(19)

$$\begin{aligned} \hbox {pr}(|1\rangle )&= \frac{1}{4}\left[ (\theta _{0,0} \!-\!\theta _{1,0} )^{2}\!+\!(\theta _{0,1} \!-\!\theta _{1,1} )^{2}\!+\!(\theta _{0,2} \!-\!\theta _{1,2} )^{2}\!+\!\cdots (\theta _{0,2^{n}-1} \!-\!\theta _{1,2^{n}-1} )^{2}\right] \nonumber \\&= \frac{1}{4}\sum _{i=0}^{2^{n}-1} {(\theta _{0,i} -\theta _{1,i} )^{2}}\end{aligned}$$

(20)

$$\begin{aligned}&\hbox {pr}(|0\rangle )+\hbox {pr}(|1\rangle )=1 \end{aligned}$$

(21)

Among them, $\hbox {pr}(|1\rangle )$ reflects the differences between the two images. Moreover, according to the above derivation, in the two different cases, the probability solution is same. Hence, we only calculate the $\hbox {pr}(|1\rangle )$ by massive measurement outcomes, and the similarity value will be acquired. Coupled with the H gate operation in Sect. 4.3, the corresponding circuit can be seen in Fig. 9:

Fig. 9

Circuit for operations in Sects. 4.3 and 4.4

Summing up the above discussion, the schematic diagram of measurement and calculation is shown in Fig. 10.

Fig. 10

Measurement and calculation

When measuring N same states prepared in advance, the measure output with $\hbox {pr}(|0\rangle )$ and $\hbox {pr}(|1\rangle )$ obeys a binomial distribution. That is $\hbox {pr}(x=k)=C_N^k p^{k}(1-p)^{N-k}$, here $p=\hbox {pr}(|1\rangle )$, $k$ is the number of appear $xx \ldots 1$, and $k$ ranges from 0 to $N$.

For a specific measurement result such as$|000\ldots 0\rangle$, only if its probability distribution value becomes steady, i.e., its difference between two adjacent outcomes is less than a small number like 0.00001, and the measurement can be stopped.

Considering $\hbox {pr}(|1\rangle )$ is no more than 0.5 $(\frac{1}{4}\sum \nolimits _{i=0}^{2^{\mathrm{n}}-1}{(\theta _{0,i} -\theta _{1,i})^{2}}<\frac{1}{4}\times 2)$, therefore, when the two quantum multidimensional images are totally not the same, the max probability is 0.5. And if both are identical, let $y=\hbox {pr}(1)$ (pr(1) refers to the $(\hbox {pr}|1\rangle ))$, color difference ${x}=(\theta _{0,i} -\theta _{1,i} )$, based on (20), and the relationship of probability pr(1) and color difference $({y}=\frac{1}{4}x^{2})$ is shown in Fig. 11,

Fig. 11

The relationship between pr(1) and color difference

To illustrate the concept of similarity more clear and convenient, we make the following Definition 1:

Definition 1

quantum multidimensional color images’ similarity is defined by

$$\begin{aligned} \hbox {SIM(A,B)}=1-2\hbox {pr}(1), \end{aligned}$$

(22)

From the Fig. 11 and the definition, we can draw a conclusion that the color image similarity SIM(A,B) will decreases with the increase in the probability pr(1). pr(1) is a key indicator of the similarity between A and B. The larger probability pr(1), the greater the difference of two quantum color images.

5 Experimental simulation and similarity analysis

Because of the difficulties in preparing stable and practical quantum state through physical means, there has not yet had the practical quantum computer appeared. Consequently, we utilize a group of color images to simulate on a classical computer with Inter Core 5, Duo 1.6 GHz CPU and 4 RAM with the Matlab 2013b simulation environment.

Two satellite cloud color images at pm 15:00 and 15:30 in one day, color image Peppers and its counterpart after pseudo-color processing, two partially color-alike images with corresponding partition information, and Lena color image and its counterpart by simple color threshold processing are used.

The first experiment of satellite cloud images at different time indicates that the weather change is small in a relatively short period, and the final similarity is 0.9902, which is consistent with the actual situation (Fig. 12).

Fig. 12

The experiment 1: two satellite cloud color images with 30 min interval result: $\hbox {pr}(1)= 0.0049$, $\hbox {SIM}=0.9902$ (Color figure online)

The second experiment, for color image Peppers, using a pseudo-transformation, turns $R$ into $G$, $G$ into $B$, $B$ into $R$ and then calculates the similarity between the two. The simulation result is 0.8654 (Fig. 13).

Fig. 13

The experiment 2: Peppers and pseudo-color Peppers Result: $\hbox {pr}(1)=0.0673$, $\hbox {SIM}=0.8654$ (Color figure online)

The third experiment reflects the uniqueness of the proposed implement scheme sufficiently, through solving the probability pr(1) of two color images with the corresponding four partition labels 00, 01, 10, 11. And, finally, their similarity is 0.7876, which is mainly in virtue of the two images of 3/4 same color information that we can clearly find (Fig. 14).

Fig. 14

The experiment 3: two 3/4-color-alike images with partition label Result: $\hbox {pr}(1)= 0.1062$, $\hbox {SIM}=0.7876$ (Color figure online)

The last experiment demonstrates the similarity of Lena color image and its counterpart after threshold processing. It also receives a very good result of SIM 0.1174. As a contrast, two entirely same Lena color images are chosen, and what this experiment shows is exactly 1 (Figs. 15, 16).

Fig. 15

The experiment 4.a : lena and lena after threshold processing result: $\hbox {pr}(1)=0.4413$, $\hbox {SIM}=0.1174$

Fig. 16

The experiment 4.b : lena and lena result: $\hbox {pr}(1)=0$, $\hbox {SIM}=1$

At last, all the similarity values are presented in Table 2.

Table 2 Experiment data analysis

In brief, the four simulation experiment results (including the two different cases, with segmentation information and without segmentation information) have clearly shown that the whole implement for quantum multidimensional color image similarity comparison, from connect, transformation to measurement, is effective.

See from the whole, it should be noted that compared with the Iliyasu’ work, the main difference or contribution of this paper includes the following:

• (1) The aimed object is entirely different, and the Iliyasu’ work merely focus on the gray image, but the objective we process is the commonly used color image, it is an improvement and progress faced the practical application.

• (2) The image dimension is also expanded, and the qubits cost is small. Our scheme focuses on the multidimensional quantum color image, while the other is only the two dimension, which is advanced. It is mainly because the basis is different. The basis in this paper is not FRQI but NAQSS. In NAQSS, there is no qubit representing for the color information, while it needs one qubit in FRQI. So all the cost of qubits decreases dramatically.

• (3) Introduce new element. In our similarity scheme, the color images are divided into two cases, with segmentation information and without segmentation information, which facilitates the similarity analysis and further image retrieval.

Besides, in Iliyasu’ scheme, some work is slightly deficient. But in this paper, particularly, the circuit implement for connecting two different quantum multidimensional images is given, which provides a solid foundation for further image processing. In conclusion, the solution in this paper makes big leaps.

6 Conclusion and future work

In this paper, based on NAQSS representation, an entire solution to compute the similarity of quantum multidimensional color images in two different cases is explored. The experimental results of a group of color images, especially the two satellite clouds pictures comparison, and the two 3/4-color-alike color images with corresponding partition information similarity comparison, imply that the solution to obtain two multidimensional color images’ similarity is feasible and effective, which takes a step forward in the field of quantum color image processing. More new methods and achievements on multiple quantum multidimensional color images will be continually enriched and enlarged.