The optical exact soliton solutions of Shynaray-IIA equation with $\Phi ^6$-model expansion approach

Abstract

This paper investigates the Shynaray-IIA equation (S-IIAE), a type of partial differential parametric equation, using the $\Phi ^6$-model expansion method. The Shynaray-IIA equation is coupled system of differential equations which is integrable and contain soliton solutions. It addresses the integrable motion of space curves and have a lot of applications in nonlinear optics, water waves, plasma physics and other modern sciences. Prior to this study, no previous research has achieved solutions of this kind. In order to fill this gap, the $\Phi ^6$-model expansion method is employing to Shynaray-IIA equation and obtains new exact solutions for the perturbed form of the Shynaray-IIA equation, including bright, singular, periodic, and combined singular soliton solutions. These findings enhance our understanding of the equation’s nonlinear dynamical properties and offer a practical and efficient approach to solving various nonlinear partial differential equations. The research also explores specific parameter values that meet constraint conditions to reveal the dynamic behavior of the solutions. To present these findings effectively, the study utilizes visually appealing graphs that highlight the solutions’ characteristics. Overall, this work contributes to advancing our knowledge of the Shynaray-IIA equation and demonstrates the applicability of the $\Phi ^6$-model expansion method in studying nonlinear systems.

1 Introduction

The nonlinear partial differential equation is a fundamental mathematical tool (Ali et al. 2023a; Faridi et al. 2023) used to analyze the behavior of complex physical phenomena with nonlinear characteristics. By applying this equation, scientists can rigorously study intricate systems that would be challenging to understand otherwise. One such area of active research is the investigation of optical solitons in nonlinear media (Debnath and Debnath 2005). Optical solitons are enduring wave packets, crucial for high-speed data transmission in optical fibers and all-optical switches. Their remarkable ability to maintain shape and intensity over long distances ensures distortion-free propagation, enhancing modern telecommunication systems’ efficiency and reliability. This research area aims to deepen our understanding of soliton dynamics and further enhance their practical applications, thus contributing significantly to advancements in communication technology.

Currently, using diverse approaches to find accurate solutions for nonlinear evolution equations and partial differential equations (NLEEs) proves highly advantageous and effective. One effective approach is the new modified extended direct algebraic (MEDA) technique (Iqbal et al. 2022), the Hirota bilinear method (Rizvi et al. 2022; Kumar et al. 2022), the new Kudryashov approach (Malik et al. 2023), a new auxiliary equation approach (Rahman et al. 2023), the sinh-Gordon equation expansion method (Wazwaz and El-Tantawy 2022), the modified Exp-function and Kudryshov methods (Zafar et al. 2022; Nisar et al. 2022), The generalized Riccati equation mapping method (GREMM) and the q-HATM approaches (Akinyemi et al. 2022). the Khater-II (Khat II) method and Sardar Sub-equation method (Khater 2023), the generalized Khater (GK) technique and utilizing Atangana’s conformable fractional (ACF) derivative operator (Khater 2022), the auto-Backlund transformation approach (Singh and Saha Ray 2023), the Jacobi elliptic function technique (Tarla et al. 2022), the Jacobi elliptic function expansion (JEFE) method (Tarla et al. 2022), the modified exponential rational functional method (Shaikh et al. 2023), the integration algorithm used to achieve this retrieval is the method of undetermined coefficients (Biswas et al. 2023) and so on.

A lot of work has been done in this field. Alquran (2021, 2022, 2023a) has presented the classification of single-wave and bi-wave motion, constructed the soliton solutions of Schrödinger and new two-mode extension of the coupled KdV-Schrödinger equations by using the analytical techniques. Alquran et al. (2023b, c); Alquran and Jaradat (2023) investigated the dual-wave solutions to the Kadomtsev-Petviashvili model and derived the analytical soliton solutions of the modified regularized long wave equation and Nizhnik-Novikov-Veselov equation. Ali et al. (2023b); Jaradat et al. (2018); Alquran and Smadi (2023) developed the interesting variety of solutions of two-mode generalized KdV equation, weak-dissipative two-mode perturbed Burgers’ and Ostrovsky models and the generalized doubly dispersive equation. Ali et al. (2023c, 2023d, 2023e) examined the perturbed Fokas-Lenells equation, the Ivancevic option pricing model and nonlinear Schrödinger equation. Rasool et al. (2023) have been constructed the fractional soliton solutions. Demirbilek and Ala (2022) developed the exact solutions of Kundu-Mukherjee-Naskar mode via improved Bernoulli sub-equation function method. Muhammad Abubakar and Yokus (2023); Isah and Yokus (2022); Yokus and Isah (2023) applied the $\Phi ^{6}-$model expansion scheme to the complex Ginzburg–Landau equation and the reaction-diffusion equation to drive the analytical soliton solutions and also discussed the solitary wave solutions of the Korteweg-de Vries equation with the Hirota bilinear technique. Duran et al. (2023) investigated the Murnaghan model of the doubly dispersive equation analytically and numerically.

In this article, the Shynaray-IIA model (Umurzakhova et al. 2022) is investigated using the recently developed $\Phi ^6$-model expansion method (Asjad et al. 2023; Faridi et al. 2022; Zayed et al. 2018; Zayed and Al-Nowehy 2020, 2017), that the existence of many solitons type solutions remains an enigma and a significant gap in the current body of literature. Additionally, there is no mention of any conditions under which these solutions are valid. To address this gap, a generalized approach called the $\Phi ^6$-model expansion method is employed, which offers a more comprehensive solution. As a result of this analysis, the study successfully restores optical solitary wave solutions, contributing to a deeper understanding of the model’s behavior and its potential applications in relevant fields.

We consider the following Shynaray-IIA equation (S-IIAE) (Umurzakhova et al. 2022; Zayed and Al-Nowehy 2018; Sagidullayeva et al. 2022; Myrzakulova et al. 2022; Sagidullayeva et al. 2022; Myrzakulova et al. 2022):

$$\begin{aligned} \begin{aligned}&iq_t+q_{xt}-i(vq)_x=0,\\&ir_t-r_{xt}-i(vr)_x=0,\\&v_x-\frac{n^{2} }{m}(rq)_t=0. \end{aligned} \end{aligned}$$

(1)

The above mentioned Eq. (1) is transformed into following model by taking $r = \epsilon \bar{q}\, (\epsilon =\pm 1),$

$$\begin{aligned} \begin{aligned}&iq_t+q_{xt}-i(vq)_x=0,\\&v_x-\frac{n^{2}\epsilon }{m}(|q|^2)_t=0, \end{aligned} \end{aligned}$$

(2)

where, n, m and $\epsilon$ are real constants. The above mentioned mathematical model is coupled nonlinear differential equations system. The complex wave function and real wave function are representing by q(x, t) and v(x, t), respectively. The Shynaray-IIA equation is coupled system of differential equations which is integrable and contain soliton solutions. It addresses the integrable motion of space curves and have a lot of applications in nonlinear optics, water waves, plasma physics and other modern sciences.

Recently, Umurzakhova et al. (2022) examined the integrability of the Shynaray-IIA equation and other properties. But prior to this study, no previous research has achieved solutions of this kind. The soliton solutions are important because soliton can propagate through a medium over long distances without changing shape or amplitude. This stability is crucial in applications where the integrity of a wave or signal must be preserved, such as in optical communication, where data transmission requires minimal distortion. In order to fill this gap, we use the generalized analytical scheme and tried to develop the analytical exact solutions. The obtained solutions are novel and generalized in the literature and might be significant. There are a lot other techniques are available which can be used by anyone to find the other mystery soliton solutions to visualize the deep insights.

The paper is structured as follows: Sect. 2 outlines the $\Phi ^6$-model expansion method’s core algorithm. Section 3 derives exact solutions for the Shynaray-IIA equation using the proposed method. The graphical demonstration is presented in Sect. 4. The study concludes in Sect. 5.

2 Description of the method

In this section, the $\Phi ^6$-model expansion method will be explained in details.

Let us take the general representation of nonlinear equation with the function $T=T(x,t),$

$$\begin{aligned} \Xi (T, T_{x}, T_{t}, T_{xx}, T_{xx}, T_{tt},...)=0, \end{aligned}$$

(3)

where $\Xi$ is a polynomial involving T(x, t) and its highest-order partial derivatives with independent variables x and t and the non-linear components are implicated. To turn Eq. (1) into a simple form of ordinary differential equation, use the wave transformation $T(x,t)=T(\chi )$, $\chi$= x-$c\, t$:

$$\begin{aligned} \Omega (T, T^{'},c~T^{'}, c^{2}~T^{''}, c^2~T^{''}, ... )=0. \end{aligned}$$

(4)

The prime of T represent the derivatives. A possible initial solution for Eq. (4) is as follows:

$$\begin{aligned} T(\chi )=\sum _{i=0}^{2N} a_{i}Q^{i}(\chi ), \end{aligned}$$

(5)

where $a_{0}$, $a_{1}$, $a_{2}$,..., $a_{N}$ are unknown constants which will be determined and N is homogeneous balancing constant.

$$\begin{aligned} \begin{aligned}&Q^{'2}(\chi )=h_{0}+h_{2}Q^{2}(\chi )+h_4Q^{4}(\chi )+h_6Q^{6}(\chi ),\\&Q^{''}(\chi )=h_{2}Q(\chi )+2h_4Q^{3}(\chi )+3h_6Q^{6}(\chi ), \end{aligned} \end{aligned}$$

(6)

where $l_{0}$, $l_{2}$, $l_{4}$,$l_{6}$ are real constant to be determined.

$$\begin{aligned} Q(\chi )=\frac{P(\chi )}{\sqrt{fP^{2}(\chi )+g}}, \end{aligned}$$

(7)

where $fP^{2}(\chi )+g>0$ and $P(\chi )$ represents the solution that satisfies the Jacobi elliptic equation,

$$\begin{aligned} P^{'2}(\chi )=l_0+l_2P^2(\chi )+l_4P^4(\chi ), \end{aligned}$$

(8)

while f and g are given by,

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}f=\frac{h_4(l_2-h_2)}{(l_2-h_2)^2+3l_0l_4-2l_2(l_2-h_2)}\\ &{}g=\frac{3l_0h_4}{(l_2-h_2)^2+3l_2l_4-2l_2(l_2-h_2)} \end{array}\right. } \end{aligned}$$

(9)

under the constrain condition,

$$\begin{aligned} {h_{{4}}}^{2}(l_2-h_2)(9l_0l_4-(l_2-h_2)(2l_2+h_2))+3h_6(-{l_{{2}}}^{2}+{h_{{2}}}^{2}+3l_0l_4)^2. \end{aligned}$$

(10)

Table 1 Limiting cases for functions

3 Application of the $\Phi ^6$-model expansion method

In order to get the generalized soliton solutions of Shynaray-IIA equation, the $\Phi ^{6}-$model expansion method will take into account.

$$\begin{aligned} \begin{aligned}&q(x,t)=T(\chi )e^{i\gamma (x,t)},\quad v(x,t)=G(\chi ),\\&\gamma (x,t)=-\delta x+\omega t+\theta ,\quad \chi =x-c\,t. \end{aligned} \end{aligned}$$

(11)

The values of c, $\omega$, $\theta$ and $\delta$ determine the soliton’s frequency, wave number, phase constant, and velocity. When Eq. (11) is inserted into Eq. (2), a result is obtained:

$$\begin{aligned} \begin{aligned}&cT^{''}(\chi )+\omega (1-\delta )T(\chi )+\delta G(\chi )T(\chi )+i((\omega -c(1-\delta ))T^{'}(\chi )-G(\chi )T^{'}(\chi )-G^{'}(\chi )T(\chi ))=0,\\ \textit{and}\\&G^{'}(\chi )+\frac{2c\epsilon n^{2}}{m}T(\chi )T^{'}(\chi )=0. \end{aligned} \end{aligned}$$

(12)

The second equation of system (12) is integrated and get,

$$\begin{aligned} G(\chi )=-\frac{c\epsilon n^{2}}{m}T^{2}(\chi ). \end{aligned}$$

(13)

Equation (13) is plugging into first equation of system (12) and get the real part as,

$$\begin{aligned} cT^{''}(\chi )+\omega (1-\delta )T(\chi )-\frac{\delta \epsilon cn^2}{m}T^{3}(\chi )=0, \end{aligned}$$

(14)

and the imaginary part is,

$$\begin{aligned} (\omega -c(1-\delta ))T^{'}(\chi )+\frac{3c\epsilon n^{2}}{m}T^{2}(\chi )T^{'}(\chi )=0, \end{aligned}$$

(15)

and the constraint condition is,

$$\begin{aligned} \omega = c(1-\delta ). \end{aligned}$$

In order to find the homogeneous balancing constant from Eq. (14), we took highest order term $T^{''}$ and highest nonlinear term $T^{3}$. Thus, $N+2=3N$, therefore, $N=1$ is obtained as a result of the balance principle and the solution form can be expressed as,

$$\begin{aligned} T(\chi )=a_0+a_1Q(\chi )+a_2Q^{2}(\chi ), \end{aligned}$$

(16)

where $a_0,a_{1}$ and $a_2$ are constant to be determined. We obtain the following algebraic system of equations by substituting Eq. (16) along with Eq. (6) into Eq. (14) and setting the coefficients of all powers of $Q_{i}(\chi ), i=0,1,...,6$ to be equal to zero;

$$\begin{aligned} \begin{aligned} Q^{0}(\chi )&:2ca_2h_0+\omega a_0-\omega \delta a_0-\frac{\delta c \epsilon n^2a_0^3}{m}=0,\\ Q^{1}(\chi )&:ca_1h_2+\omega a_1-\omega \delta a_1-\frac{3\delta c \epsilon n^2a_0^2a_1}{m}=0,\\ Q^{2}(\chi )&:4ca_2h_2+\omega a_2-\omega \delta a_2-\frac{3\delta c \epsilon n^2a_0^2a_2}{m}-\frac{3\delta c \epsilon n^2a_1^2a_0}{m}=0,\\ Q^{3}(\chi )&:2ca_1h_4-\frac{6\delta c \epsilon n^2a_0a_1a_2}{m}-\frac{\delta c \epsilon n^2a_1^3}{m}=0,\\ Q^{4}(\chi )&:6ca_2h_4-\frac{3\delta c \epsilon n^2a_2^2a_0}{m}-\frac{3\delta c \epsilon n^2a_1^2a_2}{m}=0,\\ Q^{5}(\chi )&:3ca_1h_6-\frac{3\delta c \epsilon n^2a_2^2a_1}{m}=0,\\ Q^{6}(\chi )&:8ca_2h_6-\frac{\delta c \epsilon n^2a_2^3}{m}=0.\\ \end{aligned} \end{aligned}$$

(17)

Solving the resulting system and obtain,

$$\begin{aligned} \begin{aligned}&a_0=\pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}},\, a_1=0,\,a_2=\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}}},\,h_6=-{\frac{9m{h_{{4}}}^{2}c}{2\mathfrak {A}}},\\&h_0={\frac{2\,ch_{{2}}w\delta -2\,ch_{{2}}w+8\,{c}^{2}{h_{{2}}}^{2}-(\omega (\delta -1))^2}{18{c}^{2}h_{{4}}}}, \end{aligned} \end{aligned}$$

(18)

where $\mathfrak {A}=-12\,ch_{{2}}m-3\,wm+3\,w\delta \,m$. Considering Eqs. (7), (16), and (17), along with the Jacobi elliptic function provided in Table 1, we deduce the exact solution for the Eq. (2) as follows:

1. If $l_0=1, l_2=-(1+k^2),l_4=k^2,\, 0<k<1,$ then $P(\chi )=sn(\chi ,k)\, or\, P(\chi )=cd(\chi ,k),$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_1=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}sn^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fsn^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_1=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}sn^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fsn^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(19)

or

$$\begin{aligned} \begin{aligned}&q(x,t)_2=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}cd^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fcd^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_2=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}cd^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fcd^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(20)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f={\frac{h_{{4}} \left( 1+{k}^{2}+h_{{2}} \right) }{1-{k}^{2}+{k}^{4}-{ h_{{2}}}^{2}}}, \, \,g=-{\frac{3h_{{4}}}{1-{k}^{2}+{k}^{4}-{ h_{{2}}}^{2}}}, \end{aligned}$$

(21)

under the constraint condition,

$$\begin{aligned} \left( -1-{k}^{2}-h_{{2}} \right) (5k^2-2k^4-2-h_2-k^2h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,{\frac{mc{(-1+k^2-{k}^{4}+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}}=0. \end{aligned}$$

(22)

When $k\rightarrow 1,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{1,1}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)tanh^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((2+h_2)tanh^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{1,1}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)tanh^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((2+h_2)tanh^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(23)

such that,

$$\begin{aligned} \left( -2-h_{{2}}\right) (1-2h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,\frac{mc{(-1+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(24)

When $k\rightarrow 0,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{1,2}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)sin^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((1+h_2)sin^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{1,2}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)sin^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((1+h_2)sin^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(25)

or

$$\begin{aligned} \begin{aligned}&q(x,t)_{1,3}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)cos^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((1+h_2)cos^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{1,3}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)cos^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((1+h_2)cos^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(26)

with the condition that,

$$\begin{aligned} \left( -1-h_{{2}} \right) (-2-h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,\frac{mc{(-1+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(27)

2. If $l_0=1-k^2, l_2=2k^2-1,l_4=-k^2,\, 0<k<1,$ then $P(\chi )=cn(\chi ,k)$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_3=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_4m\sqrt{{c\delta \,\epsilon }}cn^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fcn^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{3}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_4m\sqrt{{c\delta \,\epsilon }}cn^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fcn^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(28)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f=-{\frac{h_{{4}} \left( 2\,{k}^{2}-1-h_{{2}} \right) }{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}}, \, \, g=\frac{3\,h_{{4}} {\left( -1+k^2 \right) }{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}}{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}, \end{aligned}$$

(29)

provided that,

$$\begin{aligned} \left( 2k^{2}-1-h_{2} \right) \left( -k^2+k^4+2k^{2}h_{2}-2-h_2+{h_{2}}^{2}\right) -{\frac{27}{2}}\,\frac{mc{(-1+k^2-{k}^{4}+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(30)

3. If $l_0=k^2-1, l_2=2-k^2,l_4=-1,\, 0<k<1,$ then $P(\chi )=dn(\chi ,k)$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_4=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_4m\sqrt{{c\delta \,\epsilon }}dn^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fdn^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{4}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_4m\sqrt{{c\delta \,\epsilon }}dn^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fdn^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(31)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f={\frac{h_{4} \left( -2\,+{k}^{2}+h_{2} \right) }{1-{k}^{2}+{k}^{4}-{h_{2}}^{2}}}, \, \, g=-\frac{3\,h_{4}( -1+k^{2}) }{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}, \end{aligned}$$

(32)

with the condition that,

$$\begin{aligned} \left( 2-k^2-h_{2} \right) (-k^2-2k^4-k^2h_2+1+2h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,\frac{mc{(-1+k^2-{k}^{4}+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(33)

4. If $l_0=k^2, l_2=-(1+k^2),l_4=1,\, 0<k<1,$ then $P(\chi )=ns(\chi ,k)\, or\, P(\chi )=dc(\chi ,k),$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_5=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}ns^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fns^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{5}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}ns^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fns^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(34)

or

$$\begin{aligned} \begin{aligned}&q(x,t)_6=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}dc^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fdc^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{6}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}dc^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fdc^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(35)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f={\frac{h_{{4}} \left( 1+{k}^{2}+h_{{2}} \right) }{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}},\,\, g=-{\frac{3k^2h_{{4}}}{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}}, \end{aligned}$$

(36)

under the constraint condition,

$$\begin{aligned} \left( -1-{k}^{2}-h_{{2}} \right) (5k^2-2k^4-2-h_2-k^2h_2+{h_{{2}}}^{2})-{ \frac{27}{2}}\,{\frac{mc{(-1+k^2-{k}^{4}+{h_{{2}}}^{2})}^{2}}{\mathfrak {A} }}=0. \end{aligned}$$

(37)

When $k\rightarrow 1,$ solitary wave solution is obtained,

$$\begin{aligned} \begin{aligned}&q(x,t)_{5,1}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)coth^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((2+h_2)coth^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{5,1}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)coth^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((2+h_2)coth^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(38)

with the condition that,

$$\begin{aligned} ( -2-h_{{2}} ) (1-2h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,\frac{mc{(-1+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(39)

5. If $l_0=-k^2, l_2=2k^2-1,l_4=1-k^2,\, 0<k<1,$ then $\, P(\chi )=nc(\chi ,k),$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_7=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}nc^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fnc^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{7}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}nc^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fnc^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(40)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f=-{\frac{h_{{4}} \left( -1+2{k}^{2}-h_{{2}} \right) }{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}},\,\,g={\frac{3k^2h_{{4}}}{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}}, \end{aligned}$$

(41)

under the constraint condition,

$$\begin{aligned} \left( -1+2{k}^{2}-h_{{2}} \right) (-k^2+k^4-2-h_2+2k^2h_2+{h_{{2}}}^{2} )-{\frac{27}{2}}\,{\frac{mc{(-1+k^2-{k}^{4}+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}}=0. \end{aligned}$$

(42)

When $k\rightarrow 1,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{7,1}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)cosh^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((h_2-1)cosh^2(\chi )+3)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{7,1}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)cosh^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((h_2-1)cosh^2(\chi )+3)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(43)

with the condition that,

$$\begin{aligned} \left( -2-h_{{2}} \right) (1-2h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,\frac{mc{(-1+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(44)

6. If $l_0=-1, l_2=2-k^2,l_4=-(1-k^2),\, 0<k<1,$ then $P(\chi )=nd(\chi ,k)$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_8=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}nd^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fnd^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{8}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}nd^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fnd^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(45)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f={\frac{h_{{4}} \left( -2+{k}^{2}+h_{{2}} \right) }{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}},\,\, g={\frac{3h_{{4}}}{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}}, \end{aligned}$$

(46)

under the constraint condition,

$$\begin{aligned} \left( 2-{k}^{2}-h_{{2}} \right) (1-k^2-2k^4+2h_2-k^2h_2+{h_{{2}}}^{2} )-{\frac{27}{2}}\,{\frac{mc{(-1+k^2-{k}^{4}+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}}=0. \end{aligned}$$

(47)

When $k\rightarrow 1,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{8,1}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2cosh^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((h_2-1)cosh^2(\chi )+3)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{8,1}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2cosh^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((h_2-1)cosh^2(\chi )+3)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(48)

with the condition that,

$$\begin{aligned} \left( -2-h_{{2}} \right) (1-2h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,\frac{mc{(-1+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(49)

7. If $l_0=1, l_2=2-k^2,l_4=1-k^2,\, 0<k<1,$ then $P(\chi )=sc(\chi ,k)$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_9=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}sc^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fsc^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{9}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}sc^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fsc^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(50)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f={\frac{h_{{4}} \left( -2+{k}^{2}+h_{{2}} \right) }{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}},\,\, g=-{\frac{3h_{{4}}}{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}}, \end{aligned}$$

(51)

under the constraint condition,

$$\begin{aligned} \left( 2-{k}^{2}-h_{{2}} \right) (1-k^2+2h_2-2k^4-k^2h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,\frac{mc(-1+k^2-{k}^{4}+{h_{{2}}}^{2})^{2}}{\mathfrak {A}}=0, \end{aligned}$$

(52)

When $k\rightarrow 1,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{9,1}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)sinh^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((h_2-1)sinh^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{9,1}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)sinh^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((h_2-1)sinh^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(53)

such that,

$$\begin{aligned} \left( -2-h_{{2}} \right) (1-2h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,\frac{mc{(-1+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(54)

When $k\rightarrow 0,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{9,2}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)tan^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((h_2-2)tan^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{9,2}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)tan^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((h_2-2)tan^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(55)

with the condition that,

$$\begin{aligned} \left( 2-h_{{2}} \right) (1+2h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,\frac{mc{(-1+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(56)

8. If $l_0=1, l_2=2k^2-1,l_4=-k^2(1-k^2),\, 0<k<1,$ then $P(\chi )=sd(\chi ,k)$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_{10}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}sd^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fsd^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{10}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}sd^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fsd^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(57)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f=-{\frac{h_{{4}} \left( -1+2{k}^{2}-h_{{2}} \right) }{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}},\,\, g=-{\frac{3h_{{4}}}{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}}, \end{aligned}$$

(58)

under the constraint condition,

$$\begin{aligned} \left( -1+2{k}^{2}-h_{{2}} \right) (-k^2+k^4-2-h_2+2k^2h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,{\frac{mc{(-1+k^2-{k}^{4}+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}}=0. \end{aligned}$$

(59)

When $k\rightarrow 0,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{10,1}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2sin^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((h_2+1)sin^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{10,1}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2sin^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((h_2+1)sin^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(60)

with the condition that,

$$\begin{aligned} \left( 2-h_2 \right) (1+2h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,\frac{mc{(-1+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(61)

9. If $l_0=1-k^2, l_2=2-k^2,l_4=1,0<k<1,$ then $P(\chi )=cs(\chi ,k)$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_{11}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}cs^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fcs^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{11}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}cs^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fcs^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(62)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f={\frac{h_{{4}} \left( -2+{k}^{2}+h_{{2}} \right) }{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}},\,\, g={\frac{3(-1+k^2)h_{{4}}}{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}}, \end{aligned}$$

(63)

under the constraint condition,

$$\begin{aligned} \left( 2-{k}^{2}-h_{{2}} \right) (1-k^2+2h_2-2k^4-k^2h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,\frac{m{c{(-1+k^2-{k}^{4}+{h_{{2}}}^{2})}^{2}}{ \mathfrak {A}}}{=}0. \end{aligned}$$

(64)

When $k\rightarrow 0,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{11,2}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)cot^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((h_2-2)cot^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{11,2}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,m\sqrt{{c\delta \,\epsilon }}(1-h_2^2)cot^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}((h_2-2)cot^2(\chi )-3)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(65)

with the condition that,

$$\begin{aligned} \left( 2-h_{{2}} \right) (1+2h_2+{h_{{2}}}^{2})-{\frac{27}{2}}\,\frac{mc{(-1+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(66)

10. If $l_0=-k^2(1-k^2), l_2=2k^2-1,l_4=1,\, 0<k<1,$ then $P(\chi )=ds(\chi ,k)$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_{12}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}ds^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fds^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{12}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}ds^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fds^2(\chi ,k)+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(67)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f=-{\frac{h_{{4}} \left( -1+2{k}^{2}-h_{{2}} \right) }{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}},\,\, g=-{\frac{3k^2(-1+k^2)h_{{4}}}{1-{k}^{2}+{k}^{4}-{h_{{2}}}^{2}}}, \end{aligned}$$

(68)

under the constraint condition,

$$\begin{aligned} \left( -1+2{k}^{2}-h_{{2}} \right) (-k^2+k^4-2-h_2+2k^2h_2+{h_{{2}}}^{2} )-{\frac{27}{2}}\,{\frac{mc{(-1+k^2-{k}^{4}+{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}}=0. \end{aligned}$$

(69)

11. If $l_0=\frac{1-k^2}{4}, l_2=\frac{1+k^2}{2},l_4=\frac{1-k^2}{4},\, 0<k<1,$ then $P(\chi )=nc(\chi ,k)\pm sc(\chi ,k)\, or\, P(\chi )=\frac{cn(\chi ,k)}{1\pm sn(\chi ,k)},$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_{13}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}[nc(\chi ,k)\pm sc(\chi ,k)]^2}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(f[nc(\chi ,k)\pm sc(\chi ,k)]^2+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{13}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}[nc(\chi ,k)\pm sc(\chi ,k)]^2}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(f[nc(\chi ,k)\pm sc(\chi ,k)]^2+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(70)

or

$$\begin{aligned} \begin{aligned}&q(x,t)_{14}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}cn^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fcn^2(\chi ,k)+g[1\pm sn(\chi ,k)]^2)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{14}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}cn^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fcn^2(\chi ,k)+g[1\pm sn(\chi ,k)]^2)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(71)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f=-{\frac{8h_{{4}} \left( 1+{k}^{2}-2h_{{2}} \right) }{1+14{k}^{2}+{k}^{4}-{16h_{{2}}}^{2}}},\,\, g={\frac{12(-1+k^2)h_{{4}}}{1+14{k}^{2}+{k}^{4}-{16h_{{2}}}^{2}}}, \end{aligned}$$

(72)

under the constraint condition,

$$\begin{aligned} 16\left( 1+{k}^{2}-2h_{{2}} \right) (1-34k^2+k^4+8h_2+8k^2h_2+16{h_{{2}}}^{2})-\frac{27\, mc{(-1-14k^2-{k}^{4}+16{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(73)

When $k\rightarrow 0,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{13,2}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{3\,m\sqrt{{c\delta \,\epsilon }}(1-16{h_{{2}}}^{2})[sec(\chi )\pm tan(\chi )]^2}{2\, \delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(2(2h_2-1)[sec(\chi )\pm tan(\chi )]^2-3)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{13,2}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{3\,m\sqrt{{c\delta \,\epsilon }}(1-16{h_{{2}}}^{2})[sec(\chi )\pm tan(\chi )]^2}{2\, \delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(2(2h_2-1)[sec(\chi )\pm tan(\chi )]^2-3)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(74)

or

$$\begin{aligned} \begin{aligned}&q(x,t)_{14,2}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{3\,m\sqrt{{c\delta \,\epsilon }}(1-16{h_{{2}}}^{2})cos^2(\chi )}{2\, \delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(2(2h_2-1)cos^2(\chi )-3(1\pm sin(\chi ))^2)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{14,2}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{3\,m\sqrt{{c\delta \,\epsilon }}(1-16{h_{{2}}}^{2})cos^2(\chi )}{2\, \delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(2(2h_2-1)cos^2(\chi )-3(1\pm sin(\chi ))^2)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(75)

with the condition that,

$$\begin{aligned} 16\left( 1-2h_{{2}} \right) (1+8h_2+16{h_{{2}}}^{2})-\frac{27\, mc{(-1+{16h_{{2}}}^{2})}^{2}}{ \mathfrak {A}}=0. \end{aligned}$$

(76)

12. If $l_0=-\frac{(1-k^2)^2}{4}, l_2=\frac{1+k^2}{2},l_4=-\frac{1}{4},0<k<1,$ then $P(\chi )=kcn(\chi ,k)\pm dn(\chi ,k),$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_{15}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}[kcn(\chi ,k)\pm dn(\chi ,k)]^2}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(f[kcn(\chi ,k)\pm dn(\chi ,k)]^2+g)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{15}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}[kcn(\chi ,k)\pm dn(\chi ,k)]^2}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(f[kcn(\chi ,k)\pm dn(\chi ,k)]^2+g)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(77)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f=-{\frac{8h_{{4}} \left( 1+{k}^{2}-2h_{{2}} \right) }{1+14{k}^{2}+{k}^{4}-{16h_{{2}}}^{2}}},\,\, g={\frac{12(-1+k^2)h_{{4}}}{1+14{k}^{2}+{k}^{4}-{16h_{{2}}}^{2}}}, \end{aligned}$$

(78)

under the constraint condition,

$$\begin{aligned} 16\left( 1+{k}^{2}-2h_{{2}} \right) (1-34k^2+k^4+8h_2+8k^2h_2+16{h_{{2}}}^{2})-\frac{27\, mc{(-1-14k^2-{k}^{4}+16{h_{{2}}}^{2}))}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(79)

When $k\rightarrow 0,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{15,2}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{3\,m\sqrt{{c\delta \,\epsilon }}(1-16{h_{{2}}}^{2})[cos(\chi )\pm 1]^2}{2\, \delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(2(2h_2-1)[cos(\chi )\pm 1]^2-3)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{15,2}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{3\,m\sqrt{{c\delta \,\epsilon }}(1-16{h_{{2}}}^{2})[cos(\chi )\pm 1]^2}{2\, \delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(2(2h_2-1)[cos(\chi )\pm 1]^2-3)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(80)

with the condition that,

$$\begin{aligned} 16\left( 1-2h_{{2}} \right) (1+8h_2+16{h_{{2}}}^{2})-\frac{27\, mc{(-1+{16h_{{2}}}^{2})}^{2}}{ \mathfrak {A}}=0. \end{aligned}$$

(81)

13. If $l_0=\frac{1}{4}, l_2=\frac{1-2k^2}{2},l_4=\frac{1}{4},0<k<1,$ then $P(\chi )=\frac{sn(\chi ,k)}{1\pm cn(\chi ,k)},$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_{16}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}sn^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fsn^2(\chi ,k)+g[1\pm cn(\chi ,k)]^2)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{16}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}sn^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fsn^2(\chi ,k)+g[1\pm cn(\chi ,k)]^2)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(82)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f={\frac{8h_{{4}} \left( -1+2{k}^{2}+2h_{{2}} \right) }{1-16{k}^{2}+16{k}^{4}-{16h_{{2}}}^{2}}},\,\, g=-{\frac{12h_{{4}}}{1-16{k}^{2}+16{k}^{4}-{16h_{{2}}}^{2}}}, \end{aligned}$$

(83)

under the constraint condition,

$$\begin{aligned} 16\left( 1-2{k}^{2}-2h_{{2}} \right) (1+32k^2-32k^4+8h_2-16k^2h_2+16{h_{{2}}}^{2})-\frac{27\, mc{(-1+16k^2-16{k}^{4}+16{h_{{2}}}^{2})}^{2}}{\mathfrak {A}}=0. \end{aligned}$$

(84)

When $k\rightarrow 1,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{16,1}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{3\,m\sqrt{{c\delta \,\epsilon }}(1-16{h_{{2}}}^{2})tanh^2(\chi )}{2\, \delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(2(2h_2+1)tanh^2(\chi )-3[1\pm sech(\chi )]^2)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{16,1}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{3\,m\sqrt{{c\delta \,\epsilon }}(1-16{h_{{2}}}^{2})tanh^2(\chi )}{2\, \delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(2(2h_2+1)tanh^2(\chi )-3[1\pm sech(\chi )]^2)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(85)

with the condition that,

$$\begin{aligned} 16\left( -1-2h_{{2}} \right) (1-8h_2+16{h_{{2}}}^{2})-\frac{27\, mc{(-1+{16h_{{2}}}^{2})}^{2}}{ \mathfrak {A}}=0. \end{aligned}$$

(86)

When $k\rightarrow 0,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{16,2}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{3\,m\sqrt{{c\delta \,\epsilon }}(1-16{h_{{2}}}^{2})sin^2(\chi )}{2\, \delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(2(2h_2-1)sin^2(\chi )-3[1\pm cos(\chi )]^2)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{16,2}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{3\,m\sqrt{{c\delta \,\epsilon }}(1-16{h_{{2}}}^{2})sin^2(\chi )}{2\, \delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(2(2h_2-1)sin^2(\chi )-3[1\pm cos(\chi )]^2)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(87)

with the condition that,

$$\begin{aligned} 16\left( 1-2h_{{2}} \right) (1+8h_2+16{h_{{2}}}^{2})-\frac{27\, mc{(-1+{16h_{{2}}}^{2})}^{2}}{ \mathfrak {A}}=0. \end{aligned}$$

(88)

14. If $l_0=\frac{1}{4}, l_2=\frac{1+k^2}{2},l_4=\frac{(1-k^2)^2}{4},0<k<1,$ then $P(\chi )=\frac{sn(\chi ,k)}{cn(\chi ,k)\pm dn(\chi ,k)},$ and we have,

$$\begin{aligned} \begin{aligned}&q(x,t)_{17}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}sn^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fsn^2(\chi ,k)+g[cn(\chi ,k)\pm dn(\chi ,k)]^2)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{17}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{6\,h_{{4}}m\sqrt{{c\delta \,\epsilon }}sn^2(\chi ,k)}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(fsn^2(\chi ,k)+g[cn(\chi ,k)\pm dn(\chi ,k)]^2)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(89)

such that $\chi =x-c\,t$, the functions f and g are,

$$\begin{aligned} f=-{\frac{8h_{{4}} \left( 1+{k}^{2}-2h_{{2}} \right) }{1+14{k}^{2}+{k}^{4}-{16h_{{2}}}^{2}}},\,\,g=-{\frac{12h_{{4}}}{1+14{k}^{2}+{k}^{4}-{16h_{{2}}}^{2}}}, \end{aligned}$$

(90)

under the constraint condition,

$$\begin{aligned} 16\left( 1+{k}^{2}-2h_{{2}} \right) (1-34k^2+k^4+8h_2+8k^2h_2+16{h_{{2}}}^{2})-{\frac{27mc{(-1-14k^2-{k}^{4}+16{h_{{2}}}^{2})}^{2}}{\mathfrak {A} }}=0. \end{aligned}$$

(91)

When $k\rightarrow 1,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{17,1}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{24\, m\sqrt{{c\delta \,\epsilon }}(1-{h_{{2}}}^{2})tanh^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(4(h_2-1)tanh^2(\chi )-3sech^2(\chi ))}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{17,1}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{24\, m\sqrt{{c\delta \,\epsilon }}(1-{h_{{2}}}^{2})tanh^2(\chi )}{\delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(4(h_2-1)tanh^2(\chi )-3sech^2(\chi ))}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(92)

with the condition that,

$$\begin{aligned} 16\left( 1-h_{{2}} \right) (-2+h_2+{h_{{2}}}^{2})-\frac{27}{2}\frac{mc{(-1+{h_{{2}}}^{2})}^{2}}{ \mathfrak {A}}=0. \end{aligned}$$

(93)

When $k\rightarrow 0,$ the solution takes the form of a solitary wave,

$$\begin{aligned} \begin{aligned}&q(x,t)_{17,2}=\left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{3\,m\sqrt{{c\delta \,\epsilon }}(1-16{h_{{2}}}^{2})sin^2(\chi )}{2\, \delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(2(2h_2-1)sin^2(\chi )-3[cos(\chi )\pm 1]^2)}}\right) e^{i(-\delta x+\omega t+\theta )},\\&v(x,t)_{17,2}=-\frac{c\epsilon n^{2}}{m}\left( \left( \pm \frac{1}{3n}\,\sqrt{-{\frac{\mathfrak {A}}{c\delta \,\epsilon }}}\pm {\frac{3\,m\sqrt{{c\delta \,\epsilon }}(1-16{h_{{2}}}^{2})sin^2(\chi )}{2\, \delta \epsilon n\sqrt{-{{\mathfrak {A}}}}(2(2h_2-1)sin^2(\chi )-3[cos(\chi )\pm 1]^2)}}\right) e^{i(-\delta x+\omega t+\theta )}\right) ^{2}, \end{aligned} \end{aligned}$$

(94)

with the condition that

$$\begin{aligned} 16\left( 1-2h_{{2}} \right) (1+8h_2+16{h_{{2}}}^{2})-\frac{27\, mc{(-1+{16h_{{2}}}^{2})}^{2}}{ \mathfrak {A}}=0. \end{aligned}$$

(95)

4 Graphical demonstration and discussion

In this section, the graphical propagation of the obtained solution will visualizes and discuss their behaviour.

Fig. 1

3D, 2D-contour and 2D are solitary wave profile of $|q_{1,1}|$ for c=1.1

Fig. 2

3D, 2D-contour and 2D are solitary wave profile of $|q_{1,1}|$ for $c=0.09$

Fig. 3

3D, 2D-contour and 2D are solitary wave profile of $|q_{1,1}|$ for $c=-0.59$

Fig. 4

3D, 2D-contour and 2D are solitary wave profile of $|v_{1,1}|$ for $c=1.1$

Fig. 5

3D, 2D-contour and 2D are solitary wave profile of $|v_{1,1}|$ for $c=0.09$

Fig. 6

3D, 2D-contour and 2D are solitary wave profile of $|v_{1,1}|$ for $c=-0.59$

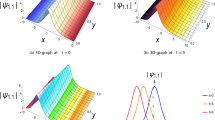
Figures 1, 2 and 3 are demonstrating the impact of c on the behaviour of solution $|q_{1,1}|$ at $h_{2}=1.2,\, m=1.12,\,\epsilon =0.9,\,\delta =0.5,\,n=1.2,\,h_{4}=0.3,\,w=1.5,\,\theta =0.5$ and $k=0.5$. The figures are presenting the dark soliton. Figures 4, 5 and 6 are demonstrating the impact of c on the behaviour of solution $|v_{1,1}|$ at $h_{2}=1.2,\, m=1.12,\,\epsilon =0.9,\,\delta =0.5,\,n=1.2,\,h_{4}=0.3,\,w=1.5,\,\theta =0.5$ and $k=0.5$. The figures are presenting the dark soliton.

Remark: It is observed that, the parameter c is controlling the propagation of dark soliton.

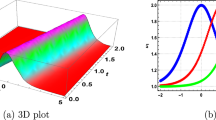
Figures 7, 8 and 9 are demonstrating the impact of c on the behaviour of solution $|q_{7,1}|$ at $h_{2}=-1.1,\, m=1.022,\,\epsilon =-1,\,\delta =1,\,n=1.2,\,h_{4}=0.4,\,w=1.5,\,\theta =0.5$ and $k=0.5$. The figures are presenting the bright stumpons and w-shaped stumpons. Figures 10, 11 and 12 are demonstrating the impact of c on the behaviour of solution $|v_{7,1}|$ at $h_{2}=-1.1,\, m=1.022,\,\epsilon =-1,\,\delta =1,\,n=1.2,\,h_{4}=0.4,\,w=1.5,\,\theta =0.5$ and $k=0.5$. The figures are presenting the bright stumpons and w-shaped stumpons.

Fig. 7

3D, 2D-contour and 2D are solitary wave profile of $|q_{7,1}|$ for $c=1.025$

Fig. 8

3D, 2D-contour and 2D are solitary wave profile of $|q_{7,1}|$ for $c=0.015$

Fig. 9

3D, 2D-contour and 2D are solitary wave profile of $|q_{7,1}|$ for $c=0.094$

Fig. 10

3D, 2D-contour and 2D are solitary wave profile of $|v_{7,1}|$ for $c=1.025$

Fig. 11

3D, 2D-contour and 2D are solitary wave profile of $|v_{7,1}|$ for $c=0.015$

Fig. 12

3D, 2D-contour and 2D are solitary wave profile of $|v_{7,1}|$ for $c=0.094$

Remark: It is observed that, the parameter c is controlling the propagation of the bright stumpons and w-shaped stumpons.

Figures 13, 14 and 15 are demonstrating the impact of c on the behaviour of solution $|q_{16,1}|$ at $h_{2}=0.9,\, m=1.022,\,\epsilon =-1,\,\delta =1,\,n=0.5,\,h_{4}=0.4,\,w=1.5,\,\theta =0.5$ and $k=0.5$. The figures are presenting the bright and w-shaped soliton behaviour. Figures 16, 17 and 18 are demonstrating the impact of c on the behaviour of solution $|v_{16,1}|$ at $h_{2}=0.9,\, m=1.022,\,\epsilon =-1,\,\delta =1,\,n=0.5,\,h_{4}=0.4,\,w=1.5,\,\theta =0.5$ and $k=0.5$. The figures are presenting the the bright and w-shaped soliton behaviour.

Fig. 13

3D, 2D-contour and 2D are solitary wave profile of $|q_{16,1}|$ for $c=0.0019$

Fig. 14

3D, 2D-contour and 2D are solitary wave profile of $|q_{16,1}|$ for c=0.0158

Fig. 15

3D, 2D-contour and 2D are solitary wave profile of $|q_{16,1}|$ for $c=0.07$

Fig. 16

3D, 2D-contour and 2D are solitary wave profile of $|v_{16,1}|$ for c=0.0019

Fig. 17

3D, 2D-contour and 2D are solitary wave profile of $|v_{16,1}|$ for c=0.0158

Fig. 18

3D, 2D-contour and 2D are solitary wave profile of $|v_{16,1}|$ for $c=0.07$

Remark: It is observed that, the parameter c is controlling the propagation of the bright and w-shaped soliton.

5 Conclusion

This study focuses on the Shynaray-IIA equation, exploring its behavior using the $\Phi ^6$-model expansion method. The study successfully obtained exact solutions for the model, which displayed interesting behaviors in different limiting cases. When the parameter $k\rightarrow 1$, the solutions converged to hyperbolic function solutions, while they approached trigonometric function solutions as $k\rightarrow 0$. The visual representations in figures illustrate the soliton solutions at different time points, which are crucial for understanding energy movement between locations. The study reveals the internal dynamics of traveling waves for different parameter values, indicating varying traveling wave behavior. The results revealed various types of solitary wave solutions, such as bright, dark, singular, and periodic solitons, providing valuable insights into the governing model’s dynamics. The research offers significant contributions to the understanding of nonlinear wave phenomena and presents an effective methodology for solving similar nonlinear models in the future.