Introduction

The idea of fractional derivatives has its roots in the well-known communication between G.A. de L’Hospital and G.W. Leibniz in the year 1695. Over the last six decades, fractional calculus (FC) has significantly influenced a wide range of disciplines, including physics, chemistry, electricity, economics, biology, signal and image processing, aerodynamics, and numerous other fields. In the past decade, fractional calculus has gained recognition as a premier tool for characterizing long-memory processes. These models hold appeal not only for engineers and physicists but also for pure mathematicians [1]. Understanding the solutions to fractional differential equations is crucial for improving our comprehension of the behaviors exhibited by physical processes with fractional orders. Furthermore, this knowledge significantly contributes to their practical application and real-world implications [2]. Ordinary differential equations (ODEs) and partial differential equations (PDEs) find application in diverse fields such as image processing [3], fluid dynamics [4], system identification, control theory, and related disciplines to elucidate intricate phenomena [5].

Fractional calculus is a field of research that broadens the scope of traditional derivatives, typically defined for integer orders, to encompass non-integer orders. This expansion leads to diverse fractional derivative formulations, including the Riemann–Liouville [6], He’s [7], Caputo [8], conformable [9], local fractional derivative [10–11], and truncated M-fractional derivatives [12]. The Riemann–Liouville fractional derivative constitutes a fundamental methodology utilizing integrals, whereas the He’s fractional derivative employs He’s polynomials to characterize fractional derivatives. On the contrary, the Caputo fractional derivative integrates integer-order derivatives with the Riemann–Liouville method, typically employed in solving initial value problems. The conformable fractional derivative, a relatively recent formulation, relies on ordinary product rules and adeptly manages functions featuring singularities. Finally, the truncated M-fractional derivative alters the Riemann–Liouville method by selectively truncating the integral component for specified fractional orders. Each of these definitions provides unique benefits and is applied in diverse domains, including physics, engineering, and signal processing, addressing scenarios where non-integer-order systems and phenomena are integral.

Soliton solutions to nonlinear events allow us to unveil the authentic structure of nonlinear behaviors. A traveling wave is a wave that progresses in a specific direction while maintaining a constant shape and velocity throughout its propagation. This phenomenon is evident in various scientific domains. Exploring traveling wave solutions is valuable for both theoretical and numerical investigations of model systems. Consequently, the pursuit of traveling wave solutions in nonlinear equations is essential for a comprehensive understanding of these equations. The examination of traveling wave solutions in fractional nonlinear partial differential equations (FNLPDEs) is significant for gaining insights into the intricate internal mechanisms of complex physical phenomena. In 1834, the first recorded observation of a soliton was made by the British experimentalist J. Scott Russell while he was riding on horseback along a narrow barge channel. Over the past two decades, optical solitons have emerged as a critical area of study within nonlinear optics, revolutionizing applications from telecommunications to optical computing. In fiber-optic communications, they are especially valued for their ability to travel long distances without distortion, ensuring data is transmitted across networks with minimal signal degradation. This capability is crucial for high-speed, long-distance communication, improving bandwidth utilization and data transmission rates significantly. Beyond telecommunications, optical solitons contribute to advancements in ultrafast laser systems and optical computing, underscoring their versatility and pivotal role in modern photonics research and technological development. Their sustained study and application highlight the ongoing importance of optical solitons in enhancing the efficiency and capability of optical systems across various fields [13,14,15,16,17,18,19,20,21,22]. These solitons are capable of transmitting signals with remarkable precision over extensive distances, paving the way for innovation and development in future communication technology. The study of optical solitons with non-Kerr law nonlinearities is an emerging area of focus in the field of nonlinear photonics [23,24,25].

The research findings present a multifaceted approach to enhancing the performance of soliton propagation, which in turn contributes to the mitigation of issues like four-wave mixing (FWM) and six-wave mixing (SWM), and offers a novel strategy for controlling Internet bottlenecks. By optimizing the inherent properties of solitons, such as phase and amplitude, and employing advanced dispersion management techniques, the propagation of solitons through fiber optic cables is significantly improved. These solitons maintain their shape and energy over extended distances, which is critical for the transmission of data across the vast networks that constitute the Internet. This optimization ensures minimal loss and distortion, essential for maintaining high-quality communication channels. In addressing the nonlinear optical phenomena of FWM and SWM, the research highlights the effectiveness of carefully adjusting system parameters, including channel spacing and the utilization of specific types of fiber (such as dispersion-shifted fibers). These adjustments are crucial for reducing the interactions that lead to FWM and SWM, phenomena that can cause signal degradation and crosstalk in densely packed wavelength-division multiplexing systems. By mitigating these effects, the research ensures clearer, more reliable signal transmission, a key component in enhancing overall network performance and reducing data loss. The implications of these findings on controlling the Internet bottleneck are significant. By enhancing soliton propagation and reducing FWM and SWM, the efficiency and reliability of data transmission are improved, addressing one of the critical challenges in network management. This improvement directly impacts the Internet’s ability to handle large volumes of data, mitigating the bottleneck effect that can lead to slow data transmission rates and increased latency [26–27]. Essentially, this research proposes a method that not only enhances the physical layer of Internet infrastructure through better soliton propagation but also offers a systemic solution to network congestion. This comprehensive approach to solving both technical and systemic issues presents a promising path forward in the ongoing effort to optimize global Internet performance.

At present, fractional nonlinear evolution equations (FNLEEs) are gaining widespread recognition. Numerous researchers have employed diverse strategies to achieve accurate soliton solutions for nonlinear physical models, with some of these approaches detailed here the exp\((-\Phi (\eta ))\)-expansion method [28], the improved modified extended tanh-expansion method [29], the modified generalized rational exponential function method [30,31,32], the Khater II method [33,34,35,36,37,38], the improved projective Riccati equations method [39], the rational extended sinh-Gordon equation expansion method [40], the generalized logistic equation technique [41], the extended simplest equation method [42], the extended Khater method [43], the generalized Khater method [44], the direct algebraic method [45], the modified Khater method [46], the extended Fan-expansion [47], the new Kudryashov method [48,49,50,51,52], the Wang’s direct mapping method-II [53], the Hirota bilinear method [54,55,56], the Bernoulli sub-equation function approach [57], the new homoclinic approach [58], the ansatz function method [59], the semi inverse method [60], the direct mapping method [61], the novel exponential ansatz method [62], the N-fold Darboux transformation technique [63], the Sine–Cosine method [64], and many more.

This paper utilizes an innovative approach based on Sardar sub-equation technique to generate numerous novel optical soliton solutions. The current approach enables researchers to generate precise optical solutions for both integer and fractional order applied differential equations. In 2023, Muhammad Amin Sadiq Murad derived the optical soliton solutions for Time-Fractional Ginzburg–Landau Equation by using the MSSEM [65]. This paper talks about finding new solutions for a particular equation related to optics, using this special approach. In 2023, Jamshad Ahmad explored chaotic patterns, bifurcation, and soliton solutions in a study analyzing the fractional Boussinesq model by using this novel approach [66]. In 2024, Waqas Ali Faridi and Zhaidary Myrzakulova [67] conducted a study comparing two improved techniques, the new extended direct algebraic method and the MSSEM to understand how optical soliton wave profiles form in the Shynaray-IIA equation. In 2024, Younes Chahlaoui studied how a soliton solution behaves, examined modulation instability, and conducted a sensitive analysis on a fractional nonlinear Schrödinger model with Kerr Law nonlinearity [68].

The exploration of the nonlinear Schrödinger equation (NLSE) across various disciplines underscores its pivotal role in nonlinear mathematical physics, illustrating its utility in deciphering the complexities of nonlinear optical fibers and Bose–Einstein condensation (BEC), among other phenomena [69]. This equation’s versatility extends its relevance to fields as diverse as fluid mechanics, plasma physics, and finance, highlighting its capacity to model wave propagation within nonlinear dispersive media [70,71,72]. While establishing a broad context for the significance of the NLSE, the discussion could be further enhanced by honing in on the specific challenges and areas of inquiry that the truncated M-fractional resonant nonlinear Schrödinger equation (RNLSE) with Kerr Law nonlinearity presents, particularly in the realm of optical soliton solutions. By centering the discussion on the unique aspects and difficulties associated with the RNLSE, and introducing the modified Sardar sub-equation method (MSSEM) as a novel investigative tool, the paper stands to offer a clearer understanding of its objectives and the anticipated contributions to the field. Highlighting how MSSEM diverges from or builds upon existing methodologies could clarify the study’s innovative edge. A focus on the exploration of optical soliton solutions within the truncated M-fractional RNLSE framework would not only clarify the research’s specific goals but also emphasize the potential broader impacts of these findings in advancing our understanding of nonlinear optical physics and its applications. Addressing the limitations of the truncated M-fractional resonant nonlinear Schrödinger equation with a Kerr law nonlinearity and suggesting possible extensions or modifications is crucial for ensuring the robustness and validity of research findings, guiding future investigations towards more accurate models, and fostering innovation in the field of nonlinear dynamics and soliton theory.

The Truncated M-Fractional Resonant Nonlinear Schrödinger Equation (RNLSE) finds practical application in modeling optical solitons within nonlinear optical fibers, crucial for optimizing data transmission in fiber-optic communication systems. Additionally, its insights into nonlinear phenomena extend to various fields like plasma physics, quantum mechanics, and fluid dynamics, contributing to advancements in diverse scientific and technological domains. The RNLSE represents a variant of the NLSE, providing an explanation for the dynamics of solitons and Madelung fluids within nonlinear systems. Various methods exist for finding optical solitons, exact solutions, and traveling wave solutions for the RNLSE. For instance, In 2021, Aly R. Seadawy explored resonant optical solitons using the extended rational sine–cosine technique within the framework of the conformable time-fractional NLSE [73]. Gulnur Yel in 2022, introduced a new wave approach, the rational sine-Gordon expansion method to the conformable resonant NLSE, incorporating Kerr-law nonlinearity [74]. In 2023, Yesim Saglam Özkan used the Adomian decomposition method to investigate the structures of exact solutions for the modified NLSE using the framework of conformable fractional derivatives [75]. And now in 2024, Dean Chou delved into probing wave dynamics within the modified fractional NLSE, offering insights with potential implications for the field of ocean engineering by using two powerful techniques named as, the Jacobi elliptic function method and unified solver method [76].

Truncated M-fractional derivative

The truncated M-fractional derivative offers a fresh perspective on understanding the dynamics of complex systems, diverging from conventional fractional calculus. Unlike its predecessors, it focuses on finite portions of a system’s evolution, effectively limiting the memory of past states. This selective memory retention enables the analysis of systems with memory effects while maintaining computational feasibility. Moreover, it allows for the isolation and examination of specific temporal segments, unveiling deeper insights into underlying physical processes. The Truncated M-fractional derivative is chosen for its tailored approach to fractional differentiation, selectively truncating the integral component for specified fractional orders, thus reducing computational complexity while maintaining numerical stability and efficiency. This makes it a practical choice for deriving soliton solutions in the nonlinear model under consideration, reflecting a balance between mathematical properties, suitability for the problem, and computational benefits.

Definition 1.1

The definition of the truncated M-fractional derivative of s with order \(\delta \in (0,1]\) can be expressed as follows

$$\begin{aligned} _\vartheta {\mathcal {D}}_{M,t}^{\gamma , \beta }s(t)&=\lim _{\varepsilon \rightarrow 0}\frac{s(_\vartheta E_{\beta }+t)(\varepsilon t^{-\gamma }))-s(t)}{\varepsilon },\quad s:(0,\infty )\nonumber \\&\rightarrow {\mathbb {R}}, \end{aligned}$$
(1)

for \(t>0, \text {and}~E_{\beta }\gamma \in (0, 1), \beta >0\) is a truncated Mittag–Leffler function of one parameter. The definition of the truncated Mittag–Leffler function with one parameter can be defined as

$$\begin{aligned} _\vartheta E_{\beta }(x)=\sum _{r=0}^\vartheta \frac{x^r}{\Gamma (\beta r+1)}. \end{aligned}$$
(2)

If \(c>0\), \(\lim _{t \rightarrow 0^+}(_i{\mathcal {D}}_{N}^{\gamma , \beta }s(t))\) and s is \(\gamma \)-differentiable in some open interval (0,c). Then we get

$$\begin{aligned} _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }s(0)=\lim _{t\rightarrow 0^+}(_\vartheta {\mathcal {D}}_{N}^{\gamma , \beta }s(t)). \end{aligned}$$
(3)

Theorem 1.1

s is continuous at \(t_0\), if \(s: (0, \infty )\rightarrow {\mathbb {R}}\) is \(\gamma \)-differentiable for \(t_0>0\), with \(\gamma \in (0, 1], \beta >0\).

Theorem 1.2

Let \(0 <\gamma \le 1, \beta > 0, a, b \in {\mathbb {R}}, s, q, \xi -\)differentiable, at a point \(t>0\). Then

$$\begin{aligned} \begin{aligned}&\bullet \,\, _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }(a s + bq)=a \, _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }(s) + b \, _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }(q),~~ a, b \in {\mathbb {R}}\\&\bullet \,\, _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }(t^\varkappa )=\varkappa t^{\varkappa - \gamma }, \varkappa \in {\mathbb {R}}\\&\bullet \,\, _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }(sq)= s\, _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }(q)+q\, _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }(s),\\&\bullet \,\, _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }(\frac{s}{q})=\frac{q \, _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }(s)-s \, _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }(q)}{q^2},\\&\bullet \,\, \text {If f is differentiable, then}~\, _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }(s)(t)=\frac{t^{1-\gamma }}{\Gamma (\beta +1)}\frac{ds}{ds},\\&\bullet \,\, _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }(soq)(t)=s' (q(t)) \, _\vartheta {\mathcal {D}}_{M}^{\gamma , \beta }q(t),\text { for} s \text {differential at} q. \end{aligned} \end{aligned}$$
(4)

Governing equation

The truncated M-fractional resonant nonlinear Schrödinger equation (RNLSE) is expressed as [77]

$$\begin{aligned}{} & {} i \, _\vartheta {\mathcal {D}}_{M,t}^{\gamma , \delta }u +\alpha _{1}\, _\vartheta {\mathcal {D}}_{M,x}^{2\gamma , \delta }u +\alpha _{2}F(\vert u \vert ^2)u \nonumber \\{} & {} \quad +\alpha _{3} \lbrace \dfrac{ \, _\vartheta {\mathcal {D}}_{M,x}^{2\gamma , \delta }\vert u \vert }{\vert u \vert }\rbrace u=0,\quad \gamma \in (0, 1],~\delta >0. \end{aligned}$$
(5)

Consider a complex function \(u = u(x, t)\) where \(x\) and \(t\) represent spatial and temporal variables respectively. The parameter \(\gamma \) belongs to the interval \((0, 1]\). In this context, \(\alpha _{1}\) denotes the coefficient related to group-velocity dispersion, \(\alpha _{3}\) signifies the coefficient associated with resonant nonlinearity, and \(\alpha _{2}\) represents the non-Kerr nonlinearity. The operator \( _\vartheta {\mathcal {D}}_{M,t}^{\gamma , \delta }\) acting on \(u(x, t)\) represents the truncated M-fractional derivative.

$$\begin{aligned}{} & {} i \, _\vartheta {\mathcal {D}}_{M,t}^{\gamma , \delta }u +\alpha _{1}\, _\vartheta {\mathcal {D}}_{M,x}^{2\gamma , \delta }u +\alpha _{2}(\vert u \vert ^2)u\nonumber \\{} & {} \quad +\alpha _{3} \left\{ \dfrac{ \, _\vartheta {\mathcal {D}}_{M,x}^{2\gamma , \delta }\vert u \vert }{\vert u \vert }\right\} u=0. \end{aligned}$$
(6)

The article’s structure is organized as follows: The introduction, discussed in Section “Introduction”, provides a brief overview. Section “Governing equation” presents the mathematical model. A summary of the MSSEM is detailed in Section “Summary of method”. Section “The truncated M-fractional resonant nonlinear Schrödinger equation” explores various structures of soliton solutions within the truncated M-fractional resonant nonlinear Schrödinger equation. The physical behavior of this equation is addressed in Section “Results and discussion”. Finally, concluding remarks are drawn in Section “Conclusion” to wrap up the article.

Summary of method

In this section, we use a modification of the Sardar sub-equation approach, designed to create a spectrum of inventive optical solutions for the truncated M-fractional resonant nonlinear Schrödinger equation. The Sardar sub-equation method is utilized due to its efficiency, accuracy, and capability in deriving soliton solutions for nonlinear models. Despite its not being new, its effectiveness in generating precise optical soliton solutions, including those for fractional differential equations, makes it a valuable tool in research. Let us consider the general fractional nonlinear partial differential equation (FNLPDE).

$$\begin{aligned}{} & {} Q\left( u,~_\vartheta {\mathcal {D}}_{M,t}^{\gamma , \delta }u,~_\vartheta {\mathcal {D}}_{M,x}^{\gamma , \delta }u_x,~ _\vartheta {\mathcal {D}}_{M,2t}^{\gamma , \delta }u,~_\vartheta {\mathcal {D}}_{M,2x}^{\gamma , \delta }u_x, \ldots \right) \nonumber \\{} & {} \quad =0,\quad \gamma \in (0, 1],\quad \delta >0, \end{aligned}$$
(7)

where Q is a polynomial in u(x, t) and its partial derivatives. Applying the subsequent fractional wave transformation

$$\begin{aligned}{} & {} u(x, t)=U(\zeta ) \exp ^{i \varrho (x, t)},\quad \zeta =\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-k t^{\gamma }\right) }{\gamma }, \nonumber \\{} & {} \varrho (x, t)=\frac{\Gamma (\beta +1) \left( \eta x^{\gamma }+\mu t^{\gamma }\right) }{\gamma }. \end{aligned}$$
(8)

By applying the transformation mentioned earlier, Eq. (7) undergoes a conversion into a nonlinear ordinary differential equation (NLODE)

$$\begin{aligned} P(u, u', u'', u''', u'''', \ldots )=0. \end{aligned}$$
(9)

The series solution of the above obtained NLODE is

$$\begin{aligned} U(\zeta )=f_0+\sum _{j=1}^{N}{f_j}{\phi ^j}(\zeta ). \end{aligned}$$
(10)

The determination of \({f_j}\), \((j=0, 1, 2, 3, \ldots , N)\), and the computation of additional constants are required. Through the equilibrium of the highest-order derivative and nonlinear variables, the integer M in Eq. (9) can be identified. The following differential equation is satisfied for \({\phi (\zeta )}\) [78,79,80]

$$\begin{aligned} (\phi '(\zeta ))^2={h_2}(\phi (\zeta ))^4+{h_1}(\phi (\zeta ))^2+{h_0}, \end{aligned}$$
(11)

where \({h_0},~{h_1}\), and \({h_2}\) are constants, then Eq. (11) has following cases.

Case-1:

If \({h_0}=0\), \({h_1}>0\) and \({h_2}\ne 0\), then

$$\begin{aligned} \phi _{1}(\zeta )=\sqrt{-\frac{h_1}{h_2}} \text {sech}\left( \sqrt{h_1} (\zeta +\kappa )\right) , \end{aligned}$$
(12)
$$\begin{aligned} \phi _{2}(\zeta )=\sqrt{-\frac{h_1}{h_2}} \text {csch}\left( \sqrt{h_1} (\zeta +\kappa )\right) . \end{aligned}$$
(13)

 Case-2:

For constants \(g_{1}\) and \(g_{2}\), let \({h_0}=0,~{h_1}>0\), and \({h_2}=+4\times g_{1}\times g_{2}\), then

$$\begin{aligned} \phi _{3}(\zeta )=\frac{4 g_1 \sqrt{h_1}}{\left( 4 g_1^2-h_2\right) \sinh \left( \sqrt{h_1} (\zeta +\kappa )\right) +\left( 4 g_1^2-h_2\right) \cosh \left( \sqrt{h_1} (\zeta +\kappa )\right) }, \end{aligned}$$
(14)

where \(g_1\) and \(g_2\) are real constants.

 Case-3:

For constants \(S_1\) and \(S_2\), let \(h_{0}=\frac{{h_1}^2}{4{h_2}}~h_{1}<0\), and \(h_{2}>0\), then

$$\begin{aligned} \phi _{4}(\zeta )= & {} \sqrt{-\frac{h_1}{2 h_2}} \tanh \left( \sqrt{-\frac{h_1}{2}} (\zeta +\kappa )\right) , \end{aligned}$$
(15)
$$\begin{aligned} \phi _{5}(\zeta )= & {} \sqrt{-\frac{h_1}{2 h_2}} \coth \left( \sqrt{-\frac{h_1}{2}} (\zeta +\kappa )\right) , \end{aligned}$$
(16)
$$\begin{aligned} \phi _{6}(\zeta )= & {} \sqrt{-\frac{h_1}{2 h_2}} \left( \tanh \left( \sqrt{-\frac{h_1}{2}} (\zeta +\kappa )\right) \right. \nonumber \\{} & {} \left. +i \text {sech}\left( \sqrt{-2 h_1} (\zeta +\kappa )\right) \right) , \end{aligned}$$
(17)
$$\begin{aligned} \phi _{7}(\zeta )= & {} \sqrt{-\frac{h_1}{8 h_2}} \left( \tanh \left( \sqrt{-\frac{h_1}{8}} (\zeta +\kappa )\right) \right. \nonumber \\{} & {} \left. +\coth \left( \sqrt{-\frac{h_1}{8}} (\zeta +\kappa )\right) \right) , \end{aligned}$$
(18)
$$\begin{aligned} \phi _{8}(\zeta )= & {} \frac{\sqrt{-\frac{h_1}{2 h_2}} \left( \sqrt{S_1^2-S_2^2}-S_1 \cosh \left( \sqrt{-2 h_1} (\zeta +\kappa )\right) \right) }{S_1 \sinh \left( \sqrt{-2 h_1} (\zeta +\kappa )\right) +S_2}, \end{aligned}$$
(19)
$$\begin{aligned} \phi _{9}(\zeta )= & {} \frac{\sqrt{-\frac{h_1}{2 h_2}} \cosh \left( \sqrt{-2 h_1} (\zeta +\kappa )\right) }{\sinh \left( \sqrt{-2 h_1} (\zeta +\kappa )\right) +i}, \end{aligned}$$
(20)

where \(S_1\) and \(S_2\) are real constants.

 Case-4:

If \(h_{0}=0,~h_{1}<0\), and \(h_{2}\ne 0\), then

$$\begin{aligned}{} & {} \phi _{10}(\zeta )=\sqrt{-\frac{h_1}{h_2}} \sec \left( \sqrt{-h_1} (\zeta +\kappa )\right) , \end{aligned}$$
(21)
$$\begin{aligned}{} & {} \phi _{11}(\zeta )=\sqrt{-\frac{h_1}{h_2}} \csc \left( \sqrt{-h_1} (\zeta +\kappa )\right) . \end{aligned}$$
(22)

 Case-5:

If \(h_{0}=\frac{h_1^2}{4{h_2}},~h_{1}>0,~h_{2}>0\), and \(S_1^2-S_2^2>0\), then

$$\begin{aligned} \phi _{12}(\zeta )= & {} \sqrt{-\frac{h_1}{2 h_2}} \tan \left( \sqrt{\frac{h_1}{2}} (\zeta +\kappa )\right) , \end{aligned}$$
(23)
$$\begin{aligned} \phi _{13}(\zeta )= & {} \sqrt{-\frac{h_1}{2 h_2}} \cot \left( \sqrt{\frac{h_1}{2}} (\zeta +\kappa )\right) , \end{aligned}$$
(24)
$$\begin{aligned} \phi _{14}(\zeta )= & {} \sqrt{-\frac{h_1}{2 h_2}} \left( \tan \left( \sqrt{2 h_1} (\zeta +\kappa )\right) \right. \nonumber \\{} & {} \left. -\sec \left( \sqrt{2 h_1} (\zeta +\kappa )\right) \right) , \end{aligned}$$
(25)
$$\begin{aligned} \phi _{15}(\zeta )= & {} \sqrt{-\frac{h_1}{8 h_2}} \left( \tan \left( \sqrt{\frac{h_1}{8}} (\zeta +\kappa )\right) \right. \nonumber \\{} & {} \left. -\cot \left( \sqrt{\frac{h_1}{8}} (\zeta +\kappa )\right) \right) , \end{aligned}$$
(26)
$$\begin{aligned} \phi _{16}(\zeta )= & {} \frac{\sqrt{-\frac{h_1}{2 h_2}} \left( \sqrt{S_1^2-S_2^2}-S_1 \cos \left( \sqrt{2 h_1} (\zeta +\kappa )\right) \right) }{S_1 \sin \left( \sqrt{2 h_1} (\zeta +\kappa )\right) +S_2}, \end{aligned}$$
(27)
$$\begin{aligned} \phi _{17}(\zeta )= & {} \frac{\sqrt{-\frac{h_1}{2 h_2}} \cos \left( \sqrt{2 h_1} (\zeta +\kappa )\right) }{\sin \left( \sqrt{2 h_1} (\zeta +\kappa )\right) -1}. \end{aligned}$$
(28)

 Case-6:

If \(h_{0}=0\) and \(h_{1}>0\), then

$$\begin{aligned}{} & {} \phi _{18}(\zeta )=\frac{4 h_1 e^{\sqrt{h_1} (\zeta +\kappa )}}{e^{2 \sqrt{h_1} (\zeta +\kappa )}-4 h_1 h_2}, \end{aligned}$$
(29)
$$\begin{aligned}{} & {} \phi _{19}(\zeta )=\frac{4 h_1 e^{\sqrt{h_1} (\zeta +\kappa )}}{1-4 h_1 h_2 e^{2 \sqrt{h_1} (\zeta +\kappa )}}. \end{aligned}$$
(30)

 Case-7:

If \(h_{0}=0,~h_{1}=0\), and \(h_{2}>0\), then

$$\begin{aligned}{} & {} \phi _{20}(\zeta )=\frac{1}{\sqrt{h_2} (\zeta +\kappa )}, \end{aligned}$$
(31)
$$\begin{aligned}{} & {} \phi _{21}(\zeta )=\frac{i}{\sqrt{h_2} (\zeta +\kappa )}. \end{aligned}$$
(32)

Upon inserting Eqs. (9) and (10) into Eq. (11), we consolidate coefficients of \(\phi (\zeta )\) with identical powers. Subsequently, by equating each coefficient to zero, an algebraic system for the equation is established. Ultimately, we solve a set of algebraic equations to determine the parameter values using Wolfram Mathematica. It offers a computationally efficient approach, reducing the time and resources required for solution generation. Additionally, the method ensures accurate results across various parameter values and system configurations, contributing to the reliability of the obtained solutions. However, like any mathematical method, it has limitations. These include potential challenges in handling extremely complex systems and the reliance on certain assumptions and initial guesses, which may affect its applicability in certain scenarios. Despite these limitations, the method remains a valuable tool for researchers, aiding in the exploration of nonlinear dynamics and advancing our understanding of complex physical phenomena. However, its effectiveness may be limited in cases where equations lack clear symmetries, possess highly nonlinear or discontinuous coefficients, or exhibit complex dynamics with non-local interactions.

The truncated M-fractional resonant nonlinear Schrödinger equation

First, we examine the truncated M-fractional resonant nonlinear Schrödinger equation (RNLSE). We employ a fractional complex transformation, converting the nonlinear fractional differential equation (NLFDE) into NLODE. Using a transformation, we separate the real and imaginary parts [81]

$$\begin{aligned}{} & {} \alpha _2 U^3+\alpha _1 \lambda ^2 U''+\alpha _3 \lambda ^2 U''-\alpha _1 \eta ^2 U-\mu U=0. \end{aligned}$$
(33)
$$\begin{aligned}{} & {} U' \left( k-2 \alpha _1 \eta \lambda \right) =0. \end{aligned}$$
(34)

Following the balancing principle, balance number 1 is obtained from Eq. (33). Subsequently, the solution to Eq. (33) assumes the following form

$$\begin{aligned} U(\zeta )=f_1 \psi (\zeta )+f_0, \end{aligned}$$
(35)

where \(f_0\) and \(f_1\) are unknowns. A system of equations, featuring unknown parameters, is constructed by transforming Eq. (34) into Eqs. (33) and (11), while setting all powers of \(\phi (\zeta )\) to zero. Computational software such as Maple or Mathematica can be utilized to handle the challenges associated with the unknown parameters in this model. These software tools facilitate the derivation of the subsequent results.

$$\begin{aligned} A_0 +A_1\phi (\zeta ) +A_2\phi (\zeta )^2 +A_3\phi (\zeta )^3 =0, \end{aligned}$$
(36)

where \(A_0=-\alpha _1 b_0 \eta ^2+\alpha _2 b_0^3-b_0 \mu \), \(A_1=\alpha _1 \left( -b_1\right) \eta ^2+3 \alpha _2 b_0^2 b_1+\alpha _1 b_1 c_1 \lambda ^2+\alpha _3 b_1 c_1 \lambda ^2-b_1 \mu \), \(A_2=3 \alpha _2 b_0 b_1^2 \), \(A_3=\alpha _2 b_1^3+2 \alpha _1 b_1 c_2 \lambda ^2+2 \alpha _3 b_1 c_2 \lambda ^2 \).

Then find the solution set for the above system of equations

$$\begin{aligned} \left\{ \alpha _2 = 0,\alpha _3 = -\alpha _1,\mu = \alpha _1 \left( -\eta ^2\right) \right\} . \end{aligned}$$
(37)

Using Eq. (37) in (35) and cases of Eqs. (12)–(5) to get the required solutions.

 Case-1:

If \({h_0}=0\), \({h_1}>0\) and \({h_2}\ne 0\), then

$$\begin{aligned}{} & {} u_{1}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( b_1 \sqrt{-\frac{h_1}{h_2}} \text {sech}\left( \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) +b_0\right) , \end{aligned}$$
(38)
$$\begin{aligned}{} & {} u_{2}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( b_1 \sqrt{-\frac{h_1}{h_2}} \text {csch}\left( \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) +b_0\right) . \end{aligned}$$
(39)

 Case-2:

For constants \(g_{1}\) and \(g_{2}\), let \({h_1}=0, {h_1}>0\) and \({h_2}=+4\times g_{1}\times g_{2}\), then

$$\begin{aligned}{} & {} u_{3}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( \frac{4 b_1 g_1 \sqrt{h_1}}{\left( 4 g_1^2-4 g_1 g_2\right) \cosh \left( \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) +\left( 4 g_1^2-4 g_1 g_2\right) \sinh \left( \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) }+b_0\right) . \end{aligned}$$
(40)

 Case-3:

For constants \(S_1\) and \(S_2\), let \(h_{0}=\frac{{h_1}^2}{4{h_2}}, h_{1}<0\) and \(h_{2}>0\), then

$$\begin{aligned}{} & {} u_{4}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( \frac{b_1 \sqrt{-\frac{h_1}{h_2}} \tanh \left( \frac{\sqrt{-h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) }{\sqrt{2}}\right) }{\sqrt{2}}+b_0\right) , \end{aligned}$$
(41)
$$\begin{aligned}{} & {} u_{5}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( \frac{b_1 \sqrt{-\frac{h_1}{h_2}} \coth \left( \frac{\sqrt{-h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) }{\sqrt{2}}\right) }{\sqrt{2}}+b_0\right) , \end{aligned}$$
(42)
$$\begin{aligned}{} & {} u_{6}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( b_0+\frac{b_1 \sqrt{-\frac{h_1}{h_2}} \left( \tanh \left( \frac{\sqrt{-h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) }{\sqrt{2}}\right) +i \text {sech}\left( \sqrt{2} \sqrt{-h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) \right) }{\sqrt{2}}\right) , \end{aligned}$$
(43)
$$\begin{aligned}{} & {} u_{7}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( \frac{b_1 \sqrt{-\frac{h_1}{h_2}} \left( \coth \left( \frac{\sqrt{-h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) }{2 \sqrt{2}}\right) +\tanh \left( \frac{\sqrt{-h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) }{2 \sqrt{2}}\right) \right) }{2 \sqrt{2}}+b_0\right) , \end{aligned}$$
(44)
$$\begin{aligned}{} & {} u_{8}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( \frac{b_1 \sqrt{-\frac{h_1}{h_2}} \left( \sqrt{S_1^2-S_2^2}-S_1 \cosh \left( \sqrt{2} \sqrt{-h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) \right) }{\sqrt{2} \left( S_1 \sinh \left( \sqrt{2} \sqrt{-h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) +S_2\right) }+b_0\right) , \end{aligned}$$
(45)
$$\begin{aligned}{} & {} u_{9}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }}\nonumber \\{} & {} \quad \left( b_0+\frac{b_1 \sqrt{-\frac{h_1}{h_2}} \cosh \left( \sqrt{2} \sqrt{-h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) }{\sqrt{2} \left( \sinh \left( \sqrt{2} \sqrt{-h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) +i\right) }\right) . \end{aligned}$$
(46)

 Case-4:

If \(h_{0}=0, h_{1}<0\) and \(h_{2}\ne 0\), then

$$\begin{aligned}{} & {} u_{10}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( b_1 \sqrt{-\frac{h_1}{h_2}} \sec \left( \sqrt{-h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) +b_0\right) , \end{aligned}$$
(47)
$$\begin{aligned}{} & {} u_{11}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( b_1 \sqrt{-\frac{h_1}{h_2}} \csc \left( \sqrt{-h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) +b_0\right) . \end{aligned}$$
(48)

 Case-5:

If \(h_{0}=\frac{h_1^2}{4{h_2}}, h_{1}>0\) and \(h_{2}>0\) and \(S_1^2-S_2^2>0\), then

$$\begin{aligned}{} & {} u_{12}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( \frac{b_1 \sqrt{-\frac{h_1}{h_2}} \tan \left( \frac{\sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) }{\sqrt{2}}\right) }{\sqrt{2}}+b_0\right) , \end{aligned}$$
(49)
$$\begin{aligned}{} & {} u_{13}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }}\nonumber \\{} & {} \quad \left( \frac{b_1 \sqrt{-\frac{h_1}{h_2}} \cot \left( \frac{\sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) }{\sqrt{2}}\right) }{\sqrt{2}}+b_0\right) , \end{aligned}$$
(50)
$$\begin{aligned}{} & {} u_{14}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( \frac{b_1 \sqrt{-\frac{h_1}{h_2}} \left( \tan \left( \sqrt{2} \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) -\sec \left( \sqrt{2} \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) \right) }{\sqrt{2}}+b_0\right) , \end{aligned}$$
(51)
$$\begin{aligned}{} & {} u_{15}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( \frac{b_1 \sqrt{-\frac{h_1}{h_2}} \left( \tan \left( \frac{\sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) }{2 \sqrt{2}}\right) -\cot \left( \frac{\sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) }{2 \sqrt{2}}\right) \right) }{2 \sqrt{2}}+b_0\right) , \end{aligned}$$
(52)
$$\begin{aligned}{} & {} u_{16}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( \frac{b_1 \sqrt{-\frac{h_1}{h_2}} \left( \sqrt{S_1^2-S_2^2}-S_1 \cos \left( \sqrt{2} \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) \right) }{\sqrt{2} \left( S_1 \sin \left( \sqrt{2} \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) +S_2\right) }+b_0\right) , \end{aligned}$$
(53)
$$\begin{aligned}{} & {} u_{17}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( \frac{b_1 \sqrt{-\frac{h_1}{h_2}} \cos \left( \sqrt{2} \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) }{\sqrt{2} \left( \sin \left( \sqrt{2} \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) -1\right) }+b_0\right) . \end{aligned}$$
(54)

 Case-6:

If \(h_{0}=0\) and \(h_{1}>0\), then

$$\begin{aligned}{} & {} u_{18}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( \frac{4 b_1 h_1 \exp \left( \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) }{\exp \left( 2 \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) -4 h_1 h_2}+b_0\right) , \end{aligned}$$
(55)
$$\begin{aligned}{} & {} u_{19}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }} \nonumber \\{} & {} \quad \left( \frac{4 b_1 h_1 \exp \left( \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) }{1-4 h_1 h_2 \exp \left( 2 \sqrt{h_1} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) \right) }+b_0\right) . \end{aligned}$$
(56)

 Case-7:

If \(h_{0}=0\), \(h_{1}=0\) and \(h_{2}>0\), then

$$\begin{aligned}{} & {} u_{20}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }}\nonumber \\{} & {} \quad \left( \frac{b_1}{\sqrt{h_2} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) }+b_0\right) , \end{aligned}$$
(57)
$$\begin{aligned}{} & {} u_{21}(x,~t)=e^{\frac{i \Gamma (\beta +1) \left( \eta x^{\gamma }-\alpha _1 \eta ^2 t^{\gamma }\right) }{\gamma }}\nonumber \\{} & {} \quad \left( b_0+\frac{i b_1}{\sqrt{h_2} \left( \kappa +\frac{\Gamma (\beta +1) \left( \lambda x^{\gamma }-2 \alpha _1 \eta \lambda t^{\gamma }\right) }{\gamma }\right) }\right) . \end{aligned}$$
(58)

Results and discussion

In this section, the distinctive originality and novelty of the present study is showcased through a comparison of the derived solutions with those from prior research. Mohammad Mirzazadeh et al. explored optical solitons within an extended-dimensional nonlinear conformable Schrödinger equation that incorporates cubic–quintic nonlinearity by applying the extended hyperbolic method and Nucci’s reduction method [82]. They obtained solutions for periodic waves, solitary waves, and rational waves for the given equation. In this study, we have derived diverse solutions, including dark, singular, periodic, and bright wave solutions, employing the MSSEM. Our findings exhibit variations from those presented in [82] when compared, yet by adjusting the values of the involved components, similar outcomes can be obtained. Unlike previous studies, the uniqueness of this research lies in its examination of the influence of model parameters on soliton behavior. Although the applied techinque is novel for the model under investigation, resulting in the creation of several solitons, the primary emphasis of this study is on understanding how model parameters impact the actions of solitons.

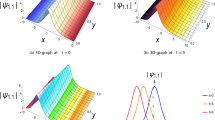
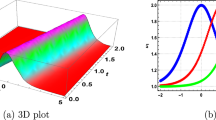
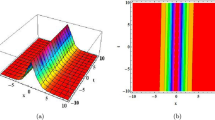
The sequence of figures, referenced from Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 and 17, meticulously portrays a diverse range of soliton solutions through 3D, 2D, contour, and density plots, each corresponding to unique equations from Eqs. (38) to (58). These visual representations encapsulate a broad spectrum of soliton phenomena: Fig. (1) illustrates the bright soliton emerging from Eq. (38), showcasing a localized wave structure. In contrast, Fig. 2 presents the singular periodic soliton arising from Eq. (39), characterized by abrupt and distinctive bends within the wave pattern. Figure 3 showcases hyperbolic soliton solutions sourced from Eq. (40), featuring localized regions of decreased amplitude within the wave solutions. Figure 4 exhibits dark soliton solutions sourced from Eq. (41), exhibiting stable waveforms preserving their shape during propagation. Furthermore, Fig. 5 illustrates the periodic dark soliton solution derived from Eq. (42), displaying localized regions of increasing amplitude within the wave. Figure 6 exhibits the combo dark–bright soliton solution from Eq. (43), featuring localized regions of increased amplitude within the wave solutions. Additionally, Fig. 7 showcases the compactons soliton derived from Eq. (44), maintaining a localized form without dispersing during propagation. Figures 8 and 9 portray hyperbolic soliton solutions originating from Eqs. (45) and (46), respectively, showcasing periodic behavior while preserving localized shapes. Moving forward, Fig. 10 represents another kink soliton solution derived from Eq. (49). Similarly, Figs. 11 and 12 demonstrate the periodic soliton derived from Eqs. (51) and (52). Furthermore, Fig. 13 portrays the peakon kink soliton obtained from Eq. (54), featuring abrupt changes or bends within the wave. Figures 14 and 15 showcase another compacton soliton from Eq. (55) and another singular kink soliton from Eq. (56), displaying peaked structures and abrupt changes within their waveforms, respectively. Finally, Fig. 16 illustrates a bright soliton solution derived from Eq. (57), displaying a stable, peaked waveform, while Fig. 17 represents the bright peakon soliton derived from Eq. (58), featuring localized regions of decreased amplitude within the wave solutions. These diverse soliton solutions span various scientific fields, including signal processing, nonlinear optics, fluid dynamics, atomic physics, plasma studies, and biological wave phenomena, providing critical insights into wave behavior across different contexts and systems.

Fig. 1
figure 1

The graphics of \(u_{1}(x,~t)\) in Eq. (38) at \(\beta =1.5\), \(\gamma =0.2\), \(\eta =0.1\), \(b_{0}=2.5\), \(b_{1}=1.7\), \(c_{0}=1.5\), \(\alpha _{1} =2.5\), \(\alpha _{3}=2.8\), \(h_{1}=1.3\), \(h_{2}=0.6\), \(\kappa =2.8\), and \(\lambda =0.6\)

Full size image
Fig. 2
figure 2

The graphics of \(u_{2}(x,~t)\) in Eq. (39) at \(\beta =2.6\), \(\gamma =0.99\), \(\eta =2.1\), \(b_{0}=0.45\), \(b_{1}=1.7\), \(c_{0}=1.4\), \(\alpha _{1} =0.5\), \(\alpha _{3}=0.6\), \(h_{1}=0.3\), \(h_{2}=0.45\), \(\kappa =2.6\), and \(\lambda =1.2.\)

Full size image
Fig. 3
figure 3

The graphics of \(u_{3}(x,~t)\) in Eq. (40) at \(\beta =2.1\), \(\gamma =0.99\), \(\eta =1.9\), \(b_{0}=0.8\), \(b_{1}=0.57\), \(c_{0}=1.5\), \(\alpha _{1} =1.5\), \(\alpha _{3}=0.7\), \(h_{0}=0\), \(h_{1}=0.66\), \(h_{2}=0.96\), \(\kappa =1.5\), \(\lambda =0.5\), \(g_1=0.4\) and \(g_2=0.6\)

Full size image
Fig. 4
figure 4

The graphics of \(u_{4}(x,~t)\) in Eq. (41) at \(\beta =1.3\), \(\gamma =0.99\), \(\eta =1.9\), \(b_{0}=1.4\), \(b_{1}=1.5\), \(c_{0}=0.7\), \(\alpha _{1} =0.5\), \(\alpha _{3}=1.7\), \(h_{0}=0.88\), \(h_{1}=-1.4\), \(h_{2}=1.8\), \(\kappa =0.76\), and \(\lambda =0.35\)

Full size image
Fig. 5
figure 5

The graphics of \(u_{5}(x,~t)\) in Eq. (42) at \(\beta =2.1\), \(\gamma =0.99\), \(\eta =2.1\), \(b_{0}=1.4\), \(b_{1}=1.5\), \(c_{0}=1.7\), \(\alpha _{1}=1.5\), \(\alpha _{3} =1.6\), \(h_{0}=0.13\), \(h_{1}=-0.9\), \(h_{2}=0.68\), \(\kappa =0.67\), and \(\lambda =0.9\)

Full size image
Fig. 6
figure 6

The graphics of \(u_{6}(x,~t)\) in Eq. (43) at \(\beta =1.9\), \(\gamma =0.99\), \(\eta =1.8\), \(b_{0}=1.8\), \(b_{1}=1.2\), \(c_{0}=2.7\), \(\alpha _{1}=1.5\), \(\alpha _{3} =2.6\), \(h_{0}=1.62\), \(h_{1}=-0.9\), \(h_{2}=1.8\), \(\kappa =1.8\), and \(\lambda =0.9\)

Full size image
Fig. 7
figure 7

The graphics of \(u_{7}(x,~t)\) in Eq. (44) at \(\beta =0.9\), \(\gamma =0.99\), \(\eta =0.5\), \(b_{0}=0.9\), \(b_{1}=0.6\), \(b_{2}=0.5\), \(c_{0}=0.8\), \(\alpha _{1} =0.66\), \(\alpha _{3}=0.8\), \(h_{0}=0.06\), \(h_{1}=-0.3\), \(h_{2}=2.8\), \(\kappa =3.3\), and \(\lambda =0.8\)

Full size image
Fig. 8
figure 8

The graphics of \(u_{8}(x,~t)\) in Eq. (45) at \(\beta =2.9\), \(\gamma =0.78\), \(\eta =2.4\), \(b_{0}=2.6\), \(b_{1}=3.1\), \(c_{0}=2.4\), \(\alpha _{1} =0.6\), \(\alpha _{3}=1.1\), \(h_{0}=0.22\), \(h_{1}=-0.8\), \(h_{2}=1.4\), \(\kappa =1.5\), \(\lambda =0.5\), \(S_1=1.2\), and \(S_2=1.1\)

Full size image
Fig. 9
figure 9

The graphics of \(u_{9}(x,~t)\) in Eq. (46) at \(\beta =1.1\), \(\gamma =0.99\), \(\eta =1.9\), \(b_{0}=0.55\), \(b_{1}=1.3\), \(b_{2}=1.5\), \(c_{0}=0.2\), \(\alpha _{1} =0.6\), \(\alpha _{3}=0.77\), \(h_{0}=0.72\), \(h_{1}=-1.8\), \(h_{2}=0.9\), \(\kappa =0.66\), and \(\lambda =0.8\)

Full size image
Fig. 10
figure 10

The graphics of \(u_{12}(x,~t)\) in Eq. (49) at \(\beta =1.5\), \(\gamma =0.99\), \(\eta =1.3\), \(b_{0}=0.8\), \(b_{1}=1.1\), \(c_{0}=0.77\), \(\alpha _{1}=1.5\), \(\alpha _{3} =2.5\), \(h_{0}=0.05\), \(h_{1}=0.5\), \(h_{2}=0.8\), \(\kappa =0.6\), and \(\lambda =0.6\)

Full size image
Fig. 11
figure 11

The graphics of \(u_{14}(x,~t)\) in Eq. (51) at \(\beta =2.1\), \(\gamma =0.96\), \(\eta =0.6\), \(b_{0}=0.9\), \(b_{1}=0.6\), \(b_{2}=0.7\), \(c_{0}=0.8\), \(\alpha _{1} =0.5\), \(\alpha _{3}=0.8\), \(h_{0}=0.018\), \(h_{1}=0.2\), \(h_{2}=1.8\), \(\kappa =2.3\), and \(\lambda =0.3\)

Full size image
Fig. 12
figure 12

The graphics of \(u_{15}(x,~t)\) in Eq. (52) at \(\beta =1.4\), \(\gamma =0.92\), \(\eta =1.7\), \(b_{0}=0.9\), \(b_{1}=0.6\), \(c_{0}=3.8\), \(\alpha _{1}=1.5\), \(\alpha _{3}=0.8\), \(h_{0}=0.018\), \(h_{1}=0.5\), \(h_{2}=1.8\), \(\kappa =1.3\), and \(\lambda =0.9\)

Full size image
Fig. 13
figure 13

The graphics of \(u_{17}(x,~t)\) in Eq. (54) at \(\beta =0.9\), \(\gamma =0.99\), \(\eta =0.5\), \(b_{0}=0.1\), \(b_{1}=0.3\), \(c_{0}=0.1\), \(\alpha _{1}=0.1\), \(\alpha _{3}=0.2\), \(h_{0}=1.62\), \(h_{1}=0.92\), \(h_{2}=0.2\), \(\kappa =0.5\), and \(\lambda =0.9\)

Full size image
Fig. 14
figure 14

The graphics of \(u_{18}(x,~t)\) in Eq. (55) at \(\beta =1.9\), \(\gamma =0.99\), \(\eta =1.6\), \(b_{0}=1.2\), \(b_{1}=0.3\), \(c_{0}=0.5\), \(\alpha _{1}=1.4\), \(\alpha _{3}=2.2\), \(h_{0}=0\), \(h_{1}=1.56\), \(h_{2}=0.78\), \(\kappa =1.8\), and \(\lambda =1.9\)

Full size image
Fig. 15
figure 15

The graphics of \(u_{19}(x,~t)\) in Eq. (56) at \(\beta =0.9\), \(\gamma =0.98\), \(\eta =0.2\), \(b_{0}=1.6\), \(b_{1}=0.89\), \(c_{0}=1.5\), \(\alpha _{1}=0.7\), \(\alpha _{3}=3.5\), \(h_{0}=1.62\), \(h_{1}=0.88\), \(h_{2}=0.4\), \(\kappa =0.4\), and \(\lambda =0.2\)

Full size image
Fig. 16
figure 16

The graphics of \(u_{20}(x,~t)\) in Eq. (57) at \(\beta =0.4\), \(\gamma =0.7\), \(\eta =0.3\), \(b_{0}=0.1\), \(b_{1}=0.2\), \(b_{2}=0.1\), \(c_{0}=0.8\), \(\alpha _{1}=0.5\), \(\alpha _{3}=0.8\), \(h_{0}=0\), \(h_{1}=0\), \(h_{2}=0.8\), \(\kappa =0.9\), and \(\lambda =0.1\)

Full size image
Fig. 17
figure 17

The graphics of \(u_{21}(x,~t)\) in Eq. (58) at \(\beta =0.9\), \(\gamma =0.99\), \(\eta =0.2\), \(b_{0}=0.1\), \(b_{1}=0.3\), \(c_{0}=0.1\), \(\alpha _{1}=0.1\), \(\alpha _{3}=0.2\), \(h_{0}=0\), \(h_{1}=0\), \(h_{2}=0.2\), \(\kappa =0.5\), and \(\lambda =1.9\)

Full size image

The solutions presented in this study hold physical significance. For example, a dark soliton, characterized by an intensity lower than the background, emerges distinctively from a conventional pulse. Instead, it primarily lacks energy within a continuous-time beam. Additional varieties of solitary waves, known as singular solitons, exhibit singularities often characterized by infinite discontinuities. When the center of the solitary wave is positioned imaginarily, these singular solitons may be associated with solitary waves. This solution category incorporates spikes, making it a potential descriptor for the formation of rogue waves. Examples of such solitary waves encompass compactions, characterized by finite (compact) support, and peakons, distinguished by peaks with a discontinuous first derivative. A bright soliton refers to solitary waves with a peak intensity surpassing that of the background. Bright solitons play a crucial role in signal transmission due to their localized nature [83]. Applications of bright solitons extend to plasma studies, while compactons are utilized in modeling localized waves. Bright solitons provide insights into fluid dynamics, and singular dark solitons find relevance in atomic physics. Periodic soliton solution is characterized by a recurring and continuous pattern, determining both its wavelength and frequency. The period is defined as the time needed to complete one cycle of the waveform, while frequency represents the number of cycles per second. These solitons facilitate periodic signal transmission in wave guides and optical fibers. Kink waves either ascend or descend from one asymptotic state to another, reaching a constant value at infinity, while singular kink solitons contribute to nonlinear optics and signal processing. The application of combo dark–bright solitons extends to various fields such as optical communications and nonlinear optics for manipulating lightwave properties. Compactons, being solitons, possess a confined spatial support, limited to a finite core. These solitons lack an exponential tail and have a finite wavelength. Moreover, they possess resilient soliton-like solutions. Combo dark–bright and singular combo dark–bright solitons enhance our understanding of complex wave behaviors, especially in biological systems. Singular kink solitons are valuable for identifying abrupt waveform changes in various physical systems. Bright peakon solitons and bright solitons are employed in nonlinear optics and photonics for their stable waveform characteristics. Bright peakons find application in oceanography for understanding localized amplitude reductions in water wave dynamics. Collectively, these soliton solutions contribute to insights and manipulations across scientific disciplines, covering a broad spectrum of wave phenomena with distinct characteristics. Periodic solitons maintain their form and speed over time, while dark and bright solitons represent specific areas of heightened or decreased intensity. Peakons are characterized by sharp peaks traveling at steady speeds, and kink waves reach a constant value at infinity by rising or falling from one asymptotic state to another. Compactons, limited to a finite core, are solitons due to their compact spatial support.

Conclusion

In this paper, the MSSEM recognized as a robust method for solving nonlinear evolution equations (NLEEs), is employed for the truncated M-fractional resonant nonlinear Schrödinger equation (RNLSE). By applying this technique, we identified solutions in various forms, including dark, bright, periodic, combo dark bright, peakons, kink, and compactons soliton solutions. It’s important to emphasize that Mathematica is a widely acknowledged and extensively validated software tool employed across diverse scientific and mathematical domains. Although no software is completely immune to errors, Mathematica has undergone thorough testing and validation procedures to mitigate such risks. Additionally, we utilized the most recent version of Mathematica to leverage any updates or enhancements in its algorithms. Utilizing this software, we have generated 3D, 2D, contour, and density plots for these solutions. The solutions obtained in this research align strongly with the original equation, underscoring their reliability. The methodologies introduced here demonstrate impressive adaptability, capable of addressing a wide range of NLPDEs. Notably unprecedented, the outcomes presented in this paper establish the developed method as a dependable and effective approach for exact solutions in NLPDEs. Our future work aims to explore further into dynamic NLPDE analysis, using the modified Sardar sub-equation method to examine the fractional-stochastic quantum Zakharov–Kuznetsov equation under additive or color multiplicative noise conditions. Additionally, our proposed method holds potential for solving systems like the Drinfel’d–Sokolov–Wilson system and other integrable NLPDEs, fostering advancements in these intricate domains through ongoing research efforts.

Optical solitons have emerged as indispensable tools in modern telecommunications, offering a unique solution to the challenges of long-distance data transmission. These self-reinforcing solitary wave packets, governed by a delicate balance of nonlinear and dispersive effects, have transformed the landscape of fiber optic communication. By maintaining their shape and speed over vast distances, solitons effectively mitigate the detrimental effects of dispersion, ensuring that data signals remain intact and coherent. This breakthrough technology has enabled the development of high-speed internet connections and global communication networks that can reliably transmit massive amounts of data over thousands of kilometers without significant degradation. Despite their remarkable utility, the deployment of optical solitons is not without its complexities and limitations. Managing soliton dynamics, including interactions between solitons and dispersive waves, requires precise control over various parameters within the optical medium. Moreover, the interaction of solitons with other signals in densely populated fiber optic networks poses challenges in maintaining signal integrity and minimizing interference. However, ongoing research and technological advancements continue to address these challenges, driving innovation in soliton-based communication systems and paving the way for even faster, more efficient, and reliable data transmission in the future [84,85,86,87,88,89,90,91,92,93,94,95,96,97].

The implications of these findings span various fields including optical fibers, plasma physics, nuclear physics, mathematical biosciences, and beyond. For instance, the derived soliton solutions may drive the innovation of novel devices like all-optical switches and amplifiers, enhancing the efficiency and reliability of fiber optic communication networks. Furthermore, in plasma physics, these solutions hold promise for unraveling intricate plasma phenomena, potentially advancing the development of fusion reactors and other plasma-based technologies. Moreover, insights gleaned from these soliton solutions could reshape models of biological systems within mathematical biosciences, offering fresh perspectives on phenomena such as neuronal signaling and protein dynamics [98].