1 Introduction

The nonlinear partial differential equation is one of the significant tools to examine the features of nonlinear physical phenomenons rigorously. The Schrödinger type governing equation is a remarkable mechanism to interpret the complex physical nonlinear model more accurately and has vital applications in the fields of plasma, fiber-optic, mathematical physics, telecommunication engineering, and optics. The extraction of analytical exact solutions for the Schrodinger equations is a glaring research area because exact solutions have a consequential role to express the physical aspects of non-linear systems in applied mathematics Gao et al. (2020a, 2020b); Ali et al. (2020).

There are so many schemes and approaches have been established to secure analytical exact solutions for non-linear partial differential equations like as, Kudryashov method Zafar et al. (2022); Srivastava et al. (2020), sine-Gordon expansion scheme Fahim et al. (2021); Abdul Kayum et al. (2020), bilinear neural network technique Zhang et al. (2021); Zhang and Bilige (2019), extended simple equation method Khater et al. (2021), F-expansion method Karaman (2021); Yildirim (2021), unified auxiliary equation method Zayed and Shohib (2019); Zayed et al. (2021), \(\frac{G'}{G}-\)expansion approach Ismael et al. (2020), Hirota bilinear method Abdulkadir Sulaiman and Yusuf (2021), the generalized exponential function method Khodadad et al. (2021), and many others Ghanbari et al. (2021); Lü (2005); Baskonus et al. (2018); Rehman et al. (2020); Zhang et al. (2021).

Ghanbari et al. (2019) have discussed the fractional obliquely propagating wave solutions extended Zakharov–Kuznetsov by via the generalized exponential rational function method. The optical solitons solutions have been established for the temporal evolution model, Fokas-Lenells equation, and nonlinear Schrödinger equations by using the Liu’s extended trial function scheme, generalized exponential function method, and sine-Gordon expansion algorithm Rezazadeh et al. (2018); Osman and Ghanbari (2018); Ali et al. (2020). Osman has investigated the inelastic collision phenomenon of the Sawada–Kotera equation with the aid of a generalized unified approach Osman (2019). Aktar et al. (2022) have applied a simple equation method to predator-prey systems and secured the analytical solutions. Adel et al. (2022) have studied the time-fractional Burger-Fisher and the space-time regularized long-wave equations and applied the extended tanh-function method to get exact solutions. Ali et al. (2022) have acquired one lump solution, one-, and two-soliton solution, exploding and periodic wave solutions, localized and breather wave solutions, multi-lump wave solutions, and interaction of lump waves with solitary waves through the symbolic computational method. Tarla et al. (2022) have investigated the Radhakrishnan-Kundu-Lakshmanan equation with Jacobi elliptic function in sort of solitons. Ismael et al. (2022) have presented the traveling wave solutions of the Yu–Toda–Sasa–Fukuyama equation. Kumar et al. (2022) have developed the Lie algebra analysis, closed-form solutions, and numerous soliton solutions for Kadomtsev–Petviashvili equation.

The oscillations section of the differential equations is a glowing avenue of research in the current decade. The remarkable inventions and results have generated and researchers made significant contributions in this field like oscillations of delay differential equations, even-order and 4th order differential equations with different properties, etc Moaaz et al. (2020); Bazighifan (2020); Bazighifan et al. (2021a); Bazighifan and Kuman (2020); Bazighifan et al. (2021b); Santra et al. (2020). The soliton and wave theory have tedious applications in the different fields of science. The exact analytical solutions are getting sound attention from researchers due to their wide applications in the physical phenomenon. Extensive work has been done in the field of soliton theory and researchers have discussed numerous remarkable partial differential equations and governing systems and established traveling wave solutions Akinyemi et al. (2022); Khodadad et al. (2021); Khater et al. (2021); Inan et al. (2022); Raheel et al. (2022); Zafar et al. (2022).

The Chirp free bright optical solitons and Chirped optical solitons have been investigated by prosecuting the semi inverse technique and extended trial equation method for Chen-Lee-Liu model by Biswas (2018); Biswas et al. (2018). Kudryashov Kudryashov (2019), analyzed the Chen-Lee-Liu equation with perturbation effect and established a general traveling wave solution by the Weierstrass function method. Yildirim et al. (2020), has applied the Riccati equation method on the perturbed Chen-Lee-Liu model and explored solitary wave patterns. Esen et al. (2021), developed some new analytical solutions via Sardar sub-equation method for Chen-Lee-Liu governing model. Recently in (2022), Tarla et al. (2022) employed Jacobi elliptic function technique to the perturbed Chen-Lee-Liu model and obtained twelve solutions that cover trigonometric, hyperbolic trigonometric, exponential, periodic, singular, and dark-bright soliton solution. It means that numerous solitons type solutions are still a mystery and gap in the literature. The second thing is that there is not any condition discussed for the existence of obtained solutions. To fulfill this gap, a generalized approach \(\Phi ^{6}-\)model expansion method is utilized that provides the more generalized and new solitary waves with more than twenty-eight analytical solutions and demonstrates the constraint condition corresponding to each solution for their existence. The \(\Phi ^{6}-\)model expansion method is the generalization of the Jacobi elliptic function method.

1.1 Governing model

We consider the Chen-Lee-Liu (CLL) governing equation with perturbation effect Tarla et al. (2022),

$$\begin{aligned} i\mathcal {H}_{t}+\alpha \mathcal {H}_{xx}+i\beta |\mathcal {H}|^{2}\mathcal {H}_{x}=i\bigg [\gamma \mathcal {H}_{x}+\mu \left( |\mathcal {H}|^{2n}\mathcal {H}\right) _{x}+\delta \left( |\mathcal {H}|^{2n}\right) _{x}\mathcal {H}\bigg ], \end{aligned}$$
(1)

where, \(\mathcal {H}\) is a function for profile of optical soliton, \(\gamma\) symbolize coefficient of the inter model dispersion, \(\delta\) and \(\mu\) are the coefficient of non-linear dispersion and self-steeping for short pulses, respectively. \(\alpha\) is the coefficient of group velocity dispersion and \(\beta\) is the coefficient of the non-linearity. In above Eq. (1) n stipulates the density of the complex wave function. The (CLL) model describes the dynamics of solitary waves in optical fiber and also has applications in optical couplers, optoelectronic devices, solitons cooling, and meta-material Tarla et al. (2022). The Chen-Lee-Liu Eq. (1) becomes,

$$\begin{aligned} i\mathcal {H}_{t}+\alpha \mathcal {H}_{xx}+i\beta |\mathcal {H}|^{2}\mathcal {H}_{x}=i\bigg [\gamma \mathcal {H}_{x}+\mu \left( |\mathcal {H}|^{2}\mathcal {H}\right) _{x}+\delta \left( |\mathcal {H}|^{2}\right) _{x}\mathcal {H}\bigg ]. \end{aligned}$$
(2)

at \(n=1\). We develop a variety of solitons with the aid of \(\Phi ^{6}-\)model expansion method to perturbed (CLL) equation.

This work is organized as, Sect. 1 is presenting introduction, description of the scheme and application is given in Sects. 2, and 3 is devoted for graphical presentation and at last, Sect. 4 is giving concluding remarks.

2 Analytical solutions

2.1 The \(\Phi ^{6}-\)model expansion method

In this section, we will propose the procedure of the scheme as follow Bibi (2021).

Let a non-linear partial differential equation:

$$\begin{aligned} \mathcal {P}(\mathcal {H} ,\mathcal {H}_{t},\mathcal {H}_{x},\mathcal {H}_{tt},\mathcal {H}_{xx},...) = 0, \end{aligned}$$
(3)

where the polynomial function \(\mathcal {P}\) contains \(\mathcal {H}(x,t)\) and it’s partial derivatives.

It can be transformed into ordinary differential equation:

$$\begin{aligned} \mathcal {Q}(\Upsilon ,\Upsilon ',\Upsilon '',...) = 0. \end{aligned}$$
(4)

By applying the below given transformation Bibi (2021):

$$\begin{aligned} \mathcal {H}(x,t)=\Upsilon (\mho )e^{\iota \theta }, \end{aligned}$$
(5)

where, \(\mho =k_{1}x+k_{2}t,~~\theta =k_{3}x+k_{4}t\), \(k_{1},k_{2},k_{3},\) and \(k_{4}\) are the constant, which can be labelled according to phenomenon like frequency, amplitude, and wave number, etc. Assume the solution of Eq. (4) is in the form:

$$\begin{aligned} \Upsilon (\mho )=\sum _{m=0}^{2j} \bigg [a_{m}\mathcal {R}^{m}(\mho )\bigg ], \end{aligned}$$
(6)

where \(a_{m},~0\le m \le 2j\) are constants to be determined later and j is homogeneous balancing constant of the non-linear ordinary differential equation. The function \(\mathcal {R}(\mho )\) satisfies the given below auxiliary non-linear ordinary partial differential equations,

$$\begin{aligned} \begin{aligned} \mathcal {R}'^{2}(\mho )=h_{0}+h_{2}\mathcal {R}^{2}(\mho )+h_{4}\mathcal {R}^{4}(\mho )+h_{6}\mathcal {R}^{6}(\mho ),\\ \mathcal {R}''(\mho )=h_{2}\mathcal {R}(\mho )+2h_{4}\mathcal {R}^{3}(\mho )+3h_{6}\mathcal {R}^{5}(\mho ). \end{aligned} \end{aligned}$$
(7)

The Eq. (7) has the following solutions,

$$\begin{aligned} \mathcal {R}(\mho )=\frac{\Phi (\mho )}{\sqrt{f\Phi ^{2}(\mho )+g}}, \end{aligned}$$
(8)

where \(f\Phi ^{2}(\mho )+g>0\) and \(\Phi (\mho )\) is the solution of Jacobi elliptic equation,

$$\begin{aligned} \Phi '^{2}(\mho )=l_{0}+l_{2}\Phi ^{2}(\mho )+l_{4}\Phi ^{4}(\mho ), \end{aligned}$$
(9)

where \(l_{0},~l_{},\) and \(l_{4}\) are constants to be determined, while f and g are the given as,

$$\begin{aligned} f=\frac{h_{4}(l_{2}-h_{2})}{3l_{0}l_{4}+(h^{2}_{2}-l^{2}_{2})},~~ g=\frac{3h_{4}l_{0}}{3l_{0}l_{4}+(h^{2}_{2}-l^{2}_{2})}, \end{aligned}$$
(10)

under the constraint,

$$\begin{aligned} h^{2}_{4}(l_{2}-h_{2})[9l_{0}l_{4}-(l_{2}-h_{2})(2l_{2}+h_{2})]+3h_{6}[-l^{2}_{2}+h^{2}_{2}+3l_{0}l_{4}]^{2}=0. \end{aligned}$$

2.2 Application to the Eq. (3)

In order to find solutions of the Eq. (2), we develop a traveling wave transformation:

$$\begin{aligned} \mathcal {H}(x,t)=\Upsilon (\mho )e^{i\theta },~~\text {where},~\mho =x-\lambda t,~~\theta (x,t)=(-\kappa x+\omega t+\eta ). \end{aligned}$$
(11)

The traveling wave transformation (11) is prosecuting on the Eq. (2) and get an ordinary differential equation.

$$\begin{gathered} i\lambda \Upsilon ^{\prime} - \omega \Upsilon + \alpha \Upsilon ^{\prime\prime} - 2i\kappa \alpha \Upsilon ^{\prime} - \kappa ^{2} \alpha \Upsilon + i\beta \Upsilon ^{\prime}\Upsilon ^{2} \hfill \\ + ~\kappa \beta \Upsilon ^{3} - i\gamma \Upsilon ^{\prime} - \kappa \gamma \Upsilon - 3i\mu \Upsilon ^{\prime}\Upsilon ^{2} - \kappa \mu \Upsilon ^{3} - 2i\delta \Upsilon ^{\prime}\Upsilon ^{2} = 0. \hfill \\ \end{gathered}$$
(12)

Now, one can get real and imaginary parts of the obtained ordinary differential Eq. (12) respectively.

$$\begin{aligned}&\kappa (\beta -\mu )\Upsilon ^{3}+\alpha \Upsilon ''-(\omega +\alpha \kappa ^{2}+\gamma \kappa )\Upsilon =0. \end{aligned}$$
(13)
$$\begin{aligned}&(\beta -3\mu -2\delta )\Upsilon '\Upsilon ^{2}-(\lambda +2\alpha \kappa +\gamma )\Upsilon '=0. \end{aligned}$$
(14)

We get \(\beta =3\mu +2\delta\) and \(\lambda =-(\gamma +2\alpha \kappa )\) by setting the components of imaginary part equal to zero. Under the above mentioned two constraints, the real part (13) becomes,

$$\begin{aligned} 2\kappa (\delta +\mu )\Upsilon ^{3}+\alpha \Upsilon ''-(\omega +\alpha \kappa ^{2}+\gamma \kappa )\Upsilon =0. \end{aligned}$$
(15)

The homogeneous balancing principle yields \(j=1\) for Eq. (15). Therefore, the solution (21) for the Eq. (15) can be expressed as,

$$\begin{aligned} \Upsilon (\mho )=a_{0}+a_{1}\mathcal {R}(\mho )+a_{2}\mathcal {R}^{2}(\mho ), \end{aligned}$$
(16)

where,

$$\begin{aligned} \begin{aligned} \mathcal {R}'^{2}(\mho )=h_{0}+h_{2}\mathcal {R}^{2}(\mho )+h_{4}\mathcal {R}^{4}(\mho )+h_{6}\mathcal {R}^{6}(\mho ),\\ \mathcal {R}''(\mho )=h_{2}\mathcal {R}(\mho )+2h_{4}\mathcal {R}^{3}(\mho )+3h_{6}\mathcal {R}^{5}(\mho ). \end{aligned} \end{aligned}$$
(17)

The Eq. (16) is placing along with (17) into Eq. (15) and get a system of algebraic equations by separating the distinct powers of \({\mathcal {R}}\).

$$\begin{aligned} \begin{aligned}&\mathcal {R}^{0}:3\delta \kappa a^{3}_{0}+2\kappa \mu a^{3}_{0}-\alpha \kappa ^{2}a_{0}+2\alpha a_{2}h_{0}-\gamma \kappa a_{0}-\omega a_{0}=0,\\&\mathcal {R}^1:6\delta \kappa a^{2}_{0}a_{1}+6\mu \kappa a^{2}_{0}a_{1}-\alpha \kappa ^{2}a_{1}+\alpha a_{1}h_{2}-\gamma \kappa a_{1}-\omega a_{1}=0,\\&\mathcal {R}^2:=6\delta \kappa a^{2}_{0}a_{2}+6\delta \kappa a_{0}a^{2}_{1}+6\kappa \mu a^{2}_{0}a_{2}+6\kappa \mu a_{0}a^{2}_{1}-\alpha \kappa ^{2} a_{2}+4\alpha a_{2}h_{2}-\gamma \kappa a_{2}-\omega a_{2}=0,\\&\mathcal {R}^3:12\delta \kappa a_{0}a_{1}a_{2}+2\delta \kappa a^{3}_{1}+12\kappa \mu a_{0}a_{1}a_{2}+2\kappa \mu a^{2}_{1}+2\alpha a_{1}h_{4}=0,\\&\mathcal {R}^4:6\delta \kappa a_{0}a^{2}_{2}+6\delta \kappa a^{2}_{1}a_{2}+6\kappa \mu a_{0}a^{2}_{2}+6\kappa \mu a^{2}_{1}a_{2}+6\alpha a_{2}h_{4}=0,\\&\mathcal {R}^5:6\delta \kappa a_{1}a^{2}_{2}+6\kappa \mu a_{1}a^{2}_{2}+3\alpha a_{1} h_{6}=0,\\&\mathcal {R}^6:2\delta \kappa a^{3}_{2}+2\kappa \mu a^{3}_{2}+8\alpha a_{2}h_{6}=0. \end{aligned} \end{aligned}$$
(18)

The Maple Software is utilized to solve the system (18) and get a set of solutions,

$$\begin{aligned} \bigg [a_{0}=\pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}},~a_{1}=0,~a_{2}=\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}},\end{aligned}$$
(19)
$$\begin{aligned} ~h_{0}=-\frac{(\alpha \kappa ^{2}+2\alpha h_{2}+\gamma \kappa +\omega )\Lambda }{18\alpha ^{2}h_{4}},~h_{6}=-\frac{3\alpha h^{2}_{4}}{2\Lambda }\bigg ]. \end{aligned}$$
(20)

After substituting (20) into (16), we get,

$$\begin{aligned} \mathcal {H}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\mathcal {R}^2(x-\lambda t)\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(21)

where \(\Lambda =\alpha \kappa ^{2}-4\alpha h_{2}+\gamma \kappa +\omega\). We acquire the exact solutions of (2) by taking Eq. (21) along with (8) and Jacobi elliptic functions from Table (1).

Table 1 Limiting cases for functions
Full size table

Result 1 if \(l_{0}=1,~l_{2}=-1-n^{2},~l_{4}=n^{2}, ~0<n<1,\) then \(\Phi (\mho )=sn(\mho ,n)\) or \(\Phi (\mho )=cd(\mho ,n)\), thus we have,

$$\begin{aligned} \mathcal {H}_{1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {sn}^{2}(\mho ,n)}{{f \text {sn}^{2}(\mho ,n)+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(22)

or

$$\begin{aligned} \mathcal {H}_{2}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {cd}^{2}(\mho ,n)}{{f \text {cd}^{2}(\mho ,n)+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(23)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=\frac{h_{4}(n^{2}+h_{2}+1)}{n^{4}-n^{2}-h^{2}_{2}+1},~~g=-\frac{3h_{4}}{n^{4}-n^{2}-h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned}&h^{2}_{4}\left( -n^{2}-h_{2}-1)(9n^{2}-(n^{2}+h_{2}+1)(2n^{2}-h_{2}+2)\right) \\&-\frac{9\alpha h^{2}_{4}\left( n^{2}-n^{4}-1+h^{2}_{2}\right) ^{2}}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {1},\)

$$\begin{aligned} \mathcal {H}_{1,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\tanh ^{2}(\mho )}{{f \tanh ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(24)

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(-h_{2}-2)(9-(h_{2}+2)(4-h_{2}))-\frac{9\alpha h^{2}_{4}\left( -1+h^{2}_{2}\right) ^{2}}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a periodic wave solution, when \(n\rightarrow {0},\)

$$\begin{aligned} \mathcal {H}_{2,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\sin ^{2}(\mho )}{{f \sin ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(25)

or

$$\begin{aligned} \mathcal {H}_{2,2}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\cos ^{2}(\mho )}{{f \cos ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(26)

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(-h_{2}-1)(h_{2}+1)(h_{2}-2)-\frac{9\alpha h^{2}_{4}(h^{2}_{2}-1)^{2}}{2\Lambda }=0. \end{aligned}$$

Result 2 if \(l_{0}=1-n^{2},~l_{2}=2n^{2}-1,~l_{4}=-n^{2}, ~0<n<1,\) then \(\Phi (\mho )=cn(\mho ,n)\) , thus we have,

$$\begin{aligned} \mathcal {H}_{3}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {cn}^{2}(\mho ,n)}{{f \text {cn}^{2}(\mho ,n)+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(27)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=\frac{h_{4}(2n^{2}-h_{2}-1)}{n^{4}-n^{2}-h^{2}_{2}+1},~~g=-\frac{3h_{4}(n^{2}-1)}{n^{4}-n^{2}-h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(2n^{2}-h_{2}-1)(-9n^{2}(1-n^{2})-(2n^{2}-h_{2}-1)(4n^{2}+h_{2}-2))-\frac{9\alpha h^{2}_{4}(n^{2}-n^{4}-1+h^{2}_{2})}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {1},\)

$$\begin{aligned} \mathcal {H}_{3,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{{{\,\mathrm{sech}\,}}^{2}(\mho )}{{f {{\,\mathrm{sech}\,}}^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(28)

under the constraint condition,

$$\begin{aligned} -h^{2}_{4}(h_{2}-1)^{3}-\frac{9\alpha h^{2}_{4}(h^{2}_{2}-3)^{2}}{2\Lambda }=0. \end{aligned}$$

Result 3 if \(l_{0}=n^{2}-1,~l_{2}=2-n^{2},~l_{4}=-1, ~0<n<1,\) then \(\Phi (\mho )=dn(\mho ,n)\) , thus we have,

$$\begin{aligned} \mathcal {H}_{4}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {dn}^{2}(\mho ,n)}{{f \text {dn}^{2}(\mho ,n)+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(29)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=\frac{h_{4}(n^{2}+h_{2}-2)}{n^{4}-n^{2}-h^{2}_{2}+1},~~g=-\frac{3h_{4}(n^{2}-1)}{n^{4}-n^{2}-h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(-n^{2}-h_{2}+2)(-9n^{2}+9-(n^{2}-h_{2}+2)(-2n^{2}+h_{2}+4))-\frac{9\alpha h^{2}_{4}(n^{2}-n^{4}-1+h^{2}_{2})}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {1},\)

$$\begin{aligned} \mathcal {H}_{4,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{{{\,\mathrm{sech}\,}}^{2}(\mho )}{{f {{\,\mathrm{sech}\,}}^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(30)

under the constraint condition,

$$\begin{aligned} -h^{2}_{4}(1-h_{2})(3-h_{2})(2+h_{2})-\frac{9\alpha h^{2}_{4}(h^{2}_{2}-1)^{2}}{2\Lambda }=0. \end{aligned}$$

Result 4 if \(l_{0}=n^{2},~l_{2}=-1-n^{2},~l_{4}=1, ~0<n<1,\) then \(\Phi (\mho )=ns(\mho ,n)\) or \(\Phi (\mho )=dc(\mho ,n)\) , thus we have,

$$\begin{aligned} \mathcal {H}_{5}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {ns}^{2}(\mho ,n)}{{f \text {ns}^{2}(\mho ,n)+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(31)

or

$$\begin{aligned} \mathcal {H}_{6}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {dc}^{2}(\mho ,n)}{{f \text {dc}^{2}(\mho ,n)+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(32)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=\frac{h_{4}(n^{2}+h_{2}+1)}{n^{4}-n^{2}-h^{2}_{2}+1},~~g=-\frac{3h_{4}n^{2}}{n^{4}-n^{2}-h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(-n^{2}-h_{2}-1)(9n^{2}-(-n^{2}-h_{2}-1)(-2n^{2}+h_{2}-2))-\frac{9\alpha h^{2}_{4}(n^{2}-n^{4}-1+h^{2}_{2})}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {1},\)

$$\begin{aligned} \mathcal {H}_{5,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\coth ^{2}(\mho )}{{f \coth ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(33)

under the constraint condition,

$$\begin{aligned} -h^{2}_{4}(-h_{2}-2)(9-(-h_{2}-2)(h_{2}-4))-\frac{9\alpha h^{2}_{4}(h^{2}_{2}-1)^{2}}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {0},\)

$$\begin{aligned} \mathcal {H}_{5,2}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\csc ^{2}(\mho )}{{f \csc ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(34)

or

$$\begin{aligned} \mathcal {H}_{6,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\sec ^{2}(\mho )}{{f \sec ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(35)

under the constraint condition,

$$\begin{aligned} -h^{2}_{4}(h_{2}+1)^{2}(h_{2}-2))-\frac{9\alpha h^{2}_{4}(h^{2}_{2}-1)^{2}}{2\Lambda }=0. \end{aligned}$$

Result 5 if \(l_{0}=-n^{2},~l_{2}=-1+2n^{2},~l_{4}=1-n^{2}, ~0<n<1,\) then \(\Phi (\mho )=nc(\mho ,n)\) , thus we have,

$$\begin{aligned} \mathcal {H}_{7}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {nc}^{2}(\mho ,n)}{{f \text {nc}^{2}(\mho ,n)+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(36)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=\frac{h_{4}(2n^{2}-h_{2}-1)}{n^{4}-n^{2}-h^{2}_{2}+1},~~g=-\frac{3h_{4}n^{2}}{n^{4}-n^{2}-h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(2n^{2}-h_{2}-1)(9n^{4}-9n^{2}-(2n^{2}-h_{2}-1)(4n^{2}+h_{2}-2))-\frac{9\alpha h^{2}_{4}(n^{2}-n^{4}-1+h^{2}_{2})}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {1},\)

$$\begin{aligned} \mathcal {H}_{7,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\cosh ^{2}(\mho )}{{f \cosh ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(37)

under the constraint condition,

$$\begin{aligned} -h^{2}_{4}(h_{2}-1)^{2}(h_{2}+2)-\frac{9\alpha h^{2}_{4}(h^{2}_{2}-1)^{2}}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {0},\)

$$\begin{aligned} \mathcal {H}_{7,2}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\sec ^{2}(\mho )}{{f \sec ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(38)

under the constraint condition,

$$\begin{aligned} -h^{2}_{4}(h_{2}+1)^{2}(h_{2}-1)-\frac{9\alpha h^{2}_{4}(h^{2}_{2}-1)^{2}}{2\Lambda }=0. \end{aligned}$$

Result 6 if \(l_{0}=-1,~l_{2}=2-n^{2},~l_{4}=-1+n^{2}, ~0<n<1,\) then \(\Phi (\mho )=nd(\mho ,n)\) , thus we have,

$$\begin{aligned} \mathcal {H}_{8}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {nd}^{2}(\mho ,n)}{{f \text {nd}^{2}(\mho ,n)+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(39)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=\frac{h_{4}(n^{2}+h_{2}-2)}{n^{4}-n^{2}-h^{2}_{2}+1},~~g=-\frac{3h_{4}}{n^{4}-n^{2}-h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(-n^{2}-h_{2}+2)(-9n^{2}+9-(-n^{2}-h_{2}+2)(-2n^{2}+h_{2}+4))-\frac{9\alpha h^{2}_{4}(n^{2}+n^{4}-1+h^{2}_{2})}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {1},\)

$$\begin{aligned} \mathcal {H}_{8,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\cosh ^{2}(\mho )}{{f \cosh ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(40)

under the constraint condition,

$$\begin{aligned} -h^{2}_{4}(-h_{2}+1)^{2}(h_{2}+2)-\frac{9\alpha h^{2}_{4}(h^{2}_{2}+1)^{2}}{2\Lambda }=0. \end{aligned}$$

Result 7 if \(l_{0}=1,~l_{2}=2-n^{2},~l_{4}=1-n^{2}, ~0<n<1,\) then \(\Phi (\mho )=sc(\mho ,n)\) , thus we have,

$$\begin{aligned} \mathcal {H}_{9}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {sc}^{2}(\mho ,n)}{{f \text {sc}^{2}(\mho ,n)+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(41)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=\frac{h_{4}(n^{2}+h_{2}-2)}{n^{4}-n^{2}-h^{2}_{2}+1},~~g=-\frac{3h_{4}}{n^{4}-n^{2}-h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(-n^{2}-h_{2}+2)(-9n^{2}+9-(-n^{2}-h_{2}+2)(-2n^{2}+h_{2}+4))-\frac{9\alpha h^{2}_{4}(n^{2}+n^{4}-1+h^{2}_{2})}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {1},\)

$$\begin{aligned} \mathcal {H}_{9,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\sinh ^{2}(\mho )}{{f \sinh ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(42)

under the constraint condition,

$$\begin{aligned} -h^{2}_{4}(-h_{2}+1)^{2}(h_{2}+2)-\frac{9\alpha h^{2}_{4}(h^{2}_{2}+1)^{2}}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a periodic wave solution, when \(n\rightarrow {0},\)

$$\begin{aligned} \mathcal {H}_{9,2}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\tan ^{2}(\mho )}{{f \tan ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(43)

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(-h_{2}+2)(9-(2-h_{2})(h_{2}+4))-\frac{9\alpha h^{2}_{4}(h^{2}_{2}-1)^{2}}{2\Lambda }=0. \end{aligned}$$

Result 8 if \(l_{0}=1,~l_{2}=2n^{2}-1,~l_{4}=-n^{2}(1-n^{2}), ~0<n<1,\) then \(\Phi (\mho )=sd(\mho ,n)\) , thus we have,

$$\begin{aligned} \mathcal {H}_{10}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {sd}^{2}(\mho ,n)}{{f \text {sd}^{2}(\mho ,n)+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(44)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=-\frac{h_{4}(2n^{2}-h_{2}-1)}{n^{4}-n^{2}-h^{2}_{2}+1},~~g=-\frac{3h_{4}}{n^{4}-n^{2}-h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(2n^{2}-h_{2}-1)(9n^{4}-9n^{2}-(2n^{2}-h_{2}-1)(4n^{2}+h_{2}-2))-\frac{9\alpha h^{2}_{4}(n^{2}-n^{4}-1+h^{2}_{2})}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {0},\)

$$\begin{aligned} \mathcal {H}_{10,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\sin ^{2}(\mho )}{{f \sin ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(45)

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(h_{2}+1)^{2}(h_{2}-2)-\frac{9\alpha h^{2}_{4}(h^{2}_{2}-1)^{2}}{2\Lambda }=0. \end{aligned}$$

Result 9 if \(l_{0}=1-n^{2},~l_{2}=2-n^{2},~l_{4}=1, ~0<n<1,\) then \(\Phi (\mho )=cs(\mho ,n)\) , thus we have,

$$\begin{aligned} \mathcal {H}_{11}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {cs}^{2}(\mho ,n)}{{f \text {cs}^{2}(\mho ,n)+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(46)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=\frac{h_{4}(n^{2}+h_{2}-2)}{n^{4}-n^{2}-h^{2}_{2}+1},~~g=\frac{3h_{4}(n^{2}-1)}{n^{4}-n^{2}-h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(-n^{2}-h_{2}+2)(-9n^{2}+9-(-n^{2}-h_{2}+1)(-2n^{2}+h_{2}+4))-\frac{9\alpha h^{2}_{4}(n^{2}-n^{4}-1+h^{2}_{2})}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {1},\)

$$\begin{aligned} \mathcal {H}_{11,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{{{\,\mathrm{csch}\,}}^{2}(\mho )}{{f {{\,\mathrm{csch}\,}}^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(47)

under the constraint condition,

$$\begin{aligned} -h^{2}_{4}(-h_{2}+1)^{2}(h_{2}+2)-\frac{9\alpha h^{2}_{4}(h^{2}_{2}-1)^{2}}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a periodic wave solution, when \(n\rightarrow {0},\)

$$\begin{aligned} \mathcal {H}_{11,2}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\cot ^{2}(\mho )}{{f \cot ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(48)

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(-h_{2}+2)(9-(-h_{2}+2)(4+h_{4}))-\frac{9\alpha h^{2}_{4}(h^{2}_{2}-1)^{2}}{2\Lambda }=0. \end{aligned}$$

Result 10 if \(l_{0}=-n^{2}(1-n^{2}),~l_{2}=2n^{2}-1,~l_{4}=1, ~0<n<1,\) then \(\Phi (\mho )=ds(\mho ,n)\) , thus we have,

$$\begin{aligned} \mathcal {H}_{12}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {ds}^{2}(\mho ,n)}{{f \text {ds}^{2}(\mho ,n)+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(49)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=-\frac{h_{4}(2n^{2}-h_{2}-1)}{n^{4}-n^{2}-h^{2}_{2}+1},~~g=-\frac{3h_{4}n^{2}}{n^{4}-n^{2}-h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(2n^{2}-h_{2}-1)(9n^{4}-9n^{2}-(2n^{2}-h_{2}-1)(4n^{2}+h_{2}-2))-\frac{9\alpha h^{2}_{4}(n^{2}-n^{4}-1+h^{2}_{2})}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {1},\)

$$\begin{aligned} \mathcal {H}_{12,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{{{\,\mathrm{csch}\,}}^{2}(\mho )}{{f {{\,\mathrm{csch}\,}}^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(50)

under the constraint condition,

$$\begin{aligned} -h^{2}_{4}(-h_{2}+1)^{2}(h_{2}+2)-\frac{9\alpha h^{2}_{4}(h^{2}_{2}-1)^{2}}{2\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {0},\)

$$\begin{aligned} \mathcal {H}_{12,2}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\csc ^{2}(\mho )}{{f \csc ^{2}(\mho )+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(51)

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(h_{2}+1)^{2}(h_{2}-1)-\frac{9\alpha h^{2}_{4}(h^{2}_{2}-1)^{2}}{2\Lambda }=0. \end{aligned}$$

Result 11 if \(l_{0}=\frac{1-n^{2}}{4},~l_{2}=\frac{1+n^{2}}{2},~l_{4}=\frac{1-n^{2}}{4}, ~0<n<1,\) then \(\Phi (\mho )=nc(\mho ,n)\pm sc(\mho ,n)\) or \(\Phi (\mho )=\frac{cn(\mho ,n)}{1\pm sn(\mho ,n)}\) , thus we have,

$$\begin{aligned} \mathcal {H}_{13}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{(\text {nc}(\mho ,n)\pm \text {sc}(\mho ,n))^{2}}{{f (\text {nc}(\mho ,n)\pm \text {sc}(\mho ,n))^{2}+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(52)

or

$$\begin{aligned} \mathcal {H}_{14}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {cn}^{2}(\mho ,n)}{f \text {cn}^{2}(\mho ,n)+g(1\pm \text {sn}(\mho ,n))^{2}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(53)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=-\frac{8h_{4}(n^{2}-2h_{2}+1)}{n^{4}+14n^{2}-16h^{2}_{2}+1},~~g=\frac{12h_{4}(n^{2}-1)}{n^{4}+14n^{2}-16h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned} \frac{h^{2}_{4}}{32}(n^{2}-2h_{2}+1)(n^{4}-34n^{2}+1+8n^{2}h_{2}+8h_{2}+16h^{2}_{2})-\frac{9\alpha h^{2}_{4}(n^{4}+14n^{2}+1-16h^{2}_{2})}{512\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {1},\)

$$\begin{aligned} \mathcal {H}_{13,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{(\cosh (\mho ,n)\pm \sinh (\mho ,n))^{2}}{{f (\cosh (\mho ,n)\pm \sinh (\mho ,n))^{2}+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(54)

or

$$\begin{aligned} \mathcal {H}_{14,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{{{\,\mathrm{sech}\,}}^{2}(\mho ,n)}{f {{\,\mathrm{sech}\,}}^{2}(\mho ,n)+g(1\pm \tanh (\mho ,n))^{2}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(55)

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(-h_{2}+1)(h_{2}+h^{2}_{2}-1)-\frac{9\alpha h^{2}_{4}(-h^{2}_{2}+1)^{2}}{32\Lambda }=0. \end{aligned}$$

We are able to acquire a periodic wave solution, when \(n\rightarrow {0},\)

$$\begin{aligned} \mathcal {H}_{13,2}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{(\sec (\mho ,n)\pm \tan (\mho ,n))^{2}}{{f (\sec (\mho ,n)\pm \tan (\mho ,n))^{2}+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(56)

or

$$\begin{aligned} \mathcal {H}_{14,2}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\cos ^{2}(\mho ,n)}{f \cos ^{2}(\mho ,n)+g(1\pm \sin (\mho ,n))^{2}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(57)

under the constraint condition,

$$\begin{aligned} \frac{h^{2}_{4}}{32}(-2h_{2}+1)(1+8h_{2}+16h^{2}_{2})-\frac{9\alpha h^{2}_{4}(1-16h^{2}_{2})}{512\Lambda }=0. \end{aligned}$$

Result 12 if \(l_{0}=-\frac{(1-n^{2})^{2}}{4},~l_{2}=\frac{1+n^{2}}{2},~l_{4}=-\frac{1}{4}, ~0<n<1,\) then \(\Phi (\mho )=n~cn(\mho ,n)\pm dn(\mho ,n)\) , thus we have,

$$\begin{aligned} \mathcal {H}_{15}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{(n\,\text {cn}(\mho ,n)\pm \text {dn}(\mho ,n))^{2}}{{f (n\,\text {cn}(\mho ,n)\pm \text {dn}(\mho ,n))^{2}+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(58)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=-\frac{8h_{4}(n^{2}-2h_{2}+1)}{n^{4}+14n^{2}-16h^{2}_{2}+1},~~g=\frac{12h_{4}(n^{2}-1}{n^{4}+14n^{2}-16h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned} \frac{h^{2}_{4}}{32}(n^{2}-2h_{2}+1)(n^{4}-34n^{2}+1+8n^{2}h_{2}+8h_{2}+16h^{2}_{2})-\frac{9\alpha h^{2}_{4}(n^{4}+14n^{2}+1-16h^{2}_{2})}{512\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {1},\)

$$\begin{aligned} \mathcal {H}_{15,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{({{\,\mathrm{sech}\,}}(\mho ,n)\pm {{\,\mathrm{sech}\,}}(\mho ,n))^{2}}{{f ({{\,\mathrm{sech}\,}}(\mho ,n)\pm {{\,\mathrm{sech}\,}}(\mho ,n))^{2}+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(59)

under the constraint condition,

$$\begin{aligned} h^{2}_{4}(-h_{2}+1)(h_{2}+h^{2}_{2}-1)-\frac{9\alpha h^{2}_{4}(-h^{2}_{2}+1)^{2}}{32\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {0},\)

$$\begin{aligned} \mathcal {H}_{15,2}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{(\cos (\mho ,n)\pm 1)^{2}}{{f (\cos (\mho ,n)\pm 1)^{2}+g}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(60)

under the constraint condition,

$$\begin{aligned} \frac{h^{2}_{4}}{32}(-2h_{2}+1)(1+8h_{2}+16h^{2}_{2})-\frac{9\alpha h^{2}_{4}(1-16h^{2}_{2})}{512\Lambda }=0. \end{aligned}$$

Result 13 if \(l_{0}=\frac{1}{4},~l_{2}=\frac{1-2n^{2}}{2},~l_{4}=\frac{1}{4}, ~0<n<1,\) then \(\Phi (\mho )=\frac{sn(\mho ,n)}{1\pm cn(\mho ,n)}\) , thus we have,

$$\begin{aligned} \mathcal {H}_{16}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {sn}^{2}(\mho ,n)}{f \text {sn}^{2}(\mho ,n)+g(1\pm \text {cn}(\mho ,n))^{2}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(61)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=\frac{8h_{4}(2n^{2}+2h_{2}-1)}{16n^{4}-16n^{2}-16h^{2}_{2}+1},~~g=-\frac{12h_{4}(n^{2}-1)}{16n^{4}-16n^{2}-16h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned} \frac{h^{2}_{4}}{32}(-2n^{2}-2h_{2}+1)(-32n^{4}+32n^{2}+1-16n^{2}h_{2}+8h_{2}+16h^{2}_{2})-\frac{9\alpha h^{2}_{4}(16n^{4}-16n^{2}+1-16h^{2}_{2})}{512\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {1},\)

$$\begin{aligned} \mathcal {H}_{16,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\tanh ^{2}(\mho ,n)}{f \tanh ^{2}(\mho ,n)+g(1\pm {{\,\mathrm{sech}\,}}(\mho ,n))^{2}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(62)

under the constraint condition,

$$\begin{aligned} \frac{h^{2}_{4}}{32}(-2h_{2}-1)(-8h_{2}+16h^{2}_{2}+1)-\frac{9\alpha h^{2}_{4}(-16h^{2}_{2}+1)^{2}}{512\Lambda }=0. \end{aligned}$$

We are able to acquire a periodic wave solution, when \(n\rightarrow {0},\)

$$\begin{aligned} \mathcal {H}_{16,2}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\sin ^{2}(\mho ,n)}{f \sin ^{2}(\mho ,n)+g(1\pm \cos (\mho ,n))^{2}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(63)

under the constraint condition,

$$\begin{aligned} \frac{h^{2}_{4}}{32}(-2h_{2}+1)(1+8h_{2}+16h^{2}_{2})-\frac{9\alpha h^{2}_{4}(1-16h^{2}_{2})}{512\Lambda }=0. \end{aligned}$$

Result 14 if \(l_{0}=\frac{1}{4},~l_{2}=\frac{1+n^{2}}{2},~l_{4}=\frac{(1-n^{2})^{2}}{4}, ~0<n<1,\) then \(\Phi (\mho )=\frac{sn(\mho ,n)}{cn(\mho ,n)\pm dn(\mho ,n)}\) , thus we have,

$$\begin{aligned} \mathcal {H}_{17}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\text {sn}^{2}(\mho ,n)}{f \text {sn}^{2}(\mho ,n)+g(\text {cn}(\mho ,n)\pm \text {dn}(\mho ,n))^{2}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(64)

where \(\Lambda \kappa (\mu +\delta )>0\) and \(\mho =x-\lambda t\) and the functions f and g are,

$$\begin{aligned} f=-\frac{8h_{4}(n^{2}-2h_{2}+1)}{n^{4}+14n^{2}-16h^{2}_{2}+1},~~g=-\frac{12h_{4}}{n^{4}+14n^{2}-16h^{2}_{2}+1}, \end{aligned}$$

under the constraint condition,

$$\begin{aligned} \frac{h^{2}_{4}}{32}(-2n^{2}-2h_{2}+1)(-32n^{4}+32n^{2}+1-16n^{2}h_{2}+8h_{2}+16h^{2}_{2})-\frac{9\alpha h^{2}_{4}(16n^{4}-16n^{2}+1-16h^{2}_{2})}{512\Lambda }=0. \end{aligned}$$

We are able to acquire a solitary wave solution, when \(n\rightarrow {1},\)

$$\begin{aligned} \mathcal {H}_{17,1}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\tanh ^{2}(\mho ,n)}{f \tanh ^{2}(\mho ,n)+g({{\,\mathrm{sech}\,}}(\mho ,n)\pm {{\,\mathrm{sech}\,}}(\mho ,n))^{2}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(65)

under the constraint condition,

$$\begin{aligned} {h^{2}_{4}}(-2h_{2}+1)(h_{2}+h^{2}_{2}-2)-\frac{9\alpha h^{2}_{4}(-16h^{2}_{2}+1)^{2}}{322\Lambda }=0. \end{aligned}$$

We are able to acquire a periodic wave solution, when \(n\rightarrow {0},\)

$$\begin{aligned} \mathcal {H}_{16,2}(x,t)=\left( \pm \frac{\sqrt{\Lambda }}{\sqrt{6\kappa (\mu +\delta )}}\mp \frac{\sqrt{6}\alpha h_{4}}{\sqrt{\Lambda \kappa (\mu +\delta )}}\frac{\sin ^{2}(\mho ,n)}{f \sin ^{2}(\mho ,n)+g(\cos (\mho ,n)\pm 1)^{2}}\right) e^{i(-\kappa x+\omega t+\eta )}, \end{aligned}$$
(66)

under the constraint condition,

$$\begin{aligned} {h^{2}_{4}}(-2h_{2}+1)(1+16h_{2}+16h^{2}_{2})-\frac{9\alpha h^{2}_{4}(1-16h^{2}_{2})}{512\Lambda }=0. \end{aligned}$$

3 Graphical representation and discussion

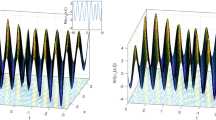
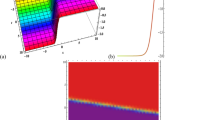
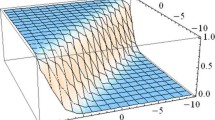
In this section, we will display 2-D, 3-D, and Contour visualization of the acquired results.

Fig. 1
figure 1

Real and Imaginary new solitary behaviour of \(\mathcal {H}_{1,1}(x,t)\) at \(\alpha =0.01,\kappa =-0.01,\mu =0.9,\delta =0.9,\gamma =0.01,\eta =0.05,\omega =-2,h_{1}=0.5,h_{4}=0.5\)

Full size image
Fig. 2
figure 2

Real and Imaginary new solitary behaviour of \(\mathcal {H}_{2,1}(x,t)\) at \(\alpha =0.01,\kappa =-0.01,\mu =0.9,\delta =0.9,\gamma =0.01,\eta =0.05,\omega =-2,h_{1}=0.5,h_{4}=0.5\)

Full size image
Fig. 3
figure 3

Real and Imaginary new solitary behaviour of \(\mathcal {H}_{5,1}(x,t)\) at \(\alpha =0.1,\kappa =1,\mu =0.9,\delta =0.9,\gamma =-0.5,\eta =1,\omega =-2,h_{1}=0.5,h_{4}=0.5\)

Full size image
Fig. 4
figure 4

Real and Imaginary new solitary behaviour of \(\mathcal {H}_{5,2}(x,t)\) at \(\alpha =0.1,\kappa =1,\mu =0.9,\delta =0.9,\gamma =-0.5,\eta =1,\omega =-2,h_{1}=0.5,h_{4}=0.5\)

Full size image

The complex analytical exact solutions of the considered governing model (2) are visually shown in this section. The [result 1] of the paper Tarla et al. (2022) is presenting the dark-bright soliton because \(\tanh\) and \({{\,\mathrm{sech}\,}}\) functions are appeared in solution in series form but taking the same case, we secured a new solitary wave solutions [result 1], in which tanh, sin and cosine functions are appearing in fraction with more number of constants that are determined. Similarly, by comparing the results of this work to the results of Tarla et al. (2022), we concluded that many new solitary wave exact solutions are being generated in the form of trigonometric function solutions, Jacobi elliptic function solutions, and hyperbolic function solutions. The 2-D surface graph, 3-D surface graph, and contour surface graph are all shown using an appropriate set of parametric values that satisfy the constraint criteria for solutions. Figures 1, 2, 3 and 4 are plotted for \((n=0.75,~h_{2}=400.0014569)\), \((n=0.4,~h_{2}=-0.6830188661)\), \((n=0.8,~h_{2}=1.429681116)\), and \((n=0.4,~h_{2}=47083116200)\) respectively.

4 Conclusion

In this work, the perturbed Chen-Lee-Liu equation is considered to investigate which delineates the phenomenon of propagation pulse in the optical fiber. The generalized soliton solutions are acquired for the Chen-Lee-Liu model with perturbation term by executing one of the reliable expansion schemes. The \(\Phi ^{6}-\)model expansion technique provided generally fourteen families of different types of soliton patterns based on Jacobi elliptic functions.

  • Twenty-eight analytical solutions are obtained.

  • The secured solitary wave patterns are based on the Jacobi elliptic functions, on limiting case \(n\rightarrow {1},\) will get hyperbolic solution and on limiting case \(n\rightarrow {0}\) will get trigonometric solutions.

  • The condition corresponding to every obtained traveling wave solution is developed which ensured the existence of acquired solution.

  • 2-D, 3-D, and contour real and imaginary profiles of the solutions are depicted.

  • The used parametric values satisfies the developed constrains.

Some suitable values are taken for involved free parameters to interpret the graphical behavior of optical pulsed by using the generated analytical solutions. The secured solutions can be authoritative to interpret the physical view of the non-linear model. The \(\Phi ^{6}-\)model expansion approach is an effective and powerful mathematical tool that can be prosecuted to get the analytical solutions to many other complex mathematical phenomenons. The future planes are to perform bifurcation analysis, chaos analysis, modulation instability, and sensitivity visualization for deep understanding the dynamical properties of the propagating pulse in the field of optical fiber.