1 Introduction

Nonlinear evolution equations (NL-EEs) play a pivotal role in comprehending a multitude of intricate phenomena, spanning fields such as biophysics, fluid thermodynamics, marine physics, ocean engineering, neurophysics, optics, nuclear physics, quantum theory, thermodynamics, physiology, ecology, social science, and economics (Aslan 2017; Biswas et al. 2013; Bokhari et al. 2007; Biswas et al. 2013). The realm of nonlinear partial differential equations has garnered extensive attention from researchers and mathematicians, who have diligently explored mathematical and analytical methods to attain accurate periodic solutions, traveling wave solutions, solitary wave solutions, and other relevant outcomes (Liu et al. 2023; Muhammad et al. 2024; Zayed et al. 2018, 2019, 2022, 2021).

Many scholars have created various methods in recent decades to acquire the exact results of NL-EEs, including the Bifurcation method, Riccati method (Ping 2010), Hirota bilinear method (Hietarinta 2007), extended Riccati-expansion method (Khater and Salama 2022), Lie symmetry technique (Bokhari et al. 2011; Usman et al. 2024a, b; Al-Ali et al. 2016; Abbas et al. 2024; Al-Omari et al. 2023; Hussain et al. 2024; Usman et al. 2024c), Bäcklund transformation method (Yan et al. 2018), Auxiliary equation technique (Guo et al. 2011), exp-function method (Ma et al. 2010), modified F-expansion method, the Jacobi elliptic function expansion method (Yel 2020), the Darboux transformations method (Guo et al. 2012), the inverse-scattering method (Bock and Kruskal 1979), and the F-expansion method, rational expansion approach (Akbar et al. 2016), modified simple equation approach (Hossain and Akbar 2017) and others. This study focuses on the Kudryashov-Sinelshchikov equation, which is given by

$$\begin{aligned} u_{t}+\alpha uu_{x}+\beta u_{xxx}+\kappa (uu_{x})_{xx}+\eta u_{x}u_{xx}=0. \end{aligned}$$
(1)

The arbitrary constants \(\alpha\), \(\beta\), \(\kappa\), and \(\eta\) serve as the parameters.  Kudryashov and Sinelshchikov established this equation (Kudryashov and Sinelshchikov 2010) to explain the pressure waves in a combination of liquid and gas bubbles under the influence of fluid viscosity and heat transfer. To find the periodic wave and traveling wave solutions to the KS equation, Marly Randrüüt (2011) used undistorted traveling wave transformation. Ryabov (2010), Ryabov et al. (2011) used a modified version of the truncated expansion approach to get certain accurate solutions when the constant \(\beta =-3,-4\) was chosen. Li and Chen (2012) employed a dynamical systems technique to research the KS equation’s traveling structure. In various parametric regions of the plane, they studied all bifurcations of phase portraits for the KS equation traveling systems. He et al. (2012) use the bifurcation theory of system dynamics and the concept of phase portraiture analysis to solve the KS problem.

Peakon, single waveforms, smoother and quasi-periodic waves are all shown to exist from a dynamical perspective, and the necessary conditions are presented for the presence of the aforementioned solutions in various regions of the parameterized space. He et al. (2012) investigated the periodical loop solutions and associated limit forms of the KS problem using the bifurcation idea and the phase portraits estimation procedure. They demonstrate that the limit forms include solutions for loop solitary waves, smooth periodic waveforms, and periodic cusp waves. The Lie symmetry analysis approach was utilized by Nadjafikhah et al. (2011) to look at the one- and two-dimensional optimum systems of Lie subalgebras, exact solutions, and the initial structure of the group-invariant solutions. The \((G'/G)\)-expansion method and its variations were used by He et al. (2013) to find the waveform solutions to the KS equation.

The main objective of this article is to use the SSE (Rezazadeh et al. 2020a, b) and JEF (Elboree 2011; Allahyani et al. 2022) techniques to get analytical soliton solutions to the KS equation depending upon four parameters. These methods are productive, efficient, and easy to use and produce a variety of exact analytical solutions in the form of trigonometric, hyperbolic, exponential and rational functions. The dynamical behavior of solutions shows the solitary wave profile, singletons, dark-singular-mixed, combined dark-bright, single, bright, shock waves, solitary waves, periodic and double periodic solitons. In contrast to the work in the literature stated above, the produced families of solutions represent a wide variety of physical phenomena since the solutions are derived with free parameters. Due to the use of arbitrary parameters, our solutions are more generalized. We demonstrate the suitable value of the arbitrary constants involved in the discovered families of solutions, we depict the two-dimensional and related three-dimensional graphics in the appropriate range space. The resulting KS equation solutions are original and have never been documented in any other work, to the author’s knowledge.

The manuscript is structured into distinct sections, each serving a specific purpose. The introductory section initiates the paper, setting the stage for the subsequent content. In the second section, the focus shifts toward introducing two analytical techniques rooted in ansatz-based approaches. The third section delves into the application of the efficient and effective SSE technique to pinpoint solutions for the KS equation. Moving forward, the fourth section elaborates on the utilization of the JEF technique, demonstrating its capacity to identify a range of analytical wave solutions categorized into families such as trigonometric, hyperbolic, exponential function, and rational forms. Section 5 takes the spotlight by visually demonstrating the physical existence of analytical soliton solutions. This is achieved through the incorporation of two- and three-dimensional graphics, facilitated by parameter selection and the computational tool Mathematica. By observing the diverse dynamical behaviors, the significance of the identified solutions becomes apparent. The manuscript culminates in Sect. 6, offering a concluding statement to wrap up the study.

2 Integrated schemes

The expression for the KS equation is provided as follows

$$\begin{aligned} u_{t}+\alpha uu_{x}+\beta u_{xxx}+\kappa (uu_{x}){xx}+\eta u{x}u_{xx}=0, \end{aligned}$$

where the parameters \(\alpha\), \(\beta\), \(\kappa\), and \(\eta\) are arbitrary constants. This equation explains the emergence of pressure waves within a medium containing a mixture of liquid and gas bubbles while being subjected to the influences of fluid viscosity and heat transfer. In its general form, the nonlinear partial differential equation (NL-PDE) is considered as follows

$$\begin{aligned} \mathcal {Y}(u, u_{t}, u_{x}, u_{tt}, u_{xx},....)=0. \end{aligned}$$
(2)

The subsequent wave change

$$\begin{aligned} u(x,t)=\mathcal {V}(\mu ),\,\,\, \mu =x-\omega t, \end{aligned}$$
(3)

where \(\omega\) is the wave speed. Equation (3) is converted into a nonlinear ODE

$$\begin{aligned} \mathcal {H}(\mathcal {V}, \mathcal {V}', \mathcal {V}'', \mathcal{V}''',...)=0. \end{aligned}$$
(4)

We next apply two ansatz-based techniques here.

2.1 SSE technique

The SSE is briefly described in this part by using the steps below:

Step 1 We assume the solution of nonlinear ODE (4) as

$$\begin{aligned} \mathcal {V}(\mu )=\sum _{i=0}^{s} b_{i}\mathcal {K}^{i}(\mu ), \end{aligned}$$
(5)

where \(b_{i}\) \((i=0, 1,\cdots , s)\) are constants and \(\mathcal {K}(\mu )\) satisfy;

$$\begin{aligned} (\mathcal{K}^{'}(\mu ))^2=\sigma +\nu \mathcal{K}^2(\mu )+\mathcal{K}^4(\mu ). \end{aligned}$$
(6)

Step 2 The output of Eq. (6), where \(\nu\) and \(\sigma\) are unknown parameters, is presented as follows;

Case i If \(\nu >0\) and \(\sigma =0\), the outcomes are as follows

$$\begin{aligned} \begin{aligned} \mathcal{K}^\pm _{1}(\mu )&=\pm \sqrt{-pq\nu }\,\,\text {sech}_{pq}\left( \sqrt{\nu }\mu \right) ,\\ \mathcal{K}^\pm _{2}(\mu )&=\pm \sqrt{pq\nu }\,\,\text {csch}_{pq}\left( \sqrt{\nu }\mu \right) , \end{aligned} \end{aligned}$$
(7)

where p,  q are positive constants known to be the deformation parameters and the trigonometric equations are defined by

$$\begin{aligned} \text {sech}_{pq}(\mu )=\frac{2}{pe^{\mu }+qe^{-\mu }},\,\, \text {csch}_{pq}(\mu )=\frac{2}{pe^{\mu }-qe^{-\mu }}\cdot \end{aligned}$$

Case ii If \(\nu <0\) and \(\sigma =0\), we obtain the outcome

$$\begin{aligned} \begin{aligned} \mathcal{K}^\pm _{3}(\mu )&=\pm \sqrt{-pq\nu }\,\,\sec _{pq} \left( \sqrt{-\nu }\mu \right) ,\\ \mathcal{K}^\pm _{4}(\mu )&=\pm \sqrt{-pq\nu }\,\,\csc _{pq} \left( \sqrt{-\nu }\mu \right) , \end{aligned} \end{aligned}$$
(8)

where the trigonometric equations are defined by

$$\begin{aligned} \sec _{pq}(\mu )=\frac{2}{pe^{l\mu }+qe^{-l\mu }}, \,\, \csc _{pq}(\mu )=\frac{2}{pe^{l\mu }-qe^{-l\mu }}\cdot \end{aligned}$$

Case iii If \(\nu <0\) and \(\sigma =\frac{\nu ^{2}}{4}\), the outcomes are as follows

$$\begin{aligned} \begin{aligned} \mathcal{K}^\pm _{5}(\mu )&=\pm \sqrt{\frac{-\nu }{2}}\,\,\tanh _{pq}\left( \sqrt{\frac{-\nu }{2}\mu }\right) ,\\ \mathcal{K}^\pm _{6}(\mu )&=\pm \sqrt{\frac{-\nu }{2}}\,\,\coth _{pq}\left( \sqrt{\frac{-\nu }{2}\mu }\right) ,\\ \mathcal{K}^\pm _{7}(\mu )&=\pm \sqrt{\frac{-\nu }{2}}\,\,\left( \tanh _{pq}\left( \sqrt{-2\nu }\mu \right) \pm l \sqrt{pq}\,\,\text {sech}_{pq}\left( \sqrt{-2\nu }\mu \right) \right) ,\\ \mathcal{K}^\pm _{8}(\mu )&=\pm \sqrt{\frac{-\nu }{2}}\,\,\left( \coth _{pq}\left( \sqrt{-2\nu }\mu \right) \pm \sqrt{pq}\,\,\text {csch}_{pq}\left( \sqrt{-2\nu }\mu \right) \right) ,\\ \mathcal{K}^\pm _{9}(\mu )&=\pm \sqrt{\frac{-\nu }{8}}\,\,\left( \tanh _{pq}\left( \sqrt{\frac{-\nu }{8}\mu }\right) + \,\,\coth _{pq}\left( \sqrt{\frac{-\nu }{8}\mu }\right) \right) ,\\ \end{aligned} \end{aligned}$$
(9)

where the trigonometric equations are defined by

$$\begin{aligned} \tanh _{pq}(\mu )=\frac{pe^{\mu }-qe^{-\mu }}{pe^{\mu }+ qe^{-\mu }},\,\, \coth _{pq}(\mu )=\frac{pe^{\mu }+qe^{-\mu }}{pe^{\mu }-qe^{-\mu }}\cdot \end{aligned}$$

Case iv If \(\nu >0\) and \(\sigma =\frac{\nu ^{2}}{4}\), the outcomes are as follows

$$\begin{aligned} \begin{aligned} \mathcal{K}^\pm _{10}(\mu )&=\pm \sqrt{\frac{\nu }{2}}\,\,\tan _{pq}\left( \sqrt{\frac{\nu }{2}\mu }\right) ,\\ \mathcal{K}^\pm _{11}(\mu )&=\pm \sqrt{\frac{\nu }{2}}\,\,\cot _{pq}\left( \sqrt{\frac{\nu }{2}\mu }\right) ,\\ \mathcal {K}^\pm _{12}(\mu )&=\pm \sqrt{\frac{\nu }{2}}\,\,\left( \tan _{pq}\left( \sqrt{2\nu }\mu \right) \pm l\sqrt{pq}\,\,\sec _{pq}\left( \sqrt{2\nu }\mu \right) \right) ,\\ \mathcal {K}^\pm _{13}(\mu )&=\pm \sqrt{\frac{\nu }{2}}\,\,\left( \cot _{pq}\left( \sqrt{2\nu }\mu \right) \pm \sqrt{pq}\,\,\csc _{pq}\left( \sqrt{2\nu }\mu \right) \right) ,\\ \mathcal {K}^\pm _{14}(\mu )&=\pm \sqrt{\frac{\nu }{8}}\,\,\left( \tan _{pq}\left( \sqrt{\frac{\nu }{8}\mu }\right) + \,\,\cot _{pq}\left( \sqrt{\frac{\nu }{8}\mu }\right) \right) ,\\ \end{aligned} \end{aligned}$$
(10)

where the trigonometric equations are defined by

$$\begin{aligned} \tan _{pq}(\mu )=-l\frac{pe^l{\mu }-qe^{-l\mu }}{pe^{l\mu }+ qe^{-l\mu }},\,\, \cot _{pq}(\mu )=l\frac{pe^{l\mu }+qe^{-l\mu }}{pe^{l\mu }-qe^{-l\mu }}\cdot \end{aligned}$$

2.2 JEF technique

The JEF technique (Elboree 2011; Allahyani et al. 2022) is used to find explicit waveform solutions for the KS Eq. (1), and it is briefly presented here. To further explain the advantages of the JEF technique in this instance, apply the technique that is described below;

Step 1 We assume the solution of nonlinear ODE (4) as

$$\begin{aligned} g(\mu )=\sum _{s=0}^{n}a_{s}P^s(\mu ), \end{aligned}$$
(11)

where \(a_s(s=1, 2, \cdots , n)\) are real parameters to be computed. The function \(P(\mu )\) satisfy the following Jacobi elliptic equation;

$$\begin{aligned} P'(\mu )=\sqrt{m_1+m_2P^2(\mu )+\frac{m_3}{2}P^4(\mu )}, \end{aligned}$$
(12)

where \(m_1,\,\,m_2\) and \(m_3\) are constants.

Step 2 We can figure out s by applying the homogeneous balancing principle.

Step 3 When Eq. (12) is replaced and Eq. (12) is applied to (4), we obtain an algebraic system with multiple \(P(\mu )\) monomials. Once this system is solved, the required collection of parameters is acquired.

Step 4 To find the solution to Eq. (12), utilise the choices for the constants \(m_1\), \(m_2\), and \(m_3\) in Table 1.

Elliptic functions fulfill the following relationships.

$$\begin{aligned} \begin{aligned} sn^{2}(\mu )+cn^{2}(\mu )=1,~dn^{2}(\mu )+\varrho ^{2}sn^{2}(\mu )=1, ~(sn(\mu ))'=cn(\mu )dn(\mu ), \\ (cn(\mu ))'=-sn(\mu )dn(\mu ),~~(dn(\mu ))'=-\varrho ^{2}sn(\mu )cn(\mu ). \end{aligned} \end{aligned}$$
(13)

Here we employ \(sn(\mu )=sn(\mu |\varrho )\).

The hyperbolic functions for \(\varrho \mapsto 1\) are shown in Table 2, but the elliptic functions for \(\varrho \mapsto 0\) typically tend to be trigonometric functions.

Table 1 Types of solutions of (13)
Full size table
Table 2 When \(\varrho \mapsto 1\)
Full size table

3 Soliton solutions to KS Eq. (1) via SSE technique

The KS equation is now subjected to the method’s aforementioned steps. Equation (1) is solved using the wave transition (3) to get

$$\begin{aligned} \frac{1}{2}\alpha \mathcal {V}^{2}-\omega \mathcal {V}+\frac{1}{2}\eta \mathcal {V}'^2+\kappa \mathcal {V}'^2+(\kappa \mathcal {V}+\beta )\mathcal {V}'=0. \end{aligned}$$
(14)

By integrating (14) with respect to the already-existing variable \(\mu\), we can lower the order of the ODE

$$\begin{aligned} \left( \frac{1}{2}\eta +\kappa \right) (\mathcal {V}')^2+ (\kappa \mathcal {V}+\beta )\mathcal {V}''+ \frac{1}{2}\alpha \mathcal {V}^2-\omega \mathcal {V}=C, \end{aligned}$$
(15)

where C indicates the integration constant. We use the balancing principle to Eq. (15) to determine the value of s and obtain \(s=2\). Equation (5) provides us with the following

$$\begin{aligned} \mathcal {V}(\mu )={b}_{0}+b_{1}\mathcal {K}(\mu )+b_{2}\mathcal {K}^2(\mu ), \,\,\,b_{2}\ne 0, \end{aligned}$$
(16)

where the arbitrary constants \(b_{0},~b_{1}\) and \(b_{2}\) are used. We substitute Eqs. (16) into (14), we get a system of algebraic equations. Solving this system we have the following set of solution parameters

Set 1

$$\begin{aligned} \ \kappa =-\frac{\eta }{5},~~~b_0=-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )},~~~b_1=0,~~~b_2=-\frac{15 \omega }{4\eta (\nu ^2-3\sigma )}, \end{aligned}$$
(17)

Set 2

$$\begin{aligned} \alpha =-\frac{1}{3}\eta \nu ,~~~\beta =-\frac{\omega }{2\nu },~~\kappa =-\frac{\eta }{6},~~~ b_{0}=-\frac{3\omega }{\eta \nu },\,\,\,b_1=\frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9V^2}{\nu \sigma }},\,\,\, b_{2}=0. \end{aligned}$$
(18)

The following solution collections are accessed using the aforementioned technique along with Set 1;

Case i If \(\nu >0\) and \(\sigma =0\), the outcomes are as follows

$$\begin{aligned} \begin{aligned} u_{1}(x,t)=&-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}+\frac{15 \omega }{4\eta (\nu ^2-3\sigma )} pq \nu \,\,\text {sech}^2_{pq}\left( \sqrt{\nu }\mu \right) ,\\ u_{2}(x,t)=&-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}-\frac{15 \omega }{4\eta (\nu ^2-3\sigma )}pq\nu \,\,\text {csch}^2_{pq}\left( \sqrt{\nu }\mu \right) . \end{aligned} \end{aligned}$$
(19)

Case ii If \(\nu <0\) and \(\sigma =0\), we obtain the outcome

$$\begin{aligned} \begin{aligned} u_{3}(x,t)&=-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}+\frac{15 \omega }{4\eta (\nu ^2-3\sigma )}pq\nu \,\,\sec ^2_{pq}\left( \sqrt{-\nu }\mu \right) ,\\ u_{4}(x,t)&=-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}+\frac{15 \omega }{4\eta (\nu ^2-3\sigma )} pq\nu \,\,\csc ^2_{pq}\left( \sqrt{-\nu }\mu \right) . \end{aligned} \end{aligned}$$
(20)

Case iii If \(\nu <0\) and \(\sigma =\frac{\nu ^{2}}{4}\), the outcomes are as follows

$$\begin{aligned} \begin{aligned} u_{5}(x,t)&=-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}+\frac{15 \omega }{4\eta (\nu ^2-3\sigma )} \frac{\nu }{2}\,\,\tanh ^2_{pq}\left( \sqrt{\frac{-\nu }{2}\mu }\right) ,\\ u_{6}(x,t)&=-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}+\frac{15 \omega }{4\eta (\nu ^2-3\sigma )} \frac{\nu }{2}\,\,\coth ^2_{pq}\left( \sqrt{\frac{-\nu }{2}\mu }\right) ,\\ u_{7}(x,t)&=-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}\pm \frac{15 \omega }{4\eta (\nu ^2-3\sigma )} \bigg (\sqrt{\frac{-\nu }{2}}\,\,\left( \tanh _{pq}\left( \sqrt{-2\nu }\mu \right) \pm l\sqrt{pq}\,\,\text {sech}_{pq}\left( \sqrt{-2\nu }\mu \right) \right) \bigg )^2,\\ u_{8}(x,t)&=-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}\pm \frac{15 \omega }{4\eta (\nu ^2-3\sigma )} \bigg (\sqrt{\frac{-\nu }{2}}\,\,(\coth _{pq}\left( \sqrt{-2\nu }\mu )\pm \sqrt{pq}\,\,\text {csch}_{pq}\left( \sqrt{-2\nu }\mu \right) \right) \bigg )^2,\\ u_{9}(x,t)&=-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}\pm -\frac{15 \omega }{4\eta (\nu ^2-3\sigma )} \bigg (\sqrt{\frac{-\nu }{8}}\,\,\left( \tanh _{pq}\left( \sqrt{\frac{-\nu }{8}\mu }\right) + \,\,\coth _{pq}\left( \sqrt{\frac{-\nu }{8}\mu }\right) \right) \bigg )^2\cdot \end{aligned} \end{aligned}$$
(21)

Case iv: If \(\nu >0\) and \(\sigma =\frac{\nu ^{2}}{4}\), the outcomes are as follows

$$\begin{aligned} \begin{aligned} u_{10}(x,t)&=-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}-\frac{15 \omega }{4\eta (\nu ^2-3\sigma )} \frac{\nu }{2}\,\,\tan ^2_{pq}\left( \sqrt{\frac{\nu }{2}\mu }\right) ,\\ u_{11}(x,t)&=-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}-\frac{15 \omega }{4\eta (\nu ^2-3\sigma )}\frac{\nu }{2}\,\,\cot ^2_{pq}\bigg (\sqrt{\frac{\nu }{2}\mu },\\ u_{12}(x,t)&=-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}\pm \frac{15 \omega }{4\eta (\nu ^2-3\sigma )} \bigg (\sqrt{\frac{\nu }{2}}\,\,(\tan _{pq}(\sqrt{2\nu }\mu )\pm l\sqrt{pq}\,\,\sec _{pq}\left( \sqrt{2\nu }\mu )\right) \bigg )^2,\\ u_{13}(x,t)&=-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}\pm \frac{15 \omega }{4\eta (\nu ^2-3\sigma )} \bigg (\sqrt{\frac{\nu }{2}}\,\,\left( \cot _{pq}\left( \sqrt{2\nu }\mu \right) \pm \sqrt{pq}\,\,\csc _{pq}\left( \sqrt{2\nu }\mu \right) \right) \bigg )^2,\\ u_{14}(x,t)&=-\frac{5\nu \omega }{4\eta (\nu ^2-3\sigma )}\pm \frac{15 \omega }{4\eta (\nu ^2-3\sigma )} \bigg (\sqrt{\frac{\nu }{8}}\,\,\left( \tan _{pq}\left( \sqrt{\frac{\nu }{8}\mu }\right) + \,\,\cot _{pq}\left( \sqrt{\frac{\nu }{8}\mu }\right) \right) \bigg )^2, \end{aligned} \end{aligned}$$
(22)

where in all above cases \(\mu =x-\omega t\).

The following solutions collections are accessed using the aforementioned technique along with Set 2;

Case i If \(\nu >0\) and \(\sigma =0\), the outcomes are as follows

$$\begin{aligned} \begin{aligned} u_{15}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }}\sqrt{-pq\nu }\,\,\text {sech}_{pq}\left( \sqrt{\nu }\mu \right) ,\\ u_{16}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }} \sqrt{pq\nu }\,\,\text {csch}_{pq}\left( \sqrt{\nu }\mu \right) . \end{aligned} \end{aligned}$$
(23)

Case ii If \(\nu <0\) and \(\sigma =0\), we obtain the outcome

$$\begin{aligned} \begin{aligned} u_{17}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }} \sqrt{-pq\nu }\,\,\sec _{pq}\left( \sqrt{-\nu }\mu \right) ,\\ u_{18}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }} \sqrt{-pq\nu }\,\,\csc _{pq}\left( \sqrt{-\nu }\mu \right) . \end{aligned} \end{aligned}$$
(24)

Case iii If \(\nu <0\) and \(\sigma =\frac{\nu ^{2}}{4}\), the outcomes are as follows

$$\begin{aligned} \begin{aligned} u_{19}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }}\sqrt{\frac{-\nu }{2}}\,\,\tanh _{pq}\left( \sqrt{\frac{-\nu }{2}\mu }\right) ,\\ u_{20}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }} \sqrt{\frac{-\nu }{2}}\,\,\coth _{pq}\left( \sqrt{\frac{-\nu }{2}\mu }\right) ,\\ u_{21}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }} \bigg (\sqrt{\frac{-\nu }{2}}\,\,\left( \tanh _{pq}\left( \sqrt{-2\nu }\mu \right) \pm l\sqrt{pq}\,\,\text {sech}_{pq}\left( \sqrt{-2\nu }\mu \right) \right) \bigg ),\\ u_{22}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }} \bigg (\sqrt{\frac{-\nu }{2}}\,\,\left( \coth _{pq}\left( \sqrt{-2\nu }\mu \right) \pm \sqrt{pq}\,\,\text {csch}_{pq}\left( \sqrt{-2\nu }\mu \right) \right) \bigg ),\\ u_{23}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }} \bigg (\sqrt{\frac{-\nu }{8}}\,\,\left( \tanh _{pq}\left( \sqrt{\frac{-\nu }{8}\mu }\right) + \,\,\coth _{pq}\left( \sqrt{\frac{-\nu }{8}\mu }\right) \right) \bigg ). \end{aligned} \end{aligned}$$
(25)

Case iv If \(\nu >0\) and \(\sigma =\frac{\nu ^{2}}{4}\), the outcomes are as follows

$$\begin{aligned} \begin{aligned} u_{24}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }} \sqrt{\frac{\nu }{2}}\,\,\tan _{pq}\left( \sqrt{\frac{\nu }{2}\mu }\right) ,\\ u_{25}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }} \sqrt{\frac{\nu }{2}}\,\,\cot _{pq}\left( \sqrt{\frac{\nu }{2}\mu }\right) ,\\ u_{26}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }} \bigg (\sqrt{\frac{\nu }{2}}\,\,\left( \tan _{pq}\left( \sqrt{2\nu }\mu \right) \pm l\sqrt{pq}\,\,\sec _{pq}\left( \sqrt{2\nu }\mu \right) \right) \bigg ),\\ u_{27}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }} \bigg (\sqrt{\frac{\nu }{2}}\,\,\left( \cot _{pq}\left( \sqrt{2\nu }\mu \right) \pm \sqrt{pq}\,\,\csc _{pq}\left( \sqrt{2\nu }\mu \right) \right) \bigg ),\\ u_{28}(x,t)&=-\frac{3\omega }{\eta \nu }\pm \frac{1}{\eta }\sqrt{\frac{6C\eta \nu -9\omega ^2}{\nu \sigma }} \bigg (\sqrt{\frac{\nu }{8}}\,\,\left( \tan _{pq}\left( \sqrt{\frac{\nu }{8}\mu }\right) + \,\,\cot _{pq}\left( \sqrt{\frac{\nu }{8}\mu }\right) \right) \bigg ), \end{aligned} \end{aligned}$$
(26)

where in all above cases \(\mu =x-\omega t\).

Next, we apply the JEF technique to additional soliton families of the KS equation.

4 Periodic solutions of the KS Eq. (1) via JEF technique

In this section, we delve into the utilization of the Jacobi elliptic function (JEF) technique to identify solutions for the KS Eq. (1) corresponding to various waveforms including shock waves, periodic waves, solitary waves, and double periodic waves. The JEF technique proves to be a reliable approach for handling such complex waveform solutions. To achieve this, we leverage the Eq. (15) to derive the solution

$$\begin{aligned} \mathcal {V}(\mu )=a_0+a_1 P(\mu )+a_2P(\mu )^2. \end{aligned}$$
(27)

The following algebraic system results from substituting (27) in Eq. (15) and then using Eq. (11). If we use the program Maple, MATLAB, or Mathematica to solve this system, we get

$$\begin{aligned} \alpha =2 \kappa m_{2},\,\,\, \beta =-\frac{\omega }{2m_2}, \,\,\, \eta =-6\kappa ,\,\, a_{0}=\frac{\omega }{2\kappa m_2},\,\,\, a_{1}=\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}},\,\,\, a_{2}=0. \end{aligned}$$
(28)

From (27), we use the conclusion for (15) as follows

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}P(\mu ). \end{aligned}$$
(29)

We can identify several solitons based on the parameters \(m_1\), \(m_2\), and \(m_3\) using the Eq. (12);

Subcase 1 When \(m_1=1,\,\,m_2=-(1+\varrho ^2),\,\,\,m_3=2\varrho ^2.\)

By interpreting \(P(\mu )= \text {sn}(\mu ,\varrho )\) in the solution of Eq. (29), we can identify a periodic wave solution to Eq. (12)

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\text {sn}(\mu ,\varrho ). \end{aligned}$$
(30)

Equation (30) degenerates into the shock wave solution of (15) in the case \(\varrho \mapsto 1\)

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\tanh (\mu ). \end{aligned}$$
(31)

Back substitution allows us to solve (1)

$$\begin{aligned} u_{29}(x,t)= \frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\tanh (x-\omega t). \end{aligned}$$
(32)

Subcase: 2 When \(m_1=-\varrho ^2(1-\varrho ^2),\,\,m_2=2\varrho ^2-1,\,\,\,m_3=2.\)

By interpreting \(P(\mu )= \text {ds}(\mu ,\varrho )\) in the solution of Eq. (29), we can identify a periodic wave solution to Eq. (12);

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\text {ds}(\mu ,\varrho ). \end{aligned}$$
(33)

When \(\varrho \mapsto 1\) occurs, Eq. (33) degenerates into

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\text {csch}(\mu ). \end{aligned}$$
(34)

Back substitution allows us to solve (1)

$$\begin{aligned} u_{30}(x,t)= \frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\text {csch}(x-\omega t). \end{aligned}$$
(35)

Subcase: 3 When \(m_1=1-\varrho ^2,\,\,m_2=2-\varrho ^2,\,\,\,m_3=2.\)

By interpreting \(P(\mu )= \text {cs}(\mu ,\varrho )\) in the solution of Eq. (29), we can identify a periodic wave solution to Eq. (12);

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\text {cs}(\mu ,\varrho ). \end{aligned}$$
(36)

When \(\varrho \mapsto 0\) occurs, Eq. (36) degenerates into

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa } \sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\coth (\mu ). \end{aligned}$$
(37)

Back substitution allows us to solve (1)

$$\begin{aligned} u_{31}(x,t)= \frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\coth (x-\omega t). \end{aligned}$$
(38)

Similarly for \(\varrho \mapsto 1\), we have

$$\begin{aligned} u_{32}(x,t)= \frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\text {csch}(x-\omega t). \end{aligned}$$
(39)

Subcase: 4 When \(m_1=1-\varrho ^2,\,\,m_2=2\varrho ^2-1,\,\,\,m_3=-2\varrho ^2.\)

By interpreting \(P(\mu )= \text {cn}(\mu ,\varrho )\) in the solution of Eq. (29), we can identify a periodic wave solution to Eq (12);

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\text {cn}(\mu ,\varrho ). \end{aligned}$$
(40)

When \(\varrho \mapsto 1\) occurs, Eq. (40) degenerates into

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\text {sech}(\mu ). \end{aligned}$$
(41)

Back substitution allows us to solve (1)

$$\begin{aligned} u_{33}(x,t)=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\text {sech}(x-\omega t). \end{aligned}$$
(42)

Subcase: 5 When \(m_1=\eta ^2-1,\,\,m_2=2-\varrho ^2,\,\,\,m_3=-2.\)

By interpreting \(P(\mu )= \text {dn}(\mu ,\varrho )\) in the solution of Eq. (29), we can identify a periodic wave solution to Eq. (12);

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\text {dn}(\mu ,\varrho ). \end{aligned}$$
(43)

When \(\varrho \mapsto 1\) occurs, Eq. (43) degenerates into

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\text {sech}(\mu ). \end{aligned}$$
(44)

Back substitution allows us to solve (1)

$$\begin{aligned} u_{34}(x,t)= \frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\text {sech}(x-\omega t). \end{aligned}$$
(45)

Subcase: 6 When \(m_1=\frac{1}{4},\,\,m_2=\frac{\varrho ^2-2}{2},\,\,\,m_3=\frac{\varrho ^2}{2}\cdot\)

By interpreting \(P(\mu )= \frac{\text {sn}(\mu ,\varrho )}{1\pm \text {dn}(\mu ,\varrho )}\) in the solution of Eq. (29), we can identify a periodic wave solution to Eq. (12);

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\text {sn}(\mu ,\varrho )}{(1\pm \text {dn}(\mu ,\varrho ))}\cdot \end{aligned}$$
(46)

When \(\varrho \mapsto 1\) occurs, Eq. (46) degenerates into

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\tanh (\mu )}{(1\pm \text {sech}(\mu ))}\cdot \end{aligned}$$
(47)

Back substitution allows us to solve (1)

$$\begin{aligned} u_{35}(x,t)=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\tanh (x-\omega t)}{(1\pm \text {sech}(x-\omega t))}. \end{aligned}$$
(48)

Subcase: 7 When \(m_1=\frac{\varrho ^2}{4},\,\,m_2=\frac{\varrho ^2-2}{2},\,\,\,m_3=\frac{\varrho ^2}{2}\cdot\)

By interpreting \(P(\mu )= \frac{\text {sn}(\mu ,\varrho )}{1\pm \text {dn}(\mu ,\varrho )}\) in the solution of Eq. (29), we can identify a double periodic wave solution to Eq. (12);

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\text {sn}(\mu ,\varrho )}{(1\pm \text {dn}(\mu ,\varrho ))}\cdot \end{aligned}$$
(49)

When \(\varrho \mapsto 1\) occurs, Eq. (49) degenerates into

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\tanh (\mu )}{(1\pm \text {sech}(\mu ))}\cdot \end{aligned}$$
(50)

Back substitution allows us to solve (1)

$$\begin{aligned} u_{36}(x,t)= \frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\tanh (x-\omega t)}{(1\pm \text {sech}(x-\omega t))}. \end{aligned}$$
(51)

Subcase: 8 When \(m_1=-\frac{(1-\varrho ^2)^2}{4},\,\,m_2=\frac{(\varrho ^2+1)}{2}, \,\,\,m_3=\frac{-1}{2}\cdot\)

By interpreting \(P(\mu )=\varrho \text {cn}(\mu ,\varrho )\pm \text {dn}(\mu ,\varrho )\) in the solution of Eq. (29), we can identify a double periodic wave solution to Eq. (12);

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}(\varrho \text {cn}(\mu ,\varrho )\pm \text {dn}(\mu ,\varrho ))\cdot \end{aligned}$$
(52)

When \(\varrho \mapsto 1\) occurs, Eq. (52) degenerates into

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}(\text {sech}(\mu )\pm \text {sech}(\mu ))\cdot \end{aligned}$$
(53)

Back substitution allows us to solve (1)

$$\begin{aligned} u_{37}(x,t)= \frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}(\text {sech}(x-\omega t)\pm \text {sech}(x-\omega t)). \end{aligned}$$
(54)

Subcase: 9 When \(m_1=\frac{\varrho ^2-1}{4},\,\,m_2=\frac{\varrho ^2+1}{2},\,\,\,m_3=\frac{\varrho ^2-1}{2}\cdot\)

By interpreting \(P(\mu )=\frac{\text {dn}(\mu ,\varrho )}{1\pm \text {sn}(\mu ,\varrho )}\) in the solution of Eq. (29), we can identify a double periodic wave solution to Eq. (12);

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\text {dn}(\mu ,\varrho )}{(1\pm \text {sn}(\mu ,\varrho ))}\cdot \end{aligned}$$
(55)

When \(\varrho \mapsto 1\) occurs, Eq. (55) degenerates into

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\text {sech}(\mu )}{(1\pm \tanh (\mu ))}\cdot \end{aligned}$$
(56)

Back substitution allows us to solve (1)

$$\begin{aligned} u_{38}(x,t)= \frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\text {sech}(x-\omega t)}{(1\pm \tanh (x-\omega t))}\cdot \end{aligned}$$
(57)

Subcase: 10 When \(m_1=\frac{1-\varrho ^2}{4},\,\,m_2=\frac{1-\varrho ^2}{2},\,\,\,m_3=\frac{1-\varrho ^2}{2}\cdot\)

By interpreting \(P(\mu )=\frac{\text {cn}(\mu ,\varrho )}{1\pm \text {sn}(\mu ,\varrho )}\) in the solution of Eq. (29), we can identify a double periodic wave solution to Eq. (12);

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\text {cn}(\mu ,\varrho )}{(1\pm \text {sn}(\mu ,\varrho ))}\cdot \end{aligned}$$
(58)

When \(\varrho \mapsto 1\) occurs, Eq. (58) degenerates into

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\text {sech}(\mu )}{(1\pm \tanh (\mu ))}\cdot \end{aligned}$$
(59)

Back substitution allows us to solve (1)

$$\begin{aligned} u_{39}(x,t)= \frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\text {sech}(x-\omega t)}{(1\pm \tanh (x-\omega t))}\cdot \end{aligned}$$
(60)

Subcase: 11 When \(m_1=\frac{1}{4},\,\,m_2=\frac{(1-\varrho ^2)^2}{2},\,\,\,m_3=\frac{(1-\varrho ^2)^2}{2}\cdot\)

By interpreting \(P(\mu )=\frac{\text {sn}(\mu ,\varrho )}{\text {dn}(\mu ,\varrho )\pm \text {cn}(\mu ,\varrho )}\) in the solution of Eq. (29), we can identify a double periodic wave solution to Eq. (12);

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}} \frac{\text {sn}(\mu ,\varrho )}{(\text {dn}(\mu ,\varrho )\pm \text {cn}(\mu ,\varrho ))}\cdot \end{aligned}$$
(61)

When \(\varrho \mapsto 1\) occurs, Eq. (61) degenerates into

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\tanh (\mu )}{(\text {sech}(\mu )\pm \text {sech}(\varrho ))}\cdot \end{aligned}$$
(62)

Back substitution allows us to solve (1)

$$\begin{aligned} u_{40}(x,t)=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\frac{\tanh (x-\omega t)}{(\text {sech}(x-\omega t)\pm \text {sech}(x-\omega t))}\cdot \end{aligned}$$
(63)

Subcase: 12 When \(m_1=0,\,\,m_2=0,\,\,\,m_3=2.\)

By interpreting \(P(\mu )=\frac{D}{\mu }\) in the solution of Eq. (29), we can identify a double periodic wave solution to Eq. (12);

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\bigg (\frac{E}{\mu }\bigg )\cdot \end{aligned}$$
(64)

Back substitution allows us to solve (1)

$$\begin{aligned} u_{41}(x,t)=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\bigg (\frac{E}{x-\omega t}\bigg )\cdot \end{aligned}$$
(65)

Subcase: 13 When \(m_1=0,\,\,m_2=1,\,\,\,m_3=0.\)

By interpreting \(P(\mu )=De^{\mu }\) in the solution of Eq. (29), we can identify a double periodic wave solution to Eq. (12);

$$\begin{aligned} \mathcal {V}(\mu )=\frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\big (Ee^{\mu }\big )\cdot \end{aligned}$$
(66)

Back substitution allows us to solve (1)

$$\begin{aligned} u_{42}(x,t)= \frac{\omega }{2\kappa m_2}+\frac{1}{\kappa }\sqrt{\frac{4C\kappa m_2+\omega ^2}{8m_1m_2}}\bigg (Ee^{x-\omega t}\bigg ). \end{aligned}$$
(67)

where in the instances outlined above, E is a constant.

5 Graphical interpretation of the solitons

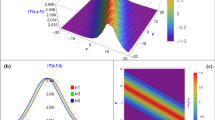
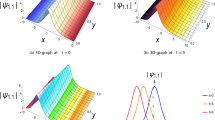
Because graphs display the physical behaviors of solutions, they play a crucial part in the article’s structure. Here, using the SSE and JEF, we investigate the behavior and physical significance of the KS equation solutions that we have obtained. It should be emphasized that the results given in Kumar et al. (2022) only take the form of traveling wave solutions, rational form solutions, dark-bright solitons, singular solitons, singular bell-shaped solitons, and periodic wave solitons. In the current approach, we provide the results as solitary wave patterns, singletons, dark-singular-mixed, combo dark-bright, single, bright, exponential, rational functions, shock waves, and periodic and double periodic solitons. The SSE yields the bright and dark solitons, respectively, from the solutions \(|u_1(x,t)|\), \(|u_5(x,t)|\), \(|u_{15}(x,t)|\) and \(|u_{19}(x,t)|\). The periodic singular solitons are represented by \(|u_2(x,t)|\), \(|u_6(x,t)|\), \(|u_8(x,t)|\), \(|u_{16}(x,t)|\), \(|u_{20}(x,t)|\) and \(|u_{22}(x,t)|\) while \(|u_3(x,t)|\), \(|u_4(x,t)|\), \(|u_{10}(x,t)|\), \(|u_{11}(x,t)|\), \(|u_{12}(x,t)|\), \(|u_{13}(x,t)|\), \(|u_{14}(x,t)|\), \(|u_{17}(x,t)|\), \(|u_{18}(x,t)|\), \(|u_{24}(x,t)|\), \(|u_{25}(x,t)|\), \(|u_{26}(x,t)|\), \(|u_{27}(x,t)|\) and \(|u_{28}(x,t)|\) show the singular solitons. By \(|u_7(x,t)|\), \(|u_{21}(x,t)|\) and \(|u_9(x,t)|\), \(|u_{23}(x,t)|\) respectively, dark-bright-combined and dark-singular-combined solitons are elaborated. Figure 1, 2, 3, 4, 5, 6 and 7 illustrates the dynamics of such soliton solutions with a specific set of parameters. The JEF method provides exponential, rational functions, shock waves, periodic and double periodic solitons. Figures 8 and 9 illustrate the dynamics of such soliton solutions with a specific set of parameters.

Fig. 1
figure 1

Wave form of the \(u_1\) with \(\eta =1,~p=1,~q=-1,~\omega =1,~\sigma =0\) and \(\nu =1\)

Full size image
Fig. 2
figure 2

Wave form of the \(u_2\) with \(\eta =1,~p=1,~q=-1,~\omega =1,~\sigma =0\) and \(\nu =1\)

Full size image
Fig. 3
figure 3

Wave form of the \(u_3\) with \(\eta =1,~p=1,~q=1,~\omega =1,~\sigma =0\) and \(\nu =-1\)

Full size image
Fig. 4
figure 4

Wave form of the \(u_5\) with \(\eta =1,~p=1,~q=1,~\omega =1,~\sigma =-2\) and \(\nu =-2\)

Full size image
Fig. 5
figure 5

Wave form of the \(u_7\) with \(\eta =1,~p=1,~q=1,~\omega =1,~\sigma =-2\) and \(\nu =-2\)

Full size image
Fig. 6
figure 6

Wave form of the \(u_{10}\) with \(\eta =1,~p=1,~q=1,~\omega =1,~\sigma =2\) and \(\nu =2\)

Full size image
Fig. 7
figure 7

Wave form of the \(u_{29}\) with \(\kappa =1,~C=1,~m_1=1,~m_2=-2,~m_3=2\) and \(\omega =1\)

Full size image
Fig. 8
figure 8

Wave form of the \(u_{30}\) with \(\kappa =1,~C=1,~m_1=1,~m_2=1,~m_3=2\) and \(\omega =1\)

Full size image
Fig. 9
figure 9

Wave form of the \(u_{42}\) with \(\kappa =1,~C=1,~m_1=1,~m_2=1,~m_3=1,~E=1\) and \(\omega =1\)

Full size image

6 Discussion and conclusions

The current investigation successfully employs both the SSE and JEF techniques to derive analytic wave solutions for the KS equation. These solutions, characterized by general expressions with multiple free parameters, encompass a variety of mathematical functions such as trigonometric, hyperbolic, exponential, and rational functions. Notably, certain solutions manifest in singularity form wave profiles, representing a novel contribution to the existing literature. Visual representation through 2D and 3D graphics, achieved by assigning appropriate values to the arbitrary parameters, enhances our comprehension of the dynamic wave profiles inherent in the KS equation. The versatility of the obtained solutions extends their applicability across various branches of nonlinear sciences, including mathematical physics, plasma physics, nonlinear dynamics, marine physics, optical fibers, ocean engineering, and related fields in nonlinear wave sciences.

Symbolic computations and the resulting solutions underscore the robustness, potency, fruitfulness, and simplicity of both the SSE and JEF techniques. The novelty of the solutions is emphasized by their absence in prior literature. Moreover, the applicability of these techniques extends to the analytical soliton solutions of diverse nonlinear evolution equations, rendering them valuable tools for exploring nonlinear phenomena. This study underscores the SSE and JEF techniques as robust, powerful, and reliable methodologies for elucidating exact solitary wave solutions in diverse nonlinear partial differential equations. The research advocates for heightened attention to this noteworthy field, highlighting the potential for investigating numerous other nonlinear partial differential equations using these formidable techniques.