1 Introduction

The integrable, nonlinear and higher-order differential equations represent many phenomena in the real world as Nanocarbon field, fluids, water propagation, Geology and earthquakes science, image processing, etc. (Sun 2018; Ramzan 2020; Malischewsky 2011). Here, we focus on a new integrable and highly nonlinear partial differential equation that is known as the integrable (3 + 1)-dimensional Date–Jimbo–Kashiwara–Miwa (DJKM) equation with variable coefficients which has the form;

$$u_{xxxxy} + 4u_{xxy} u_{x} + 2u_{xxx} u_{y} + 6u_{xy} u_{xx} - \alpha u_{yyy} - 2\beta h\left( t \right)u_{xxt} + {\text{k}}\left( {\text{t}} \right)\left( {{\text{au}}_{{\text{x}}} + {\text{bu}}_{{\text{y}}} + {\text{cu}}_{{\text{z}}} } \right)_{{{\text{xx}}}} = 0$$
(1)

which characterize the real physical phenomena for the inhomogeneous of media, \(u\left( {x,y,z,t} \right)\) is the amplitude of the wave and \(\alpha ,\beta ,a,b,c\) are arbitrary constants \(h\left( t \right)\) is a smooth function, \(k\left( t \right)\) is a function of t.

For \(h\left( t \right)\) = 1,\(k\left( t \right) = 1\), Eq. (1) minimize to (3 + 1)-dimensional Date–Jimbo–Kashiwara–Miwa.

equation with constant coefficients

$$u_{xxxxy} + 4u_{xxy} u_{x} + 2u_{xxx} u_{y} + 6u_{xy} u_{xx} - \alpha u_{yyy} - 2\beta u_{xxt} + \left( {{\text{au}}_{{\text{x}}} + {\text{bu}}_{{\text{y}}} + {\text{cu}}_{{\text{z}}} } \right)_{{{\text{xx}}}} = 0$$
(2)

Equation (2) integrable in the Painlev´e analysis and allowed multiple soliton solutions consisting of solitonic, singular, periodic solutions. When \(h\left( t \right) = 1, k\left( t \right) = 0\), Eq. (1) reduces to the (2 + 1)-dimensional Date–Jimbo–Kashiwara–Miwa (DJKM) equation.

$$u_{xxxxy} + 4u_{xxy} u_{x} + 2u_{xxx} u_{y} + 6u_{xy} u_{xx} - \alpha u_{yyy} - 2\beta u_{xxt} = 0{ }$$
(3)

which describes the propagation of nonlinear dispersive waves in inhomogeneous media, where \(\alpha\) and \(\beta\) are real constants.

This equation at \(\alpha = - 1 \;{\text{and}}\; \beta = 1\) can be written as the bilinear Hirota form as:

$${\mathcal{D}}_{x} \left( {\left( {{\mathcal{D}}_{x}^{3} {\mathcal{D}}_{y} - 3{\mathcal{D}}_{x} {\mathcal{D}}_{t} } \right)\phi .\phi } \right).\phi^{2} + {\mathcal{D}}_{y} \left( {\left( {0.5{\mathcal{D}}_{x}^{4} + 1.5{\mathcal{D}}_{y}^{3} } \right)\phi .\phi } \right).\phi^{2} = 0.$$
(4)

where \({\mathcal{D}}_{x} ,\) \({\mathcal{D}}_{y}\), \({\mathcal{D}}_{t}\) are the Hirota’s bilinear operators.

with the customary definition of Hirota’s bilinear operators (Hirota 2004; Cheng and Zhang 2017; Xu 2019; Kang and Xia 2020).

$${\mathcal{D}}_{x}^{m} {\mathcal{D}}_{t}^{n} \emptyset \cdot \omega = \left( {\frac{\partial }{\partial x} - \frac{\partial }{{\partial x^{\prime } }}} \right)^{m} \left( {\frac{\partial }{\partial t} - \frac{\partial }{{\partial t^{\prime } }}} \right)^{n} \emptyset \left( {x,t} \right)\omega \left( {x^{\prime } ,t^{\prime } } \right)\left| {t^{\prime } = t, \quad x^{\prime } = x.} \right.$$

where the D-operators’ properties

$$\frac{{{\mathcal{D}}_{x}^{2} \phi .\phi }}{{\phi^{2} }} = u ,\; \frac{{{\mathcal{D}}_{x}^{4} \phi .\phi }}{{\phi^{2} }} = u_{xx} + 3u^{2} ,\; \frac{{{\mathcal{D}}_{x}^{6} \phi .\phi }}{{\phi^{2} }} = u_{xxxx} + 15uu_{xx} + 15u^{3} .$$

Equation (1) consider the extension of the Kadomtsev–Petviashvili (KP) hierarchy (Chauhan et al. 2020; Rizvi et al. 2020a).

Many studies are applied to Eq. (1) and generated many types of solutions. Ismael et al. (2020) applied the Hirota method to explore the class of lump-typed solutions that are analytical solutions localized in all directions in space and also studied the collision phenomenon between the lump-typed solutions and other soliton solutions. Chauhan et al. (2020) used the fourth prolongation theory to generate the Lie infinitesimals for Eq. (1) and investigated some soliton solution for it. Using the bilinear Bäcklund transformation with aid of some quadratic functions, Cheng et al. (2019) explored exact solutions in the form of Lump and interacted solutions for Eq. (1). In the three dimensions and the variable coefficients, Kang and Xia (2020) generated double-solitary wave solution and rogue wave solution. Other methods (Guo and Lin 2019; Yuan 2017; Wazwaz 2020a, b; Kang and Xia 2020; Adem et al. 2019; Singh and Gupta 2018) were applied to explore more solutions for Eq. (1). Here, we studied this model using various methods and investigated new and multi different solutions as in the following sections.

2 Lump soliton solutions for Eq. (2)

We apply the Hirota Billinear Method (HBM) (Hirota 2004; Cheng and Zhang 2017; Xu 2019; Kang and Xia 2020; Ma et al. 2018) to explore soliton and Lump soliton solutions for Eq. (2). According to our observation, the resulted solutions predicate on the characteristics and physical significance of the problem. The Hirota method is effective in generating many types of soliton solutions (Sadat et al. 2018; Yang et al. 2018; Yong 2018; Li et al. 2019; Zhou et al. 2019; Zhang and Xia 2020). The interaction solutions have been studied in many nonlinear evolution equations (Ma et al. 2020; Ali and Hadhoud 2019; Ali et al. 2020; Ali and Ma 2019; Mohamed 2019; M 2015; Yu and Sun 2017; Rizvi et al. 2020b; Khater et al. 2020; Aliyu 2020). In this section, we investigate some of the lump soliton solutions and travelling wave solutions in which the medium moves in the direction of propagation of the wave, their dynamics using the Hirota method for (2). By using the singular manifold method (SMM) with two terms truncated series to derive the same ansatz in (Wazwaz 2020b);

$$u\left( {x,y,z,t} \right) = 2({\text{ln}}\left( {\phi \left( {x,y,t,z} \right)} \right)_{x}$$
(5)

where \(\phi \left( {x,y,t,z} \right)\) is a test function and will be assumed later, substitute (5) into (2) generate highly nonlinear PDE;

$$\begin{aligned} & \phi_{xxxxy} \phi^{3} - 12\phi_{xxy} \phi_{x}^{3} - 6\alpha \phi_{y} \phi_{x} \phi_{yy} \phi + 6c\phi_{xx} \phi_{z} \phi_{x} \phi + 6b\phi_{xx} \phi_{z} \phi_{x} \phi \\ & \quad - 12\beta \phi_{xx} \phi_{t} \phi_{x} \phi + 6\phi_{xx}^{2} \phi_{x} \phi_{y} - 12\phi_{x}^{2} \phi_{xxx} \phi_{y} + 12\phi_{x}^{2} \phi_{xx} \phi_{xy} - \phi_{xxxx} \phi_{xy} \phi^{2} - \alpha \phi_{yyyx} \phi^{3} \\ & \quad + 12\phi_{xxxy} \phi_{x}^{2} \phi - 2\phi_{xxxy} \phi^{2} \phi_{xx} - 6\phi_{xy} \phi_{xx}^{2} \phi + 2\phi_{xxx} \phi_{xxy} \phi^{2} - \phi_{xxxxx} \phi_{y} \phi^{2} \\ & \quad - 5\phi_{xxxxy} \phi_{x} \phi^{2} - 3a\phi_{xx}^{2} \phi^{2} + a\phi_{xxxxx} \phi^{3} + c\phi_{xxxz} \phi^{3} + b\phi_{xxxy} \phi^{3} - 2\beta \phi_{xxxt} \phi^{3} \\ & \quad + 6\alpha \phi_{y}^{3} \phi_{x} - 12\beta \phi_{xt} \phi_{x}^{2} \phi + 6\beta \phi_{xt} \phi_{xx} \phi^{2} + 2\beta \phi_{xxx} \phi_{t} \phi^{2} - 4a\phi_{xxx} \phi_{x} \phi^{2} + 12a\phi_{xx} \phi_{x}^{2} \phi \\ & \quad - b\phi_{xxx} \phi_{y} \phi^{2} - 3b\phi_{xxy} \phi_{x} \phi^{2} - 3b\phi_{xx} \phi_{xy} \phi^{2} + 6c\phi_{x}^{2} \phi_{xz} \phi + 6\phi_{xxxx} \phi_{y} \phi_{x} \phi + 3\alpha \phi_{xyy} \phi_{y} \phi^{2} \\ & \quad - 6\alpha \phi_{xy} \phi_{y}^{2} \phi + 3\alpha \phi_{xy} \phi_{yy} \phi^{2} + \alpha \phi_{yyy} \phi_{x} \phi^{2} + 6\beta \phi_{xxt} \phi_{x} \phi^{2} - 6a\phi_{xxxx} - 6c\phi_{x}^{3} \phi_{z} \\ & \quad + 12\beta \phi_{t} \phi_{x}^{3} - 6b\phi_{x}^{3} \phi_{y} = 0 \\ \end{aligned}$$
(6)

To generate a single lump-typed solution, we suppose that the test function in the form;

$$\left\{ {\begin{array}{*{20}l} {\phi = \delta^{2} + \gamma^{2} + \lambda_{11} ,} \hfill \\ {\delta = \lambda_{1} x + \lambda_{2} y + \lambda_{3} t + \lambda_{4} z + \lambda_{5} ,} \hfill \\ {\gamma = \lambda_{6} x + \lambda_{7} y + \lambda_{8} t + \lambda_{9} z + \lambda_{10} .} \hfill \\ \end{array} } \right.$$
(7)

where \(\lambda_{i} , i = 1, \ldots ,11\), are real unknown that will be determined later. A direct substitution from (7) into (6) and gather the coefficients of polynomials in \(x,y,t\) and z. We obtain a nonlinear algebraic system in \(\lambda_{i}\), by solving those equations with aid of Maple, we acquire some sets of solutions as follows;

3 Case I

$$\begin{aligned} & \lambda_{1} = \lambda_{1} ,\lambda_{2} = \lambda_{2} , \lambda_{3} = 0,\lambda_{4} = - \frac{{\left( { - \alpha \lambda_{2}^{3} + b\lambda_{1}^{2} \lambda_{2} + a\lambda_{1}^{3} + 3\alpha \lambda_{2} \lambda_{7}^{2} } \right)}}{{c \lambda_{1}^{2} }},\quad \lambda_{5} = \lambda_{5} , \lambda_{6} = 0,\lambda_{7} = \lambda_{7} ,\lambda_{8} \\ & \quad = \frac{1}{2}\frac{{\left( {b\lambda_{1}^{2} \lambda_{7} + \alpha \lambda_{7}^{3} + c\lambda_{1}^{2} \lambda_{9} - 3\alpha \lambda_{7} \lambda_{2}^{2} } \right)}}{{\beta \lambda_{1}^{2} }},\quad \lambda_{9} = \lambda_{9} ,\lambda_{10} = \lambda_{10} ,\lambda_{11} = \frac{{\lambda_{1}^{4} }}{{\alpha \lambda_{7}^{2} }}, \\ \end{aligned}$$
(8)

4 Case II

$$\begin{aligned} & \lambda_{1} = \lambda_{1} ,\lambda_{2} = \lambda_{2} , \lambda_{3} = \lambda_{3} ,\lambda_{4} = - \frac{{\left( { - \alpha \lambda_{2}^{3} + b\lambda_{1}^{2} \lambda_{2} - 2\beta \lambda_{1}^{2} \lambda_{3} + a\lambda_{1}^{3} + 3\alpha \lambda_{2} \lambda_{7}^{2} } \right)}}{{c \lambda_{1}^{2} }},\quad \lambda_{5} = \lambda_{5} ,\lambda_{6} = 0,\lambda_{7} \\ & = \lambda_{7} ,\lambda_{8} = \lambda_{8} ,\lambda_{9} = - \frac{{\left( {b\lambda_{1}^{2} \lambda_{7} - 2\beta \lambda_{1}^{2} \lambda_{8} + \alpha \lambda_{7}^{3} - 3\alpha \lambda_{7} \lambda_{2}^{2} } \right)}}{{c \lambda_{1}^{2} }},\quad \lambda_{10} = \lambda_{10} ,\lambda_{11} = \frac{{\lambda_{1}^{4} }}{{\alpha \lambda_{7}^{2} }}, \\ \end{aligned}$$
(9)

where \(\lambda_{1} \ne 0, \lambda_{7} \ne 0\).

5 Case III

$$\begin{aligned} & \lambda_{1} = 0,\lambda_{2} = \lambda_{2} , \lambda_{3} = \lambda_{3} ,\lambda_{4} = - \frac{{\left( {\alpha \lambda_{2}^{3} + b\lambda_{6}^{2} \lambda_{2} - 2\beta \lambda_{6}^{2} \lambda_{3} + a\lambda_{2}^{3} - 3\alpha \lambda_{2} \lambda_{7}^{2} } \right)}}{{c \lambda_{6}^{2} }},\quad \lambda_{5} = \lambda_{5} ,\lambda_{7} = \lambda_{7} ,\lambda_{8} \\ & \quad = \lambda_{8} ,\lambda_{9} = - \frac{{\left( {b\lambda_{6}^{2} \lambda_{7} - 2\beta \lambda_{6}^{2} \lambda_{8} - \alpha \lambda_{7}^{3} + 3\alpha \lambda_{7} \lambda_{2}^{2} } \right)}}{{c \lambda_{6}^{2} }},\quad \lambda_{10} = \lambda_{10} ,\lambda_{11} = \frac{{\lambda_{6}^{4} }}{{\alpha \lambda_{2}^{2} }} \\ \end{aligned}$$
(10)

where \(\lambda_{6} \ne 0, \lambda_{2} \ne 0\).

By substituting a result with Eqs. (7)–(9) into (5), the solution of (2) has the form;

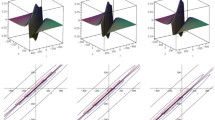
$$u = 4\frac{{ \lambda_{1} \delta + \lambda_{6} \gamma }}{\phi }$$
(11)

By selecting Case I to present three-dimensional plots for the obtained results and depicted in Fig. 1. The 3-dimensional figures are attracted to comprehend the physical phenomena for the acquired solutions.

Fig. 1
figure 1figure 1

Plots of Lump soliton solutions for Eq. (9) with specific values;\(\lambda_{1} = 1,\lambda_{5} = \lambda_{3} = \lambda_{7} = \lambda_{10} = 1,\lambda_{8} = \lambda_{2} = - 1,\;\alpha = 2,\beta = 1, a = b = c = 1\) and \(z = 0,\) \(t = 0, 1\) and 6 respectively, a–c 3D plots for Eq. (11) d-f Contour plot of (a–c), g–i the density plots, j represent a curve solutions at \(y = 0, y = 1\) and \(y = 2\)

Full size image

6 More soliton solutions

In this section, we apply some trigonometric and hyperbolic functions as an ansatz to generate new solutions for the (3 + 1) dimensional (EDJKM) (Liu et al. 2020; Kang and Xia 2020; Wazwaz 2020c; Guo et al. 2015). Assume the solution of Eq. (2) in the form;

$$u\left( {x,y,z,t} \right) = \mathop \sum \limits_{i = 0}^{n} d_{i } \phi \left( {kx + ry + sz - wt} \right)^{i} + \mathop \sum \limits_{i = 1}^{n} d_{i } \phi \left( {kx + ry + sz - wt} \right)^{ - 2n + i}$$
(12)

where \(d_{i} ,\left( { i = 1, \ldots ,n + 1} \right)\) are constants which will be determined later, n belongs to the set of integers which is determined by equaling the highest order derivatives and nonlinear terms in Eq. (2) together and the function \(\phi \left( {kx + ry + sz - wt} \right)\) satisfies the assumed trigonometric and hyperbolic functions and this will be shown in the literature;

6.1 Three-solitary solution

In this portion, to find the three-solitary wave solution of Eq. (3), we suppose

$$\begin{aligned} \theta_{1} & = p_{1} \left[ {a_{1} x + b_{1} y + c_{1} z + \int {\frac{\begin{gathered} (a_{1}^{2} P_{1}^{2} - a_{2}^{2} P_{2}^{2} )^{2} [cos\left( t \right)\left( {a_{1} + b_{1} + c_{1} ) + a_{1}^{2} b_{1} P_{1}^{2} + a_{2}^{2} P_{2}^{2} b_{1} + 2a_{1} a_{2} b_{2} P_{2}^{2} } \right] \hfill \\ - \alpha \left[ {a_{2} b_{2}^{2} P_{2}^{4} \left( {3a_{2} b_{1} - 2a_{1} b_{2} } \right) + b_{1} P_{1}^{2} P_{2}^{2} \left( {a_{2}^{2} b_{1}^{2} + 3a_{1}^{2} b_{2}^{2} - a_{2} b_{1} b_{2} } \right) + a_{1}^{2} b_{1}^{3} P_{1}^{4} } \right] \hfill \\ \end{gathered} }{{4\left( {a_{1}^{2} P_{1}^{2} - a_{2}^{2} P_{2}^{2} } \right)^{2} }}} dt} \right] \\ \theta_{2} & = p_{2} \left[ {a_{2} x + b_{2} y + c_{2} z + \int {\frac{\begin{gathered} (a_{1}^{2} P_{1}^{2} - a_{1}^{2} P_{1}^{2} )^{2} [cos\left( t \right)\left( {a_{1} \lambda_{1} + b_{2} \lambda_{2} + c_{2} \lambda_{3} ) + a_{2}^{2} b_{2} P_{2}^{2} + a_{1}^{2} b_{2} P_{1}^{2} + 2a_{1} a_{2} b_{1} P_{1}^{2} } \right] \hfill \\ \alpha \left[ {a_{1} b_{1}^{2} P_{1}^{4} \left( {3a_{1} b_{2} - 2a_{2} b_{2} } \right) + b_{2} P_{1}^{2} P_{2}^{2} \left( {a_{2}^{2} b_{2}^{2} + 3a_{2}^{2} b_{1}^{2} - { }6a_{1} a_{2} b_{1} b_{2} } \right) + a_{2}^{2} b_{2}^{3} P_{2}^{4} } \right] \hfill \\ \end{gathered} }{{4\left( {a_{1}^{2} P_{1}^{2} - a_{2}^{2} P_{2}^{2} } \right)^{2} }}} dt} \right] \\ \end{aligned}$$
(13)

where a1, a2 \(\kappa_{1} ,\kappa_{2} ,p_{1} ,p_{2} ,b_{1} ,b_{2} ,c_{1} ,c_{2}\) are arbitrary parameters.

Using Eq. (13), we get the following three-solitary solution of Eq. (2).

$$u = \frac{{2 p_{1} a_{1} \left[ {\frac{{k_{2}^{2} p_{2}^{2} [p_{1}^{2} \alpha (a_{2} b_{1} - a_{1} b_{2} )^{2} + (a_{1}^{2} a_{2} P_{1}^{2} - a_{2}^{3} P_{2}^{2} )^{2} }}{{4P_{1}^{2} \left( {P_{2}^{2} \alpha (a_{2} b_{1} - a_{1} b_{2} } \right)^{2} + (a_{1}^{3} P_{1}^{2} - a_{1} a_{2}^{2} P_{2}^{2} )^{2} }}} \right] + 2p_{2} a_{2} k_{2} \sinh \left( {\theta_{2} } \right)}}{{\frac{{k_{2}^{2} p_{2}^{2} [p_{1}^{2} \alpha (a_{2} b_{1} - a_{1} b_{2} )^{2} + (a_{1}^{2} a_{2} P_{1}^{2} - a_{2}^{3} P_{2}^{2} )^{2} }}{{4P_{1}^{2} \left( {P_{2}^{2} \alpha (a_{2} b_{1} - a_{1} b_{2} } \right)^{2} + (a_{1}^{3} P_{1}^{2} - a_{1} a_{2}^{2} P_{2}^{2} )^{2} }}e^{{\theta_{1} }} + e^{{ - \theta_{1} }} + k_{2} \cosh \left( {\theta_{2} } \right)}}{\text{ + tanh}}\left( {z + t} \right)$$
(14)

we suppose the figures of the three-solitary solution (14) u are demonstrated in Fig. 2. The drive of the solutions is shown. Figure 2. demonstrates that the interfere between waves at \(p_{1} = 1; a_{1} = 1; b_{1} = 1;k_{2} = 2; c_{1} = p_{2} = 1; a_{2} = k_{2} = 2; c_{2} = 2;\)

Fig. 2
figure 2

The three -solitary solution by the specification of a \(x = 0, y = 10,\) b with \(x = 0, y = 0\), and c with \(x = 0, y = 10.\)

Full size image

6.2 The improved tanh–coth method

To determine the parameter n, according to the following formulas for the highest exponents of the function u and its derivatives: \(u^{n} \left( \zeta \right) \to n u, u^{\prime} \to n + 1, u^{\left( k \right)} \to n + k\).

Through investigation Eq. (2), we get the value of n as, \(n + 5 = n + 2 + n + 2 \Rightarrow n = 1\). Equation (12) rewrite as;

$$u\left( {x,y,z,t} \right) = d_{0} + d_{1} {\text{tanh}}\left( {kx + ry + sz - wt} \right) + d_{2} \left( {{\text{tanh}}\left( {kx + ry + sz - wt} \right)} \right)^{ - 1}$$
(15)

where \(d_{0} ,d_{1} ,d_{2} ,k, r, s\) and w are arbitrary constants and will be obtained later. Substitute Eq. (15) into Eq. (2) and collect the coefficients of \(\left( {{\text{tanh}}\left( {kx + ry + sz - wt} \right)} \right)^{j}\) where, \(j = 0, 2, 4, 6, - 2, - 4\) and − 6. Equaling these coefficients to zero, generating an algebraic system in \(d_{0} ,d_{1} ,d_{2} ,k, r, s\) and w as follows.

$$\begin{aligned} & 60d_{1}^{2} k^{3} r - 120rk^{4} d_{1} = 0, \\ & 60d_{2}^{2} k^{3} r - 120rk^{4} d_{2} = 0, \\ \end{aligned}$$
$$\begin{aligned} & - 136d_{1} k^{4} r + 84rk^{3} d_{1}^{2} - 8\alpha r^{3} d_{1} + 8ad_{1} k^{3} + 8ck^{2} sd_{1} + 48d_{1} d_{2} rk^{3} + 8bk^{2} rd_{1} + 16\beta wk^{2} d_{1} = 0, \\ & - 136d_{2} k^{4} r + 84rk^{3} d_{2}^{2} - 8\alpha r^{3} d_{2} + 8ad_{2} k^{3} + 8ck^{2} sd_{2} + 48d_{1} d_{2} rk^{3} + 8bk^{2} rd_{2} + 16\beta wk^{2} d_{2} = 0, \\ & - 6bd_{2} k^{2} r + 240d_{2} k^{4} r - 12\beta wd_{2} k^{2} + 6\alpha r^{3} d_{2} - 132d_{2}^{2} k^{3} r - 36d_{1} d_{2} rk^{3} - 6ad_{2} k^{3} - 6csk^{2} d_{2} = 0, \\ & - 6bd_{1} k^{2} r + 240d_{1} k^{4} r - 12\beta wd_{1} k^{2} + 6\alpha r^{3} d_{1} - 132d_{1}^{2} k^{3} r - 36d_{1} d_{2} rk^{3} - 6ad_{1} k^{3} - 6csk^{2} d_{1} = 0, \\ & 16d_{2} k^{4} r - 12k^{3} d_{2}^{2} r + 16rk^{4} d_{1} - 2ad_{2} k^{3} - 12rk^{3} d_{1}^{2} + 2\alpha r^{3} d_{2} + 2\alpha r^{3} d_{1} - 2ak^{3} d_{1} \\ & - 2csk^{2} d_{1} - 24k^{3} rd_{1} d_{2} - 4\beta wd_{2} k^{2} - 4\beta wd_{1} k^{2} - 2brk^{2} d_{2} - 2csk^{2} d_{2} - 2brk^{2} d_{1} = 0. \\ \end{aligned}$$
(16)

By solving this system, we obtain the unknown constants that assumed in Eq. (15);

$$d_{0} = d_{0} ,\;d_{1} = 2k, \;d_{2} = 2k\;{\text{and}}\;w = - \frac{{16rk^{4} + csk^{2} + brk^{2} - \alpha r^{3} - ak^{3} }}{{2\beta k^{2} }}$$
(17)

Substitute Eq. (15) into Eq. (13), we get new solution for Eq. (2);

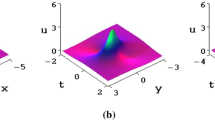
$$\begin{aligned} & u\left( {x,y,z,t} \right) = d_{0} + 2k{\text{tanh}}\left( {kx + ry + sz + \frac{{16rk^{4} + csk^{2} + brk^{2} - \alpha r^{3} - ak^{3} }}{{2\beta k^{2} }}t} \right) \\ & \quad + \frac{2k}{{{\text{tanh}}\left( {kx + ry + sz + \frac{{16rk^{4} + csk^{2} + brk^{2} - \alpha r^{3} - ak^{3} }}{{2\beta k^{2} }}t} \right)}} \\ \end{aligned}$$
(18)

Tanh Coth method demonstrated many hyperbolic functions characterized the Soliton solutions for different cases. For different values of time, we plotted the result (18) in Fig. 3.

Fig. 3
figure 3

Three dimensional plots for result in (14) with \(d_{0} = 1,a = b = c = k = s = r = z = 1,\alpha = 2\) and \(\beta = 1,\) (a) t = 0, (b) t = 1.5

Full size image

6.3 The improved tan–cot method

Application of the tanh–coth method may also lead to tanh–coth (or tan–cot) solutions that are not disguised versions of coth (or cot) solutions. Assume that;

$$u\left( {x,y,z,t} \right) = d_{0} + d_{1} {\text{tan}}\left( {kx + ry + sz - wt} \right) + d_{2} \left( {{\text{tan}}\left( {kx + ry + sz - wt} \right)} \right)^{ - 1}$$
(19)

Following the same steps in the previous section, we get the constants as;

$$d_{0} = d_{0} ,d_{1} = - 2k, d_{2} = 2k\;{\text{and}}\;w = - \frac{{ - 16rk^{4} + csk^{2} + brk^{2} - \alpha r^{3} - ak^{3} }}{{2\beta k^{2} }}$$
(20)

Back substation to the original variables;

$$\begin{aligned} & u\left( {x,y,z,t} \right) = d_{0} + d_{1} {\text{tan}}\left( {kx + ry + sz + \frac{{ - 16rk^{4} + csk^{2} + brk^{2} - \alpha r^{3} - ak^{3} }}{{2\beta k^{2} }}t} \right) \\ & \quad + d_{2} \left( {{\text{tan}}\left( {kx + ry + sz + \frac{{ - 16rk^{4} + csk^{2} + brk^{2} - \alpha r^{3} - ak^{3} }}{{2\beta k^{2} }}t} \right)} \right)^{ - 1} \\ \end{aligned}$$
(21)

This solution is plotted for different values of time in Fig. 3.

7 Results and discussion

Three-and two-dimensional simulations are presented to illustrate our results. Through our observation, we notice that;

  • Figure 1a–c represents Lump-soliton solutions for Eq. (2) that localized in space and time.

  • Figure 3a, b illustrates one soliton solution for Eq. (2) that with increasing the time, the amplitude decreasing and moves towards the right.

  • The obtained solution in Fig. 4a, b represents three soliton solutions for Eq. (2). The behavior of the solitons depends on the variety between the spatial coordinates and the time.

    Fig. 4
    figure 4

    Three dimensional plots for result in (21) with \(d_{0} = 1,a = b = c = k = s = r = z = 1,\alpha = 2\) and \(\beta = 1,\) a t = 0, b t = 2

    Full size image

8 Conclusions

In this paper, we explore diverse types of solutions for the (3 + 1)-dimensional (EDJKM) equation through many methods. Applying the Hirota- bilinear method, generate new Lump soliton solutions for Eq. (2) that localized in all directions and Using various ansatzes to explore new multi-soliton solutions for Eq. (2) by the Cole–Hopf transformation. Some of these solutions have solitary wave shapes. By using the 3D plot, we can draw the solutions.

Based on the Hirota bilinear method we can get the three-solitary solution. We find that our results are new Comparing with the published papers (Xu 2019; Kang and Xia 2020). We demonstrate the multiple soliton solutions which form a solitonic, periodic and singular solutions. We can also try to find their multiple interaction solutions. we demonstrated the kinds of solutions, such as solitary solutions and singular solitary solutions. More soliton solutions are presented. the velocity for a lump-typed solution is studied. The Tan–Cot method specified many solutions depending on the parameter n, so many Soliton solutions are demonstrated and illustrated by figures. The three-dimensional figures are demonstrated to show the physical phenomena for the obtained solutions. By using Maple calculation, we can solve the resulted system of equations and obtain the exact solutions for the (3 + 1)-dimensional VC-DJKM equation. we can extend Eq. (2) into a generalized variable-coefficient equation and obtain its novel solutions by the generalized bilinear operator. It is demonstrated that our calculations are useful to study the higher-dimensional nonlinear partial differential equations in mathematical physics.