1 Introduction

Scientific models used in research fields such as biology, nonlinear optics, nuclear physics, plasma physics and chemistry are expressed usually by nonlinear evolution equations (NLEEs). Therefore, it is an inevitable task to investigate the solutions of NLEEs. Seeking the exact solutions to NLEEs is quite difficult and is possible in only some circumstances. However, in the last three decades, there has been enormous activities for handling these equations. The Hirota’s bilinear scheme [1], multiple exp-function approach [2,3,4,5,6], exp-function procedure [7], extended transformed rational function methodology [8], sub-equation algorithm [9], Riccati–Bernoulli sub-ordinary differential equation (ODE) methodology and modified Kudryashov method [10], novel test function method [11], ansatz method [12], \(\left( G^{\prime }/G\right) \)-expansion method [13], Jacobi elliptic function algorithm [11, 13,14,15], simplest equation procedure [11, 12, 14, 15], B\(\ddot{\text{ a }}\)cklund transformation [16], Lax pair [17], Wronskian and Grammian techniques [18], lump and interaction solutions [19,20,21,22,23,24] etc. are some of the most popular techniques.

It is well known that one of the most efficient approaches in the literature is the multiple exp-function integration scheme [2,3,4,5,6]. The fundamental advantage of handling this technique is that it is profited without any requirement of the bilinear equations that must be required by means of Hirota’s bilinear procedure [1]. In this process, expressing the multiwave solutions as polynomials of exponential functions is the most important point. The obtained solutions contain generic wave frequencies with phase shifts and known as one-soliton-, two-soliton- and three-soliton-type solutions. The multiple exp-function algorithm is a generalisation of Hirota’s perturbation methodology [1].

Another interesting method for constructing analytical solutions to NLEEs is the extended transformed rational function scheme [8]. In this process, finding the rational solutions of variable-coefficient ODE transformed from the given nonlinear partial differential equation is the most important point. This algorithm relies on the Hirota bilinear form of the considered models. Complexiton solutions fall out of this integration scheme. These solutions contain singularities of unifications of both exponential and trigonometric function waves that possess novel style distinct travelling wave speeds.

The \((2+1)\)-dimensional Date–Jimbo–Kashiwara–Miwa (DJKM) equation [16,17,18] considered in this paper will be employed as follows:

$$\begin{aligned}&u_{xxxxy}+4u_{xxy}u_{x}+2u_{xxx}u_{y}+6u_{xy}u_{xx} \nonumber \\&\quad +u_{yyy}-2u_{xxt}=0. \end{aligned}$$
(1)

This equation can be derived from the following bilinear Hirota equation:

$$\begin{aligned}&D_{x}\{(D_{x}^{3}D_{y}-3D_{x}D_{t})F\cdot F\}\cdot F^{2} \nonumber \\&\quad +\frac{1}{2}D_{y} \{(D_{x}^{4}+3D_{y}^{2})F\cdot F\}\cdot F^{2}=0, \end{aligned}$$
(2)

employing \(u=2(\ln F)_{x}.\) This model characterises the time evolution of Kadomtsev–Petviashvili (KP) hierarchy as the bilinear identity [25]. Hu and Li [16] proved that the first two bilinear equations of the KP hierarchy can be constructed by bilinear equation (2), and named eq. (1) as DJKM equation.

When we look at the works done on this equation, Lax pair, multishock wave solutions as well as infinite conservation laws were imparted in [17] while nonlinear superposition formulae as well as bilinear Bäcklund transformation (BT) were extracted in [16]. In addition to these substantial studies, Wronskian and Grammian solutions were also recovered in [18]. We shall contribute to the existing works in a different way by finding multisoliton-type solutions and complexiton-type solutions which have not been worked so far.

This paper is presented as follows. The multiple exp-function methodology will be employed in order to obtain multisoliton-type solutions, namely one-soliton, two-soliton and three-soliton solutions in §2 whilst complexiton solutions are derived by the extended transformed rational function approach in §3. Some conclusions are given in §4.

2 A quick glance at the multiple exp-function methodology

The fundamental stages of this scheme are enumerated by the following steps [2,3,4,5,6]: Let us consider an NLEE:

$$\begin{aligned} Q(x,t,u_{x},u_{t},\ldots \,)=0. \end{aligned}$$
(3)

Step 1: Let the first-order auxiliary equations be

$$\begin{aligned} \phi _{l,t}=-\omega _{l}\phi _{l},\quad \phi _{l,x}=k_{l}\phi _{l},\quad 1\leqslant l\leqslant m, \end{aligned}$$
(4)

where \(k_{l}\) corresponds to the angular wave numbers while \(\omega _{l}\) corresponds to the wave frequencies for \(1\leqslant l\leqslant m\). The analytical solutions of eq. (4) are given as

$$\begin{aligned} \phi _{l}=c_{l}\,\mathrm{e}^{\xi _{l}},\quad \xi _{l}=k_{l}x-\omega _{l}t,\quad 1\leqslant l\leqslant m, \end{aligned}$$

where \(c_{l}\) signifies arbitrary constants.

Step 2: Equation (3) permits the formal solution

$$\begin{aligned} u(x,t)=\frac{p(\phi _{1},\ldots ,\phi _{m})}{q(\phi _{1},\ldots ,\phi _{m})} \end{aligned}$$
(5)
Fig. 1
figure 1

Profiles of one-soliton-type solution (11).

Full size image
Fig. 2
figure 2

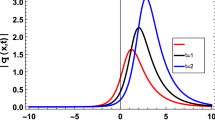
Profiles of two-soliton-type solution (13).

Full size image

with

$$\begin{aligned}&p=\sum _{r,s=1}^{m}\sum _{l,j=0}^{M}p_{rs,lj}\phi _{r}^{l}\phi _{s}^{{j}}, \nonumber \\&q=\sum _{r,s=1}^{m}\sum _{l,j=0}^{M}q_{rs,lj}\phi _{r}^{{l}}\phi _{s}^{{j}}, \end{aligned}$$
(6)

where \(p_{rs,lj}\) and \(q_{rs,lj}\) are all constants to be determined. The necessary partial derivatives in eq. (3) can be yielded by employing eq. (4). For instance, one can get

$$\begin{aligned} u_{t} =&\,\frac{q\sum \nolimits _{l=1}^{m} p_{\phi _{l}}\phi _{l,t}-p \sum \nolimits _{l=1}^{m} q_{\phi _{l}}\phi _{l,t}}{q^{2}} \nonumber \\ =&\,\frac{-q\sum \nolimits _{l=1}^{m} \omega _{l}p_{\phi _{l}}\phi _{l}+p\sum \nolimits _{l=1}^{m} \omega _{l}q_{\phi _{l}}\phi _{l}}{ q^{2}} \end{aligned}$$
(7)

and

$$\begin{aligned} u_{x} =&\,\frac{q\sum \nolimits _{l=1}^{m} p_{\phi _{l}}\phi _{l,x}-p \sum \nolimits _{l=1}^{m} q_{\phi _{l}}\phi _{l,x}}{q^{2}} \nonumber \\ =&\,\frac{q\sum \nolimits _{l=1}^{m} k_{l}p_{\phi _{l}}\phi _{l}-p \sum \nolimits _{l=1}^{m} k_{l}q_{\phi _{l}}\phi _{l}}{q^{2}}. \end{aligned}$$
(8)

Step 3: Plugging (5) throughout (6) and its necessary derivatives such as (7) and (8) into (3) lead to the following transformed equation:

$$\begin{aligned} \Lambda (x,t,\phi _{1},\phi _{2},\ldots ,\phi _{m})=0. \end{aligned}$$
(9)

Step 4: An overdetermined system which includes the terms \(k_{l}\), \(\omega _{l}\), \(p_{rs,lj}\) and \(q_{rs,lj}\) is obtained by equating the numerator of (9) to zero. Solving this system with Maple, we get the values of p, q polynomials with \(\xi _{l}\) wave exponents. So, the multiple wave solutions for eq. (3) are given by

$$\begin{aligned} u(x,t)=\frac{p(c_{1}\mathrm{e}^{k_{1}x-\omega _{1}t},\ldots ,c_{m}\mathrm{e}^{k_{m}x-\omega _{m}t})}{q(c_{1}\mathrm{e}^{k_{1}x-\omega _{1}t},\ldots ,c_{m}\mathrm{e}^{k_{m}x-\omega _{m}t})}. \end{aligned}$$
(10)

2.1 One-soliton solution

In order to obtain the one-soliton solution of eq. (1) (see figure 1), we assume

$$\begin{aligned} u(x,y,t)=\frac{p}{q}, \end{aligned}$$
(11)

where

$$\begin{aligned} p= & {} A_{{0}}+A_{{1}}{\mathrm {e}^{k_{{1}}x+l_{{1}}y-\omega _{{1}}t}}, \nonumber \\ q= & {} B_{{0}}+B_{{1}}{\mathrm {e}^{k_{{1}}x+l_{{1}}y-\omega _{{1}}t}.} \end{aligned}$$
(12)

Plugging eq. (11) and necessary derivative terms into eq. (1), one comes up with an overdetermined system having unknown parameters. Solving the overdetermined system, we conclude

$$\begin{aligned} A_{{1}}= & {} {\frac{2B_{{0}}B_{{1}}k_{{1}}+A_{{0}}B_{{1}}}{B_{{0}}}}, \\ \omega _{{1}}= & {} -{\frac{k_{1}^{4}l_{{1}}+l_{1}^{3}}{2k_{1}^{2}}},\,\,\,k_{1},\,B_{0}\ne 0. \end{aligned}$$

Remark

We note that for the one-soliton solution, this methodology corresponds to the exp-function technique [7].

2.2 Two-soliton solution

In order to construct the two-soliton solution of eq. (1) (see figure 2), we assume

$$\begin{aligned} u(x,y,t)=\frac{p}{q}, \end{aligned}$$
(13)

where

$$\begin{aligned} p=&\,2k_{{1}}{\mathrm {e}^{k_{{1}}x+l_{{1}}y-\omega _{{1}}t}}+2k_{{ 2}}{ \mathrm {e}^{k_{{2}}x+l_{{2}}y-\omega _{{2}}t}}\nonumber \\&+2A_{{12}}\left( k_{{1}}+k_{{ 2}}\right) {\mathrm {e}^{k_{{1}}x+l_{{1}}y-\omega _{{1}}t}}{\mathrm {e}^{k_{{2} }x+l_{{2}}y-\omega _{{2}}t}}, \nonumber \\ q=&\,1+{\mathrm {e}^{k_{{1}}x+l_{{1}}y-\omega _{{1}}t}}+{\mathrm {e}^{k_{{2} }x+l_{{2}}y-\omega _{{2}}t}} \nonumber \\&+A_{{12}}{\mathrm {e}^{k_{{1}}x+l_{{1}}y-\omega _{{1}}t}}{\mathrm {e}^{k_{{2}}x+l_{{2}}y-\omega _{{2}}t}.} \end{aligned}$$
(14)
Fig. 3
figure 3

Profiles of three-soliton-type solution (15).

Full size image

Plugging eq. (13) and necessary derivative terms into eq. (1), one comes up with an overdetermined system having unknown parameters. Solving the overdetermined system, we get

$$\begin{aligned}&A_{{12}}={\frac{k_{{1}}^{4}k_{{2}}^{2}-2\,k_{{1}}^{3}k_{{2}}^{3}+ k_{{1}}^{2}k_{{2}}^{4}-k_{{1}}^{2}l_{{2}}^{2}+2\,k_{{1}}k_{{2}}l_{{1} }l_{{2}}-k_{{2}}^{2}l_{{1}}^{2}}{k_{{1}}^{4}k_{{2}}^{2}+2\,k_{{1}} ^{3}k_{{2}}^{3}+k_{{1}}^{2}k_{{2}}^{4}-k_{{1}}^{2}l_{{2}}^{2}+2\,k_{{1}}k_{{2}}l_{{1}}l_{{2}}-k_{{2}}^{2} l_{{1}}^{2}}}, \\&\omega _{{1}}=-\,{\frac{l_{{1}}\left( k_{{1}}^{4}+l_{{1}}^{2}\right) }{ 2k_{{1}}^{2}}},\quad \omega _{{2}}=-\,{\frac{l_{{2}}\left( k_{{2}}^{4}+ l_{{2}}^{2}\right) }{2k_{{2}}^{2}}}. \end{aligned}$$

2.3 Three-soliton solution

For the three-soliton solution of eq. (1) (see figure 3), we assume

$$\begin{aligned} u(x,y,t)=\frac{p}{q}, \end{aligned}$$
(15)

where

$$\begin{aligned} p&=2\,k_{{1}}{\mathrm {e}^{-\omega _{{1}}t+k_{{1}}x+l_{{1}}y}}+2\,k_{{2}}{\mathrm {e}^{-\omega _{{2}}t+k_{{2}}x+l_{{2}}y}} \nonumber \\&\, \quad +2k_{{3}}{\mathrm {e}^{-\omega _{{3}}t+k_{{3}}x+l_{{3}}y}} \nonumber \\&\quad \,+2A_{{12}}\left( k_{{1}}+k_{{2}}\right) {\mathrm {e}^{-\omega _{{1}}t+k_{{ 1}}x+l_{{1}}y}}{\mathrm {e}^{-\omega _{{2}}t+k_{{2}}x+l_{{2}}y}} \nonumber \\&\,\quad +2A_{{13} }\left( k_{{1}}+k_{{3}}\right) {\mathrm {e}^{-\omega _{{1}}t+k_{{1}}x+l_{{1}}y}}{\mathrm {e}^{-\omega _{{3}}t+k_{{3}}x+l_{{3}}y}} \nonumber \\&\,\quad +2A_{{23}}\left( k_{{2}}+k_{{3}}\right) {\mathrm {e}^{-\omega _{{2}}t+k_{{2}}x+l_{{2}}y}}{\mathrm {e}^{-\omega _{{3}}t+k_{{3}}x+l_{{3}}y}} \nonumber \\&\,\quad +2A_{{12}}A_{{13}}A_{{23}}\left( k_{{\ 1}}+k_{{2}}+k_{{3}}\right) \nonumber \\&\, \quad \times {\mathrm {e}^{-\omega _{{1}}t+k_{{1}}x+l_{{1}}y}}{\mathrm {e}^{-\omega _{{2}}t+k_{{2}}x+l_{{2}}y}}{\mathrm {e}^{-\omega _{{3}}t+k_{{3}}x+l_{{3}}y}}, \nonumber \\ q&=1+{\mathrm {e}^{-\omega _{{1}}t+k_{{1}}x+l_{{1}}y}}+{\mathrm {e}^{-\omega _{{2}}t+k_{{2}}x+l_{{2}}y}} \nonumber \\&\,\quad +{\mathrm {e}^{-\omega _{{3}}t+k_{{3}}x+l_{{3}}y}} +A_{{12}}{\mathrm {e}^{-\omega _{{1}}t+k_{{1}}x+l_{{1}}y}}{\mathrm {e}^{-\omega _{{ 2}}t+k_{{2}}x+l_{{2}}y}} \nonumber \\&\,\quad +A_{{13}}{\mathrm {e}^{-\omega _{{1}}t+k_{{1}}x+yl_{{1}}}}{\mathrm {e}^{-t\omega _{{3}}+xk_{{3}}+yl_{{3}}}} \nonumber \\&\, \quad +A_{{23}}{\mathrm {e}^{-t\omega _{{2}}+xk_{{2}}+yl_{{2}}}}{\mathrm {e}^{-t\omega _{{3}}+xk_{{3}}+yl_{{3}}}} \nonumber \\&\,\quad +A_{{12}}A_{{13}}A_{{23}}{\mathrm {e}^{-\omega _{{1}}t+k_{{1}}x+yl_{{1}}}}{ \mathrm {e}^{-t\omega _{{2}}+xk_{{2}}+yl_{{2}}}} \nonumber \\&\,\quad \times {\mathrm {e}^{-t\omega _{{3}}+xk_{{3}}+yl_{{3}}}.} \end{aligned}$$
(16)

Plugging eq. (15) and necessary derivative terms into eq. (1), one comes up with an overdetermined system having unknown parameters. Solving the overdetermined system, we get

$$\begin{aligned}&A_{{12}}={\frac{k_{{1}}^{4}k_{{2}}^{2}-2\,k_{{1}}^{3}k_{{2}}^{3}+ k_{{1}}^{2}k_{{2}}^{4}-k_{{1}}^{2}l_{{2}}^{2}+2\,k_{{1}}k_{{2}}l_{{1} }l_{{2}}-k_{{2}}^{2}l_{{1}}^{2}}{k_{{1}}^{4}k_{{2}}^{2}+2\,k_{{1}}^{3}k_{{2}}^{3}+k_{{1}}^{2}k_{{2}}^{4} -k_{{1}}^{2}l_{{2}}^{2}+2\,k_{{1}}k_{{2}}l_{{1}}l_{{2}}-k_{{2}}^{2}l_{1}^{2}}}, \nonumber \\&A_{{13}}={\frac{k_{{1}}^{4}k_{{3}}^{2}-2\, k_{{1}}^{3}k_{{3}}^{3}+ k_{{1}}^{2}k_{{3}}^{4}-k_{{1}}^{2}l_{{3}}^{2}+2\,k_{{1}}k_{{3}}l_{{1} }l_{{3}}-k_{{3}}^{2}l_{{1}}^{2}}{k_{{1}}^{4}k_{{3}}^{2}+2\,k_{{1}} ^{3}k_{{3}}^{3}+k_{{1}}^{2}k_{{3}}^{4}-k_{{1}}^{2}l_{{3}} ^{2}+2\,k_{{1}}k_{{3}}l_{{1}}l_{{3}}-k_{{3}}^{2}l_{{1}}^{2}}}, \nonumber \\&A_{{23}}={\frac{k_{{2}}^{4}k_{{3}}^{2}-2\,k_{{2}}^{3}k_{{3}}^{3}+ k_{{2}}^{2}k_{{3}}^{4}-k_{{2}}^{2}l_{{3}}^{2}+2\,k_{{2}}k_{{3}}l_{{2} }l_{{3}}-k_{{3}}^{2}l_{{2}}^{2}}{k_{{2}}^{4}k_{{3}}^{2}+2\,k_{{2}} ^{3}k_{{3}}^{3}+k_{{2}}^{2}k_{{3}}^{4}-k_{{2}}^{2}l_{{3}} ^{2}+2\,k_{{2}}k_{{3}}l_{{2}}l_{{3}}-k_{{3}}^{2}l_{{2}}^{2}}}, \nonumber \\&\omega _{{1}}=-\,{\frac{l_{{1}}\left( {k^{4}_{{1}}}+{l^{2}_{{1}}}\right) }{ 2k_{{1}}^{2}}}, \nonumber \\&\omega _{{2}}=-\,{\frac{l_{{2}}\left( {k^{4}_{{2}}}+{l^{2}_{{2}}}\right) }{ 2k_{{2}}^{2}}}, \nonumber \\&\omega _{{3}}=-\,{\frac{l_{{3}}\left( {k^{4}_{{3}}}+{l^{2}_{{3}}}\right) }{ 2k_{{3}}^{2}}}. \end{aligned}$$
(17)

To the best of our knowledge the phase shifts \(A_{12},A_{13}\) and \(A_{23}\) are being shown for the first time for the DJKM equation.

3 A quick glance at the extended transformed rational function approach

The key steps of this procedure are summarised as follows [8]:

Let us consider the NLEE

$$\begin{aligned} \Delta \left( u,u_{x},u_{t},u_{xx},\ldots \right) =0. \end{aligned}$$
(18)

Step 1: Equation (18) is transformed to the so-called the Hirota bilinear form

$$\begin{aligned} H( D_{x},D_{t},\ldots ) FF=0 \end{aligned}$$
(19)

with the help of the dependent function transformation \(u=T\left( F\right) \ \)in which F accounts for an unknown function and \(D_{x}\), \(D_{t}\),..., are Hirota’s differential operators defined by

$$\begin{aligned}&D_{\zeta }^{l}F\left( \zeta \right) \cdot P\left( \zeta \right) =\left. (\partial _{\zeta }-\partial _{\zeta ^{\prime }}) ^{l}F\left( \zeta \right) P\left( \zeta ^{\prime }\right) \right| _{\zeta ^{\prime }=\zeta }\nonumber \\&\quad =\left. \partial _{\zeta ^{\prime }}^{l}F\left( \zeta +\zeta ^{\prime }\right) P\left( \zeta -\zeta ^{\prime }\right) \right| _{\zeta ^{\prime }=0} ,\quad l\ge 1. \end{aligned}$$
(20)

Step 2: Equation (19) permits the formal solution

$$\begin{aligned} F=\frac{p\left( \eta _{1},\eta _{2}\right) }{q\left( \eta _{1},\eta _{2}\right) }, \end{aligned}$$
(21)

where \(p\left( \eta _{1},\eta _{2}\right) \) and \(q\left( \eta _{1},\eta _{2}\right) \) are polynomials and \(\eta _{1}\left( \xi _{1}\right) \) and \( \eta _{2}\left( \xi _{2}\right) \) hold the following ODEs:

$$\begin{aligned}&\eta _{1}^{\prime \prime }=\frac{\mathrm{d}^{2}\eta _{1}}{\mathrm{d}\xi _{1}^{2}}=-\eta _{1}, \end{aligned}$$
(22)
$$\begin{aligned}&\eta _{2}^{\prime \prime }=\frac{\mathrm{d}^{2}\eta _{2}}{\mathrm{d}\xi _{2}^{2}}=\eta _{2}, \end{aligned}$$
(23)

respectively, together with

$$\begin{aligned} \xi _{1}=k_{1}x+\omega _{1}t+c_{1},\quad \xi _{2}=k_{2}x+\omega _{2}t+c_{2}, \end{aligned}$$

where \(k_{1}\), \(k_{2}\), \(\omega _{1}\) and \(\omega _{2}\) will be obtained subsequently and \(c_{1}\) and \(c_{2}\) are real value arbitrary constants.

The analytical solutions of eq. (22) are given through the medium of

$$\begin{aligned} \eta _{1}=\pm \sin \xi _{1}\ \ \ \text {or }\ \ \ \eta _{1}=\pm \cos \xi _{1}, \end{aligned}$$
(24)

whilst the exact solutions of eq. (23) are obtained by the equation

$$\begin{aligned} \eta _{2}=\pm \sinh \xi _{2}\ \ \ \text {or }\ \ \ \eta _{2}=\pm \cosh \xi _{2}. \end{aligned}$$
(25)

The solutions suggest that \(\eta _{i}^{2}\) and \(\eta _{i}^{\prime 2}\) admit

$$\begin{aligned} \eta _{1}^{\prime 2}=1-\eta _{1}^{2}\ \ \ \text {and }\ \ \ \eta _{2}^{\prime 2}=1+\eta _{2}^{2}. \end{aligned}$$
(26)

Step 3: We choose appropriate \(p\left( \eta _{1},\eta _{2}\right) \) and \(q\left( \eta _{1},\eta _{2}\right) \), then we substitute (21) into (19) along with (22) and (23). As a result of this substitution, we get an algebraic equation involving \(k_{i}\) and \( \omega _{i}\) under the conditions of (26). Solving this algebraic equation, analytical solutions for eq. (18) are recovered.

3.1 Complexiton solutions

The Hirota bilinear forms [16,17,18] of eq. (1) are obtained by

$$\begin{aligned}&( D_{x}^{4}+3D_{y}^{2}+\alpha D_{x}D_{z}) FF\nonumber \\&\quad =2FF_{xxxx}-8F_{x}F_{xxx}+6F_{xx}^{2}+6FF_{yy} \nonumber \\&\qquad \,\,-6F_{y}^{2}+2\alpha FF_{xz}-2\alpha F_{x}F_{z}=0 \end{aligned}$$
(27)

and

$$\begin{aligned}&\left( D_{x}^{3}D_{y}-3D_{x}D_{t}-\frac{\alpha }{2}D_{y}D_{z}\right) FF\nonumber \\&\quad =2FF_{xxxy}-2F_{xxx}F_{y}-6F_{x}F_{xxy}+6F_{xx}F_{xy} \nonumber \\&\qquad -6FF_{xt}+6F_{x}F_{t}- \alpha FF_{yz}+\alpha F_{y}F_{z}=0 \end{aligned}$$
(28)

under the transformation

$$\begin{aligned} u\left( x,y,t\right) =2\left( \ln F\left( x,y,z,t\right) \right) _{x}, \end{aligned}$$

where \(F\left( x,y,z,t\right) \) accounts for a real-valued function while z implies an auxiliary variable and \(\alpha \) corresponds to a constant.

Case 1: \(z=x\).

In this case, eqs (27) and (28) read as

$$\begin{aligned}&( D_{x}^{4}+3D_{y}^{2}+\alpha D_{x}^{2}) FF\nonumber \\&\quad =2FF_{xxxx}-8F_{x}F_{xxx}+6F_{xx}^{2}+6FF_{yy} \nonumber \\&\qquad \,-6F_{y}^{2}+2\alpha FF_{xx}-2\alpha F_{x}^{2}=0 \end{aligned}$$
(29)

and

$$\begin{aligned}&\left( D_{x}^{3}D_{y}-3D_{x}D_{t}-\frac{\alpha }{2}D_{y}D_{x}\right) FF\nonumber \\&\quad =2FF_{xxxy}-2F_{xxx}F_{y}-6F_{x}F_{xxy}+6F_{xx}F_{xy} \nonumber \\&\qquad \,-6FF_{xt}+6F_{x}F_{t}- \alpha FF_{yx}+\alpha F_{y}F_{x}=0. \end{aligned}$$
(30)

To seek complexiton solutions of eq. (1), we suppose F in eqs (29) and (30) is expressed in the following rational function form:

$$\begin{aligned} F=\frac{p\left( \eta _{1},\eta _{2}\right) }{q\left( \eta _{1},\eta _{2}\right) }, \end{aligned}$$
(31)

with

$$\begin{aligned}&p\left( \eta _{1},\eta _{2}\right) =A\eta _{1}+B\eta _{2},\quad q( \eta _{1},\eta _{2}) =1, \\&\xi _{1}=k_{1}x+l_{1}y+\omega _{1}t+c_{1}, \\&\xi _{2}=k_{2}x+l_{2}y+\omega _{2}t+c_{2} \end{aligned}$$

A, B, \(k_{i}\), \(l_{i}\) and \(\omega _{i}\) will be determined subsequently.

Fig. 4
figure 4

Profiles of complexiton-type solution (50) with (52).

Full size image

Under conditions (22) and (23), all the necessary derivatives in eqs (29) and (30) are recovered by means of

$$\begin{aligned}&F_{x}=Ak_{1}\eta _{1}^{\prime }+Bk_{2}\eta _{2}^{\prime }, \end{aligned}$$
(32)
$$\begin{aligned}&F_{y}=Al_{1}\eta _{1}^{\prime }+Bl_{2}\eta _{2}^{\prime }, \end{aligned}$$
(33)
$$\begin{aligned}&F_{t}=A\omega _{1}\eta _{1}^{\prime }+B\omega _{2}\eta _{2}^{\prime }, \end{aligned}$$
(34)
$$\begin{aligned}&F_{xx}=Ak_{1}^{2}\eta _{1}^{\prime \prime }+Bk_{2}^{2}\eta _{2}^{\prime \prime }=-Ak_{1}^{2}\eta _{1}+Bk_{2}^{2}\eta _{2}, \end{aligned}$$
(35)
$$\begin{aligned}&F_{yy}=Al_{1}^{2}\eta _{1}^{\prime \prime }+Bl_{2}^{2}\eta _{2}^{\prime \prime } =-Al_{1}^{2}\eta _{1}+Bl_{2}^{2}\eta _{2}, \end{aligned}$$
(36)
$$\begin{aligned}&F_{xt}=Ak_{1}\omega _{1}\eta _{1}^{\prime \prime }+Bk_{2}\omega _{2}\eta _{2}^{\prime \prime } =-Ak_{1}\omega _{1}\eta _{1}+Bk_{2}\omega _{2}\eta _{2}, \nonumber \\\end{aligned}$$
(37)
$$\begin{aligned}&F_{xy}=Ak_{1}l_{1}\eta _{1}^{\prime \prime }+Bk_{2}l_{2}\eta _{2}^{\prime \prime } =-Ak_{1}l_{1}\eta _{1}+Bk_{2}l_{2}\eta _{2}, \nonumber \\\end{aligned}$$
(38)
$$\begin{aligned}&F_{xxx}=Ak_{1}^{3}\eta _{1}^{\prime \prime \prime }+Bk_{2}^{3}\eta _{2}^{\prime \prime \prime } =-Ak_{1}^{3}\eta _{1}^{\prime }+Bk_{2}^{3}\eta _{2}^{\prime }, \end{aligned}$$
(39)
$$\begin{aligned}&F_{xxy}=Ak_{1}^{2}l_{1}\eta _{1}^{\prime \prime \prime }+Bk_{2}^{2}l_{2}\eta _{2}^{\prime \prime \prime } =-Ak_{1}^{2}l_{1}\eta _{1}^{\prime }+Bk_{2}^{2}l_{2}\eta _{2}^{\prime }, \nonumber \\\end{aligned}$$
(40)
$$\begin{aligned}&F_{xxxy}=Ak_{1}^{3}l_{1}\eta _{1}^{(4)}+Bk_{2}^{3}l_{2}\eta _{2}^{(4)} \nonumber \\&\qquad \quad \,\, =Ak_{1}^{3}l_{1}\eta _{1}+Bk_{2}^{3}l_{2}\eta _{2}, \end{aligned}$$
(41)
$$\begin{aligned}&F_{xxxx}=Ak_{1}^{4}\eta _{1}^{(4)}+Bk_{2}^{4}\eta _{2}^{(4)}=Ak_{1}^{4}\eta _{1}+Bk_{2}^{4}\eta _{2}. \end{aligned}$$
(42)

An algebraic equation for \(k_{i}\), \(l_{i}\) and \(\omega _{i}\) is imparted by substituting (32)–(42) into (29) and (30) and then equate all the coefficients of the same terms, namely \(\eta _{1}^{2}\), \( \eta _{2}^{2}\), \(\eta _{1}\), \(\eta _{2}\), \(\eta _{1}^{\prime }\) and \(\eta _{2}^{\prime }\) as well as constant term to zero. Under the conditions of (26), the determined equations are emerged from this system as follows:

$$\begin{aligned}&8A^{2}k_{1}^{4}-8B^{2}k_{2}^{4}-2A^{2}\alpha k_{1}^{2}-2B^{2}\alpha k_{2}^{2} \nonumber \\&\quad \quad -6A^{2}l_{1}^{2}-6B^{2}l_{2}^{2}=0, \end{aligned}$$
(43)
$$\begin{aligned}&8ABk_{1}^{3}k_{2}-8ABk_{1}k_{2}^{3}-4AB\alpha k_{1}k_{2} \nonumber \\&\quad \quad -12ABl_{1}l_{2}=0, \end{aligned}$$
(44)
$$\begin{aligned}&2ABk_{1}^{4}-12ABk_{1}^{2}k_{2}^{2}+2ABk_{2}^{4}-2AB\alpha k_{1}^{2} \nonumber \\&\quad \quad +2AB\alpha k_{2}^{2}-6ABl_{1}^{2}+6ABl_{2}^{2}=0, \end{aligned}$$
(45)
$$\begin{aligned}&2ABk_{1}^{3}l_{2}+6ABk_{1}^{2}k_{2}l_{1}-6ABk_{1}k_{2}^{2}l_{2}-2ABk_{2}^{3}l_{1} \nonumber \\&\quad \quad +AB\alpha k_{1}l_{2}+AB\alpha k_{2}l_{1}+6ABk_{1}\omega _{2}\nonumber \\&\quad \quad +6ABk_{2}\omega _{1}=0, \end{aligned}$$
(46)
$$\begin{aligned}&2ABk_{1}^{3}l_{1}-6ABk_{1}^{2}k_{2}l_{2}-6ABk_{1}k_{2}^{2}l_{1}+2ABk_{2}^{3}l_{2} \nonumber \\&\quad \quad +AB\alpha k_{1}l_{1}-AB\alpha k_{2}l_{2}+6ABk_{1}\omega _{1}\nonumber \\&\quad \quad -6ABk_{2}\omega _{2}=0, \end{aligned}$$
(47)
$$\begin{aligned}&8A^{2}k_{1}^{3}l_{1}-8B^{2}k_{2}^{3}l_{2}+A^{2}\alpha k_{1}l_{1}+B^{2}\alpha k_{2}l_{2} \nonumber \\&\quad \quad \quad \quad +6A^{2}k_{1}\omega _{1}+6B^{2}k_{1}\omega _{2}=0. \end{aligned}$$
(48)

Solving (43)–(48), we obtain the following results:

Result 1

$$\begin{aligned}&l_{1}=-k_{2}( 2A^{2}k_{1}^{2}-B^{2}k_{1}^{2}-3B^{2}k_{2}^{2}) \kappa ,\ \ l_{2}=k_{1}( 3A^{2}k_{1}^{2}+A^{2}k_{2}^{2}-2B^{2}k_{2}^{2}) \kappa , \\&\alpha =\frac{ 12A^{4}k_{1}^{4}-4A^{4}k_{1}^{2}k_{2}^{2}+3A^{2}B^{2}k_{1}^{4}-26A^{2}B^{2}k_{1}^{2}k_{2}^{2}+3A^{2}B^{2}k_{2}^{4}-4B^{4}k_{1}^{2}k_{2}^{2}+12B^{4}k_{2}^{4} }{3( A^{4}k_{1}^{2}+A^{2}B^{2}k_{1}^{2}-A^{2}B^{2}k_{2}^{2}-B^{4}k_{2}^{2}) }, \end{aligned}$$
$$\begin{aligned} \omega _{1}= & {} \frac{k_{2}\kappa }{18( A^{4}k_{1}^{2}+A^{2}B^{2}k_{1}^{2}-A^{2}B^{2}k_{2}^{2}-B^{4}k_{2}^{2})} \\&\times \left( 72A^{6}k_{1}^{6}-8A^{6}k_{1}^{4}k_{2}^{2}+36A^{4}B^{2}k_{1}^{6}\right. \\&-\,168A^{4}B^{2}k_{1}^{4}k_{2}^{2}+36A^{4}B^{2}k_{1}^{2}k_{2}^{4}-9A^{2}B^{4}k_{1}^{6}\\&-69A^{2}B^{4}k_{1}^{4}k_{2}^{2}+153A^{2}B^{4}k_{1}^{2}k_{2}^{4}-\,27A^{2}B^{4}k_{2}^{6}\\&+10B^{6}k_{1}^{4}k_{2}^{2}+\,36B^{6}k_{1}^{2}k_{2}^{4}\left. -\,54B^{6}k_{2}^{6}\right) , \end{aligned}$$
$$\begin{aligned} \omega _{2}= & {} -\frac{k_{1}\kappa }{18\left( A^{4}k_{1}^{2}+A^{2}B^{2}k_{1}^{2}-A^{2}B^{2}k_{2}^{2}-B^{4}k_{2}^{2}\right) }\nonumber \\&\times \left( 54A^{6}k_{1}^{6}-36A^{6}k_{1}^{4}k_{2}^{2}-10A^{6}k_{1}^{2}k_{2}^{4}\right. \nonumber \\&+27A^{4}B^{2}k_{1}^{6}-153A^{4}B^{2}k_{1}^{4}k_{2}^{2}+69A^{4}B^{2}k_{1}^{2}k_{2}^{4}\nonumber \\&+9A^{4}B^{2}k_{2}^{6}-36A^{2}B^{4}k_{1}^{4}k_{2}^{2}+168A^{2}B^{4}k_{1}^{2}k_{2}^{4}\nonumber \\&\left. -36A^{2}B^{4}k_{2}^{6}+8B^{6}k_{1}^{2}k_{2}^{4}-72B^{6}k_{2}^{6}\right) \nonumber \\&\times (9A^{4}k_{1}^{2}+9A^{2}B^{2}k_{1}^{2}-9A^{2}B^{2}k_{2}^{2}-9B^{4}k_{2}^{2}) \kappa ^{2}\nonumber \\&-1=0. \end{aligned}$$
(49)
Fig. 5
figure 5

Profiles of complex-valued-type solution (54) with (55).

Full size image

The complexiton solutions of (1) (see figure 4) corresponding to (49) are given by

$$\begin{aligned} u\left( x,y,t\right) =2\left( \ln F\left( x,y,t\right) \right) _{x} \end{aligned}$$
(50)

with

$$\begin{aligned} F(x,y,t)&=\pm B\sinh ( k_{2}x+k_{1}( 3A^{2}k_{1}^{2}+A^{2}k_{2}^{2}\nonumber \\&\quad \ \, -2B^{2}k_{2}^{2}) \kappa y+\omega _{2}t+c_{2}) \nonumber \\&\quad \ \, \pm A\sin ( k_{1}x-k_{2}(2A^{2}k_{1}^{2}-B^{2}k_{1}^{2}\nonumber \\&\quad \ \, -3B^{2}k_{2}^{2}) \kappa y +\omega _{1}t+c_{1}) , \end{aligned}$$
(51)
$$\begin{aligned} F( x,y,t)&=\pm B\sinh ( k_{2}x+k_{1} (3A^{2}k_{1}^{2}+A^{2}k_{2}^{2} \nonumber \\&\quad \, \ -2B^{2}k_{2}^{2})\kappa y +\omega _{2}t+c_{2}) \nonumber \\&\quad \, \ \pm A \cos ( k_{1}x-k_{2}(2A^{2}k_{1}^{2}-B^{2}k_{1}^{2} \nonumber \\&\quad \, \ -3B^{2}k_{2}^{2}) \kappa y+\omega _{1}t+c_{1}) . \end{aligned}$$
(52)

Result 2

$$\begin{aligned}&\alpha = \frac{4k_{1}^{4}+3l_{2}^{2}}{k_{1}^{2}},\quad k_{2}=\pm \mathrm {i}k_{1},\quad l_{1}=\pm \mathrm {i}l_{2}, \nonumber \\&\omega _{1}=\pm \frac{\mathrm {i}( 4k_{1}^{4}+l_{2}^{2}) l_{2}}{2k_{1}^{2}},\quad \omega _{2}=-\frac{( 4k_{1}^{4}+l_{2}^{2}) l_{2}}{2k_{1}^{2}}. \end{aligned}$$
(53)

The complex-valued solutions of (1) (see figure 5) corresponding to (53) are given by

$$\begin{aligned} u\left( x,y,t\right) =2\left( \ln F\left( x,y,t\right) \right) _{x} \end{aligned}$$
(54)

with

$$\begin{aligned}&F\left( x,y,t\right) \nonumber \\&\quad =\pm B\sinh \left( \pm \mathrm {i}k_{1}x+l_{2}y-\frac{( 4k_{1}^{4}+l_{2}^{2}) l_{2}}{2k_{1}^{2}}t+c_{2}\right) \nonumber \\&\qquad \, \ \pm A\sin \left( k_{1}x\pm \mathrm {i}l_{2}y\pm \frac{\mathrm {i}( 4k_{1}^{4}+l_{2}^{2}) l_{2}}{ 2k_{1}^{2}}t+c_{1}\right) , \end{aligned}$$
(55)
$$\begin{aligned}&F\left( x,y,t\right) \nonumber \\&\quad =\pm B\cosh \left( \pm \mathrm {i}k_{1}x+l_{2}y-\frac{(4k_{1}^{4}+l_{2}^{2}) l_{2}}{2k_{1}^{2}}t+c_{2}\right) \nonumber \\&\qquad \,\ \pm A\sin \left( k_{1}x\pm \mathrm {i}l_{2}y\pm \frac{\mathrm {i}( 4k_{1}^{4}+l_{2}^{2}) l_{2}}{2k_{1}^{2}}t+c_{1}\right) , \end{aligned}$$
(56)
$$\begin{aligned}&F\left( x,y,t\right) \nonumber \\&\quad =\pm B\sinh \left( \pm \mathrm {i}k_{1}x+l_{2}y-\frac{( 4k_{1}^{4}+l_{2}^{2}) l_{2}}{2k_{1}^{2}}t+c_{2}\right) \nonumber \\&\qquad \ \pm A\cos \left( k_{1}x\pm \mathrm {i}l_{2}y\pm \frac{\mathrm {i}( 4k_{1}^{4}+l_{2}^{2}) l_{2}}{2k_{1}^{2}}t+c_{1}\right) , \end{aligned}$$
(57)
$$\begin{aligned}&F\left( x,y,t\right) \nonumber \\&\quad =\pm B\cosh \left( \pm \mathrm {i}k_{1}x+l_{2}y-\frac{(4k_{1}^{4}+l_{2}^{2}) l_{2}}{2k_{1}^{2}}t+c_{2}\right) \nonumber \\&\qquad \,\ \pm A\cos \left( k_{1}x\pm \mathrm {i}l_{2}y\pm \frac{\mathrm {i}( 4k_{1}^{4}+l_{2}^{2}) l_{2}}{2k_{1}^{2}}t+c_{1}\right) . \end{aligned}$$
(58)

Case 2: \(z=y\).

In this case, eqs (27) and (28) read

$$\begin{aligned}&( D_{x}^{4}+3D_{y}^{2}+\alpha D_{x}D_{y}) FF\nonumber \\&\quad =2FF_{xxxx}-8F_{x}F_{xxx}+6F_{xx}^{2}+6FF_{yy}-6F_{y}^{2}\nonumber \\&\qquad +2\alpha FF_{xy}-2\alpha F_{x}F_{y}=0 \end{aligned}$$
(59)

and

$$\begin{aligned}&\left( D_{x}^{3}D_{y}-3D_{x}D_{t}-\frac{\alpha }{2}D_{y}^{2}\right) FF \nonumber \\&\quad = 2FF_{xxxy}-2F_{xxx}F_{y}-6F_{x}F_{xxy}+6F_{xx}F_{xy} \nonumber \\&\quad \quad -6FF_{xt}+6F_{x}F_{t}- \alpha FF_{yy}+\alpha F_{y}^{2}=0. \end{aligned}$$
(60)

Using the same steps described in Case 1, the following outputs are emerged:

Result 1

$$\begin{aligned}&A=\frac{\rho B}{k_{1}},\ \ \alpha =\kappa ,\ \ l_{1}=-\frac{k_{1}(-4k_{1}^{2}k_{2}+4k_{2}^{3}+\kappa l_{2}) }{\kappa k_{2}+6l_{2}}, \\&( k_{1}^{2}k_{2}l_{2}+k_{2}^{3}l_{2}) \kappa ^{3} \\&\quad +(-3k_{1}^{4}k_{2}^{2}-2k_{1}^{2}k_{2}^{4}+k_{2}^{6}+3k_{1}^{2}l_{2}^{2}+15k_{2}^{2}l_{2}^{2})\kappa ^{2}\\&\quad +( 12k_{1}^{4}k_{2}l_{2}-72k_{1}^{2}k_{2}^{3}l_{2}+12k_{2}^{5}l_{2}+72k_{2}l_{2}^{3})\kappa \\&\quad -48k_{1}^{2}k_{2}^{6}+96k_{1}^{4}k_{2}^{4}+36k_{2}^{4}l_{2}^{2}-48k_{1}^{6}k_{2}^{2}\\&\quad - 216k_{1}^{2}k_{2}^{2}l_{2}^{2}+36k_{1}^{4}l_{2}^{2}+108l_{2}^{4}=0, \\&(9k_{1}^{8}+36k_{1}^{6}k_{2}^{2}+30k_{1}^{4}k_{2}^{4}-12k_{1}^{2}k_{2}^{6}\\&\quad +k_{2}^{8}-18k_{1}^{4}l_{2}^{2}+12k_{1}^{2}k_{2}^{2}l_{2}^{2}-10k_{2}^{4}l_{2}^{2}+9l_{2}^{4})\rho ^{2}\\&\quad -12k_{1}^{6}k_{2}^{4}-24k_{1}^{4}k_{2}^{6}+4k_{1}^{2}k_{2}^{8}-3\kappa k_{1}^{6}k_{2}l_{2} \\&\quad -6k_{1}^{4}k_{2}^{3}l_{2}\kappa -3k_{1}^{2}k_{2}^{5}l_{2}\kappa -k_{1}^{2}k_{2}^{2}l_{2}^{2}\kappa ^{2}\\&\quad -\kappa ^{2}k_{2}^{4}l_{2}^{2}-9l_{2}^{2}k_{1}^{6}-18k_{1}^{4}k_{2}^{2}l_{2}^{2}-k_{1}^{2}k_{2}^{4}l_{2}^{2} \\&\quad -12\kappa k_{2}^{3}l_{2}^{3}+9k_{1}^{2}l_{2}^{4}-36l_{2}^{4}k_{2}^{2}=0, \end{aligned}$$
$$\begin{aligned} \omega _{1}&=\frac{k_{1}}{6k_{2}( k_{1}^{2}+k_{2}^{2}) ^{2}\left( \kappa k_{2}+6l_{2}\right) ^{2}} \\&\quad \times ( -24\kappa k_{1}^{8}k_{2}^{3}+16\kappa k_{1}^{6}k_{2}^{5}+32\kappa k_{1}^{4}k_{2}^{7}-16\kappa k_{1}^{2}k_{2}^{9} \\&\qquad \,-8\kappa k_{2}^{11}+7\kappa ^{2}k_{1}^{6}k_{2}^{2}l_{2}+5\kappa ^{2}k_{1}^{4}k_{2}^{4}l_{2}+5\kappa ^{2}k_{1}^{2}k_{2}^{6}l_{2} \\&\qquad \, +7\kappa ^{2}k_{2}^{8}l_{2}-96k_{1}^{8}k_{2}^{2}l_{2} +240k_{1}^{6}k_{2}^{4}l_{2} \\&\qquad \, -240k_{1}^{4}k_{2}^{6}l_{2}+144k_{1}^{2}k_{2}^{8}l_{2} -48k_{2}^{10}l_{2}\\&\qquad \,+24\kappa k_{1}^{6}k_{2}l_{2}^{2} -96\kappa k_{1}^{4}k_{2}^{3}l_{2}^{2}+312\kappa k_{1}^{2}k_{2}^{5}l_{2}^{2}\\&\qquad \, +48\kappa k_{2}^{7}l_{2}^{2}+3\kappa ^{2}k_{1}^{4}l_{2}^{3} +30\kappa ^{2}k_{1}^{2}k_{2}^{2}l_{2}^{3} \\&\qquad \,-21\kappa ^{2}k_{2}^{4}l_{2}^{3}+36k_{1}^{6}l_{2}^{3}-180k_{1}^{4}k_{2}^{2}l_{2}^{3}\\&\qquad \, +972k_{1}^{2}k_{2}^{4}l_{2}^{3}+36k_{2}^{6}l_{2}^{3}+108\kappa k_{1}^{2}k_{2}l_{2}^{4}\\&\qquad \,-180\kappa k_{2}^{3}l_{2}^{4} +108k_{1}^{2}l_{2}^{5}-324k_{2}^{2}l_{2}^{5}), \end{aligned}$$
$$\begin{aligned} \omega _{2}&=-\frac{1}{6( k_{1}^{2}+k_{2}^{2}) ^{2}( \kappa k_{2}+6l_{2}) ^{2}} \nonumber \\&\quad \ \times ( 32\kappa k_{1}^{6}k_{2}^{5}-32\kappa k_{1}^{2}k_{2}^{9}+5\kappa ^{2}k_{1}^{6}k_{2}^{2}l_{2}\nonumber \\&\qquad \, \ -9\kappa ^{2}k_{1}^{4}k_{2}^{4}l_{2}-17\kappa ^{2}k_{1}^{2}k_{2}^{6}l_{2} -3\kappa ^{2}k_{2}^{8}l_{2} \nonumber \\&\qquad \,\ -48k_{1}^{8}k_{2}^{2}l_{2}+432k_{1}^{6}k_{2}^{4}l_{2}-336k_{1}^{4}k_{2}^{6}l_{2} \nonumber \\&\qquad \,\ -48k_{1}^{2}k_{2}^{8}l_{2}+84\kappa k_{1}^{6}k_{2}l_{2}^{2} -252\kappa k_{1}^{4}k_{2}^{3}l_{2}^{2} \nonumber \\&\qquad \,\ +12\kappa k_{1}^{2}k_{2}^{5}l_{2}^{2} -36\kappa k_{2}^{7}l_{2}^{2}-3\kappa ^{2}k_{1}^{4}l_{2}^{3}\nonumber \\&\qquad \,\ +42\kappa ^{2}k_{1}^{2}k_{2}^{2}l_{2}^{3}-3\kappa ^{2}k_{2}^{4}l_{2}^{3}+180k_{1}^{6}l_{2}^{3}\nonumber \\&\qquad \,-612k_{1}^{4}k_{2}^{2}l_{2}^{3} +252k_{1}^{2}k_{2}^{4}l_{2}^{3}-108k_{2}^{6}l_{2}^{3}\nonumber \\&\qquad \,+252\kappa k_{1}^{2}k_{2}l_{2}^{4}-36\kappa k_{2}^{3}l_{2}^{4} +324k_{1}^{2}l_{2}^{5}-108k_{2}^{2}l_{2}^{5}). \end{aligned}$$
(61)

The complexiton solutions of (1) corresponding to (61) are given by

$$\begin{aligned} u\left( x,y,t\right) =2\left( \ln F\left( x,y,t\right) \right) _{x} \end{aligned}$$
(62)

with

$$\begin{aligned}&F\left( x,y,t\right) =\pm B\sinh \left( k_{2}x+l_{2}y+\omega _{2}t+c_{2}\right) \pm \frac{\rho B}{k_{1}}\nonumber \\&\quad \times \sin \left( k_{1}x-\frac{ k_{1}( -4k_{1}^{2}k_{2}+4k_{2}^{3}+\kappa l_{2}) }{\kappa k_{2}+6l_{2}}y+\omega _{1}t+c_{1}\right) , \end{aligned}$$
(63)
$$\begin{aligned}&F\left( x,y,t\right) =\pm B\sinh \left( k_{2}x+l_{2}y+\omega _{2}t+c_{2}\right) \pm \frac{\rho B}{k_{1}}\nonumber \\&\quad \times \cos \left( k_{1}x-\frac{ k_{1}( -4k_{1}^{2}k_{2}+4k_{2}^{3}+\kappa l_{2}) }{\kappa k_{2}+6l_{2}}y+\omega _{1}t+c_{1}\right) . \end{aligned}$$
(64)

Result 2

$$\begin{aligned}&9\kappa ^{4}+( 18k_{1}^{4}+6k_{2}^{4}) \kappa ^{2}+k_{1}^{8}-8k_{1}^{6}k_{2}^{2}\\&\qquad +14k_{1}^{4}k_{2}^{4}+8k_{1}^{2}k_{2}^{6}+k_{2}^{8}=0, \\&A=k_{2}B\rho ,\quad (3k_{1}^{2}+k_{2}^{2})\rho ^{2}-2=0, \\&\alpha =\frac{k_{1}^{4}-4k_{1}^{2}k_{2}^{2}-k_{2}^{4}-3\kappa ^{2}}{k_{1}\kappa }, \\&l_{1}=\kappa ,\ \ l_{2}=-\frac{k_{2}(k_{1}^{4}-4k_{1}^{2}k_{2}^{2}-k_{2}^{4}-3\kappa ^{2}) }{6k_{1}\kappa }, \end{aligned}$$
$$\begin{aligned}&\omega _{1}=\frac{3k_{1}^{10}-27k_{1}^{8}k_{2}^{2}+66k_{1}^{6}k_{2}^{4}-18k_{1}^{4}k_{2}^{6}-21k_{1}^{2}k_{2}^{8}-3k_{2}^{10}+53\kappa ^{2}k_{1}^{6}-49\kappa ^{2}k_{1}^{4}k_{2}^{2}+15\kappa ^{2}k_{1}^{2}k_{2}^{4}-19\kappa ^{2}k_{2}^{6} }{18\kappa ^{3}}, \nonumber \\&\omega _{2}=\frac{\left( 3k_{1}^{10}-26k_{1}^{8}k_{2}^{2}+58k_{1}^{6}k_{2}^{4}-4k_{1}^{4}k_{2}^{6}-13k_{1}^{2}k_{2}^{8}-2k_{2}^{10}+57\kappa ^{2}k_{1}^{6}-54\kappa ^{2}k_{1}^{4}k_{2}^{2}+39\kappa ^{2}k_{1}^{2}k_{2}^{4}-6\kappa ^{2}k_{2}^{6}\right) k_{2} }{27k_{1}\kappa ^{3}}. \nonumber \\ \end{aligned}$$
(65)
Fig. 6
figure 6

Profiles of complexiton-type solution (66) with (67).

Full size image

The complexiton solutions of (1) (see figure 6) corresponding to (65) are given by

$$\begin{aligned} u\left( x,y,t\right) =2\left( \ln F( x,y,t\right) ) _{x} \end{aligned}$$
(66)

with

(67)
(68)

Result 3

$$\begin{aligned}&B=\pm \mathrm {i}A,\ \alpha =-\frac{4k_{2}^{4}+3l_{2}^{2}}{k_{2}l_{2}},\ \ k_{1}=\pm \mathrm {i}k_{2},\ \ l_{1}=\pm \mathrm {i}l_{2},\nonumber \\&\omega _{1}=\pm \frac{\mathrm {i}( 4k_{2}^{4}l_{2}-k_{2}^{2}\omega _{2}+l_{2}^{3}) }{k_{2}^{2}}. \end{aligned}$$
(69)

The complex-valued solutions of (1) corresponding to (69) are given by

$$\begin{aligned} u\left( x,y,t\right) =2\left( \ln F( x,y,t\right) ) _{x} \end{aligned}$$
(70)

with

$$\begin{aligned}&F\left( x,y,t\right) =\pm \mathrm {i}A\sinh \left( k_{2}x+l_{2}y+\omega _{2}t+c_{2}\right) \nonumber \\&\pm A\sin \left( \pm \mathrm {i}k_{2}x\pm \mathrm {i}l_{2}y \pm \frac{\mathrm {i}(4k_{2}^{4}l_{2}-k_{2}^{2}\omega _{2}+l_{2}^{3})}{k_{2}^{2}} t+c_{1}\right) , \end{aligned}$$
(71)
$$\begin{aligned}&F\left( x,y,t\right) =\pm \mathrm {i}A\sinh \left( k_{2}x+l_{2}y+\omega _{2}t+c_{2}\right) \nonumber \\&\pm A\cos \left( \pm \mathrm {i}k_{2}x\pm \mathrm {i}l_{2}y \pm \frac{\mathrm {i}(4k_{2}^{4}l_{2}-k_{2}^{2}\omega _{2}+l_{2}^{3}) }{k_{2}^{2}}t+c_{1}\right) . \end{aligned}$$
(72)
Fig. 7
figure 7

Profiles of complex-valued-type solution (74) with (75).

Full size image

Result 4

$$\begin{aligned}&4\kappa ^{4}-3l_{2}^{2}=0,\quad \alpha =-\frac{8\kappa ^{3}}{l_{2}},\quad k_{1}=\pm \mathrm {i}\kappa ,\quad k_{2}=\kappa ,\nonumber \\&l_{1}=\pm \mathrm {i}l_{2},\ \ \omega _{1}=\pm \frac{8\mathrm {i}l_{2}\kappa ^{2}}{3},\ \ \omega _{2}=\frac{8l_{2}\kappa ^{2} }{3}. \end{aligned}$$
(73)

The complex-valued solutions of (1) (see figure 7) corresponding to (73) are given by

$$\begin{aligned} u\left( x,y,t\right) =2\left( \ln F\left( x,y,t\right) \right) _{x} \end{aligned}$$
(74)

with

$$\begin{aligned} F\left( x,y,t\right)&=\pm B\sinh \left( \kappa x+l_{2}y+\frac{8l_{2}\kappa ^{2}}{3}t+c_{2}\right) \nonumber \\&\quad \,\, \pm A\sin \left( \pm \mathrm {i}\kappa x\pm \mathrm {i}l_{2}y\pm \frac{ 8\mathrm {i}l_{2}\kappa ^{2}}{3}t+c_{1}\right) , \end{aligned}$$
(75)
$$\begin{aligned} F\left( x,y,t\right)&=\pm B\cosh \left( \kappa x+l_{2}y+\frac{8l_{2}\kappa ^{2}}{3}t+c_{2}\right) \nonumber \\&\quad \,\, \pm A\sin \left( \pm \mathrm {i}\kappa x\pm \mathrm {i}l_{2}y\pm \frac{ 8\mathrm {i}l_{2}\kappa ^{2}}{3}t+c_{1}\right) , \end{aligned}$$
(76)
$$\begin{aligned} F\left( x,y,t\right)&=\pm B\sinh \left( \kappa x+l_{2}y+\frac{8l_{2}\kappa ^{2}}{3}t+c_{2}\right) \nonumber \\&\quad \,\,\pm A\cos \left( \pm \mathrm {i}\kappa x\pm \mathrm {i}l_{2}y\pm \frac{ 8\mathrm {i}l_{2}\kappa ^{2}}{3}t+c_{1}\right) , \end{aligned}$$
(77)
$$\begin{aligned} F\left( x,y,t\right)&=\pm B\cosh \left( \kappa x+l_{2}y+\frac{8l_{2}\kappa ^{2}}{3}t+c_{2}\right) \nonumber \\&\quad \pm A\cos \left( \pm \mathrm {i}\kappa x\pm \mathrm {i}l_{2}y\pm \frac{ 8\mathrm {i}l_{2}\kappa ^{2}}{3}t+c_{1}\right) . \end{aligned}$$
(78)

Result 5

$$\begin{aligned}&\alpha =\pm \frac{\mathrm {i}( 4k_{1}^{4}+3l_{2}^{2}) }{k_{1}l_{2}},\quad k_{2}=\pm \mathrm {i}k_{1},\quad l_{1}=\pm \mathrm {i}l_{2}, \nonumber \\&\omega _{1}=\pm \frac{\mathrm {i}l_{2}( 4k_{1}^{4}+l_{2}^{2}) }{2k_{1}^{2}},\ \ \omega _{2}=-\frac{l_{2}( 4k_{1}^{4}+l_{2}^{2}) }{2k_{1}^{2}}. \end{aligned}$$
(79)

The complex-valued solutions of (1) corresponding to (79) are given by

$$\begin{aligned} u\left( x,y,t\right) =2\left( \ln F( x,y,t\right) ) _{x} \end{aligned}$$
(80)

with

$$\begin{aligned}&F\left( x,y,t\right) \nonumber \\&\quad =\pm B\sinh \left( \pm \mathrm {i}k_{1}x+l_{2}y -\frac{l_{2}(4k_{1}^{4}+l_{2}^{2}) }{2k_{1}^{2}}t+c_{2}\right) \nonumber \\&\qquad \,\, \pm A\sin \left( k_{1}x\pm \mathrm {i}l_{2}y\pm \frac{\mathrm {i}l_{2}( 4k_{1}^{4}+l_{2}^{2}) }{ 2k_{1}^{2}}t+c_{1}\right) , \end{aligned}$$
(81)
$$\begin{aligned}&F\left( x,y,t\right) \nonumber \\&\quad =\pm B\cosh \left( \pm \mathrm {i}k_{1}x+l_{2}y-\frac{l_{2}( 4k_{1}^{4}+l_{2}^{2}) }{2k_{1}^{2}}t+c_{2}\right) \nonumber \\&\qquad \,\, \pm A\sin \left( k_{1}x\pm \mathrm {i}l_{2}y\pm \frac{\mathrm {i}l_{2}( 4k_{1}^{4}+l_{2}^{2}) }{ 2k_{1}^{2}}t+c_{1}\right) , \end{aligned}$$
(82)
$$\begin{aligned}&F( x,y,t)\nonumber \\&\quad =\pm B\sinh \left( \pm \mathrm {i}k_{1}x+l_{2}y-\frac{l_{2}(4k_{1}^{4}+l_{2}^{2}) }{2k_{1}^{2}}t+c_{2}\right) \nonumber \\&\qquad \,\, \pm A\cos \left( k_{1}x\pm \mathrm {i}l_{2}y\pm \frac{\mathrm {i}l_{2}( 4k_{1}^{4}+l_{2}^{2}) }{ 2k_{1}^{2}}t+c_{1}\right) , \end{aligned}$$
(83)
$$\begin{aligned}&F\left( x,y,t\right) \nonumber \\&\quad =\pm B\cosh \left( \pm \mathrm {i}k_{1}x+l_{2}y-\frac{l_{2}( 4k_{1}^{4}+l_{2}^{2}) }{2k_{1}^{2}}t+c_{2}\right) \nonumber \\&\qquad \,\, \pm A\cos \left( k_{1}x\pm \mathrm {i}l_{2}y\pm \frac{\mathrm {i}l_{2}( 4k_{1}^{4}+l_{2}^{2}) }{ 2k_{1}^{2}}t+c_{1}\right) . \end{aligned}$$
(84)

Case 3: \(z=t\).

In this case, eqs (27) and (28) change to

$$\begin{aligned}&( D_{x}^{4}+3D_{y}^{2}+\alpha D_{x}D_{t}) \textit{FF}\nonumber \\&\quad =2\textit{FF}k_{xxxx}-8F_{x}F_{xxx}+6F_{xx}^{2}+6\textit{FF}_{yy}-6F_{y}^{2}\nonumber \\&\qquad \,\,+2\alpha \textit{FF}_{xt}-2\alpha F_{x}F_{t}=0 \end{aligned}$$
(85)

and

$$\begin{aligned}&\left( D_{x}^{3}D_{y}-3D_{x}D_{t}-\frac{\alpha }{2}D_{y}D_{t}\right) {} \textit{FF}\nonumber \\&\quad =2\textit{FF}_{xxxy}-2F_{xxx}F_{y}-6F_{x}F_{xxy} \nonumber \\&\qquad \,\,+6F_{xx}F_{xy}-6\textit{FF}_{xt}+6F_{x}F_{t}\nonumber \\&\qquad \,\,-\alpha \textit{FF}_{yt}+\alpha F_{y}F_{t}=0. \end{aligned}$$
(86)

Using the same steps mentioned in Case 1, we obtain the following result:

$$\begin{aligned}&B=A,\quad \alpha =-\frac{2k_{2}\beta _{1}}{\kappa \beta _{2}},\quad l_{2}=\kappa , \\&\omega _{1}=\frac{\kappa \beta _{2}\beta _{3}}{4k_{2}^{3}k_{1}\beta _{1}\beta _{4}}, \\&\omega _{2}=\frac{\kappa (-3k_{1}^{4}-6k_{1}^{2}k_{2}^{2}+5k_{2}^{4}+6\kappa ^{2}) \beta _{2}}{ 4k_{2}^{2}\beta _{1}}, \\&(144k_{1}^{2}-144k_{2}^{2})\kappa ^{8}+(-288k_{1}^{6}+480k_{1}^{4}k_{2}^{2} \\&\quad -992k_{1}^{2}k_{2}^{4}+288k_{2}^{6})\kappa ^{6} \\&\quad +(216k_{1}^{10}-216k_{1}^{8}k_{2}^{2}-144k_{1}^{6}k_{2}^{4} \\&\quad -816k_{1}^{4}k_{2}^{6}+1464k_{1}^{2}k_{2}^{8}-504k_{2}^{10})\kappa ^{4} \\&\quad +(-72k_{1}^{14}-72k_{1}^{12}k_{2}^{2}+1464k_{1}^{10}k_{2}^{4} \\&\quad -2184k_{1}^{8}k_{2}^{6}+744k_{1}^{6}k_{2}^{8}+1896k_{1}^{4}k_{2}^{10} \\&\quad -2136k_{1}^{2}k_{2}^{12}+360k_{2}^{14})\kappa ^{2}+9k_{1}^{18} \\&\quad +39k_{1}^{16}k_{2}^{2}+148k_{1}^{14}k_{2}^{4} -36k_{1}^{12}k_{2}^{6}-98k_{1}^{10}k_{2}^{8} \\&\quad -1230k_{1}^{8}k_{2}^{10}+2852k_{1}^{6}k_{2}^{12}-2644k_{1}^{4}k_{2}^{14} \\&\quad +1185k_{1}^{2}k_{2}^{16}-225k_{2}^{18}=0, \end{aligned}$$
$$\begin{aligned} \beta _{1}&=-27k_{1}^{22}-243k_{1}^{20}k_{2}^{2} \\&\quad -1017k_{1}^{18}k_{2}^{4}-2081k_{1}^{16}k_{2}^{6}+354k_{1}^{14}k_{2}^{8} \\&\quad +5170k_{1}^{12}k_{2}^{10}+8958k_{1}^{10}k_{2}^{12}-28306k_{1}^{8}k_{2}^{14} \\&\quad +24905k_{1}^{6}k_{2}^{16}-7983k_{1}^{4}k_{2}^{18}-405k_{1}^{2}k_{2}^{20} \\&\quad +675k_{2}^{22}-108\kappa ^{2}k_{1}^{18}-2520\kappa ^{2}k_{1}^{16}k_{2}^{2} \\&\quad -10896\kappa ^{2}k_{1}^{14}k_{2}^{4} -10368\kappa ^{2}k_{1}^{12}k_{2}^{6}+43704\kappa ^{2}k_{1}^{10}k_{2}^{8} \\&\quad -18096\kappa ^{2}k_{1}^{8}k_{2}^{10}-12816\kappa ^{2}k_{1}^{6}k_{2}^{12}+9024\kappa ^{2}k_{1}^{4}k_{2}^{14} \\&\quad +6228\kappa ^{2}k_{1}^{2}k_{2}^{16}-1080\kappa ^{2}k_{2}^{18}-4104\kappa ^{4}k_{1}^{14} \\&\quad -19656\kappa ^{4}k_{1}^{12}k_{2}^{2}+6648\kappa ^{4}k_{1}^{10}k_{2}^{4}+19704\kappa ^{4}k_{1}^{8}k_{2}^{6} \\&\quad +17832\kappa ^{4}k_{1}^{6}k_{2}^{8} -7704\kappa ^{4}k_{1}^{4}k_{2}^{10}-1944\kappa ^{4}k_{1}^{2}k_{2}^{12}\\ {}&\quad +1512\kappa ^{4}k_{2}^{14}+5184\kappa ^{6}k_{1}^{10} -864\kappa ^{6}k_{1}^{8}k_{2}^{2}\\&\quad +8448\kappa ^{6}k_{1}^{6}k_{2}^{4} +2496\kappa ^{6}k_{1}^{4}k_{2}^{6}+5568\kappa ^{6}k_{1}^{2}k_{2}^{8} \\&\quad -864\kappa ^{6}k_{2}^{10}+6480\kappa ^{8}k_{1}^{6}+3024\kappa ^{8}k_{1}^{4}k_{2}^{2} \\&\quad -720\kappa ^{8}k_{1}^{2}k_{2}^{4} +432\kappa ^{8}k_{2}^{6}+1728\kappa ^{10}k_{1}^{2}, \\ \beta _{2}&=27k_{1}^{22}+255k_{1}^{20}k_{2}^{2}+809k_{1}^{18}k_{2}^{4} \\&\quad +821k_{1}^{16}k_{2}^{6}-1442k_{1}^{14}k_{2}^{8}-3130k_{1}^{12}k_{2}^{10} \\&\quad +10914k_{1}^{10}k_{2}^{12}-20806k_{1}^{8}k_{2}^{14}+20855k_{1}^{6}k_{2}^{16} \\&\quad -10133k_{1}^{4}k_{2}^{18} +1605k_{1}^{2}k_{2}^{20}+225k_{2}^{22}+396\kappa ^{2}k_{1}^{18} \\&\quad +2088\kappa ^{2}k_{1}^{16}k_{2}^{2}+672\kappa ^{2}k_{1}^{14}k_{2}^{4}-9296\kappa ^{2}k_{1}^{12}k_{2}^{6} \\&\quad +19672\kappa ^{2}k_{1}^{10}k_{2}^{8}-10560\kappa ^{2}k_{1}^{8}k_{2}^{10} \\&\quad -11456\kappa ^{2}k_{1}^{6}k_{2}^{12}+11472\kappa ^{2}k_{1}^{4}k_{2}^{14}+444\kappa ^{2}k_{1}^{2}k_{2}^{16} \\&\quad -360\kappa ^{2}k_{2}^{18}-1368\kappa ^{4}k_{1}^{14}-9144\kappa ^{4}k_{1}^{12}k_{2}^{2} \\&\quad +2568\kappa ^{4}k_{1}^{10}k_{2}^{4} +12648\kappa ^{4}k_{1}^{8}k_{2}^{6}+13560\kappa ^{4}k_{1}^{6}k_{2}^{8} \\&\quad -11688\kappa ^{4}k_{1}^{4}k_{2}^{10}+2136\kappa ^{4}k_{1}^{2}k_{2}^{12}+504\kappa ^{4}k_{2}^{14} \\&\quad -5856\kappa ^{6}k_{1}^{8}k_{2}^{2}+4928\kappa ^{6}k_{1}^{6}k_{2}^{4}+5632\kappa ^{6}k_{1}^{4}k_{2}^{6} \\&\quad +704\kappa ^{6}k_{1}^{2}k_{2}^{8}-288\kappa ^{6}k_{2}^{10}+1584\kappa ^{8}k_{1}^{6} \\&\quad -144\kappa ^{8}k_{1}^{4}k_{2}^{2}+720\kappa ^{8}k_{1}^{2}k_{2}^{4} +144\kappa ^{8}k_{2}^{6}+576\kappa ^{10}k_{1}^{2}, \end{aligned}$$
$$\begin{aligned}&l_{1}=\frac{\kappa k_{1}\left( -9k_{1}^{8}-16k_{1}^{6}k_{2}^{2}+22k_{1}^{4}k_{2}^{4}-8k_{1}^{2}k_{2}^{6}+27k_{2}^{8}+12\kappa ^{2}k_{1}^{4}+8\kappa ^{2}k_{1}^{2}k_{2}^{2}-4\kappa ^{2}k_{2}^{4}+12\kappa ^{4}\right) }{k_{2}\left( 3k_{1}^{8}+8k_{1}^{6}k_{2}^{2}+22k_{1}^{4}k_{2}^{4}-32k_{1}^{2}k_{2}^{6}+15k_{2}^{8}+36\kappa ^{2}k_{1}^{4}+24\kappa ^{2}k_{1}^{2}k_{2}^{2}-12\kappa ^{2}k_{2}^{4} +12\kappa ^{4}\right) }, \end{aligned}$$
$$\begin{aligned} \beta _{3}&=-45k_{1}^{20}k_{2}^{2}-186k_{1}^{18}k_{2}^{4}-665k_{1}^{16}k_{2}^{6}+520k_{1}^{14}k_{2}^{8} \\&\quad +1238k_{1}^{12}k_{2}^{10} +6692k_{1}^{10}k_{2}^{12}-15242k_{1}^{8}k_{2}^{14} \\&\quad +11400k_{1}^{6}k_{2}^{16} -1833k_{1}^{4}k_{2}^{18}-1530k_{1}^{2}k_{2}^{20} \\&\quad +675k_{2}^{22}+486\kappa ^{2}k_{1}^{18}+648\kappa ^{2}k_{1}^{16}k_{2}^{2} \\&\quad -3144\kappa ^{2}k_{1}^{14}k_{2}^{4}-7872\kappa ^{2}k_{1}^{12}k_{2}^{6} +22260\kappa ^{2}k_{1}^{10}k_{2}^{8}\\&\quad -5328\kappa ^{2}k_{1}^{8}k_{2}^{10}-10152\kappa ^{2}k_{1}^{6}k_{2}^{12}+5184\kappa ^{2}k_{1}^{4}k_{2}^{14} \\&\quad +6678\kappa ^{2}k_{1}^{2}k_{2}^{16} -1080\kappa ^{2}k_{2}^{18}-1296\kappa ^{4}k_{1}^{14} \\&\quad -10008\kappa ^{4}k_{1}^{12}k_{2}^{2} +672\kappa ^{4}k_{1}^{10}k_{2}^{4}+16152\kappa ^{4}k_{1}^{8}k_{2}^{6} \\&\quad +15984\kappa ^{4}k_{1}^{6}k_{2}^{8} -6888\kappa ^{4}k_{1}^{4}k_{2}^{10} -2304\kappa ^{4}k_{1}^{2}k_{2}^{12}\\&\quad +1512\kappa ^{4}k_{2}^{14} -432\kappa ^{6}k_{1}^{10}-5472\kappa ^{6}k_{1}^{8}k_{2}^{2} \\&\quad +5280\kappa ^{6}k_{1}^{6}k_{2}^{4} +5952\kappa ^{6}k_{1}^{4}k_{2}^{6}+3984\kappa ^{6}k_{1}^{2}k_{2}^{8} \\&\quad -864\kappa ^{6}k_{2}^{10} +1728\kappa ^{8}k_{1}^{6}+432\kappa ^{8}k_{1}^{4}k_{2}^{2} \\&\quad +288\kappa ^{8}k_{1}^{2}k_{2}^{4} +432\kappa ^{8}k_{2}^{6}+864\kappa ^{10}k_{1}^{2}, \end{aligned}$$
$$\begin{aligned} \beta _{4}&=(3k_{1}^{8}+8k_{1}^{6}k_{2}^{2}+22k_{1}^{4}k_{2}^{4}-32k_{1}^{2}k_{2}^{6}+15k_{2}^{8} \nonumber \\&\quad +36\kappa ^{2}k_{1}^{4}+24\kappa ^{2}k_{1}^{2}k_{2}^{2}-12\kappa ^{2}k_{2}^{4}+12\kappa ^{4}) ^{2}. \end{aligned}$$
(87)

The complexiton solutions of (1) corresponding to (87) are given as

$$\begin{aligned} u\left( x,y,t\right) =2\left( \ln F\left( x,y,t\right) \right) _{x} \end{aligned}$$
(88)

with

(89)
(90)

4 Concluding remarks

In this work, the DJKM equation was considered from the view of analytical solutions. In this regard, multisoliton-type solutions, namely one-soliton, two-soliton and three-soliton which comprise both wave frequencies and generic phase shifts are presented by the multiple exp-function approach which falls out as a result of generalisation of Hirota’s perturbation methodology. We emphasise that the fundamental advantage of this methodology is that it does not require bilinear equations, whereas the Hirota’s bilinear procedure requires bilinear equations. The new phase shifts \(A_{12},A_{13}\) and \(A_{23}\) in (17) are given for the first time for the DJKM equation. Furthermore, complexiton solutions were recovered through the additional integration technique known as the extended transformed rational function algorithm that is based on the Hirota bilinear form. Additional solutions such as complex-valued solutions also are obtained in this integration scheme. It is emphasised that the obtained complexiton-type solutions include singularities of unifications of both exponential and trigonometric function waves that possess novel style distinct travelling wave speeds.

On the other hand, lump solutions are special exact rational solutions and contrary to soliton solutions they can be localised in all directions. We note that the lump-type or interaction solutions can be constructed in (3\(+\)1) and (4\(+\)1) dimensions using the generalised Hirota bilinear forms. The important condition for producing lump solutions is to put the given equation into Hirota bilinear form with the help of Hirota’s derivative definition and \(u=T(f)\) substitution (usually \( u=2(\log f)_{x}\) or \(u=2(\log f)_{xx}\)). Afterwards, one assumes the form of lump solutions as follows:

$$\begin{aligned} f=g^{2}+h^{2}+a_{9}, \end{aligned}$$

where

$$\begin{aligned} g= & {} a_{1}x+a_{2}y+a_{3}t+a_{4}, \\ h= & {} a_{5}x+a_{6}y+a_{7}t+a_{8} \end{aligned}$$

and \(a_{i}\) \(,\ i=1,\ldots ,9\), are arbitrary values which must be fixed in terms of themselves. We have observed that the form of lump solutions does not generate analytic solutions which are rationally localised in all directions in the space by Maple symbolic computation for eqs (29), (30), (59), (60), (85) and (86). Therefore, we could not get lump solutions. However, the interaction solutions (lump–soliton, lump–kink) stand as an open problem. Moreover, in our subsequent works, using the generalised Hirota derivative operators, lump-type solutions will be investigated.