1 Introduction

Soliton theory provides effective methods to solve nonlinear partial differential equations (PDEs) [1, 2], including soliton equations generated from zero curvature equations. The Hirota bilinear method is particularly powerful in constructing soliton solutions [3, 4]. Those solutions are analytic and exponentially localized. Let a polynomial P determine a Hirota bilinear differential equation

$$\begin{aligned} P(D_x,D_y,D_t)f\cdot f=0 \end{aligned}$$

in (2+1)-dimensions, where \(D_x,D_y\) and \(D_t\) are Hirota’s bilinear derivatives [3]. The corresponding PDE with a dependent variable u is usually determined through one of the logarithmic transformations: \(u=2(\ln f)_{x}\) or \(u=2(\ln f)_{xx}\). Based on the Hirota bilinear form, the N-soliton solution is formulated as follows:

$$\begin{aligned} f=\sum _{\mu =0,1}\text {exp}\left( \sum _{i=1}^N \mu _i \xi _i +\sum _{i<j}\mu _i\mu _j a_{ij}\right) , \end{aligned}$$

where \(\sum _{\mu =0,1}\) denotes the sum over all possibilities for \(\mu _1,\mu _2,\ldots ,\mu _N\) taking either 0 or 1, and the wave variables and the phase shifts are given by

$$\begin{aligned} \xi _i=k_ix+l_iy -\omega _i t +\xi _{i,0},\ 1\le i\le N, \end{aligned}$$

and

$$\begin{aligned} \mathrm{e}^{a_{ij}}=- \frac{P(k_i-k_j,l_i-l_j,\omega _j-\omega _i)}{P(k_i+k_j,l_i+l_j,\omega _j+\omega _i)} ,\ 1\le i< j\le N, \end{aligned}$$

in which \(k_i,l_i\) and \(\omega _i\), \(1\le i\le N,\) satisfy the corresponding dispersion relation and \(\xi _{i,0}\), \(1\le i\le N,\) are arbitrary phase shifts.

Lump solutions are rational solutions, which are analytic and localized in all directions in space (see, e.g., [5,6,7]), and they can often be obtained from computing long wave limits of soliton equations (see, e.g., [8]). Various recent studies on (2+1)-dimensional soliton equations show the striking richness of lump solutions (see, e.g., [5, 6]), which describe various dispersive wave phenomena. The KPI equation possesses diverse lump solutions (see, e.g., [9]), and special lump solutions are derived from soliton solutions [10]. Other soliton equations which possess lump solutions contain the three-dimensional three-wave resonant interaction [11], the BKP equation [12, 13], the Davey-Stewartson II equation [8], the Ishimori-I equation [14], the KPI equation with a self-consistent source [15] and the mKPI equation [16]. A crucial step in constructing lump solutions is to determine positive quadratic function solutions to Hirota bilinear equations [5]. Then lump solutions to nonlinear PDEs are generated through the logarithmic transformations from positive quadratic function solutions.

In this paper, we would like to consider a combined fourth-order soliton equation in (2+1)-dimensional dispersive waves and determine its abundant lump solution structures. The Hirota bilinear form plays a key role in our discussion (see, e.g., [5, 6, 17, 18]). We will formulate a combined fourth-order soliton equation including three fourth-order nonlinear terms and all second-order linear terms. To present lump solutions with Maple symbolic computations, we will discuss two cases of the combined model. Illustrative examples of the considered model will be presented and some three-dimensional plots and contour plots will be made for two particular lump solutions by using Maple. A conclusion and some remarks will be given at the end of the paper.

2 A combined soliton equation

We would like to consider a general combined fourth-order soliton equation as follows:

$$\begin{aligned} P(u)&=\alpha ( 6 u_x u_{xx}+ u_{xxxx} ) + \beta [3 (u_xu_t)_x+u_{xxxt}]+\gamma [3 (u_xu_y)_x+u_{xxxy}] \nonumber \\&\quad +\delta _1 u_{yt} +\delta _2 u_{xx} +\delta _3 u_{xt}+\delta _4 u_{xy}+\delta _5 u_{yy}+\delta _6 u_{tt} =0, \end{aligned}$$
(2.1)

where the constants \(\alpha , \beta \) and \(\gamma \) are not all zero, but the constants \(\delta _i,\ 1\le i\le 6,\) are all arbitrary. This equation contains three fourth-order nonlinear terms and all second-order linear terms, and it generalizes the standard KP equation.

Upon taking \(\alpha =0, \ \beta =1\) and \(\gamma =0\), and \(\delta _1=\delta _2=1\) and the other \(\delta _i\)’s as zero, we obtain an integrable \((2+1)\)-dimensional extension of the Hirota-Satsuma equation [3], namely the Hirota-Satsuma-Ito (HSI) equation in (2+1)-dimensions [19]:

$$\begin{aligned} 3 (u_xu_t)_x+u_{xxxt} + u_{yt} + u_{xx} =0, \end{aligned}$$
(2.2)

which satisfies the Hirota three-soliton condition and possesses a Hirota bilinear form under the logarithmic transformation \(u=2(\ln f)_{x}\):

$$\begin{aligned} (D_x^3D_t+ D_yD_t+ D_x^2 )f\cdot f=0. \end{aligned}$$
(2.3)

This equation is called the bilinear HSI equation.

Upon taking \(\alpha =0,\ \beta =0\) and \(\gamma =1\), and \(\delta _3=\delta _5=1\) and the other \(\delta _i\)’s as zero, we obtain a generalized Calogero–Bogoyavlenskii–Schiff equation [20]:

$$\begin{aligned} 3(u_xu_y)_x+u_{xxxy}+u_{xt}+u_{yy}=0, \end{aligned}$$
(2.4)

which also possesses a Hirota bilinear form

$$\begin{aligned} (D_x^3D_y+D_xD_t+D_y^2)f\cdot f=0, \end{aligned}$$
(2.5)

under \(u=2(\ln f)_x\), and whose lump solutions have been computed in [20].

Upon taking \(\alpha =1,\ \beta =0\) and \(\gamma =1\), and \(\delta _2=\delta _3=\delta _5=1\) and the other \(\delta _i\)’s as zero, we obtain a generalized Bogoyavlensky–Konopelchenko equation [21]:

$$\begin{aligned} 6u_xu_{xx}+ u_{xxxx}+ 3(u_xu_y)_x+u_{xxxy}+u_{xt}+ u_{xx} + u_{yy}=0, \end{aligned}$$
(2.6)

whose Hirota bilinear form is given by

$$\begin{aligned} (D_x^4+ D_x^3D_y+D_xD_t+D_x^2 +D_y^2)f\cdot f=0, \end{aligned}$$
(2.7)

under \(u=2(\ln f)_x\). It has lump solutions as well [21].

The general combined soliton equation (2.1) also presents a generalization of the nonlinear soliton equation in [22], and it has a Hirota bilinear form

$$\begin{aligned} B(f)&=(\alpha D_x^4+ \beta D^3_xD_t+ \gamma D_x^3D_y+\delta _1 D_yD_t+ \delta _2 D_x^2 \nonumber \\&\quad \, + \delta _3 D_xD_t + \delta _4 D_xD_y + \delta _5 D_y^2+\delta _6 D_t^2 )f\cdot f =0, \end{aligned}$$
(2.8)

under the logarithmic transformation

$$\begin{aligned} u=2(\ln f)_x= \frac{2f_x}{f}. \end{aligned}$$
(2.9)

In fact, we have the relation between the nonlinear and bilinear equations: \( P(u)=(\frac{B(f)}{f^2})_x, \) when u and f satisfy the link (2.9).

3 Lump solutions

In this section, we would like to determine lump solutions to the combined fourth-order soliton equation (2.1) in (2+1)-dimensions, through symbolic computations with Maple.

Let us begin with positive quadratic solutions to the combined Hirota bilinear equation (2.8):

$$\begin{aligned} f=(a_1x+a_2y+a_3t +a_4)^2+(a_5 x+a_6y+a_7 t+a_8)^2+a_9, \end{aligned}$$
(3.1)

where the constant parameters \(a_i,\ 1\le i\le 9,\) are to be determined, to present lump solutions to the combined fourth-order soliton equation (2.1). This is a general ansatz on lump solutions in (2+1)-dimensions, generated from quadratic functions [9].

3.1 The case of \(\delta _6=0\)

Let us first consider the case of \(\delta _6=0\) for the combined soliton equation (2.1). A direct symbolic computation determines a set of solutions for the parameters, where

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle a_3= -{\frac{ b_1 }{ (a_{{2}} \delta _{{1}} + a_{{1}}\delta _{{3}} ) ^{2}+ ( a_{{6}}\delta _{{ 1}} +a_{{5}}\delta _{{3}} ) ^{2}}} ,\\ \displaystyle a_7 = -{\frac{ b_2 }{( a_{{2}} \delta _{{1}} + a_{{1}}\delta _{{3}}) ^{2}+ ( a_{{6}}\delta _{{ 1}} + a_{{5}}\delta _{{3}} ) ^{2}}} , \\ \displaystyle a_9=- \frac{3\, ( a_{{1}}^{2}+a_{{5}}^{2} ) (\alpha b_3- \beta b_4 + \gamma b_5) }{ ( a _{{1}}a_{{6}}-a_{{2}}a_{{5}} ) ^{2} ( \delta _{{1}}^{2} \delta _{{2}}-\delta _{{1}}\delta _{{3}}\delta _{{4}}+\delta _{{3}}^{2} \delta _{{5}} ) } ,\end{array} \right. \end{aligned}$$
(3.2)

and all other \(a_i\)’s are arbitrary. The involved five constants \(b_i,\ 1\le i\le 5\), are given by

$$\begin{aligned} \left\{ \begin{array}{l} b_1= [ ( a_{{1}}^{2}a_{{2}}+2\,a_{{1}}a_{{5}}a_{{6}} -a_{{2}}a_{{5}}^{2} ) \delta _{{2}}+a_{{1}} ( a_{{2}}^{2 }+a_{{6}}^{2} ) \delta _{{4}}+a_{{2}} ( a_{{2}}^{2}+a_{ {6}}^{2} ) \delta _{{5}} ] \delta _{{1}}\\ \qquad + [ a_{{1}} ( a_{{1}}^{2}+a_{{5}}^{2} ) \delta _{{2}}+a_{{2}} ( a_{{1}}^{2}+a_{{5}}^{2} ) \delta _{{4}}+ ( a_{{1 }}a_{{2}}^{2}+2\,a_{{2}}a_{{5}}a_{{6}} -a_{{1}}a_{{6}}^{2}) \delta _{{5}} ] \delta _{{3}} , \\ b_2= [ ( -a_{{1}}^{2}a_{{6}}+2\,a_{{1}}a_{{2}}a_{{5} }+a_{{5}}^{2}a_{{6}} ) \delta _{{2}}+a_{{5}} ( a_{{2}}^{ 2}+a_{{6}}^{2} ) \delta _{{4}}+a_{{6}} ( a_{{2}}^{2}+a_ {{6}}^{2} ) \delta _{{5}} ] \delta _{{1}} \\ \qquad + [ a_{{5}} ( a_{{1}}^{2}+a_{{5}}^{2} ) \delta _{{2}}+a_{{6}} ( a_{{1}}^{2}+a_{{5}}^{2} ) \delta _{{4}}+ ( -a_{{2}}^{2}a_{{5}}+ 2\,a_ {{1}}a_{{2}}a_{{6}}+a_{{5}}a_{{6}}^{2} ) \delta _{{5}} ] \delta _{{3}} , \\ b_3= ( a_{{1}}^2+a_{ {5}}^2 ) [ ( a_{{1}}\delta _3 +a_{{2}}\delta _1 ) ^2+ ( a_{{5}}\delta _3 +a_{{6}} \delta _{{1}})^2 ], \\ b_4= ( a_{{1}}^{2}+a_{{5}}^{2} ) ( a_{{1}}a_{{2}}+a_{ {5}}a_{{6}} ) ( \delta _{{1}}\delta _{{2}}+\delta _{{3}} \delta _{{4}} ) + ( a_{{1}}^{2}+a_{{5}}^{2} ) ( a_{{2}}^{2}+a_{{6}}^{2} ) \delta _{{1}}\delta _{{4}} \\ \qquad +( a_{{1}}^{2}+a_{{5}}^{2} ) ^{2}\delta _{{2}}\delta _{{3 }} + ( a_{{2}}^{2}+a_{{6}}^{2} ) ( a_{{1}}a_{{2}}+ a_{{5}}a_{{6}} ) \delta _{{1}}\delta _{{5}} \\ \qquad + [ ( a_{{1} }a_{{2}}+a_{{5}}a_{{6}} ) ^{2}- ( a_{{1}}a_{{6}}-a_{{2}}a_{ {5}} ) ^{2} ] \delta _{{3}}\delta _{{5}} ,\\ b_5= ( a_{{1}}a_{{2}}+a_{ {5}}a_{{6}} ) [ ( a_{{2}}\delta _1 +a_{{1}}\delta _3 ) ^2+ ( a_{{6}}\delta _1 +a_{{5}} \delta _{{3}})^2 ] . \end{array}\right. \end{aligned}$$
(3.3)

The expressions of \(a_3\) and \(a_7\) present diverse dispersion relations in (2+1)-dimensional dispersive waves.

3.2 The case of \(\delta _5=0\)

Let us second consider the case of \(\delta _5=0\) for the combined nonlinear equation (2.1). A similar direct symbolic computation determines a set of solutions for the parameters, where

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle a_2= -{\frac{ c_1 }{ (a_{{3}} \delta _{{1}} + a_{{1}}\delta _{{4}} ) ^{2}+ ( a_{{7}}\delta _{{ 1}} +a_{{5}}\delta _{{4}} ) ^{2}}} , \\ \displaystyle a_6 = -{\frac{ c_2 }{( a_{{3}} \delta _{{1}} + a_{{1}}\delta _{{4}}) ^{2}+ ( a_{{7}}\delta _{{ 1}} + a_{{5}}\delta _{{4}} ) ^{2}}} , \\ \displaystyle a_9=- \frac{3\, ( a_{{1}}^{2}+a_{{5}}^{2} ) (\alpha c_3-\gamma c_4 + \beta c_5) }{ ( a _{{1}}a_{{7}}-a_{{3}}a_{{5}} ) ^{2} ( \delta _{{1}}^{2} \delta _{{2}}-\delta _{{1}}\delta _{{3}}\delta _{{4}}+\delta _{{4}}^{2} \delta _{{6}} ) } ,\end{array} \right. \end{aligned}$$
(3.4)

and all other \(a_i\)’s are arbitrary. The involved five constants \(c_i,\ 1\le i\le 5\), are given by

$$\begin{aligned} \left\{ \begin{array}{l} c_1= [ ( a_{{1}}^{2}a_{{3}}+2\,a_{{1}}a_{{5}}a_{{7}} -a_{{3}}a_{{5}}^{2} ) \delta _{{2}}+a_{{1}} ( a_{{3}}^{2 }+a_{{7}}^{2} ) \delta _{{3}}+a_{{3}} ( a_{{3}}^{2}+a_{ {7}}^{2} ) \delta _{{6}} ] \delta _{{1}} \\ \qquad + [ a_{{1}} ( a_{{1}}^{2}+a_{{5}}^{2} ) \delta _{{2}}+a_{{3}} ( a_{{1}}^{2}+a_{{5}}^{2} ) \delta _{{3}}+ ( a_{{1 }}a_{{3}}^{2}+2\,a_{{3}}a_{{5}}a_{{7}} -a_{{1}}a_{{7}}^{2}) \delta _{{6}} ] \delta _{{4}} , \\ c_2= [ ( -a_{{1}}^{2}a_{{7}}+2\,a_{{1}}a_{{3}}a_{{5} }+a_{{5}}^{2}a_{{7}} ) \delta _{{2}}+a_{{5}} ( a_{{3}}^{ 2}+a_{{7}}^{2} ) \delta _{{3}}+a_{{7}} ( a_{{3}}^{2}+a_ {{7}}^{2} ) \delta _{{6}} ] \delta _{{1}} \\ \qquad + [ a_{{5}} ( a_{{1}}^{2}+a_{{5}}^{2} ) \delta _{{2}}+a_{{7}} ( a_{{1}}^{2}+a_{{5}}^{2} ) \delta _{{3}}+ ( -a_{{3}}^{2}a_{{5}}+ 2\,a_ {{1}}a_{{3}}a_{{7}}+a_{{5}}a_{{7}}^{2} ) \delta _{{6}} ] \delta _{{4}} , \\ c_3= ( a_{{1}}^2+a_{ {5}}^2 ) [ ( a_{{1}}\delta _4 +a_{{3}}\delta _1 ) ^2+ ( a_{{5}}\delta _4 +a_{{7}} \delta _{{1}})^2 ], \\ c_4= ( a_{{1}}^{2}+a_{{5}}^{2} ) ( a_{{1}}a_{{3}}+a_{ {5}}a_{{7}} ) ( \delta _{{1}}\delta _{{2}}+\delta _{{3}} \delta _{{4}} ) + ( a_{{1}}^{2}+a_{{5}}^{2} ) ( a_{{3}}^{2}+a_{{7}}^{2} ) \delta _{{1}}\delta _{{3}} \\ \qquad +( a_{{1}}^{2}+a_{{5}}^{2} ) ^{2}\delta _{{2}}\delta _{{4 }} + ( a_{{3}}^{2}+a_{{7}}^{2} ) ( a_{{1}}a_{{3}}+ a_{{5}}a_{{7}} ) \delta _{{1}}\delta _{{6}} \\ \qquad + [ ( a_{{1} }a_{{3}}+a_{{5}}a_{{7}} ) ^{2}- ( a_{{1}}a_{{7}}-a_{{3}}a_{ {5}} ) ^{2} ] \delta _{{4}}\delta _{{6}} , \\ c_5= ( a_{{1}}a_{{3}}+a_{ {5}}a_{{7}} ) [ ( a_{{3}}\delta _1 +a_{{1}}\delta _4 ) ^2+ ( a_{{7}}\delta _1 +a_{{5}} \delta _{{4}})^2 ] . \end{array} \right. \end{aligned}$$
(3.5)

All the above expressions for wave frequencies and wave numbers in (3.2), (3.3), (3.4) and (3.5) have been obtained with some direct simplifications with Maple. Based on those solution expressions, we need two basic conditions:

$$\begin{aligned} \delta _1^2+\delta _3^2\ne 0, \end{aligned}$$
(3.6)

in the case of \(\delta _6=0\), and

$$\begin{aligned} \delta _1^2+\delta _4^2\ne 0, \end{aligned}$$
(3.7)

in the case of \(\delta _5=0\), to present lump solutions.

In the case of \(\delta _5=0\), to check when the set of the resulting parameters presents lumps, we work out

$$\begin{aligned} \begin{array}{l} a_1a_6-a_2a_5 \\ \quad \displaystyle = \frac{(a_1a_7-a_3a_5) [(a_1^2+a_5^2)(\delta _1 \delta _2 - \delta _3 \delta _4) -(a_3^2+a_7^2)\delta _1 \delta _6 -2 (a_1a_3+a_5a_7)\delta _4\delta _6 ] }{ (a_3\delta _1 +a_1\delta _4)^2+ (a_7 \delta _1 +a_5 \delta _4)^2 }. \end{array} \end{aligned}$$

Therefore, we can see that the condition \(a_1a_6-a_2a_5\ne 0\), which guarantees the existence of lumps, holds if and only if besides (3.7), the following two additional conditions are satisfied:

$$\begin{aligned} \left\{ \begin{array}{l} a_1a_7-a_3a_5\ne 0, \\ (a_1^2+a_5^2)(\delta _1 \delta _2 - \delta _3 \delta _4) -(a_3^2+a_7^2)\delta _1 \delta _6 -2 (a_1a_3+a_5a_7)\delta _4\delta _6 \ne 0. \end{array} \right. \end{aligned}$$
(3.8)

Together with \(a_9>0\), these three conditions ensure that the corresponding set of the parameters will lead to lump solutions.

4 Illustrative examples of the combined model

We present diverse examples of the considered combined soliton equation, on the base of the presented solution expressions above in the two cases of solutions.

4.1 The case of \(\delta _1=\delta _2=1\)

Let \(\delta _1=\delta _2=1\) and the other \(\delta _i\)’s be zero. Then the combined Hirota bilinear equation (2.8) becomes

$$\begin{aligned} (\alpha D_x^4+ \beta D_x^3D_t+\gamma D_x^3D_y +D_yD_t+D_x^2)f\cdot f=0. \end{aligned}$$
(4.1)

The subcase of \(\alpha =\beta =0\) and \(\gamma =1\) gives the dimensionally reduced Jimbo–Miwa equation with \(z=x\) [23].

The subcase of \(\beta =1\) and \(\alpha =\gamma =0\) gives us the original HSI equation in (2+1)-dimensions (2.2). The two solution classes in this case are equivalent to each other. The function f by (3.1) with (3.2) and (3.3) presents a class of lump solutions to the HSI equation (2.2), where

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle a_3= -\frac{a_1^2 a_2+2 a_1 a_5 a_6-a_2 a_5^2}{a_2^2+a_6^2}, \\ \displaystyle a_7 = \frac{a_1^2 a_6 -2 a_1 a_2 a_5- a_5^2 a_6}{a_2^2+a_6^2}, \\ \displaystyle a_9= \frac{3(a_1^2+a_5^2)^2(a_1 a_2+a_5 a_6)}{(a_1 a_6-a_2 a_5)^2 } ,\end{array} \right. \end{aligned}$$
(4.2)

and all other \(a_i\)’s are arbitrary; and the function f by (3.1) with (3.4) and (3.5) presents another class of lump solutions to the HSI equation (2.2), where [24]

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle a_2=-\frac{a_1^2 a_3+2 a_1 a_5 a_7-a_3 a_5^2}{a_3^2+a_7^2}, \\ \displaystyle a_6 = \frac{a_1^2 a_7 -2 a_1 a_3 a_5- a_5^2 a_7}{a_3^2+a_7^2}, \\ \displaystyle a_9= -\frac{3(a_1^2+a_5^2)(a_3^2+a_7^2)(a_1 a_3+a_5 a_7)}{(a_1 a_7-a_3 a_5)^2 } .\end{array} \right. \end{aligned}$$
(4.3)

Obviously, we see that

$$\begin{aligned} a_1a_3+a_5a_7=-\frac{(a_1^2+a_5^2) (a_1a_2+a_5a_6)}{a_2^2+a_6^2}, \end{aligned}$$
(4.4)

and

$$\begin{aligned} a_1a_6-a_2a_5= \frac{(a_1^2+a_5^2)(a_1a_7-a_3a_5)}{a_3^2+a_7^2}. \end{aligned}$$
(4.5)

Therefore, the conditions of

$$\begin{aligned} a_1a_2+a_5a_6>0,\ a_1a_6-a_2a_5\ne 0, \end{aligned}$$
(4.6)

under which f by (3.1) with (4.2) will present lump solutions to (2.2), are equivalent to the conditions of

$$\begin{aligned} a_1a_3+a_5a_7<0,\ a_1a_7-a_3a_5\ne 0, \end{aligned}$$
(4.7)

under which f by (3.1) with (4.3) will present lump solutions to (2.2). To conclude, the two classes of lump solutions presented in the two solution cases are the same. They can be derived from each other.

4.2 The case of \(\delta _3=\delta _5=1\)

Let \(\delta _3=\delta _5=1\) and the other \(\delta _i\)’s be zero. Then the combined Hirota bilinear equation (2.8) becomes

$$\begin{aligned} (\alpha D_x^4+ \beta D_x^3D_t+\gamma D_x^3D_y +D_xD_t+D_y^2)f\cdot f=0. \end{aligned}$$
(4.8)

The subcase of \(\alpha =\beta =1\) and \(\gamma =0\) provides a new model, for which a specific lump will be presented in the next section. The subcase of \(\alpha =\beta =0\) and \(\gamma =1\) is the generalized Calogero–Bogoyavlenskii–Schiff equation discussed previously in [20].

4.3 The case of \(\delta _4=\delta _6=1\)

Let \(\delta _4=\delta _6=1\) and the other \(\delta _i\)’s be zero. Then the combined Hirota bilinear equation (2.8) becomes

$$\begin{aligned} (\alpha D_x^4+ \beta D_x^3D_t+\gamma D_x^3D_y +D_xD_y+D_t^2)f\cdot f=0. \end{aligned}$$
(4.9)

The condition \(a_1a_6-a_2a_5\ne 0\) for the existence of lumps requires

$$\begin{aligned} a_1a_7-a_3a_5\ne 0,\ a_1a_3+a_5a_7\ne 0; \end{aligned}$$
(4.10)

and thus, \(a_9>0\) requires

$$\begin{aligned} \alpha (a_1^2 +a_5^2 )^2 + \beta (a_1a_3+a_5a_7)(a_1^2+a_5^2)+\gamma [ (a_1a_7-a_3a_5)^2- (a_1a_3+a_5a_7)^2 ] <0. \end{aligned}$$
(4.11)

Therefore, we see that if \(\beta =\gamma =0\), we need to require \(\alpha <0\) to present lumps. A specific lump in the subcase of \(\alpha =\beta =\gamma =1\) will be computed and plotted in the next section.

4.4 The case of \(\delta _1=\delta _3=\delta _4=1\)

Let \(\delta _1=\delta _3=\delta _4=1\) and the other \(\delta _i\)’s be zero. Then the combined Hirota bilinear equation (2.8) becomes

$$\begin{aligned} (\alpha D_x^4+ \beta D_x^3D_t+\gamma D_x^3D_y +D_yD_t+D_xD_t+D_xD_y)f\cdot f=0, \end{aligned}$$
(4.12)

which generate two new combined soliton equations possessing lump solutions, when \(\alpha =\beta =1\) and \( \gamma =0\) or when \(\beta =0\) and \(\alpha =\gamma =1\).

Two classes of lump solutions determined by (3.2) with (3.3) and (3.4) with (3.5) are essentially equivalent to each other. In other words, one can be generated from the other as in the first case. The first class of parameters by (3.2) with (3.3) reads

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle a_3=- \frac{ a_1 (a_2^2+a_6^2) + a_2 (a_1^2+a_5^2) }{ (a_1+a_2)^2+(a_5+a_6)^2 } , \\ \displaystyle a_7=- \frac{ a_5 (a_2^2+a_6^2) + a_6 (a_1^2+a_5^2) }{ (a_1+a_2)^2+(a_5+a_6)^2 } , \\ \displaystyle a_9=\frac{3(a_1^2+a_5^2) (\alpha b_3 -\beta b_4 +\gamma b_5) }{ (a_1a_6-a_2a_5)^2 }, \end{array}\right. \end{aligned}$$
(4.13)

where

$$\begin{aligned} \left\{ \begin{array}{l} b_3= (a_1^2+a_2^2)[(a_1+a_2)^2 +(a_5+a_6)^2], \\ b_4 =(a_1^2+a_5^2) [(a_1a_2+a_5a_6) +(a_2^2+a_6^2)], \\ b_5=(a_1a_2+a_5a_6) [(a_1+a_2)^2 +(a_5+a_6)^2]. \end{array}\right. \end{aligned}$$
(4.14)

The second class of parameters by (3.4) with (3.5) reads

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle a_2=- \frac{ a_1 (a_3^2+a_7^2) + a_3 (a_1^2+a_5^2) }{ (a_1+a_3)^2+(a_5+a_7)^2 } , \\ \displaystyle a_6=- \frac{ a_5 (a_3^2+a_7^2) + a_7 (a_1^2+a_5^2) }{ (a_1+a_3)^2+(a_5+a_7)^2 } , \\ \displaystyle a_9=\frac{3(a_1^2+a_5^2) (\alpha c_3 -\gamma c_4 +\beta c_5) }{ (a_1a_7-a_3a_5)^2 }, \end{array}\right. \end{aligned}$$
(4.15)

where

$$\begin{aligned} \left\{ \begin{array}{l} c_3= (a_1^2+a_5^2)[(a_1+a_3)^2 +(a_5+a_7)^2], \\ c_4 =(a_1^2+a_5^2) [(a_1a_3+a_5a_7) +(a_3^2+a_7^2)], \\ c_5=(a_1a_3+a_5a_7) [(a_1+a_3)^2 +(a_5+a_7)^2]. \end{array}\right. \end{aligned}$$
(4.16)

These two classes of parameters are the same, since they can be solved from each other. Moreover, one has

$$\begin{aligned} a_1a_7-a_3a_5=-\frac{ (a_1^2+a_5^2)(a_1a_6-a_2a_5)}{(a_1+a_2)^2+(a_5+a_6)^2}, \end{aligned}$$

and therefore, two classes present the exactly same set of values for the parameters.

4.5 The case of \(\delta _1=\delta _3=\delta _5=1\)

Let \(\delta _1=\delta _3=\delta _5=1\) and the other \(\delta _i\)’s be zero, Then the combined Hirota bilinear equation (2.8) becomes

$$\begin{aligned} (\alpha D_x^4+ \beta D_x^3D_t+\gamma D_x^3D_y +D_yD_t+D_xD_t+D_y^2)f\cdot f=0. \end{aligned}$$
(4.17)

Observe that \(a_1a_6-a_2a_5\ne 0\) leads to \((a_1+a_2)^2+(a_5+a_6)^2\ne 0\), which ensures that \(a_3\) and \(a_7\) in (3.2) are well defined. Therefore, besides \(a_1a_6-a_2a_5\ne 0\), the condition for guaranteeing lumps is

$$\begin{aligned}&\alpha ( a_1^2+a_5^2)[ (a_1+a_2)^2 +(a_5+a_6)^2 ] \nonumber \\&\quad - \beta [ (a_2^2+a_6^2)(a_1a_2+a_5a_6)+(a_1a_2+a_5a_6)^2-(a_1a_6-a_2a_5)^2] \nonumber \\&\quad +\gamma (a_1a_2+a_5a_6)[ (a_1+a_2)^2+(a_5+a_6)^2 ] <0, \end{aligned}$$
(4.18)

which guarantees that \(a_9\) defined in (3.2) is positive.

4.6 The case of \(\delta _1=\delta _4=\delta _6=1\)

Let \(\delta _1=\delta _4=\delta _6=1\) and the other \(\delta _i\)’s be zero. Then the combined Hirota bilinear equation (2.8) becomes

$$\begin{aligned} (\alpha D_x^4+ \beta D_x^3D_t+\gamma D_x^3D_y +D_yD_t+D_xD_y+D_t^2)f\cdot f=0. \end{aligned}$$
(4.19)

Observe that \(a_1a_7-a_3a_5\ne 0\) leads to \((a_1+a_3)^2+(a_5+a_7)^2\ne 0\), which ensures that \(a_2\) and \(a_6\) in (3.4) are well defined. Also, it is easy to see that in this case, we have

$$\begin{aligned} a_1a_6-a_2a_5 =\frac{(a_1a_7-a_3a_5)[(a_3^2+a_7^2)+2(a_1a_3+a_5a_7)]}{(a_1+a_3)^2+(a_5+a_7)^2}. \end{aligned}$$

Therefore, the conditions for guaranteeing lumps are

$$\begin{aligned} a_1a_7-a_3a_5\ne 0,\ (a_3^2+a_7^2)+2(a_1a_3+a_5a_7)\ne 0, \end{aligned}$$
(4.20)

and

$$\begin{aligned}&[\alpha (a_1^2+a_5^2) +\beta (a_1a_3+a_5a_7) ] [ (a_1+a_3)^2+(a_5+a_7)^2 ] \nonumber \\&\quad -\gamma [(a_3^2+a_7^2)(a_1a_3+a_5a_7)+(a_1a_3+a_5a_7)^2-(a_1a_7-a_3a_5)^2] <0. \end{aligned}$$
(4.21)

This guarantees, together with the first condition in (4.20), that \(a_9\) defined in (3.4) is positive.

5 Two particular lumps

Let us first take

$$\begin{aligned} \alpha =1,\ \beta =1,\ \gamma =0,\ \delta _3=\delta _5=1,\ \delta _1=\delta _2=\delta _4=\delta _6=0, \end{aligned}$$
(5.1)

which leads to a special combined soliton equation

$$\begin{aligned} u_{xxxx} + 6u_xu_{xx}+ u_{xxxt}+3(u_xu_t)_x+u_{xt}+u_{yy}=0. \end{aligned}$$
(5.2)

This has a Hirota bilinear form

$$\begin{aligned} (D_x^4+D_x^3D_t +D_xD_t+D_y^2)f\cdot f=0, \end{aligned}$$

under the logarithmic transformation (2.9). Upon further taking

$$\begin{aligned} a_1=2,\ a_2=-6,\ a_4=1, \ a_5=2,\ a_6=-5,\ a_8=2, \end{aligned}$$
(5.3)

the transformation (2.9) with (3.1) presents a lump solution to the special combined soliton equation (5.2):

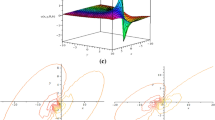
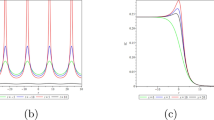
$$\begin{aligned} u_1= {\frac{2(-120 t+16 x-44 y+12 )}{ ( -\frac{71}{4} t+2x-6 y+1) ^{2}+ ( -\frac{49}{4} t +2 x - 5y+2 ) ^{2}+2496 } } . \end{aligned}$$
(5.4)

Three-dimensional plots and contour plots of this lump solution at three different times are made by using Maple in Fig. 1. 

Fig. 1
figure 1

Profiles of \(u_1\) when \(t=0,10,20\): 3d plots (top) and contour plots (bottom)

Full size image

Let us second take

$$\begin{aligned} \alpha =1,\ \beta =1,\ \gamma =1, \delta _4=\delta _6=1, \ \delta _1=\delta _2=\delta _3=\delta _5=0, \end{aligned}$$
(5.5)

which leads to another special combined soliton equation

$$\begin{aligned} u_{xxxx} + 6u_xu_{xx}+ u_{xxxt}+3(u_xu_t)_x+u_{xxxy}+3(u_xu_y)_x+ u_{xy}+u_{tt}=0. \end{aligned}$$
(5.6)

It has a Hirota bilinear form

$$\begin{aligned} (D_x^4+ D_x^3D_t +D_x^3D_y+D_xD_y +D_t^2)f\cdot f=0, \end{aligned}$$

under the logarithmic transformation (2.9). Upon further taking

$$\begin{aligned} a_1=2,\ a_3=-6,\ a_4=5, \ a_5=2,\ a_7=-8, a_8=3, \end{aligned}$$
(5.7)

the transformation (2.9) with (3.1) gives a lump solution to the special combined soliton equation (5.6):

$$\begin{aligned} u_2= {\frac{2(-56 t+16 x-192 y +32)}{ ( -6 t+2 x-17 y+5 ) ^{2}+ ( -8 t+2x-31y+3) ^{2}+1392}} . \end{aligned}$$
(5.8)

Three three-dimensional plots and contour plots of this lump solution at three different values of x are made through Maple in Fig. 2.

Fig. 2
figure 2

Profiles of \(u_2\) when \(x=0,60,120\): 3d plots (top) and contour plots (bottom)

Full size image

6 Conclusion and remarks

With Maple symbolic computations, we have formulated a combined fourth-order soliton equation in (2+1)-dimensions and determined its lump solutions in terms of the coefficients in the combined model. The presented results supplement the existing lumps and solitons in dispersive waves. Some three-dimensional plots and contour plots of two particular lump solutions were made by using Maple.

We remark that all exactly presented solutions add valuable insights into related studies on soliton solutions and dromion-type solutions in the continuous and discrete cases, achieved through effective techniques such as the generalized bilinear method (see, e.g., [25]), the Wronskian technique (see, e.g., [26, 27]), Darboux transformations (see, e.g., [28, 29]), the Riemann-Hilbert approach (see, e.g., [30]), the multiple-wave expansion method (see, e.g., [31, 32]), symmetry reductions (see, e.g., [33, 34]), and symmetry constraints (see, e.g., [35, 36] for the continuous case and [37, 38] for the discrete case). The combined equation has theoretical interest itself, and is an essential step to obtain a significant model in multiple-scale and singular perturbation theory close to integrable equations [39].

We also remark that many nonlinear equations possess lump solutions, which include generalized KP, BKP, KP-Boussinesq, Sawada-Kotera, Calogero–Bogoyavlenskii–Schiff and Bogoyavlensky–Konopelchenko equations in (2+1)-dimensions [20, 21, 40,41,42,43]. Moreover, recent studies exhibit the remarkable richness of lump solutions to linear PDEs [32, 44, 45] and nonlinear PDEs in (2+1)-dimensions (see, e.g., [46,47,48,49,50]) and (3+1)-dimensions (see, e.g., [23, 51,52,53,54,55,56]). A new kind of lumps with higher-order rational dispersion relations has been discovered as well [57]. Abundant lump solutions amend the existing theories of solutions through different kinds of combinations (see, e.g., [58,59,60,61]), and can generate interesting Lie-Bäcklund symmetries by taking derivatives with respect to the involved parameters. These symmetries can also be used to formulate conservation laws by pairs of symmetries and adjoint symmetries [62,63,64], and classify lump solutions based on an idea of determining optimal systems of solutions [65, 66]. Moreover, diverse interaction solutions [42, 67, 68] have been constructed for different soliton equations in (2+1)-dimensions, including homoclinic interaction solutions (see, e.g., [69,70,71]) and heteroclinic interaction solutions (see, e.g., [72,73,74,75]). Based on the Hirota bilinear form and the generalized bilinear forms, some general formulations have been presented for lump solutions [5, 6, 76].