1 Introduction

Differential equations featuring fractional orders are of great importance in many sciences and engineering fields since they best describe physical situations. This importance is what makes numerous researchers to devise many definitions among which the newly proposed definition by Khalil et al. (2014). Further, many researchers utilized this fractional derivative and other well-known fractional derivatives alongside some analytical methods to solve many solitary wave problems such as the variant bussinesq equations (Inan et al. 2017)

$$\left\{ \begin{array}{lll} u_t+u_x v+v_x u+v_{xxx}=0, \\ \\ v_t+u_x+vv_x=0 . \\ \end{array}\right.$$
(1)

Other analytical methods used in constructing traveling wave solutions include the Kudryashov method (Kudryashov 2012), the \(G'/G\)-expansion method (Bekir and Guner 2013), the collocation based methods (Raslan et al. 2016a, b, 2017c; Talaat 2016), the modified extended tanh method (Khalid et al. 2016), \(tan(\phi (\xi )/2)\)-expansion method (Raslan et al. 2017b), the Sine-Gordon method (Manafian and Lakestani 2016a; Bulut et al. 2017), the exp\((-\phi (\xi ))\) (Baskonus et al. 2017) and other analytical methods among others (Islam et al. 2014; Guner et al. 2015a, b; Manafian et al. 2015; Shukri and Al-Khaled 2010; Nuruddeen et al. 2018; Nuruddeen 2017a; Nuruddeen et al. 2017; Alquran et al. 2017; Inc et al. 2017a, b; Hosseini et al. 2017; Younis et al. 2016; Islam et al. 2015; Wazwaz 2017; Bakodah et al. 2017a, b; Banaja et al. 2016; Khalid et al. 2017, 2018; Nuruddeen 2017b; Lakestani and Manafian 2017; Manafian 2017; Manafian and Lakestani 2016b; Manafian et al. 2017a, b; Sindi and Manafian 2017; Manafian et al. 2017c). However, in this article, the time fractional variant bussinesq equations would be considered in the sense of the newly devised conformable fractional derivative definition. The considered problem would then be solved by employing the modified extended tanh expansion method after recasting the problem to an ordinary differentiation equation via wave transformation. The Mathematica software would be used in the solution of the system of algebraic equations obtained and also in the graphical illustrations of the solution.

2 Preliminaries

Definition 1

Let \(u:[0,\infty )\rightarrow \mathbb {R}\) be a function. The \(\alpha '\)s order conformable derivative of u is defined by

$$D_t^\alpha (u(t))=\lim \limits _{\epsilon \rightarrow 0 } \frac{u(t+\epsilon t^{1-\alpha })-u(t)}{\epsilon },$$
(2)

for all \(t>0\) and \(\alpha \in (0,1).\) Further, the following theorems gives some properties of conformable derivative:

Theorem 1

Let \(\alpha \in (0,1)\) and suppose u(t) and v(t) are \(\alpha\)-differentiable at \(t>0\). Then

  1. (i)

    \(D_t^{\alpha } (t^c)=c t^{c-\alpha },\) for all \(c\in \mathbb {R}.\)

  2. (ii)

    \(D_t^{\alpha } (a)=0, a\) for all constant function \(u(t)=a.\)

  3. (iii)

    \(D_t^{\alpha } (a u(t))=a D_t^{\alpha } (u(t)),\) for all a constant.

  4. (iv)

    \(D_t^{\alpha } \left( a u(t) + b v(t)\right) =a D_t^{\alpha } u(t)+ b D_t^{\alpha } v(t),\) for all \(a,b\in \mathbb {R}.\)

  5. (v)

    \(D_t^{\alpha } \left( v(t)u(t)\right) =v(t) D_t^{\alpha } \left( u(t)\right) +u(t)D_t^{\alpha } \left( v(t)\right) .\)

  6. (vi)

    \(D_t^{\alpha } \left( \frac{u(t)}{v(t)}\right) =\frac{v(t)D_t^{\alpha } u(t)-u(t)D_t^{\alpha } v(t)}{v^2(t)}, \ \ v(t)\ne 0.\)

  7. (vii)

    If, in addition to u(t) differentiable, then \(D_t^{\alpha } u(t)=t^{1-\alpha } \frac{du}{dt}.\)

Definition 2

Let \(\alpha \in (0,1)\) such u(t) is differentiable and also \(\alpha\)-differentiable. Let v(t) be a function defined in the range of u(t) also differentiable, then

$$D_t^{\alpha } \left( u(t)\circ v(t)\right) = t^{1-\alpha } v'(t) u'(v(t)).$$

See also [1].

3 Analysis of the method

We present the modified extended tanh expansion method by considering the following nonlinear fractional differential equation of the form:

$$G(u, D_t^{\alpha }u, D_x^{\alpha }u,D_{tt}^{2\alpha }u, D_{xx}^{2\alpha }u,D_{t}^{\alpha }D_{x}^{\alpha }u,\ldots )=0 , \quad 0< \alpha <1,$$
(3)

where \(\alpha\) is order of the derivative of the function \(u = u(x, t)\). Also, we use the wave transformation

$$u(x,t)=U(\xi ), \quad \xi =a x+b\frac{t^\alpha }{\alpha },$$
(4)

where a and b are nonzero constants. Substitution of wave transformation (4) into (3), we obtain an ordinary differential equation of the form

$$P(U, U', U'',\ldots )=0,$$
(5)

where, \('\) is a derivative w.r.t \(\xi\). Further, the solution is assumed to be of the finite series of the form:

$$U(\xi )=a_0+\sum _{n=1}^{n=N}\left( a_n\Phi ^n(\xi )+\frac{b_n}{\Phi ^n(\xi )}\right) ,$$
(6)

where \(a_0, a_n, b_n, n=1,2,\ldots N\) are nonzero constants to be computed; where N is a positive integer determined by balancing the highest order derivative with the highest nonlinear terms in the equation, and \(\Phi (\xi )\) satisfies the Riccati differential equation:

$$\Phi '(\xi )=d+\Phi ^2(\xi ),$$
(7)

where d is a constant. Further, the Riccati differential equation in (7) has solutions of the form:

  1. (i)

    If \(d<0\), then

    $$\begin{aligned} \Phi (\xi )=&-\sqrt{-d}\tanh (\sqrt{-d}\xi ), \\ \Phi (\xi )=&-\sqrt{-d}\coth (\sqrt{-d}\xi ). \end{aligned}$$
  2. (ii)

    If \(d=0\), then

    $$\Phi (\xi )=-\frac{1}{\xi }.$$
  3. (iii)

    If \(d>0\), then

    $$\begin{aligned} \Phi (\xi )=&\sqrt{d}\tan (\sqrt{d}\xi ), \\\\ \Phi (\xi )=&-\sqrt{d}\cot (\sqrt{d}\xi ). \end{aligned}$$

Therefore, substituting equation (6) and its necessary derivatives into (5) gives a polynomial in \(\Phi (\xi )\). Collecting coefficients of the obtained polynomials and subsequently setting each one to zero, we will get a set of over-determined algebraic equations for \(a_0,a_n,b_n (n=1,2,\ldots )\), and b with the aid of symbolic computation using Mathematica. Finally, solving the algebraic equations and the above possible solutions of Raccati equation into (5), we obtain the solution of Eq. (3).

4 Application

We consider the conformable time fractional variant bussinesq equations version of (1) the form

$$\left\{ \begin{array}{l} D_t^{\alpha }u+u_x v+v_x u+v_{xxx}=0,\\ D_t^{\alpha }v+u_x+vv_x=0 . \\ \end{array}\right.$$
(8)

Employing the wave transformation, Eq. (8) becomes an ordinary differential equation:

$$\left\{ \begin{array}{l} bU'+aU'V+aV'U+a^3 V'''=0,\\ bV'+aU'+aVV'=0 . \\ \end{array}\right.$$
(9)

Now, balancing Eq. (9) using the homogeneous balancing method, we get \(N_1=2\); and \(N_2=1\), Thus, Eq. (8) has a solution of the form:

$$\left\{ \begin{array}{l} U(\xi )=a_0+a_1\Phi (\xi ) +a_2\Phi ^2(\xi )+\frac{b_1}{\Phi (\xi )}+\frac{b_2}{\Phi ^2(\xi )}, \\ V(\xi )=c_0+c_1\Phi (\xi ) + \frac{d_1}{\Phi (\xi )}.\\ \end{array}\right.$$
(10)

where from (7)

$$\Phi '(\xi )=d+\Phi ^2(\xi ), \ and \ \Phi ''(\xi )=2\Phi (\xi )(d+\Phi ^2(\xi )).$$
(11)

Then, putting the values of Eq. (10) and their necessary derivatives alongside Eq. (11) into (9); collecting the coefficients of same degree of \(\Phi (\xi )\) and thereafter setting them to zero, we get the following algebraic equations:

$$\begin{aligned}&-2bb_2-2ab_2 c_0-2ab_1 d_1=0,\\&2bda_2+2ada_2 c_0+2ada_1 c_1=0,\\&-2bdb_2-2adb_2 c_0-2adb_1 d_1=0,\\&2ba_2+2aa_2 c_0+2aa_1 c_1=0,6a^3 c_1+3aa_2 c_1=0,\\&ba_1+aa_1 c_0+8a^3 dc_1+aa_0 c_1+3ada_2 c_1+aa_2 d_1=0,\\&-bdb_1-adb_1 c_0-adb_2 c_1-8a^3 d^2 d_1-ada_0 d_1-3ab_2 d_1=0,\\&ada_1-ab_1+bdc_1+adc_0 c_1-bd_1-ac_0 d_1=0,2ada_2+adc_1^2=0,\\&aa_1+bc_1+ac_0 c_1=0,2aa_2+ac_1^2=0,-6a^3 d^3 d_1-3adb_2 d_1=0,\\&-2adb_2-add_1^2=0,-adb_1-bdd_1-adc_0 d_1=0,-2ab_2-ad_1^2=0,\\&bda_1-bb_1+ada_1 c_0-ab_1 c_0+2a^3 d^2 c_1+ada_0 c_1-ab_2 c_1-2a^3 dd_1-aa_0 d_1+ada_2 d_1=0. \end{aligned}$$

Solving the above system via Mathematica software, we get the following:

Case 1

$$\begin{aligned} a_0=&-2a^2 d,\quad a_1=0,\quad a_2=-2a^2,\quad b_1=0, \quad b_2=0,\\ c_0=&-\frac{b}{a}, \quad c_1=\pm 2a, \quad d_1=0, \quad d=d. \end{aligned}$$

Hence, we get the following solutions:

$$\left\{ \begin{array}{l} u_{1,2}(x,t) = -2a^2 d+2a^2d\tanh ^2(\sqrt{-d} \xi ). \\ v_{1,2}(x,t) =-\frac{b}{a}\mp 2a\sqrt{-d} \tanh (\sqrt{-d} \xi ). \end{array}\right.$$
(12)
$$\left\{ \begin{array}{l} u_{3,4}(x,t)=-2a^2 d+2a^2d\coth ^2(\sqrt{-d} \xi ).\\ v_{3,4}(x,t) = -\frac{b}{a}\mp 2a \sqrt{-d} \coth (\sqrt{-d} \xi ). \\ \end{array}\right.$$
(13)

Case 2

$$\begin{aligned} a_0=&0, \quad a_1=0, \quad a_2=-2a^2, \quad b_1=0, \quad b_2=-2a^2d^2, \\ c_0=&-\frac{b}{a}, \quad c_1=\pm 2a, \quad d_1=\pm 2ad, \quad d=d. \end{aligned}$$

Thus, we get the following solutions:

$$\left\{ \begin{array}{l} u_{5,6}(x,t) = 2a^2d\tanh ^2(\sqrt{-d}\xi )+\frac{2a^2d}{\tanh ^2(\sqrt{-d}\xi )}. \\ v_{5,6}(x,t) = -\frac{b}{a}\mp 2a \sqrt{-d}\tanh (\sqrt{-d}\xi ) \mp \frac{2ad}{\sqrt{-d}\tanh (\sqrt{-d}\xi )}.\\ \end{array}\right.$$
(14)
$$\left\{ \begin{array}{l} u_{7,8}(x,t)= 2a^2d\coth ^2(\sqrt{-d}\xi )+\frac{2a^2d}{\coth ^2(\sqrt{-d}\xi )},\\ v_{7,8}(x,t) = -\frac{b}{a}\mp 2a \sqrt{-d}\coth (\sqrt{-d}\xi ) \mp \frac{2ad}{\sqrt{-d}\coth (\sqrt{-d}\xi )}. \\ \end{array}\right.$$
(15)

Case 3

$$\begin{aligned} a_0=&-4a^2 d, \quad a_1=0, \quad a_2=-2a^2, \quad b_1=0, \quad b_2=-2a^2d^2, \\ c_0=&-\frac{b}{a}, \quad c_1=\mp 2a,\quad d_1=\pm 2ad,\quad d=d. \end{aligned}$$

Therefore, we get the following solutions:

$$\left\{ \begin{array}{l} u_{9,10}(x,t) =-4a^2 d +2a^2d\tanh ^2(\sqrt{-d}\xi )+\frac{2a^2d}{\tanh ^2(\sqrt{-d}\xi )},\\ v_{9,10}(x,t) = -\frac{b}{a}\pm 2a\sqrt{-d} \tanh (\sqrt{-d}\xi ) \mp \frac{2ad}{ \sqrt{-d}\tanh (\sqrt{-d}\xi )}. \end{array}\right.$$
(16)
$$\left\{ \begin{array}{l} u_{11,12}(x,t)= -4a^2 d +2a^2d\coth ^2(\sqrt{-d}\xi )+\frac{2a^2d}{\coth ^2(\sqrt{-d}\xi )}, \\ v_{11,12}(x,t) = -\frac{b}{a}\mp 2a \sqrt{-d} \coth (\sqrt{-d}\xi ) \pm \frac{2ad}{\sqrt{-d} \coth (\sqrt{-d}\xi )}. \end{array}\right.$$
(17)

Case 4

$$\begin{aligned} a_0=&-2a^2 d, \quad a_1=0, \quad a_2=0, \quad b_1=0, \quad b_2=-2a^2d^2, \\ c_0=&-\frac{b}{a}, \quad c_1=0, \quad d_1=\mp 2ad,\quad d=d. \end{aligned}$$

Also, we get the following solutions:

$$\left\{ \begin{array}{l} u_{13,14}(x,t) =-2a^2 d +\frac{2a^2d}{\tanh ^2(\sqrt{-d}\xi )},\\ v_{13,14}(x,t) =-\frac{b}{a} \pm \frac{2ad}{\sqrt{-d}\tanh (\sqrt{-d}\xi )}. \end{array}\right.$$
(18)
$$\left\{ \begin{array}{l} u_{15,16}(x,t)=-2a^2 d+\frac{2a^2d}{\coth ^2(\sqrt{-d}\xi )},\\ v_{15,16}(x,t) = -\frac{b}{a} \pm \frac{2ad}{\sqrt{-d} \coth (\sqrt{-d}\xi )}. \end{array}\right.$$
(19)

Case 5

$$a_0= a_1=0, \ \ a_2=-2a^2, \ \ b_1= b_2=0, \ \ c_0=-\frac{b}{a}, \ \ c_1=\pm 2a , \ \ d_1=0,\ \ d=0.$$

Finally, we get the following solutions:

$$\left\{ \begin{array}{l} u_{17,18}(x,t) =-\frac{2a^2}{\xi ^2}, \\ v_{17,18}(x,t) = -\frac{b}{a} \pm \frac{2a}{\xi }. \end{array}\right.$$
(20)

It is also important to note that in the cases \(1-4\) above, we made use of \(d<0\) to get those solutions from Eq. (7). However, when d is taken \(>0\); these solutions containing hyperbolic functions are expected to change to trigonometric function solutions as explained in Sect. 3. Also, \(\xi\) in Cases 1–5 is given by:

$$\xi =ax +b \frac{t^\alpha }{\alpha }.$$
(21)

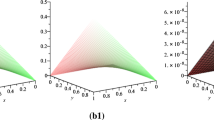
5 Graphical illustrations of the solutions

In this section, we give the graphical illustrations of the conformable time-fractional variant bussinesq equations at different time levels with different values of \(\alpha\): u(x, t) is given in Fig. 1 while their corresponding solutions of v(x, t) are given in Fig. 2, respectively.

Fig. 1
figure 1

Profiles of u(x, t) at different time levels

Full size image
Fig. 2
figure 2

Profiles of v(x, t) at different time levels

Full size image

6 Conclusion

In conclusion, various exact hyperbolic function solutions for the time fractional variant bussinesq equations are constructed using the modified extended tanh expansion method in the sense of the newly devised fractional derivative called the conformable fractional derivative. We made use of the wave transformation to convert the problem to an ordinary differentiation equation. The Mathematica software is used for the solution of the system of algebraic equations and also for the graphical illustrations, respectively.