1 Introduction

The fractional calculus deals with derivatives and integrals to an arbitrary order. In recent years, a large number of scientific and engineering problems involving fractional calculus. It provides more accurate models of systems under consideration. The applications of fractional calculus have been demonstrated by many authors. Many systems in interdisciplinary fields, such as biological systems (Ahmed and Elgazzar 2007; Zalp and Demirci 2011), turbulence (Chen 2006), anomalous diffusion (Chen et al. 2010; Sun et al. 2009), viscoelastic systems (Rossikhin and Shitikova 1997), and partial bed-load transport (Sun et al. 2015), can be described with the help of fractional derivatives. Moreover, various problems in fluid mechanics, biology, physics, physiology, optics, and climatology can be modeled by fractional integral equations (Atanackovic and Stankovic 2004; Evans et al. 2017). In many situations, analytic solutions of fractional integral and differential equations are not available, or may these equations not be directly solvable. Therefore, finding efficient numerical methods to approximate the solutions of these equations has become the main objective of many mathematicians. For a review on numerical methods, see, for instance, (Amin et al. 2021; Aminikhah et al. 2017; Dahaghin and Hassani 2017; Esmaeili et al. 2011; Fathizadeh et al. 2017; Hassani et al. 2019; Hassani and Naraghirad 2019; Hesameddini and Shahbazi 2018; Hassani et al. 2019a, b; Jabari Sabeg et al. 2017; Kılıçman and Al Zhour 2007; Li and Shah 2017; Mohammadi Rick and Rashidinia 2019; Maleknejad et al. 2018, 2020a, b, c; Mashoof and Refahi Shekhani 2017; Mirzaee and Samadyar 2019; Najafalizadeh and Ezzati 2016; Nouri et al. 2018; Pourbabaee and Saadatmandi 2019; Permoon et al. 2016; Rahimkhani et al. 2018; Samadyar and Mirzaee 2019; Shah and Wang 2019; Zhu and Fan 2012).

In this research study, the following fractional integral equations of the second kind are considered:

Two-dimensional nonlinear fractional Volterra integral equations (2D-NFVIEs):

$$\begin{aligned}&f(x,y) = g(x,y) \nonumber \\&\quad + \dfrac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}{k}(x,y,\tau ,\varsigma ,{{f}(\tau ,\varsigma )})\mathrm {d}\varsigma } \mathrm {d}\tau }, \end{aligned}$$
(1)

Two-dimensional nonlinear fractional Fredholm integral equations (2D-NFFIEs):

$$\begin{aligned}&f(x,y) = g(x,y) \nonumber \\&\quad + \dfrac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{\ell _1} {\int _0^{\ell _2} {{{({\ell _1} - \tau )}^{{\iota _1} - 1}}{{({\ell _2} - \varsigma )}^{{\iota _2} - 1}}{k}(x,y,\tau ,\varsigma ,{{f}(\tau ,\varsigma )})\mathrm {d}\varsigma } \mathrm {d}\tau }, \end{aligned}$$
(2)

where f(x, y) , \( {k}(x,y,\tau ,\varsigma ,f(\tau ,\varsigma )) \) are unknown functions and g(x, y) is a given function. Also, \( {\iota _1},~ {\iota _2}>0 \) and \( (x,y) \in \varOmega = [0,{\ell _1}] \times [0,{\ell _2}] \).

The outline of this paper is as follows. First, in Sect. 2, a review of two definitions required in this paper is given. In Sect. 3, sufficient conditions for the existence and uniqueness of solutions for 2D-NFVIEs and 2D-NFFIEs are provided. Also, in Sect. 4, the hybrid of two-dimensional block-pulse functions and two-variable shifted Legendre polynomials (2D-HBPSLs) and their operational matrices of product and fractional integration are introduced. Afterward, in Sect. 5, we explain numerical solutions of 2D-NFVIEs and 2D-NFFIEs, respectively, by using what was introduced in Sect. 4. Moreover, in Sect. 6, error bound and convergence analysis of the proposed method are discussed. To demonstrate the effectiveness of the presented method, three numerical examples are given in Sect. 7. Finally, in Sect. 8, a conclusion is given.

2 Preliminary knowledge

Here, we give two necessary definitions of the fractional calculus theory which are used throughout this paper.

Definition 1

(See Podlubony 1999) The Riemann–Liouville fractional integral of order \( \alpha >0 \) is defined by

$$\begin{aligned} {I_\upsilon ^\alpha }f(x)&= \dfrac{1}{\varGamma (\alpha )}\int _\upsilon ^ x {{{( x - \tau )}^{\alpha - 1}}f( \tau ) {\text {d}} \tau }, \end{aligned}$$

where \( \upsilon >0 \). If \( \upsilon =0 \), for simplicity, we will denote the Riemann–Liouville fractional integral of order \( \alpha \) of f(x) with \( {I^\alpha }f(x) \).

Definition 2

(See Abbas and Benchohra 2014) The left-sided mixed Riemann–Liouville fractional integral of order \( \iota :=({\iota _1},{\iota _2}) \in (0,\infty ) \times (0,\infty ) \) of f is defined by

$$\begin{aligned} {I_{\sigma }^\iota }f(x,y)= \dfrac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _{\sigma _1}^x {\int _{\sigma _2}^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}f(\tau ,\varsigma )\mathrm {d}\varsigma } \mathrm {d} \tau }, \end{aligned}$$

where \( \sigma = ({\sigma _1},{\sigma _2}) \). If \( \sigma = (0,0) \), for simplicity, we will denote the left-sided mixed Riemann–Liouville fractional integral of order \( \iota \) of f(x, y) with \( {I^\iota }f(x,y) \).

3 Existence and uniqueness of solutions

In this section, we provide sufficient conditions for the existence and uniqueness of solutions for 2D-NFVIEs (1) and 2D-NFFIEs (2) in a Banach space. To do this, we need the following theorems.

Theorem 1

(The Arzela-Ascoli theorem (Conway 2007)) If E is compact and \( B \subseteq C(E) \), then B is totally bounded if and only if B is bounded and equicontinuous.

Corollary 1

(See Conway 2007) If E is compact and \( B \subseteq C(E) \), then B is compact if and only if B is bounded, closed, and equicontinuous.

Theorem 2

(Schauder’s fixed-point theorem (Zeidler 1995)) If \( {\varPi _0} \) is a bounded, closed, convex, nonempty subset of a Banach space V and \( T : {\varPi _0} \rightarrow {\varPi _0} \) is completely continuous, then T has a fixed point.

Theorem 3

(Tychonoff’s fixed-point theorem (Zeidler 1995)) Let V be a complete, locally convex, linear space and \( V_0 \) be a closed, convex, nonempty subset of V. Assume that the mapping \( T : V \rightarrow V \) is continuous and \( T({V_0}) \subset {V_0} \). If the closure of \( T({V_0}) \) is compact, then T has a fixed point in \( V_0 \).

In the following theorem, we prove the local existence of the solutions for 2D-NFVIEs using Schauder’s fixed-point theorem.

Theorem 4

Assume that

(C1):

f , v , g , \( {g_1} \in C(\varOmega ,{\mathbb {R}}^n) \) and \( k \in C(\varOmega \times \varOmega \times {\mathbb {R}}^n,{\mathbb {R}}^n) \), for \( 0 \le \tau \le x \le {\ell _1} \) and \( 0 \le \varsigma \le y \le {\ell _2} \).

(C2):

\( \left| {{g}(x,y) - {g_1}(x,y)} \right| <\frac{\varepsilon }{2} \).

(C3):

\( \left| {k(x,y,\tau ,\varsigma ,{f}(\tau ,\varsigma )) - k(x,y,\tau ,\varsigma ,{v}(\tau ,\varsigma ))} \right| < \frac{{\varepsilon \varGamma (1 + {\iota _1})\varGamma (1 + {\iota _2})}}{{2{\alpha ^{{\iota _1}}}{\beta ^{{\iota _2}}}}} \), for some \( 0< \alpha < {\ell _1} \) and \( 0< \beta < {\ell _2} \).

Then, the 2D-NFVIE has at least one solution on \( 0 \le x \le \alpha ,\, 0 \le y \le \beta \).

Proof

Consider the set \( D =\{ (x,y,\tau ,\varsigma ,f) : (x,y,\tau ,\varsigma )\in \varOmega \times \varOmega , |f| \le b \} \). Let \( |{g}(x,y)|\le \frac{b}{2} \) and \( |k(x,y,\tau ,\varsigma ,{f}(\tau ,\varsigma ))|\le {\xi } \) on D. Choose \( \frac{{{\xi }{\alpha ^{{\iota _1}}}{\beta ^{{\iota _2}}}}}{{\varGamma (1+{\iota _1})\varGamma (1+{\iota _2})}} \le \frac{b}{2} \) and let \( {\varPi _0}=\{f : f\in C({\varOmega _0},{\mathbb {R}}^n) ,~ \left\| f \right\| \le b\} \), where \( \left\| f \right\| = {\mathop {\max }\limits _{(x,y) \in {\varOmega _0}}} |f(x,y)| \) and \( {\varOmega _0}=[0,\alpha ]\times [0,\beta ] \). Clearly, the set \( {\varPi _0} \) is bounded, closed, and convex.

For any \(f \in {\varPi _0}\), define the operator

$$\begin{aligned}&Tf(x,y) = {g}(x,y) \nonumber \\&\quad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}k(x,y,\tau ,\varsigma ,f(\tau ,\varsigma )){\mathrm{d}}\varsigma } {\mathrm{d}}\tau },\quad {(x,y) \in {\varOmega _0}}. \end{aligned}$$
(3)

Clearly, we have

$$\begin{aligned} \left| {Tf(x,y)} \right|&\le \left| {g(x,y)} \right| \\&\quad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}\left| {k(x,y,\tau ,\varsigma ,f(\tau ,\varsigma ))} \right| {\mathrm{d}}\varsigma } {\mathrm{d}}\tau } \\&\le \frac{b}{2} + \frac{\xi }{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}{\mathrm{d}}\varsigma } {\mathrm{d}}\tau } \\&\le \frac{b}{2} + \frac{{{\xi }{\alpha ^{{\iota _1}}}{\beta ^{{\iota _2}}}}}{{\varGamma (1+{\iota _1})\varGamma (1+{\iota _2})}} \le b . \end{aligned}$$

Therefore, we obtain \( \left\| {Tf} \right\| \le b \), which implies that \( T({\varPi _0}) \subset {\varPi _0} \). Furthermore, for any \( ({x_1},{y_1}),\, ({x_2},{y_2}) \in \varOmega _0 \) such that \( {x_2}>{x_1} \) and \( {y_2}>{y_1} \), we have

$$\begin{aligned}&{Tf({x_2},{y_2}) - Tf({x_1},{y_1})} = {g({x_2},{y_2}) - g({x_1},{y_1})} \nonumber \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{{x_2}} {\int _0^{{y_2}} {{{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}}k({x_2},{y_2},\tau ,\varsigma ,f(\tau ,\varsigma )){\mathrm{d}}\varsigma } {\mathrm{d}}\tau }\nonumber \\&\qquad - \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{{x_1}} {\int _0^{{y_1}} {{{({x_1} - \tau )}^{{\iota _1} - 1}}{{({y_1} - \varsigma )}^{{\iota _2} - 1}}k({x_1},{y_1},\tau ,\varsigma ,f(\tau ,\varsigma )){\mathrm{d}}\varsigma } {\mathrm{d}}\tau } \nonumber \\&\quad = {g({x_2},{y_2}) - g({x_1},{y_1})} \nonumber \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{{x_1}} {\int _0^{{y_1}} {{{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}}k({x_2},{y_2},\tau ,\varsigma ,f(\tau ,\varsigma )){\mathrm{d}}\varsigma } {\mathrm{d}}\tau }\nonumber \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _{{x_1}}^{{x_2}} {\int _{{y_1}}^{{y_2}} {{{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}}k({x_2},{y_2},\tau ,\varsigma ,f(\tau ,\varsigma )){\mathrm{d}}\varsigma } {\mathrm{d}}\tau } \nonumber \\&\qquad - \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{{x_1}} {\int _0^{{y_1}} {{{({x_1} - \tau )}^{{\iota _1} - 1}}{{({y_1} - \varsigma )}^{{\iota _2} - 1}}k({x_1},{y_1},\tau ,\varsigma ,f(\tau ,\varsigma )){\mathrm{d}}\varsigma } {\mathrm{d}}\tau } \nonumber \\&\quad = {g({x_2},{y_2}) - g({x_1},{y_1})} \nonumber \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{{x_1}} \int _0^{{y_1}} \left( {{{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}} k({x_2},{y_2},\tau ,\varsigma ,f(\tau ,\varsigma ))} \right. \nonumber \\&\qquad \left. - {{({x_1} - \tau )}^{{\iota _1} - 1}}{{({y_1} - \varsigma )}^{{\iota _2} - 1}} k({x_1},{y_1},\tau ,\varsigma ,f(\tau ,\varsigma ))\right) {\mathrm{d}}\varsigma {\mathrm{d}}\tau \nonumber \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _{{x_1}}^{{x_2}} {\int _{{y_1}}^{{y_2}} {{{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}} k({x_2},{y_2},\tau ,\varsigma ,f(\tau ,\varsigma )) {\mathrm{d}}\varsigma } {\mathrm{d}}\tau } . \end{aligned}$$
(4)

Now adding and subtracting \( {{{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}} k({x_1},{y_1},\tau ,\varsigma ,f(\tau ,\varsigma ))} \) to the right-hand side of the inequality (4) yields

$$\begin{aligned}&{Tf({x_2},{y_2}) - Tf({x_1},{y_1})} = {g({x_2},{y_2}) - g({x_1},{y_1})} \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{{x_1}} \int _0^{{y_1}} \left( {{{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}} k({x_2},{y_2},\tau ,\varsigma ,f(\tau ,\varsigma ))} \right. \\&\qquad - {{{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}} k({x_1},{y_1},\tau ,\varsigma ,f(\tau ,\varsigma ))} \\&\qquad + {{{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}} k({x_1},{y_1},\tau ,\varsigma ,f(\tau ,\varsigma ))} \\&\qquad \left. - {{({x_1} - \tau )}^{{\iota _1} - 1}}{{({y_1} - \varsigma )}^{{\iota _2} - 1}} k({x_1},{y_1},\tau ,\varsigma ,f(\tau ,\varsigma ))\right) {\mathrm{d}}\varsigma {\mathrm{d}}\tau \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _{{x_1}}^{{x_2}} {\int _{{y_1}}^{{y_2}} {{{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}} k({x_2},{y_2},\tau ,\varsigma ,f(\tau ,\varsigma )) {\mathrm{d}}\varsigma } {\mathrm{d}}\tau } \\&\quad = {g({x_2},{y_2}) - g({x_1},{y_1})} \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{{x_1}} \int _0^{{y_1}} \left( {{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}} \left( {k({x_2},{y_2},\tau ,\varsigma ,f(\tau ,\varsigma ))} \right. \right. \\&\qquad \left. - {k({x_1},{y_1},\tau ,\varsigma ,f(\tau ,\varsigma ))}\right) \\&\qquad \left. + k({x_1},{y_1},\tau ,\varsigma ,f(\tau ,\varsigma )) \left( {{{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}} } \right. \right. \\&\qquad \left. \left. - {{({x_1} - \tau )}^{{\iota _1} - 1}}{{({y_1} - \varsigma )}^{{\iota _2} - 1}}\right) \right) {\mathrm{d}}\varsigma {\mathrm{d}}\tau \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _{{x_1}}^{{x_2}} {\int _{{y_1}}^{{y_2}} {{{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}} k({x_2},{y_2},\tau ,\varsigma ,f(\tau ,\varsigma )) {\mathrm{d}}\varsigma } {\mathrm{d}}\tau } . \end{aligned}$$

Let

$$\begin{aligned}&\left| {k({x_1},{y_1},\tau ,\varsigma ,f(\tau ,\varsigma ))} \right| \le \eta _1, \\&\left| {k({x_2},{y_2},\tau ,\varsigma ,f(\tau ,\varsigma ))} \right| \le \eta _2 , \end{aligned}$$

and

$$\begin{aligned} \left| {k({x_2},{y_2},\tau ,\varsigma ,f(\tau ,\varsigma ))} - {k({x_1},{y_1},\tau ,\varsigma ,f(\tau ,\varsigma ))} \right| \le \eta _3 , \end{aligned}$$

for \( (\tau ,\varsigma )\in \varOmega \), then we can write

$$\begin{aligned}&\left| {Tf({x_2},{y_2}) - Tf({x_1},{y_1})} \right| \le \left| {g({x_2},{y_2}) - g({x_1},{y_1})} \right| \nonumber \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{{x_1}} \int _0^{{y_1}} \left( ({\eta _1}+{\eta _3}) {{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}} \right. \nonumber \\&\qquad \left. + {\eta _1} {{({x_1} - \tau )}^{{\iota _1} - 1}}{{({y_1} - \varsigma )}^{{\iota _2} - 1}} \right) {\mathrm{d}}\varsigma {\mathrm{d}}\tau \nonumber \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _{{x_1}}^{{x_2}} {\int _{{y_1}}^{{y_2}} {{\eta _2} {{({x_2} - \tau )}^{{\iota _1} - 1}}{{({y_2} - \varsigma )}^{{\iota _2} - 1}} {\mathrm{d}}\varsigma } {\mathrm{d}}\tau } \nonumber \\&\quad = \left| {g({x_2},{y_2}) - g({x_1},{y_1})} \right| + \frac{1}{{\varGamma (1 + {\iota _1})\varGamma (1 + {\iota _2})}}\left( ({\eta _1}+{\eta _3}-{\eta _2}) {{({x_2} - {x_1})}^{{\iota _1}}}{{({y_2} - {y_1})}^{{\iota _2}}} \right. \nonumber \\&\qquad \left. - ({\eta _1}+{\eta _3}) x_2^{{\iota _1}}y_2^{{\iota _2}} - {\eta _1} x_1^{{\iota _1}}y_1^{{\iota _2}} \right) \nonumber \\&\quad \le \left| {g({x_2},{y_2}) - g({x_1},{y_1})} \right| + \frac{{\eta _1}+{\eta _3}}{{\varGamma (1 + {\iota _1})\varGamma (1 + {\iota _2})}} { {{({x_2} - {x_1})}^{{\iota _1}}}{{({y_2} - {y_1})}^{{\iota _2}}} } . \end{aligned}$$
(5)

Note that the right-hand side in the inequality (5) tends to zero as \( {x_2}\rightarrow {x_1} , \, {y_2}\rightarrow {y_1} \). Therefore, \( T : {\varPi _0} \rightarrow {\varPi _0} \) is equicontinuous and consequently, from Theorem 1, the closure of \( T({\varPi _0}) \) is compact.

To show that T is a continuous map, let

$$\begin{aligned} {Tv(x,y)}&= {{g_1}(x,y)} \\&\quad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}} {k(x,y,\tau ,\varsigma ,{v}(\tau ,\varsigma ))} {\mathrm{d}}\varsigma } {\mathrm{d}}\tau } , \end{aligned}$$

where \( v \in {\varPi _0} \). Clearly, we have

$$\begin{aligned}&\left| {Tf(x,y) - Tv(x,y)} \right| \le \left| {{g}(x,y) - {g_1}(x,y)} \right| \\&\quad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x \int _0^y {{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}\left| k(x,y,\tau ,\varsigma ,{f}(\tau ,\varsigma )) \right. \\&\quad \left. - k(x,y,\tau ,\varsigma ,{v}(\tau ,\varsigma )) \right| {\mathrm{d}}\varsigma {\mathrm{d}}\tau . \end{aligned}$$

Since k is uniformly continuous, for an arbitrary \( \varepsilon > 0 \), there exists a \( \delta > 0 \) such that \( | f(x,y)-v(x,y) |<\delta \). Assume that conditions \( (\mathbf{C1} )\)–\((\mathbf{C3} ) \) are satisfied, then we obtain

$$\begin{aligned}&\left| {Tf(x,y) - Tv(x,y)} \right| \le \frac{\varepsilon }{2} \\&\quad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\frac{{\varepsilon \varGamma (1 + {\iota _1})\varGamma (1 + {\iota _2})}}{{2{\alpha ^{{\iota _1}}}{\beta ^{{\iota _2}}}}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}{\mathrm{d}}\varsigma } {\mathrm{d}}\tau } \le \varepsilon , \end{aligned}$$

and the proof is completed. \(\square \)

We shall next discuss a global existence result for the 2D-NFVIEs using Tychonoff’s fixed-point theorem.

Theorem 5

Assume that

(D1):

\( k \in C({\mathbb {R}}_ + ^4 \times {\mathbb {R}}^n ,{\mathbb {R}}^n) \) and \( G \in C({\mathbb {R}}_ + ^5 ,{\mathbb {R}}^n) \).

(D2):

\( G(x,y,\tau ,\varsigma ,u) \) is monotone nondecreasing in u, for each \( (x,y,\tau ,\varsigma )\in {\mathbb {R}}_ + ^4 \).

(D3):

\( \left| {k(x,y,\tau ,\varsigma ,f)} \right| \le G(x,y,\tau ,\varsigma ,\left| f \right| )\), for \((x,y,\tau ,\varsigma ,f) \in {\mathbb {R}}_ + ^4 \times {{\mathbb {R}}^n} \).

Then, the fractional integral equation

$$\begin{aligned} u(x,y)&= q(x,y) \nonumber \\&\quad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}G(x,y,\tau ,\varsigma ,u(\tau ,\varsigma )){\mathrm{d}}\varsigma } {\mathrm{d}}\tau }, \end{aligned}$$
(6)

has a solution u(x, y) , for every \( x,y\ge 0 \), and then for every \( q(x,y)\in {\mathbb {R}}_ + ^2 \) such that \( \left| g(x,y) \right| \le q(x,y) \), there exists a solution f(x, y) for 2D-NFVIE satisfying \( \left| f(x,y) \right| \le u(x,y) \).

Proof

Assume that the real vector space V consists of all continuous functions from \( (0,\infty )\times (0,\infty ) \) into \( {\mathbb {R}}^n \). The topology on V being that induced by the family of pseudo-norms \( \{ {V_{n,m}}(f)\} _{{n,m} = 1}^\infty \), where \( {V_{n,m}}(f) = {\mathop {\sup }\nolimits _{0 \le x \le n,0 \le y \le m}} \left| {f(x,y)} \right| \), for \( f \in V \). Let \( \{{S_{n,m}}\} _{n,m = 1}^\infty \) be a fundamental system of neighborhoods, where \( {S_{n,m}} = \{ f \in V:{V_{n,m}}(f) \le 1\} \). Under this topology, V is complete and locally convex linear space.

Now define the subset \({V_0}\) of V as follows:

$$\begin{aligned} {V_0} = \left\{ f \in V:\left| {f(x,y)} \right| \le u(x,y),~ x,y \ge 0 \right\} \subseteq V , \end{aligned}$$

where u(x, y) is a solution of Eq. (6). It is clear that in the topology of V, \( V_0 \) is closed, convex, and bounded.

Consider the Eq. (6) whose fixed point corresponds to a solution of Eq. (1). Evidently, in the topology of V, the operator T is compact. Hence, in view of the boundedness of \( {V_0} \), the closure of \( T({V_0}) \) is compact.

Now using conditions \( (\mathbf{D1} )\)–\((\mathbf{D3} ) \), we observe that for any \( f\in {V_0} \),

$$\begin{aligned}&\left| {Tf(x,y)} \right| \le \left| {g(x,y)} \right| \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}\left| {k(x,y,\tau ,\varsigma ,f(\tau ,\varsigma ))} \right| {\mathrm{d}}\varsigma } {\mathrm{d}}\tau } \\&\quad \le \left| {g(x,y)} \right| + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}G(x,y,\tau ,\varsigma ,\left| {f(\tau ,\varsigma )} \right| ){\mathrm{d}}\varsigma } {\mathrm{d}}\tau } \\&\quad \le q(x,y) \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}G(x,y,\tau ,\varsigma ,u(\tau ,\varsigma )){\mathrm{d}}\varsigma } {\mathrm{d}}\tau } = u(x,y). \end{aligned}$$

It is clear that using the fact that u(x, y) is a solution of 2D-NFVIE and from the definition of \(V_0\), we can obtain \( \left| {Tf(x,y)} \right| \le u(x,y) \), which implies that \(T({V_0}) \subset {V_0}\). Therefore, by Tychonoff’s fixed-point theorem, the mapping T has a fixed point in \( {V_0} \), which completes the proof of this theorem. \(\square \)

In the following theorem, we prove the uniqueness of the solution for 2D-NFVIEs.

Theorem 6

Let \( f \in C(\varOmega ,{\mathbb {R}}^n) \) and \( k \in C(\varOmega \times \varOmega \times {\mathbb {R}}^n ,{\mathbb {R}}^n) \). Suppose that there exists \( 0< L_1 < 1 \) such that the following Lipschitz condition is satisfied:

$$\begin{aligned} \left| {k}(x,y,\tau ,\varsigma ,f(\tau ,\varsigma )) - {k}(x,y,\tau ,\varsigma ,{f_1}(\tau ,\varsigma )) \right| \le {L_1} \left| f(\tau ,\varsigma ) - {f_1}(\tau ,\varsigma ) \right| . \end{aligned}$$

If \( \frac{{{L_1}{{\ell }_1^{\iota _1}}{{\ell }_2^{\iota _2}}}}{{\varGamma ({\iota _1}+1)\varGamma ({\iota _2}+1)}} < 1 \), then the 2D-NFVIE has a unique solution.

Proof

Let

$$\begin{aligned}&Tf(x,y) = {g}(x,y) \\&\quad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}k(x,y,\tau ,\varsigma ,f(\tau ,\varsigma )){\mathrm{d}}\varsigma } {\mathrm{d}}\tau },\quad (x,y) \in \varOmega , \end{aligned}$$

then, for any \( {f},~ {f_1} \in C(\varOmega ,{\mathbb {R}}^n) \) and \( (x,y) \in \varOmega \), we have

$$\begin{aligned}&\left| {Tf(x,y) - T{f_1}(x,y)} \right| \\&\quad = \left| {g(x,y) + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}k(x,y,\tau ,\varsigma ,f(\tau ,\varsigma )){\mathrm{d}}\varsigma } {\mathrm{d}}\tau } } \right. \\&\qquad \left. { - g(x,y) - \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}k(x,y,\tau ,\varsigma ,{f_1}(\tau ,\varsigma )){\mathrm{d}}\varsigma } {\mathrm{d}}\tau } } \right| \\&\quad \le \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x \int _0^y {{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}\left| k(x,y,\tau ,\varsigma ,f(\tau ,\varsigma )) \right. \\&\qquad \left. - k(x,y,\tau ,\varsigma ,{f_1}(\tau ,\varsigma )) \right| {\mathrm{d}}\varsigma {\mathrm{d}}\tau \\&\quad \le \frac{{{L_1}}}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}\left| f(\tau ,\varsigma ) - {f_1}(\tau ,\varsigma ) \right| {\mathrm{d}}\varsigma } {\mathrm{d}}\tau } \\&\quad \le \frac{{{L_1}{{\ell }_1^{\iota _1}}{{\ell }_2^{\iota _2}}}}{{\varGamma ({\iota _1}+1)\varGamma ({\iota _2}+1)}} \left\| f - {f_1} \right\| . \end{aligned}$$

Therefore,

$$\begin{aligned} \left\| {Tf - T{f_1}} \right\| \le \frac{{{L_1}{{\ell }_1^{\iota _1}}{{\ell }_2^{\iota _2}}}}{{\varGamma ({\iota _1}+1)\varGamma ({\iota _2}+1)}} \left\| f - {f_1} \right\| . \end{aligned}$$

Since \( \frac{{{L_1}{{\ell }_1^{\iota _1}}{{\ell }_2^{\iota _2}}}}{{\varGamma ({\iota _1}+1)\varGamma ({\iota _2}+1)}} < 1 \), it follows that T is a contraction in \( C(\varOmega ,{\mathbb {R}}^n) \). Consequently, T has a unique fixed point and therefore the 2D-NFVIE has a unique solution \( {f} \in C(\varOmega ,{\mathbb {R}}^n) \). \(\square \)

Now, in the following theorems, we are going to investigate a result of the existence and uniqueness of the solution for 2D-NFFIEs.

Theorem 7

Assume that conditions \( (\mathbf{C1} )\)–\((\mathbf{C3} ) \) in Theorem 4 hold. Then the 2D-NFFIE has at least one solution on \( 0 \le x \le \alpha ,\, 0 \le y \le \beta \).

Proof

The proof of this theorem is similar to the proof of Theorem 4. \(\square \)

Theorem 8

Assume that conditions \( (\mathbf{D1} )\)–\((\mathbf{D3} ) \) in Theorem 5 hold. Then, the fractional integral equation

$$\begin{aligned}&u(x,y) = q(x,y) \nonumber \\&\quad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{\ell _1} {\int _0^{\ell _2} {{{({\ell _1} - \tau )}^{{\iota _1} - 1}}{{({\ell _2} - \varsigma )}^{{\iota _2} - 1}}G(x,y,\tau ,\varsigma ,u(\tau ,\varsigma )){\mathrm{d}}\varsigma } {\mathrm{d}}\tau }, \end{aligned}$$
(7)

has a solution u(x, y) existing for every \( x,y\ge 0 \), and then for every \( q(x,y)\in {\mathbb {R}}_ + ^2 \), such that \( \left| g(x,y) \right| \le q(x,y) \), there exists a solution f(x, y) of the 2D-NFFIE for \( x,y\ge 0 \) satisfying \( \left| f(x,y) \right| \le u(x,y) \).

Proof

The proof of this theorem is similar to the proof of Theorem 5. \(\square \)

Theorem 9

Let \( f \in C(\varOmega ,{\mathbb {R}}^n) \) and \( k \in C(\varOmega \times \varOmega \times {\mathbb {R}}^n ,{\mathbb {R}}^n) \). Suppose that there exists \( 0< L_2 < 1 \) such that the following Lipschitz condition is satisfied:

$$\begin{aligned} \left| {k}(x,y,\tau ,\varsigma ,f(\tau ,\varsigma )) - {k}(x,y,\tau ,\varsigma ,{f_1}(\tau ,\varsigma )) \right| \le {L_2} \left| f(\tau ,\varsigma ) - {f_1}(\tau ,\varsigma ) \right| . \end{aligned}$$

If \( \frac{{{L_2}{{\ell }_1^{\iota _1}}{{\ell }_2^{\iota _2}}}}{{\varGamma ({\iota _1}+1)\varGamma ({\iota _2}+1)}} < 1 \), then the 2D-NFFIE has a unique solution.

Proof

The proof of this theorem is similar to the proof of Theorem 6. \(\square \)

4 The 2D-HBPSLs and the operational matrices

Here, we present the 2D-HBPSLs and use them to obtain the approximation of two-variable functions. Then, we review the operational matrices of fractional integration and product.

First, consider the 1D-HBPSLs on the interval \( [0,{\ell }) \) as follows:

$$\begin{aligned} {\hslash }_{nm}(x)= {\left\{ \begin{array}{ll} \phi _{m}(\frac{2N}{\ell } x-2n+1), &{} x\in [\frac{n-1}{N} {\ell },\frac{n}{N} {\ell }),\\ 0, &{} \mathrm {otherwise}, \end{array}\right. } \end{aligned}$$

for \(n=1,2,\dots ,N,~ m=0,1,\dots ,M-1\), where N and M are positive integers. Here, \(\phi _{m}\) is Legendre polynomial of degree m which is defined on \([-1,1]\) with the analytic form

$$\begin{aligned} {\phi _m}( x) = {2^m}\sum \limits _{j = 0}^m {{ x^j}\left( \begin{array}{c} m\\ j \end{array} \right) \left( \begin{array}{c} \frac{{m + j - 1}}{2}\\ m \end{array} \right) }. \end{aligned}$$

The orthogonality property of the 1D-HBPSLs on the interval \( [0,{\ell }) \) is as follows:

$$\begin{aligned} \int _{0}^{\ell }{{\hslash }_{nm}(x) {\hslash }_{ij}(x) \mathrm {d}x}= {\left\{ \begin{array}{ll} \frac{{\ell }}{N(2m+1)},&{} n=i,m=j,\\ 0,&{} \mathrm {otherwise}. \end{array}\right. } \end{aligned}$$

Similarly, the 2D-HBPSLs on the domain \( \varOmega =[0,{\ell _1})\times [0,{\ell _2}) \) is defined as follows:

$$\begin{aligned}&{\hslash }_{n_{1}m_{1}n_{2}m_{2}}(x,y)\\&\quad = {\left\{ \begin{array}{ll} \phi _{m_{1}}\left( \frac{2N}{\ell _1}x-2n_{1}+1\right) \phi _{m_{2}}\left( \frac{2N}{\ell _2}y-2n_{2}+1\right) , &{} (x,y) \in [\frac{n_{1}-1}{N} {\ell _1},\frac{n_{1}}{N} {\ell _1})\times [\frac{n_{2}-1}{N} {\ell _2},\frac{n_{2}}{N} {\ell _2}),\\ 0, &{} \mathrm {otherwise}. \end{array}\right. } \end{aligned}$$

Here \(\phi _{m_{1}}\) and \(\phi _{m_{2}}\) are Legendre polynomials of degrees \(m_{1}\) and \(m_{2}\), respectively, where \(n_{1},n_{2}=1,2,\dots ,N,~ m_{1},m_{2}=0,1,\dots ,M-1\).

The orthogonality property of the 2D-HBPSLs on the domain \( \varOmega \) is

$$\begin{aligned}&\int _{0}^{\ell _1}\int _{0}^{\ell _2} {\hslash }_{n_{1}m_{1}n_{2}m_{2}}(x,y) {\hslash }_{i_{1}j_{1}i_{2}j_{2}}(x,y)\,\mathrm {d}y\,\mathrm {d}x\\&\quad = {\left\{ \begin{array}{ll} \frac{{\ell _1}{\ell _2}}{N^{2}(2m_{1}+1)(2m_{2}+1)},&{} n_{1}=i_{1},n_{2}=i_{2},m_{1}=j_{1},m_{2}=j_{2},\\ 0,&{} \mathrm {otherwise}. \end{array}\right. } \end{aligned}$$

Now consider the space \(X=L^{2}(\varOmega )\) with the norm

$$\begin{aligned} \left\| f \right\| _{2}=\left\langle {f,f} \right\rangle ^{\frac{1}{2}}=\left( \int _{0}^{\ell _1}\int _{0}^{\ell _2} |f(x,y) |^{2}\,\mathrm {d}y \mathrm {d}x\right) ^{\frac{1}{2}}, \end{aligned}$$

where \( \left\langle {.,.} \right\rangle \) denotes the inner product. Let

$$\begin{aligned} X_{N,M}&=span\lbrace {\hslash }_{1010}(x,y),\dots ,{\hslash }_{101(M-1)}(x,y),{\hslash }_{1020}(x,y),\dots , {\hslash }_{102(M-1)}(x,y),\\&\dots ,{\hslash }_{N(M-1)N0}(x,y),\dots , {\hslash }_{N(M-1)N(M-1)}(x,y)\rbrace . \end{aligned}$$

Since \(X_{N,M} \subset X \) is a finite dimensional vector space, for every \( f \in X \) there exists a unique best approximation \( f_{N,M} \in X_{N,M} \) such that

$$\begin{aligned} {\left\| f-f_{N,M} \right\| _2} = \mathop {\inf }\limits _{u\in X_{N,M}} \left\| f-u \right\| _{2}. \end{aligned}$$

A proof of this result is given by Cheney (1966), Davis (1975), and Kreyszig (1989). Since \( f_{N,M} \in X_{N,M} \), we have

$$\begin{aligned} f(x,y)\simeq f_{N,M}(x,y)=\sum \limits _{n_{1}=1}^{N}\sum \limits _{m_{1}=0}^{M-1}\sum \limits _{n_{2}=1}^{N}\sum \limits _{m_{2=0}}^{M-1} {{\hat{f}}}_{n_{1}m_{1}n_{2}m_{2}} {\hslash }_{n_{1}m_{1}n_{2}m_{2}}(x,y)={{\hat{F}}}^{T}H(x,y), \end{aligned}$$
(8)

where

$$\begin{aligned}&{{\hat{F}}}=[{{\hat{f}}}_{1010},\dots ,{{\hat{f}}}_{101(M-1)},{{\hat{f}}}_{1020},\dots ,{{\hat{f}}}_{102(M-1)},\dots ,{{\hat{f}}}_{N(M-1)N0},\dots ,{{\hat{f}}}_{N(M-1)N(M-1)}]^{T}, \end{aligned}$$
(9)
$$\begin{aligned}&H(x,y)=[{\hslash }_{1010}(x,y),\dots ,{\hslash }_{101(M-1)}(x,y),{\hslash }_{1020}(x,y),\dots ,{\hslash }_{102(M-1)}(x,y),\nonumber \\&\qquad \qquad \quad \dots , {\hslash }_{N(M-1)N0}(x,y),\dots , {\hslash }_{N(M-1)N(M-1)}(x,y)]^{T}, \end{aligned}$$
(10)

and hybrid coefficients are uniquely obtained by

$$\begin{aligned} {{\hat{f}}}_{n_{1}m_{1}n_{2}m_{2}}=\dfrac{\left\langle f,{{\hslash }_{n_{1}m_{1}n_{2}m_{2}}}\right\rangle }{\left\langle {{\hslash }_{n_{1}m_{1}n_{2}m_{2}}}, {{\hslash }_{n_{1}m_{1}n_{2}m_{2}}}\right\rangle } . \end{aligned}$$
(11)

Now consider \(X =L^{2}(\varOmega \times \varOmega )\) with

$$\begin{aligned} \Vert k \Vert _{2}=\left\langle k,k \right\rangle ^{\frac{1}{2}}=\left( \int _0^{\ell _1} \int _0^{\ell _2}\int _0^{\ell _1} \int _0^{\ell _2}|k(x,y, \tau ,\varsigma )|^{2}\,\mathrm {d}\varsigma \,\mathrm {d} \tau \,\mathrm {d}y\,\mathrm {d}x\right) ^{\frac{1}{2}}. \end{aligned}$$

Also, a function k in X can be expanded as follows:

$$\begin{aligned} k( x,y, \tau ,\varsigma ) \simeq H^{T}(x,y) K H( \tau ,\varsigma ), \end{aligned}$$
(12)

where K is the \( N^{2}M^{2} \times N^{2}M^{2} \) known matrix and its entries are given by

$$\begin{aligned} K_{n,m}=\dfrac{\int _0^{\ell _1}\int _0^{\ell _2}\int _0^{\ell _1}\int _0^{\ell _2}H_{(n)}(x,y)k(x,y, \tau ,\varsigma )H_{(m)}( \tau ,\varsigma )\,\mathrm {d}\varsigma \,\mathrm {d} \tau \,\mathrm {d}y\,\mathrm {d}x}{\left( \int _0^{\ell _1}\int _0^{\ell _2}|H_{(n)}(x,y)|^{2}\,\mathrm {d}y\,\mathrm {d}x\right) \left( \int _0^{\ell _1}\int _0^{\ell _2}|H_{(m)}( \tau ,\varsigma )|^{2}\,\mathrm {d}\varsigma \,\mathrm {d} \tau \right) }. \end{aligned}$$
(13)

Here \(H_{(n)}(x,y)\) denotes the nth element of H(x, y).

4.1 The operational matrix of fractional integration

Maleknejad et al. (2020a) obtained the left-sided mixed Riemann–Liouville fractional integral of order \( \iota := ({\iota _1},{\iota _2}) \) of 2D-HBPSLs as follows:

$$\begin{aligned} {I^{({\iota _1},{\iota _2})}}{H}(x,y) \simeq \left( {\mathbf{I }^{{\iota _1}}} \otimes {\mathbf{I }^{{\iota _2}}}\right) {H}(x,y). \end{aligned}$$
(14)

Here, \( \otimes \) denotes the Kronecker product and \( {\mathbf{I }^{{\iota _1}}} \otimes {\mathbf{I }^{{\iota _2}}} \) is the operational matrix of fractional integration of 2D-HBPSLs, where

$$\begin{aligned} {\mathbf{I }^{{\iota _i}}} = \varPsi {\mathbf{P }^{\iota _i}}{\varPsi ^{ - 1}},\qquad i=1,2, \end{aligned}$$
(15)

and

$$\begin{aligned} {\mathbf{P }^{\iota _i}} = {\left( \frac{{{\ell _i}}}{{{NM}}}\right) ^{\iota _i}}\dfrac{1}{\varGamma ({\iota _i} + 2)}\left[ {\begin{array}{*{20}{c}} 1&{}{{\kappa _{_1}}}&{}{{\kappa _{_2}}}&{} \ldots &{}{{\kappa _{_{NM - 1}}}}\\ 0&{}1&{}{{\kappa _{_1}}}&{} \ldots &{}{{\kappa _{_{NM - 2}}}}\\ 0&{}0&{}1&{} \ldots &{}{{\kappa _{_{NM - 3}}}}\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0&{}0&{}0&{} \ldots &{}1 \end{array}} \right] , \end{aligned}$$

with \( {\kappa _{_l}} = {(l + 1)^{{\iota _i} + 1}} - 2{l^{{\iota _i} + 1}} + {(l - 1)^{{\iota _i}+ 1}} \), \( l=1,2,\ldots ,NM-1 \), is the operational matrix of fractional integration of block-pulse functions given by Kılıçman and Al Zhour (2007). Also, \( \varPsi _i \) is an \( NM\times NM \) matrix given by

$$\begin{aligned} \varPsi _i \triangleq \left[ {H\left( {\frac{{\ell _i}}{{2NM}}} \right) ,H\left( {\frac{3{\ell _i}}{{2NM}}} \right) , \ldots ,H\left( {\frac{({2NM - 1}){\ell _i}}{{2NM}}} \right) } \right] _{NM\times NM}, \end{aligned}$$

where

$$\begin{aligned} H(x) = [{\hslash }_{10}(x),\dots ,{\hslash }_{1(M-1)}(x),{\hslash }_{20}(x),\dots ,{\hslash }_{N(M-1)}(x)]^{T}, \end{aligned}$$

is an \( NM\times 1 \) vector of 1D-HBPSLs.

Moreover, from Maleknejad et al. (2020a), we have

$$\begin{aligned}&\frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{{\ell _1}} {\int _0^{{\ell _2}} {{{({\ell _1} - \tau )}^{{\iota _1} - 1}}{{({\ell _2} - \varsigma )}^{{\iota _2} - 1}}{H}(\tau ,\varsigma )\mathrm {d}\varsigma } \mathrm {d}\tau } = {\varXi _1} \otimes {\varXi _2} , \end{aligned}$$
(16)

where

$$\begin{aligned} {\varXi _1} = \frac{1}{{\varGamma ({\iota _1})}}\int _0^{{\ell _1}} {{{({\ell _1} - \tau )}^{{\iota _1} - 1}}{H}(\tau )\mathrm {d}\tau }, \end{aligned}$$

and

$$\begin{aligned} {\varXi _2} ={\frac{1}{{\varGamma ({\iota _2})}}\int _0^{{\ell _2}} {{{({\ell _2} - \varsigma )}^{{\iota _2} - 1}}{H}(\varsigma )\mathrm {d}\varsigma } }. \end{aligned}$$

4.2 The product operational matrix

Let H(x, y) be the 2D-HBPSLs vector defined in (10), then we have

$$\begin{aligned} H(x,y)H^{T}(x,y){{\hat{F}}}\simeq \tilde{{{\hat{F}}}}H(x,y), \end{aligned}$$
(17)

where \({{\hat{F}}}\) is defined by (9) and \(\tilde{{{\hat{F}}}}\) is an \( {N^2}{M^2}\times {N^2}{M^2} \) product operational matrix. Maleknejad et al. (2020a) have computed the entries of \(\tilde{{{\hat{F}}}}=diag(C_{i_{1}})_{i_{1}=1,2,\dots ,N} \) as follows:

$$\begin{aligned} C_{i_{1}}&=\left[ C_{i_{1}}^{(j_{1},m_{1})} \right] _{j_{1},m_{1}=0,1,\dots ,M-1},\\ C_{i_{1}}^{(j_{1},m_{1})}&=\dfrac{N(2m_{1}+1)}{\ell _1}\sum \limits _{{h}_{1}=0}^{M-1} w_{i_{1}j_{1}{h}_{1}m_{1}} B_{i_{1}{h}_{1}}, \quad j_{1},m_{1}=0,1,\dots ,M-1,\\ w_{i_{1}j_{1}{h}_{1}m_{1}}&=\int _{\frac{i_{1}-1}{N}{\ell _1}}^{\frac{i_{1}}{N}{\ell _1}} \phi _{j_{1}}\left( \frac{2N}{\ell _1} x -2i_{1}+1 \right) \phi _{{h}_{1}}\left( \frac{2N}{\ell _1} x -2i_{1}+1 \right) \phi _{m_{1}}\nonumber \\&\qquad \times \left( \frac{2N}{\ell _1} x -2{i_{1}}+1 \right) \,\mathrm {d}x,\\ B_{i_{1}{h}_{1}}&={\text {diag}}(A_{i_{1},{h}_{1},i_{2}})_{i_{2}=1,2,\dots ,N},\\ A_{i_{1},{h}_{1},i_{2}}&=\left[ A_{i_{1},{h}_{1},i_{2}}^{(j_{2},m_{2})} \right] _{ j_{2},m_{2}=0,\dots ,M-1},\\ A_{i_{1},{h}_{1},i_{2}}^{(j_{2},m_{2})}&=\dfrac{N(2 m_{2}+1)}{\ell _2}\sum \limits _{{h}_{2}=0}^{M-1}w_{i_{2}j_{2}{h}_{2}m_{2}}{{\hat{f}}}_{i_{1}{h}_{1}i_{2}{h}_{2}},\quad j_{2},m_{2}=0,\dots ,M-1,\\ w_{i_{2}j_{2}{h}_{2}m_{2}}&=\int _{\frac{i_{2}-1}{N}{\ell _2}}^{\frac{i_{2}}{N}{\ell _2}} \phi _{j_{2}}\left( \frac{2N}{\ell _2} y -2i_{2}+1 \right) \phi _{{h}_{2}}\left( \frac{2N}{\ell _2} y -2i_{2}+1 \right) \phi _{m_{2}}\\&\qquad \times \left( \frac{2N}{\ell _2} y -2{i_{2}}+1 \right) \,\mathrm {d}y . \end{aligned}$$

5 Method of solution

In this section, we suppose that \({k}(x,y,\tau ,\varsigma ,f(\tau ,\varsigma ))={k}(x,y,\tau ,\varsigma ){f^p}(\tau ,\varsigma ) \) and then we use 2D-HBPSLs and their operational matrices for solving Eqs. (1) and (2).

5.1 The method for 2D-NFVIEs

Here, we are going to convert Eq. (1) to a nonlinear system using 2D-HBPSLs. First, we can write

$$\begin{aligned}&g(x,y) \simeq {{H}^T}(x,y)G, \end{aligned}$$
(18)

Using (8) and (17) for the function f(x, y) , we obtain

$$\begin{aligned} {[f(x,y)]^2}&\simeq {{{{\hat{F}}}}^T}{H}(x,y){{H}^T}(x,y){{\hat{F}}} = \underbrace{{{{{\hat{F}}}}^T}{\tilde{{{\hat{F}}}}}}_{{{{\hat{F}}}_2}}{H}(x,y) = {{{\hat{F}}}_2}{H}(x,y),\\ {[f(x,y)]^3}&\simeq {{{{\hat{F}}}}^T}{H}(x,y){{{\hat{F}}}_2}{H}(x,y) = {{{{\hat{F}}}}^T}{H}(x,y){{H}^T}(x,y){{\hat{F}}}_2^T = \underbrace{{{{{\hat{F}}}}^T}\widetilde{{{\hat{F}}}_2^T}}_{{{{\hat{F}}}_3}}{H}(x,y) \\&= {{{\hat{F}}}_3}{H}(x,y). \end{aligned}$$

where \({\widetilde{{{\hat{F}}}_2^T}}\) is an \( {N^2}{M^2}\times {N^2}{M^2} \) product operational matrix. By expanding the method for an arbitrary \( p\in \mathbb {N} \), the result is as follows:

$$\begin{aligned} {[f(x,y)]^p} \simeq {{{\hat{F}}}_p}{H}(x,y). \end{aligned}$$
(19)

Now, using (8), (12), (14), (17) -(19), we get

$$\begin{aligned}&{{H}^T}(x,y){{{\hat{F}}}} \simeq {{H}^T}(x,y)G \\&\quad + \dfrac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}{{H}^T}(x,y){K}{H}(\tau ,\varsigma ){{{\hat{F}}}_p} {H}(\tau ,\varsigma )\mathrm {d}\varsigma } \mathrm {d}\tau } \\&\simeq {{H}^T}(x,y)G \\&\quad + \dfrac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}{{H}^T}(x,y){K}{\widetilde{{{\hat{F}}}_p^T}} {H}(\tau ,\varsigma )\mathrm {d}\varsigma } \mathrm {d}\tau } \\&={{H}^T}(x,y)G \\&\quad + {{H}^T}(x,y){K}{\widetilde{{{\hat{F}}}_p^T}} \left( \dfrac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}{H}(\tau ,\varsigma )\mathrm {d}\varsigma } \mathrm {d}\tau }\right) \\&\simeq {{H}^T}(x,y)G + {{H}^T}(x,y){K}{\widetilde{{{\hat{F}}}_p^T}} \left( {{\mathbf{I }^{{\iota _1}}} \otimes {\mathbf{I }^{{\iota _2}}}} \right) {H}(x,y). \end{aligned}$$

Therefore, we have

$$\begin{aligned} {{H}^T}(x,y){{{\hat{F}}}}&\simeq {{H}^T}(x,y)G + {{H}^T}(x,y){K}{\widetilde{{{\hat{F}}}_p^T}}\left( {{\mathbf{I }^{{\iota _1}}} \otimes {\mathbf{I }^{{\iota _2}}}} \right) {H}(x,y). \end{aligned}$$
(20)

To obtain unknown coefficients \( {{{\hat{f}}}_{n_{1}m_{1}n_{2}m_{2}}} \), for \( n_{1},n_{2}=1,2,\dots ,N,~ m_{1},m_{2}=0,1,\dots ,M-1 \), we collocate Eq. (20) at \( {N^2}{M^2} \) collocation points \( \{({x_i},{y_j})\}_{i,j=1}^{NM} \) in the domain \(\varOmega = [0,{\ell _1}) \times [0,{\ell _2})\), where

$$\begin{aligned} {x_i}=\dfrac{2i-1}{2NM},~ {y_j}= \dfrac{2j-1}{2NM},\quad i,j=1,2,\ldots , NM, \end{aligned}$$

are the Newton-Cotes nodes. Therefore, we have \( {N^2}{M^2} \) nonlinear equations. By solving this system, we determine an approximate solution for 2D-NFVIE from (8).

5.2 The method for 2D-NFFIEs

Now we want to convert Eq. (2) to a nonlinear system using 2D-HBPSLs. For this purpose, we apply (8), (12), (16)–(19) in (2) and, therefore, we obtain

$$\begin{aligned}&{{H}^T}(x,y){{{\hat{F}}}} \simeq {{H}^T}(x,y)G \\&\qquad + \dfrac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{\ell _1} {\int _0^{\ell _2} {{{({\ell _1} - \tau )}^{{\iota _1} - 1}}{{({\ell _2} - \varsigma )}^{{\iota _2} - 1}}{{H}^T}(x,y){K}{H}(\tau ,\varsigma ) {{{\hat{F}}}_p} {H}(\tau ,\varsigma )\mathrm {d}\varsigma } \mathrm {d}\tau } \\&\quad \simeq {{H}^T}(x,y)G \\&\qquad + \dfrac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{\ell _1} {\int _0^{\ell _2} {{{({\ell _1} - \tau )}^{{\iota _1} - 1}}{{({\ell _2} - \varsigma )}^{{\iota _2} - 1}}{{H}^T}(x,y){K}{\widetilde{{{\hat{F}}}_p^T}} {H}(\tau ,\varsigma )\mathrm {d}\varsigma } \mathrm {d}\tau } \\&\quad = {{H}^T}(x,y)G \\&\qquad + {{H}^T}(x,y){K}{\widetilde{{{\hat{F}}}_p^T}} \left( \dfrac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^{\ell _1} {\int _0^{\ell _2} {{{({\ell _1} - \tau )}^{{\iota _1} - 1}}{{({\ell _2} - \varsigma )}^{{\iota _2} - 1}}{H}(\tau ,\varsigma )\mathrm {d}\varsigma } \mathrm {d}\tau }\right) \\&\quad \simeq {{H}^T}(x,y)G + {{H}^T}(x,y){K}{\widetilde{{{\hat{F}}}_p^T}} ({\varXi _1}\otimes {\varXi _2}). \end{aligned}$$

So, we have

$$\begin{aligned} {{H}^T}(x,y){{{\hat{F}}}} \simeq {{H}^T}(x,y)G + {{H}^T}(x,y){K}{\widetilde{{{\hat{F}}}_p^T}} ({\varXi _1}\otimes {\varXi _2}). \end{aligned}$$
(21)

Obtaining the unknown coefficients \( {{{\hat{f}}}_{n_{1}m_{1}n_{2}m_{2}}} \) in the above system is similar to (20). Therefore, we can determine an approximate solution for 2D-NFFIE from (8).

6 Error bound and convergence analysis

Theorem 10

Suppose that \( f \in {C^{(2M)}}(\varOmega ) \). Let f(x, y) be the exact solution of the 2D-NFVIE and \(f_{N,M}(x,y)\) be its approximate solution obtained by the proposed method. Assume that for \( (x,y)\in \varOmega =[0,{\ell _1})\times [0,{\ell _2}) \), the following assumptions hold:

(H1):

\( g \in {C^{(2M)}}(\varOmega ) \) and \( k \in {C^{(4M)}}(\varOmega \times \varOmega ) \).

(H2):

There exists a Lipschitz constant L such that

$$\begin{aligned} \left| {{f^{p}}(x,y) - f_{N,M}^{p}(x,y)} \right| \le {L}\left| {f(x,y) - {f_{N,M}}(x,y)} \right| . \end{aligned}$$
(H3):

\(\sup _{\varOmega }|{{{f}}^{p}}(x,y) |= a' <\infty \).

(H4):

\(\sup _{\varOmega \times \varOmega }|{k}(x,y,\tau ,\varsigma )|= b' <\infty \).

Then, there exist positive constants \({\mu _1}\) and \({\mu _2}\) such that

$$\begin{aligned} \Vert f-{f}_{N,M}\Vert _{2} \le \left( \frac{{{c'}\varGamma ({\iota _1} + 1)\varGamma ({\iota _2} + 1) + {\mu _1} \ell _1^{{\iota _1}}\ell _2^{{\iota _2}}} }{{ { \varGamma ({\iota _1} + 1)\varGamma ({\iota _2} + 1) - {\mu _2} \ell _1^{{\iota _1}}\ell _2^{{\iota _2}} } }} \right) \dfrac{{\sqrt{{\ell _1}{\ell _2}}}}{2^{2M-1}N^{M}M!}. \end{aligned}$$
(22)

Proof

Considering the two-dimensional hybrid expansions of f(x, y) and \( {k}(x,y, \tau ,\varsigma ) \) and also using assumptions \( (\mathbf{H1} )\)–\((\mathbf{H4} ) \) lead to

$$\begin{aligned}&\left| {f(x,y) - {{f}_{N,M}}(x,y)} \right| = \left| {g(x,y) - {g_{N,M}}(x,y)} \right. \nonumber \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}k(x,y,\tau ,\varsigma ){f^p}(\tau ,\varsigma ){\mathrm{d}}\varsigma } {\mathrm{d}}\tau } \nonumber \\&\qquad \left. { - \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}{k_{N,M}}(x,y,\tau ,\varsigma ){f}_{N,M}^p(\tau ,\varsigma ){\mathrm{d}}\varsigma } {\mathrm{d}}\tau } } \right| \nonumber \\&\quad \le \left| {g(x,y) - {g_{N,M}}(x,y)} \right| \nonumber \\&\qquad + \left| {\frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}\left( {k(x,y,\tau ,\varsigma )\left( {{f^p}(\tau ,\varsigma ) - {f}_{N,M}^p(\tau ,\varsigma )} \right) } \right. } } } \right. \nonumber \\&\qquad \left. { + \left. {\left( {k(x,y,\tau ,\varsigma ) - {k_{N,M}}(x,y,\tau ,\varsigma )} \right) f_{N,M}^p(\tau ,\varsigma )} \right) {\mathrm{d}}\varsigma {\mathrm{d}}\tau } \right| \nonumber \\&\quad \le \left| {g(x,y) - {g_{N,M}}(x,y)} \right| \nonumber \\&\qquad + \frac{1}{{\varGamma ({\iota _1})\varGamma ({\iota _2})}}\int _0^x {\int _0^y {{{(x - \tau )}^{{\iota _1} - 1}}{{(y - \varsigma )}^{{\iota _2} - 1}}\left( {{b'}{L}\left| {f(\tau ,\varsigma ) - {{f}_{N,M}}(\tau ,\varsigma )} \right| } \right. } } \nonumber \\&\qquad + \left. {{a'}\left| {k(x,y,\tau ,\varsigma ) - {k_{N,M}}(x,y,\tau ,\varsigma )} \right| } \right) {\mathrm{d}}\varsigma {\mathrm{d}}\tau . \end{aligned}$$
(23)

Now from Maleknejad et al. (2020a) (see Theorem 6, page 16), we can write

$$\begin{aligned} \left\| g - {g_{N,M}} \right\| _{2}\le \dfrac{{c'} {\sqrt{{\ell _1}{\ell _2}}}}{2^{2M-1}N^{M}M!}, \end{aligned}$$

and

$$\begin{aligned} \Vert k - k_{N,M} \Vert _{2} \le \dfrac{{d'} {\sqrt{{\ell _1}{\ell _2}}}}{2^{2M-1}N^{M}M!}. \end{aligned}$$

Also, by taking \( {L^2}- \)norm in the inequality (23), we obtain

$$\begin{aligned} \Vert f - f_{N,M} \Vert _{2}&\le {\left\| {g - {g_{N,M}}} \right\| _2} \\&\quad +\frac{{\ell _1^{{\iota _1}}\ell _2^{{\iota _2}}}}{{\varGamma ({\iota _1} + 1)\varGamma ({\iota _2} + 1)}} \left( {{b'}{L}\Vert f - f_{N,M} \Vert _{2} + {a'}{\left\| {k - {k_{N,M}}} \right\| _2}} \right) \\&\le \dfrac{{c'} {\sqrt{{\ell _1}{\ell _2}}}}{2^{2M-1}N^{M}M!}\\&\quad +\frac{{\ell _1^{{\iota _1}}\ell _2^{{\iota _2}}}}{{\varGamma ({\iota _1} + 1)\varGamma ({\iota _2} + 1)}} \left( {{b'}{L}\Vert f - f_{N,M} \Vert _{2} + \dfrac{{a'}{d'} {\sqrt{{\ell _1}{\ell _2}}}}{2^{2M-1}N^{M}M!}} \right) \\&\le \left( {c'} + \frac{{a'}{d'}{\ell _1^{{\iota _1}}\ell _2^{{\iota _2}}}}{{\varGamma ({\iota _1} + 1)\varGamma ({\iota _2} + 1)}} \right) \dfrac{ {\sqrt{{\ell _1}{\ell _2}}}}{2^{2M-1}N^{M}M!} \\&\quad + \frac{{b'}{L}{\ell _1^{{\iota _1}}\ell _2^{{\iota _2}}}}{{\varGamma ({\iota _1} + 1)\varGamma ({\iota _2} + 1)}}\Vert f - f_{N,M} \Vert _{2} . \end{aligned}$$

By simplifying the above relation and also setting \( {\mu _1} = {a'}{d'} \) and \( {\mu _2} = {b'}{L} \), we get the inequality (22) which completes the proof of the theorem. \(\square \)

Remark 1

To obtain an upper error bound for 2D-NFFIEs, since \( (x,y) \in \varOmega \), we can use a similar way that has been used in Theorem 10.

Remark 2

It is obvious that the right-hand side of the inequality (22) tends to zero as \(N,M \rightarrow \infty \), so \( f - {f}_{N,M} \rightarrow 0 \) and this proves the convergence of the proposed method.

7 Illustrative examples

In this section, we present three examples to demonstrate the accuracy and efficiency of the proposed method. In all these examples, \( {{\hat{n}}} \) denotes the number of bases. All examples are tested on an Intel(R) Core(TM) i5-2450M CPU @ 2.50GHz Processor with 4 GB of RAM using Maple 2018 software on Windows 7 (64 bit) operating system with 16 significant digits (Digits:= 16). The absolute errors in the solutions are obtained by

$$\begin{aligned} \left| {{f}(x,y) - {f_{N,M}}(x,y)} \right| , \qquad (x,y) \in [0,{\ell _1})\times [0,{\ell _2}) , ~ N,M\in \mathbb {N}. \end{aligned}$$

Also, the maximum absolute errors

$$\begin{aligned} \mathop {\max }\limits _{i,j=1,\ldots ,NM} \left\{ {\left| {f({x_i},{y_j}) - {f_{N,M}}({x_i},{y_j})} \right| } \right\} , \end{aligned}$$

are calculated at points \( ({x_i},{y_j}),~ i,j=1,\ldots ,NM \) which are Newton-Cotes nodes in \( [0,{\ell _1})\times [0,{\ell _2}) \).

Moreover, plots of maximum absolute errors are displayed by using

$$\begin{aligned} \mathop {\max }\limits _{j=1,\ldots ,NM}\left\{ \left| {f(x,{y_j}) - {f_{N,M}}(x,{y_j})} \right| \right\} ,\qquad x \in [0,{\ell _1}), \end{aligned}$$

where points \( {y_j},~ j=1,\ldots ,NM \) are Newton-Cotes nodes in \( [0,{\ell _2}) \).

Example 1

Consider the following two-dimensional fractional Fredholm integral equation studied by Hesameddini and Shahbazi (2018); Najafalizadeh and Ezzati (2016):

$$\begin{aligned} f(x,y) = \frac{{2362}}{{4725}} x y + \frac{1}{{\varGamma (\frac{7}{2})\varGamma (\frac{7}{2})}}\int _0^1 {\int _0^1 {{{(1 - \tau )}^{\frac{5}{2}}}{{(1 - \varsigma )}^{\frac{5}{2}}} x y\sqrt{\varsigma }f( \tau ,\varsigma )\mathrm {d}\varsigma } \mathrm {d} \tau }, \end{aligned}$$

with the exact solution \( f(x,y) = \frac{1}{2} x y \).

In Tables 1 and 2, respectively, we report the exact and approximate solutions and also the absolute errors in the solutions for \( N=2,~M = 2,3 \) at some selected nodes. These tables state that by using \( {{\hat{n}}} = {N^2}{M^2} = 36 \) numbers of bases, we obtain more accurate results than the 2D-SLPOM and 2D-BPFs methods reported by Hesameddini and Shahbazi (2018); Najafalizadeh and Ezzati (2016), respectively, that used \( {{\hat{n}}} = {(N+1)^2} = {129^2}=16641 \) 2D-SLPOM and \( {{\hat{n}}} = {m^2} = {128^2}=16384 \) 2D-BPFs to solve this problem. Figures 1 and 2 illustrate the accuracy and efficiency of the presented method.

Table 1 Numerical results for Example 1
Full size table
Table 2 Absolute errors for Example 1
Full size table
Fig. 1
figure 1

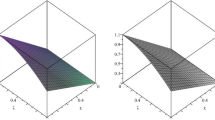
Plots of: a1 the exact solution, b1 the approximate solution, c1 the absolute error with \( N = 2 \) and \( M=3 \) for Example 1

Full size image
Fig. 2
figure 2

Plots of: d1 the comparison of the exact and approximate solutions, e1 the maximum absolute error with \( N = 2 \) and \( M=3 \) at \( y=0.3 \) for Example 1

Full size image
Table 3 Numerical results for Example 2
Full size table
Table 4 Absolute errors for Example 2
Full size table
Fig. 3
figure 3

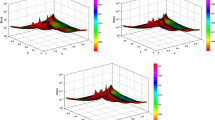
Plots of: a2 the exact solution, b2 the approximate solution, c2 the absolute error with \( N = 2 \) and \( M=3 \) for Example 2

Full size image
Fig. 4
figure 4

Plots of: d2 the comparison of the exact and approximate solutions, e2 the maximum absolute error with \( N = 2 \) and \( M=3 \) at \( y=0.3 \) for Example 2

Full size image
Table 5 Numerical results for Example 3
Full size table
Table 6 Absolute errors for Example 3
Full size table

Example 2

Consider the following two-dimensional fractional Fredholm integral equation studied by Hesameddini and Shahbazi (2018) and Najafalizadeh and Ezzati (2016):

$$\begin{aligned} f(x,y) = g(x,y) + \frac{1}{{\varGamma (\frac{9}{2})\varGamma (\frac{3}{2})}}\int _0^1 {\int _0^1 {{{(1 - \tau )}^{\frac{7}{2}}}{{(1 - \varsigma )}^{\frac{1}{2}}}5\sqrt{\tau }(y - x){{f^2}(\tau ,\varsigma )}\mathrm {d}\varsigma } \mathrm {d}\tau } , \end{aligned}$$

where

$$\begin{aligned} g(x,y) = \frac{{322560{x^2} - 322349x + 161069y}}{{322560}}, \end{aligned}$$

with the exact solution \( f(x,y) = {x^2} - x + \frac{1}{2}y \).

In Tables 3 and 4, respectively, we report the exact and approximate solutions and also the absolute errors in the solutions for \( N=2,~M = 2,3 \) at some selected nodes. These tables state that using \( {{\hat{n}}} = {N^2}{M^2} = 36 \) numbers of bases, we obtain more accurate results than the 2D-SLPOM and 2D-BPFs methods reported by Hesameddini and Shahbazi (2018); Najafalizadeh and Ezzati (2016), respectively, that used \( {{\hat{n}}} = {(N+1)^2} = {129^2}=16641 \) 2D-SLPOM and \( {{\hat{n}}} = {m^2} = {128^2}=16384 \) 2D-BPFs to solve this problem. Figures 3 and 4 illustrate the accuracy and efficiency of the presented method.

Example 3

Consider the following two-dimensional nonlinear fractional Volterra integral equation studied by Jabari Sabeg et al. (2017) and Najafalizadeh and Ezzati (2016):

$$\begin{aligned} f(x,y)= & {} \sqrt{y} \left( { - \frac{1}{{180}}{ x^3}{ y^{\frac{7}{2}}} + \sqrt{\frac{x}{3}} } \right) \\&+ \frac{1}{{\varGamma \left( \frac{3}{2}\right) \varGamma \left( \frac{5}{2}\right) }}\int _0^ x {\int _0^ y {{{( x - \tau )}^{\frac{1}{2}}}{{(y - \varsigma )}^{\frac{3}{2}}}\sqrt{ x y\varsigma } {{f^2}( \tau ,\varsigma )}\mathrm {d}\varsigma } \mathrm {d} \tau } , \end{aligned}$$

with the exact solution \( f(x,y) = \frac{{\sqrt{3 x y} }}{3} \).

The exact and approximate solutions and also the absolute errors in the solutions, respectively, are reported in Tables 5 and 6 for \( N=2,~M = 3,4 \). These tables state that by using \( {{\hat{n}}} = {N^2}{M^2} = 64 \) numbers of bases, we obtain more accurate results than the 2D-TFs and 2D-BPFs methods reported by Jabari Sabeg et al. (2017) and Najafalizadeh and Ezzati (2016), respectively, that used \( {{\hat{n}}} = 4{m^2} =256 \) 2D-TFs and \( {{\hat{n}}} = {m^2} = {32^2}=1024 \) 2D-BPFs to solve this problem. Figures 5 and 6 illustrate the accuracy and efficiency of the presented method.

Fig. 5
figure 5

Plots of: a3 the exact solution, b3 the approximate solution, c3 the absolute error with \( N = 2 \) and \( M=4 \) for Example 3

Full size image
Fig. 6
figure 6

Plots of: d3 the comparison of the exact and approximate solutions, e3 the maximum absolute error with \( N = 2 \) and \( M=4 \) at \( y=0.3 \) for Example 3

Full size image

8 Conclusion

In the presented paper, sufficient conditions were provided for the local and global existence of solutions for 2D-NFVIEs and 2D-NFFIEs, based on the Schauder’s and Tychonoff’s fixed-point theorems. Also, sufficient conditions were provided for the uniqueness of the solutions. Moreover, operational matrices of 2D-HBPSLs via collocation method were applied to find approximate solutions for 2D-NFVIEs and 2D-NFFIEs. The obtained results introduced the presented method as a powerful mathematical tool for solving these fractional integral equations with lower numbers of bases than the other methods studied by Hesameddini and Shahbazi (2018); Jabari Sabeg et al. (2017); Najafalizadeh and Ezzati (2016).