1 Introduction

In recent years, to model and describe phenomena in various fields of science such as plasma physics, nonlinear optics, nonlinear transmission lines, solid state physics, chemical kinematics, and biology, to mention a few, we have generally used nonlinear equations. The popularity of these equations is because of their capacity to model many real systems. In fact, it has been discovered that many models in mathematics and physics are described by nonlinear partial differential equations. Accordingly, nonlinear equations have gained a very significant place in the current research. In this way, a challenging task is to look for solutions for these nonlinear equations. There has been an overwhelming progress in this line of research (Wang and Winful 1988; Matula 1979; Pelap and Faye 2005; Wazwaz 2006). The literature is replete with many methods for building exact solutions including the Exp-function method (Dehghan et al. 2011; Ekici et al. 2017; Manafian and Lakestani 2015c; Manafian 2015), the generalized Kudryashov method (Zhou et al. 2005), the extended Jacobi elliptic function expansion method (Ekici et al. 2017; Chen and Wang 2005; Zhou and Liu 2015; Mirzazadeh et al. 2016), the improve \(\tan (\phi /2)\)-expansion method (Manafian 2016a, b, 2017; Manafian and Lakestani 2015a, 2016a, b; Manafian et al. 2016a, b, c, d; Aghdaei and Manafian 2016; Zinati and Manafian 2017), the \(G'/G\)-expansion method (Manafian and Lakestani 2015b, 2017; Manafian et al. 2016c; Sindi and Manafian 2016; Sonmezoglu et al. 2017), the Bernoulli sub-equation function method (Baskonus and Bulut 2016a; Baskonus et al. 2016a; Bulut and Baskonus 2016), the sine-Gordon expansion method (Baskonus et al. 2016b; Baskonus and Bulut 2016b), the ansatz scheme (Zhou et al. 2016), the Ricatti equation expansion (Zhou 2016), the formal linearization method (Mirzazadeh and Eslami 2015), the extend \(\exp (-\Psi (\tau ))\)-expansion method (Taghizadeh et al. 2017; Mirzazadeh et al. 2017a), the Riccati method (Inc et al. 2016), and the Lie symmetry (Tchier et al. 2017). However, these methods can not satisfy all the existing nonlinear equations. For this reason, several new methods have to be explored. In this paper, building upon the improved Bernoulli sub-ODE method (Bulut and Baskonus 2016; Foroutan et al. 2017) and the extended trial equation method (Foroutan et al. 2017; Mohyud-Din and Irshad 2017; Mirzazadeha et al. 2017b), we derive many solutions which can help to understand the mechanism underlying different phenomena observed through a nonlinear transmission line described through the modified Zakharov–Kuznetsov (mZK) equation.

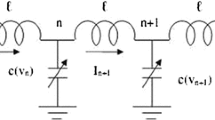
The model studied here is given by Fig. 1. Nonlinear electrical transmission lines (NETLs) (Tala-Tebue et al. 2014) are good examples to provide a useful way to check how the nonlinear excitations behave inside the nonlinear medium. They are constructed by periodically loading a normal transmission line with varactors or, alternatively, by arranging inductors and varactors in a 1-D lattice. The model used in this work consists of a nonlinear network with many coupled nonlinear LC dispersive transmission lines. We imagine that there are many identical dispersive lines which are coupled by means of capacitance \(C_s\) at each node, as shown in Fig. 1. Each section of line consists of a constant inductor L in the series branch and a nonlinear capacitor of capacitance \(C(V_{n,m})\) in the shunt branch. The nodes in the system are labeled with two discrete coordinates n and m, where n specifies the nodes in the direction of propagation of the wave, and m labels the lines in the transverse direction. The same model has been studied in Duan (2004). In his work, Duan derive a coupled Zakharov–Kuznetsov equation for a nonlinear transmission line and study the instability of this equation.

Fig. 1
figure 1

Schematic representation of the nonlinear electrical transmission line

Full size image

Applying the Kirchhoff law on the model, one can easily obtain the following discrete differential equation:

$$\begin{aligned} \frac{\partial ^2 Q_{n,m}}{\partial T^2}=\frac{1}{L}\left( V_{n+1,m}-V_{n,m}+V_{n-1,m}\right) +C_s\frac{\partial ^2 }{\partial T^2}\left( V_{n,m+1}-V_{n,m}+V_{n,m-1}\right) , \end{aligned}$$
(1.1)

where \(V_{n,m}=V_{n,m}(T)\) is the voltage in the transmission lines. The nonlinear charge in the shunt branch are voltage dependent and are given by

$$\begin{aligned} Q_{n,m}=C_0\left( V_{n,m}+\frac{\beta _1}{2}V_{n,m}^2 +\frac{\beta _2}{3}V_{n,m}^3\right) , \end{aligned}$$
(1.2)

where \(\beta _1\) and \(\beta _2\) are constants. Inserting (1.2) into Eq. (1.1), we obtain

$$\begin{aligned}&C_0\frac{\partial ^2 }{\partial T^2}\left( V_{n,m}+\frac{\beta _1}{2}V_{n,m}^2+\frac{\beta _2}{3}V_{n,m}^3\right) \nonumber \\&\quad = \frac{1}{L}\left( V_{n+1,m}-V_{n,m}+V_{n-1,m}\right) +C_s\frac{\partial ^2 }{\partial T^2}\left( V_{n,m+1}-V_{n,m}+V_{n,m-1}\right) . \end{aligned}$$
(1.3)

Setting \(V_{n,m}(T)=V(n,m,T)\), which means that n and m are treated as the continuous variables, we get the following equation

$$\begin{aligned} C_0\frac{\partial ^2 }{\partial T^2}\left( V+\frac{\beta _1}{2}V^2+\frac{\beta _2}{3}V^3\right) = \frac{1}{L}\frac{\partial ^2 }{\partial n^2}\left( V+\frac{1}{12}\frac{\partial ^2 V}{\partial n^2}\right) +C_s \frac{\partial ^2 }{\partial T^2\partial m^2}\left( V+\frac{1}{12}\frac{\partial ^2 V}{\partial m^2}\right) . \end{aligned}$$
(1.4)

Via the independent variable transformations

$$\begin{aligned} x=\chi ^{1/2}(n-v_sT),\quad y=\chi ^{1/2}m, \quad t=\chi ^{1/2}T, \quad V(n,m,T)=\chi u(x,y,t), \end{aligned}$$
(1.5)

where \(\chi\) is the formal parameter, \(v_s=1/(LC_0)\), and with the help of the reductive perturbation technique, then Eq. (1.4) can be reduced to the following modified mZK equation (Duan 2004; Sardar et al. 2015) as

$$\begin{aligned} u_t+Auu_x+Bu^2u_x+Mu_{xxx}+Nu_{xyy}=0, \end{aligned}$$
(1.6)

where

$$\begin{aligned} A=-\beta _1v_s, \quad B=-\beta _2v_s, \quad M=\frac{1}{24\beta _1Lv_s}, \quad N=\frac{\beta _1}{288L^2v_sC_0^2}. \end{aligned}$$
(1.7)

Therefore, u(x, y, t) represents the first-order perturbation voltage in the coupled nonlinear electrical transmission lines, and the subscripts x, y and t denote the partial derivatives. The modified ZK equation (Yu et al. 2007) has received a great among of attention. Zhen et al. (2014) have given different expressions of the parameters of the mZK equation and by means of the Hirota method, bilinear forms and soliton solutions of the this equation were obtained. In the same way, Sardar et al. (2015) applied the (\(G'/G\))-expansion method, extended tanh method and sine-cosine method to obtain different kinds of solutions which are solitary, shock, singular, periodic, rational and kink-shaped solitons. For further information in about the mZK equation see Krishnan and Biswas (2010), Naranmandula and Wang (2005), Nozaki and Bekki (1983) and Panthee and Scialom (2010). The rest of the paper is organized as follows: In Sect. 2, we offer the improved Bernoulli sub-ODE method and its application to mZK equation. Also, in Sect. 3, we present the extended trial equation method along and discuss its use for the mZK equation. Finally conclusion is given in Sect. 4.

2 The improved Bernoulli sub-ODE method

The IBSOM is well-known analytical method which was improved and developed by Baskonus and Bulut (2016a). We consider the following stages

Step 1 We suppose that given nonlinear partial differential equation for u(x, t) to be in the form

$$\begin{aligned} {\mathcal {N}}(u, u_x, u_y, u_t, u_{xx}, u_{tt},\ldots ) = 0, \end{aligned}$$
(2.1)

which can be converted to an ODE

$$\begin{aligned} {\mathcal {Q}}(U, r_1U', r_2U', -r_3U', r_1^2U'', r_3^2U'',\ldots )=0, \end{aligned}$$
(2.2)

by the transformation \(\xi =r_1x+r_2y-r_3t\) is the wave variable. Also, \(r_1, r_2\) and \(r_3\) are constants to be determined later.

Step 2 Considering trial equation of solution in Eq. (2.2), it can be written as follows:

$$\begin{aligned} U(\xi )=\frac{\sum _{k=0}^{n}a_kF^k(\xi )}{\sum _{k=0}^{m}a_kF^k(\xi )} =\frac{a_0+a_1F(\xi )+a_2F^2(\xi )+\cdots +a_nF^n(\xi )}{b_0+b_1F(\xi )+b_2F^2(\xi )+\cdots +b_mF^m(\xi )}, \end{aligned}$$
(2.3)

and according to the Bernoulli theory,

$$\begin{aligned} F'(\xi )=bF(\xi )+dF^\theta (\xi ), \quad b\ne 0, \quad d\ne 0, \quad \theta \in {\mathbb {R}}-\{0,1,2\}, \end{aligned}$$
(2.4)

where \(F(\xi )\) is Bernoulli differential polynomial. Substituting the above relations in Eq. (2.2), we have an equation of polynomial \(\Psi (F(\xi ))\) of \(F(\xi )\):

$$\begin{aligned} \Psi (F(\xi ))=\rho _sF^s(\xi )+\cdots \rho _1F(\xi )+\rho _0=0. \end{aligned}$$
(2.5)

According to the homogenous balance method, we can obtain the relationship between n, m, and \(\theta\).

Step 3 Let the coefficients of \(\Psi (F(\xi ))\) all be zero. Then it yields an equation system as follows:

$$\begin{aligned} \rho _k=0, \quad k=0,1,\ldots ,s. \end{aligned}$$
(2.6)

Solving this system, we will determine the values of \(a_0, a_n\) and \(b_0, b_m\).

Step 4 By solving nonlinear Bernoulli differential equation (2.4), we obtain two cases according to b and d situations as follows:

$$\begin{aligned} F(\xi )= \left[ \frac{-d}{b}+\frac{E}{e^{b(\theta -1)\xi }}\right] ^{\frac{1}{\theta -1}}, \quad b\ne d,\end{aligned}$$
(2.7)
$$\begin{aligned} F(\xi )= & {} \left[ \frac{E-1+(E+1)\tanh \left( \frac{b(1-\theta )\xi }{2}\right) }{1-\tanh \left( \frac{b(1-\theta )\xi }{2}\right) }\right] ^{\frac{1}{\theta -1}}, \quad b=d, \quad E\in {\mathbb {R}}, \end{aligned}$$
(2.8)

where E is both the constant of integration and non-zero. Using a complete discrimination system for polynomial of \(F(\xi )\), we solve Eq. (2.6) with the help of Maple 13 and classify the exact solutions for Eq. (2.2). For a better interpretations of solutions obtained in this way, we can plot two- and three-dimensional surfaces of the solutions by taking suitable parameters.

2.1 Implementations of IBSOM

This illustrates the performance of the analytical algorithm proposed. To this end, we use the transformation \(u(x,y,t)=u(\xi )\) and \(\xi =r_1x+r_2y-r_3t\) to reduce Eq. (1.1) to the following nonlinear ODE:

$$\begin{aligned} -r_3u+Ar_1\frac{u^2}{2}+Br_1\frac{u^3}{3}+(Mr_1^3+Nr_1r_2^2)u''=0. \end{aligned}$$
(2.9)

Considering the Eqs. (2.3) and (2.4) for the homogenous balance method between \(u^3\) and \(u''\), we obtain the following relationship for m, n, and \(\theta\):

$$\begin{aligned} \theta +m=n+1. \end{aligned}$$
(2.10)

For different values of \(\theta , m,\) and n, we have the following cases:

Case I \(\theta =n=3, m=1\).

If we take \(\theta =n=3\) and \(m=1\) for Eq. (2.9), then we obtain

$$\begin{aligned} U(\xi )= & \frac{a_0+a_1F(\xi )+a_2F^2(\xi )+a_3F^3(\xi )}{b_0+b_1F(\xi )}=\frac{\Theta _1(\xi )}{\Phi _1(\xi )},\end{aligned}$$
(2.11)
$$\begin{aligned} U'(\xi )= & \frac{\Theta _1'(\xi )\Phi _1(\xi )-\Theta _1(\xi ) \Phi _1'(\xi )}{\Phi _1^2(\xi )},\end{aligned}$$
(2.12)
$$\begin{aligned} U''(\xi )= & {} \frac{\Theta _1''(\xi )\Phi _1(\xi )-\Theta _1(\xi )\Phi _1'(\xi )}{\Phi _1^2(\xi )}- \frac{[\Theta _1(\xi )\Phi _1'(\xi )]'\Phi _1^2(\xi )-2\Theta _1(\xi ) [\Phi _1'(\xi )]^2\Phi _1(\xi )}{\Phi _1^4(\xi )}, \end{aligned}$$
(2.13)

where \(F'=bF + dF^3\), \(b\ne 0\), \(d\ne 0\), \(a_3\ne 0\) and \(b_1\ne 0\). When we use Eqs. (2.11) and (2.13) in Eq. (2.9), we get a system of algebraic equations. Therefore, we attain a system of equations from the coefficients of polynomial of F. This system of equations is solved for the above parameters with the following cases of solutions:

Subcase I

$$\begin{aligned} b= & {} b, \,\,d =\frac{ba_3B}{Ab_1}, \,\,b_0=a_0=a_1=a_2=0, \,\,a_3 =a_3, \,\, b_1=b_1, \,\,r_1=\pm \frac{\sqrt{-6BM(24Nr_2^2b^2B+A^2)}}{12BMb}, \nonumber \\ r_2= & {} r_2, \,\,r_3=-\frac{A^2r_1}{6B}. \end{aligned}$$
(2.14)

Subcase II

$$\begin{aligned} b= & {} -\frac{A\sqrt{-6(Mr_1^2+Nr_2^2)B}}{2}, \,\,d =\frac{a_3\sqrt{-6(Mr_1^2+Nr_2^2)B}}{12b_1(Mr_1^2+Nr_2^2)}, \,\,a_0=a_1=0, \,\,a_2=a_2, \,\,a_3=a_3, \,\, \nonumber \\ b_0= & {} \frac{a_2b_1}{a_3},\,\,b_1=b_1, \,\,r_1 =r_1, \,\,r_2=r_2, \,\,r_3=-\frac{A^2r_1}{6B}. \end{aligned}$$
(2.15)

Subcase III

$$\begin{aligned} b= & {} \frac{Adb_1}{Ba_3}, \,\,d =d, \,\,a_0=-\frac{Aa_2b_1}{a_3B}, \,\,a_1 =-\frac{Ab_1}{B}, \,\,a_2=a_2, \,\,a_3=a_3, \,\, \nonumber \\ b_0= & {} \frac{a_2b_1}{a_3}, \,\,b_1=b_1, \,\, r_1=\pm \frac{\sqrt{-6BM(24Nr_2^2d^2b_1^2+Ba_3^2)}}{12Mb_1d}, \,\,r_2=r_2, \,\,r_3=-\frac{A^2r_1}{6B}. \end{aligned}$$
(2.16)

For Subcase I, we have the following solution

$$\begin{aligned} U(\xi )=\frac{a_3}{b_1}F(\xi ). \end{aligned}$$
(2.17)

For Subcase II, we have the following solution

$$\begin{aligned} U(\xi )=\frac{a_2F^2(\xi )+a_3F^3(\xi )}{\frac{a_2b_1}{a_3}+b_1F(\xi )}=\frac{a_3}{b_1}F^2(\xi ). \end{aligned}$$
(2.18)

For Subcase III, we have the following solution

$$\begin{aligned} U(\xi )=\frac{-\frac{Aa_2b_1}{a_3B}-\frac{Ab_1}{B}F(\xi )+a_2F^2(\xi )+a_3F^3(\xi )}{b_0+\frac{a_2b_1}{a_3}F(\xi )}. \end{aligned}$$
(2.19)

Result 1 If we take (2.7) and (2.8), then we have the following solutions based on (2.14) and (2.17) as:

$$\begin{aligned} u_1(x,y,t)= & {} \frac{a_3}{b_1}\left[ -\frac{a_3B}{Ab_1} +\frac{E}{e^{2b\left( \pm \frac{\sqrt{-6BM(24Nr_2^2b^2B+A^2)}}{12BMb}x+r_2y\mp \frac{A^2\sqrt{-6BM(24Nr_2^2b^2B+A^2)}}{72B^2Mb}t\right) }}\right] ^{\frac{1}{2}}, \quad \end{aligned}$$
(2.20)
$$\begin{aligned} u_2(x,y,t)= & {} \frac{A}{B}\left[ \frac{E-1-(E+1)\tanh \left( \pm \frac{\sqrt{-6BM(24Nr_2^2b^2B+A^2)}}{12BM}x+br_2y\mp \frac{A^2\sqrt{-6BM(24Nr_2^2b^2B+A^2)}}{72B^2M}t\right) }{1+\tanh \left( \pm \frac{\sqrt{-6BM(24Nr_2^2b^2B+A^2)}}{12BM}x+br_2y\mp \frac{A^2\sqrt{-6BM(24Nr_2^2b^2B+A^2)}}{72B^2M}t\right) }\right] ^{\frac{1}{2}} . \end{aligned}$$
(2.21)

Result 2 If we take (2.7) and (2.8), then we have the following solutions based on (2.15) and (2.18) as:

$$\begin{aligned} u_3(x,y,t)= & {} \frac{a_3}{b_1}\left[ \frac{a_3}{12Ab_1(Mr_1^2+Nr_2^2)}+ \frac{E}{e^{2b\left( r_1x+r_2y-\frac{r_1A^2}{6B}t\right) }}\right] ,\end{aligned}$$
(2.22)
$$\begin{aligned} u_4(x,y,t)= & {} -6(Mr_1^2+Nr_2^2)\left[ \frac{E-1-(E+1)\tanh \left( r_1x+r_2y-\frac{r_1A^2}{6B}t\right) }{1+\tanh \left( r_1x+r_2y-\frac{r_1A^2}{6B}t\right) }\right] . \end{aligned}$$
(2.23)

Result 3 If we take (2.7) and (2.8), then we have the following solutions based on (2.16) and (2.19) as:

$$\begin{aligned} u_5(\xi )=\frac{-\frac{Aa_2b_1}{a_3B}-\frac{Ab_1}{B}F(\xi )+a_2F^2(\xi )+a_3F^3(\xi )}{b_0+\frac{a_2b_1}{a_3}F(\xi )}, \end{aligned}$$
(2.24)

where

$$\begin{aligned} F(x,y,t)= & {} \left[ -\frac{Ba_3}{Ab_1}+\frac{E}{e^{2b \left( \pm \frac{\sqrt{-6BM(24Nr_2^2d^2b_1^2+Ba_3^2)}}{12Mb_1d}x +r_2y\mp \frac{A^2\sqrt{-6BM(24Nr_2^2d^2b_1^2+Ba_3^2)}}{72BMb_1d}t\right) }}\right] ^{\frac{1}{2}},\nonumber \\ u_6(\xi )= & {} \frac{-a_2-a_3F(\xi )+a_2F^2(\xi )+a_3F^3(\xi )}{b_0+\frac{a_2B}{A}F(\xi )}, \end{aligned}$$
(2.25)

where

$$\begin{aligned} F(x,y,t)=\left[ \frac{E-1-(E+1)\tanh \left( \pm \frac{\sqrt{-6BM(24Nr_2^2d^2b_1^2+Ba_3^2)}}{12Mb_1}x+br_2y\mp \frac{A^2\sqrt{-6BM(24Nr_2^2d^2b_1^2+Ba_3^2)}}{72BMb_1}t\right) }{1+\tanh \left( \pm \frac{\sqrt{-6BM(24Nr_2^2d^2b_1^2+Ba_3^2)}}{12Mb_1}x+br_2y \mp \frac{A^2\sqrt{-6BM(24Nr_2^2d^2b_1^2+Ba_3^2)}}{72BMb_1}t\right) }\right] ^{\frac{1}{2}}. \end{aligned}$$

Case II \(\theta =3, n=2\), and \(m=0\).

If we take \(\theta =3, n=2,\) and \(m=0\) for Eq. (2.9), then we obtain

$$\begin{aligned} U(\xi )= & {} \frac{a_0+a_1F(\xi )+a_2F^2(\xi )}{b_0}=\frac{\Theta _2(\xi )}{\Phi _2(\xi )},\end{aligned}$$
(2.26)
$$\begin{aligned} U'(\xi )= & {} \frac{\Theta _2'(\xi )\Phi _2(\xi )-\Theta _2(\xi )\Phi _2'(\xi )}{\Phi _2^2(\xi )},\end{aligned}$$
(2.27)
$$\begin{aligned} U''(\xi )= & {} \frac{\Theta _2''(\xi )\Phi _2(\xi )-\Theta _2(\xi )\Phi _2'(\xi )}{\Phi _2^2(\xi )}- \frac{[\Theta _2(\xi )\Phi _2'(\xi )]'\Phi _2^2(\xi )-2\Theta _2(\xi ) [\Phi _2'(\xi )]^2\Phi _2(\xi )}{\Phi _2^4(\xi )}, \end{aligned}$$
(2.28)

where \(F'=bF + dF^3\), \(b\ne 0\), \(d\ne 0\), \(a_2\ne 0\) and \(b_0\ne 0\). When we use Eqs. (2.26) and (2.28) in Eq. (2.9), we get a system of algebraic equations. Therefore, we attain a system of equations from the coefficients of polynomial of F. This system of equations is solved for the above parameters with the following cases of solutions as:

Subcase I

$$\begin{aligned} b= & {} \frac{A}{\sqrt{-24B(Mr_1^2+Nr_2^2)}}, \,\,d =d, \,\,a_0=a_1=0, \,\,a_2=-\frac{24b_0d(Mr_1^2+Nr_2^2)}{\sqrt{-24B(Mr_1^2+Nr_2^2)}}, \,\, b_0=b_0, \nonumber \\ r_1= & {} r_1, \,\,r_2=r_2, \,\,r_3=-\frac{A^2r_1}{6B}. \end{aligned}$$
(2.29)

Subcase II

$$\begin{aligned} b= & {} -\frac{Adb_0}{Ba_2}, \quad d =d, \quad a_0=-\frac{A}{B}b_0, \quad a_1=0, \quad a_2=a_2, \quad b_0=b_0, \quad \nonumber \\ r_1= & {} \frac{1}{b_0d}\sqrt{-\frac{24b_0^2r_2^2d^2N+Ba_2^2}{24M}}, \,\,r_2=r_2, \,\,r_3=-\frac{A^2r_1}{6B}. \end{aligned}$$
(2.30)

For Subcase I, we have the following solution

$$\begin{aligned} U(\xi )=\frac{a_2}{b_0}F^2(\xi ). \end{aligned}$$
(2.31)

For Subcase II, we have the following solution

$$\begin{aligned} U(\xi )=\frac{a_0+a_2F^2(\xi )}{b_0}. \end{aligned}$$
(2.32)

Result 1 If we take (2.7) and (2.8), then we have the following solutions based on (2.29) and (2.31) as:

$$\begin{aligned} u_1(x,y,t)=-\frac{24d(Mr_1^2+Nr_2^2)}{\sqrt{-24B(Mr_1^2+Nr_2^2)}} \left[ -\frac{d\sqrt{-24B(Mr_1^2+Nr_2^2)}}{A}+\frac{E}{e^{2b \left( r_1x+r_2y-\frac{A^2r_1}{6B}t\right) }}\right] . \quad \end{aligned}$$
(2.33)

Result 2 If we take (2.7) and (2.8), then we have the following solutions based on (2.30) and (2.32) as:

$$\begin{aligned} u_2(x,y,t)= & {} -\frac{A}{B}+\frac{a_2}{b_0}\left[ \frac{Ba_2}{Ab_0}+ \frac{E}{e^{2b\left( \frac{1}{b_0d}\sqrt{-\frac{24b_0^2r_2^2d^2N+Ba_2^2}{24M}}x+r_2y-\frac{A^2}{6Bb_0d}\sqrt{-\frac{24b_0^2r_2^2d^2N+Ba_2^2}{24M}}t\right) }}\right] ,\end{aligned}$$
(2.34)
$$\begin{aligned} u_3(x,y,t)= & {} -\frac{A}{B}\left[ 1+\frac{E-1-(E+1)\tanh \left( \frac{1}{b_0d}\sqrt{-\frac{24b_0^2r_2^2d^2N+Ba_2^2}{24M}}x+r_2y-\frac{A^2}{6Bb_0d}\sqrt{-\frac{24b_0^2r_2^2d^2N+Ba_2^2}{24M}}t\right) }{1+\tanh \left( \frac{1}{b_0d}\sqrt{-\frac{24b_0^2r_2^2d^2N+Ba_2^2}{24M}}x+r_2y-\frac{A^2}{6Bb_0d}\sqrt{-\frac{24b_0^2r_2^2d^2N+Ba_2^2}{24M}}t\right) }\right] . \end{aligned}$$
(2.35)

3 Extended trial equation method

The second method described here is the extended trial equation method used to find traveling wave solutions of nonlinear models which can be understood through the following steps:

Step 1 We assume that the given nonlinear PDE

$$\begin{aligned} {\mathcal {N}}(u, u_x, u_y, u_z, u_t, u_{xx}, u_{tt},\ldots )=0. \end{aligned}$$
(3.1)

Utilizing the wave transformation

$$\begin{aligned} u(x_1,x_2,\ldots ,x_N,t)=u(\eta ), \quad \eta =\lambda \left( \sum _{j=1}^{N}x_j-ct \right) , \end{aligned}$$
(3.2)

where \(\lambda \ne 0\) and \(c\ne 0\). Substituting (3.2) into Eq. (3.1) yields a nonlinear ordinary differential equation,

$$\begin{aligned} {\mathcal {Q}}(u, \lambda u', \lambda u', \lambda u', -c\lambda u',\lambda ^2u'',\ldots )=0. \end{aligned}$$
(3.3)

Step 2 Take the transformation and trial equation as follows:

$$\begin{aligned} u(\eta )=\sum _{i=0}^{\delta }\tau _i\Gamma ^i, \end{aligned}$$
(3.4)

where

$$\begin{aligned} (\Gamma ')^2=\Omega (\Gamma )=\frac{\Phi (\Gamma )}{\Psi (\Gamma )} =\frac{\xi _\theta \Gamma ^\theta +\cdots +\xi _1\Gamma +\xi _0}{\zeta _\epsilon \Gamma ^\epsilon +\cdots +\zeta _1\Gamma +\zeta _0}. \end{aligned}$$
(3.5)

Using the Eqs. (3.4) and (3.5), we can find

$$\begin{aligned} (u')^2= & {} \frac{\Phi (\Gamma )}{\Psi (\Gamma )}\left( \sum _{i=0}^{\delta }i\tau _i\Gamma ^{i-1}\right) ^2, \end{aligned}$$
(3.6)
$$\begin{aligned} u''= & {} \frac{\Phi '(\Gamma )\Psi (\Gamma )-\Phi (\Gamma )\Psi '(\Gamma )}{2\Psi ^2(\Gamma )} \left( \sum _{i=0}^{\delta }i\tau _i\Gamma ^{i-1}\right) + \frac{\Phi (\Gamma )}{\Psi (\Gamma )}\left( \sum _{i=0}^{\delta }i(i-1)\tau _i\Gamma ^{i-2} \right) , \end{aligned}$$
(3.7)

where \(\Phi (\Gamma )\) and \(\Psi (\Gamma )\) are polynomials. Substituting these terms into Eq. (3.1) yields an equation of polynomial \(\Lambda (\Gamma )\) of \(\Gamma\):

$$\begin{aligned} \Lambda (\Gamma )=\varrho _s\Gamma ^s+\cdots +\varrho _1\Gamma +\varrho _0=0, \end{aligned}$$
(3.8)

According to the balance principle on (3.8), we can arrive at a relation of \(\theta , \epsilon\) and \(\delta\). We can take some values of \(\theta , \epsilon\) and \(\delta\).

Step 3 Setting each coefficient of polynomial \(\Lambda (\Gamma )\) to zero to derive a system of algebraic equations:

$$\begin{aligned} \varrho _i=0, \quad i=1,2,\ldots ,s. \end{aligned}$$
(3.9)

By solving the system (3.9), we will obtain the values of \(\xi _0,\xi _1,\ldots ,\xi _\theta\), \(\zeta _0,\zeta _1,\ldots ,\zeta _\sigma\) and \(\tau _0,\tau _1,\ldots ,\tau _\delta\).

Step 4In the following step, we obtain the elementary form of the integral by reduction of Eq. (3.5), as follows

$$\begin{aligned} \pm (\eta -\eta _0)=\int \frac{d\Gamma }{\sqrt{\Omega (\Gamma )}}=\int \sqrt{\frac{\Psi (\Gamma )}{\Phi (\Gamma )}}d\Gamma , \end{aligned}$$
(3.10)

where \(\eta _0\) is an arbitrary constant. We can classify the roots of \(\Phi (\Gamma )\) with the help of complete discrimination system for polynomials. Furthermore, we can write the exact traveling wave solutions to Eq. (3.1) respectively.

3.1 Implementations of ETEM

By processing manipulations on Eq. (1.1) and reducing to ODE by help the transformations \(u(x,y,t)=u(\eta )\) and \(\eta =r_1x+r_2y-r_3t\) get to the following nonlinear ODE:

$$\begin{aligned} -r_3u+Ar_1\frac{u^2}{2}+Br_1\frac{u^3}{3}+(Mr_1^3+Nr_1r_2^2)u''=0. \end{aligned}$$
(3.11)

Multiplying \(u'\) in (3.11) and integrating it we get the following equation

$$\begin{aligned} -\frac{1}{2}r_3u^2+\frac{1}{6}Ar_1u^3+\frac{1}{12}Br_1u^4+\frac{1}{2} (Mr_1^3+Nr_1r_2^2)u'^2=0. \end{aligned}$$
(3.12)

Substituting Eq. (3.7) in Eq. (3.12) and using the balance principle technique, between \(u^3\) and \(u''\), we obtain the following relationship for \(\delta , \theta\), and \(\epsilon\):

$$\begin{aligned} 2\delta =\theta -\epsilon -2. \end{aligned}$$
(3.13)

For different values of \(\delta , \theta\) and \(\epsilon\), we have the following cases:

Case I \(\delta =1, \theta =4, \epsilon =0\).

If we take \(\delta =1, \theta =4\), \(\epsilon =0\) for Eq. (2.9), then we obtain

$$\begin{aligned} u(\eta )= & {} \tau _0+\tau _1\Gamma ,\end{aligned}$$
(3.14)
$$\begin{aligned} (u'(\eta ))^2= & {} \frac{\tau _1^2(\xi _4\Gamma ^4+\xi _3\Gamma ^3 +\xi _2\Gamma ^2+\xi _1\Gamma +\xi _0)}{\zeta _0}, \end{aligned}$$
(3.15)

where \(\xi _4\ne 0\) and \(\zeta _0\ne 0\). Solving the system of (3.9) yields

$$\begin{aligned} r_1= & {} r_1, \quad r_2=r_2, \quad r_3=r_3, \quad \tau _0=\tau _0, \quad \tau _1=\tau _1, \quad \xi _0=\frac{\xi _4\tau _0^2(-6r_3+2Ar_1\tau _0+Br_1\tau _0^2)}{r_1\tau _1^4B},\nonumber \\ \xi _1= & {} \frac{2\xi _4\tau _0(-6r_3+2Br_1\tau _0^2+3Ar_1\tau _0)}{r_1\tau _1^3B}, \quad \xi _2=\frac{6\xi _4(-r_3+Ar_1\tau _0+Br_1\tau _0^2)}{\tau _1^2Br_1}, \quad \xi _3=\frac{2\xi _4(A+2\tau _0B)}{B\tau _1}, \quad \nonumber \\ \xi _4= & {} \xi _4, \quad \zeta _0=-\frac{6\xi _4(Mr_1^2+Nr_2^2)}{\tau _1^2B}. \end{aligned}$$
(3.16)

Substituting these results into Eqs. (3.5) and (3.10), we get

$$\begin{aligned} \pm (\eta -\eta _0)=\int \frac{\sqrt{-\frac{6\xi _4(Mr_1^2+Nr_2^2)}{\xi _4\tau _1^2B}}d\Gamma }{\sqrt{\Gamma ^4+\frac{2\xi _4(A+2\tau _0B)}{\xi _4B\tau _1}\Gamma ^3+ \frac{6\xi _4(-r_3+Ar_1\tau _0+Br_1\tau _0^2)}{\xi _4\tau _1^2Br_1}\Gamma ^2+ \frac{2\xi _4\tau _0(-6r_3+2Br_1\tau _0^2+3Ar_1\tau _0)}{\xi _4r_1\tau _1^3B}\Gamma + \frac{\xi _4\tau _0^2(-6r_3+2Ar_1\tau _0+Br_1\tau _0^2)}{\xi _4r_1\tau _1^4B}}}. \end{aligned}$$
(3.17)

Integrating Eq. (3.17), we obtain the solutions for Eq. (1.1) as follows:

$$\begin{aligned} \pm (\eta -\eta _0)= & {} -\frac{\Pi }{\Gamma -\alpha _1},\end{aligned}$$
(3.18)
$$\begin{aligned} \pm (\eta -\eta _0)= & {} \frac{2\Pi }{\alpha _1-\alpha _2}\sqrt{\frac{\Gamma -\alpha _2}{\Gamma -\alpha _1}}, \,\,\,\alpha _2>\alpha _1,\end{aligned}$$
(3.19)
$$\begin{aligned} \pm (\eta -\eta _0)= & {} \frac{\Pi }{\alpha _1-\alpha _2}\ln \left| \frac{\Gamma -\alpha _1}{\Gamma -\alpha _2}\right| , \end{aligned}$$
(3.20)
$$\begin{aligned} \pm (\eta -\eta _0)= & {} \frac{\Pi }{\sqrt{(\alpha _1-\alpha _2)(\alpha _1-\alpha _3)}} \ln \left| \frac{\sqrt{(\alpha _1-\alpha _3)(\Gamma -\alpha _2)}- \sqrt{(\alpha _1-\alpha _2)(\Gamma -\alpha _3)}}{\sqrt{(\alpha _1-\alpha _3) (\Gamma -\alpha _2)}+ \sqrt{(\alpha _1-\alpha _2)(\Gamma -\alpha _3)}}\right| , \end{aligned}$$
(3.21)
$$\begin{aligned} \pm (\eta -\eta _0)= & {} \frac{2\Pi }{\sqrt{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)}} F(\varphi ,l), \,\,\,\alpha _1>\alpha _2>\alpha _3>\alpha _4, \end{aligned}$$
(3.22)

where

$$\begin{aligned} \Pi =\sqrt{-\frac{6\xi _4(Mr_1^2+Nr_2^2)}{\xi _4\tau _1^2B}}, \,\,\, F(\varphi ,l)=\int _{0}^{\varphi }\frac{d\psi }{\sqrt{1-l^2\sin ^2\psi }}, \end{aligned}$$
(3.23)

and

$$\begin{aligned} \varphi =\arcsin \sqrt{\frac{(\alpha _2-\alpha _4)(\Gamma -\alpha _1)}{(\alpha _1-\alpha _4)(\Gamma -\alpha _2)}}, \quad l^2=\frac{(\alpha _2-\alpha _3)(\alpha _1-\alpha _4)}{(\alpha _1-\alpha _3) (\alpha _2-\alpha _4)}. \end{aligned}$$
(3.24)

Also \(\alpha _1,\alpha _2,\alpha _3\) and \(\alpha _4\) are the roots of the polynomial equation

$$\begin{aligned} \Gamma ^4+\frac{\xi _3}{\xi _4}\Gamma ^3+\frac{\xi _2}{\xi _4}\Gamma ^2 +\frac{\xi _1}{\xi _4}\Gamma +\frac{\xi _0}{\xi _4}=0. \end{aligned}$$
(3.25)

Substituting the solutions (3.18)–(3.23) into (3.4), we obtain the following traveling wave solutions for Eq. (1.1):

$$\begin{aligned} u_1(x,y,t)= & {} \tau _0+\tau _1\alpha _1-\frac{\Pi }{r_1x+r_2y-r_3t-\eta _0},\end{aligned}$$
(3.26)
$$\begin{aligned} u_2(x,y,t)= & {} \tau _0+\tau _1\alpha _1+\frac{4(\alpha _2-\alpha _1)\tau _1\Pi ^2}{4\Pi ^2-(\alpha _1-\alpha _2)^2(r_1x+r_2y-r_3t-\eta _0)^2},\end{aligned}$$
(3.27)
$$\begin{aligned} u_3(x,y,t)= & {} \tau _0+\tau _1\alpha _2\pm \frac{(\alpha _2-\alpha _1)\tau _1}{\exp \left[ \frac{\alpha _1-\alpha _2}{\Pi }\left( r_1x+r_2y-r_3t-\eta _0\right) \right] -1},\end{aligned}$$
(3.28)
$$\begin{aligned} u_4(x,y,t)= & {} \tau _0+\tau _1\alpha _1-\frac{2(\alpha _1-\alpha _2)(\alpha _1-\alpha _3)\tau _1}{2\alpha _1-\alpha _2-\alpha _3+(\alpha _3-\alpha _2)\cosh \left[ \frac{\sqrt{(\alpha _1-\alpha _2)(\alpha _1-\alpha _3)}}{\Pi } \left( r_1x+r_2y-r_3t-\eta _0\right) \right] },\end{aligned}$$
(3.29)
$$\begin{aligned} u_5(x,y,t)= & {} \tau _0+\tau _1\alpha _2+\frac{2(\alpha _1-\alpha _2) (\alpha _4-\alpha _2)\tau _1}{\alpha _4-\alpha _2+(\alpha _1-\alpha _4)sn^2 \left[ \mp \frac{\sqrt{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)}}{2\Pi } \left( r_1x+r_2y-r_3t-\eta _0\right) ,\frac{(\alpha _2-\alpha _3) (\alpha _1-\alpha _4)}{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)}\right] }, \end{aligned}$$
(3.30)

If we take \(\tau _0=-\tau _1\alpha _1\) and \(\eta _0=0\), then the solutions (3.26)–(3.30) can reduce to rational function solutions

$$\begin{aligned} u_6(x,y,t)= & {} -\frac{\Pi }{r_1x+r_2y-r_3t},\end{aligned}$$
(3.31)
$$\begin{aligned} u_7(x,y,t)= & {} \frac{4(\alpha _2-\alpha _1)\tau _1\Pi ^2}{4\Pi ^2-(\alpha _1-\alpha _2)^2(r_1x+r_2y-r_3t)^2}, \end{aligned}$$
(3.32)

traveling wave solutions

$$\begin{aligned} u_8(x,y,t)=\frac{(\alpha _2-\alpha _1)\tau _1}{2}\left\{ 1\mp \coth \left[ \frac{\alpha _1-\alpha _2}{2\Pi }(r_1x+r_2y-r_3t) \right] \right\} , \end{aligned}$$
(3.33)

soliton solution

$$\begin{aligned} u_9(x,y,t)=-\frac{2(\alpha _1-\alpha _2)(\alpha _1-\alpha _3)\tau _1}{2\alpha _1-\alpha _2-\alpha _3+(\alpha _3-\alpha _2)\cosh \left[ \frac{\sqrt{(\alpha _1-\alpha _2)(\alpha _1-\alpha _3)}}{\Pi } (r_1x+r_2y-r_3t)\right] }, \end{aligned}$$
(3.34)

where \(\Pi _1=2(\alpha _1-\alpha _2)(\alpha _1-\alpha _3)\tau _1\) is the amplitude of the soliton, while \(v=r_3\) is the velocity and \(\Pi _2=\frac{\sqrt{(\alpha _1-\alpha _2)(\alpha _1-\alpha _3)}}{\Pi }\) is the inverse width of the soliton. On the other hand, if we take \(\tau _0=-\tau _1\alpha _2\) and \(\eta _0=0\), the Jacobi elliptic function solution (3.30) can be written in the form

$$\begin{aligned} u_{10}(x,y,t)=\frac{2(\alpha _1-\alpha _2)(\alpha _4-\alpha _2)\tau _1}{\alpha _4-\alpha _2+(\alpha _1-\alpha _4)sn^2 \left[ \mp \frac{\sqrt{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)}}{2\Pi } \left( r_1x+r_2y-r_3t\right) , \frac{(\alpha _2-\alpha _3)(\alpha _1-\alpha _4)}{(\alpha _1-\alpha _3) (\alpha _2-\alpha _4)}\right] }. \end{aligned}$$
(3.35)

If the modulus \(l\rightarrow 1\), then the solution (3.35) can be reduced to the solitary wave solution

$$\begin{aligned} u_{10_1}(x,y,t)=\frac{2(\alpha _1-\alpha _2)(\alpha _4-\alpha _2)\tau _1}{\alpha _4-\alpha _2+(\alpha _1-\alpha _4)\tanh ^2\left[ \mp \frac{\sqrt{(\alpha _1-\alpha _4) (\alpha _2-\alpha _4)}}{2\Pi } (r_1x+r_2y-r_3t)\right] }, \end{aligned}$$
(3.36)

where \(\alpha _3=\alpha _4\). If the modulus \(l\rightarrow 0\), then the solution (3.35) can be reduced to the solitary wave solution

$$\begin{aligned} u_{10_2}(x,y,t)=\frac{2(\alpha _1-\alpha _3)(\alpha _4-\alpha _3)\tau _1}{\alpha _4-\alpha _3+(\alpha _1-\alpha _4)\sin ^2\left[ \mp \frac{\sqrt{(\alpha _1-\alpha _3)(\alpha _3-\alpha _4)}}{2\Pi } (r_1x+r_2y-r_3t)\right] }, \end{aligned}$$
(3.37)

where \(\alpha _2=\alpha _3\).

Case II \(\delta =1, \theta =5, \epsilon =1\).

If we take \(\delta =1, \theta =5\), and \(\epsilon =1\) for Eq. (2.9), then we obtain

$$\begin{aligned} u(\eta )= & {} \tau _0+\tau _1\Gamma ,\end{aligned}$$
(3.38)
$$\begin{aligned} (u'(\eta ))^2= & {} \frac{\tau _1^2(\xi _5\Gamma ^5+\xi _4\Gamma ^4+\xi _3\Gamma ^3+\xi _2\Gamma ^2+\xi _1\Gamma +\xi _0)}{\zeta _0+\zeta _1\Gamma }, \end{aligned}$$
(3.39)

where \(\xi _5\ne 0\) and \(\zeta _1\ne 0\). Solving the system of (3.9) yields

$$\begin{aligned} r_1= & {} r_1, \quad r_2=r_2, \quad r_3=r_3, \quad \tau _0=\tau _0, \quad \tau _1=\tau _1, \quad \xi _4=\xi _4, \quad \xi _5=\xi _5,\nonumber \\ \xi _0= & {} -\frac{\tau _0^2(B^2r_1(4\tau _0^3\xi _5-\tau _0^2\xi _4\tau _1)+4A^2r_1\tau _0\xi _5+2ABr_1(5\tau _0^2\xi _5- \tau _0\xi _4\tau _1)-12r_3A\xi _5+6r_3B(\xi _4\tau _1-4\tau _0\xi _5))}{r_1\tau _1^5B^2},\nonumber \\ \xi _1= & {} -\frac{\tau _0(6ABr_1(5\tau _0^2\xi _5-\tau _0\xi _4\tau _1)+B^2r_1(15\tau _0^3\xi _5-4\tau _0^2\xi _4\tau _1)+ 12A^2r_1\tau _0\xi _5+6r_3Br_3(2\xi _4\tau _1-7\tau _0\xi _5)-24r_3A\xi _5)}{r_1\tau _1^4B^2},\nonumber \\ \xi _2= & {} -\frac{2(B^2r_1(10\tau _0^3\xi _5-3\tau _0^2\xi _4\tau _1)+6A^2r_1\tau _0\xi _5+ 3ABr_1(5\tau _0^2\xi _5-\tau _0\xi _4\tau _1)+3r_3B(\xi _4\tau _1-2\tau _0\xi _5) -6r_3A\xi _5)}{r_1\tau _1^3B^2},\nonumber \\ \xi _3= & {} -\frac{2(5\xi _5Ar_1\tau _0B+ 5\xi _5B^2r_1\tau _0^2+2r_1A^2\xi _5-2r_1\tau _0B^2\xi _4\tau _1-r_1A\xi _4\tau _1B +3\xi _5r_3B)}{r_1\tau _1^2B^2},\nonumber \\ \zeta _0= & {} \frac{6(r_1^2M+Nr_2^2)(2A\xi _5-\xi _4\tau _1B+4\tau _0\xi _5B)}{\tau _1^3B^2}, \,\,\zeta _1=-\frac{6\xi _5(r_1^2M+Nr_2^2)}{\tau _1^2B}, \end{aligned}$$
(3.40)

Substituting these results into Eqs. (3.5) and (3.10), we get

$$\begin{aligned} \pm (\eta -\eta _0)=\int \frac{\sqrt{\frac{\zeta _0}{\xi _5}+\frac{\zeta _1}{\xi _5}\Gamma }\ d\Gamma }{\sqrt{\Gamma ^5+\frac{\xi _4}{\xi _5}\Gamma ^4+ \frac{\xi _3}{\xi _5}\Gamma ^3+\frac{\xi _2}{\xi _5}\Gamma ^2+\frac{\xi _1}{\xi _5} \Gamma +\frac{\xi _0}{\xi _5}}}. \end{aligned}$$
(3.41)

To integrate Eq. (3.41), we must discuss the following families:

Family 1 If \(\Gamma ^5+\frac{\xi _4}{\xi _5}\Gamma ^4+ \frac{\xi _3}{\xi _5}\Gamma ^3+\frac{\xi _2}{\xi _5}\Gamma ^2+\frac{\xi _1}{\xi _5}\Gamma +\frac{\xi _0}{\xi _5}\) can be written in the following form:

$$\begin{aligned} \Gamma ^5+\frac{\xi _4}{\xi _5}\Gamma ^4+ \frac{\xi _3}{\xi _5}\Gamma ^3+\frac{\xi _2}{\xi _5}\Gamma ^2+\frac{\xi _1}{\xi _5} \Gamma +\frac{\xi _0}{\xi _5}=(\Gamma -\alpha _1)^5, \end{aligned}$$
(3.42)

where \(\alpha _1\) is an arbitrary constant. Then, we have

$$\begin{aligned} \pm (\eta -\eta _0)=\int \frac{\sqrt{\frac{\zeta _0}{\xi _5}+\frac{\zeta _1}{\xi _5}\Gamma }\ d\Gamma }{(\Gamma -\alpha _1)^2\sqrt{\Gamma -\alpha _1}}= -\frac{2}{3}\frac{\left( \frac{\zeta _0}{\xi _5}+\frac{\zeta _1}{\xi _5}\Gamma \right) ^{\frac{3}{2}}}{\left( \frac{\zeta _0}{\xi _5}+\frac{\zeta _1}{\xi _5}\alpha _1\right) (\Gamma -\alpha _1)^{\frac{3}{2}}}, \end{aligned}$$
(3.43)

or

$$\begin{aligned} \Gamma =\frac{\frac{\zeta _0}{\xi _5}+\alpha _1 \left[ -\frac{3}{2}\left( \frac{\zeta _0}{\xi _5} +\frac{\zeta _1}{\xi _5}\alpha _1\right) (\eta -\eta _0)\right] ^{\frac{3}{2}}}{\left[ -\frac{3}{2}\left( \frac{\zeta _0}{\xi _5} +\frac{\zeta _1}{\xi _5}\alpha _1\right) (\eta -\eta _0)\right] ^{\frac{3}{2}} -\frac{\zeta _1}{\xi _5}}. \end{aligned}$$
(3.44)

Substituting (3.44) into (3.14), we get the exact solution of Eq. (1.1) in the form of:

$$\begin{aligned} u_1(x,y,t)=\tau _0+\tau _1\alpha _1+\frac{\frac{\zeta _0}{\xi _5}+\alpha _1 \frac{\zeta _1}{\xi _5}}{\left[ -\frac{3}{2}\left( \frac{\zeta _0}{\xi _5}+\frac{\zeta _1}{\xi _5} \alpha _1\right) (r_1x+r_2y-r_3t-\eta _0)\right] ^{\frac{3}{2}}-\frac{\zeta _1}{\xi _5}}. \end{aligned}$$
(3.45)

Family 2 If \(\Gamma ^5+\frac{\xi _4}{\xi _5}\Gamma ^4+ \frac{\xi _3}{\xi _5}\Gamma ^3+\frac{\xi _2}{\xi _5}\Gamma ^2+\frac{\xi _1}{\xi _5}\Gamma +\frac{\xi _0}{\xi _5}\) can be written in the following form:

$$\begin{aligned} \Gamma ^5+\frac{\xi _4}{\xi _5}\Gamma ^4+ \frac{\xi _3}{\xi _5}\Gamma ^3+\frac{\xi _2}{\xi _5}\Gamma ^2+\frac{\xi _1}{\xi _5}\Gamma +\frac{\xi _0}{\xi _5}=(\Gamma -\alpha _1)^4(\Gamma -\alpha _2), \end{aligned}$$
(3.46)

where \(\alpha _1\) and \(\alpha _2\) are arbitrary constants. Then, we have

$$\begin{aligned} \pm (\eta -\eta _0)=\int \frac{\sqrt{\frac{\zeta _0}{\xi _5}+\frac{\zeta _1}{\xi _5}\Gamma }\ d\Gamma }{(\Gamma -\alpha _1)^2\sqrt{\Gamma -\alpha _2}}= -\frac{1}{2}\frac{(\Gamma -\alpha _1)(\Gamma -\alpha _2) \sqrt{\frac{\zeta _0}{\xi _5}+\frac{\zeta _1}{\xi _5}\Gamma }\ [2\Pi _1\Pi _2+\Pi _3\ln (Y)]}{(\alpha _1-\alpha _2)\Pi _1\Pi _2\sqrt{(\Gamma -\alpha _1)^4(\Gamma -\alpha _2)}}, \end{aligned}$$
(3.47)

where

$$\begin{aligned} \Pi _1= & {} \sqrt{(\alpha _1-\alpha _2)\left( \frac{\zeta _0}{\xi _5} +\frac{\zeta _1}{\xi _5}\alpha _1\right) }, \,\,\, \Pi _2=\sqrt{\frac{\zeta _1}{\xi _5}\Gamma ^2+\left( \frac{\zeta _0}{\xi _5} -\frac{\zeta _1}{\xi _5}\alpha _2\right) \Gamma -\frac{\zeta _0}{\xi _5}\alpha _2}, \,\,\,\Pi _3=(\alpha _1-\Gamma )\left( \frac{\zeta _0}{\xi _5} -\frac{\zeta _1}{\xi _5}\alpha _2\right) , \end{aligned}$$
(3.48)
$$\begin{aligned} \Pi _4= & {} \Gamma \left( \frac{\zeta _0}{\xi _5}-\frac{\zeta _1}{\xi _5}\alpha _2 +2\frac{\zeta _1}{\xi _5}\alpha _1\right) + \frac{\zeta _0}{\xi _5}\alpha _1-2\frac{\zeta _0}{\xi _5}\alpha _2 -\frac{\zeta _1}{\xi _5}\alpha _1\alpha _2, \quad Y=\frac{\Pi _4+2\Pi _1\Pi _2}{\Gamma -\alpha _1}. \end{aligned}$$
(3.49)

Family 3 If \(\Gamma ^5+\frac{\xi _4}{\xi _5}\Gamma ^4+ \frac{\xi _3}{\xi _5}\Gamma ^3+\frac{\xi _2}{\xi _5}\Gamma ^2 +\frac{\xi _1}{\xi _5}\Gamma +\frac{\xi _0}{\xi _5}\) can be written in the following form:

$$\begin{aligned} \Gamma ^5+\frac{\xi _4}{\xi _5}\Gamma ^4+ \frac{\xi _3}{\xi _5}\Gamma ^3+\frac{\xi _2}{\xi _5}\Gamma ^2+\frac{\xi _1}{\xi _5} \Gamma +\frac{\xi _0}{\xi _5}=(\Gamma -\alpha _1)^3(\Gamma -\alpha _2)^2, \end{aligned}$$
(3.50)

where \(\alpha _1\) and \(\alpha _2\) are arbitrary constants. Then, we have

$$\begin{aligned} \pm (\eta -\eta _0)=\int \frac{\sqrt{\frac{\zeta _0}{\xi _5}+\frac{\zeta _1}{\xi _5}\Gamma }\ d\Gamma }{\sqrt{(\Gamma -\alpha _1)^3(\Gamma -\alpha _2)^2}}= -\frac{\sqrt{\frac{\zeta _0}{\xi _5}+\frac{\zeta _1}{\xi _5}\Gamma }\ [2(\alpha _1-\alpha _2)\Pi _2+(\Gamma -\alpha _1)\Pi _1\ln (Y)]}{(\alpha _1-\alpha _2)^2\Pi _2\sqrt{\Gamma -\alpha _1}}, \end{aligned}$$
(3.51)

where

$$\begin{aligned} \Pi _1= & {} \sqrt{-(\alpha _1-\alpha _2)\left( \frac{\zeta _0}{\xi _5} +\frac{\zeta _1}{\xi _5}\alpha _2\right) }, \quad \Pi _2=\sqrt{\frac{\zeta _1}{\xi _5}\Gamma ^2+\left( \frac{\zeta _0}{\xi _5} -\frac{\zeta _1}{\xi _5}\alpha _1\right) \Gamma -\frac{\zeta _0}{\xi _5}\alpha _1}, \,\,\, \end{aligned}$$
(3.52)
$$\begin{aligned} \Pi _3= & {} \Gamma \left( \frac{\zeta _0}{\xi _5}-\frac{\zeta _1}{\xi _5}\alpha _1 +2\frac{\zeta _1}{\xi _5}\alpha _2\right) + \frac{\zeta _0}{\xi _5}\alpha _2-2\frac{\zeta _0}{\xi _5}\alpha _1 -\frac{\zeta _1}{\xi _5}\alpha _1\alpha _2, \quad Y=\frac{\Pi _3+2\Pi _1\Pi _2}{\Gamma -\alpha _2}. \end{aligned}$$
(3.53)

Family 4 If \(\Gamma ^5+\frac{\xi _4}{\xi _5}\Gamma ^4+ \frac{\xi _3}{\xi _5}\Gamma ^3+\frac{\xi _2}{\xi _5}\Gamma ^2+\frac{\xi _1}{\xi _5}\Gamma +\frac{\xi _0}{\xi _5}\) can be written in the following form:

$$\begin{aligned} \Gamma ^5+\frac{\xi _4}{\xi _5}\Gamma ^4+ \frac{\xi _3}{\xi _5}\Gamma ^3+\frac{\xi _2}{\xi _5}\Gamma ^2+\frac{\xi _1}{\xi _5}\Gamma +\frac{\xi _0}{\xi _5}= (\Gamma -\alpha _1)^2(\Gamma -\alpha _2)^2(\Gamma -\alpha _3), \end{aligned}$$
(3.54)

where \(\alpha _1, \alpha _2\) and \(\alpha _3\) are arbitrary constants. Then, we have

$$\begin{aligned} \pm (\eta -\eta _0)=\int \frac{\sqrt{\frac{\zeta _0}{\xi _5}+\frac{\zeta _1}{\xi _5}\Gamma }\ d\Gamma }{\sqrt{(\Gamma -\alpha _1)^3(\Gamma -\alpha _2)^2}}= -\frac{\sqrt{\Gamma -\alpha _3}\sqrt{\frac{\zeta _0}{\xi _5}+\frac{\zeta _1}{\xi _5}\Gamma }\ [(\alpha _2-\alpha _3)\Pi _1\ln (Y_1)-(\alpha _1-\alpha _3)\Pi _2\ln (Y_2)]}{\Pi _3\Pi _6}, \end{aligned}$$
(3.55)

where

$$\begin{aligned} \Pi _1= & {} \sqrt{(\alpha _1-\alpha _3)\left( \frac{\zeta _0}{\xi _5}+\frac{\zeta _1}{\xi _5}\alpha _1\right) },\, \Pi _2=\sqrt{(\alpha _2-\alpha _3)\left( \frac{\zeta _0}{\xi _5}+\frac{\zeta _1}{\xi _5}\alpha _2\right) },\, \end{aligned}$$
(3.56)
$$\begin{aligned} \Pi _3= & {} \sqrt{\frac{\zeta _1}{\xi _5}\Gamma ^2+\left( \frac{\zeta _0}{\xi _5}-\frac{\zeta _1}{\xi _5}\alpha _3\right) \Gamma -\frac{\zeta _0}{\xi _5}\alpha _3}, \,\, \Pi _4=\Gamma \left( \frac{\zeta _0}{\xi _5}-\frac{\zeta _1}{\xi _5}\alpha _3+2\frac{\zeta _1}{\xi _5}\alpha _1\right) + \frac{\zeta _0}{\xi _5}\alpha _1-2\frac{\zeta _0}{\xi _5}\alpha _3-\frac{\zeta _1}{\xi _5}\alpha _1\alpha _3, \end{aligned}$$
(3.57)
$$\begin{aligned} \Pi _5= & {} \Gamma \left( \frac{\zeta _0}{\xi _5}-\frac{\zeta _1}{\xi _5}\alpha _3+2\frac{\zeta _1}{\xi _5}\alpha _2\right) + \frac{\zeta _0}{\xi _5}\alpha _2-2\frac{\zeta _0}{\xi _5}\alpha _3-\frac{\zeta _1}{\xi _5}\alpha _2\alpha _3, \end{aligned}$$
(3.58)
$$\begin{aligned} \Pi _6= & {} (\alpha _1-\alpha _2)(\alpha _1-\alpha _3)(\alpha _2-\alpha _3), \,\,\, Y_1=\frac{\Pi _4+2\Pi _1\Pi _3}{\Gamma -\alpha _1}, \,\,\,Y_2=\frac{\Pi _5+2\Pi _2\Pi _3}{\Gamma -\alpha _2}. \end{aligned}$$
(3.59)

Remark 1

The other Families are ignored for simplicity.

Remark 2

We also observe that some solutions found in this paper are the same as those obtained in Sardar et al. (2015) when \(l\rightarrow 1\) or when \(l\rightarrow 0\). The other results are new solutions not yet reported in the literature. We then suppose that these exact solutions may have significant applications in telecommunication systems where solitons are used to codify or for the transmission of data.

Note that All the obtained results have been checked with Maple 13 by putting them back into the original equation and found correct.

4 Conclusion

In this paper, we have used the improved Bernoulli sub-ODE method and the extended trial equation method for building exact soliton solutions of nonlinear electrical transmission lines described by a mZK equation. A comparison of our results and with those obtained in (Sardar et al. 2015; Zhen et al. 2014) by using the (\(G'/G\))-expansion method, the extended tanh method, the sine–cosine method and the Hirota method shows, that there are many new solutions in the present work. It is worth noting that the new solutions obtained by means of aforementioned methods confirm the correctness of those obtained by other methods. Not only, the newly obtained solutions are identical to already published results, but also further solutions have obtained. The solutions obtained in this paper can help to explain many phenomena observed in nonlinear electrical transmission lines. Therefore, these methods can be applied to study many other nonlinear partial differential equations which frequently arise in engineering, mathematical physics.