Abundant soliton solutions of the resonant nonlinear Schrödinger equation with time-dependent coefficients by ITEM and He’s semi-inverse method

Abstract

The improved $\tan (\phi /2)$-expansion method (ITEM) and He’s semi-inverse variational method (HSIVM) are the efficient methods for obtaining exact solutions of nonlinear differential equations. In this paper, the ITEM and HSIVM are applied to construct exact solutions of the resonant nonlinear Schrödinger equation (RNLSE) with time-dependent coefficients for parabolic law nonlinearity. The resonant nonlinear Schrödinger equation plays a very important role in mathematical physics and nonlinear optics. We compare analytical findings with the results of the other analytical schemes describing the ansatz method approach and expansion method are used to carry out the integration. Description of the ITEM is given and the obtained results reveal that the ITEM is a new significant method for exploring nonlinear partial differential models. Moreover, by help of the HSIVM we obtained the bright and dark soliton wave solutions. Finally, by using Matlab, some graphical simulations were drawn to see the behavior of these solutions.

1 Introduction

The study of optical solitons has been going on for the recent years. There has been an overwhelming progress in this direction of research. There are lots of new results that have been produced in this field (Hasegawa and Kodama 1995). There have been many advances made in the area of Nonlinear Optics (Biswas et al. 2012a). In fact, optical solitons are nowadays a reality. Of important equations for optical soliton theory is nonlinear Schrödinger equation. The tanh method and the sine-cosine method are effectively used for reliable analysis for the nonlinear Schrödinger equations with cubic and power law nonlinearities by Wazwaz (2006). Manafian (2016) studied the Schrödinger type nonlinear evolution equations by the improved $\tan (\phi /2)$-expansion method. The resonant nonlinear Schrödinger equation has been exhibited the usual cubic nonlinearity present in the classical nonlinear Schrödinger equation together with an additional nonlinear term involving the modulus of the wave envelope by Tang et al. (2009). A resonant Davey–Stewartson capillary model system has been worked by Rogers et al. (2009). Mirzazadeh et al. (2014) have applied the $G^{\prime }/G$-expansion method for the resonant nonlinear Schrödinger equation with dual-power law nonlinearity. Moreover, Ekici et al. (2017) studied the resonant nonlinear Schrödinger equation with the Kerr-law and parabolic-law nonlinearities by the extended Jacobi elliptic function expansion method. There are many analytical and numerical methods for solving nonlinear partial differential equations (PDEs), some of these methods which solve PDEs are: the homotopy analysis method (Dehghan et al. 2010), the Exp-function method (Dehghan et al. 2011; Manafian and Lakestani 2015a; Manafian 2015), the exp($-\phi (\xi )$)-expansion method (Hafez et al. 2015), the generalized Kudryashov method (Zhou et al. 2016), the $G^{\prime }/G$-expansion method (Aghdaei and Manafianheris 2011; Mirzazadeh et al. 2015; Younis 2017; Rizva et al. 2017), the formal linearization method (Mirzazadeh and Eslami 2015), the Jacobi elliptic function method (Chen and Wang 2005), the homogeneous balance method (Zhao et al. 2006), the fractional extended Fan sub-equation method (Younis et al. 2017a), trial solution method (Arnous et al. 2017), the complex ansatz method (Younis et al. 2017b; Islam et al. 2017), the Jacobi elliptic function method (Cheemaa et al. 2017), the improved $\tan (\phi /2)$-expansion method (Manafian and Lakestani 2015b, 2016a, b, c, d; Manafian 2016; Manafian et al. 2016a, b; Aghdaei and Manafian 2016) and so on. Also, of applied methods for solving nonlinear partial differential equation is He’s semi-inverse variational principle, which introduced by He (2006). For further information see references therein (Kohl et al. 2009; Zhang 2007; Biswas et al. 2012c, d; Sassaman et al. 2010). Consider the dimensionless form of the resonant nonlinear Schrödinger equation which is given in Eslami et al. (2014)

$$i\psi _t+a_1(t)\psi _{xx}+r(t)F(|\psi |^2)\psi +d_1(t)\left( \frac{|\psi |_{xx}}{|\psi |}\right) \psi = i\lambda (t)\psi ,$$

(1.1)

where $\psi = \psi (x, t)$ is a complex valued function, while x and t are the independent spatial and temporal variables, respectively. The coefficients $a_1(t), r(t), d_1(t)$ and $\lambda (t)$ are all functions of t. The coefficients $a_1(t), r(t)$ and $d_1(t)$ respectively represent the group velocity dispersion, the nonlinear term and the resonant term. On the right-hand side, the coefficient of $\lambda (t)$ is the linear attenuation. Thus, there are two nonlinear terms in Eq. (1.1) which are the coefficients of r(t) and $d_1(t)$. The coefficient of $\gamma (t)$ is sometimes referred to as the quantum potential or Bohm potential (Biswas and Milovic 2010, 2011; Biswas et al. 2011; Nishino et al. 1998). This term commonly appears in the study of chiral solitons in quantum Hall effect. The RNLSE appears in quantum mechanics and in the study of Madelung fluid (Pashaev and Lee 2002). The function F is a real-valued algebraic function and in order to satisfy the necessary condition of having smoothness of the complex function $F(|q|^2)q$, the function $F(|q|^2)q$ is considered to be k times continuously differentiable (Triki et al. 2012), so that

$$F(|q|^2)q\in \bigcup _{m,n=1}^{\infty }C^k((-n,n)\times (-m,m);R^2).$$

(1.2)

Equation (1.1) is a nonlinear, non-integrable partial differential equation where non-integrability is not necessarily associated with the nonlinear term present in the equation. In this paper we search for the stationary solution to (1.1). We use the following transformations as

$$\psi (x,t)=u(\xi )\exp (i\phi ), \quad \xi =x-v(t)t, \quad \phi =-k x+w(t) t,$$

(1.3)

where v(t) is the soliton velocity, k is the wave number of the soliton, while w(t) is the frequency of the soliton velocity, and by using of derivations of $\psi (x,t)$ we will have

$$\psi _t=\left[ i\left( t\frac{d w(t)}{dt}+w(t)\right) u-\left( t\frac{d v(t)}{dt}+v(t)\right) u^{\prime }\right] e^{i(-k x+w(t) t)},$$

(1.4)

$$\psi _{xx}=\left[ u^{\prime \prime }-2iku^{\prime }-k^2u\right] e^{i(-k x+w(t) t)},$$

(1.5)

$$\left( \frac{|\psi |_{xx}}{|\psi |}\right) \psi =u^{\prime \prime }e^{i(-k x+w(t) t)},$$

(1.6)

where the primes denote derivatives with respect to $\xi$. Inserting (1.3)–(1.6) into (1.1), and separating into real and imaginary parts and by supposing $\lambda (t)=0$, the results are

$$t\frac{d v(t)}{dt}+v(t)+2ka_1(t)=0,$$

(1.7)

$$(\alpha (t)+\gamma (t))u^{\prime \prime }-\left( t\frac{d w(t)}{dt}+w(t)+k^2a_1(t)\right) u+r(t)F(u^2)u=0.$$

(1.8)

By integrating (1.7) with respect to t yields

$$v(t)=-\frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma .$$

(1.9)

Also, we remark from (1.9) that the pulse velocity is only affected by the varying dispersion coefficient $a_1(t)$. The outline of this paper is organized as follows:

In Sect. 2, we describe the ITEM and solve with it the RNLSE with time-dependent coefficients. In Sect. 3, we apply He’s semi-inverse variational principle to solve Eq. (2.8). In Sect. 4, the physical explanation of the obtained solutions is given. Also conclusion is given in Sect. 5.

2 Description of the ITEM

The ITEM is well-known analytical method which was improved and developed by Manafian.

Step 1

We suppose that given nonlinear partial differential equation for u(x, t) to be in the form

$$\begin{aligned} \mathcal {N}(u, u_x, u_t, u_{xx}, u_{tt},\ldots )=0, \end{aligned}$$

(2.1)

which can be converted to an ODE

$$\begin{aligned} \mathcal {Q}(u, u^{\prime }, -\mu u^{\prime }, u^{\prime \prime }, \mu ^2u^{\prime \prime },\ldots )=0, \end{aligned}$$

(2.2)

by the transformation $\xi =x-\mu t$ is the wave variable. Also, $\mu$ is constant to be determined later.

Step 2

Suppose the traveling wave solution of Eq. (2.2) can be expressed as follows:

$$\begin{aligned} u(\xi )=S(\phi )=\sum _{k=-m}^{m}A_k\left[ p+\tan (\phi /2)\right] ^k, \end{aligned}$$

(2.3)

where $A_k (0\le k \le m)$ and $A_{-k}=B_k (1\le k \le m)$ are constants to be determined, such that $A_m\ne 0, B_m\ne 0$ and $\phi =\phi (\xi )$ satisfies the following ordinary differential equation:

$$\begin{aligned} \phi ^{\prime }(\xi )=a\sin (\phi (\xi ))+b\cos (\phi (\xi ))+c. \end{aligned}$$

(2.4)

We will consider the following special solutions of equation (2.4):

Family 1::

When $\Delta =a^2+b^2-c^2<0$ and $b-c\ne 0$, then $\phi (\xi )=2\tan ^{-1}\left[ \frac{a}{b-c}-\frac{\sqrt{-\Delta }}{b-c}\tan \left( \frac{\sqrt{-\Delta }}{2}\overline{\xi }\right) \right] .$

Family 2::

When $\Delta =a^2+b^2-c^2>0$ and $b-c\ne 0$, then $\phi (\xi )=2\tan ^{-1}\left[ \frac{a}{b-c}+\frac{\sqrt{\Delta }}{b-c}\tanh \left( \frac{\sqrt{\Delta }}{2}\overline{\xi }\right) \right] .$

Family 3::

When $\Delta =a^2+b^2-c^2>0$, $b\ne 0$ and $c=0,$ then $\phi (\xi )=2\tan ^{-1}\left[ \frac{a}{b}+\frac{\sqrt{b^2+a^2}}{b}\tanh \left( \frac{\sqrt{b^2+a^2}}{2}\overline{\xi }\right) \right] .$

Family 4::

When $\Delta =a^2+b^2-c^2<0$, $c\ne 0$ and $b=0,$ then $\phi (\xi )=2\tan ^{-1}\left[ -\frac{a}{c}+\frac{\sqrt{c^2-a^2}}{c}\tan \left( \frac{\sqrt{c^2-a^2}}{2}\overline{\xi }\right) \right] .$

Family 5::

When $\Delta =a^2+b^2-c^2>0$, $b-c\ne 0$ and $a=0,$ then $\phi (\xi )=2\tan ^{-1}\left[ \sqrt{\frac{b+c}{b-c}}\tanh \left( \frac{\sqrt{b^2-c^2}}{2}\overline{\xi }\right) \right] .$

Family 6::

When $a=0$ and $\mathrm {c=0,}$ then $\phi (\xi )=\tan ^{-1}\left[ \frac{e^{2b\overline{\xi }}-1}{e^{2b\overline{\xi }}+1}, \frac{2e^{b\overline{\xi }}}{e^{2b\overline{\xi }}+1}\right] .$

Family 7::

When $b=0$ and $c=0,$ then $\phi (\xi )=\tan ^{-1}\left[ \frac{2e^{a\overline{\xi }}}{e^{2a\overline{\xi }}+1},\ \frac{e^{2a\overline{\xi }}-1}{e^{2a\overline{\xi }}+1}\right] .$

Family 8::

When $a^2+b^2=c^2$, then $\phi (\xi )=2\tan ^{-1}\left[ \frac{a\overline{\xi }+2}{(b-c)\overline{\xi }}\right] .$

Family 9::

When $a=b=c=ka$, then $\phi (\xi )=2\tan ^{-1}\left[ e^{ka\overline{\xi }}-1\right] .$

Family 10::

When $a=c=ka$ and $\mathrm {b=-ka}$, then $\phi (\xi )=-2\tan ^{-1}\left[ \frac{e^{ka\overline{\xi }}}{-1+e^{ka\overline{\xi }}}\right] .$

Family 11::

When $c=a$, then $\phi (\xi )=-2\tan ^{-1}\left[ \frac{(a+b)e^{b\overline{\xi }}-1}{(a-b)e^{b\overline{\xi }}-1}\right] .$

Family 12::

When $a=c$, then $\phi (\xi )=2\tan ^{-1}\left[ \frac{(b+c)e^{b\overline{\xi }}+1}{(b-c)e^{b\overline{\xi }}-1}\right] .$

Family 13::

When $c=-a$, then $\phi (\xi )=2\tan ^{-1}\left[ \frac{e^{b\overline{\xi }}+b-a}{e^{b\overline{\xi }}-b-a}\right] .$

Family 14::

When $b=-c$, then $\phi (\xi )=2\tan ^{-1}\left[ \frac{ae^{a\overline{\xi }}}{1-ce^{a\overline{\xi }}}\right] .$

Family 15::

When $b=0$ and $\mathrm {a=c}$, then $\phi (\xi )=-2\tan ^{-1}\left[ \frac{c\overline{\xi }+2}{c\overline{\xi }}\right] .$

Family 16::

When $a=0$ and $b=c$, then $\phi (\xi )=2\tan ^{-1}\left[ c\overline{\xi }\right] .$

Family 17::

When $a=0$ and $b=-c$, then $\phi (\xi )=-2\tan ^{-1}\left[ \frac{1}{c\overline{\xi }}\right] .$

Family 18::

When $a=0$ and $b=0$, then $\phi (\xi )=c\xi +C.$

Family 19::

When $b=c$ then $\phi (\xi )=2\tan ^{-1}\left[ \frac{e^{a\overline{\xi }}-c}{a}\right] ,$ where $\overline{\xi }=\xi +C, p, A_0, A_k, B_k (k=1,2,\ldots ,m), a, b$ and c are constants to be determined later.

Step 3

Determine m. This, usually, can be accomplished by balancing the linear term(s) of highest order with the highest-order nonlinear term(s) in Eq. (2.2). But, the positive integer m can be determined by considering the homogeneous balance between the highest order derivatives and nonlinear terms appearing in Eq. (2.2). If $m = q/p$ (where $m = q/p$ be a fraction in the lowest terms), we let

$$\begin{aligned} u(\xi )=v^{q/p}(\xi ), \end{aligned}$$

(2.5)

then substitute Eq. (2.5) into Eq. (2.2) and then determine the value of m in new Eq. (2.2). If m be a negative integer, we let

$$\begin{aligned} u(\xi )=v^m(\xi ), \end{aligned}$$

(2.6)

then substitute Eq. (2.6) into Eq. (2.2). Then we determine the new value of m in obtained equation.

Step 4

Substituting (2.3) into Eq. (2.2) with the value of m obtained in Step 2. Collecting the coefficients of $\tan (\phi /2)^k$, $\cot (\phi /2)^k (k=0,1,2,\ldots )$, then setting each coefficient to zero, we can get a set of over-determined equations for $A_0, A_k, B_k (k = 1, 2,\ldots , m)$ a, b, c and p and solving it with the aid of symbolic computation using Maple.

Step 5

Solving the algebraic equations in Step 3, then substituting $A_0, A_1, B_1, \ldots , A_m, B_m, \mu , p$ in (2.3).

The parabolic law nonlinearity is the case when $F(s)=b_1(t)s+c_1(t)s^2$, where $b_1(t)$ and $c_1(t)$ are in general constants. Such a kind of nonlinearity appears also in fiber optics (Biswas et al. 2012b; Gagnon 1989). For parabolic law nonlinearity, the considered generalized RNLSE with time-varying coefficients is given by

$$\begin{aligned} i\psi _t+a_1(t)\psi _{xx}+(b_1(t)|\psi |^2+c_1(t)|\psi |^4)\psi +d_1(t)\left( \frac{|\psi |_{xx}}{|\psi |}\right) \psi = i\lambda (t)\psi , \end{aligned}$$

(2.7)

where is considered $r(t)=1$. By using (1.4)–(1.6) and supposing $\lambda (t)=0$, then (2.7) transformed to

$$\begin{aligned}&(a_1(t)+d_1(t))u^{\prime \prime }-\left( t\frac{d w(t)}{dt}+w(t)+k^2a_1(t)\right) u+b_1(t)u^3+c_1(t)u^5=0, \end{aligned}$$

(2.8)

$$\begin{aligned}&v(t)=-\frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma . \end{aligned}$$

(2.9)

By balancing the $\mathrm {u^{\prime \prime }}$ and $\mathrm {u^5}$ gives $m=\frac{1}{2}$. To get a closed form solution, we use the transformation

$$\begin{aligned} u(x,t)=U(x,t)^{\frac{1}{2}}, \end{aligned}$$

(2.10)

that will carry Eq. (2.8) into the ODE,

$$\begin{aligned} (a_1(t)+d_1(t))(2UU^{\prime \prime }-(U^{\prime })^2)-4\left( t\frac{d w(t)}{dt}+w(t)+k^2a_1(t)\right) U^2+4b_1(t)U^3+4c_1(t)U^4=0. \end{aligned}$$

(2.11)

By balancing the $\mathrm {UU^{\prime \prime }}$ and $\mathrm {U^4}$ gives $m=1$. By supposing $p=0$ in (2.3), the trail solution will be as

$$\begin{aligned} U(\xi )=A_{0}+A_1\tan (\phi /2)+ B_1\cot (\phi /2). \end{aligned}$$

(2.12)

Substituting (2.12) and (2.4) into Eq. (2.11), we get the following results:

Case I

First set is:

$$a=\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}, b=-c, c=c,k=k, A_{0}=0,A_{1} =-\frac{c}{2}\sqrt{-\frac{3(a_1(t)+d_1(t))}{c_1(t)}}, B_{1} =0,$$

(2.13)

$$w(t)=-\frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma , U(\xi )= A_{1}\tan \left( \frac{\Phi (\xi )}{2}\right) .$$

(2.14)

By using of (2.13), (2.14) and Families 1, 2 and 14 can be written, respectively, as

$$\begin{aligned} \psi _{1}(x,t)= \left\{ \frac{3b_1(t)}{8c_1(t)}-\frac{3b_1(t)i}{8c_1(t)}\tan \left( \frac{\sqrt{-\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right\} ^{\frac{1}{2}} \times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.15)

where $\Delta =\frac{-3b_1^2(t)}{4c_1(t)(a_1(t)+d_1(t))}<0$.

$$\begin{aligned} \psi _{2}(x,t)= \left\{ \frac{3b_1(t)}{8c_1(t)}+\frac{3b_1(t)}{8c_1(t)}\tanh \left( \frac{\sqrt{\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right\} ^{\frac{1}{2}} \times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.16)

where $\Delta =\frac{-3b_1^2(t)}{4c_1(t)(a_1(t)+d_1(t))}>0$.

$$\begin{aligned} \psi _{3}(x,t) &= \left\{ \frac{-\frac{3b_1(t)c}{4c_1(t)} e^{\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] }}{1-ce^{\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] }}\right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.17)

where C is constant.

Case II

Second set is:

$$\begin{aligned}&a=\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}, \quad b=c, \quad c=c,\quad k=k,\quad A_{0}=0,\quad A_{1} =0, \quad B_{1} =-\frac{c}{2}\sqrt{-\frac{3(a_1(t)+d_1(t))}{c_1(t)}}, \end{aligned}$$

(2.18)

$$\begin{aligned}&w(t)=-\frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma , U(\xi )= B_{1}\cot \left( \frac{\Phi (\xi )}{2}\right) . \end{aligned}$$

(2.19)

By using of (2.18), (2.19) and Family 19 can be written as

$$\begin{aligned} \psi _{4}(x,t)= \left\{ \frac{\frac{3cb_1(t)}{4c_1(t)}}{e^{\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] }-c}\right\} ^{\frac{1}{2}}e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.20)

where C is constant.

Case III

Third set is:

$$\begin{aligned} a= & {} a, \quad b=-\frac{(64A_1^2c_1^2+12d_1a^2c_1+12a_1a^2c_1+9b_1^2)\sqrt{-3072c_1(a_1+d_1)}}{3072A_1c_1^2(a_1+d_1)}, c=\frac{12a_1a^2c_1-64A_1^2c_1^2+9b_1^2+12d_1a^2c_1}{c_1A_1\sqrt{-3072c_1(a_1+d_1)}}, \\ k= & {} k,A_{0}=-\frac{48b_1(t)+a\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}}{128c_1(t)},\quad A_{1} = A_1,\quad B_1=0, \end{aligned}$$

(2.21)

$$\begin{aligned} w(t)= & {} -\frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma , \Delta =a^2+b^2-c^2=-\frac{3b_1^2}{4c_1(a_1+d_1)},u(\xi )= A_0+A_{1}\tan \left( \frac{\Phi (\xi )}{2}\right) . \end{aligned}$$

(2.22)

By using of (2.21), (2.22) and Families 1, 2, 6, 11, 15 and 17 can be written, respectively, as

$$\begin{aligned} \psi _{5}(x,t)= & {} \left\{ -\frac{48b_1(t)}{128c_1(t)}-\frac{\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}\sqrt{-\Delta }}{128c_1(t)} \tan \left( \frac{\sqrt{-\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right\} ^{\frac{1}{2}} \\&\quad \times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.23)

where $\Delta =-\frac{3b_1^2}{4c_1(a_1+d_1)}<0.$

$$\begin{aligned} \psi _{6}(x,t)= & {} \left\{ -\frac{48b_1(t)}{128c_1(t)}+\frac{\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}\sqrt{\Delta }}{128c_1(t)} \tanh \left( \frac{\sqrt{\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right\} ^{\frac{1}{2}} \nonumber \\&\quad\times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.24)

where $\Delta =-\frac{3b_1^2}{4c_1(a_1+d_1)}>0.$

$$\begin{aligned} \psi _{7}(x,t)= & {} \left\{ -\frac{48b_1(t)}{128c_1(t)}+A_1\tan \left( \frac{1}{2}\arctan \left[ \frac{e^{ \frac{8A_1\sqrt{-3c_1(t)(a_1(t)+d_1(t))}}{3(a_1(t)+d_1(t))}\xi }-1}{e^{ \frac{8A_1\sqrt{-3c_1(t)(a_1(t)+d_1(t))}}{3(a_1(t)+d_1(t))}\xi }+1}, \ \frac{2e^{ \frac{4A_1\sqrt{-3c_1(t)(a_1(t)+d_1(t))}}{3(a_1(t)+d_1(t))}\xi }}{e^{ \frac{8A_1\sqrt{-3c_1(t)(a_1(t)+d_1(t))}}{3(a_1(t)+d_1(t))}\xi }+1}\right] \right) \right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.25)

where $\xi =x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C$ and C is arbitrary constant.

$$\begin{aligned} \psi _{8}(x,t)= & {} \left\{ -\frac{48b_1(t)+a\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}}{128c_1(t)}+ A_1\left[ \frac{(a+b)e^{b(\xi +C)}-1}{(a-b)e^{b(\xi +C)}-1}\right] \right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.26)

where $a=\pm \frac{8A_1c_1(t)\pm 3b_1(t)}{2\sqrt{-3c_1(t)(a_1(t)+d_1(t))}}$ and $\xi =x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C$ and C is arbitrary constant.

$$\begin{aligned} \psi _{9}(x,t)= & {} \left\{ -\frac{48b_1(t)+a\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}}{128c_1(t)}-A_1\left[ \frac{c\left( x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right) +2}{c\left( x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right) }\right] \right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.27)

where $a=c=-\frac{128A_1c_1(t)}{\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}}$ and C is arbitrary constant.

$$\begin{aligned} \psi _{10}(x,t)= \sqrt{A_1}\left\{ -c\left( x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right) \right\} ^{\frac{-1}{2}} e^{i\left[ -kx- \left( \int _{0}^{t}k^2a_1(\sigma )d\sigma \right) \right] }, \end{aligned}$$

(2.28)

where $c=\frac{-2A_1c_1(t)}{2\sqrt{-3c_1(t)(a_1(t)+d_1(t))}}$, $A_1$ and C are arbitrary constants.

Case IV

Fourth set is:

$$\begin{aligned} a= & {} a, \quad b=\frac{(64B_1^2c_1^2+12d_1a^2c_1+12a_1a^2c_1+9b_1^2)\sqrt{-3072c_1(a_1+d_1)}}{3072B_1c_1^2(a_1+d_1)}, \quad c=\frac{12a_1a^2c_1-64B_1^2c_1^2+9b_1^2+12d_1a^2c_1}{c_1B_1\sqrt{-3072c_1(a_1+d_1)}}, \nonumber \\ k= & {} k,\quad A_{0}=-\frac{48b_1(t)+a\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}}{128c_1(t)},A_{1} =0, \quad B_1=B_1, \end{aligned}$$

(2.29)

$$\begin{aligned} w(t)= & {} -\frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma , \Delta =a^2+b^2-c^2=-\frac{3b_1^2}{4c_1(a_1+d_1)},u(\xi )= A_0+B_{1}\cot \left( \frac{\Phi (\xi )}{2}\right) . \end{aligned}$$

(2.30)

By using of (2.29), (2.30) and Families 1, 2, 6, 11, 15 and 18 can be written, respectively, as

$$\begin{aligned} \psi _{11}(x,t)= & {} \left\{ -\frac{48b_1(t)+a\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}}{128c_1(t)}+\frac{128B_1^2c_1(t)}{\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}}\right. \\&\quad\left. \left[ a-\sqrt{-\Delta } \tan \left( \frac{\sqrt{-\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right] ^{-1}\right\} ^{\frac{1}{2}} e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.31)

where $\Delta =-\frac{3b_1^2}{4c_1(a_1+d_1)}<0.$

$$\begin{aligned} \psi _{12}(x,t)= & {} \left\{ -\frac{48b_1(t)+a\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}}{128c_1(t)}+\frac{128B_1^2c_1(t)}{\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}}\right. \\&\quad\left. \left[ a+\sqrt{\Delta } \tanh \left( \frac{\sqrt{\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right] ^{-1}\right\} ^{\frac{1}{2}} e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.32)

where $\Delta =-\frac{3b_1^2}{4c_1(a_1+d_1)}>0.$

$$\begin{aligned} \psi _{13}(x,t)= & {} \left\{ -\frac{48b_1(t)}{128c_1(t)}+\frac{3b_1(t)}{8c_1(t)}\cot \left( \frac{1}{2}\arctan \left[ \frac{e^{ \frac{b_1(t)\sqrt{-3c_1(t)(a_1(t)+d_1(t))}}{c_1(t)(a_1(t)+d_1(t))}\xi }-1}{e^{ \frac{b_1(t)\sqrt{-3c_1(t)(a_1(t)+d_1(t))}}{c_1(t)(a_1(t)+d_1(t))}\xi }+1}, \ \frac{2e^{ \frac{b_1(t)\sqrt{-3c_1(t)(a_1(t)+d_1(t))}}{2c_1(t)(a_1(t)+d_1(t))}\xi }}{e^{ \frac{b_1(t)\sqrt{-3c_1(t)(a_1(t)+d_1(t))}}{c_1(t)(a_1(t)+d_1(t))}\xi }+1}\right] \right) \right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.33)

where $\xi =x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C$ and C is arbitrary constant.

$$\begin{aligned} \psi _{14}(x,t)= & {} \left\{ -\frac{48b_1(t)+a\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}}{128c_1(t)}+ B_1\left[ \frac{(a-b)e^{b(\xi +C)}-1}{(a+b)e^{b(\xi +C)}-1}\right] \right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.34)

where $a=\pm \frac{8A_1c_1(t)\pm 3b_1(t)}{2\sqrt{-3c_1(t)(a_1(t)+d_1(t))}}$ and $\xi =x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C$ and C is arbitrary constant.

$$\begin{aligned} \psi _{15}(x,t)= & {} \left\{ -\frac{48b_1(t)+a\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}}{128c_1(t)}-B_1\left[ \frac{c\left( x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right) }{c\left( x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right) +2}\right] \right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.35)

where $c=-\frac{128A_1c_1(t)}{\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}}$, $a=\sqrt{-\frac{9b_1^2(t)+64A_1c_1^2(t)}{12c_1(t)(a_1(t)+d_1(t))}}$ and C is arbitrary constant.

$$\begin{aligned} \psi _{16}(x,t)= \left\{ -\frac{48b_1(t)}{128c_1(t)}+\frac{3cb_1(t)}{8c_1(t)}i\left( x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right) ^{-1}\right\} ^{\frac{1}{2}} e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.36)

where $c=\frac{6b_1(t)i}{2\sqrt{-3072c_1(t)(a_1(t)+d_1(t))}}$, $i=\sqrt{-1}$ and C is arbitrary constant.

Case V

Fifth set is:

$$\begin{aligned}&\small {a=\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}, \quad b=-c, \quad c=c,\quad k=k,\quad A_{0}=-\frac{3b_1(t)}{4c_1(t)},\quad A_{1} =-\frac{c}{2}\sqrt{-\frac{3(a_1(t)+d_1(t))}{c_1(t)}}, } \end{aligned}$$

(2.37)

$$\begin{aligned}&B_{1} =0,\quad w(t)=-\frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma , \quad U(\xi )=A_0+A_{1}\tan \left( \frac{\Phi (\xi )}{2}\right) . \end{aligned}$$

(2.38)

By using of (2.37), (2.38) and Families 1, 2 and 14 can be written, respectively, as

$$\begin{aligned} \psi _{17}(x,t)= & {} \left\{ -\frac{3b_1(t)}{8c_1(t)}-\frac{3b_1(t)i}{8c_1(t)}\tan \left( \frac{\sqrt{-\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.39)

where $\Delta =\frac{-3b_1^2(t)}{4c_1(t)(a_1(t)+d_1(t))}<0$.

$$\begin{aligned} \psi _{18}(x,t)= & {} \left\{ -\frac{3b_1(t)}{8c_1(t)}+\frac{3b_1(t)}{8c_1(t)}\tanh \left( \frac{\sqrt{\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.40)

where $\Delta =\frac{-3b_1^2(t)}{4c_1(t)(a_1(t)+d_1(t))}>0$.

$$\begin{aligned} \psi _{19}(x,t)= & {} \left\{ -\frac{3b_1(t)}{4c_1(t)}-\frac{\frac{3b_1(t)c}{4c_1(t)} e^{\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] }}{1-ce^{\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] }}\right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \left( \frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma \right) t\right] }, \end{aligned}$$

(2.41)

where C is constant.

Case VI

Sixth set is:

$$\begin{aligned}&\small {a=\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}, \quad b=c, \quad c=c,\quad k=k,\quad A_{0}=-\frac{3b_1(t)}{4c_1(t)},\quad A_{1} =0, \quad B_{1} =-\frac{c}{2}\sqrt{-\frac{3(a_1(t)+d_1(t))}{c_1(t)}}, } \end{aligned}$$

(2.42)

$$\begin{aligned}&w(t)=-\frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma , \quad U(\xi )= A_0+B_{1}\cot \left( \frac{\Phi (\xi )}{2}\right) . \end{aligned}$$

(2.43)

By using of (2.42), (2.43) and Family 19 can be written as

$$\begin{aligned} \psi _{20}(x,t)= \left\{ -\frac{3b_1(t)}{4c_1(t)}+\frac{\frac{3cb_1(t)}{4c_1(t)}}{e^{\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] }-c}\right\} ^{\frac{1}{2}}e^{i\left[ -kx- \frac{1}{16}\int _{0}^{t}\frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}d\sigma \right] }, \end{aligned}$$

(2.44)

where C is constant.

Case VII

Seventh set is:

$$\begin{aligned}&\small {a=0, \quad b=\frac{b_1(t)}{4}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}, \quad c=0,\quad k=k,\quad A_{0}=-\frac{3b_1(t)}{8c_1(t)},\,\,\,A_{1} =\frac{3b_1(t)}{16c_1(t)}, \,\,\,B_{1} =\frac{3b_1(t)}{16c_1(t)},\,\,\, } \end{aligned}$$

(2.45)

$$\begin{aligned}&w(t)=-\frac{1}{16t}\int _{0}^{t}\left[ \frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma , \quad U(\xi )= A_0+A_{1}\tan \left( \frac{\Phi (\xi )}{2}\right) +B_{1}\cot \left( \frac{\Phi (\xi )}{2}\right) . \end{aligned}$$

(2.46)

By using of (2.45), (2.46) and Family 6 can be written as

$$\begin{aligned} \psi _{21}(x,t)= & {} \left\{ -\frac{3b_1(t)}{8c_1(t)} \pm \frac{3b_1(t)}{16c_1(t)}\tan \left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }-1}{e^{\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }+1}, \ \frac{2e^{\frac{b_1(t)}{4}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }}{e^{\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }+1}\right] \right) \right. \\&\quad\left. \pm \frac{3b_1(t)}{16c_1(t)}\cot \left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }-1}{e^{\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }+1}, \ \frac{2e^{\frac{b_1(t)}{4}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }}{e^{\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }+1}\right] \right) \right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \frac{1}{16}\int _{0}^{t}\frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}d\sigma \right] } \end{aligned}$$

(2.47)

where $\xi =x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C$ and C is constant.

Case VIII

Eighth set is:

$$\begin{aligned}&\small {a=0, \,\,\,b=\frac{b_1(t)}{4}\sqrt{\frac{3}{c_1(t)(a_1(t)+d_1(t))}}, \,\,\,c=0,\,\,\,k=k,\,\,\, A_{0}=-\frac{3b_1(t)}{8c_1(t)},\,\,\,A_{1} =\frac{3b_1(t)i}{16c_1(t)}, \,\,\,B_{1} =-\frac{3b_1(t)i}{16c_1(t)},\quad } \end{aligned}$$

(2.48)

$$\begin{aligned}&w(t)=-\frac{1}{64t}\int _{0}^{t}\left[ \frac{15b_1^2(\sigma )+64a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}\right] d\sigma , \quad U(\xi )= A_0+A_{1}\tan \left( \frac{\Phi (\xi )}{2}\right) +B_{1}\cot \left( \frac{\Phi (\xi )}{2}\right) . \end{aligned}$$

(2.49)

By using of (2.48), (2.49) and Family 6 can be written as

$$\begin{aligned} \psi _{22}(x,t)= & {} \left\{ -\frac{3b_1(t)}{8c_1(t)} +\frac{3b_1(t)i}{16c_1(t)}\tan \left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{b_1(t)}{2}\sqrt{\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }-1}{e^{\frac{b_1(t)}{2}\sqrt{\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }+1}, \ \frac{2e^{\frac{b_1(t)}{4}\sqrt{\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }}{e^{\frac{b_1(t)}{2}\sqrt{\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }+1}\right] \right) \right. \\&\quad\left. -\frac{3b_1(t)i}{16c_1(t)}\cot \left( \frac{1}{2}\arctan \left[ \frac{e^{\frac{b_1(t)}{2}\sqrt{\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }-1}{e^{\frac{b_1(t)}{2}\sqrt{\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }+1}, \ \frac{2e^{\frac{b_1(t)}{4}\sqrt{\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }}{e^{\frac{b_1(t)}{2}\sqrt{\frac{3}{c_1(t)(a_1(t)+d_1(t))}}\xi }+1}\right] \right) \right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \frac{1}{64}\int _{0}^{t}\frac{15b_1^2(\sigma )+64a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}d\sigma \right] }, \end{aligned}$$

(2.50)

where $\xi =x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C$ and C is constant.

Case IX

Ninth set is:

$$\begin{aligned}&\small {a=0, \,\,\,b=-\frac{256B_1^2c_1^2(t)+9b_1^2(t)}{B_1c_1(t)\sqrt{-49152c_1(t)(a_1(t)+d_1(t))}}, \,\,\,c=\frac{256B_1^2c_1^2(t)-9b_1^2(t)}{B_1c_1(t)\sqrt{-49152c_1(t)(a_1(t)+d_1(t))}},\,\,\,k=k,\,\,\, A_{0}=-\frac{3b_1(t)}{8c_1(t)}, } \end{aligned}$$

(2.51)

$$\begin{aligned}&A_{1} =\frac{9b_1^2(t)}{256B_1c_1^2(t)}, \,B_{1} =B_1,\,w(t)=-\frac{1}{16t}\int _{0}^{t}\frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}d\sigma , \,U(\xi )=A_0+ A_{1}\tan \left( \frac{\Phi (\xi )}{2}\right) +B_{1}\cot \left( \frac{\Phi (\xi )}{2}\right) . \end{aligned}$$

(2.52)

By using of (2.51), (2.52) and Family 5 can be written as

$$\begin{aligned} \psi _{23}(x,t)= & {} \left\{ -\frac{3b_1(t)}{8c_1(t)}+\frac{3b_1(t)}{16c_1(t)}\tanh \left( \frac{\sqrt{\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right. \\&\quad\times\left. \frac{3b_1(t)}{16c_1(t)}\coth \left( \frac{\sqrt{\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right\} ^{\frac{1}{2}}e^{i\left[ -kx- \frac{1}{16}\int _{0}^{t}\frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}d\sigma \right] }, \end{aligned}$$

(2.53)

where $\Delta =\frac{-3b_1^2(t)}{16c_1(t)(a_1(t)+d_1(t))}>0$.

Case X

Tenth set is:

$$\begin{aligned}&\small {a=0, \,\,\,b=-\frac{256B_1^2c_1^2(t)-9b_1^2(t)}{B_1c_1(t)\sqrt{-49152c_1(t)(a_1(t)+d_1(t))}}, \,\,\,c=\frac{256B_1^2c_1^2(t)+9b_1^2(t)}{B_1c_1(t)\sqrt{-49152c_1(t)(a_1(t)+d_1(t))}},\,\,\,k=k, A_{0}=-\frac{3b_1(t)}{8c_1(t)}, } \end{aligned}$$

(2.54)

$$\begin{aligned}&A_{1} =\frac{9b_1^2(t)}{256B_1c_1^2(t)}, B_{1} =B_1,\,\,w(t)=-\frac{1}{64t}\int _{0}^{t}\frac{15b_1^2(\sigma )+64a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}d\sigma , \,U(\xi )=A_0+ A_{1}\tan \left( \frac{\Phi (\xi )}{2}\right) +B_{1}\cot \left( \frac{\Phi (\xi )}{2}\right) . \end{aligned}$$

(2.55)

By using of (2.54), (2.55) and Families 5 and 14 can be written, respectively, as

$$\begin{aligned} \psi _{24}(x,t)= & {} \left\{ -\frac{3b_1(t)}{8c_1(t)}+\frac{3b_1(t)i}{16c_1(t)}\tanh \left( \frac{\sqrt{\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right. \quad \\&\quad\left. \frac{3b_1(t)i}{16c_1(t)}\coth \left( \frac{\sqrt{\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right\} ^{\frac{1}{2}}e^{i\left[ -kx- \frac{1}{64}\int _{0}^{t}\frac{15b_1^2(\sigma )+64a_1(\sigma )c_1(\sigma )k^2}{c_1(\sigma )}d\sigma \right] }, \end{aligned}$$

(2.56)

where $\Delta =\frac{3b_1^2(t)}{16c_1(t)(a_1(t)+d_1(t))}>0$.

Case XI

Eleventh set is:

$$\begin{aligned}&\small {a=-\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}, \,b=b, c=c,\,\,k=k,\,\, A_{0}=-\frac{3b_1(t)}{4c_1(t)},\,A_{1} =-\frac{b-c}{4}\sqrt{\frac{-3(a_1(t)+d_1(t))}{{c_1(t)}}}, } \end{aligned}$$

(2.57)

$$\begin{aligned}&B_{1} =\frac{b+c}{4}\sqrt{\frac{-3(a_1(t)+d_1(t))}{{c_1(t)}}}, \,w(t)=-\frac{1}{16t}\int _{0}^{t}\frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2-4(b^2-c^2)c_1(\sigma )(a_1(\sigma )+ d_1(\sigma ))}{c_1(\sigma )}d\sigma , \,\, \\&\quad U(\xi )=A_0+ A_{1}\tan \left( \frac{\Phi (\xi )}{2}\right) +B_{1}\cot \left( \frac{\Phi (\xi )}{2}\right) . \end{aligned}$$

(2.58)

By using of (2.57), (2.58) and Families 1, 2, 11 and 15 can be written, respectively, as

$$\begin{aligned} \psi _{25}(x,t)= & {} \left\{ -\frac{3b_1(t)}{4c_1(t)} -\frac{1}{4}\sqrt{\frac{-3(a_1(t)+d_1(t))}{{c_1(t)}}}\left[ a-\sqrt{-\Delta } \tan \left( \frac{\sqrt{-\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right] \right. \\&\quad\left. +\frac{b^2-c^2}{4}\sqrt{\frac{-3(a_1(t)+d_1(t))}{{c_1(t)}}}\left[ a-\sqrt{-\Delta } \tan \left( \frac{\sqrt{-\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right] ^{-1}\right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \frac{1}{16}\int _{0}^{t}\frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2-4(b^2-c^2)c_1(\sigma )(a_1(\sigma )+ d_1(\sigma ))}{c_1(\sigma )}d\sigma \right] }, \end{aligned}$$

(2.59)

where $\Delta =b^2-\frac{3b_1^2(t)}{4c_1(t)(a_1(t)+d_1(t))}-c^2<0$.

$$\begin{aligned} \psi _{26}(x,t)= & {} \left\{ -\frac{3b_1(t)}{4c_1(t)}-\frac{1}{4}\sqrt{\frac{-3(a_1(t)+d_1(t))}{{c_1(t)}}}\left[ a+\sqrt{\Delta } \tanh \left( \frac{\sqrt{\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right] \right. \\&\quad\left. +\frac{b^2-c^2}{4}\sqrt{\frac{-3(a_1(t)+d_1(t))}{{c_1(t)}}}\left[ a+\sqrt{\Delta } \tanh \left( \frac{\sqrt{\Delta }}{2}\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] \right) \right] ^{-1}\right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \frac{1}{16}\int _{0}^{t}\frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2-4(b^2-c^2)c_1(\sigma )(a_1(\sigma )+ d_1(\sigma ))}{c_1(\sigma )}d\sigma \right] }, \end{aligned}$$

(2.60)

where $\Delta =b^2-\frac{3b_1^2(t)}{4c_1(t)(a_1(t)+d_1(t))}-c^2>0$.

$$\begin{aligned} \psi _{27}(x,t)= & {} \left\{ -\frac{3b_1(t)}{4c_1(t)}-\frac{1}{4}\sqrt{\frac{-3(a_1(t)+d_1(t))}{{c_1(t)}}}\left[ \frac{\left( -\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}+b\right) e^{b\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] }-1}{\left( -\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}-b\right) e^{b\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] }-1}\right] \right. \\&\quad\left. +\frac{b^2-c^2}{4}\sqrt{\frac{-3(a_1(t)+d_1(t))}{{c_1(t)}}} \left[ \frac{\left( -\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}-b\right) e^{b\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] }-1}{\left( -\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}+b\right) e^{b\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] }-1}\right] \right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \frac{1}{16}\int _{0}^{t}\frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2-4(b^2-c^2)c_1(\sigma )(a_1(\sigma )+ d_1(\sigma ))}{c_1(\sigma )}d\sigma \right] }, \end{aligned}$$

(2.61)

$$\begin{aligned} \psi _{28}(x,t)= & {} \left\{ -\frac{3b_1(t)}{4c_1(t)}+\frac{1}{4}\sqrt{\frac{-3(a_1(t)+d_1(t))}{{c_1(t)}}}\left[ \frac{c\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] +2}{c\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] }\right] \right. \,\, \\&\quad\left. -\frac{b^2-c^2}{4}\sqrt{\frac{-3(a_1(t)+d_1(t))}{{c_1(t)}}} \left[ \frac{c\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] }{c\left[ x+\left( \frac{2k}{t}\int _{0}^{t} a_1(\sigma ) d\sigma \right) t+C\right] +2}\right] \right\} ^{\frac{1}{2}} \\&\quad\times e^{i\left[ -kx- \frac{1}{16}\int _{0}^{t}\frac{3b_1^2(\sigma )+16a_1(\sigma )c_1(\sigma )k^2-4(b^2-c^2)c_1(\sigma )(a_1(\sigma )+ d_1(\sigma ))}{c_1(\sigma )}d\sigma \right] }, \end{aligned}$$

(2.62)

where $c=-\frac{b_1(t)}{2}\sqrt{-\frac{3}{c_1(t)(a_1(t)+d_1(t))}}$ and C is constant.

3 The He’s semi-inverse variational principle method

Step 1

We suppose that given nonlinear partial differential equation for u(x, t) to be in the form

$$\mathcal {N}(u, u_x, u_t, u_{xx}, u_{tt},\ldots )=0,$$

(3.1)

which can be converted to an ODE

$$\mathcal {Q}(u, u^{\prime }, -\mu u^{\prime }, u^{\prime \prime }, \mu ^2u^{\prime \prime },\ldots )=0,$$

(3.2)

by the transformation $\xi =x-\mu t$ is the wave variable. Also, $\mu$ is constant to be determined later.

Step 2

According to He’s semi-inverse method, we construct the following trial-functional

$$J(U)=\int Ld\xi ,$$

(3.3)

where L is an unknown function of U and its derivatives.

Step 3

By the Ritz method, we can obtain different forms of solitary wave solutions, such as

$$U(\xi )=A sech(B\xi ),\quad U(\xi )=A csch(B\xi ),\quad U(\xi )=A \tanh (B\xi ),\quad U(\xi )=A \coth (B\xi ),$$

(3.4)

and so on. For example in this paper, we search a solitary wave solution in the form

$$U(\xi )=A sech(B\xi ),$$

(3.5)

and

$$U(\xi )=A \tanh (B\xi ),$$

(3.6)

where A and B are constants to be further determined. Substituting Eq. (3.5) or (3.6) into Eq. (3.3) and making J stationary with respect to A and B results in

$$\frac{\partial J}{\partial A}=0,$$

(3.7)

$$\frac{\partial J}{\partial B}=0.$$

(3.8)

Solving Eqs. (3.7) and (3.8), we obtain A and B. Hence the solitary wave solutions (3.5) or (3.6) are well determined. By He’s semi-inverse principle (He 2006; Kohl et al. 2009; Zhang 2007), we can obtain the following variational formulation for (2.8)

$$J=\int _{0}^{\infty }\left[ \frac{1}{2}(a_1(t)+d_1(t))(u^{\prime })^2-\frac{1}{2}\left( t\frac{d w(t)}{dt}+w(t)+k^2a_1(t)\right) u^2+\frac{1}{4}b_1(t)u^4+\frac{1}{6}c_1(t)u^6\right] d\xi .$$

(3.9)

By a Ritz-like method, we search a solitary wave solution in the form

$$u(\xi )=A sech(B\xi ),$$

(3.10)

where A and B are unknown constants to be further determined. Substituting Eq. (3.10) into Eq. (3.9), we have

$$\begin{aligned} J= \int _{0}^{\infty }\left[ \frac{1}{2}(a_1(t)+d_1(t))A^2sech(B\xi )^2\tanh (B\xi )^2B^2-\frac{1}{2}\left( t\frac{d w(t)}{dt}+w(t)+k^2\alpha (t)\right) A^2sech(B\xi )^2\;\;+ \frac{b_1(t)}{4}A^4sech(B\xi )^4+\frac{c_1(t)}{6}A^6sech(B\xi )^6\right] d\xi = \frac{1}{6}(a_1(t)+d_1(t))A^2B-\frac{1}{2B}\left( t\frac{d w(t)}{dt}+w(t)+k^2\alpha (t)\right) A^2+\frac{b_1(t)}{6B}A^4+\frac{4c_1(t)}{45B}A^6. \end{aligned}$$

(3.11)

Making J stationary with A and B yields

$$\frac{\partial J(A,B)}{\partial A}=\frac{1}{3}(a_1(t)+d_1(t))AB-\frac{1}{B}\left( t\frac{d w(t)}{dt}+w(t)+k^2\alpha (t)\right) A+\frac{2b_1(t)}{3B}A^3+\frac{8c_1(t)}{15B}A^5=0,$$

(3.12)

$$\frac{\partial J(A,B)}{\partial B}=\frac{1}{6}(a_1(t)+d_1(t))A^2+\frac{1}{2B^2}\left( t\frac{d w(t)}{dt}+w(t)+k^2\alpha (t)\right) A^2-\frac{b_1(t)}{6B^2}A^4-\frac{4c_1(t)}{45B^2}A^6=0.$$

(3.13)

Solving Eqs. (3.12) and (3.13), we obtain

$$\begin{aligned} A= \pm \frac{1}{8}\sqrt{\frac{1}{c_1(t)}\left[ -45b_1(t)\pm 3\sqrt{225b_1^2(t)+1280c_1(t)S(t)}\right] }, B= \pm \frac{1}{2}\sqrt{\frac{1}{a_1(t)+d_1(t)}\left( -6S(t)+\frac{3b_1(t)}{64c_1(t)} \left[ -15b_1(t)\pm \sqrt{225b_1^2(t)+1280c_1(t)S(t)}\right] \right) }, \end{aligned}$$

(3.14)

where

$$S(t)=t\frac{d w(t)}{dt}+w(t)+k^2\alpha (t).$$

By using the transformations (1.3), we will have

$$\begin{aligned} \psi (x,t)= \pm \frac{1}{8}\sqrt{\frac{1}{c_1(t)}\left[ -45b_1(t)\pm 3\sqrt{225b_1^2(t)+1280c_1(t)S(t)}\right] }\exp [-kx+w(t)t] \times sech\left[ \pm \frac{1}{2}\sqrt{\frac{1}{a_1(t)+d_1(t)}\left( -6S(t)+\frac{3b_1(t)}{64c_1(t)} \left[ -15b_1(t)\pm \sqrt{225b_1^2(t)+1280c_1(t)S(t)}\right] \right) }\left( x+2k\int _{0}^{t} \alpha (\sigma ) d\sigma \right) \right] . \end{aligned}$$

(3.15)

Also, we search a solitary wave solution in the form

$$u(\xi )=A \tanh (B\xi ),$$

(3.16)

where A and B are unknown constants to be further determined. Substituting Eq. (3.16) into Eq. (3.9), we have

$$\begin{aligned} J= \int _{0}^{\infty }\left[ \frac{1}{2}(a_1(t)+d_1(t))A^2(1-\tanh (Bx)^2)^2B^2-\frac{1}{2}\left( t\frac{d w(t)}{dt}+w(t)+k^2\alpha (t)\right) A^2\tanh (Bx)^2+ \frac{1}{4}b_1(t)A^4\tanh (Bx)^4+\frac{1}{6}c_1(t)A^6\tanh (Bx)^6\right] =\frac{1}{3}(a_1(t)+d_1(t))A^2B+ \frac{1}{2B}A^2\left( t\frac{d w(t)}{dt}+w(t)+k^2\alpha (t)\right) -\frac{1}{3B}b_1(t)A^4-\frac{23}{90B}c_1(t)A^6. \end{aligned}$$

(3.17)

Making J stationary with A and B yields

$$\frac{\partial J(A,B)}{\partial A}=\frac{2}{3}(a_1(t)+d_1(t))AB+\frac{1}{B}A\left( t\frac{d w(t)}{dt}+w(t)+k^2\alpha (t)\right) -\frac{4}{3B}b_1(t)A^3-\frac{23}{15B}c_1(t)A^5=0,$$

(3.18)

$$\frac{\partial J(A,B)}{\partial B}=\frac{1}{3}(a_1(t)+d_1(t))A^2- \frac{1}{2B^2}A^2\left( t\frac{d w(t)}{dt}+w(t)+k^2\alpha (t)\right) +\frac{1}{3B^2}b_1(t)A^4+\frac{23}{90B^2}c_1(t)A^6=0.$$

(3.19)

Solving Eqs. (3.18) and (3.19), we obtain

$$\begin{aligned} A= \pm \frac{\sqrt{69}}{46}\sqrt{\frac{1}{c_1(t)}\left[ -15b_1(t)\pm \sqrt{225b_1^2(t)+920c_1(t)S(t)}\right] }, B= \pm \frac{1}{2}\sqrt{\frac{1}{a_1(t)+d_1(t)}\left( 3S(t)-\frac{69b_1(t)}{2116c_1(t)} \left[ -15b_1(t)\pm \sqrt{225b_1^2(t)+920c_1(t)S(t)}\right] \right) }, \end{aligned}$$

(3.20)

where

$$S(t)=t\frac{d w(t)}{dt}+w(t)+k^2\alpha (t).$$

By using the transformations (1.3), we will have

$$\begin{aligned} \psi (x,t)= \pm \frac{\sqrt{69}}{46}\sqrt{\frac{1}{c_1(t)}\left[ -15b_1(t)\pm \sqrt{225b_1^2(t)+920c_1(t)S(t)}\right] }\exp [-kx+w(t)t] \times \tanh \left[ \pm \frac{1}{2}\sqrt{\pm \frac{1}{2}\sqrt{\frac{1}{a_1(t)+d_1(t)}\left( 3S(t)-\frac{69b_1(t)}{2116c_1(t)} \left[ -15b_1(t)\pm \sqrt{225b_1^2(t)+920c_1(t)S(t)}\right] \right) }}\left( x+2k\int _{0}^{t} \alpha (\sigma ) d\sigma \right) \right] . \end{aligned}$$

(3.21)

Fig. 1

Profile of the optical soliton $\psi _5$ with parabolic law nonlinearity

Fig. 2

Profile of the optical soliton $\psi _6$ with parabolic law nonlinearity

Fig. 3

Profile of the optical soliton $\psi _7$ with parabolic law nonlinearity

Fig. 4

Profile of the optical soliton $\psi _9$ with parabolic law nonlinearity

Fig. 5

Profile of the optical soliton $\psi _{10}$ with parabolic law nonlinearity

4 The physical explanation of the obtained solutions

Triki et al. (2012) studied the exact solutions of RNLSE equation with time-dependent coefficients through ansatz method approach and found bright soliton solutions and dark soliton solutions for five forms of nonlinearity. On the other hand, by means of the ITEM we have obtained 28 solutions for parabolic law nonlinearity. Moreover, for particular values of the free parameters, some of our solutions coincide with solutions of Triki et al. (2012). It proves that the other solutions are newly derived through the improved $\tan (\phi )$-expansion method. Similarly, it can be shown that Eslami et al. (2014) with first integral method have obtained 6 solutions for parabolic law nonlinearity. One see some of solutions by first integral method concur to the solutions of our considered method in this paper. Also, Mirzazadeh et al. (2014) with help of two methods, namely, $G^{\prime }/G$-expansion method and improved $G^{\prime }/G$-expansion method for dual-power law nonlinearity have found sufficient solutions that some of the solutions similar with the solutions of ITEM.

In this section, the numerical simulations of the RNLSE equation with time-dependent coefficients with parabolic law nonlinearity will be given. Now, we will discuss all possible physical significance for each parameter.

Remark

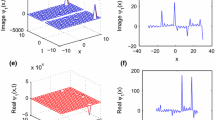
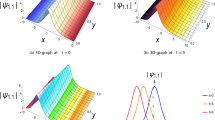
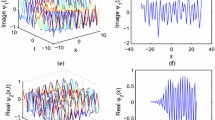
In Figs. 1, 2, 3, 4 and 5, we plot three dimensional and two dimensional graphics of absolute values of parabolic law nonlinearity solutions, which denote the dynamics of solutions with appropriate parametric selections. We plot three dimensional graphics of in Figs. 1, 2, 3, 4 and 5 for $-10<x<10, -10<t<10$. Moreover, we plot two dimensional graphics of Figs. 1, 2, 3, 4 and 5 when $-30<x<30, t=2$. In Fig. 1, we plot graphs for profiles from $\mathbf a$ to $\mathbf d$ with $k=2, a_1=t, b_1=2t, c_1=3t, d_1=4t$, and $\mathbf e$ to $\mathbf h$ with $k=2, a_1=\sin (t), b_1=\cos (t), c_1=\cos (t), d_1=\cos (t)-\sin (t)$. Moreover, in Fig. 2, we plot graphs for profiles from $\mathbf a$ to $\mathbf d$ with $k=2, a_1=t, b_1=2t, c_1=-3t, d_1=4t$, and $\mathbf e$ to $\mathbf h$ with $k=2, a_1=\sin (t), b_1=\cos (t), c_1=-\cos (t), d_1=\cos (t)-\sin (t)$. Also, in Fig. 3, for profiles $\mathbf a$ to $\mathbf d$ with $A_1=2, k=2, a_1=t, c_1=3t, d_1=4t$, and $\mathbf e$ to $\mathbf h$ with $A_1=2, k=2, a_1=\sin (t), c_1=\cos (t), d_1=\cos (t)-\sin (t)$. In Fig. 4, we plot graphs for profiles from $\mathbf a$ to $\mathbf d$ with $A_1=3, k=2, a_1=t, c_1=3t, d_1=4t$, and $\mathbf e$ to $\mathbf h$ with $A_1=3, k=2, a_1=sin(t), c_1=cos(t), d_1=sin(2t)+cos(2t)$. Finally, in Fig. 5, we plot graphs for profiles from $\mathbf a$ to $\mathbf d$ with $A_1=3, k=2, a_1=t, b_1=2t, c_1=3t, d_1=4t$, and $\mathbf e$ to $\mathbf h$ with $A_1=3, k=2, a_1=sin(t), b_1=cos(t), c_1=cos(t), d_1=sin(2t)+cos(2t)$.

For parabolic nonlinearity, $\psi _5$ as periodic solution, $\psi _6$ as dark soliton solution, $\psi _7$ as singular periodic solution, $\psi _9$ as singular solution, $\psi _{10}$ as polynomial solution. The analytical solutions and figures obtained in this paper give us a different physical interpretation for the RNLSE equation with time-dependent coefficients.

5 Conclusion

The integrable, resonant nonlinear Schrödinger equation has been shown to arise, in particular, in modeling of many physical, engineering, chemistry, biology, etc. The resonant nonlinear Schrödinger equation is studied with parabolic law nonlinearity. We compare analytical findings with the results of the other analytical schemes describing the ansatz method approach (Eslami et al. 2014; Triki et al. 2012) are used to carry out the integration. Description of the methods are given and the obtained results reveal that the ITEM and HSIVM are new significant methods for exploring nonlinear partial differential models. The obtained results are useful in gaining understanding of behavior of solitons.