1 Introduction

Higher dimensional integrable systems have been dealt with recently from physical and mathematical points of view. Because of its significant effects in scientific areas, immense research has been invested in constructing and studying integrable models. The higher dimensional integrable equations have attracted lot of studies in various fields, such as solitary waves theory, ion-acoustic waves in plasmas, and many other scientific fields. The Painlevé integrable systems exhibit multiple solitons solutions and infinite conservation laws [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16].

In [1], a (3 + 1)-dimensional Kadomtsev–Petviashvili-type equation was introduced as

$$\begin{aligned}{} & {} au_{xt}-\frac{a^4+b^4-6a^2b^2}{16}u_{xxxx}-\frac{3(b^2-a^2)}{4}(u^2)_{xx}\nonumber \\{} & {} \quad -\frac{3}{4}u_{yy}+\frac{3}{4}u_{zz}=0, \end{aligned}$$
(1)

which admits a weak dispersion term \(u_{xxxx}\), was introduced in [1]. The Bäcklund transformation was used to investigate its integrability [1]. However, equation (1) is not Painlevé integrable in its given form.

Researchers invested a great deal of works to extend and generalize the integrable systems [11,12,13,14,15,16,17,18,19,20] to higher dimensional models. These works have led to the formation of many higher dimensional integrable systems. The higher-dimensional integrable models allow us to explore the solution dynamics through using a variety of powerful techniques [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. Two comprehensive review papers appeared recently in [33, 34] in the area of nonlinear wave structures in many physical settings, including nonlinear optics and photonics and matter waves in Bose–Einstein condensates. Researchers in [33] examined the two- and three-dimensional solitons and related states, such as quantum droplets, that can appear in optical systems, atomic Bose–Einstein condensates, and liquid crystals, among other physical settings. However, in the overview presented in [34], new findings concerning light bullets, the creation and diverse applications of few-cycle (ultra-narrow) optical pulses, and the emergence of rogue waves in various media were formally furnished.

We now propose an extended (3 + 1)-dimensional Painlevé integrable equation that reads

$$\begin{aligned}{} & {} au_{xt}-\frac{a^4-6a^2b^2+b^4}{16}u_{xxxx}-\frac{3(b^2-a^2)}{4}(u^2)_{xx}\nonumber \\{} & {} \quad +\alpha u_{xx}+\beta u_{xy}+\gamma u_{xz}+\lambda u_{zz}+\mu u_{yz}\nonumber \\{} & {} \quad +\frac{\mu ^2}{4\lambda } u_{yy}=0, \end{aligned}$$
(2)

that extends (1) by adding more linear terms, where \(a, b, \alpha , \beta , \gamma , \lambda ,\) and \(\mu \) are real numbers, but \(a, \lambda \ne 0\), and \(u = u(x, y, z, t)\) is a sufficiently differentiable function with respect to the spatial and the temporal variables.

It is to be noted that for \(\gamma =0, \lambda =0\), and \(\mu =0\), equation (2) will be transformed to a (2 + 1)-dimensional equation as

$$\begin{aligned}{} & {} au_{xt}-\frac{a^4-6a^2b^2+b^4}{16}u_{xxxx}-\frac{3(b^2-a^2)}{4}(u^2)_{xx}\nonumber \\{} & {} \quad +\alpha u_{xx}+\beta u_{xy} +\eta u_{yy}=0, \end{aligned}$$
(3)

where \( u = u(x, y, t)\). Equation (3) will be studied later in details. However, each equation (2) or (3) involves one nonlinear term \((u^2)_{xx}\) in addition to the remaining linear terms.

Studies on multiple soliton solutions and lump solutions have been flourishing recently for their important roles in nonlinear scientific fields. Lumps are characterized by locality with high amplitude. Lumps and solitons can be obtained via using the Hirota bilinear form [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Physically a lump may be detached (or emitted) from a line soliton, survives for a brief transient period in time, and then merges with the next adjacent soliton. Several powerful schemes, such as the Hirota method, and Darboux transformation method, have been formally employed for studying nonlinear integrable models [30,31,32,33,34].

In this article, we will first confirm THE complete integrability of the extended (3 + 1)- and (2 + 1)-dimensional KP equation (2) and (3) via using the Painlevé test to show each retrieves Painlevé integrability, whereas Eq. (1) is not Painlevé integrable. Consequently, multiple soliton solutions can be derived for both extended equations. In addition, a class of lump solutions will be furnished for both extended KP equations (2) and (3) by using distinct values of the employed parameters.

2 Extended (3 + 1)-dimensional nonlinear KP equation

We will first emphasize the Painlevé integrability for the extended (3 + 1)-dimensional nonlinear KP equation (2). Next, the Hirota’s method will be used to formally derive the multiple soliton solutions for this extended model. A class of lump solutions will be furnished, and we will select two cases of the employed parameters to derive lump solutions. Other lump solutions will be furnished.

2.1 Painlevé analysis to Eq. (2)

Many powerful tools, such as Lax pair, and Painlevé Analysis, can be used to test integrability of any nonlinear evolution equation [1,2,3,4,5,6,7,8,9,10]. To show that Eq. (2) retrieves its integrability, although some linear terms were added, we employ the Painlevé analysis method [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20].

We assume that Eq. (2) has a solution, given as a Laurent expansion about a singular manifold \(\psi =\psi (x,y,z,t)\) as

$$\begin{aligned} u(x,y,z,t)=\sum _{k=0}^{\infty }\,u_k(x,y,z,t)\,\psi ^{k-\gamma }. \end{aligned}$$
(4)

This in turn gives a characteristic equation with one branch for resonances at \(k=-1, 4, 5,\) and 6. The resonance at \(k = -1\) corresponds to \(\psi (x,y,z,t) = 0\). Moreover, explicit expressions for \(u_1, u_{2}\), and \(u_3\) were furnished. However, we found that \( u_{4}, u_5, u_{6}\) turn out to be arbitrary functions for all real values of the parameters \( \alpha , \beta , \gamma , \lambda , \mu , a\) and b. Moreover, it is necessary to note that \(a \ne 0, a\ne \pm b,\) and \(\lambda \ne 0\). This confirms the Painlevé integrability of the (3 + 1)-dimensional Eq. (2).

However, for \(\gamma =0, \lambda =0\), and \(\mu =0\), the reduced (2 + 1)-dimensional equation is also Painlevé integrable via using Painlevé analysis. Based on this, we will study briefly this case related to the multiple soliton solutions in the next section.

2.2 Multiple soliton solutions

To derive the multiple soliton solutions of Eq. (2), we substitute

$$\begin{aligned} u(x, y, z, t)=e^{k_ix+r_iy+s_iz-c_i t}, \end{aligned}$$
(5)

into the linear terms of (2) to obtain the dispersion relations as

$$\begin{aligned} c_i= \frac{-(a^4-6a^2b^2+b^4)\, \lambda k_i^4+16\lambda k_i(\beta r_i+\gamma s_i)+4\mu r_i(4\lambda s_i+\mu r_i)+16\lambda (\alpha k_i^2+\lambda s_i^2) }{16a\lambda k_i}, \end{aligned}$$
(6)

and hence, the phase variables

$$\begin{aligned}{} & {} \theta _i=k_i x+r_i y+s_i z \nonumber \\{} & {} \quad -\frac{-(a^4-6a^2b^2+b^4)\,\lambda k_i^4+16\lambda k_i(\beta r_i+\gamma s_i)+4\mu r_i(4\lambda s_i+\mu r_i)+16\lambda (\alpha k_i^2+\lambda s_i^2) }{16a\lambda k_i}\, t, \end{aligned}$$
(7)

follow immediately for \(i=1, 2, \cdots , N\). We next use the transformation

$$\begin{aligned} u(x,y,z,t)=R(\ln \,f(x,y,z,t))_{xx}, \end{aligned}$$
(8)

into Eq. (2), where the auxiliary function f(x, y, z, t) reads

$$\begin{aligned}{} & {} f(x,y,z,t)=1+e^{\theta _1}=1+e^{k_1 x+r_1 y+s_1 z -\frac{-(a^4-6a^2b^2+b^4)\lambda k_1^4+16\lambda k_1(\beta r_1+\gamma s_1)+4\mu r_1(4\lambda s_1+\mu r_1)+16\lambda (\alpha k_1^2+\lambda s_1^2) }{16a\lambda k_1}\, t}, \end{aligned}$$
(9)

used for deriving the single soliton solution. This gives

$$\begin{aligned} R=-\frac{(a^4-6a^2b^2+b^4)}{2(a^2-b^2)}. \end{aligned}$$
(10)

Based on this, the single soliton solution follows upon substituting (10) and (9) into (8) as

$$\begin{aligned} u(x,y,z,t)=-\frac{ (a^4-6a^2b^2+b^4) e^{k_1x+r_1y+s_1z- \frac{-\lambda (a^4-6a^2b^2+b^4)k_1^4 +16\lambda k_1(\beta r_1+\gamma s_1)+4\mu r_1(4\lambda s_1+\mu r_1)+16\lambda (\alpha k_1^2+\lambda s_1^2)}{16a\lambda k_1}} }{2(a^2-b^2)(1+e^{k_1x+r_1y+s_1z- \frac{-\lambda (a^4-6a^2b^2+b^4)k_1^4 +16\lambda k_1(\beta r_1+\gamma s_1)+4\mu r_1(4\lambda s_1+\mu r_1)+16\lambda (\alpha k_1^2+\lambda s_1^2)}{16a\lambda k_1}}}. \end{aligned}$$
(11)

For the two soliton solutions, we use the auxiliary function as

$$\begin{aligned} \begin{array}{rcl} f(x,y,z,t)= & {} 1+e^{\theta _1}+e^{\theta _2}+a_{12}e^{\theta _1+\theta _2}, \end{array} \end{aligned}$$
(12)

where \(a_{12}\) is the phase shift of the interaction of solitons. To determine the phase shift \(a_{12}\), we substitute (12) into (2), and solving we obtain

$$\begin{aligned} a_{12}= & {} \frac{3\lambda (a^4-6a^2b^2+b^4)k_1^2k_2^2(k_1-k_2)^2 +16\lambda ^2(k_1s_2-k_2s_1)^2+4\mu ^2(k_1r_2-k_2r_1)^2+16\lambda \mu (k_1r_2-k_2r_1)(k_1s_2-k_2s_1)}{3\lambda (a^4-6a^2b^2+b^4)k_1^2k_2^2(k_1+k_2)^2 +16\lambda ^2(k_1s_2-k_2s_1)^2+4\mu ^2(k_1r_2-k_2r_1)^2+16\lambda \mu (k_1r_2-k_2r_1)(k_1s_2-k_2s_1)},\nonumber \\ \end{aligned}$$
(13)

which can be generalized as

$$\begin{aligned} a_{ij}= & {} \frac{3\lambda (a^4-6a^2b^2+b^4)k_i^2k_j^2(k_i-k_j)^2 +16\lambda ^2(k_is_j-k_js_i)^2+4\mu ^2(k_ir_j-k_jr_i)^2+16\lambda \mu (k_ir_j-k_jr_i)(k_is_j-k_js_i)}{3\lambda (a^4-6a^2b^2+b^4)k_i^2k_j^2(k_i+k_j)^2 +16\lambda ^2(k_is_j-k_js_i)^2+4\mu ^2(k_ir_j-k_jr_i)^2+16\lambda \mu (k_ir_j-k_jr_i)(k_is_j-k_js_i)}, \nonumber \\ \end{aligned}$$
(14)

for \( \,\,1\le i<j\le 3.\) This result shows that the phase shifts (14) depend only on \(a, b, \lambda \) and \(\mu \) as well as on the coefficients of the spatial parameters \(k_n, r_n\) and \(s_n, n=1,2,3\). Substituting (13) and (12) into (8) provides the two soliton solutions.

For the three soliton solutions, we apply the auxiliary function f(x, y, z, t) as

$$\begin{aligned}{} & {} f(x,y,z,t)=1+e^{\theta _1}+e^{\theta _2}+e^{\theta _3}+a_{12}e^{\theta _1+\theta _2}\nonumber \\{} & {} \quad +a_{13}e^{\theta _1+\theta _3}+a_{23}e^{\theta _2+\theta _3}+a_{12}a_{23}a_{13}e^{\theta _1+\theta _2+\theta _3}\nonumber \\ \end{aligned}$$
(15)

Substituting (15) into (8) provides three soliton solutions.

2.3 The (3 + 1)-dimensional model: lump solutions

Lump solution is a kind of rational function solution localized in all spatial directions [20,21,22,23,24,25,26,27,28,29,30,31,32]. This is unlike a soliton solution which is exponentially localized in all directions in spatial and temporal variables [1,2,3,4,5,6,7,8,9,10,11,12]. Usually, we use the generalized positive quadratic function to study the lump solutions. To derive lump solutions, we transform the (3 + 1)-dimensional KP equation (2) into a bilinear equation in operators as

$$\begin{aligned}{} & {} \left( aD_xD_t-\frac{a^4-6a^2b^2+b^4}{16}D_x^4+ \alpha D_x^2+\beta D_xD_y\right. \nonumber \\{} & {} \left. +\gamma D_xD_z+\lambda D_z^2+\mu D_yD_z+\frac{\mu ^2}{4\lambda } D_y^2\right) f\cdot f=0, \nonumber \\ \end{aligned}$$
(16)

where \(D_t, D_x, D_y,\) and \(D_z\) are the Hirota’s bilinear derivative operators. To ease computational works, we substitute \(\alpha =\beta =\gamma \), and \( \mu =2\lambda \) in (3 + 1)-dimensional KP equation (2) to obtain

$$\begin{aligned}{} & {} au_{xt}-\frac{a^4-6a^2b^2+b^4}{16}u_{xxxx}\nonumber \\{} & {} \quad -\frac{3(b^2-a^2)}{4}(u^2)_{xx}+\alpha (u_{xx}+u_{xy}+ u_{xz})\nonumber \\{} & {} \quad +\lambda ( u_{zz}+2 u_{yz}+u_{yy})=0. \end{aligned}$$
(17)

Consequently, equation (16) is transformed to

$$\begin{aligned} \begin{array}{ll} &{}a(ff_{xt}-f_xf_t)-\frac{a^4-6a^2b^2+b^4}{16}\\ &{}\quad \times (ff_{xxxx}-4f_{xxx}f_{x}+3(f_{xx})^2)\\ &{} \quad + \alpha \left( (ff_{xx}-f_xf_x)+ (ff_{xy}-f_xf_y) \right. \\ &{}\quad \left. + (ff_{xz}-f_xf_z)\right) \\ &{} \quad + \lambda \left( (ff_{zz}-f_zf_z)+ 2(ff_{yz}-f_yf_z) \right. \\ &{}\quad \left. + (ff_{yy}-f_yf_y)\right) =0, \end{array} \end{aligned}$$
(18)

obtained upon using

$$\begin{aligned} u(x,y,z,t)=-\frac{a^4-6a^2b^2+b^4}{2(a^2-b^2)}(\ln f(x,y,z,t))_{xx}. \end{aligned}$$
(19)

To obtain the quadratic soliton solutions for (17), we set

$$\begin{aligned} \begin{array}{rcl} g&{}=&{}a_1x+a_2y+a_3z+a_4t+a_5,\\ h&{}=&{}a_6x+a_7y+a_8z+a_9t+a_{10},\\ f&{}=&{}g^2+h^2+a_{11}, \end{array} \end{aligned}$$
(20)

where \(a_j, 1\le j\le 11\) are real parameters that we will be derived. Substituting (20) in (18), we get a polynomial of the variables x, y, z,  and t. To determine the parameters \(a_j, 1\le j\le 11\), we build up a system of equations of the coefficients of the variables and the constant terms. In what follows, we highlight some cases of a variety of parameters.

Case 1.

We first select

$$\begin{aligned}&a_1=a_1, a_2=a_2, a_3=a_3, a_4=a_4,a_{10}=a_{10},\nonumber \\&a_5=\frac{a_{1} a_{10} \left( \alpha ( a_{1}+ a_{2}+a_{3})+a a_{4}\right) }{\sqrt{\lambda a_1\left( \alpha ( a_{1}+ a_{2}+a_{3})+a a_{4}\right) }\, \left( a_{2}+a_{3}\right) }, a_{2} \ne -a_{3},\nonumber \\&a_6= \frac{\sqrt{\lambda a_1 \left( \alpha (a_{1}+a_{2}+a_{3})+a a_{4}\right) }\, \left( a_{2}+a_{3}\right) }{\alpha ( a_{1}+ a_{2}+a_{3})+a a_{4}},\nonumber \\&a_{7}= -\frac{a_{1} a_{2} \left( \alpha ( a_{1}+ a_{2}+a_{3})+a a_{4}\right) }{\sqrt{\lambda a_1\left( \alpha ( a_{1}+ a_{2}+a_{3})+a a_{4}\right) }\, \left( a_{2}+a_{3}\right) }, a_{2} \ne -a_{3},\nonumber \\&a_8=-\frac{a_{1} a_{3} \left( \alpha ( a_{1}+ a_{2}+a_{3})+a a_{4}\right) }{\sqrt{\lambda a_1\left( \alpha ( a_{1}+ a_{2}+a_{3})+a a_{4}\right) }\, \left( a_{2}+a_{3}\right) }, a_{2} \ne -a_{3},\nonumber \\&a_9=\frac{\alpha ^2(a_1^2+a_1a_2+a_1a_3)+\alpha \lambda (a_2+a_3)^2+\lambda a a_4(a_2+a_3)+\alpha a a_1 a_4}{a\sqrt{\lambda a_1\left( \alpha ( a_{1}+ a_{2}+a_{3})+a a_{4}\right) }},\nonumber \\&a_{11}= \frac{3 \left( a^{4}-6 a^{2}b^{2} +b^{4}\right) \left( \alpha (a_{1}^{2}+a_{1} a_{2}+a_{1} a_{3}) +\lambda (a_{2} + a_{3})^2+a a_{1} a_{4}\right) a_{1}^{2}}{16 \left( \alpha (a_{1}+a_{2} a_{3})+a a_{4}\right) ^{2}}, \end{aligned}$$
(21)

which needs to satisfy

$$\begin{aligned}{} & {} \alpha (a_{1}+a_{2} a_{3})+a a_{4}\ne 0, \, \text{ and } \nonumber \\{} & {} \quad \lambda a_1(\alpha (a_{1}+a_{2} a_{3})+a a_{4})>0, \end{aligned}$$
(22)

to obtain a well-defined function f(x, y, z, t) and its positiveness. We can furnish a class of lump solutions to Eq. (17) by using u(x, y, z, t)) as follows

$$\begin{aligned} u(x,y,z,t)= & {} -\frac{(b^4-6a^2b^2+b^4)}{2(a^2-b^2)}\nonumber \\{} & {} \times (\ln (f(x,y,z,t))_{xx},\nonumber \\= & {} -\frac{(b^4-6a^2b^2+b^4)}{2(a^2-b^2)}\nonumber \\{} & {} \times \frac{2(a_1^2+a_6^2)f-4(a_1g+a_6h)^2}{f^2}, \end{aligned}$$
(23)

where f, g,  and h are given earlier in (20). Note that the obtained lump solutions \(u(x,y,z,t)\rightarrow 0\) if and only if \( g^2+h^2 \rightarrow \infty \).

For example, selecting

$$\begin{aligned}{} & {} a_1=1, a_2=2,a_3=1, a_4=2,a_{10}=2,a=6,\nonumber \\{} & {} b=2,\lambda =4,\alpha =1, \end{aligned}$$
(24)

gives

$$\begin{aligned} a_5= & {} \frac{4}{3}, a_6=\frac{3}{2},a_7= -\frac{4}{3}, a_8=-\frac{2}{3},\nonumber \\ a_9= & {} \frac{49}{12}, a_{11}=\frac{273}{16}. \end{aligned}$$
(25)

The lump solution follows as

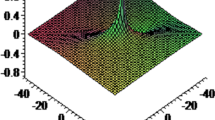
$$\begin{aligned} u= \frac{111384 t^{2}+\left( 90720 x +16128 y +8064 z +120960\right) t +18144 x^{2}-32256 y^{2}-32256 y z -8064 z^{2}+48384 x -63000}{\left( 229 t^{2}+180 t x -32 t y -16 t z +36 x^{2}+64 y^{2}+64 y z +16 z^{2}+240 t +96 x +253\right) ^{2}}. \end{aligned}$$
(26)

Using the parameters as given earlier, and substituting \(z=1, t=2\) leads to (Figs. 1, 2, 3)

$$\begin{aligned} u(x,y,z,t)= \frac{504(36x^2-64y^2+456x+1255)}{(36x^2 +64y^2+456x+163)^2}. \nonumber \\ \end{aligned}$$
(27)
Fig. 1
figure 1

Profile of the lump solution for (27), \(-20\le x, y\le 20 \)

Full size image
Fig. 2
figure 2

Profile of the contour plot for (27), \(-40\le x, y\le 40 \)

Full size image
Fig. 3
figure 3

Profile of the density plot for (27), \(-50\le x, y\le 50\)

Full size image

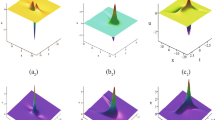
Case 2.

We next select

$$\begin{aligned} \begin{array}{ll} &{}a_1=a_1, a_2=a_2, a_3=a_3, a_5=a_5,a_6=a_6,a_7=a_7,a_8=a_8,a_{10}=a_{10},\\ &{}a_4=-{\frac{\alpha (a_1+a_2+a_3)(a_1^2+a_6^2)+\lambda a_1(a_2+a_3)^2 -\lambda a_1(a_7+a_8)^2 +2\lambda a_6(a_2+a_3)(a_7+a_8)}{a \left( {a_{{1}}}^{2}+{a_{{6}}}^{2} \right) }},\\ &{}a_9= -{\frac{ \alpha (a_6+a_7+a_8)(a_1^2+a_6^2)+2\lambda a_1(a_2+a_3)(a_7+a_8) -\lambda a_6(a_2+a_3)^2+\lambda a_6(a_7+a_8)^2}{a \left( {a_{{1}}}^{2}+{a_{{6}}}^{2} \right) }},\\ &{}a_{11}= \frac{3(a^4-6a^2b^2+b^4)(a_1^2+a_6^2)^3}{16\lambda \left( a_{{1}}a_{{7 }}+a_{{1}}a_{{8}}-a_{{2}}a_{{6}}-a_{{3}}a_{{6}} \right) ^{2}}, \end{array} \end{aligned}$$
(28)

where \(a \ne 0, \lambda \ne 0\), to derive a well-defined function f(x, y, z, t) as furnished earlier. A class of lump solutions to the Eq. (17) is furnished by using u(x, y, z, t)) as follows

$$\begin{aligned} \begin{array}{rcl} &{}&{}u(x,y,z,t)=-\frac{a^4-6a^2b^2+b^4}{2(a^2-b^2)} (\ln (f(x,y,z,t))_{xx},\\ &{}&{}\quad = -\frac{a^4-6a^2b^2+b^4}{2(a^2-b^2)}\left( \frac{2(a_1^2+a_6^2)f-4(a_1g+a_6h)^2}{f^2}\right) , \end{array} \end{aligned}$$
(29)

where f, g,  and h are given earlier in (20). Note that the obtained lump solutions \(u(x,y,z,t)\rightarrow 0\) if and only if \( g^2+h^2 \rightarrow \infty \).

3 Extended (2 + 1)-dimensional nonlinear KP equation

Setting \(\gamma =0, \lambda =0\) and \(\mu =0\) in (2), the (3 + 1)-dimensional Painlevé integrable (2) reduces to the (2 + 1)-dimensional equation

$$\begin{aligned}{} & {} au_{xt}-\frac{a^4-6a^2b^2+b^4}{16}u_{xxxx}-\frac{3(b^2-a^2)}{4}(u^2)_{xx}\nonumber \\{} & {} \quad +\alpha u_{xx}+\beta u_{xy}+\eta u_{yy}=0, \end{aligned}$$
(30)

where \(a, b, \alpha , \beta \) and \(\eta \), are real parameters, \(a \ne 0\), and \(u = u(x, y,t)\) is a sufficiently differentiable function with respect to the spatial and the temporal variables x, y,  and t.

3.1 Painlevé analysis

Following the Painlevé analysis that we employed earlier for the (3 + 1)-dimensional structure (2) shows that the (2 + 1)-dimensional equation (30) is completely Painlevé integrable. Moreover, the resonance points were derived as \(-1, 4, 5, 6\), the same as obtained for the (3 + 1)-dimensional model (2).

3.2 Multiple soliton solutions

Substituting

$$\begin{aligned} u(x, y, t)=e^{k_ix+r_iy-c_i t}, \end{aligned}$$
(31)

into the linear terms of (30) gives the dispersion relation as

$$\begin{aligned} c_i= & {} \frac{-(a^4-6a^2b^2+b^4)k_i^4+16(\alpha k_i^2+ \beta k_i r_i+\eta r_i^2)}{16ak_i}, \nonumber \\{} & {} \quad i=1, 2, \ldots , N, \end{aligned}$$
(32)

that gives the phase variable as

$$\begin{aligned}{} & {} \theta _i=k_i x+r_i y \nonumber \\{} & {} \quad - \frac{-(a^4-6a^2b^2+b^4)k_i^4+16(\alpha k_i^2+ \beta k_i r_i+\eta r_i^2)}{16ak_i}\nonumber \\{} & {} \qquad t, i=1, 2, \ldots , N, \end{aligned}$$
(33)

follows immediately. We next use the transformation

$$\begin{aligned} u(x,y,t)=-\frac{a^4-6a^2b^2+b^4}{2(a^2-b^2)}(\ln \,f(x,y,t))_{xx}, \end{aligned}$$
(34)

into Eq. (30), where the auxiliary function f(x, y, t) is

$$\begin{aligned}{} & {} f(x,y,t)=1+e^{\theta _1} \nonumber \\{} & {} \quad =1+e^{k_1 x+r_1y- \frac{-(a^4-6a^2b^2+b^4)k_1^4+16(\alpha k_1^2+ \beta k_1 r_1+\eta r_1^2)}{16ak_1}\, t,}, \end{aligned}$$
(35)

and hence, the single soliton solution reads

$$\begin{aligned}{} & {} u(x,y,t)=-\frac{(a^4-6a^2b^2+b^4)k_1^2e^{k_1 x+r_1y- \frac{-(a^4-6a^2b^2+b^4)k_1^4+16(\alpha k_1^2+ \beta k_1 r_1+\eta r_1^2)}{16ak_1}\, t}}{2(a^2-b^2)\left( 1+e^{k_1 x+r_1y- \frac{-(a^4-6a^2b^2+b^4)k_1^4+16(\alpha k_1^2+ \beta k_1 r_1+\eta r_1^2)}{16ak_1}\, t}\right) ^2}. \end{aligned}$$
(36)

For the two soliton solutions, the auxiliary function reads

$$\begin{aligned} f(x,y,t)=1+e^{\theta _1}+e^{\theta _2}+a_{12}e^{\theta _1+\theta _2}, \end{aligned}$$
(37)

that will lead to the following phase shifts

$$\begin{aligned} a_{12}=\frac{3(a^4-6a^2b^2-b^4)k_1^2k_2^2(k_1-k_2)^2 +16\eta (k_1r_2-k_2r_1)^2}{3(a^4-6a^2b^2-b^4)k_1^2k_2^2(k_1+k_2)^2 +16\eta (k_1r_2-k_2r_1)^2}, \end{aligned}$$
(38)

which can be generalized as

$$\begin{aligned} a_{ij}=\frac{3(a^4-6a^2b^2-b^4)k_i^2k_2^2(k_i-k_j)^2 +16\eta (k_ir_j-k_jr_i)^2}{3(a^4-6a^2b^2-b^4)k_i^2k_j^2(k_i+k_j)^2 +16\eta (k_ir_j-k_jr_i)^2}, 1\le i<j\le 3, \end{aligned}$$
(39)

where the phase shifts (39) depend only on the parameters a, b,  and \(\eta \), and on the spatial coefficients \(k_n,\) and \(r_n, n=1,2,3\). Substituting (38) and (37) into (34) gives the two soliton solutions. In addition, the three soliton solutions can be obtained as employed earlier.

3.3 The (2 + 1)-dimensional model: lump solutions

The bilinear equation of the KP equation (30) can be set as

$$\begin{aligned}{} & {} \left( aD_xD_t-\frac{a^4-6a^2b^2+b^4}{16}D_x^4+ \alpha D_x^2+\beta D_xD_y+\eta D_y^2\right) \nonumber \\{} & {} \quad f\cdot f=0, \end{aligned}$$
(40)

where \(D_t, D_x,\) and \(D_y\) are the Hirota’s bilinear derivative operators. To ease computational works, we substitute \(\alpha =\beta \), in (2 + 1)-dimensional KP equation (30) to obtain

$$\begin{aligned}{} & {} au_{xt}-\frac{a^4-6a^2b^2+b^4}{16}u_{xxxx}-\frac{3(b^2-a^2)}{4}(u^2)_{xx} \nonumber \\{} & {} \quad +\alpha (u_{xx}+u_{xy})+\eta u_{yy}=0. \end{aligned}$$
(41)

Consequently, Eq. (40) is transformed to

$$\begin{aligned} \begin{array}{ll} &{}a(ff_{xt}-f_xf_t)\\ &{}\quad -\frac{a^4-6a^2b^2+b^4}{16}(ff_{xxxx}-4f_{xxx}f_{x}+3(f_{xx})^2) \\ &{}+ \alpha \left( (ff_{xx}-f_xf_x)+ (ff_{xy}-f_xf_y)\right) \\ &{}\quad +\eta (ff_{yy}-f_yf_y) =0, \end{array} \end{aligned}$$
(42)

where we applied

$$\begin{aligned} u(x,y,t)=-\frac{b^4-6a^2b^2+b^4}{2(a^2-b^2)}(\ln f(x,y,t))_{xx}. \end{aligned}$$
(43)

The quadratic soliton solutions for Eq. (41) can be obtained by using the assumptions

$$\begin{aligned} \begin{array}{rcl} g&{}=&{}a_1x+a_2y+a_3t+a_4,\\ h&{}=&{}a_5x+a_6y+a_7t+a_{8},\\ f&{}=&{}g^2+h^2+a_{9}, \end{array} \end{aligned}$$
(44)

where \(a_j, 1\le j\le 9\) are real parameters that we will be derived. Substituting (44) in (42), we get a polynomial of the variables x, y,  and t, where the parameters \(a_j, 1\le j\le 9\), can be obtained as furnished earlier:

Case 1.

In this case, we select

$$\begin{aligned} \begin{aligned} a_1&= \frac{a_6\sqrt{\alpha \eta }}{\alpha },\\ a_2&=-\frac{a a_3}{\alpha },\\ a_4&=\frac{a_6 a_8 \alpha }{a a_3},\\ a_5&= \frac{a a_3\sqrt{\alpha \eta }}{\alpha ^2},\\ a_7&= -\frac{a_6 \alpha }{a},\\ a_9&= \frac{ 2\eta \left( \alpha ^2 a_6^2(a^4-6a^2b^2+b^4)(\alpha ^2 a_6^2+a^2a_3^2)\right) }{16\alpha ^4}, \end{aligned} \end{aligned}$$
(45)

where

$$\begin{aligned} a, a_3, \alpha \ne 0, \end{aligned}$$
(46)

to obtain a well-defined function f(x, y, t), and to strengthen the localization of u(x, y, t) in all directions in the space. Hence, lump solutions to the KP equation (41) read

$$\begin{aligned} \begin{array}{rcl} u(x,y,t)&{}=&{}-\frac{b^4-6a^2b^2+b^4}{2(a^2-b^2)} (\ln (f(x,y,z,t))_{xx},\\ &{}=&{} -\frac{b^4-6a^2b^2+b^4}{2(a^2-b^2)} \frac{2(a_1^2+a_5^2)f-4(a_1g+a_5h)^2}{f^2}, \end{array} \end{aligned}$$
(47)

where f, g,  and h are given earlier in (44).

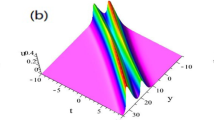
For example, selecting

$$\begin{aligned}{} & {} a_3=1, a_6=2,a_{8}=2,a=6,b=2,\eta =2,\nonumber \\{} & {} \alpha =1,t=2, \end{aligned}$$
(48)

gives the lump solution as

$$\begin{aligned} \begin{array}{rcl} &{}&{}u(x,y,t)\\ {} &{}&{}\quad = 1008\times {\frac{24\,\sqrt{2}x-{t}^{2}+12\,ty+72\,{x}^{2}-36\,{y}^{2}- 6044}{ \left( 24\,\sqrt{2}x+{t}^{2}-12\,ty+72\,{x}^{2}+36\,{y}^{2}+ 6052 \right) ^{2}}}. \end{array} \end{aligned}$$
(49)

Case 2.

We next choose

$$\begin{aligned} a_1= & {} a_1, a_2=a_2, a_4=a_4, a_5=a_5,a_6=a_6,a_8=a_8,\nonumber \\ a_3= & {} \frac{\alpha (a_1+a_2)(a_1^2+a_5^2) +\eta (a_1a_2^2-a_1a_6^2+2a_2 a_5 a_6)}{a(a_1^2+a_5^2)},\nonumber \\{} & {} a \ne 0, \nonumber \\ a_7= & {} -\frac{\alpha (a_5+a_6)(a_1^2+a_5^2) + \eta (2a_1a_2a_6-a_5a_2^2+a_5a_6^2)}{a(a_1^2+a_5^2)},\nonumber \\{} & {} a\ne 0, \nonumber \\ a_9= & {} \frac{3(a^4-6a^2b^2+b^4)(a_1^2+a_5^2)^3)}{16\eta (a_1a_6-a_2a_5)^2}, \end{aligned}$$
(50)

where \(a \ne 0, \eta \ne 0\), and the determinant condition

$$\begin{aligned} \Delta =\left( a_1a_6-a_2a_5\right) =\left| \begin{array}{cc} a_1 &{}a_2\\ a_5&{}a_6 \end{array} \right| \ne 0, \end{aligned}$$
(51)

to secure a well-defined function f(x, y, t), and localization of u(x, y, t) in all spatial sides, respectively. This gives lump solutions to the (3 + 1)-dimensional KP equation (41) as

$$\begin{aligned} \begin{array}{rcl} &{}&{}u(x,y,t)=-\frac{b^4-6a^2b^2+b^4}{2(a^2-b^2)} (\ln (f(x,y,t))_{xx},\\ &{}&{}\quad = -\frac{b^4-6a^2b^2+b^4}{\times }{2(a^2-b^2)} \frac{2(a_1^2+a_5^2)f-4(a_1g+a_5h)^2}{f^2}, \end{array} \end{aligned}$$
(52)

where f, g,  and h are given earlier in (44).

For example, selecting the same values of the parameters as in the previous case the lump solution as

$$\begin{aligned} \begin{array}{rcl} &{}&{}u(x,y,t)\\ &{}&{}\quad = {\frac{35000\,{x}^{2}+ \left( 56000\,y-8400 \right) x+16800\,{y}^{2}- 2240\,y-9187892}{ \left( 50\,{x}^{2}+80\,xy+40\,{y}^{2}-12\,x-16\,y+ 13127 \right) ^{2}}}. \end{array} \end{aligned}$$
(53)

4 Conclusions

We gave two extended (3 + 1)- and (2 + 1)-dimensional Kadomtsev–Petviashvili (KP) equations in shallow water waves. Shallow water waves play an important role in the study of fluid dynamics, which involves the development of ground water resources, sea water intrusion, marine engineering, and many other fields. The two extended KP equations were proposed to explore new multiple solitons solutions and more lump solutions as well. We used the Painlevé analysis method to ensure the integrability of each extended equation and to confirm that the newly added linear terms did not end the integrability feature. The Hirota’s method was employed to exhibit multiple soliton solutions for each examined equation. Two sets of lump solutions were derived for proposed model. The results are helpful to understand the dynamic properties of extended KP equations in fluid mechanics.