A new (3 + 1)-dimensional Schrödinger equation: derivation, soliton solutions and conservation laws

Abstract

In the present paper, a new (3 + 1)-dimensional Schrödinger equation in Quantum Mechanics is derived. Based on the extended (3 + 1)-dimensional zero curvature equation, this equation is derived for the first time via the compatibility condition. Meanwhile, some soliton solutions are presented. Finally, conservation laws also obtained.

1 Introduction

Nonlinear evolution equations play a very important role in many fields, as many nonlinear phenomena can be described by them. It is well-known that many scientific application fields exist a rich variety of nonlinear phenomena. Studying the analytical solutions of these equations becomes a hot research topic. Various systematic methods have been proposed and developed to seek analytical solutions of NLEEs. For example, some of the most important approaches are inverse scattering transformation [1], Hirotas bilinear direct method [2], B$\ddot{a}$cklund transformation [3], Darboux transformations [4, 5], generalized multi-symplectic method [6,7,8,9], Lax pairs [10], symmetry method [11,12,13,14,15,16,17,18,19], auxiliary function method [20, 21], and other methods. These methods have powerful features that perform it practical for dealing with a great many of nonlinear evolution equations.

The nonlinear Schr$\ddot{o}$dinger equation (NLSE) [1] is widely considered as a general mathematical model to describe the evolution of slow wave packets in general nonlinear wave systems. It plays an important role in nonlinear optics, condensed state physics and other physical sciences. With the development of science and technology and the continuous deepening of research, we need to use more complex equations to describe the nonlinear phenomena in reality. Therefore, equations have been extended on the basis of standard form of NLSE, which includes variable coefficients, high order, multi-dimensional, non-local, fractional order and their combined forms.

Recently, Wang [22] considered a new (3 + 1)-dimensional sine-Gordon and sinh-Gordon equation from extended (3 + 1)-dimensional zero curvature equation. Also, Wang et al. [13] studied a new (2 + 1)-dimensional sine-Gordon and sinh-Gordon equation. In paper [23], they get almost-periodic solutions of the (2 + 1)-dimensional three-wave equation. In paper [24], they derive Schr$\ddot{o}$dinger equation and give some analytic solutions. In paper [17], a (2 + 1)-dimensional KdV and mKdV equation are derived from positive case. In this paper, we try to derive a (3 + 1)-dimensional Schr$\ddot{o}$dinger equation via extended (3 + 1)-dimensional zero curvature equation. In fact, this paper is a continuous paper of the previous ones [13, 17, 22].

This paper is mainly divided into the following parts to carry out research; in the second section, we derived the (3 + 1)-dimensional Schr$\ddot{o}$dinger equation from the extended zero curvature equation. In the third section, some soliton solutions and analytic solutions are obtained. In the last section, some conclusions of this paper are displayed.

2 Derivation of the new (3 + 1)-dimensional Schr$\ddot{o}$dinger equation

Recently, Wang [22] from the following Lax pairs compatibility equation,

$$\begin{aligned} \left\{ \begin{array}{l} \varphi _z=\varphi _x+\varphi _y+M\varphi ,\\ \varphi _t=\varphi _x+\varphi _y+N\varphi , \end{array}\right. \end{aligned}$$

(1)

where $\varphi$ is function of x, y, z and t. $\varphi$ is an n-dimensional vector and M and N are $n\times n$ matrices. Wang [22] considered $\varphi _{zt}=\varphi _{tz}$ and derived the following (3 + 1)-dimensional zero curvature equation

$$\begin{aligned} M_t+N_x+N_y-M_x-M_y-N_z+[M,N]=0, \end{aligned}$$

(2)

where $[M,N]=MN-NM$, and M, N are [1, 13, 17, 22, 24]

$$\begin{aligned} M=\left( \begin{array}{ccc} -i\zeta &{} q \\ r &{} i\zeta \\ \end{array} \right) , \ N=\left( \begin{array}{ccc} A &{} B \\ C &{} D\\ \end{array} \right) , \end{aligned}$$

(3)

where A, B, C and D are scalar functions of $q(x, y,z,t), r(x,y,z, t)$, and their derivatives, and $\zeta$, where q, r are functions of x, y, z, t, $\zeta$ is the spectral parameter. Substituting (3) into (2), one can find $D=-A$, and one can have

$$\begin{aligned} \left\{ \begin{aligned}&A_x+A_y-A_z=rB-qC,\\&B_x+B_y-B_z=q_x+q_y-q_t+2iB\zeta +2Aq,\\&C_x+C_y-C_z=r_x+r_y-r_t-2iC\zeta -2rA. \end{aligned}\right. \nonumber \\ \end{aligned}$$

(4)

In general, it is difficult to solve these equations. Since $\zeta$ is the eigenvalue and it is a free parameter, in order to solve A, B and C, by seeking finite power series expansions. In this paper, unlike the previous work [22], we consider positive case for $n=2$, one can get

$$\begin{aligned} \begin{aligned} A&=a_2(x,y,z,t)\zeta ^{2}+a_1(x,y,z,t)\zeta +{a_0(x,y,z,t)},\\ B&=b_2(x,y,z,t)\zeta ^{2}+b_1(x,y,z,t)\zeta +{b_0(x,y,z,t)},\\ C&=c_2(x,y,z,t)\zeta ^{2}+c_1(x,y,z,t)\zeta +{c_0(x,y,z,t)}. \end{aligned}\nonumber \\ \end{aligned}$$

(5)

Putting (5) into (4) and from the second and third equation of Eq. (4), from the coefficients of $\zeta ^3$ immediately generates $b_2=c_2=0.$ Thus, we rewrite Eq. (5) as follows

$$\begin{aligned} \begin{aligned} A&=a_2(x,y,z,t)\zeta ^{2}+a_1(x,y,z,t)\zeta +{a_0(x,y,z,t)},\\ B&=b_1(x,y,z,t)\zeta +{b_0(x,y,z,t)},\\ C&=c_1(x,y,z,t)\zeta +{c_0(x,y,z,t)}. \end{aligned} \end{aligned}$$

(6)

Substituting Eq. (6) into Eq. (4), from the different coefficients of $\zeta$, we can obtain

$$\begin{aligned} \begin{aligned} A&=2i\zeta ^{2}+iqr,\ B=-2q\zeta +i\left( q_x+q_y-q_z\right) ,\\ C&=-2r\zeta -i\left( r_x+r_y-r_z\right) . \end{aligned} \end{aligned}$$

(7)

Finally, let $r=q^{*}$, and then we get the new (3 + 1)-dimensional Schr$\ddot{o}$dinger equation as follows

$$\begin{aligned}&i\left( q_t-q_x-q_y\right) \nonumber \\&\quad -\left( q_{xx}+q_{yy}+q_{zz}+2q_{xy}-2q_{xz}-2q_{yz}\right) \nonumber \\&\quad +2|q|^2q=0. \end{aligned}$$

(8)

To eliminate items $q_x$ and $q_y$, consider the transformation $q(x,y,z,,t)=U(\xi ,\eta ,\tau ,Z),\xi =x+t,\eta =y+t,\tau =t,Z=z$, substitute them into Eq. (8), one can get

$$\begin{aligned}&i\left( U_\tau \right) -\left( U_{\xi \xi }+U_{\eta \eta }+U_{ZZ}\right. \nonumber \\&\quad \left. +2U_{\xi \eta }-2U_{\xi Z}-2U_{\eta Z}\right) +2|U|^2U=0. \end{aligned}$$

(9)

In order to write in a common form, we rewrite Eq. (9) as follows (3 + 1)-dimensional Schr$\ddot{o}$dinger equation

$$\begin{aligned}&iu_t-\left( u_{xx}+u_{yy}+u_{zz}+2u_{xy}-2u_{xz}-2u_{yz}\right) \nonumber \\&\quad +2|u|^2u=0. \end{aligned}$$

(10)

In the following Sections, we will study Eq. (10).

3 Symmetries analysis and analytical solutions of the new (3 + 1)-dimensional Schr$\ddot{o}$dinger equation

3.1 Symmetry analysis for transformation $u=p+iq$

In order to get the Lie point symmetry of Eq. (10), assume that $u=p+iq$, where p(x, y, z, t), q(x, y, z, t) are real functions. By separating the real and imaginary parts of this equation, we can obtain the following system of equations

$$\begin{aligned}&p_t-\left( q_{xx}+q_{yy}+q_{zz}+2q_{xy}-2q_{xz}-2q_{yz}\right) \nonumber \\&\quad +2(p^2+q^2)q=0, \end{aligned}$$

(11)

$$\begin{aligned}&q_t+\left( p_{xx}+p_{yy}+p_{zz}+2p_{xy}-2p_{xz}-2p_{yz}\right) \nonumber \\&\quad -2(p^2+q^2)p=0. \end{aligned}$$

(12)

For the vector fields [11,12,13,14,15,16,17, 22]

$$\begin{aligned} \begin{aligned} V&=\xi ^t(x,y,z,t,{p,q})\frac{\partial }{\partial {t}}\\&\quad +\xi ^x(x,y,z,t,p,q)\frac{\partial }{\partial {x}}\\&\quad +\xi ^y(x,y,z,t,{p,q})\frac{\partial }{\partial {y}}\\&\quad +\xi ^z(x,y,z,t,{p,q})\frac{\partial }{\partial {z}}\\&\quad +\eta ^p(x,y,z,t,p,q)\frac{\partial }{\partial {p}}\\&\quad +\eta ^q(x,y,z,t,{p,q})\frac{\partial }{\partial {q}}, \end{aligned} \end{aligned}$$

(13)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} {\hat{t}}=t+\epsilon \xi ^t(x,y,z,t,p,q)+O(\epsilon ^2),\\ {\hat{x}}=x+\epsilon \xi ^x(x,y,z,t,p,q)+O(\epsilon ^2),\\ {\hat{y}}=y+\epsilon \xi ^y(x,y,z,t,p,q)+O(\epsilon ^2),\\ {\hat{z}}=z+\epsilon \xi ^z(x,y,z,t,p,q)+O(\epsilon ^2), \\ {\hat{p}}=p+\epsilon \eta ^p(x,y,z,t,p,q)+O(\epsilon ^2),\\ {\hat{q}}=q+\epsilon \eta ^q(x,y,z,t,p,q)+O(\epsilon ^2). \end{array}\right. } \end{aligned}$$

(14)

On the basis of the symmetry method (For more details refer to Refs. [11, 12]), applying the second prolongation $pr^{(2)}V$ to (11) and (12), and get

$$\begin{aligned} pr^{(2)}V(\varDelta _1,\varDelta _2)|_{\varDelta _1=0,\varDelta _2=0}=0, \end{aligned}$$

(15)

where

$$\begin{aligned} \varDelta _1= & {} p_t-\left( q_{xx}+q_{yy}+q_{zz}+2q_{xy}-2q_{xz}\right. \nonumber \\&\left. -2q_{yz}\right) +2(p^2+q^2)q, \end{aligned}$$

(16)

$$\begin{aligned} \varDelta _2= & {} q_t+\left( p_{xx}+p_{yy}+p_{zz}+2p_{xy}-2p_{xz}\right. \nonumber \\&\left. -2p_{yz}\right) -2(p^2+q^2)p, \end{aligned}$$

(17)

and $pr^{(2)}$ is the second prolongation

$$\begin{aligned} pr^{(2)}V= {\left\{ \begin{array}{ll}V+\eta ^{px}(x,y,t,p,q)\frac{\partial }{\partial {p_x}} +\eta ^{py}(x,y,z,t,p,q)\frac{\partial }{\partial {p_y}}+\eta ^{pt}(x,y,z,t,p,q)\frac{\partial }{\partial {p_t}}\\ +\eta ^{pxt}(x,y,z,t,p,q)\frac{\partial }{\partial {p_{xt}}}+\eta ^{pxy}(x,y,z,t,p,q)\frac{\partial }{\partial {p_{xy}}}\\ +\eta ^{pzt}(x,y,z,t,p,q)\frac{\partial }{\partial {p_{zt}}} +\eta ^{pyt}(x,y,z,t,p,q)\frac{\partial }{\partial {p_{yt}}}\\ +\eta ^{pxz}(x,y,z,t,p,q)\frac{\partial }{\partial {p_{xz}}} +\eta ^{pxx}(x,y,z,t,p,q)\frac{\partial }{\partial {p_{xx}}}+\eta ^{pzy}(x,y,z,t,p,q)\frac{\partial }{\partial {p_{zy}}}\\ +\eta ^{pyy}(x,y,z,t,p,q)\frac{\partial }{\partial {p_{yy}}}+\eta ^{pzz}(x,y,z,t,p,q)\frac{\partial }{\partial {p_{zz}}}\\ +\eta ^{qx}(x,y,t,p,q)\frac{\partial }{\partial {q_x}} +\eta ^{qy}(x,y,z,t,p,q)\frac{\partial }{\partial {q_y}}+\eta ^{qt}(x,y,z,t,p,q)\frac{\partial }{\partial {q_t}}\\ +\eta ^{qxt}(x,y,z,t,p,q)\frac{\partial }{\partial {q_{xt}}}+\eta ^{qxy}(x,y,z,t,p,q)\frac{\partial }{\partial {q_{xy}}}\\ +\eta ^{qzt}(x,y,z,t,p,q)\frac{\partial }{\partial {q_{zt}}} +\eta ^{qyt}(x,y,z,t,p,q)\frac{\partial }{\partial {q_{yt}}}\\ +\eta ^{qxz}(x,y,z,t,p,q)\frac{\partial }{\partial {q_{xz}}} +\eta ^{qxx}(x,y,z,t,p,q)\frac{\partial }{\partial {q_{xx}}}+\eta ^{qzy}(x,y,z,t,p,q)\frac{\partial }{\partial {q_{zy}}}\\ + +\eta ^{qyy}(x,y,z,t,p,q)\frac{\partial }{\partial {q_{yy}}}+\eta ^{qzz}(x,y,z,t,p,q)\frac{\partial }{\partial {q_{zz}}}. \end{array}\right. } \end{aligned}$$

(18)

Thus, the infinitesimal criterion reads as follows

$$\begin{aligned}&\eta ^{pt}-\left( \eta ^{qxx}+\eta ^{qyy}+\eta ^{qzz}+2\eta ^{qxy}\right. \nonumber \\&\quad \left. -2\eta ^{qxz}-2\eta ^{qyz}\right) \end{aligned}$$

(19)

$$\begin{aligned}&+4pq\eta ^{p}+2p^2\eta ^{q}+6q^2\eta ^{q}=0, \end{aligned}$$

(20)

$$\begin{aligned}&\eta ^{qt}+\left( \eta ^{pxx}+\eta ^{pyy}+\eta ^{pzz}+2\eta ^{pxy}\right. \nonumber \\&\quad \left. -2\eta ^{pxz}-2\eta ^{pyz}\right) \end{aligned}$$

(21)

$$\begin{aligned}&-6p^2\eta ^{p}-4pq\eta ^{q}-2q^2\eta ^{p}=0. \end{aligned}$$

(22)

where

$$\begin{aligned} \begin{aligned} \eta ^{pt}&=D_t(\eta ^{p})-p_xD_t(\xi ^1) -p_yD_t(\xi ^2)-p_tD_t(\xi ^3)\\&\quad -p_zD_t(\xi ^4),\\ \eta ^{px}&=D_x(\eta ^{p})-p_xD_x(\xi ^1) -p_yD_x(\xi ^2)-p_tD_x(\xi ^3)\\&\quad -p_zD_x(\xi ^4),\\ \eta ^y&=D_y(\eta )-u_xD_y(\xi ^1) -u_yD_y(\xi ^2)-u_tD_y(\xi ^3)\\&\quad -u_tD_y(\xi ^4),\\ \eta ^{xx}&=D_x(\eta ^x)-u_{xt}D_{x}(\xi ^3) -u_{xx}D_{x}(\xi ^1)-u_{xy}D_{x}(\xi ^2)\\&\quad -u_{xz}D_{x}(\xi ^4),\\ \eta ^{yy}&=D_y(\eta ^y)-u_{yt}D_{y}(\xi ^3) -u_{xy}D_{y}(\xi ^1)-u_{yy}D_{y}(\xi ^2)\\&\quad -u_{zy}D_{y}(\xi ^4),\\ \eta ^{tt}&=D_t(\eta ^t)-u_{tt}D_{t}(\xi ^3) -u_{xt}D_{t}(\xi ^1)-u_{yt}D_{t}(\xi ^2)\\&\quad -u_{zt}D_{t}(\xi ^4), \end{aligned}\nonumber \\ \end{aligned}$$

(23)

and so on. $D_i$ express the total derivative operator.

Lastly, we get the following results

$$\begin{aligned} \eta _p= & {} -\frac{1}{2}xqF_7+qF_{11}-\frac{1}{2}F_3p, \nonumber \\ \eta _q= & {} \frac{1}{2}xpF_7-pF_{11}-\frac{1}{2}F_3q, \nonumber \\ \xi ^t= & {} tF_3+F_4, \nonumber \\ \xi ^x= & {} -tF_7+\frac{1}{2}xF_3+F_9, \nonumber \\ \xi ^y= & {} -tF_7+\frac{1}{2}xF_3+F_{10},\nonumber \\ \xi ^z= & {} tF_7-\frac{1}{2}xF_3+F_{8}, \end{aligned}$$

(24)

where $F_i(i=1,2,3\cdots 11$ are functions of $(-x+y,x+z)$.

3.2 Symmetry analysis for transformation $u=Pe^{i\phi }$

First, consider the following hypothesis

$$\begin{aligned} \begin{aligned} u(x,y,z,t)=P(x,y,z,t)e^{i\phi (x,y,z,t)}, \end{aligned} \end{aligned}$$

(25)

where P(x, y, z, t) is the shape of the pulse and $\phi (x,y,z,t)$ represents the phase portion of the solutions [25]. In this way, one separates real and imaginary parts; one can get

$$\begin{aligned}&P_t-2P_x\phi _x-2P_y\phi _y-2P_z\phi _z\nonumber \\&\quad -P\phi _{xx}-P\phi _{yy}-P\phi _{zz} -2P_x\phi _y-2P_y\phi _x\nonumber \\&\quad -2P\phi _{xy}+2P_x\phi _z+2P_z\phi _x +P\phi _{xz}+2P_y\phi _z\nonumber \\&\quad +2P_z\phi _y+2P\phi _{yz}=0, \end{aligned}$$

(26)

$$\begin{aligned}&-P\phi _t-P_{xx}+P\phi _x^2-P_{yy}+P\phi _y^2-P_{zz}\nonumber \\&\quad +P\phi _z^2-2P_{xy}-2P\phi _x\phi _y\nonumber \\&\quad +2P_{xz}-2P\phi _x\phi _z+2P_{yz}\nonumber \\&\quad -2P\phi _y\phi _z+P^3=0. \end{aligned}$$

(27)

3.3 Symmetry analysis (26) and (27)

In this subsection, once again, we consider (26) and (27) using symmetry method. Repeat previous steps, we can get

$$\begin{aligned} \eta _P&=-c_1P, \eta _\phi =c_3z+c_5, \xi _t=2c_1t+c_2, \nonumber \\ \xi _x&=c_1x+2c_3t+c_4, \nonumber \\ \xi _y&=c_1y+2c_3t+c_6,\nonumber \\ \xi _z&=c_1z-2c_3t+c_7, \end{aligned}$$

(28)

where $c_i(i=1,2,3,4,5,6,7)$ are arbitrary constants. Therefore, we obtain following infinitesimal generators

$$\begin{aligned} \begin{aligned} V=V_1+V_2+V_3+V_4+V_5+V_6+V_7, \end{aligned} \end{aligned}$$

(29)

where

$$\begin{aligned} \begin{aligned} V_1&=\frac{\partial }{\partial {x}},V_2=\frac{\partial }{\partial {y}},V_3=\frac{\partial }{\partial {z}}, V_4=\frac{\partial }{\partial {t}},\\ V_5&=\frac{\partial }{\partial {\phi }},V_6=2t\frac{\partial }{\partial {t}}+x\frac{\partial }{\partial {x}} +y\frac{\partial }{\partial {y}}\\&\quad +z\frac{\partial }{\partial {z}}-P\frac{\partial }{\partial {P}},\\ V_7&=2t\frac{\partial }{\partial {x}}+2t\frac{\partial }{\partial {y}}+2t\frac{\partial }{\partial {z}} +z\frac{\partial }{\partial {\phi }}. \end{aligned} \end{aligned}$$

(30)

From (30), one can get one-parameter groups $G_{i}$,

$$\begin{aligned} \begin{aligned}&G_1{:}\, \left( x+\varepsilon ,y,z,t,P,\phi \right) ,\\&G_2{:}\, \left( x,y+\varepsilon ,z,t,P,\phi \right) ,\\&G_3{:}\, \left( x,y,z+\varepsilon ,t,P,\phi \right) ,\\&G_4{:}\, \left( x,y,z,t+\varepsilon ,P,\phi \right) ,\\&G_5{:}\, \left( x,y,z,t,P+\varepsilon ,\phi \right) ,\\&G_6{:}\, \left( \mathrm{{e}^{\varepsilon }}x,\mathrm{{e}^{\varepsilon }}y,\mathrm{{e}^{\varepsilon } }z,\mathrm{{e}^{\varepsilon 2}}t,\mathrm{{e}^{-\varepsilon }}P,\phi \right) ,\\&G_7{:}\, \left( x+2\varepsilon t,y+2\varepsilon t,z+2\varepsilon t,P,\phi +z\varepsilon +2\varepsilon ^2t\right) . \end{aligned} \end{aligned}$$

(31)

It is clear that all of them are symmetry group; this implies that if $P= f(x,y,z, t),g(x,y,z,t)=\varphi$ are solutions of the new Schr$\ddot{o}$dinger equation, the following functions also are solutions of (10)

$$\begin{aligned} \begin{aligned} P_1&=f \left( x-\varepsilon ,y,z,t,\right) ,\phi _1=g\left( x-\varepsilon ,y,z,t\right) ,\\ P_2&=f \left( x,y-\varepsilon ,z,t,\right) ,\phi _2=g\left( x,y-\varepsilon ,z,t\right) ,\\ P_3&=f \left( x,y,z-\varepsilon ,t,\right) ,\phi _3=g\left( x,y,z-\varepsilon ,t\right) ,\\ P_4&=f \left( x,y,z,t-\varepsilon ,\right) ,\phi _4=g\left( x,y,z,t-\varepsilon \right) ,\\ P_5&=\varepsilon +f \left( x,y,z,t,\right) ,\phi _5=g\left( x,y,z,t\right) ,\\ P_6&=\mathrm{{e}^{-\varepsilon }}f\left( \mathrm{{e}^{-\varepsilon }}x,\mathrm{{e}^{-\varepsilon }}y,\mathrm{{e}^{-\varepsilon } }z,\mathrm{{e}^{-\varepsilon 2}}t\right) ,\\ \phi _6&=g\left( \mathrm{{e}^{-\varepsilon }}x,\mathrm{{e}^{-\varepsilon }}y,\mathrm{{e}^{-\varepsilon } }z,\mathrm{{e}^{-\varepsilon 2}}t\right) ,\\ P_7&=f\left( x+2\varepsilon t,y+2\varepsilon t,z+2\varepsilon t\right) ,\\ \phi _7&=\left( g+z\varepsilon +2\varepsilon ^2t\right) \left( x+2\varepsilon t,y+2\varepsilon t,z+2\varepsilon t\right) . \end{aligned} \end{aligned}$$

(32)

From above analysis, one can see that if we choose different transformation, we get different vector fields.

3.4 Soliton solutions of the new (3 + 1)-dimensional Schr$\ddot{o}$dinger equation

3.4.1 Soliton solutions

In general, the wave number of the solution should be constant quantity, that is to say, $\phi _{xx},\phi _{yy},\phi _{xy},\phi _{xz},\phi _{yz}$ and $\phi _{zz}$ should be equal to zero. Therefore, Eqs. (26), (27) reduced to

$$\begin{aligned}&P_t-2P_x\phi _x-2P_y\phi _y-2P_z\phi _z -2P_x\phi _y-2P_y\phi _x\nonumber \\&\quad +2P_x\phi _z+2P_z\phi _x +2P_y\phi _z+2P_z\phi _y=0, \end{aligned}$$

(33)

$$\begin{aligned}&-P\phi _t-P_{xx}+P\phi _x^2-P_{yy}+P\phi _y^2\nonumber \\&\quad -P_{zz}+P\phi _z^2-2P_{xy}-2P\phi _x\phi _y\nonumber \\&\quad +2P_{xz}-2P\phi _x\phi _z+2P_{yz}\nonumber \\&\quad -2P\phi _y\phi _z+P^3=0. \end{aligned}$$

(34)

3.4.2 Bright solutions

In order to get solutions, let us consider the following hypothesis [25, 26]

$$\begin{aligned} P=A {{\,\mathrm{sech}\,}}^p\tau , \end{aligned}$$

(35)

where

$$\begin{aligned} \tau =B_1x+B_2y+B_3z-vt, \end{aligned}$$

(36)

and the phase of solutions is given by

$$\begin{aligned} \phi =-k_1x-k_2y-k_3z+\omega t+\theta , \end{aligned}$$

(37)

A is the amplitude, $B_i(i=1,2,3)$ is the inverse width and v is the velocity of the solutions, respectively, the wave number are given by $k_1,k_2$ and $k_3$, $\omega$ is the frequency, the center of the phase represents $\theta$, for more details see [25, 26].

Substituting (35) into (33) and (34), one can get

$$\begin{aligned} \begin{aligned}&pvA{{\,\mathrm{sech}\,}}^p\tau \tanh \tau -2k_1pAB_1{{\,\mathrm{sech}\,}}^p\tau \tanh \tau \\&\quad -2k_2pAB_2{{\,\mathrm{sech}\,}}^p\tau \tanh \tau \\&\quad -2k_3pAB_3{{\,\mathrm{sech}\,}}^p\tau \tanh \tau \\&\quad -2k_2pAB_1{{\,\mathrm{sech}\,}}^p\tau \tanh \tau \\&\quad -2k_1pAB_2{{\,\mathrm{sech}\,}}^p\tau \tanh \tau \\&\quad +2k_3pAB_1{{\,\mathrm{sech}\,}}^p\tau \tanh \tau \\&\quad +2k_1pAB_3{{\,\mathrm{sech}\,}}^p\tau \tanh \tau \\&\quad +2k_3pAB_2{{\,\mathrm{sech}\,}}^p\tau \tanh \tau \\&\quad +2k_2pAB_3{{\,\mathrm{sech}\,}}^p\tau \tanh \tau =0, \end{aligned} \end{aligned}$$

(38)

and

$$\begin{aligned}&-\omega A{{\,\mathrm{sech}\,}}^p\tau -p^2AB_1^2{{\,\mathrm{sech}\,}}^p\tau \nonumber \\&\quad +p(p+1)AB_1^2{{\,\mathrm{sech}\,}}^{p+2}\tau + k_1^2pA{{\,\mathrm{sech}\,}}^p\tau \nonumber \\&\quad -p^2AB_2^2{{\,\mathrm{sech}\,}}^p\tau +p(p+1)AB_2^2{{\,\mathrm{sech}\,}}^{p+2}\tau \nonumber \\&\quad +k_2^2pA{{\,\mathrm{sech}\,}}^p\tau -p^2AB_3^2{{\,\mathrm{sech}\,}}^p\tau \nonumber \\&\quad +p(p+1)AB_3^2{{\,\mathrm{sech}\,}}^{p+2}\tau \nonumber \\&\quad +k_3^2pA{{\,\mathrm{sech}\,}}^p\tau -2p^2AB_2B_1{{\,\mathrm{sech}\,}}^p\tau \nonumber \\&\quad +2p(p+1)AB_2B_1{{\,\mathrm{sech}\,}}^{p+2}\tau -2k_1k_2A{{\,\mathrm{sech}\,}}^p\tau \nonumber \\&\quad +2p^2AB_3B_1{{\,\mathrm{sech}\,}}^p\tau \nonumber \\&\quad -2p(p+1)AB_3B_1{{\,\mathrm{sech}\,}}^{p+2}-2k_1k_3A{{\,\mathrm{sech}\,}}^p\tau \nonumber \\&\quad +2p^2AB_2B_3{{\,\mathrm{sech}\,}}^p\tau \nonumber \\&\quad -2p(p+1)AB_2B_3{{\,\mathrm{sech}\,}}^{p+2}\tau \nonumber \\&\quad -2k_2k_3A{{\,\mathrm{sech}\,}}^p\tau +A^3{{\,\mathrm{sech}\,}}^{3p}\tau =0. \end{aligned}$$

(39)

From Eq. (38), one can derive

$$\begin{aligned} \begin{aligned} v&=2k_1B_1+2k_2B_2+2k_3B_3+2k_2B_1\\&\quad +2k_1B_2-2k_3B_1-2k_1B_3-2k_3B_2-2k_2B_3. \end{aligned}\nonumber \\ \end{aligned}$$

(40)

Now, consider Eq. (39), we find that the exponents 3p and $p+2$ should be equal. Thus, one can have $p=1.$ Therefore, from Eq. (39) we derive

$$\begin{aligned} {\left\{ \begin{array}{ll} \omega =-B_1^2+k_1^2-B_2^2+k_2^2-B_3^2+k_3^2-2B_1B_2\\ \qquad -2k_1k_2+2B_1B_3-2k_1k_3+2B_2B_3-2k_3k_3,\\ A=\sqrt{4B_2B_3+4B_1B_3-4B_1B_2-2B_3^2-2B_2^2-2B_1^2}. \end{array}\right. }\nonumber \\ \end{aligned}$$

(41)

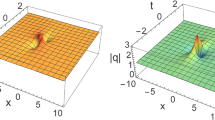
Thus, from the condition it requires that $\left( 4B_2B_3+4B_1B_3-4B_1B_2-2B_3^2-2B_2^2-2B_1^2\right) >0$. Finally, the bright soliton solution of (10) is given by

$$\begin{aligned} \begin{aligned}&u(x,y,z,t)\\&\quad =A {{\,\mathrm{sech}\,}}(B_1x+B_2y+B_3y-vt)e^{i(-k_1x-k_2y-k_3z-\omega t+\theta )}, \end{aligned}\nonumber \\ \end{aligned}$$

(42)

the relation the amplitude A and width B, the frequency $\omega$ are presented by (41). The velocity v is decided by (40). Only when these conditions are satisfied, the solutions can exist.

3.4.3 Dark solutions

Let us assume the following hypothesis [25, 26]

$$\begin{aligned} P=A \tanh ^p\tau , \end{aligned}$$

(43)

where $\tau$ also is Eq. (36).

Inserting (43) into (10), one can derive

$$\begin{aligned}&-pvA\left( \tanh ^{p-1} \tau -\tanh ^{p+1} \tau \right) \nonumber \\&\quad +2k_1pAB_1\left( \tanh ^{p-1} \tau -\tanh ^{p+1} \tau \right) \nonumber \\&\quad +2k_2pAB_2\left( \tanh ^{p-1} \tau -\tanh ^{p+1} \tau \right) \nonumber \\&\quad +2k_3pAB_3\left( \tanh ^{p-1} \tau -\tanh ^{p+1} \tau \right) \nonumber \\&\quad +2k_2pAB_1\left( \tanh ^{p-1} \tau -\tanh ^{p+1} \tau \right) \nonumber \\&\quad +2k_1PAB_2\left( \tanh ^{p-1} \tau -\tanh ^{p+1} \tau \right) \nonumber \\&\quad -2k_3PAB_1\left( \tanh ^{p-1} \tau -\tanh ^{p+1} \tau \right) \nonumber \\&\quad -2k_1PAB_3\left( \tanh ^{p-1} \tau -\tanh ^{p+1} \tau \right) \nonumber \\&\quad -2k_3PAB_2\left( \tanh ^{p-1} \tau -\tanh ^{p+1} \tau \right) \nonumber \\&\quad -2k_2PAB_3\left( \tanh ^{p-1} \tau -\tanh ^{p+1} \tau \right) =0, \end{aligned}$$

(44)

and

$$\begin{aligned} \begin{aligned}&-\left( pAB_1^2+pAB_2^2+pAB_3^2+2pAB_1B_2\right. \\&\quad \left. -2pAB_1B_3-2pAB_2B_3\right) \\&\quad \Bigg \{\left( p-1\right) \tanh ^{p-2}\tau -2p\tanh ^{p} \tau \\&\quad +(p+1)\tanh ^{p+2}\tau \Bigg \}\\&\quad +\left( -\omega +k_1^2+k_2^2+k_3^2-2k_1k_2-2k_1k_3-2k_2k_3\right) \\&\quad A\tanh ^{p} \tau +A^3\tanh ^{3p} \tau =0. \end{aligned} \end{aligned}$$

(45)

For v, we also get the same value as the dark solutions,

$$\begin{aligned} \begin{aligned} v&=2k_1B_1+2k_2B_2+2k_3B_3+2k_2B_1\\&\quad +2k_1B_2-2k_3B_1-2k_1B_3-2k_3B_2-2k_2B_3. \end{aligned}\nonumber \\ \end{aligned}$$

(46)

Balancing the exponents 3p and $p+2$, one can also arrive at $p=1.$ If we repeat the previous steps, we can get,

$$\begin{aligned} {\left\{ \begin{array}{ll} \omega =-B_1^2+k_1^2-B_2^2+k_2^2-B_3^2+k_3^2-2B_1B_2\\ \qquad -2k_1k_2+2B_1B_3-2k_1k_3+2B_2B_3-2k_3k_3,\\ A=\sqrt{-4B_2B_3-4B_1B_3+4B_1B_2+2B_3^2+2B_2^2-2B_1^2}. \end{array}\right. }\nonumber \\ \end{aligned}$$

(47)

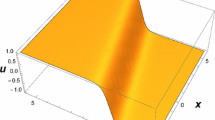
For A, it is easy to see that this is just a minus sign from the previous one. Therefore, condition (47) requires $-4B_2B_3-4B_1B_3+4B_1B_2+2B_3^2+2B_2^2-2B_1^2>0$. Finally, we get the dark solution of (10)

$$\begin{aligned} \begin{aligned}&u(x,y,z,t)\\&\quad =A \tanh (B_1x+B_2y+B_3z-vt)e^{i(-k_1x-k_2y-k_3z-\omega t+\theta )}, \end{aligned}\nonumber \\ \end{aligned}$$

(48)

the amplitude A and width $B_i(i=1,2,3)$ are linked by (47), the frequency $\omega$ is shown (47). The velocity v is decided by (46).

3.4.4 Complexitons

By employing the following assumption [25, 26]

$$\begin{aligned} \begin{aligned}&u(x,y,z,t)\\&\quad =f(l_1x+l_2y+l_3z-vt+\theta _1)e^{i(\alpha _1x+\alpha _2y+\alpha _3z+\beta t+\theta _0)}, \end{aligned}\nonumber \\ \end{aligned}$$

(49)

where $f(\xi )=f(l_1x+l_2y+l_3z-vt+\theta _1)$ is a real function. Putting (49) into (10), we have

$$\begin{aligned} \begin{aligned} Z_1f''+Z_2f'+Z_3f+2f^3=0, \end{aligned} \end{aligned}$$

(50)

where $Z_1=-l_1^2-l_2^2-l_3^2-2l_1l_2+2l_1l_3+2l_2l_3$, $Z_3=-\beta +\alpha _1^2+\alpha _2^2+\alpha _3^2+2\alpha _1\alpha _2+2\alpha _1\alpha _3-2\alpha _2\alpha _3$, $Z_2=-iv-2i\alpha _1l_1-2i\alpha _2l_2-2i\alpha _3l_3-2i\alpha _2l_1-2i\alpha _1l_2+2i \alpha _3l_1+2i\alpha _1l_3+2i\alpha _3l_2+2i\alpha _2l_3$. Since f is a real value function, therefore $Z_2=0$. In other words, $v=-2\alpha _1l_1-2\alpha _2l_2-2\alpha _3l_3-2\alpha _2l_1-2\alpha _1l_2 +2\alpha _3l_1+2\alpha _1l_3+2\alpha _3l_2+2\alpha _2l_3$. So, Eq. (50) reduced to

$$\begin{aligned} \begin{aligned} Z_1f''+Z_3f+2f^3=0, \end{aligned} \end{aligned}$$

(51)

this equation has many solutions, such as

$$\begin{aligned} \begin{aligned} f(\xi )&=A{{\,\mathrm{sn}\,}}(\mu \xi ,k) =\pm k \sqrt{\frac{-Z_3}{1+k^2}}{{\,\mathrm{sn}\,}}\\&\quad \left( \sqrt{\frac{Z_3}{(1+k^2)Z_1}}(\xi -\xi _0),k\right) , \end{aligned} \end{aligned}$$

(52)

if $k\longrightarrow 1$, one can get $f(\xi )=\pm \sqrt{\frac{-Z_3}{2}}\tanh \left( \sqrt{\frac{Z_3}{2Z_1}}(\xi -\xi _0)\right) ,$ and

$$\begin{aligned} \begin{aligned} f(\xi )&=A{{\,\mathrm{dn}\,}}(\mu \xi ,k) =\pm \sqrt{\frac{-Z_3}{2-k^2}}{{\,\mathrm{dn}\,}}\\&\quad \left( \sqrt{\frac{-Z_3}{(2-k^2)Z_1}}(\xi -\xi _0),k\right) , \end{aligned} \end{aligned}$$

(53)

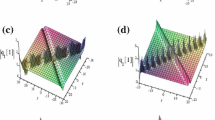
if $k\longrightarrow 1$, one can get $f(\xi )=\pm \sqrt{{-Z_3}}{{\,\mathrm{sech}\,}}\left( \sqrt{\frac{-Z_3}{Z_1}}(\xi -\xi _0)\right)$. We have get many other forms of solutions, we do not list all of them. Finally, we can get analytic solutions of Eq. (10)

$$\begin{aligned} \begin{aligned}&u(x,y,z,t)=\pm k \sqrt{\frac{-Z_3}{1+k^2}}{{\,\mathrm{sn}\,}}\\&\quad \left( \sqrt{\frac{Z_3}{(1+k^2)Z_1}}(\xi -\xi _0),k\right) e^{i(\alpha _1x+\alpha _2y+\alpha _3z+\beta t+\theta _0)}, \end{aligned}\nonumber \\ \end{aligned}$$

(54)

if $k\longrightarrow 1$, we have $u(x,y,z,t)=\pm \sqrt{\frac{-Z_3}{2}}\tanh \left( \sqrt{\frac{Z_3}{2Z_1}}(\xi -\xi _0)\right) e^{i(\alpha _1x+\alpha _2y+\alpha _3z+\beta t+\theta _0)},$ and

$$\begin{aligned} \begin{aligned}&u(x,y,z,t) =\pm \sqrt{\frac{-Z_3}{2-k^2}}{{\,\mathrm{dn}\,}}\\&\quad \left( \sqrt{\frac{-Z_3}{(2-k^2)Z_1}}(\xi -\xi _0),k\right) e^{i(\alpha _1x+\alpha _2y+\alpha _3z+\beta t+\theta _0)}, \end{aligned}\nonumber \\ \end{aligned}$$

(55)

if $k\longrightarrow 1$, one obtains $u(x,y,z,t)=\pm \sqrt{{-Z_3}}{{\,\mathrm{sech}\,}}\left( \sqrt{\frac{-Z_3}{Z_1}}(\xi -\xi _0)\right) e^{i(\alpha _1x+\alpha _2y+\alpha _3z+\beta t+\theta _0)}.$

4 Conservation laws

Based on the conservation law multiplier method [12], using the transformation $u(x,y,z,t)=p(x,y,z,t)+iq(x,y,z,t)$, we get

$$\begin{aligned} \begin{aligned} R[u]&=p_t-\left( q_{xx}+q_{yy}+q_{zz}+2q_{xy}-2q_{xz}-2q_{yz}\right) \\&\quad +2(p^2+q^2)q\\&\quad +q_t+\left( p_{xx}+p_{yy}+p_{zz}+2p_{xy}-2p_{xz}-2p_{yz}\right) \\&\quad -2(p^2+q^2)p. \end{aligned}\nonumber \\ \end{aligned}$$

(56)

Therefore, for the following multiplier, we should get

$$\begin{aligned} \begin{aligned} \varLambda _1&=-F_3(y+z)q_x+F_4(-x+y,y+z)p,\\ \varLambda _2&=F_3(y+z)p_x+F_4(-x+y,y+z)q, \end{aligned} \end{aligned}$$

(57)

where $F_4(-x+y,y+z)$ is arbitrary function $(-x+y,y+z)$, $F_3(y+z)$ is arbitrary function $(y+z)$. Therefore, we get the following statement

Theorem 1

Equation (56) possess a conservation law for multiplier $\varLambda _1=-F_3q_x, \varLambda _2=F_3p_x$,

$$\begin{aligned} \begin{aligned} T&=\left( -\frac{1}{2} p F_3 q_x+\frac{1}{2} qF_3p_x\right) , \\ X&=-\frac{1}{2}F_3\Bigg (p^4+2p^2q^2+q^4-2pp_{xy}+2pp_{xz}-pp_{yy}\\&\quad +2pp_{yz}-pp_{zz}-pq_t+p_tq-p_x^2-2p_xp_y\\&\quad +2p_xp_z-2qq_{xy}+2qq_{xz}-qq_{yy}\\&\quad +2qq_{yz}-qq_{zz}-q_x^2-2q_xq_y+2q_xq_z\Bigg ),\\ Y&=\Bigg (-qF_3q_{xx}-\frac{1}{2}D(F_3)pp_x-\frac{1}{2}qF_3q_{xy}\\&\quad +\frac{1}{2}q_xq_yF_3-F_3q_xq_z-F_3pp_{xx}-\frac{1}{2}D(F_3)pp_x\\&\quad -\frac{1}{2}F_3pp_{xy}+\frac{1}{2}F_3p_xp_y-F_3p_xp_z\Bigg ),\\ Z&=\Bigg (F_3qq_{xx}+\frac{1}{2}D(F_3)qq_x+F_3qq_{xy}-\frac{1}{2}F_3qq_{xz}\\&\quad +\frac{1}{2}F_3q_zq_x+F_3pp_{xx}+\frac{1}{2}D(F_3)pp_x\\&\quad +F_3pp_{xy}-\frac{1}{2}F_3pp_{xz}+\frac{1}{2}F_3p_zp_x\Bigg ). \end{aligned}\nonumber \\ \end{aligned}$$

(58)

Equation (56) has a conservation law for multiplier $\varLambda _1=F_4p, \varLambda _2=F_4q$,

$$\begin{aligned} \begin{aligned} T&=\left( \frac{1}{2}p^2F_4+\frac{1}{2}q^2F_4\right) , \\ X&=\Bigg (-q_xpF_4-F_4q_yp+F_4pq_z\\&\quad +F_4p_xq+F_4p_yq-F_4p_zq\Bigg ),\\ Y&=\Bigg (-F_4q_xp-F_4q_yp+F_4q_zp\\&\quad +F_4p_xq+F_4p_yq-F_4p_zq\Bigg ),\\ Z&=\Bigg (F_4q_xp+F_4q_yp-F_4q_zp\\&\quad -F_4p_xq-F_4p_yq+F_4p_zq\Bigg ). \end{aligned} \end{aligned}$$

(59)

5 Conclusions

In the present paper, based on the (3 + 1)-dimensional zero curvature equation, we have derived a new (3 + 1)-dimensional Schr$\ddot{o}$dinger equation. Moreover, from compatibility conditions, we obtained that (3 + 1)-dimensional zero curvature equation and then derived this equation from the positive case. Subsequently, we get two systems of partial differential equations with two different types of transformations. Meanwhile, we studied these two systems by the Lie group method, and we obtained their symmetries and infinitesimal operators. Simultaneously, we find that if we choose different transformations, we get different symmetries. According to different infinitesimal operators, this equation can be reduced to the (2 + 1)-dimensional Schr$\ddot{o}$dinger equation in literature [24], and of course it can be further reduced to the classical (1+1)-dimensional Schr$\ddot{o}$dinger equation by using Lie groups again. Furthermore, some soliton solutions and analytic solutions are derived, including bright solutions and dark solutions, Jacobi elliptic function solutions, and so on. In addition, some conservation laws are also given based on the multiplier method.

This paper only derived the equation and shows some analytical solutions, but there are still many issues to be reported, such as using Hirota bilinear method to study more soliton solutions, studying the B$\ddot{a}$cklund transformation and Darboux transformation of the new (3 + 1)-dimensional Schr$\ddot{o}$dinger equation. In addition, the fractional order version, the discretization as well as variable coefficients cases of the equation will be presented in future research papers.