1 Introduction

Memristor, as a special nonlinear component with inner state, has essential difference with most conventional nonlinear components [1, 2]. A memristor remembers the charge flowing through it and exhibits the property of pinched hysteresis loops [3]. Due to the special nonlinearity, memristors were widely applied in vast continuous dynamical systems and the obtained memristor-based dynamical systems can demonstrate complex initial condition-dependent dynamical behaviors [4,5,6]. These complex dynamical behaviors include self-excited or hidden period and chaos, coexisting multiple attractors, periodic window, chaotic bubble, period-doubling bifurcation, Hopf bifurcation, Neimark–Sacker bifurcation, tangent bifurcation, and so on [7, 8]. Therefore, the newly introduced memristors have the dynamical effects on the original dynamical systems and can induce more complex dynamical behaviors. However, the application of memristors in discrete dynamical systems has not received enough attention, yet [9]. Hence, it is an interesting and challenging work to apply memristors to discrete dynamical systems and study complex dynamical behaviors of the obtained memristor-based discrete systems.

Generally, the basin of attraction of a self-excited attractor is associated with the unstable equilibrium of the system, and thus the initial orbit beginning from an unstable manifold in an equilibrium neighborhood can readily tends to be unstable oscillations [10]. Different from the self-excited attractor, a hidden attractor is a completely new class of attractors and its attracting basin does not intersect with the neighborhoods of unstable equilibrium points [10,11,12]. Since the hidden attractors were found, a lot of continuous dynamical systems with hidden oscillations have been reported [13,14,15,16,17,18,19]. It is relatively easy to generate hidden attractors by constructing some continuous dynamical systems with only stable equilibrium points or with no equilibrium points [20]. Different from a continuous dynamical system, a discrete dynamical system is a particular case of dynamical system whose instantaneous states are described by discrete variables. Recently, the hidden attractors have also been discovered in some discrete dynamical systems such as the sine hyperchaotic map [21], Vertigo-2 and Vertigo-10 maps [22], polynomial maps [23], and quadratic chaotic maps [24]. Furthermore, Ref. [25] proposed a new two-dimensional (2D) chaotic map with hidden attractors and tested the complexity of output time series, while Ref [26] constructed a fractional-order map with hidden attractors and studied its dynamical behaviors by deriving the fractional Caputo-type version of a standard integer-order map. Therefore, the hidden attractors in discrete dynamical systems have been accepted much attention. Nevertheless, the internal bifurcation mechanism of such a hidden attractor has not been reported in any literature, yet. Toward this end, a three-dimensional (3D) memristive Hénon map with no invariant points is presented in this paper and its hidden Neimark–Sacker bifurcations are investigated in depth.

More recently, using some discrete models of memristors, several memristor-based discrete dynamical systems have been successively presented [9, 27,28,29,30,31]. By coupling a discrete model of memristor to an existing chaotic map, Ref. [9] constructed a general two-dimensional (2D) memristive mapping model and applied it to secure communication application. According to the difference modeling theory, Ref. [27] designed a discrete model of memristor and then proposed a discrete memristor-based Hénon map. By building a unified discrete memristor mapping model, Ref. [28] devised four 2D discrete memristor-based hyperchaotic maps directly. By applying a discrete model of memristor to the sine map, Ref. [29] established a discrete memristor-based hyperchaotic map and explored its nonparametric bifurcation mechanism. Moreover, Ref. [30] implemented a 2D sine hyperchaotic map using a discrete model of memristor and disclosed its initials-boosted coexisting behaviors, and Ref. [31] proposed a 3D memristive Rulkov neuron model through employing a discrete memristor to simulate the magnetic induction effects and found its regime transition behaviors, transient chaotic bursting regimes, and hyperchaotic firing behaviors. As the same with the continuous model of memristor, these presented discrete models of memristors can also be applied to some existing chaotic maps. Therefore, constructing memristor-based chaotic maps are an important research area with theoretical meanings and application values.

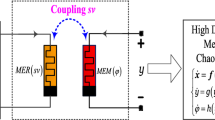
Motivated by the above idea of constructing memristor-based chaotic maps, this paper presents a novel memristive Hénon map and studies its hidden Neimark–Sacker bifurcations. The contributions of our paper are summarized as follows. (1) A memristive Hénon map with no invariant points is presented by introducing a discrete memristor into the classical Hénon map and its complex hidden dynamical behaviors are thereby revealed using the parameter-plane plots and phase orbits. (2) A dimension-reduction conversion method is firstly proposed by converting the memristor inner state into the cumulative sum form of the memristor input variable, and then the hidden Neimark–Sacker bifurcations of the memristive Hénon map are effectively interpreted. (3) A digital hardware set is exploited to implement the memristive Hénon map based on a high-performance microcontroller, and the chaotic attractors are experimentally acquired to validate the numerical simulations. As a result, the discrete memristor can make the presented map have complex hidden dynamical behaviors, which greatly enhances the fractal structure complexity of the chaotic attractors.

The remainder of the paper is arranged as follows. In Sect. 2, a memristive Hénon map is presented and the dynamical effects induced by memristor are studied. In Sect. 3, a dimension-reduction conversion method for studying the memristor-induced hidden Neimark–Sacker bifurcations is proposed. Complex hidden dynamical behaviors with multistability are disclosed in Sect. 4 and the chaotic attractors are physically acquired in Sect. 5. The last section concludes this paper.

2 Discrete memristor-based Hénon map

This section presents a memristive Hénon map with no invariant points by introducing a discrete model of memristor into the classical Hénon map. The parameter-plane plots and phase orbits are used for studying the dynamical effect of the memristor on the memristive Hénon map.

2.1 Discrete model with no invariant points

The well-known Hénon map is a 2D discrete system [32], and it is one of the most studied paradigms of discrete systems owning chaotic dynamics. The 2D Hénon map is described as

$$ \left\{ {\begin{array}{*{20}l} {x_{{n + 1}} = 1 - ax_{n}^{2} + y_{n} ,} \hfill \\ {y_{{n + 1}} = bx_{n} ,} \hfill \\ \end{array} } \right. $$
(1)

where x and y represent two state variables, and a and b represent two adjustable parameters. For the classical values a = 1.4 and b = 0.3, the Hénon map has two invariant points and displays a chaotic attractor [32]. However, the chaotic attractor fractal structure is relatively simple.

Following the continuous model of memristor presented in [33], a discrete model of memristor can be easily derived using the Euler difference method. For the input vn, output in and inner flux φn at the n-th iteration as well as the inner flux φn+1 at the (n + 1)-th iteration, the discrete model of memristor can be modeled as

$$ \left\{ {\begin{array}{*{20}l} {i_{n} = W(\varphi _{n} )v_{n} = \tanh (\varphi _{n} )v_{n} ,} \hfill \\ {\varphi _{{n + 1}} = \varphi _{n} + v_{n} ,{\text{ }}} \hfill \\ \end{array} } \right. $$
(2)

Therefore, the memductance \(W(\varphi_{n} ) = \tanh (\varphi_{n} )\) in (2) is threshold as the hyperbolic tangent function is bounded above and below.

To enhance the fractal structure complexity of the chaotic attractor generated by the Hénon map, a novel 3D memristor-based Hénon map is presented by introducing the discrete model of memristor in (2) into the existing Hénon map. Denote the state yn in the Hénon map as the input of the discrete model of memristor and the state zn as the inner state of memristor. Then the 3D memristive Hénon map is mathematically modeled as

$$ \left\{ {\begin{array}{*{20}l} {x_{{n + 1}} = 1 - ax_{n}^{2} + y_{n} ,} \hfill \\ {y_{{n + 1}} = bx_{n} + ky_{n} \tanh (z_{n} ),} \hfill \\ {z_{{n + 1}} = y_{n} + z_{n} ,} \hfill \\ \end{array} } \right. $$
(3)

where k represents the coupling strength of the discrete memristor and Hénon map. Due to the introduction of the memristor, the 3D memristive Hénon map has more complex algebraic structure, resulting in the emergence of complex dynamics.

The 3D memristive Hénon map described by (3) is completely distinguishing from the memristor-based Hénon map designed in [27]. The inner state of the memristor always has an unbounded divergent behavior, which means that the memristor-based Hénon map in [27] is invalid. However, our presented memristive Hénon map has a bounded iterative behavior in the appropriate parameter regions.

Assume P = (X, Y, Z) as an invariant point of the memristive Hénon map. So the invariant point P must satisfy the following conditional equations

$$ \left\{ {\begin{array}{*{20}l} {X = 1 - aX^{2} + Y,} \hfill \\ {Y = bX + kY\tanh Z,} \hfill \\ {Z = Y + Z.} \hfill \\ \end{array} } \right. $$
(4)

From the third equation of (4), one gets Y = 0. Substituting Y = 0 into the second equation of (4), there yields X = 0. However, when substituting X = 0 and Y = 0 into the first equation of (4), the first equation of (4) does not have a solution, indicating that P = (X, Y, Z) is not a solution to (4). In other words, the memristive Hénon map can not map any point into itself. Thus, the memristive Hénon map has no invariant points. It indicates that once various bounded iterative oscillations occur in the memristive Hénon map, all its dynamical behaviors are hidden. Consequently, the memristive Hénon map is a hidden discrete system and can also be named a hidden memristive Hénon map.

2.2 Memristor-induced dynamical effects

A colorful 2D parameter-plane plot is depicted by detecting the periodicities of the iteration sequence in a discrete-time map [27]. Using the colorful 2D parameter-plane plots, we can demonstrate the dynamical effects of the memristor on the 3D memristive Hénon map, as shown in Figs. 1 (left), 2 and 3, where the truncated interval of iteration sequence is [4900, 5000]. The initial conditions are fixed as (x0, y0, z0) = (0, 0, 0), and the two adjustable parameters a and b are used to build the 2D parameter-plane. The parameter regions emerging the iteration sequences with different periodicities are painted by different colors. The red marked by CH stands for chaos, the dark green by QP for quasi-period, the purple by MP for multi-period (i.e., the periodicities greater than 8), the magenta by SP for stable point, and the other colors by P2 to P8 for period-2 to period-8. Note that the quasi-period QP is examined by the first Lyapunov exponents of the 3D memristive Hénon map being zero.

Fig. 1
figure 1

For fixed (x0, y0, z0) = (0, 0, 0), the colorful 2D parameter-plane plot (left) and representative chaotic attractor (right) of the 2D Hénon map

Full size image

If the coupling strength is set as k = 0, the 3D memristive Hénon map degenerates to the original 2D Hénon map. When the parameter regions are considered to be adjusted in a ∈ [0, 2] and b ∈ [−1,1], the colorful 2D parameter-plane plot of the original 2D Hénon map is depicted, as shown in Fig. 1 (left). The 2D parameter-plane plot is composed of bounded dynamical behavior in color and unbounded dynamical behavior in white. The bounded dynamical behavior mainly presents chaotic behavior in red and periodic behaviors in other colors. When setting the adjustable parameters as a = 1.4 and b = 0.3, the well-known representative chaotic attractor with fractal structure is displayed in the x-y plane and shown in Fig. 1 (right), where the iteration length is set as 3 × 105. Using the Wolf’s algorithm with the iteration length 2 × 105, the two Lyapunov exponents (LE1, LE2) of the representative chaotic attractor are calculated and also marked in Fig. 1 (right). As shown in Fig. 1 (left), as the increase of the adjustable parameters a and b in a specific region, the 2D Hénon map has a route to chaos via period-doubling bifurcation and exhibits the dynamics of period, chaos, and periodic windows.

Figure 2 displays the colorful 2D parameter-plane plots of the 3D memristive Hénon map under four different negative values of the coupling strength k by setting the parameter regions a ∈ [0, 0.9] and b ∈ [0, 1.1]. Similarly, Fig. 3 reveals the colorful 2D parameter-plane plots of the 3D memristive Hénon map under four different positive values of the coupling strength k by setting the parameter regions a ∈ [0, 0.8] and b ∈ [−1.1, −0.6]. The colorful 2D parameter-plane plots in Figs. 2 and 3 intuitively exhibit the dynamical effects of the memristor on the 3D memristive Hénon map. In summary, the memristor can greatly affect the bounded dynamical distributions and dynamical behaviors of the 3D memristive Hénon map, and the bounded dynamical regions are relatively narrowed as the increase or decrease of the coupling strength k. However, with the introduction of memristor with an appropriate coupling strength, the dynamical distribution of the 3D memristive Hénon map becomes more complex.

Fig. 2
figure 2

For fixed (x0, y0, z0) = (0, 0, 0), the colorful 2D parameter-plane plots of the 3D memristive Hénon map under different negative values of the coupling strength k. a k =  −0.9. b k =  −0.7. c k =  −0.5. d k =  −0.3

Full size image
Fig. 3
figure 3

For fixed (x0, y0, z0) = (0, 0, 0), the colorful 2D parameter-plane plots of the 3D memristive Hénon map under different positive values of the coupling strength k. a k = 0.5. b k = 0.7. c k = 0.8. d k = 1

Full size image

The colorful 2D parameter-plane plots in Figs. 2 and 3 are composed of bounded dynamical behaviors in colors and unbounded dynamical behavior in white. The bounded dynamical behavior in Fig. 2 mainly possesses the period-2 in dark-blue, period-4 in pink, period-8 in yellow, and chaos in red. For the fixed adjustable parameter b, the 3D memristive Hénon map has the route to chaos via forward or reverse period-doubling bifurcation as the increase or decrease of the adjustable parameter a. By contrast, the bounded dynamical behaviors in Fig. 3 have quite complicated and irregularly distributions in the parameter-plane and are greatly affected by the coupling strength k. All in all, these results in Figs. 2 and 3 indicate that the memristor has complex dynamical effects on the 3D memristive Hénon map.

Accordingly, one parameter point (k, a, b) (or model parameters) is picked from the red-painted region of each of the eight figures in Figs. 2 and 3. The phase orbits of the 3D memristive Hénon map under these eight parameter points are drawn and shown in Fig. 4, where the iteration length 3 × 105 is used. As can be found, eight strange chaotic attractors are demonstrated, and their fractal structures are much more complex than that of the original Hénon map. Besides, we also calculate out three Lyapunov exponents (LE1, LE2, and LE3) of the 3D memristive Hénon map for these eight parameter points using the Wolf’s algorithm with the iteration length 2 × 105, and the results are simultaneously marked in Fig. 4. Note that, for convenience, only the first two Lyapunov exponents (LE1, LE2) are labeled in Fig. 4, because the third Lyapunov exponent (LE3) is always negative. Comparatively speaking, the 3D memristive Hénon map exhibits hyperchaotic behavior with two positive Lyapunov exponents at the parameter point (k, a, b) = (−0.9, 0.25, 0.51), and chaotic behaviors with the largest first Lyapunov exponent at (k, a, b) = (−0.5, 0.79, 0.6) and the smallest first Lyapunov exponent at (k, a, b) = (−0.3, 0.09, 0.87). Consequently, the memristor can significantly improve the complexity of the chaotic attractor fractal structure of the original 2D Hénon map, in other words, compared with most discrete chaotic maps reported in the literature [21,22,23,24,25,26,27,28,29,30], the 3D memristive Hénon map can produce the chaotic attractor with more complex fractal structures.

Fig. 4
figure 4

The phase orbits of the 3D memristive Hénon map for eight sets of model parameters under the initial conditions (x0, y0, z0) = (0, 0, 0). The model parameters k, a, b are also provided in the figures. a Four negative values of k. b Four positive values of k

Full size image

3 Memristor-induced hidden Neimark–Sacker bifurcations

Neimmark–Sacker bifurcation is a qualitative change [34, 35] that a closed invariant curve is born from a fixed point in a discrete-time dynamical system (iteration map) when the fixed point changes its stability through a pair of complex eigenvalues with unit modules [36, 37]. Because the memristive Hénon map has no invariant points, we can not study the map stability using the stable manifold and unstable manifold of the invariant points. To solve this issue, we propose a novel dimension-reduction conversion method for studying the memristor-induced hidden Neimark–Sacker bifurcations in the memristive Hénon map.

3.1 Dimension-reduction conversion method

The variable z (i.e., the memristor inner state) in the third equation of (3) is expressed as the difference iteration form of the variable y (i.e., the memristor input), which can be converted into the cumulative sum form of the variable y [29]. Thus, the memristive Hénon map in (3) can be rewritten in the following form as

$$ \left\{ {\begin{array}{*{20}l} {x_{{n + 1}} = 1 - ax_{n}^{2} + y_{n} ,} \hfill \\ {y_{{n + 1}} = bx_{n} + ky_{n} \tanh (z_{0} + \sum\limits_{{l = 0}}^{{n - 1}} {y_{l} } ),} \hfill \\ \end{array} } \right. $$
(5)

where z0 is the initial state of the memristor.

Denote

$$ M = k\tanh (z_{0} + \sum\limits_{l = 0}^{n - 1} {y_{l} } ), $$
(6)

as a memristor-related parameter. Since the hyperbolic tangent function tanh(·) is a monotonic continuous function bounded above and below, i.e., − 1 < tanh(·) < 1, we have

$$ - k < M < k. $$
(7)

Thus, a dimension-reduction model of the memristive Hénon map can be deduced as

$$ \left\{ {\begin{array}{*{20}l} {x_{{n + 1}} = 1 - ax_{n}^{2} + y_{n} ,} \hfill \\ {y_{{n + 1}} = bx_{n} + My_{n} ,} \hfill \\ \end{array} } \right. $$
(8)

where the memristor-related parameter M is an adjustable parameter in the interval [−k, k].

The stability of the dimension-reduction model (8) can be discussed using its determined invariant point. The invariant point F = (X, Y) of (8) is obtained by solving the following equations

$$ \left\{ {\begin{array}{*{20}l} {X = 1 - aX^{2} + Y,} \hfill \\ {Y = bX + MY} \hfill \\ \end{array} } \right. $$
(9)

There yields

$$ \begin{gathered} F_{ + } = (X_{ + } ,b^{\prime}X_{ + } ), \hfill \\ F_{ - } = (X_{ - } ,b^{\prime}X_{ - } ), \hfill \\ \end{gathered} $$
(10)

where \(b^{\prime} = {b \mathord{\left/ {\vphantom {b {(1 - M)}}} \right. \kern-\nulldelimiterspace} {(1 - M)}}\), \(X_{ + } = \tfrac{{(b^{\prime} - 1) + \sqrt {(b^{\prime} - 1)^{2} + 4a} }}{2a}\), and \(X_{ - } = \tfrac{{(b^{\prime} - 1) - \sqrt {(b^{\prime} - 1)^{2} + 4a} }}{2a}\). Since b' is a nonlinear function of M, the positions of the two invariant points F± in the phase space change with the value of M.

The Jacobian matrix at these two determined invariant points F± is given as

$$ {\mathbf{J}}_{{F_{ \pm } }} = \left[ {\begin{array}{*{20}c} { - 2aX_{ \pm } } & 1 \\ b & M \\ \end{array} } \right]. $$
(11)

Thereafter, the corresponding characteristic polynomial is generated by

$$ P(\lambda ) = \lambda^{2} + (2aX_{ \pm } - M)\lambda - 2aMX_{ \pm } - b. $$
(12)

Hence, two eigenvalues λ1 and λ2 are finally solved as

$$ \lambda_{1,2} = (0.5M - aX_{ \pm } ) \pm \sqrt {(0.5M + aX_{ \pm } )^{2} + b} . $$
(13)

The results given in (13) indicate that the memristor-related parameter can alter the stability of the dimension-reduction model (8).

Clearly, if |λ1|< 1 and |λ2|< 1, the invariant points F± are stable; otherwise they are unstable. Thus, once the adjustable parameters a, b and memristor-related parameter M are fixed, the eigenvalues λ1 and λ2 in (13) can be figured out and the stability of the memristive Hénon map can be then obtained.

First, a set of adjustable parameters are fixed as a = 0.27 and b =  − 1.05. For the invariant point F+, the stable interval of the memristor-related parameter is yielded from (13) as

$$ 0.2288 < M < 0.8754. $$
(14)

i.e., if the memristor-related parameter is located into the stable interval given in (14), the invariant point F+ is stable. Thus, when M = 0.2288 and 0.8754, there exists |λ1,2|= 1, leading to the occurrence of Neimark–Sacker bifurcations. However, the invariant point F− is always unstable, regardless of the memristor-related parameter.

Second, another set of adjustable parameters are fixed as a = 0.27 and b =  − 0.82. For the invariant points F+ and F−, the stable intervals of the memristor-related parameter can be obtained from (13) as

$$ -0.5618 < M < 1.0000, $$
(15)

and

$$ 1.0000 < M < 1.1833, $$
(16)

respectively. Thus, when M =  −0.5618, the Neimark–Sacker bifurcation occurs at the invariant point F+; whereas when M = 1.1833, the Neimark–Sacker bifurcation occurs at the invariant point F−.

In particular, when M = 1, the dimension-reduction model given in (8) has a unique invariant point F = (0, − 1). Thus, the two eigenvalues λ1 and λ2 at F = (0, − 1) are transformed from (13) as

$$ \lambda_{1,2} = 0.5b \pm \sqrt {0.25 + b} , $$
(17)

indicating that λ1 and λ2 are only dependent on the adjustable parameter b. Accordingly, the stable interval of the adjustable parameter b can be solved from (17) as

$$ - 1 < b < 0.3944. $$
(18)

When b =  −1, there are |λ1,2|= 1, leading to the occurrence of the Neimark–Sacker bifurcation at the unique invariant point F. By contrast, when b = 0.3944, there are λ1 = 1 and λ2 =  −0.6055, resulting in the occurrence of fold bifurcation at the same invariant point.

3.2 Memristor-induced hidden Neimark–Sacker bifurcations

When the memristor-related parameter M increases within the respective regions under these two sets of adjustable parameters, we can calculate the two eigenvalues λ1 and λ2 in (13) and draw their loci in Fig. 5. As illustrated in Fig. 5a and 5c, when M = 0.2288 or −0.5618, the loci of the conjugate complex eigenvalues at the invariant point F+ are going from outside the unit circle to inside the unit circle, leading to the occurrence of the Neimark–Sacker bifurcation. As demonstrated in Fig. 5b, when M = 0.8754, the loci of the conjugate complex eigenvalues at the invariant point F+ are crossing the unit circle from inside to outside, resulting in the occurrence of the Neimark–Sacker bifurcation. Moreover, as shown in Fig. 5d, when M = 1.1833, the loci of the conjugate complex eigenvalues at the invariant point F– are passing the unit circle from inside to outside, also indicating the occurrence of the Neimark–Sacker bifurcation. Consequently, the results in Fig. 5 show that the invariant points of the dimension-reduction model become unstable via the Neimark–Sacker bifurcations.

Fig. 5
figure 5

The loci of two eigenvalues relative to the memristor-related parameter M, demonstrating the occurrence of the Neimark–Sacker bifurcations in the dimension-reduction model. For fixed (a, b) = (0.27, −1.05), a M increasing from 0.1 to 0.5 and b M increasing from 0.59 to 0.99. For fixed (a, b) = (0.27, −0.82), c M increasing from −0.7 to −0.3 and d M increasing from 1.05 to 1.35

Full size image

Using the dimension-reduction model described by (8), the initial conditions are determined as (x0, y0) = (0, 0) and the memristor-related parameter M is regarded as a variable parameter. Corresponding to the loci of the two eigenvalues shown in Fig. 5, the bifurcation diagrams of the two variables x and y relative to M can be numerically depicted in Fig. 6. It demonstrates that the dimension-reduction model undergoes a quasi-periodic bifurcation scenario with respect to the memristor-related parameter and the four Neimark–Sacker bifurcation points are consistent with the theoretical results in (14), (15), and (16). Since there are no invariant points, all the quasi-periodic bifurcations of the memristive Hénon map are hidden. Therefore, using the proposed dimension-reduction conversion method, the memristor-induced hidden Neimark–Sacker bifurcations can be intuitively revealed and effectively interpreted. Interestingly, such a hidden Neimark–Sacker bifurcation has not been reported in the literature.

Fig. 6
figure 6

The bifurcation diagrams relative to the memristor-related parameter M, illustrating the quasi-periodic bifurcation scenarios in the dimension-reduction model. For fixed (a, b) = (0.27, −1.05), a M increasing from 0.1 to 0.5 and b M increasing from 0.59 to 0.99. For fixed (a, b) = (0.27, −0.82), c M increasing from − 0.7 to −0.3 and d M increasing from 1.05 to 1.35

Full size image

It should be noticed that the dimension-reduction model given in (8) has the unique invariant point F = (0, −1) at M = 1, and its stability only relates to the adjustable parameter b. For the special case M = 1, when b increases within b ∈ [−1.1, −0.9] and b ∈ [0.3, 0.5], respectively, the two eigenvalues λ1 and λ2 in (17) are calculated and their loci can be drawn in Fig. 7a and b. As can be seen, when b =  −1, the loci of the conjugate complex eigenvalues at the unique invariant point F are crossing the unit circle from outside to inside, resulting in the occurrence of Neimark–Sacker bifurcation. Conversely, when b = 0.3944, the locus of λ1 at the unique invariant point F passes through the unit circle from inside to outside at +1, while that of λ2 at the invariant point F remains inside the unit circle, meaning the occurrence of the fold bifurcation rather than the Neimark–Sacker bifurcation at this parameter point. Accordingly, for three different settings of the adjustable parameter a, the bifurcation diagrams of the variable x with respect to the adjustable parameter b are numerically depicted based on the dimension-reduction model (8), and they are shown in Fig. 7c. One can see that the dimension-reduction model undergoes exactly the same quasi-periodic bifurcation scenario with respect to the adjustable parameter b for three different settings of a. The results in Fig. 7 confirm that the numerically simulated Neimark–Sacker bifurcation point is consistent with the theoretical result given in (18), no matter what the adjustable parameter a is. Besides, the numerical result clarifies that if b > 0, an unbounded dynamical behavior appears in the dimension-reduction model.

Fig. 7
figure 7

For the special memristor-related parameter M = 1, the loci of two eigenvalues and bifurcation diagrams with respect to the adjustable parameter b with respect to the memristor-related parameter. a The loci of two eigenvalues when b increases from −1.1 to −0.9. b The loci of two eigenvalues when b increases from 0.3 to 0.5. c The bifurcation diagrams under three different values of the adjustable parameter a when b increases from −1.1 to −0.9

Full size image

4 Bifurcation plots and basins of attraction

In this section, we explore the bifurcation plots and local basins of attraction to disclose rich and complex hidden dynamical behaviors with multistability in the memristive Hénon map.

4.1 Coupling strength-dependent bifurcation plots

To obtain the bifurcation plots of the memristive Hénon map, the adjustable parameters are determined as (a, b) = (0.25, 0.51) and (0.27, −0.82), respectively, the initial conditions are fixed as (x0, y0, z0) = (0, 0, 0), and the coupling strength k is taken as a bifurcation parameter. When k increases within the regions [−0.9, −0.85] and [0.7, 1.05] respectively, the bifurcation diagrams of variables x, y, z and corresponding Lyapunov exponent (LE) spectra are depicted and shown in Fig. 8, where the LEs are computed using the Wolf’s Jacobian algorithm.

Fig. 8
figure 8

For fixed initial conditions (x0, y0, z0) = (0, 0, 0), the coupling strength-dependent bifurcation diagrams of the variables x, y, z (bottom) and corresponding LE spectra (top). a For fixed (a, b) = (0.25, 0.51), numerical plots of the memristive Hénon map with k ∈ [−0.9, −0.85]. b For fixed (a, b) = (0.27, −0.82), numerical plots of the 3D memristive Hénon map with k ∈ [0.7, 1.05]

Full size image

As demonstrated in Fig. 8a, the memristive Hénon map can display hyperchaos and has a reverse period-doubling route to chaos with the increase of k. When decreasing k, the orbit of the map begins with period-2 with negative first LE at k =  −0.85, breaks into period-4 at k =  −0.8546, period-8 at k =  −0.8633, and period-16 at k =  −0.8675 via the reverse period-doubling bifurcation successively, then enters into chaos with one positive LE at k =  −0.8708, and finally goes into hyperchaos with two positive LEs at k =  −0.8916.

Meanwhile, as illustrated in Fig. 8b, the memristive Hénon map can display chaos and has a quasi-periodic route to chaos with the increase of k. When increasing k, the orbit of the map starts with period-3 limit cycle with negative first LE at k = 0.7, goes into quasi-period with zero first LE at k = 0.7568 via the quasi-periodic bifurcation, then mutates into multi-period with negative first LE at k = 0.8204, and finally turns into chaos with one positive LE at k = 0.8316.

It should be noted that there are some obvious periodic windows within a relatively wider chaotic interval. Therefore, the memristive Hénon map can generate complex dynamical behaviors, including chaos, hyperchaos, quasi-period, period, and periodic windows. The bifurcation analyses show that with the intervention of memristor, the dynamical behaviors of the memristive Hénon map become richer and more complex.

Besides, the original Hénon map in [32] only has the period-doubling route to chaos with the variations of its adjustable parameters. However, with the increase of the coupling strength k, the presented memristive Hénon map has not only the period-doubling route to chaos, but also the quasi-periodic route to chaos [38]. The results indicate that the memristive Hénon map possesses more complex hidden bifurcation scenarios than most reported maps.

4.2 Basins of attraction for detecting multistability

Multistability is an intrinsic characteristic for many nonlinear dynamical systems [39] and it can cause multiple attractors to be coexisted in the initial space. With the multistability, the long-term motions of a nonlinear dynamical system are different and they are totally dependent on the initial conditions in the basin of attraction. In particular, the multistability can be readily found in the dynamical systems based on continuous or discrete models of memristors [2, 40]. As discussed in Sect. 3, the 3D memristive Hénon map has no invariant points, but the memristor-related parameter can induce the hidden Neimark–Sacker bifurcations therein, leading to the emergence of the stable manifold and unstable manifold of hidden invariant points. Thus, for some specific adjustable parameters, the memristive Hénon map can show multistability and has coexisting multiple attractors when some initial conditions are chosen in the initial space.

To measure the coexisting multiple attractors’ behaviors, the basins of attraction are painted with different colors to divide the initial space according to the long-term motions of the memristive Hénon map. When two sets of model parameters (k, a, b) = (1, 0.25, −0.75) and (−0.3, 0.05, 0.85) are considered, their basins of attraction are depicted through detecting every initial condition in the x0–y0 plane with z0 = 0, as shown in Fig. 9a1 and b1. The red, black, and orange regions represent chaos (CH), multi-period (MP), and period-2 (P2), respectively. Note that the white region represents the unbounded behavior. As can be seen, the bi-stability or tri-stability phenomenon of the coexisting attractors can be indeed disclosed in the memristive Hénon map.

Fig. 9
figure 9

Coexisting multiple attractors’ behaviors in the memristive Hénon map for two sets of model parameters. a The basin of attraction a1 and coexisting bi-stable attractors a2 for fixed (k, a, b) = (1, 0.25, −0.75). b The basin of attraction b1 and coexisting tri-stable attractors b2 for fixed (k, a, b) = (−0.3, 0.05, 0.85)

Full size image

Furthermore, Fig. 9a2 and b2 exhibits the phase orbits of coexisting attractors for the two sets of model parameters. The initial conditions of the chaotic attractors are selected from the red regions of Fig. 9a1 and b1, the limit cycles with multi-periods are obtained using the initial conditions from the black regions of Fig. 9a1 and b1, whereas the limit cycle with period-2 are generated using the initial conditions from the orange regions of Fig. 9b1. The results well validate the emergences of bi-stability or tri-stability in the memristive Hénon map.

5 Digital hardware experiments

In order to facilitate the implementation of the memristive Hénon map, a digitally circuit-implemented hardware set is exploited using a high-performance microcontroller [7, 28, 41]. Based on the hardware set, the generated chaotic attractors in Fig. 4 can be physically acquired by a digital oscilloscope in the XY mode.

The powerful STM32F407 family with in-built ARM Cortex-M4 32-bit RISC core is chosen as the microcontroller. The hardware set mainly consists of 32-bit microcontroller STM32F407VET6, 16-bit digital-to-analog converter DAC8563, and interface level conversion circuit. The 32-bit microcontroller is employed to digitally implement the memristive Hénon map, the digital-to-analog converter outputs the analog voltage, and the interface level conversion circuit completes the voltage polarity conversion. The executable program for the memristive Hénon map is programmed in C language and loaded to the 32-bit microcontroller. All the model parameters and initial conditions are preloaded to the built hardware set. In addition, a digital oscilloscope is used to acquire the phase orbits of the chaotic attractors generated from the memristive Hénon map.

In the following hardware experiments, the selected model parameters and initial conditions are exactly the same as those in Fig. 4. Utilizing the digitally circuit-implemented hardware set, the phase orbits for eight sets of model parameters under the initial conditions (x0, y0, z0) = (0, 0, 0) are experimentally acquired on the digital oscilloscope, as shown in Fig. 10. Note that Ch1 and Ch2 labeled in the captured figures represent the channels of x-axis and y-axis, respectively, and their values represent the scales of each division in both directions. To better show the visual effect, the iteration number of the memristive Hénon map is set to 2 × 105 and the time scale of the digital oscilloscope is adjusted to 10 s. This can make sure that more points can be captured in each unit time. The experimental results in Fig. 10 well validate the numerical simulations in Fig. 4, implying the feasibility of the digital hardware implementation for the presented 3D memristive Hénon map.

Fig. 10
figure 10

Based on the hardware set, the experimentally acquired phase orbits for eight sets of model parameters under the initial conditions (x0, y0, z0) = (0, 0, 0). The model parameters (k, a, b) are also provided in the figures. a Four negative values of k. b Four positive values of k

Full size image

6 Conclusion

In this paper, a memristor-based Hénon map with hidden Neimark–Sacker bifurcations has been presented. The 3D memristive Hénon map was achieved by coupling a memristor to the classical Hénon map [32]. Using numerical measures, the memristor effects were exhibited and the complex dynamical behaviors with multistability were disclosed. Due to no invariant points in the presented map, the dimension-reduction conversion method was firstly proposed and the hidden Neimark–Sacker bifurcations were effectively interpreted. It was demonstrated that the memristive Hénon map can exhibit the bounded iteration behaviors, and the memristor can bring complex hidden dynamical behaviors to the presented map and greatly enhances the fractal structure complexity of the generated chaotic attractors. Besides, the generated chaotic attractors have been physically acquired by the digitally circuit-implemented hardware experiments. However, how to introduce the discrete model of memristor to ensure that the memristive Hénon map exhibits the bounded iterative behaviors and what is the application prospect for complex hidden dynamical behaviors? These issues deserve further investigation.