4-D Memristive Chaotic System with Different Families of Hidden Attractors

Abstract

The design of systems without equilibrium or with line of equilibrium points is a subject which has started to attract the interest of the research community the last decade. In this direction, various chaotic systems with hidden attractors, which are based on memristors or memristive systems, have been proposed. In this chapter a new 4-D memristive system is presented. The peculiarity of the model is that it displays a line of equilibrium points for a range of the parameters as well as no-equilibrium for another range of the parameters. System in both occasions presents a chaotic behavior with hidden attractors. The behavior of the proposed system is investigated through numerical simulations, by using phase portraits, Lyapunov exponents and bifurcation diagrams. The adaptive control scheme of the system is presented in order to prove that the memristive system’s dynamical behavior can be controlled. Also, we have designed an electronic circuit to confirm the feasibility of the system in both cases.

1 Introduction

The forth missing curcuit element, the memristor, was introduced for the first time in 1971 (Chua 1971). A general concept of memristive systems expanded in 1976, (Chua and Kang 1976). In 2008 the realization of a two terminal memristor was announced (Strukov et al. 2008). This announcement influenced many researchers and paved the way for various scientific fields. n 2009, other elements with memory from the nano-world, memcapacitor and meminductor was introduced (Ventra et al. 2009).

There are systems, such as thermistors, with phenomena in which internal state depends on the temperature (Sapoff and Oppenheim 1963), spintronic devices in which resistance varies according to their spin polarization (Pershin and Di Ventra 2008) and molecules in which resistance changes according to their atomic configuration (Chen et al. 2003), could be explained now with the use of the memristor. Also, electronic circuits with memory could simulate processes typical of biological systems, such as the adaptive behavior of unicellular organisms (Pershin et al. 2009) and the learning and associative memory (Pershin and Di Ventra 2010). Mem-elemets also are used in order to replace nonlinear parts of the electrical circuits.

At present, many applications of memristors based on their properties, such as memristor-based neural networks, memristor-based chaotic oscillators, memristor-based charge pump locked loops etc. have been introduced (Itoh and Chua 2008; Zhao et al. 2013; Wu et al. 2011). Research on memristor-based chaotic systems becomes a focal research topic in both the technological and the application domain (Volos et al. 2011; Yang et al. 2013; Driscoll et al. 2010; Wang et al. 2012; Shang et al. 2012; Shin et al. 2011; Cepisca et al. 2008; Cepisca and Bardis 2011; Bogdan et al. 2011; Corinto and Ascoli 2012a, b). Also, the design of memristor- based chaotic oscillators, by replacing the nonlinear part of chaotic dynamical systems with memristors has been introduced (Sabarathinam et al. 2016; Chen et al. 2015; Bao et al. 2016; Wu et al. 2016).

The last decades researchers introduced some memristor-based hyperchaotic systems, motivated by the complex dynamical behaviors of hyperchaotic systems and the special features of memristor in order to investigate whether there exists a memristor-based system that is hyperchaotic. Hyperchaos was generated by combining a memristor with its non-linear characteristics and a chaotic oscillator (Biswas et al. 2016; Ponomarenko et al. 2013; Özkaynak and Yavuz 2013; Ye and Wong 2013; Banerjee et al. 2012a, b; Banerjee and Biswas 2013).

Leonov and Kuznetsov (Kuznetsov et al. 2010; Leonov et al. 2011) in their research categorized periodic and chaotic attractors as either self-excited or hidden. A self-excited attractor has a basin of attraction that is associated with an unstable equilibrium, whereas a hidden attractor (HA) has a basin of attraction that does not intersect with small neighborhoods of any equilibrium points. The classical attractors of Lorenz, Rössler, Chen, Sprott (cases B to S), and other widely-known attractors are those excited from unstable equilibria. From a computational point of view this allows one to use a numerical method in which a trajectory started from a point on the unstable manifold in the neighborhood of an unstable equilibrium, reaches an attractor and identifies it. Hidden attractors cannot be found by this method and are important in engineering applications because they allow unexpected and potentially disastrous responses to perturbations in a structure like a bridge or an airplane wing.

Furthermore, the last two decades the subject of chaos control has attracted the interest of the research community. The control of a chaotic system aims to stabilize or regulate the system with the help of feedback control. There are many methods available for controlling a chaotic system such as active control (Sundarapandian 2010; Vaidyanathan 2011, 2016), adaptive control (Sundarapandian 2013; Vaidyanathan 2012, 2013, 2014; Azar and Vaidyanathan 2015), sliding mode control (Vaidyanathan 2012) and backstepping control (Njah and Sunday 2012; Vincent et al. 2007). Adaptive control is an active field in the design of control systems, especially of systems with hidden attractors (Vaidyanathan and Volos 2012; Wei et al. 2014; Pham et al. 2016), and deal with uncertainties. The key difference between adaptive controllers and linear controllers is the adaptive controller’s ability to adjust itself in order to handle unknown model’s uncertainties. Recently, much effort has been placed in adaptive control in both theory and applications. New controller design techniques are introduced to handle nonlinear and time-varying uncertainties. Broader systems with larger nonlinear uncertainties can be covered by these developments. As a result, adaptive control is used in various real world applications (Cao et al. 2012; Vaidyanathan 2015).

This research work is organized as follows. In Sect. 2 the model of the memristive system, as well as the new system are presented. In Sect. 3 the simulation results of the memristive system are also presented. The adaptive control scheme of the system is studied in Sect. 4. In Sect. 5 the circuit realization of the system is described in detail, while Sect. 6 concludes this work with a summary of the main results.

2 The Memristive System with Hidden Attractors

In this section a new memristive system with different families of hidden attractors is presented. First of all, the model of the memristive device will be analyzed, while next the mathematical description of the 4-D system will be introduced.

2.1 Model of the Memristive Device

As it is mentioned, Chua and Kang introduced the memristive device by generalizing the original definition of a memristor (Chua and Kang 1976). A memristive system can be described by:

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} \dot{w}_m=F(w_m,u_m,t), \\ &{} f_m=G(w_m,u_m,t)u_m \end{array} \end{aligned}$$

(1)

where $w_m,f_m$ and $u_m$ denote the state of memristive system, output and input, respectively. The function G is a continuous and n-dimensional scalar function and F is a vector function. Based on the definition of memristive system (1), a memristive device is introduced in this section and used in our whole paper. This memristive device is described by the following equations:

$$\begin{aligned} \dot{w}_m=u_m, \end{aligned}$$

(2a)

$$\begin{aligned} f_m=(1+0.25 w_{m}^{2}-0.002 w_{m}^{4})u_m . \end{aligned}$$

(2b)

In order to investigate the behavior of the memristive system an external sinusoidal signal $u_m$ is applied. The form of $u_m$ is:

$$\begin{aligned} \begin{array}{l@{}l@{}l}&u_m=A sin(2 \uppi \upnu t) \end{array} \end{aligned}$$

(3)

where A is the amplitude and $\upnu$ is the frequency. From the first equation of the system (3) we can find $w_m$:

$$\begin{aligned} \begin{array}{l@{}l@{}l}&w_m=w_m(0)+\frac{A}{2\uppi t}(1- cos(2\pi \upnu t)) \end{array} \end{aligned}$$

(4)

where $w_m(0)= \int _{-\infty }^{0} u_m(\tau )d\tau$ is the initial condition of the internal state $w_m$.

Substituting Eqs. (3) and (4) into Eq. (2b) it is easy to derive the output of the memristive device. Therefore, the output $f_m$ depends on frequency and amplitude of the applied input stimulus.

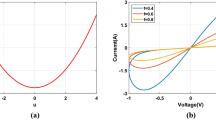
The figures below show the hysteresis loops of the proposed memristive system driven by a sinusoidal stimulus, when it is driven by a periodic signal (4).

• Figure 1 with $A = 1$, $w_0=0$ while $\upnu = 0.1$ (green line), $\upnu = 0.2$ (blue line) and $\upnu = 0.5$ (red line).

• Figure 2 for $\upnu = 0.1$, $w_0=0$ while $A = 0.5$ (green line), $A=1$ (blue line) and $A=1.5$ (red line).

• Figure 3 for $\upnu = 0.1$, $A=1$ while $w_0 = -1$ (green line), $w_0 = 0$ (blue line) and $w_0 = 1$ (red line).

Obviously, the proposed memristive device exhibits a pinched hysteresis loop in the input-output plane.

Fig. 1

Hysteresis loops of the proposed memristive device driven by a sinusoidal stimulus with $A=1$ and $w_0=0$, for frequencies $\upnu =0.1$ (green line), $\upnu =0.2$ (blue line), $\upnu =0.5$ (red line)

Fig. 2

Hysteresis loops of the proposed memristive device driven by a sinusoidal stimulus with $\upnu =0.1$ and $w_0=0$, for amplitude $A=0.5$ (red line), $A=1$ (blue line), $A=1.5$ (green line)

Fig. 3

Hysteresis loops of the proposed memristive device driven by a sinusoidal stimulus with $A=1$ and $\upnu =0.1$, for $w_0 = -1$ (green line), $w_0 = 0$ (blue line) and $w_0 = 1$ (red line)

2.2 The New Memristive System

Finally, based on the aforementioned memristive device, the following new dynamical system can be obtained.

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} \dot{x}=-\upalpha x+\upgamma f(y,w)\\ &{} \dot{y}=\upbeta x-\updelta xz+\varepsilon \\ &{} \dot{z}=-\upzeta z+ xy\\ &{} \dot{w}=y \end{array} \end{aligned}$$

(5)

where $y=u_m$ the input, $w=w_m$ the state, $f(y,w)=f_m=(1+0.25 w^{2}-0.002 w^{4})y$ the output of the memristor device and $\upalpha , \upbeta , \upgamma , \updelta , \varepsilon , \upzeta$ are real positive parameters. So, the fourth-order memristive system (5) is obtained and used in the following sections.

2.2.1 Analysis of the New Hyperchaotic Memristive System

The equilibria of system (5) can be derived by solving the following equations:

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} -\upalpha x+\upgamma f(y,w)=0\\ &{} \upbeta x-\updelta xz+\varepsilon =0\\ &{} -\upzeta z+ xy=0\\ &{} y=0 \end{array} \end{aligned}$$

(6)

The 4-D memristive system (5) for $\varepsilon =0$ and for every $\upalpha ,\upbeta ,\upgamma ,\updelta ,\upzeta$ set of values has line of equilibrium E(0, 0, 0, w). Moreover for $\varepsilon \not =0$ and for every $\upalpha ,\upbeta ,\upgamma ,\updelta ,\upzeta$ has no equilibria. As a result, this memristive hyperchaotic system can be considered as a dynamical system with hidden attractors because it is impossible to verify the chaotic attractor by choosing an arbitrary initial condition in the vicinity of the unstable equilibria. This system’s feature is noteworthy especially in the case of using these systems in applications, such as chaos encryption, because of its complexity.

The Jacobian of the system (5), $\mathbf J$ at any point is calculated as:

$$\begin{aligned} \begin{array}{l@{}l@{}l} \mathbf J = \left( \begin{array}{ c c c c } -\upalpha &{} \upgamma Q &{} 0 &{} \upgamma R\\ \upbeta - \updelta z &{} 0 &{} -\updelta x &{} 0 \\ y &{} x &{} - \upzeta &{} 0\\ 0 &{} 1 &{} 0 &{} 0 \end{array}\right) \end{array} \end{aligned}$$

(7)

where,

$$Q= \frac{\partial f(y,w)}{\partial y}=1+0.25 w^{2}-0.002 w^{4}$$

$$R= \frac{\partial f(y,w)}{\partial w}=0.5wy-0.008w^3 y$$

For the case of $\varepsilon =0$ there are infinite equilibrium points. In this case the eigenvalues of the matrix of Eq. (7), for $\upalpha =1,$ $\upgamma =1,$ $\upbeta =7,$ $\updelta =1$, $\upzeta =1$, are:

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{}\qquad \qquad \quad \quad \,\lambda _1=-1\\ &{}\qquad \qquad \quad \quad \,\,\,\lambda _2=0 \\ &{}\lambda _3=0.5 (-1 - (29 + 7 w^2 - 0.056 w^4)^{1/2})\\ &{}\lambda _4=0.5 (-1 + (29 + 7 w^2 - 0.056 w^4)^{1/2}) \end{array} \end{aligned}$$

(8)

As it is clear the eigenvalue $\lambda _1=-1$ shows that there is a stable multiplicity, $\lambda _2=0$ is as expected because the system has a line equilibrium and the eigenvalues $\lambda _3$ and $\lambda _4$ of the Jacobian Matrix depend on the variable w. So, it is difficult to determine the stability of the equilibrium points.

For the case of $\varepsilon \not =0$ there are no equilibrium points. As a result there cannot be analysis of the equilibrium points.

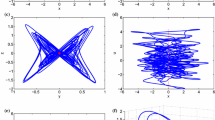
The chaotic attractor in the (x, y, z) phase space, for $\varepsilon =0$, $\upalpha =1,$ $\upgamma =1,$ $\upbeta =8.5,$ $\updelta =1$, $\upzeta =1$ is depicted in Fig. 4.

Fig. 4

Chaotic attractor in (x, y, z) phase space, for $\varepsilon =0$, $\upalpha =1,$ $\upgamma =1,$ $\upbeta =8.5,$ $\updelta =1$, $\upzeta =1$

The chaotic attractor in the (x, y, z) phase space, for $\varepsilon =0.01$, $\upalpha =1,$ $\upgamma =1,$ $\upbeta =7,$ $\updelta =2$, $\upzeta =1$ is depicted in Fig. 5.

Fig. 5

Chaotic attractor in (x, y, z) phase space, for $\varepsilon =0.01$, $\upalpha =1,$ $\upgamma =1,$ $\upbeta =7,$ $\updelta =2$, $\upzeta =1$

According to system (5), the divergence of the system is

$$\begin{aligned} \begin{array}{l@{}l@{}l}&\nabla {V}=\frac{\partial {\dot{x}}}{\partial {x}}+\frac{\partial {\dot{y}}}{\partial {y}}+\frac{\partial {\dot{z}}}{\partial {z}}+\frac{\partial {\dot{w}}}{\partial {w}}=-\upalpha -\upzeta \end{array} \end{aligned}$$

(9)

where $\nabla {V}<0$ for $\upalpha$ and $\upzeta$ positive.

The Lyapunov exponents for $\varepsilon =0.1$ have been calculated as: $L_1=0.01044,$ $L_2=0.05774$, $L_3=0$ and $L_4=-2.95934$. There are two positive Lyapunov exponents, so the system is hyperchaotic. In addition the Kaplan-Yorke dimension of the system is found as:

$$\begin{aligned} \begin{array}{l@{}l@{}l}&D_{KY}= 3+\frac{L_1+L_2+L_3}{|L_4|}=3.023038 \end{array} \end{aligned}$$

(10)

3 Simulation Results

In order to study the behavior of the new system, usual tools of the theory of dynamical systems such as phase portaits, bifurcation diagrams, continuation diagrams and diagram of Lyapunov exponents have been used.

Firstly, the bifurcation diagram of y versus $\upbeta$, for various values of the parameter $\varepsilon$, is obtained by plotting the variable x when the trajectory cuts the plane $w = 0$ with $dy/dt < 0$, as the control parameter $\upbeta$ is decreased in tiny steps in the range of $7 \le \upbeta \le 10$. Also, the continuations diagrams of y versus $\upbeta$, in which the initial conditions in each iteration have different values, and the diagram of system’s (5) Lyapunov exponents versus $\upbeta$ are presented for different sets of values of the system’s parameters. At the Lyapunov diagrams the fourth Lyapunov exponent is ignored because it takes negative values far from the zero value. Especially, the hyperchaotic behavior is shown in the Lyapunov diagrams in the region where two Lyapunov exponents become positive and one zero.

For values of the parameters $\varepsilon =0$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =1$, $\upzeta =1$ in Figs. 6, 7 and 8 the bifurcation diagram of y versus $\upbeta$, the continuation diagram of y versus $\upbeta$ and the diagram of systems Lyapunov exponents versus $\upbeta$ are presented.

Fig. 6

The bifurcation diagram of y versus $\upbeta$ for $\varepsilon =0$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =2$, $\upzeta =1$

Fig. 7

The continuation diagram of y versus $\upbeta$ for $\varepsilon =0$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =2$, $\upzeta =1$

Fig. 8

The Lyapunov diagram of Lyapunov exponents versus $\upbeta$ for $\varepsilon =0$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =2$, $\upzeta =1$

In more details, system (5) presents the following dynamical behavior, in respect to $\upbeta$ for $\varepsilon =0$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =2$, $\upzeta =1$:

• A region of periodic behavior for $\upbeta <7.162$

• A region of chaotic behavior for $7.162<\upbeta <7.204$

• A region of quasi-periodic behavior for $7.204<\upbeta <7.216$

• A region of chaotic behavior for $7.216<\upbeta <7.228$

• A region of quasi-periodic behavior for $7.228<\upbeta <7.246$

• A region of chaotic behavior for $7.246<\upbeta <7.294$

• A region of quasi-periodic behavior for $7.294<\upbeta <7.306$

• A region of chaotic behavior for $7.306<\upbeta <8.134$

• A region of hyperchaotic behavior for $8.134<\upbeta <8.152$

• A region of chaotic behavior for $8.152<\upbeta <8.212$

• A region of hyperchaotic behavior for $8.212<\upbeta <8.224$

• A region of chaotic behavior for $8.224<\upbeta <8.242$

• A region of hyperchaotic behavior for $8.242<\upbeta <8.254$

• A region of chaotic behavior for $8.254<\upbeta <9.472$

• A region of hyperchaotic behavior for $9.472<\upbeta <10$.

For values of the parameters $\varepsilon =0.0001$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =1$, $\upzeta =1$ in Figs. 9, 10 and 11 the bifurcation diagram of y versus $\upbeta$, the continuation diagram of y versus $\upbeta$ and the diagram of systems Lyapunov exponents versus $\upbeta$ are presented.

Fig. 9

The bifurcation diagram of y versus $\upbeta$ for $\varepsilon =0.0001$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =1$, $\upzeta =1$

Fig. 10

The continuation diagram of y versus $\upbeta$ for $\varepsilon =0.0001$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =1$, $\upzeta =1$

Fig. 11

The Lyapunov Diagram of Lyapunov exponents versus $\upbeta$ for $\varepsilon =0.0001$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =1$, $\upzeta =1$

In more details, system (5) presents the following dynamical behavior, in respect to $\upbeta$ for $\varepsilon =0.0001$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =1$, $\upzeta =1$:

• A region of periodic behavior for $\upbeta <7.216$

• A region of chaotic for $7.216<\upbeta <8.11$

• A region of hyperchaotic behavior for $8.11<\upbeta <8.158$

• A region of chaotic behavior for $8.158<\upbeta <9.49$

• A region of hyperchaotic behavior for $9.49<\upbeta <10$.

For values of the parameters $\varepsilon =0.001$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =1$, $\upzeta =1$ in Figs. 12, 13 and 14 the bifurcation diagram of y versus $\upbeta$, the continuation diagram of y versus $\upbeta$ and the diagram of systems Lyapunov exponents versus $\upbeta$ are presented.

Fig. 12

The bifurcation diagram of y versus $\upbeta$ for $\varepsilon =0.001$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =1$, $\upzeta =1$

Fig. 13

The continuation diagram of y versus $\upbeta$ for $\varepsilon =0.001$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =1$, $\upzeta =1$

Fig. 14

The Lyapunov Diagram of Lyapunov exponents versus $\upbeta$ for $\varepsilon =0.001$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =1$, $\upzeta =1$

In more details, system (5) presents the following dynamical behavior, in respect to $\upbeta$ for $\varepsilon =0.001$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =1$, $\upzeta =1$:

• A region of periodic behavior for $\upbeta <7.138$

• A region of quasi-periodic behavior for $7.144<\upbeta <7.204$

• A region of chaotic behavior for $7.204<\upbeta <7.234$

• A region of quasi-periodic behavior for $7.234<\upbeta <7.246$

• A region of chaotic behavior for $7.246<\upbeta <8.164$

• A region of hyperchaotic behavior for $8.164<\upbeta <8.254$

• A region of chaotic behavior for $8.254<\upbeta <9.502$

• A region of hyperchaotic behavior for $9.502<\upbeta <10$.

For values of the parameters $\varepsilon =0.01$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =1$, $\upzeta =1$ in Figs. 15, 16 and 17 the bifurcation diagram of y versus $\upbeta$, the continuation diagram of y versus $\upbeta$ and the diagram of systems Lyapunov exponents versus $\upbeta$ are presented.

Fig. 15

The bifurcation diagram of y versus $\upbeta$ for $\varepsilon =0.01$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =2$, $\upzeta =1$

Fig. 16

The continuation diagram of y versus $\upbeta$ for $\varepsilon =0.01$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =2$, $\upzeta =1$

Fig. 17

The Lyapunov Diagram of Lyapunov exponents versus $\upbeta$ for $\varepsilon =0.01$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =2$, $\upzeta =1$

In more details, system (5) presents the following dynamical behavior, in respect to $\upbeta$ for $\varepsilon =0.01$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =2$, $\upzeta =1$:

• A region of periodic behavior for $\upbeta <7.048$

• A region of chaotic behavior for $7.048<\upbeta <7.06$

• A region of quasi-periodic behavior for $7.06<\upbeta <7.066$

• A region of chaotic behavior for $7.066<\upbeta <7.732$

• A region of periodic behavior for $7.732<\upbeta <7.75$

• A region of chaotic behavior for $7.732<\upbeta <9.508$

• A region of hyperchaotic behavior for $9.508<\upbeta <10$.

For values of the parameters $\varepsilon =0.1$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =1$, $\upzeta =1$ in Figs. 18, 19 and 20 the bifurcation diagram of y versus $\upbeta$, the continuation diagram of y versus $\upbeta$ and the diagram of systems Lyapunov exponents versus $\upbeta$ are presented.

Fig. 18

The bifurcation diagram of y versus $\upbeta$ for $\varepsilon =0.1$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =2$, $\upzeta =1$

Fig. 19

The continuation diagram of y versus $\upbeta$ for $\varepsilon =0.1$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =2$, $\upzeta =1$

Fig. 20

The Lyapunov diagram of Lyapunov exponents versus $\upbeta$ for $\varepsilon =0.1$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =2$, $\upzeta =1$

In more details, system (5) presents the following dynamical behavior, in respect to $\upbeta$ for $\varepsilon =0.1$, $\upalpha =1,$ $\upgamma =1,$ $\updelta =2$, $\upzeta =1$.:

• A region of periodic behavior for $7.108<\upbeta <7.126$

• A region of quasi-periodic behavior for $7.126<\upbeta <7.156$

• A region of periodic behavior for $7.156<\upbeta <7.258$

• A region of chaotic behavior for $7.258<\upbeta <8.83$

• A region of periodic behavior for $8.83<\upbeta <8.842$

• A region of quasi-periodic behavior for $8.842<\upbeta <8.854$

• A region of periodic behavior for $8.854<\upbeta <8.872$

• A region of chaotic behavior for $8.872<\upbeta <8.896$

• A region of periodic behavior for $8.896<\upbeta <8.902$

• A region of quasi-periodic behavior for $8.902<\upbeta <8.92$

• A region of chaotic behavior for $8.92<\upbeta <9.46$

• A region of hyperchaotic behavior for $9.46<\upbeta <10$.

4 Adaptive Control of the 4-D Hyperchaotic Memristive Dynamical System

From the results of the simulations it is shown that the memristor adds an extra complexity to the system’s dynamical behavior. So it is useful to see if the new 4-D memristive system can be controlled by using the adaptive control method, in order to derive an adaptive feedback control law for globally stabilization of the system with unknown parameters.

The controlled 4-D hyperchaotic memristive dynamical system given by following state equilibrium for $\upgamma =1,$ $\varepsilon =0, \upzeta =1$:

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} \dot{x}=-\upalpha x+f(y,w)+u_1\\ &{} \dot{y}=\upbeta x-\updelta xz+u_2\\ &{} \dot{z}=-z+ xy+u_3\\ &{} \dot{w}=y+u_4 \end{array} \end{aligned}$$

(11)

where x, y, z, w are the states and $u_1$, $u_2$, $u_3$, $u_4$ are the adaptive controls and $\upalpha$, $\upbeta$ and $\updelta$ are the unknown parameters of the system.

The problem is finding the adaptive controls $u_1$, $u_2$, $u_3$, $u_4$ so as to regulate the variables x, y, z, w.

Consider the adaptive feedback control law:

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} u_1=\hat{\upalpha }(t)x-f(y,w)-k_1 x\\ &{} u_2=-\hat{\upbeta }(t)x+\hat{\updelta }(t) x z -k_2 y\\ &{} u_3=z-xy-k_3 z\\ &{} u_4=-y-k_4 w \end{array} \end{aligned}$$

(12)

where $k_1,k_2,k_3,k_4$ are the positive gain constants.

Substituting Eq. (12) into Eq. (11), the closed-loop plant dynamics is given as:

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} \dot{x}=-(\upalpha -\hat{\upalpha }(t))x-k_1 x\\ &{} \dot{y}=(\upbeta -\hat{\upbeta }(t))x-(\updelta -\hat{\updelta }(t)) x z-k_2 y\\ &{} \dot{z}=-k_3 z\\ &{} \dot{w}=-k_4 w \end{array} \end{aligned}$$

(13)

The parameter estimation errors are defined as:

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} e_\alpha =\upalpha -\hat{\upalpha }(t)\\ &{} e_\beta =\upbeta -\hat{\upbeta }(t)\\ &{} e_\delta =\updelta -\hat{\updelta }(t) \end{array} \end{aligned}$$

(14)

Differentiating the Eq. (14) with respect to t

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} \dot{e_{\upalpha }}=-{\dot{\hat{\upalpha }}}(t)\\ &{} \dot{e_{\upbeta }}=-{\dot{\hat{\upbeta }}}(t)\\ &{} \dot{e_{\updelta }}=-{\dot{\hat{\updelta }}}(t) \end{array} \end{aligned}$$

(15)

In the view of Eq. (15) the plant dynamics can be simplified as:

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} \dot{x}=-e_{\upalpha } x-k_1 x\\ &{} \dot{y}=e_{\upbeta } x-e_{\updelta } x z-k_2 y\\ &{} \dot{z}=-k_3 z\\ &{} \dot{w}=-k_4 w \end{array} \end{aligned}$$

(16)

Next the adaptive control theory is used in order to find an update law for the parameter estimates. Consider the quadratic candidate Lyapunov function defined by

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} V(x,y,z,w,e_{\upalpha },e_{\upbeta },e_{\updelta })=\\ &{} =\frac{1}{2}(x^2+y^2+z^2+w^2)+\frac{1}{2}(e_{\upalpha }^2+e_{\upbeta }^2+e_{\updelta }^2) \end{array} \end{aligned}$$

(17)

Differentiating the Eq. (17) with respect to t

$$\begin{aligned} \begin{array}{l@{}l@{}l} \dot{V}=x \dot{x}+y \dot{y}+z \dot{z}+w \dot{w}+e_{\upalpha } \dot{e_{\upalpha }}+e_{\upbeta } \dot{e_{\upbeta }}+e_{\updelta } \dot{e_{\updelta }}\\ \end{array} \end{aligned}$$

(18)

Finally,

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} \dot{V}=-k_1 x^2-k_2 y^2-k_3 z^2-k_4 w^2+ \\ &{} +e_{\upalpha } (x^2-{\dot{\hat{\upalpha }}})+e_{\upbeta } (x y -{\dot{\hat{\upbeta }}})-e_{\updelta } (z x y \dot{\hat{\updelta }}) \end{array} \end{aligned}$$

(19)

From Eq. (19) the parameter update law is

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} {\dot{\hat{\upalpha }}}(t)=-x^2\\ &{} \dot{\hat{\upbeta }}(t)=x y\\ &{} \dot{\hat{\updelta }}(t)=-z x y \end{array} \end{aligned}$$

(20)

Theorem 1

The states x, y, z, w of the 4-D hyperchaotic memristive dynamical system (5) with unknown system parameters are globaly and exponentially regulated for all initial conditions to the desired constant values $\upalpha$, $\upbeta$, $\updelta$ by the adaptive control law (11) and the parameter update law (19), where $k_1$, $k_2$, $k_3$ and $k_4$ are positive gain constants.

Proof

This result will be prooved by applying Lyapunov stability theory (Khalil 2001).

The quadratic Lyapunov function defined by Eq. (17), which is a positive definite function on $\mathfrak {R}^7$, is considered.

By substituting the Eq. (15) into Eq. (14) the time derivative of V is obtained as:

$$\begin{aligned} \begin{array}{l@{}l@{}l}&\dot{V}=-k_1 x^2-k_2 y^2-k_3 z^2-k_4 w^2 \end{array} \end{aligned}$$

(21)

From the above equation (21) it is obvious that the derivative of V respect to t, $\frac{dV}{dt}<0$ is a negative semi-definite function on $\mathfrak {R}^7$. So the state vector x(t) and the parameter estimation error can be concluded that are globally bounded, i.e.

$$[x \, y\, z\, w\, e_{\upalpha }(t)\, e_{\upbeta }(t)\, e_{\updelta }(t)]^T \in L_\infty $$

where the function space $L_\infty$ consists of all functions of the form h(t) that satisfies $\mid h(\cdot ,t) \mid <\infty$ for all t.

If $k=min\{k_1,k_2,k_3,k_4\}$, then it follows from the Eq. (16) that

$$\begin{aligned} \begin{array}{l@{}l@{}l}&\dot{V}\le -k||\mathbf x (t)||^2 \end{array} \end{aligned}$$

(22)

Thus

$$\begin{aligned} \begin{array}{l@{}l@{}l}&k||\mathbf x (t)||^2 \le \dot{V} \end{array} \end{aligned}$$

(23)

Integrating the inequality (23)

$$\begin{aligned} \begin{array}{l@{}l@{}l}&k \int _{0}^{t} ||\mathbf x (t)||^2 d\tau \le V(0)-V(t) \end{array} \end{aligned}$$

(24)

From Eq. (24) it follows that $x,y,z,w \in L_2$, where the function space $L_2$ consists of all functions h(t) with properties such that the integral $\int _{0}^{\infty } \sqrt{h(t)^2}$ exists for all t. By using Barbalat’s lemma (Khalil 2001), the $x,y,z,w \rightarrow 0$ exponentially as $t \rightarrow \infty$ for all initial conditions x(0), y(0), z(0), w(0) $\in \mathfrak {R}^4$. Then it follows that ths states x, y, z, w of the system with the unknown parameters $\upalpha ,\upbeta ,\updelta$ are globally exponentially regulated for all the initial conditions, by the adaptive control laws (12) and the parameter update law (20).

Fig. 21

Time-series of the controlled states $x,\,y,\,z,\,w$

Fig. 22

Time-series of the controlled states $x,\,y,\,z,\,w$

Here the proof is completed.

For the numerical simulations the parameter values are $\upalpha = 1$, $\upbeta = 8$, $\updelta = 2$ as used before. Also the positive gain constants are chosen $k_1=k_2=k_3=k_4=5$. Futhermore the initial conditions are $x(0)=-1.1$, $y(0) = 0.6$, $z(0) = -1.5$, $w(0) = 0.2$, and $\hat{\upalpha }(0)= -0.5$, $\hat{\upbeta }(0) = -0.2$, $\hat{\updelta }(0) = -0.1$. In Fig. 21 the exponential convergence of the controlled states of the system, is depicted.

In Fig. 22 the parameter values are $\upalpha = 1$, $\upbeta = 8$, $\updelta = 2$, while the initial conditions are $x(0)=-1.1$, $y(0) = 1$, $z(0) = -0.5$, $w(0) = 0.7$, and $\hat{\upalpha }(0)= -0.5$, $\hat{\upbeta }(0) = -0.2$, $\hat{\updelta }(0) = -0.1$.

In Fig. 23 the parameter values are $\upalpha = 1$, $\upbeta = 8$, $\updelta = 2$, while the initial conditions are $x(0)=1.1$, $y(0) = 0.8$, $z(0) = -1.5$, $w(0) = 0.2$, and $\hat{a}(0)= -0.5$, $\hat{b}(0) = -0.2$, $\hat{\delta }(0) = -0.1$.

Fig. 23

Time-series of the controlled states $x,\,y,\,z,\,w$

5 Circuit Realization

The classical approach for the verification of the feasibility of theoretical chaotic models is the physical realization through electronic circuits (Borah et al. 2016; Bouali et al. 2012; Kingni et al. 2016; Wu et al. 2015; Zhou et al. 2015). Furthermore, the circuital realization of chaotic systems has been applied in numerous engineering applications, for example in secure communications (Banerjee 2010; Cicek et al. 2010), liquid mixing (Sahin and Guzelic 2013), robotics (Volos et al. 2012), image encryption process (Volos et al. 2013), audio encryption scheme (Liu et al. 2016), target detection (Wang et al. 2015) or random signal generation (Fatemi-Behbahani et al. 2016; Yalcin et al. 2004). For this reason, analog and digital approaches have been applied to realize chaotic oscillators by using different kinds of electronic devices such as common off-the-shelf electronic components (Elwakil and Ozoguz 2003; Piper and Sprott 2010), integrated circuit technology (Trejo-Guerra et al. 2012, 2013), microcontroller (Pano-Azucena et al. 2017) or field-programmable gate array (FPGA) (Koyuncu et al. 2014; Tlelo-Cuautle et al. 2015).

Therefore, in this section, we will confirm the feasibility of the proposed memristive system by discussing its circuital realization by using the general operational amplier–based approach. The third state variable (z) of the memristive system has been rescaled as $Z= z/2$, in order to avoid the limitations problems of the components of our electronic circuit. Therefore, the memristive system is transformed into the following equivalent system:

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} \dot{X}=- X+F(Y,W)\\ &{} \dot{Y}=\beta X-2 \delta XZ+\varepsilon \\ &{} \dot{Z}=-Z+ \frac{1}{2} XY\\ &{} \dot{W}=Y \end{array} \end{aligned}$$

(25)

where $F(Y,W)=(1+0.25 W^{2}-0.002 W^{4})Y$ the output of the memristive device. Figure 24 shows the schematic of the circuit for realizing the system (5). As shown in this figure, the circuit includes sixteen resistors, four capacitors, seven operational amplifiers (TL081) and five analog multipliers (AD633). By applying Kirchhoffs circuit laws into the designed circuit, we get the following circuital equation:

$$\begin{aligned} \begin{array}{l@{}l@{}l} &{} \dot{x}=\frac{1}{R \cdot C}[ -X + F(Y, W) ] y + \frac{R}{10V \cdot R_1} y \cdot z ]\\ &{} \dot{y}=\frac{1}{R \cdot C}[\frac{R}{R_\beta }X- \frac{R}{10V \cdot R_\delta } XZ+V+\varepsilon ] \\ &{} \dot{z}=\frac{1}{R \cdot C}[ -Z + \frac{R}{10V \cdot R_1} X \cdot Y]\\ &{} \dot{w}=\frac{1}{R \cdot C} Y \\ \end{array} \end{aligned}$$

(26)

where

$$\begin{aligned} \begin{array}{l@{}l@{}l}&F(Y, W) =[\frac{R}{10V \cdot R_a} V_f + \frac{R}{(10V)^2 \cdot R_b} W^2 - \frac{R}{(10V)^4 \cdot R_c} W^4 ] y \end{array} \end{aligned}$$

(27)

is the output of the memristive circuit in the dotted frame of the schematic in Fig. 16, which implements the opposite of the memristive function of Eq. (2).

In system (26), X, Y, Z and W correspond to the voltages on the integrators (U1–U4), respectively, while the power supply is $\pm 15V_{DC}$. System (26) is normalized by using $\tau = t/RC$. It can thus be suggested that system (26) is equivalent to system (5), with $a =\frac{R}{10V \cdot R_a}$, $b =\frac{R}{(10V)^2 \cdot R_b}$, $c = \frac{R}{(10V)^4 \cdot R_c}$, $d = R/R_\delta$, $2e =\frac{R}{10\,V \cdot R_e}$, $m = V_m$ and $\frac{R}{10\,V \cdot R_1}= 0.5$. So, the values of circuit components are: $R = 10\,\mathrm{k}\Omega$, $R_a = 1\,\mathrm{k}\Omega$, $R_b = 0.4\,\mathrm{k}\Omega$, $R_c = 0.5\,\mathrm{k}\Omega$, $R_\delta = 1\,\mathrm{k}\Omega$, $Re = 0.5\,\mathrm{k}\Omega$, $R_1 = 2\,\mathrm{k}\Omega$, $C = 10\,\mathrm{nF}$, $V_f = 1\,\mathrm{V}$ and $V_\varepsilon = 0\,\mathrm{V}$ (for the case of $\varepsilon = 0$). The designed circuit has been implemented in Multisim and PSpice results are reported in Fig. 24. It is easy to see the good agreement between the circuit’s simulation results (Figs. 25, 26 and 27) and numerical results (Fig. 2).

Fig. 24

Schematic of the circuit including sixeteen resistors, four capacitors, seven operational amplifiers and five analog multipliers. The power supplies of all operational amplifiers and analog multipliers are $\pm 15V_{DC}$

Fig. 25

a PSpice chaotic attractors of the designed circuit in (a) $X - Y$ plane, b $X - Z$ plane for $\varepsilon =0$

Fig. 26

a PSpice chaotic attractors of the designed circuit in (a) $X - W$ plane, b $Y - Z$ plane for $\varepsilon =0$

Fig. 27

a PSpice chaotic attractors of the designed circuit in (a) $Y - W$ plane, b $Z - W$ plane for $\varepsilon =0$

6 Conclusion

The existence of a memristor-based hyperchaotic system with line of equibria and with no equilibria has been studied in this paper. Although 4-D memristive systems often only generate chaos, the presence of a memristive device leads the proposed system to a hyperchaotic system with hidden attractors. The system has rich dynamical behavior as confirmed by the reported example of attractor and by the presented numerical bifurcation diagrams and Lyapunov exponents. It is worth noting that the possibilities of control of such system with unknown parameters is verified by constructing an adaptive controller. Also, the designed circuit emulates very well the proposed hyperchaotic memristive system. Because there is little knowledge about the special features of such systems, future works will continue focusing on their dynamical behaviors, as well as the possibility of synchronization of such systems. Furthermore, the robustness of the control technique with respect to noise is very crucial especially in practical applications. For this reason, the investigation of noise effect on the control scheme will be taken as a future work.