1 Introduction

The memristor was first proposed by Chua [1], referring to a kind of two-terminal device that exhibits a pinched hysteresis loop in the voltage–current plane. All memristors can be classified into ideal memristor, generic memristor, and extended memristor [2]. Later, Chua [3] proposed that the concept of memristor can be extended to a much more general class of dynamical systems called memristive systems (or generalized memristors), and the memristor is only a special case of the systems.

In 2008, HP Laboratory constructed the first real memristor by using TiO2 [4]. Later, Chew et al. [5] realized a real discrete memristor by ZnO nanowires synthesized on a printed circuit board. Due to the unique nonlinear properties of memristors, there have been lots of literatures about its theoretical exploration and practical applications in many fields, such as neural networks [6, 7], information encryption [8, 9], chaotic memristive systems [10, 11], and nonlinear electronic circuits [12,13,14,15,16]. It is important to note that compared with CMs, DMs have not been received adequate attention. In recent years, Karthikeyan et al. [17] proposed a discrete fractional-order differential memristor system and its dynamic properties were explored. Sun et al. [18, 19] were put forward to a discrete mathematical model of the charge-controlled memristor and a higher-dimensional chaotic map with discrete memristor, and the authors held the opinion that the DM can expand the scope of the memristor. In Ref. [20], a discrete charge-controlled HP memristor model was proposed by using backward differential theory, and its application in Hénon map was investigated. In Ref. [21], a new DM-based map was proposed based on a sampling switch-based memristor–capacitor circuit, which can generate hyperchaos. In Ref. [22], a general two-dimensional memristive map model was studied by coupling the discrete memristor with an existing discrete map. These literatures presented some ideal charge-controlled DM models and verified that they could be directly introduced into the discrete systems. In this paper, a n-dimensional generalized discrete model conforming to the definition of memristor is proposed. As far as we know, there are no reports on the modeling of the n-dimensional generalized DM.

Compared with chaotic systems, hyperchaotic systems have more complex behaviors and a relatively better application prospect, especially discrete hyperchaotic maps, because it only needs two dimensions and less resources’ cost [23,24,25]. However, most of existing discrete maps cannot generate hyperchaotic sequences, such as sine map, logistic map, Hénon map, and so on. Hence, designing a discrete hyperchaotic map is still a novel and valuable research topic.

Meanwhile, a lot of works have been done on the dynamical analysis of memristor-based systems, in which nonparametric bifurcation is a hot topic often occurring in CM-based systems [26,27,28,29]. Due to the special form of the CM model, infinite number of equilibria may exist and be formed m-dimensional manifolds of equilibria, where m is the number of memristor in n-dimensional systems (n > m). Normally hyperbolic manifolds of equilibria are characterized by m zero eigenvalues, whereas other eigenvalues are not equal to zero or purely imagine. This kind of systems with normally hyperbolic manifolds of equilibria have a significant property of the existence of nonparametric bifurcation when the requirements of normal hyperbolicity are not satisfied at some equilibria. So far, this phenomenon has not been reported in DM-based systems.

In this paper, a new n-dimensional generalized model of DM is proposed, whose memristance is controlled by a discrete function. At present, most of the existing CMs are designed based on the analog circuits and various materials. However, the DMs can be naturally realized in digital circuits such as DSP and FPGA. As Chua mentioned in Ref. [3], the input and the output signals of the generalized memristors are not only limited to voltage and current. If it exhibits a pinched hysteresis loop for the periodic input current signals, regardless of the state x which incorporates the memory effect, it is a memristor [3]. Hence, DM could extend the input and output of memristors to other signals. Moreover, many complex problems that occur in the real world are necessarily described by discrete systems. Thus, we can apply those potential DMs but not the CMs to discrete systems.

In order to provide the potential application, an ideal and a nonideal DM mathematical model is designed. Their i–v cures are explored by numerical simulations, and the results show that two DM models accord with the characteristics of memristors. Introducing the mathematical model of the proposed ideal DM into the sine map yields a new second-order discrete map called DM-S map, which can generate hyperchaos under some suitable parameters. Compared with the original sine map, the DM-S map has a line of fixed points, whose eigenvalue λ1 is always equal to 1 and the other eigenvalue λ2 depends on both the parameters and the initial position of the fixed point on the y-axis. Because of this, the DM-S map has a significant property of nonparametric bifurcation. In addition, the DM-S map has a larger chaotic region, a lager parameter space and a greater Lyapunov exponent than that of the original sine map. The hyperchaotic sequence generated by DM-S map is implemented by DSP platform and tested by using SP800-22 NIST software. The results show that the hyperchaotic sequence passes through all the subtests, which means it has great randomness.

The rest of the paper is summarized as follows: In Sect. 2, a new generalized model of DM is deduced. An ideal and a nonideal DM model is proposed based on the generalized model, and their properties are simulated. In Sect. 3, applying the mathematical model of the proposed ideal DM into the sine map yields a new second-order DM-S map. Then, the stability for a line of fixed points is investigated. Section 4 explores the bifurcation without or with parameters in detail. Section 5 contains the DSP hardware implementation of the DM and the DM-S map. The random sequences are generated by the DM-S map and tested by SP800-22 NIST software. Finally, conclusions are drawn in the last section.

2 A generalized DM mathematical model

2.1 Derivation of generalized DM mathematical model

A continuous-time n-dimensional generalized memristor model [3, 30] can be expressed as

$$ \left\{ \begin{array}{l} y(t) = g(x,u)u(t) \hfill \\ \dot{x}(t) = f(x,u) \hfill \\ \end{array} \right. $$
(1)

where g(x) is sectional continuous scalar function. x, y and u are the state, input, and output of the memristors. f(x, u) is a continuous n-dimensional vector function, expressed as its state-space model Ax + Bu in this paper, where A and B are n-dimensional constant vectors. Hence, the generalized CM model can be rewritten as

$$ \left\{ \begin{array}{l} y(t) = g(x,u)u(t) \hfill \\ \dot{x}(t) = Ax + Bu \hfill \\ \end{array} \right. $$
(2)

The sampling discrete method is an effective discrete method, which makes continuous models transform to their discrete models. In this paper, a discretization method for time-invariant continuous systems is used, whose mathematical essence is to derive an equivalent discrete state-space model from its corresponding continuous state-space model and establish the relationship between each coefficient matrix of the two. Suppose the sampling period is T, so the continuous state space model Eq. (2) can transform to the discrete state-space model, which is expressed as

$$ \left\{ \begin{array}{l} y(KT) = g(x,u)u(KT) \hfill \\ x(KT + T) = G(T)x(KT) + H(T)u(KT) \hfill \\ \end{array} \right. $$
(3)

It is worth noting that discretization is mainly for differential equations describing dynamic characteristics. For the static equation, the first equation in Eq. (3), it is unchanged after discretization. Hence, we just derive an equivalent discrete state-space model of the second equation in Eq. (3). Next, the relationship between each coefficient matrix of Eqs. (2) and (3) will be analyzed.

The solution formula of the continuous state equation is given as

$$ x(t) = \Phi (t - t_{0} )x(t_{0} ) + \int_{{t_{0} }}^{t} {\Phi (t - \tau )} Bu(\tau ){\text{d}}\tau $$
(4)

where Φ is the state transition matrix of A. In order to make the discretization be an equivalent transformation process from continuous system to discrete system, the values of state variables, input variables and output variables of the system at each sampling moment remain unchanged after discretization. Considering the state response during a sampling period from the sampling time KT to the time (K + 1)T, and assuming that u(KT) is constant over the sampling period, that is u(τ) = u(KT), Eq. (4) can be derived as Eq. (5) by letting t0 = KT and t = (K + 1)T.

$$ x((K + 1)T) = \Phi (T)x(KT) + \int_{KT}^{(K + 1)T} {\Phi [(K + 1)} T - \tau ]{\text{d}}\tau Bu(KT) $$
(5)

Assuming t* = (K + 1)T – τ, Eq. (5) can be rewritten as

$$ x((K + 1)T) = \Phi (T)x(KT) + \int_{0}^{T} {\Phi (t^{*} )} {\text{d}}t^{*} Bu(KT) $$
(6)

Compared with Eqs. (3) and (6), one gets

$$ \left\{ \begin{array}{l} G(T) = \Phi (T) = {\text{e}}^{AT} \hfill \\ H(T) = \int_{0}^{T} {\Phi (t)} {\text{d}}tB = \int_{0}^{T} {{\text{e}}^{At} } {\text{d}}tB \hfill \\ \end{array} \right. $$
(7)

Letting tn = KT and tn+1 = KT + T, a n-dimensional generalized DM model can be derived as

$$ \left\{ \begin{array}{l} y(t_{n} ) = g(x,u)u(t_{n} ) \hfill \\ x(t_{n + 1} ) = {\text{e}}^{AT} x(t_{n} ) + \int_{0}^{T} {{\text{e}}^{At} } {\text{d}}tBu(t_{n} ) \hfill \\ \end{array} \right. $$
(8)

Hence, the other types of DM mathematical models can be obtained as Table 1

Table 1 Different kinds of DM mathematical models
Full size table

2.2 Two mathematical DM models

In this subsection, two mathematical voltage-controlled DM models are proposed as follows:

$$ {\text{Model}}\,1:\left\{ \begin{array}{l} i(t_{n} ) = [a\varphi (t_{n} ) + b\varphi^{2} (t_{n} )]v(t_{n} ) \hfill \\ \varphi (t_{n + 1} ) = Tv(t_{n} ) + \varphi (t_{n} ) \hfill \\ \end{array} \right. $$
$$ {\text{Model}}\,2:\left\{ \begin{array}{l} i(t_{n} ) = \left( { - G_{a} + G_{b} v_{0}^{2} (t_{n} )} \right)v(t_{n} ) \hfill \\ v_{0} (t_{n + 1} ) = {\text{e}}^{ - bT} v_{0} (t_{n} ) + \frac{a}{b}({\text{e}}^{ - bT} - 1)v(t_{n} ) \hfill \\ \end{array} \right. $$

We can see Model 1 is an ideal DM, where the variables a and b are coefficients controlling the memristance. Model 2 is a non-ideal memristor, whose continuous model was proposed in Ref. [31]. Variable v0 is the internal voltage that controls the memristor, whose memristance depends on the control parameters Ga, and Gb.

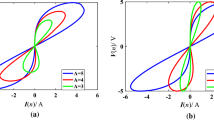
Set the parameters of Model 1 and Model 2 as Table 2, and the excitation signal is given by v(n) = A sin(wtn), where tn is a discretized time with step T. Varying the frequency w, the different v–i curves for two models are plotted in Fig. 1a, b, respectively.

Table 2 Simulation parameters for Model 1 and Model 2
Full size table
Fig. 1
figure 1

The i–v curves with different frequencies of a Model 1 and b Model 2 with setting initial values as 0.1. The v–i curves of the DM model and CM model of c Model 1 and d Model 2

Full size image

All the results indicate that the hysteresis loops confined to the first and third quadrants on the v–i plane are always pinched at the origin, which satisfy the character of a memristor [2, 31]. In addition, the enclosed lobe area of the hysteresis loop increases monotonically with the decrease of the frequency w. Finally, the hysteresis loop will shrink to a single-valued function when the frequency w ≈ 10 kHz for Model 1 and 100 Hz for Model 2 under the above parameters in Table 2. Thus, these three fingerprint characteristics indicate that the DM models are accorded to the definition of the memristor. In addition, when the frequency w = 1 Hz, while the other parameters are set as Table 2, the v–i curves of their DM models and CM models of Model 1 and Model 2 are shown in Fig. 1c, d, where the blue curves represent the results of CM and the red dots represent DM. It can be seen that the curves of DM and CM basically match. Hence, the DM model can retain the properties of the CM.

Non-volatile analog memories refer to a class of memory devices that can store a continuous ranges of resistance values [2]. In the past, Chua proposed the following criterions (not all) for non-volatile memristors in Refs. [2, 32, 33]. First, all ideal memristors are non-volatile analog memories [2]. Second, a memristor is non-volatile, when its power-off plot (POP), just a curve in the f(x, 0) versus x plane, intersects the x-axis at 2 or more points with a negative slope [32, 33]. The next but not the last one, if a memristor whose pinched hysteresis loop depends not only on the input waveform i(t) or v(t), but also on the initial conditions of the relevant state variables, is non-volatile [33].

As we know, the DM models are accorded to the definition of the memristor, and they can retain the properties of the CM. Thus, we can exert the criterions of non-volatile to the DM.

Letting v = 0 for Model 1; it is easy to see that f(x, 0) = 0, which means the POP intersects the x-axis at an infinite number of points. For Model 2, f(x, 0) is a linear function, f(x, 0) = \({\text{e}}^{ - bT} x\), where \({\text{e}}^{ - bT}\) is coefficient. Thus, the POP for Model 2 intersects the x-axis at only one point. In short, Model 1 is non-volatile, and Model 2 is volatile.

Setting the parameters as Table 2, the i–v curves with different initial values for Model 1 and Model 2 are shown in Fig. 2. It can be clearly seen that the i–v curve of Model 1 changes with the varying of the initial value, while the i–v curve of Model 2 does not change. In terms of the third criterion, we also can directly indicate that the Model 1 is non-volatile, and Model 2 is volatile.

Fig. 2
figure 2

The i–v curves with different initial values for a Model 1 with w = 10 and b Model 2 with w = 1

Full size image

3 The application of DM mathematical model in the Sine map

3.1 A DM-S map

Since the special form of the DM, it is more suitable to use in discrete systems and digital circuits than the CM. In this section, we construct a DM-based map by using the proposed Model 1.

The equation of the Sine map is expressed by

$$ x(n + 1) = \mu \sin [\pi x(n)] $$
(11)

where μ is a constant.

In mathematical sense, the second equation in Eq. (9) can be transformed into

$$ \varphi (t_{n + 1} ) = \varphi (1) + T\sum\limits_{j = 1}^{n} {v(t_{j} )} $$
(12)

Combining with Eqs. (9) and (12) yields

$$ i(t_{n} ) = \left[ {a\varphi (1) + aT\sum\limits_{j = 1}^{n - 1} {v(t_{j} )} + b\left[ {\varphi (1) + T\sum\limits_{j = 1}^{n - 1} {v(t_{j} )} } \right]^{2} } \right]v(t_{n} ) $$
(13)

Assuming that x(n) = v(tn), x(j) = v(tj), A(n) = i(tn), and k = T, so the DM model is presented as

$$ A(n) = \left[ {a\varphi (1) + ak\sum\limits_{j = 1}^{n - 1} {x(j)} + b\left[ {\varphi (1) + k\sum\limits_{j = 1}^{n - 1} {x(j)} } \right]^{2} } \right]x(n) $$
(14)

Adding the DM model into the original Sine map for the state x(n) control, a new map called the DM-S map is designed. The model structure of the new map is given in Fig. 3, and its equation can be expressed as

$$ x(n + 1) = \mu \sin \left[ {\pi \left[ {a\varphi (1) + ak\sum\limits_{j = 1}^{n - 1} {x(j)} + b\left[ {\varphi (1) + k\sum\limits_{j = 1}^{n - 1} {x(j)} } \right]^{2} } \right]x(n)} \right] $$
(15)
Fig. 3
figure 3

The structure of the DM-S map

Full size image

The equation shows that the present state of x depends on the initial state of the DM and the sum of all the past states of x. Therefore, the special “memory effect” is reflected in the new map. Moreover, due to adding a DM to the sine map, the new map increases one dimension. Therefore, Eq. (15) can be derived into the 2-D equations expressed as Eq. (16) by assuming

$$ y(n) = \varphi (1) + k\sum\limits_{j = 1}^{n - 1} {x(j)} $$
$$ \left\{ \begin{array}{l} x(n + 1) = \mu \sin [\pi (ay(n) + by^{2} (n))x(n)] \hfill \\ y(n + 1) - y(n) = kx(n) \hfill \\ \end{array} \right. $$
(16)

The parameters are selected as a = 7.2, b = 50, k = 1.2, and the initial values are set as x(1) = 0.2 and y(1) = 0.2. Set different values of parameter u as shown in Table 3 and Lyapunov exponents are obtained in Table 3.

Table 3 Lyapunov exponents and dynamic behaviors for different values of parameter μ
Full size table

In order to make the simulation results more accurate, we set the number of calculations as 100,000. The results show that if the value of the Lyapunov exponent is greater than about 0.01, it can be considered as a positive value.

It is obvious that the proposed DM-S map has three kinds of dynamic behaviors and their phase portraits and iterative sequences are plotted in Fig. 4, where the iterative sequences are limited to the first 150 iterations to make the graphs clear. When μ = 0.24, the map behaves the irregular movements at the beginning and then enters a stable state. When μ = 0.14, the map is chaotic because of a positive exponent, and the points on the trajectory are uniformly distributed in the plane. As μ changes to 2.9, the scope of the map becomes larger, and more points appear in the boundary and negative region. Because the Lyapunov exponents are all greater than zero, the map can generate hyperchaos.

Fig. 4
figure 4

Some simulation results for the map: a phase portrait for μ = 0.24 and b the corresponding iterative sequences, c phase portrait for μ = 0.12 and d the corresponding iterative sequences, e phase portrait for μ = 2.9 and f the corresponding iterative sequences

Full size image

Furthermore, without the sine function, the accumulator will cause the value of y(n) to increase infinitely, resulting in the divergence of the map. It is because the sine function can always keep the sequence of x(n) balance between positive and negative values, that the y(n) sequence will not diverge.

3.2 Stability for DM-S map

The stability of a discrete map depends on its fixed point that is regarded as an element mapping to itself in its domain [34]. For the original sine map xn+1 = μ sin(πxn), the number of the fixed points and the stability relies on the parameter μ. For example, if setting μ = 4, the original sine map has two fixed unstable points E0 = 0 and Em = xm, where xm is solved by xm = 4 sin(πxm); if setting μ = 0.5, the original sine map has two fixed stable points E0 = 0 and Em = 0.5; if setting μ = 0.1, the original sine map has only one fixed stable point E0 = 0.

The fixed points of the DM-S map marked as (x*, y*) are obtained by the following equations

$$ \left\{ \begin{array}{l} x^{ * } = \mu \sin [\pi (ay^{ * } + by^{ * 2} )x^{ * } ] \hfill \\ y^{ * } = y^{ * } + kx^{ * } \hfill \\ \end{array} \right. $$
(17)

Obviously, the DM-S map has infinitely many line fixed points, denoted as (x*, y*) = (0, M), where M is an arbitrary constant.

The Jacobin matrix J at the fixed points can be calculated as

$$ J = \left[ {\begin{array}{*{20}c} {\mu \pi (aM + bM^{2} )} & {0} \\ k & {1} \\ \end{array} } \right] $$
(18)

The characteristic equation of the Jacobin matrix is derived as

$$ (\lambda - 1)[\lambda - \mu \pi (aM + bM^{2} )] = 0 $$
(19)

One gets

$$ \lambda_{1} = { 1},\lambda_{{2}} = \mu \pi (M + bM^{2} ) $$
(20)

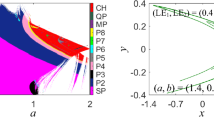
In terms of the stability criterion of discrete systems [34], if the absolute values of both eigenvalues are less than 1, the fixed point is stable; otherwise, it is unstable. Note that the term unstable (or stable) point means the trajectories are attracted (or repelled) in the neighborhood of the fixed point. Obviously, the Jacobin matrix (18) has one eigenvalue that is always equal to 1. The other eigenvalue depends on both the parameters and the initial position of the fixed point on the y-axis. When |λ2| > 1, the fixed points are unstable. When |λ2| < 1, the fixed points are critically stable. Hence, we can consider the set |λ2| = 1 as the condition of the critical bifurcation. For example, if the parameter u and initial state M are set as μ = 1 and M = 1, respectively, the stability region of DM-S map with the varying of parameters a and b is obtained as Fig. 5. When the parameters a and b locate in the closed blue area, the DM-S map is critically stable. When a and b locate in red lines, the system shows the critical bifurcation at a fixed point.

Fig. 5
figure 5

The stability region of DM-S map with the varying of parameters a and b for parameter u = 1 and initial state M = 1

Full size image

4 Bifurcations without or with parameters

4.1 Nonparametric bifurcations

Based on the above analyses of stability, the eigenvalue λ1 of each fixed point is always on the unit circle, whereas the second eigenvalue λ2 is in or out of the unit circle in most instances. However, when the second eigenvalue λ2 is on the unit circle, the DM-S map has a significant property of nonparametric bifurcations.

Suppose parameter μ = 1/π yields

$$ \lambda_{{2}} = aM + bM^{2} $$
(21)

For different ranges of parameter b, the corresponding unstable regions are obtained in Table 4. In case b <  − a2/4, starting from the vicinity of the stable point (0, M1), where \(\frac{{ - a + \sqrt {a^{2} - 4b} }}{2b} < M_{1} < \frac{{ - a - \sqrt {a^{2} - 4b} }}{2b}\), the phase point moves away from the initial state and then settles down into a stable point or periodically oscillates with different amplitudes.

Table 4 Unstable regions related to different ranges of b
Full size table

Instead, if the phase point starts from the vicinity of unstable points, it may behave different motions. Thus, one can observe that for fixed parameters, any changes of initial values give rise to the bifurcational changes in phase trajectories, which is called nonparametric bifurcations in this paper.

Let the parameters as a = 2, k = 0.1, μ = 1/π, and initial values x(1) = 0.1. For different values of parameter b, bifurcation diagrams of various initial values y(1) are plotted in Fig. 6a–c, respectively. According to Table 4, when b =  − 2 and 2, the stable regions are − 0.366 < M < 1.366 and − 1.366 < M < 0.366. The corresponding bifurcation diagrams are shown in Fig. 6a, b, respectively. Note that when − a2/4 < b < a2/4, there are two continuous stable ranges. In case b =  − 0.5, the stable ranges are − 0.45 < M < 0.58 and 3.41 < M < 4.45, and the corresponding bifurcation diagram is shown in Fig. 6c. One can observe that these structures of a bifurcation consist of three parts. One is a set of rest points on the x-axis, another is a set of periodic points moving up and down around the x-axis, and the last is a set of disorganized points on limited two-dimensional plane. All figures indicate that if the phase point starts from the vicinity of stable points, it behaves the first motion. As the initial value changes to the critical value that makes the stability change, the behavior of trajectory becomes the second type. Otherwise, when the initial value is very far from stable fixed points, it is chaotic.

Fig. 6
figure 6

Bifurcation diagrams of various initial values y(1) for different parameter b: a b =  − 2, b b = 2, and c b =  − 0.5. Note that, the first 100 iterations are ignored to intuitively describe bifurcation diagrams

Full size image

In order to investigate the mechanism of nonparametric bifurcations, we focus on attractor evolutions with the varying initial values y(1). Let the parameters as a = 2, k = 0.1, μ = 1/π, and b =  − 0.5. Starting from the initial point (0.1, − 2), near a set of unstable fixed points (shown by the red dashed line in Fig. 7a), the phase point moves away from the initial point and behaves irregular movements in a limited space because of the repellency from unstable points.

Fig. 7
figure 7

Phase portraits of various initial values y(1) for b =  − 0.5: a y(1) =  − 2, b y(1) =  − 1, c y(1) = 0.1, and d y(1) = 1.5

Full size image

As the initial value gets closer to the stable fixed points, the map will lose the chaotic state. When the phase point starts from point S (0.1, − 1), whose trajectory is plotted as Fig. 7b, where a set of stable (unstable) fixed points are described by black (red) dashed line. The sequence of x(n) always shifts symmetrically about the x-axis, resulting in the sequence of y(n) oscillates with a small amplitude. Hence, the phase point moves upward along a spiral-like trajectory to the vicinity of stable fixed points and then culminates in motion shifting between two points marked T1 and T2 in Fig. 7b.

As shown in Fig. 6c, when the phase point starts from the vicinity of unstable points (− 0.45 < y(1) < 0.58 and 3.41 < y(1) < 4.45), it will move toward and quickly settle down into a stable point, which can be observed in Fig. 7c with y(1) = 0.1. Another case is that when the initial value y(1) is located in the unstable range close to two stable ranges, the phase point is also attracted to a fixed point on the x-axis. Suppose the initial values y(1) = 1.5 and x(1) = 0.1, whose phase portrait is shown in Fig. 7d. The phase point moves rapidly with the increase in the number of iterations, until it arrives at the vicinity of unstable points. Since the attraction of the stable points, the phase point enters into a stable state of a single point.

4.2 Bifurcations with parameters

This subsection shows the bifurcation and Lyapunov exponents of the sine map and the DM-S map with the varying parameters. The parameters of the DM-S map are set as a = 7.2, b = 50, k = 1.2, and the initial values are selected as x(1) = 0.2 and y(1) = 0.2. Changing the parameter μ in the range of [0.01, 3] with the step of 0.001, the bifurcation diagram and the corresponding Lyapunov exponent spectrum of the sine map are illustrated in Fig. 8a, b, and those of the DM-S map are shown in Fig. 8c, d, respectively.

Fig. 8
figure 8

Bifurcation diagram and its corresponding Lyapunov exponent spectrum with varying u a bifurcation diagram of sine map, b Lyapunov exponent spectrum of sine map, c bifurcation diagram of DM-S map and d Lyapunov exponent spectrum of memristor-based sine map

Full size image

We can see from Fig. 8 that the bifurcation diagrams and their corresponding Lyapunov exponent spectrums are consistent. The chaotic ranges of the sine map are discontinuous, which means that a small change of μ may lead the sine map to be periodic. However, the chaotic region of the DM-S map is continuous when μ is approximately greater than 0.6. Furthermore, compared with Fig. 8b, d, the maximum Lyapunov exponent of the DM-S map is much greater than that of the original Sine map.

Since the DM-S map has more control parameters than that of the sine map, it has more complex dynamical behaviors and larger parameter space. Setting the parameters as μ = 2 and k = 1.2, two Lyapunov exponents with the varying parameters a and b in the range of [1, 50] are shown in Fig. 9. One can see that the first Lyapunov exponent is almost always positive over the parameter ranges, and the second one is also positive in a large range.

Fig. 9
figure 9

Two Lyapunov exponents of the DM-S map with varying parameters a and b: a LE1 and b LE2

Full size image

5 Hardware implementation and NIST test

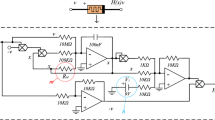
In this section, the hardware implementation of the DMs and the DM-S map is obtained by DSP board, whose experiment device mainly consists of core processing chip (TMS320C5509) with an evaluation board (ICETEK-VC5509-AE) and a digital oscilloscope (DSO-X3034A). The data are generated through the microcontroller, then converted and shown by the converter and the oscilloscope, respectively.

Set the parameters of the DMs as Table 2, and the hysteresis loops of the Model 1 and Model 2 are obtained as Fig. 10a, b, respectively. These results are consistent with the simulation results shown in Fig. 1, which indicates that the DM can naturally be realized by digital circuit.

Fig. 10
figure 10

Hardware implementation obtained by DSP: a the hysteresis loop for Model 1, b the hysteresis loop for Model 2, c sequences of yn and xn, and d experimental prototype

Full size image

Set the parameters of the map as a = 7.2, b = 50, k = 1.2, and μ = 2.9. The obtained sequences of xn and yn, and the experimental prototype are shown as Fig. 10c, d, respectively. These results are consistent with the simulation results shown in Fig. 4f.

In order to verify the randomness of the sequences obtained by the proposed DM-S map, the National Institute of Standards and Technology (NIST) SP800-22 test is applied, which consists of 15 subtests. Each subtest can produce two results, P value and proportion of the passed binary sequences.

Since the DA converter only owns 8 bits, we select the last 8-bit [21: 28] of each sequence to generate the test sequences and export them into binary files. In our experiment, we generate 50 sequences, and the length of each sequence is 1,048,576. The test results are listed as Table 5. According to the criteria, the minimum proportion and P value are 0.9628 and 0.0001, respectively. One can see that two sequences pass all the subtests, which means the hyperchaotic sequences generated by DM-S map have high randomness.

Table 5 NIST performance test report
Full size table

6 Conclusions

In this paper, a new n-dimensional generalized model of discrete memristor is proposed by using the precise discrete method. Two different mathematical models of DM are obtained and their i–v cures are explored, whose results show that the DM models accord with the characteristics of memristors. Applying the mathematical model into the sine map, it yields a new discrete map called DM-S map. From the simulation results, we can find that DMs can be used to increase the complexity of the nonlinear chaotic map and construct the low-dimensional hyperchaotic map. Moreover, the hardware implementation of the DMs and the DM-S map is obtained by DSP.

Indeed, the DM proposed in this paper is different from the existing memristors that designed by various materials and analog circuits. The DM can be naturally realized in digital circuits (such as DSP and FPGA). As we know, systems can be divided into continuous systems and discrete systems. At present, DM can be used into discrete maps to increase the complexity and even generate hyperchaotic sequences because of the ease of implementation. Hence, the DM may have long-term application prospects. Moreover, DMs, whose values are changed with the input, can be applied to simulate cognitive function, neuromorphic computations, modulators, and other applications such as information encryption, programmable digital circuit and logical operations.

Compared with the real memristor, the research of discrete memristor is still in its infancy, and many theories have not been applied yet. Just like other researchers working on DMs, we hold the opinion that the input and the output of the memristors are not only limited to voltage and current but can be extended to other signals. We expect DM will expand the scope of the memristor, and more interested scholars will join and continue this work.