1 Introduction

Chaos plays an important role in image encryption [1,2,3,4,5], secure communication [6,7,8,9], computer engineering [10], and even other fields [11,12,13,14]. The discrete chaotic map shows its potential power as a continuous chaotic system. Amplitude control and polarity adjustment of the chaotic sequence obtain much flexibility for chaos-based applications and therefore introduce much more value in information engineering [15,16,17,18,19]. Although the amplitude and offset control of continuous chaotic systems have been systematically explored and reported [20, 21], the geometric control of discrete chaotic maps is still in the beginning stages. The nonlinearity of the trigonometric function leaves a chance for chaos producing [22], but it also increases the difficulty of amplitude control and poses a great risk for multistability [23,24,25,26,27]. It is of great theoretical significance and engineering values to design chaotic maps based on trigonometric function nonlinearity and study their controllability. A couple of 2-D chaotic maps with trigonometric functions have been studied [28,29,30,31], with abundant dynamics for multistability. However, we cannot find any single knob for amplitude control. Amplitude control along with offset boosting seems to be well addressed in continuous chaotic systems [32], but all chaotic systems ignore the nonlinearity of the trigonometric function. Continuous chaotic systems have been investigated, mainly focusing on polarity balance and attractor self-reproduction [33, 34], generalized synchronization [35, 36], or attractor growing [37, 38] rather than amplitude control. Amplitude control in chaotic maps seems much more difficult to design since the coefficient for variable rescaling has a broader distribution on the right side of the map; therefore, the control of chaotic maps has not received enough attention in the field of nonlinear dynamics. Additionally, homogenous multistability plays an important role in amplitude control, where an initial condition can be selected for easy variable rescaling.

Aiming to design a chaotic map with amplitude control and rich dynamics, in this paper, a three-dimensional (3-D) hyperchaotic map is created by resorting to sinusoidal feedback. As a result, the map is gifted with two independent knobs for total and partial amplitude control. In Sect. 2, the hyperchaotic model is constructed, and the dynamic development is discussed, including fixed points and bifurcation analysis. In Sect. 3, the principle of amplitude control is explained. In Sect. 4, the special homogenous multistability is demonstrated, where two-leaf and three-leaf attractors are selected by the initial condition under a set of unified Lyapunov exponents. In Sect. 5, a digital platform based on STM32 is set up for experimental verification. In Sect. 6, the hyperchaotic sequence is applied to image encryption, where the performance of encryption affected by amplitude control and homogenous multistability is exhaustively explored. The conclusions are presented in the last section.

2 A 3-D hyperchaotic map and its basic dynamics

2.1 Map model

Based on the continuous jerk system, a new 3-D discrete chaotic map is derived by introducing a sinusoidal function,

$$ \left\{ \begin{gathered} x_{{n + 1}} = x_{n} + ax_{n} \sin (by_{n} ) \hfill \\ y_{{n + 1}} = z_{n} \hfill \\ z_{{n + 1}} = cx_{n} - y_{n} - z_{n} \hfill \\ \end{gathered} \right. $$
(1)

where xn, yn, zn (n = 0, 1, 2, …) are discrete sequences, and map parameters a, b, c are not equal to 0. The fixed points S = (x*, y*, z*) of map (1) is solved by Eq. (2),

$$ \left\{ \begin{gathered} x^{{\text{*}}} = x^{{\text{*}}} + ax^{{\text{*}}} \sin (by^{{\text{*}}} ) \hfill \\ y^{{\text{*}}} = z^{{\text{*}}} \hfill \\ z^{{\text{*}}} = cx^{{\text{*}}} - y^{{\text{*}}} - z^{{\text{*}}} \hfill \\ \end{gathered} \right. $$
(2)

Therefore, the fixed points are,

$$ S = (x^{*} ,y^{*} ,z^{*} ) = \left(\frac{{3m\pi }}{{bc}},\frac{{m\pi }}{b},\frac{{m\pi }}{b}\right) $$
(3)

where m is an integer.

When a = 0.9, b = 1, and c = − 2, the Jacobian matrix of the discrete map at the fixed point (x *, y *, z *) = (− 3mπ/2, mπ, mπ) (m = 0,1,2, …) can be described as

$$ J = \left[ {\begin{array}{*{20}c} 1 & { - 1.35m\pi \cos (m\pi )} & 0 \\ 0 & 0 & 1 \\ { - 2} & { - 1} & { - 1} \\ \end{array} } \right] $$
(4)

The Jacobian characteristic equation satisfies λ3 = 1+2.7mπcos(mπ) (m = 0, 1, 2, …). For m = 0, 1, 2…, |1 + 2.7mπcos(mπ)| ≥ 1, so |λ1,2,3| < 1, it cannot be satisfied at the same time. The map has unstable fixed points.

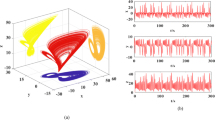
When a = 0.9, b = , c = − 2, and IC = (− 0.1, − 0.1, 0.1), map (1) exhibits hyperchaos with three positive Lyapunov exponents, LE1 = 0.095, LE2 = 0.057, and LE3 = 0.011. The corresponding hyperchaotic sequences and attractors are shown in Fig. 1.

Fig. 1
figure 1

Hyperchaotic sequences and attractor of map (1) with a = 0.9, b = 1, c = − 2, IC = (− 0.1, − 0.1, 0.1): a x(n), b y(n), c z(n), and d phase portrait in the x–y plane

Full size image

2.2 Bifurcation analysis

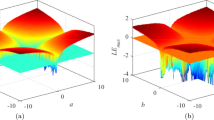
For map (1) with b = 1 and c = − 2, IC = (− 0.1, − 0.1, 0.1), and a varies in [0.85, 0.95], the dynamical behavior can be indicated by the Lyapunov exponent spectrum and corresponding bifurcation as displayed in Fig. 2. When a ∈ [0.85, 0.862] and a = 0.95, all Lyapunov exponents are negative, and the map is periodic. The typical x–y plane phase portraits are shown in Fig. 3a, d. When a ∈ [0.863, 0.868], map (1) has one positive Lyapunov exponent showing its chaotic state. The typical x–y plane phase portraits are shown in Fig. 3b. When a ∈ [0.9, 0.94] and a ∈ [1, 1.02], three Lyapunov exponents are all positive indicating that map (1) is hyperchaotic, corresponding phase portraits are demonstrated in Fig. 3c (Table 1).

Fig. 2
figure 2

Dynamical analysis of map (1) when b = 1, c = − 2, and IC = (− 0.1, − 0.1, 0.1): a Lyapunov exponent spectrum and b bifurcation evolvement

Full size image
Fig. 3
figure 3

Typical phase portraits of map (1) with b = 1, c = − 2, IC = (− 0.1, − 0.1, 0.1) under given parameters: a a = 0.86, b a = 0.866, c a = 0.9, and d a = 0.95

Full size image
Table 1 LEs and attractor type for different values of a under fixed IC = (− 0.1, − 0.1, 0.1), \(b = - 1\), \(c = - 2\)
Full size table

3 Amplitude control analysis

3.1 Total amplitude control

Theorem 1

In map (1), b is a total amplitude controller.

Proof 1

Let un+1 = xn+1/b, vn+1 = yn+1/b and wn+1 = zn+1/b, the resulting map is.

$$ \left\{ \begin{gathered} u_{{n + 1}} = u_{n} + au_{n} \sin (v_{n} ) \hfill \\ v_{{n + 1}} = w_{n} \hfill \\ w_{{n + 1}} = cu_{n} - v_{n} - w_{n} \hfill \\ \end{gathered} \right. $$
(5)

which is identical to Eq. (1) with b = 1. Therefore, the parameter b adjusts the amplitude of all sequences of x, y, and z according to 1/b, which means that b is a total amplitude controller.

Here the parameter b controls the amplitude of all variables, and therefore b is a non-bifurcation parameter, as shown in Fig. 4, the attractor projection in all plane is rescaled by b in inverse proportion. In map (1), a = 0.9, c = − 2, and IC = (− 0.1, − 0.1, 0.1).

Fig. 4
figure 4

Rescaled phase portraits of map (1) with a = 0.9, c = − 2, and IC = (− 0.1, − 0.1, 0.1), where parameter b takes different values: a x–y plane and b y–z plane

Full size image

Further verification can be seen in Fig. 5, where the averages of the absolute values of x, y, and z decrease with the parameter b but almost without revising the Lyapunov exponents. Unrevised Lyapunov exponents prove that the frequency of the sequence in map (1) remains independent with the parameter b.

Fig. 5
figure 5

Amplitude control in map (1) with a = 0.9, c = − 2, and IC = (− 0.1, − 0.1, 0.1): a almost invariable Lyapunov exponents, b bifurcation diagram, and c average absolute value of the sequences

Full size image

3.2 Partial amplitude control

Theorem 2

The c in map (1) is a partial amplitude controller.

Proof 2

Let un+1 = xn+1/c, vn+1 = yn+1, and wn+1 = zn+1 the resulting map is.

$$ \left\{ \begin{gathered} u_{{n + 1}} = u_{n} + au_{n} \sin (bv_{n} ) \hfill \\ v_{{n + 1}} = w_{n} \hfill \\ w_{{n + 1}} = u_{n} - v_{n} - w_{n} \hfill \\ \end{gathered} \right. $$
(6)

Therefore, the parameter c controls the amplitude of the sequence of x according to 1/c without changing the other two series of y and z. Therefore, parameter c is a non-bifurcation partial amplitude controller for the variable x.

As shown in Fig. 6b, the amplitude of the x signal is controlled under different c. When c = − 2, the amplitude of x is larger, and when c = − 20, the amplitude is greatly reduced. Further verification can be seen in Fig. 6c, where the average of the |x(n)| increases with parameter c but almost without revising the Lyapunov exponents. This also further proves that the frequency of the sequence in map (1) is not affected by parameter c.

Fig. 6
figure 6

Amplitude control in map (1) with a = 0.9, b = 1, and IC = (− 0.1, − 0.1, 0.1): a Lyapunov exponents spectrum, b bifurcation diagram of x(n), c average value of |x(n)|, and d rescaled phase portraits under different c

Full size image

4 Homogeneous multistability

Different initial conditions in chaotic systems may lead to different attractors with the same shape (sometimes with different amplitudes and/or frequencies or offsets). This special multistability is defined as homogeneous multistability.

To show the complex dynamics of map (1) with infinitely many attractors, a bifurcation diagram under the initial value is plotted in Fig. 7 where a = 0.9, b = 1, c = − 1, and IC = (− 1, y0, 1). It proves that the map displays homogeneous multistability indicated by almost unchanged Lyapunov exponents and gap-enlarged bifurcation.

Fig. 7
figure 7

Dynamical transition controlled by the initial condition of map (1) with a = 0.9, b = 1, c = − 1, and IC = (− 1, y0, 1): a Lyapunov exponents and b bifurcation diagram

Full size image

Set to a = 0.9, b = 1, c = − 1, and IC = (− 1, y0, 1) in map (1), and rescaled coexisting two-leaf and three-leaf attractors are plotted in Fig. 8. Map (1) has infinite coexisting attractors with unified Lyapunov exponents.

Fig. 8
figure 8

Rescaled coexisting two-leaf and three-leaf attractors of map (1) with a = 0.9, b = 1, c = − 1, IC = (− 1, y0, 1) under different initial conditions of y0

Full size image

The dynamical behavior can be further observed by setting a = 0.9, b = 1, c = − 1, and IC = (− 1, − 1, z0), corresponding Lyapunov exponent spectrum and bifurcation diagram of the signal y are plotted in Fig. 9. Rescaled coexisting two-leaf and three-leaf hyperchaotic attractors share the same set of unified Lyapunov exponents. Moreover, the discrete periodic points are scattered between any two hyperchaotic states. To the best of our knowledge, this is a brand new phenomenon in nonlinear mapping. Also with the increase of z0 in the 3-D map, two-leaf and three-leaf attractors with different leaf distances are born. More strikingly, the initial data modifies the distance between any two leaves in a positive correlation. Figure 10 shows the typical coexisting phase portraits of map (1) accordingly. Note that the homogeneous multistability found here shows the characteristic of coexisting attractors with enlarged distance, which is close to the regime of megamultistability [39, 40].

Fig. 9
figure 9

Dynamical development of map (1) with a = 0.9, b = 1, c = − 1, and IC = (− 1, − 1, z0): a Lyapunov exponent spectrum and b rescaled bifurcation

Full size image
Fig. 10
figure 10

Rescaled coexisting two-leaf and three-leaf attractors of map (1) with a = 0.9, b = 1, c = − 1, IC = (− 1, − 1, z0) under different initial conditions of z

Full size image

5 Hardware implementation based on STM32

An experimental test can be given for further demonstration. In this work, the MCU development suite was used for experimental exploration. Here the electronic platform and components mainly include STM32F103 MCU and TLV5618, 12-bit DAC modules. To meet the requirement of the precision, here we select ∆T = 1 and the TLV5618 is applied for giving two separate sequences. The phase trajectories of map (1) are captured in the oscilloscope which is displayed in Fig. 11. The experimental process is shown in Fig. 12.

Fig. 11
figure 11

Phase portraits of map (1) displayed in the oscilloscope when a = 0.9, b = 1, c = − 1, and IC = (− 1, y0, 1): a y0 = 1 + 3π and b y0 = 1

Full size image
Fig. 12
figure 12

Hardware equipment of the experimental device

Full size image

6 Application of the hyperchaotic map in image encryption

Hyperchaotic systems provide a larger key space and higher complexity and therefore become more applicable for encryption and secure communication. In the following, the image encryption is studied based on the above-proposed hyperchaotic map. Furthermore, the amplitude control and coexisting two-leaf or three-leaf hyperchaotic sequences are applied as shown later that in fact the information entropy of the three-channel encrypted image does not change dramatically.

6.1 Algorithm design

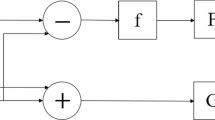
Here, DNA coding is applied in hyperchaotic mapping (1) for image encryption. Compared with other algorithms, the encryption key space becomes larger with stronger sensitivity, showing robustness to attacks. The main encryption flowchart is shown in Fig. 13: First, the image is encrypted by a logistic map, then encrypted by the hyperchaotic sequence combining with the DNA coding.

Fig. 13
figure 13

Encryption schematic diagram

Full size image

The specific encryption process can be described as follows:

  • Step 1: Add the horizontal and vertical pixels with M0 = 0 and N0 = 0, so that they are divisible by the block size S.

  • Step 2: Given the initial condition of x0 and the variable μ of the logistic map, discrete signals {Pi}(i = 2001, 2002, …, M × N + 2000) with the length of M × N + 2000 is obtained.

  • Step 3: All the numbers in the discrete signals are transformed to [0, 255] and then randomly formed into a 2-D matrix R of M × N.

  • Step 4: Set S = 4, and correspondingly the size of each block of the matrix R and the image are S × S.

  • Step 5: Given the initial conditions X0, Y0, Z0 and the values of a and b in map (1), three discrete time series {xi}, {yi}, and {zi} can be obtained (i = 4002, 4003, …, 4001 + M/S + N/S).

  • Step 6: The DNA coding pattern of each image matrix and a stochastic matrix is determined by the sequences {xi} and {yi}, respectively. Taking image matrix as an example, this process of encoding mode is defined as follows,

    $$ x_{i} = \bmod (round(x_{i} \times 10^{4} ),8) + 1 $$
    (7)

    Transform the grayscale values of all image elements into the binary numbers and get DNA coding pattern according to the value of xi.

  • Step 7: DNA coding between random matrix and image matrix according to {zi}. The conversion of {zi} is as follows,

    $$ z_{i} = \bmod (round(z_{i} \times 10^{4} ),4) $$
    (8)

    when zi = 0, the random matrix block and the corresponding elements in the image matrix block execute DNA addition, and when zi = 1, subtraction, zi = 2, exclusive or (XOR), and zi = 3, the equivalence gate (XNOR) operation.

  • Step 8: The encryption performance can be optimized by adding a diffusion algorithm. {zi} also determines the relationship between two adjacent image blocks after encryption. In the case of zi = 0, the encryption results ci can be expressed:

    $$ c_{i} = c_{{i - 1}} + I_{i} + R_{i} $$
    (9)

    The process of decryption and encryption are inverse to each other. The operation mode of random matrix and DNA encoding can be obtained by the keys shown below.

6.2 Chaotic encryption with DNA coding

In the following, we test with a standard RGB image, as displayed in Fig. 14. The initial value x0 is 0.5475 and the parameter μ of Logistic map is 3.999. Set the parameters of hyperchaotic map (1) as a = 0.9, b = 1, c = − 1 along with the initial condition: X0 = − 1, Y0 = − 1, Z0 = 1, and therefore, the coding rule of DNA is determined randomly by the corresponding hyperchaotic sequence. As shown in Table 2, the selected keys of M0 and N0 during the encryption process are given; k1 and k2 are the average gray levels of the B channel and G channel in the unencrypted image, respectively. The encrypted image is shown in Fig. 14b, where the information disappears and shows nothing. Figure 14c shows the decrypted image which is the same as the unencrypted image.

Fig. 14
figure 14

Encryption experiment: a unencrypted image, b encrypted image, and c decrypted image

Full size image
Table 2 Algorithm keys
Full size table

6.3 Safety performance analysis

Security is the essential requirement of the encryption system. Generally, the encryption system requires a large key space, a reversible encryption process, and strong anti-attack property. Detailed analysis of the hyperchaotic encryption algorithm is given from the following five aspects.

6.3.1 Key space analysis

An excellent encryption method typically obtains its high performance by its large key space in order to against strong attack. In the above encryption algorithm, the initial conditions of the 3-D hyperchaotic map are applied as the keys, where the accuracy reaches 10–16, and therefore the key space is 10160. Furthermore, the logistic chaotic map is used for the key generation. Its initial value and parameter are also be introduced as a part of the key. By this means, the key space is enlarged for resisting attacks more effectively.

6.3.2 Histogram analysis

The R, G, B components are extracted from the original color image and its encrypted image, and their histograms are shown in Fig. 15. It can be easily observed from Fig. 15 that the histograms of the R, G, B are completely changed when they are encrypted.

Fig. 15
figure 15

Histogram of the original and encrypted image: a original image and b encrypted image

Full size image

6.3.3 Information entropy analysis

The uncertainty of image information can be analyzed by information entropy. The size of information entropy is proportional to the strength of randomness. To ensure the random distribution of pixel values, we use the following method,

$$ H(x) = - \sum\limits_{{i = 1}}^{N} {p(x_{i} )} \log _{2} p(x_{i} ) $$
(10)

where N is the number of gray levels, xi is a gray level of the image, and P(xi) is the frequency of the grayscale. Generally speaking, the pixel value of a completely random gray image is scattered between [0, 255], p(xi) = 1/256, i ∈ [0, 255], and the entropy is computed to be of 8 bits. Therefore, for the information entropy of the encrypted image, the value closer to 8 wins the better encoding performance. The information entropy of the three channels of the image before and after encryption is displayed in Table 3. The information entropy calculated by our method is higher than that in reference [8] indicating better image encryption performance.

Table 3 Information entropy of three channels of the unencrypted and encoded images
Full size table

Figure 16 shows the information entropy of the encrypted image of the amplitude-controllable map under different scales. Figure 17 shows the information entropy of three channels of encrypted images under multistable hyperchaotic sequences.

Fig. 16
figure 16

Information entropy of encrypted image in the R, G, and B channels by the sequences from map (1) with a = 0.9, b = 1, and IC = (− 1, − 1, 1)

Full size image
Fig. 17
figure 17

Information entropy of the three-channel encrypted image by the multistable sequences from map (1) with a = 0.9, b = 1, c = − 1 and IC = (− 1, y0, 1)

Full size image

6.3.4 Correlation analysis of images before and after encryption

The degree of correlation between adjacent pixels is directly proportional to its correlation coefficient, and security is inversely proportional. To calculate the correlation between the pixels next to each other of the image before and after encryption, N pairs of adjacent pixels are stochastically picked to analyze in vertical, horizontal, and diagonal directions.

$$ E(x) = \frac{1}{N}\sum\limits_{{i = 1}}^{N} {x_{i} } $$
(11)
$$ D(x) = \frac{1}{N}\sum\limits_{{i = 1}}^{N} {(x_{i} - E(x))} ^{2} $$
(12)
$$ \text{cov} (x,y) = \frac{1}{N}\sum\limits_{{i = 1}}^{N} {(x_{i} - E(x))} ^{2} $$
(13)
$$ r_{{xy}} = \frac{{\text{cov} (x,y)}}{{\sqrt {D(x)D(y)} }} $$
(14)

where cov(x, y) is the correlation function and D(x) means square error. Table 4 shows that all the pixels of the encrypted image are distributed with high dispersion.

Table 4 Correlation of the original image and encrypted one
Full size table

6.3.5 Analysis of resistance to noise

In the application of communication engineering, encrypted image will be inevitably disturbed in the channel. The most common disturb is the salt-and-pepper noise. Figure 18 shows the decrypted image in the R channel with different intensities of salt-and-pepper noise. Although there is some distortion in the decrypted image, it does not affect the access to valid information.

Fig. 18
figure 18

Decrypted images with salt-and-pepper noise of various density n: a n = 0, b n = 0.05, c n = 0.1, and d n = 0.2

Full size image

7 Conclusion

In this paper, a class of three-dimensional maps with homogenous multistability and amplitude control is proposed. A set of united positive Lyapunov exponents is well maintained in attractors with two-leaf and three-leaf even when they stand at different distances. The complex dynamical properties of the 3-D map are studied by Lyapunov exponents and bifurcation diagrams. The proposed hyperchaotic map can be freely controlled in one dimension or all three dimensions by a single coefficient. These two isolated amplitude controllers provide a quick passage for hyperchaotic sequence rescaling, which is generally a great challenge for typical chaotic systems.

Furthermore, the newly found hyperchaotic map with a sinusoidal function has an infinite number of coexisting attractors with united Lyapunov exponents, in which the special phenomenon called homogeneous multistability is found. Experimental results verify the findings from the numerical simulations. A typical application of image encryption is analyzed in detail. Applying the hyperchaotic sequence generated by the map, a color image can be easily encrypted and decrypted in the key space. The lack of correlation between the histograms and the pixels next to each other proves that the hyperchaotic map shows high performance for image encryption.