1 Introduction

The integrable NLS equation along with its higher-order ones has numerous applications, such as nonlinear optics, Bose–Einstein condensates, biophysics and water waves [1,2,3,4,5]. It is solvable based on the inverse scattering transform, DT and Hirota bilinear method [6,7,8,9,10,11]. The nonlocal NLS equation has been proposed by Ablowitz and Musslimimain [12]

$$\begin{aligned} iq_{t}(x,t)=q_{xx}(x,t)+2\sigma q^{2}(x,t)q^{*}(-x,t), \end{aligned}$$
(1)

which is non-Hermitian and \(PT \)-symmetric, q(x, t) is a complex-valued function of real variables x, t, and can become the local NLS equation under the variable transformations \(x\rightarrow ix,t\rightarrow -t\). Here \(\sigma =\pm 1\) denotes the focusing NLS equation or defocusing NLS equation, respectively. The soliton solutions and RW solutions have been obtained by DT in determinant form for the two cases [13, 14]. Gauge equivalent structure of Eq. (1) has been studied in [15, 16]. For the past few years, a series of nonlocal integrable nonlinear equations have been studied, which includes the \(PT \)-symmetric nonlocal NLS equation [17,18,19], reverse space–time complex modified Korteweg–de Vries (mKdV) equation [20,21,22,23], reverse space–time nonlocal Sasa–Satsuma equation [24, 25] and \(PT \)-symmetric Davey–Stewartson equation [26,27,28,29]. Integrable discrete version of the nonlocal NLS equation is also discussed [30]. In recent months, Ablowitz and Musslimimain have introduced a series of new integrable space–time shifted nonlocal nonlinear equations in [31], which contain the space shifted nonlocal NLS equation, time shifted nonlocal NLS equation and space–time shifted nonlocal NLS equation as well as the real and complex space–time shifted nonlocal mKdV equation. The one of the space shifted nonlocal NLS equations reads

$$\begin{aligned} iq_{t}(x,t)=q_{xx}(x,t)+2\sigma q^{2}(x,t)q^{*}(x_{0}-x,t), \end{aligned}$$
(2)

where \(x_{0}\) is an arbitrary real parameter. The Lax pair and the infinite number of conserved quantities have been given, which indicates that Eq. (2) is integrable. The exact one-soliton solution is obtained via the inverse scattering transform in Ref. [19]. Soon after, the periodic wave solution and one-, two-soliton solutions of the shifted nonlocal NLS and mKdV equations are obtained by using the Hirota bilinear method [32]. On the variable transformation scale, one cannot get the local NLS equation from the space shifted nonlocal NLS equation, which is different from the nonlocal NLS equation [33]. Therefore, we consider the focusing and defocusing nonlocal space shifted NLS equation. Our main attention focuses on the space shifted coefficient \(x_{0}\), which can cause the spatial displacement of the wave propagation of solitons and RWs.

The paper is organized as follows. In Sect. 2, we derive the nonsingular N-soliton solutions and the dynamic behavior of two-soliton solutions are analyzed for the defocusing space shifted nonlocal NLS equation. In Sect. 3, using the known DT, we construct the higher-order RW solutions for focusing space shifted nonlocal NLS equation. The first-, second-order RWs are studied by the analysis of the space shifted factor \(x_{0}\). The conclusion is summarized in the last section.

2 Soliton solutions for defocusing nonlocal space shifted NLS Eq. (2)

In this section, we construct the exact solutions of the defocusing space shifted nonlocal NLS Eq. (2) on nonzero seed solution via DT. The dynamic behavior of the solitons with respect to the space shift \(x_{0}\) is also investigated.

The Lax pair of Eq. (2) is

$$\begin{aligned} \Phi _{x}&=U(Q,z)\Phi \end{aligned}$$
(3a)
$$\begin{aligned} \Phi _{t}&=V(Q,z)\Phi \end{aligned}$$
(3b)

with

$$\begin{aligned} U(Q,z)&=z\sigma _{3}+Q, \\ V(Q,z)&=-2iz^{2}\sigma _{3}-2izQ-i\sigma _{3}(Q_{x}-Q^{2}),\\ Q(x,t)&=\left( \begin{array}{cc} 0 &{} q(x,t) \\ -\sigma q^{*}(x_{0}-x,t) &{} 0 \\ \end{array} \right) ,\\ \sigma _{3}&=\mathrm diag(1,-1), \end{aligned}$$

where \(\Phi =(\phi _{1},\phi _{2})^{T}\) is the vector eigenfunction and z is the spectral parameter. One can check that the space shifted nonlocal NLS equation can derive from the compatibility condition \(U_{t}-V_{x}+[U,V]=0\).

Following the method of constructing the DT for nonlocal NLS equation in [13], we directly give the Nth iterated potential transformations

$$\begin{aligned} q_{_{N}}(x,t)&=q(x,t)+2\frac{\tau _{N+1,N-1}}{\tau _{N,N}}, \end{aligned}$$
(4a)
$$\begin{aligned} q^{*}_{_{N}}(x,t)&=q^{*}(-x,t)-2\frac{\tau _{N-1,N+1}}{\tau _{N,N}}, \end{aligned}$$
(4b)

with

$$\begin{aligned} \tau _{_{M,2N-M}}=\left| \begin{array}{cc} F_{N\times M} &{} G_{N\times (2N-M)} \\ G^{*}_{N\times M} &{} F^{*}_{N\times (2N-M)} \\ \end{array} \right| , \end{aligned}$$
(5)

where \(M=N-1\), N, or \(N+1\), the block matrices \(F_{N\times M},G_{N\times (2N-M)}, G^{*}_{N\times M},F^{*}_{N\times (2N-M)}\) are defined as below

$$\begin{aligned} F_{N\times N}&=[z_{k}^{m-1}f_{k}(x,t)]_{1\ll k,m\ll N},\\ G_{N\times N}&=[(-z_{k})^{m-1}g_{k}(x,t)]_{1\ll k,m\ll N},\\ F^{*}_{N\times N}&=[(-z_{k}^{*})^{m-1}f_{k}^{*}(x,t)]_{1\ll k,m\ll N},\\ G^{*}_{N\times N}&=[(z_{k}^{*})^{m-1}g_{k}^{*}(x,t)]_{1\ll k,m\ll N}. \end{aligned}$$

To obtain the exact solutions, we start from the plane-wave solution \(q=c e^{2ic^{2}t}\) with \(\sigma =-1\), where c is a real parameter, and solve the system (3a) and (3b). Then we get the eigenfunctions

$$\begin{aligned} \left( \begin{array}{c} f_{k} \\ g_{k} \\ \end{array} \right) =\left( \begin{array}{c} e^{i c^{2}t}(a_{k}e^{s_{k}\xi _{k}}+b_{k}e^{-s_{k}\xi _{k}})\\ e^{-ic^{2}t}(\frac{(s_{k}-z_{k})a_{k}}{c}e^{s_{k}\xi _{k}}- \frac{(s_{k}+z_{k})b_{k}}{c}e^{-s_{k}\xi _{k}}) \\ \end{array} \right) \end{aligned}$$
(6)

with \(s_{k}=\sqrt{z^2+c^2}\) and \(\xi _{k}=x-2iz_{k}t\), where \(a_{k}\) and \(b_{k}(1\ll k \ll N)\) are complex parameters. Taking the above eigenfunction into the Nth iterated solution (4a) and (4b), we can get the exact solutions of the defocusing space shifted nonlocal NLS equation (2). Here we stress that the conjugate eigenfunction in (5) is essentially connected with the space shifted parameter \(x_{0}\) in symmetric forms, e.g., \((f_{k}^{*}(x_{0}-x,t),g_{k}^{*}(x_{0}-x,t))\). In order to seek the soliton solutions, we impose \(s_{k}\) to be real numbers, \(z_{k}\) pure imaginary and \(0<|\mathrm Im(z_{k})|<c\), which results in the existence of the \(\xi _{k}\)-solitary wave.

When \(N=1\), the solution (4a) is reduced to

$$\begin{aligned} q =c e^{2ic^{2}} \left[ 1-\frac{2z_{\mathrm{1I}} (e^{2s_{1}\xi _{1}}+\gamma _{1})(\mu _{1}e^{2s_{1}(x_{0}-\eta _{1})}+\mu _{1}^{*}\gamma _{1}^{*})}{c^{2}e^{2s_{1}(\xi _{1}+x_{0}-\eta _{1})}+z_{\mathrm{1I}}\mu _{1}\gamma _{1}e^{2s_{1} (x_{0}-\eta _{1})}+z_{\mathrm{1I}}\mu _{1}^{*}\gamma _{1}^{*}e^{2s_{1}\xi _{1}}+c^{2}|\gamma _{1}|^{2} }\right] , \end{aligned}$$
(7)

where \(\xi _{1}=x+2z_\mathrm{1I}t,\eta _{1}=x-2z_\mathrm{1I}t, \mu _{1}=z_\mathrm{1I}-is_{1},s_{1}=\sqrt{c^{2}-z_\mathrm{1I}^{2}},\gamma _{1}=a_{1}/b_{1}\) and \(z_{1}=z_\mathrm{1R} +iz_\mathrm{1I}\). The singularity problem can be avoid with the constraint condition \(\mathrm sgn(z_\mathrm{1I})\mathrm Re(\mu _{1}\gamma _{1})>0\) or \(\mathrm Im(\mu _{1}\gamma _{1}) \ne 0\). Under the nonsingular conditions, the exact solution (7) contains two waves, i.e., \(\xi _{1}\)-wave and \(\eta _{1}\)-wave. Let us consider the asymptotic analysis for the soliton solution (7).

(i) Along the line \(x+2z_\mathrm{1I}t=0\) as \(|t|\rightarrow \infty \), we have

$$\begin{aligned}&q\rightarrow q^{\pm }_{1} =c e^{2ic^2t}\left[ 1-\frac{2z_\mathrm{1I}(e^{2s_{1}\xi _{1}}+\gamma _{1})}{\zeta _{1}^{\pm }e^{2s_{1}\xi _{1}}+\vartheta _{1}^{\pm }}\right] , \end{aligned}$$
(8a)
$$\begin{aligned}&|q|^{2}\rightarrow | q^{\pm }_{1}|^2 =c^{2} \nonumber \\&\quad \!\left[ \!1-\frac{2\gamma _\mathrm{1I}s_1}{sgn(z_\mathrm{1I})c|\gamma _{1}|\cosh (2s_{1}\xi _{1}+\Lambda _{1}^{\pm })+ Re(\mu _{1}\gamma _{1})}\!\right] , \end{aligned}$$
(8b)

where \(\zeta _{1}^{-}=z_{1\mathrm{I}},\vartheta _{1}^{-}=\mu _{1}\gamma _{1}, \zeta _{1}^{+}=\mu _{1}^{*},\vartheta _{1}^{+}=z_\mathrm{1I}\gamma _{1}, \Lambda _{1}^{-}=\ln \frac{|z_\mathrm{1I}|}{c|\gamma _{1}|}, \Lambda _{1}^{+}=\ln \frac{c}{|z_\mathrm{1I}||\gamma _{1}|}\). The minus sign corresponds to \(z_\mathrm{1I}>0\) as \(t\rightarrow -\infty \) or \(z_\mathrm{1I}<0\) as \(t\rightarrow \infty \) and the plus sign to \(z_\mathrm{1I}<0\) as \(t\rightarrow -\infty \) or \(z_\mathrm{1I}>0\) as \(t\rightarrow \infty \).

(ii) Along the line \(x-2z_\mathrm{1I}t=0\) as \(|t|\rightarrow \infty \), we have

$$\begin{aligned}&q\rightarrow q^{\pm }_{2} =c e^{2ic^2t}\left[ 1-\frac{2z_\mathrm{1I}(\mu _1e^{2s_{1}(x_0-\eta _{1}})+\mu _{1}^{*}\gamma ^{*}_{1})}{\omega _{1}^{\pm }e^{2s_{1}(x_0-\eta _{1})}+\varphi _{1}^{\pm }}\right] , \end{aligned}$$
(9a)
$$\begin{aligned}&|q|^{2}\rightarrow | q^{\pm }_{2}|^2 =c^{2} \nonumber \\&+\frac{2s_1 Im(\mu _{1}^2\gamma _{1})}{ sgn(z_\mathrm{1I})c|\gamma _{1}|\cosh (2s_{1} (\eta _1-x_{0})-\Lambda _{1}^{\pm })+ Re(\mu _{1}\gamma _{1})}, \end{aligned}$$
(9b)

where \(\eta _{1}^{-}=\mu _{1}z_\mathrm{1I},\varphi _{1}^{-}=c^2\gamma _{1}^{*}, \eta _{1}^{+}=c^2,\varphi _{1}^{+}=\mu _{1}^{*}z_\mathrm{1I}\gamma _{1}^{*}\). The minus sign corresponds to \(z_\mathrm{1I}>0\) as \(t\rightarrow -\infty \) or \(z_\mathrm{1I}<0\) as \(t\rightarrow \infty \) and the plus sign to \(z_\mathrm{1I}<0\) as \(t\rightarrow -\infty \) or \(z_\mathrm{1I}>0\) as \(t\rightarrow \infty \).

From the above expression, we can deduce that Eq. (8a) represents the dark soliton for \(\mathrm z_\mathrm{1I}\gamma _\mathrm{1I}>0\) or antidark soliton for \(\mathrm z_\mathrm{1I}\gamma _\mathrm{1I}<0\), while Eq. (9a) represents the dark soliton for \(\mathrm z_\mathrm{1I}\mathrm Im(\mu _{1}^2\gamma _{1})<0\) or antidark soliton for \(\mathrm z_\mathrm{1I}\mathrm Im(\mu _{1}^2\gamma _{1})>0\) under the nonsingular constraints. Asymptotic analysis expressions (8b) and (9b) reveal that the velocities and amplitudes of two solitons maintain unchanged before and after collisions but a phase shift \(|\Lambda _{1}^{+}-\Lambda _{1}^{-}|=2\ln \frac{c}{|z_\mathrm{1I}||\gamma _{1}|}\).

Fig. 1
figure 1

The soliton solution (7) of the space shifted nonlocal defocusing NLS Eq. (1): a two antidark solitons with \(c=1,z_{1}=0.2i,\gamma _{1}=1-2i, x_0=1\); b dark and antidark solitons with \(c=2,z_{1}=i,\gamma _{1}=1-i,x_0=-1\); c two dark solitons with \(c=2,z_{1}=0.2i,\gamma _{1}=1+2i,x_0=-2\)

Full size image

Next, we exhibit several typical solitons with specific parameter values \(z_{1},\mu _{1}\) and \(\gamma _{1}\). Figure 1 shows the elastic interactions of exact two-soliton solutions (7) with three profiles: two antidark soliton, dark and antidark soliton and two dark soliton. However, for the case \(\gamma _\mathrm{1I}=0\) or \(\mathrm Im(\mu _{1}^2\gamma _{1})=0\), the two solitons degrade into a single soliton, which is not a trivial single soliton as the existence of phase shift (see Fig. 2). In Fig. 3, contour plots of the soliton solution (7) are displayed with the different space shifts. We see that the space shift \(x_{0}\) only has the effect of translation on the \(q_{2}\) soliton.

Fig. 2
figure 2

Degenerate two-soliton interactions a dark soliton with \(c=2,z_{1}=\gamma _{1}=1,x_0=1\) and b antidark soliton with \(c=2,z_{1}=1,\gamma _{1}=1-\sqrt{3}i,x_0=-1\)

Full size image
Fig. 3
figure 3

Contour plots of the soliton solution (7) with \(c=1,z_{1}=\frac{i}{7},\gamma _{1}=\frac{1}{4}-\frac{i}{2}\) at \(x_0=-3,0,3\) from left to right, respectively

Full size image

3 Rogue wave solutions of focusing space shifted nonlocal NLS Eq. (2)

In this section, we construct the RW solutions for focusing space shifted nonlocal NLS equation (2) through the DT. This derivation follows the DT [14] with the Lax pair (3a) and (3b) under the spectrum transformation \(z=i\lambda \), which implies the symmetric condition

$$\begin{aligned} \sigma _{1}Q^{*}(x_{0}-x,t)\sigma _{1}=-Q(x,t), \end{aligned}$$
(10)

where

$$\begin{aligned} \sigma _{1}=\left( \begin{array}{cc} 0 &{} 1 \\ 1 &{} 0 \\ \end{array} \right) . \end{aligned}$$

Let’s review the DT in the ZS-AKNS system

$$\begin{aligned} T=I+\frac{\zeta _{1}-\lambda _{1}}{\lambda -\zeta _{1}}P_{1},~~~P_{1}=\frac{\Phi _{1}\Psi _{1}}{\Psi _{1}\Phi _{1}}, \end{aligned}$$
(11)

where \(\Phi _{1}\) is the column eigenvectors solution of the transformed Lax pair with \(\lambda =\lambda _{1}\) and \(\Psi _{1}\) is row eigenvectors solution of the one with \(\lambda =\zeta _{1}\). The relationship between the old and new potentials is

$$\begin{aligned} Q[1]=Q+i(\zeta _{1}-\lambda _{1})[\sigma _{3},P_{1}], \end{aligned}$$
(12)

For Eq. (2), the Lax pair satisfies the following symmetry

$$\begin{aligned} \sigma _{1}U^{*}(x_{0}-x,t,-\lambda ^{*})\sigma _{1}&=-U(x,t,\lambda ), \nonumber \\ \sigma _{1}V^{*}(x_{0}-x,t,-\lambda ^{*})\sigma _{1}&=-V(x,t,\lambda ), \end{aligned}$$
(13)

Using the above symmetries, we can obtain the symmetries of wave functions \(\Phi \) and adjoint wave functions \(\Psi \). Applying these symmetries to the Lax pair, we have

$$\begin{aligned} {[}\sigma _{1}\Phi ^{*}(x_{0}-x)]_{x}&=U(x,-\lambda ^{*})[\sigma _{1}\Phi ^{*}(x_{0}-x)], \nonumber \\ {[}\sigma _{1}\Phi ^{*}(x_{0}-x)]_{t}&=V(x,-\lambda ^{*})[\sigma _{1}\Phi ^{*}(x_{0}-x)], \end{aligned}$$
(14)

Thus, if \(\Phi (x)\) is a wave function of the linear system at \(\lambda \), then \(\sigma _{1}\Phi ^{*}(x_{0}-x)\) is a wave function of this same system at \(-\lambda ^{*}\). In the same wave, if \(\Psi (x)\) is a wave function of the linear system at \(\zeta \), then \(\Psi ^{*}(x_{0}-x)\sigma _{1}\) is a wave function of this same system at \(-\zeta ^{*}\).

Fig. 4
figure 4

The nonsingular first-order RW with a \(r_{0}=-1/3,s_{0}=1/7,=-4\); b \(r_{0}=-1/3,s_{0}=1/7,=0\); c \(r_{0}=-1/4,s_{0}=-1/3,=4\). d– f are density plots of the above 3D figures

Full size image
Fig. 5
figure 5

The singular first-order RW with \(r_{0}=1,s_{0}=-2,x_{0}=2\) (left). On the right is density plot

Full size image
Fig. 6
figure 6

Density plot of second-order rogue waves for strong interaction (above) with \(r_{0}=1/5, s_{0}=-1/5, r_{1}=s_{1}=0\) and weak interaction (below) with \(r_{0}=1/2, s_{0}=-1/4, r_{1}=-s_{1}=200\) at \(x_0=-2,0,2\) from left to right, respectively

Full size image

Under the above symmetric condition, if \(\lambda _{1},\zeta _{1}\in i\mathbb {R}\) and the wave functions satisfy

$$\begin{aligned} \sigma _{1}\Phi _{1}^{*}(x_{0}-x)=\alpha \Phi _{1}(x),~~~~\Psi _{1}^{*}(x_{0}-x)\sigma _{1}=\beta \Psi _{1}(x), \end{aligned}$$
(15)

where \(\alpha ,\beta \) are complex constants, the transformation (11) is the DT of the focusing space shifted nonlocal NLS equation (2). Thus we directly give the multi-RW solutions of the focusing space shifted nonlocal NLS equation

$$\begin{aligned} q^{[N]}(x,t)=e^{-2it}\left( 1+2i\frac{\tau _{1}^{(1)}}{\tau _{0}^{(1)}}\right) , \end{aligned}$$
(16)

where

$$\begin{aligned} \begin{aligned} \tau _{0}^{(1)}&= \mathop {\mathrm{det}}\limits _{1\ll i,j\ll N}\left( m_{i,j}^{(1)}\right) ,\\ \tau _{1}^{(1)}&= {\mathrm{det}} \left( \begin{array}{cc} \left( m_{i,j}^{(1)}\right) _{1\ll i,j\ll N} &{} \nu ^{(1)} \\ \mu ^{(1)} &{} 0 \\ \end{array} \right) ,\\ \mu ^{(1)}&=\left( \phi _{1}^{(0)},\phi _{1}^{(1)},\ldots ,\phi _{1}^{(n-1)}\right) ,\\ \phi _{1}^{(k)}&=\mathop {\mathrm{lim}}\limits _{\epsilon _1\rightarrow 0}\frac{\partial ^{2k}\phi _{1}(\lambda )}{(2k)!\partial \epsilon _1^{2k}},\\ \nu ^{(1)}&=\left( \psi _{1}^{(0)},\psi _{1}^{(1)},\ldots ,\psi _{1}^{(n-1)}\right) ^{T},\\ \psi _{2}^{(k)}&=\mathop {\mathrm{lim}}\limits _{\epsilon _2\rightarrow 0}\frac{\partial ^{2k}\psi _{2}(\zeta )}{(2k)!\partial \epsilon _2^{2k}},\\ m_{i,j}^{(1)}&=\mathop {\mathrm{lim}}\limits _{\epsilon _1,\epsilon _2\rightarrow 0} \frac{1}{(2i-2)!(2j-2)!}\\&\qquad \frac{\partial ^{2i+2j-4}}{\partial \epsilon _2^{2i-2} \partial \epsilon _1^{2j-2}} \left( \frac{\psi (\zeta )\phi (\lambda )}{\lambda -\zeta }\right) ,\\ \lambda&=i(1+\epsilon _1^{2}),\zeta =-i(1+\epsilon _2^{2}). \end{aligned} \end{aligned}$$

The eigenfunctions \(\phi (\lambda )=(\phi _{1},\phi _{2})^{T}\) and \(\psi (\zeta )=(\psi _{1},\psi _{2})\) are given by

$$\begin{aligned} \phi (\lambda )&=\frac{1}{\sqrt{h_{1}-1}}\\&\quad \left( \begin{array}{c} \sinh \left[ A_1+\frac{1}{2}\mathrm ln(h_1+\sqrt{h_1^{2}-1})\right] \\ \sinh \left[ -A_1+\frac{1}{2}\mathrm ln(h_1+\sqrt{h_1^{2}-1})\right] \\ \end{array} \right) , \\ \lambda&=ih_1, h_1=1+\epsilon _1^{2}, \\ A_1&=\sqrt{h_1^{2}-1}(x-\frac{x_{0}}{2}-2ih_1t+i\theta _1), \\ \theta _1&=\sum _{k=1}^{n-1}s_{k}\epsilon _1^{2k},\\ \psi ^T(\zeta )&=\frac{1}{\sqrt{h_{2}-1}}\\&\quad \left( \begin{array}{c} \sinh \left[ A_2+\frac{1}{2}\mathrm ln(h_{2}+\sqrt{h_{2}^{2}-1})\right] \\ \sinh \left[ -A_2+\frac{1}{2}\mathrm ln(h_{2}+\sqrt{h_{2}^{2}-1})\right] \\ \end{array} \right) , \\ \zeta&=-ih_2, h_2=1+\epsilon _2^{2}, \\ A_2&=\sqrt{h_2^{2}-1}(x-\frac{x_{0}}{2}+2ih_2t+i\theta _2), \\ \theta _2&=\sum _{k=1}^{n-1}r_{k}\epsilon _2^{2k}, \end{aligned}$$

where \(s_{k}\) and \(r_{k}~(k=0,1,\ldots ,n-1)\) are arbitrary real parameters.

Fig. 7
figure 7

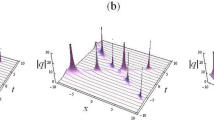
Six collapsing second-order RWs. a \(r_{0}=2, s_{0}=2, r_{1}=40, s_{1}=40, x_{0}=1\); b \(r_{0}=s_{0}=4, r_{1}=s_{1}=-30, x_{0}=-\frac{1}{2}\); c \(r_{0}=-s_{0}=1, r_{1}=s_{1}=20, x_{0}=1\); d \(r_{0}=s_{0}=8, r_{1}=-s_{1}=30, x_{0}=2\); e \(r_{0}=s_{0}=8, r_{1}=-s_{1}=-30, x_{0}=0\); f \(r_{0}=s_{0}=8, r_{1}=s_{1}=-30, x_{0}=-2\)

Full size image

When \(N=1\), we derive the first-order RW from (16) as

$$\begin{aligned} q^{[1]}=e^{-2it} \left( 1-\frac{2(4t-2ix+i(1+x_{0})+2r_{0})(4t+2ix+i(1-x_{0})-2s_{0})}{16t^{2}+4x^{2}+8(r_{0}-s_{0})t+4i(r_{0}+s_{0}+ix_{0})x-2ix_{0}(r_{0}+s_{0})-4r_{0}s_{0}+x_{0}^{2}+1}\right) . \end{aligned}$$
(17)

If we set \(t_{0}=(r_{0}-s_{0})/4\) and \(b=(r_{0}+s_{0})/2\), the solution can be rewritten as

$$\begin{aligned} q^{[1]}=-e^{-2it}\left( 1+\frac{4(4i\hat{t}-1)}{16\hat{t}^{2}+4(\hat{x}+ib)^{2}+1}\right) , \end{aligned}$$
(18)

where \(\hat{t}=t+t_{0}, \hat{x}=x-x_{0}/2\). The first-order RW (18) is nonsingular when \(b^{2}<1/4\). To understand the properties of this RW solution, the intensity minus background is

$$\begin{aligned}&|q^{[1]}|^2-1 \nonumber \\&\quad =\frac{8(16\hat{t}^2+32b\hat{t}\hat{x}-4\hat{x}^2+4b^2+1)}{(16\hat{t}^2-4b^2+1)^2+8(16\hat{t}^2+4b^2+1)\hat{x}^2+16\hat{x}^4}, \end{aligned}$$
(19)

The nonsingular first-order RW solution (18) has three critical points: \((x_{1},t_{1})=(\frac{x_{0}}{2},-t_{0}),(x_{2,3},t_{2,3})= (\frac{x_{0}}{2}\mp \frac{1}{2}\sqrt{\frac{4b^2+3}{b^2+1}},-t_{0}\pm \frac{b}{4}\sqrt{\frac{4b^2+3}{b^2+1}})\). The first point \((x_{1},t_{1})\) is a maximum amplitude with \(|{q[1]|}_\mathrm{max}=3+\frac{16b^2}{1-4b^2}\) and the other two critical points \((x_{2,3},t_{2,3})\) are minimum, at which the amplitudes reduce to zero. We can see the background value \(|q[1]|\rightarrow 1\) as \(x,t\rightarrow \infty \) and the space shift \(x_{0}\) produces \(x_{0}/2\) spatial translation on RWs (18) (see Fig. 4). When \(b^{2}>1/4\), the RW solution collapses at point \((x,t)=(\frac{x_0}{2},-t_{0}\pm \frac{1}{4}\sqrt{4b^{2}-1})\) (see Fig. 5).

We remark here that the RWs cannot be considered as time-translation invariance since the time shift transformation \(\hat{t}\) and peak amplitude associates with the same parameters \(s_{0},r_{0}\).

When \(N=2\), we get the second-order RWs from the formula (16). The explicit expressions of the solutions are given in Appendix, which has five parameters \(s_{j},r_{j},(j=0,1)\) and \(x_0\). If we changed these parameters, the different types of singular and nonsingular RWs are derived.

  • When \(r_{1}=s_{1}=0\), the second-order RW exists in the regime of strong interaction, with the corresponding density graphs exhibited in Fig. 6a–c.

  • When \(r_{1}s_{1}\ne 0\), the weak interaction occurs and the second-order RW splits into three first-order RWs, which form a triangular pattern, see Fig. 6d–f.

Moreover, the abundant collapsing second-order RW solutions can be obtained by choosing proper parameters. They display a variety of profiles, including the quadrilaterals, triangles as well as cyclic structures, which represent singular second-order RWs (see Fig. 7). Interestingly, among the collapsing RWs, there exist two kinds of nonsingular RWs. The ones is on the horizontal x-axis (see Fig. 7a) and the other is located in the centre of quadrilateral structures (see Fig. 7b). The rest of six collapsing second-order RWs with the corresponding density plots are displayed in Fig. 7c–f. These models have appeared in the local NLS equation, but each of which has no “space shift” effect on RWs [33].

Thus, it demonstrates that the peak and depression points increase spatial translational displacement of \(x_{0}/2\) for each of the RWs, which is quite distinct from the ones in solitons with the increase of \(x_{0}\). We should point out that, by the reconstruction of different eigenfunction in the DT, we can also obtain type-II and type-III RW solutions as in the nonlocal NLS equation [14]. Although these RW solutions have the similar properties except the space translation, they cannot be obtained from a simple variable transformation.

4 Conclusions

In this paper, we have constructed the N-soliton solutions and multi-rogue wave solutions for defocusing and focusing space shifted nonlocal NLS equation on different plane-wave solutions. The asymptotic analysis has indicated that the elastic two-soliton solutions have rich soliton types. The effect of the space shift \(x_{0}\) on soliton solutions and multi-rogue wave solutions have been investigated. It is shown that the solitons of the space shifted nonlocal NLS equation possess the spatial translational distance with \(x_{0}\) and the RWs have the distance \(x_{0}/2\) compared with the same solutions in nonlocal NLS equation. But the space shift \(x_0\) does not affect the amplitude of solutions. Besides the results of the nonlocal NLS equation with space shifts obtained in this paper, it is worth studying other real and complex space–time shifted nonlocal equations.