1 Introduction

The local focusing nonlinear Schrödinger (LF-NLS) equation

$$\begin{aligned} iq_{t}\left( x,t\right) =q_{xx}\left( x,t\right) +2|q\left( x,t\right) |^2q\left( x,t\right) \end{aligned}$$
(1.1)

and the local defocusing nonlinear Schrödinger (LD-NLS) equation

$$\begin{aligned} iq_{t}\left( x,t\right) =q_{xx}\left( x,t\right) -2|q\left( x,t\right) |^2q\left( x,t\right) \end{aligned}$$
(1.2)

are known to be two integrable equations in water wave theory, fiber optics, acoustics, Bose–Einstein condensation, etc [1,2,3]. In these two equations, \(q=q(x,t)\) denotes a complex-valued function of two real variables x, t. The focusing case and the defocusing case are relevant to the positive nonlinearity and the negative nonlinearity, respectively. It is known that there are many physical contexts where Eqs. (1.1) and (1.2) appear. For example, the LF-NLS equation (1.1) describes the weakly nonlinear surface wave in the deep water, while the LD-NLS equation (1.2) governs the weakly nonlinear surface wave in the shallow water. In optical fibers, the LF-NLS equation (1.1) models the envelope bright-soliton propagation where the group velocity dispersion and the self-phase modulation effects are considered, while the LD-NLS equation (1.2) does not admit bright-soliton solutions vanishing at infinity. In fact, the LD-NLS equation (1.2) is obtained when the dispersion is normal, and it has dark-soliton solutions having a nontrivial background intensity. Moreover, the LF-NLS equation (1.1) is gauge equivalent to the Heisenberg ferromagnetic equation. Physically significant, Eqs. (1.1) and (1.2) have many important relations to a few of celebrated equations, e.g., the Ginzburg–Landau equation, the Gross–Pitaevskii equation, and others. Mathematically, Eqs. (1.1) and (1.2) are both known to be completely integrable and they can be solved via the inverse scattering transform (IST) [4] based on the known Ablowitz–Kaup–Newell–Segur (AKNS) spectral problem [5].

Recently, the nonlocal focusing nonlinear Schrödinger (NF-NLS) equation

$$\begin{aligned} iq_{t}\left( x,t\right) =q_{xx}\left( x,t\right) +2 q^2\left( x,t\right) q^*\left( -x,t\right) \end{aligned}$$
(1.3)

and the nonlocal defocusing nonlinear Schrödinger (ND-NLS) equation

$$\begin{aligned} iq_{t}\left( x,t\right) =q_{xx}\left( x,t\right) -2 q^2\left( x,t\right) q^*\left( -x,t\right) \end{aligned}$$
(1.4)

have been proposed in [6] by considering the nonlocal reductions of the AKNS spectral problem. In Eqs. (1.3) and (1.4), the asterisk \(*\) denotes the complex conjugation and \(q=q(x,t)\) is complex-valued. Similar to Eqs. (1.1)–(1.2), the difference in Eqs. (1.3)–(1.4) is the positive nonlinearity and the negative nonlinearity corresponding to the focusing case and the defocusing case, respectively. The word nonlocal comes from the fact that the evolution of the field depends on not only the solution values at x but also the values at \(-x\). From Refs. [6,7,8], we know that Eqs. (1.3)–(1.4) are also completely integrable since they have Lax pair formulations and infinitely many conservation laws. Physically, (1.3) and (1.4) are \({{{\mathcal {P}}}{{\mathcal {T}}}}\)-symmetric [9, 10] since they are invariant under the combined action of parity operator \({{\mathcal {P}}}\ (x\rightarrow -x\)) and time-reversal operator \({{\mathcal {T}}}\ (t\rightarrow -t,i\rightarrow -i\)). We note that the \({{{\mathcal {P}}}{{\mathcal {T}}}}\)-symmetric systems have attracted more and more attention recently, which is a hot topic in modern physics. Moreover, the potential applications of these nonlocal NLS equations in magnetics were reported in Ref. [11]. In the literature, a lot of exact solutions have been found for (1.3) and (1.4), such as soliton solutions, breather solutions, rogue wave solutions, periodic solutions, hyperbolic soliton solutions, and others [6,7,8, 12,13,14,15]. In this paper, we aim to investigate the nonlinear dynamics in the ND-NLS equation (1.4) by extending the RH method [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31] to this equation.

This paper is organized as follows. In Sect. 2, we will study the direct scattering transform of the ND-NLS equation (1.4) by formulating its RH problems. Then the spectral structure of the equation will be investigated and compared with the other three NLS-type equations. In Sect. 3, multi-soliton solutions will be obtained for (1.4). Moreover, we will point out, upon choosing suitable parameters, the soliton solutions of (1.4) can be reduced to special kinds of solutions of the LF-NLS equation (1.1) and the LD-NLS equation (1.2). In Sect. 4, the nonlinear dynamics in the ND-NLS equation (1.4) will be analyzed and demonstrated by using Mathematica symbolic computations. In general, the multi-soliton solutions often collapse repeatedly, but they can remain analytic for a wide range of soliton parameters. Section 5 gives the conclusions.

2 The Riemann–Hilbert approach

2.1 Riemann–Hilbert problem

The ND-NLS equation (1.4) admits the Lax pair [6]

$$\begin{aligned} \Psi _x= & {} \left( \begin{array}{ll} i\lambda &{}q\left( x,t\right) \\ q^*\left( -x,t\right) &{}-i\lambda \end{array} \right) \Psi , \end{aligned}$$
(2.1a)
$$\begin{aligned} \Psi _t= & {} \left( \begin{array}{ll} 2i\lambda ^2+i q\left( x,t\right) q^*\left( -x,t\right) &{}\quad 2\lambda q-iq_x\left( x,t\right) \\ 2\lambda q^*\left( -x,t\right) +i q^*_x\left( -x,t\right) &{}\quad -2i\lambda ^2-i q\left( x,t\right) q^*\left( -x,t\right) \end{array} \right) \Psi , \end{aligned}$$
(2.1b)

where \(\Psi =\Psi (x,t;\lambda )\) is a column vector function of the complex iso-spectral spectral parameter \(\lambda \), and q(x, t) is a complex-valued function. In fact, one can check that (1.4) comes as the compatibility condition of the system (2.1).

In order to perform spectral analysis conveniently, we first rewrite the original Lax pair (2.1) in an equivalent form

$$\begin{aligned} J_x= & {} i\lambda \left[ \sigma _3, J\right] +QJ, \end{aligned}$$
(2.2a)
$$\begin{aligned} J_t= & {} 2i\lambda ^2 \left[ \sigma _3, J\right] +{\widetilde{Q}}J, \end{aligned}$$
(2.2b)

where the square bracket is the matrix commutator, and

$$\begin{aligned} \sigma _3=\left( \begin{array}{ll} 1&{} \quad 0\\ 0&{} \quad -1 \end{array} \right) ,\ Q=Q(x,t)=\left( \begin{array}{ll} 0&{} \quad q(x,t)\\ q^*(-x,t)&{} \quad 0 \end{array} \right) , \quad {{\widetilde{Q}}}=2\lambda Q+i\left( Q^2+Q_x\right) \sigma _3. \end{aligned}$$

Remark 1

The Lax pairs of the other three NLS-type equations (1.1)–(1.3) are all reduced AKNS spectral problems admitting the same form as (2.2a)–(2.2b), except for the difference in \(Q=Q(x,t)\) that

  • \(Q(x,t)=\big (\begin{array}{ll} 0&{} \quad q(x,t)\\ -q^*(x,t)&{} \quad 0 \end{array} \big )\) for Eq. (1.1), which satisfies the symmetry relation \(Q^\dagger (x,t)=-Q(x,t)\). Here the dagger \(\dag \) represents the Hermitian conjugation.

  • \(Q(x,t)=\big (\begin{array}{ll} 0&{} \quad q(x,t)\\ q^*(x,t)&{} \quad 0 \end{array} \big )\) for Eq. (1.2), which satisfies the symmetry relation \(Q^\dagger (x,t)=-\sigma _3 Q(x,t)\sigma _3\).

  • \(Q(x,t)=\big (\begin{array}{ll} 0&{} \quad q(x,t)\\ -q^*(-x,t)&{} \quad 0 \end{array} \big )\) for Eq. (1.3), which satisfies the symmetry relation \(Q^*(-x,t)=-\sigma _1Q(x,t)\sigma _1\). Here \(\sigma _1=\left( \begin{array}{ll} 0&{} \quad 1\\ 1&{} \quad 0 \end{array} \right) \).

Following the procedure in deriving RH problems of the AKNS spectral problem [16, 17], we can establish the RH problem of the ND-NLS equation (1.4) as

$$\begin{aligned}&\displaystyle P^-(\lambda )P^+(\lambda )=\left( \begin{array}{ll} 1&{} \quad s_{12}e^{2i\lambda x}\\ r_{21}e^{-2i\lambda x}&{} \quad 1 \end{array} \right) ,\quad \lambda \in {\mathbb {R}}, \end{aligned}$$
(2.3)
$$\begin{aligned}&\displaystyle P_1(\lambda )\rightarrow {\mathbb {I}},\quad \lambda \in {\mathbb {C}}^{+}\rightarrow \infty , \end{aligned}$$
(2.4)
$$\begin{aligned}&\displaystyle P_2(\lambda )\rightarrow {\mathbb {I}},\quad \lambda \in {\mathbb {C}}^{-}\rightarrow \infty , \end{aligned}$$
(2.5)

where (2.4)–(2.5) are the canonical normalization conditions. Here \(P_1=P_1(x,\lambda )\) and \(P_2=P_2(x,\lambda )\) are two matrix functions which are analytic in the upper half \(\lambda \)-plane \({\mathbb {C}}^+\) and the lower half \(\lambda \)-plane \({\mathbb {C}}^-\), respectively. In fact, \(P_1\) and \(P_2\) are constructed as

$$\begin{aligned} P_1=([J_{+}]_1,[J_{-}]_2),\quad P_2=\left( \begin{array}{l} {[J_{+}^{-1}]}^1\\ {[J_{-}^{-1}]}^2 \end{array} \right) , \end{aligned}$$

where each \([J_{\pm }]_l\ (l=1,2)\) denotes the lth column of the Jost solutions \(J_{\pm }\) of (2.2a) satisfying \(J_{\pm }\rightarrow {\mathbb {I}}\) as \(x\rightarrow \pm \infty \), and each \([J_\pm ^{-1}]^l\ (l=1,2)\) represents the lth row of the matrix inverse \(J_\pm ^{-1}\). In addition, the symbols \(P^\pm \) are the limits of \(P_1\) or \(P_2\) taken from the left-hand side (LHS) or the right-hand side (RHS) of the real \(\lambda \)-axis. In addition, \(s_{12}\) and \(r_{21}\) are two reflection coefficients defined on the real \(\lambda \)-axis in general.

2.2 Spectral structure

To solve the RH problem (2.3)–(2.5) for the ND-NLS equation (1.4), we have to investigate its zero structure completely. Before we do this, let us first recall the zero structures of the three NLS-type equations (1.1)–(1.3) [16, 17]. It is known that the RH methods for the NLS-type equations (1.1)–(1.3) rely heavily on their respective symmetry relations of the potential matrix Q(x, t) in Remark 1. Indeed, these three symmetry relations lead to the different zero structures of the three NLS-type equations. The zero structures of the LF-NLS equation (1.1) and the LD-NLS equation (1.2) are similar [17]: \(\text {det}P_1\) has N simple zeros \(\{\lambda _j\}^{N}_1\) in \({\mathbb {C}}^+\), where \(\lambda _j\) are complex-valued, while \(\text {det}P_2\) has N simple zeros \(\{{\hat{\lambda _j\}}}^{N}_1\) in \({\mathbb {C}}^-\) with \({\hat{\lambda }}_{j}=\lambda ^*_j\). Obviously, the zeros \(\lambda _j\) and \({\hat{\lambda }_j}\) are complex conjugate to each other. The zero structure of the NF-NLS equation (1.3) corresponding to soliton solution is [16]: \(\text {det}P_1\) has \(2N+M\) simple zeros \(\{\lambda _j\}^{2N+M}_1\) in \({\mathbb {C}}^+\), where \(\lambda _{N+l}=-\lambda ^*_l\ (1\le l\le N)\) are non-purely imaginary and \(\lambda _{2N+l}\ (1\le l\le M)\) are purely imaginary, while \(\text {det}P_2\) has \(2N+M\) simple zeros \(\{{\hat{\lambda _j\}}}^{2N+M}_1\) in \({\mathbb {C}}^-\), where \({\hat{\lambda }}_{n+l}=-{\hat{\lambda }}^*_l\ (1\le l\le n)\) are non-purely imaginary and \({\hat{\lambda }}_{2n+l}\ (1\le l\le 2N+M-2n)\) are purely imaginary. In general, the zeros \(\lambda _j\) and \({\hat{\lambda }_j}\) have no definite relations.

Now, compared with Eqs. (1.1)–(1.3), there will be rather different symmetry relation of the spectral data for the ND-NLS equation (1.4), which is the consequence of the symmetry property of the potential matrix Q in (2.2a). This symmetry relation will be our main concern hereafter. Notice that the matrix \(Q=Q(x,t)\) in (2.2a) satisfies the symmetry relation

$$\begin{aligned} Q^*(-x,t)=-\sigma ^{-1}Q(x,t)\sigma , \end{aligned}$$
(2.6)

where \(\sigma =\big (\begin{array}{ll} 0&{} \quad 1\\ -1&{} \quad 0 \end{array} \big ).\) Obviously, the symmetry property (2.6) in the ND-NLS equation (1.4) is different from the three symmetry relations for the NLS-type equations (1.1)–(1.3), as indicated in Remark 1.

By performing spectral analysis on (2.2a) by using (2.6), we have a relation of the matrix spectral functions \(J_\pm \) that \(J_\pm (x,\lambda )=\sigma ^{-1} J^*_\mp (-x,-\lambda ^*)\sigma .\) Then it follows from the definitions of \(P_1\) and \(P_2\) that

$$\begin{aligned} P_1\left( x,\lambda \right)= & {} \sigma ^{-1} P^*_1\left( -x,-\lambda ^*\right) \sigma ,\quad \lambda \in {\mathbb {C}}^+, \end{aligned}$$
(2.7)
$$\begin{aligned} P_2\left( x,\lambda \right)= & {} \sigma ^{-1} P^*_2\left( -x,-\lambda ^*\right) \sigma ,\quad \lambda \in {\mathbb {C}}^-. \end{aligned}$$
(2.8)

Using (2.7)–(2.8), the zero structure of the RH problem of the ND-NLS equation (1.4) can be given. In fact, from (2.7) we know that \(\text {det}[P_1(x,\lambda )]=\text {det}[P^*_1(-x,-\lambda ^*)]\). Therefore, if \(\lambda _j\) is a zero of \(\text {det}P_1\), so is \(-\lambda _j^*\). Likewise, from (2.8) we know that \(\text {det}[P_2(x,\lambda )]=\text {det}[P^*_2(-x,-\lambda ^*)]\). Therefore, if \({\hat{\lambda }_j}\) is a zero of \(\text {det}P_2\), so is \(-{\hat{\lambda }_j}^*\). We note that this property for the zero structure is the same as that of the NF-NLS equation (1.3) [16]. However, a remarkable difference we shall show here is that the zero structure of the ND-NLS equation (1.4) only involves pairwise zeros \((\lambda _j,-\lambda _j^*)\) and \(({\hat{\lambda }_j},-{\hat{\lambda }_j}^*)\), where \(\lambda _j\) and \({\hat{\lambda }_j}\) are non-purely imaginary, i.e., Re\((\lambda _j)\ne 0\) and Re\(({\hat{\lambda }_j})\ne 0\). In other words, for the ND-NLS equation (1.4), its RH problem cannot admit purely imaginary zeros. Now we shall prove this via the contradiction approach. If \(\text {det}P_1\) and \(\text {det}P_2\) in the RH problem of the ND-NLS equation (1.4) has purely imaginary simple zeros \(\lambda _j,{\hat{\lambda }_j}\), we have \(\lambda _j=-\lambda _j^*\) and \({\hat{\lambda }_j}=-{\hat{\lambda }_j}^*\). Now let us consider the kernels of \(P_1(\lambda _j)\) and \(P_2({\hat{\lambda }_j})\) spanned by a nonzero column vector \(v_j\) and a nonzero row vector \({{\hat{v}}}_j\), respectively,

$$\begin{aligned} P_1\left( \lambda _j\right) v_j=0,\quad {\hat{v}}_jP_2\left( {\hat{\lambda }}_j\right) =0. \end{aligned}$$
(2.9)

Using the first equation in (2.9) and the Lax pair (2.2), we can obtain that

$$\begin{aligned} v_j=e^{(i\lambda _j x+2i\lambda ^2_jt)\sigma _3}v_{j,0}, \end{aligned}$$

where \(v_{j,0}\) is a nonzero two-component column vector. Then it follows from (2.7) and the first equation in (2.9) that \(v^*_{j,0}=c_j\sigma v_{j,0}\), where \(c_j\) is a constant. Therefore, by setting \(v_{j,0}=(\alpha _j, \beta _j)^T\) with \(\beta _j\ne 0\) without loss of generality, we can arrive at the conclusion \(c_j=0\). Here the symbol T represents the matrix transpose. This obviously means that \(v_j\equiv 0\), which is a contradiction to the definition of \(v_j\). In a similar way, by using (2.8) and the second equation in (2.9), we can arrive at \({{\hat{v}}}_j\equiv 0\), which is a contradiction to the definition of \({{\hat{v}}}_j\).

Summarizing the above results, the general zero structure for the ND-NLS equation (1.4) corresponding to soliton solution is: \(\text {det}P_1\) has 2K non-purely imaginary zeros \(\{\lambda _j\}^{2K}_1\) in \({\mathbb {C}}^+\), where \(\lambda _{K+l}=-\lambda ^*_l\ (1\le l\le K)\), while \(\text {det}P_2\) has 2K non-purely imaginary zeros \(\{{\hat{\lambda _j\}}}^{2K}_1\) in \({\mathbb {C}}^-\), where \({\hat{\lambda }}_{K+l}=-{\hat{\lambda }}^*_l\ (1\le l\le K)\). To solve the RH problem (2.3)–(2.5) with this zero structure, we need the discrete scattering data \(\{\lambda _j,{{\hat{\lambda }}}_j,v_j,{{\hat{v}}}_j\}\). Here \(\lambda _j,{{\hat{\lambda }}}_j\) are the indicated zeros above, and \(v_j,{\hat{v}}_j\) are the corresponding vectors defined in (2.9). Following a similar procedure for the NF-NLS equation (1.3) [16], the vectors \(v_j\) and \({{\hat{v}}}_j\) for the ND-NLS equation (1.4) can be determined via the definitions in (2.9) and the Lax pair (2.2)

$$\begin{aligned}&v_j=\left\{ \begin{array}{ll} e^{\theta _j\sigma _3}v_{j,0},&{}\quad 1\le j\le K,\\ \sigma e^{\theta ^*_{j-K}(-x,t)\sigma _3 }v^*_{j-K,0},&{}\quad K+1\le j\le 2K, \end{array} \right. \end{aligned}$$
(2.10a)
$$\begin{aligned}&{{\hat{v}}}_j=\left\{ \begin{array}{ll} {{\hat{v}}}_{j,0}e^{{\hat{\theta _j\sigma }}_3}, &{}\quad 1\le j\le K,\\ {{\hat{v}}}^*_{j-K,0}e^{{\hat{\theta }}^*_{j-K}(-x,t)\sigma _3}\sigma ,&{}\quad K+1\le j\le 2K, \end{array} \right. \end{aligned}$$
(2.10b)

with \(\theta _j=i\lambda _j x+2i\lambda ^2_jt, \, {{\hat{\theta }}}_j=-i{\hat{\lambda }_j} x-2i{\hat{\lambda }}^2_jt\), and

$$\begin{aligned}&\lambda _j\in {\mathbb {C}}^+,\ 1\le j\le K, \quad \mathrm{with} \,\, \mathrm{Re}\,\,(\lambda _j)\ne 0,\\&{\hat{\lambda _j\in {\mathbb {C}}}}^-,\ 1\le j\le K, \quad \mathrm{with}\,\, \mathrm{Re}\,\,({\hat{\lambda }_j})\ne 0,\\&v_{j,0}=\left( \begin{array}{l} \alpha _j\\ 1 \end{array} \right) , \quad 1\le j\le K, \quad \mathrm{with}\,\,\alpha _j \quad \mathrm{being\ complex\ constants},\\&{{\hat{v}}}_{j,0}=\left( {\hat{\alpha _j}},1\right) ,\ 1\le j\le K, \quad \mathrm{with} \,\, {\hat{\alpha _j}} \quad \mathrm{being\ complex\ constants}. \end{aligned}$$

Note that the second components of \(v_{j,0}\) and \({{\hat{v}}}_{j,0}\) are normalized without loss of generality.

2.3 Solutions of the Riemann–Hilbert problem

Now, for the ND-NLS equation (1.4), we can regulate the RH problem (2.3)–(2.5) with the indicated zero structure above to a regular one without zeros. Then its RH problem (2.3)–(2.5) in the reflection-less case can be uniquely solved via (2.10a)–(2.10b) as

$$\begin{aligned}&P_1(\lambda )={\mathbb {I}}-\sum ^{2K}_{k=1}\sum ^{2K}_{j=1}\frac{v_k{\hat{v}}_j\left( A^{-1}\right) _{kj}}{\lambda -{\hat{\lambda }}_j}, \end{aligned}$$
(2.11a)
$$\begin{aligned}&P_2(\lambda )={\mathbb {I}}+\sum ^{2K}_{k=1}\sum ^{2K}_{j=1}\frac{v_k{\hat{v}}_j\left( A^{-1}\right) _{kj}}{\lambda -\lambda _k}, \end{aligned}$$
(2.11b)

where \(A=(a_{kj})\) is a 2Kth-order matrix whose elements are

$$\begin{aligned} a_{kj}=\frac{{\hat{v}}_kv_j}{\lambda _j-{\hat{\lambda }}_k},\quad 1\le k, j\le 2K. \end{aligned}$$

3 Multi-soliton solutions

Now we are ready to derive a multi–soliton solution of the ND-NLS equation (1.4). To this end, we expand \(P_1(\lambda )\) in (2.11a) as

$$\begin{aligned} P_1(\lambda )={\mathbb {I}}+\lambda ^{-1}P^{(1)}_1+\lambda ^{-2}P^{(2)}_1+\ldots , \quad \lambda \rightarrow \infty . \end{aligned}$$
(3.1)

Then substituting it into (2.2a) and equating the O(1) terms, we get

$$\begin{aligned} Q=-i\left[ \sigma _3,P^{(1)}_1\right] , \end{aligned}$$
(3.2)

which implies that

$$\begin{aligned} q(x,t)= & {} -2i\left( P^{(1)}_1\right) _{12}, \end{aligned}$$
(3.3a)
$$\begin{aligned} q^*(-x,t)= & {} 2i\left( P^{(1)}_1\right) _{21} \end{aligned}$$
(3.3b)

where \((P^{(1)}_1)_{12}\) is the (1, 2)-element of the matrix function \(P^{(1)}_1\). Here the matrix \(P^{(1)}_1\) can be found from (2.11a) as

$$\begin{aligned} P^{(1)}_1=-\sum ^{2K}_{k=1}\sum ^{2K}_{j=1}v_k{\hat{v}}_j\left( A^{-1}\right) _{kj}, \end{aligned}$$
(3.4)

Remark 2

It should be noted that the explicit expression \(P_1(\lambda )\) in (2.11a) can be shown to satisfy the relation in (2.7) through some algebraic calculations. Then using the expansion (3.1), one can verify the consistency of Eqs. (3.3a)–(3.3b).

Now let us substitute the corresponding vectors in (2.10a)–(2.10b) into (3.4). Then a general multi-soliton solution is obtained for the ND-NLS equation (1.4) from (3.3a)

$$\begin{aligned} q(x,t)= & {} 2i\sum ^K_{k=1}\sum ^K_{j=1}\alpha _ke^{\theta _k-{\hat{\theta _j}}}\left( A^{-1}\right) _{kj} +2i\sum ^K_{k=1}\sum ^{2K}_{j=K+1}\alpha _k{\hat{\alpha }}^*_{j-K}e^{\theta _k+{\hat{\theta }}^*_{j-K}(-x,t)}\left( A^{-1}\right) _{kj}\nonumber \\&+2i\sum ^{2K}_{k=K+1}\sum ^K_{j=1}e^{-\theta ^*_{k-K}(-x,t)-{\hat{\theta }}_{j}}\left( A^{-1}\right) _{kj}\nonumber \\&+2i\sum ^{2K}_{k=K+1}\sum ^{2K}_{j=K+1}{\hat{\alpha }}^*_{j-K} e^{-\theta ^*_{k-K}(-x,t)+{\hat{\theta }}^*_{j-K}(-x,t)}(A^{-1})_{kj}, \end{aligned}$$
(3.5)

where \(A=(a_{kj})_{(2K)\times (2K)}\) with the matrix entries

$$\begin{aligned} a_{kj}=\left\{ \begin{array}{ll} \frac{{\hat{\alpha _k\alpha _je}}^{{\hat{\theta _k}}+\theta _j}+e^{-{\hat{\theta _k}}-\theta _j}}{\lambda _j-{\hat{\lambda _k}}}, &{} \quad 1\le k,j\le K;\\ \frac{{\hat{\alpha }}_{k}e^{{\hat{\theta _k}}-\theta ^*_{j-K}(-x,t)}-\alpha ^*_{j-K}{e^{-{\hat{\theta }}_{k} +\theta ^*_{j-K}(-x,t)}}}{-\lambda ^*_{j-K}-{\hat{\lambda _k}}}, &{} \quad 1\le k\le K,\ K+1\le j\le 2K;\\ \frac{-\alpha _{j}e^{-{\hat{\theta }}^*_{k-K}(-x,t)+\theta _{j}}+{\hat{\alpha }}^*_{k-K}{e^{{\hat{\theta }}^*_{k-K}(-x,t) -\theta _{j}}}}{\lambda _{j}+{\hat{\lambda }}^*_{k-K}}, &{} \quad K+1\le k\le 2K,\ 1\le j\le K;\\ \frac{-{\hat{\alpha }}^*_{k-K}\alpha ^*_{j-K}e^{{\hat{\theta }}^*_{k-K}(-x,t)+\theta ^*_{j-K}(-x,t)} -{e^{-{\hat{\theta }}^*_{k-K}(-x,t)-\theta ^*_{j-K}(-x,t)}}}{-\lambda ^*_{j-K}+{\hat{\lambda }}^*_{k-K}}, &{} \quad K+1\le k,j\le 2K. \end{array} \right. \end{aligned}$$

Till now, we have derived a general multi-soliton solution for the ND-NLS equation (1.4). Indeed, it is the zero structure of the RH problem that leads to this multi-soliton solution. Then, a mathematically interesting question arises that: Whether we can establish any relationships between the multi-soliton solution (3.5) of the ND-NLS equation (1.4) and those of the other three NLS-type equations (1.1)–(1.3) in the framework of RH approach? In the following remark, we shall establish the relationships of the multi-soliton solutions between the ND-NLS equation (1.4) and Eqs. (1.1)–(1.2).

Remark 3

We note that if \({\hat{\lambda }_j}=\lambda ^*_j\) and \({{\hat{\alpha }}}_{j}=\alpha ^*_{j}\) for each j in the vectors in (2.10a)–(2.10b), the multi-soliton solution (3.5) of the ND-NLS equation (1.4) can be reduced to a kind of analytic 2K-soliton solution of the LF-NLS equation (1.1). In fact, in this case, \(\text {det}P_1\) and \(\text {det}P_2\) have the same number of zeros which are complex conjugate to each other. Moreover, the vectors \(v_{j},{{\hat{v}}}_{j}\) in (2.10a)–(2.10b) satisfy the relations \({{\hat{v}}}_j=v^\dagger _j\). This case just corresponds to the scattering data that generates analytic multi-soliton solutions of the LF-NLS equation (1.1) [17]. Similarly, if \({\hat{\lambda }_j}=\lambda ^*_j\) and \({{\hat{\alpha }}}_{j}=-\alpha ^*_{j}\) for each j in (2.10a)–(2.10b), then the vectors \(v_{j}\) and \({{\hat{v}}}_{j}\) obey the relations \({{\hat{v}}}_j=-v^\dagger _j\sigma _3\). In this case, the multi-soliton solution (3.5) of the ND-NLS equation(1.4) can be reduced to a kind of singular 2K-soliton solution of the LD-NLS equation (1.2). In fact, this case corresponds to the scattering data that generates singular multi-soliton solutions of the LD-NLS equation (1.2) [17].

4 Nonlinear dynamics

It is easy to see that for a positive integer K, the multi-soliton solution (3.5) of the ND-NLS equation (1.4) totally involves 4K independent parameters

$$\begin{aligned}&\lambda _1,\lambda _2,\ldots ,\lambda _K, \quad \alpha _1,\ldots ,\alpha _K,\\&{\hat{\lambda }}_1,{\hat{\lambda }}_2,\ldots ,{\hat{\lambda _K}}, \quad {\hat{\alpha }}_1,\ldots ,{\hat{\alpha _K}}, \end{aligned}$$

where \(\lambda _{j}\in {\mathbb {C}}^+\), \({\hat{\lambda }}_{j}\in {\mathbb {C}}^-\), \(\mathrm{Re}(\lambda _j)\ne 0\), \(\mathrm{Re}({\hat{\lambda }_j})\ne 0\), \(\alpha _j\) and \({\hat{\alpha _j}}\) are complex-valued for \(1\le j\le K\). In what follows, to demonstrate the corresponding nonlinear dynamics via (3.5), we shall investigate a representative case: \(K=1\), which corresponds to two-soliton solutions of the ND-NLS equation (1.4).

To demonstrate, we firstly choose the corresponding parameters in (3.5) as

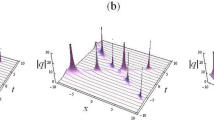
$$\begin{aligned} \lambda _1=0.8+1.5i, \quad {\hat{\lambda }}_1=0.6-0.5i, \quad \alpha _1=1, \quad {\hat{\alpha }}_1=i. \end{aligned}$$
(4.1)

With the parameters in (4.1), Eq. (3.5) gives a two-soliton solution for the ND-NLS equation (1.4). In this case where \(\mathrm{Re}(\lambda _1) \ne \mathrm{Re}({\hat{\lambda }}_1)\), the left-direction wave gradually becomes smaller and even disappear after some time, while the right-direction wave emerges from a zero background and becomes larger and larger during the propagation process. The interaction characteristic is shown in Fig. 1.

Fig. 1
figure 1

Two-soliton solution (3.5) with the parameters in (4.1): 3d plot and density plot

Full size image

Secondly, we choose the parameters in (3.5) as

$$\begin{aligned} \lambda _1=0.2+0.5i, \quad {\hat{\lambda }}_1=0.2-1.2i, \quad \alpha _1=1, \quad {\hat{\alpha }}_1=i. \end{aligned}$$
(4.2)

Under these parameters, Eq. (3.5) also denotes a two-soliton solution for ND-NLS equation (1.4), which is displayed in Fig. 2. As shown in Fig. 2, this two-soliton collision is more regular compared with that in Fig. 1. It is obvious that the breathers have one breather-form before the interaction and keep another breather-form after the interaction. The collision visually looks like the two breathers are bounced back by the collision. Therefore, we call this kind of collision as breather reflection. We note that a kind of bell-soliton reflection phenomenon has been reported for a general coupled NLS equation [19]. However, to our knowledge, the breather-type reflection in Fig. 2 has not been discovered before for the ND-NLS equation (1.4).

Fig. 2
figure 2

Two-soliton solution (3.5) with the parameters in (4.2): 3d plot and density plot

Full size image

Thirdly, we set the parameters in (3.5) to be

$$\begin{aligned} \lambda _1=0.3+0.5i, \quad {\hat{\lambda }}_1=0.4-0.5i, \quad \alpha _1=1, \quad {\hat{\alpha }}_1=i. \end{aligned}$$
(4.3)

In this case where \(\mathrm{Im}(\lambda _1)=-\mathrm{Im}({\hat{\lambda }}_1)\), the two-soliton solution (3.5) via (4.3) is demonstrated in Fig. 3. It is obvious here that the right-direction wave gradually becomes smaller and smaller, while the left-direction wave becomes larger and larger along the propagation process. Therefore, a lot of power has been transferred from one wave to the other. In addition, in Fig. 3, the right-direction wave after the interaction has finite amplitude at all times and even approaches to zero when \(t\rightarrow +\infty \). On the other hand, the left-direction wave emerges from the zero background and its amplitude is finite before the collision.

Fig. 3
figure 3

Two-soliton solution (3.5) with the parameters in (4.3): 3d plot and density plot

Full size image

Now our further task is to demonstrate the relationships between the ND-NLS equation (1.4) and Eqs. (1.1)–(1.2). To this end, we take the following two cases of parameters:

$$\begin{aligned}&\lambda _1=0.2+0.5i, \quad {\hat{\lambda }}_1=0.2-0.5i, \quad \alpha _1=0.5+0.7i, \quad {\hat{\alpha }}_1=-0.5+0.7i, \end{aligned}$$
(4.4)
$$\begin{aligned}&\lambda _1=0.2+0.5i, \quad {\hat{\lambda }}_1=0.2-0.5i, \quad \alpha _1=0.5+0.7i, \quad {\hat{\alpha }}_1=0.5-0.7i. \end{aligned}$$
(4.5)

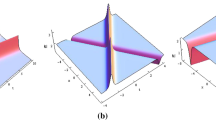
Obviously, the parameters in (4.4) satisfy \({\hat{\lambda }}_1=\lambda ^*_1\) and \({{\hat{\alpha }}}_{1}=-\alpha ^*_{1}\). While, the parameters in (4.5) satisfy that \({\hat{\lambda }}_1=\lambda ^*_1\) and \({{\hat{\alpha }}}_{1}=\alpha ^*_{1}\). Therefore, using the assertions in Remark 3, we obtain two conclusions: (a) under the parameters in (4.4), the two-soliton solution via (3.5) for the ND-NLS equation (1.4) is reduced to a two-soliton solution for the LD-NLS equation (1.2); (b) under the parameters in (4.5), the two-soliton solution via (3.5) for the ND-NLS equation (1.4) is reduced to a two-soliton solution for the LF-NLS equation (1.1). The two-soliton interactions corresponding to (4.4) and (4.5) are graphically illustrated in Figs. 4 and 5, respectively. In Fig. 4, the two-soliton involves two singular bell solitons with the same widths. In Fig. 5, it is a two-soliton with two analytic bell solitons. These two bell solitons have the same amplitudes.

Fig. 4
figure 4

Two-soliton solution (3.5) with the parameters in (4.4): 3d plot and density plot

Full size image
Fig. 5
figure 5

Two-soliton solution (3.5) with the parameters in (4.5): 3d plot and density plot

Full size image

For the multi-soliton solution (3.5), if it is also a solution of the LD-NLS equation (1.2), it will be singular. However, if (3.5) is singular, it is not always a solution of the LD-NLS equation (1.2). In fact, we observe that if the parameters in (3.5) are chosen as

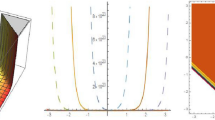
$$\begin{aligned} \lambda _1=0.2+0.5i,\ \ {\hat{\lambda }}_1=0.2-0.5i,\ \ \alpha _1=0.1i,\ \ {\hat{\alpha }}_1=0.6i, \end{aligned}$$
(4.6)

then the solution (3.5) is demonstrated in Fig. 6. We notice that though this solution is singular, it does not satisfy the LD-NLS equation (1.2). Otherwise, due to the form of Eq. (1.2), we can conclude that \(q(x,t)=q(-x,t)\) for arbitrary time t. This means that |q(x, t)| must be symmetric in x. However, as can be seen clearly in Fig. 6, |q(x, t)| is asymmetric in x.

Fig. 6
figure 6

Two-soliton solution (3.5) with the parameters in (4.6): 3d plot and density plot

Full size image

Similarly, if the multi-soliton solution (3.5) is also a solution of the LF-NLS equation (1.1), it will be analytic. However, if (3.5) is analytic, it is not always a solution of the LF-NLS equation (1.1). In fact, if the parameters in (3.5) are chosen as

$$\begin{aligned} \lambda _1=0.2+0.5i, \quad {\hat{\lambda }}_1=0.2-0.5i, \quad \alpha _1=0.2i, \quad {\hat{\alpha }}_1=0.6i, \end{aligned}$$
(4.7)

the solution (3.5) of the ND-NLS equation (1.4) is demonstrated in Fig. 7. We note that though this solution still consists of two analytic bell solitons, it does not satisfy the LF-NLS equation (1.1). Otherwise, in view of the form of Eq. (1.1), we can conclude that \(q(x,t)=-q(-x,t)\) for arbitrary time t. This means that |q(x, t)| must also be symmetric in x. However, as can be seen in Fig. 7, |q(x, t)| is obviously asymmetric in x.

Fig. 7
figure 7

Two-soliton solution (3.5) with the parameters in (4.7): 3d plot and density plot

Full size image

5 Concluding remarks

In this paper, the RH approach for nonlinear evolution equations [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31] is extended to the ND-NLS equation (1.4). By performing spectral analysis and considering the symmetry relation (2.6), we have explored the novel spectral structure of the RH problem, from which the multi-soliton solution (3.5) is presented. Specifically, we prove that the RH problem of the ND-NLS equation (1.4) admit only pairwise non-purely imaginary zeros. That is to say, the zero structure of the ND-NLS equation (1.4) has sharp difference compared with those of Eqs. (1.1)–(1.3). This difference is the main basis for performing RH approach throughout this paper.

Concerning the mathematical aspects of the multi-soliton solution (3.5), we have proved that under some parameter selections, the solution (3.5) can be reduced to special kinds of solutions of Eqs. (1.1)–(1.2). For physical aspects, we graphically illustrated some soliton interactions via the multi-soliton solution (3.5) by choosing suitable parameters via Mathematica symbolic computations. Some figures correspond to the multi-soliton solution with repeated singularities, e.g., Figs. 1 and 2. Some figures reveal the multi-soliton solution with persistent singularities, e.g., Figs. 4 and 6. Some figures are about the analytic multi-soliton solutions, e.g., Figs. 5 and 7. Interestingly, Fig. 2 reveals a kind of collision as breather-type reflection, which is novel for Eq. (1.4). In Fig. 3, the solution remains analytic before a certain time and will become singular after a period of time. More interesting, each individual soliton in Fig. 4 possesses the same width and this solution is also that of the LD-NLS equation (1.2). Similarly, each individual soliton in Fig. 5 possesses the same amplitude and this solution is also that of the LF-NLS equation (1.1). However, though the solution demonstrated in Fig. 6 is singular, we have proved that this solution is not a solution of the LD-NLS equation (1.2). Likewise, though the solution demonstrated in Fig. 7 is analytic, we have proved that this solution is not a solution of the LF-NLS equation (1.1). These results indicate that the zero structure of the ND-NLS equation (1.4) is novel and has sharp contrast to those of Eqs. (1.1)–(1.3). In addition, the obtained solution (3.5) has very rich solution structures since it can be repeatedly singular, persistently singular, even analytic, depending on the parameter selections.

Compared with the other methods for investigating multi-soliton structures of soliton equations, such as the Darboux transformation [32, 33], the bilinear method [34, 35], the Wronskian technique [36, 37], and others, the RH method in this paper not only paves a way for deriving multi-soliton solutions for the ND-NLS equation (1.4) but also can reveal the novel spectral structure of the corresponding equation. Therefore, our findings expand the understanding of the spectral structure of the ND-NLS equation (1.4). We hope that this method can be applied to other nonlocal integrable systems in the future. In addition, it is known that once the RH problem is formulated, the Cauchy problem and the initial-boundary value problem as well as the long time behaviors can be discussed using the nonlinear steepest descent method [38, 39]. More recently, based on the RH approach, the nonlinear steepest descent method was also extended to study soliton equations associated with the \(3\times 3\) matrix spectral problems [40, 41]. Naturally, we hope that the nonlinear steepest descent method can also be applied to Eq. (1.4) and other nonlocal integrable systems in the future.