Integrability and gauge equivalence of the reverse space–time nonlocal Sasa–Satsuma equation

Abstract

The integrability of the reverse space–time nonlocal Sasa–Satsuma equation in the Liouville sense is established by showing the existence of infinitely many conservation laws and putting into a bi-Hamiltonian form. Further, we show that the nonlocal Sasa–Satsuma equation for focusing case and defocusing case is, respectively, gauge equivalent to a generalized Heisenberg-like equation and a modified generalized Heisenberg-like equation. Finally, by using of special variable transformations, various kinds of nonlinear waves are obtained from those of the classical counterpart.

1 Introduction

Nonlinear Schrödinger (NLS) equation and its various generalized versions (continuous and discrete) have been playing an important role in describing various physical phenomena [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. In the literature [3], Sasa and Satsuma proposed the following higher-order extension of the NLS equation

$$\begin{aligned}&iQ_{T}+\frac{\varepsilon }{2}Q_{XX}+|Q|^2Q \nonumber \\&\quad +\,i ( Q_{XXX}+6 \varepsilon |Q|^2 Q_X+3 \varepsilon Q |Q|^2_X )=0, \end{aligned}$$

(1.1)

where $Q=Q(X,T)$ is a complex valued function of the real variables X and T, $\varepsilon =\mp \,1$ and subscript denotes the partial derivative with respect to the corresponding variables. Taking the transformations [24]

$$\begin{aligned} u(x,t)= & {} Q(X,T) \hbox {e}^{-i\frac{\varepsilon }{6} \big (X-\frac{T}{18}\big )}, \nonumber \\ t= & {} T, \qquad x=X-\frac{T}{12}, \end{aligned}$$

(1.2)

Eq. (1.1) is reduced to

$$\begin{aligned}&u_{t}(x,t)+u_{xxx}(x,t)+6 \varepsilon |u(x,t)|^2 u_x(x,t)\nonumber \\&\quad +\,3 \varepsilon u(x,t) |u(x,t)|^2_x=0. \end{aligned}$$

(1.3)

This system, referred as Sasa–Satsuma (SS) equation, has many important physical applications, such as dynamics of deep water waves [16, 17], pulse propagation in optical fibers [18, 19], and generally in dispersive nonlinear media [20]. Besides, many other achievements have been made for the model including the conserved quantities, the Hamiltonian structure, the inverse scattering transformation, the Darboux transformation, the Hirota bilinear representation and various kinds of solutions [21,22,23,24,25,26].

Very recently, investigations about the corresponding integrable nonlocal model have grown tremendously [27,28,29,30,31,32,33,34,35,36,37]. The physical application of these models can be found in various wave mixing phenomena under appropriate ${\mathcal {P}}{\mathcal {T}}$ symmetric settings. This work is concerned the reverse space–time nonlocal SS equation

$$\begin{aligned}&u_{t}(x,t)+u_{xxx}(x,t)+6 \sigma {\bar{u}}(-x,-t) u(x,t) u_x(x,t)\nonumber \\&\quad +\,3\sigma u(x,t) [ {\bar{u}}(-x,-t) u(x,t)]_x=0. \end{aligned}$$

(1.4)

Here and below, the bar refers to the complex conjugate, and coefficient $\sigma$ defines the sign of the nonlinearity. It should be mentioned that the nonlinearities are nonlocal in case of optical beams in nonlinear dielectric waveguides or waveguide arrays with random variation of refractive index, size, or waveguide spacing [36]. In addition, the Lax pair for the nonlocal SS equation as well as its binary Darboux transformation were found in Ref. [31]. However, to the best of our knowledge, some important integrable properties of the nonlocal model including infinite number of conservation laws and bi-Hamiltonian structure have not been reported. It is known that the gauge equivalence of the nonlocal NLS equation with a Heisenberg-like equation and discrete version, as well as the SS equation related to the generalized Landau Lifshitz equation were described in Refs. [22, 38,39,40]. It is, therefore, natural to ask what is the gauge equivalent equation of the nonlocal SS equation. We further, from a different point of view, find different types of nonlinear waves of the nonlocal equation from those of the classical SS equation by making use of special variable transformations.

The rest of the paper is organized as follows. In Sects. 2 and 3, we report the derivation of an infinite number of conservation laws and bi-Hamiltonian structure for the nonlocal SS equation. In Sect. 4, the relation between nonlocal SS equation and a generalized Heisenberg-like equation is established with the explicit construction of the equivalent Lax pair. Finally, in Sect. 5 we study some different types of nonlinear waves of the nonlocal SS equation by special variable transformations.

2 Conservation laws

The existence of infinite number of conservation laws is an important indicator for the complete integrability. The Lax pair for Eq. (1.4) is given by [31]

$$\begin{aligned} \varphi _x=M \varphi ,\quad \varphi _t=N \varphi , \end{aligned}$$

(2.1)

where

$$\begin{aligned} M&=-\,i\lambda J+U,\\ N&=-\,4i\lambda ^3 J+4 \lambda ^2 U-2i\lambda J(U^2-U_x)\\&\qquad +U_x U -U U_x-U_{xx}+2 U^3, \end{aligned}$$

with

$$\begin{aligned} J&=\left( \begin{array}{ccc} 1 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 1 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad -\,1 \\ \end{array}\right) ,\nonumber \\ U&=\left( \begin{array}{ccc} 0 &{} \quad 0 &{} \quad u(x,t) \\ 0 &{} \quad 0 &{} \quad \sigma {\bar{u}}(-x,-t) \\ -\sigma {\bar{u}}(-x,-t) &{} \quad -u(x,t) &{} \quad 0 \\ \end{array}\right) . \end{aligned}$$

Here $\varphi =(\varphi _{1}(x,t,\lambda ),\varphi _{2}(x,t,\lambda ),\varphi _{3}(x,t,\lambda ))^T$ is a vector eigenfunction and $\lambda$ is a complex spectral parameter. The zero curvature condition $M_t-N_x+[M,N]=0$ can yield Eq. (1.4).

By means of the Lax representation, we can derive infinitely many conservation laws for the nonlocal SS equation. Introducing the variables

$$\begin{aligned} \omega _2=\frac{\varphi _{2}(x,t,\lambda )}{\varphi _{3}(x,t,\lambda )}, \qquad \omega _3=\frac{\varphi _{1}(x,t,\lambda )}{\varphi _{3}(x,t,\lambda )}, \end{aligned}$$

(2.3)

the first equation of spectral problem (2.1) is written as a set of coupled Riccati equations

$$\begin{aligned} \omega _{2,x}= & {} \sigma {\bar{u}}(-x,-t) -2 i \lambda \omega _2+u(x,t) \omega ^2_{2} \nonumber \\&+\,\sigma {\bar{u}}(-x,-t) \omega _{2} \omega _{3}, \end{aligned}$$

(2.4a)

$$\begin{aligned} \omega _{3,x}= & {} u(x,t) -2 i \lambda \omega _3+u(x,t) \omega _{2}\omega _{3} \nonumber \\&+\sigma {\bar{u}}(-x,-t) \omega ^2_{3}. \end{aligned}$$

(2.4b)

Next, we expand $\omega _{j}$ as series,

$$\begin{aligned} \omega _{j}=\sum ^{\infty }_{k=1} \chi ^{(k)}_j (2 i \lambda )^{-\,k}, \quad j=2,3. \end{aligned}$$

(2.5)

By substituting (2.5) into (2.4) and comparing the coefficients of $\lambda$, we raise

$$\begin{aligned}&\chi ^{(1)}_2=\sigma {\bar{u}}(-x,-t), \qquad \chi ^{(1)}_3= u(x,t),\\&\chi ^{(2)}_2=-\sigma \frac{\partial }{\partial x} {\bar{u}}(-x,-t), \qquad \chi ^{(2)}_3= -\frac{\partial }{\partial x} u(x,t), \\&\chi ^{(3)}_2=\sigma \frac{\partial ^2 }{\partial x^2} {\bar{u}}(-x,-t)+2 u(x,t) [{\bar{u}}(-x,-t)]^2,\\&\chi ^{(3)}_3= \frac{\partial ^2 }{\partial x^2} u(x,t)+2 \sigma {\bar{u}}(-x,-t) [u(x,t)]^2, \end{aligned}$$

and the recursion formulas

$$\begin{aligned} \chi ^{(k+1)}_2&=-\frac{\partial }{\partial x} \chi ^{(k)}_2+u(x,t)\sum ^{k-1}_{j=1}\chi ^{(j)}_2 \chi ^{(k-j)}_2 \\&\quad +\,\sigma {\bar{u}}(-x,-t)\sum ^{k-1}_{j=1}\chi ^{(j)}_2 \chi ^{(k-j)}_3,\\ \chi ^{(k+1)}_3&=-\frac{\partial }{\partial x} \chi ^{(k)}_3+u(x,t)\sum ^{k-1}_{j=1}\chi ^{(j)}_2 \chi ^{(k-j)}_3\\&\quad +\,\sigma {\bar{u}}(-x,-t)\sum ^{k-1}_{j=1}\chi ^{(j)}_3 \chi ^{(k-j)}_3. \end{aligned}$$

On the other hand, it is easy to see that $[\ln \varphi _{3}(x,t,\lambda )]_{xt}=[\ln \varphi _{3}(x,t,\lambda )]_{tx}$, which implies

$$\begin{aligned} \frac{\partial }{\partial t}\rho = \frac{\partial }{\partial x} \mathcal {J}, \end{aligned}$$

(2.6)

where

$$\begin{aligned} \rho&= u(x,t) \omega _2+\sigma {\bar{u}}(-x,-t)\omega _3, \\ \mathcal {J}&= [4 \sigma \lambda ^2 {\bar{u}}(-x,-t)- 2 \sigma i \lambda \frac{\partial }{\partial x} {\bar{u}}(-x,-t) \\&\quad - \,\sigma \frac{\partial ^2 }{\partial x^2} {\bar{u}}(-x,-t)-\,4 ({\bar{u}}(-x,-t))^2 u(x,t) ] \omega _3 \\&\quad +\,[4 \lambda ^2 u(x,t)- 2 i \lambda \frac{\partial }{\partial x} u(x,t) - \frac{\partial ^2 }{\partial x^2} u(x,t)\\&\quad -\,4 \sigma (u(x,t))^2 {\bar{u}}(-x,-t) ] \omega _2 \\&\quad +\,4 i \sigma \lambda {\bar{u}}(-x,-t) u(x,t). \end{aligned}$$

Then, we expand $\rho$ and $\mathcal {J}$ as

$$\begin{aligned} \rho =\sum ^{\infty }_{k=1} \rho _k (2 i \lambda )^{-k}, \qquad \mathcal {J}=\sum ^{\infty }_{k=1} \mathcal {J}_k (2 i \lambda )^{-k}, \end{aligned}$$

(2.7)

In comparison with the powers of $\lambda$ on both sides of Eq. (2.6), we obtain an infinite number of conservation laws for the model

$$\begin{aligned} \frac{\partial }{\partial t}\rho _k = \frac{\partial }{\partial x} \mathcal {J}_k, \end{aligned}$$

(2.8)

where

$$\begin{aligned} \rho _1= & {} \sigma u(x,t) {\bar{u}}(-x,-t), \\ \rho _2= & {} \sigma [u(x,t) {\bar{u}}(-x,-t)]_x, \\ \rho _3= & {} \sigma u(x,t) \frac{\partial ^2 }{\partial x^2} {\bar{u}}(-x,-t)+ 4[u(x,t){\bar{u}}(-x,-t)]^2 \\&+\,\sigma {\bar{u}}(-x,-t) \frac{\partial ^2 }{\partial x^2} u(x,t), \\ \rho _k= & {} u(x,t)\chi ^{(k)}_2+\sigma {\bar{u}}(-x,-t)\chi ^{(k)}_3, \quad k=4,5,\ldots , \\ \mathcal {J}_1= & {} \sigma u(x,t) \frac{\partial ^2 }{\partial x^2} {\bar{u}}(-x,-t)\\&+\,\sigma {\bar{u}}(-x,-t) \frac{\partial ^2 }{\partial x^2} u(x,t) \\&+\, 6[u(x,t){\bar{u}}(-x,-t)]^2\\&- \,\sigma \frac{\partial }{\partial x } u(x,t) \frac{\partial }{\partial x } {\bar{u}}(-x,-t), \\ \mathcal {J}_2= & {} \sigma u(x,t) \frac{\partial ^3 }{\partial x^3} {\bar{u}}(-x,-t)\\&+\,\sigma {\bar{u}}(-x,-t) \frac{\partial ^3 }{\partial x^3} u(x,t) \\&+ \,12 u(x,t){\bar{u}}(-x,-t) \frac{\partial }{\partial x } [u(x,t){\bar{u}}(-x,-t)], \\ \mathcal {J}_k= & {} - \sigma {\bar{u}}(-x,-t) \chi ^{(k+2)}_3 \\&-\left[ \sigma \frac{\partial ^2 }{\partial x^2} {\bar{u}}(-x,-t)\right. \\&\left. +\,4 ({\bar{u}}(-x,-t))^2 u(x,t) \right] \chi ^{(k)}_3 \\&- \, u(x,t) \chi ^{(k+2)}_2 - \left[ \frac{\partial ^2 }{\partial x^2} u(x,t)\right. \\&\left. +\,4 \sigma (u(x,t))^2 {\bar{u}}(-x,-t) \right] \chi ^{(k)}_2 \\&-\, \sigma \frac{\partial }{\partial x} {\bar{u}}(-x,-t) \chi ^{(k+1)}_3 - \frac{\partial }{\partial x} u(x,t) \chi ^{(k+1)}_2, \\&k=3,4,5,\ldots \end{aligned}$$

3 Hamiltonian structure

To establish the Hamiltonian structure of the nonlocal SS equation, we introduce a basic Hamiltonian operator

$$\begin{aligned}\Theta _1=\left( \begin{array}{cc} u(x,t) \partial ^{-1}_x u(x,t) &{} \quad -\sigma \partial _x - u(x,t) \partial ^{-1}_x {\bar{u}}(-x,-t) \\ -\sigma \partial _x - {\bar{u}}(-x,-t) \partial ^{-1}_x u(x,t) &{} \quad {\bar{u}}(-x,-t) \partial ^{-1}_x {\bar{u}}(-x,-t) \end{array}\right) ,\end{aligned}$$

and a symplectic structure

$$\begin{aligned}\mathcal {S}=\left( \begin{array}{cc} 0 &{} \quad \partial _x - 8 \sigma u(x,t) \partial ^{-1}_x {\bar{u}}(-x,-t) \\ \partial _x - 8 {\bar{u}}(-x,-t) \partial ^{-1}_x u(x,t) &{} \quad 0 \end{array}\right) .\end{aligned}$$

Then, a hereditary recursion operator $\mathcal {R}=\Theta _1 \mathcal {S}$ that can be written as

$$\begin{aligned}\mathcal {R}=\left( \begin{array}{cc} {\mathfrak {P}}(u(x,t),{\bar{u}}_x(-x,-t)) &{} \quad {\mathfrak {Q}}(u(x,t),{\bar{u}}_x(-x,-t)) \\ {\mathfrak {Q}}({\bar{u}}_x(-x,-t),u(x,t)) &{} \quad {\mathfrak {P}}({\bar{u}}_x(-x,-t), u(x,t)) \end{array}\right) ,\end{aligned}$$

where

$$\begin{aligned} {\mathfrak {Q}}({\mathbf {u}},{\mathbf {v}})= & {} {\mathbf {u}}^2-{\mathbf {u}} \partial ^{-1}_x {\mathbf {u}}_x+8\sigma {\mathbf {u}} \big [\partial ^{-1}_x {\mathbf {u}}^2\big ] \partial ^{-1}_x {\mathbf {v}}\\&- \,8 \sigma {\mathbf {u}} \partial ^{-1}_x [\partial ^{-1}_x {\mathbf {u}}^2] {\mathbf {v}}, \qquad \qquad \qquad \qquad \end{aligned}$$

$$\begin{aligned} {\mathfrak {P}}({\mathbf {u}},{\mathbf {v}})= & {} -\sigma \frac{\partial ^2 }{\partial x^2} -8 {\mathbf {v}}_x \partial ^{-1}_x {\mathbf {u}}-9 {\mathbf {u}} {\mathbf {v}}+{\mathbf {u}} \partial ^{-1}_x {\mathbf {v}}_x \\&- \,8 \sigma {\mathbf {u}} \big [\partial ^{-1}_x {\mathbf {v}}^2\big ] \partial ^{-1}_x {\mathbf {u}}+8\sigma {\mathbf {u}} \partial ^{-1}_x \big [\partial ^{-1}_x {\mathbf {v}}^2\big ] {\mathbf {u}}. \end{aligned}$$

Hence, due to the Magri [41] and Olver [42], the nonlocal SS equation has an infinite hierarchy of compatible Hamiltonian structures $\Theta _j=\mathcal {R}^{j-1} \Theta _1$, $j=2,3,\ldots$. and an infinite hierarchy of commuting symmetries of the form $\mathcal {K}_j=\mathcal {R}^{j-1} \mathcal {K}_1$, $j=2,3,\ldots$ where $\mathcal {K}_1= \sigma ( u_x(x,t),{\bar{u}}_x(-x,-t))^T$. Therefore, the nonlocal SS equation is a bi-Hamiltonian system

$$\begin{aligned} \left( \begin{array}{ccc} u(x, t) \\ {\bar{u}}(-x,-t) \end{array}\right) _t= & {} \Theta _1 \left( \begin{array}{ccc} \frac{\delta }{\delta u(x, t)} \\ \frac{\delta }{\delta {\bar{u}}(-x,-t)} \end{array}\right) H_2 \nonumber \\= & {} \Theta _2 \left( \begin{array}{ccc} \frac{\delta }{\delta u(x, t)} \\ \frac{\delta }{\delta {\bar{u}}(-x,-t)} \end{array}\right) H_1, \end{aligned}$$

(3.1)

where the Hamiltonian functions are

$$\begin{aligned} H_1= & {} -\int ^{+ \infty }_{-\infty } u(x,t) {\bar{u}}(-x,-t) \hbox {d}x, \qquad \qquad \qquad \qquad \qquad \end{aligned}$$

(3.2)

$$\begin{aligned} H_2= & {} \int ^{+ \infty }_{-\infty } 2 u^2(x,t) {\bar{u}}^2(-x,-t) \nonumber \\&-\,\sigma u_x(x,t){\bar{u}}_x(-x,-t) \hbox {d}x. \end{aligned}$$

(3.3)

Here $\frac{\delta }{\delta {\mathbf {u}}}$ denotes variational derivative with respect to ${\mathbf {u}}$.

4 Gauge equivalent system

In this section, we show that the nonlocal focusing ($\sigma =1$) SS equation and the nonlocal defocusing ($\sigma =-\,1$) SS equation are gauge equivalent to a generalized Heisenberg-like equation and a modified generalized Heisenberg-like equation, respectively.

We first make the following gauge transformation

$$\begin{aligned} {\tilde{\varphi }}= & {} G^{-1}\varphi ,\quad {\tilde{M}}=G^{-1}M G-G^{-1}G_{x}, \nonumber \\ {\tilde{N}}= & {} G^{-1}N G-G^{-1}G_{t}, \end{aligned}$$

(4.1a)

where G is a solution of system (2.1) for $\lambda =0$, i.e.,

$$\begin{aligned} G_{x}=M(0)G, \quad G_{t}=N(0)G. \end{aligned}$$

(4.1b)

For the focusing case, we obtain

$$\begin{aligned}&{\tilde{M}}=-\,i\lambda G^{-1}J G \triangleq -\,i\lambda S, \end{aligned}$$

(4.2a)

$$\begin{aligned}&{\tilde{N}}=-\,4i\lambda ^3S+2\lambda ^2 SS_x+i\lambda \left( S_{xx}+\frac{3}{2}SS_x^2\right) , \end{aligned}$$

(4.2b)

in which we have used the following important identities

$$\begin{aligned}&SS_x=2G^{-1}UG, \quad SS_x^2=-\,4G^{-1}JU^2G,\\&S_{xx}+SS_x^2=2G^{-1}JU_xG. \end{aligned}$$

The integrability condition ${\tilde{M}}_t-{\tilde{N}}_x+[{\tilde{M}},{\tilde{N}}]=0$ for new linear equation

$$\begin{aligned} {\tilde{\varphi }}_x={\tilde{M}} {\tilde{\varphi }},\quad {\tilde{\varphi }}_t={\tilde{N}} {\tilde{\varphi }}, \end{aligned}$$

(4.3)

yields a generalized integrable Heisenberg-like equation

$$\begin{aligned} S_t+S_{xxx}+\frac{3}{2}\left( S_x^3+SS_{xx}S_{x}+SS_{x}S_{xx}\right) =0. \end{aligned}$$

(4.4)

For the defocusing case, setting $S=-iG^{-\,1}J G$, from gauge transformation (4.1), we have

$$\begin{aligned}&{\tilde{M}}=\lambda S, \end{aligned}$$

(4.5a)

$$\begin{aligned}&{\tilde{N}}=4\lambda ^3S-2\lambda ^2 SS_x+\lambda \left( \frac{3}{2}SS_x^2-S_{xx}\right) , \end{aligned}$$

(4.5b)

where the following three important identities have been used

$$\begin{aligned}&SS_x=-\,2G^{-1}UG, \quad SS_x^2=-\,4iG^{-1}\sigma _3U^2G,\\&S_{xx}-SS_x^2=-\,2iG^{-\,1}\sigma _3U_xG. \end{aligned}$$

The zero curvature condition of (4.5) leads to a modified generalized integrable Heisenberg-like equation

$$\begin{aligned} S_t+S_{xxx}-\frac{3}{2}\left( S_x^3+SS_{xx}S_{x}+SS_{x}S_{xx}\right) =0. \end{aligned}$$

(4.6)

Fig. 1

a Evolution plot of the module of solution (5.2); b evolution plot of the module of solution (5.3); c evolution plot of $\text {Re}(u(x,t){\bar{u}}(-x,-t))$ of (5.3); d evolution plot of $\text {Im}(u(x,t){\bar{u}}(-x,-t))$ of (5.3). a Focusing SS. b Nonlocal defocusing SS

5 Different types of nonlinear waves

In this section, we construct analytical solutions of the nonlocal SS equation from those of the classical SS equation through some special variable transformations. Dynamical properties of the analytical solutions present the structural diversity of the nonlinear waves. Notice that nonlocal SS equation (1.4) can be converted to classical SS equation (1.3) by introducing the variable transformations [43]

$$\begin{aligned} x=i {\hat{x}},\quad t=-i {\hat{t}},\quad u(x,t)\triangleq {\hat{u}}({\hat{x}},{\hat{t}}), \end{aligned}$$

(5.1)

but with the opposite sign of nonlinearity. We have omitted the symbol  $\hat{}$  for the SS equation. It means that x and t in nonlocal SS equation are treated as real variables when taking complex conjugate of ${\bar{u}}(-x,-t)$, however, the transformations, $x=i {\hat{x}},~ t=-i {\hat{t}}$ with real ${\hat{x}}, {\hat{t}}$, change sign of x, t, which convert the nonlocal term ${\bar{u}}(-x,-t)$ of (1.4) to the local term $\bar{{\hat{u}}}({\hat{x}},{\hat{t}})$ of (1.3).

Fig. 2

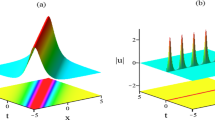
a Double-hump soliton solution of the focusing SS equation; b module $|u(x,t)|^2$ of solution (5.5) to nonlocal defocusing SS equation; c, d $\text {Re}(u(x,t){\bar{u}}(-x,-t))$ and $\text {Im}(u(x,t){\bar{u}}(-x,-t))$ with periods $T_\mathrm{space}=\frac{\pi }{2\eta }$ and $T_\mathrm{time}=\frac{\pi }{8(\eta ^2-3\xi ^2)}$, respectively. Parameters $\xi =1/4,\eta =1$

5.1 Nonlinear waves of nonlocal defocusing SS equation

Case 1 (periodic wave) Choosing the one-soliton solution of the classical focusing ($\varepsilon =1$) SS equation [3]

$$\begin{aligned} \begin{aligned}&u(x,t)= \hbox {e}^{ia(x+(a^2-3c^2)t+w)}\frac{2c\hbox {e}^{\eta }(\hbox {e}^{2\eta }+k)}{\hbox {e}^{4\eta }+2\hbox {e}^{2\eta }+|k|^2},\\&k=\frac{a}{a+i c},\quad \eta =c(x+(3a^2-c^2)t+\delta ), \end{aligned}\end{aligned}$$

(5.2)

and using the reverse of transformations (5.1), i.e., ${\hat{x}}=-ix, {\hat{t}}=it$, we get the solution of the nonlocal defocusing ($\sigma =-1$) SS equation

$$\begin{aligned} \begin{aligned}&u(x,t)= \hbox {e}^{a(x-(a^2-3c^2)t+iw)}\frac{2c\hbox {e}^{\eta _1}(\hbox {e}^{2\eta _1+k})}{\hbox {e}^{4\eta _1}+2\hbox {e}^{2\eta _1}+|k|^2},\\&k=\frac{a}{a+i c},\quad \eta _1=c(-ix+(3a^2-c^2)it+\delta ). \end{aligned}\end{aligned}$$

(5.3)

The dynamics for $|u(x,t)|^2$, $\text {Re}(u(x,t){\bar{u}}(-x,-t))$ and $\text {Im}(u(x,t){\bar{u}}(-x,-t))$ are illustrated in Fig. 1, where parameters are taken as $a=1,c=1,w=1/2,\delta =1$. We can see that $\text {Re}(u(x,t){\bar{u}}(-x,-t))$ and $\text {Im}(u(x,t){\bar{u}}(-x,-t))$ are periodic in both space and time with periods $T_\mathrm{space}=\frac{\pi }{c}$ and $T_\mathrm{time}=\frac{\pi }{c(3a^2-c^2)}$, respectively.

Fig. 3

a Breather solution of the focusing SS equation; b, c singular solution of the nonlocal defocusing SS equation; d Density plot of breather soliton of the focusing SS equation; e and f are density plot of b and c, respectively. Parameters $\xi =1/2,\eta =1/2$

Case 2 For the double-hump soliton solution of the classical focusing SS equation [24]

$$\begin{aligned}&u(x,t)=\frac{4\eta \hbox {e}^{-2i(\xi +i\eta )(x-4(\eta -i\xi )^2t)}(\xi (\xi {+}i\eta ) {+}(\xi ^2{+}\eta ^2)\hbox {e}^{\beta })}{\xi ^2{+}2(\xi ^2{+}\eta ^2)\hbox {e}^{\beta }{+}(\xi ^2{+}\eta ^2)\hbox {e}^{2\beta }},\nonumber \\&\beta =4\eta (x-4t(\eta ^2-3\xi ^2)), \end{aligned}$$

(5.4)

where $\xi ,\eta \in R$ and $|\xi |<|\eta |$, the reverse of transformations (5.1) yields the following solution of the nonlocal defocusing SS equation

$$\begin{aligned}&u(x,t)=\frac{4\eta \hbox {e}^{-2(\xi +i\eta )(x+4(\eta -i\xi )^2t)}(\xi (\xi +i\eta ) +(\xi ^2{+}\eta ^2)\hbox {e}^{\beta _1})}{\xi ^2{+}2(\xi ^2{+}\eta ^2)\hbox {e}^{\beta _1}{+}(\xi ^2{+}\eta ^2)\hbox {e}^{2\beta _1}},\nonumber \\&\beta _1=4\eta (-ix-4it(\eta ^2-3\xi ^2)). \end{aligned}$$

(5.5)

This solution is displayed in Fig. 2 when $\xi =1/4,\eta =1$. The module of solution (5.5) grows exponentially, but $\text {Re}(u(x,t){\bar{u}}(-x,-t))$ and $\text {Im}(u(x,t){\bar{u}}(-x,-t))$ are still periodic in both space and time with periods $T_\mathrm{space}=\frac{\pi }{2\eta }$ and $T_\mathrm{time}=\frac{\pi }{8(\eta ^2-3\xi ^2)}$, respectively.

Case 3 For the breather solution of the classical focusing SS equation [24], setting

$$\begin{aligned}&\alpha =(x+4(\eta +i\xi )^2t)(\eta +i\xi ),\nonumber \\&\beta =-x+4(\xi ^2-3\eta ^2)t,\quad \gamma =x+4(\eta ^2-3\xi ^2)t,\nonumber \\ \end{aligned}$$

(5.6)

and employing the reverse of transformations (5.1), we obtain a singular solution for the nonlocal defocusing SS equation

$$\begin{aligned} \begin{aligned} u(x,t)=8\eta \hbox {e}^{-2i\alpha }\frac{2(\xi +i\eta )(5\xi -3i\eta )+(\xi -i\eta )(5\xi -3i\eta )\hbox {e}^{4\beta \xi }+8\xi (\xi -i\eta )\hbox {e}^{-\,4i\gamma \eta }+4\xi (\xi +i\eta )\hbox {e}^{4i\alpha }}{(9\eta ^2+41\xi ^2)\cos (4\gamma \eta )-32\eta ^2\cosh (4\beta \xi )+(\eta ^2+\xi ^2)(40-9i\sin (4\gamma \eta ))}. \end{aligned} \end{aligned}$$

(5.7)

The singular point (x, t) satisfies

$$\begin{aligned} \begin{aligned}&2\eta (x+4(\eta ^2-3\xi ^2)t)=k\pi , \\&\quad 81\xi ^2+49\eta ^2=32\eta ^2 \cosh (4\xi (-x+4(\xi ^2-3\eta ^2)t)). \end{aligned}\end{aligned}$$

(5.8)

This solution is displayed in Fig. 3 with $\xi =1/2,\eta =1/2$.

Case 4 (W-type and dark soliton solution) The classical focusing SS equation admits the following periodic solution

$$\begin{aligned} \begin{aligned} u(x,t)=-\rho +\frac{2(\lambda ^2-2)\rho ^3}{-2\rho ^2-\lambda \tau \cos (2 \tau x-2 m t)+\lambda ^2\sin (2 \tau x-2 m t)}, \end{aligned} \end{aligned}$$

(5.9)

where $\tau =\sqrt{2\rho ^2-\lambda ^2},m=4\tau (\rho ^2+\lambda ^2),\lambda ,\rho \in R$ and $2|\rho |>|\lambda |$. Using the reverse of transformations (5.1), we yield a W-type solution of the nonlocal defocusing SS equation

$$\begin{aligned} \begin{aligned} u(x,t)=-\rho -\frac{2(\lambda ^2-2)\rho ^3}{2\rho ^2+\lambda \tau \cosh (2 \tau x+2 m t)+i \lambda ^2\sinh (2 \tau x+2 m t)}. \end{aligned}\end{aligned}$$

(5.10)

When $\lambda =1/2,\rho =1$, the dynamical profile of solution (5.10) is displayed in Fig. 4. If we choose $\lambda =1,\rho =1$, dark soliton solution can be obtained, which is depicted in Fig. 5.

Fig. 4

a Periodic soliton solution of the focusing SS equation; b–d W-type solution of nonlocal defocusing SS equation. Parameters $\lambda =1/2,\rho =1$

Fig. 5

a–c Dark soliton solution of nonlocal defocusing SS equation with $\lambda =1,\rho =1$

Fig. 6

a Breather solution (5.11) of the nonlocal defocusing SS equation with $\rho =1,\lambda =1$; b semi-periodical solution (5.13) of the focusing SS equation; c $x=1$. a Nonlocal defocusing SS. b Focusing SS. c Focusing SS

Fig. 7

Periodic solution (5.14) of the nonlocal focusing SS equation with $a=2,b=2,c=1,\xi =1/2$. a Defocusing SS. b Nonlocal focusing SS

Here we remark that, by choosing proper parameters, W-type (or M-type) and dark soliton solutions of nonlocal defocusing SS equation can also be derived from the periodic solution of the focusing SS equation under the variable transformations. These solutions have been obtained by Darboux transformation in [31].

On the other hand, one can check that the solution of nonlocal SS equation can also be converted into those of classical SS equation by means of transformations (5.1). For example, the breather solution of the nonlocal defocusing SS equation is given by [31]

$$\begin{aligned} \begin{aligned} u(x,t)=\rho \left( 1-\frac{\lambda \hbox {e}^{i\lambda \xi }(\lambda +i\tau +(\lambda -i\tau ) \hbox {e}^{2\eta })\left( 2i\tau \hbox {e}^\eta +(\lambda ^2+\tau ^2)(1+\hbox {e}^{2\eta })\hbox {e}^{i\lambda \xi }\right) }{\tau ^2\hbox {e}^{2\eta }+\rho ^2\hbox {e}^{2i\lambda \xi }\left( \lambda (\lambda +i\tau +(\lambda -i\tau ) \hbox {e}^{4\eta })+4\rho ^2\hbox {e}^{2\eta }\right) }\right) , \end{aligned}\end{aligned}$$

(5.11)

where $\xi =x+4\lambda ^2t, \eta =\tau x+mt,\tau =\sqrt{2\rho ^2-\lambda ^2},m=4\tau (\rho ^2+\lambda ^2)$. Under the transformation

$$\begin{aligned} x\rightarrow i x,\quad t=-i t, \end{aligned}$$

(5.12)

we arrive to a semi-periodical solution of the focusing SS equation

$$\begin{aligned} \begin{aligned} u(x,t)=\rho \left( 1-\frac{\lambda \hbox {e}^{-\lambda \xi _1}(\lambda +i\tau +(\lambda -i\tau ) \hbox {e}^{2i\eta _1})\left( 2i\tau \hbox {e}^{i\eta _1}+(\lambda ^2+\tau ^2)(1+\hbox {e}^{2i\eta _1})\hbox {e}^{-\lambda \xi _1}\right) }{\tau ^2\hbox {e}^{2i\eta _1}+\rho ^2\hbox {e}^{-2\lambda \xi _1}\left( \lambda (\lambda +i\tau +(\lambda -i\tau ) \hbox {e}^{4i\eta _1})+4\rho ^2\hbox {e}^{2i\eta _1}\right) }\right) , \end{aligned}\end{aligned}$$

(5.13)

where $\xi _1=x-4\lambda ^2t, \eta _1=\tau x-mt$. The dynamics of the solution is displayed in Fig. 6b. We can see that the expression of (5.13) tends to a constant $\rho$ as $t\rightarrow -\infty$, but to quasi-periodic oscillation as $t\rightarrow +\infty$.

5.2 Periodic wave solution of nonlocal focusing SS equation

For the dark one-soliton solution of the defocusing ($\varepsilon =-\,1$) SS equation [25], under the reverse of transformations (5.1), i.e., ${\hat{x}}=-ix, {\hat{t}}=it$, we derive a periodic wave solution of the nonlocal focusing SS equation

$$\begin{aligned} u(x,t)= & {} c(\tanh \phi -i B \mathrm{sech}\phi ),\quad B=\sqrt{\frac{2\xi }{\xi +\mu }}\nonumber \\ \phi= & {} -i(\mu -\xi )x-4i((\xi ^2-c^2)\mu -\xi ^3)t\nonumber \\&+\frac{1}{2}\ln \frac{2b^2{+}\mu ^2}{a^2\xi (\xi {+}\mu )},\quad \mu \,{=}\,\sqrt{\xi ^2{+}2c^2}. \end{aligned}$$

(5.14)

We thus see that the solution is periodic in both space and time with periods $T_\mathrm{space}=\frac{\pi }{\mu -\xi }$ and $T_\mathrm{time}=\frac{\pi }{4(\xi ^3+(c^2-\xi ^2)\mu )}$. The dynamics of the solution is shown in Fig. 7 as $a=2,b=2,c=1,\xi =1/2$.

In short, some other kinds of solutions for the nonlocal focusing or defocusing SS equations can be studied through the transformation based on corresponding solutions of defocusing or focusing SS equation, respectively. The symbols x and t should be regarded as imaginary variables under the transformation of (5.1), but real variables within the scope of the nonlocal system. This provides an effective tool in search for explicit solutions of nonlocal systems.

6 Conclusion

In this paper, we have investigated the integrability of the reverse space–time Sasa–Satsuma equation in the Liouville sense including the infinite many conservation laws and bi-Hamiltonian form. We have also shown that, under the gauge transformations, the nonlocal Sasa–Satsuma equation for focusing case and defocusing case are, respectively, gauge equivalent to a generalized Heisenberg-like equation and a modified generalized Heisenberg-like equation. By using of special variable transformations, various kinds of explicit solutions of the reverse space–time Sasa–Satsuma equation are derived from those of the classical counterpart.