1 Introduction

It is well-known that the following coupled system of nonlinear evolution equations with two potential functions \(q=q(x,t),r=r(x,t)\),

$$\begin{aligned}{} & {} { i}q_t(x,t)=q_{xx}(x,t)-2q^2(x,t)r(x,t), \end{aligned}$$
(1.1a)
$$\begin{aligned}{} & {} -{i}r_t(x,t)=r_{xx}(x,t)-2r^2(x,t)q(x,t), \end{aligned}$$
(1.1b)

comes as a compatibility condition of the celebrated Ablowitz–Kaup–Newell–Segur (AKNS) spectral problem [1]. Therefore, the coupled system (1.1) is usually referred to as the AKNS “\((q,r)\ \textrm{system}\)” in the literature. Also is known that the physically and mathematically significant nonlinear Schrödinger (NLS) equation [2]:

$$\begin{aligned} {i} q_{t}(x,t)=q_{xx}(x,t)-2\varepsilon q^2(x,t) q^*(x,t),\quad \varepsilon ={\mp } 1,\nonumber \\ \end{aligned}$$
(1.2)

is a symmetry reduction of the AKNS “\((q,r)\ \textrm{system}\)” (1.1). In fact, if \(r=\varepsilon q^*\), the AKNS “\((q,r)\ \textrm{system}\)” (1.1) exactly reduces to the NLS Eq. (1.2). In (1.2), q(x, t) represents a complex-valued function of x, t, the symbol i denotes the imaginary unit, and the asterisk \(*\) is the complex conjugation. The NLS Eq. (1.2) appears in many physical contexts, such as nonlinear fiber optics, plasma physics, magneto-static spin waves, deep water waves, and others. Mathematically, the NLS Eq. (1.2) is known to be integrable by the inverse scattering transform (IST) from which soliton solutions can be found. In addition, other integrability properties, such as infinite number of conserved quantities, the Hamiltonian structure, and so on, have also been discovered for (1.2). We also note that the cases \(\varepsilon =\mp 1\) in the NLS Eq. (1.2) represent the focusing and the defocusing nonlinearities, respectively. The defocusing case of (1.2), compared with its focusing counterpart, does not admit soliton solutions that vanish at infinity. In fact, the defocusing NLS equation, i.e., (1.2) with \(\varepsilon =1\), admits soliton solutions which have the nontrivial background intensity.

In 2013, an integrable nonlocal type soliton equation [3]:

$$\begin{aligned} { i} q_{t}(x,t)=q_{xx}(x,t)-2\varepsilon q^2(x,t) q^*(-x,t),\quad \varepsilon =\mp 1,\nonumber \\ \end{aligned}$$
(1.3)

was proposed and studied by Ablowitz and Musslimani via imposing a novel nonlocal symmetry reduction \(r(x,t)=\varepsilon q^*(-x,t)\) in the AKNS “\((q,r)\ \textrm{system}\)” (1.1). This is rather surprising since many researchers generally believe that it is not easy to obtain intrinsically new integrable systems in soliton theory. Via the nonlocal NLS Eq. (1.3), the solution states at positions x and \(-x\) are directly coupled, which is reminiscent of quantum entanglement between pairs of particles in quantum mechanics. It has been shown that as a nonlocal reduction of the AKNS “\((q,r)\ \textrm{system}\)” (1.1), the nonlocal NLS Eq. (1.3) still admits Lax pair formulation, has an infinite number of conservation laws. It is also easy to check that the nonlocal NLS Eq. (1.3) is invariant under the parity-time transformation: \(x\rightarrow -x,t\rightarrow -t\) as well as complex conjugation. In this sense, the nonlocal NLS Eq. (1.3) is said to be parity-time (\({\mathcal{P}\mathcal{T}}\)) symmetric which is a hot topic in modern physics [4]. Significantly, the nonlocal NLS Eq. (1.3) can also be viewed as asymptotic quasi-momochromatic reductions of some other nonlinear evolution systems [5]. Moreover, the relations between the nonlocal NLS Eq. (1.3) and other physically important equations were established in [6, 7]. In the literature, many classical tools for local soliton equations have been extended to the nonlocal NLS Eq. (1.3), such as the IST, the Riemann–Hilbert (RH) approach, the Darboux transformation, the Hirota bilinear method, and others [8,9,10,11,12,13,14]. Nowadays, the study of nonlocal type soliton equations has become a hot research direction and has attracted considerable interests in integrable theory [15,16,17,18,19,20,21].

What is more interesting is that, after the discovery of the nonlocal NLS Eq. (1.3), Ablowitz and Musslimani subsequently in 2021 further introduced the shifted versions of the nonlocal NLS Eq. (1.3) [22], which are now referred to as the focusing shifted nonlocal NLS equation:

$$\begin{aligned} {i}q_{t}(x,t)=q_{xx}(x,t)+2 q^2(x,t) q^*(x_0-x,t), \end{aligned}$$
(1.4)

and the defocusing shifted nonlocal NLS equation:

$$\begin{aligned} { i}q_{t}(x,t)=q_{xx}(x,t)-2 q^2(x,t) q^*(x_0-x,t), \end{aligned}$$
(1.5)

by imposing the shifted nonlocal symmetry reductions \(r(x,t)=- q^*(x_0-x,t)\) and \(r(x,t)= q^*(x_0-x,t)\), respectively, in the AKNS “\((q,r)\ \textrm{system}\)” (1.1). In Eqs. (1.4)–(1.5), \(x_0\) is an arbitrary real parameter denoting the space shift. Obviously, when \(x_0\) is set to be zero, Eqs. (1.4)–(1.5) will reduce back to their corresponding standard unshifted nonlocal NLS Eq. (1.3). Regarding the focusing shifted nonlocal NLS Eq. (1.4), the IST method and single- and two-soliton solutions for it were studied in [22]. Subsequently, three types of Darboux transformations and general soliton solutions for (1.4) were presented in [23]. In addition, several reduction techniques for (1.4) based on Hirota bilinear formulation and RH approach were studied in [24,25,26]. Very recently, multiple double-pole solitons and multiple negaton-type solitons were derived for (1.4) via a long-wave technique [27]. However, to our knowledge, there are rare results about the defocusing shifted nonlocal NLS Eq. (1.5) apart from the reduction techniques investigated by using the bilinear approach in [24, 25].

In this paper, we shall focus on the defocusing shifted nonlocal NLS Eq. (1.5) in the framework of RH approach. It is known that the RH approach is a modern version of IST for integrable soliton equations. Though the IST method in the perspective of RH problem for the focusing shifted NLS Eq. (1.4) was revealed in [22], whether the RH approach applies to the defocusing shifted NLS Eq. (1.5) was still an open problem. Moreover, it has been shown that the focusing and the defocusing cases of the unshifted nonlocal NLS Eq. (1.3) share different spectral structures, and thus their RH approaches differ from each other [28]. Hence we are motivated that the defocusing shifted nonlocal NLS Eq. (1.5) with general \(x_0\) might have diverse spectral structures compared with its focusing counterpart (1.4). In turn, their soliton solutions might also be different. This paper will focus on these aspects.

This paper is organized as follows. In Sect. 2, we shall perform spectral analysis of the Lax pair of the defocusing shifted nonlocal NLS Eq. (1.5). Particularly, we explore in detail the spectral structure of the defocusing shifted nonlocal NLS Eq. (1.5). It will be shown that the zeros of the RH problem of the defocusing shifted nonlocal NLS Eq. (1.5) do not allow for purely imaginary ones, which is rather different from that of its focusing counterpart (1.4). Moreover, based on the revealed spectral structure, the even-order soliton solutions of the defocusing shifted nonlocal NLS Eq. (1.5) will be rigorously obtained. In addition, the dynamical properties underlying the obtained soliton solutions will be analyzed and then graphically illustrated by highlighting the role that the space-shifted parameter \(x_0\) plays. Section 3 gives our conclusions.

2 RH approach

In this section, by employing the RH approach [29,30,31,32,33,34,35,36,37,38,39,40,41,42], we intend to perform spectral analysis and then derive soliton solutions for the defocusing shifted nonlocal NLS Eq. (1.5). It is known the RH approach heavily relies on the RH problem constructed via the corresponding Lax pair.

2.1 Lax pair and RH problem

An important property of the AKNS spectral theory is that a reduced version of a Lax-integrable equation is still integrable admitting the corresponding Lax pair formulation. Therefore, we can obtain the Lax pair of the defocusing shifted nonlocal NLS Eq. (1.5) by imposing the defocusing shifted nonlocal symmetry reduction: \(r(x,t)= q^*(x_0-x,t)\) in that of the AKNS “\((q,r)\ \textrm{system}\)” (1.1) [22],

$$\begin{aligned} \Psi _x=\textbf{U}\Psi ,\quad \quad \Psi _t=\textbf{V}\Psi , \end{aligned}$$
(2.1)

in which \(\Psi =\Psi (x,t,\lambda )\) is a matrix function of the complex spectral parameter \(\lambda \), and

$$\begin{aligned}{} & {} \textbf{U}={ i}\lambda \sigma _3+Q, \\{} & {} \textbf{V}=2 { i}\lambda ^2\sigma _3+2\lambda Q+{i} (Q^2+Q_x)\sigma _3, \end{aligned}$$

with

$$\begin{aligned}{} & {} Q=Q(x,t)=\left( \begin{array}{cc} 0&{}q(x,t)\\ q^*(x_0-x,t)&{}0 \end{array}\right) ,\\{} & {} \sigma _3=\left( \begin{array}{cc} 1&{}0\\ 0&{}-1 \end{array}\right) . \end{aligned}$$

Indeed, one can check that the compatibility condition of (2.1), \(\Psi _{xt}=\Psi _{tx}\), yields the zero-curvature equation, \(\textbf{U}_t-\textbf{V}_x+[\textbf{U},\textbf{V}]=\textbf{0}\), which exactly gives the defocusing shifted nonlocal NLS Eq. (1.5). This equation belongs to the shifted nonlocal reverse-space type since the evolution of the field depends on both the values at (x, t) and \((x_0-x,t)\). Based on the Lax pair (2.1), we shall perform spectral analysis and then derive soliton solutions for the defocusing shifted nonlocal NLS Eq. (1.5).

To perform spectral analysis conveniently on the Lax pair (2.1), we first introduce a new matrix spectral function \(J=J(x,t,\lambda )\) defined as

$$\begin{aligned} \Psi =JE,\quad E=\textrm{e}^{{ i}\lambda \sigma _3 x+2{i} \lambda ^2\sigma _3 t}. \end{aligned}$$
(2.2)

Using (2.2), the Lax pair (2.1) can be rewritten in another form

$$\begin{aligned} J_x={ i}\lambda [\sigma _3, J]+QJ,\quad \quad J_t=2{i} \lambda ^2 [\sigma _3, J]+\widetilde{Q}J,\nonumber \\ \end{aligned}$$
(2.3)

where Q is the potential matrix in (2.1), and \(\widetilde{Q}=2\lambda Q+ { i} (Q^2+Q_x)\sigma _3\).

Since the defocusing shifted nonlocal NLS Eq. (1.5) comes as a reduction of the AKNS “\((q,r)\ \textrm{system}\)” (1.1), the procedure for deriving an RH problem for sufficiently decaying potentials is similar as that of the unreduced AKNS “\((q,r)\ \textrm{system}\)” (1.1). In fact, we can establish an RH problem for the defocusing shifted nonlocal NLS Eq. (1.5) as

$$\begin{aligned} \left\{ \begin{array}{ll} P^-(\lambda )P^+(\lambda )\\ \quad = \left( \begin{array}{cc} 1&{}s_{12}(0,\lambda )\textrm{e}^{2{ i}\lambda x+4{ i}\lambda ^2 t}\\ r_{21}(0,\lambda )\textrm{e}^{-2{ i}\lambda x-4{ i}\lambda ^2 t}&{}1 \end{array}\right) , \quad \lambda \in \mathbb {R},\\ P_1(\lambda )\rightarrow {\mathbb {I}}, \quad \ \lambda \in {\mathbb {C}}^+\rightarrow \infty ,\\ P_2(\lambda )\rightarrow {\mathbb {I}}, \quad \ \lambda \in {\mathbb {C}}^-\rightarrow \infty , \end{array}\right. \nonumber \\ \end{aligned}$$
(2.4)

by following the way to arrive at the RH problem for the AKNS “\((q,r)\ \textrm{system}\)” (1.1) [29]. In the RH problem (2.4), \(P^+(\lambda )\) is the limit of an analytic matrix function \(P_1(\lambda )\) from the left-hand side of \(\mathbb {R}\), \(P^-(\lambda )\) is the limit of another analytic matrix function \(P_2(\lambda )\) from the right-hand side of \(\mathbb {R}\), while the symbol \({\mathbb {I}}\) denotes the \(2\times 2\) identity matrix. The asymptotic states in (2.4) are canonical normalization conditions of the RH problem, while \(s_{12}(0,\lambda ),r_{21}(0,\lambda )\) are two reflection coefficients defined on the real \(\lambda \)-axis at the initial states. In fact, the two sectionally analytic matrix functions \(P_1(\lambda )\) and \(P_2(\lambda )\) are constructed as

$$\begin{aligned} P_1=([J_{+}]_1,[J_{-}]_2), \quad \quad P_2=\left( \begin{array}{c} {[J^{-1}_{+}]}^1\\ {[J^{-1}_{-}]}^2 \end{array}\right) , \end{aligned}$$
(2.5)

where each \([J_{\pm }]_l\ (l=1,2)\) denotes the l-th column of the Jost solutions \(J_{\pm }=J_{\pm }(x,t,\lambda )\) of (2.3) satisfying \(J_{\pm }\rightarrow {\mathbb {I}}\) as \(x\rightarrow \pm \infty \), and each \([J_\pm ^{-1}]^l\ (l=1,2)\) represents the l-th row of the matrix inverse \(J_\pm ^{-1}\). In fact, \(J_{\pm }\) are uniquely determined by the Volterra integral equations [29]

$$\begin{aligned}{} & {} J_{+}(x,t,\lambda )\\{} & {} \quad = {\mathbb {I}}-\int ^{+\infty }_x \textrm{e}^{{ i}\lambda \sigma _3(x-\xi )}Q(\xi ,t)J_+ (\xi ,t,\lambda )\textrm{e}^{-{ i}\lambda \sigma _3(x-\xi )}d\xi ,\\{} & {} J_{-}(x,t,\lambda )\\{} & {} \quad = {\mathbb {I}}+\int ^x_{-\infty }\textrm{e}^{{i} \lambda \sigma _3(x-\xi )}Q(\xi ,t)J_-(\xi ,t,\lambda ) \textrm{e}^{-{i}\lambda \sigma _3(x-\xi )}d\xi . \end{aligned}$$

2.2 Scattering data and symmetry relations

In this section, we shall explore the scattering data and the corresponding symmetry relations determined by the Lax pair (2.3). Indeed, these are the core aspects in the RH approach. Generally, we assume the RH problem (2.4) is an irregular one which means that \(\textrm{det}\ P_1\) and \(\textrm{det}\ P_2\) have certain zeros in their analytic domains. Notice that the potential matrix \(Q=Q(x,t)\) in (2.3) satisfies the following symmetry relation

$$\begin{aligned} Q^*(x_0-x,t)=-\sigma ^{-1} Q(x,t)\sigma ,\quad \quad \sigma =\left( \begin{array}{cc} 0&{}1\\ -1&{}0 \end{array}\right) . \end{aligned}$$
(2.6)

Then using the symmetry relation (2.6) and the Lax pair (2.3), we can arrive at the symmetry relations of \(P_1=P_1(x,t,\lambda )\) and \(P_2=P_2(x,t,\lambda )\), respectively

$$\begin{aligned}&P_1^*(x_0-x,t,-\lambda ^*)=\sigma ^{-1} P_1(x,t,\lambda )\sigma ,\quad \quad \lambda \in {\mathbb {C}}^+, \end{aligned}$$
(2.7)
$$\begin{aligned}&P_2^*(x_0-x,t,-\hat{\lambda }^*)=\sigma ^{-1} P_2(x,t,\hat{\lambda })\sigma ,\quad \quad \lambda \in {\mathbb {C}}^-, \end{aligned}$$
(2.8)

which are the key relations for establishing the symmetry relations of the scattering data. In fact, it follows from the symmetry relations (2.7)–(2.8) that the zeros of \(\textrm{det}\ P_1\) and \(\textrm{det}\ P_2\) appear as \((\lambda _l,-\lambda ^*_l)\) and \((\hat{\lambda }_l,-\hat{\lambda }^*_l)\) coupled types, where l is an integer. Correspondingly, we shall consider the kernels Ker \((P_1(\lambda _l))\), Ker \((P_1(-\lambda ^*_l))\), Ker\(\ (P_2(\hat{\lambda }_l))\), Ker \((P_2(-\hat{\lambda }^*_l))\), which are spanned by column vectors \(v_l=v_l(x,t),\nu _l=\nu _l(x,t)\) and row vectors \(\hat{v}_l=\hat{v}_l(x,t),\hat{\nu }_l=\hat{\nu }_l(x,t)\), respectively,

$$\begin{aligned}{} & {} P_1(\lambda _l)v_l=0, \quad \quad \quad \hat{v}_l P_2(\hat{\lambda }_l)=0, \end{aligned}$$
(2.9)
$$\begin{aligned}{} & {} P_1(-\lambda ^*_l)\nu _l=0, \quad \quad \quad \hat{\nu }_lP_2(-\hat{\lambda }^*_l)=0. \end{aligned}$$
(2.10)

Using the Lax pair (2.3), the vectors \(v_l\) and \(\hat{v}_l\) can be readily calculated as

$$\begin{aligned} v_l=\textrm{e}^{\theta _l\sigma _3}v_{l,0}, \quad \quad \quad \hat{v}_l=\hat{v}_{l,0} \textrm{e}^{\hat{\theta }_l\sigma _3}, \end{aligned}$$
(2.11)

in which \(\theta _l=\theta _l(x,t)={i}\lambda _lx+2{ i}\lambda ^2_lt, \hat{\theta }_l=\hat{\theta }_l(x,t)=-{i}\hat{\lambda }_lx-2{i} \hat{\lambda }^2_lt,\) and \(v_{l,0},\hat{v}_{l,0}\) are complex column and row vectors, respectively. Obviously, \(v_{l,0},\hat{v}_{l,0}\) are independent of x, t. However, they rely on the space-shifted parameter \(x_0\). In a parallel way, the vectors \(\nu _l\) and \(\hat{\nu }_l\) can also be obtained from the Lax pair (2.3) as

$$\begin{aligned} \nu _l=\textrm{e}^{\vartheta _l\sigma _3}\nu _{l,0}, \quad \quad \hat{\nu }_l=\hat{\nu }_{l,0} \textrm{e}^{\hat{\vartheta }_l\sigma _3}, \end{aligned}$$
(2.12)

where \(\vartheta _l=\vartheta _l(x,t)={ i}(-\lambda ^*_l)x+2{ i}(-\lambda ^*_l)^2t, \hat{\vartheta }_l=\hat{\vartheta }_l(x,t)=-{ i}(-\hat{\lambda }^*_l)x-2{ i}(-\hat{\lambda }_l^*)^2t,\) and \(\nu _{l,0},\hat{\nu }_{l,0}\) are complex column and row vectors, respectively. Similarly, \(\nu _{l,0},\hat{\nu }_{l,0}\) are independent of x, t, but they depend on the space-shifted parameter \(x_0\). Here we normally scale the second components of all \(v_{l,0},\hat{v}_{l,0},\nu _{l,0},\hat{\nu }_{l,0}\) as 1 without loss of generality, i.e.,

$$\begin{aligned}{} & {} v_{l,0}=(\alpha _l,1)^T,\quad \hat{v}_{l,0}=(\hat{\alpha }_l,1),\\{} & {} \nu _{l,0}=(\beta _l,1)^T,\quad \hat{\nu }_{l,0}=(\hat{\beta }_l,1). \end{aligned}$$

For symmetry relations of \(v_l,\hat{v}_{l},\nu _{l},\hat{\nu }_{l}\), we have from (2.7) that \(\nu ^*_l(x_0-x,t)=C\sigma ^{-1}v_l(x,t)\), and from (2.8) that \(\hat{\nu }^*_l(x_0-x,t)=\hat{C}\hat{v}_l(x,t)\sigma \), where \(C,\hat{C}\) are complex constants independent of \(x,t,x_0\). Therefore, we finally arrive at

$$\begin{aligned}{} & {} \alpha _l\beta ^*_l=-\textrm{e}^{-2{ i}\lambda _lx_0}, \end{aligned}$$
(2.13)
$$\begin{aligned}{} & {} \hat{\alpha }_l\hat{\beta }^*_l=-\textrm{e}^{2{ i}\hat{\lambda }_lx_0}. \end{aligned}$$
(2.14)

From Eqs. (2.13)–(2.14), we know that \(\alpha _l,\hat{\alpha }_l,\beta _l,\hat{\beta }_l\) are all nonzero. Furthermore, (2.13)–(2.14) imply that the following conclusions about the zeros of \(\textrm{det}\ P_1\) and \(\textrm{det}\ P_2\) for the defocusing shifted nonlocal NLS Eq. (1.5).

Proposition 1

The defocusing shifted nonlocal NLS Eq. (1.5) does not allow for purely imaginary zeros for \(\textrm{det}\ P_1\) and \(\textrm{det}\ P_2\).

Proof

On the one hand, if \(\textrm{det}\ P_1\) has the purely imaginary zero \(\lambda _l={ i}\eta _l\ (\eta _l>0)\), then \(-\lambda ^*_l=\lambda _l\). In this situation, we have \(\alpha _l=\beta _l\), and thus, (2.13) becomes \(|\alpha _l|^2=-\textrm{e}^{2\eta _lx_0}\) which is a contradiction with \(|\alpha _l|^2> 0\) since \(\alpha _l\ne 0\). On the other hand, if \(\textrm{det}\ P_2\) has the purely imaginary zero \(\hat{\lambda }_l={ i}\hat{\eta }_l\ (\hat{\eta }_l<0)\), then \(-\hat{\lambda }^*_l=\hat{\lambda }_l\). Consequently, we have \(\hat{\alpha }_l=\hat{\beta }_l\). Thus, (2.14) would be \(|\hat{\alpha }_l|^2=-\textrm{e}^{-2\hat{\eta }_lx_0}\) which is a contradiction with \(|\hat{\alpha }_l|^2>0\) since \(\hat{\alpha }_l\ne 0\). \(\square \)

2.3 Soliton solutions

In what follows, we shall derive soliton solutions for the defocusing shifted nonlocal NLS Eq. (1.5) under general initial conditions. To this end, we assume that \(\textrm{det}\ P_1(\lambda )\) has N pairs of zeros \((\lambda _j, \lambda _{N+j})\) in \({\mathbb {C}}^+\) with \(\lambda _{N+j}=-\lambda ^*_j\) and \(\lambda _j\) being not purely imaginary, while \(\textrm{det}\ P_2(\lambda )\) has N pairs of zeros \((\hat{\lambda }_j, \hat{\lambda }_{N+j})\) in \({\mathbb {C}}^-\) with \(\hat{\lambda }_{N+j}=-\hat{\lambda }^*_j\) and \(\hat{\lambda }_j\) being not purely imaginary. Now, inspired by the restrictions in (2.13)–(2.14), we assume that the kernels of \(\textrm{det}\ P_1(\lambda _j)\) and \(\textrm{det}\ P_2(\hat{\lambda }_j)\) are spanned by the column vectors \(v_j\) and the row vectors \(\hat{v}_j\), respectively, i.e., \(P_1(\lambda _j)v_j=0\) and \(\hat{v}_j P_2(\hat{\lambda }_j)=0\), where

$$\begin{aligned} v_j=\textrm{e}^{\theta _j\sigma _3}v_{j,0},\quad \hat{v}_j =\hat{v}_{j,0}\textrm{e}^{\hat{\theta }_j\sigma _3}, \quad 1\le j\le 2N, \end{aligned}$$
(2.15)

in which \(\theta _j=\theta _j(x,t)={i}\lambda _jx+2{ i}\lambda ^2_jt,\ \hat{\theta }_j =\hat{\theta }_j(x,t)=-{ i}\hat{\lambda }_jx-2{ i}\hat{\lambda }^2_jt\), and

$$\begin{aligned}&v_{j,0}=(\alpha _j,1)^T,\nonumber \\&v_{N+j,0} =\left( -\frac{\textrm{e}^{2{ i} \lambda _j^*x_0}}{\alpha ^*_j},1\right) ^T, \quad \quad \quad 1\le j\le N, \end{aligned}$$
(2.16)
$$\begin{aligned}&\hat{v}_{j,0}=(\hat{\alpha }_j,1),\nonumber \\&\hat{v}_{N+j,0}=\left( -\frac{\textrm{e}^{-2{i} \hat{\lambda }_j^*x_0}}{\hat{\alpha }^*_j},1\right) , \quad \quad 1\le j\le N, \end{aligned}$$
(2.17)

where \(\lambda _j\in {\mathbb {C}}^+\) and \(\hat{\lambda }_j\in {\mathbb {C}}^-\) are free complex-valued parameters.

Using the prescribed conditions (2.15)–(2.17) of the scattering data, we can explicitly solve the RH problem (2.4) in the reflectionless case, i.e., \(s_{12}(0,\lambda )=r_{21}(0,\lambda )\), as

$$\begin{aligned}&P_1(\lambda )={\mathbb {I}}-\sum ^{2N}_{k=1}\sum ^{2N}_{j=1} \frac{v_k(M^{-1})_{kj}\widehat{v}_j}{\lambda -\widehat{\lambda }_j},\nonumber \\&P_2(\lambda )={\mathbb {I}}+\sum ^{2N}_{k=1}\sum ^{2N}_{j=1} \frac{v_k(M^{-1})_{kj}\widehat{v}_j}{\lambda -\lambda _k}, \end{aligned}$$
(2.18)

where \(M=(m_{kj})_{2N\times 2N}\) with \(m_{kj}=\frac{\hat{v}_kv_j}{\lambda _j-\hat{\lambda }_k}\). Moreover, \(P_1(\lambda )\) satisfies

$$\begin{aligned} P_{1,x}(\lambda )= & {} { i}\lambda [\sigma _3, P_1(\lambda )] +\bar{Q}P_1(\lambda ), \end{aligned}$$
(2.19a)
$$\begin{aligned} P_{1,t}(\lambda )= & {} 2{i}\lambda ^2 [\sigma _3, P_1(\lambda )]\nonumber \\{} & {} +\big (2\lambda \bar{Q}+{ i} (\bar{Q}^2+\bar{Q}_x)\sigma _3\big )P_1(\lambda ), \end{aligned}$$
(2.19b)

where \(\bar{Q}=-{ i}[\sigma _3,P_1^{(1)}]\) with \(P_1^{(1)}=P_1^{(1)}(x,t)\) being determined by

$$\begin{aligned} P_1(\lambda )={\mathbb {I}}+\lambda ^{-1}P^{(1)}_1 +\lambda ^{-2}P^{(2)}_1+\cdots ,\quad \lambda \rightarrow \infty . \end{aligned}$$
(2.20)

Now we shall prove that \(\bar{Q}=(\bar{Q}_{kj})_{2\times 2} =-{i}[\sigma _3,P_1^{(1)}]\) keeps the same matrix structure of Q as in the original Lax pair (2.3) such that the system (2.19) also constitutes a Lax pair for the defocusing shifted nonlocal NLS Eq. (1.5). This means that we have to prove that

$$\begin{aligned} \left( P^{(1)}_1\right) ^*_{12}(x_0-x,t) =\left( P^{(1)}_1\right) _{21}(x,t), \end{aligned}$$
(2.21)

with \((P^{(1)}_1)_{kl}\) denoting the (k, l)-entry of \(P^{(1)}_1\) which is determined in (2.20). In fact, it is not difficult to check that \(P_1(\lambda )\) given in (2.18) satisfies the symmetry relation:

$$\begin{aligned} P_1^*(x_0-x,t,-\lambda ^*)=\sigma ^{-1} P_1(x,t,\lambda )\sigma ,\quad \quad \lambda \in {\mathbb {C}}^+,\nonumber \\ \end{aligned}$$
(2.22)

where \(\sigma =\left( \begin{array}{cc} 0&{}1\\ -1&{}0 \end{array}\right) \). Then, we obtain from the expansion (2.20) as well as (2.22) that

$$\begin{aligned} \left( P_1^{(1)}\right) ^*(x_0-x,t)=-\sigma ^{-1} \left( P_1^{(1)}\right) (x,t)\sigma . \end{aligned}$$
(2.23)

Using the relation (2.23), one can easily check that the desired relation (2.21) holds. Consequently, the system (2.19) indeed defines a Lax pair for the defocusing shifted nonlocal NLS Eq. (1.5). As a result,

$$\begin{aligned} q(x,t)=\bar{Q}_{12}=-2{ i}\left( P^{(1)}_1\right) _{12}, \end{aligned}$$
(2.24)

yields a soliton solution of the defocusing shifted nonlocal NLS Eq. (1.5). To write out the soliton solutions (2.24) explicitly, we get from the form of \(P_1(\lambda )\) in (2.18) and its expansion (2.20), that the matrix function \(P^{(1)}_1\) can be found as

$$\begin{aligned} P^{(1)}_1=-\sum ^{2N}_{k=1}\sum ^{2N}_{j=1}v_k\hat{v}_j(M^{-1})_{kj}. \end{aligned}$$
(2.25)

Then, substituting (2.25) into (2.24), we finally obtain an explicit 2N-soliton solution of the defocusing shifted nonlocal NLS Eq. (1.5) as

$$\begin{aligned} q(x,t)&=2{ i}\sum ^{N}_{k=1}\sum ^{2N}_{j=1}\alpha _k\textrm{e}^{\theta _k -\hat{\theta }_j}(M^{-1})_{kj} \nonumber \\&\quad -2{i}\sum ^{2N}_{k=N+1}\sum ^{2N}_{j=1} \frac{\textrm{e}^{2{i}\lambda ^*_{k-N}x_0}}{\alpha ^*_{k-N}} \textrm{e}^{\theta _k-\hat{\theta }_j}(M^{-1})_{kj}, \end{aligned}$$
(2.26)

where \(M=(m_{kj})_{2N\times 2N}\) with \(m_{kj}=\frac{\hat{v}_kv_j}{\lambda _j-\hat{\lambda }_k}\) in which \(\hat{v}_k\) and \(v_j\) take the expressions in (2.15).

Remark 1

The representation (2.26) is said to be a 2N-soliton solution since \(\textrm{det}\ P_1\) and \(\textrm{det}\ P_2\) possess 2N zeros, respectively. That is to say, the soliton solutions expressed as (2.26) are in even orders. This is remarkably different compared with the focusing shifted nonlocal NLS Eq. (1.4). In fact, as aforementioned, the zeros of the RH problem of the defocusing shifted nonlocal NLS Eq. (1.5) cannot be allow for purely imaginary ones, while those of its focusing counterpart (1.4) do can [22].

2.4 Dynamical behaviors

Note that the form of the 2N-soliton solution (2.26) is not obvious to analyze its underlying dynamical behaviors. To reveal the properties of the 2N-soliton solution (2.26), we first rewrite it in an equivalent form, i.e., a ratio of two determinants:

$$\begin{aligned}&q(x,t)\nonumber \\&\quad =-2{ i}\frac{\left| \begin{array}{ccccccc} 0&{}\alpha _1e^{\theta _1}&{}\cdots &{}\alpha _{N}e^{\theta _{N}}&{}-\frac{\textrm{e}^{2{ i}\lambda ^*_{1}x_0}}{\alpha ^*_{1}}e^{\theta _{N+1}} &{}\cdots &{}-\frac{\textrm{e}^{2{ i}\lambda ^*_{N}x_0}}{\alpha ^*_{N}}e^{\theta _{2N}}\\ e^{-\hat{\theta }_1}&{}m_{11}&{}\cdots &{}m_{1,N}&{}m_{1,N+1}&{}\cdots &{}m_{1,2N}\\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ e^{-\hat{\theta }_{N}}&{}m_{N,1}&{}\cdots &{}m_{N,N}&{}m_{N,N+1}&{}\cdots &{}m_{N,2N}\\ e^{-\hat{\theta }_{N+1}}&{}m_{N+1,1}&{}\cdots &{}m_{N+1,N}&{}m_{N+1,N+1}&{}\cdots &{}m_{N+1,2N}\\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ \\ e^{-\hat{\theta }_{2N}}&{}m_{2N,1}&{}\cdots &{}m_{2N,N}&{}m_{2N,N+1}&{}\cdots &{}m_{2N,2N} \end{array}\right| }{\left| \begin{array}{ccccccc} m_{11}&{}\cdots &{}m_{1,N}&{}m_{1,N+1}&{}\cdots &{}m_{1,2N}\\ \vdots &{}\ddots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ m_{N,1}&{}\cdots &{}m_{N,N}&{}m_{N,N+1}&{}\cdots &{}m_{N,2N}\\ m_{N+1,1}&{}\cdots &{}m_{N+1,N}&{}m_{N+1,N+1}&{}\cdots &{}m_{N+1,2N}\\ \vdots &{}\ddots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ \\ m_{2N,1}&{}\cdots &{}m_{2N,N}&{}m_{2N,N+1}&{}\cdots &{}m_{2N,2N} \end{array}\right| }, \end{aligned}$$
(2.27)

where \(\hat{\theta }_k=-{i}\hat{\lambda }_k x-2{ i}\hat{\lambda }^2_kt,\theta _j= { i}\lambda _j x+2 { i}\lambda ^2_jt\), \(\lambda _{N+j}=-\lambda ^*_j\), \(\hat{\lambda }_{N+j}=-\hat{\lambda }^*_j\), and \(m_{kj}=\frac{\hat{v}_kv_j}{\lambda _j-\hat{\lambda }_k}\) with \(\hat{v}_k, v_j\) given in (2.15).

Fig. 1
figure 1

Two-soliton solutions via (2.27) with \(N=1\) and (2.28). a singular collapsing two-soliton behavior with \(x_0=-5\), b singular collapsing two-soliton behavior with \(x_0=0\), c singular collapsing two-soliton behavior with \(x_0=5\)

Full size image
Fig. 2
figure 2

Two-soliton solutions via (2.27) with \(N=1\) and (2.29). a singular collapsing two-soliton behavior with \(x_0=-5\), b singular collapsing two-soliton behavior with \(x_0=0\), c singular collapsing two-soliton behavior with \(x_0=5\)

Full size image
Fig. 3
figure 3

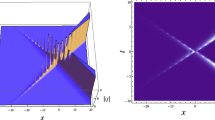
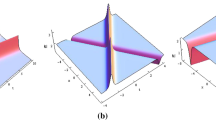
Two-soliton behaviors via (2.27) with \(N=1\) and (2.30). a analytic exponentially-growing or decaying two-soliton behavior with \(x_0=-5\), b analytic exponentially-growing or decaying two-soliton behavior with \(x_0=0\), c analytic exponentially-growing or decaying two-soliton behavior with \(x_0=5\)

Full size image

In order to explore the 2N-soliton solution (2.27), we take \(N=1\) as an representative example, which corresponds to a two-soliton solution for the defocusing shifted nonlocal NLS Eq. (1.5). According to the spectral structure revealed in (2.15)–(2.17), we investigate the soliton dynamical behaviors underlying (2.27) by selecting the following lists of parameters:

$$\begin{aligned}{} & {} \lambda _1=0.3+0.4{ i}, \quad \hat{\lambda }_1=0.4-0.8 { i},\nonumber \\{} & {} \alpha _1=1,\quad \hat{\alpha }_1={ i}, \end{aligned}$$
(2.28)
$$\begin{aligned}{} & {} \lambda _1=0.3+0.4{ i},\quad \hat{\lambda }_1=0.3-0.8 { i},\nonumber \\{} & {} \alpha _1=1,\quad \hat{\alpha }_1={i}, \end{aligned}$$
(2.29)
$$\begin{aligned}{} & {} \lambda _1=0.3+0.4{ i},\quad \hat{\lambda }_1=0.2-0.4{ i},\nonumber \\{} & {} \alpha _1=1, \quad \hat{\alpha }_1={i}, \end{aligned}$$
(2.30)
$$\begin{aligned}{} & {} \lambda _1=0.3+0.4{ i}, \quad \hat{\lambda }_1=0.3-0.4{i},\nonumber \\{} & {} \quad \alpha _1=0.6{ i},\quad \hat{\alpha }_1=-0.8{ i}, \end{aligned}$$
(2.31)
$$\begin{aligned}{} & {} \lambda _1=0.3+0.4{ i},\quad \hat{\lambda }_1=0.3-0.4{ i},\nonumber \\{} & {} \quad \alpha _1=0.6{ i}\quad \hat{\alpha }_1=0.8{ i}. \end{aligned}$$
(2.32)
Fig. 4
figure 4

Two-soliton behaviors via (2.27) with \(N=1\) and (2.31). a singular bell-type two-soliton interaction with \(x_0=-5\), b singular bell-type two-soliton interaction with \(x_0=0\), c singular bell-type two-soliton interaction with \(x_0=5\)

Full size image
Fig. 5
figure 5

Two-soliton behaviors via (2.27) with \(N=1\) and (2.32). a analytic bell-type two-soliton interaction with \(x_0=-5\), b analytic bell-type two-soliton interaction with \(x_0=0\), c analytic bell-type two-soliton interaction with \(x_0=5\)

Full size image

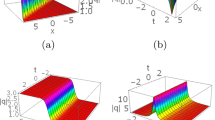
In fact, the parameters in (2.28)–(2.30) respectively satisfy: (I) \(\textrm{Re}\ \lambda _1\ne \textrm{Re}\ \hat{\lambda }_1\) and \(\textrm{Im}\ \lambda _1\ne -\textrm{Im}\ \hat{\lambda }_1\), (II) \(\textrm{Re}\ \lambda _1=\textrm{Re}\ \hat{\lambda }_1\) and \(\textrm{Im}\ \lambda _1\ne -\textrm{Im}\ \hat{\lambda }_1\), (III) \(\textrm{Re}\ \lambda _1\ne \textrm{Re}\ \hat{\lambda }_1\) and \(\textrm{Im}\ \lambda _1=-\textrm{Im}\ \hat{\lambda }_1\). Corresponding to (2.28) and (2.29), the two-soliton solutions are singular periodic solitons that collapse repeatedly which are shown in Figures 1 and 2. It is demonstrated in Fig. 1a-c that each right-propagation collapsing soliton decreases in its amplitude, while each left-propagation collapsing soliton increases in its amplitude. In contrast, in Fig. 2a–c, each right-propagation collapsing soliton increases in its amplitude, while each left-propagation collapsing soliton decreases in its amplitude. Remarkably different from the singular profiles in Figs. 1 and 2, the two-soliton interactions corresponding to (2.30) are analytic exponentially-growing or decaying types which are clearly shown in Fig. 3. Obviously, the two-soliton interactions revealed in Figs. 1, 2 and 3 have the properties that the two individual solitons change their forms before and after their interactions. That is to say, the two-soliton collisions are non-regular for the parameters in (2.28)–(2.30). Comparatively, the parameters in (2.31)–(2.32) obey the conditions: \(\textrm{Re}\ \lambda _1=\textrm{Re}\ \hat{\lambda }_1\) and \(\textrm{Im}\ \lambda _1=-\textrm{Im}\ \hat{\lambda }_1\). The difference for (2.31) and (2.32) lies in the different selections of \(\hat{\alpha }_1\). Consequently, the two-soliton solutions for (2.31)–(2.32) evolve as Figs. 4 and 5, which are all regular since the individual solitons do not change their respective forms before and after the collisions. However, due to the different choices of \(\hat{\alpha }_1\), the two-soliton solutions in Fig. 4 are singular bell types, while those in Fig. 5 are analytic bell types. Regarding the role that the space-shifted parameter \(x_0\) plays in the two-soliton solutions corresponding to (2.28)–(2.32), we highlight that the space-shifted parameter \(x_0\) affects the interaction positions which can be clearly seen in Figs. 1, 2, 3, 4 and 5 where \(x_0\) is selected as \(x_0=-5, 0, 5\), respectively.

3 Conclusions

By extending the RH approach to the defocusing shifted nonlocal NLS Eq. (1.5), we have explored and revealed the spectral structure of the equation, i.e., the scattering data and the their corresponding symmetry relations. Then soliton solutions in even orders are rigorously derived for the defocusing shifted nonlocal NLS Eq. (1.5). We showed that the zeros of the RH problem of the defocusing shifted nonlocal NLS Eq. (1.5) do not allow for purely imaginary ones, which is different from the focusing shifted nonlocal NLS Eq. (1.4) [22]. Finally, by selecting five representative lists of parameters, we explored the dynamical properties underlying the obtained solitons and then graphically illustrated them by highlighting the role that the space-shifted parameter \(x_0\) plays. The graphical illustrations show that the defocusing shifted nonlocal NLS Eq. (1.5) possesses diverse soliton dynamical behaviors which stem from its particular spectral structure revealed in (2.15)–(2.17). Before ending this paper, we point out that it is also meaningful to investigate the long-time behaviors of the solutions of (1.5) by performing asymptotic analysis of the corresponding RH problem (2.4) by utilizing the Deift-Zhou method [43, 44]. In addition, it is also possible to study other aspects of the defocusing shifted nonlocal NLS Eq. (1.5), such as the bright or dark soliton solutions [45,46,47], the neural network-based symbol calculation method [48,49,50], the Painlevé integrability properties [51, 52], and others. These are left for future discussions.