1 Introduction

The investigations on vibration, impact, noise, and nonlinear dynamics for gear transmission system have been the hot subjects in recent decades [1,2,3,4]. Analysis of vibration and dynamic responses for a gear drive, such nonlinear factors including time-varying mesh stiffness and damping, backlash, as well as static transmission error are generally considered but the oil film stiffness and damping are neglected in conventional system models to study the gear dynamics. However, it is generally accepted that the major contributions to stiffness and damping of gear pairs are from gear tooth and lubricated contacts between the teeth [5]. Therefore, it plays significant role in full understanding of the lubrication dynamic responses of gear drive that considering the hydrodynamic oil film stiffness and damping.

In the development of gear dynamics, Kahraman and Sigh have contributed significantly to gear dynamics theories. A spur gear dynamic model was established in their study. The dynamics equations were derived and full numerical analysis was conducted. Specifically, the time-varying mesh stiffness was closed to the realistic gear tooth stiffness by obtaining the best approximation of experimental results [6, 7]. Further, they studied the contact stiffness and damping of bearing by taking rolling bearings as flexible bodies into spur gear drive system [8]. Moreover, Velex and Baud conducted experiments based on a high-accuracy single stage spur and helical geared system and compared numerical simulations with experiment results to confirm the system model validation [9]. Chen and Tang analyzed the nonlinear dynamic characteristics of double-helical gear [10] and face gear transmission system [11] considering the effect of modification.

The gear drive generally operates in elastohydrodynamic lubrication contacts and the oil film between meshing gear teeth is beneficial to reduce vibration noise as well as tooth wear, and to enhance transmission stability. Therefore, the investigations on elastohydrodynamic lubrication for gear pairs have received considerable research attention. Gear lubrication has been investigated since the numerical model of elastohydrodynamic lubrication was established [12]. Then, the non-Newtonian behaviors of lubricant [13], squeeze film and thermal effects were studied in elastohydrodynamic line contacts for spur gears [14]. Khonsari et al. discussed the characteristics of various non-Newtonian rheological models under different lubrication boundary conditions and analyzed the validity of various rheological models over a wide range of the shear rate [15]. Further, the same authors investigated the effects of starvation degree on lubricant traction and film thickness in thermal elastohydrodynamic line contacts by using Carreau rheological model [16]. Recently, Liu et al. discussed the effect of starvation condition on film thickness, lubricant temperature rise, and friction coefficient for a spur gear drive [17].

In gear dynamics analysis, the time-varying mesh stiffness and damping are crucial factors to the dynamic response of gear drive system. Given that the lubricant is the viscous-elastic fluid, the oil film at interactive gear profiles generates elastic deformation and occurs energy dissipation during the dynamic contact. Consequently, the oil film stiffness and damping should be included in gear dynamics equations to meet the requirements of practical operating condition. Qin et al. investigated the stiffness of elastohydrodynamic lubrication line contacts along with various loads, entrainment velocities, and curvature radii [18]. Liu studied the oil film normal stiffness and damping based on a line contact-vibration elastohydrodynamic model [19]. Further, the effects of applied load, entrainment velocity, surface roughness, and starvation degree on the oil film normal stiffness were investigated as well [20]. Velex et al. deduced a linear viscous damping formula according to a series of elastohydrodynamically numerical results in line contacts [21] and further studied the normal and tangential damping of the oil film [5]. More recently, the authors modeled the oil film stiffness and damping both in normal and tangential directions and discussed the effects of gear geometric and operating parameters on them [22, 23]. According to elastohydrodynamic lubrication and gear dynamics theories, Li and Kahraman established a viscous damping model by incorporating the elastohydrodynamic model with the torsional dynamic model of spur gear drive [24]. Then, the same author extended the modeling strategy to investigate the gear dynamics both with torsional and transverse degrees of freedom by utilizing a tribo-dynamic model [25]. Guilbault et al. deduced a squeeze damping expression of oil film according to the Reynolds equation and explained the generation mechanism of viscous damping for cylindrical gear systems [26].

Although the oil film stiffness and damping have been studied by researchers, the systematic investigations for the combined stiffness and damping of both the lubricant and gear teeth are rarely performed, and their impacts on gear dynamics are lacking. Following the advances in elastohydrodynamic theory and conventional gear dynamics, the combined stiffness and damping have to be considered in the developed tribo-dynamic model for a gear drive. This study established an enhanced spur gear dynamic model by considering the stiffness and damping of both the gear tooth and oil film, and the models for oil film stiffness and damping in normal and tangential directions are developed. The combined stiffness is deduced from the stiffness of both the gear tooth and oil film, while the combined damping is derived from the damping of these parts. Effects of oil film stiffness and damping in normal and tangential directions on spur gear dynamics are investigated. Finally, the comparison of dynamic response between the developed model and the conventional model is discussed.

Fig. 1
figure 1

Gear pair dynamic model

Full size image

2 Dynamic model for spur gears

2.1 Enhanced dynamic model for spur gear pairs

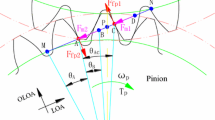
The dynamic model for a spur gear pair is sketched in Fig. 1, and the gear geometry is shown in Fig. 2. In the present study, an enhanced dynamic model for spur gear pairs including the backlash and static transmission error and stimulatingly incorporating the combined stiffness in the normal direction as well as the combined damping both in normal and tangential directions is developed from a conventional model [6, 7]. And the conventional model refers to the spur gear dynamic model in which the oil film stiffness and damping are not considered and the friction is not included as well. The combined stiffness and damping are derived from the counterparts of gear pair and oil film. The gear mesh is described as a pair of rigid disk connected by a linear spring and damper acting on the line of action (LOA) normal to the tooth flank called the normal direction. Given that the vibration of gear pair along off the line of action (OLOA) tangential to the tooth flank called the tangential direction is closely related to the tangential damping [5], it is included in the present dynamic model as well. The equations of torsional motion of 2-degree-of-freedom model for a spur gear pair neglecting the effects of tangential stiffness of oil film and gear pair, and of shift as well as bearing are written as:

$$\begin{aligned}&I_p \ddot{\theta }_p +R_p c_m \left( {\bar{{t}}} \right) \left( {R_p \dot{\theta }_p -R_g \dot{\theta }_g -\dot{e}\left( {\bar{{t}}} \right) } \right) \nonumber \\&\quad +\tan \varphi R_a c_n \left( {\bar{{t}}} \right) \left( {R_p \dot{\theta }_p -R_g \dot{\theta }_g -\dot{e}\left( {\bar{{t}}} \right) } \right) \nonumber \\&\quad +\, R_p k_m \left( {\bar{{t}}} \right) f\left( {R_p \theta _p -R_g \theta _g -e\left( {\bar{{t}}} \right) } \right) =T_p \end{aligned}$$
(1)
$$\begin{aligned}&I_g \ddot{\theta }_g -R_g c_m \left( {\bar{{t}}} \right) \left( {R_p \dot{\theta }_p -R_g \dot{\theta }_g -e\left( {\bar{{t}}} \right) } \right) \nonumber \\&\quad -\tan \varphi R_b c_n \left( {\bar{{t}}} \right) \left( {R_p \dot{\theta }_p -R_g \dot{\theta }_g -e\left( {\bar{{t}}} \right) } \right) \nonumber \\&\quad -\, R_g k_m \left( {\bar{{t}}} \right) f\left( {R_p \theta _p -R_g \theta _g -e\left( {\bar{{t}}} \right) } \right) =-T_g \end{aligned}$$
(2)
Fig. 2
figure 2

Gear geometry

Full size image

where \({\theta }_{p}\) and \({\theta }_{g}\) denote the angular displacements of pinion and gear, respectively. \(R_{p}\) and \(R_{g}\) are the base circle radii of gears, \(I_{p}\) and \(I_{g}\) are the mass moment of inertia of gears. \(k_{m}\) and \(c_{m}\) represent the combined normal stiffness and damping respectively. \(c_{n}\) denotes the combined tangential damping. \(R_{a}\) and \(R_{b}\) shown in Fig. 2 are the acting arms of tangential forces on the pinion and gear respectively, which are the distances between the mesh point and points \(N_{1}\) and \(N_{2}\) respectively and they vary along LOA. \(N_{1 }\)and \(N_{2}\) are the tangent points where the action line is tangent to the base circles of pinion and gear, respectively. \(\varphi \) is the pressure angle. f is the backlash function ande denotes the static transmission error. \(T_{p}\) and \(T_{g}\) are the external torques acting on the pinion and gear, respectively. \(\bar{{t}}\) denotes the time. For simplifying dynamics equations, introducing the dynamic transmission error expressed as

$$\begin{aligned} \bar{{x}}\left( {\bar{{t}}} \right) =R_p \theta _p \left( {\bar{{t}}} \right) -R_g \theta _g \left( {\bar{{t}}} \right) -e\left( {\bar{{t}}} \right) \end{aligned}$$
(3)

Substituting Eq. (3) into Eqs. (1) and (2) yields

$$\begin{aligned}&m_e \ddot{\bar{{x}}}\left( {\bar{{t}}} \right) +c_m \left( {\bar{{t}}} \right) \dot{x}\left( {\bar{{t}}} \right) \nonumber \\&\quad +\, \mu c_n \left( {\bar{{t}}} \right) \dot{x}\left( {\bar{{t}}} \right) \nonumber \\&\quad +\, k_m \left( {\bar{{t}}} \right) f\left( {\bar{{x}}} \right) =\bar{{F}}_m -m_e \ddot{e}\left( {\bar{{t}}} \right) \end{aligned}$$
(4)

where \(\mu =\tan \varphi {\left( {R_a R_p I_g +R_b R_g I_p } \right) }\big /\big (I_p R_g^2+I_g R_p^2\big )\), \(m_e ={I_p I_g }/{\left( {I_p R_g^2 +I_g R_p^2 } \right) }\) is the equivalent mass and \(\bar{{F}}_m ={T_p }/{R_p }\) is external excitation. The ode45 command in MATLAB that adopts the Runge–Kutta method is used to solve Eq. (4) where the initial condition is zero. And an adaptive integration step is utilized in this algorithm. The gear pair has a clearance equal to 2b along LOA and the backlash function is expressed as:

$$\begin{aligned} f(\bar{{x}},b)=\left\{ {\begin{array}{ll} \bar{{x}}-b &{}\quad \bar{{x}}>b \\ 0 &{}\quad -b\le \bar{{x}}\le b \\ \bar{{x}}+b&{} \quad \bar{{x}}<-b \\ \end{array}} \right. \end{aligned}$$
(5)

The static transmission error caused by manufacture error and teeth deformations can be approximated as a periodic function and its fundamental frequency is the gear meshing frequency, \(\bar{{\omega }}_e \). Therefore, the static transmission error is written as:

$$\begin{aligned} e\left( {\bar{{t}}} \right) =\tilde{e}\sin \bar{{\omega }}_e \bar{{t}} \end{aligned}$$
(6)

where \(\tilde{e}\) is the internal excitation amplitude. Introducing the following dimensionless parameters

$$\begin{aligned}&x={\bar{{x}}}/b, \quad t=\bar{{t}}\omega _n ,\\&\omega _n =\sqrt{{\bar{{k}}_m }/{m_e }}, \\&\xi ={c_m }/{\left( {2m_e \omega _n } \right) },\\&\varsigma ={\mu c_n }/{\left( {2m_e \omega _n } \right) }, \\&\omega _e ={\bar{{\omega }}_e }/{\omega _n }, \\&F_m ={\bar{{F}}_m }/{\left( {b\bar{{k}}_m } \right) }, \quad F_e ={\tilde{e}}/b \end{aligned}$$

where \(\omega _{n}\) is the natural frequency and \(\bar{{k}}_m \) is the mean combined normal stiffness. Therefore, the dimensionless dynamics equation is written as:

$$\begin{aligned}&\ddot{x}\left( t \right) +2\xi \dot{x}\left( t \right) +2\varsigma \dot{x}\left( t \right) \nonumber \\&+\, kf\left( {x\left( t \right) } \right) =F_m +F_e \omega _e^2 \sin \left( {\omega _e t} \right) \end{aligned}$$
(7)

where \(k={k_m }/{\bar{{k}}_m }\) is the dimensionless combined normal stiffness. \(\xi \) and \(\varsigma \) denote the combined normal and tangential damping ratios, respectively. f(x(t)) is expressed as

$$\begin{aligned} f(x(t))=\left\{ {\begin{array}{ll} x\left( t \right) -1 &{}\quad x\left( t \right) >1 \\ 0 &{}\quad -1<x\left( t \right)<1 \\ x\left( t \right) +1&{}\quad x\left( t \right) <-1\\ \end{array}} \right. \end{aligned}$$
(8)

where x is the dimensionless dynamic transmission error and t denote the time.

2.2 Mesh stiffness and damping of gear pairs

The Ishikawa formula is used to calculate the mesh stiffness of spur gear drive in this work. Given that the tooth profile can be considered as the combination of a rectangle and a trapezoid that are the deformation components in Ishikawa formula, the elastic deformation of gear tooth including bending, shear, and contact deformations is written as [27]

$$\begin{aligned} \delta =\delta _{br} +\delta _{bt} +\delta _s +\delta _g \hbox {+}\delta _p \end{aligned}$$
(9)

where \(\delta _{br}\) and \(\delta _{bt}\) are the bending deformations of the rectangular and trapezoidal sections, respectively. \(\delta _{s}\) and \(\delta _{g}\) represent the shear and contact deformations of the gear pair. \(\delta _{p}\) denotes the shear deformation resulting from the basic part sloping.

The total deformation of the meshing gear pair can be written as

$$\begin{aligned} \delta =\sum _{i=1}^2 {\left( {\delta _{bri} +\delta _{bti} +\delta _{si} +\delta _{gi} } \right) } +\delta _p \end{aligned}$$
(10)

where \(i=2\) denotes the gear teeth pair. The gear mesh stiffness is given as

$$\begin{aligned} k_g \left( t \right) =\frac{F_n }{\delta } \end{aligned}$$
(11)

where \(F_n \) denotes the normal contact force. The mesh damping based on conventional dynamic model for spur gear pairs is written as

$$\begin{aligned} c_g \left( t \right) \hbox {=}2\xi \sqrt{k_g m_e } \end{aligned}$$
(12)

where the value of \(\xi \) is fixed at 0.07 because the mesh damping ratio for analysis of spur gear dynamics is commonly chosen between 0.05 and 0.08. Hence, a medium mesh damping ratio is adopted in this study.

3 Oil film stiffness and damping

In conventional gear dynamic model, the stiffness and damping of gear tooth are considered, while the oil film stiffness and damping are neglected. In fact, the meshing gear pair is generally required in elastohydrodynamic lubrication contacts. The stiffness and damping of oil film which contributes to the stability improvement and life prolongation as well as energy dissipation for the gear drive are included in the present enhanced gear dynamic model for acquiring more practical gear dynamic responses.

3.1 Elastohydrodynamic lubrication equations

The hydrodynamic oil film between a meshing gear pair is general the non-Newtonian fluid due to the complex operating conditions and load distribution of gear drive. Therefore, the pressure distribution of oil film taking into account the non-Newtonian and squeeze film effects in line contacts is governed by the one-dimensional generalized Reynolds equation modified by Yang and Wen [28] and expressed as:

$$\begin{aligned} \frac{\partial }{\partial x}\left( {\varepsilon \frac{\partial p}{\partial x}} \right) =12u_e \frac{\partial \left( {\rho ^{*}h} \right) }{\partial x}+12\frac{\partial \left( {\rho _e h} \right) }{\partial t} \end{aligned}$$
(13)

where

$$\begin{aligned}&\varepsilon =\left( {\frac{\rho }{\eta }} \right) _e \frac{h^{3}}{\lambda } \quad {\lambda =\frac{3}{4}\pi ^{2}\frac{\overline{U} }{\overline{W} ^{2}}} \\&\left( {\frac{\rho }{\eta }} \right) _e =12\left( {\eta _e {\rho }'_e /{\eta }'_e -{\rho }''_e } \right) \\&\frac{1}{\eta _e }=\frac{1}{h}\int _0^h {\frac{\mathrm{d}z}{\eta ^{{*}}}} \quad {\frac{1}{{\eta }'_e }=\frac{1}{h^{2}}\int _0^h {\frac{z\mathrm{d}z}{\eta ^{{*}}}} } \\&{\rho ^{*}=\frac{{\rho }'_e \eta _e (u_g -u_p )+\rho _e u_p }{u_e }}\\ \\&\rho _e =\frac{1}{h}\int _o^h {\rho \mathrm{d}z}\quad {{\rho }'_e =\frac{1}{h^{2}}\int _0^h {\rho \int _0^z {\frac{\mathrm{d}{z}'}{\eta ^{{*}}}} } \mathrm{d}z}\\&{{\rho }''_e =\frac{1}{h^{3}}\int _0^h \rho \int _0^z {\frac{{z}'\mathrm{d}{z}'}{\eta ^{{*}}}} \mathrm{d}z} \end{aligned}$$

Specifically, p, h, \(\rho \), and \(\eta ^{*}\) are the pressure, film thickness, density and equivalent viscosity of the non-Newtonian fluid, respectively. x and z denote the coordinates along the rolling direction and across the oil film, respectively. \(u_{p}\) and \(u_{g}\) represent the surface velocities of the driving pinion and driven gear, respectively. And \(u_{e}\) denotes the entrainment velocity. For the boundary conditions of Reynolds equation, ambient pressure is used at the inlet and outlet of the contact domain. The corresponding coordinates, \(x_{\mathrm{in}}\) and \(x_{\mathrm{out}}\) are fixed at \(x_{\mathrm{in}}=-4.5c\) and \(x_{\mathrm{out}}=1.5c\), respectively. c is the Hertzian contact half-width. The finite difference method is used to solve Eq. (13), and the number of nodes in the contact domain is \(n=961\). The Ree–Eyring rheological model is used to describe the non-Newtonian behavior of lubricant in elastohydrodynamic lubrication and the non-Newtonian effect is considered by employing the generalized Reynolds equation where the equivalent viscosity is used. The equivalent lubricant viscosity of the Ree–Eyring fluid is written as

$$\begin{aligned} \eta ^{{*}}={\eta \left( {\frac{\tau }{\tau _0 }} \right) }/{\sinh \left( {\frac{\tau }{\tau _0 }} \right) } \end{aligned}$$
(14)

where \(\tau \) and \({\tau }_{0}\) represent the shear stress and Eyring stress of the lubricant, respectively.

Fig. 3
figure 3

Elastohydrodynamic line contact

Full size image

The film thickness equation in elastohydrodynamic lubrication line contact is expressed as:

$$\begin{aligned} h=h_0 +\frac{x^{2}}{2R}-\frac{2}{\pi {E}'}\int _{x_{\mathrm{in}} }^{x_{\mathrm{out}} } p \ln \left( {x-{x}'} \right) ^{2}\mathrm{d}x' \end{aligned}$$
(15)

where \(h_{0}\) is the mutual approach between the rigid contacting bodies. R and \(E'\) are the equivalent curvature radius and elastic modulus, respectively. The last term in Eq. (15) denotes the total elastic deformation of two contact surfaces.

In elastohydrodynamic lubrication contacts, high fluid pressure will lead to the sharp increase of the fluid viscosity. The pressure-viscosity relationship proposed by Roelands [29] and used in this study is expressed as:

$$\begin{aligned} \eta =\eta _0 \exp \left\{ {(\ln \eta _0 +9.67)\left[ {\left( {1+5.1\times 10^{-9}p} \right) ^{z_0 }-1} \right] } \right\} \nonumber \\ \end{aligned}$$
(16)

where \(\eta _{0}\) represents the lubricant ambient viscosity and \(z_{0}\) denotes the pressure-viscosity coefficient. The lubricant density related to the fluid pressure varies in accordance with pressure-density relationship presented by Dowson and Higginson [30], which is expressed as:

$$\begin{aligned} \rho =\rho _{0} \left[ {1+\left( {0.6\times 10^{-9}p} \right) /\left( {1+1.7\times 10^{-9}p} \right) } \right] \end{aligned}$$
(17)

where \({\rho }_{0}\) represents the lubricant ambient density.

The applied load acting on the fluid is balanced by the fluid pressure. Hence, the load equation is written as

$$\begin{aligned} \int _{x_{\mathrm{in}} }^{x_{\mathrm{out}} } {p\mathrm{d}x=w} \end{aligned}$$
(18)

where w denotes the load per unit width that is known. The mutual approach, \(h_{0}\), is a variable at each time step and it can be solved by combining the Reynolds equation with the applied load equation.

The shear stress of a Ree–Eyring fluid is given as

$$\begin{aligned} \tau= & {} \tau _p +z\frac{\partial p}{\partial x} \end{aligned}$$
(19)
$$\begin{aligned} \tau _p= & {} \tau _0 \ln \frac{\sqrt{\left( {u_p -u_g } \right) ^{2}+\left( {F_1^2 -F_2^2 } \right) }-\left( {u_p -u_g } \right) }{F_1 +F_2 }\nonumber \\ \end{aligned}$$
(20)

where \({\tau }_{p}\) is the shear stress on the surface of driving pinion. \(F_{1}\) and \(F_{2}\) are the integrals in Eq. (20) which are written as:

$$\begin{aligned} F_1= & {} \int _0^h {\frac{\tau _0 }{\eta }\cosh \left( {\frac{z}{\tau _0 }\cdot \frac{\partial p}{\partial x}} \right) \mathrm{d}z} \hbox { and} \\ F_2= & {} \int _0^h {\frac{\tau _0 }{\eta }\sinh \left( {\frac{z}{\tau _0 }\cdot \frac{\partial p}{\partial x}} \right) \mathrm{d}z} . \end{aligned}$$

The velocity gradient of non-Newtonian lubricant in the direction across the oil film can be expressed as

$$\begin{aligned} \frac{\partial u}{\partial z}=\frac{\tau }{\eta ^{*}} \end{aligned}$$
(21)

By integrating Eq. (21) with respect to variable z, the fluid velocity along the rolling direction is derived as

$$\begin{aligned} u=u_p +\int _0^z {\frac{\partial u}{\partial z}} \mathrm{d}{z}' \end{aligned}$$
(22)

3.2 Oil film normal stiffness

Elastohydrodynamic line contacts can be assumed as the contacts between two cylinders and is further simplified as the contacts between an elastic cylinder with an equivalent curvature radius R and a semi-infinite rigid plane as shown in Fig. 3. The equivalent elastic cylinder will move toward the rigid plane under the action of normal load. Owing to the pressure-viscosity relationship of the lubricant, the oil film will be compressed and generate the compression deformation in the contact domain. At each mesh position of the spur gear mesh cycle, the film pressure, p(x, t), is obtained by solving Eq. (13), and the film thickness, h(x, t), is obtained by using Eq. (15). If an applied load increment, \(\Delta w(t)\), that is derived from the known quasi-steady state load spectrum of a spur gear transmission [22] is given, the film pressure increment, \(\Delta p(x,t)\), and the compression deformation increment of the film thickness, \(\Delta h(x,t)\), can be obtained. As the viscous-elastic fluid, the oil film between the meshing gear pair is modeled as a massless spring element shown in Fig. 4. Hence, the oil film normal stiffness is derived as [22],

$$\begin{aligned} k_o \left( t \right) =\frac{\Delta F_n }{\Delta h}=\frac{B\times \Delta ^{k}\sum _{i=1}^n {\Delta p\left( {x,t} \right) } }{\frac{1}{n}\sum _{i=1}^n {\Delta h\left( {x,t} \right) } } \end{aligned}$$
(23)

where B denotes the face width. \(\Delta \) denotes increment and \(\Delta ^{k}\) represents the grid size in the rolling direction. n is the nodal number within the nominal contact domain.

Fig. 4
figure 4

Equivalent spring model of the oil film normal stiffness

Full size image

3.3 Oil film normal damping

In one mesh cycle of spur gear transmission, both the fluid pressure and film thickness in transient elastohydrodynamic contact are re-calculated at each mesh position along LOA, which makes it possible to gain the compression speed of the oil film in the direction across film thickness. As the viscous-elastic fluid, the oil film between the meshing gear pair is equivalent to a damping element shown in Fig. 5. Hence, the oil film normal damping is expressed as [23]

$$\begin{aligned} c_{no} \left( t \right)= & {} \frac{\Delta F_n }{\Delta \dot{h}}\nonumber \\= & {} \frac{B\times \Delta ^{k}\sum _{i=1}^n {\Delta p\left( {x,t} \right) } }{\Delta \left( {{\frac{1}{n}\sum _{i=1}^n {\left( {h\left( {x,t} \right) -\tilde{h}\left( {x,\tilde{t}} \right) } \right) } }/{dt}} \right) } \end{aligned}$$
(24)

where \({\dot{h}}\) denotes the normal compression speed of the oil film in which h and \({\tilde{h}}\) are the film thicknesses at present and last mesh positions, respectively. dt represents the oil film compression time.

3.4 Oil film tangential damping

The oil film tangential damping is computed on the basis of the first derivative of the fluid tangential force, \(F_{\tau }\), with respect to tangential velocity. The fluid shear stress, \(\tau \)(x, z, t), is calculated by utilizing Eq. (19) and the velocity of oil film along the rolling direction, u(x, z, t), is computed by using Eq. (22). With a applied load increment, \(\Delta w(t)\), the fluid shear stress increment, \(\Delta \tau (x,z,t)\), and the flow velocity increment of the oil film, \(\Delta u(x,z,t)\), can be obtained. As the viscous-elastic fluid, the oil film the meshing gear pair is modeled as a massless damping element shown in Fig. 5. Thus, the oil film tangential damping is defined as:

$$\begin{aligned} c_{\tau o} \left( t \right) =\frac{\Delta F_\tau }{\Delta u}=\frac{B\times \Delta ^{k}\sum _{i=1}^n {\Delta \tau \left( {x,z,t} \right) } }{\frac{1}{n}\sum _{i=1}^n {\Delta u\left( {x,z,t} \right) } } \end{aligned}$$
(25)
Fig. 5
figure 5

Oil film normal and tangential damping models

Full size image

4 Results and discussion

4.1 Numerical analysis and validation

Given that the oil film stiffness and damping are considered to investigate the spur gear dynamics, the combined normal stiffness, \(k_{m}(t)\), derived from gear mesh stiffness and oil film normal stiffness and included in the present enhanced dynamic model of spur gear is expressed as:

$$\begin{aligned} k_m \left( t \right) =\sum _{i=1}^I {\left( {\frac{1}{k_g }+\frac{1}{k_o }} \right) } _i^{-1} \end{aligned}$$
(26)

where \(I=1\) or \(I=2\) indicates that one or two tooth pairs are in the mesh, respectively. The combined normal stiffness is a time-varying parameter varying along LOA.

According to Ref. [31], the tangential stiffness of gear pair and oil film are far less than the normal stiffness of these parts. Therefore, they are both neglected in this study and it is noted that the oil film normal stiffness is simply called oil film stiffness in following sections since the tangential stiffness of oil film is neglected. The combined normal damping, \(c_{m}(t)\), derived from gear mesh damping and oil film normal damping and included in the present enhanced dynamic model as well is written as

$$\begin{aligned} c_m \left( t \right) =\sum _{i=1}^I {\left( {\frac{1}{c_g }+\frac{1}{c_{no} }} \right) } _i^{-1} \end{aligned}$$
(27)

In the tangential direction of tooth flank perpendicular to LOA, according to Ref. [31], the tangential damping of gear pair is far larger than that of oil film, which indicates that it plays a minor role in combined tangential damping. To simplify the calculation process, only the oil film tangential damping is taken into account. Here, the combined tangential damping, \(c_{n}(t)\), involved in the enhanced dynamic model is given by

$$\begin{aligned} c_n \left( t \right) =c_{\tau o} \end{aligned}$$
(28)
Table 1 Gear and lubricant parameters
Full size table
Fig. 6
figure 6

Dynamic response of a displacement, b velocity and c acceleration

Full size image
Fig. 7
figure 7

Pressure and film thickness distributions at a approach point, b pitch point and c recession point

Full size image

Given that the combined normal stiffness and damping as well as combined tangential damping are obtained, the dynamic analysis using the enhanced dynamic model for spur gear pairs can be conducted. Table 1 lists the spur gear and lubricant properties parameters. To check the validity of numerical solution, the conventional gear dynamics analysis is shown in Fig. 6, in which the oil film stiffness and damping are neglected. It can been seen that the displacement fluctuation or called dynamic transmission error fluctuation which is caused by the external excitation gradually decreases and finally reaches the steady state. The similar variation can be observed in velocity and acceleration versus time. Stimulatingly, for elastohydrodynamic lubrication analysis, the lubricant pressure and film thickness profiles at approach, pitch and recession points are shown in Fig. 7 to evaluate the calculation procedure of oil film stiffness and damping. The lubricant pressure decreases when the film thickness increases, and the pressure at approach or recession point is less than that at pitch point because the applied load at pitch point is the largest. Moreover, the second pressure spike is clearly observed in the pressure curve at pitch point, which is a significant characteristic in elastohydrodynamic line contacts. This can be attributed to the fluid flow hindered by oil film rupture, which leads to the second pressure spike of oil film described in the published literature [24, 32]. The pressure and film thickness distributions at approach point are similar to those at recession point owing to the same applied load.

As shown in Fig. 8a, the oil film normal stiffness at single-tooth contact is larger than that at double-teeth contact because the applied load at single-tooth is larger. Moreover, the variations of oil film normal stiffness and applied load along LOA are similar. Figure 8b shows the variation of oil film normal damping along LOA. Since the squeeze film action is taken into account in the gear mesh, the transient variation can be observed in the oil film normal damping. The fluctuation of the oil film normal damping at single-to-double and double-to-single tooth contacts can be attributed to the sudden changes in the applied load.

Fig. 8
figure 8

a Oil film normal stiffness and b damping

Full size image
Fig. 9
figure 9

The variations of stiffness and damping along LOA

Full size image
Fig. 10
figure 10

Effect of oil film stiffness on the dynamic responses of a displacement, b velocity, c acceleration, d phase-plane portrait, and e Poincaré map

Full size image

As shown in Fig. 9a, the combined normal stiffness is smaller than gear mesh stiffness along LOA because the stiffness of oil film and gear tooth are in series resulting in combined normal stiffness smaller than each stiffness. Additionally, small fluctuations of combined normal stiffness at single-to-double and double-to-single tooth contacts are observed. Comparing Figs. 9a and 8a reveals that oil film stiffness are larger than the gear mesh stiffness and the combined normal stiffness is closer to the mesh stiffness. Figure 9b shows the combined normal damping is smaller than the gear mesh damping ascribed to the same reason for the combined normal stiffness. Comparing Figs. 9b and 8b reveals that oil film normal damping are larger than gear mesh damping and the combined normal damping is closer to the gear mesh damping. Moreover, the fluctuation in the combined normal damping at single-to-double and double-to-single tooth contacts is observed as well. The combined normal stiffness and damping at single-tooth contact is large than those at double-teeth contact. Fig. 9c depicts the variation of the combined tangential damping along LOA. At pitch point, it reaches minimum due to the effect of slide-to-roll ratio. Comparing Fig. 9b, c reveals that the combined tangential damping is far smaller than combined normal damping and gear mesh damping.

4.2 Effect of oil film stiffness

As shown in Fig. 10, when oil film stiffness is considered in the gear mesh, the fluctuation amplitude of displacement, velocity and acceleration slightly increase. The changes in the dynamic responses can be ascribed to the fact that the combined normal stiffness is smaller than gear mesh stiffness and smaller stiffness leads to larger vibration amplitude. Additionally, the displacement response reaches steady stage fast when the oil film stiffness is included. The fluctuations of velocity and acceleration responses in the period converting from transient stage to steady stage is smaller compared to the results of conventional model. It indicates that oil film stiffness is valid to impact resistance for gear drive. Comparing the dynamic responses in velocity, and acceleration of enhanced model included oil film stiffness with those of conventional model versus time, the transient responses faster convent to steady response and their response curves are smoother due to the effect of oil film stiffness. The phase-plane portrait and Poincaré map show obvious differences with or without considering the oil film stiffness. However, the systems are both in period-1 motion in the two cases.

4.3 Effect of oil film normal damping

Figure 11 shows the effect of oil film normal damping on dynamic responses. The fluctuation amplitude of displacement, velocity, and acceleration in transient stage is larger than the results from the conventional model, which can be explained that the combined normal damping is smaller than gear mesh damping and leads to dissipating vibration energy slowly. While in steady stage, the response curves of enhanced model and conventional model have no obvious difference. The reason for that is the dynamic system reaches energy-balanced state and oil film damping plays slight role in current steady stage. The phase-plane portrait and Poincaré map show slight differences with or without considering the oil film normal damping. However, the system is in period-1 motion in conventional model and it transfers from period-1 motion for period-2 motion when considering the oil film normal damping.

Fig. 11
figure 11

Effect of oil film normal damping on the dynamic responses of a displacement, b velocity, c acceleration, d phase-plane portrait, and e Poincaré map

Full size image

4.4 Effect of oil film tangential damping

As shown in Fig. 12, the oil film tangential damping has no obvious effect on the dynamic responses of displacement, velocity, and acceleration both in transient and steady stages. This can be ascribed to the fact that the oil film tangential damping shown in Fig. 9c are far smaller than the combined damping which is in the normal direction and shown in Fig. 9b; thus, it plays a minor role in dynamic responses. Moreover, the oil film tangential damping is mainly contributed to alleviate shear vibration and frictional heat generation in the tangential direction not the normal direction of tooth flank. The phase-plane portrait and Poincaré map show no obvious differences with or without considering the oil film tangential damping.

Fig. 12
figure 12

Effect of oil film tangential damping on the dynamic responses of a displacement, b velocity, c acceleration, d phase-plane portrait, and e Poincaré map

Full size image

4.5 Combined effects of oil film stiffness and damping

Figure 13 shows the combined effects of oil film stiffness and damping on the dynamic responses versus time. The oil stiffness and damping slightly increase the fluctuation amplitudes of displacement, velocity, and acceleration because the combined normal stiffness and damping are smaller than the corresponding gear mesh stiffness and damping. Compared to results of conventional model, the dynamic responses of the present enhanced model reaches steady stage in shorter time, which indicates the oil film stiffness and damping is benefit for gear drive to resist impact and vibration. The response amplitude of speed and acceleration in the period converting from transient stage to steady stage is obviously smaller, and smoother transition is achieved when the oil film stiffness and damping are included in gear dynamic model. The response curves of speed and acceleration obtained from the present enhanced gear dynamic model are smoother in steady stage, which means the transmission stability of gear system is improved. The phase-plane portrait and Poincaré map show obvious differences between the present enhanced dynamic model and conventional model. However, in the two models, the systems are both in period-1 motion, which indicates oil film stiffness plays a larger effect than oil film damping on the spur gear dynamics.

Fig. 13
figure 13

Combined effects of oil film stiffness and damping on the dynamic responses of a displacement, b velocity, c acceleration, d phase-plane portrait, and e Poincaré map

Full size image

5 Conclusions

In this study, an enhanced spur gear dynamic model considering the combined stiffness and damping of both gear tooth and oil film was established. The models of oil film stiffness and damping in normal and tangential directions were, respectively, developed according to elastohydrodynamic lubrication theory. The combined stiffness was deduced from the stiffness of both the oil film and gear tooth, while the combined damping was derived from the damping of these parts. Effects of oil film stiffness in normal direction and damping in normal and tangential directions on spur gear dynamics were investigated, and the comparison of dynamic response between the enhanced model and the conventional model was discussed. The oil film stiffness is larger than gear mesh stiffness, and oil film normal damping is larger than gear mesh damping as well. Thus, the combined normal stiffness and damping is closer to the gear mesh stiffness and damping. The oil film tangential damping is far smaller than the oil film normal damping as well as the combined normal damping. The fluctuation amplitude of dynamic responses obtained from the enhanced spur gear dynamic model is slightly larger than that from conventional model. Given considering the oil film stiffness and damping, the displacement fluctuation in transient stage fast decays and displacement response reaches steady state in shorter time. The speed and acceleration fluctuation in this period converting from transient stage to steady stage obviously smaller, and the response curves of speed and acceleration in steady stage are smoother. This reveals that oil film stiffness is prone to alleviate impact effectively and the oil film damping is inclined to reduce vibration and frictional heat substantially for a gear drive. Moreover, the phase-plane portrait and Poincaré map show obvious differences between the present enhanced dynamic model and conventional model and the gear system transfers from period-1 motion for period-2 motion when only considering the effect of oil film normal damping.