An improved nonlinear dynamic model of gear pair with tooth surface microscopic features

Abstract

In view of the issue that current gear dynamics model contains no parameters about tooth surface topography, this paper puts forward an improved nonlinear dynamic model of gear pair with tooth surface microscopic features through revision of the backlash equation by W–M function from fractal theory and combination with the tradition gear torsional model. The model sets up a mathematical relationship between gear dynamic characteristics and surface microscopic parameters such as surface roughness and fractal dimension. Results of the numerical simulations indicate that as surface roughness decreases, meshing stiffness increases and viscous damping rises, the gear dynamic performance tends to be better, which is consistent with the existing research reports. Furthermore, it is found that dropping of fractal dimension is good to improve gear dynamic performance, so gear dynamics can be enhanced by decreasing the fractal dimension if surface roughness is set or cannot be decreased anymore. Moreover, it is also shown that initial backlash has little impact on the rule of gear dynamics response but influences the size of start-up or stop shock. Finally, the model is validated by a series of simulations and comparison with experimental data and existing model. The theory here opens up a mathematical methodology to analyze gear dynamics with respect to tooth surface microscopic features, which lays a theoretical basis for design of tooth surface topography to obtain better performance of gear transmission in the future.

1 Introduction

Research on gear dynamics has been studied over the past 50 years [1,2,3,4,5,6], and the topic about the mathematical modeling for gear pairs is always the scholars’ interests. Among the existing mathematical models of gear pair, the effect of time-varying stiffness, viscous damping and backlash nonlinearity on gear dynamics is, especially, the research focus in recent years.

Kahraman et al. [7,8,9] started earlier to research on dynamic response influenced by time-variant stiffness and backlash nonlinearity and presented two mathematical models: One is about a single degree of freedom (SDOF) for a gear pair; the other is concerned with a three degree of freedom (TDOF) system for a geared rotor-bearing system. Özgüven et al. [10] presented a six degree of freedom (DOF) nonlinear semi-definite model of geared system with consideration of time-variant mesh stiffness and damping, gear backlash, and profile modification, etc.; Wang et al. [11] formulated a SDOF nonlinear time-varying dynamic model for a hypoid gear-pair system and studied gear dynamic response influenced by mesh stiffness asymmetry, in which they concluded that increasing mesh stiffness variation (a similar parameter to stiffness coefficient in this paper) has a negative effect on gear dynamics. Kim et al. [12] analyzed the dynamic response of a pair of spur gears considering translational motion caused by bearing deformation and showed the influences of various mechanical factors on dynamic behavior, including gear mesh stiffness which is also found having a negative relation to the amplitude of the vibration. Amabili et al. [13] researched on an improved SDOF model for a low-contact-ratio spur gear involving time-varying stiffness and damping that is assumed proportional to stiffness, and stated that damping has a positive correlation with gear stability. Theodossiades et al. [14] applied a new analytical methodology into a gear-pair nonlinear model to determine periodic steady-state motions, and then demonstrated the validation by observing several typical dynamic responses of some parameters such as stiffness and damping, where it is verified adding damping tends to improve gear dynamics. Walha et al. [15] employed the elastic gear load discontinuous function to describe backlash nonlinearity, and considered the effects of the essential bodies’ deformability on nonlinear dynamic behavior in geared systems. Moradi et al. [16] established a third-order polynomial function of backlash nonlinearity for the SDOF gear dynamic model, and analyzed the system responses and dynamic transmission error (DTE) of spur gear pairs.

Besides the above researches on modeling of time-variant stiffness, damping and nonlinear backlash, there are also some scholars who concentrated on the influence of friction on tooth surface. Chen et al. [17] studied the effects of both the friction and dynamic backlash with effect of central distance error on dynamic responses in the multi-degree of freedom (MDOF) nonlinear gear system except the parameter of time-varying stiffness; Fang et al. [18] investigated the transient characteristics influenced by surface sliding friction in a geared system with stochastic load.

Through the above analyses, it is clear that the factors such as time-varying meshing stiffness and damping, backlash nonlinearity or friction are emphatically discussed; however, the tooth surface microscopic features such as roughness and topography are often paid little attention. While gear meshing is accompanied with the process of tooth surface contacting, tooth surface micro-structure is bound to play an important role on gear dynamics.

Our team [19] has begun firstly to investigate the effect of tooth surface topography on gear dynamics since 2014, and introduced a new backlash equation by W–M function into traditional dynamic model of gear pair, and then, the relationship between gear dynamics and fractal dimension (a parameter that can reflect the micro-structure of tooth surface) is established; and later Li et al. [20] discussed a MDOF gear nonlinear model which can address the tooth tribological characters on the gear dynamic response for coal cutters, while the basic theory inherits from our paper [19]; Recently, we also obtained a MDOF model to characterize the static transmission error based on fractal theory and built an indirect relationship between dynamic responses and surface roughness [21]. But there are two drawbacks in our previous researches. One is that we assumed that the relationship between surface roughness and fractal dimension is negatively correlated; however, now we find they have no association; the other one is that we only set up the indirect connection of gear dynamics and surface roughness, and the analysis is inconvenient. So, a new gear dynamic model containing both these two parameters is waited to be solved for improving the analytic accuracy and efficiency.

In order to build a direct mathematical relationship between gear dynamics and microscopic features such as surface roughness and fractal dimension, this paper will present the detailed process of establishing an improved nonlinear dynamic model of gear pair. Through executing a series of numerical simulations, the effects of surface roughness and fractal dimension on gear dynamics are analyzed. The simulation results as well as the comparison of the theory with existing experimental data indicate that the model is correct and reasonable. An important contribution of the theory here is to prove that reducing the surface roughness is beneficial for gear transmission by analytical method but not experimental way. The other factors such as initial backlash, time-varying stiffness and damping related to the gear dynamics will also be discussed, and some fresh results are obtained there.

The rest of the paper is organized as follows. Section 2 is the review of traditional torsional vibration model; Sect. 3 provides the detailed process of setting up the mathematical model for gear-pair system considering tooth surface microscopic features; Sect. 4 is the simulation and discussion of the model, where effects of main parameters in the model on gear dynamic performance are analyzed and relevant results are discussed; Sect. 5 shows the experimental validation; Summary and conclusions are given in Sect. 6.

2 Review of traditional torsional vibration model of gear pairs

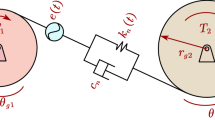
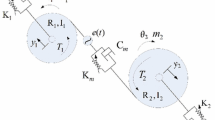
There are usually four models for gear pair, such as dynamic load factor model, torsional vibration model, drive system model and gear system model, where the torsional vibration model is the most general [9], as shown in Fig. 1.

Fig. 1

The torsional vibration model of gear pair

According to Ref. [9], the gear dynamic equation is represented as follows:

$$\begin{aligned}&m_{\mathrm{e}} \frac{\mathrm{d}^{2}p}{\mathrm{d}t^{2}}+c_\mathrm{h} \frac{\mathrm{d}p}{\mathrm{d}t}+k_\mathrm{h} (t)f_\mathrm{h} (p) \nonumber \\&\quad = f_\mathrm{m} -m_\mathrm{e} \frac{\mathrm{d}^{2}e(t)}{\mathrm{d}t^{2}} \end{aligned}$$

(1)

Here, $m_\mathrm{e}$ is the equivalent mass of gear pair; $c_\mathrm{h}$ is damping coefficient; p(t) is the difference between the dynamic transmission error (DTE) and static transmission error (STE) changing with time (t); $f_\mathrm{m}$ is the external static load.

$k_\mathrm{h} (t)$ is time-varying stiffness. Choose the first-order harmonic component, then $k_\mathrm{h} (t)$ is shown as follows [9]:

$$\begin{aligned} k_\mathrm{h} (t)=k_{\mathrm{hm}} +k_{\mathrm{har}} \hbox {cos} ({\omega _\mathrm{h} t + {\phi }_\mathrm{h}}) \end{aligned}$$

(2)

where $k_{\mathrm{hm}}$ is average meshing stiffness, $k_\mathrm{har} \hbox {cos}({\omega _\mathrm{h} t+ {\phi }_\mathrm{h}})$ is the first-order harmonic component; $\omega _\mathrm{h}$ is gear meshing frequency; ${\phi }_\mathrm{h}$ is the initial phase of time-varying stiffness.

e(t) is static transmission error. Suppose it fits monogenetic harmonic function.

$$\begin{aligned} e(t)=e_\mathrm{r} \cos ({\omega _\mathrm{h} t+ {\phi }_\mathrm{e}}) \end{aligned}$$

(3)

where $e_\mathrm{r}$ is the comprehensive error amplitude, ${\phi }_\mathrm{e}$ is the initial phase of static transmission error.

$f_\mathrm{h} (p)$ is backlash function, which is usually calculated by the Eq. (4).

$$\begin{aligned} f_\mathrm{h} (p)=\left\{ \begin{array}{l} {p-b_\mathrm{h}, \qquad x>b_\mathrm{h} } \\ {0, \quad \qquad -b_\mathrm{h}<x<b_\mathrm{h} } \\ {p+b_\mathrm{h}, \qquad x<-b_\mathrm{h} } \\ \end{array} \right. \end{aligned}$$

(4)

where $b_\mathrm{h}$ is backlash of gear pair.

(Note: Please find the rest of variable meaning in the list of symbols.)

3 Mathematical model for a gear-pair system considering tooth surface microscopic features

3.1 Mathematical representation of gear backlash

Figure 2 shows the structure of gear meshing, where A is the highest point of tooth asperities in gear 1; B is the highest point of tooth asperities in gear 2; $b_0$ is the initial backlash which is the gap between A and B.

Fig. 2

The micro-structure of the tooth surface

Based on the literature [22], gear backlash is usually represented as the following two forms:

• (a) a fixed value.

• (b) a steady random number which meets the normal distribution.

While these two types of gear backlashes ignore the influence affected by the microscopic features, such as surface roughness and fractal dimension.

Fig. 3

The simulation of backlash ($b^{\prime }$). a$\xi =0.5$, b$\xi =2.0$

According to the results in [23,24,25], rough surfaces of machined metal have fractal characteristics and can be simulated by W–M function [26,27,28], so we assume that gear backlash also meets fractal law, which can be called the third form:

• (c) a fractal law given by W–M function

  $$\begin{aligned} b(t)= \sum \limits _{k=0}^{+\infty } \lambda ^{({D-2})k}\sin ({\lambda ^{k}t}) \end{aligned}$$

  (5)

Here, b(t) is the backlash varying with time. $\lambda$ is the characteristic scale coefficient (let $\lambda =1.5$ according to literature [28] for we also suppose tooth surface is random and normally distributed); D is fractal dimension. (Set $1< D < 2$, because only two-dimensional fractal is discussed here).

Through Eq. (5), we can set up an indirect relationship between gear dynamic performance and tooth surface features, which can be utilized to improve the gear dynamic performance through designing the gear surface morphology. The study about this topic had been finished by our group on 2014, and the detailed content can be found in the literature [19].

But recently, we find a drawback in the above methodology. That is, the calculation by Eq. (5) is not unique even if we set D as a fixed value. For example, when we multiply a scale factor ($\xi$) to the right side of Eq. (5), the D is unchanged but the value of b is changed, which can be shown as:

$$\begin{aligned} b^{\prime }(t)=\xi *\sum \limits _{k=0}^{+\infty } \lambda ^{({D-2})k}\sin ({\lambda ^{k}t}) \end{aligned}$$

(6)

Here, $b^{\prime }(t)$ is the backlash with $\xi$; $\xi$ is a scale factor (let $\xi > 0$).

Figure 3 displays the simulation result by Eq. (6) with $\xi =0.5$ and $\xi =2.0$.

It is shown clearly in Fig. 3 that fractal dimension D is also equal to 1.1 as $\xi$ changes, but the values of backlash are different. So, how to get a determinate value of backlash when D is fixed is the following difficulty. In order to resolve the above puzzle, we will firstly revise the W–M function so as to obtain the accurate amplitude of surface topography, and then redesign the formula of gear backlash.

Considering that arithmetic mean deviation ($R_\mathrm{a}$) can be used to precisely measure surface roughness, the parameter ($R_\mathrm{a}$) is introduced to calibrate the value of surface topography amplitude coupled with W–M function.

Suppose $\xi =1$ and then the $R_\mathrm{a}$ corresponding to D is easily obtained by programming, shown in Table 1.

Table 1 Values of $R_\mathrm{a}$ with different D

However, when the fractal dimension (D) is fixed (such as $D =1.1$), the actual surface roughness ($R_\mathrm{a}$) is not just the results listed in Table 1. In order to establish the mathematical relationship between the height of surface asperities by the W–M function and the actual surface roughness, the scale factor is defined as:

$$\begin{aligned} \xi = \frac{R_\mathrm{a}}{R_\mathrm{a} D(D)} \end{aligned}$$

(7)

where $R_\mathrm{a}$ is the actual surface roughness; $R_\mathrm{a} D$ is the function to get the corresponding $R_\mathrm{a}$ with a definite D, which can be obtained from Table 1. For example, if $D=1.1$, $R_\mathrm{a} D = 0.8727$; if $D =1.2$, $R_\mathrm{a} D =1.2181$; and so on. Then, the new W–M function is changed to

$$\begin{aligned} z^{\prime }(t)=\frac{R_\mathrm{a} }{R_\mathrm{a} D(D)} \cdot \sum \limits _{k=0}^{+\infty } \lambda ^{({D-2})k}\sin ({\lambda ^{k}t}) \end{aligned}$$

(8)

where $z^{\prime }(t)$ is the new height of surface asperities. Through the revised W–M function (here called $\hbox {W}{-}{\hbox {M}}^{\prime }$), a real tooth topography and its unevenness can be simulated and calculated by mathematical equation including tooth surface microscopic features ($R_\mathrm{a}$ and D).

According to Eq. (8) and considering the difference of the two teeth roughness ($R_\mathrm{a}$) and fractal dimension (D), gear backlash is redefined as

$$\begin{aligned} b_\mathrm{h}^{\prime } (t)= & {} b_0 -\frac{R_{\mathrm{a}_1}}{R_\mathrm{a} D({D_1})} \cdot \sum \limits _{k=0}^{+\infty } \lambda ^{({D_1 -2})k}\sin ({\lambda ^{k}t})\nonumber \\&-\frac{R_{\mathrm{a}_2}}{R_\mathrm{a} D({D_2})} \cdot \sum \limits _{k=0}^{+\infty } \lambda ^{({D_2 -2})k}\sin ({\lambda ^{k}t}) \end{aligned}$$

(9)

where $b_\mathrm{h}^{\prime }$ is updated backlash of gear pair; $b_0$ is the initial backlash (see Fig. 2). If $b_0 =0$, there is no backlash, which is an ideal state for gear installation; $R_{\mathrm{a}1}, \, R_{\mathrm{a}2}$ is the surface roughness of gear 1 and gear 2, respectively; $D_1, \, D_2$ is the fractal dimension of gear 1 and gear 2, respectively.

3.2 Mathematical model for a gear-pair system considering tooth surface microscopic features

Substituting Eq. (9) into Eq. (4), a new backlash function with tooth surface microscopic features is gained:

$$\begin{aligned} f_\mathrm{h}^{\prime } (p)=\left\{ \begin{array}{l} p-b_\mathrm{h}^{\prime }, \quad x>b_\mathrm{h}^{\prime } \\ 0, \quad -b_\mathrm{h}^{\prime }<x<b_\mathrm{h}^{\prime } \\ p+b_\mathrm{h}^{\prime }, \quad x<-b_\mathrm{h}^{\prime } \\ \end{array} \right. \end{aligned}$$

(10)

where $f^{\prime }_h (p)$ is modified backlash function.

Combining Eqs. (10) and (1), and based on the result in [9], we can get the revised model of gear dynamics considering tooth surface microscopic features in the dimensionless form:

$$\begin{aligned}&{\ddot{p^{\prime }}} ({t^{\prime }})+2\zeta _{33} {\dot{p^{\prime }}} ({t^{\prime }})+ [1-\varepsilon \cdot \cos (\varOmega _h t^{\prime })]) f_\mathrm{h} (p^{\prime }(t^{\prime })) \nonumber \\&\quad =F_\mathrm{m} +F_{\mathrm{ah}} {\varOmega }_\mathrm{h}^2 \cos ({\varOmega }_\mathrm{h} t^{\prime }) \end{aligned}$$

(11)

(Note: in Eq. (11) we only consider the internal excitation for the sake of convenience [9].)

where $p^{\prime } (t^{\prime })$ is the dimensionless difference between the dynamic transmission error (DTE) and static transmission error (STE) changing with nominal time ($t^{\prime }$), $t^{\prime }$ is nominal time.

Let $\omega _\mathrm{n} = \sqrt{\frac{k_{\mathrm{hm}}}{m_\mathrm{e}}}$, ${p}^{\prime } = \frac{p}{b_\mathrm{h}^{\prime }}$, $t^{\prime } = \frac{t}{\omega _\mathrm{n}}$; ${\varOmega }_\mathrm{h}$ is dimensionless excitation frequency, ${\varOmega }_\mathrm{h} =\omega _\mathrm{h} /\omega _\mathrm{n}$.

${\upzeta }_{33}$ is the dimensionless gear mesh damping ($\zeta _{33} = c_\mathrm{h} / ({2m_\mathrm{e} \omega _\mathrm{n}}))$, $\varepsilon$ is time-varying stiffness coefficient ($\varepsilon =k_\mathrm{har}/k_{\mathrm{hm}}$); $F_\mathrm{m}$ is dimensionless external load $({F_\mathrm{m} = f_\mathrm{m}/ ({m_\mathrm{e} b_\mathrm{c} \omega _\mathrm{n}^2})})$, $F_{\mathrm{ah}}$ is dimensionless error amplitude ($F_{\mathrm{ah}} =e_\mathrm{r} / b_\mathrm{c}$). (Here, we set ${\phi }_\mathrm{h} = \pi$, and ${\phi }_\mathrm{e} =0$ referencing to [9].) $f_\mathrm{h}^{\prime } ({p^{\prime }})$ is the dimensionless modified backlash function of gear pair given as follows:

$$\begin{aligned} f_\mathrm{h}^{\prime } ({p^{\prime }}) = \left\{ \begin{array}{l} p^{\prime }-b^{\prime }_h /b_\mathrm{c}, \quad x>b_\mathrm{h} /b_\mathrm{c} \\ 0, \quad b_\mathrm{h} /b_\mathrm{c}<x<b_\mathrm{h} /b_\mathrm{c} \\ p^{\prime }+b^{\prime }_h /b_\mathrm{c}, \quad x<-b_\mathrm{h} /b_\mathrm{c} \\ \end{array} \right. \end{aligned}$$

(12)

Here, $b_\mathrm{c}$ is the characteristic length (let $b_\mathrm{c} =1$ in this paper for the sake of convenience).

The main difference of this updated model by Eq. (11) from the existing ones is that the model established a mathematical relationship between gear dynamics and tooth micro-information such as surface roughness $({R_\mathrm{a}})$ and fractal dimension (D), which can be used to analyze the effect of tooth surface microscopic structures on gear dynamics by analytic way, and to optimize the design of tooth topography for better gear transmission performance.

4 Numerical simulation and discussion

In this section, we will utilize Eq. (11) to evaluate the effect of main parameters in the new model on gear dynamics, especially focusing on the microscopic features such as surface roughness ($R_\mathrm{a}$) and fractal dimension (D), aiming at validating the model as well as looking for some fresh results.

As the model is a nonlinear equation, a fifth–sixth-order Runge–Kutta numerical integration algorithm with variable time step is employed here to solve Eq. (11), which is implemented in MATLAB SIMULINK.

4.1 Gear dynamics influenced by surface roughness ($R_\mathrm{a}$)

Table 2 Lists of analysis data with variety of $R_\mathrm{a}$

Referring to the examples in [9], we set the parameters values as follows: $b_0 = 0$, $\varepsilon =0.1$, $\zeta _{33} =0.1$, $F_\mathrm{m} =0.2$, $F_{\mathrm{ah}} =0.05$, ${\Omega }_\mathrm{h} =0.85$.

Here, we suppose $R_\mathrm{a}$ changes from 0.8 to $12.5\,\upmu \hbox {m}$, and D varies from 1.1 to 1.9. Considering the concision of the paper, we only list part of the analysis data related to Table 2, where we assume that $R_{\mathrm{a}1}$ and $R_{\mathrm{a}2}$ change together when $D_1$ and $D_2$ are fixed and equal.

Fig. 4

The dynamic characteristics with variety of $R_\mathrm{a}$, where $R_{\mathrm{a}1} =R_{\mathrm{a}2}$, $D_1 =D_2 =1.1$. a$R_{\mathrm{a}1} =R_{\mathrm{a}2} =0.8\,\upmu \hbox {m}$, b$R_{\mathrm{a}1} =R_{\mathrm{a}2} =3.2\,\upmu \hbox {m}$, c$R_{\mathrm{a}1} =R_{\mathrm{a}2} =12.5\,\upmu \hbox {m}$. Here, AMP means the amplitude of the signal ($p^{\prime }$). Note: Here, we only display part of the results corresponding to Table 2 for succinctness of the paper

From Fig. 4, we know that as the surface roughness of both gears adds, the time histories $p^{\prime } ({t^{\prime }})$ gradually increase from 0.3532, 0.3683 to 0.4272 (Fig. 4(i) ‘Time History Chart’), and the shape of phase diagram changes from regular circles to irregular circles progressively (Fig. 4(ii) ‘Phase Diagram’); the point distribution tends to be dispersed from centralized (Fig. 4(iii) ‘Poincaré Perception Mapping’) and the system frequency number grows observably, especially at 0–0.05 Hz and 0.1–0.15 Hz (Fig. 4(iv) ‘FFT Spectrogram’); so gear system shows a transform from periodic to chaotic response, and the stability of gear transmission deteriorates when $R_{\mathrm{a}1}$ and $R_{\mathrm{a}2}$ turn from 0.8 to $12.5\,\upmu \hbox {m}$.

Table 3 Lists of analysis data with variety of D

Fig. 5

The dynamic characteristics with variety of D, where $D_1 = D_2$, $R_{\mathrm{a}1} =R_{\mathrm{a}2} =1.6\,\upmu \hbox {m}$. a$D_1 =D_2 =1.1$, b$D_1 =D_2 =1.5$, c$D_1 =D_2 =1.9$

Fig. 6

The dynamic characteristics with variety of $b_0$. a$b_0 =0$, b$b_0 =0.5$, c$b_0 =1.0$

(Note: We also find the law of gear dynamics to be similar to the above when only one of the surface roughness adds leaving the other one unchanged. Here, these related results of graphs are not presented for avoiding the redundant display and boring reading.)

Thus, we can draw a conclusion that tooth surface roughness has a strong impact on gear dynamics, and reducing surface roughness (both or one of the tooth surfaces) will improve the performance of gear dynamics, which is a common fact that higher quality of tooth surface will bring better gear transmission. The reasonable result can preliminarily prove that the model is correct.

Discussion In fact, the result by the model here is not novel, but the model firstly sets up a mathematical expression between gear dynamics and tooth surface roughness, and with this model we can prove that decreasing the surface roughness is good to improve the performance of gear transmission by analytic method but not experiment way.

4.2 Gear dynamics influenced by fractal dimension (D)

Firstly, we also set the main parameters as follows: $b_0 =0$, $\varepsilon =0.1$, $\zeta _{33} =0.1$, $F_\mathrm{m} =0.2$, $F_{\mathrm{ah}} =0.05$, ${\Omega }_\mathrm{h} =0.85$.

Table 3 lists part of analysis data, where we suppose that $D_1$ and $D_2$ vary together when $R_{\mathrm{a}1}$ and $R_{\mathrm{a}2}$ are the same and fixed.

Figure 5 displays the plots of time histories, phase diagram, poincaré perception mapping and FFT spectrogram corresponding to Table 3.

Here, we also present some of the figures only with $D = 1.1$, $D = 1.5$ and $D =1.9$ for the sake of compactness of the paper.

From Fig. 5, we can see that when surface roughness keeps fixed, as adding the fractal dimension of both teeth surfaces, the time histories $p^{\prime } (t^{\prime })$ rise continuously with the values fluctuating from 0.3582, 0.3615 to 0.3693 [Fig. 5(i)]; the phase diagram alters to thick circles from thin circles [Fig. 5(ii)]; the range of points becomes to bigger one from small one gradually [Fig. 5(iii)]; the number of frequency around 0.05 Hz and 0.15 Hz increases noticeably as D adds [Fig. 5(iv)]. So, the gear dynamics experiences a single-cycle response to multiple-cycle response when $D_1$ and $D_2$ vary from 1.1 to 1.9.

Fig. 7

Gear meshing with initial backlash $b_0$

Fig. 8

Time-varying stiffness with variety of $\varepsilon$

(Note: When we only change one of the fractal dimensions and keep surface roughness of the two teeth surface fixed and different, the effect rule of fractal dimension on gear dynamics is the same to the above.)

Therefore, we can conclude that with the increase in fractal dimension, the performance of gear dynamics declines, which is compatible with our previous conclusion [19].

Discussion According to the above conclusion, we can acquire a new way to make gear dynamic characteristics better through changing the surface topography besides the surface roughness. That is, when surface roughness is set or can decreased no more, we can further better the gear transmission by decreasing the fractal dimension through micromachining techniques such as femtosecond laser, micro-ultrasonic machining (micro-USM) or micro-electrical discharge machining (micro-EDM) [29], which will be our next plan and research focus.

4.3 Gear dynamics influenced by initial backlash $({{\varvec{b}}}_\mathbf{0})$

Here, we assume the main parameters as follows: $\varepsilon =0.1$, $\zeta _{33} =0.1$, $F_\mathrm{m} =0.2$, $F_{\mathrm{ah}} =0.05$, ${\Omega }_\mathrm{h} =0.85$, $R_{\mathrm{a}1} =0.8$, $R_{\mathrm{a}2} =0.8$, $D_1 =1.5$, $D_2 =1.5$.

Fig. 9

The dynamic characteristics with variety of $\varepsilon$. a$\varepsilon =0$, b$\varepsilon =0.1$, c$\varepsilon =0.2$

Fig. 10

The dynamic characteristics with variety of dimensionless damping -$\zeta _{33}$. a$\zeta _{33} =0.01$, b$\zeta _{33} =0.05$, c$\zeta _{33} =0.10$

From Fig. 6, we can find clearly that when tooth surface roughness and fractal dimension are fixed, as initial backlash rises, the amplitude of the time histories $p^{\prime } (t^{\prime })$ are the same, whereas the average value of displacement increases from about 0.2, 0.7 to 1.2; the results at phase diagram, Poincaré Perception Mapping and FFT spectrogram are identical.

Thus, variety of initial backlash will not alter the rule of gear dynamic response, but change the average size of difference between the dynamic transmission error and static transmission error ($p^{\prime } (t^{\prime })$).

Discussion We can explain the above result by observing the process of gear meshing. Figure 7 demonstrates the meshing state of a gear pair. When the driving gear 1 rotates, the driven gear 2 will not rotate until the initial backlash is eliminated. Once the two gears contact, they will not depart and the initial backlash disappears. So, the value of initial backlash will not influence the vibration amplitude of the gear pairs, but only affect the size of transmission error when the gear transmission starts, stops or changes the rotate direction. That is the reason why the above three conditions with different initial backlashes all display the same vibration response, only leaving the absolute value of $p^{\prime } (t^{\prime })$ altered.

In addition, we can also conclude that if the gear system is one-way movement or can bear the start-up or stop shock in a very short time, we can accept a little initial backlash for it will be missing after the system steps in stable operation, which will bring convenience for gear installation as a reward.

4.4 Gear dynamics influenced by time-varying stiffness coefficient $(\varvec{\varepsilon })$

Let the main parameters be as follows: $b_0 =0.1$, $\zeta _{33} =0.1$, $F_\mathrm{m} =0.2$, $F_{\mathrm{ah}} =0.05$, ${\Omega }_\mathrm{h} =0.85$, $R_{\mathrm{a}1} =1.6$, $R_{\mathrm{a}2} =0.8$, $D_1 =1.2$, $D_2 =1.8$.

(Note: We modify some of the parameters for the universality of the result)

Figure 8 shows the result with $\varepsilon =0, 0.1$ and 0.2, where it is clear that the amplitude of dimensionless time-varying stiffness becomes bigger as $\varepsilon$ rises; it is constant when $\varepsilon =0$.

From Fig. 9, we can observe that when time-varying stiffness coefficient grows, the time histories $p^{\prime } (t^{\prime })$ fluctuate stronger from 0.2319, 0.3582 to 0.8335, and there exits multilateral shock when $\varepsilon =0.2$ because the displacement appears to be a negative value [Fig. 9c(i)]; the shape of phase diagram changes from circle to noncircular [Fig. 9(ii)], and the points also turn to be dispersed progressively [Fig. 9(iii)]; besides, frequency size grows gradually at $\sim \,0.22 \, \hbox {Hz}$ [(Fig. 9(iv)], and the system tends to be chaotic from stable.

Thus, decreasing the time-varying stiffness coefficient and making the stiffness steady is advantageous to improve the gear dynamics.

Discussion Based on the definition of time-varying stiffness coefficient in Eq. (11) ($\varepsilon =k_\mathrm{har} /k_{\mathrm{hm}}$, here $k_{\mathrm{hm}}$ is the average stiffness), reducing $\varepsilon$ means increasing average stiffness, and then, the vibration is restrained, so the vibration extent descents, and the system dynamics will be better. Therefore, the result about $\varepsilon$ is reliable, which is also consistent with the existing studies [9, 11, 12].

4.5 Gear dynamics influenced by dimensionless damping (${\varvec{\zeta }}_{33}$)

Give the main parameters as follows: $b_0 =0.1$, $\varepsilon =0.1$, $F_\mathrm{m} =0.2$, $F_{\mathrm{ah}} =0.05$, ${\Omega }_\mathrm{h} =0.85$, $R_{\mathrm{a}1} =1.6$, $R_{\mathrm{a}2} =1.6$, $D_1 =1.3$, $D_2 =1.7$.

From Fig. 10, we can know that when dimensionless damping rises, the time histories $p^{\prime } (t^{\prime })$ drop apparently from 1.4625, 1.1587 to 0.3622; moreover, the gear system varies from multilateral shock to unilateral shock because there is only positive values when $\zeta _{33} =0.10$ (Fig. 10c), while there are negative and positive values both in Fig. 10a, b; the shape of phase diagram alters from disordered shape, noncircular to regular circle [Fig. 10(ii)], and the points also tend to be concentrated gradually [Fig. 10(iii)]; the number of frequency at 0.22 Hz drops progressively [Fig. 10(iv)], and the system tends to be stable from chaotic.

Thus, adding the damping is beneficial for improvement in gear transmission, which is identical with the result from most of the studies [9, 13, 14].

Table 4 Main parameters of Kubo’s test rig [30]

Fig. 11

Comparison of theory with Kubo’s experiment and Kahraman’s model

Discussion As we know, when the damping rises, the systematic response will become non-sensitive or dull to the excitation, and the system has more power to keep the original state, and then, the dynamic characteristic will be better. So, the result about the damping here is reasonable. But the increase in damping will also bring the loss of power; therefore, the proper increment of the damping is helpful for better dynamic performance.

5 Experimental validation

For the sake of verifying the above model efficiently, here we will compare our theory with Kubo’s experiment results as well as Kahraman’s model [9]. Table 4 shows the parameters of the setup in Kubo’s experiment.

Fig. 12

Dynamic transmission error (DTE) changing with surface roughness

Fig. 13

Dynamic transmission error (DTE) changing with fractal dimension

Here, we inherit the definition of dynamic factor as the dynamic to static mesh force ratio from Kahraman [9], which is equivalent to the meaning of dynamic factor given by Kubo according to Kahraman’s explanation. Figure 11 presents the result of comparison among Kubo’s experiment, Kahraman’s model and our theory. It is clearly shown that during the lower frequency (0.2–0.5), our model is perfectly compatible with the Kubo’s; when the frequency goes to 0.5–0.8, our model is consistent with Kahraman’s; and as the frequency comes to 0.8–1.3, our model is between the Kubo’s and Kahraman’s. Based on the above analysis, we can see that our model can reflect the correct tendency of dynamic factor changing with frequency.

Discussion One of the reasons that our model does not display the exactly compatible result with Kubo’s experimental data is that we cannot get more detailed parameters of tooth surface characters such as fractal dimension and surface roughness under Kubo’s work condition, so we just set $R_\mathrm{a} =1.6\, \upmu \hbox {m}$ and $D =1.4$ because the result by these two values is most suitable after our tremendous simulations and calculations; furthermore, the wear condition is also omitted in this paper. They will all bring some possible calculation errors. The main purpose of the comparison here is to validate our model preliminarily by the contrast; in the next step, we will start to take some corresponding experiments with respect to our model.

In order to verify those previous conclusions at Sects. 4.1 and 4.2, we investigate the effect of tooth surface roughness and fractal dimension on dynamic transmission error (DTE).

Figure 12 shows that as surface roughness decreases, DTE also drops; conversely, when surface roughness adds, DTE increases too. Therefore, reducing surface roughness is beneficial to improve gear dynamic performance, which is consistent with the result at Sect. 4.1 and the actual application experience.

Figure 13 gives the results of DTE with different fractal dimensions. It is clear that dropping D is effective to reduce DTE and thereby to promote gear dynamic characteristics, which also bring us the enlightenment that we can further improve the gear dynamics by decreasing the D if $R_\mathrm{a}$ is set or can be decreased no more.

6 Conclusion

This paper presented a revised nonlinear dynamic model of gear pair with tooth surface micro-characters through combining a new backlash equation given by updated W–M function from the fractal theory and traditional gear torsional model. The model here built a mathematical correlation between gear dynamics and surface microscopic parameters such as surface roughness and fractal dimension. By means of a series of numerical simulations and comparison with exiting experimental data, the model is validated. The main results by the model are as follows.

• (1) Tooth surface roughness has an important impact on gear dynamics; reducing surface roughness (both or one of the tooth surfaces) will improve the performance of gear dynamics, which is corresponding with the common understanding. Although this is not a fresh conclusion, here we proved it by analytic method but not experimental way.

• (2) Fractal dimension lays a definite influence on gear dynamics; when fractal dimension declines, gear dynamic performance escalates. Thus, if surface roughness is set or cannot be decreased more, we can further enhance the gear dynamics by decreasing the fractal dimension through modern manufacture techniques such as femtosecond laser, micro-USM and micro-EDM.

• (3) Initial backlash puts a little effect on the rule of gear dynamic response but changes the size of start-up or stop shock. That is, when initial backlash rises, the vibration amplitude and cycle number keep unchanged, only the average value of difference between the dynamic transmission error and static transmission error increases, which will bring start-up and stop shock. Thus, if the gear system is one-way movement and can bear the start-up or stop shock in a short time, we may allow a little initial backlash for the economy.

• (4) With the growth of time-varying stiffness and damping, the system tends to be more steady. Thus, properly increasing the value of meshing stiffness and damping is good for the betterment of gear dynamics. The result is consistent with most of the research reports.

The theory here updated the nonlinear model of a gear pair which can analyze the effect of tooth surface microscopic features on gear dynamics by mathematical methodology. Our next plan will focus on the design of tooth surface topography for better performance of gear transmission as well as related experiments.