1 Introduction

Fractional calculus is widely used in research fields such as electrochemical systems, fluid mechanics and viscoelastic materials [1,2,3]. The chemical properties of many physical materials show strong fractional-order dynamic behavior. A large number of references show that the use of fractional-order system model modeling and identification can better express this dynamic behavior than integer-order systems. Fractional calculus, as a tool that can accurately reflect the operating state of the system, is currently focused on the research of fractional-order modeling and identification and fractional-order control methods.

The application of fractional calculus in the field of control is relatively mature compared to the field of modeling and identification, and some researchers have achieved fruitful results. Many researchers have combined fractional calculus and control algorithms to produce many new control algorithms, such as fractional-order nonlinear time-delay multi-agent control [4]; fractional state feedback control [5, 6]; fractional output feedback control [7]; adaptive internal model control with fractional parameters [8]; and fractional fuzzy control [9, 10] control algorithms. The modeling and identification of the system are the prerequisite that the system can be accurately controlled. Therefore, it is particularly important to use fractional calculus to model and identify the dynamic behavior of the system.

The difficulty of modeling and identification of fractional-order systems compared with integer-order systems is that it not only needs to identify the structural parameters of the system but also the fractional order of the system, so that the difficulty of system identification is greatly increased. According to the identification model, the system fractional-order model can be divided into fractional-order transfer function model and state-space model. For these two different models, researchers have carried out a lot of research and achieved rich results. In the identification of fractional-order state-space model, Jonscher et al. [11] established a fractional-order state-space model of inductance and capacitance; Tan Cheng et al. [12] used Lyapunov stability theory to design a fractional-order nonlinear controller and successfully controlled the pseudo-continuous Boost circuit in mode; Karima Hammar et al. [13] used the Levenberg–Marquardt algorithm to identify the state-space model of the fractional-order Hammerstein system.

In the identification of the fractional-order transfer function model, Victor et al. [14] used a fractional filter to propose a time domain identification method based on equation error and output error; Fahim et al. [15] extended the auxiliary variable method to the fractional-order system and improved it; Shalaby et al. [16] proposed an identification method for fractional-order continuous systems based on orthogonal basis functions and block impulse functions; Karima Hammar et al. [17] used Levenberg–Marquardt algorithm to study Hammerstein-Wiener nonlinear fractional-order system identification problem and successfully identified the system structure parameters and system fractional order. In the identification of fractional-order Hammerstein nonlinear ARMAX system with colored noise, some scholars have also made a series of research. Cheng Songsong et al. [18] proposed a multi-innovation fractional stochastic gradient algorithm to identify Hammerstein nonlinear ARMAX system. Jin Qibing et al. [19] proposed adaptive differential evolution with the local search strategy (ADELS) algorithm with the steepest descent method and the overparameterization-based auxiliary model recursive least squares (OAMRLS) algorithm to deal with the identification of the fractional-order Hammerstein model. There are some problems in the identification methods of systems with colored noise, such as slow convergence speed and low accuracy. Therefore, based on the Levenberg–Marquardt (L–M) algorithm, combined with the multi-innovation identification algorithm, this paper proposes the multi-innovation Levenberg–Marquardt (MILM) algorithm to identify the fractional-order Hammerstein nonlinear ARMAX system that contains colored noise. At the same time, the auxiliary model is used to deal with the unknown noise variables. It can identify the structural parameters and fractional order of the system with colored noise, and it can also improve the convergence speed and accuracy of the algorithm.

The contributions of this paper are as follows:

  1. (1)

    Solved the problem of high identification difficulty for the fractional-order Hammerstein nonlinear ARMAX system with colored noise;

  2. (2)

    Combine the multiple innovation algorithm with the L-M identification algorithm to improve the convergence speed and accuracy of the algorithm;

  3. (3)

    Using auxiliary model method to solve the problem of unknown noise term;

  4. (4)

    Solve the problem of parameter coupling and multiple identification parameters.

The overall structure of this paper is as follows: Sect. 2 describes the fractional-order calculation and fractional-order linear model; Sect. 3 constructed a fractional-order Hammerstein nonlinear ARMAX system with colored noise; Sect. 4 first introduces the L–M algorithm and the multi-innovation identification algorithm, and then combines the two algorithms to propose the MILM identification algorithm and finally makes an overall summary of the algorithm proposed in this paper; Sect. 5 uses academic example and flexible robotic arm example to verify the proposed method.

2 Mathematical description

This part introduces the basic concepts related to fractional-order calculations and the fractional-order linear Hammerstein model. First, the principle part of fractional-order calculation gives the calculus used in this paper. Then, the linear model of the fractional-order Hammerstein transfer function is described and defined in detail.

2.1 Calculation of fractional-order system

In the past decades in system modeling and control, fractional-order systems have attracted continually an increasing interesting among researchers. The most commonly used in discrete cases are GL fractional calculus [20], RL fractional calculus [21] and Caputo fractional calculus [22], which is used in this paper is the definition of GL calculus is expressed as follows:

$$ \Delta^{\alpha } x(kh) = \frac{1}{{h^{\alpha } }}\sum\limits_{j = 0}^{k} {( - 1)^{j} \left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right)x(k - j)} . $$
(1)

where \(\Delta^{\alpha }\) is the fractional-order difference operator of order \(\alpha\); \(x(kh)\) denotes a function of \(t = kh\), which k is the k-th sampling, and h is assumed to be equal to 1. The term \(\left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right)\) is the binomial term defined by

$$ \left( {\begin{array}{*{20}l} \alpha \\ j \\ \end{array} } \right) = \left\{ {\begin{array}{*{20}l} 1 & {{\text{for}}\;j = 0} \\ {\frac{\alpha (\alpha - 1) \cdots (\alpha - j + 1)}{{j!}}} & {{\text{for}}\;j > 0} \\ \end{array} } \right.. $$
(2)

According to (1) and (2), we give the following recurrence equation:

$$ \left\{ {\begin{array}{*{20}l} {w(0) = 1} \hfill \\ {w(j) = \left( {1 - \frac{{\alpha + 1}}{j}} \right)w(j - 1)\quad {\text{for}}\;j = 1,2,...,k} \hfill \\ \end{array} } \right.. $$
(3)

where

$$ w(j) = \left( { - 1} \right)^{j} \left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right). $$
(4)

According to (4), (1) can be written as the following equation,

$$ \Delta^{\alpha } x(k) = \sum\limits_{j = 0}^{k} {w(j)x(k - j)} . $$
(5)

In this paper, we use (5) as the fractional calculation to study the modeling of the fractional-order Hammerstein system (FOHS) in subsequent sections.

2.2 Fractional-order linear models

In fractional-order systems, there exist different linear models defined from the fractional-order systems [23,24,25]. In this paper, we use the transfer function model of the fractional-order description. This linear transfer function is defined as follows:

$$ y(k) = G(z)u(k) = \frac{B(z)}{{A(z)}}u(k). $$
(6)

where \(u(k)\) and \(y(k)\) are the system input and the system output, respectively. \(A(z)\) and \(B(z)\) are the denominator polynomial and the numerator polynomial, respectively,

$$ \begin{aligned} A(z) & = 1 + a_{1} z^{{ - \alpha _{1} }} + a_{2} z^{{ - \alpha _{2} }} + \cdots + a_{{n_{a} }} z^{{ - \alpha _{{n_{a} }} }} , \\ B(z) & = b_{1} z^{{ - \gamma _{1} }} + b_{2} z^{{ - \gamma _{2} }} + \cdots + b_{{n_{b} }} z^{{ - \gamma _{{n_{b} }} }} ; \\ \end{aligned} $$

\(\alpha_{i}\) and \(\gamma_{j}\)(\(i = 1,2,...,n_{a}\), and \(j = 1,2,...,n_{b}\)) are the corresponding fractional orders of the polynomials, \(\alpha_{i} \in {\mathbb{R}}^{ + }\) and \(\gamma_{j} \in {\mathbb{R}}^{ + }\), and \(z^{ - 1}\) is a unit backward shift operator with \(z^{ - 1} y(k) = y(k - 1)\).

When the fractional orders of the denominator polynomial and the numerator polynomial in (6) are completely different, the fractional-order models of (6) are generally non-identical (disproportionate) order systems; otherwise, each fractional order is an integer multiple of the base order (\(\alpha\) is order factor), αi = iα, γi = jα \((i = 1,2...,n_{a} ;\;j = 1,2...,n_{b} )\), such a model is defined as a homogeneous (proportionate) order system. In this paper, consider a proportional fractional-order system. Then, (6) can be written as:

$$ \begin{aligned} y(k) & = \frac{{B(z)}}{{A(z)}}u(k) \\ & = \frac{{b_{1} z^{{ - \alpha }} + b_{2} z^{{ - 2\alpha }} + \cdots + b_{{n_{b} }} z^{{ - n_{b} \alpha }} }}{{1 + a_{1} z^{{ - \alpha }} + a_{2} z^{{ - 2\alpha }} + \cdots + a_{{n_{a} }} z^{{ - n_{a} \alpha }} }}u(k). \\ \end{aligned} $$
(7)

By means of the discrete fractional-order operator \(\Delta\) and the derivation [17], (7) can be derived as follows:

$$ \begin{aligned} y(k) & = [1 - A(z)]y(k) + B(z)u(k) \\ & = - a_{1} \Delta^{\alpha } y(k - 1) - a_{2} \Delta^{\alpha } y(k - 2) - \cdots \\ & \quad - a_{{n_{a} }} \Delta^{\alpha } y(k - n_{a} ) + b_{1} \Delta^{\alpha } u(k - 1) \\ & \quad + b_{2} \Delta^{\alpha } u(k - 2) + \cdots + b_{{n_{b} }} \Delta^{\alpha } u(k - n_{b} ) \\ & { = } - \sum\limits_{i = 1}^{{n_{a} }} {a_{i} \Delta^{\alpha } } y(k - i){ + }\sum\limits_{i = 1}^{{n_{b} }} {b_{i} \Delta^{\alpha } } u(k - i). \\ \end{aligned} $$
(8)

This linear model in (8) is employed as the model of the linear part of the fractional-order Hammerstein system.

3 Problem description

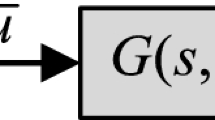
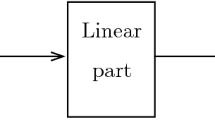
Assume that the general structure of a Hammerstein system in Fig. 1 is defined by the series connection of one nonlinear block with a linear fractional dynamic block, which is described by an ARMAX model.

Fig. 1
figure 1

The structure diagram of the nonlinear fractional-order stochastic system

Full size image

In Fig. 1, the nonlinear ARMAX model of the Hammerstein system is shown as follows:

$$ y(k) = x(k) + w(k). $$
(9)
$$ x(k) = G(z)\overline{u}(k) = \frac{B(z)}{{A(z)}}\overline{u}(k). $$
(10)
$$ w(k) = N(z)v(k) = \frac{D(z)}{{A(z)}}v(k). $$
(11)

where \(u(k)\) and \(y(k)\) are the input signal and the output signal of the overall system, respectively. \(\overline{u}(k)\) and \(x(k)\) are the input and the output of the linear block, respectively. Meanwhile, \(\overline{u}(k)\) is the output of the nonlinear block. \(v(k)\) is the outside noise signal. \(w(k)\) is a contaminated noise signal. Here, \(A(z)\), \(B(z)\) and \(D(z)\) are polynomials in the shift operator given the following polynomials:

$$ \begin{aligned} A(z) & = 1 + a_{1} z^{{ - \alpha_{1} }} + a_{{2}} z^{{ - \alpha_{2} }} + \cdots + a_{{n_{a} }} z^{{ - \alpha_{{n_{a} }} }} \\ & = 1 + \sum\limits_{i = 1}^{{n_{a} }} {a_{i} } z^{{ - \alpha_{i} }} \\ \end{aligned} $$
(12)
$$ \begin{aligned} B(z) & = b_{1} z^{{ - \beta_{1} }} + b_{2} z^{{ - \beta_{2} }} + \cdots + b_{{n_{b} }} z^{{ - \beta_{{n_{b} }} }} \\ & = \sum\limits_{i = 1}^{{n_{b} }} {b_{i} } z^{{ - \beta_{i} }} . \\ \end{aligned} $$
(13)
$$ \begin{aligned} D(z) & = 1 + d_{1} z^{{ - \gamma_{1} }} + d_{2} z^{{ - \gamma_{2} }} + \cdots + d_{{n_{d} }} z^{{ - \gamma_{{n_{d} }} }} \\ & = {1 + }\sum\limits_{i = 1}^{{n_{d} }} {d_{i} } z^{{ - \gamma_{i} }} . \\ \end{aligned} $$
(14)

The nonlinear block is represented by the nonlinear function \(f( \cdot )\), which is expressed as a linear combination of a known basis functions. It is written as the following equation:

$$ \overline{u}(k) = f(u(k)) = c_{1} f_{1} (u(k)) + c_{2} f_{2} (u(k)) + \cdots + c_{m} f_{m} (u(k)). $$
(15)

From (1)–(3), the Hammerstein nonlinear ARMAX model is given as the following form,

$$ A(z)y(k) = B(z)\overline{u}(k) + D(z)v(k). $$
(16)
$$ \overline{u}(k) = f(u(k)) = c_{1} f_{1} (u(k)) + c_{2} f_{2} (u(k)) + \cdots + c_{m} f_{m} (u(k)). $$
(17)

For the motivation of this paper, the identification method is developed to identify the parameters \(a_{i}\), \(b_{i}\), \(c_{i}\), \(d_{i}\) and fractional orders \(\alpha_{i}\), \(\beta_{i}\), \(\gamma_{i}\).

Using (12)–(14), replacing \(A(z)\), \(B(z)\) and \(D(z)\) in (16) gives

$$ \begin{aligned} y(k) & = - \sum\limits_{i = 1}^{{n_{a} }} {a_{i} z^{{ - \alpha_{i} }} y(k)} + \sum\limits_{i = 1}^{{n_{b} }} {b_{i} z^{{ - \beta_{i} }} f(u(k))} \\ & \quad + \sum\limits_{i = 1}^{{n_{d} }} {d_{i} z^{{ - \gamma_{i} }} v(k) + v(k)} . \\ \end{aligned} $$
(18)

Substituting (17) in (18) results in the overall model:

$$ \begin{aligned} y(k) & = - \sum\limits_{i = 1}^{{n_{a} }} {a_{i} z^{{ - \alpha_{i} }} y(k)} + \sum\limits_{i = 1}^{{n_{b} }} {b_{i} z^{{ - \beta_{i} }} \sum\limits_{j = 1}^{m} {c_{j} f_{j} (u(k))} } \\ & \quad + \sum\limits_{i = 1}^{{n_{d} }} {d_{i} z^{{ - \gamma_{i} }} v(k) + v(k)} . \\ \end{aligned} $$
(19)

In this paper, consider the commensurate order in (19), \(\alpha_{i} = i\tilde{\alpha }\), \(\beta_{j} = j\tilde{\alpha }\), \(\gamma_{l} = l\tilde{\alpha }\). (19) can be rearranged in the time domain, using the difference operator \(\Delta\) in [17]:

$$ \begin{aligned} y(k) & = - \sum\limits_{i = 1}^{{n_{a} }} {a_{i} \Delta^{{\tilde{\alpha }}} y(k - i)} + \sum\limits_{i = 1}^{{n_{b} }} {b_{i} \sum\limits_{j = 1}^{m} {c_{j} \Delta^{{\tilde{\alpha }}} f_{j} (u(k))} } \\ & \quad + \sum\limits_{i = 1}^{{n_{d} }} {d_{i} \Delta^{{\tilde{\alpha }}} v(k - i) + v(k)} \\ & { = } - \sum\limits_{i = 1}^{{n_{a} }} {a_{i} \Delta^{{\tilde{\alpha }}} y(k - i)} + c_{1} \sum\limits_{i = 1}^{{n_{b} }} {b_{i} \Delta^{{\tilde{\alpha }}} f_{1} (u(k - i)) + \cdots } \\ & \quad + c_{m} \sum\limits_{i = 1}^{{n_{b} }} {b_{i} \Delta^{{\tilde{\alpha }}} f_{m} (u(k - i))} + \sum\limits_{i = 1}^{{n_{d} }} {d_{i} \Delta^{{\tilde{\alpha }}} v(k - i) + v(k)} \\ \end{aligned} $$
(20)

In this paper, the main work is to design or develop a new identification method to estimate the unknown parameters and fractional commensurate order of the Hammerstein nonlinear model.

4 Identification method

The identification goal consists in confirming the parameters \(a_{i}\), \(b_{i}\), \(c_{i}\), \(d_{i}\) as well as the order \(\tilde{\alpha }\) in (20). The L–M algorithm is proposed to identify these parameters and the corresponding fractional order. It is a robust nonlinear optimization approach which includes the Gauss–Newton optimization and the gradient descent. However, this method suffers from the drawback points, including multiple parameters coupling, complex computation and slow convergence. This paper extends the multi-innovation L–M algorithm for the identification of the Hammerstein model by the multi-innovation identification principle. The principle of multi-innovation identification is proposed in [26,27,28,29]. The basic idea of multi-innovation identification is to extend scalar innovation to multi-innovation vector and innovation vector to innovation matrix, which uses both current data and past data. The research results of many papers have shown that the proposed multi-innovation identification algorithms can improve the convergence of the algorithms and the accuracy of parameters estimation. Therefore, this paper introduces it into the identification algorithm. For (20), the regression representation of the nonlinear relationship is written as the following form,

$$ y(k){ = }{\varvec{\varphi }}^{{\text{T}}} (k,\tilde{\alpha })\tilde{\theta }{ + }v(k). $$
(21)

where the parameter vector \(\tilde{\theta }\) and information vector \({\varvec{\varphi }}(k,\tilde{\alpha })\) are defined as

$$ \tilde{\theta } = \left[ {\begin{array}{*{20}l} {\mathbf{a}} \\ {c_{1} {\mathbf{b}}} \\ {c_{2} {\mathbf{b}}} \\ \vdots \\ {c_{m} {\mathbf{b}}} \\ {\mathbf{d}} \\ \end{array} } \right] \in {\mathbb{R}}^{n} ,\quad {\mathbf{\varphi }}(k,\tilde{\alpha }) = \left[ {\begin{array}{*{20}l} {{{\varvec{\uppsi}}}(k,\tilde{\alpha })} \\ {\Delta^{{\tilde{\alpha }}} v(k - 1)} \\ {\Delta^{{\tilde{\alpha }}} v(k - 2)} \\ \vdots \\ {\Delta^{{\tilde{\alpha }}} v(k - n_{d} )} \\ \end{array} } \right] \in {\mathbb{R}}^{n} ,\quad n = n_{a} + mn_{b} + n_{d} $$

where \({\mathbf{a}} = \left[ {\begin{array}{*{20}l} {a_{1} } \\ {a_{2} } \\ \vdots \\ {a_{{n_{a} }} } \\ \end{array} } \right] \in {\mathbb{R}}^{{n_{a} }}\), \({\mathbf{b}} = \left[ {\begin{array}{*{20}l} {b_{1} } \\ {b_{2} } \\ \vdots \\ {b_{{n_{b} }} } \\ \end{array} } \right] \in {\mathbb{R}}^{{n_{b} }}\), \({\mathbf{c}} = \left[ {\begin{array}{*{20}l} {c_{1} } \\ {c_{2} } \\ \vdots \\ {c_{m} } \\ \end{array} } \right] \in {\mathbb{R}}^{m}\), \({\mathbf{d}} = \left[ {\begin{array}{*{20}c} {d_{1} } \\ {d_{2} } \\ \vdots \\ {d_{{n_{d} }} } \\ \end{array} } \right] \in {\mathbb{R}}^{{n_{d} }}\)

$$ {{\varvec{\uppsi}}}(k,\tilde{\alpha }) = \left[ {\begin{array}{*{20}c} {{{\varvec{\uppsi}}}_{0} (k,\tilde{\alpha })} \\ {{{\varvec{\uppsi}}}_{1} (k,\tilde{\alpha })} \\ {{{\varvec{\uppsi}}}_{2} (k,\tilde{\alpha })} \\ \vdots \\ {{{\varvec{\uppsi}}}_{m} (k,\tilde{\alpha })} \\ \end{array} } \right] \in {\mathbb{R}}^{n} , $$
$$ {{\varvec{\uppsi}}}_{0} (k,\tilde{\alpha }) = \left[ {\begin{array}{*{20}c} { - \Delta^{{\tilde{\alpha }}} y(k - 1)} \\ { - \Delta^{{\tilde{\alpha }}} y(k - 2)} \\ { - \Delta^{{\tilde{\alpha }}} y(k - 3)} \\ \vdots \\ { - \Delta^{{\tilde{\alpha }}} y(k - n_{a} )} \\ \end{array} } \right] \in {\mathbb{R}}^{{n_{a} }} , $$
$$ {{\varvec{\uppsi}}}_{j} (k,\tilde{\alpha }) = \left[ {\begin{array}{*{20}l} {\Delta^{{\tilde{\alpha }}} f_{i} (u(k - 1))} \\ {\Delta^{{\tilde{\alpha }}} f_{i} (u(k - 2))} \\ {\Delta^{{\tilde{\alpha }}} f_{i} (u(k - 3))} \\ \vdots \\ {\Delta^{{\tilde{\alpha }}} f_{i} (u(k - n_{b} ))} \\ \end{array} } \right] \in {\mathbb{R}}^{{n_{b} }} ,\quad j = 1,2,...,m. $$

The identification process of the Hammerstein system requires the estimation of the total parameter vector \({{\varvec{\uptheta}}}\) which includes the parameter vectors \({\mathbf{a}}{,}\;{\mathbf{b}}{,}\;{\mathbf{d}}\) of the linear block and the parameters \(c_{i}\)(\(i = 1,2,...,m\)) of the nonlinear block as well as the fractional order. The total parameter vector is defined as,

$$ {{\varvec{\uptheta}}} = \left[ {{\tilde{\varvec{\uptheta }}}^{{\text{T}}} \quad \alpha } \right]^{{\text{T}}} \in {\mathbb{R}}_{\theta } ,\;{\mathbb{R}}_{\theta } = n + 1. $$

Consider the quadratic output criterion,

$$ J = \frac{1}{N}\sum\limits_{k = 1}^{N} {e^{2} (k)} . $$
(22)

where \(N\) is the total number of the sampled data.\(e(k)\) is the estimation error to be minimized,

$$ e(k) = y(k) - \hat{y}(k) = y(k) - {\mathbf{\varphi }}^{{\text{T}}} (k,\hat{\tilde{\alpha }})\hat{\tilde{\theta }}. $$
(23)

where \(\hat{y}(k)\), \({\mathbf{\hat{\tilde{\theta }}}}\) and \(\hat{\tilde{\alpha }}\) are the estimates of \(y(k)\), \({\tilde{\mathbf{\theta }}}\) and \(\tilde{\alpha }\). The iterative L–M algorithm is used to confirm the total parameter vector as the following form:

$$ {{\varvec{\uptheta}}}^{(i + 1)} = {{\varvec{\uptheta}}}^{(i)} + \left\{ {\left[ {J^{\prime \prime } + \lambda I} \right]^{ - 1} J^{\prime } } \right\}_{{\hat{\theta } = \theta^{(i)} }} . $$
(24)

Based on the calculation of the gradient \(J^{\prime }\), and the Hessian calculation \(J^{\prime \prime }\) with respect to all parameters of \({{\varvec{\uptheta}}}\). Using the calculation in (21), a difficulty of arises because \(\Delta^{{\tilde{\alpha }}} v(k - i)\) and the fractional order \(\tilde{\alpha }\) are unknown in \({\mathbf{\varphi }}(k)\), thus \({\mathbf{\varphi }}(k)\) in the expression on the right-hand side of (23) contains the unknown elements \(- \Delta^{{\tilde{\alpha }}} y(k - 1)\), \(\Delta^{{\tilde{\alpha }}} f_{i} (u(k - 1))\), \(\Delta^{{\tilde{\alpha }}} v(k - i),\) so it is impossible to estimate the parameter vector \({{\varvec{\uptheta}}}\) by (24). In order to deal with this problem, combine with auxiliary model ideas [30], use their corresponding estimates \(- \Delta^{{\hat{\tilde{\alpha }}}} y(k - 1)\), \(\Delta^{{\hat{\tilde{\alpha }}}} f_{i} (u(k - 1))\), \(\Delta^{{\hat{\tilde{\alpha }}}} \hat{v}(k - i)\) to replace the unknown variables \(- \Delta^{{\tilde{\alpha }}} y(k - 1)\), \(\Delta^{{\tilde{\alpha }}} f_{i} (u(k - 1))\), \(\Delta^{{\tilde{\alpha }}} v(k - i)\). From (21), the estimates \(\hat{v}(k)\) are given by

$$ \hat{v}(k){ = }y(k) - \hat{y}(k){ = }y(k) - {\hat{\mathbf{\varphi }}}^{{\text{T}}} (k,\hat{\tilde{\alpha }})\hat{\tilde{\theta }}. $$
(25)

where \({\hat{\mathbf{\varphi }}}(k,\hat{\tilde{\alpha }})\) and \(\hat{\tilde{\theta }}\) are

$$ \hat{\tilde{\theta }} = \left[ {\begin{array}{*{20}c} {{\hat{\mathbf{a}}}} \\ {\hat{c}_{1} {\hat{\mathbf{b}}}} \\ {\hat{c}_{2} {\hat{\mathbf{b}}}} \\ \vdots \\ {\hat{c}_{m} {\hat{\mathbf{b}}}} \\ {{\hat{\mathbf{d}}}} \\ \end{array} } \right] \in {\mathbb{R}}^{n} ,\quad {\hat{\mathbf{\varphi }}}(k,\hat{\tilde{\alpha }}) = \left[ {\begin{array}{*{20}c} {{\hat{\mathbf{\psi }}}(k,\hat{\tilde{\alpha }})} \\ {\Delta^{{\hat{\tilde{\alpha }}}} \hat{v}(k - 1)} \\ {\Delta^{{\hat{\tilde{\alpha }}}} \hat{v}(k - 2)} \\ \vdots \\ {\Delta^{{\hat{\tilde{\alpha }}}} \hat{v}(k - n_{d} )} \\ \end{array} } \right] \in {\mathbb{R}}^{n} , $$

where

\({\hat{\mathbf{a}}} = \left[ {\begin{array}{*{20}c} {\hat{a}_{1} } \\ {\hat{a}_{2} } \\ \vdots \\ {\hat{a}_{{n_{a} }} } \\ \end{array} } \right] \in {\mathbb{R}}^{{n_{a} }}\), \({\hat{\mathbf{b}}} = \left[ {\begin{array}{*{20}c} {\hat{b}_{1} } \\ {\hat{b}_{2} } \\ \vdots \\ {\hat{b}_{{n_{b} }} } \\ \end{array} } \right] \in {\mathbb{R}}^{{n_{b} }}\), \({\hat{\mathbf{c}}} = \left[ {\begin{array}{*{20}c} {\hat{c}_{1} } \\ {\hat{c}_{2} } \\ \vdots \\ {\hat{c}_{m} } \\ \end{array} } \right] \in {\mathbb{R}}^{m}\), \({\hat{\mathbf{d}}} = \left[ {\begin{array}{*{20}c} {\hat{d}_{1} } \\ {\hat{d}_{2} } \\ \vdots \\ {\hat{d}_{{n_{d} }} } \\ \end{array} } \right] \in {\mathbb{R}}^{{n_{d} }}\).

Define \(\otimes\) as Kronecker product or direct product, e.g., \({\hat{\mathbf{c}}} \otimes {\hat{\mathbf{b}}} = \left[ {\begin{array}{*{20}c} {\hat{c}_{1} {\hat{\mathbf{b}}}} \\ {\hat{c}_{2} {\hat{\mathbf{b}}}} \\ \vdots \\ {\hat{c}_{m} {\hat{\mathbf{b}}}} \\ \end{array} } \right]\),

$$ {\hat{\mathbf{\psi }}}(k,\hat{\tilde{\alpha }}) = \left[ {\begin{array}{*{20}c} {{\hat{\mathbf{\psi }}}_{0} (k,\hat{\tilde{\alpha }})} \\ {{\hat{\mathbf{\psi }}}_{1} (k,\hat{\tilde{\alpha }})} \\ {{\hat{\mathbf{\psi }}}_{2} (k,\hat{\tilde{\alpha }})} \\ \vdots \\ {{\hat{\mathbf{\psi }}}_{m} (k,\hat{\tilde{\alpha }})} \\ \end{array} } \right] \in {\mathbb{R}}^{n} , $$
$$ {\hat{\mathbf{\psi }}}_{0} (k,\hat{\tilde{\alpha }}) = \left[ {\begin{array}{*{20}c} { - \Delta^{{\hat{\tilde{\alpha }}}} y(k - 1)} \\ { - \Delta^{{\hat{\tilde{\alpha }}}} y(k - 2)} \\ { - \Delta^{{\hat{\tilde{\alpha }}}} y(k - 3)} \\ \vdots \\ { - \Delta^{{\hat{\tilde{\alpha }}}} y(k - n_{a} )} \\ \end{array} } \right] \in {\mathbb{R}}^{{n_{a} }} , $$
$$ {\hat{\mathbf{\psi }}}_{j} (k,\hat{\tilde{\alpha }}) = \left[ {\begin{array}{*{20}c} {\Delta^{{\hat{\tilde{\alpha }}}} f_{i} (u(k - 1))} \\ {\Delta^{{\hat{\tilde{\alpha }}}} f_{i} (u(k - 2))} \\ {\Delta^{{\hat{\tilde{\alpha }}}} f_{i} (u(k - 3))} \\ \vdots \\ {\Delta^{{\hat{\tilde{\alpha }}}} f_{i} (u(k - n_{b} ))} \\ \end{array} } \right] \in {\mathbb{R}}^{{n_{b} }} ,\quad j = 1,2,...,m. $$

Based on (25), \(\Delta^{{\hat{\tilde{\alpha }}}} \hat{v}(k - i)\) is calculated as the following equations,

$$ \Delta^{{\hat{\tilde{\alpha }}}} \hat{v}(k - i){ = }\sum\limits_{j = 0}^{k - i} {w(j)\hat{v}(k - i - j)} . $$
(26)
$$ \left\{ {\begin{array}{*{20}c} {\hat{w}(0) = 1} \\ {\hat{w}(j) = \left( {1 - \frac{{\hat{\tilde{\alpha }} + 1}}{j}} \right)w(j - 1),\quad {\text{for}}\;j = 1, \ldots ,k - i} \\ \end{array} } \right. $$
(27)

In addition, \(\lambda\) in (24) is a tuning coefficient for the convergence. Based on the recursive equation of the prediction error in (22), the estimated parameters can be computed by the following gradient and the Hessian equations with respect to \(\hat{\tilde{\theta }}\):

$$ J_{{\hat{\tilde{\theta }}}}^{^{\prime}} = - \frac{2}{N}{\hat{\mathbf{\varphi }}}(k,\hat{\tilde{\alpha }})\left[ {y(k) - {\hat{\mathbf{\varphi }}}^{{\text{T}}} (k,\hat{\tilde{\alpha }})\hat{\tilde{\theta }}} \right]. $$
(28)
$$ J_{{\hat{\tilde{\theta }}}}^{\prime \prime } = \frac{2}{N}{\hat{\mathbf{\varphi }}}(k,\hat{\tilde{\alpha }}){\hat{\mathbf{\varphi }}}^{{\text{T}}} (k,\hat{\tilde{\alpha }}). $$
(29)

The calculation equation of the gradient and the Hessian of fractional order \(\hat{\tilde{\alpha }}\) is as follows:

$$ \begin{aligned} J_{{\hat{\tilde{\alpha }}}}^{\prime } & = - \frac{2}{N}\left[ {\frac{{\partial {\hat{\mathbf{\varphi }}}^{{\text{T}}} (k,\hat{\tilde{\alpha }}){\mathbf{\hat{\tilde{\theta }}}}}}{{\partial \hat{\tilde{\alpha }}}}} \right]^{{\text{T}}} \left[ {y(k) - {\hat{\mathbf{\varphi }}}^{{\text{T}}} (k,\hat{\tilde{\alpha }}){\mathbf{\hat{\tilde{\theta }}}}} \right] \\ & = - \frac{2}{N}\left[ {\frac{{\partial \hat{y}(k)}}{{\partial \hat{\tilde{\alpha }}}}} \right]^{{\text{T}}} \left[ {y(k) - {\hat{\mathbf{\varphi }}}^{{\text{T}}} (k,\hat{\tilde{\alpha }}){\mathbf{\hat{\tilde{\theta }}}}} \right] \\ & = - \frac{2}{N}\left[ {\sigma \hat{y}(k)/\hat{\tilde{\alpha }}} \right]^{{\text{T}}} \left[ {y(k) - {\hat{\mathbf{\varphi }}}^{{\text{T}}} (k,\hat{\tilde{\alpha }}){\mathbf{\hat{\tilde{\theta }}}}} \right] \\ \end{aligned} $$

where \(\sigma \hat{y}(k)/\hat{\tilde{\alpha }}\)\(= \frac{{\partial \hat{y}(k)}}{{\partial \hat{\tilde{\alpha }}}}\) is the output sensitivity function with respect to \(\hat{\tilde{\alpha }}\). The sensitivity function is shown as follows:

$$ \sigma \hat{y}(k)/\hat{\tilde{\alpha }} \approx \frac{{\hat{y}(k,\hat{\tilde{\alpha }} + \delta \hat{\tilde{\alpha }}) - \hat{y}(k,\hat{\tilde{\alpha }})}}{{\delta \hat{\tilde{\alpha }}}}. $$
(30)

where \(\delta \hat{\tilde{\alpha }}\) is a small variation of \(\hat{\tilde{\alpha }}\).

The Hessian \(J_{{\hat{\tilde{\alpha }}}}^{^{\prime\prime}}\) can be calculated by

$$ \begin{aligned} J_{{\hat{\tilde{\alpha }}}}^{^{\prime\prime}} & = \frac{2}{N}\left( {\frac{{\partial \hat{y}(k)}}{{\partial \hat{\tilde{\alpha }}}}} \right)^{{\text{T}}} \left( {\frac{{\partial \hat{y}(k)}}{{\partial \hat{\tilde{\alpha }}}}} \right) \\ & = \frac{2}{N}\left( {\sigma \hat{y}(k)/\hat{\tilde{\alpha }}} \right)^{{\text{T}}} \left( {\sigma \hat{y}(k)/\hat{\tilde{\alpha }}} \right). \\ \end{aligned} $$
(31)

Hence, the gradient \(J_{\theta }^{^{\prime}}\) and the Hessian calculation \(J_{\theta }^{^{\prime\prime}}\) are shown as follows:

$$ \begin{aligned} J_{\theta }^{\prime } & = \left[ {\begin{array}{*{20}c} {J_{{\hat{\tilde{\theta }}}}^{\prime } } \\ {J_{{\hat{\tilde{\alpha }}}}^{^{\prime}} } \\ \end{array} } \right] \\ & = - \frac{2}{N}\left[ {\begin{array}{*{20}c} {{\hat{\mathbf{\varphi }}}(k,\hat{\tilde{\alpha }})\left[ {y(k) - {\hat{\mathbf{\varphi }}}^{{\text{T}}} (k,\hat{\tilde{\alpha }})\hat{\tilde{\theta }}} \right]} \\ {\left[ {\sigma \hat{y}(k)/\hat{\tilde{\alpha }}} \right]^{{\text{T}}} \left[ {y(k) - {\hat{\mathbf{\varphi }}}^{{\text{T}}} (k,\hat{\tilde{\alpha }}){\mathbf{\hat{\tilde{\theta }}}}} \right]} \\ \end{array} } \right]. \\ \end{aligned} $$
(32a)
$$ J_{\theta }^{\prime \prime } = \left[ {\begin{array}{*{20}c} {J_{{\hat{\tilde{\theta }}}}^{\prime \prime } } \\ {J_{{\hat{\tilde{\alpha }}}}^{^{\prime\prime}} } \\ \end{array} } \right] = \frac{2}{N}\left[ {\begin{array}{*{20}c} {{\hat{\mathbf{\varphi }}}(k,\hat{\tilde{\alpha }}){\hat{\mathbf{\varphi }}}^{{\text{T}}} (k,\hat{\tilde{\alpha }})} \\ {\left[ {\sigma \hat{y}(k)/\hat{\tilde{\alpha }}} \right]^{{\text{T}}} \left[ {\sigma \hat{y}(k)/\hat{\tilde{\alpha }}} \right]} \\ \end{array} } \right]. $$
(32b)

For the L–M algorithm in (24), it can be considered as the single-innovation estimation algorithm by using the error \(y(k) - \hat{\varphi }^{{\text{T}}} (k,\hat{\tilde{\alpha }})\hat{\tilde{\theta }}\). For the single-innovation L–M algorithm, it can suffer from low convergence speed and low modeling accuracy. For this reason, propose a multi-innovation L–M identification algorithm (MILM).

First, define the L-dimensional innovation vector \({\mathbf{E}}(L,k,\hat{\tilde{\alpha }})\), the input–output information matrix \({\hat{\mathbf{\Phi }}}(L,k,\hat{\tilde{\alpha }})\), the stacked output vector \({\mathbf{Y}}(L,k)\) as follows:

$$ \begin{array}{*{20}c} \begin{aligned} {\mathbf{E}}(L,k,\hat{\tilde{\alpha }}) & = [y(k) - \hat{\varphi }^{T} (k,\hat{\tilde{\alpha }})\hat{\tilde{\theta }},y(k - 1) - \hat{\varphi }^{T} (k - 1,\hat{\tilde{\alpha }})\hat{\tilde{\theta }},..., \\ & \quad y(k - L + 1) - \hat{\varphi }^{T} (k - L + 1,\hat{\tilde{\alpha }})\hat{\tilde{\theta }}]^{T} \in {\mathbb{R}}^{L} \\ \end{aligned} & \begin{aligned} {\hat{\mathbf{\Phi }}}(L,k,\hat{\tilde{\alpha }}) & = [{\hat{\mathbf{\varphi }}}(k,\hat{\tilde{\alpha }}),{\hat{\mathbf{\varphi }}}(k - 1,\hat{\tilde{\alpha }}),..., \\ & \quad {\hat{\mathbf{\varphi }}}(k - L + 1,\hat{\tilde{\alpha }})] \in {\mathbb{R}}^{n \times L} \\ \end{aligned} \\ \end{array} , $$
(33a)
$$ {\mathbf{Y}}(L,k) = \left[ {y(k),y(k - 1),...,y(k - L + 1)} \right]^{{\text{T}}} \in {\mathbb{R}}^{L} ,\quad n = n_{a} + mn_{b} + n_{d} . $$
(33b)

The L-dimensional innovation vector \({\mathbf{E}}(L,k,\hat{\tilde{\alpha }})\) can be also expressed as

$$ {\mathbf{E}}(L,k,\hat{\tilde{\alpha }}) = {\mathbf{Y}}(L,k) - {\hat{\mathbf{\Phi }}}^{{\text{T}}} (L,k,\hat{\tilde{\alpha }}){\mathbf{\hat{\tilde{\theta }}}}. $$
(34)

Define the stacked sensitivity function vector \({{\varvec{\Xi}}}(L,k,\hat{\tilde{\alpha }})\) as

$$ {{\varvec{\Xi}}}(L,k,\hat{\tilde{\alpha }}) = [\sigma \hat{y}(k)/\hat{\tilde{\alpha }},\sigma \hat{y}(k - 1)/\hat{\tilde{\alpha }},...,\sigma \hat{y}(k - L + 1)/\hat{\tilde{\alpha }}]^{{\text{T}}} \in {\mathbb{R}}^{L} . $$
(35)

Thus, the gradient \(J_{\theta }^{\prime }\) and the Hessian calculation \(J_{\theta }^{\prime \prime }\) are rearranged by the above multi-innovation variable definitions,

$$ \begin{aligned} J_{\theta }^{^{\prime}} & = \left[ {\begin{array}{*{20}c} {J_{{\hat{\tilde{\theta }}}}^{^{\prime}} } \\ {J_{{\hat{\tilde{\alpha }}}}^{^{\prime}} } \\ \end{array} } \right] \\ & = - \frac{2}{N}\left[ {\begin{array}{*{20}c} {{\hat{\mathbf{\Phi }}}(L,k,\hat{\tilde{\alpha }})\left[ {Y(k) - {\hat{\mathbf{\Phi }}}^{{\text{T}}} (L,k,\hat{\tilde{\alpha }})\hat{\tilde{\theta }}} \right]} \\ {\left[ {{{\varvec{\Xi}}}(L,k,\hat{\tilde{\alpha }})} \right]^{{\text{T}}} \left[ {Y(k) - {\hat{\mathbf{\Phi }}}^{{\text{T}}} (L,k,\hat{\tilde{\alpha }})\hat{\tilde{\theta }}} \right]} \\ \end{array} } \right]. \\ \end{aligned} $$
(36a)
$$ J_{\theta }^{\prime \prime } = \left[ {\begin{array}{*{20}c} {J_{{\hat{\tilde{\theta }}}}^{\prime \prime } } \\ {J_{{\hat{\tilde{\alpha }}}}^{\prime \prime } } \\ \end{array} } \right] = \frac{2}{N}\left[ {\begin{array}{*{20}c} {{\hat{\mathbf{\Phi }}}(L,k,\hat{\tilde{\alpha }}){\hat{\mathbf{\Phi }}}^{{\text{T}}} (L,k,\hat{\tilde{\alpha }})} \\ {\left[ {{{\varvec{\Xi}}}(L,k,\hat{\tilde{\alpha }})} \right]^{{\text{T}}} \left[ {{{\varvec{\Xi}}}(L,k,\hat{\tilde{\alpha }})} \right]} \\ \end{array} } \right]. $$
(36b)

Using the definitions of \({\hat{\mathbf{\Phi }}}(L,k,\hat{\alpha })\) and \({\mathbf{Y}}(L,k)\), the multi-innovation L–M identification algorithm is organized as follows:

$$ \hat{\tilde{\theta }}^{(m + 1)} = \hat{\tilde{\theta }}^{(m)} + \frac{2}{N}\left\{ {\left[ {\frac{2}{N}{\hat{\mathbf{\Phi }}}(L,k,\hat{\tilde{\alpha }}){\hat{\mathbf{\Phi }}}^{{\text{T}}} (L,k,\hat{\tilde{\alpha }}) + \lambda I} \right]^{ - 1} {\hat{\mathbf{\Phi }}}(L,k,\hat{\tilde{\alpha }})\left[ {Y(L,k) - {\hat{\mathbf{\Phi }}}^{{\text{T}}} (L,k,\hat{\tilde{\alpha }})\hat{\tilde{\theta }}} \right]} \right\}_{{\hat{\tilde{\theta }} = \hat{\tilde{\theta }}^{(m)} }} . $$
(37a)
$$ \hat{\tilde{\alpha }}^{(m + 1)} = \hat{\tilde{\alpha }}^{(m)} + \frac{2}{N}\left\{ {\left[ {\frac{2}{N}{{\varvec{\Xi}}}^{{\text{T}}} (L,k,\hat{\tilde{\alpha }}){{\varvec{\Xi}}}(L,k,\hat{\tilde{\alpha }}) + \lambda I} \right]^{ - 1} {{\varvec{\Xi}}}^{{\text{T}}} (L,k,\hat{\tilde{\alpha }})[{\mathbf{Y}}(L,k) - {\hat{\mathbf{\Phi }}}^{{\text{T}}} (L,k,\hat{\tilde{\alpha }})\hat{\tilde{\theta }}]} \right\}_{{\hat{\tilde{\alpha }} = \hat{\tilde{\alpha }}^{(m)} }} . $$
(37b)

After obtaining the estimated parameter vector \({\hat{\mathbf{\theta }}}\), the first \(n_{a}\) element in \({\hat{\mathbf{\theta }}}\) is the estimate of the vector \({\hat{\mathbf{a}}}\), and the element \(n_{a} { + 1}\) to the \(n_{a} { + }m \times n_{b}\) in \({\hat{\mathbf{\theta }}}\) is the estimate of the vector \({\hat{\mathbf{c}}} \otimes {\hat{\mathbf{b}}}\). By observing the parameter vector \({\hat{\mathbf{\theta }}}\), there are \(n_{b}\) estimate \(\hat{c}_{m}\), the last \(n_{d}\) element in \({\hat{\mathbf{\theta }}}\) is the estimate of the vector \(\hat{d}\). To this end, they are calculated by the average method.

$$ \hat{c}_{j} = \frac{1}{{n_{b} }}\sum\limits_{i = 1}^{{n_{b} }} {\frac{{\theta_{{n_{a} + n_{b} (j - 1) + i}} }}{{b_{i} }}} ,\quad j = 2,3,...,m. $$
(38)

In this paper, the MILM method is proposed to deal with the parameter identification of FOHS and to estimate the fractional order. The whole steps of the proposed method can be summarized as follows:

Step 1 Collect the input and output data set \(\left\{ {u(k),y(k)} \right\}\) of the system;

Step 2 Let \(i = 1\), and set the initial values \(\tilde{\theta }^{0}\), \(\tilde{\alpha }^{0}\), \(\hat{v}(k)^{0}\) and \(\delta \hat{\alpha }\);

Step 3 Construct the information matrix \({\hat{\mathbf{\Phi }}}(L,k_{s} ,\hat{\alpha })\), the stacked output vector \({\mathbf{Y}}(L,k_{s} )\) using (33a) and (33b), respectively, and compute the output fractional-order sensitivity function \(\sigma \hat{y}_{0} (k_{s} )/\hat{\alpha }\) using (30);

Step 4 Construct the stacked sensitivity function vector \({{\varvec{\Xi}}}(L,k_{s} ,\hat{\alpha })\) using (35);

Step 5 Compute \(J_{\theta }^{^{\prime\prime}}\) using (36b) and \(J_{\theta }^{^{\prime}}\) using (36a), update the fractional order estimate \(\tilde{\alpha }\) using (37b) and the parameter estimate \(\tilde{\theta }\) using (37a);

Step 6 Update the noise sequence according to (25), compute the objective function in (22);

Step 7 If \(\frac{{\left| {J({\hat{\mathbf{\theta }}}^{(m + 1)} ) - J({\hat{\mathbf{\theta }}}^{(m)} )} \right|}}{{\left| {J({\hat{\mathbf{\theta }}}^{(m)} )} \right|}} \le \xi\), increase \(\lambda\), otherwise decrease \(\lambda\) and set \(\hat{\theta } = \theta^{(m)}\) and \(J(\hat{\theta }) = J(\theta^{i} )\), then go to Step 3.

The overall algorithm process is summarized as follows:

5 Simulation examples

This part uses two examples to verify the effectiveness of the proposed method. The first example is an academic example of a fractional-order Hammerstein nonlinear ARMAX system, which proves the theoretical feasibility of the method in this paper. Secondly, the method of this paper is applied to the actual system example of the second flexible manipulator experiment, which proves that the modeling effect of this paper is better and the degree of fitting with the actual system is relatively high (Fig. 2).

Fig. 2
figure 2

Overall algorithm flow chart

Full size image

5.1 Academic example

In order to verify the effectiveness of the proposed algorithm, consider the following fractional-order Hammerstein nonlinear ARMAX system, the system structure coefficient is \(n_{a} = 2,\)\(n_{b} = 3,\)\(n_{d} = 2,\) nonlinear output block adopts the polynomial form of \(m = 3\), and the fractional order of the system is \(\alpha = 0.6\), respectively.

$$ \begin{array}{*{20}l} {A(z) = a_{1} z^{ - \alpha } + a_{2} z^{ - 2\alpha } } \\ {B(z) = b_{1} z^{ - \alpha } + b_{2} z^{ - 2\alpha } + b_{3} z^{ - 3\alpha } } \\ {D(z) = d_{1} z^{ - \alpha } + d_{{_{2} }} z^{ - 2\alpha } } \\ \end{array} , $$
$$ f(u(k)) = \sum\limits_{m = 1}^{3} {c_{m} } f_{m} (u(k)). $$

The overall output of the system is expressed as follows:

\(\begin{aligned} y(k) & = - \sum\limits_{i = 1}^{2} {a_{i} } \Delta^{0.6} (y(k - i) + c_{1} \sum\limits_{i = 1}^{3} {b_{i} } \Delta^{0.6} f_{1} (u(k - i) \\ & \quad + c_{2} \sum\limits_{i = 1}^{3} {b_{i} } \Delta^{0.6} f_{2} (u(k - i) + c_{3} \sum\limits_{i = 1}^{3} {b_{i} } \Delta^{0.6} f_{3} (u(k - i) \\ & \quad + \sum\limits_{i = 1}^{2} {d_{i} } \Delta^{0.6} v(k - i) + v(k). \\ \end{aligned}\).with:

$$ \begin{array}{*{20}l} {f_{1} (u(k - i)) = u(k - i)} \hfill \\ \begin{gathered} f_{2} (u(k - i)) = u^{2} (k - i) \hfill \\ f_{3} (u(k - i)) = u^{3} (k - i) \hfill \\ \end{gathered} \hfill \\ \end{array} , $$
$$ \begin{aligned} y(k) & = - a_{1} \Delta^{0.6} y(k - 1) - a_{2} \Delta^{0.6} y(k - 2) + c_{1} b_{1} \Delta^{0.6} u(k - 1) \\ & \quad + c_{1} b_{2} \Delta^{0.6} u(k - 2) + c_{1} b_{3} \Delta^{0.6} u(k - 3) \\ & \quad + c_{2} b_{1} \Delta^{0.6} u^{2} (k - 1) + c_{2} b_{2} \Delta^{0.6} u^{2} (k - 2) \\ & \quad + c_{2} b_{3} \Delta^{0.6} u^{2} (k - 3) + c_{3} b_{1} \Delta^{0.6} u^{3} (k - 1) \\ & \quad + c_{3} b_{2} \Delta^{0.6} u^{3} (k - 2) + c_{3} b_{3} \Delta^{0.6} u^{3} (k - 3) \\ & \quad + d_{1} \Delta^{0.6} v(k - 1) + d_{2} \Delta^{0.6} v(k - 2) + v(k). \\ \end{aligned} $$

The true values of the parameter vector to be estimated are:

$$ \begin{aligned} a & = \left[ {\begin{array}{*{20}l} {a_{1} } \hfill & {a_{2} } \hfill \\ \end{array} } \right]^{{\text{T}}} = \left[ {\begin{array}{*{20}l} {0.1} \hfill & {0.2} \hfill \\ \end{array} } \right]^{{\text{T}}} \\ b & = \left[ {\begin{array}{*{20}l} {b_{1} } \hfill & {b_{2} \, b_{3} } \hfill \\ \end{array} } \right]^{{\text{T}}} = \left[ {\begin{array}{*{20}l} {0.3} \hfill & {0.2{ 0}{\text{.4}}} \hfill \\ \end{array} } \right]^{{\text{T}}} \\ c & = \left[ {\begin{array}{*{20}l} {c_{1} } \hfill & {c_{2} \, c_{3} } \hfill \\ \end{array} } \right]^{{\text{T}}} = \left[ {\begin{array}{*{20}l} 1 \hfill & {0.7{ 0}{\text{.5}}} \hfill \\ \end{array} } \right]^{{\text{T}}} \\ d & = \left[ {\begin{array}{*{20}l} {d_{1} } \hfill & {d_{2} } \hfill \\ \end{array} } \right]^{{\text{T}}} = \left[ {0.25{ 0}{\text{.5}}} \right]^{{\text{T}}} . \\ \end{aligned} $$

The input signal \(u(k)\) is a random signal with a mean value of 0 and a variance of 1, and the noise signal \(v(k)\) is a Gaussian random signal with a mean value of zero and a variance of \(\sigma^{{2}} { = 0}{\text{.01}}\). The data set length is \(N = 1000\), and the number of iterations is 50 times. Before parameter estimation, we must first determine the best structure of the system and test various combinations of \(n_{a} ,n_{b} ,n_{d}\) and \(m\). The index value \(J\) under various test combinations is shown in Table 1 and Fig. 3. It can be clearly seen that the structural parameters when the combination is \([n_{a} ,n_{b} ,n_{d} ,m] = [2,3,2,3]\) [2,3,2,3], the index value is the smallest, so this parameter combination is determined as the best structure.

Table 1 Structure test results of academic example
Full size table
Fig. 3
figure 3

\(J\) under different structure combinations

Full size image

In the study, the length of multiple innovations is selected as \(L = 1,3,5\). In order to verify the effectiveness of the proposed method, the relative error of parameter estimation \({\text{RMSE}} = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {(\hat{\theta } - \theta )^{2} }\), the relative error of fractional-order estimation \(\delta : = \left\| {\hat{\alpha } - \alpha } \right\|\) and the secondary index \(J\) are used as indicators to verify. Following Table 2 continues to show the identification results of parameters and fractional orders under different innovation numbers. Figure 4 shows the \(J\) index curves of different multi-innovation systems.

Table 2 Partial parameter identification results of the fractional-order nonlinear system (L = 1, 3, 5)
Full size table
Fig. 4
figure 4

\(J\) under different number of innovationscxs

Full size image

Figure 5a shows the estimated relative error curves of system parameters with different multi-innovation systems, and Fig. 5b shows the estimated relative error results of the fractional orders of different multi-innovation systems. Through the analysis and comparison of these results, it is obvious that appropriately increasing the length of multiple innovations can speed up the identification convergence speed, and the identification accuracy is higher. Through appropriate partial enlargement of Figs. 4 and 5, it can be found that when the number of innovations \(L = 5\), the relative error of parameter estimation and the relative error of fractional-order estimation are the smallest.

Fig. 5
figure 5

a Relative error of parameter estimation \((L = 1,3,5)\), b relative error of fractional-order estimation \((L = 1,3,5)\)

Full size image

Figures 6a and 7 are the parameter estimation curve and the fractional-order estimation curve of the system when the innovation length \(L = 5\). The estimated value is basically consistent with the true value. The final convergence value and estimation error of the parameters are shown in Fig. 6b. The estimated value can be seen in Table 1. Figure 8 compares the estimated output of the identification model under the innovation length \(L = 5\) with the actual output of the system. After partial amplification and comparison and combined with the system estimation error shown in Fig. 9, the output has a high degree of fit and basically coincides.

Fig. 6
figure 6

a System parameter estimation \((L = 5)\), b parameter estimates and error values

Full size image
Fig. 7
figure 7

Estimated and true values of the fractional order of the system

Full size image
Fig. 8
figure 8

System estimation and actual output

Full size image
Fig. 9
figure 9

System estimation error

Full size image

5.2 Example of a flexible manipulator

The flexible manipulator data obtained in the standard database DAISY [31] are further used to verify the effectiveness of the method proposed in this paper. The measured data set contains 1024 data samples. The input of this system is the reaction torque of the structure on the ground, and the output is the acceleration of the flexible manipulator. Same as Example 1, we first determine the best structure combination of the system. The index value \(J\) under different structure combinations is shown in Table 3 and Fig. 10. When the combination structure is \([n_{a} ,n_{b} ,m,n_{d} ] = [1,3,2,1]\), the index value \(J\) is the smallest. The structure combination of is the best structure combination.

Table 3 Structure test results of flexible manipulator
Full size table
Fig. 10
figure 10

\(J\) under different structure combinations

Full size image

Therefore, the optimal structure of the fractional-order Hammerstein nonlinear ARMAX model of the flexible manipulator system is determined as follows, the parameter vector \([a_{1} ,b_{1,} b_{2} ,b_{3} ,c_{1} ,c_{2} ,d_{1} ]\) is the parameter to be identified, and \(\alpha\) is the fractional order to be identified. From the conclusion of the calculation example 1, it can be seen that an appropriate increase in the innovation number \(L\) can speed up the convergence speed and improve the identification accuracy, and the effect is best when the innovation number \(L = 5\). Therefore, this flexible manipulator calculation example directly uses the innovation number \(L = 5\), and the system parameters and fractional-order identification results are shown in Table 4 and Figs. 11 and 12. The specific values can be seen in Table 4.

$$ \begin{array}{*{20}l} {A(z) = a_{1} z^{{ - \alpha }} } \hfill \\ {B(z) = b_{1} z^{{ - \alpha }} + b_{2} z^{{ - 2\alpha }} + b_{3} z^{{ - 3\alpha }} } \hfill \\ {D(z) = d_{1} z^{{ - \alpha }} } \hfill \\ \end{array} , $$
$$ f(u(k)) = c_{1} f_{1} (u(k)) + c_{2} f_{2} (u(k)). $$
Table 4 Parameter identification results of the fractional-order nonlinear system
Full size table
Fig. 11
figure 11

System parameter estimation

Full size image
Fig. 12
figure 12

System fractional-order estimation

Full size image

The overall output system equation is as follows:

$$ \begin{aligned} y(k) & = - a_{1} \Delta^{\alpha } (y(k - 1)) + c_{1} \sum\limits_{i = 1}^{3} {b_{i} } \Delta^{\alpha } f_{1} (u(k - i) \\ & \quad + c_{2} \sum\limits_{i = 1}^{3} {b_{i} } \Delta^{\alpha } f_{2} (u(k - i) + d_{1} \Delta^{\alpha } v(k - i) + v(k), \\ \end{aligned} $$
$$ \begin{array}{*{20}l} {f_{1} (u(k - i)) = u(k - i)} \hfill \\ {f_{2} (u(k - i)) = u^{2} (k - i)} \hfill \\ \end{array} , $$
$$ \begin{aligned} y(k) & = - a_{1} \Delta^{\alpha } y(k - 1) + c_{1} b_{1} \Delta^{\alpha } u(k - 1) \\ & \quad + c_{1} b_{2} \Delta^{\alpha } u(k - 2) + c_{1} b_{3} \Delta^{\alpha } u(k - 3) \\ & \quad + c_{2} b_{1} \Delta^{\alpha } u^{2} (k - 1) + c_{2} b_{2} \Delta^{\alpha } u^{2} (k - 2) \\ & \quad + c_{2} b_{3} \Delta^{\alpha } u^{2} (k - 3) + d_{1} \Delta^{\alpha } v(k - 1) + v(k). \\ \end{aligned} $$

Using the method proposed in this paper, the model output and actual output identified by the flexible manipulator system are shown in Fig. 13. After partial magnification and combined with the identification output error results of Fig. 14, it can be clearly seen that the accuracy of the identification model is high, which is basically the same as the actual output. Fittingly, the error is almost 0.

Fig. 13
figure 13

System estimation and actual output

Full size image
Fig. 14
figure 14

System estimation error

Full size image

6 Conclusion

Based on the Levenberg–Marquardt algorithm and combined with the multiple innovation identification algorithm, this paper proposes a new MILM algorithm to model and identify the fractional-order Hammerstein nonlinear ARMAX system with colored noise. The innovation vector composed of multiple fractional variables is used as the model input. The proposed MILM algorithm not only identifies the parameters and fractional order of the system, but also solves the problem of slow convergence speed and low accuracy of the pure Levenberg–Marquardt algorithm. Finally, two examples are combined to verify the accuracy and effectiveness of the method proposed in this paper. The control problem of the fractional-order Hammerstein nonlinear ARMAX system with colored noise is the author's future research direction.