1 Introduction

As the research process of system control, fault diagnosis, life prediction, etc. [1,2,3,4,5] requires higher and higher accuracy of the system model, the emergence of fractional operators has attracted extensive attention of scholars. Researchers have integrated fractional operators with various disciplines to derive fractional systems in various industries such as fractional financial risk systems, fractional power systems, fractional sticky systems, and fractional novel coronavirus transmission systems [6,7,8,9,10]. Fractional-order phenomena with heredity and memory have been proven to be ubiquitous in practical systems.

Accurate system model and parameters are prerequisites for accurate design of controllers for the system, so the research on modeling and identification methods for fractional-order systems is particularly important. In recent years, some scholars have proposed a series of methods for the research on the identification methods of fractional order systems. It mainly includes methods based on the least squares method and gradient method. For least squares algorithms, Ahmed et al. assumed that the fractional order is known to identify the fractional order system, and used the integral equation method to study the fractional order model identification problem of the step response, and used the least squares to estimate the time delay and system coefficients of the system at the same time [11]. Djouambi et al. studied the difference between least squares and recursive least squares when the fractional order is known, and used the recursive method to weaken the influence of the singular matrix. The experiment proved that using recursive least squares can get better parameter estimation of fractional order system [12]. Zhao used the least squares method to identify the coefficients of the KiBaM nonlinear fractional order system, and successfully identified the fractional order of the system using the P-type order learning rate [13]. For gradient algorithms, Karima Hammar et al. proposed to use the Levenberg–Marquardt (LM) algorithm to simultaneously identify fractional system parameters and fractional orders, and applied it to two actual systems of flexible manipulator system [14] and halogen lamp heating system [15], the established model can better fit the actual output of the system. Wang et al. studied the nonlinear fractional order system with colored noise, and proposed to use the multi-innovation gradient descent algorithm to identify the system coefficients and fractional order, and successfully completed the identification task combined with the method of key item separation [16]. Zhang and other scholars designed an LM identification algorithm based on the principle of multi-innovation in order to improve the convergence speed and identification accuracy of the algorithm. First, it solved the difficult identification problem of the fractional-order Hammerstein system containing colored noise [17]. Secondly, in order to separate the static nonlinear term and the dynamic linear term of the fractional-order Hammerstein system, a method based on neuro-fuzzy is proposed to fit the polynomial of the nonlinear term, thereby linearizing the system as a whole and reducing the identification difficulty [18]. Recently, Zhang et al. proposed a hybrid identification algorithm, using the multi-innovation stochastic gradient method and the multi-innovation LM algorithm to separate the identification of system parameters from the fractional order, and the two algorithms work alternately [19]. The above methods are all proposed for homogeneous fractional order systems. However, in practical systems, non-homogeneous order is ubiquitous, and homogeneous order is a special assumption of non-homogeneous systems. Therefore, the research on the identification methods of non-homogeneous fractional order systems needs to be paid attention to. Although some scholars have conducted research on the identification methods of non-homogeneous systems. For example, scholars such as Abir and Stéphane studied the use of irrational number fitting combined with the LM algorithm to identify non-homogeneous fractional orders, and proposed a three-stage identification method to reduce the calculation amount of non-homogeneous system identification [20, 21]. However, no in-depth research has been carried out on the solution methods for non-homogeneous fractional partial derivative irrational numbers. For the problem of solving partial derivatives of irrational numbers based on the fractional order identification based on the minimum error, Wang J and other scholars have carried out detailed and clear derivations, but the calculation of the results is too large [22]. There are also some studies that completely entrust the identification problem of fractional order to the swarm intelligence algorithm [23,24,25]. Although these methods can identify the fractional orders of the system, the obtained results are not stable enough, and in non-homogeneous systems, when the number of fractional orders to be identified is large, the calculation time of the identification algorithm is often longer.

At present, the system identification methods are generally divided into two types: online identification and offline identification. Some scholars have proposed a series of offline identification methods for fractional order systems. Tang et al. proposed a numerical calculation method for fractional linear systems using block pulses, and proposed to transform the system and use the interior point method to identify the system parameters with time delay [26]. Similarly, Kothari et al. used Haar wavelet to numerically transform fractional order systems, and also studied the problem of parameter identification of fractional order systems with time delays [27, 28]. In the follow-up work, Wang et al. studied the advantages and disadvantages of various wavelets for modulating fractional system signals. Through experimental comparison, Legendre wavelet is used to fit the system, and Legendre wavelet is used to filter the system at the same time. Finally, the parameter identification of the fractional order system with nonlinear terms is successfully identified.

The above methods are generally based on signal modulation, and these methods have high identification accuracy and have a certain ability to suppress signal noise. However, since this method does not have too many restrictions on calculation time, it can only be used for offline identification work, resulting in a large amount of data storage and high memory requirements [29]. In addition, in the actual production process, some reaction processes cannot be interrupted, resulting in the inapplicability of offline identification methods. At this time, it is imminent to develop a series of online identification methods for such systems that cannot be interrupted. Therefore, the purpose of this paper is to propose an online identification method for non-homogeneous Hammerstein fractional order system parameters. The main contributions are as follows: (1) Combining with Riemann–Liouville (RL) fractional order operator, a new gradient calculation method is proposed, which solves the problem of simultaneous identification of multiple different fractional orders of non-homogeneous fractional order system models. (2) The multi-innovation principle is introduced into the iterative process of the algorithm, and the historical information is used to speed up the convergence speed of the algorithm and improve the identification accuracy. (3) The online identification equation based on the multi-innovation LM algorithm is derived, which provides a real-time identification strategy for non-stop systems.

The sections of this paper are arranged as follows: Sect. 2 introduces the relevant knowledge of the basic theory of fractional order, and explains the representation of fractional order operators and Laplace fractional calculus. Section 3 introduces the structure of Hammerstein non-homogeneous fractional order system, deduces the system representation convenient for system identification, and extracts all the parameters to be identified. Section 4 introduces the LM algorithm based on the multi-innovation principle and identifies the system model parameters in Sect. 3. It introduces the calculation process of identifying fractional gradients in detail, and summarizes the algorithm flow. Section 5 uses a numerical example and a flexible manipulator system to verify the algorithm of this paper. The experimental results show that the method of this paper has good performance in identifying parameters and fitting the actual system.

2 Fundamentals of fractional calculus

2.1 Fractional calculus

Unlike the integer-order system whose order is an integer, the order \(\alpha \in {\mathbb{C}}\) of the fractional-order system, when the real part of \(\alpha\) is \({\text{Re}} (\alpha ) > 0\), then the fractional-order calculus of any integrable function \(f(t)\) can be defined by the fractional-order RL integral operator as follows [30]:

$$ t_{0} I_{t}^{\alpha } f(t) = t_{0} D_{t}^{ - \alpha } f(t) = \frac{1}{\Gamma (\alpha )}\int_{{t_{0} }}^{t} {\frac{f(\tau )}{{(t - \tau )^{1 - \alpha } }}} {\text{d}}\tau $$
(1)

In Eq. (1), \(t_{0} I_{t}^{\alpha }\) represents the fractional integral operator with order \(\alpha\), \(t_{0} D_{t}^{ - \alpha }\) represents the fractional differential operator with order \(- \alpha\), and \(t_{0}\) represents the initial time of the system, when \(t_{0} = 0\), \(t_{0} I_{t}^{\alpha }\) can be abbreviated as \(I^{\alpha }\), and \(t_{0} D_{t}^{ - \alpha }\) can be abbreviated as \(D_{{}}^{ - \alpha }\).

\(\Gamma (\alpha )\) represents the Gamma function [31], it is defined as:

$$ \Gamma (\alpha ) = \int_{0}^{\infty } {e^{ - t} } t^{\alpha - 1} {\text{d}}t $$
(2)

When the real part of \(\alpha\) is \({\text{Re}} (\alpha ) < 0\), the value of \(\Gamma (\alpha )\) will be infinite due to the Eq. (2), which means that the fractional differential of the function \(f(t)\) cannot be calculated directly using the Eq. (1). Therefore, the function \(f(t)\) is integrated by the fractional RL integral operator first, and then the function \(f(t)\) is differentiated by the integer differentiation rule. The RL differential is defined as follows [32]:

$$ t_{0} D_{t}^{\beta } f(t) = t_{0} I_{t}^{ - \beta } f(t) = \frac{1}{\Gamma (n - \beta )}\left( {\frac{{\text{d}}}{{{\text{d}}t}}} \right)^{n} \int_{{t_{0} }}^{t} {\frac{f(\tau )}{{(t - \tau )^{1 + \beta - n} }}} {\text{d}}\tau $$
(3)

where \(\beta = - \alpha\), under zero initial condition (\(t_{0} = 0\)), \(t_{0} I_{t}^{ - \beta }\) can be abbreviated as \(I^{ - \beta }\), and \(t_{0} D_{t}^{\beta }\) can be abbreviated as \(D_{{}}^{\beta }\).

2.2 Fractional Laplace transform

Like the calculus of integer order systems, the Laplace transform can also be used to describe fractional order systems. The Laplace transform of RL fractional calculus is defined as [29]:

$$ {\mathcal{L}}\left\{ {_{0} D_{t}^{\alpha } f(t)} \right\} = s^{\alpha } F(s) - \sum\limits_{k = 0}^{n - 1} {s^{k} } \left[ {_{0} D_{t}^{\alpha - k - 1} f(t)} \right]_{t = 0} $$
(4)

Under zero initial conditions, the Laplace transform of the fractional derivative simplifies to:

$$ {\mathcal{L}}\left\{ {_{0} {\text{D}}_{t}^{\alpha } f(t)} \right\} = s^{\alpha } F(s) $$
(5)

The Laplace transform of the fractional integral under zero initial conditions is given by:

$$ {\mathcal{L}}\left\{ {I_{0}^{\alpha } f(t)} \right\} = s^{ - \alpha } F(s) $$
(6)

3 Hammerstein non-homogeneous fractional order model

The Hammerstein non-homogeneous fractional order system essentially adds the nonlinear term of the input link to the non-homogeneous linear fractional order system. Among them, the non-homogeneous system assumption is to better adapt to the actual system. Although the homogeneous system has rich research results, in the real world, the non-homogeneous system can better describe the actual system. However, the introduction of non-homogeneous elements also makes system identification difficult. Next, we will describe the system identification of non-homogeneous elements in detail.

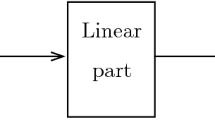
Figure 1 is a non-homogeneous fractional system of Hammerstein. There is a static nonlinear link at its input, and the forward path of the system input is composed of a nonlinear link and a transfer function in series.

Fig.1
figure 1

Structure of Hammerstein non-homogeneous fractional order system

Full size image

In Fig. 1, the system input/output equations are expressed as follows:

$$ y(t) = G(s,{{\varvec{\upalpha}}},{{\varvec{\upbeta}}})\overline{u}(t) $$
(7)
$$ G(s,{{\varvec{\upalpha}}},{{\varvec{\upbeta}}}) = \frac{{B(s,{{\varvec{\upbeta}}})}}{{A(s,{{\varvec{\upalpha}}})}} $$
(8)
$$ \overline{u}(t) = f(u(t)) $$
(9)

Therefore, the complete system by Eqs. (7)-(9) can be expressed as follows:

$$ y(t) = \frac{{B(s,{{\varvec{\upbeta}}})}}{{A(s,{{\varvec{\upalpha}}})}}f(u(t)) $$
(10)

Multiplying both sides of the equation by \(A(s,{{\varvec{\upalpha}}})\), can be expressed as:

$$ A(s,{{\varvec{\upalpha}}})y(t) = B(s,{{\varvec{\upbeta}}})f(u(t)) $$
(11)

where \(A(s,{{\varvec{\upalpha}}})\) and \(B(s,{{\varvec{\upbeta}}})\) in Eq. (11) are expressed as follows:

$$ A(s,{{\varvec{\upalpha}}}) = 1 + a_{1} s^{{\alpha_{1} }} + a_{2} s^{{\alpha_{2} }} + \cdots + a_{{n_{a} }} s^{{\alpha_{{n_{a} }} }} $$
(12)
$$ B(s,{{\varvec{\upbeta}}}) = b_{1} s^{{\beta_{1} }} + b_{2} s^{{\beta_{2} }} + \cdots + b_{{n_{b} }} s^{{\beta_{{n_{b} }} }} $$
(13)

The nonlinear module \(f(u(t))\) in Eq. (11) is expressed as follows:

$$ \begin{aligned} & f(u(t)) = p_{1} f_{1} (u(t)) + \cdots \cdots + p_{{n_{p} }} f_{{n_{p} }} (u(t)) \\ & \quad \quad \quad \quad = \mathop \sum \limits_{i = 1}^{{n_{p} }} p_{i} f_{i} (u(t)) \\ \end{aligned} $$
(14)

Therefore, by Eq. (7) and Eqs. (12)-(14), then Eq. (12) can be expressed as:

$$ y(t) + \mathop \sum \limits_{i = 1}^{{n_{a} }} a_{i} s^{{\alpha_{i} }} y(t) = \mathop \sum \limits_{j = 1}^{{n_{b} }} b_{j} s^{{\beta_{j} }} \overline{u}(t) $$
(15)

Under zero initial conditions, according to Eq. (5) and inverse Laplace transform. Through the transposition operation, then Eq. (15) can be expressed as:

$$ y(t) = - \mathop \sum \limits_{i = 1}^{{n_{a} }} a_{i} D^{{\alpha_{i} }} y(t) + \mathop \sum \limits_{j = 1}^{{n_{b} }} b_{j} D^{{\beta_{j} }} \overline{u}(t) $$
(16)

Considering the actual situation, the system usually contains noise. And for the convenience of reading, the symbol \({\Delta }^{\alpha }\) is used instead of \(D^{\alpha }\). According to Eq. (14), Eq. (16) can be expressed as:

$$ \begin{gathered} y(t) = - \sum\limits_{i = 1}^{{n_{a} }} {a_{i} } \Delta^{{\alpha_{i} }} y(t) + p_{1} \sum\limits_{i = 1}^{{n_{b} }} {b_{i} } \Delta^{{\beta_{i} }} f_{1} (u(t)) + \cdots \hfill \\ \, + p_{{n_{p} }} \sum\limits_{i = 1}^{{n_{b} }} {b_{i} } \Delta^{{\beta_{i} }} f_{{n_{p} }} (u(t)) + v(t) \hfill \\ \end{gathered} $$
(17)

It is worth noting that in order to ensure the uniqueness of the system parameters in the case of the same system input and output, the model parameters must be standardized. Here, we set \(p_{1}\) to 1, then Eq. (17) can be rewritten as:

$$ \begin{gathered} y(t) = - \sum\limits_{i = 1}^{{n_{a} }} {a_{i} } \Delta^{{\alpha_{i} }} y(t) + \sum\limits_{i = 1}^{{n_{b} }} {b_{i} } \Delta^{{\beta_{i} }} f_{1} (u(t)) \hfill \\ \, + p_{{2}} \sum\limits_{i = 1}^{{n_{b} }} {b_{i} } \Delta^{{\beta_{i} }} f_{{2}} (u(t)) + \cdots + p_{{n_{p} }} \sum\limits_{i = 1}^{{n_{b} }} {b_{i} } \Delta^{{\beta_{i} }} f_{{n_{p} }} (u(t)) \hfill \\ \, + v(t) \hfill \\ \end{gathered} $$
(18)

From Eq. (18), it can be concluded that all the parameters of the system to be identified, including the coefficients and orders of non-homogeneous fractions of the system, can be summarized as the following form:

$$ \begin{gathered} {\mathbf{a}} = \left[ {\begin{array}{*{20}l} {a_{1} } \hfill & {a_{2} \cdots a_{{n_{a} }} } \hfill \\ \end{array} } \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{a} }} \hfill \\ {\mathbf{b}} = \left[ {\begin{array}{*{20}l} {b_{1} } \hfill & {b_{2} \cdots b_{{n_{b} }} } \hfill \\ \end{array} } \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{b} }} \hfill \\ {{\varvec{\upalpha}}} = \left[ {\begin{array}{*{20}l} {\alpha_{1} } \hfill & {\alpha_{2} \cdots \alpha_{{n_{a} }} } \hfill \\ \end{array} } \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{a} }} \hfill \\ {{\varvec{\upbeta}}} = \left[ {\begin{array}{*{20}l} {\beta_{1} } \hfill & {\beta_{2} \cdots \beta_{{n_{b} }} } \hfill \\ \end{array} } \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{b} }} \hfill \\ {\mathbf{p}} = \left[ {\begin{array}{*{20}c} {p_{2} } & \cdots & {p_{{n_{p} }} } \\ \end{array} } \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{p} - 1}} \hfill \\ \end{gathered} $$
(19)

Next, we present the contribution of this work. We have developed a new method to identify all the parameters listed in Eq. (19), especially the fractional order in the system. This method can be adapted to the Hammerstein non-homogeneous fractional order model in Eq. (10).

4 Multi-innovation LM identification method

The identification method in this paper is based on the output error method using the LM algorithm. This method combines the advantages of the steepest descent algorithm and Newton's method. To further adapt the algorithm, first the system of Eq. (18) is rewritten as:

$$ y(t) = {\mathbf{\varphi }}^{{\text{T}}} (t,{\tilde{\mathbf{\alpha }}}){\tilde{\mathbf{\theta }}} + v(t) $$
(20)

where information vector \(\varphi (t,{\tilde{\mathbf{\alpha }}})\) is defined as:

$$ {\mathbf{\varphi }}(t,{\tilde{\mathbf{\alpha }}}) = \left[ {\begin{array}{*{20}c} {\phi (t,{{\varvec{\upalpha}}})} \\ {\tilde{\phi }(t,{{\varvec{\upbeta}}})} \\ \end{array} } \right] \in {\mathbb{R}}^{{[n_{a} + n_{b} n_{p} ] \times 1}} $$
(21)
$$ \phi (t,{{\varvec{\upalpha}}}) = \left[ { - \Delta^{{\alpha_{1} }} y(t), \cdots , - \Delta^{{\alpha_{{n_{a} }} }} y(t)} \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{a} \times 1}} $$
(22)
$$ \begin{gathered} \tilde{\phi }(t,{{\varvec{\upbeta}}}) = \left[ {\tilde{\phi }_{1} (t,{{\varvec{\upbeta}}}),\tilde{\phi }_{2} (t,{{\varvec{\upbeta}}}), \cdots ,\tilde{\phi }_{{n_{p} }} (t,{{\varvec{\upbeta}}})} \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{b} n_{p} \times 1}} \hfill \\ \tilde{\phi }_{j} (t,{{\varvec{\upbeta}}}) = \left[ {\Delta^{{\beta_{1} }} f_{j} (u(t)), \cdots ,\Delta^{{\beta_{{n_{b} }} }} f_{j} (u(t))} \right] \, \in {\mathbb{R}}^{{1 \times n_{p} }} \hfill \\ {\text{,for }}j = 1, \ldots ,n_{p} \hfill \\ \end{gathered} $$
(23)

In addition, the coefficients of the information vector \(\varphi (t,{\tilde{\mathbf{\alpha }}})\) are expressed as follows:

$$ \widetilde{{{\varvec{\uptheta}}}} = \left[ {\begin{array}{*{20}c} {\mathbf{a}} & {\mathbf{b}} & {p_{2} {\mathbf{b}}} & \cdots & {p_{{n_{p} }} {\mathbf{b}}} \\ \end{array} } \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{{\tilde{\theta }}} }} ,n_{{\tilde{\theta }}} = n_{a} + n_{b} n_{p} $$
(24)

All fractional orders of the system are integrated as follows:

$$ {\tilde{\mathbf{\alpha }}} = \left[ \begin{gathered} \tilde{\alpha }_{1} \\ \vdots \\ \tilde{\alpha }_{{n_{a} }} \\ \tilde{\alpha }_{{n_{a} + 1}} \\ \vdots \\ \tilde{\alpha }_{{n_{a} + n_{b} }} \\ \end{gathered} \right]^{{\text{T}}} = \left[ \begin{gathered} {{\varvec{\upalpha}}} \hfill \\ {{\varvec{\upbeta}}} \hfill \\ \end{gathered} \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{{\tilde{\alpha }}} }} ,n_{{\tilde{\alpha }}} = n_{a} + n_{b} $$
(25)

It can be seen from Eqs. (20)-(25) that the parameters to be identified are the coefficient \({\tilde{\mathbf{\theta }}}\) and the fractional order \({\tilde{\mathbf{\alpha }}}\) of the information vector \({\mathbf{\varphi }}(t,{\tilde{\mathbf{\alpha }}})\) respectively.

Then all the parameters of the system to be identified, namely the information vector coefficients and fractional order, can be collectively referred to as:

$$ {{\varvec{\uptheta}}} = \left[ {\begin{array}{*{20}l} {\widetilde{{{\varvec{\uptheta}}}}^{{\text{T}}} } \hfill & {{\tilde{\mathbf{\alpha }}}^{{\text{T}}} } \hfill \\ \end{array} } \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{\theta } }} ,n_{\theta } = 2n_{a} + n_{b} (n_{p} + 1) $$
(26)

In order to identify the above parameters of \({{\varvec{\uptheta}}}\), the following objective function is defined:

$$ \min J(t) = \varepsilon^{2} (t) $$
(27)

where \(\varepsilon (t)\) represents the estimation error, and the equation is expressed as follows:

$$ \varepsilon (t) = y(t) - \hat{y}(t,{{\varvec{\uptheta}}}) = y(t) - {\mathbf{\varphi }}^{{\text{T}}} (t,{\mathbf{\hat{\tilde{\alpha }}}}){\varvec{\theta}} $$
(28)

In order to minimize the objective function and achieve the purpose of identification, iterative optimization of the parameters to be identified is required. Obviously, according to the LM algorithm, the system coefficient vector \({\tilde{\mathbf{\theta }}}\) can be iterated by the following method:

$$ {\tilde{\mathbf{\theta }}}(t) = {\tilde{\mathbf{\theta }}}(t - h) - \left\{ {\left[ {{\mathbf{J}}_{{{\tilde{\mathbf{\theta }}}}}^{\prime \prime } + \lambda {\mathbf{I}}} \right]^{ - 1} {\mathbf{J}}_{{{\tilde{\mathbf{\theta }}}}}^{\prime } } \right\}_{{{\tilde{\mathbf{\theta }}} = {\tilde{\mathbf{\theta }}}(t)}} $$
(29)

where \({\tilde{\mathbf{\theta }}}(t)\) represents the identification parameter value at time \(t\), \(h\) represents the sampling time, \(\lambda\) is the harmonic coefficient, \({\mathbf{J}}_{{{\tilde{\mathbf{\theta }}}}}{\prime}\) and \({\mathbf{J}}_{{{\tilde{\mathbf{\theta }}}}}^{^{\prime\prime}}\) are the first-order derivative and the Hessian matrix of the objective function \(J(t)\) to the system coefficient vector \({\tilde{\mathbf{\theta }}}(t)\) respectively, which can be expressed as follows:

$$\begin{aligned} & \mathbf{J}_{\tilde{\theta}}^{\prime}=-2 \varphi(t, \tilde{\alpha})\left[y(t)- \varphi^{\mathrm{T}}(t, \tilde{\alpha}) \tilde{\theta}\right] \\ & \mathbf{J}_{\tilde{\theta}}^{\prime \prime}=2 \varphi(t, \tilde{\alpha}) \varphi^{\mathrm{T}}(t, \tilde{\alpha}) \end{aligned}$$
(30)

It can be seen from Eq. (30) that it is very simple to use Eq. (20) to calculate the gradient information about \({\tilde{\mathbf{\theta }}}(t)\), which makes Eq. (29) very easy to implement. However, in non-homogeneous systems, it is very difficult to identify the fractional order, because the sensitivity function method is usually used for the homogeneous fractional order identification [14], which cannot be used for non-homogeneous systems great. Therefore, we designed a new identification method based on the LM algorithm for the difficulty in identifying the non-homogeneous order of the system such as Eq. (20), and the iterative method is as follows:

$$\tilde{\alpha}(t)=\tilde{\alpha}(t-h)-\left \{\left[\mathbf{J}_{\tilde{\alpha}}^{\prime \prime}+\lambda \mathbf{I}\right]^{-1} \mathbf{J}_{\tilde{\alpha}}^{\prime}\right \}_{\tilde{\alpha}=\tilde{\alpha}(t)}$$
(31)

where \({\tilde{\mathbf{\alpha }}}(t)\) represents the order to be identified at time \(t\), \({\mathbf{J}}_{{{\tilde{\mathbf{\alpha }}}}}{\prime}\) and \({\mathbf{J}}_{{{\tilde{\mathbf{\alpha }}}}}^{^{\prime\prime}}\) are the first-order derivative and the Hessian matrix of the objective function with respect to the fractional order parameter respectively, and the calculation method is as follows:

$$\begin{aligned} & \mathbf{J}_{\tilde{\alpha}}^{\prime}=-2 \boldsymbol{\sigma}_{\hat{y} / \tilde{\alpha}}\left[y(t)- \varphi^{\mathrm{T}}(t, \tilde{\alpha}) \tilde{\theta}\right] \\ & \mathbf{J}_{\tilde{\alpha}}^{\prime \prime}=2 \left[\boldsymbol{\sigma}_{\hat{y} / \tilde{\alpha}} \boldsymbol{\sigma}_{\hat{y} / \tilde{\alpha}}^{\mathrm{T}}- \boldsymbol{\xi}_{\hat{y} / \tilde{\alpha}}\left(y(t)- \varphi^{\mathrm{T}}(t, \tilde{\alpha}) \tilde{\theta}\right)\right] \end{aligned}$$
(32)

where \({{\varvec{\upxi}}}_{{\hat{y}/\tilde{\alpha }}}\) represents the second-order partial derivative matrix of \({\mathbf{\varphi }}^{{\text{T}}} (t,{\tilde{\mathbf{\alpha }}}){\tilde{\mathbf{\theta }}}\) for the fractional vector \({\tilde{\mathbf{\alpha }}}\), which can be derived as follows:

$$ {{\varvec{\upxi}}}_{{\hat{y}/\tilde{\alpha }}} = \frac{{\text{d}}}{{{\text{d}}{\tilde{\mathbf{\alpha }}}}}{{\varvec{\upsigma}}}_{{\hat{y}/\tilde{\alpha }}} \approx {\text{diag}}\left( {\frac{{{{\varvec{\upsigma}}}_{{\hat{y}/(\tilde{\alpha } + \delta \alpha )}} - {{\varvec{\upsigma}}}_{{\hat{y}/\tilde{\alpha }}} }}{{\delta {\tilde{\mathbf{\alpha }}}}}} \right) $$
(33)

where the algebraic representation of \({{\varvec{\upsigma}}}_{{\hat{y}/\tilde{\alpha }}}\) is the key to iterative identification of parameter \({\tilde{\mathbf{\alpha }}}(t)\), which represents the first-order partial derivative of \({\mathbf{\varphi }}^{{\text{T}}} (t,{\tilde{\mathbf{\alpha }}}){\tilde{\mathbf{\theta }}}\) in Eq. (20) with respect to non-homogeneous fractional differential order vector. From Eq. (25), \({{\varvec{\upsigma}}}_{{\hat{y}/\tilde{\alpha }}}\) can be expressed as follows:

$$ {{\varvec{\upsigma}}}_{{\hat{y}/\tilde{\alpha }}} = \left[ \begin{gathered} \sigma_{{\hat{y}/\tilde{\alpha }_{1} }} \\ \vdots \\ \sigma_{{\hat{y}/\tilde{\alpha }_{i} }} \\ \vdots \\ \sigma_{{\hat{y}/\tilde{\alpha }_{{n_{{\tilde{\alpha }}} }} }} \\ \end{gathered} \right] \in {\mathbb{R}}^{{n_{{\tilde{\alpha }}} }} ,\tilde{\alpha }_{i} \in {\tilde{\mathbf{\alpha }}},i = 1, \cdots ,n_{{\tilde{\alpha }}} $$
(34)

It can be seen from Eq. (34) that before giving the result of \({{\varvec{\upsigma}}}_{{\hat{y}/\tilde{\alpha }}}\), we need to derive the partial derivative \(\sigma_{{\hat{y}/\tilde{\alpha }_{i} }}\) of \({\mathbf{\varphi }}^{{\text{T}}} (t,{\tilde{\mathbf{\alpha }}}){\tilde{\mathbf{\theta }}}\) to fractional order \(\tilde{\alpha }_{i}\) first, and the derivation process is based on the RL differential operator. The derivation process is as follows:

First, for the convenience of derivation, we define:

$$ g(t) = {\mathbf{\varphi }}^{{\text{T}}} (t,{\tilde{\mathbf{\alpha }}}){\tilde{\mathbf{\theta }}} = \sum\nolimits_{i = 1}^{{n_{{\tilde{\alpha }}} }} {D_{{}}^{{\tilde{\alpha }_{i} }} g_{{_{i} }} (t,{\tilde{\mathbf{\theta }}})} $$
(35)

It is worth noting that, as can be seen from Eq. (21), Eq. (24) and Eq. (35), \(g(t)\) represents the sum of multiple sub-items of information vector \({\mathbf{\varphi }}^{{\text{T}}} (t,{\tilde{\mathbf{\alpha }}})\) and sub-items of coefficient vector \({\tilde{\mathbf{\theta }}}\). \(D_{{}}^{{\tilde{\alpha }_{i} }} g_{{_{i} }} (t,{\tilde{\mathbf{\theta }}})\) represents sub-items related to fractional order \(\tilde{\alpha }_{i}\) in \(g(t)\), for example:

When \(n_{a} = 2\),\(n_{b} = 2\),\(n_{p} = 3\), using Eq. (18), then sub-items of \(g(t)\) are represented by:

\( \begin{gathered} D_{{}}^{{\tilde{\alpha }_{1} }} g_{1} (t,\widetilde{{\mathbf{\theta }}}) = - a_{1} \Delta ^{{\alpha _{1} }} y(t) \hfill \\ D_{{}}^{{\tilde{\alpha }_{2} }} g_{2} (t,\widetilde{{\mathbf{\theta }}}) = - a_{2} \Delta ^{{\alpha _{2} }} y(t) \hfill \\ D_{{}}^{{\tilde{\alpha }_{3} }} g_{3} (t,\widetilde{{\mathbf{\theta }}}) = b_{1} \Delta ^{{\beta _{1} }} u(t) + p_{2} b_{1} \Delta ^{{\beta _{1} }} u^{2} (t) + p_{3} b_{1} \Delta ^{{\beta _{1} }} u^{3} (t) \hfill \\ D_{{}}^{{\tilde{\alpha }_{4} }} g_{4} (t,\widetilde{{\mathbf{\theta }}}) = b_{2} \Delta ^{{\beta _{2} }} u(t) + p_{2} b_{2} \Delta ^{{\beta _{2} }} u^{2} (t) + p_{3} b_{2} \Delta ^{{\beta _{2} }} u^{3} (t) \hfill \\ \end{gathered} \).

Therefore,

$$ \sigma_{{\hat{y}/\tilde{\alpha }_{i} }} = \frac{{{\text{d}}\left( {D_{{}}^{{\tilde{\alpha }_{i} }} g_{{_{i} }} (t,{\tilde{\mathbf{\theta }}})} \right)}}{{{\text{d}}\tilde{\alpha }_{i} }}, \, i = 1, \cdots ,n_{{\tilde{\alpha }}} $$
(36)

Under zero initial conditions, according to Eq. (3), we can get:

$$ \begin{gathered} \frac{{{\text{d}}\left( {D_{{}}^{{\tilde{\alpha }_{i} }} g_{{_{i} }} (t,{\tilde{\mathbf{\theta }}})} \right)}}{{{\text{d}}\tilde{\alpha }_{i} }} = \frac{{\psi (n - \tilde{\alpha }_{i} )}}{{\Gamma (n - \tilde{\alpha }_{i} )}}\left( {\frac{{\text{d}}}{{{\text{d}}t}}} \right)^{n} \int_{0}^{t} {\frac{{g_{{_{i} }} (\tau ,{\tilde{\mathbf{\theta }}})}}{{(t - \tau )^{1 + \alpha - n} }}} {\text{d}}\tau \hfill \\ \, - \frac{1}{{\Gamma (n - \tilde{\alpha }_{i} )}}\left( {\frac{{\text{d}}}{{{\text{d}}t}}} \right)^{n} \int_{0}^{t} {\frac{{g_{{_{i} }} (\tau ,{\tilde{\mathbf{\theta }}})}}{{(t - \tau )^{1 + \alpha - n} }}} \ln (t - \tau ){\text{d}}\tau \hfill \\ \end{gathered} $$
(37)

where \(\psi ( \cdot )\) represents the Psi function, it is defined as [33]:

$$ \psi ( \cdot ) = \frac{{\text{d}}}{{{\text{d}} \cdot }}\ln \Gamma ( \cdot ) = \frac{{\Gamma^{\prime } ( \cdot )}}{\Gamma ( \cdot )} $$

And the Eq. (37) is integrated and simplified, and the Eq. (37) can be rewritten as:

$$ \frac{{{\text{d}}\left( {D_{{}}^{{\tilde{\alpha }_{i} }} g_{{_{i} }} (t,{\tilde{\mathbf{\theta }}})} \right)}}{{{\text{d}}\tilde{\alpha }_{i} }} = r(t,\tilde{\alpha }_{i} ) + w(t,\tilde{\alpha }_{i} ) $$
(38)

where

$$ r(t,\tilde{\alpha }_{i} ) = \frac{{\psi (n - \tilde{\alpha }_{i} )}}{{\Gamma (n - \tilde{\alpha }_{i} )}}\left( {\frac{{\text{d}}}{{{\text{d}}t}}} \right)^{n} \int_{0}^{t} {\frac{{g_{{_{i} }} (\tau ,{\tilde{\mathbf{\theta }}})}}{{(t - \tau )^{1 + \alpha - n} }}} {\text{d}}\tau $$
(39)
$$ w(t,\tilde{\alpha }_{i} ) = - \frac{1}{{\Gamma (n - \tilde{\alpha }_{i} )}}\left( {\frac{{\text{d}}}{{{\text{d}}t}}} \right)^{n} \int_{0}^{t} {\frac{{g_{{_{i} }} (\tau ,{\tilde{\mathbf{\theta }}})}}{{(t - \tau )^{{1 + \tilde{\alpha }_{i} - n}} }}} \ln (t - \tau ){\text{d}}\tau $$
(40)

It can be seen that Eq. (39) can be simplified as:

$$ \begin{gathered} r(t,\tilde{\alpha }_{i} ) = \frac{{\psi (n - \tilde{\alpha }_{i} )}}{{\Gamma (n - \tilde{\alpha }_{i} )}}\left( {\frac{{\text{d}}}{{{\text{d}}t}}} \right)^{n} \int_{0}^{t} {\frac{{g_{{_{i} }} (\tau ,{\tilde{\mathbf{\theta }}})}}{{(t - \tau )^{1 + \alpha - n} }}} {\text{d}}\tau \hfill \\ \, _{{_{{}} }} \, = \psi (n - \tilde{\alpha }_{i} )D_{{}}^{{\tilde{\alpha }_{i} }} g_{{_{i} }} (t,{\tilde{\mathbf{\theta }}}) \hfill \\ \end{gathered} $$
(41)

Combining Eqs. (36), (38) and (41), we can get:

$$ \sigma_{{\hat{y}/\tilde{\alpha }_{i} }} = \psi (n - \tilde{\alpha }_{i} )D_{{}}^{{\tilde{\alpha }_{i} }} g_{{_{i} }} (t,{\tilde{\mathbf{\theta }}}) + w(t,\tilde{\alpha }_{i} ) $$
(42)

Obviously, the key to calculating \(\sigma_{{\hat{y}/\tilde{\alpha }_{i} }}\) is to calculate \(w(t,\tilde{\alpha }_{i} )\), but since the integral term in Eq. (40) is not easy to be calculated directly, it is transformed into discrete fitting, and because in this study, \(\left\| {{\tilde{\mathbf{\alpha }}}} \right\| < 1\), so \(n = 1\), then Eq. (40) can be simplified as follows:

$$ \begin{gathered} w(t,\tilde{\alpha }_{i} ) \approx - \frac{1}{{\Gamma (1 - \tilde{\alpha }_{i} )}}\left( {\frac{{\text{d}}}{{{\text{d}}t}}} \right)^{1} \sum\limits_{j = 0}^{k} {\frac{{g_{i} (jh,{\tilde{\mathbf{\theta }}})}}{{(kh - jh)^{{1 + \tilde{\alpha }_{i} - n}} }}\ln (kh - jh)} h \hfill \\ \approx - \frac{1}{{\Gamma (1 - \tilde{\alpha }_{i} )}}\frac{{g_{i} (h,{\tilde{\mathbf{\theta }}})}}{{h^{{1 + \tilde{\alpha }_{i} - n}} }}\ln (h)h = - \frac{1}{{\Gamma (1 - \tilde{\alpha }_{i} )}}\frac{{g_{i} (h,{\tilde{\mathbf{\theta }}})}}{{h^{{\tilde{\alpha }_{i} - n}} }}\ln (h) \hfill \\ \end{gathered} $$
(43)

So far, the calculation method for \(\sigma_{{\hat{y}/\tilde{\alpha }_{i} }}\) has been deduced. According to the Eq. (34), we can calculate the vector \({{\varvec{\upsigma}}}_{{\hat{y}/\tilde{\alpha }}}\), and then use the LM algorithm to use the Eq. (29) and Eq. (31) to iterate the parameters to be identified. However, the convergence speed of the common LM algorithm is not fast enough, and the convergence accuracy is not high enough. In order to overcome the above difficulties, we introduce the principle of multi-innovation on the basis of the traditional LM algorithm to enhance the convergence speed and accuracy of the algorithm. Firstly, the objective function of Eq. (27) is extended to multi-innovation objective function, and Eq. (27) is redefined as follows:

$$ \min J(t) = \, \left\| {{\mathbf{E}}(t,P,{{\varvec{\uptheta}}})} \right\|^{2} $$
(44)

where \(P\) represents the length of multi-innovation,

$$ \begin{gathered} {\mathbf{E}}(t,P,{{\varvec{\uptheta}}}) = {[}y(t) - \hat{y}(t,{{\varvec{\uptheta}}}),y(t - h) - \hat{y}(t - h,{{\varvec{\uptheta}}}),..., \hfill \\ \, y(t - Ph + h) - \hat{y}(t - Ph + h,{{\varvec{\uptheta}}}){]}^{{\text{T}}} \in {\mathbb{R}}^{P} \hfill \\ \, \hfill \\ \end{gathered} $$
(45)

In order to simplify Eq. (45) and facilitate the subsequent derivation, the system multi-innovation output vector \({\mathbf{Y}}(t,P)\) and its estimated vector \({\hat{\mathbf{Y}}}(t,P,{{\varvec{\uptheta}}})\) are defined as follows:

$$ {\mathbf{Y}}(t,P) = \left[ {y(t),y(t - h),...,y(t - Ph + h)} \right]^{{\text{T}}} \in {\mathbb{R}}^{P} $$
(46)
$$ {\hat{\mathbf{Y}}}(t,P,{{\varvec{\uptheta}}}) = \left[ {\hat{y}(t),\hat{y}(t - h,{{\varvec{\uptheta}}}),...,\hat{y}(t - Ph + h,{{\varvec{\uptheta}}})} \right]^{{\text{T}}} \in {\mathbb{R}}^{P} $$
(47)

From Eq. (46) and Eq. (47), Eq. (45) can be rewritten as:

$$ {\mathbf{E}}(t,P,{{\varvec{\uptheta}}}) = {\mathbf{Y}}(t,P) - {\hat{\mathbf{Y}}}(t,P,{{\varvec{\uptheta}}}) $$
(48)

Obviously, according to Eq. (48), Eq. (44) can be smoothly rewritten as:

$$ \min J(t) = \left\| {{\mathbf{Y}}(t,P) - {\hat{\mathbf{Y}}}(t,P,{{\varvec{\uptheta}}})} \right\|^{2} $$
(49)

where \(\left\| \cdot \right\|^{2}\) represents the sum of the square values of all elements in a vector.

According to the Eq. (26), the parameter \({{\varvec{\uptheta}}}\) includes the information vector coefficient \({\tilde{\mathbf{\theta }}}\) and the fractional order \({\tilde{\mathbf{\alpha }}}\), where the parameter adjustment method of \({\tilde{\mathbf{\theta }}}\) is described by the following equation:

$$ {\tilde{\mathbf{\theta }}}(t) = {\tilde{\mathbf{\theta }}}(t - h) - \left\{ {\left[ {{\mathbf{J}}_{{{\tilde{\mathbf{\theta }}}}}^{^{\prime\prime}P} + \lambda {\mathbf{I}}} \right]^{ - 1} {\mathbf{J}}_{{{\tilde{\mathbf{\theta }}}}}^{^{\prime}P} } \right\}_{{{\tilde{\mathbf{\theta }}} = {\tilde{\mathbf{\theta }}}(t)}} $$
(50)

where \({\mathbf{J}}_{{{\tilde{\mathbf{\theta }}}}}^{^{\prime}P}\) and \({\mathbf{J}}_{{{\tilde{\mathbf{\theta }}}}}^{^{\prime\prime}P}\) contain the multi-innovation data about \({\tilde{\mathbf{\theta }}}\), which is expressed as follows:

$$ {\mathbf{J}}_{{{\tilde{\mathbf{\theta }}}}}^{^{\prime}P} = - 2{\tilde{\mathbf{\Phi }}}(t,P,{\tilde{\mathbf{\alpha }}}){\mathbf{E}}(t,P,{{\varvec{\uptheta}}}) $$
(51)
$$ {\mathbf{J}}_{{{\tilde{\mathbf{\theta }}}}}^{^{\prime\prime}P} = 2{\tilde{\mathbf{\Phi }}}(t,P,{\tilde{\mathbf{\alpha }}}){\tilde{\mathbf{\Phi }}}^{T} (t,P,{\tilde{\mathbf{\alpha }}}) $$
(52)

where \({\tilde{\mathbf{\Phi }}}(t,P,{\tilde{\mathbf{\alpha }}})\) is composed of \(P\) information vector matrices, expressed as follows:

$$ {\tilde{\mathbf{\Phi }}}(t,P,{\tilde{\mathbf{\alpha }}}) = [{\mathbf{\varphi }}(t,{\tilde{\mathbf{\alpha }}}),{\mathbf{\varphi }}(t - h,{\tilde{\mathbf{\alpha }}}), \cdots ,{\mathbf{\varphi }}(t - Ph + h,{\tilde{\mathbf{\alpha }}})] \in {\mathbb{R}}^{{n_{{\tilde{\theta }}} \times P}} $$
(53)

So far, it can be seen that the multi-innovation principle LM algorithm not only uses the information of the current moment, but also uses historical data as the basis for adjusting parameters. Similarly, the identification method of the non-homogeneous fractional vector \({\tilde{\mathbf{\alpha }}}\) of the system using the multi-innovation principle is as follows:

$$ {\tilde{\mathbf{\alpha }}}(t) = {\tilde{\mathbf{\alpha }}}(t - h) - \left\{ {\left[ {{\mathbf{J}}_{{{\tilde{\mathbf{\alpha }}}}}^{^{\prime\prime}P} + \lambda {\mathbf{I}}} \right]^{ - 1} {\mathbf{J}}_{{{\tilde{\mathbf{\alpha }}}}}^{^{\prime}P} } \right\}_{{{\tilde{\mathbf{\alpha }}} = {\tilde{\mathbf{\alpha }}}(t)}} $$
(54)

where

$$ {\mathbf{J}}_{{\tilde{\alpha }}}^{^{\prime}P} = - 2{{\varvec{\Xi}}}(t,P,{{\varvec{\uptheta}}}){\mathbf{E}}(t,P,{{\varvec{\uptheta}}}) $$
(55)
$$ {\mathbf{J}}_{{\tilde{\alpha }}}^{^{\prime\prime}P} = 2\left[ {{{\varvec{\Xi}}}(t,P,{{\varvec{\uptheta}}}){{\varvec{\Xi}}}^{{\text{T}}} (t,P,{{\varvec{\uptheta}}}) - {\mathbf{\rm H}}(t,P,{{\varvec{\uptheta}}}){\mathbf{E}}(t,P,{{\varvec{\uptheta}}})} \right] $$
(56)

Similarly, \({{\varvec{\Xi}}}(t,P,{{\varvec{\uptheta}}})\) and \({\mathbf{\rm H}}(t,P,{{\varvec{\uptheta}}})\) contain multiple time-point innovations about the fractional order vector \({\tilde{\mathbf{\alpha }}}\), which are calculated by Eqs. (33) and (34), expressed as follows:

$$ {{\varvec{\Xi}}}(t,P,{{\varvec{\uptheta}}}) = [{{\varvec{\upsigma}}}_{{\hat{y}(t)/\tilde{\alpha }}} ,{{\varvec{\upsigma}}}_{{\hat{y}(t - h)/\tilde{\alpha }}} , \cdots ,{{\varvec{\upsigma}}}_{{\hat{y}(t - Ph + h)/\tilde{\alpha }}} ]^{{\text{T}}} \in {\mathbb{R}}^{{n_{{\tilde{\alpha }}} \times P}} $$
(57)
(58)

where

means to stack multiple two-dimensional matrices with the same dimension into a three-dimensional matrix.

So far, the introduction of the multi-innovation LM algorithm for the identification of non-homogeneous fractional order systems has been completed. In order to facilitate readers to use the algorithm, we provide Fig. 2, which is used to visually present the identification process of the algorithm, and we will the entire algorithm flow is summarized as follows:

Fig. 2
figure 2

Algorithm overall flow chart

Full size image

Step 1: Set the initial value of the estimated parameter \({{\varvec{\uptheta}}}_{0}\), the sampling time \(h\), let \(t = h\), initialize the harmonic coefficient \(\lambda\), set the innovation length \(P\), and start identification;

Step 2: Collect input/output data \(\left\{ {u(t),y(t)} \right\}\), construct information vector \({\mathbf{\varphi }}(t,{\tilde{\mathbf{\alpha }}})\) according to Eq. (21) and \(\left\{ {u(t),y(t)} \right\}\);

Step 3: Construct \({\mathbf{E}}(t,P,{{\varvec{\uptheta}}})\) according to Eqs. (45)-(48), and calculate the objective function value \(J\) according to Eq. (44);

Step 4: According to Eq. (21) calculate the multi-innovation subitem of \({\tilde{\mathbf{\Phi }}}(t,P,{\tilde{\mathbf{\alpha }}})\) in Eq. (53), calculate \({\mathbf{J}}_{{{\tilde{\mathbf{\theta }}}}}^{^{\prime}P}\) and \({\mathbf{J}}_{{{\tilde{\mathbf{\theta }}}}}^{^{\prime\prime}P}\) according to Eqs. (51) and (52), and update \({\tilde{\mathbf{\theta }}}(t)\) according to Eq. (50);

Step 5: First calculate the multi-innovation sub-item of \({{\varvec{\Xi}}}(t,P,{{\varvec{\uptheta}}})\) in Eq. (57) according to Eq. (34), and calculate the multi-innovation sub-item of \({\mathbf{\rm H}}(t,P,{{\varvec{\uptheta}}})\) in Eq. (58) according to Eq. (33), then calculate \({\mathbf{J}}_{{\tilde{\alpha }}}^{^{\prime}P}\) and \({\mathbf{J}}_{{\tilde{\alpha }}}^{^{\prime\prime}P}\) according to Eq. (55)-(56), update \({\tilde{\mathbf{\alpha }}}(t)\) according to Eq. (54) at last;

Step 6: Judgment, If \(J < J_{0}\), then increase \(\lambda\), else decrease \(\lambda\);

Step 7: Let \(J_{0} = J\), \(t = t + h\), If \(t < t_{\max }\),then go to Step 2, else go to Step 8;

Step 8: After the identification is completed, the estimated value \({\hat{\mathbf{\theta }}}\) of the identification is output.

5 Simulation examples

In order to illustrate that the algorithm is effective, this section gives an academic example simulation experiment and an actual example simulation of a mechanical system, where the actual example data comes from the flexible manipulator data in Daisy (system identification database) [34]. Next, two calculation examples will be introduced in detail.

5.1 An academic example

In order to illustrate the reliability of the method, an academic example is used to simulate and verify the theory. Consider a Hammerstein non-homogeneous fractional order continuous system with structural orders \(n_{a} = 2\), \(n_{b} = 2\), \(n_{p} = 3\) as follows:

$$ \begin{gathered} y(t) = - a_{1} \Delta^{{\alpha_{1} }} y(t) - a_{2} \Delta^{{\alpha_{2} }} y(t) + b_{1} \Delta^{{\beta_{1} }} u(t) + b_{2} \Delta^{{\beta_{2} }} u(t) \hfill \\ \, _{{}} \, + p_{{2}} b_{1} \Delta^{{\beta_{1} }} u^{2} (t) + p_{{2}} b_{2} \Delta^{{\beta_{2} }} u^{2} (t) \hfill \\ \, ^{{}} \, + p_{3} b_{1} \Delta^{{\beta_{1} }} u^{3} (t) + p_{3} b_{2} \Delta^{{\beta_{2} }} u^{3} (t) + v(t) \hfill \\ \end{gathered} $$

The parameter assignment is:

$$ \begin{array}{*{20}l} \hline {{\mathbf{a}} = \left[ {\begin{array}{*{20}l} 1 \hfill & {0.3} \hfill \\ \end{array} } \right]^{{\text{T}}} } \hfill & {{{\varvec{\upalpha}}} = \left[ {\begin{array}{*{20}l} {0.8} \hfill & {0.6} \hfill \\ \end{array} } \right]^{{\text{T}}} } \hfill &\vline & {} \hfill \\ {{\mathbf{b}} = \left[ {\begin{array}{*{20}l} {0.8} \hfill & 2 \hfill \\ \end{array} } \right]_{{_{{}} }}^{{\text{T}}} } \hfill & {{{\varvec{\upbeta}}} = \left[ {\begin{array}{*{20}l} {0.1} \hfill & {0.3} \hfill \\ \end{array} } \right]^{{\text{T}}} } \hfill &\vline & {{\mathbf{p}} = \left[ {\begin{array}{*{20}c} 1 & 2 & 4 \\ \end{array} } \right]^{{\text{T}}} } \hfill \\ \hline \end{array} $$

where the initial state of the system is 0, the input \(u(t)\) is a Gaussian random sequence with a mean value of 0 and a variance of 1, and \(v(t)\) is a Gaussian white noise with a mean value of 0.

Using the above system as a basis to carry out simulation experiments, using the algorithm proposed in this paper to identify the parameters of the system, the experiment compares the decline curve of the identification objective function under the conditions of different innovation lengths \(P = \{ 1,3,5\}\) and different signal-to-noise ratios \({\text{SNRs}} = \{ 25{\text{dB}}, \, 34{\text{dB\} }}\). The experimental results are shown in Fig. 3 and Fig. 4, and \(K\) in the figure represents the sampling times at equal time intervals. It can be seen from Fig. 3 that under different signal-to-noise ratios (SNRs), the longer the innovation length, the faster the objective function declines and the objective function value can converge to a smaller value. Figure 4 shows more clearly the convergence difference of the objective function with different SNRs under different lengths of innovations. It can be seen that although high SNR leads to better experimental results, the deterioration of results caused by low SNR is weakened as the innovation time prolongs. When the innovation length increases to 3, the convergence result of the objective function value hardly deteriorates due to the decrease of SNR. When the innovation length increases to 5, the objective function value for low SNR drops at almost the same rate as for high SNR. This proves that the performance improvement of the LM algorithm through multiple innovations is still very objective.

Fig. 3
figure 3

The descending curve of the objective function with different innovation lengths

Full size image
Fig. 4
figure 4

Descent curves of objective functions for different SNRs

Full size image

In order to reduce the influence of the random initial value of the algorithm on the results of different fractional order algorithms, we use the innovation lengths {1, 3, 5} for system identification, and the experiment counts the objective function value of 1000 Monte Carlo experiments. As shown in Fig. 5, it can be seen that Fig. 5 consists of a distribution histogram with a Kernel Smooth distribution curve and whiskers below the horizontal axis. It can be seen from the distribution curve and distribution histogram that when the length of innovation is longer, the distribution curve and histogram are denser near the objective function of 0. In addition, it can be seen from the whiskers that the longer the innovation length is, the smaller the final optimized objective function value is, and the higher the accuracy of the algorithm is. Figure 6 depicts the comparison of the statistical boxplot of the objective function value estimation with its true value. It can be seen that for the estimated coefficient values (the first 8 boxes), the boxes are all narrow, and the median line and mean almost coincide with the true values of the corresponding coefficients. For the estimated fractional order value (the last 4 boxes), the box has been coincident into a straight line, and almost coincides with the corresponding true value, and the estimation result is better. Table 1 and Table 2 respectively show the comparison of a group of estimated coefficient values with the real coefficient values, and the comparison of the estimated fractional order values with the true fractional order values for the same group. It can be seen that the estimated parameter values are basically the same as the real values, and the algorithm is effective.

Fig. 5
figure 5

Boxplot of objective function values with different innovation lengths

Full size image
Fig. 6
figure 6

Comparison of parameter estimation boxplot and true value

Full size image
Table 1 Estimated coefficient values and true values
Full size table
Table 2 Estimated fractional order values and true values
Full size table

Figure 7 shows the comparison between the output of the estimated system and the output of the real system. The almost coincidence of the red dotted line and the black dotted line proves the accuracy of the estimated system, and the partially enlarged part further illustrates this point. The blue straight line in Fig. 7 represents the difference between the estimated system output and the actual system output. It is clear that the error is almost distributed around 0, which further proves that the algorithm proposed in this paper is effective.

Fig. 7
figure 7

Comparison and error between estimated output and actual output

Full size image

5.2 Flexible manipulator system identification

In order to further explore the effectiveness of the algorithm in real systems, taking a flexible manipulator system as an example, the fractional-order system in Fig. 1 is used as a model to identify system parameters and explore its system structure. The data is provided by KU Leuven, and the data length is 1024. The input of the system is the reaction force of the ground structure, and the output is the acceleration of the end of the manipulator. When the output signal is similar to a sinusoidal signal, its input and output signals are shown in Fig. 8. The purpose of the experiment is to use the algorithm proposed in this paper to explore the relationship between the ground reaction force and the terminal acceleration of the flexible manipulator system.

Fig. 8
figure 8

Input and output of the flexible manipulator system

Full size image

In order to ensure the reliability of the experiment, the data is divided into two groups on average, which are respectively used as identification training data and test data. In the experiment, the system structure was first determined to ensure the accuracy of the identification model. For this part of the work, we chose to refer to the existing work content, including [14] and [17]. The structural orders include the linear part \([n_{a} ,n_{b} ]\) and the nonlinear part \([n_{p} ]\) of the system. For convenience, the structure orders are denoted as \([n_{a} ,n_{b} ,n_{p} ]\) in the experiments. We select well-tested structures in [14] and [17], and used the method proposed in this paper to carry out system identification work on known inputs and outputs, and record the decline curve of the objective function. A total of 5 system structures are tested in the experiment, and the experimental results are shown in Fig. 9. Obviously, using the algorithm proposed in this paper, the objective function value can be well optimized for systems with different structures. In addition, it can be seen from the partially enlarged diagram in Fig. 9 that when the system structure is \([2,2,2]\), the value of the experimental objective function is the smallest at this time. Therefore, the Hammerstein non-homogeneous fractional continuous system model with system structure \([2,2,2][2,2,2]\) is chosen as the fitting model of the flexible manipulator system.

Fig. 9
figure 9

Objective function descent curves under different system structures

Full size image

In order to further illustrate the effectiveness of the combination of multi-innovation theory and LM algorithm, the experimental statistics of the convergence boxplot of the objective function value of the innovation length \(P = \{ 1,3,5\}\) are shown in Fig. 10. It can be seen that with the increase of the innovation length, the box keeps compressing, the mean value keeps decreasing, and the statistical outliers keep approaching the box. This shows that in the process of parameter identification of the system using the LM algorithm combined with the principle of multi-innovation, with the increase of the length of innovations, in addition to the faster identification speed and the continuous improvement of accuracy, the longer length of innovations also makes the algorithm more likely that finding good parameter combinations.

Fig. 10
figure 10

Boxplot of objective function values with different innovation lengths

Full size image

Figures 11 and 12 show the parameter change curves in the process of identifying the system when the length of innovations is 5. It can be seen that when the initial value of the parameter is random, in the process of parameter identification of the non-homogeneous fractional order system using the multi-innovation LM algorithm, with the increase of online data sampling, the parameter can change rapidly and converge. The algorithm makes only minor adjustments to the parameters between 200 and 300 samples. After 300 samples, the parameters of the system coefficients hardly change, and the fractional order changes almost stop, the algorithm shows convergence, and the value of the objective function almost stops decreasing. At this time, the system parameters are close to the optimal value.

Fig. 11
figure 11

Variation curve of system coefficients in the process of system identification

Full size image
Fig. 12
figure 12

Fractional order changes in the process of system identification

Full size image

Figure 13 shows the output of the estimated system identified using our method compared with the actual output. It can be seen that with the same system input, the output of the estimated system is almost the same as that of the actual flexible manipulator system, which is shown in detail in the partial enlargement of Fig. 13. To further illustrate the accuracy of the estimation system, we add the output error plots of the estimation system and the flexible manipulator system, as shown in Fig. 14. It can be seen that the output errors of the estimation system and the flexible manipulator system are small, except for a small error in the early stage due to online identification. This shows that with the increase of sampling times, the identification algorithm converges, and the estimation system has successfully fitted the flexible manipulator system, which shows the effectiveness of the theory in this paper in actual engineering.

Fig. 13
figure 13

Comparison of estimated output and actual output

Full size image
Fig. 14
figure 14

Estimation error between estimated output and actual output

Full size image

Finally, in order to show the performance of the method in this paper, we compared the methods in [14, 17,18,19]. The content of the comparison is the estimated error range of the test set. The results are shown in Table 3. It can be seen that for the same flexible manipulator system data, the method in this paper has a smaller estimation error range.

Table 3 Comparison of algorithm estimation error range
Full size table

6 Conclusion

This paper proposes a LM algorithm based on the principle of multiple innovations, which is used for the online identification of Hammerstein non-homogeneous fractional order continuous systems. The algorithm deduces the identification process for system parameters in detail. Among them, for the identification of non-homogeneous fractional orders, this paper theoretically abandons traditional methods of using numerical differentiation. The partial derivative equation of the objective function with respect to non-homogeneous fractional order is deduced when the range of fractional order to be identified is (0,1). Combined with the principle of multi-innovation and LM algorithm, the parameters of an academic example and a flexible manipulator system are identified online. The conclusions of the experiment are as follows:

  • Monte Carlo experiments prove that the principle of multiple innovations has a significant effect on improving the accuracy and speed of the LM algorithm. Under different signal-to-noise ratios, the performance of the multi-innovation LM algorithm is better than that of the traditional LM algorithm.

  • The identification method for non-homogeneous fractional orders proposed in this paper can effectively reduce the value of the objective function, and can effectively identify all fractional orders of the system.

Although the algorithm in this paper can be effectively used in the identification of non-homogeneous fractional orders, and has better identification results in mechanical system examples. But the algorithm can only be used for single-input single-output systems, so our follow-up work will focus on extending the algorithm to multiple-input and multiple-output systems.