1 Introduction

The fractional calculus that was started by the ideas of Leibniz in 1695 represents the generalization of standard differential calculus up to non-integer orders [1, 2]. This field remained ignored by applied sciences during several centuries, due to the lack of application backgrounds, insufficient geometrical interpretation, and many conflicting definitions of fractional means. However, in the last years, because of their increased flexibility (with respect to integer order equations) which allows a more precise modeling of complex systems, the fractional order equations have progressively attracted attention and play a considerable role in various areas, such as: mathematics, physics, electronics, chemistry, mechanics, and control theory [3,4,5,6,7].

Furthermore, fractional order controllers (FOCs) have so far been implemented to modify the robustness and the performance of the control applications. In 1996, Oustaloup proposed the idea of fractional calculus in control of dynamic systems [8] where he demonstrated the superior performance of the CRONE (French abbreviation for Commande Robuste d’Ordre NonEntier) method over the classical PID controller. Later, Podlubny introduced a fractional order PID controller and demonstrated the better efficiency of this type of controllers, in comparison with the integer PID controllers, when used to control of fractional order systems (FOSs) [9]. The control of FOSs by FOCs has begun to receive a lot of consideration recently [10,11,12,13,14] and different fractional order stability theorems have been presented to provide better using of the FOCs [15,16,17,18,19,20]. Newly, due to the broad applications, many different control methods have been utilized to synchronize the fractional order nonlinear systems such as chaotic systems [21,22,23,24,25,26,27]. In [28] a fractional order adaptive controller (FOAC) has been proposed to synchronize two chaotic systems. FOAC uses a gradient-based adaptation mechanism to adjust its coefficients and parameters. Aghababa has presented a new hierarchical terminal sliding mode control (HTSC) scheme for finite time stabilization of non-autonomous dynamic FOSs [29].

Inadequacy and insufficiency of information and the uncertainty of environment demand the use of intelligent decision systems for control of ill-defined and complex plants. Fuzzy logic is one of the powerful tools for data processing and is generally applicable to systems that are mathematically poorly understood [14, 30, 31]. Fuzzy control has also found extensive application in a broad variety of industrial systems due to a model-free approach and being capable of approximating any continuous unknown nonlinear functions to arbitrary accuracy [30, 32]. In addition, the adaptive fuzzy controller (an important class of fuzzy control) has been developed to estimate the plant structure online and their stability is guaranteed by the Lyapunov theorems [33, 37]. However, it is proved that if the membership functions are not correctly determined, either the function approximation ability may not be good enough or the learning inefficient owing to the correlations among rules [34, 38].

In recent years, adaptive fuzzy methods have been presented to control fractional (or integer) order systems. Efe has firstly proposed a fractional adaptive fuzzy sliding mode controller that utilizes fractional order integration in the parameter tuning stage to control a robot arm with integer order equations [39]. An indirect adaptive fuzzy sliding mode system has been introduced to synchronize uncertain fractional order chaotic systems [40] and time delayed ones [41]. In [42], an adaptive fuzzy controller with an H \(\infty \) tracking design technique has been presented to control a class of fractional order nonlinear systems. However, in [40,41,42], the fractional order calculations have carelessly treated as ordinary ones. Hence the main results of these works have some fallacies [27, 43]. In [44] a hybrid adaptive fuzzy sliding mode control has been used to achieve tracking performance for uncertain fractional order nonlinear systems. Though in that, the fractional order calculus is used inappropriately and the corollary of integer order Barbalat’s lemma is applied erroneously in fractional order computations. Ullah et al. have introduced a fractional order adaptive fuzzy sliding mode scheme to control uncertain integer order dynamic systems [45, 46]. Although their results are noticeable, there is no guarantee that the error will be successfully converged to zero.

Motivated by the above discussion and inspired by the work of Tang et al. [34], we propose a novel direct adaptive fuzzy system with compensation control for a certain class of fractional order nonlinear systems with unknown nonlinearities. A fractional order adaptation law is employed to update the free parameters in the consequence part of the fuzzy system. By using the compensation control signal, the fractional order nonlinear plant, which is little known, can be controlled effectively no matter whether the membership functions of the adaptive fuzzy controller are suitable or not. In this work, using fractional order Lyapunov’s direct method and Brabalat’s lemma, the boundness of all signals in a closed-loop system and some convergence properties of the tracking error are analytically proven for an uncertain fractional order nonlinear system. In addition, the free parameters are uniformly bounded by applying a projection algorithm in an adaptation law. In a new application, a supervisory controller accompanies the compensation control signal and the adaptive fuzzy controller to guarantee the generalized Mittag–Leffler stability of the closed-loop system. It should be noted that Mittag–Leffler stability implies Lyapunov asymptotic stability. If the nonlinear system tends to be unstable, especially in the transient time, the supervisory controller will be activated to cooperate with the controller for stabilizing the closed-loop system. Moreover, if the adaptive fuzzy and the compensatory controller operate well, the supervisory controller will be deactivated. Finally, some illustrative Examples and simulations are presented to demonstrate the validity of proposed control scheme.

This paper is organized as follows. After this introduction section, basic definitions of fractional order calculus are described in Sect. 2. A brief explanation of the fuzzy systems is presented in Sect. 3. Section 4 involves system description and problem formulation. The new direct adaptive fuzzy controller with compensation and supervisory control is designed in Sect. 5. Section 6 comprises simulation Examples to demonstrate the performance of the proposed method. Finally, the conclusions of the advocated design procedure are listed in Sect. 7.

2 Brief introduction to fractional calculus

In fractional calculus, the traditional definitions of the integral and derivative of a function are generalized from integer orders to real or complex orders. In this section, some basic notations and properties of fractional calculus are summarized. Afterward, a numerical algorithm for solving fractional order differential equations is presented.

Definition 1

[27]: The fractional order integral \(_{ 0} I_t^q \) with the order \(q\in \mathrm{R}^{+}\) of function \(x\left( t \right) \) is computed by:

$$\begin{aligned} {}_{t_0 } I_t^q x(t)=\frac{1}{\Gamma (q)}\int _{ t_0 }^{ t} {\frac{x(\tau )}{({t-\tau })^{1-q}}d\tau } \end{aligned}$$
(1)

where \(t_0 \) is an initial time, \(t>t_0 \) and \(\Gamma \left( \cdot \right) \) is Gamma function.

Definition 2

[2]: The Riemann–Liouville (RL) derivative with the order \(q\in {\mathbb {R}}^{+}\) of function x(t) with respect to t is calculated as below:

$$\begin{aligned} {}_{t_0}^{RL} D_t^q x\left( t \right) =\frac{1}{\Gamma \left( {m-q} \right) }\frac{d^{m}}{dt^{m}}\int _{ t_0 }^{ t} {\frac{x\left( \tau \right) }{\left( {t-\tau } \right) ^{q+1-m}}d\tau } \end{aligned}$$
(2)

where \(m-1<q\le m, t>t_0\) and \(m\in {\mathbb {N}}\).

Definition 3

[2]: The Caputo (C) derivative with the order \(q\in {\mathbb {R}}^{+}\) of function \(x\left( t \right) \) with respect to t is defined as (3). Where \(m-1<q\le m, t>t_0\) and \(m\in {\mathbb {N}}\).

$$\begin{aligned} {}_{t_0}^C D_t^q x\left( t \right) =\frac{1}{\Gamma \left( {m-q} \right) }\int _{ t_0 }^{ t} {\frac{x^{\left( m \right) }\left( \tau \right) }{\left( {t-\tau } \right) ^{q+1-m}}d\tau } \end{aligned}$$
(3)

Definition 4

[2]: The original definition of the Grunwald–Letnikov (GL) fractional derivative is given by:

$$\begin{aligned} {}_{t_0}^{GL} D_t^q x\left( t \right) \!=\! \mathop {\lim }\limits _{{\begin{array}{c} h\rightarrow 0 \\ Nh\!=\!t\!-\!t_0 \end{array}}} \frac{1}{h^{q}}\sum _{j=0}^N {\left( {-1} \right) ^{j}\left( {\begin{array}{l} q \\ j \\ \end{array}} \right) x\left( {t\!-\!jh} \right) } \end{aligned}$$
(4)

where h is the sample time.

Lemma 1

[13]: If \(x\left( t \right) \) is continuous and \(\dot{x}\left( t \right) \) is integrable in the interval \(\left[ {t_0 ,t} \right] \), then for every \(q (0<q<1)\) both RL and GL derivatives exist and can be written as below

$$\begin{aligned} _{t_0 }^{GL} D_t^q x\left( t \right) \,=\,_{t_0 }^{RL} D_t^q x\left( t\right) \end{aligned}$$
(5)

Lemma 2

[13]: For \(0<q<1\), the relationship between Caputo and RL derivative is as

$$\begin{aligned} _{t_0 }^C D_t^q x\left( t \right) \,=\,_{t_0}^{RL} D_t^q x\left( t \right) -\frac{x\left( {t_0 } \right) }{\Gamma \left( {1-q} \right) }\left( {t-t_0 } \right) ^{-q} \end{aligned}$$
(6)

In this study, Caputo definition is considered to describe FOSs due to its well-understood physical interpretation, wide engineering applications, and many stability theorems. The relationship between Caputo derivative and fractional order integral in \(0<q<1\) is expressed as follow [2]:

$$\begin{aligned} _{ 0} I{_t^q }\; {_0^C }D_t^q V =V\left( t \right) -V \left( 0 \right) \end{aligned}$$
(7)

Lemma 3

[13]: If \(x\left( t \right) \in C^{1}\left[ {0,T} \right] \) (the first derivative of \(x\left( t \right) \) is continuous for \(T>0\)) and \(q_1 +q_2 \le 1\) then

$$\begin{aligned} {_0^C} D_t^{q_{1} }\; {_0^C}D_t^{q_{2} } x\left( t \right) = {_0^C}D_t^{q_{2} } \;{_0^C}D_t^{q_{1} } x\left( t \right) = {_0^C}D_t^{q_{1} +q_{2} } x\left( t \right) \end{aligned}$$
(8)

where \(q_1 ,q_{2} \in {\mathbb {R}}^{+}\).

In order to simplicity, the notations \(I^{q}x\left( t \right) \) and \(D^{q}x\left( t \right) \) (or \(x^{\left( q \right) }\left( t \right) \)) denote fractional order integral (\({_0}^I_{t^q} x\left( t \right) \)) and Caputo derivative (\( _0^C D_t^q x\left( t \right) \)), respectively. Furthermore, throughout this paper, the lower limit of the fractional integral and derivative is assumed zero.

Theorem 1

[2]: Let a linear time invariant fractional order system be given by

$$\begin{aligned} D^{q}{} \mathbf{x}=\mathbf{Ax},\;\;\;\;\;\;\mathbf{x}\left( 0 \right) =\mathbf{x}_\mathbf{0} \end{aligned}$$
(9)

where \(0<q\le 1, \mathbf{x}\in {\mathbb {R}}^{n}\) and \(\mathbf{A}\in {\mathbb {R}}^{n\times n}\). The system has asymptotical stability if and only if \(\left| {\arg \left( {\lambda _i } \right) } \right| >q\pi /2\) is satisfied for all eigenvalues. \(\lambda _i \) denotes the \(i\hbox {th}\) eigenvalue of \(\mathbf{A}\).

Theorem 2

[18]: (Fractional order Lyapunov theorem) Let \(x=0\) be an equilibrium point for the non-autonomous fractional order system \(D{^q} x\;\left( t \right) =f\left( {t,x} \right) \), where \(f\left( {t,x} \right) \) is piecewise continuous in t and locally Lipschitz in x and \(q\in \left( {0,1} \right) \). Assume is a domain containing the origin and is a continuously differentiable function and locally Lipschitz with respect to x such that

$$\begin{aligned}&k_1 \left\| x \right\| ^{a} \le V\left( {t,x\left( t \right) } \right) \le k_2 \left\| x \right\| ^{ab} \end{aligned}$$
(10)
$$\begin{aligned}&D^\beta V\left( {t,x\left( t \right) } \right) \le -k_3 \left\| x \right\| ^{ab} \end{aligned}$$
(11)

then \(x=0\) is Mittag–Leffler stable. Here, , \(k_{1} , k_{2} , k_{3} , a\) and b are arbitrary positive constants and \(\left\| \cdot \right\| \) is an arbitrary norm. If the assumptions hold globally on \({\mathbb {R}}^{n}, x=0\) is globally Mittag–Leffler stable and (12) is obtained.

$$\begin{aligned} \left\| {x\left( t \right) } \right\| \le \left[ {\frac{V\left( 0 \right) }{k_1 }E_\beta \left( {-\frac{k_3 }{k_2 }t^{\beta }} \right) } \right] ^{\frac{1}{a}} \end{aligned}$$
(12)

\(E_\beta \left( z \right) \) is the one parameter Mittag–Leffler function frequently used in the solutions of FOSs and is defined as below

$$\begin{aligned} E_\beta \left( z \right) =\sum _{k=0}^\infty {\frac{z^{k}}{\Gamma \left( {\beta k+1} \right) }} \end{aligned}$$
(13)

Theorem 2 extends the Lyapunov direct method and it is called the generalized Mittag–Leffler stability theory. It should be considered that Mittag–Leffler asymptotic stability connotes the Lyapunov asymptotic stability.

Lemma 4

[47]: Let \(\mathbf{x}\left( t \right) \in {\mathbb {R}}^{n}\) be a real-valued continuous and differentiable vector function. Then, for any time instant \(t\ge t_0 \) and \( q\in \left( {0,1} \right) \), the following inequality holds that:

$$\begin{aligned} \frac{1}{2}D^q \left( {\mathbf{x}^{T}\left( t \right) \mathbf{Px}\left( t \right) } \right) \le \mathbf{x}^{T}\left( t \right) \mathbf{P}D^q \mathbf{x}\left( t \right) \end{aligned}$$
(14)

where \(\mathbf{P}\in {\mathbb {R}}^{n\times n}\) is a constant, square, symmetric and positive definite matrix.

Lemma 5

[48]: Let \(\mathbf{P}\in {\mathbb {R}}^{n\times n}\) be a symmetric and positive semidefinite matrix, then for any vector \(\mathbf{x}\in {\mathbb {R}}^{n}\)

$$\begin{aligned} \lambda _{\min \mathbf{P}} \left\| \mathbf{x} \right\| ^{2}\le \mathbf{x}^{T}{} \mathbf{Px}\le \lambda _{\max \mathbf{P}} \left\| \mathbf{x} \right\| ^{2} \end{aligned}$$
(15)

\(\lambda _{\min \mathbf{P}} \) and \(\lambda _{\max \mathbf{P}} \) are the minimum and maximum eigenvalue of \(\mathbf{P}\), respectively.

Theorem 3

[16] (Fractional order Barbalat lemma): Let \(V\left( t \right) \in C^{1}\left( {{\mathbb {R}}^{+}} \right) \) be a bounded uniformly continuous function and \(\mathop {\lim }\limits _{t\rightarrow \infty } I^{q}V\left( t \right) \rightarrow L\), where L is an arbitrary constant. If \(V\left( t \right) \) is a positive function then \(V\left( t \right) \) converges to zero as t goes to infinity.

The numerical simulation of a fractional order differential equation is not as simple as an ordinary one. Here, an algorithm derived from the GL definition which is the core idea for numerical computation of a FOS is used. Consider the following differential equation:

$$\begin{aligned} _0^{RL} D_t^q x\left( t \right) =f\left( {x\left( t \right) ,t} \right) \end{aligned}$$
(16)

According to Lemma 1, discretization of the fractional order differential equation (16) can be expressed as

$$\begin{aligned} x\left( {t_{k} } \right) =h^{q}f\left( {x\left( {t_{k-1} } \right) ,t_{k} } \right) -\sum _{j=1}^k {c_{j}^x\left( {t_{k-j} } \right) } \end{aligned}$$
(17)

where \(m-1<q\le m, t_k =kh, h\) is the sample time and \(c_j \left( {j=0,1,\cdots } \right) \) are binomial coefficients which are calculated by the following expression [1].

$$\begin{aligned} c_{0} =1,\;\;\;\;\;\;c_{j} =\left( {1-\frac{1+q}{j}} \right) c_{j-1} \end{aligned}$$
(18)

If Caputo derivative is used in (16), on the basis of Lemma 2 and (17), we can use (19) in the numerical simulation.

$$\begin{aligned} x\left( {t_k } \right)= & {} h^{q}f\left( {x\left( {t_{k-1} } \right) ,t_k } \right) -\sum _{j=1}^k c_j^ x\left( {t_{k-j} } \right) \nonumber \\&+\,h^{q}\frac{x\left( {t_0 } \right) }{\Gamma \left( {1-q} \right) }\left( {t-t_0 } \right) ^{-q} \end{aligned}$$
(19)

3 Basic description of Fuzzy system

In this article, the proposed adaptive fuzzy controller uses a fuzzy logic system as a model of the plant dynamics to achieve desired tracking performance. The parameters of the fuzzy controller are tuned to reduce the error between the output plant and a given desired signal. Two auxiliary control signals, compensation and supervisory control, are incorporated with the adaptive fuzzy system to make an appropriate operation in the closed-loop system.

The fuzzy inference engine employs fuzzy IF-THEN rules to perform a mapping from \(\mathbf{x}=\left[ {x_{1} ,x_{2} ,}{\cdots ,x_{n} } \right] ^{T}\) (input vector) to \(y\left( \mathbf{x} \right) \in {\mathbb {R}}\) (output variable). Assume that there are M rules in the fuzzy system and the \(\ell \) th rule is written in the following form:

Rule \(\ell \): IF \(x_1\) is \(A_1^\ell \) and \(\cdots \) and \(x_n \) is \(A_n^\ell \) THEN \(y^{\ell }\left( \mathbf{x} \right) \) is \(B^{\ell }\) \(y^{\ell }\left( \mathbf{x} \right) \) is the crisp output and \(A_i^\ell (i=,\cdots ,n)\) and \(B^{\ell }\) are the fuzzy sets in the \(\ell \)th rule. The output of the fuzzy system with the singleton fuzzification, product inference, and central-average defuzzification is expressed as follows

$$\begin{aligned} y\left( \mathbf{x} \right) =\frac{\sum \limits _{\ell =1}^M {\bar{{y}}^{\ell }\prod \limits _{i=1}^n {\mu _{A_{i}^\ell } \left( {x_{i} } \right) } } }{\sum \limits _{\ell =1}^M {\left( {\prod \limits _{i=1}^n {\mu _{A_{i}^\ell } \left( {x_{i} } \right) } } \right) } }={{{\varvec{\uptheta }} }^{T}} {{{\varvec{\upxi }} }\left( \mathbf{x} \right) } \end{aligned}$$
(20)

where \(\mu _{A_i^\ell } \left( {x_i } \right) \) is the degree of the membership function of \(x_i \) to \(A_i^\ell , \bar{{y}}^{\ell }\) is the point at which the membership function of the output fuzzy set \(B^{\ell }\) achieves its maximum value. \({\varvec{\uptheta }}=\left[ {\bar{{y}}^{1},\cdots ,\bar{{y}}^{n}} \right] ^{T}\) and \(\varvec{\upxi }\left( \mathbf{x} \right) =\left[ {\xi ^{1}\left( \mathbf{x} \right) ,\cdots ,\xi ^{M}\left( \mathbf{x} \right) } \right] ^{T}\) are an adaptive parameters (free parameters) vector and a vector of normalized firing strength, respectively. \(\xi ^{\ell }\left( \mathbf{x} \right) \) is equivalent to

$$\begin{aligned} {{\xi }} ^{\ell }\left( \mathbf{x} \right) =\frac{\prod \limits _{i=1}^n {\mu _{A_i^\ell } \left( {x_i } \right) } }{\sum \limits _{\ell =1}^M {\left( {\prod \limits _{i=1}^n {\mu _{A_i^\ell } \left( {x_i } \right) } } \right) } }=\frac{v^{\ell }}{\sum \limits _{\ell =1}^M {v^{\ell }} } \end{aligned}$$
(21)

where \(v^{\ell }\) is firing strength of the \(\ell \) th rule [34, 39, 41, 49].

According to the universal approximation theorem [50], the fuzzy system in the form of (20) is proven to be capable of uniformly approximating any well-defined nonlinear function over a compact set to any degree of accuracy if its parameters are suitable. In fact, there are not practically enough experiences about the plant especially in the fractional order one. Thus, the necessary conditions of general approximation theorem are not established. Under this circumstance, the designing proper membership functions are not possible and the fuzzy system is operated inappropriately. Accordingly, the standard fuzzy systems cannot control the plant efficiently. The compensation control is a reasonable strategy to overcome the adverse effects of the undesirable membership functions [34].

If the fuzzy system is equipped with a stable training algorithm to maintain a consistent performance under plant uncertainties, this system is an adaptive fuzzy system. The adaptive fuzzy controller can adjust itself to the changing environment and needs less information about the plant because the adaptation law can help to learn the dynamics of the plant during real-time operation. The most significant advantage of the adaptive fuzzy controller over the conventional adaptive controller is that adaptive fuzzy controllers can incorporate linguistic information from human, whereas conventional adaptive controllers are not. This property is important for the systems with a high degree of uncertainty [14, 37, 41, 49, 51].

4 System description and problem formulation

We consider a class of commensurate FOCs as

$$\begin{aligned} \left\{ {\begin{array}{l} x_i^{\left( q \right) } =x_{i+1} , i=1,\cdots ,n-1, q\in \left( {0,1} \right) \\ x_n^{\left( q \right) } =f\left( \mathbf{x} \right) +b u\left( t \right) \\ y=x_1 \\ \end{array}} \right. \end{aligned}$$
(22)

where q is the system order with Caputo definition and n is the number of state variables. \(\mathbf{x}=\left[ {x_{1} ,x_{2} ,\cdots ,x_{n} } \right] ^{T}, u\in {\mathbb {R}}\) and \(y\in {\mathbb {R}}\) are the measurable state vector, control input and system output, respectively. \(f\left( \cdot \right) \) is an unknown but bounded continues nonlinear function and b is the nonzero known control gain. In addition, it is assumed that this system has bounded output or at least all the states locate in the bounded area in the presence of the control signal. Since the disturbance and uncertainty are not considered in separate functions, \(f\left( \cdot \right) \) involves both of them. Nonlinear systems represented in this form can be called the commensurate fractional order Brunovsky form [52] or normal form. According to Lemma 3 and assuming \(y=x=x_1\), provided that \(nq\le 1\), the system’s equation can be rewritten as

$$\begin{aligned} \left\{ {\begin{array}{l} x_{i}^{\left( q \right) }=x^{\left( {iq} \right) }=x_{i+1} \\ x_{n}^{\left( q \right) } =x^{\left( {nq} \right) }=f\left( \mathbf{x} \right) +b u\left( t \right) \\ \end{array}} \right. \end{aligned}$$
(23)

where \(\mathbf{x}=\left[ {x,x^{\left( q \right) },x^{\left( {2q} \right) },\cdots ,x^{\left( {\left( {n-1} \right) q} \right) }} \right] ^{T}\). The control problem is the designing of the control input \(u\left( t \right) \) such that the output of (23) follows a given continues bounded reference signal \((y_{d} \left( t \right) =x_{d} \left( t \right) )\). Furthermore, the tracking error \((e\left( t \right) =x_d \left( t \right) -x\left( t \right) )\) should be as small as possible, under the condition that all involved signals in the close-loop remain bounded; i.e., \(\left\| {\mathbf{x}\left( t \right) } \right\| \le M_x <\infty \) and \(\left| {u\left( t \right) } \right| \le M_u <\infty \) for all \(t>0\). Where \(M_x \) and \(M_u \) stand for the maximum amount of \(\left\| {\mathbf{x}\left( t \right) } \right\| \) and \(\left| {u\left( t \right) } \right| \), respectively. To meet this goal, a feedback control \(u=u\left( {\mathbf{x}|{\varvec{\uptheta }}} \right) \) based on adaptive fuzzy system (20) is designed. \({{\varvec{\uptheta }}}\) is an adjustable parameter vector and \(\left\| {\varvec{\uptheta }}\left( t \right) \right\| \le M_{\varvec{\uptheta }} <\infty \). \(M_x ,M_u \) and \(M_{\varvec{\uptheta }} \) are specified by the designer. By defining \(e\left( t \right) \), the vector of tracking errors is obtained as below:

$$\begin{aligned} \mathbf{e}=\mathbf{x}_\mathbf{d} -\mathbf{x}=\left[ {e,e^{\left( q \right) },e^{\left( {2q} \right) },\cdots ,e^{\left( {\left( {n-1} \right) q} \right) }} \right] ^{T} \end{aligned}$$
(24)

where \(\mathbf{x}_d =\left[ {x_d ,x_d^{\left( q \right) } ,\cdots ,x_{d}^{\left( {\left( {n-1} \right) q} \right) } } \right] ^{T}\) is the desired state vector. If the function \(f\left( \mathbf{x} \right) \) is known, by the feedback linearization technique, the control law can be written as follow [53].

$$\begin{aligned} u^{{*}}=\frac{1}{b}\left[ {-f\left( \mathbf{x} \right) +x_d^{\left( {nq} \right) } +\mathbf{k}^{T}{} \mathbf{e}} \right] \end{aligned}$$
(25)

Let \(\mathbf{k}=\left[ {k_{1} ,k_{2} ,\cdots ,k_{n} } \right] ^{T}\in \mathrm{R}^{n}\) be chosen such that all roots (\(\lambda _{i} , i=1,\cdots ,n)\) of the polynomial \(\Delta \left( s \right) =s^{nq}+k_{n} s^{\left( {n-{1}} \right) q}+\cdots +k_{1} \) satisfy \(\left| {\arg \left( {\lambda _{i} } \right) } \right| >q\pi /2\). Where s is the Laplace operator. From (25) and (23), the error equation is calculated as

$$\begin{aligned} e^{\left( {nq} \right) } +k_n e^{\left( {\left( {n-1} \right) q} \right) }+\cdots +k_1 e=0 \end{aligned}$$
(26)

which implies \(\mathop {\lim }\limits _{t\rightarrow \infty } e\left( t \right) =0\) and the system can achieve the asymptotically stable tracking. However, \(f\left( \mathbf{x} \right) \) is unknown in real applications, obtaining a control input similar to (25) is impossible. In this situation, the approximation by the adaptive fuzzy system is employed to treat this tracking control design problem. Suppose that the control input \(u\left( t \right) \) is considered as

$$\begin{aligned} u\left( t \right) =u_f \left( {\mathbf{x}|{\varvec{\uptheta }}} \right) +u_s \left( t \right) +u_c \left( t \right) \end{aligned}$$
(27)

where \(u_c \left( t \right) \) is a measurable compensatory control signal related to the previous amount of system variables and has the basic duty to the control. \(u_f \left( {\mathbf{x}|{\varvec{\uptheta }}} \right) \) is the output of an adaptive fuzzy controller in the form of (20) which is added to eliminate the error between the ideal and compensatory control signal. \(u_s \left( t \right) \) is a supervisory control signal and determined to ensure the stability of the closed-loop system. In the proposed strategy, the boundedness of the states is ensured by using the supervisory control signal and the asymptotical stability is guaranteed by the compensatory and the adaptive fuzzy control signals. Based on (27) and (23), \(x^{\left( {nq} \right) }\) is equivalent to

$$\begin{aligned} x^{\left( {nq} \right) } =f\left( \mathbf{x} \right) +b \left( {u_f \left( {\mathbf{x}|{\varvec{\uptheta }}} \right) +u_s \left( t \right) +u_c \left( t \right) } \right) \end{aligned}$$
(28)

By adding and subtracting \(bu^{{*}}\) to (28), considering (25), and after straightforward calculations, the error equation of the closed-loop system is computed as below

$$\begin{aligned} e^{\left( {nq} \right) }= & {} -\mathbf{k}^{T}{} \mathbf{e}+b \left( {u^{{*}}-u_f \left( {\mathbf{x}|\varvec{\uptheta }} \right) -u_s \left( t \right) -u_c \left( t \right) } \right) \nonumber \\ nq\le & {} 1 \end{aligned}$$
(29)

Equivalently, the vector representation is obtained as

$$\begin{aligned} \mathbf{e}^{\left( q \right) }=\varvec{\Lambda }_c \mathbf{e}+\mathbf{b}_c \left( {u^{{*}}-u_f \left( {\mathbf{x}|\varvec{\uptheta }} \right) -u_s \left( t \right) -u_c \left( t \right) } \right) \end{aligned}$$
(30)

where

$$\begin{aligned} \varvec{\Lambda }_c =\left[ {{\begin{array}{cccc} 0&{} 1&{} &{} 0 \\ 0&{} 0&{} &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0&{} 0&{} &{} 1 \\ {-k_1 }&{} {-k_2 }&{} \cdots &{} {-k_n } \\ \end{array} }} \right] , \mathbf{b}_c =\left[ {\begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \\ b \\ \end{array}} \right] \end{aligned}$$
(31)

One can define a Lyapunov function of the error in (32).

$$\begin{aligned} V_e =\mathbf{e}^{T}{} \mathbf{Pe} \end{aligned}$$
(32)

where \(\mathbf{P}\in \mathrm{R}^{n\times n}\) is a constant and symmetric positive definite matrix. So referring to lemma 5, \(V_e \) is bounded as \(\lambda _{\min \mathbf{P}} \left\| \mathbf{e} \right\| ^{2}\le V_e \le \lambda _{\max \mathbf{P}} \left\| \mathbf{e} \right\| ^{2}\). Also according to Lemma 4, \(V_e^{\left( q \right) } \) can be easily calculated.

$$\begin{aligned} V_e^{^{\left( q \right) }} \le \left( {\mathbf{e}^{T}} \right) ^{\left( q \right) } \mathbf{P} \mathbf{e}+\mathbf{e}^{T} \mathbf{Pe}^{\left( q \right) } \end{aligned}$$
(33)

Based on Theorem 2, if for any positive definite symmetric matrix \(\mathbf{Q}\), there exists a positive definite symmetric solution \(\mathbf{P}\) to the Lyapunov equation \(\varvec{\Lambda }_c^T \mathbf{P}+ \mathbf{P} \varvec{\Lambda }_c =-\mathbf{Q}\), then the error equation \(\mathbf{e}^{\left( q \right) }=\varvec{\Lambda }_c \mathbf{e}\) is intrinsically (without control input) Mittag–Leffler stable. According to (30), (33), and Lemma 5, we have:

$$\begin{aligned} V_e^{^{\left( q \right) }} \le -\mathbf{e}^{T} \mathbf{Qe}\le -\lambda _{\min \mathbf{Q}} \left\| \mathbf{e} \right\| ^{2} \end{aligned}$$
(34)

Furthermore, by using (12) and (34) \(\left\| {\mathbf{e}\left( t \right) } \right\| \) is always bounded as below:

$$\begin{aligned} \left\| {\mathbf{e}\left( t \right) } \right\| \le \left[ {\frac{\mathbf{e}^{T}\left( 0 \right) \mathbf{Pe}\left( 0 \right) }{\lambda _{\min \mathbf{P}} }E_q \left( {-\frac{\lambda _{\min \mathbf{Q}} }{\lambda _{\max \mathbf{P}} }t^{q}} \right) } \right] ^{\frac{1}{2}} \end{aligned}$$
(35)

If the control signal is nonzero then \(V_e^{\left( q \right) } \) is written as

$$\begin{aligned} V_e^{\left( q \right) }\le & {} -\mathbf{e}^{T}{} \mathbf{Qe}+ 2\mathbf{e}^{T}\mathbf{Pb}_{c} \left( {u^{{*}}-u_{f} \left( {\mathbf{x}|\varvec{\uptheta }} \right) -u_{s} -u_{c} } \right) \nonumber \\\le & {} -\mathbf{e}^{T}{} \mathbf{Qe} + 2\left| {\mathbf{e}^{T}{} \mathbf{Pb}_{c} } \right| \left( {\left| {u^{{*}}} \right| +\left| {u_{f} \left( {\mathbf{x}|\varvec{\uptheta }} \right) } \right| +\left| {u_{c} } \right| } \right) \nonumber \\&-2\mathbf{e}^{T}{} \mathbf{Pb}_{c} u_{s} \end{aligned}$$
(36)

The supervisory control signal is designed to guarantee \(V_e^{\left( q \right) } \le 0\). To this purpose, the following assumption is considered.

Assumption: we can determine a function \(f^{U}\left( \mathbf{x} \right) \) such that \(\left| {f\left( \mathbf{x} \right) } \right| \le f^{U}\left( \mathbf{x} \right) \). By observing (36) and based on \(f^{U}\left( \mathbf{x} \right) \), the supervisory control \(u_s \left( t \right) \) is chosen as

$$\begin{aligned} u_s \left( t \right)= & {} I^{{*}}\hbox {sgn}\left( {\mathbf{e}^{T}{} \mathbf{Pb}_c } \right) \left( \left| {u_c \left( t \right) } \right| +\left| {u_f \left( {\mathbf{x}|\varvec{\uptheta }} \right) } \right| \right. \nonumber \\&\left. +\frac{1}{b}\left( {f^{U}+\left| {x_d^{\left( {nq} \right) } } \right| +\left| {\mathbf{k}^{T}{} \mathbf{e}} \right| } \right) \right) \end{aligned}$$
(37)
Fig. 1
figure 1

Overall scheme of direct adaptive fuzzy controller with compensation

Full size image

Because b (or \(\mathbf{b}_\mathbf{c} \)) is known, \(sgn\left( {\mathbf{e}^{T}{} \mathbf{Pb}_c } \right) \) can be easily computed. Where \(I^{{*}}=1\) if \(V_e >V_{\max } \) (\(V_{\max } \) is constant and upper bound of \(V_e \) that the close-loop system remains stable and determined by the designer), \(I^{{*}}=0\) if \(V_e \le V_{\max } \), and \(\hbox {sgn}\left( r \right) =1\left( {-1} \right) \) if \(r\ge 0\left( {<0} \right) \). Considering the case \(V_e >V_{\max } \), and inserting (37) and (25) into (36) we have

$$\begin{aligned} V_e^{\left( q \right) } \le -\mathbf{e}^{T}{} \mathbf{Qe}<0 \end{aligned}$$
(38)

If the system tends to be unstable, especially in transient time, then \(u_s \left( t \right) \) begins operating to force \(V_e \le V_{\max } \). If the closed-loop system with the adaptive fuzzy controller and compensatory control well behaves in the sense that the error is sufficiently small (\(V_e \le V_{\max } )\), subsequently \(u_s \left( t \right) \) will be zero. In view of control energy, this strategy is a very economical design methodology. Since the supervisory control is usually very large and it may increase the implementation cost, this technique causes \(u_s \left( t\right) \) to operate only in short specific time. Therefore we always have \(V_e \le V_{\max } \) by using (37). Also, the boundedness of \(V_e \) implies the limitation of \(\mathbf{e}\).

$$\begin{aligned} \left\| \mathbf{e} \right\| \le \left( {\frac{V_{\max } }{\lambda _{\min \mathbf{P}} }} \right) ^{\frac{1}{2}} \end{aligned}$$
(39)

Considering (24) and (39), the boundedness of \(\mathbf{x}\) is concluded, as well.

$$\begin{aligned} \left\| \mathbf{x} \right\| \le \left( {\frac{V_{\max } }{\lambda _{\min \mathbf{P}} }} \right) ^{\frac{1}{2}}+\left\| {\mathbf{x}_\mathbf{d} } \right\| =M_x \end{aligned}$$
(40)

Thus by applying the supervisory control, the tracking error vector and the state variables vector always remain bounded.

5 Adaptive Fuzzy controller with compensation

In this section, the direct adaptive fuzzy system with compensatory control is designed, in which a fractional order adaptation law is applied to update the free parameters in consequence of the fuzzy controller.

First, let us define an ideal parameters vector (\(\varvec{\uptheta }^{{*}})\) and the minimum approximation error (\(\Omega \)) as follows:

$$\begin{aligned}&\varvec{\uptheta }^{{*}}\equiv \mathop {\arg \min }\limits _{\left| \varvec{\uptheta } \right| \le M_\theta } \left[ {\mathop {\sup }\limits _{\left| \mathbf{x} \right| \le M_x } \left| {u^{{*}}\left( t \right) -u_f \left( {\mathbf{x}|\varvec{\uptheta }} \right) -u_c \left( t \right) } \right| } \right] \end{aligned}$$
(41)
$$\begin{aligned}&\Omega \left( t \right) \buildrel \Delta \over = u^{{*}}\left( t \right) -u_c \left( t \right) -u_f \left( {\mathbf{x}|\varvec{\uptheta }^{{*}}} \right) =\omega \left( t \right) -u_c \left( t \right) \end{aligned}$$
(42)

where \(u_f \left( {\mathbf{x}|\varvec{\uptheta }^{{*}}} \right) \) is the output of the fuzzy system in the ideal parameters vector and \(\omega \left( t \right) =u^{{*}}\left( t \right) -u_f \left( {\mathbf{x}|\varvec{\uptheta }^{{*}}} \right) \). By adding and subtracting \(\mathbf{b}_c u_f \left( {\mathbf{x}|\varvec{\uptheta }^{{*}}} \right) \) to (30), according to (20) and (42), and after some simple manipulations, the error dynamics can be expressed as

$$\begin{aligned} \mathbf{e}^{\left( q \right) }=\varvec{\Lambda }_c \mathbf{e}+\mathbf{b}_c \varvec{\tilde{\uptheta }}^{T}\varvec{\upxi }\left( {\mathbf{x}\left( t \right) } \right) -\mathbf{b}_c u_s +\mathbf{b}_c \omega \left( t \right) -\mathbf{b}_\mathbf{c} u_c \end{aligned}$$
(43)

where \(\varvec{\tilde{\uptheta }}=\varvec{\uptheta }^{{*}}-\varvec{\uptheta }\) is the free parameters error.

Theorem 4

Considering the fractional order nonlinear system (22) with \(nq\le 1\) and control input (27), if the fractional order adaptation law is chosen as (44) and the compensator control is defined as (46), the overall adaptive scheme guarantees the stability of the resulting closed-loop system in the sense that all involved signals are uniformly bounded and the error will converge to zero asymptotically.

$$\begin{aligned}&\varvec{\uptheta }^{\left( q \right) }=2\gamma \mathbf{e}^{T}{} \mathbf{p}_n \varvec{\Psi }\left( {\mathbf{x}\left( t \right) } \right) -2I_\theta \gamma \mathbf{e}^{T}{} \mathbf{p}_n \frac{\varvec{\uptheta }{\varvec{\uptheta }}^{T}\varvec{\Psi }\left( {\mathbf{x}\left( t \right) } \right) }{\left\| \varvec{\uptheta } \right\| ^{2}} \nonumber \\ \end{aligned}$$
(44)
$$\begin{aligned}&I_\theta \,=\,\left\{ {\begin{array}{l} 0 \left\| \varvec{\uptheta } \right\| <M_\theta or \left( {\left\| \varvec{\uptheta } \right\| \!=\!M_\theta , \mathbf{e}^{T}{} \mathbf{p}_n \varvec{\uptheta }^{T}\varvec{\Psi }\left( \mathbf{x} \right) \le 0} \right) \\ 1 \left\| \varvec{\uptheta } \right\| \!=\!M_\theta , \mathbf{e}^{T}{} \mathbf{p}_n \varvec{\uptheta }^{T}\varvec{\Psi }\left( \mathbf{x} \right) >0 \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(45)
$$\begin{aligned}&u_c \left( t \right) =u\left( {t-1} \right) -\varvec{\uptheta }^{\mathbf{T}}\left( t \right) \varvec{\upxi }\left( {\mathbf{x}\left( {t-1} \right) } \right) \nonumber \\&~~~~~~~~~~~~~~+\, \frac{1}{b}\left( {x_d^{\left( {nq} \right) } \left( {t-1} \right) -x^{\left( {nq} \right) }\left( {t-1} \right) }\right. \nonumber \\&~~~~~~~~~~~~~~\left. +\,\mathbf{k}^{\mathbf{T}}{} \mathbf{e}\left( {t-1} \right) \right) \end{aligned}$$
(46)

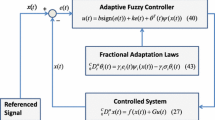
where \(\varvec{\Psi }\left( {\mathbf{x}\left( t \right) } \right) =\varvec{\upxi }\left( {\mathbf{x}\left( t \right) } \right) -\varvec{\upxi }\left( {\mathbf{x}\left( {t-1} \right) } \right) \), \(\mathbf{p}_n \) is the last column of \(\mathbf{P}\), and \(\gamma \) is a positive constant. Figure 1 shows the general scheme of the proposed approach.

Proof

: The Lyapunov function candidate is chosen as below to analyze the closed-loop stability.

$$\begin{aligned} V=\mathbf{e}^{T}{} \mathbf{Pe}+\frac{b}{2\gamma }\varvec{\tilde{\uptheta }}^{T}\varvec{\tilde{\uptheta }} \end{aligned}$$
(47)

Using (42), Lemma 4, and differentiating (47) with q order and respect to time along the trajectory (43), we obtain

$$\begin{aligned} V^{\left( q \right) }\le & {} -\mathbf{e}^{T}{} \mathbf{Qe}+\frac{b}{\gamma }\varvec{\tilde{\uptheta }}^{T} \varvec{\tilde{\uptheta }}^{\left( q \right) } \nonumber \\&+ 2\mathbf{e}^{T}{} \mathbf{Pb}_c \left( {\varvec{\tilde{\uptheta }}^{T}\varvec{\upxi }\left( {\mathbf{x}\left( t \right) } \right) -u_s +\Omega \left( t \right) } \right) \end{aligned}$$
(48)

Let \(\mathbf{p}_n \) be the last column of \(\mathbf{P}\) then \(\mathbf{e}^{T}{} \mathbf{Pb}_c =\mathbf{e}^{T}{} \mathbf{p}_n b\) and we have

$$\begin{aligned} V^{\left( q \right) }\le & {} -\mathbf{e}^{T}{} \mathbf{Qe}-2 \mathbf{e}^{T}{} \mathbf{Pb}_c u_s +\frac{b}{\gamma }\varvec{\tilde{\uptheta }}^{T} \varvec{\tilde{\uptheta }}^{\left( q \right) } \nonumber \\&+2 \mathbf{e}^{T}{} \mathbf{p}_n b\left( {\omega \left( t \right) -u_c \left( t \right) +\varvec{\tilde{\uptheta }}^{T}\varvec{\upxi }\left( {\mathbf{x}\left( t \right) } \right) } \right) \end{aligned}$$
(49)

The compensator control is constructed as below

$$\begin{aligned} u_c \left( t \right) =u^{{*}}\left( {t-1} \right) -\varvec{\uptheta }^{\mathbf{T}}\left( t \right) \varvec{\upxi }\left( {\mathbf{x}\left( {t-1} \right) } \right) \end{aligned}$$
(50)

From (25), we have

$$\begin{aligned} u^{{*}}\left( {t-1} \right)= & {} \frac{1}{b}\left( {-f\left( {\mathbf{x}\left( {t-1} \right) } \right) +x_d^{\left( {nq} \right) } \left( {t-1} \right) }\right. \nonumber \\&\left. {+\,\mathbf{k}^{\mathbf{T}}{} \mathbf{e}\left( {t-1} \right) } \right) \end{aligned}$$
(51)

where \(f\left( {\mathbf{x}\left( {t-1} \right) } \right) \) can be calculated from (23).

$$\begin{aligned} f\left( {\mathbf{x}\left( {t-1} \right) } \right) =x^{\left( {nq} \right) }\left( {t-1} \right) -bu\left( {t-1} \right) \end{aligned}$$
(52)

Substituting (52) into (51), \(u^{{*}}\left( {t-1} \right) \) is computable because all terms are available for measurement. Then the compensator control is measurable as below

$$\begin{aligned} u_{c} \left( t \right)= & {} u\left( {t-1} \right) -\varvec{\uptheta }^{\mathbf{T}}\left( t \right) \varvec{\upxi }\left( {\mathbf{x}\left( {t-1} \right) } \right) \nonumber \\&+\frac{1}{b}\left( {x_d^{\left( {nq} \right) } \left( {t-1} \right) -x^{\left( {nq} \right) }\left( {t-1} \right) }\right. \nonumber \\&\left. {+\,\mathbf{k}^{\mathbf{T}}{} \mathbf{e}\left( {t-1} \right) } \right) \end{aligned}$$
(53)

Combining (49) and (50) and after adding and subtracting \(2\mathbf{e}^{T}{} \mathbf{p}_\mathbf{n} b \varvec{\uptheta }^{T}\varvec{\upxi }\left( {\mathbf{x}\left( {t-1} \right) } \right) , V{\left( ^q \right) }\) is equivalent to

$$\begin{aligned} V^{\left( q \right) }\le & {} -\,\mathbf{e}^{\mathbf{T}}{} \mathbf{Qe}+2\mathbf{e}^{T}\mathbf{p}_\mathbf{n} b\left( {\omega \left( t \right) -\omega \left( {t-1} \right) } \right) \nonumber \\&-\,2\mathbf{e}^{T}{} \mathbf{Pb}_c u_s \!+ \!\frac{b}{\gamma }\varvec{\tilde{\uptheta }}^{T}\left[ {\varvec{\tilde{\uptheta }}^{\left( q \right) }\!+\!2\gamma \mathbf{e}^{T}{} \mathbf{p}_\mathbf{n} \left( {\varvec{\upxi }\left( {\mathbf{x}\left( t \right) } \right) }\right. }\right. \nonumber \\&-\,\left. {\left. {\varvec{\upxi }\left( {\mathbf{x}\left( {t-1} \right) } \right) } \right) } \right] \end{aligned}$$
(54)

By the fact \(\varvec{\uptheta }^{{*(q)}}=0\) and \(\varvec{\tilde{\uptheta }}^{\left( q \right) }=-\varvec{\uptheta }^{\left( q \right) }\), we can choose the adaptation law as

$$\begin{aligned} \varvec{\uptheta }^{\left( q \right) }=2\gamma \mathbf{e}^{T}{} \mathbf{p}_\mathbf{n} \left( {\varvec{\upxi }\left( {\mathbf{x}\left( t \right) } \right) -\varvec{\upxi }\left( {\mathbf{x}\left( {t-1} \right) } \right) } \right) \end{aligned}$$
(55)

Observing from (37), \(\mathbf{e}^{T}{} \mathbf{Pb}_c u_s \left( t \right) \ge 0\) is straightforward and \(V^{\left( q \right) }\) can be written as below

$$\begin{aligned} V^{\left( q \right) }\le -\mathbf{e}^{\mathbf{T}}{} \mathbf{Qe}+2\mathbf{e}^{T}\mathbf{p}_\mathbf{n} b\left( {\omega \left( t \right) -\omega \left( {t-1} \right) } \right) \end{aligned}$$
(56)

This inequality is the best we can hope to obtain since \(2\mathbf{e}^{T}{} \mathbf{p}_\mathbf{n} b\left( {\omega \left( t \right) -\omega \left( {t-1} \right) } \right) \) is of the order of the minimum approximation error. The variations of \(u^{{*}}\left( t \right) \) and \(u_f \left( {\mathbf{x}|\varvec{\uptheta }^{{*}}} \right) \) with time are smooth. In other words, the gradient of \(u^{{*}}\left( t \right) \) or \(u_f \left( {\mathbf{x}|\varvec{\uptheta }^{{*}}} \right) \) with respect to t does not change much. So the values of \(u^{{*}}\left( t \right) -u^{{*}}\left( {t-1} \right) \) and \(u_{f} \left( {\mathbf{x}\left( t \right) |{\varvec{\uptheta }}^{{*}}} \right) -u_{f} \left( {\mathbf{x}\left( {t-1} \right) |{\varvec{\uptheta }}^{{*}}} \right) \) in \(\omega \left( t \right) -\omega \left( {t-1} \right) \) are very small even if the value of \(u^{{*}}\left( t \right) -u_{f} \left( {\mathbf{x}\left( t \right) |{\varvec{\uptheta }}^{{*}}} \right) \) is significant. To guarantee \(\left\| {\varvec{\uptheta }} \right\| \le M_{\varvec{\uptheta }} \), the adaptation law (55) must be modified by the projection algorithm as shown in (57) where the projection factor \(I_{\varvec{\uptheta }} \) is defined as (58).

$$\begin{aligned}&\varvec{\uptheta }^{\left( q \right) }=2\gamma \mathbf{e}^{T}{} \mathbf{p}_n \varvec{\Psi }\left( {\mathbf{x}\left( t \right) } \right) -2I_\theta \gamma \mathbf{e}^{T}{} \mathbf{p}_n \frac{\varvec{\uptheta }{\varvec{\uptheta }}^{T}\varvec{\Psi }\left( {\mathbf{x}\left( t \right) } \right) }{\left\| \varvec{\uptheta } \right\| ^{2}}\nonumber \\ \end{aligned}$$
(57)
$$\begin{aligned}&I_\theta =\left\{ {\begin{array}{l@{\quad }l} 0 &{}\left\| \varvec{\uptheta } \right\| <M_\theta or \left( {\left\| \varvec{\uptheta } \right\| =M_\theta , \mathbf{e}^{T}{} \mathbf{p}_n \varvec{\uptheta }^{T}\varvec{\Psi }\left( {\mathbf{x}\left( t \right) } \right) \le 0} \right) \\ 1 &{} \left\| \varvec{\uptheta } \right\| =M_\theta , \mathbf{e}^{T}{} \mathbf{p}_n \varvec{\uptheta }^{T}\varvec{\Psi }\left( {\mathbf{x}\left( t \right) } \right) >0 \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(58)

where \(\varvec{\uppsi }\left( \mathbf{x} \right) =\varvec{\upxi }\left( {\mathbf{x}\left( t \right) } \right) -\varvec{\upxi }\left( {\mathbf{x}\left( {t-1} \right) } \right) \). To prove \(\left\| \varvec{\uptheta } \right\| \le M_{\varvec{\uptheta }} \), let \(V_{\varvec{\uptheta }} =\frac{1}{2}\varvec{\uptheta }^{T}\varvec{\uptheta }\). If the first line of (58) is right, we have either \(\left\| \varvec{\uptheta } \right\| <M_{\varvec{\uptheta }} \) or (59) for \(\left\| \varvec{\uptheta } \right\| =M_{\varvec{\uptheta }} \), then \(\left\| \varvec{\uptheta } \right\| \le M_{\varvec{\uptheta }} \) is always true.

$$\begin{aligned} V_{\varvec{\uptheta }}^{\left( q \right) } \le \varvec{\uptheta }^{T}\varvec{\uptheta }^{\left( q \right) }\le 2\gamma \mathbf{e}^{T}{} \mathbf{p}_n \varvec{\uptheta }^{T} \varvec{\upxi }\left( \mathbf{x} \right) \le 0 \end{aligned}$$
(59)

If the second line of (58) is correct, we have \(\left\| \varvec{\uptheta } \right\| =M_{\varvec{\uptheta }} \) and

$$\begin{aligned} V_{\varvec{\uptheta }}^{\left( q \right) } \le \varvec{\uptheta }^{T}\varvec{\uptheta }^{\left( q \right) } = 2\gamma \mathbf{e}^{T}{} \mathbf{p}_n \left( { \varvec{\uptheta }^{T} - \frac{\varvec{\uptheta }^{T}\varvec{\uptheta \theta }^{T}}{\left\| \varvec{\uptheta } \right\| ^{2}}} \right) \varvec{\Psi }\left( \mathbf{x} \right) =0 \end{aligned}$$
(60)

Then \(V_{\varvec{\uptheta }}^{\left( q \right) } \le 0\) and \(\left\| \varvec{\uptheta } \right\| \) is remain in the enclosed area like \(M_{\varvec{\uptheta }} \). Therefore, \(\left\| \varvec{\uptheta } \right\| \le M_{\varvec{\uptheta }} \) is always true for \(t\ge 0\). According to (21), it is obvious that \(\left\| {\varvec{\upxi }\left( \mathbf{x} \right) } \right\| \le 1\) and base on (20), the output of the fuzzy controller is as

$$\begin{aligned} \left| {u_f \left( {\mathbf{x}|\varvec{\uptheta }} \right) } \right| \le \left\| \varvec{\uptheta } \right\| \le M_\theta \end{aligned}$$
(61)

Because based on (20), \(\left| {u_f \left( {\mathbf{x}|\varvec{\uptheta }} \right) } \right| \) is a weighted average of the elements \(\varvec{\uptheta }\). Then, invoking (25), (39), and (50) the compensation signal will be bounded.

$$\begin{aligned} \left| {u_c \left( t\right) } \right|\le & {} \left| {u^{{*}}\left( {t-1} \right) } \right| +\left| {\varvec{\uptheta }^{\mathbf{T}}\left( t \right) \varvec{\upxi }\left( {\mathbf{x}\left( {t-1} \right) } \right) } \right| \nonumber \\\le & {} \left| {\frac{1}{b}\left[ {-f\left( {\mathbf{x}\left( {t-1} \right) } \right) +x_d^{\left( {nq} \right) } \left( {t-1} \right) +\mathbf{k}^{T}{} \mathbf{e}\left( {t-1} \right) } \right] }\right| \nonumber \\&+\left| {\varvec{\uptheta }^{\mathbf{T}}\left( t \right) \varvec{\upxi }\left( {\mathbf{x}\left( {t-1} \right) } \right) } \right| \nonumber \\\le & {} \frac{f^{U}\left( \mathbf{x} \right) \!+\!\left| {x_d^{\left( {nq} \right) } \left( {t-1} \right) } \right| \!+\!\left\| {\mathbf{k}^{T}} \right\| \left( {\frac{V_{\max } }{\lambda _{\min \mathbf{P}} }} \right) ^{\frac{1}{2}}}{b}+M_{\varvec{\uptheta }}\nonumber \\ \end{aligned}$$
(62)

Using (39), (61) and (62), the inequality of the control signal is computed as follows:

$$\begin{aligned} \left| {u\left( t \right) } \right|\le & {} \left| {u_f \left( {\mathbf{x}|\varvec{\uptheta }} \right) } \right| +\left| {u_c \left( t \right) } \right| +\left| {u_s \left( t \right) } \right| \nonumber \\\le & {} 4M_{\varvec{\uptheta }} +\frac{3}{b}\left( f^{U}\left( \mathbf{x} \right) +\left\| {\mathbf{k}^{T}} \right\| \right. \nonumber \\&\left. \times \left( {\frac{V_{\max } }{\lambda _{\min \mathbf{P}} }} \right) ^{\frac{1}{2}}+M_{x_d } \right) =M_u \end{aligned}$$
(63)

where \(M_{x_d } \) is the known upper bound for \(\left| {x_d^{\left( {nq} \right) } } \right| \).

In order to show that the closed-loop system is Mittag–Leffler stable, and the system error converges to zero asymptotically, according to Theorem 3, it is necessary to demonstrate that \(I^{q}\left\| \mathbf{e} \right\| \) is bounded. In order to show this property by Substituting (57) into (54) and considering \(\mathbf{e}^{T}{} \mathbf{Pb}_c u_s \left( t \right) \ge 0\), we obtain

$$\begin{aligned} V^{\left( q \right) }\le & {} -\mathbf{e}^{\mathbf{T}}{} \mathbf{Qe}+2\mathbf{e}^{T}\mathbf{p}_\mathbf{n} b\left( {\omega \left( t \right) -\omega \left( {t-1} \right) } \right) \nonumber \\&+\,2b \mathbf{e}^{T}{} \mathbf{p}_n I_\theta \frac{\varvec{\tilde{\theta }}^{T}\varvec{\uptheta }\varvec{\uptheta }^{T}\varvec{\Psi }\left( {\mathbf{x}\left( t \right) } \right) }{\left\| \varvec{\uptheta } \right\| ^{2}} \end{aligned}$$
(64)

Let us assume that \(I_{\varvec{\uptheta }} =1\) and \(\mathbf{e}^{T}{} \mathbf{p}_{n} \varvec{\uptheta }^{T}\varvec{\Psi }\left( {\mathbf{x}\left( t \right) } \right) >0\), because \(\varvec{\uptheta }^{{*T}}\varvec{\uptheta }=\varvec{\uptheta }^{T}\varvec{\uptheta }^{{*}}\), the following simplification is reasonable:

$$\begin{aligned} \varvec{\tilde{\theta }}^{T}\varvec{\uptheta }=\frac{1}{2}\left( {\left\| {\varvec{\uptheta }^{{*}}} \right\| ^{2}-\left\| \varvec{\uptheta } \right\| ^{2}-\left\| {\varvec{\uptheta }-\varvec{\uptheta }^{{*}}} \right\| ^{2}} \right) \end{aligned}$$
(65)

Since \(M_\theta \) is selected in such a way that always involves \(\varvec{\uptheta }^{{*}}\) and \(\left\| {\varvec{\uptheta }^{{*}}} \right\| \le \left\| \varvec{\uptheta } \right\| =M_\theta \), this yields that \(\varvec{\tilde{\theta }}^{T}\varvec{\uptheta }\le 0\). Therefore, due to the \(\mathbf{e}^{T}{} \mathbf{p}_n \varvec{\uptheta }^{T}\varvec{\Psi }\left( {\mathbf{x}\left( t \right) } \right) >0\) last term of (64) is nonpositive and it is straightforward that

$$\begin{aligned} V^{\left( q \right) }\le -\mathbf{e}^{T}{} \mathbf{Qe}+2 \mathbf{e}^{T}\mathbf{Pb}_c \left( {\omega \left( t \right) -\omega \left( {t-1} \right) } \right) \end{aligned}$$
(66)

On the other hand, if \(I_\theta =0\), (66) is directly achieved from (64). According to \(\lambda _{\min \mathbf{Q}} \left\| \mathbf{e} \right\| ^{2}\le \mathbf{e}^{T}{} \mathbf{Qe}\), (66) can be further simplified to

$$\begin{aligned} V^{\left( q \right) }\le & {} -\left( {\lambda _{\min Q} -2} \right) \left\| \mathbf{e} \right\| ^{2}-2\left( {\mathbf{e}+\,\frac{1}{2}{} \mathbf{Pb}_c^ \upsilon \left( t \right) } \right) ^{2}\nonumber \\&+\,\frac{1}{2}\left\| {\mathbf{Pb}_c^ \upsilon \left( t \right) } \right\| ^{2}\nonumber \\\le & {} -\left( {\lambda _{\min Q} -2} \right) \left\| \mathbf{e} \right\| ^{2}+\frac{1}{2}\left\| {\mathbf{Pb}_c^ \upsilon \left( t \right) } \right\| ^{2} \end{aligned}$$
(67)

where \(\upsilon \left( t \right) =\omega \left( {t-1} \right) -\omega \left( t \right) \). Let us assume \(\lambda _{\min Q} >2 (\mathbf{Q}\) is determined by the designer). On the basis of (4), by fractional order integrating both sides of (67), we can obtain

$$\begin{aligned} I^{q}\left\| \mathbf{e} \right\| ^{2}\le & {} \frac{1}{\lambda _{\min Q} -2}\left( {V\left( 0 \right) -V\left( t \right) } \right) \nonumber \\&+\,\frac{1}{2\left( {\lambda _{\min Q} -2} \right) }I^{q}\left\| {\mathbf{Pb}_c^ \upsilon \left( t \right) } \right\| ^{2} \end{aligned}$$
(68)

Because \(\mathbf{e}\) and \(\varvec{\uptheta }\) are bounded, we can claim that V is finite and (68) is changed to:

$$\begin{aligned} I^{q}\left\| \mathbf{e} \right\| ^{2}\le & {} \frac{1}{\lambda _{\min Q} -2}\left( {V\left( 0 \right) +\mathop {\sup }\limits _{t\ge 0} \left| {V\left( t \right) } \right| } \right) \nonumber \\&+\,\frac{1}{2\left( {\lambda _{\min Q} -2} \right) }\left\| {\mathbf{Pb}_c } \right\| ^{2}I^{q}\left\| {\upsilon \left( t \right) } \right\| ^{2} \end{aligned}$$
(69)

If \(I^{q}\left\| {\upsilon \left( t \right) } \right\| ^{2}\) is limited, then \(I^{q}\left\| \mathbf{e} \right\| ^{2}\) is bounded and according to (33), \(I^{q}V_e \) is also bounded. If \({\dot{\mathbf{e}}}\) is continuous, inspire by the fractional order Barbalat’s lemma (Theorem 3), we achieve that \(V_e \) and the tracking error (\(\mathbf{e})\) can converge to zero when t goes to infinity. This equation completes the proof. \(\square \)

6 Simulation

In this section, two illustrative examples are provided to clarify the effectiveness and robustness of the proposed scheme to confirm the theoretical results of this investigation. For the purpose of comparison, two different controllers including the adaptive fractional order PID [28] and the hierarchical terminal sliding mode control (HTSC) [29] are implemented. In all numerical simulations, the sample time is assumed \(h=10^{-3}\) second and the Lyapunov matrix \(\mathbf{Q}\) is equaled to \(3\mathbf{I}_{n\times n} \). Where \(\mathbf{I}\in \mathrm{R}^{n\times n}\)is identity matrix and n shows the number of system states. Also, the free parameters vector \(\varvec{\uptheta }\) is chosen randomly at the start time of control.

Fig. 2
figure 2

State trajectories of the master and slave system a first states, b second states

Full size image
Fig. 3
figure 3

Arbitrary membership functions defined over the state space in Example 2 for \(x_{1}\) and \(x_{2}\)

Full size image

Example 1

: Synchronization of two fractional order non-identical chaotic systems

The following example confirms the suitability of the proposed method to synchronize two fractional order non-identical chaotic systems. Consider the following uncertain fractional order system as a slave system:

$$\begin{aligned} \left\{ {\begin{array}{l} x_1^{\left( q \right) } \left( t\right) =x_2 \left( t \right) \\ x_2^{\left( q \right) } \left( t \right) =\tilde{a}x_{1} \left( t \right) +\tilde{b}x_2 \left( t \right) +\tilde{c}x_1^2\left( t \right) +\tilde{d}\cos \left( t\right) \\ \qquad \qquad \quad +\,d_{1} \left( t\right) +u\left( t \right) +\Delta f\left( \mathbf{x}\right) \end{array}} \right. \nonumber \\ \end{aligned}$$
(70)

where \(d_1 \left( t \right) =\sin (3t)\) is an internal disturbance, \(\Delta f\left( \mathbf{x} \right) =1.5\sin \left( {x_1 } \right) \sin \left( {x_2 } \right) \) is a system uncertainty, and \(\tilde{a}=a+\Delta a\), \(\tilde{b}=b+\Delta b, \tilde{c}=c+\Delta c\), and \(\tilde{d}=d+\Delta d\) are uncertain coefficients of the slave system. In this example, we set \(a=1.2, b=-1, c=-1, d=2\), \(\Delta a=0.2a\sin \left( {2t} \right) \), \(\Delta b=0.3b\cos \left( {3t} \right) , \Delta c=0.25c\sin \left( {3t} \right) \), and \(d=0.15d\cos \left( {2t} \right) \). The controller must force the output variable \(y=x_1 \) to track the output variable \(y_d =x_{d1} \) of a master system which is considered a fractional order version of Duffing–Holmes system in (71) [54].

$$\begin{aligned} \left\{ {\begin{array}{l} x_{d1}^{\left( q \right) } \left( t \right) =x_{d2} \left( t \right) \\ x_{d2}^{\left( q \right) } \left( t \right) =x_{d1} (t) -0.25x_{d2} \left( t \right) -x_{d1}^3 \left( t \right) \\ \qquad \qquad \qquad +\,0.3\cos \left( t \right) +\Delta g\left( {\mathbf{x}_\mathbf{d} } \right) +d_2 \left( t \right) \\ \end{array}} \right. \end{aligned}$$
(71)

Let us assume that the master system is perturbed by \(\Delta g\left( {\mathbf{x}_\mathbf{d} } \right) =1.5\sin \left( {x_{d} {2} } \right) \cos \left( {x_{d1} } \right) \) as an uncertainty term and \(d_{2} \left( t \right) =\cos (3t)\) as the internal disturbance. State trajectories of the slave and master system are plotted in Fig. 2 when the input control is zero and \(\mathbf{x}\left( 0 \right) =\left[ {-0.1,0.2} \right] \), \(\mathbf{x}_\mathbf{d} \left( 0 \right) =\left[ {0.3,-0.2} \right] \) are chosen as initial conditions.

For demonstrating the ability of the proposed controller in synchronization of chaotic systems, the design parameters are chosen as \(f^{U}=5, V_{\max } =2\) and according to (29), \(q=0.5\). Referring to theorem 1 and (26), the coefficient vector of the error equation is considered as \(\mathbf{k}=\left[ {{\begin{array}{cc} 2&{} 3 \\ \end{array} }} \right] ^{T}\) to guarantee the stability of the error equation. Let us assume that the Gaussian membership functions are arbitrarily defined with random centers and variances in the antecedent part of the fuzzy controller as Fig. 3. The performance of the fractional order direct adaptive fuzzy with compensation (FDAFC), the fractional order adaptive controller (FoAC) [28] and the hierarchical terminal sliding mode control (HTSC) [29] are compared in Fig. 4 when the control signal is activated at \(t=2^{s}\). Figure 4c, d which focuses on the range between \(40^{s}\) and \(50^{s}\) indicates that FDAFC has better accuracy in signal tracking than two other strategies. Furthermore, to illustrate the acceptable efficiency of FDAFC, Fig. 5 shows the time history of the control signal and state variables error. These results confirm that the system can be controlled to track the reference trajectory and the error is asymptotically regulated to zero. To ascertain the importance of the adaptive fuzzy controller in the described strategy, time history of the fuzzy control signal is indicated in Fig. 6a. In addition, the states variable error is also shown in Fig. 6b when the fuzzy controller is considered inactive. As can be seen that the error signal has the nonzero bias and does not converge to zero, hence the compensation signal cannot appropriately control the plant alone.

Fig. 4
figure 4

Simulation results of Example 1 a state trajectories of \(x_1\), b state trajectories of \(x_2\), c zoomed view of state trajectory of \(x_1\), d zoomed view of state trajectory of \(x_2\)

Full size image
Fig. 5
figure 5

a Time history of the control signal in FDAFC, b error convergence in FDAFC in Example 1

Full size image
Fig. 6
figure 6

a Time history of the fuzzy control signal in FDAFC, b error convergence in the proposed method when the adaptive fuzzy is inactive in Example 1

Full size image

Example 2

Stabilization the non-autonomous fractional order gyro

This example verified the usefulness and efficiency of FDAFC by using stabilization of the non-autonomous fractional order gyro. The gyro is one of the most interesting and everlasting dynamic systems which has various useful applications in optics, navigation, aeronautics and space engineering fields [55]. Therefore, the chaos stabilization procedure of chaotic gyroscope systems in this brief may have practical applications in the future. Since in real-world applications, model uncertainties, and external disturbances affect the dynamics of the system, in this article the following uncertain fractional order gyro with a control input is taken into account [29].

$$\begin{aligned} \left\{ {\begin{array}{l} x_1^{\left( q \right) } =x_2 \left( t \right) \\ x_2^{\left( q \right) } =-\frac{100\left( {1-\cos \left( {x_1 \left( t \right) } \right) } \right) ^{2}}{\sin ^{3}\left( {x_1 \left( t \right) } \right) }-\tilde{a} \left( t \right) x_2 \left( t \right) \\ \qquad \qquad - \frac{x_2^3 \left( t \right) }{20}+\sin \left( {x_1 \left( t \right) } \right) +\Delta f\left( {\mathbf{x},t} \right) +d\left( t \right) \\ \qquad \qquad +\tilde{b}\left( t \right) \sin \left( {25t} \right) \sin \left( {x_1 \left( t \right) } \right) +u\left( t \right) \\ \end{array}} \right. \end{aligned}$$
(72)

where \(x_1 \) denotes the rotation angle, \(x_2 \) represents the rotation angle velocity, \(u\left( t \right) \) is the control input, \(\Delta f\left( {\mathbf{x},t} \right) =2\sin \left( {x_1 \left( t \right) } \right) \sin \left( {x_2 \left( t \right) } \right) \) is the time-varying model uncertainty and \(d\left( t \right) =\cos \left( {4t} \right) \) shows the disturbance. \(\tilde{a}\left( t \right) =0.5+0.5\Delta a\left( t \right) \) and \(\tilde{b}\left( t \right) =35.5+35.5\Delta b\left( t \right) \) are uncertain coefficients of the slave system where \(\Delta a\left( t \right) =0.4\sin \left( {2t} \right) \) and \(\Delta b\left( t \right) =0.2\cos \left( t \right) \). The order of fractional derivative (q) is set to 0.5 and the initial condition of the gyro system is selected as \(\mathbf{x}\left( 0 \right) =\left[ {1,-1} \right] \). Time trajectories of state variables are shown in Fig. 7 in which the control signal is chosen to be zero.

Fig. 7
figure 7

State trajectories of the gyro system a \(x_1 \), b \(x_2 \) in Example 2

Full size image
Fig. 8
figure 8

Arbitrary membership functions defined over the state space in Example 2 for \(x_1\) and \(x_2\)

Full size image
Fig. 9
figure 9

Simulation results of Example 2 a State trajectories of \(x_1 \), b state trajectories of \(x_2 \)

Full size image

Another design parameters are determined as \(f^{U}=5, V_{\max } =5\) and referring to theorem 1 and (26), the coefficient vector of the error equation is considered as \(\mathbf{k}=\left[ {{\begin{array}{cc} 2&{} 3 \\ \end{array} }} \right] ^{T}\). In this example, the Gaussian membership functions in the antecedent part of the fuzzy controller are depicted in Fig. 8. Figure 9 compares the performance of FDAFC, FoAC [28] and HTSC [29] while the control input is activated at \(t=4^{s}\). In addition, the control signal of FDAFC and the fuzzy control signal are shown in Fig. 10. These results express that the output can be stabilized significantly and the error is asymptotically converged to zero. It is noteworthy that if the fuzzy controller is set to be inactive, the state variables error cannot converge to zero and has undesirable variations as shown in Fig. 11.

Table 1 represents Sum of Integral Absolute Error (SIAE) and Integral Absolute Control Signal (IACS) as two well-known criteria in order to compare the performance of the proposed method, FDAFC, with the previously proposed methods: FoAC and HTSC. SIAE and IACS are computed by:

$$\begin{aligned} \mathbf{SIAE}\!=\!\sum _{i=1}^n {\int {\left| {e_i \left( t \right) } \right| dt} } ,\quad \mathbf{IACS}\!=\!\int {\left| {u\left( t \right) } \right| dt} \end{aligned}$$
(73)
Fig. 10
figure 10

Time history of a the control signal, b the adaptive fuzzy control signal in Example 2

Full size image
Fig. 11
figure 11

Error convergence in the proposed method

Full size image
Table 1 Performance of various control methods
Full size table

The values of the resulted criteria show the significant improvement of the control performance of FDAFC in comparison to FoAC and HTSC. In Example 1, the SIAE of the proposed scheme is lower and therefore more acceptable than the other approaches above. This improvement is also observed in Example 2. Furthermore, the control signal energy of FDAFC is approximately less than or equal to FoAC and HTSC in two simulations. It is remarkable that in the introduced method, the model function (\(f(\mathbf{x})\)), the uncertainty, and the disturbance are all unknown. However, in the HTSC, \(f(\mathbf{x})\) is pre-specified and only the uncertainty and disturbance are unknown. Based on this property, the FDAFC is more practical and useful and outperforms the previously introduced adaptive controllers.

7 Conclusion

In this paper, a novel direct adaptive fuzzy controller with compensation signal is proposed for controlling and stabilizing the specific fractional order nonlinear systems. The new fractional order adaptation law is obtained from fractional order Lyapunov theorem which is applied to adjust free parameters in the consequence part of the adaptive fuzzy controller. Moreover, in advanced application of the supervisory control, we proved that the supervisory control is sufficient to constrain the output error in fractional order systems. On the top of that, due to the less experience about the fractional order plant, it is not practically possible to design proper membership functions and the common adaptive fuzzy systems cannot control the plant effectively while the proposed approach does not demand suitable membership functions in the antecedent part of the fuzzy system. Furthermore, the fractional order nonlinear system can be involved in disturbance and uncertainty since the introduced method does not require a plant model function. In addition, the proposed approach guarantees the global Mittag–Leffler stability of the resulting closed-loop system in which all signals are uniformly bounded. Also, it ensures that the output error has asymptotic convergence to zero by using the fractional order Barbalat lemma. Another advantage of this proposed approach compared to the literature is the utilization of valid fractional order equations in the direct adaptive fuzzy controller; moreover, the application of the projection algorithm in the fractional order adaptation law is investigated in order to prevent free parameters from being excessively large. Simulation studies are finally presented to show the advantages of the proposed approach. Different fractional order nonlinear systems are adequately controlled by the proposed method. In the end, simulation results on two applications express the satisfying achievements on the controlling performance of the recommended approach, while yielding asymptotic convergence to zero for the error vector.