Analysis of supercritical pitchfork bifurcation in active magnetic bearing-rotor system with current saturation

Abstract

The bifurcation characteristics of the active magnetic bearing-rotor system subjected to the external excitation were investigated analytically when it was operating at a speed far away from its natural frequencies. During operation of the system, some nonlinear factors may be prominent, for example, the nonlinearity of bearing force and current saturation. Nonlinear factors can lead to some complicated behaviors, which have negative effects on the operating performance and stability. To analyze the bifurcations happening at the speed far away from harmonic resonances, an approximate analytical method that can be applicable to the bifurcation analysis of the forced vibration system was proposed. By applying it to the active magnetic bearing-rotor system, multiple static equilibriums and periodic solutions were obtained, and then, the stability analysis was conducted based on Floquet theory. The validity and accuracy of the approximate analytical method were verified by the numerical integration method and generalized cell mapping digraph method. It was found that there was supercritical pitchfork bifurcation of static equilibrium in the active magnetic bearing-rotor system. The influences of external excitation and controller parameters on dynamical characteristics were discussed. Based on analysis results, controller parameters were also improved to prevent nonlinear behaviors and improve system performance.

1 Introduction

1.1 Nonlinear AMB-rotor system

Active magnetic bearing (AMB) is a typical mechatronic product consisting of sensors, power amplifier, controller, and electromagnetic actuator. In rotating machines, AMBs can generate proper electromagnetic forces in time through the cooperation of their components to achieve the suspension support of rotors [1]. During operation, once the rotor deviates from the reference position, the sensor measures the rotor displacement and transmits measurement signal to the controller. Then the controller gives control command based on its control law. The power amplifier outputs corresponding control current. Thereby the electromagnetic forces are adjusted and the rotor is driven to return to the reference position through this way.

Compared with mechanical bearings, AMBs have many advantages. There is no contact between the rotor and stator. Accordingly, there is no mechanical wear. The additional lubrication system is also unnecessary. The extremely high-speed operation can also be achieved due to non-contacting support. What’s more, the dynamical characteristics including stiffness and damping can be adjusted flexibly by the controller. Due to these advantages, AMBs have been widely used in high-speed rotating machines, especially those operating in harsh environments, the primary helium circulator for high-temperature gas-cooled nuclear reactor[2,3,4] for example.

In the process of design and commissioning, it is necessary to obtain accurate models which can describe the characteristics of AMB-rotor systems. The most common models are linearized. They can be obtained by linearizing the electromagnetic force with respect to the rotor displacement and current near the reference position [1]. In the vicinity of reference position, linearized models can accurately describe dynamical characteristics of systems and play key roles in system design, performance analysis, system identification and controller design of AMB-rotor systems [5, 6].

However, AMB-rotor systems are inherently nonlinear and there exist nonlinear factors in most of their components. Nonlinear factors can be divided into two types according to involved components, namely the bearing nonlinearities and the rotor nonlinearities. The nonlinear factors in bearings and related components are called bearing nonlinearities. One of the important bearing nonlinearities is the nonlinear relationship of the electromagnetic force with respect to the rotor displacement, current in bearing, which is called the nonlinearity of electromagnetic force in this paper. Besides, bearing nonlinearities also include the nonlinear magnetization, magnetic saturation, hysteresis due to the feature of ferromagnetic material [7], the voltage or current saturation due to the capacity of power amplifier [8, 9], etc. The nonlinear factors in rotating parts are called rotor nonlinearities, which include the internal friction of rotor [10, 11], and even some faults [12,13,14] such as rotor crack and rub-impact. When the AMB-rotor systems are operating under some harsh conditions, subjected to heavy load and large disturbance for example, these nonlinear factors may lead to some complicated phenomena, which always have important influences on the system performance and stability. In addition, with the increasing trend of operation speed of rotating machines, the nonlinear factors in AMB-rotor systems are becoming more and more prominent. Thereby many nonlinear behaviors happen frequently in AMB-rotor systems.

In AMB-rotor systems, many nonlinear phenomena such as jump phenomenon [15], pitchfork bifurcation [16], period doubling, quasi-periodic motion and even chaos [17] have been observed. In cases of jump phenomenon and supercritical pitchfork bifurcation, the maximum displacement of rotor will increase obviously, which will make the system performance deteriorate and even lead to instability. In case of the period doubling, quasi-periodic motion and chaos, non-synchronous vibrations occurring in the system will generate alternating stress in the rotor, which will damage the system structure and shorten the operating life. These nonlinear dynamical behaviors have significant influences on the performance, stability and operating life of the AMB-rotor systems.

However, analyses based on the linearized models cannot explain these complicated behaviors. Accordingly, no effective measures can be proposed to avoid these phenomena. On the basis of this research background, it is necessary to conduct dynamical analyses of the AMB-rotor systems by taking nonlinear factors into consideration. It can help to get a comprehensive understanding of dynamical characteristics under various operating conditions from nonlinear perspective and propose effective measures to improve the system performance.

1.2 Nonlinear analysis methods

The nonlinear dynamics of rotating machinery has always been the research hot spot. In this field, many effective analysis methods were developed and some valuable results were found [10, 12, 14, 18,19,20,21,22]. These papers focused on nonlinear bearing forces (mainly nonlinear oil-film forces), rotor cracks, internal friction, internal damping, rub-impact and other possible nonlinear factors in bearing-rotor systems. Various nonlinear phenomena such as oil whirl, jump phenomenon, bifurcation, quasi-periodic motion and chaos were investigated. The mechanisms and conditions of these complicated behaviors were illustrated in detail.

The analysis methods adapted in these papers can be classified into numerical methods, approximate analytical methods and qualitative analysis methods.

Numerical methods mainly included the numerical integration method and cell mapping methods. References [13, 20, 23] used the numerical integration method to study nonlinear phenomena in the bearing-rotor systems. The period doubling, quasi-periodic motion and chaos were investigated using bifurcation diagrams, time domain responses, shaft center trajectories, Poincaré map and power spectrum comprehensively. Some analysis results were validated through experiments. In numerical analyses of nonlinear dynamics of bearing-rotor systems, the largest Lyapunov exponent can be calculated and regarded as the judgment of the chaos [14, 24, 25].

References [16, 26] applied cell mapping methods to rotor systems to obtain global nonlinear dynamical characteristics including attractors and their domains of attraction. Hsu proposed the simple cell mapping method firstly in [27]. Consequent on this, various improved methods such as the generalized cell mapping method [28, 29], generalized cell mapping digraph method [30, 31] and Poincaré-like simple cell mapping method [32] were developed. Compared with traditional point mapping methods, these cell mapping methods have the advantages of low computation cost and wide application. They have shown great potential to be used in nonlinear dynamical analysis of bearing-rotor systems.

The approximate analytical methods include the harmonic balance method, the method of multiple scales, the averaging method, the asymptotic method, etc. Compared with numerical methods, they can help to understand mechanisms of nonlinear phenomena in the systems, calculate the critical parameter domains quantitatively and determine the stability conditions. Reference [33] used the harmonic balance method to study responses of a dual-rotor system with transverse crack. The super-harmonic responses were found, and influences of depth and position of the crack were also discussed. Reference [12] applied the method of multiple scales to analyze nonlinear dynamical characteristics in 2:1 and 3:1 super-harmonic resonances of an aircraft cracked rotor. The calculation accuracy of the method of multiple scales was improved by expanding orders of time-scale in [34]. The method of multiple scales is widely used and can be applied to the dynamical behaviors of the bearing-rotor systems with different nonlinear factors. But in solving process, the solvability is dependent on the secular term which is always obtained according to conditions of resonances or harmonic resonances. Therefore, the method of multiple scales focuses on the dynamical characteristics of bearing-rotor systems in harmonic resonance regions. The whirling motions and stability of bearing-rotor systems with hysteretic internal friction were analyzed using averaging methods in [10, 11, 35, 36]. The authors discussed influences of hysteretic internal friction on the system stability and pointed out that proper stiffness anisotropy of the supports is beneficial to stability of systems.

Besides numerical methods and approximate analytical methods, there are also some analysis methods which can be applied to the bifurcation and stability analyses of nonlinear systems. These methods are always used to analyze the topological properties of nonlinear governing equations qualitatively, which can help to understand the whole nonlinear characteristics of the systems. References [37, 38] obtained the nonlinear viscoelastic shaft models based on Hamilton principle and then used the method of normal form and center manifold theory to study Hopf bifurcations and double Hopf bifurcations. The bifurcations and stability of nonlinear rotor system with viscoelastic damping were discussed. Reference [22] also used the center manifold theory to analyze the supercritical and subcritical bifurcations in the floating ring bearing-rotor system and discussed the oil whirl and whip. However this kind of method are mostly applicable to bifurcation analyses of autonomous and parameter-excited systems. In bearing-rotor systems, rotor eccentricities are inherent, and the external excitation is unavoidable during operation. Therefore, the systems are substantially forced vibration systems in which the applications of qualitative analysis methods are limited.

In the field of nonlinear dynamics of rotating machines, there are many different forms of analysis methods applicable for different situations. In the above papers, numerical methods, analytical methods and qualitative analysis methods were applied to different systems operating in different working conditions. Many valuable results have been obtained.

1.3 Applications of nonlinear analysis methods in AMB-rotor systems

As one type of bearing-rotor systems, AMB-rotor systems have similarities with others in some aspects, for example some similar nonlinear factors in rotors and bearings. On the other hand, the AMB-rotor systems may be special in some ways. There are some special nonlinear factors due to peculiarities of AMB-rotor systems. Meanwhile, for the same nonlinear factors of the rotor, behaviors of rotor systems supported by AMBs may be very different from those in rotor systems supported by other bearings. In addition, controllers of AMB systems also have influences on dynamical behaviors due to nonlinear factors of the rotor [39].

Different from mechanical bearings, support forces of the AMBs are electromagnetic forces, which have a more definite relation with system parameters. Thus, models of bearing forces can be obtained more easily. The nonlinearity of electromagnetic forces is more prominent due to the large range of rotor displacement in AMB-rotor systems. Electrical components and ferromagnetic materials used in the systems may lead to the current or voltage saturation, nonlinear magnetization, magnetic saturation and hysteresis possibly, which will never happen in mechanical bearings. These unique nonlinear factors will make AMB-rotor systems exhibit some different nonlinear dynamical behaviors. The complicated behaviors caused by bearing and rotor nonlinearities need further analyses. However the nonlinear dynamical analyses of mechanical bearing-rotor systems can provide some methodological guidances. These analysis results have immense heuristic values.

The methods mentioned in Sect. 1.2 have been used in nonlinear analyses of AMB-rotor systems, and some analysis results were similar to those in other bearing-rotor systems. References [17, 40, 41] used the numerical integration method to study complicated dynamical behaviors of AMB-rotor systems by considering the nonlinearity of bearing forces. The period doubling, quasi-periodic motions and chaos were found. They illustrated the influences of system parameters on dynamical characteristics and identified some key factors. Reference [15] obtained the approximate analytical solutions of a nonlinear AMB-rotor system in the main resonance region by using the method of multiple scales. The jump phenomenon and local bifurcation behaviors were illustrated based on the solutions. The influences of external excitation amplitude and controller parameters on dynamical characteristics were also discussed. Besides, the harmonic balance method can also be utilized to analyze the nonlinear responses of the AMB-rotor system in the main resonance and harmonic resonance regions [42]. These reports proved the universality of analysis methods in the nonlinear dynamics of rotating machines.

However, the characteristics of AMB-rotor systems are more complicated than those of mechanical bearing-rotor systems. The digital controllers are adopted, and then, the control delay is inevitable. Although the time delay is a linear dynamical characteristic, the extremely short time delay still has significant influences on support characteristics, rotor dynamics and the stability of high-speed rotating machines supported by AMBs. If the nonlinearity of electromagnetic force is prominent, the effect of control delay will be more obvious. By considering both the nonlinearity of bearing force and control delay, references [43, 44] conducted nonlinear analyses and found the soft spring characteristic and jump phenomenon. It was pointed out that control delay made the effect of nonlinear electromagnetic force more prominent.

Additionally, the stiffness can be designed to be time-varying by choosing appropriate control strategies due to the flexible adjustment of the AMB characteristics. This design strategy may get larger stable parameter domains and improve the performance of AMB-rotor systems. Nevertheless, the time-varying stiffness may make the systems with nonlinearity of bearing forces show more complicated characteristics. References [45,46,47,48] used the asymptotic method, method of multiple scales and numerical integration method to investigate the dynamical characteristics of nonlinear AMB-rotor systems with time-varying stiffness. The Shilnikov type multi-pulse chaotic motions, quasi-periodic motions, and jump phenomena were found. What’s more, it was pointed out that the rational designed parameters of PD (proportional differential) controller can generate control force to make the chaotic motion turn into period-2 motions, which emphasized the role of the controller in nonlinear AMB-rotor systems [45].

These above reports about nonlinear dynamical analyses of AMB-rotor systems show there are some special nonlinear effects in AMB-rotor systems, and they have important influences on the dynamical characteristics. In the field of nonlinear analyses of AMB-rotor systems, the main nonlinear factor was the nonlinearity of electromagnetic force. And some also took both the nonlinearity of electromagnetic force and dynamical characteristic of the controller into consideration. As for analysis methods, there were two common ones. One was the method of multiple scales, which was utilized to analyze the nonlinear dynamical behaviors near the resonances and harmonic resonances. The other was the numerical integration method, which can investigate period doubling, quasi-periodic motions and chaos by taking the rotor speed as distinguish variable.

During operation of the AMB-rotor system, the rotor suspends at a steady position. The steady suspension position of rotor is called static equilibrium in this paper. Different from mechanical bearing system in which the rotor is fixed at a very limited extent, the larger mechanical clearance of AMBs can make the static equilibrium vary in a much larger range. In some situations, the static equilibrium can make a significant contribution to the rotor displacement. Therefore the static equilibrium has significant influences on the system performance and stability as well as the rotor vibration amplitude. During the design and operation, it is expected that the mechanical clearance between the rotor and stator in all directions is uniform. To achieve this goal, the reference position is designed to locate in the center of mechanical clearance. During operation, the static equilibrium is supposed to coincide with the reference position. It can effectively avoid that the clearance in an arbitrary direction becomes too small to cause rub-impact. When the static equilibrium locates in the reference position, we call it trivial equilibrium. However, the static equilibrium can deviate from the reference position during actual operation. In this situation, it is called nontrivial equilibrium.

In the following, both vibration and static equilibriums are investigated.

In above reports, the characteristics of rotor vibration amplitudes and phases in AMB-rotor systems were complicated due to their nonlinear factors. The static equilibrium was not considered. However there is no doubt that static equilibrium will affect dynamical characteristics of the systems. There is few research about the static equilibrium of the AMB-rotor system. Reference [8] studied the influence of current saturation on the dynamical characteristics of a permanent magnet-based homopolar magnetic bearing system and found the current saturation would make the rotor vibrate steadily at a position deviating from the reference position. Although the structure of this system is different from those of AMB-rotor systems, the similar phenomena are possible in the AMB-rotor systems.

Reference [16] studied the effects of current saturation on the static equilibrium of AMB-rotor system. The generalized cell mapping digraph method was used to investigate global dynamical characteristics of an AMB-rotor system with current saturation. There were multiple static equilibriums in the non-resonance region. The bifurcation behaviors occurred. The larger mechanical clearance of AMB makes it possible that multiple static equilibriums can be exhibited during actual operation, even if they are not trivial equilibriums. This deviation of static equilibrium from reference position is detrimental to the performance and stability of the system and needs further investigation. However, the further application of the generalized cell mapping digraph method used in [16] was limited due to its expensive computational cost.

The approximate analytical methods have small computational cost and can be used to explore mechanisms of nonlinear phenomena. The common one is the method of multiple scales. It has been applied in nonlinear analyses of AMB-rotor systems. But as mentioned above, in this field, the method of multiple scales was mostly used to analyze nonlinear behaviors in resonance and harmonic resonance regions. In some situations, it can also be used to explore the behaviors in non-resonance region [21], but the systems are parameter-excited vibration systems. The qualitative analysis methods including bifurcation theory can be applied to study bifurcation behaviors of autonomous and parameter-excited vibration systems in non-resonance region. But most of them did not work for forced vibration systems.

Based on an AMB-rotor system considering the nonlinearity of electromagnetic force and current saturation, this paper developed a novel method of multiple scales to investigate bifurcation characteristics of the AMB-rotor system in non-resonance region. The multiple static equilibriums of the nonlinear model can be obtained through the method and the supercritical pitchfork bifurcation was found. After transforming the non-autonomous governing equation into the autonomous form through state augment, the stability analysis of multiple solutions can be conducted based on Floquet theory. The validity of the method was verified by numerical methods. It was found that there was supercritical pitchfork bifurcation of static equilibrium in the AMB-rotor system with current saturation, which could give the reason why the rotor deviated from the reference position when the system was operating at its working speed. The supercritical pitchfork bifurcation makes the maximum instantaneous displacement of the rotor increase a lot and has negative influences on the performance and stability of the system. The influences of controller parameters were also discussed, and the adjustment of the controller parameters was conducted based on the analysis results. Changing the controller parameters can prevent the supercritical pitchfork bifurcation effectively to improve the system performance. The research generalized applications of the method of multiple scales in the field of nonlinear dynamics of rotating machines. The system structure design and controller design based on the nonlinear analysis results can help the AMB-rotor system keep in high-performance operation even if the operating condition is harsh.

2 Model description

The research object is a blower rotor supported by AMBs, whose operating speed is $\Omega _0=27{,}000\,\mathrm{rpm}$, see details in [16]. Different from mechanical bearings, AMBs use the electromagnetic force to achieve the non-contact support of the rotor and have larger mechanical clearance. Figure 1 shows the structural sketch of the AMB-rotor system. The static equilibrium is designed to locate in the reference position exactly, as shown in Fig. 1a. In this case, the rotor vibrates at the reference position. The maximum displacement of the rotor is exactly the vibration amplitude. According to the analysis based on linear theory, the designed system has enough stability margin and can vibrate stably for different conditions. However, during the actual operation, an unexpected phenomenon happened. The static equilibrium deviated from the reference position and the rotor vibrated at a new static equilibrium, as shown in Fig. 1b. In this case, the maximum displacement of rotor becomes much larger, that is sum value of the vibration amplitude and static equilibrium. The system performance deteriorates. It is easy for the rotor to exceed the physical limit to cause instability. By analyzing the operational data, the current saturation was found. The AMB-rotor system showed typical nonlinear characteristics.

Fig. 1

Structural sketch of AMB-rotor system

In order to explore this phenomenon, this paper planned to do the nonlinear dynamical analysis through an approximate analytical method. A model that can describe the nonlinear characteristics accurately was needed. During actual operation, unexpected phenomenon was more prominent in one direction due to the tiny differences among all directions. Therefore, this paper focused on one direction and obtained the single-degree-of-freedom (SDOF) model by neglecting the coupled relationship between different directions. For simple analysis, the actual controller was simplified into a PD controller at the operating speed. Summing up the above, this paper would conduct the nonlinear dynamical analysis based a SDOF model with PD controller.

2.1 Mathematical model

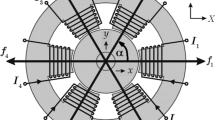
During operation, the AMB-rotor system always suffers external excitations such as unbalance excitation and air load. In general, external excitations are synchronous with the rotor speed. Under the combined effects of bearing force generated by currents and external excitation, the AMB-rotor system can keep vibrating stably. However, there are limitations in the capacity of the power amplifier. The actual currents are not infinite and have extreme values. The relationship between the electromagnetic force and rotor displacement and currents are also nonlinear. If the external excitation is large, the system will prominently exhibit the nonlinearity of bearing force and current saturation. It is more accurate to describe dynamical characteristics of the AMB-rotor system by considering them. These two nonlinear factors are taken into consideration to build a nonlinear SDOF model. The modeling process is as follows [1, 16].

The control current according to the control law of the PD controller can be formulated in

$$\begin{aligned} i=K_{\mathrm{p}} y+K_\mathrm{d} \dot{y} , \end{aligned}$$

(1)

where y is the rotor displacement, $\dot{y}$ is the velocity of the rotor, $K_{\mathrm{p}}$ and $K_\mathrm{d}$ represent the proportional and differential gains of PD controller, respectively. The control current i will work with the bias current $i_0$ together in the electromagnets in differential arrangement. But due to the output capacity of power amplifier, the currents in a pair of opposite electromagnets $i_+$ and $i_-$ have limits and can be expressed as

$$\begin{aligned} i_\pm= & {} \mathrm{med}\left( 0,i_0\pm i,i_m\right) \nonumber \\= & {} \left\{ \begin{array}{ll}0&{}i_0\pm i<0\\ i_0\pm i&{}0\le i_0\pm i\le i_m\\ i_m&{}i_m\le i_0\pm i \end{array}\right. , \end{aligned}$$

(2)

where $i_m$ is the maximum current that the power amplifier can output, 0 is the minimum, and ‘med’ means taking the median.

The currents $i_+$ and $i_-$ generate the nonlinear electromagnetic force,

$$\begin{aligned} F=\frac{1}{4}K_F\left( \left( \frac{i_+}{s_0+y}\right) ^2- \left( \frac{i_-}{s_0-y}\right) ^2\right) , \end{aligned}$$

(3)

where $s_0$ is the air gap of the bearing, and $K_F$ is the force coefficient determined by the system structure.

During operation, the AMB-rotor system is subjected to the external excitation inevitably. The differential equation of motion can be expressed in

$$\begin{aligned} \ddot{y}=\frac{1}{m}\left( -F+f\cos \left( \Omega \text {t}\right) \right) , \end{aligned}$$

(4)

where f is the excitation amplitude.

Equations (1)–(4) can describe the nonlinear dynamical characteristics of the AMB-rotor system with PD controller. Shown as Eq. (3), the electromagnetic force is a nonlinear function with respect to the rotor displacement and currents in the system. Compared with the linearized model, this model is more accurate to describe the actual system. Different from most reports about the nonlinear investigations of AMB-rotor systems [15, 17, 40,41,42], the actual limitation about the currents is considered as well as the nonlinearity of the bearing force. If the operating condition becomes harsh, the system will need large electromagnetic force to suppress vibration. Accordingly, large control current is needed. If the expected currents exceed the limitations, the current saturation will happen. The current saturation will make the electromagnetic force shown in Eq. (3) more complicated. Based on the above SDOF nonlinear model, the complicated behaviors of the AMB-rotor system can be investigated.

2.2 Non-dimensional equation of motion

This paper introduced these non-dimensional variables shown in Eq. (5) to transform the nonlinear differential equation of motion shown in Eq. (4) into a non-dimensional one.

$$\begin{aligned} {\tilde{y}}= & {} \frac{y}{s_0},\quad {\tilde{\Omega }}=\frac{\Omega }{\Omega _0},\quad {\tilde{t}}={\Omega _0} t,\nonumber \\ {\tilde{i}}= & {} \frac{i}{i_m},\quad {{\tilde{i}}_0}=\frac{i_0}{i_m},\quad {{\tilde{i}}_\pm }=\frac{i_\pm }{i_m} . \end{aligned}$$

(5)

By substituting Eq. (5) into Eqs. (1)–(4), we can obtain the non-dimensional equation,

$$\begin{aligned} \ddot{\tilde{y}}=-{\tilde{F}}+{\tilde{f}}\cos \left( {\tilde{\Omega }}{\tilde{t}}\right) , \end{aligned}$$

(6a)

$$\begin{aligned} {\tilde{F}}={{\tilde{K}}_F}\left( \left( \frac{{{\tilde{i}}_+}}{1+{\tilde{y}}}\right) ^2 -\left( \frac{{{\tilde{i}}_-}}{1-{\tilde{y}}}\right) ^2\right) , \end{aligned}$$

(6b)

$$\begin{aligned} {{\tilde{i}}\pm }=\mathrm{med}\left( 0,{{\tilde{i}}_0} \pm {\tilde{i}},1\right) , \end{aligned}$$

(6c)

$$\begin{aligned} {\tilde{i}}={{\tilde{K}}_{\mathrm{p}}} {\tilde{y}}+{{\tilde{K}}_\mathrm{d}} \dot{\tilde{y}} , \end{aligned}$$

(6d)

where ${{\tilde{K}}_F}=\frac{K_F i_m^2}{4 m \Omega _0^2 s_0^3},{{\tilde{K}}_{\mathrm{p}}}=\frac{K_{\mathrm{p}} s_0}{i_m},{{\tilde{K}}_\mathrm{d}}=\frac{{\Omega _0} K_\mathrm{d} s_0}{i_m}$, ${\tilde{f}}=\frac{f}{m s_0 \Omega ^2}$.

3 Analytical analysis

This paper used the approximate analytical method to investigate nonlinear dynamical characteristics of the AMB-rotor system when it was operating far away from resonances. The polynomial fitting was employed firstly to transform the non-smooth model (6) into a polynomial expression that can be solved analytically. Then a novel method of multiple scales was proposed to get the approximate solutions, which could obtain both static equilibrium and vibration characteristics. At last, Floquet theory was used to carry out the stability analysis of approximate solutions.

3.1 Approximation of electromagnetic force

Due to current saturation, the characteristic of actual electromagnetic force is complicated. As shown in Eq. (6b), the function of electromagnetic force with respect to the rotor displacement and currents is a rational fraction one. At critical points where current saturation occurs, the change of electromagnetic force is non-smooth. If the approximate analytical method is applied to the non-smooth model directly, a large number of section-by-section calculations depending on the piecewise function of electromagnetic force will be needed. It brings a challenge to the application of approximate analytical method. In order to solve the problem, this paper conducted a polynomial fitting of the electromagnetic force and got an approximate expression of the model which can describe the characteristics of electromagnetic force approximately.

In the possible operating region, namely ${\tilde{y}}\in \left[ -0.8,0.8\right]$, ${\tilde{i}}\in \left[ -2.8,2.8\right]$, this paper used a eleven-order polynomial to fit the electromagnetic force ${\tilde{F}}$ with respect to the control current ${\tilde{i}}$ and rotor displacement ${\tilde{y}}$. The error of mean square of fitting is $\mathrm{RMSE}=0.0030$. The original electromagnetic force, fitting one, and their difference are shown in Fig. 2. It can be seen that they generally fit precisely. The difference between them is much smaller compared with absolute value of the original electromagnetic force. In most operating regions, the difference value can be neglected. The difference has little influence on the subsequent analysis. The fitting electromagnetic force can reflect characteristics of the actual electromagnetic force accurately.

Substitute the control current (6d) into the fitting polynomial of the electromagnetic force with respect to ${\tilde{i}}$ and ${\tilde{y}}$, then obtain the expression of the fitting electromagnetic force with respect to the rotor displacement ${\tilde{y}}$ and its first-order derivative $\dot{\tilde{y}}$, shown in Eq. (7) .

Fig. 2

Fitting result of electromagnetic forces. a Actual electromagnetic forces. b Fitting electromagnetic forces. c Difference between actual and fitting electromagnetic forces

$$\begin{aligned} {{\tilde{F}}_f} =\sum _{1\le m+n \le 11} k_{m,n}{\tilde{y}}^m \dot{\tilde{y}}^n, \end{aligned}$$

(7)

where $k_{m,n}=0$ if $m+n$ is even number. Otherwise $k_{m,n}$ are the relational expressions about controller parameters ${{\tilde{K}}_{\mathrm{p}}}$, ${{\tilde{K}}_\mathrm{d}}$, see the details in “Appendix A”. The nonlinearity of electromagnetic force and current saturation can be reflected in fitting electromagnetic force (7).

The non-dimensional model in Eq. (6) is transformed into the fitting model by the polynomial fitting, shown in Eq. (8).

$$\begin{aligned} \ddot{\tilde{y}}=-{{\tilde{F}}_f}+{\tilde{f}}\cos \left( {\tilde{\Omega }} {\tilde{t}}\right) . \end{aligned}$$

(8)

The nonlinear dynamical analysis of the AMB-rotor system can be carried out based on the fitting model (8).

3.2 Analytical solutions

This paper utilized the method of multiple scales to study complicated behaviors in the AMB-rotor system analytically. The method of multiple scales is one of the common approximate analytical methods to investigate the dynamical characteristics of nonlinear systems. In the field of nonlinear dynamical analyses of rotor-bearing systems, the method of multiple scales is usually applied in two cases. The one usage of the method of multiple scales is to investigate the free vibration to obtain nonlinear relationship between the vibration amplitude and vibration phase. The other is to study the nonlinear behaviors of the forced or parameter-excited vibration systems in primary and harmonic resonance regions. In above both usages, it only can obtain the magnitude-frequency characteristics of rotor vibration. The secular term is obtained by using the resonance conditions, and the solvability condition is the secular term equal zero.

In this paper, the aim is to investigate the forced vibration of the AMB-rotor system when it is operating far away from resonances. Moreover, the complicated behaviors are reflected in the static equilibrium rather than the magnitude-frequency characteristics. Obviously, the traditional method of multiple scales is not applicable. Aiming at the problem, this paper improved the traditional method of multiple scales to get both vibration amplitude and static equilibrium and then analyzed nonlinear dynamical characteristics of the AMB-rotor systems. Although the idea of multiple time scales including the fast and slow scales was still adopted, the minor perturbation term chosen and the form of solution were different from the traditional ones [15]. Accordingly, the way to derive the secular term was also different.

The nonlinear rotor systems show complicated behaviors in terms of vibration amplitude. The reasons why nonlinear behaviors occur lie in the intrinsic properties of systems. However, the AMB-rotor system in this paper exhibited complicated nonlinear responses when it operated at a speed far away from the resonances, which was obviously different from the jump phenomena and bifurcations in resonance regions. The unexpected behaviors were mostly caused by the forced vibration, namely affected by the external excitation. Therefore, the different minor perturbation term was chosen, then Eq. (9) was obtained.

$$\begin{aligned} \ddot{\tilde{y}}+\varepsilon {{\tilde{F}}_f}={\tilde{f}}\cos \left( {\tilde{\Omega }} {\tilde{t}}\right) , \end{aligned}$$

(9)

where $\varepsilon$ is the non-dimensional perturbation parameter, which denotes the corresponding term is minor perturbation term. This paper only considered the first-order approximation of solutions. Then the form of analytical solution can be formulated in

$$\begin{aligned} {\tilde{y}}=y_0+\varepsilon y_1 . \end{aligned}$$

(10)

The dynamical characteristics can be analyzed from two time scales, namely $T_0={\tilde{t}}$ and $T_1=\varepsilon {\tilde{t}}$. From the algebraic relationship between ${\tilde{t}}$ and $T_0, T_1$, the following equation can be derived,

$$\begin{aligned} \frac{\text {d}}{{\text {d}} {{\tilde{t}}}}={\text {D}}_0+{\varepsilon } {{\text {D}}_1}, \qquad \frac{{\text {d}}^2}{{\text {d}} {\tilde{t}}^2}={{\text {D}}_0^2}+{\varepsilon } 2 {{\text {D}}_0} {{\text {D}}_1}+{{\varepsilon }^2} {{\text {D}}_1^2} , \end{aligned}$$

(11)

where $\mathrm{D}_0$ and $\mathrm{D}_1$ denote to derivative with respect to $T_0$, $T_1$ respectively. Substitute Eqs. (10) and (11) into Eq. (9), then equate the powers of perturbation parameter $\varepsilon$, we can obtain two linear differential equations,

$$\begin{aligned} \varepsilon ^0:{\mathrm{D}_0^2}{y_0}={\tilde{f}}\cos \left( {\tilde{\Omega }} {\tilde{t}}\right) , \end{aligned}$$

(12)

$$\begin{aligned} \varepsilon ^1: {\mathrm{D}_0^2} y_1= -2\mathrm{D}_0 {{\text {D}}_1}y_0-\sum _{1\le m+n \le 11} k_{m,n}{\tilde{y}}^m \dot{\tilde{y}}^n. \end{aligned}$$

(13)

The stationary solutions of the periodically excited AMB-rotor system must be periodic. Therefore only periodic solutions were considered in this paper. The solution of Eq. (12) was supposed to be

$$\begin{aligned} y_0= & {} C_0+A\cos \left( {\tilde{\Omega }}T_0 \right) = C_0+a\mathrm{e}^{-{\mathrm{D}}{{\tilde{\Omega }}} T_0}\nonumber \\&+\,\bar{a}\mathrm{e}^{\mathrm{j}{\tilde{\Omega }} T_0}, \end{aligned}$$

(14)

where $C_0$ is the static equilibrium, a is the complex vibration amplitude, and $\bar{a}$ is its conjugate. The vibration amplitude of rotor is $\left| A\right|$, and $A=2\mathrm{Re}\left( a\right)$. The solution form is different from that in the traditional method of multiple scales, which only includes the vibration amplitude and phase. It contains both vibration and static equilibrium terms and can reflect dynamical characteristics of the AMB-rotor system comprehensively.

The term $A\cos \left( {\tilde{\Omega }}T_0 \right)$ or $a\mathrm{e}^{-\mathrm{j}{\tilde{\Omega }} T_0}+\bar{a}\mathrm{e}^{\mathrm{j}{\tilde{\Omega }} T_0}$ is the harmonic term describing the rotor vibration. Because the operating speed is much larger than the natural frequency. The value of A can be approximately determined by the external excitation amplitude $\tilde{f}$ and operating speed ${\tilde{\Omega }}$. And when the system is operating steadily at working speed, the influence of vibration phase of the rotor on the system stability is very weak and can be ignored. Based on this, a is a real number and we can obtain,

$$\begin{aligned} A=2a=-\frac{{\tilde{f}}}{{\tilde{\Omega }} ^2}. \end{aligned}$$

(15)

In order to get $C_0$, by substituting Eq. (14) into Eq. (13), we can get

$$\begin{aligned} {\mathrm{D}_0^2} y_1= & {} b_1 C_0+b_2 {C_0}^3+b_3{C_0}^5+b_4{C_0}^7+b_5{C_0}^9\nonumber \\&+b_6{C_0}^{11}+b_7 \mathrm{e}^{-\mathrm{j}{\tilde{\Omega }} T_0} + b_8 \mathrm{e}^{-2\mathrm{j}{\tilde{\Omega }} T_0} \nonumber \\&+b_9 \mathrm{e}^{-3\mathrm{j}{\tilde{\Omega }} T_0}+ b_{10} \mathrm{e}^{-4\mathrm{j}{\tilde{\Omega }} T_0}+ b_{11} \mathrm{e}^{-5\mathrm{j}{\tilde{\Omega }} T_0}\nonumber \\&+b_{12} \mathrm{e}^{-6\mathrm{j} {\tilde{\Omega }} T_0}+b_{13} \mathrm{e}^{-7\mathrm{j}{\tilde{\Omega }} T_0}+ b_{14} \mathrm{e}^{-8\mathrm{j}{\tilde{\Omega }} T_0}\nonumber \\&+b_{15} \mathrm{e}^{-9\mathrm{j} {\tilde{\Omega }} T_0}+b_{16} \mathrm{e}^{-10\mathrm{j}{\tilde{\Omega }} T_0}+ b_{17} \mathrm{e}^{-11\mathrm{j}{\tilde{\Omega }} T_0}\nonumber \\&+ \mathrm{CC} , \end{aligned}$$

(16)

where $b_1$–$b_{17}$ are functions with respect to coefficients of fitting electromagnetic force $k_{m,n}$, a and ${\tilde{\Omega }}$, see the details in “Appendix B,” and $\mathrm{CC}$ represents the complex conjugate of the harmonic terms. Equation (16) is too complicated to be solved directly. Luckily, it is unnecessary to obtain the complete solution. In the equation, only $C_0$ needs to be determined. It is found there is a constant term on the right-hand side. Set it as $G\left( C_0\right)$, we can get,

$$\begin{aligned} G\left( C_0\right)= & {} b_1 C_0+b_2 {C_0}^3+b_3{C_0}^5+b_4{C_0}^7\nonumber \\&+\,b_5{C_0}^9+b_6{C_0}^{11}. \end{aligned}$$

(17)

It has nothing to do with time $T_0$. However, there is no term on the left-hand side in Eq. (16) to balance it. If the constant term does not equal to zero, Eq. (16) cannot have any periodic convergent solutions, which is inconsistent with the actual situations. Therefore, the term is the secular term. In this paper, the secular term is an expression with respect to the static equilibrium $C_0$ rather than harmonic terms determined by resonance conditions.

According to the solvability of the method of multiple scales, we can obtain,

$$\begin{aligned} G\left( C_0\right)= & {} b_1 C_0+b_2 {C_0}^3+b_3{C_0}^5+b_4{C_0}^7\nonumber \\&+\,b_5{C_0}^9+b_6{C_0}^{11}=0. \end{aligned}$$

(18)

It is a polynomial equation that can have multiple real solutions. There may be other static equilibriums besides $C_0=0$, which means the AMB-rotor system may have multiple static equilibriums. The solution meets the condition $C_0=0$ is the trivial equilibrium, otherwise nontrivial equilibrium. After getting static equilibriums, the approximate solutions of Eq. (8) can be obtained,

$$\begin{aligned} {\tilde{y}}=y_0=C_0+A\cos \left( {\tilde{\Omega }}{{\tilde{t}}}\right) . \end{aligned}$$

(19)

This subsection used the improved method of multiple scales to investigate dynamical characteristics of the AMB-rotor system at its operating speed. The analysis results show that characteristics of vibration amplitude $\left| A \right|$ are simple. But the characteristics of static equilibrium are complicated. There may be multiple static equilibriums. During operation, complicated responses are mainly reflected in the suspension position of rotor represented by the static equilibrium $C_0$.

3.3 Stability analysis

According to the solving procedure in Sect. 3.2, this paper can obtain multiple periodic solutions of the AMB-rotor system. The stability of each solution can be analyzed based on Floquet theory.

Before stability analysis, this paper augmented the states by introducing $\xi _1=\dot{{\tilde{y}}}$, $\xi _2={\tilde{y}}$, $\xi _3= {\tilde{\Omega }} {\tilde{t}}$. Then the polynomial model of the AMB-system (8) with external excitation can be transformed into

$$\begin{aligned} {{\dot{{\xi }}}}= & {} \left[ \begin{array}{l} {\dot{\xi }_{1}} \\ {\dot{\xi }_{2}} \\ {\dot{\xi }_{3}} \end{array} \right] = \left[ \begin{array}{l} -{{\tilde{F}}_{f}}\left( {\xi _{1}},{\xi _{2}} \right) + {\tilde{f}} \cos \left( {\xi _{3}} \right) \\ {\xi _{1}} \\ {\tilde{\Omega }} \end{array} \right] \nonumber \\= & {} \mathbf{{G}} \left( {{\xi }} \right) , \end{aligned}$$

(20)

where ${{\tilde{F}}_f}\left( \xi _1,\xi _2\right)$ is the fitting electromagnetic force expressed by the extended states, see the details in “Appendix C”. After state augment, the governing Eq. (8) becomes an autonomous one which does not include explicitly time term. The stability analysis can be conducted based on Eq. (20). The eigenvalue of corresponding monodromy matrix can determine the stability of solutions.

The state Eq. (20) is a periodic function with $T=\frac{2\pi }{{\tilde{\Omega }}}$. The monodromy matrix of the system can be determined by the following equation,

$$\begin{aligned} \frac{\mathrm{d} \mathbf{{M}}\left( {\tilde{t}}\right) }{\mathrm{d}{\tilde{t}}}= & {} \frac{{\partial } {\mathbf{{G}}\left( \mathbf{{\xi }} \right) }}{{\partial }\mathbf{{\xi }}}\big |_{\mathbf{{\xi }_0}} \mathbf{{M}} \left( {\tilde{t}} \right) ,\nonumber \\ \mathbf{{M}}\left( 0 \right)= & {} \mathbf{{I}}, \end{aligned}$$

(21)

where $\mathbf {I}$ is an identity matrix. The monodromy matrix $\mathbf {M}$ is the solution at time T of Eq. (21).

The procedure of stability analysis is as follows. Substitute solutions $\xi _2=C_0+A\cos \left( \xi _3 \right) , \xi _1=\dot{\xi }_2$ obtained in Sect. 3.2 into Eq. (20), then obtain corresponding monodromy matrix $\mathbf {M}$. The stability of analytical solutions can be determined by eigenvalues of $\mathbf {M}$, namely Floquet multipliers $\lambda _i\left( \mathbf {M} \right)$.

The monodromy matrix $\mathbf {M}$ is obtained based on the autonomous Eq. (20). There is always an immutable Floquet multiplier, that is $\lambda _3=1$. It is corresponding to the periodic excitation. The stability of solution is decided by the moduli of the other two Floquet multipliers. If both moduli of these two Floquet multipliers are less than 1, the corresponding solution is stable. Otherwise, the solution is unstable.

Through above processing, the stability problem of multiple solutions is transformed into the eigenvalue problem of monodromy matrix. The stability of the solutions can be determined by solving the eigenvalues of the monodromy matrix.

This section can obtain multiple solutions of the AMB-rotor system and judge their stability through analysis procedure introduced in Sects. 3.2 and 3.3. The specific procedure is as follows. By substituting system parameters including the rotor speed ${\tilde{\Omega }}$, controller parameters ${{\tilde{K}}_{\mathrm{p}}}$ and ${{\tilde{K}}_\mathrm{d}}$, and external excitation amplitude ${\tilde{f}}$ into Eqs. (15) and (18), the vibration amplitude $\left| A\right|$ and static equilibrium $C_0$ can be obtained. After that, the periodic solutions can be obtained according to Eq. (19). The stability of each solution can be judged by solving the eigenvalues of the monodromy matrix $\mathbf {M}$.

4 Analytical results

4.1 Analysis procedure with an example

As mentioned above, the research object is a blower supported by AMBs. Non-dimensionalize the AMB-rotor system according to the process in Sect. 2.2. In the non-dimensional model, the electromagnetic force coefficient is ${{\tilde{K}}_F}=0.0097$, and the bias current is ${{\tilde{i}}_0}=0.5$. The operating speed of system is ${\tilde{\Omega }}=1$. The controller was designed based on the classical linear control theory. In the linear theoretical framework, the designed controller parameters have sufficient stability margin and can make the system keep globally stable. Based on the frequency domain method, the original controller parameters can be transformed into the proportional and differential gains of PD controller at a certain speed [16]. Then the non-dimensional PD controller parameters are ${{\tilde{K}}_{\mathrm{p}}}=1.9044$, ${{\tilde{K}}_\mathrm{d}}=4.8006$, respectively. Under the combination of above system parameters, the AMB-rotor system are expected to vibrate at the reference position with a small amplitude. However, unexpected complicated behaviors happened during the actual operation.

This paper takes this system as an example to investigate the unexpected behaviors, and the approximate analytical method introduced in Sect. 3 is the main analysis method. In this subsection, this paper explains how to use the proposed method to conduct the nonlinear dynamical analysis of the AMB-system.

For different external harmonic excitation, the number and stability of periodic solution in the AMB-rotor system can be different.

For example, when the operating speed is ${\tilde{\Omega }}=1$ and external amplitude is set as ${\tilde{f}}=0.1$, we can obtain the vibration amplitude $\left| A\right| =0.1000$ according to Eq. (15). Then substitute system parameters ${{\tilde{K}}_F}=0.0097$, ${{\tilde{i}}_0}=0.5$, ${\tilde{\Omega }}=1$, ${{\tilde{K}}_{\mathrm{p}}}=1.9044$ and ${{\tilde{K}}_\mathrm{d}}=4.8006$ into Eq. (18) and solve the polynomial equation. The static equilibriums can be obtained. The relationship between $G\left( C_0 \right)$ and $C_0$ is shown in Fig. 3. There are three static equilibriums, namely

$$\begin{aligned} C_0=0,\pm 0.7656. \end{aligned}$$

It should also be noted that we chose the fitting range ${{\tilde{y}}}\in \left[ -0.8,0.8\right]$,${{\tilde{i}}}\in \left[ -2.8,2.8\right]$ during the fitting process of electromagnetic force, which completely covered the possible operation range of the AMB-rotor system. In the fitting range, in order to make the fitting electromagnetic force as close as possible to the actual force, a sufficiently high-order polynomial was used to fit the relationship of electromagnetic force with respect to rotor displacement and control current. This high-order fitting caused overfitting outside the fitting range, and the fitting electromagnetic force is only valid for the selected range and not extrapolative. Therefore, the validity of solutions obtained based on the fitting model should be tested by telling whether solutions are in the fitting range. By considering $C_0$ and $\left| A \right|$ simultaneously, the actual static equilibrium should locate in the region $\left[ -0.8+\left| A \right| ,0.8-\left| A \right| \right]$, which is also marked in Fig. 3. The static equilibriums outside the region are extraneous roots. It can be seen that there is only one trivial equilibrium in this situation.

Fig. 3

Static equilibriums for ${{\tilde{f}}}=0.1$

At last, we obtain the static equilibrium and periodic solution of the AMB-rotor system when ${\tilde{f}}=0.1$,

$$\begin{aligned} C_{01}=0, \end{aligned}$$

$$\begin{aligned} {\tilde{y}}_1=-0.1000\cos {\tilde{t}}. \end{aligned}$$

After obtaining the periodic solution ${\tilde{y}}=-0.1000\cos {\tilde{t}}$, the corresponding monodromy matrix can be calculated according to Eqs. (20) and (21). After state augment, the solution can be expressed as

$$\begin{aligned} \xi _1&=0.1000\sin {\tilde{t}}, \\ \xi _2&=-0.1000\cos {\tilde{t}}, \\ \xi _3&={\tilde{t}}. \end{aligned}$$

Substitute it into Eq. (20), and calculate the monodromy matrix $\mathbf{M}$ according to Eq. (21). The corresponding Floquet multipliers are

$$\begin{aligned} \lambda _1{=}0.5833+{j}0.5422, \lambda _2{=}0.5833-{j} 0.5422, \lambda _3{=}1. \end{aligned}$$

All the eigenvalues are not greater than 1. The solution is stable. The analysis shows when ${\tilde{f}}=0.1$, there is one stable periodic solution in the AMB-rotor system.

However when ${\tilde{f}}=0.2$, we can obtain the static equilibriums $C_0=0,\pm 0.3282,\pm 0.6835$ and vibration amplitude $\left| A \right| =0.2000$. Figure 4 shows the static equilibriums for ${\tilde{f}}=0.2$. As we can see, there are three actual equilibriums and two extraneous roots. In this situation, the static equilibriums of the AMB-rotor system are

$$\begin{aligned} C_{02}=\left\{ \begin{array}{l} 0, \\ 0.3282, \\ -0.3282. \end{array} \right. \end{aligned}$$

Then further three possible periodic solutions can be obtained according to Eq. (19); they are

$$\begin{aligned} \tilde{y}_2=\left\{ \begin{array}{l} -0.2000\cos {\tilde{t}} , \\ 0.3282-0.2000\cos {\tilde{t}} , \\ -0.3282-0.2000\cos {\tilde{t}}. \end{array} \right. \end{aligned}$$

Fig. 4

Static equilibrium for ${\tilde{f}}=0.2$

By substituting the periodic solutions into the monodromy matrix $\mathbf {M}$ and getting $\lambda \left( \mathbf {M} \right)$, their stability can be determined, respectively. The trivial solution ${\tilde{y}}_2=-0.2000\cos {\tilde{t}}$ is unstable, while two nontrivial solutions ${\tilde{y}}_2=\pm 0.3282 -0.2000\cos {\tilde{t}}$ are stable.

This paper regards the external excitation amplitude ${\tilde{f}}$ as the distinguishing variable and uses the approximate analytical method to solve the static equilibrium $C_0$ and vibration amplitude $\left| A \right|$, and further periodic solutions ${\tilde{y}}$. After removing extraneous roots and conducting stability analysis based on Floquet theory, the nonlinear dynamical characteristics can be explored in depth. Table 1 gives calculation results for some external excitation amplitudes, and the corresponding stability is also noted.

Table 1 Calculation results for some ${\tilde{f}}$

Through above procedures, this paper can get the multiple solutions and their stability in the AMB-rotor system with nonlinear electromagnetic force and current saturation. The nonlinear dynamical analysis can be conducted based on the solved results.

4.2 Supercritical pitchfork bifurcation

The dynamical characteristics of the AMB-rotor system for different external excitations can be analyzed according to the analysis procedure introduced in Sect. 4.1. The system parameters are fixed at ${\tilde{\Omega }}=1$, ${{\tilde{K}}_{\mathrm{p}}}=1.9044$, ${{\tilde{K}}_\mathrm{d}}=4.8006$. The analytical results show that the characteristic of vibration amplitude is simple and nonlinear behaviors of the AMB-rotor system with current saturation are mainly reflected in the static equilibrium $C_0$. The analysis results are introduced in this subsection.

Figure 5 gives the relationship between static equilibrium $C_0$ and excitation amplitude ${\tilde{f}}$. Its abscissa is ${\tilde{f}}$, while the ordinate is $C_0$. The red line represents stable solutions and the blue are unstable ones. It can be seen there are multiple static equilibriums for some values of ${\tilde{f}}$ in the nonlinear AMB-rotor system with current saturation.

Fig. 5

Static equilibrium $C_0$ with respect to excitation amplitude ${\tilde{f}}$

Under the effects of nonlinearity of electromagnetic force and current saturation, the AMB-rotor system shows complicated characteristics. Different from expected behavior that there is always one stable trivial equilibrium, multiple static equilibriums are found in the AMB-rotor system. Accordingly there are multiple periodic solutions and their stability characteristics are complicated. As ${\tilde{f}}$ is small, there is only one static equilibrium, namely stable trivial equilibrium. In this situation, the system does not exhibit nonlinear behaviors. However, the number and stability of static equilibriums will change with the increase of ${\tilde{f}}$. It can be seen that the trivial equilibrium loses its stability in the vicinity of ${\tilde{f}}=0.16$, and in the meantime two stable nontrivial equilibriums appear. After that, there are three static equilibriums in the system. Two of them are stable, and one is unstable. It is a typical supercritical pitchfork bifurcation. If ${\tilde{f}}$ continues to enlarge, the bifurcation will become more and more prominent.

Only stable static equilibriums can be exhibited during actual operation of the AMB-rotor system. The corresponding dynamical behaviors are introduced as follows. For the small ${\tilde{f}}$, the system is operating at the trivial equilibrium. As for large ${\tilde{f}}$, the trivial equilibrium loses its stability and the rotor deviates from the trivial equilibrium and starts to vibrate at one of two new nontrivial equilibriums. Which one of nontrivial equilibriums will be exhibited during operation depends on initial conditions. When ${\tilde{f}}$ is small and supercritical pitchfork bifurcation does not occur, the rotor displacement only depends on the vibration. In this situation, the maximum displacement of rotor is the vibration amplitude, i.e., ${\tilde{y}}_\mathrm{max}=\left| A\right| =\frac{{\tilde{f}}}{{\tilde{\Omega }}^2}$. However, after bifurcation, the rotor displacement depends on both static equilibrium and vibration amplitude and is the sum value of static equilibrium and vibration amplitude, namely ${\tilde{y}}_\mathrm{max}=C_0+\left| A \right|$. The deviation of static equilibrium makes system performance deteriorate and even threatens stable operation of the system.

To illustrate that intuitively, the relationship between rotor displacement ${\tilde{y}}$ and external excitation amplitude ${\tilde{f}}$ can be obtained by adding the vibration amplitude $\left| A \right|$. The nontrivial equilibriums are symmetrical about the trivial equilibrium based on the static equilibriums, as shown in Fig. 5. We only focus on one of nontrivial equilibriums and the trivial equilibrium to get rotor displacement when the system is operating stably at them. Figure 6 shows the rotor displacement when the system is operating at stable trivial equilibrium or nontrivial equilibrium. The abscissa is ${\tilde{f}}$, while the ordinate is the rotor displacement ${\tilde{y}}$ whose reference substance is the reference position of the rotor. The green line represents the physical limit which depends on the mechanical clearance between the rotor and stator. The rotor will rush into the stator if it exceeds the limit, which will lead to instability.

Fig. 6

Rotor displacement ${\tilde{y}}$ with respect to external excitation amplitude ${\tilde{f}}$

It is found that the nonlinearity of electromagnetic force and current saturation have major impact on the dynamical behaviors of the AMB-rotor system. For small ${\tilde{f}}$, the nonlinear factors in the AMB-rotor system are not prominent and complicated behaviors do not appear. The maximum displacement is not large and appears to increase linearly with the increase of ${\tilde{f}}$. In this situation, the rotor vibrates at the trivial equilibrium and can keep far away from the physical limit. The system can keep in a good performance during operation. However, when ${\tilde{f}}$ increases to a certain level, nonlinear factors become prominent, and supercritical pitchfork bifurcation occurs. In this case, the rotor displacement is affected by both the static equilibrium and vibration amplitude. It has a more complicated relationship with respect to ${\tilde{f}}$. Even a small change of ${\tilde{f}}$ will make the rotor displacement increase a lot. The rotor operates within an inch of the physical limit. The system performance deteriorates. If ${\tilde{f}}$ continues to enlarge, the rotor displacement will even exceeds the physical limit, and the rotor will crash into the stator, which will lead to direct instability and damage the system structure. It can be seen from Fig. 6, the theoretical maximum value of external excitation which can avoid rub-impact and keep system stable is ${\tilde{f}}=0.1940$. However considering the disturbances during the actual operation, the acceptable ${\tilde{f}}$ is much smaller. When the rotor displacement is close to the physical limit, a small disturbance may lead to the rub-impact between the rotor and stator, and instability occurs frequently. There is no doubt the supercritical pitchfork bifurcation is harmful to the system and should be prevented.

When the AMB-rotor system is operating at a speed far away from resonances, the vibration amplitude of the rotor is simple and nearly consistent with the analysis result based on linear theory. However, the static equilibrium $C_0$ shows complicated characteristics. With the increase of ${\tilde{f}}$, the trivial equilibrium loses its stability, and the rotor deviates from the reference position. In other words, the supercritical pitchfork bifurcation in the AMB-rotor system is reflected in the static equilibrium $C_0$ rather than the vibration amplitude A, which is different from the phenomenon in fluid film bearing-rotor system in [22]. The AMB has a larger bearing mechanical clearance; it can make the stable nontrivial solution be exhibited during operation when the nonlinear factors are prominent.

5 Numerical validation

In order to verify the validity of the method of multiple scales, two numerical methods were used. They are the numerical integration method and the generalized cell mapping digraph method. The numerical results were obtained by them and compared with the analytical results.

The numerical integration method was used to verify the time series responses. The time series responses obtained through the numerical integration method and the method of multiple scales were compared. Take ${\tilde{f}}=0.1, 0.18$ as examples to show the time series responses before and after supercritical pitchfork bifurcation. Figures 7 and 8 show the time series responses for ${\tilde{f}}=0.1, 0.18$, respectively. In the case of ${\tilde{f}}=0.1$, the analytical result is highly consistent with the numerical. There is only one stable static equilibrium. The rotor vibrates at the trivial equilibrium, and the maximum displacement of rotor is exactly the vibration amplitude $\left| A\right| =0.1$. During operation, the mechanical clearance between the rotor and stator is large enough to avoid rub-impact. The high performance of the system can be ensured. While in the case of ${\tilde{f}}=0.18$, there are three static equilibriums. Accordingly, there are three periodic solutions. The rotor can operate at any one of nontrivial equilibriums, and the maximum displacement is large. During numerical simulation, the rotor cannot keep vibrating stably at the unstable trivial equilibrium for a long time. But any nontrivial equilibrium can be exhibited. The stable analytical solutions can fit numerical results very well. In Fig. 8, we can only get the stable time series responses through numerical integration method. The comparison of numerical and analytical results shows the method of multiple scales can get accurate stable solutions. However, the numerical integration method cannot test the accuracy of unstable solutions because it cannot simulate unstable time series responses steadily. The following numerical results obtained by the generalized cell mapping digraph method will show the unstable solution is a saddle-node point. We cannot use inverse-time numerical integration method to get the unstable solution neither.

Fig. 7

Steady-state response for ${\tilde{f}}=0.1$

Fig. 8

Steady-state response for ${\tilde{f}}=0.18$

Aiming at the problem that unstable solution cannot be verified by the numerical integration method, the generalized cell mapping digraph method was adopted to get both stable and unstable solutions to provide reference substances for analytical solutions. Reference [16] introduced how to use the generalized cell mapping digraph method to do global dynamical analysis of the nonlinear AMB-rotor system. The analysis results include stable attractors and their domains and unstable attractor and its stable/unstable manifolds. In results of generalized cell mapping digraph method, this paper only focuses on the stable and unstable solutions to verify the accuracy of analytical solutions.

The validation process is introduced as follows. Firstly, choose four different values of external excitation amplitude, namely set ${\tilde{f}}=0.05,0.1,0.15,0.2$. Then get four phase diagrams and regard them as four slices in a three-dimensional diagram shown in Fig. 9. At last, deal with the analytical results shown in Fig. 6 and get the rotor displacement for $\tilde{f} \in \left[ 0.05,0.24 \right]$ based on static equilibrium $C_0$ and vibration amplitude $\left| A \right|$. The method of multiple scales neglects vibration phase in Eq. (14). This paper sets $\dot{\tilde{y}}=0$ directly when putting analytical solutions into Fig. 9.

Fig. 9

Comparison between analytical and numerical solutions

To show the comparison of numerical and analytical results in details, take ${\tilde{f}}=0.2$ as an example to point out analytical and numerical solutions in a phase diagram. The results of generalized cell mapping method contain the stable solutions and their domains of attraction, unstable solution and its stable/unstable manifold. The solutions are marked by $\times$. The analytical solutions are marked by $\circ$. The red are stable solutions, and the blue represent unstable ones.

It can be seen from Fig. 9 that the results obtained by the method of multiple scales and generalized cell mapping method are consistent. The number and stability of analytical solutions are in accordance with numerical ones. The numerical and analytical results are highly consistent, and the differences in ${\tilde{y}}$ and $\dot{\tilde{y}}$ are very tiny. Although Eq. (14) only considers the static equilibrium $C_0$ and vibration amplitude A and ignores the vibration phase in the method of multiple scales, the handling method do not cause substantive effects on the analytical results, which can also be proved by Figs. 7 and 8.

In summary, this section obtained numerical results through the numerical integration method and generalized cell mapping digraph method. The comparisons between analytical results and numerical results prove the validity and accuracy of the approximate analytical method.

6 Effects of controller parameters

According to the analysis results in Sect. 4.2, it is known the AMB-rotor system with current saturation exhibits supercritical pitchfork bifurcation that is detrimental to the operating performance. Decreasing the external excitation amplitude ${\tilde{f}}$ can suppress the bifurcation effectively. However, limited by the operation load and rotor eccentricity, it is always difficult to decrease ${\tilde{f}}$ further. Other measures to change the system characteristics are needed. Compared with mechanical bearings, AMBs have a superiority, namely the stiffness and damping characteristics can be adjusted flexibly through controller. There is no doubt that controller parameters have significant influences on dynamical characteristics of the AMB-rotor system. The influences of controller on nonlinear behaviors should be explored in depth. In this paper, the actual high-order controller was simplified into a PD controller equivalently in order to investigate effects of controller parameters.

The analysis results show the supercritical pitchfork bifurcation with respect to controller parameters ${{\tilde{K}}_{\mathrm{p}}}$ and ${{\tilde{K}}_\mathrm{d}}$ also exist. In order to investigate the dynamical characteristics under the action of different controller parameter combinations, the relationship between static equilibrium $C_0$ and controller parameters ${{\tilde{K}}_{\mathrm{p}}}$, ${{\tilde{K}}_\mathrm{d}}$ were obtained for ${\tilde{f}}=0.18$, as shown in Fig. 10. There is only one stable trivial equilibrium for large ${{\tilde{K}}_{\mathrm{p}}}$ and small ${{\tilde{K}}_\mathrm{d}}$. However, for small ${{\tilde{K}}_{\mathrm{p}}}$ and large ${{\tilde{K}}_\mathrm{d}}$, the trivial equilibrium loses stability, and two stable nontrivial equilibriums appear. This phenomenon means the different controller parameters can make the system show very different dynamical characteristics.

Fig. 10

Static equilibrium $C_0$ with respect to ${{\tilde{K}}_{\mathrm{p}}}$ and ${{\tilde{K}}_\mathrm{d}}$

The results can provide guidance for the controller design of the AMB-rotor system when nonlinear factors are prominent. In the controller design based on the linear theory, the large stiffness is expected for heavy bearing capacity, which always means large proportional gain ${{\tilde{K}}_{\mathrm{p}}}$. In the meantime, in order to suppress the vibration, a large damping is expected too, which needs large differential gain ${{\tilde{K}}_\mathrm{d}}$. However, such controller design principle seems not perfect from the perspective of nonlinear dynamics. Large ${{\tilde{K}}_\mathrm{d}}$ may cause supercritical pitchfork bifurcation of static equilibrium in the system, which will have bad influences on the system instead.

This paper conducted the nonlinear dynamical analysis of the AMB-rotor system by considering the nonlinearity of electromagnetic force and current saturation. The controller parameters can be modified based on the analysis results to prevent nonlinear behaviors and improve system performance. In this paper, the controller parameters were changed into ${{\tilde{K}}_{\mathrm{p}}}=2.0074$, ${{\tilde{K}}_\mathrm{d}}=1.8527$ according to Fig. 10. Under action of the controller parameters, the supercritical pitchfork bifurcation disappears, as shown in Fig. 11. For any ${\tilde{f}} \in \left[ 0.05,0.24 \right]$, there is only one stable trivial equilibrium. In this situation, even if the external excitation is large, the AMB-rotor system can stay at the trivial equilibrium and vibrate at a small amplitude. The modified controller parameters can keep $C_0=0$ for a wide range of ${\tilde{f}}$, and the maximum displacement of the rotor decreases a lot.

Fig. 11

Static equilibrium $C_0$ with respect to ${\tilde{f}}$ before and after controller parameter modification

The results imply that the controller design principle based on nonlinear dynamics should be considered. It can provide the supplement to the linear controller design principle and prevent nonlinear behaviors under some harsh operating conditions. Take the results in this paper as an example, the large differential gain ${{\tilde{K}}_\mathrm{d}}$ will lead to bifurcation. In the case of bifurcation, although vibration amplitude can be suppressed effectively, the deviation of the rotor from trivial equilibrium will enlarge the rotor displacement. It makes instability happen more easily. Therefore, during the controller design, the parameters should be chosen by considering both effects of vibration amplitude and static equilibrium comprehensively. Proper controller parameters can prevent the occurrence of bifurcation and keep system in high-performance operation even for some complicated and harsh operating conditions.

7 Conclusions and prospect

In this paper, nonlinear behaviors of the AMB-rotor system were investigated by considering the nonlinearity of electromagnetic force and current saturation. A novel method of multiple scales was developed to analyze bifurcation behaviors of the periodically excited AMB-rotor system, and corresponding stability analysis of multiple solutions was carried out based on Floquet theory. The comparison of the results with those based on the numerical methods proved the validity and accuracy of the proposed method. It is the first time to use the method of multiple scales for the bifurcation analysis of a forced bearing-rotor system when it is operating at a speed far away from resonances. It is found there is supercritical pitchfork bifurcation in the AMB-rotor system. The bifurcation is not reflected in vibration amplitude but the static equilibrium. The influences of controller parameters and external excitation on supercritical pitchfork bifurcation were discussed. Based on analysis results, the modification of controller parameters can prevent the nonlinear behaviors and improve the system performance effectively.

Although the bifurcation in the AMB-rotor system was investigated through the method of multiple scales, the actual high-order controller was simplified into a PD controller. In the future, other analytical methods are to be proposed and applied to the AMB-rotor system with higher-oder controller. The more accurate results are needed to help get a comprehensive understanding of nonlinear characteristics of the AMB-rotor system.

Appendices

Appendix A

The coefficients $k_{m,n}$ in Eq. (7):

$k_{1,0}=0.02287{{\tilde{K}_{\mathrm{p}}}}-0.01033 , k_{3,0}=-0.02308{{\tilde{K}_{\mathrm{p}}}}^3-0.02852{{\tilde{K}_{\mathrm{p}}}}^2+0.06079{{\tilde{K}_{\mathrm{p}}}}-0.05111, k_{5,0}=0.01302{{\tilde{K}_{\mathrm{p}}}}^5+0.02609{{\tilde{K}_{\mathrm{p}}}}^4-0.06087{{\tilde{K}_{\mathrm{p}}}}^3 -0.0412{{\tilde{K}_{\mathrm{p}}}}^2+0.1919{{\tilde{K}_{\mathrm{p}}}}+0.3458 , k_{7,0}=0.003566{{\tilde{K}_{\mathrm{p}}}}^7-0.009379{{\tilde{K}_{\mathrm{p}}}}^6+0.02636{{\tilde{K}_{\mathrm{p}}}}^5 +0.0287{{\tilde{K}_{\mathrm{p}}}}^4-0.0713{{\tilde{K}_{\mathrm{p}}}}^3-0.05661{{\tilde{K}_{\mathrm{p}}}}^2 -0.1839{{\tilde{K}_{\mathrm{p}}}}-1.968 , k_{9,0}=0.000455{{\tilde{K}_{\mathrm{p}}}}^9+0.001425{{\tilde{K}_{\mathrm{p}}}}^8-0.004855{{\tilde{K}_{\mathrm{p}}}}^7 -0.00675{{\tilde{K}_{\mathrm{p}}}}^6+0.02344{{\tilde{K}_{\mathrm{p}}}}^5+0.02136{{\tilde{K}_{\mathrm{p}}}}^4-0.07812{{\tilde{K}_{\mathrm{p}}}}^3 -0.008971{{\tilde{K}_{\mathrm{p}}}}^2+0.4281{{\tilde{K}_{\mathrm{p}}}}+4.045 , k_{11,0}=-0.000022{{\tilde{K}_{\mathrm{p}}}}^{11}-0.000077{{\tilde{K}_{\mathrm{p}}}}^{10}+0.00031{{\tilde{K}_{\mathrm{p}}}}^9 +0.000514{{\tilde{K}_{\mathrm{p}}}}^8-0.002422{{\tilde{K}_{\mathrm{p}}}}^7-0.00299{{\tilde{K}_{\mathrm{p}}}}^6+0.01789{{\tilde{K}_{\mathrm{p}}}}^5 +0.016{{\tilde{K}_{\mathrm{p}}}}^4-0.117{{\tilde{K}_{\mathrm{p}}}}^3-0.08791{{\tilde{K}_{\mathrm{p}}}}^2+0.5638{{\tilde{K}_{\mathrm{p}}}}-3.368 , k_{0,1}=0.02287{{\tilde{K}_\mathrm{d}}} , k_{2,1}=-0.06924{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}-0.05704{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}+0.06079{{\tilde{K}_\mathrm{d}}} , k_{4,1}=0.0651{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}}+0.10436{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}} - 0.18261{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}} - 0.0824{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}+0.1919{{\tilde{K}_\mathrm{d}}} ,$ $k_{6,1}=- 0.024962{{\tilde{K}_{\mathrm{p}}}}^6{{\tilde{K}_\mathrm{d}}}- 0.056274{{\tilde{K}_{\mathrm{p}}}}^5{{\tilde{K}_\mathrm{d}}} + 0.1318{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}}+0.1148{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}} - 0.2139{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}- 0.11322{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}- 0.1839{{\tilde{K}_\mathrm{d}}},$ $k_{8,1}=0.004094{{\tilde{K}_{\mathrm{p}}}}^8{{\tilde{K}_\mathrm{d}}} + 0.0114{{\tilde{K}_{\mathrm{p}}}}^7{{\tilde{K}_\mathrm{d}}} - 0.033985{{\tilde{K}_{\mathrm{p}}}}^6{{\tilde{K}_\mathrm{d}}}- 0.0405{{\tilde{K}_{\mathrm{p}}}}^5{{\tilde{K}_\mathrm{d}}} + 0.1172{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}}+ 0.08544{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}} - 0.23436{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}- 0.017942{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}} + 0.428{{\tilde{K}_\mathrm{d}}},$ $k_{10,1}=- 0.000238{{\tilde{K}_{\mathrm{p}}}}^{10}{{\tilde{K}_\mathrm{d}}} - 0.000767{{\tilde{K}_{\mathrm{p}}}}^9{{\tilde{K}_\mathrm{d}}} + 0.0027891{{\tilde{K}_{\mathrm{p}}}}^8{{\tilde{K}_\mathrm{d}}}+ 0.004114{{\tilde{K}_{\mathrm{p}}}}^7{{\tilde{K}_\mathrm{d}}} - 0.016954{{\tilde{K}_{\mathrm{p}}}}^6{{\tilde{K}_\mathrm{d}}} - 0.01794{{\tilde{K}_{\mathrm{p}}}}^5{{\tilde{K}_\mathrm{d}}} + 0.08945{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}} + 0.064{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}} - 0.351{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}} - 0.17582{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}+ 0.5638{{\tilde{K}_\mathrm{d}}}, k_{1,2}=- 0.06924{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^2-0.02852{{\tilde{K}_\mathrm{d}}}^2, k_{3,2}=0.1302{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^2 + 0.15654{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^2 - 0.18261{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^2 - 0.0412{{\tilde{K}_\mathrm{d}}}^2, k_{5,2}=- 0.074886{{\tilde{K}_{\mathrm{p}}}}^5{{\tilde{K}_\mathrm{d}}}^2 - 0.140685{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}}^2 + 0.2636{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^2 + 0.1722{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^2 - 0.2139{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^2 - 0.05661{{\tilde{K}_\mathrm{d}}}^2 ,$ $k_{7,2}=0.016376{{\tilde{K}_{\mathrm{p}}}}^7{{\tilde{K}_\mathrm{d}}}^2 +0.0399{{\tilde{K}_{\mathrm{p}}}}^6{{\tilde{K}_\mathrm{d}}}^2 - 0.101955{{\tilde{K}_{\mathrm{p}}}}^5{{\tilde{K}_\mathrm{d}}}^2- 0.10125{{\tilde{K}_{\mathrm{p}}}}^4 {{\tilde{K}_\mathrm{d}}}^2 + 0.2344{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^2 + 0.12816{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^2 - 0.23436{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^2 - 0.008971{{\tilde{K}_{\mathrm{p}}}}^2, k_{9,2}=-0.00119{{\tilde{K}_{\mathrm{p}}}}^9{{\tilde{K}_\mathrm{d}}}^2 - 0.00345{{\tilde{K}_{\mathrm{p}}}}^8{{\tilde{K}_\mathrm{d}}}^2 + 0.011156{{\tilde{K}_{\mathrm{p}}}}^7{{\tilde{K}_\mathrm{d}}}^2+ 0.0144{{\tilde{K}_{\mathrm{p}}}}^6{{\tilde{K}_\mathrm{d}}}^2 - 0.050862{{\tilde{K}_{\mathrm{p}}}}^5{{\tilde{K}_\mathrm{d}}}^2 - 0.04485{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}}^2 + 0.1789{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^2 + 0.096{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^2 - 0.351{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^2 - 0.08791{{\tilde{K}_\mathrm{d}}}^2 ,$ $k_{0,3}=-0.02308{{\tilde{K}_\mathrm{d}}}^3 , k_{2,3}=0.1302{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^3 + 0.10436{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^3 - 0.06087{{\tilde{K}_\mathrm{d}}}^3 , k_{4,3}=- 0.12481{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}}^3 - 0.18758{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^3 + 0.2636{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^3 + 0.1148{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^3 - 0.0713{{\tilde{K}_\mathrm{d}}}^3 ,$ $k_{6,3}=0.038212{{\tilde{K}_{\mathrm{p}}}}^6{{\tilde{K}_\mathrm{d}}}^3+ 0.0798{{\tilde{K}_{\mathrm{p}}}}^5{{\tilde{K}_\mathrm{d}}}^3 - 0.169925{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}}^3 - 0.135{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^3 + 0.2344{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^3 + 0.08544{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^3 - 0.07812{{\tilde{K}_\mathrm{d}}}^3 , k_{8,3}=- 0.003571{{\tilde{K}_{\mathrm{p}}}}^8{{\tilde{K}_\mathrm{d}}}^3 - 0.0092{{\tilde{K}_{\mathrm{p}}}}^7{{\tilde{K}_\mathrm{d}}}^3 + 0.026032{{\tilde{K}_{\mathrm{p}}}}^6{{\tilde{K}_\mathrm{d}}}^3 + 0.028801{{\tilde{K}_{\mathrm{p}}}}^5{{\tilde{K}_\mathrm{d}}}^3 - 0.08477{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}}^3 - 0.0598{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^3 + 0.1789{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^3 + 0.064{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^3 - 0.117{{\tilde{K}_\mathrm{d}}}^3 , k_{1,4}=0.0651{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^4+ 0.02609{{\tilde{K}_\mathrm{d}}}^4 , k_{3,4}=- 0.12481{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^4 - 0.140685{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^4 + 0.1318{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^4 + 0.0287{{\tilde{K}_\mathrm{d}}}^4 , k_{5,4}=0.057317{{\tilde{K}_{\mathrm{p}}}}^5{{\tilde{K}_\mathrm{d}}}^4 + 0.09975{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}}^4 - 0.169925{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^4 - 0.10125{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^4 + 0.1172{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^4 + 0.02136{{\tilde{K}_\mathrm{d}}}^4 ,$ $k_{7,4}=- 0.007141{{\tilde{K}_{\mathrm{p}}}}^7{{\tilde{K}_\mathrm{d}}}^4 - 0.016101{{\tilde{K}_{\mathrm{p}}}}^6{{\tilde{K}_\mathrm{d}}}^4 + 0.039047{{\tilde{K}_{\mathrm{p}}}}^5{{\tilde{K}_\mathrm{d}}}^4 + 0.036001{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}}^4 - 0.08477{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^4 - 0.04485{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^4 + 0.08945{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^4 + 0.016{{\tilde{K}_\mathrm{d}}}^4 ,$ $k_{0,5}=0.01302{{\tilde{K}_\mathrm{d}}}^5 , k_{2,5}=- 0.074886{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^5 - 0.056274{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^5 + 0.02636{{\tilde{K}_\mathrm{d}}}^5 ,$ $k_{4,5}=0.057317{{\tilde{K}_{\mathrm{p}}}}^4 {{\tilde{K}_\mathrm{d}}}^5 + 0.0798{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^5 - 0.101955{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^5 - 0.0405{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^5 + 0.02344 {{\tilde{K}_\mathrm{d}}}^5 , k_{6,5}=- 0.009998{{\tilde{K}_{\mathrm{p}}}}^6{{\tilde{K}_\mathrm{d}}}^5 - 0.019321{{\tilde{K}_{\mathrm{p}}}}^5{{\tilde{K}_\mathrm{d}}}^5 + 0.039047{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}}^5 + 0.028801{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^5 - 0.050862{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^5 - 0.01794{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^5 + 0.01789{{\tilde{K}_\mathrm{d}}}^5 , k_{1,6}=- 0.024962{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^6 - 0.009379{{\tilde{K}_\mathrm{d}}}^6 , k_{3,6}=0.038212{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^6 + 0.0399{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^6 - 0.033985{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^6 - 0.00675{{\tilde{K}_\mathrm{d}}}^6 , k_{5,6}=- 0.009998{{\tilde{K}_{\mathrm{p}}}}^5 {{\tilde{K}_\mathrm{d}}}^6- 0.016101{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}}^6 + 0.026032{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^6 + 0.0144{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^6 - 0.016954{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^6 - 0.00299{{\tilde{K}_\mathrm{d}}}^6 , k_{0,7}=-0.003566{{\tilde{K}_\mathrm{d}}}^7 , k_{2,7}=0.016376{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^7 + 0.0114{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^7 - 0.004855{{\tilde{K}_\mathrm{d}}}^7 , k_{4,7}=- 0.007141{{\tilde{K}_{\mathrm{p}}}}^4{{\tilde{K}_\mathrm{d}}}^7 - 0.0092{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^7 + 0.011156{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^7 + 0.004114{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^7 - 0.002422{{\tilde{K}_\mathrm{d}}}^7 , k_{1,8}=0.004094{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^8 + 0.001425{{\tilde{K}_\mathrm{d}}}^8 ,$ $k_{3,8}=- 0.003571{{\tilde{K}_{\mathrm{p}}}}^3{{\tilde{K}_\mathrm{d}}}^8 - 0.00345{{\tilde{K}_{\mathrm{p}}}}^2{{\tilde{K}_\mathrm{d}}}^8 + 0.002789{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^8 + 0.000514{{\tilde{K}_\mathrm{d}}}^8 ,$ $k_{0,9}=0.000455{{\tilde{K}_\mathrm{d}}}^9 , k_{2,9}=- 0.00119{{\tilde{K}_{\mathrm{p}}}}^2 {{\tilde{K}_\mathrm{d}}}^9- 0.000767{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^9 + 0.00031{{\tilde{K}_\mathrm{d}}}^9 , k_{1,10}=- 0.000238{{\tilde{K}_{\mathrm{p}}}}{{\tilde{K}_\mathrm{d}}}^{10} - 0.000077{{\tilde{K}_\mathrm{d}}}^{10} , k_{0,11}=-0.000022{{\tilde{K}_\mathrm{d}}}^{11} .$

Appendix B

The coefficients in Eq. (16): $b_1=-k_{1,0} -6 k_{3,0} a\bar{a}-30 k_{5,0}a^2\bar{a}^2-140 k_{7,0} a^3\bar{a}^3 -630 k_{9,0} a^4\bar{a}^4-2772 k_{11,0}a^5\bar{a}^5-2 k_{1,2}{\tilde{\Omega }} ^2 a\bar{a}-6 k_{3,2} {\tilde{\Omega }} ^2 a^2\bar{a}-20 k_{5,2} {\tilde{\Omega }} ^2 a^3\bar{a}^3-70 k_{7,2} {\tilde{\Omega }} ^2 a^4\bar{a}^4 -252 k_{9,2} {\tilde{\Omega }} ^2a^5\bar{a}^5-6 k_{1,4} {\tilde{\Omega }} ^4 a^2\bar{a}^2 -12 k_{3,4} {\tilde{\Omega }} ^4 a^3\bar{a}^3-30 k_{5,4} {\tilde{\Omega }} ^4 a^4\bar{a}^4-84 k_{7,4} {\tilde{\Omega }} ^4 a^5\bar{a}^5-20 k_{1,6} {\tilde{\Omega }} ^6 a^3\bar{a}^3-30 k_{3,6} {\tilde{\Omega }} ^6 a^4\bar{a}^4-60 k_{5,6} {\tilde{\Omega }} ^6 a^5\bar{a}^5-70 k_{1,8} {\tilde{\Omega }} ^8 a^4 \bar{a}^4-84 k_{3,8} {\tilde{\Omega }} ^8 a^5\bar{a}^5-252 k_{1,10} {\tilde{\Omega }} ^{10} a^5\bar{a}^5 ,$

$b_2=-k_{3,0}-20k_{5,0} a\bar{a}-210k_{7,0}a^2\bar{a}^2-1680 k_{9,0} a^3 \bar{a}^3-11550 k_{11,0} a^4\bar{a}^4-2k_{3,2}{\tilde{\Omega }} ^2a\bar{a} -20 k_{5,2} {\tilde{\Omega }} ^2 a^2\bar{a}^2-140 k_{7,2}{\tilde{\Omega }} ^2a^3 \bar{a}^3-840 k_{9,2}{\tilde{\Omega }}^2 a^4\bar{a}^4-6 k_{3,4}{\tilde{\Omega }} ^4 a^2\bar{a}^2-40k_{5,4}{\tilde{\Omega }} ^4a^3\bar{a}^3-210 k_{7,4}{\tilde{\Omega }} ^4 a^4\bar{a}^4-20 k_{3,6}{\tilde{\Omega }} ^6 a^3\bar{a}^3 -100 k_{5,6} {\tilde{\Omega }} ^6 a^4\bar{a}^4-70k_{3,8}{\tilde{\Omega }} ^8a^4\bar{a}^4 ,$

$b_3=-k_{5,0}- 42 k_{7,0} a\bar{a} - 756 k_{9,0} a^2\bar{a}^2 - 9240 k_{11,0}a^3 \bar{a}^3 - 2 k_{5,2}{\tilde{\Omega }} ^2 a\bar{a}- 42 k_{7,2} {\tilde{\Omega }} ^2 a^2\bar{a}^2 -504 k_{9,2} {\tilde{\Omega }} ^2 a^3\bar{a}^3- 6 k_{5,4} {\tilde{\Omega }} ^4 a^2\bar{a}^2 - 84 k_{7,4} {\tilde{\Omega }} ^4 a^3\bar{a}^3 - 20 k_{5,6}{\tilde{\Omega }} ^6 a^3\bar{a}^3 ,$

$b_4=-k_{7,0}-72 k_{9,0} a\bar{a}-1980 k_{11,0} a^2\bar{a}^2 -2 k_{7,2} {\tilde{\Omega }} ^2 a\bar{a}-72 k_{9,2} {\tilde{\Omega }} ^2 a^2\bar{a}^2-6 k_{7,4} {\tilde{\Omega }} ^4 a^2\bar{a}^2 ,$

$b_5=-k_{9,0}-110 k_{11,0}a\bar{a} -2 k_{9,2} {\tilde{\Omega }} ^2 a\bar{a} ,$

$b_6=-k_{11,0} ,$

$b_7=-k_{1,0}a-k_{3,0}a^2\bar{a}-3k_{3,0}a{C_0}^2-10k_{5,0}a^3\bar{a}^2-30k_{5,0} a^2\bar{a}{C_0}^2-5k_{5,0}a{C_0}^4-35k_{7,0}a^4\bar{a}^3-210k_{7,0}a^3\bar{a}^2 {C_0}^2-105k_{7,0}a^2\bar{a}{C_0}^4-7k_{7,0}a{C_0}^6-126k_{9,0}a^5\bar{a}^4 -1260k_{9,0}a^4\bar{a}^3{C_0}^2-1260k_{9,0}a^3\bar{a}^2{C_0}^4-252k_{9,0}a^2 \bar{a}{C_0}^6-9k_{9,0}a{C_0}^8-462k_{11,0}a^6\bar{a}^5-6930k_{11,0}a^5 \bar{a}^4{C_0}^2-11550k_{11,0} a^4\bar{a}^3{C_0}^4-4620k_{11,0} a^3\bar{a}^2 {C_0}^6-495k_{11,0}a^2\bar{a}{C_0}^8-11k_{11,0}a{C_0}^{10}+5\mathrm{j}k_{6,1} {\tilde{\Omega }} a^4\bar{a}^3+30\mathrm{j}k_{6,1}{\tilde{\Omega }} a^3\bar{a}^2{C_0}^2 +15\mathrm{j}k_{6,1}{\tilde{\Omega }} a^2\bar{a}{C_0}^4+\mathrm{j}k_{6,1}{\tilde{\Omega }} a{C_0}^6+14\mathrm{j}k_{6,1}{\tilde{\Omega }} a^5\bar{a}^4+140\mathrm{j}k_{8,1}{\tilde{\Omega }} a^4\bar{a}^3{C_0}^2+140\mathrm{j}k_{8,1}{\tilde{\Omega }} a^3\bar{a}^2{C_0}^4+28\mathrm{j} k_{8,1}{\tilde{\Omega }} a^2\bar{a}{C_0}^6+\mathrm{j}k_{8,1}{\tilde{\Omega }} a{C_0}^8 +42\mathrm{j}k_{10,1}{\tilde{\Omega }} a^6\bar{a}^5+630\mathrm{j}k_{10,1}{\tilde{\Omega }} a^5\bar{a}^4{C_0}^2+1050\mathrm{j}k_{10,1}{\tilde{\Omega }} a^4\bar{a}^3{C_0}^4 +420\mathrm{j}k_{10,1}{\tilde{\Omega }} a^3\bar{a}^2{C_0}^6+45\mathrm{j}k_{10,1}{\tilde{\Omega }} a^2\bar{a}{C_0}^8+\mathrm{j}k_{10,1}{\tilde{\Omega }} a{C_0}^{10}+\mathrm{j}k_{0,1} {\tilde{\Omega }} a+\mathrm{j}k_{2,1}{\tilde{\Omega }} a^2\bar{a}+\mathrm{j}k_{2,1} {\tilde{\Omega }} a{C_0}^2+2\mathrm{j}k_{4,1}{\tilde{\Omega }} a^3\bar{a}^2+6\mathrm{j} k_{4,1}{\tilde{\Omega }} a^2\bar{a}{C_0}^2+\mathrm{j}k_{4,1}{\tilde{\Omega }} a {C_0}^4-k_{1,2}{{\tilde{\Omega }}}^2 a^2 \bar{a}-2k_{3,2}{{\tilde{\Omega }}}^2 a^3 \bar{a}^2-3k_{3,2}{{\tilde{\Omega }}}^2 a^2 \bar{a} {C_0}^2-5k_{5,2}{{\tilde{\Omega }}}^2 a^4 \bar{a}^3-20k_{5,2}{{\tilde{\Omega }}}^2 a^3 \bar{a}^2 {C_0}^2 -5k_{5,2} {{\tilde{\Omega }}}^2 a^2 \bar{a} {C_0}^4-14k_{7,2}{{\tilde{\Omega }}}^2 a^5 \bar{a}^4 -105k_{7,2}{{\tilde{\Omega }}}^2 a^4 \bar{a}^3 {C_0}^2 -70k_{7,2} {{\tilde{\Omega }}}^2 a^3 \bar{a}^2 {C_0}^4 -7k_{7,2}{{\tilde{\Omega }}}^2 a^2 \bar{a} {C_0}^6-42k_{9,2}{{\tilde{\Omega }}}^2 a^6 \bar{a}^5-504k_{9,2} {{\tilde{\Omega }}}^2 a^5 \bar{a}^4 {C_0}^2 -630k_{9,2}{{\tilde{\Omega }}}^2 a^4 \bar{a}^3 {C_0}^2 -168k_{9,2}{{\tilde{\Omega }}}^2 a^3 \bar{a}^2 {C_0}^6 -9k_{9,2}{{\tilde{\Omega }}}^2 a^2 \bar{a}{C_0}^8+ 3\mathrm{j}k_{0,3} {{\tilde{\Omega }}}^3 a^2\bar{a}+ 2\mathrm{j}k_{2,3} {{\tilde{\mathrm{\Omega }}}}^3 a^3 \bar{a}^2+3\mathrm{j}k_{2,3} {{\tilde{\Omega }}}^3 a^2\bar{a} {C_0}^2+3\mathrm{j}k_{4,3} {{\tilde{\Omega }}}^3 a^4\bar{a}^3+12\mathrm{j}k_{4,3} {{\tilde{\Omega }}}^3 a^3 \bar{a}^2{C_0}^2+3\mathrm{j}k_{4,3} {{\tilde{\Omega }}}^3 a^2\bar{a}{C_0}^4+6\mathrm{j} k_{6,3} {{\tilde{\Omega }}}^3 a^5\bar{a}^4+45\mathrm{j}k_{6,3} {{\tilde{\Omega }}}^3 a^4\bar{a}^3{C_0}^2+30\mathrm{j}k_{6,3} {{\tilde{\Omega }}}^3 a^2\bar{a}{C_0}^4 +3\mathrm{j}k_{6,3} {{\tilde{\Omega }}}^3 a^2\bar{a}{C_0}^6 +14\mathrm{j}k_{8,3} {{\tilde{\Omega }}}^3 a^6\bar{a}^5+168\mathrm{j}k_{8,3} {{\tilde{\Omega }}}^3 a^5 \bar{a}^4{C_0}^2+210\mathrm{j}k_{8,3} {{\tilde{\Omega }}}^3 a^4\bar{a}^3{C_0}^4 +56\mathrm{j}k_{8,3} {{\tilde{\Omega }}}^3 a^3\bar{a}^2{C_0}^6+3\mathrm{j}k_{8,3} {{\tilde{\Omega }}}^3 a^2\bar{a}{C_0}^8-2k_{1,4} {{\tilde{\Omega }}}^4 a^3\bar{a}^2 -3k_{3,4} {{\tilde{\Omega }}}^4 a^4\bar{a}^3-6k_{3,4} {{\tilde{\Omega }}}^4 a^3 \bar{a}^2{C_0}^2-6k_{5,4} {{\tilde{\Omega }}}^4 a^5\bar{a}^4-30k_{5,4} {\Omega }^4 a^4\bar{a}^3{C_0}^2 -10k_{5,4} {{\tilde{\Omega }}}^4 a^3\bar{a}^2{C_0}^4-14k_{7,4} {{\tilde{\Omega }}}^4 a^6\bar{a}^5-126k_{7,4} {{\tilde{\Omega }}}^4 a^5\bar{a}^4{C_0}^2 -10k_{7,4} {{\tilde{\Omega }}}^4 a^4\bar{a}^3{C_0}^4-14k_{7,4} {{\tilde{\Omega }}}^4 a^3\bar{a}^2{C_0}^6+10\mathrm{j}k_{0,5}{{\tilde{\Omega }}}^5 a^3 \bar{a}^2+5\mathrm{j}k_{2,5} {{\tilde{\Omega }}}^5 a^4 \bar{a}^3+10\mathrm{j}k_{2,5}{{\tilde{\Omega }}}^5 a^3 \bar{a}^2{C_0}^2+6\mathrm{j}k_{4,5}{{\tilde{\Omega }}}^5 a^5 \bar{a}^4+30\mathrm{j} k_{4,5}{{\tilde{\Omega }}}^5 a^4 \bar{a}^3{C_0}^2+10\mathrm{j}k_{4,5} {{\tilde{\Omega }}}^5 a^3 \bar{a}^2{C_0}^4+10\mathrm{j}k_{6,5}{{\tilde{\Omega }}}^5 a^6 \bar{a}^5+90\mathrm{j}k_{6,5}{{\tilde{\Omega }}}^5 a^4 \bar{a}^4{C_0}^2+75\mathrm{j} k_{6,5}{{\tilde{\Omega }}}^5 a^4 \bar{a}^3{C_0}^4+10\mathrm{j}k_{6,5}{{\tilde{\Omega }}}^5 a^3 \bar{a}^2{C_0}^6-5k_{1,6}{{\tilde{\Omega }}}^6 a^4 \bar{a}^3-6k_{3,6} {{\tilde{\Omega }}}^6 a^5 \bar{a}^4-15k_{3,6}{{\tilde{\Omega }}}^6 a^4 \bar{a}^3 {C_0}^2-10k_{5,6}{{\tilde{\Omega }}}^6 a^6 \bar{a}^5-60k_{5,6}{{\tilde{\Omega }}}^6 a^5 \bar{a}^4{C_0}^2-25k_{5,6}{{\tilde{\Omega }}}^6 a^4 \bar{a}^3{C_0}^4+35\mathrm{j} k_{0,7}{{\tilde{\Omega }}}^7 a^4 \bar{a}^3+14\mathrm{j}k_{2,7}{{\tilde{\Omega }}}^7 a^5 \bar{a}^4+35\mathrm{j}k_{2,7}{{\tilde{\Omega }}}^7 a^4 \bar{a}^3{C_0}^2+14\mathrm{j}k_{4,7} {{\tilde{\Omega }}}^7 a^6 \bar{a}^5+84\mathrm{j}k_{4,7}{{\tilde{\Omega }}}^7 a^5 \bar{a}^4{C_0}^2+35\mathrm{j}k_{4,7}{{\tilde{\Omega }}}^7 a^4 \bar{a}^3{C_0}^4-14k_{1,8} {{\tilde{\Omega }}}^8 a^5 \bar{a}^4-14k_{3,8}{{\tilde{\Omega }}}^8 a^6 \bar{a}^5-42k_{3,8} {{\tilde{\Omega }}}^8 a^5 \bar{a}^4{C_0}^2+126\mathrm{j}k_{0,9}{{\tilde{\Omega }}}^9 a^5 \bar{a}^4+42\mathrm{j}k_{2,9}{{\tilde{\Omega }}}^9 a^6 \bar{a}^5+126\mathrm{j}k_{2,9} {{\tilde{\Omega }}}^9 a^5 \bar{a}^4{C_0}^2-42k_{1,10}{{\tilde{\Omega }}}^{10} a^6 \bar{a}^5+462\mathrm{j}k_{0,11}{{\tilde{\mathrm{\Omega }}}}^{11} a^6 \bar{a}^5 ,$

$b_8=-3k_{3,0}a^2{C_0}-20k_{5,0}a^3\bar{a}{C_0}^3-10k_{5,0}a^2{C_0}^3-105k_{7,0}a^4 \bar{a}^2{C_0}-140k_{7,0}a^3\bar{a}{C_0}^3-210k_{7,0}a^2{C_0}^5-504k_{9,0}a^5 \bar{a}^3{C_0}-1260k_{9,0}a^4\bar{a}^2{C_0}^3-504k_{9,0}a^3\bar{a}{C_0}^5-36k_{9,0} a^2{C_0}^7-2310k_{11,0}a^6\bar{a}{C_0}-9240k_{11,0}a^5\bar{a}^3{C_0}^3-6930k_{11,0} a^4\bar{a}^2{C_0}^5-1320k_{11,0}a^3\bar{a}{C_0}^7-55k_{11,0}a^2{C_0}^9+30\mathrm{j}k_{6,1} {\tilde{\Omega }} a^4\bar{a}^2{C_0}+40\mathrm{j}k_{6,1}{\tilde{\Omega }} a^3\bar{a}{C_0}^3 +6\mathrm{j}k_{6,1}{\tilde{\Omega }} a^2{C_0}^5+112\mathrm{j}k_{8,1}{\tilde{\Omega }} a^5 \bar{a}^3{C_0}+280\mathrm{j}k_{8,1}{\tilde{\Omega }} a^4\bar{a}^2{C_0}^3+112\mathrm{j}k_{8,1} {\tilde{\Omega }} a^3\bar{a}{C_0}^5+8\mathrm{j}k_{8,1}{\tilde{\Omega }} a^2{C_0}^7 +420\mathrm{j}k_{10,1}{\tilde{\Omega }} a^6\bar{a}^4{C_0}+1680\mathrm{j}k_{10,1} {\tilde{\Omega }} a^5\bar{a}^3{C_0}^3+1260\mathrm{j}k_{10,1}{\tilde{\Omega }} a^4 \bar{a}^2{C_0}^5+240\mathrm{j}k_{10,1}{\tilde{\Omega }} a^3\bar{a}{C_0}^7+10\mathrm{j}k_{10,1} {\tilde{\Omega }} a^2{C_0}^9+2\mathrm{j}k_{2,1}{\tilde{\Omega }} a^2{C_0}+8\mathrm{j}k_{4,1} {\tilde{\Omega }} a^3\bar{a}{C_0}+4\mathrm{j}k_{4,1}{\tilde{\Omega }} a^2{C_0}^3+k_{1,2} {\tilde{\Omega }}^2 a^2{C_0}+k_{3,2}{\tilde{\Omega }}^2 a^2{C_0}^3-5k_{5,2} {\tilde{\Omega }}^2 a^4\bar{a}^2{C_0}+k_{5,2}{\tilde{\Omega }}^2 a^2{C_0}^5-128k_{7,2} {\tilde{\Omega }}^2 a^5\bar{a}^3{C_0}-35k_{7,2}{\tilde{\Omega }}^2 a^4\bar{a}^2{C_0}^3 +k_{7,2}{\tilde{\Omega }}^2 a^2{C_0}^7-126k_{9,2}{\tilde{\Omega }}^2 a^6\bar{a}^4{C_0} -336k_{9,2}{\tilde{\Omega }}^2 a^5\bar{a}^3{C_0}^3-126k_{9,2}{\tilde{\Omega }}^2 a^4 \bar{a}^2{C_0}^5+k_{9,2}{\tilde{\Omega }}^2 a^2{C_0}^9+4\mathrm{j}k_{2,3} {\tilde{\Omega }}^3 a^3\bar{a}{C_0}+12\mathrm{j}k_{4,3}{\tilde{\Omega }}^3 a^4\bar{a}^2{C_0} +8\mathrm{j}k_{4,3}{\tilde{\Omega }}^3 a^3\bar{a}{C_0}^3+36\mathrm{j}k_{6,3}{\tilde{\Omega }}^3 a^5\bar{a}^3{C_0}+60\mathrm{j}k_{6,3}{\tilde{\Omega }}^3 a^4\bar{a}^2{C_0}^3+12\mathrm{j}k_{6,3} {\tilde{\Omega }}^3 a^3\bar{a}{C_0}^5+112\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^6\bar{a}^4{C_0} +336\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^5\bar{a}^3{C_0}^3+168\mathrm{j}k_{8,3} {\tilde{\Omega }}^3 a^4\bar{a}^2{C_0}^5+16\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^3 \bar{a}{C_0}^7+4k_{1,4}{\tilde{\Omega }}^4 a^3\bar{a}{C_0}+3k_{3,4} {\tilde{\Omega }}^4 a^4\bar{a}^2{C_0}+4k_{3,4}{\tilde{\Omega }}^4 a^3\bar{a}{C_0}^3 +10k_{5,4}{\tilde{\Omega }}^4 a^4\bar{a}^2{C_0}^3+4k_{5,4}{\tilde{\Omega }}^4 a^3 \bar{a}{C_0}^5-14k_{7,4}{\tilde{\Omega }}^4 a^6\bar{a}^4{C_0}+21k_{7,4}{\tilde{\Omega }}^4 a^4\bar{a}^2{C_0}^5+4k_{7,4}{\tilde{\Omega }}^4 a^3\bar{a}{C_0}^7+10\mathrm{j}k_{2,5} {\tilde{\Omega }}^5 a^4\bar{a}^2{C_0}+24\mathrm{j}k_{4,5}{\tilde{\Omega }}^5 a^5 \bar{a}^3{C_0}+20\mathrm{j}k_{4,5}{\tilde{\Omega }}^5 a^4\bar{a}^2{C_0}^3+60\mathrm{j}k_{6,5} {\tilde{\Omega }}^5 a^6\bar{a}^4{C_0}+120\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^5 \bar{a}^3{C_0}^3+30\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^4\bar{a}^2{C_0}^5+15k_{1,6} {\tilde{\Omega }}^6 a^4\bar{a}^2{C_0}+12k_{3,6}{\tilde{\Omega }}^6 a^5\bar{a}^3{C_0} +12k_{3,6}{\tilde{\Omega }}^6 a^5\bar{a}^3{C_0}+15k_{3,6}{\tilde{\Omega }}^6 a^4 \bar{a}^2{C_0}^3+10k_{5,6}{\tilde{\Omega }}^6 a^6\bar{a}^4{C_0}+40k_{5,6} {\tilde{\Omega }}^6 a^5\bar{a}^3{C_0}^3+15k_{5,6}{\tilde{\Omega }}^6 a^4\bar{a}^2{C_0}^5 +28\mathrm{j}k_{2,7}{\tilde{\Omega }}^7 a^5\bar{a}^3{C_0}+56\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^6\bar{a}^4{C_0}+56\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^5\bar{a}^3{C_0}^3+56k_{1,8} {\tilde{\Omega }}^8 a^5\bar{a}^3{C_0}+42k_{3,8}{\tilde{\Omega }}^8 a^6\bar{a}^4{C_0} +56k_{3,8}{\tilde{\Omega }}^8 a^5\bar{a}^3{C_0}^3+84\mathrm{j}k_{2,9}{\tilde{\Omega }}^9 a^6\bar{a}^4{C_0}+210k_{1,10}{\tilde{\Omega }}^{10} a^6\bar{a}^4{C_0} ,$

$b_9=-k_{3,0}a^3-5k_{5,0}a^4\bar{a}-10k_{5,0}a^3{C_0}^2-21k_{7,0}a^5\bar{a}^2 -105k_{7,0}a^4\bar{a}{C_0}^2-35k_{7,0}a^3{C_0}^4-84k_{9,0}a^6\bar{a}^3-756k_{9,0} a^5\bar{a}^2{C_0}^2-630k_{9,0}a^4\bar{a}{C_0}^4-84k_{9,0}a^3{C_0}^6-330k_{11,0}a^7 \bar{a}^4-4620k_{11,0}a^6\bar{a}^3{C_0}^2-6930k_{11,0}a^5\bar{a}^2{C_0}^4-2310k_{11,0} a^4\bar{a}{C_0}^6-165k_{11,0}a^3{C_0}^8+9\mathrm{j}k_{6,1}{\tilde{\Omega }} a^5\bar{a}^2 +45\mathrm{j}k_{6,1}{\tilde{\Omega }} a^4\bar{a}{C_0}^2+15\mathrm{j}k_{6,1}{\tilde{\Omega }} a^3{C_0}^4+28\mathrm{j}k_{8,1}{\tilde{\Omega }} a^6\bar{a}^3+252\mathrm{j}k_{8,1}{\tilde{\Omega }} a^5\bar{a}^2{C_0}^2+210\mathrm{j}k_{8,1}{\tilde{\Omega }} a^4\bar{a}{C_0}^4+28\mathrm{j}k_{8,1} {\tilde{\Omega }} a^3{C_0}^6+90\mathrm{j}k_{10,1}{\tilde{\Omega }} a^7\bar{a}^4+1260\mathrm{j} k_{10,1}{\tilde{\Omega }} a^6\bar{a}^3{C_0}^2+1890\mathrm{j}k_{10,1}{\tilde{\Omega }} a^5 \bar{a}^2{C_0}^4+630\mathrm{j}k_{10,1}{\tilde{\Omega }} a^4\bar{a}{C_0}^6+45\mathrm{j}k_{10,1} {\tilde{\Omega }} a^3{C_0}^8+\mathrm{j}k_{2,1}{\tilde{\Omega }} a^3+3\mathrm{j}k_{4,1} {\tilde{\Omega }} a^4\bar{a}+6\mathrm{j}k_{4,1}{\tilde{\Omega }} a^3{C_0}^2+k_{1,2} {\tilde{\Omega }}^2 a^3+k_{3,2}{\tilde{\Omega }}^2 a^4 \bar{a}+3k_{3,2}{\tilde{\Omega }}^2 a^3{C_0}^2+k_{5,2}{\tilde{\Omega }}^2 a^5 \bar{a}^2+10k_{5,2}{\tilde{\Omega }}^2 a^4 \bar{a}{C_0}^2+5k_{5,2}{\tilde{\Omega }}^2 a^3 {C_0}^4+21k_{7,2}{\tilde{\Omega }}^2 a^5 \bar{a}^2{C_0}^2+35k_{7,2}{\tilde{\Omega }}^2 a^4 \bar{a}{C_0}^4+7k_{7,2} {\tilde{\Omega }}^2 a^3{C_0}^6-6k_{9,2}{\tilde{\Omega }}^2 a^7 \bar{a}^4+126k_{9,2} {\tilde{\Omega }}^2 a^5 \bar{a}^2{C_0}^4+84k_{9,2}{\tilde{\Omega }}^2 a^4 \bar{a}{C_0}^6 +9k_{9,2}{\tilde{\Omega }}^2 a^3 {C_0}^8-\mathrm{j}k_{0,3}{\tilde{\Omega }}^3 a^3+\mathrm{j} k_{2,3}{\tilde{\Omega }}^3 a^4\bar{a}-\mathrm{j}k_{2,3}{\tilde{\Omega }}^3 a^3{C_0}^2 +3\mathrm{j}k_{4,3}{\tilde{\Omega }}^3 a^5\bar{a}^2+6\mathrm{j}k_{4,3}{\tilde{\Omega }}^3 a^4\bar{a}{C_0}^2-\mathrm{j}k_{4,3}{\tilde{\Omega }}^3 a^3{C_0}^4+8\mathrm{j}k_{6,3} {\tilde{\Omega }}^3 a^6\bar{a}^3+45\mathrm{j}k_{6,3}{\tilde{\Omega }}^3 a^5\bar{a}^2{C_0}^2 +15\mathrm{j}k_{6,3}{\tilde{\Omega }}^3 a^4\bar{a}{C_0}^4-\mathrm{j}k_{6,3}{\tilde{\Omega }}^3 a^3{C_0}^6+22\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^7\bar{a}^4+224\mathrm{j}k_{8,3} {\tilde{\Omega }}^3 a^6\bar{a}^3{C_0}^2+210\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^5 \bar{a}^2{C_0}^4+28\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^4\bar{a}{C_0}^6-\mathrm{j}k_{8,3} {\tilde{\Omega }}^3 a^3{C_0}^8+3k_{1,4}{\tilde{\Omega }}^4 a^4\bar{a}+3k_{3,4} {\tilde{\Omega }}^4 a^5\bar{a}^2+9k_{3,4}{\tilde{\Omega }}^4 a^4\bar{a}{C_0}^2+4k_{5,4} {\tilde{\Omega }}^4 a^6\bar{a}^3+30k_{5,4}{\tilde{\Omega }}^4 a^5\bar{a}^2{C_0}^2+15k_{5,4} {\tilde{\Omega }}^4 a^4\bar{a}{C_0}^4+6k_{7,4}{\tilde{\Omega }}^4 a^7\bar{a}^4+84k_{7,4} {\tilde{\Omega }}^4 a^6\bar{a}^3{C_0}^2+105k_{7,4}{\tilde{\Omega }}^4 a^5\bar{a}^2{C_0}^4 +21k_{7,4}{\tilde{\Omega }}^4 a^4\bar{a}{C_0}^6-5\mathrm{j}k_{0,5}{\tilde{\Omega }}^5 a^4 \bar{a}+\mathrm{j}k_{2,5}{\tilde{\Omega }}^5 a^5\bar{a}^2-5\mathrm{j}k_{2,5}{\tilde{\Omega }}^5 a^4\bar{a}{C_0}^2+4\mathrm{j}k_{4,5}{\tilde{\Omega }}^5 a^6\bar{a}^3+6\mathrm{j}k_{4,5} {\tilde{\Omega }}^5 a^5\bar{a}^2{C_0}^2-5\mathrm{j}k_{4,5}{\tilde{\Omega }}^5 a^4\bar{a} {C_0}^4+10\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^7\bar{a}^4+60\mathrm{j}k_{6,5} {\tilde{\Omega }}^5 a^6\bar{a}^3{C_0}^2+15\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^5 \bar{a}^2{C_0}^4-5\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^4\bar{a}{C_0}^6+9k_{1,6} {\tilde{\Omega }}^6 a^5\bar{a}^2+8k_{3,6}{\tilde{\Omega }}^6 a^6\bar{a}^3+27k_{3,6} {\tilde{\Omega }}^6 a^5\bar{a}^2{C_0}^2+10k_{5,6}{\tilde{\Omega }}^6 a^7\bar{a}^4 +80k_{5,6}{\tilde{\Omega }}^6 a^6\bar{a}^3{C_0}^2+45k_{5,6}{\tilde{\Omega }}^6 a^5 \bar{a}^2{C_0}^4-21\mathrm{j}k_{0,7}{\tilde{\Omega }}^7 a^5\bar{a}^2-21\mathrm{j}k_{2,7} {\tilde{\Omega }}^7 a^5\bar{a}^2{C_0}^2+6\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^4-21\mathrm{j} k_{4,7}{\tilde{\Omega }}^7 a^5\bar{a}^2{C_0}^4+28k_{0,7}{\tilde{\Omega }}^8 a^6 \bar{a}^3+22k_{3,8}{\tilde{\Omega }}^8 a^7\bar{a}^4+84k_{3,8}{\tilde{\Omega }}^8 a^6\bar{a}^3{C_0}^2-84\mathrm{j}k_{0,9}{\tilde{\Omega }}^9 a^6\bar{a}^3-6\mathrm{j} k_{2,9}{\tilde{\Omega }}^9 a^7\bar{a}^4-84\mathrm{j}k_{2,9}{\tilde{\Omega }}^9 a^6 \bar{a}^3{C_0}^2+90k_{1,10}{\tilde{\Omega }}^{10} a^7\bar{a}^4-330\mathrm{j}k_{0,11} {\tilde{\Omega }}^{11} a^7\bar{a}^4 ,$

$b_{10}=-5k_{5,0}a^4C_0-42k_{7,0}a^5\bar{a}C_0-35k_{7,0}a^4{C_0}^3-252k_{9,0}a^6 \bar{a}^2C_0-504k_{9,0}a^5\bar{a}{C_0}^3-126k_{9,0}a^4{C_0}^5-1320k_{11,0}a^7 \bar{a}^3{C_0}-4620k_{11,0}a^6\bar{a}^2{C_0}^3-2772k_{11,0}a^5\bar{a}{C_0}^5-330 k_{11,0}a^4{C_0}^7+24\mathrm{j}k_{6,1}{\tilde{\Omega }} a^5\bar{a}{C_0}+20\mathrm{j}k_{6,1} {\tilde{\Omega }} a^4{C_0}^3+112\mathrm{j}k_{8,1}{\tilde{\Omega }} a^6\bar{a}^2{C_0} +224\mathrm{j}k_{8,1}{\tilde{\Omega }} a^5\bar{a} {C_0}^3+56\mathrm{j}k_{8,1}{\tilde{\Omega }} a^4{C_0}^5+480\mathrm{j}k_{10,1}{\tilde{\Omega }} a^7\bar{a}^3{C_0}+1680\mathrm{j}k_{10,1} {\tilde{\Omega }} a^6\bar{a}^2{C_0}^3+1008\mathrm{j}k_{10,1}{\tilde{\Omega }} a^5\bar{a} {C_0}^5+120\mathrm{j}k_{10,1}{\tilde{\Omega }} a^4{C_0}^7+4\mathrm{j}k_{4,1}{\tilde{\Omega }} a^4{C_0}+3k_{3,2}{\tilde{\Omega }}^2 a^4{C_0}+10k_{5,2}{\tilde{\Omega }}^2 a^5\bar{a} {C_0}+10k_{5,2}{\tilde{\Omega }}^2 a^4 {C_0}^3+28k_{7,2}{\tilde{\Omega }}^2 a^6\bar{a}^2 {C_0}+70k_{7,2}{\tilde{\Omega }}^2 a^5\bar{a} {C_0}^3+21k_{7,2}{\tilde{\Omega }}^2 a^4 {C_0}^5+72k_{9,2}{\tilde{\Omega }}^2 a^7\bar{a}^3 {C_0}+336k_{9,2}{\tilde{\Omega }}^2 a^6\bar{a}^2 {C_0}^3+252k_{9,2}{\tilde{\Omega }}^2 a^5\bar{a} {C_0}^5+36k_{9,2} {\tilde{\Omega }}^2 a^4 {C_0}^7-2\mathrm{j}k_{2,3}{\tilde{\Omega }}^3 a^4{C_0}-4\mathrm{j} k_{4,3}{\tilde{\Omega }}^3 a^4{C_0}^3+12\mathrm{j}k_{6,3}{\tilde{\Omega }}^3 a^6 \bar{a}^2 {C_0}-6\mathrm{j}k_{6,3}{\tilde{\Omega }}^3 a^4 {C_0}^5+64\mathrm{j}k_{8,3} {\tilde{\Omega }}^3 a^7 \bar{a}^3 {C_0}+112\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^6 \bar{a}^2 {C_0}^3-8\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^4 {C_0}^7-k_{1,4} {\tilde{\Omega }}^4 a^4 {C_0}+6k_{3,4}{\tilde{\Omega }}^4 a^5 \bar{a} {C_0}-k_{3,4} {\tilde{\Omega }}^4 a^4 {C_0}^3+20k_{5,4}{\tilde{\Omega }}^4 a^6 \bar{a}^2 {C_0} +20k_{5,4}{\tilde{\Omega }}^4 a^5 \bar{a} {C_0}^3-k_{5,4}{\tilde{\Omega }}^4 a^4 {C_0}^5+56k_{7,4}{\tilde{\Omega }}^4 a^7 \bar{a}^3 {C_0}+140k_{7,4}{\tilde{\Omega }}^4 a^6 \bar{a}^2 {C_0}^3+42k_{7,4}{\tilde{\Omega }}^4 a^5 \bar{a} {C_0}^5-k_{7,4} {\tilde{\Omega }}^4 a^4 {C_0}^7-8\mathrm{j}k_{2,5}{\tilde{\Omega }}^5 a^5 \bar{a}{C_0} -8\mathrm{j}k_{4,5}{\tilde{\Omega }}^5 a^6 \bar{a}^2 {C_0}-16\mathrm{j}k_{4,5}{\tilde{\Omega }}^5 a^5 \bar{a} {C_0}^3-40\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^6 \bar{a}^2 {C_0}^3-24\mathrm{j} k_{6,5}{\tilde{\Omega }}^5 a^5 \bar{a} {C_0}^5-6k_{1,6}{\tilde{\Omega }}^6 a^6 \bar{a} {C_0}+12k_{3,6}{\tilde{\Omega }}^6 a^6 \bar{a}^2 {C_0}-6k_{3,6}{\tilde{\Omega }}^6 a^5 \bar{a} {C_0}^3+40k_{5,6}{\tilde{\Omega }}^6 a^5 \bar{a} {C_0}^3+40k_{5,6} {\tilde{\Omega }}^6 a^7 \bar{a}^3 {C_0}+40k_{5,6}{\tilde{\Omega }}^6 a^6 \bar{a}^2 {C_0}^3-6k_{5,6}{\tilde{\Omega }}^6 a^5 \bar{a} {C_0}^5-28\mathrm{j}k_{2,7} {\tilde{\Omega }}^7 a^6 \bar{a}^2 {C_0}-32\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^7 \bar{a}^3 {C_0}-56\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^6 \bar{a}^2 {C_0}^3-28k_{1,8} {\tilde{\Omega }}^8 a^6 \bar{a}^2 {C_0}+24k_{3,8}{\tilde{\Omega }}^8 a^7 \bar{a}^3 {C_0}-28k_{3,8}{\tilde{\Omega }}^8 a^6 \bar{a}^2 {C_0}^3-96\mathrm{j}k_{2,9}{\tilde{\Omega }}^9 a^7 \bar{a}^3 {C_0}-120k_{1,10}{\tilde{\Omega }}^{10} a^7 \bar{a}^3 {C_0} ,$

$b_{11}=-k_{5,0}a^5-7k_{7,0}a^6\bar{a}-21k_{7,0}a^5{C_0}^2-36k_{9,0}a^7\bar{a}^2-252 k_{9,0}a^6\bar{a}{C_0}^2-126k_{9,0}a^5{C_0}^4-165k_{11,0}a^8\bar{a}^3-1980k_{11,0}a^7 \bar{a}^2{C_0}^2-2310k_{11,0}a^6\bar{a}{C_0}^4-462k_{11,0}a^5{C_0}^6+5\mathrm{j}k_{6,1} a^6 \bar{a}+15\mathrm{j}k_{6,1}{\tilde{\Omega }} a^5 {C_0}^2+20\mathrm{j}k_{8,1}{\tilde{\Omega }} a^7 \bar{a}^2+140\mathrm{j}k_{8,1} a^6 \bar{a} {C_0}^2+70\mathrm{j}k_{8,1}{\tilde{\Omega }} a^5 {C_0}^4+75\mathrm{j}k_{10,1}{\tilde{\Omega }} a^8 \bar{a}^3 +900\mathrm{j}k_{10,1} {\tilde{\mathrm{\Omega }}} a^7 \bar{a}^2 {C_0}^2+1050\mathrm{j}k_{10,1}{\tilde{\Omega }} a^6 \bar{a}^2 {C_0}^4+210\mathrm{j}k_{10,1}{\tilde{\Omega }} a^5 {C_0}^6+\mathrm{j}k_{4,1} {\tilde{\Omega }} a^5+k_{3,2}{\tilde{\Omega }}^2 a^5+3k_{5,2}{\tilde{\Omega }}^2 a^6 \bar{a} +10k_{5,2}{\tilde{\Omega }}^2 a^5 {C_0}^2+8k_{7,2}{\tilde{\Omega }}^2 a^7 \bar{a}^2+63k_{7,2}{\tilde{\Omega }}^2 a^6 \bar{a} {C_0}^2+35k_{7,2}{\tilde{\Omega }}^2 a^5 {C_0}^4+21k_{9,2}{\tilde{\Omega }}^2 a^8 \bar{a}^3+288k_{9,2}{\tilde{\Omega }}^2 a^7 \bar{a}^2 {C_0}^2+378k_{9,2}{\tilde{\Omega }}^2 a^6 \bar{a} {C_0}^4+84k_{9,2} {\tilde{\Omega }}^2 a^5 {C_0}^6-\mathrm{j}k_{2,3}{\tilde{\Omega }}^3 a^5-\mathrm{j}k_{4,3} {\tilde{\Omega }}^3 a^6 \bar{a} -6\mathrm{j}k_{4,3} {\tilde{\Omega }}^3 a^5 {C_0}^2-15\mathrm{j} k_{6,3} {\tilde{\Omega }}^3 a^6 \bar{a} {C_0}^2-15\mathrm{j}k_{6,3} {\tilde{\Omega }}^3 a^5 {C_0}^4+5\mathrm{j}k_{8,3} {\tilde{\Omega }}^3 a^8 \bar{a}^3-70\mathrm{j}k_{8,3} {\tilde{\Omega }}^3 a^6 \bar{a} {C_0}^4-28\mathrm{j}k_{8,3} {\tilde{\Omega }}^3 a^5 {C_0}^6-k_{1,4}{\tilde{\Omega }}^4 a^5+k_{3,4}{\tilde{\Omega }}^4 a^6 \bar{a}-3k_{3,4} {\tilde{\Omega }}^4 a^5 {C_0}^2+4k_{5,4}{\tilde{\Omega }}^4 a^7 \bar{a}^2+10k_{5,4} {\tilde{\Omega }}^4 a^6 \bar{a}{C_0}^2-5k_{5,4}{\tilde{\Omega }}^4 a^5 {C_0}^4+11k_{7,4} {\tilde{\Omega }}^4 a^8 \bar{a}^3+84k_{7,4}{\tilde{\Omega }}^4 a^7 \bar{a}^2{C_0}^2 +35k_{7,4}{\tilde{\Omega }}^4 a^6 \bar{a}{C_0}^4-7k_{7,4}{\tilde{\Omega }}^4 a^5 {C_0}^6 +\mathrm{j}k_{0,5} {\tilde{\Omega }}^5 a^5-3\mathrm{j}k_{2,5} {\tilde{\Omega }}^5 a^6\bar{a} +\mathrm{j}k_{2,5} {\tilde{\Omega }}^5 a^5{C_0}^2-4\mathrm{j}k_{4,5} {\tilde{\Omega }}^5 a^7 \bar{a}^2-18\mathrm{j}k_{4,5} {\tilde{\Omega }}^5 a^6\bar{a}{C_0}^2+\mathrm{j}k_{4,5} {\tilde{\Omega }}^5 a^5{C_0}^4-5\mathrm{j}k_{6,5} {\tilde{\Omega }}^5 a^8\bar{a}^3-60 \mathrm{j}k_{6,5} {\tilde{\Omega }}^5 a^7\bar{a}^2{C_0}^2-45\mathrm{j}k_{6,5} {\tilde{\Omega }}^5 a^6\bar{a}{C_0}^4+\mathrm{j}k_{6,5} {\tilde{\Omega }}^5 a^5{C_0}^6-5k_{1,6} {\tilde{\Omega }}^6 a^6\bar{a}-15k_{3,6} {\tilde{\Omega }}^6 a^6\bar{a}{C_0}^2+5k_{5,6} {\tilde{\Omega }}^6 a^8\bar{a}^3-25k_{5,6} {\tilde{\Omega }}^6 a^6\bar{a}{C_0}^4 +7\mathrm{j}k_{0,7} {\tilde{\Omega }}^7 a^6\bar{a}-8\mathrm{j}k_{2,7} {\tilde{\Omega }}^7 a^7\bar{a}^2+7\mathrm{j}k_{2,7} {\tilde{\Omega }}^7 a^6\bar{a}{C_0}^2-11\mathrm{j}k_{4,7} {\tilde{\Omega }}^7 a^8\bar{a}^3-48\mathrm{j}k_{4,7} {\tilde{\Omega }}^7 a^7\bar{a}^2{C_0}^2 +7\mathrm{j}k_{4,7} {\tilde{\Omega }}^7 a^6\bar{a}{C_0}^4-20k_{1,8} {\tilde{\Omega }}^8 a^7 \bar{a}^2-5k_{3,8} {\tilde{\Omega }}^8 a^8\bar{a}^3-60k_{3,8} {\tilde{\Omega }}^8 a^7 \bar{a}^2{C_0}^2+36\mathrm{j}k_{0,9} {\tilde{\Omega }}^9 a^7\bar{a}^2-21\mathrm{j}k_{2,9} {\tilde{\Omega }}^9 a^8\bar{a}^3+36\mathrm{j}k_{2,9} {\tilde{\Omega }}^9 a^7\bar{a}^2{C_0}^2 -75k_{1,10} {\tilde{\Omega }}^{10} a^8\bar{a}^3+165\mathrm{j}k_{0,11} {\tilde{\Omega }}^{11} a^8\bar{a}^3 ,$

$b_{12}=-7k_{7,0}a^6{C_0}-72k_{9,0}a^7\bar{a}{C_0}-84k_{9,0}a^6{C_0}^3-495k_{11,0} a^8\bar{a}^2{C_0}-1320k_{11,0}a^7\bar{a}{C_0}^3-462k_{11,0}a^6{C_0}^5+6\mathrm{j}k_{6,1} {\tilde{\Omega }} a^6{C_0}+48\mathrm{j}k_{8,1}{\tilde{\Omega }} a^7\bar{a}{C_0}+56\mathrm{j}k_{8,1} {\tilde{\Omega }} a^6{C_0}^3+270\mathrm{j}k_{10,1}{\tilde{\Omega }} a^8\bar{a}^2{C_0}+720\mathrm{j} k_{10,1}{\tilde{\Omega }} a^7\bar{a}{C_0}^3+252\mathrm{j}k_{10,1}{\tilde{\Omega }} a^6{C_0}^5 +5k_{5,2}{\tilde{\Omega }}^2 a^6{C_0}+28k_{7,2}{\tilde{\Omega }}^2 a^7\bar{a}{C_0}+35k_{7,2} {\tilde{\Omega }}^2 a^6{C_0}^3+117k_{9,2}{\tilde{\Omega }}^2 a^8\bar{a}^2{C_0}+336k_{9,2} {\tilde{\Omega }}^2 a^7\bar{a}{C_0}^3+126k_{9,2}{\tilde{\Omega }}^2 a^6{C_0}^5-4\mathrm{j}k_{4,3} {\tilde{\Omega }}^3 a^6{C_0}-12\mathrm{j}k_{6,3}{\tilde{\Omega }}^3 a^7\bar{a}{C_0}-20\mathrm{j} k_{6,3}{\tilde{\Omega }}^3 a^6{C_0}^3-24\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^8\bar{a}^2{C_0} -112\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^7\bar{a}{C_0}^3-56\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^6{C_0}^5-3k_{3,4}{\tilde{\Omega }}^4 a^6\bar{a}{C_0}-10k_{5,4}{\tilde{\Omega }}^4 a^6{C_0}^3 +21k_{7,4}{\tilde{\Omega }}^4 a^8\bar{a}^2{C_0}-21k_{7,4}{\tilde{\Omega }}^4 a^6{C_0}^5 +2\mathrm{j}k_{2,5}{\tilde{\Omega }}^5 a^6{C_0}-8\mathrm{j}k_{4,5}{\tilde{\Omega }}^5 a^7 \bar{a}{C_0}+4\mathrm{j}k_{4,5}{\tilde{\Omega }}^5 a^6{C_0}^3-30\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^8\bar{a}^2{C_0}-40\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^7\bar{a}{C_0}^3+6\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^6\bar{a}^6{C_0}^5+k_{1,6}{\tilde{\Omega }}^6 a^6{C_0}-12k_{3,6}{\tilde{\Omega }}^6 a^7\bar{a}{C_0}+k_{5,6}{\tilde{\Omega }}^6 a^6{C_0}^3-15k_{5,6}{\tilde{\Omega }}^6 a^8\bar{a}^2-40k_{5,6}{\tilde{\Omega }}^6 a^7\bar{a}{C_0}^3+k_{5,6}{\tilde{\Omega }}^6 a^6{C_0}^5+12\mathrm{j}k_{2,7}{\tilde{\Omega }}^7 a^7\bar{a}{C_0}-12\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^8\bar{a}^2{C_0}+24\mathrm{j}k_{4,7}\tilde{\Omega }^7 a^7\bar{a}{C_0}^3+8k_{1,8}\tilde{\Omega }^8 a^7\bar{a}{C_0}-39k_{3,8}{\tilde{\Omega }}^8 a^8\bar{a}^2{C_0}+8k_{3,8}{\tilde{\Omega }}^8 a^7\bar{a}{C_0}^3+54\mathrm{j}k_{2,9}{\tilde{\Omega }}^9 a^8\bar{a}^2{C_0}+45k_{1,10}{\tilde{\Omega }}^{10} a^8\bar{a}^2{C_0} ,$

$b_{13}=-k_{7,0}a^7-9k_{9,0}a^8\bar{a}-36k_{9,0}a^7{C_0}^2-55k_{11,0}a^9\bar{a}^2 -495k_{11,0}a^8\bar{a}{C_0}^2-330k_{11,0}a^7{C_0}^4+\mathrm{j}k_{6,1}{\tilde{\Omega }} a^7+7\mathrm{j}k_{8,1}{\tilde{\Omega }} a^8\bar{a}+28\mathrm{j}k_{8,1}{\tilde{\Omega }} a^7{C_0}^2+35\mathrm{j}k_{10,1}{\tilde{\Omega }} a^9\bar{a}^2+315\mathrm{j}k_{10,1}{\tilde{\Omega }} a^8\bar{a}{C_0}^2+210\mathrm{j}k_{10,1}{\tilde{\Omega }} a^7{C_0}^4+k_{5,2}{\tilde{\Omega }}^2a^7+5k_{7,2}{\tilde{\Omega }}^2 a^8\bar{a}+210k_{7,2}{\tilde{\Omega }}^2 a^7{C_0}^2+19k_{9,2}{\tilde{\Omega }}^2 a^9\bar{a}^2+180k_{9,2}{\tilde{\Omega }}^2 a^8\bar{a}{C_0}^2+126k_{9,2}{\tilde{\Omega }}^2 a^7{C_0}^4-\mathrm{j}k_{4,3}{\tilde{\Omega }}^3 a^7-3\mathrm{j}k_{6,3}{\tilde{\Omega }}^3 a^8 \bar{a}-15\mathrm{j}k_{6,3}{\tilde{\Omega }}^3 a^7 {C_0}^2-7\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^9 \bar{a}^2-84\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^8 \bar{a}{C_0}^2-70\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^7 {C_0}^4-k_{3,4}{\tilde{\Omega }}^4 a^7-k_{5,4}{\tilde{\Omega }}^4 a^8\bar{a}-10k_{5,4}{\tilde{\Omega }}^4 a^7{C_0}^2+k_{7,4}{\tilde{\Omega }}^4 a^9\bar{a}^2-21k_{7,4}{\tilde{\Omega }}^4 a^8\bar{a}{C_0}^2-35k_{7,4}{\tilde{\Omega }}^4 a^7{C_0}^4+\mathrm{j}k_{2,5}{\tilde{\Omega }}^5 a^7 -\mathrm{j}k_{4,5}{\tilde{\Omega }}^5 a^8 \bar{a} +6\mathrm{j}k_{4,5}{\tilde{\Omega }}^5 a^7 {C_0}^2-5\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^9 \bar{a}^2-15\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^8 \bar{a} {C_0}^2+15\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^7 {C_0}^4+k_{1,6}{\tilde{\Omega }}^6 a^7-3k_{3,6}{\tilde{\Omega }}^6 a^8 \bar{a}+3k_{3,6}{\tilde{\Omega }}^6 a^7 {C_0}^2+5k_{5,6}{\tilde{\Omega }}^6 a^9 \bar{a}^2-30k_{5,6}{\tilde{\Omega }}^6 a^8 \bar{a} {C_0}^2+5k_{5,6}{\tilde{\Omega }}^6 a^7 {C_0}^4-\mathrm{j}k_{0,7}{\tilde{\Omega }}^7 a^7+5\mathrm{j}k_{2,7}{\tilde{\Omega }}^7 a^8 \bar{a}-\mathrm{j}k_{2,7}{\tilde{\Omega }}^7 a^7{C_0}^2+\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^9 \bar{a}^2+30\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^8 \bar{a} {C_0}^2-\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^7 {C_0}^4+7k_{1,8}{\tilde{\Omega }}^8 a^8 \bar{a}-7k_{3,8}{\tilde{\Omega }}^8 a^9 \bar{a}^2+21k_{3,8}{\tilde{\Omega }}^8 a^8 \bar{a} {C_0}^2-9\mathrm{j}k_{0,9}{\tilde{\Omega }}^9 a^8 \bar{a}+19\mathrm{j}k_{2,9}{\tilde{\Omega }}^9 a^9 \bar{a}^2-9\mathrm{j}k_{2,9}{\tilde{\Omega }}^9 a^8 \bar{a} {C_0}^2+35k_{1,10}{\tilde{\Omega }}^{10} a^9 \bar{a}^2-55\mathrm{j}k_{0,11}{\tilde{\Omega }}^{11} a^9 \bar{a}^2 ,$

$b_{14}=-9k_{9,0}a^8{C_0}-110k_{11,0}a^8\bar{a}{C_0}-165k_{11,0}a^8{C_0}^3+8\mathrm{j}k_{8,1}{\tilde{\Omega }} a^8{C_0}+80\mathrm{j}k_{10,1}{\tilde{\Omega }} a^9 \bar{a}{C_0}+120\mathrm{j}k_{10,1}{\tilde{\Omega }} a^8 {C_0}^3+7k_{7,2}{\tilde{\Omega }}^2 a^8{C_0}+54k_{9,2}{\tilde{\Omega }}^2 a^9 \bar{a}{C_0}+84k_{9,2}{\tilde{\Omega }}^2 a^8 {C_0}^3-6\mathrm{j}k_{6,3}{\tilde{\Omega }}^3 a^8 {C_0}-32\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^9 \bar{a}{C_0}-56\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^8 {C_0}^3-5k_{5,4}{\tilde{\Omega }}^4 a^8{C_0}-14k_{7,4}{\tilde{\Omega }}^4 a^9 \bar{a}{C_0}-35k_{7,4}{\tilde{\Omega }}^4 a^8{C_0}^3+4\mathrm{j}k_{4,5}{\tilde{\Omega }}^5 a^8{C_0}+20\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^8{C_0}^3+3k_{3,6}{\tilde{\Omega }}^6 a^8{C_0}-10k_{5,6}{\tilde{\Omega }}^6 a^9 \bar{a}{C_0}+10k_{5,6}{\tilde{\Omega }}^6 a^8 {C_0}^3-2\mathrm{j}k_{2,7}{\tilde{\Omega }}^7 a^8{C_0}+16\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^9\bar{a}{C_0}-4\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^8{C_0}^3-k_{1,8}{\tilde{\Omega }}^8 a^8{C_0}+18k_{3,8}{\tilde{\Omega }}^8 a^9\bar{a}{C_0}-k_{3,8}{\tilde{\Omega }}^8 a^8{C_0}^3-16\mathrm{j}k_{2,9}{\tilde{\Omega }}^9 a^9\bar{a}{C_0}-10k_{1,10}{\tilde{\Omega }}^{10} a^9\bar{a}{C_0} ,$

$b_{15}=-k_{9,0}a^9-11k_{11,0}a^{10}\bar{a}-55k_{11,0}a^9{C_0}^2+\mathrm{j}k_{8,1}{\tilde{\Omega }} a^9+9\mathrm{j}k_{10,1}{\tilde{\Omega }} a^{10} \bar{a}+45\mathrm{j}k_{10,1}{\tilde{\Omega }} a^9{C_0}^2+k_{7,2}{\tilde{\Omega }}^2 a^9+7k_{9,2}{\tilde{\Omega }}^2 a^{10}\bar{a}+36k_{9,2}{\tilde{\Omega }}^2 a^9{C_0}^2-\mathrm{j}k_{6,3}{\tilde{\Omega }}^3 a^9-5\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^{10} \bar{a}-28\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^9{C_0}^2-k_{5,4}{\tilde{\Omega }}^4 a^9-3k_{7,4}{\tilde{\Omega }}^4 a^{10} \bar{a}-21k_{7,4}{\tilde{\Omega }}^4 a^9 {C_0}^2+\mathrm{j}k_{4,5}{\tilde{\Omega }}^5 a^9+\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^{10}\bar{a}+15\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^9{C_0}^2+k_{3,6}{\tilde{\Omega }}^6 a^9-k_{5,6}{\tilde{\Omega }}^6 a^{10}\bar{a}+k_{5,6}{\tilde{\Omega }}^6 a^9{C_0}^2-\mathrm{j}k_{2,7}{\tilde{\Omega }}^7 a^9+3k_{4,7}{\tilde{\Omega }}^7 a^{10}\bar{a}-6\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^9{C_0}^2-k_{1,8}{\tilde{\Omega }}^8 a^9+5k_{3,8}{\tilde{\Omega }}^8 a^{10}\bar{a}-3k_{3,8}{\tilde{\mathrm{\Omega }}}^8 a^9{C_0}^2+\mathrm{j}k_{0,9}{\tilde{\Omega }}^9 a^9-7\mathrm{j}k_{2,9}{\tilde{\Omega }}^9 a^{10}\bar{a}+\mathrm{j}k_{2,9}{\tilde{\Omega }}^9 a^9{C_0}^2-9k_{1,10}{\tilde{\Omega }}^{10} a^{10}\bar{a}+11\mathrm{j}k_{0,11}{\tilde{\Omega }}^{11} a^{10}\bar{a} ,$

$b_{16}=-11k_{11,0}a^{10}{C_0}+10\mathrm{j}k_{10,1}{\tilde{\Omega }} a^{10}{C_0}+9k_{9,2}{\tilde{\Omega }}^2 a^{10}{C_0}-8\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^{10}{C_0}^3-7k_{7,4}{\tilde{\Omega }}^4 a^{10}{C_0}+6\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^{10}{C_0}+5k_{5,6}{\tilde{\Omega }}^6 a^{10}{C_0}-4\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^{10}{C_0}-3k_{3,8}\tilde{\Omega }^8 a^{10}{C_0}+2\mathrm{j}k_{2,9}\tilde{\Omega }^9 a^{10}{C_0}+k_{1,10}\tilde{\Omega }^{10} a^{10}{C_0} ,$

$b_{17}=-k_{11,0}a^{11}+\mathrm{j}k_{10,1}{\tilde{\Omega }} a^{11}+k_{9,2}{\tilde{\Omega }}^2 a^{11}-\mathrm{j}k_{8,3}{\tilde{\Omega }}^3 a^{11}-k_{7,4}{\tilde{\Omega }}^4 a^{11}+\mathrm{j}k_{6,5}{\tilde{\Omega }}^5 a^{11}+k_{5,6}{\tilde{\Omega }}^6 a^{11}-\mathrm{j}k_{4,7}{\tilde{\Omega }}^7 a^{11}-k_{3,8}{\tilde{\Omega }}^8 a^{11}+\mathrm{j}k_{2,9}{\tilde{\Omega }}^9 a^{11}+\mathrm{j}k_{1,10}{\tilde{\Omega }}^{10} a^{11}-\mathrm{j}k_{0,11}{\tilde{\Omega }}^{11}a^{11} .$

Appendix C

In Eq. (20),

$\tilde{F_f}\left( \xi _1,\xi _2\right) = k_{1,0}\xi _2 + k_{3,0}{{\xi _2}^3} + k_{5,0}{{\xi _2}^5} + k_{7,0}{{\xi _2}^7} + k_{9,0}{{\xi _2}^9} + k_{11,0}{{\xi _2}^{11}} + k_{0,1}\xi _1 + k_{2,1}{{\xi _2}^2}\xi _1 + k_{4,1}{{\xi _2}^4}\xi _1 + k_{6,1}{{\xi _2}^6}\xi _1 + k_{8,1}{{\xi _2}^8}\xi _1 + k_{10,1}{{\xi _2}^{10}}\xi _1 + k_{1,2}{\xi _2}{{\xi _1}^2} + k_{3,2}{{\xi _2}^3}{{\xi _1}^2} + k_{5,2}{{\xi _2}^5}{{\xi _1}^2} + k_{7,2}{{\xi _2}^7}{{\xi _1}^2}+ k_{9,2}{{\xi _2}^9}{{\xi _1}^2} + k_{0,3}{{\xi _1}^3} + k_{2,3}{{\xi _2}^2}{{\xi _1}^3} + k_{4,3}{{\xi _2}^4}{{\xi _1}^3} + k_{6,3}{{\xi _2}^6}{{\xi _1}^3} + k_{8,3}{{\xi _2}^8}{{\xi _1}^3} + k_{1,4}{\xi _2}{{\xi _1}^4} + k_{3,4}{{\xi _2}^3}{{\xi _1}^4} + k_{5,4}{{\xi _2}^5}{{\xi _1}^4} + k_{7,4}{{\xi _2}^7}{{\xi _1}^4} + k_{0,5}{{\xi _1}^5} + k_{2,5}{{\xi _2}^2}{{\xi _1}^5} + k_{4,5}{{\xi _2}^4}{{\xi _1}^5} + k_{6,5}{{\xi _2}^6}{{\xi _1}^5} + k_{1,6}{\xi _2}{{\xi _1}^6} + k_{3,6}{{\xi _2}^3}{{\xi _1}^6} + k_{5,6}{{\xi _2}^5}{{\xi _1}^6} + k_{0,7}{{\xi _1}^7} + k_{2,7}{{\xi _2}^2}{{\xi _1}^7} + k_{4,7}{{\xi _2}^4}{{\xi _1}^7} + k_{1,8}{\xi _2}{{\xi _1}^8} + k_{3,8}{{\xi _2}^3}{{\xi _1}^8} + k_{0,9}{{\xi _1}^9} + k_{2,9}{{\xi _2}^2}{{\xi _1}^9} + k_{1,10}{\xi _2}{{\xi _1}^{10}} + k_{0,11}{{\xi _1}^{11}} .$