Dynamic simulation and experimental study of an asymmetric double-disk rotor-bearing system with rub-impact and oil-film instability

Abstract

This study deals with numerical analysis and experimental investigations where the nonlinear dynamic behaviors of an asymmetric double-disk rotor-bearing system are reproduced considering rub-impact and oil-film instability. A dedicated experimental setup was designed to validate the interaction between rubs and oil-film vibration. A model considering nonlinear rub-impact forces and nonlinear oil-film forces is put forward to analyze the complicated nonlinear vibrations of the rotor-bearing system. The experimental study focuses on the interaction of oil-whirl/whip and rub-impact faults, and the results show that the oil-whirl is restrained or even removed, but the whip is uninfluenced when the rub becomes heavy contact. The numerical simulation focuses on the effect of eccentricity and the stator stiffness on the onset of instability and nonlinear responses of the rotor-bearing system by using bifurcation diagrams, Poincaré maps, frequency spectrum and three-dimension spectral plots. Agreeing with the experimental results, the results from simulation indicate that the motion of system becomes simple and the oil-whirl gets diminished or even disappeared, but the whip keeps unchanged when the eccentricity or the stator stiffness increases. The research discloses the worthy energy exchange phenomenon of multi-fault system and presents the nonlinear dynamical characteristics of the interaction between rub-impact and oil-film instability for such a rotor-bearing system.

1 Introduction

Studies of the characteristics of rotor-bearing systems are necessary in the design of rotating systems and their industrial applications, and for the diagnosis of system malfunctions. The safe operation of turbo-machine is threatened by danger situations such as oil-film instability and rub-impact. The occurrence of rotor lateral self-excited vibration known as “whirl,” “whip” or “instability” arises from the presence of nonlinear fluid. The instability would induce excessive vibration at the first- or second-mode whirl/whip frequency, and it would contribute to unstable operation of the system, high-level vibration and potential damage of the rotating machinery [1]. The oil-whirl is a kind of self-exciting movement that vibrates at a frequency close to half of the rotation speed. When the rotation speed reaches twice the first natural frequency, the self-excited vibration frequency remains constant and close to the first resonance frequency. The new behavior is the oil-whip instability. Oil-whip instability, in particular, can be seriously harmful to the rotor-bearing system. The rubbing impact is a movement that vibrates at multi-frequency of the rotation speed. The rub-impact is one of the common nonlinear faults in rotor systems and can bring a serious hazard to machines. Under many circumstances, the rub-impact usually results from excessive vibration caused by other faults in practical rotor systems, such as imbalance, rotor crack and oil-film instability. In modern industry, the machinery is becoming more precise, and the faults of these machineries are also becoming more complicated. The multiple or coupled faults such as oil-whirl and rubs often occur at the same time. The rotor-bearing model with nonlinear oil-film forces should also takes the nonlinear rub-impact forces into account, and the relevant multi-fault experiment should not be neglected.

Many literature reported the typical nonlinear vibration phenomena caused by oil-film instability, such as sub-harmonic and super-harmonic vibration. Adiletta et al. [2] studied the chaotic motions of a rigid rotor in short journal bearings. Diken [3] presented the nonlinear vibration analysis and sub-harmonic whirl frequencies of the Jeffcott rotor mode. Jing et al. [4] considered the nonlinear model proposed by Capone to analyze the nonlinear dynamic behavior of bearings, taking into account the oil-whip phenomenon. Boedo [5] reported the extensive numerical simulation studies with a short-bearing film model, which showed that a balanced dual offset rotor can improve bearing. Wang et al. [6] analyzed the bifurcation behavior of a flexible rotor supported by two fluid-film journal bearing. Whirl and whip instabilities were studied in rotor-bearing system considering a nonlinear force model [7]. Zhang and Xu [8] proposed an effective model for unsteady oil-film force to express time-varying boundaries of the film that whirled rapidly around the journal center. Chen and Yau [9] studied chaotic behavior of a flexible rotor supported by oil-film bearings with nonlinear suspension by using the long-bearing approximation. There are also experimental works to verify the theory model by using different forms of test rigs. By a test rig, Fan et al. [10] investigated the phenomena in start-up vibration responses and presented a method for predicting instabilities of rotor systems in the coexistence of oil-whip and dry whip. Zhou et al. [11] reported an experimental method to recognize these coefficients and establish their characteristics under varieties of operating conditions. EI-Shafei et al. [12] studied the onset of instability on a flexible rotor mounted on two plain cylindrical journal bearings and analyzed the influence of rotor imbalance, oil pressure and misalignment to the initial instability speed. Experiment was observed on fault detection for a direct coupled rotor-bearing system [13]. The nonlinear dynamic behaviors of a rotor-bearing coupled system were reported in simulation and experiment [14].

The dynamics of rotor-to-stator contact dynamics have been studied extensively in the past by many researches. Muszynska [15] presented a comprehensive literary survey on rub-related phenomena. In the 1990, a great deal of work treated the nonlinear analysis on rotor-to-stator contact dynamics. Studies on these rubbing phenomena revealed that the rotating system showed a rich class of nonlinear related dynamics such as sub- and super-synchronous responses, quasi-periodic responses and even chaotic motions. Lankarani and Nikravesh [16] suggested a contact force model with hysteresis damping to analyze the impact of multi-body system. Goldman and Muszynska [17] reported that the chaotic motion in a nonlinear study is more likely to occur if a proper impact model is employed. Chu and Zhang [18] investigated the nonlinear vibration characteristics of a rub-impact Jeffcott rotor. They also found that when the rotating speed is increased, the grazing bifurcation, the quasi-periodic motion and chaotic motion occur after the rub-impact. Abu-Mahfouz and Banerjee [19] used numerical analysis and evolutionary algorithms to analyze the nonlinear dynamics of a rotor with rub-impact. The dynamic model of a disk-drum-shaft rotor system with rub-impact is established, and its dynamic characteristics are analyzed [20]. Flores [21] reported the numerical and experimental investigation on multi-body systems with revolute clearance joints. Lahriri and Santos [22, 23] conducted the experimental quantification of contact forces and theoretical analysis of rub-impact rotor-bearing system. The study [24] performed a dynamic analysis of the rub-impact rotor supported by two couple stress fluid-film journal bearings, and the strong nonlinear couple stress fluid-film force, nonlinear rub-impact force and nonlinear suspension (hard spring) are presented and coupled together.

Of the existing work, numerous studies are often more focused on the numerical simulation of nonlinearity than on the dynamical behavior of real rotating machinery, but some researchers [24–26] have thrown light to nonlinear coupled or interaction dynamics considering different forces or different influences, but little researchers [27–29] have been carried out on nonlinear coupled dynamics of an asymmetric double-disk rotor-bearing system considering rub-impact and oil-film forces. The studies on interaction between rub-impact and oil-film instability are still not enough either in numerical analysis or in experimental results. Thus, some new attempt will be presented in this paper. In order to observe the physical phenomena of rub-impact and oil-film instability, the experiments were performed, while the theoretical predictions were done for verifying the results from tests. The Bently test rig has been used allowing for oil-whirl, oil-whip and rub-impact on some operating conditions, and it could reveal some valuable vibration characteristics of the rotor-bearing system, sub-serving the fault diagnostics for rotating machinery. Numeral results reveal a nonlinear dynamic process including periodic, quasi-periodic, multi-periodic and almost-periodic, which agree with results from experimental study.

2 Description of the experimental equipment

The experimental tests of oil-film whirl and rub-impact were performed on the Bently test rig which has been employed for several researched in the fields of rotor dynamics (see Cheng et al. [14] and Cong et al. [30]). The experimental test facility is designed to measure the rotor dynamic characteristic under a series of conditions, such as rotating speed, eccentricity and stator stiffness. These experimental results can be used to validate the result from numerical simulation.

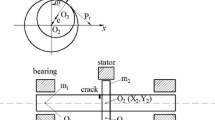
The workbench is an oil-fluid supporting rotor-bearing system (see Fig. 1). An electrical motor is attached to the shaft that carries two disks by a flexible coupling. The first natural frequency of the rotor system is approximately 31 Hz. The oil-film journal bearing is part of an assembly connected to the oil pump assembly, as shown in Fig. 2. A key-phase sensor closed to the coupling is fixed to measure the rotating speed. The bearing is equipped with two proximity probes in the horizontal and vertical directions. Probes, located near each bearing and near the contact position, measure the shaft vibrations in vertical and horizontal direction. In order to preferably simulate the real process of the rub, we have designed a special setup that can make it possible to perform a safe and reliable contact experiment, as shown in Fig. 3. The rub-impact force occurs and increases by tightening the rubbing copper bar at a constant rotor speed for every experiment.

Fig. 1

Picture of Bently test rig

Fig. 2

Experimental test map

Fig. 3

View of the rub-impact stator

3 Mathematical model

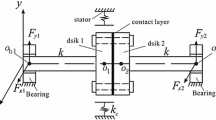
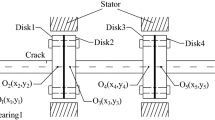
The model of rotor-bearing system consists of two disks at point B and C and a massless shaft mounted by two oil-film journal bearings at each end (point A and D), as shown in Fig. 1. The two disks have a lumped mass $m_2$ and $m_3$, while the two bearings take lumped mass $m_1$ and $m_4$. The influence of torsional vibration, shear deformation and gyroscopic couple is all neglected in order to highlight the effect of oil-film force.

3.1 Nonlinear oil-film force

Considering the nonlinear oil-film force model, a dynamic model is established using short-bearing theory [2]. The nondimensional Reynolds equation and nondimensional oil-film force components $\overline{fx}$ and $\overline{fy}$ can be written as

$$\begin{aligned}&\left( {\frac{R}{L}} \right) ^{2}\frac{\partial }{\partial \mathrm{Z}}\left( {h^{3}\frac{\partial p}{\partial \mathrm{Z}}} \right) =x\sin \theta -y\cos \theta \nonumber \\&\quad -2\left( x^{{\prime }}\cos \theta +y^{{\prime }}\sin \theta \right) \nonumber \\&\left\{ {\begin{array}{l} f_X =\sigma \bar{{f}}_x ; \\ f_Y =\sigma \bar{{f}}_y \\ \end{array}} \right. \nonumber \\&\sigma =\mu \omega RL\left( {\frac{R}{C}} \right) ^{2}\left( {\frac{L}{2R}} \right) ^{2} \nonumber \\&\left[ {{\begin{array}{l} {\bar{{f}}_x } \\ {\bar{{f}}_y } \\ \end{array} }} \right] =-\frac{\left[ {\left( {x-2\dot{y}} \right) ^{2}+\left( {x+2\dot{x}} \right) ^{2}} \right] ^{1/2}}{1-x^{2}-y^{2}}\nonumber \\&\quad \times \left[ {\begin{array}{l} 3xV\left( {x,y,\alpha } \right) \!-\!\sin \alpha G\left( {x,y,\alpha } \right) \!-\!2\cos \alpha S\left( {x,y,\alpha } \right) \\ 3xV\left( {x,y,\alpha } \right) \!+\!\hbox {cos}\alpha G\left( {x,y,\alpha } \right) \!-\!2\hbox {sin}\alpha S\left( {x,y,\alpha } \right) \\ \end{array}} \right] \nonumber \\ \end{aligned}$$

(1)

where R is the radius of bearing. C is the bearing radial clearance, $\mu$ is the lubricating oil viscosity described, and L is the length of bearing.

The nondimensional parameters are introduced as below

$$\begin{aligned}&\alpha \!=\!\arctan \frac{y\!+\!2\dot{x}}{x-2\dot{y}}\!-\!\frac{\pi }{2}\sin \left( {\frac{y\!+\!2\dot{x}}{x-2\dot{y}}} \right) \!-\!\frac{\pi }{2}\sin \left( {y\!+\!2\dot{x}} \right) \nonumber \\&V\left( {x,y,\alpha } \right) =\frac{2+\left( {y\cos \alpha -x\sin \alpha } \right) G\left( {x,y,\alpha } \right) }{1-x^{2}-y^{2}} \nonumber \\&G\left( {x,y,\alpha } \right) =\frac{2}{\left( 1-x^{2}-y^{2}\right) ^{1/2}}\nonumber \\&\quad \times \left[ {\frac{\pi }{2}+\arctan \frac{y\cos \alpha -x\sin \alpha }{1-x^{2}-y^{2}}} \right] \nonumber \\&S\left( {x,y,\alpha } \right) =\frac{x\cos \alpha +y\sin \alpha }{1-\left( {x\cos \alpha +y\sin \alpha } \right) ^{2}} \end{aligned}$$

(2)

3.2 Nonlinear rub-impact force

The rub-impact model of this rotor-bearing system is shown in Fig. 4. It is assumed that the rub-impact occurs with a Hertz contact and a Coulomb friction. The striking force $F_N$ is represented following linear elastic deformation theory. The frictional force $F_T$ is brought up by Coulomb law.

$$\begin{aligned} F_N= & {} \left\{ {{\begin{array}{ll} 0,&{} \quad {(r<\delta )} \\ {(r-\delta )K_c },&{} \quad {(r\ge \delta )} \\ \end{array} }}\right. \nonumber \\ F_T= & {} fF_N \end{aligned}$$

(3)

where $\delta$ is the clearance between rotor and stator, r is the displacement of shaft center in radial direction and $r=\sqrt{x^{2}+y^{2}}$.

Fig. 4

Rotor-bearing system with two asymmetric disks

The equations of rub-impact force in x and y direction are formulated as follows,

(4)

3.3 Model of rotor-bearing system

The model of rotor-bearing system from test rig is shown in Fig. 4. The mathematical model based on rotor dynamics theory is established in Eq. (5)

$$\begin{aligned}&\hbox {M}\ddot{\hbox {Z}}+C\dot{\hbox {Z}}+\hbox {KZ}=\hbox {F}_\mathrm{o} +\hbox {F}_\mathrm{e} +\hbox {F}_\mathrm{g} +\hbox {F}_\mathrm{p} \nonumber \\&\hbox {F}_\mathrm{o}, \hbox {F}_\mathrm{e}, \hbox {F}_\mathrm{g}, \hbox {F}_\mathrm{p} \in C^{4} \end{aligned}$$

(5)

where M,C,K are mass, damping and stiffness matrix.

Matrix $\hbox {Z}=\hbox {[Z}_{1}, \hbox {Z}_{2} ,\hbox {Z}_{3}, \hbox {Z}_{4} ]^{\mathrm{T}}\in C^{4}\left( \hbox {Z}_\mathrm{i} =x_i +jy_i \right)$ is the displacement matrix corresponding to each mass. The damping coefficient of the ith mass is $c_i$.

$$\begin{aligned} \hbox {M}= & {} {\hbox {diaf}}[m_i ](i=1,2,3,4)\\ \hbox {C}= & {} {\hbox {diag}}[c_i ](i=1,2,3,4) \end{aligned}$$

The stiffness matrix is:

$$\begin{aligned} \hbox {K}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {k_{1} }&{} {-k_{1} }&{} &{} \\ {-k_{1} }&{} {k_{1} +k_2 }&{} {-k_2 }&{} \\ &{} {-k_2 }&{} {k_2 +k_3 }&{} {-k_3 } \\ &{} &{} {-k_3 }&{} {k_3 } \\ \end{array} }} \right] \end{aligned}$$

(6)

The stiffness of each axis according to structural relationships of plane beam is as follows: The stiffness of support axis in both ends is $k_i =3EI_i /l_i ^{3},i=1,3$, and the stiffness of middle axis is $k_i =12EI_i /l_i ^{3},i=2$. $I_i$ is the section inertia of that axis, and the symbol $l_i$ is the length of each axis.

$$\begin{aligned} I_i =\frac{\pi d_i^4 }{64}\quad (i=1,2,3) \end{aligned}$$

(7)

where $d_i$ is the diameter of section in each axis. Notations $F_o ,F_e ,F_g ,F_p \in C^{4}$ are the plural oil-film force, plural unbalance, plural gravity and plural rub-impact force matrix:

$$\begin{aligned} \hbox {F}_\mathrm{o}= & {} \left[ F_{\mathrm{o1}} {\begin{array}{ccc} 0&{} 0&{} {F_{{\mathrm{O}4}} } \\ \end{array} }\right] ^{\hbox {T}}\nonumber \\ \hbox {F}_\mathrm{p}= & {} \left[ {{\begin{array}{cccc} 0&{} {F_{p2} }&{} {F_{p3} }&{} 0 \\ \end{array} }} \right] ^{\hbox {T}} \nonumber \\ \hbox {F}_\mathrm{e}= & {} \left[ {\begin{array}{cccc} 0&{} {F_{ex} }&{} {F_{ey} }&{} 0 \\ \end{array} }\right] ^{\hbox {T}} \nonumber \\ \hbox {F}_\mathrm{g}= & {} -jg\left[ {\begin{array}{cccc} {m_1 }&{} {m_2 }&{} {m_3 }&{} {m_4 } \\ \end{array} }\right] ^{\hbox {T}} \end{aligned}$$

(8)

The unbalanced eccentric force is:

$$\begin{aligned} \left[ {{\begin{array}{lll} {F_{\hbox {exi}} } \\ {F_{\hbox {eyi}} } \\ \end{array} }} \right] =\left[ {{\begin{array}{c} {m_i b_i \omega _r ^{2}\cos \left( \omega _r t+\varphi _i \right) } \\ {m_i b_i \omega _r ^{2}\sin \left( \omega _r t+\varphi _i \right) } \\ \end{array} }} \right] ,\quad i=2,3 \end{aligned}$$

(9)

where $b_2$ and $b_3$ are the mass eccentricity of disks.

The nondimensional equation for Eq. (5) is displayed in Eq. (10)

$$\begin{aligned}&\ddot{x}_1 +\frac{c_1 }{m_1 \omega }\dot{x}_1 +\frac{k_1 }{m_1 }(x_1 -x_2 )=-\frac{f_{X1} }{m_1 C\omega ^{2}} \nonumber \\&\ddot{y}_1 +\frac{c_1 }{m_1 \omega }\dot{y}_1 +\frac{k_1 }{m_1 }(y_1 -y_2 )=-\frac{f_{Y1} }{m_1 C\omega ^{2}}-\frac{g}{C\omega ^{2}} \nonumber \\&\ddot{x}_2 +\frac{c_2 }{m_2 \omega }\dot{x}_2 +\frac{k_1 }{m_2 }(x_2 -x_1 )-\frac{k_2 }{m_2 }(x_3 -x_2 )\nonumber \\&\quad =\frac{F_{x2} }{m_2 C\omega ^{2}}+\frac{b_2 }{C}\cos t \nonumber \\&\ddot{y}_2 +\frac{c_2 }{m_2 \omega }\dot{y}_2 +\frac{k_1 }{m_2 }(y_2 -y_1 )-\frac{k_2 }{m_2 }(y_3 -y_2 )\nonumber \\&\quad =\frac{F_{y2} }{m_2 C\omega ^{2}}+\frac{b_2 }{C}\sin t-\frac{g}{C\omega ^{2}} \nonumber \\&\ddot{x}_3 +\frac{c_3 }{m_3 \omega }\dot{x}_3 -\frac{k_2 }{m_3 }(x_2 -x_3 )-\frac{k_3 }{m_3 }(x_4 -x_3 )\nonumber \\&\quad =\frac{F_{x3} }{m_3 C\omega ^{2}}+\frac{b_3 }{C}\cos t\nonumber \\&\ddot{y}_3 +\frac{c_3 }{m_3 \omega }\dot{y}_3 -\frac{k_2 }{m_3 }(y_2 -y_3 )-\frac{k_3 }{m_3 }(y_4 -y_3 )\nonumber \\&\quad =\frac{F_{y3} }{m_3 C\omega ^{2}}+\frac{b_3 }{C}\sin t-\frac{g}{C\omega ^{2}} \nonumber \\&\ddot{x}_4 +\frac{c_4 }{m_4 \omega }\dot{x}_4 -\frac{k_3 }{m_4 }(x_3 -x_4 )=\frac{F_{x4} }{m_4 C\omega ^{2}}\nonumber \\&\ddot{y}_4 +\frac{c_4 }{m_4 \omega }\dot{y}_4 -\frac{k_3 }{m_4 }(y_3 -y_4 )=\frac{F_{y4} }{m_4 C\omega ^{2}}-\frac{g}{C\omega ^{2}} \end{aligned}$$

(10)

4 Analysis of experimental results

Since oil-whirl/whip and rubbing are nonlinear phenomena, the experimental results cannot be the same at every time. In this respect, several experiments for a setup need to confirm a peculiar physical phenomenon. Through these several experiments, the vibration signal can be manifested. In the case, tests were carried out several times in order to ensure a “repeatability” of the experimental results. After rigging up the workbench, experiments were carried out under different conditions. Results obtained during the rundown will be shown in terms of shaft orbits, contact duration, rotational speed variation and time–frequency spectrum. Orbit amplitudes in present vibration are obtained, which are the interacting results of oil-whirl/whip and rub-impact faults.

4.1 Case of light oil-whirl

Light oil-whirl conditions are generated when the rotating speed approaches to the first-order critical speed 1900 r/min. The experimental data are collected when the rotating speed stays at 1800 r/min after an accelerating process. Thus, a light oil-whirl vibration occurs in the rotor-bearing system. The rub-impact force is enlarged by tightening the rubbing copper bar when the time is at 26.81 s. When the rub-impact force increases, vibration displacements of shaft center become obviously smaller. A sudden heavy impulse is exerted on the disk, so the motion of the system has changed and is developed as shown in Fig. 5. Figure 6a, b shows the orbit and frequency spectrum of the system motion in the range of [10–15] s, and Fig. 6c, d shows those plots in the range of [30–35] s. From Fig. 6c, it is indicated that the shaft orbit is concave after increasing the rub-impact force, but the orbit is elliptical in lighter rubbing (see Fig. 6a).

Table 1 The simulated model parameters of rotor-bearing system

Fig. 5

Experiment at 1800 r/min: time series x-motion

Fig. 6

Experiment at 1800 r/min: a trajectories of the center of the disk within light rub, b frequency spectrum x-motion within light rub c trajectories of the center of the disk within heavy rub, b frequency spectrum x-motion within heavy rub

The rotating speed frequency is 30 Hz, and the oil-whirl frequency is approximately half of rotating speed frequency (shown in Figs. 6b, 7). From Figs. 6d and 7, a special phenomenon can be seen that the oil-whirl frequency disappears and rub-impact frequencies (multi-fundamental frequency) arise. The results indicate that the rotor system will have different motions and will present energy exchange phenomenon in interaction of multi-fault vibration.

Fig. 7

Experiment at 1800 r/min: time–frequency distribution

4.2 Case of medium oil-whirl

The system vibration will intensify with the rotating speed increasing. The experimental data are collected when the rotating speed stays at 2000 r/min after an accelerating process. Thus, a medium oil-whirl vibration appears in the rotor-bearing system. The rub-impact force is enlarged by tightening the rubbing copper bar when the time is at 26.81 s. When the rub-impact force increases, vibration displacements of shaft center become obviously, as shown in Fig. 8. Before heavy rub, the vibration includes two main frequencies, which are the oil-whirl frequency 16 Hz and the rotating speed frequency 33.2 Hz, as shown in Fig. 9b. Figure 9a shows that the orbit is elliptical, but it becomes toughly concave as shown in Fig. 9c. From Figs. 9d and 10, a special phenomenon can also be seen that the oil-whirl frequency disappears and rub-impact frequencies (multi-fundamental frequency) arise. The results also indicate that the rotor system has transformed the energy and presented different motion in interaction of multi-fault vibration.

Fig. 8

Experiment at 2000 r/min: time series x-motion

Fig. 9

Experiment at 2000 r/min: a trajectories of the center of the disk within light rub, b frequency spectrum x-motion within light rub, c trajectories of the center of the disk within heavy rub, b frequency spectrum x-motion within heavy rub

Fig. 10

Experiment at 2000 r/min: time–frequency distribution

4.3 Case of oil-whip

The oil-whip will occur, and its frequency equals the first natural frequency, when the rotating speed reaches or exceeds double critical speed of system. Figure 11 shows the waveform of the oil-whip vibration with rotating speed 4000 r/min. Figure 12a, b shows the orbit and frequency spectrum of the system motion in the range of [10–15] s, and Fig. 13c, d shows those plots in the range of [30–35] s. The amplitude of the oil-whip vibration (see Fig. 11) is significantly larger than that of the oil-whirl vibration, compared with Figs. 5 and 8. In this condition, the oil-whip frequency (31.33 Hz) is less than half of fundamental frequency (66.66 Hz), and the amplitude of oil-whip vibration overtops that of the fundamental vibration (see Fig. 12b). Now the system has a frequency-locked phenomenon, and the oil-whip occupied most of energy. After the rub-impact force is intensified at time 21.3 s, the orbit and time series have unchanged (see Figs. 11, 12a, c), but the amplitude of oil-whip has been decreased (see Fig. 12b, d). The time–frequency distribution (Fig. 13) also reveals the motion of the rotor-bearing system.

Fig. 11

Experiment at 4000 r/min: time series x-motion

Fig. 12

Experiment at 4000 r/min: a trajectories of the center of the disk within light rub, b frequency spectrum x-motion within light rub, c trajectories of the center of the disk within heavy rub, b frequency spectrum x-motion within heavy rub

Fig. 13

Experiment at 4000 r/min: time–frequency distribution

The experimental study demonstrates that the friction contact force can influence on the oil-film instability. Energy exchanging occurs in the process of the rub-impact force increasing, and the rotor-bearing system presents different nonlinear dynamical characteristics. The eccentricity of shaft can make the rub-impact force have a change, and the stiffness of the stator can also change the level of the rubs. Therefore, the two parameters are used in simulation of the rotor-bearing system as following.

5 Modeling and simulation results

The model of the test rig has been developed to analyze the dynamical behavior as displayed in Fig. 4. The fourth-order Runge–Kutta formula is used to solve the numerical Eq. (5) for a steady data analysis. The system parameters associated are defined in Table 1, and they can be systematically changed in different conditions. To illuminate the numerical results, lots of plots are used to display, such as time series, shaft orbit, Poincare maps, frequency spectrum and cascade spectrum.

In the following, all the simulation analyses are based on the rotating speed. The two parameters (eccentricity and stiffness) are used in simulation of the rotor-bearing system.

5.1 Influence of varying eccentricity

The bifurcation diagram of rotor-bearing system is shown in Fig. 14 at the eccentricity $b_3 =0.1$ with $\omega$ as control parameter. All the parameters are taken from Table 1. The rotor-bearing system is found to display a rich diversity of responses with very intricate dynamics. The dynamic motion of this system is synchronous with period one (P1) before $\omega =418$ rad/s. The period two (P2) is observed at $\omega$ = [418–520] rad/s. It takes the general form

Fig. 14

Bifurcation diagram at $b_3 =0.1$ mm and $K_c =7\times 10^{6}N\cdot m^{-1}$

$\{\hbox {P}4\rightarrow \hbox {P}8{\ldots }\hbox {chaos}\rightarrow \hbox {P}8\rightarrow \hbox {P}4\rightarrow \hbox {P}2\}$ as the rotating speed is varied between the values $[520\rightarrow 865]$ rad/s. The classic oil-whirl shaft orbit turns up in Fig. 15 at $\omega =650$ rad/s. The half-frequency amplitude almost equals the amplitude of fundamental frequency. And there are continuous frequency bands on the frequency spectrum. Two strange attractors appear in Poincare map. Hence, the system is caught in chaos. The system motion is entering quasi-periodic motion seen in the Poincare map. And the quasi-periodic motion is undergoing when $\omega =1400$ rad/s is deduced by the Poincare map in Fig. 16. There are distinct “beat” signals in time series. The amplitude of oil-whip frequency is considerably larger than that of fundamental frequency. Corresponding with the bifurcation in Fig. 14, Fig. 17 reveals the whole vibration journey of system. The oil-whirl frequency appears at $\omega =450$ rad/s, increases as half of fundamental frequency and turns into oil-whip frequency (f0) at $\omega =1000$ rad/s. Meanwhile, the rub-impact gets stronger.

Fig. 15

Time series, shaft orbit, frequency spectrum and Poincare map at $\omega =650$ rad/s

Fig. 16

Time series, shaft orbit, frequency spectrum and Poincare map at $\omega =1400$ rad/s

Fig. 17

Cascade spectrum of rotor-bearing system at $b_3=0.1$ mm and $K_c =7\times 10^{6}N\cdot m^{-1}$

Figure 18 represents the bifurcation diagram with a bigger eccentricity ($b_3 =0.2$ mm), compared with Fig. 14 $(b_3 =0.1$ mm). In this case, the responses of this system exhibit simpler dynamic phenomena. The system takes a series of motions $\{\hbox {P}1\rightarrow \hbox {Pn}\rightarrow \hbox {P}2\rightarrow \hbox {P}3\rightarrow \hbox {P}1\rightarrow \hbox {quasiperiod}\rightarrow \hbox {chaos}\}$. Larger imbalance force may simplify the system motion at the same rotating speed. The dynamic response undergoes synchronous vibration with period one until $\omega =634$ rad/s (see Fig. 18). When the $\omega$ = [634–1000] rad/s, oil-whirl arises with a small value and the motion is multiple periodic (see Fig. 19). The system experiences period one motion at $\omega$ = [1000–1240] with only rub-impact. After the oil-whip occurs, the system vibrations go through quasi-periodic and chaotic motion (see Fig. 20). The frequency components of oil-whip are uninfluenced, but the frequency components of oil-whirl are restrained when the imbalance force increases. In this circumstance, the frequency components of rub-impact exist in all way (shown in Fig. 21).

Fig. 18

Bifurcation diagram at $b_3 =0.2$ mm

Fig. 19

Time series, shaft orbit, frequency spectrum and Poincare map at $\omega =700$ rad/s

Fig. 20

Time series, shaft orbit, frequency spectra and Poincare map at $\omega =1400$ rad/s

Fig. 21

Cascade spectrum of rotor-bearing system at $b_3 =0.2$ mm

The eccentricity further adds to 0.3 mm. It reveals a more brief vibration curve in the bifurcation diagram (see Fig. 22). Neither oil-whirl nor oil-whip comes up until $\omega =1312$ rad/s. It shows a typical Hopf bifurcation at $\omega =1312$ rad/s and oil-whip takes place later, and the system motion becomes quasi-periodic. Figure 23 shows oil-whip has appeared at $\omega =1400$ with the system entering quasi-periodic motion. The cascade spectrum in Fig. 24 shows that the oil-whirl frequency disappeared after enlarging the eccentricity, and there are only fundamental frequency fr and rub-impact frequency when $\omega \le 1312$ rad/s. The oil-whip appears later and occupies most energy of this system.

Fig. 22

Bifurcation diagram at $b_3 =0.3$ mm

Fig. 23

Time series, shaft orbit, frequency spectra and Poincare map at $\omega =1400$ rad/s

Fig. 24

Cascade spectrum of rotor-bearing system at $b_3 =0.3$ mm

5.2 Influence of varying stator stiffness

The stator stiffness, which is directly proportional to rub-impact force shown in Eq. (4), plays a significant role in dynamic analysis of rub-impact rotor system. Bifurcation diagram for stator stiffness parameter $K_c =9\times 10^{6}N\cdot m^{-1}$ is shown in Fig. 25. The nonlinear motion components have become less than $K_c =7\times 10^{6}N\cdot m^{-1}$ in Fig. 14. From Fig. 25, it can be seen that the system experiences a vibration journey as $\{\hbox {P}1\rightarrow \hbox {P}2\rightarrow \hbox {P}1\rightarrow \hbox {quasiperiod}\rightarrow \hbox {P}1\rightarrow \hbox {chaos}\rightarrow \hbox {quasiperiod}\}$. Period two exists at $\omega$  = [721–941] rad/s, while slight oil-whirl has been in system. Figure 26 shows the waveform, shaft orbit, frequency spectrum and Poincare map of the system at $\omega =800$ rad/s. The system goes into chaos at $\omega =1400$ rad/s by a strange attractor in the Poincare map shown in Fig. 27, and the oil-whip frequency emerges in the frequency spectrum. But its amplitude gets diminished, compared with that in a less stiffness as shown in Fig. 16. The cascade spectrum of system as shown in Fig. 28 demonstrates that oil-whirl frequency range decreases at larger stator stiffness, but the oil-whip frequency does not change.

Fig. 25

Bifurcation diagram at $K_c =9\times 10^{6}N\cdot m^{-1}$

Fig. 26

Time series, shaft orbit, frequency spectrum and Poincare map at $\omega =800$ rad/s

Fig. 27

Time series, shaft orbit, frequency spectrum and Poincare map at $\omega =1400$ rad/s

Fig. 28

Cascade spectrum of rotor-bearing system at $K_c =9\times 10^{6}N\cdot m^{-1}$

Fig. 29

Bifurcation diagram at $K_c =1.1\times 10^{7}N\cdot m^{-1}$

Fig. 30

Time series, shaft orbit, frequency spectrum and Poincare map at $\omega =1550$ rad/s

Fig. 31

Time series, shaft orbit, frequency spectrum and Poincare map at $\omega =1700$ rad/s

Fig. 32

Cascade spectrum of rotor-bearing system at $K_c =9\times 10^{6}N\cdot m^{-1}$

To further discover the dynamical influence of the stator stiffness to coupled system, the stator stiffness is added to $K_c =1.1\times 10^{7}N\cdot m^{-1}$, and the bifurcation of system is displayed in Fig. 29. The nonlinear behaviors get simpler than that the stator stiffness takes two less values before. Analyzing all the characteristic plots Figs. 29, 30, 31 and 32 synthetically, it can be found that the system motion goes through a process $\{\hbox {P}1\rightarrow \hbox {quasi-period}\rightarrow \hbox {P}1\rightarrow \hbox {quasi-period}\}$. The oil-whirl motion does not occur. The oil-whip frequency comes out about at $\omega =1350$ rad/s and keeps a uniform value when $\omega \ge 1350$ rad/s (see Fig. 32). Rub-impact frequencies get higher amplitude with this bigger stator stiffness.

The above results from the simulation declare that the bigger eccentricity in limited value may keep the stability of the system. Some special phenomenon has occurred that the oil-whirl gets diminished or even disappeared with the eccentricity and stator stiffness increasing, but the oil-whip is uninfluenced. The numerical analysis also shows that the nonlinear dynamic behavior of the system varies with the rotational speed and model parameters.

6 Conclusion

The emphasis of this paper was twofold: to assess the correlation between the responses from the theoretical model and the experiments for the rotor-bearing system, and to focus on the interaction between nonlinear rub-impact and oil-film instability.

To do so, an experimental setup and a numerical model were performed to investigate the responses of a multi-fault rotor-bearing system. The dedicated experimental workbench is accepted to be competent to reproduce the rub-impact and oil-film instability phenomena which may happen in real rotating machinery. Three different tests, including light oil-whirl, medium oil-film whirl and oil-film whip, were conducted on the workbench. The rub-impact force could be adjusted in the rubbing copper bar. A nonlinear model was formulated to explore the coupled behaviors of the asymmetric double-disk rotor-bearing system with interaction between rub-impact and oil-film force. Various observation and dynamic behaviors of system obtained from experiments and numerical analysis can be concluded as follows:

• (1) The multi-fault vibration of rotor-bearing system with two asymmetric disks revealed abundant nonlinear behaviors, consisted of the characteristics of oil-whirl, oil-whip and rub-impact. The system’s responses presented sub-harmonic, multiple periodic, quasi-periodic and chaotic motions and showed frequency lock, phase lock and some special phenomena.

• (2) In the process of the experiment, the contact could be changed by tightening the rubbing copper bar, so the rubbing force can be controlled and increased. The results from experimental study indicated that the oil-whirl was restrained or even removed, but the whip was uninfluenced when the rub became heavy contact.

• (3) The eccentricity and the stator stiffness affected the vibration and instability of the system with varied rotating speed. In conclusion, when the value of the eccentricity or the stator stiffness increases, the motion of system also becomes simple and the oil-whirl gets weak or even removed, but the oil-whip is uninfluenced, while the two parameters represent unbalance force and rub-impact force, respectively. The results of the numerical simulation agree with those of the experiment, which indicate that the fault forces are interacted and the system with different faults may have energy exchange phenomena and self-healed ability.