1 Introduction

Rotating shafts are used for power transmission in many modern machines. Accurate prediction of stability and post-critical behavior of rotating shafts are necessary for a successful design. Bolotin [1] analyzed the vibration of a rotating shaft considering geometric stiffening effect. Yamamoto et al. [2] considered the combination resonances in a symmetrical rotating shaft system with nonlinear spring characteristics. The theoretical results were validated with experiments. Using the Hopf bifurcation theory, Kurnik [3] analyzed self-excited vibrations of a rotating geometrically nonlinear shaft caused by internal friction. Shaw and Shaw [4] analyzed stability and bifurcations of an extensional rotating shaft made of a viscoelastic material. They included the effects of large transverse displacements and external sources of dissipations. In addition, they examined the forced vibration of a rotating shaft with internal damping [5]. They used the center manifold approach and showed that the resonance is an example of a periodically perturbed Hopf bifurcation. Dynamics and instability of an extensional rotating shaft-disk with large transverse displacement were analyzed by Chang and Cheng [6]. They used the center manifold theory to examine the bifurcation of the double zero eigenvalue point on the stability boundaries. Ishida and Yamamoto [7] considered the forced vibrations of a rotating shaft with nonlinear restoring force and internal damping. They examined the 1/2 order subharmonic oscillations of forward and backward whirling modes. They showed that a self-excited oscillation occurs in a wide range above the major critical speeds. To validate the theoretical results, they carried out experiments using an elastic rotating shaft with a disc. Noah and Sundararajan [8] considered the works about nonlinear rotor dynamics up to 1995 and their relevance to the design, analysis, and monitoring of rotating machinery. They discussed available analytical/computational methods and various reduction techniques. Ishida et al. [9] discussed the nonlinear forced oscillations of a rotor with distributed mass. The geometric nonlinearity in the rotor was due to the extension of the rotor center-line. They showed that the primary resonances curve is of a hard spring type and only some kinds of combination resonances may occur. Kurnik [10] analyzed the stability and self-excited postcritical whirling of a rotating shaft with the aid of bifurcation theory. The shaft was made of a material with elastic and viscous nonlinearities. He derived the equations of motion by neglecting rotary inertia, gyroscopic forces and effects of Von-Karman nonlinearity, but he considered the geometric curvature nonlinearity. The vibrations of the spinning rotor with nonlinear elastic and geometric properties were considered by Cveticanin [11]. The method of multiple scales was applied to analyze the free and forced vibration of nonlinear rotor-bearing systems by Ji and Zu [12]. The rotating shaft was described by the Timoshenko beam theory. They used a nonlinear spring and linear damping to model the nonlinear bearing pedestal. A geometrically nonlinear model of a rotating shaft was introduced by Luczko [13]. The model included Von-Karman nonlinearity, nonlinear curvature effects, large displacements and rotations as well as gyroscopic and shear effects. To solve the system, he used Galerkin and continuation methods and analyzed the internal resonances by this model. The dynamic analysis of a rotor shaft system with nonlinear elastic bearings mounted on a viscoelastic suspension was analyzed by Shabaneh and Zu [14]. Ji and Leung [15] examined the superharmonic resonances of a rotating shaft with nonlinear magnetic forces. It was shown that the stability of superharmonic periodic solutions was lost by saddle-node or Hopf bifurcations. Ishida and Inoue [16] used a Jeffcott rotor to examine nonlinear phenomena and internal resonances in one, two, and three times of the major critical speed. They showed theoretically and experimentally that the almost periodic motions could occur. They concluded that the use of the Jeffcott model in nonlinear analysis of rotor systems might lead to incorrect results. Nonlinear bearing pedestal was modeled by a cubic nonlinear spring and linear damper. The viscoelastic supports were modeled by the Kelvin–Voigt model. Viana Serra Villa et al. [17] used the invariant manifold approach to explore the dynamics of a nonlinear rotor. They constructed a reduced order model with the aid of nonlinear normal modes and evaluated its performance. Cveticanin [18] considered the free vibration of a Jeffcott rotor with cubic nonlinear elastic property. He applied the Krylov–Bogolubov method to solve the nonlinear equations of motion. Wang and Wang [19] studied the nonlinear vibration and bifurcation of a rigid rotor supported by relative short aerodynamic journal bearings. They showed that the response of a rotor was composed of periodic and subharmonic motions. Dimentberg [20] investigated the random vibration of a simple Jeffcott rotor with both external and internal damping. He assumed that the coefficient of internal damping had temporal random variations. The Krylov–Bogoliubov averaging method was applied to the complex equation of motion. Shahgholi and Khadem [21] studied the nonlinear vibrations of an asymmetrical rotating shaft with unequal mass moments of inertia. They considered both harmonic and parametric resonances. Wang and Wang [22] studied the bifurcation and nonlinear dynamic behaviors of a rigid rotor supported by a noncircular aerodynamic journal bearing system. They used a hybrid numerical method to calculate pressure distribution of the bearing and rotor orbits. Han and Chu [23] investigated the parametric instability of a Jeffcott rotor with asymmetric disk and open transverse crack using a four degrees-of-freedom system.

We considered the dynamic behavior of an in-extensional rotating shaft with nonlinear curvature and inertia in the following papers: free vibrations [24], primary resonances [25], and combination resonances [26, 27]. Perturbation methods were applied to analyze the system and only external damping was considered as a dissipating mechanism.

The present paper is continuation of our previous works [24–27]. The effect of internal damping was neglected in the above articles and the shaft was always stable. The instability and post-critical behavior of a nonlinear in-extensional viscoelastic rotating shaft have yet not been considered in the literatures and in this article we will study this problem. Here, stability and bifurcations in a simply supported rotating shaft are investigated. The shaft is modeled as an in-extensional spinning beam with large amplitude, which includes the effects of nonlinear curvature and inertia. To include the internal damping, it is assumed that the shaft is made of a viscoelastic material modeled as the Kelvin–Voigt model. In addition, the torsional stiffness and external damping of the shaft are considered. Using these assumptions, with the aid of Hamilton principle, the equations of motion are derived. Applying single-mode Galerkin method, two coupled differential equations of motion in two transverse planes are obtained. To find the boundaries of stability, the linearized equations of motion are used. Following Shaw and Shaw [4], the bifurcations considered here are Hopf and double zero eigenvalues. Using center manifold theory and the method of normal form, analytical expressions are obtained, which describe the behavior of the rotating shaft in the neighborhood of the bifurcations; and consequently, the post-critical behavior of the shaft is clarified. It is shown that depending on the system parameters, the synchronous and nonsynchronous whirling of the rotating shaft are expectable.

2 Equations of motion

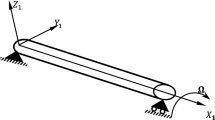
The schematic of a continuous rotating shaft has been shown in Fig. 1. The length of the undeformed shaft centerline is l and X 0–Y 0–Z 0 axes constitute an inertial frame. Displacement of any particle of a shaft is described in floating frame X–Y–Z, which follows the rigid body motion of the shaft, i.e., it rotates about X 0 axis with a constant speed Ω. Therefore, the equations of motion of the rotating shaft are described in the floating frame X–Y–Z. The x–y–z constitutes a local coordinate which are principal axes of the beam cross section at position s (Fig. 1). Here, s is the axial coordinate along the shaft centerline before deformation. Displacements of a particle in arbitrary location s along X, Y, and Z axes are u(s,t), v(s,t), and w(s,t), respectively, and torsional angle is ϕ(s,t).

Fig. 1
figure 1

Schematic of the rotating shaft and related coordinates

Full size image

The following assumptions are employed: (1) the shaft has uniform circular cross section, and it spins about longitudinal axis X with a constant speed Ω; (2) the effect of gravity is neglected; (3) the shaft is slender, and consequently, shear deformation and rotary inertia effects are neglected; (4) the shaft is simply supported; (5) support O is fixed but support O′ is free to move along the X axis (Fig. 1). This assumption implies that the stretching effect is negligible. This situation is more realistic than some previous works in which nonlinearity was due to the stretching of the shaft centerline [4, 6, 9], i.e., both supports to be fixed in the longitudinal direction; (6) external damping force is linearly proportional to the absolute velocity of any shaft particle and it is uniformly distributed along the shaft axis; (7) to model the internal damping, it is assumed that the shaft is made of a Kelvin–Voigt viscoelastic material; (8) vibrations of the rotating shaft are of large amplitude and the shortening effect due to in-extensibility assumption is considered [26, 28]. Therefore, only nonlinear effects of curvature and inertia are studied here.

2.1 Kinetic and potential energy

The relation between the original frame X–Y–Z and the deformed frame x–y–z can be described by three successive Euler-angle rotations [29]. Here, we use a 3–2–1 body rotation with angles of rotation ψ(s,t), θ(s,t) and ϕ(s,t) as shown in Fig. 2.

Fig. 2
figure 2

Schematic of the 3–2–1 Euler angles

Full size image

Position and velocity of a particle on the deformed shaft are

$$\begin{aligned} &{\boldsymbol{R} = (s + u)\mathbf{e}_{x} + v\mathbf{e}_{y} + w \mathbf{e}_{z}} \end{aligned}$$
(1)
$$\begin{aligned} &{\dot{\boldsymbol{R}} = \dot{u}\mathbf{e}_{\mathbf{X}} + (\dot{v} - w\varOmega ) \mathbf{e}_{\mathbf{Y}} + (\dot{w} + v\varOmega )\mathbf{e}_{\mathbf{Z}}} \end{aligned}$$
(2)

Neglecting rotary inertia effect, kinetic energy may be computed as

$$ T = \frac{1}{2}\int_{0}^{l} \int _{A} \rho \dot{\boldsymbol{R}}.\dot{\boldsymbol{R}} \,dA\,ds $$
(3)

where ρ is mass density. Defining m=∫ A ρ  dA, Eqs. (2) and (3) give

$$ T = \frac{1}{2}\int_{0}^{l} m \bigl[ \dot{u}^{2} + (\dot{v} - w\varOmega )^{2} + (\dot{w} + v \varOmega )^{2}\bigr] \,ds $$
(4)

Because the shaft is circular, it is better to use polar coordinates (r,α) in which y=rcosα, z=rsinα. If shear deformation is neglected, strains ε xx , ε xα , and ε xr at a point with coordinates (x,r,α) are

$$ \begin{array}{l} \varepsilon _{xx} = e - r\cos \alpha \rho _{3} + r \sin \alpha \rho _{2},\qquad \varepsilon _{x\alpha} = r\rho _{1},\\ \varepsilon _{xr} = 0 \end{array} $$
(5)

where the strain along the shaft centerline is

$$ e = \sqrt{\bigl(1 + u'\bigr)^{2} + v'^{2} + w'^{2}} - 1 $$
(6)

and ρ i (i=1–3) is curvatures of the shaft. Prime denotes the derivative with respect to variable s. The variation of strain energy is

$$ \delta \varPi = \int_{0}^{l} \int _{A} (\sigma _{xx}\delta \varepsilon _{xx} + \sigma _{x\alpha} \delta \varepsilon _{x\alpha} ) \,dA\,ds $$
(7)

Using Eq. (5), the strain energy is computed as

$$\begin{aligned} \delta \varPi =& \int_{0}^{l}\!\! \int _{A} \bigl[(\sigma _{xx}(\delta e - r\cos \alpha \delta \rho _{3} + r\sin \alpha \delta \rho _{2}) \\&{} + \sigma _{x\alpha} ( - r\delta \rho _{1}) \bigr]\,dA\,ds \end{aligned}$$
(8)

We assumed that the shaft is made of a Voigt viscoelastic material; therefore, the stress in an element is linear function of strain as well as the time rate of the strain, i.e.,

$$ \begin{array}{l} \sigma _{xx} = E(\varepsilon _{xx} + \mu _{in} \dot{\varepsilon} _{xx}),\\ \sigma _{x\alpha} = G(\varepsilon _{x\alpha} + \mu _{is}\dot{\varepsilon} _{x\alpha} ) \end{array} $$
(9)

In the above equations, E and G are elasticity and shear modulus, respectively, and μ ij (j=n,s) is internal damping coefficient. Here, the internal damping coefficient associated with normal and shear deformations are assumed equal, i.e., μ in =μ is =μ i  [30]. Using Eqs. (8) and (9), after some algebraic simplifications, one can obtain strain energy for an isotropic viscoelastic circular shaft as

$$\begin{aligned} \delta \varPi =& \int_{0}^{l} \bigl[A_{11}(e + \mu _{i}\dot{e})\delta e + D_{11} (\rho _{1} + \mu _{i}\dot{\rho} _{1})\delta \rho _{1} \\&{} + D_{22}(\rho _{2} + \mu _{i}\dot{ \rho} _{2})\delta \rho _{2} \\&{}+ D_{22}(\rho _{3} + \mu _{i}\dot{\rho} _{3})\delta \rho _{3}\bigr]\,ds \end{aligned}$$
(10)

where

$$ \begin{array}{l} A_{11} = \displaystyle\int_{A} E\,dA,\qquad D_{11} = \int _{A} Gr^{2}\,dA,\\ D_{22} = \displaystyle\int _{A} E r^{2}\sin ^{2}\alpha\, dA = \int _{A} Er^{2}\cos ^{2}\alpha\, dA \end{array} $$
(11)

Using Euler angles, the shaft curvature ρ i (i=1–3) can be computed as [26]

$$\begin{aligned} \boldsymbol{\rho} =& \rho _{1}\mathbf{e}_{\mathbf{1}} + \rho _{2}\mathbf{e}_{\mathbf{2}} + \rho _{3}\mathbf{e}_{\mathbf{3}} \\=& \bigl(\phi ' - \psi '\sin \theta \bigr)\mathbf{e}_{\mathbf{1}} + \bigl(\psi '\sin \phi \cos \theta + \theta '\cos \phi \bigr)\mathbf{e}_{\mathbf{2}} \\&{} + \bigl(\psi '\cos \phi \cos \theta - \theta '\sin \phi \bigr)\mathbf{e}_{\mathbf{3}} \end{aligned}$$
(12)

Because the shear deformation is negligible, angles ψ and θ can be related to the displacements (Fig. 2) [26]

$$ \begin{array}{l} \psi = \sin ^{ - 1}\displaystyle\frac{v'}{\sqrt{(1 + u')^{2} + v'^{2}}},\\ \theta = \sin ^{ - 1} \displaystyle\frac{ -w'}{\sqrt{(1 + u')^{2} + v'^{2} + w'^{2}}} \end{array} $$
(13)

Using Eq. (2), the virtual work due to the external damping force is computed as

$$\begin{aligned} \delta W =& \int_{0}^{l} - \mu _{e} \dot{\boldsymbol{R}}. \delta \boldsymbol{R}\,ds \\=& - \int_{0}^{l} \mu _{e}\bigl[(\dot{v} - \varOmega w)\delta v + (\dot{w} + \varOmega v) \delta w\bigr]\,ds \end{aligned}$$
(14)

where μ e is external damping coefficient. It is noted that the external damping arising from longitudinal and torsional motion have been neglected.

2.2 In-extensionality assumption

Equations (4) and (10) are expressions for kinetic and strain energy of an isotropic viscoelastic rotating shaft. It was noted earlier that support O′ in Fig. 1 is movable in X direction. So, the in-extensionality assumption can be employed, which implies that the strain along the shaft centroid is zero [28, 29]. Equation (6) gives

$$ e = 0 \quad \Longrightarrow\quad \bigl(1 + u'\bigr)^{2} + v'^{2} + w'^{2} = 1 $$
(15)

Expanding Eq. (15) into a Taylor series

$$\begin{aligned} u' =& \sqrt{1 - v'^{2} - w'^{2}} - 1 \\\simeq& - \frac{1}{2}\bigl(v'^{2} + w'^{2}\bigr) +\cdots \end{aligned}$$
(16)

Therefore, if \(v = O(\hat{\varepsilon} )\) and \(w = O(\hat{\varepsilon} )\), then \(u = O(\hat{\varepsilon} ^{2})\), where \(\hat{\varepsilon} \ll 1\) is a bookkeeping parameter. Substituting Eq. (13) into Eq. (12), expanding the outcomes in Taylor series and retaining terms up to \(O(\hat{\varepsilon} ^{3})\), one can compute curvatures up to \(O(\hat{\varepsilon} ^{3})\). Substituting these curvatures into Eqs. (10), and using Eqs. (4), the final form of kinetic and strain energies is obtained. Applying extended Hamilton principal to these kinetic and strain energies, and using Eqs. (14) and (16), one may obtain differential equations of motion governing the nonlinear bending-bending-torsional vibration of a viscoelastic rotating shaft. These differential equations can be simplified using following assumption: the shaft is circular; so, its fundamental torsional frequency is much higher than the frequency of flexural modes [29], i.e., in the torsional motion only the effect of stiffness is significant. Consequently, the time dependent terms in the differential equations corresponding to torsional motion can be neglected [29], which gives

$$ \phi = - \int_{0}^{s} v''w'\,ds+\cdots $$
(17)

Substituting Eq. (17) into the other differential equations corresponding to bending–bending motion and using the following nondimensional quantities:

$$ \begin{array}{l} s^{ *} = s/l,\qquad v^{ *} = v/l,\qquad w^{ *} = w/l,\\ t^{ *} = \sqrt{\displaystyle\frac{D_{22}}{ml^{4}}} t \equiv \chi t, \\ \varOmega ^{ *} = \varOmega /\chi,\qquad \mu _{i}^{ *} = \chi \mu _{i},\qquad \mu _{e}^{ *} = \displaystyle\frac{\mu_{e}l^{2}}{\sqrt{mD_{22}}} \end{array} $$
(18)

one may obtain the following equations of motion governing the flexural–flexural nonlinear vibrations of an in-extensional viscoelastic rotating shaft:

$$\begin{aligned} &{\ddot{v} + v^{(IV)} + \varOmega ( - 2 \dot{w} - \varOmega v) + \mu _{e}(\dot{v} - \varOmega w)} \\&{\quad {} + v'\int_{0}^{s} \bigl(\dot{v}^{\prime2} + \ddot{v}'v' + \dot{w}^{\prime2} + \ddot{w}^{\prime2}w' \bigr) \,ds} \\&{\quad {} + v''\int_{l}^{s} \!\!\! \int_{0}^{s} \bigl(\dot{v}^{\prime2} + \ddot{v}'v' + \dot{w}^{\prime2} + \ddot{w}'w'\bigr) \,ds \,ds} \\&{\quad {} + v'^{2}v^{(IV)} + v'w^{(IV)}w' + 3w'''w''v'} \\&{\quad {} + v''w''^{2} + v''^{3} + w'''v''w' + 4v'v''v'''} \\&{\quad {} + \mu _{i} \biggl[\dot{v}^{(IV)} - w^{(IV)}\int_{0}^{s} \bigl( \dot{v}''w' + v'' \dot{w}' \bigr)\, ds} \\&{\quad {} - \dot{v}'''w'w'' - \dot{v}''w'w''' + \dot{v}'w'w^{(IV)} + 3\dot{v}''v''^{2}} \\&{\quad {} + 3w'''w'' \dot{v}' + \dot{v}^{(IV)}v^{\prime2} + 3v'\dot{v}''v''' + 4\dot{v}'''v'v''} \\&{\quad {} + 3v'\dot{w}''w''' + 3w''\dot{w}''v'' + 2v''w'\dot{w}''' + v'''w'\dot{w}''} \\&{\quad {} + v'\dot{v}'v^{(IV)} + v'w'\dot{w}^{(IV)} + 3v'' \dot{v}'v''' + 3v'w''\dot{w}'''} \\&{\quad {} + v'\dot{w}'w^{(IV)}\biggr] = 0,} \end{aligned}$$
(19)
$$\begin{aligned} &{\ddot{w} + w^{(IV)} + \varOmega (2\dot{v} - \varOmega w) + \mu _{e}(\dot{w} + \varOmega v)} \\&{\quad {} + w'\int_{0}^{s} \bigl(\dot{v}^{\prime2} + \ddot{v}'v' + \dot{w}'^{2} + \ddot{w}'w' \bigr)\,ds} \\&{\quad {} + w''\int_{l}^{s} \int_{0}^{s} \bigl(\dot{v}^{\prime2} + \ddot{v}'v' + \dot{w}'^{2} + \ddot{w}'w'\bigr)\,ds\,ds} \\&{\quad {} + w''v''^{2} + v'v'''w'' + 3w'v''v''' + w'v'v^{(IV)}} \\&{\quad {} + w'^{2}w^{(IV)} + w''^{3} + 4w'w''w''' } \\&{\quad {}+ \mu _{i} \biggl[\dot{w}^{(IV)} + v^{(IV)}\int_{0}^{s} \bigl(\dot{v}''w' + v'' \dot{w}'\bigr)\,ds } \\&{\quad {}+ 3w'' \dot{w}'w''' + \dot{w}^{(IV)}w'^{2} + 3v''\dot{w}'v''' + 3\dot{v}'''w'v''} \\&{\quad {}+ 4\dot{w}'''w''w' + 3\dot{v}''v'''w' + v''^{2}\dot{w}'' + w'\dot{w}'w^{(IV)} } \\&{\quad {}+ w'' \dot{v}'''v' + 2\dot{v}''v''w'' + w'\dot{v}^{(IV)}v' } \\&{\quad {}+ 3w''^{2} \dot{w}'' + 3w'\dot{w}''w''' \biggr] = 0} \end{aligned}$$
(20)

The boundary conditions are

$$\begin{aligned} &{v = 0,\quad v'' = 0,\quad w = 0,\quad w'' = 0} \\&{\quad \mathrm{at}\ s = 0\ \mbox{and}\ s = 1} \end{aligned}$$
(21)

For ease of notation, the asterisks in the above equations have been dropped. It is noted that if Eqs. (19)–(20) are transformed to the inertial frame X 0–Y 0–Z 0, and internal damping coefficient μ i are set to zero, the resulting differential equations reduce to Eq. (13) of our previous paper [26].

To analyze the dynamical behavior of the rotating shaft, the partial differential equation of motion is discretized. We assume that only one mode to be excited and this mode does not attend any internal resonances. Therefore, one may use the single mode Galerkin method

$$ v(s,t) = \phi _{n}(s)V_{n}(t),\qquad w(s,t) = \phi _{n}(s)W_{n}(t) $$
(22)

where n is the mode number and ϕ n (s) is the linear mode shape of the shaft

$$ \phi _{n}(s) = \sqrt{2} \sin n\pi s $$
(23)

Substituting Eq. (22) into Eqs. (19)–(20), taking the inner product of each equation with its corresponding mode shape, and using the orthogonality properties of the mode shapes; one can obtain the following discretized equations of motion:

$$\begin{aligned} &{\ddot{V}_{n} + \pi ^{4}n^{4}\mu _{i}\dot{V}_{n} - 2\varOmega \dot{W}_{n} + \bigl( \pi ^{4}n^{4} - \varOmega ^{2}\bigr)V_{n}} \\&{\quad {} + \mu _{e}(\dot{V}_{n} - \varOmega W_{n}) + n^{2}\pi ^{2}\biggl(\frac{1}{3}\pi ^{2}n^{2} - \frac{3}{8}\biggr)} \\&{\quad {}\times \bigl(V_{n}\dot{W}_{n}^{2} + V_{n}W_{n}\ddot{W}_{n} + \ddot{V}_{n}V_{n}^{2} + V_{n}\dot{V}_{n}^{2}\bigr)} \\&{\quad {} + \pi ^{6}n^{6}V_{n} \bigl(W_{n}^{2} + V_{n}^{2}\bigr) + \frac{1}{4}\pi ^{6}n^{6}\mu _{i} \bigl(7W_{n}V_{n}\dot{W}_{n}} \\&{\quad {} + 7W_{n}^{2}\dot{V}_{n} + 6V_{n}^{2}\dot{V}_{n}\bigr) = 0} \end{aligned}$$
(24)
$$\begin{aligned} &{\ddot{W}_{n} + \pi ^{4}n^{4}\mu _{i}\dot{W}_{n} + 2\varOmega \dot{V}_{n} + \bigl( \pi ^{4}n^{4} - \varOmega ^{2}\bigr)W_{n}} \\&{\quad {} + \mu _{e}(\dot{W}_{n} + \varOmega V_{n}) + n^{2}\pi ^{2}\biggl(\frac{1}{3}\pi ^{2}n^{2} - \frac{3}{8}\biggr)} \\&{\quad {}\times \bigl(W_{n}\dot{V}_{n}^{2} + W_{n}\dot{W}_{n}^{2} + W_{n}^{2} \ddot{W}_{n} + V_{n}W_{n}\ddot{V}_{n} \bigr)} \\&{\quad {} + n^{6}\pi ^{6}W_{n} \bigl(V_{n}^{2} + W_{n}^{2}\bigr) + \frac{1}{4}n^{6}\pi ^{6}\mu _{i} \bigl(V_{n}W_{n}\dot{V}_{n}} \\&{\quad {} - 3V_{n}^{2}\dot{W}_{n} + 6 \dot{W}_{n}W_{n}^{2}\bigr) = 0} \end{aligned}$$
(25)

Equations (24)–(25) may be written in the form of first-order differential equations as

$$ \dot{\mathbf{A}} = \mathbf{CA} + \mathbf{N}(\mathbf{A}, \dot{\mathbf{A}}),\quad \mathbf{A} = (V,W,Q,R)^{T} $$
(26)

where

$$ \begin{array}{l} \mathbf{C} = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\- n^{4}\pi ^{4} + \varOmega ^{2} & \mu _{e}\varOmega & - \mu _{e} - n^{4}\pi ^{4}\mu _{i} & 2\varOmega \\- \mu _{e}\varOmega & - n^{4}\pi ^{4} + \varOmega ^{2} & - 2\varOmega & - \mu _{e} - n^{4}\pi ^{4}\mu _{i} \end{array} \right ]\\ \mathbf{N}(\mathbf{A},\dot{\mathbf{A}}) = (0,0,N_{3},N_{4})^{T} \end{array} $$
(27)

and

$$\begin{aligned} &{N_{3} = - n^{2}\pi ^{2}\biggl( \frac{m^{2}\pi ^{2}}{3} - \frac{3}{8}\biggr)V\bigl(R^{2} + Q^{2} + V\dot{Q}} \\&{\hphantom{N_{3} =} {} + W\dot{R}\bigr) - \frac{7}{4}n^{6}\pi ^{6}\mu _{i}W(VR + WQ)} \\&{\hphantom{N_{3} =} {} - n^{6}\pi ^{6}V \bigl(V^{2} + W^{2}\bigr) - \frac{3}{2}n^{6} \pi ^{6}\mu _{i}QV^{2}} \\ \\&{N_{4} = - n^{2}\pi ^{2}\biggl( \frac{m^{2}\pi ^{2}}{3} - \frac{3}{8}\biggr)W\bigl(R^{2} + Q^{2} + V\dot{Q}} \\&{\hphantom{N_{4} =} {} + W\dot{R}\bigr) + \frac{1}{4}n^{6}\pi ^{6}\mu _{i}V(3VR - WQ)} \\&{\hphantom{N_{4} =} {} - n^{6}\pi ^{6}W \bigl(V^{2} + W^{2}\bigr) - \frac{3}{2}n^{6} \pi ^{6}\mu _{i}RW^{2}} \end{aligned}$$
(28)

3 Stability and bifurcation analysis—linear case

It is clear that (V n ,W n )=(0,0) is a trivial solution of the system, which is corresponding to the undeformed rotation of the shaft. Linearization of Eqs. (24)–(25) about this trivial solution gives

$$ \begin{array}{l} \ddot{V}_{n} + \bigl(\pi ^{4}n^{4}\mu _{i} + \mu _{e} \bigr)\dot{V}_{n} - 2\varOmega \dot{W}_{n} \\ \quad {} + \bigl(\pi ^{4}n^{4} - \varOmega ^{2} \bigr)V_{n} - \varOmega \mu _{e}W_{n} = 0 \\ \ddot{W}_{n} + \bigl(\pi ^{4}n^{4}\mu _{i} + \mu _{e} \bigr)\dot{W}_{n} + 2\varOmega \dot{V}_{n} \\ \quad {}+ \bigl(\pi ^{4}n^{4} - \varOmega ^{2} \bigr)W_{n} + \varOmega \mu _{e}V_{n} = 0 \end{array} $$
(29)

To study the solution of the above equations, substituting V n =A 1 e λt, W n =A 2 e λt into Eq. (29), which gives the characteristic equation as

$$\begin{aligned} &{\lambda ^{4} + 2\bigl(n^{4}\pi ^{4}\mu _{i} + \mu _{e}\bigr)\lambda ^{3} + \bigl(n^{8}\pi ^{8}\mu _{i}^{2} + 2n^{4}\pi ^{4}} \\&{\quad {} + 2n^{4}\pi ^{4}\mu _{e}\mu _{i} + \mu _{e}^{2} + 2\varOmega ^{2}\bigr)\lambda ^{2} + \bigl(2n^{8}\pi ^{8}\mu _{i}} \\&{\quad {} + 2n^{4}\pi ^{4}\mu _{e} - 2n^{4}\pi ^{4}\varOmega ^{2}\mu _{i} + 2\mu _{e}\varOmega ^{2}\bigr)\lambda} \\&{\quad {} + n^{8}\pi ^{8} - 2n^{4}\pi ^{4}\varOmega ^{2} + \varOmega ^{4} + \mu _{e}^{2} \varOmega ^{2} = 0} \end{aligned}$$
(30)

The roots of characteristic equation are the eigenvalues of the matrix C in Eq. (27). Now we can determine the stability of the solution using the Routh criteria. According to this criteria, the system is stable if

$$\begin{aligned} &{4n^{4}\pi ^{4}\bigl(\mu _{e} + n^{2}\pi ^{2}\mu _{i}\varOmega + n^{4}\pi ^{4}\mu _{i}\bigr)} \\&{\quad {}\times \bigl(\mu _{e} - n^{2}\pi ^{2} \mu _{i}\varOmega + n^{4}\pi ^{4}\mu _{i} \bigr)} \\&{\quad {} \times \bigl(\mu _{e}^{2} + n^{8}\pi ^{8}\mu _{i}^{2} + 4\varOmega ^{2} + 2n^{4}\pi ^{4}\mu _{i}\mu _{e}\bigr) \ge 0} \end{aligned}$$
(31)

After simplification, we obtain

$$ \varOmega \le n^{2}\pi ^{2} + \frac{\mu _{e}}{n^{2}\pi ^{2}\mu _{i}} \equiv \varOmega _{n} $$
(32)

Therefore, if the spinning speed of the shaft exceeds Ω n ≡n 2 π 2+μ e /(n 2 π 2 μ i ), the shaft motion becomes unstable. It is seen that the external damping delays the instability and internal damping speeds up the occurrence of instability. If internal damping approaches zero, the right hand side of Eq. (32) approaches infinity. It means that in the absence of internal damping the system is stable; Ehrich [31] has presented a complete explanation about this topic.

If Ω=n 2 π 2+μ e /(n 2 π 2 μ i ), the eigenvalues of Eq. (29) become

$$ \begin{array}{l} \lambda _{1,2} = \pm \displaystyle\frac{\mu _{e}i}{n^{2}\pi ^{2}\mu _{i}},\\ \lambda _{3,4} = - \bigl(n^{4}\pi ^{4}\mu _{i} + \mu _{e}\bigr) \pm \biggl(2n^{2}\pi ^{2} + \displaystyle\frac{\mu _{e}}{n^{2}\pi ^{2}\mu _{i}}\biggr)i \end{array} $$
(33)

It is seen that in the boundary of stability, there exists one pair of pure imaginary eigenvalues, while the other two eigenvalues have negative real parts. Therefore, a Hopf bifurcation is expected to occur, when spinning speed exceeds critical value Ω=Ω n , i.e., in all regions which the relation Ω=n 2 π 2+μ e /(n 2 π 2 μ i ) is satisfied. In addition, Eq. (33) shows that when external damping vanishes, μ e =0, Eq. (29) has two zero eigenvalues as well as two complex eigenvalues with negative real parts as

$$ \lambda _{1,2} = 0,\qquad \lambda _{3,4} = - \bigl(n^{4}\pi ^{4}\mu _{i}\bigr) \pm \bigl(2n^{2}\pi ^{2}\bigr)i $$
(34)

Hence, a double zero eigenvalue bifurcation is expected to occur at points with μ e =0,Ω=n 2 π 2. It is noted that for certain values of spinning speed and external damping, i.e., Ω=(n+1)π 2,μ e =n 2(n+1)2 π 4 μ i , a double Hopf bifurcation may occur [4], which is not considered here. In the next section, we use nonlinear analysis to study double zero eigenvalue and Hopf bifurcation in the rotating shaft.

4 Stability and bifurcation analysis—nonlinear case

In this section, we use nonlinear analysis to study the bifurcation and stability of the rotating shaft. This investigation will be in the neighborhood of the double zero eigenvalues and Hopf bifurcations. We use the center manifold theory and the method of normal form to study the post critical behavior of the rotating shaft.

The existence of nontrivial steady state solutions may be examined by considering the equilibrium points of the shaft in the floating frame X–Y–Z. First, the time dependent terms of Eq. (29) are set to zero

$$ \begin{array}{l} \bigl(n^{4}\pi ^{4} - \varOmega ^{2}\bigr)V_{n} - \mu _{e}\varOmega W_{n} + n^{6}\pi ^{6}V_{n}\bigl(W_{n}^{2} + V_{n}^{2}\bigr)\\ \quad = 0 \\ \bigl(n^{4}\pi ^{4} - \varOmega ^{2}\bigr)W_{n} + \mu _{e}\varOmega V_{n} + n^{6}\pi ^{6}W_{n}\bigl(W_{n}^{2} + V_{n}^{2}\bigr)\\ \quad = 0 \end{array} $$
(35)

Using relation \(R_{n}^{2} = W_{n}^{2} + V_{n}^{2}\), the above equations may be written as

$$ \begin{array}{l} \bigl(n^{4}\pi ^{4} - \varOmega ^{2}\bigr)V_{n} - \mu _{e}\varOmega W_{n} + n^{6}\pi ^{6}V_{n}R_{n}^{2} = 0 \\ \bigl(n^{4}\pi ^{4} - \varOmega ^{2}\bigr)W_{n} + \mu _{e}\varOmega V_{n} + n^{6}\pi ^{6}W_{n}R_{n}^{2} = 0 \end{array} $$
(36)

Equation (36) has a nontrivial steady state solution if μ e =0. Therefore, if external damping in Eq. (36) is set to zero, the following expression is obtained:

$$ R_{n}^{2} = V_{n}^{2} + W_{n}^{2} = \frac{(\varOmega ^{2} - n^{4}\pi ^{4})}{n^{6}\pi ^{6}} $$
(37)

Equation (37) has a solution if Ω≥n 2 π 2. So, the rotating shaft may whirl at nth mode, where the corresponding radius of whirling is \(R_{n}^{2} = \frac{(\varOmega ^{2} - n^{4}\pi ^{4})}{n^{6}\pi ^{6}}\).

4.1 Double zero eigenvalue bifurcation

In this section, we use the center manifold theory in the neighborhood of a double zero eigenvalue bifurcation to reduce the original full nonlinear equations to a set of differential equations in center manifold, which captures the essential parts of the system dynamics. It will be shown that the results are in the standard normal form for the related bifurcation and consequent analysis may be easily done.

As explained earlier for μ e =0, Ω=m 2 π 2, the linear system (29) has a double zero eigenvalues, in which a codimension two bifurcation may occur. So, we need two parameters to fully describe the bifurcation. We use ε=(ε 1,ε 2) as a vector of unfolding parameters which is defined

$$ \varepsilon _{1} = \varOmega - n^{2}\pi ^{2},\qquad \varepsilon _{2} = \mu _{e} $$
(38)

In fact, theses parameters are a measure of deviation of the spinning speed and external damping in the neighborhood of bifurcation point. Using unfolding parameters ε 1, ε 2, Eq. (26) may be written as

$$ \dot{\mathbf{A}} = (\mathbf{C}_{0} + \mathbf{C}_{\varepsilon} ) \mathbf{A} + \mathbf{N}\bigl(\mathbf{A},\dot{\mathbf{A}}\bigr) $$
(39)

where

$$\begin{aligned} \begin{array}{l} \mathbf{C}_{0} = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\0 & 0 & - n^{4}\pi ^{4}\mu _{i} & 2n^{2}\pi ^{2} \\0 & 0 & - 2n^{2}\pi ^{2} & - n^{4}\pi ^{4}\mu _{i} \end{array} \right ]\\ \mathbf{C}_{\varepsilon} = \mbox{\small$\left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \\\varepsilon _{1}^{2} + 2n^{2}\pi ^{2}\varepsilon _{1} & (\varepsilon _{1} + n^{2}\pi ^{2})\varepsilon _{2} & - \varepsilon _{2} & 2\varepsilon _{1} \\- (\varepsilon _{1} + n^{2}\pi ^{2})\varepsilon _{2} & \varepsilon _{1}^{2} + 2n^{2}\pi ^{2}\varepsilon _{1} & - 2\varepsilon _{1} & - \varepsilon _{2} \end{array} \right ] $} \end{array} \end{aligned}$$
(40)

It is noted that the C 0 has two zero and a pair of complex conjugate eigenvalues with negative real parts (Eq. (34)). Using similarity transformation A=PZ, the Jordan form of Eq. (39) becomes

$$ \dot{\mathbf{Z}} = \mathbf{P}^{ - 1}(\mathbf{C}_{0} + \mathbf{C}_{\varepsilon} )\mathbf{PZ} + \mathbf{P}^{ - 1}\mathbf{N}\bigl( \mathbf{Z},\dot{\mathbf{Z}}\bigr) $$
(41)

where

$$ \begin{array}{l} \mathbf{P} = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 & 0 & \frac{1}{2n^{2}\pi ^{2}i - n^{4}\pi ^{4}\mu _{i}} & \frac{ - i}{2n^{2}\pi ^{2}i + n^{4}\pi ^{4}\mu _{i}} \\0 & 1 & \frac{i}{2n^{2}\pi ^{2}i - n^{4}\pi ^{4}\mu _{i}} & \frac{ - 1}{2n^{2}\pi ^{2}i + n^{4}\pi ^{4}\mu _{i}} \\0 & 0 & 1 & i \\0 & 0 & i & 1 \end{array} \right ]\\ \mathbf{Z} = (Z_{1},Z_{2},Z_{3},Z_{4})^{T} \end{array} $$
(42)

Columns of P are eigenvectors of the matrix C 0. Rewriting Eq. (41) in form of

$$ \left [ \begin{array}{c} \dot{\mathbf{S}} \\\dot{\mathbf{T}} \end{array} \right ] = \left [ \begin{array}{c@{\quad}c} \mathbf{D}_{11} & \mathbf{D}_{12} \\\mathbf{D}_{21} & \mathbf{D}_{22} \end{array} \right ]\left [ \begin{array}{c} \mathbf{S} \\\mathbf{T} \end{array} \right ] + \left [ \begin{array}{c} \mathbf{n}_{1}(\mathbf{S},\mathbf{T},\dot{\mathbf{S}},\dot{\mathbf{T}}) \\\mathbf{n}_{2}(\mathbf{S},\mathbf{T},\dot{\mathbf{S}},\dot{\mathbf{T}}) \end{array} \right ] $$
(43)

where

$$ \begin{array}{l} \left [ \begin{array}{c} \mathbf{S} \\\mathbf{T} \end{array} \right ] = (Z_{1},Z_{2},Z_{3},Z_{4})^{T}\\ \left [ \begin{array}{c@{\quad}c} \mathbf{D}_{11} & \mathbf{D}_{12} \\\mathbf{D}_{21} & \mathbf{D}_{22} \end{array} \right ] = \mathbf{P}^{ - 1}( \mathbf{C}_{0} + \mathbf{C}_{\varepsilon} )\mathbf{P}\\ \left \{ \begin{array}{c} \mathbf{n}_{1}(\mathbf{S},\mathbf{T},\dot{\mathbf{S}},\dot{\mathbf{T}}) \\\mathbf{n}_{2}(\mathbf{S},\mathbf{T},\dot{\mathbf{S}},\dot{\mathbf{T}}) \end{array} \right \} = \mathbf{P}^{ - 1}\mathbf{N}(\mathbf{Z},\dot{ \mathbf{Z}}) \end{array} $$
(44)

Considering ε as a new dependent variable and separating dynamics in the center manifold from the dynamics in the stable manifold, one may obtain

$$\begin{aligned} &{\dot{\mathbf{S}} = \mathbf{D}_{11}\mathbf{S} + \mathbf{D}_{12} \mathbf{T} + \mathbf{n}_{1}\bigl(\mathbf{S}, \mathbf{T},\dot{\mathbf{S}}, \dot{\mathbf{T}}\bigr)} \end{aligned}$$
(45)
$$\begin{aligned} &{\dot{\mathbf{T}} = \mathbf{D}_{21}\mathbf{S} + \mathbf{D}_{22} \mathbf{T} + \mathbf{n}_{2}\bigl(\mathbf{S}, \mathbf{T},\dot{\mathbf{S}},\dot{ \mathbf{T}}\bigr)} \end{aligned}$$
(46)

According to the center manifold theory, there is an invariant manifold in the neighborhood of (S,T,ε)=(0,0,0), which can locally be presented as

$$ \mathbf{T} = \mathbf{h}(\mathbf{S},\boldsymbol{\varepsilon} ),\qquad \vert \mathbf{S}_{1} \vert < \delta,\qquad \vert \boldsymbol{\varepsilon} \vert < \delta $$
(47)

for sufficiently small δ.

Substitution of Eq. (47) into Eq. (46) gives

$$\begin{aligned} &{\frac{\partial}{\partial \mathbf{S}}\mathbf{h}(\mathbf{S},\boldsymbol{\varepsilon} )\dot{ \mathbf{S}} + \frac{\partial}{\partial \boldsymbol{\varepsilon}} \mathbf{h}(\mathbf{S},\boldsymbol{\varepsilon} ) \dot{\boldsymbol{\varepsilon}} = \mathbf{D}_{21}\mathbf{S} + \mathbf{D}_{22}\mathbf{h}(\mathbf{S},\boldsymbol{\varepsilon} )} \\&{\quad {} + \mathbf{n}_{2}\bigl(\boldsymbol{\varepsilon},\mathbf{S},\dot{\mathbf{S}}\bigr)} \end{aligned}$$
(48)

Using Eq. (45), one may write Eq. (48) in form of

$$\begin{aligned} &{\frac{\partial}{\partial \mathbf{S}}\mathbf{h}(\mathbf{S},\boldsymbol{\varepsilon} )\bigl[ \mathbf{D}_{11}\mathbf{S} + \mathbf{D}_{12}\mathbf{h}( \mathbf{S},\boldsymbol{\varepsilon} )\bigr] + \mathbf{n}_{1}\bigl( \boldsymbol{\varepsilon},\mathbf{S},\dot{\mathbf{S}}\bigr) - \mathbf{D}_{21} \mathbf{S}} \\&{\quad {} - \mathbf{D}_{22}\mathbf{h}(\mathbf{S},\boldsymbol{ \varepsilon} ) - \mathbf{n}_{2}\bigl(\boldsymbol{\varepsilon},\mathbf{S}, \dot{\mathbf{S}}\bigr) = 0} \end{aligned}$$
(49)

Since the above partial differential equation can not be solved explicitly, h(S,ε)is usually approximated with polynomials [32]. Here, we use quadratic polynomial to approximate the h(S,ε) as

$$ \mathbf{T} = \mathbf{h}(\mathbf{S},\boldsymbol{\varepsilon} ) = \mathbf{h}_{2}(\mathbf{S},\boldsymbol{\varepsilon} ) + O\bigl(\vert \mathbf{S},\boldsymbol{\varepsilon} \vert ^{3}\bigr) $$
(50)

It should be noted that the center manifold is tangent to the center subspace of the corresponding linear equation at point (S,T,ε)=(0,0,0). Therefore, the assumed quadratic polynomial h 2(S,ε) does not contain constant and linear terms. Substituting Eq. (50) into Eq. (49) and equating coefficients of quadratic terms, one may obtain h 2(S,ε) as follows:

$$\begin{aligned} &{\mathbf{h}_{2}(\mathbf{S},\boldsymbol{\varepsilon} ) = (\varXi, i\bar{ \varXi} ),} \\&{\quad \varXi = \frac{n^{2}\pi ^{2}(Z_{1}i + Z_{2})(\varepsilon _{2} - 2i\varepsilon _{1})}{2(2n^{2}\pi ^{2}i - n^{4}\pi ^{4}\mu _{i})}} \end{aligned}$$
(51)

where \(\bar{\varXi}\) is the complex conjugate of Ξ. Substitution of Eqs. (50)–(51) in Eq. (45) gives the dynamics of the nonlinear system in the center manifold as

$$\begin{aligned} \left [ \begin{array}{c} \dot{Z}_{1} \\\dot{Z}_{2} \end{array} \right ] =& \left [ \begin{array}{c@{\quad}c} \frac{2n^{2}\pi ^{2}\mu _{i}\varepsilon _{1} - 2\varepsilon _{2}}{n^{4}\pi ^{4}\mu _{i}^{2} + 4} + g_{1}(\varepsilon _{1},\varepsilon _{2}) & \frac{n^{2}\pi ^{2}\mu _{i}\varepsilon _{2} + 4\varepsilon _{1}}{n^{4}\pi ^{4}\mu _{i}^{2} + 4} + g_{2}(\varepsilon _{1},\varepsilon _{2})\\\frac{ - n^{2}\pi ^{2}\mu _{i}\varepsilon _{2} - 4\varepsilon _{1}}{n^{4}\pi ^{4}\mu _{i}^{2} + 4} - g_{2}(\varepsilon _{1},\varepsilon _{2}) & \frac{2n^{2}\pi ^{2}\mu _{i}\varepsilon _{1} - 2\varepsilon _{2}}{n^{4}\pi ^{4}\mu _{i}^{2} + 4} + g_{1}(\varepsilon _{1},\varepsilon _{2}) \end{array} \right ]\left [ \begin{array}{c} Z_{1} \\Z_{2} \end{array} \right ] \\&{} + \left [ \begin{array}{c} - \frac{n^{6}\pi ^{6}\mu _{i}Z_{1}(Z_{1}^{2} + Z_{2}^{2}) + 2n^{4}\pi ^{4}Z_{2}(Z_{1}^{2} + Z_{2}^{2})}{n^{4}\pi ^{4}\mu _{i}^{2} + 4} \\- \frac{n^{6}\pi ^{6}\mu _{i}Z_{2}(Z_{1}^{2} + Z_{2}^{2}) - 2n^{4}\pi ^{4}Z_{1}(Z_{1}^{2} + Z_{2}^{2})}{n^{4}\pi ^{4}\mu _{i}^{2} + 4} \end{array} \right ] + O\bigl(\vert \mathbf{A},\boldsymbol{ \varepsilon} \vert ^{4}\bigr) \end{aligned}$$
(52)

where g j (ε 1,ε 2),j=1,2 is nonlinear function of ε 1,ε 2. Using polar coordinates Z 1=Rcos(θ),Z 2=Rsin(θ), and neglecting g j (ε 1,ε 2),j=1,2, the above equation becomes

$$\begin{aligned} &{\dot{R} = \frac{ - 2\varepsilon _{2} + 2n^{2}\pi ^{2}\mu _{i}\varepsilon _{1}}{n^{4}\pi ^{4}\mu _{i}^{2} + 4}R - \frac{n^{6}\pi ^{6}\mu _{i}}{n^{4}\pi ^{4}\mu _{i}^{2} + 4}R^{3}} \end{aligned}$$
(53)
$$\begin{aligned} &{\dot{\theta} = - \frac{4\varepsilon _{1} + n^{2}\pi ^{2}\mu _{i}\varepsilon _{2}}{n^{4}\pi ^{4}\mu _{i}^{2} + 4} + \frac{2n^{4}\pi ^{4}}{n^{4}\pi ^{4}\mu _{i}^{2} + 4}R^{2}} \end{aligned}$$
(54)

This equation describes the double zero eigenvalue bifurcation of Eq. (26) with unfolding parameters ε 1, ε 2. It is obvious that Eqs. (53)–(54) are on the standard normal form for this bifurcation. These equations were derived for arbitrary mode n, but for modes of higher than one, the results are valid in the center manifold, which is not useful for our object [4]. Therefore, we present the results only for the first mode: n=1. In Eqs. (53)–(54), variable R presents the amplitude of the shaft and θ is the phase difference between the shaft and floating frame X–Y–Z. Two cases ε 2=0 and ε 2>0 are studied here in the following [4]:

1. Case ε 2=0. Equation (53) shows that for this case (no external damping), the trivial solution is asymptotically stable if ε 1<0, and it is unstable if ε 1>0. The synchronous whirling of the shaft occurs when \(\dot{\theta} = 0\) and R is a constant. Such solutions appear as a circle of equilibria [4]. If ε 2=0, a nontrivial circle of equilibria bifurcates from the zero solution at ε 1=0. This solution is stable for ε 1>0, and it may be presented as \(R^{2} = \frac{2\varepsilon _{1}}{\pi ^{4}} = \frac{2(\varOmega - \pi ^{2})}{\pi ^{4}}\), \(\dot{\theta} = 0\), i.e., the shaft is whirling synchronously. It is interesting to compare the recent result with the one obtained in Eq. (37). This equation gave the radius of the synchronous first-mode whirling as

$$\begin{aligned} R_{1}^{2} =& \frac{(\varOmega ^{2} - \pi ^{4})}{\pi ^{6}} = \frac{(\varOmega - \pi ^{2})(\varOmega + \pi ^{2})}{\pi ^{6}} \\\simeq& \frac{2(\varOmega - \pi ^{2})}{\pi ^{4}} \end{aligned}$$
(55)

Since ε 1 is very small, i.e., Ω≃π 2, the above approximation is valid. It is seen that in this case the result of center manifold is the same as the one obtained in Eq. (37).

2. Case ε 2>0. In this case, Eqs. (53)–(54) are in standard normal form for a Hopf bifurcation. It is clear that the Hopf bifurcation occurs at boundary ε 1=ε 2/(π 2 μ i ).

The sign of R 3 determines the type of bifurcation. Because the coefficient of R 3 is always negative, the resulting Hopf bifurcation is supercritical. Therefore, the trivial solution becomes unstable and a limit cycle appears for \(\varepsilon _{1} > \frac{\varepsilon _{2}}{\pi ^{2}\mu _{i}}\). Figure 3 shows the corresponding phase portraits. The radius of the limit cycle is

$$ R^{2} = \frac{2\varepsilon _{1}}{\pi ^{4}} - \frac{2\varepsilon _{2}}{\pi ^{6}\mu _{i}} $$
(56)

It is seen that R 2 (square of the limit cycle radius) is linearly dependent on spinning speed and the ratio of external damping to internal damping, μ e /μ i . The increase of spinning speed and internal damping increases the radius of limit cycle and the increase of external damping decreases it. Substitution of Eq. (56) into Eq. (54) yields

$$ \dot{\theta} = - \frac{\varepsilon _{2}}{\pi ^{2}\mu _{i}} $$
(57)

Equation (57) shows that the whirling motion of the shaft is nonsynchronous. Precession rate \(\dot{\theta}\) of the shaft is proportional to the ratio of external damping to internal damping, μ e /μ i and is independent of the spinning speed.

Fig. 3
figure 3

Phase portraits of Eqs. (53)–(54)

Full size image

4.2 The Hopf bifurcation

As mentioned in Sect. 3 that if Ω=n 2 π 2+μ e /(n 2 π 2 μ i ), μ e ≠0, linear system, Eq. (29), has one pair of pure imaginary eigenvalues (Eq. (33)). Therefore, bifurcation of a limit cycle from the trivial solution is expected for mode n. Again, we use the center manifold theory and method of normal form in the neighborhood of the Hopf bifurcation to reduce the original full nonlinear Eq. (26) to a set of differential equations in center manifold, which captures the essential parts of the system dynamics. Since a codimension one bifurcation may occur, only one parameter is required. We use the spinning speed parameter and define

$$\varepsilon = \varOmega - n^{2}\pi ^{2} - \mu _{e}/\bigl(n^{2}\pi ^{2}\mu _{i}\bigr) $$

as an unfolding parameter for the bifurcation. Indeed, this parameter is a measure of deviation of the spinning speed in the neighborhood of the bifurcation. Using parameter ε, Eq. (26) may be written as

$$ \dot{\mathbf{A}} = (\mathbf{D}_{0} + \mathbf{D}_{\varepsilon} ) \mathbf{A} + \mathbf{N}\bigl(\mathbf{A},\dot{\mathbf{A}}\bigr) $$
(58)

where

$$ \begin{array}{l} \mathbf{D}_{0} = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\\frac{\mu _{e}^{2}}{\mu _{i}^{2}n^{4}\pi ^{4}} + 2\frac{\mu _{e}}{\mu _{i}} & \frac{\mu _{e}(\mu _{e} + n^{4}\pi ^{4}\mu _{i})}{n^{2}\pi ^{2}\mu _{i}} & - \mu _{e} - n^{4}\pi ^{4}\mu _{i} & \frac{2(\mu _{e} + n^{4}\pi ^{4}\mu _{i})}{n^{2}\pi ^{2}\mu _{i}} \\- \frac{\mu _{e}(\mu _{e} + n^{4}\pi ^{4}\mu _{i})}{n^{2}\pi ^{2}\mu _{i}} & \frac{\mu _{e}^{2}}{\mu _{i}^{2}n^{4}\pi ^{4}} + 2\frac{\mu _{e}}{\mu _{i}} & - \frac{2(\mu _{e} + n^{4}\pi ^{4}\mu _{i})}{n^{2}\pi ^{2}\mu _{i}} & - \mu _{e} - n^{4}\pi ^{4}\mu _{i} \end{array} \right ],\\ \mathbf{D}_{\varepsilon} = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \\\frac{\varepsilon (n^{2}\pi ^{2}\mu _{i}\varepsilon + 2\mu _{e} + 2n^{4}\pi ^{4}\mu _{i})}{n^{2}\pi ^{2}\mu _{i}} & \mu _{e}\varepsilon & 0 & 2\varepsilon \\- \mu _{e}\varepsilon & \frac{\varepsilon (n^{2}\pi ^{2}\mu _{i}\varepsilon + 2\mu _{e} + 2n^{4}\pi ^{4}\mu _{i})}{n^{2}\pi ^{2}\mu _{i}} & - 2\varepsilon & 0 \end{array} \right ] \end{array} $$
(59)

The matrix D 0 has a pair of imaginary eigenvalues and a pair of complex eigenvalues with negative real part, i.e., Eq. (33). Equation (58) may be written in the Jordan form using transformation A=QZ as

$$ \dot{\mathbf{Z}} = \mathbf{Q}^{ - 1}(\mathbf{D}_{0} + \mathbf{D}_{\varepsilon} )\mathbf{QZ} + \mathbf{Q}^{ - 1}\mathbf{N}\bigl( \mathbf{Z},\dot{\mathbf{Z}}\bigr) $$
(60)

where

$$ \begin{array}{l} \mathbf{Q} = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} - 1 & 0 & - \frac{\varpi _{2}\varpi _{1}}{\varpi _{2}^{2} + \varpi _{3}^{2}} & - \frac{\varpi _{3}\varpi _{1}}{\varpi _{2}^{2} + \varpi _{3}^{2}} \\0 & 1 & - \frac{\varpi _{3}\varpi _{1}}{\varpi _{2}^{2} + \varpi _{3}^{2}} & \frac{\varpi _{2}\varpi _{1}}{\varpi _{2}^{2} + \varpi _{3}^{2}} \\0 & \varpi _{1} & 0 & \varpi _{1} \\\varpi _{1} & 0 & \varpi _{1} & 0 \end{array} \right ]\\ \mathbf{Z} = (Z_{1},Z_{2},Z_{3},Z_{4})^{T} \end{array} $$
(61)

and

$$ \begin{array}{l} \varpi _{1} = \displaystyle\frac{\mu _{e}}{n^{2}\pi ^{2}\mu _{i}},\qquad \varpi _{2} = \frac{\mu _{e}}{n^{2}\pi ^{2}\mu _{i}} + 2n^{2}\pi ^{2}\\ \varpi _{3} = n^{4}\pi ^{4}\mu _{i} + \mu _{e} \end{array} $$
(62)

Again columns of Q are eigenvectors of the matrix D 0. Using the same procedure described earlier, the following equations are obtained in analogy to Eqs. (45) and (49):

$$\begin{aligned} &{\dot{\mathbf{S}} = \mathbf{E}_{11}\mathbf{S} + \mathbf{E}_{12} \mathbf{T} + \mathbf{m}_{1}\bigl(\mathbf{S},\mathbf{T},\dot{\mathbf{S}}, \dot{\mathbf{T}}\bigr)} \end{aligned}$$
(63)
$$\begin{aligned} &{\frac{\partial}{\partial \mathbf{S}}\mathbf{h}(\mathbf{S},\boldsymbol{\varepsilon} )\bigl[ \mathbf{E}_{11}\mathbf{S} + \mathbf{E}_{12}\mathbf{h}( \mathbf{S},\boldsymbol{\varepsilon} )\bigr] + \mathbf{m}_{1}( \boldsymbol{\varepsilon},\mathbf{S},\dot{\mathbf{S}}) - \mathbf{E}_{21} \mathbf{S}} \\&{\quad {} - \mathbf{E}_{22}\mathbf{h}(\mathbf{S},\boldsymbol{ \varepsilon} ) - \mathbf{m}_{2}\bigl(\boldsymbol{\varepsilon},\mathbf{S}, \dot{\mathbf{S}}\bigr) = 0} \end{aligned}$$
(64)

where

$$ \begin{array}{l} \left [ \begin{array}{c@{\quad}c} \mathbf{E}_{11} & \mathbf{E}_{12} \\\mathbf{E}_{21} & \mathbf{E}_{22} \end{array} \right ] = \mathbf{Q}^{ - 1}(\mathbf{D}_{0} + \mathbf{D}_{\varepsilon} )\mathbf{Q}\\ \left [ \begin{array}{c} \mathbf{m}_{1}(\mathbf{S},\mathbf{T},\dot{\mathbf{S}},\dot{\mathbf{T}}) \\\mathbf{m}_{2}(\mathbf{S},\mathbf{T},\dot{\mathbf{S}},\dot{\mathbf{T}}) \end{array} \right ] = \mathbf{Q}^{ - 1}\mathbf{N}\bigl(\mathbf{Z},\dot{\mathbf{Z}}\bigr) \end{array} $$
(65)

Other symbols are the same as the ones used in Sect. 4.1. Again, the above partial differential equation can not be solved explicitly. Therefore, h(S,ε) is approximated by a quadratic polynomial similar to Eq. (50). Substituting Eq. (50) into Eq. (64), and equating coefficients of quadratic terms, one may determine h 2(S,ε). Substitution of this h 2(S,ε) into Eq. (63) gives the dynamics of the nonlinear system in the center manifold as

$$\begin{aligned} \left [ \begin{array}{c} \dot{Z}_{1} \\\dot{Z}_{2} \end{array} \right ] =& \left [ \begin{array}{c@{\quad}c} \varLambda _{1}\varepsilon + \varLambda _{2}\varepsilon ^{2} & - (\omega + \varLambda _{3}\varepsilon + \varLambda _{4}\varepsilon ^{2}) \\\omega + \varLambda _{3}\varepsilon + \varLambda _{4}\varepsilon ^{2} & \varLambda _{1}\varepsilon + \varLambda _{2}\varepsilon ^{2} \end{array} \right ] \\&{}\times \left [ \begin{array}{c} Z_{1} \\Z_{2} \end{array} \right ] \\&{} + \left [ \begin{array}{c} \Delta _{1}Z_{1}^{3} + \Delta _{2}Z_{2}^{3} + \Delta _{3}Z_{1}Z_{2}^{2} + \Delta _{4}Z_{1}^{2}Z_{2} \\\Delta _{5}Z_{1}^{3} + \Delta _{6}Z_{2}^{3} + \Delta _{7}Z_{1}Z_{2}^{2} + \Delta _{8}Z_{1}^{2}Z_{2} \end{array} \right ] \\&{} + \left [ \begin{array}{c} (\varTheta _{1}Z_{1} + \varTheta _{2}Z_{2})(Z_{1}\dot{Z}_{2} - Z_{2}\dot{Z}_{1}) \\(\varTheta _{1}Z_{2} - \varTheta _{2}Z_{2})(Z_{1}\dot{Z}_{2} - Z_{2}\dot{Z}_{1}) \end{array} \right ] \\&{} + O\bigl(\vert \mathbf{A},\boldsymbol{\varepsilon} \vert ^{4}\bigr) \end{aligned}$$
(66)

where ω, Λ j (j=1–4), Δ j (j=1–8) and Θ j (j=1,2) are defined in Appendix A. It is seen that Eq. (66) is not in a standard form for the Hopf bifurcation. So, the method of normal form is applied to Eq. (66), to transform it to a standard form [33]. Using relations ζ=Z 1+iZ 2, \(\bar{\zeta} = Z_{1} - iZ_{2}\), Eq. (66) is written in complex form as

$$\begin{aligned} \dot{\zeta} =& \varPsi _{5}i\zeta + \hat{\varepsilon} \bigl[\varPsi _{1}\bigl(\zeta ^{2}\dot{\bar{\zeta}} - \zeta \bar{\zeta} \dot{\zeta} \bigr) + \varPsi _{2}\zeta ^{3} + \varPsi _{3}\bar{\zeta} \zeta ^{2} \\&{} + \varPsi _{4}\zeta \bar{\zeta} ^{2} + \varPsi _{6}\zeta + \varPsi _{7}\bar{\zeta} ^{3}\bigr] \end{aligned}$$
(67)

where Ψ j (j=1–7) is defined in Appendix B, and \(\hat{\varepsilon}\) is a small nondimensional bookkeeping parameter. To apply the normal form method, a near-identity transformation is defined as [33]

$$ \zeta = \eta + \hat{\varepsilon} H(\eta,\bar{\eta} ),\qquad \bar{\zeta} = \bar{\eta} + \hat{\varepsilon} \bar{H}(\eta,\bar{\eta} ) $$
(68)

Substitution of Eq. (68) into Eq. (67) gives

$$\begin{aligned} \dot{\eta} =& \hat{\varepsilon} \varPsi _{1}\bigl(\eta + \hat{ \varepsilon} H(\eta,\bar{\eta} )\bigr) \bigl(\eta + \hat{\varepsilon} H(\eta,\bar{ \eta} )\bigr) \\&{}\times \frac{\partial}{\partial t}\bigl(\bar{\eta} + \hat{\varepsilon} \bar{H}(\eta, \bar{\eta} )\bigr) - \hat{\varepsilon} \varPsi _{1}\bigl(\eta + \hat{\varepsilon} H( \eta,\bar{\eta} )\bigr) \\&{}\times \bigl(\bar{\eta} + \hat{\varepsilon} \bar{H}(\eta,\bar{ \eta} )\bigr)\frac{\partial}{\partial t}\bigl(\eta + \hat{\varepsilon} H(\eta,\bar{\eta} ) \bigr) \\&{} + \hat{\varepsilon} \varPsi _{2}\bigl(\eta + \hat{\varepsilon} H( \eta,\bar{\eta} )\bigr)^{3} + \hat{\varepsilon} \varPsi _{3} \bigl(\bar{\eta} + \hat{\varepsilon} \bar{H}(\eta,\bar{\eta} )\bigr) \\&{}\times \bigl(\eta + \hat{\varepsilon} H(\eta,\bar{\eta} )\bigr)^{2} + \hat{\varepsilon} \varPsi _{4}\bigl(\eta + \hat{\varepsilon} H( \eta,\bar{\eta} )\bigr) \\&{}\times \bigl(\bar{\eta} + \hat{\varepsilon} \bar{H}(\eta,\bar{ \eta} )\bigr)^{2} + (\hat{\varepsilon} \varPsi _{6} + \varPsi _{5}i) \\&{}\times \bigl(\eta + \hat{\varepsilon} H(\eta,\bar{\eta} )\bigr) + \hat{\varepsilon} \varPsi _{7}\bigl(\bar{\eta} + \hat{ \varepsilon} \bar{H}(\eta,\bar{\eta} )\bigr)^{3} \end{aligned}$$
(69)

Because the perturbation in Eq. (69) contains linear and third-order terms, \(H(\eta,\bar{\eta} )\) are expressed as

$$ H(\eta,\bar{\eta} ) = \kappa _{0}\eta + \kappa _{1}\eta ^{3} + \kappa _{2}\bar{\eta} ^{3} + \kappa _{3}\bar{\eta} \eta ^{2} + \kappa _{4}\eta \bar{ \eta} ^{2} $$
(70)

In addition to the first approximation, we have

$$ \dot{\eta} = \varPsi _{5}i\eta,\qquad \dot{\bar{\eta}} = - \varPsi _{5}i\bar{\eta} $$
(71)

Substituting Eqs. (70)–(71) into the right-hand side of Eq. (69) and retaining terms up to \(O(\hat{\varepsilon} )\), one may obtain

$$\begin{aligned} \dot{\eta} =& ( - 2i\kappa _{1}\varPsi _{5} + \varPsi _{2})\eta ^{3} + (\varPsi _{3} - 2\varPsi _{1}\varPsi _{5}i)\bar{\eta} \eta ^{2} \\&{} + (\varPsi _{6} + \varPsi _{5}i)\eta + (\varPsi _{4} + 2i\kappa _{4}\varPsi _{5})\eta \bar{\eta} ^{2} \\&{} + (\varPsi _{7} + 4i\kappa _{2}\varPsi _{5})\bar{\eta} ^{3} \end{aligned}$$
(72)

Now, one can choose κ j (j=1,2,4), so that Eq. (72) takes the simplest form

$$ \kappa _{1} = \frac{ - i\varPsi _{2}}{2\varPsi _{5}},\qquad \kappa _{2} = \frac{i\varPsi _{7}}{4\varPsi _{5}},\qquad \kappa _{4} = \frac{i\varPsi _{4}}{2\varPsi _{5}} $$
(73)

with this choice, the normal form of Eq. (72) becomes

$$ \dot{\eta} = (\varPsi _{3} - 2\varPsi _{1}\varPsi _{5}i)\bar{\eta} \eta ^{2} + (\varPsi _{6} + \varPsi _{5}i)\eta $$
(74)

It is clear that the parameters κ j (j=0,3) do not appear in Eq. (72), and hence they are arbitrary. These parameters are related to the resonance terms. Finally, transforming Eq. (74) to the polar coordinates (\(\eta = \operatorname{Re} ^{i\theta}\)), and using Appendices A and B, the normal form of the Hopf bifurcation in terms of the system parameters becomes

$$\begin{aligned} &{\dot{R} = \bigl[n^{8}\pi ^{8}\mu _{i}^{2}\bigl(n^{4}\pi ^{4}\mu _{i} + \mu _{e}\bigr) \bigl(\vartheta - 16n^{4}\pi ^{4}\bigr)\varepsilon ^{2}\big/\vartheta ^{3} } \\&{\hphantom{\dot{R} =} {}+ 2n^{6}\pi ^{6}\mu _{i}/\vartheta \varepsilon \bigr]r + n^{10}\pi ^{10} \mu _{i}/\vartheta r^{3}} \end{aligned}$$
(75)
$$\begin{aligned} &{\dot{\theta} = \bigl(\mu _{e}^{3} + 2n^{4}\pi ^{4}\mu _{i}\mu _{e}^{2} + n^{8}\pi ^{8}\mu _{e}\mu _{i}^{2} } \\&{\hphantom{\dot{\theta} =} {} + 4n^{4}\pi ^{4}\mu _{e}\bigr)\big/\bigl(\vartheta n^{2}\pi ^{2}\mu _{i}\bigr) } \\&{\hphantom{\dot{\theta} =} {}+ \bigl(n^{4}\pi ^{4}\mu _{e} \mu _{i} + 4n^{4}\pi ^{4} + \mu _{e}^{2}\bigr)/\vartheta \varepsilon} \\&{\hphantom{\dot{\theta} =} {}+ 2n^{10}\pi ^{10}\mu _{i}^{2}\big/\vartheta ^{3}\bigl( - 4n^{4}\pi ^{4}+ 3\mu _{e}^{2}} \\&{\hphantom{\dot{\theta} =} {} + 3n^{8}\pi ^{8}\mu _{i}^{2} + 6n^{4}\pi ^{4}\mu _{e}\mu _{i}\bigr) \varepsilon ^{2}} \\&{\hphantom{\dot{\theta} =} {} - 1/\bigl(2\vartheta n^{2}\pi ^{2}\mu _{i}\bigr) \bigl(n^{6}\pi ^{6}\mu _{i}\mu _{e}^{2} + n^{10}\pi ^{10}\mu _{e}\mu _{i}^{2}} \\&{\hphantom{\dot{\theta} =} {}+ 4n^{10}\pi ^{10}\mu _{i}\bigr)r^{2}} \end{aligned}$$
(76)

Now, we can use Eqs. (75)–(76) to analyze the dynamical behavior of the rotating shaft near the Hopf bifurcation. Equation (75) shows that the trivial solution is stable if ε<0 and it is unstable for ε>0. Since the coefficient of R 3 in Eq. (75) is always negative, the resulting Hopf bifurcation is supercritical. Therefore, the trivial solution becomes unstable and a limit cycle creates for ε>0. A scenario of the bifurcation is shown in Fig. 4. The corresponding phase portraits are similar to Fig. 3. Neglecting the ε 2 term, the radius of the limit cycle becomes

$$ R^{2} = \frac{2\varepsilon}{n^{4}\pi ^{4}} $$
(77)

Equation (77) shows that the R 2 (square of the limit cycle radius) is linearly dependent on spinning speed and the ratio of external damping to internal damping, μ e /μ i . Again, the increase of spinning speed and internal damping increase the radius of limit cycle. To find the precession rate \(\dot{\theta}\), one may substitute Eq. (77) into Eq. (76) to obtain

$$\begin{aligned} \dot{\theta} =& \mu _{e}/\bigl(n^{2}\pi ^{2}\mu _{i}\bigr) - 1/\bigl(2\vartheta ^{2}\bigr) \bigl(\mu _{e}^{3} + 2n^{4}\pi ^{4}\mu _{i}\mu _{e}^{2} \\&{} + n^{8}\pi ^{8}\mu _{e}\mu _{i}^{2} - 12n^{4}\pi ^{4}\mu _{e}- 8n^{8}\pi ^{8}\mu _{i}\bigr) \\&{}\times n^{2} \pi ^{2}\mu _{i}\varepsilon ^{2} \end{aligned}$$
(78)

Equation (78) shows that the whirling motion of the shaft is nonsynchronous. The increase of external damping increases the precession rate \(\dot{\theta}\) and the increase of internal damping decreases it. An interesting result is that the precession rate \(\dot{\theta}\) is independent of ε and it just is a function of ε 2. Since ε is a small parameter, the term ε 2 is very small. Hence,

$$ \dot{\theta} \simeq \mu _{e}/\bigl(n^{2}\pi ^{2} \mu _{i}\bigr) $$
(79)

The whirling speed Ω W of the shaft may be written as

$$ \varOmega _{W} = \varOmega + \dot{\theta} $$
(80)

In the neighborhood of the bifurcation,

$$ \varOmega \simeq n^{2}\pi ^{2} + \frac{\mu _{e}}{n^{2}\pi ^{2}\mu _{i}} $$
(81)

Equations (79)–(81) give

$$ \varOmega _{W} \simeq n^{2}\pi ^{2} $$
(82)

It may be concluded that in the neighborhood of the Hopf bifurcation, the shaft centerline will whirl at a rate approximately equal to the nth critical speed [4, 31].

Fig. 4
figure 4

Diagram of the Hopf bifurcation

Full size image

5 Conclusions

Bifurcations in a simply supported rotating shaft were studied. The shaft was modeled as an in-extensional viscoelastic spinning beam with large amplitudes, which includes the effects of nonlinear curvature and inertia. Torsional stiffness and external damping of the shaft were considered, but shear deformation and rotary inertia were neglected. To find the boundaries of stability, the linearized shaft model was used. Using center manifold theory and the method of normal form, analytical expressions were obtained, which describe the behavior of the rotating shaft in the neighborhood of the double zero eigenvalues and Hopf bifurcations. It was shown that dependent on the system parameters, the synchronous and nonsynchronous whirling of the rotating shaft are possible. The most important results of the paper are as follows:

  • For case μ e =0, the trivial solution is asymptotically stable if spinning speed does not exceed the critical speeds. In this case, a nontrivial circle of equilibria bifurcates from the zero solution as the spinning speed exceeds the critical speeds. In this case, the shaft whirls synchronously.

  • For case μ e >0, a Hopf bifurcation occurs at boundary ε 1=ε 2/(π 2 μ i ). Therefore, the trivial solution becomes unstable and a limit cycle appears for ε 1>ε 2/(π 2 μ i ). In this case, R 2 (square of the limit cycle radius) is linearly dependent on spinning speed and the ratio of external damping to internal damping, μ e /μ i . Precession rate \(\dot{\theta}\) of the shaft is proportional to the ratio of external damping to internal damping, μ e /μ i and is independent of the spinning speed.

  • As spinning speed exceeds the boundaries n 2 π 2+μ e /(n 2 π 2 μ i ), a Hopf bifurcation occurs and a creation of a limit cycle from the trivial solution is expected for mode n. In this case, the square of the limit cycle radius is linearly dependent on spinning speed and the ratio of external damping to internal damping, μ e /μ i . In addition, increase of external damping increases the precession rate \(\dot{\theta}\) and the increase of internal damping decreases it. In the neighborhood of the Hopf bifurcation, the shaft centerline will whirl at a rate approximately equal to the nth critical speed.