1 Introduction

Crack fault, which is one of the most serious damage in aircraft engines and other rotating machines, has been paid more and more attention in the last four decades [1]. Wauer [2], Gasch [3] and Dimarogonas [4] have reviewed the dynamical behavior of rotor systems with transverse cracks, where many complex nonlinear dynamic phenomena are shown. Based on the switching crack model (also known as hinge model) [3] and the response-dependent breathing crack model [5, 6], the critical speed was investigated to detect the nonlinear dynamics of various cracked rotor systems, that is influenced by the crack breathing and the rotor imbalance orientation [7], and the stabilities of periodic movements [8–10] and nonlinear responses [11] in cracked rotor systems were also discussed. In addition, the harmonic balance method [12], the alternate frequency/time domain approach [13] and some experimental methods [14, 15] were developed to gain an insight into the dynamical characteristics of cracked rotors, respectively. Throughout these studies, it was shown that the \(2\times \) and \(3\times \) super-harmonic frequency responses can be viewed as distinct signals for crack fault detections. Accordingly, the diagnostic tools for the changes in evolution of the nonlinear behavior at the super-harmonic frequency components are proposed to gain crack detection strategies [16–22]. However, to our knowledge, analytical investigations for the super-harmonic resonances affected by system parameters and their local bifurcation characteristics have been rarely seen in the current references.

The gravity, which plays an important role called weight dominance in the crack breathing, is a constant in general rotor systems [23, 24]. In an aircraft rotor system, however, the maneuver load playing the same role as the gravity may change from 0 to highly 10 times of the gravity during the maneuvering flight [25, 26]. Therefore, it will make great effect on the nonlinear dynamics and bifurcations of the rotor system. Lin et al. [27] investigated the dynamics of a rotor system maneuvering with either a constant flight speed or a constant acceleration, wherein it has been shown that the climbing angle, acceleration and other flight parameters make significant influence on the parameter range for bifurcation, quasi-periodic response and chaotic response as well as system stability. Hou et al. [28, 29] discussed the occurrence of the subharmonic resonance in an aircraft rotor system due to the effect of the maneuver load from hovering flight, which indicates that the subharmonic resonance may induce a rub-impact phenomena in the proposed rotor system. Yang et al. [30] found three different ways for the vibration response going to chaos in a cracked rotor system during hovering flight, that are quasi-periodic, intermittence and period-3 bifurcation. Moreover, the dynamic response of a cracked rotor-bearing system under time-dependent base movements was studied by Han and Chu [31], and the effects of various base angular motions, frequency and amplitude of base excitations, and crack depths on the system dynamic behaviors were discussed. However, the dynamical effects of the maneuver load on the super-harmonic resonances in aircraft rotor system with early crack fault and their local bifurcation characteristics have not been discussed in the above literature.

This problem is subjected to combined parametric and external excitations. Many researches working on this subject have been carried out. The primary resonance dynamics of a weak nonlinear system subjected to parametric and external excitations was investigated in [32], where it was found that stable multimodal responses may exist in the first-order asymptotic solution, even though only one mode was involved in the resonance and no internal resonance condition was present. For a nonlinear parametrically self-excited system under harmonic external excitation, the vibration amplitudes and the width of synchronization areas close to the first and second free vibration frequency were demonstrated in [33]. A nonlinear oscillator with a bias parameter that breaks the symmetry of the motion was considered in [34], wherein it was found that the dynamics and stability of the system under external and parametric excitations significantly depended on the bias parameter. Nonlinear phenomena including various types of bifurcations [35], resonant hysteresis [36] and routes to chaos [35–37] were found in different dynamic systems driven by combined parametric and external excitations. Besides, the dynamic analysis of controlling chaos in a one degree-of-freedom system with quadratic and cubic nonlinearities subjected to external and parametric excitations with incommensurate frequencies was carried out in [38].

According to the previous investigations, the primary resonance of cracked rotor systems has been deeply discussed [7, 32], and it has been shown that the 2:1 and 3:1 super-harmonic resonances are representative phenomena in cracked rotor systems [16]. Thus, the objective of this paper is mainly to detect the local bifurcation characteristics for the 2:1 and 3:1 super-harmonic resonances of an aircraft cracked rotor system considering the maneuver load, which is a dynamic system subjected to not only parametric and harmonic external excitations, but also inertial excitation. In the motion equations of the system, the maneuver load is in the vertical direction only, which breaks the symmetry of the motion. The multiple scales method is used to obtain the bifurcation equations of the system, which enables us to analyze the response characteristics of the system affected by the maneuver load combined with the crack breathing. Moreover, the two-state variable singularity method is employed to analyze the bifurcation characteristics of the system affected by the parameter combination between the maneuver load and the crack coefficient, and different bifurcation modes are demonstrated accordingly.

The remaining parts of the paper are organized as follows. In Sect. 2, the equations of motion of the system are formulated with the consideration of the nonlinear stiffness of the Duffing type and the breathing of a transverse crack on the shaft, as well as the maneuver load induced by a climbing and diving flight model. In Sect. 3, the bifurcation equations for 2:1 and 3:1 super-harmonic resonances are obtained by utilizing the multiple scales method to solve the motion equations analytically, respectively. Accordingly, the response characteristics of the system affected by the crack coefficient and the maneuver load are analyzed. In addition, the numerical computations are also carried out by using the fourth-order Runge–Kutta method to verify the correctness of the above-mentioned theoretical results. In Sect. 4, the local bifurcation characteristics of the system affected by the crack coefficient and the maneuver load are analyzed by using the two-state variable singularity method for both 2:1 and 3:1 super-harmonic resonance cases. For each case, two curves of hysteresis set dividing \(K-G\) parameter plane into three regions are demonstrated. Different bifurcation modes for different parameter combinations from the three regions and the two curves are obtained accordingly. Finally, in Sect. 5, the principle results of this study and conclusions are summarized.

2 Mathematical modeling

2.1 Rotor system model

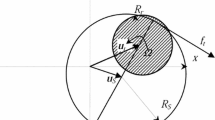
A symmetrical rotor system model considering the nonlinear stiffness of Duffing type [39–41] and a transverse crack on the shaft is presented in this paper as shown in Fig. 1, where \(m\) and \(e\) are the mass and the eccentricity of the disk, \(k\) and \(\alpha \) are, respectively, the linear and nonlinear coefficients of the shaft stiffness, \(\omega \) is the rotation speed. The motion equations of the system are presented by

$$\begin{aligned}&\!\!\!m\ddot{y}+c\dot{y}+ky-F_y +\alpha y^{3}=me\omega ^{2}\cos \omega t+G_y , \nonumber \\ \end{aligned}$$
(1a)
$$\begin{aligned}&\!\!\! m\ddot{z}+c\dot{z}+kz-F_z +\alpha z^{3}=me\omega ^{2}\sin \omega t+G_z ,\nonumber \\ \end{aligned}$$
(1b)

in which, \(c=2\xi m\omega \) is the damping of the shaft, \(F_y\) and \(F_z\) are the forces representing the effects of the crack, \(G_y\) and \(G_z\) are the additional exciting forces caused by the maneuvering flight of the aircraft, i.e., the maneuver load.

Fig. 1
figure 1

Schematic diagram of a cracked rotor system

Full size image

2.2 Maneuvering flight model

Figure 2 shows the maneuvering flight model discussed in this paper, where it is assumed that the angular velocity \(\omega _\mathrm{m}\) and the speed \(v\) of the aircraft are constants in the climbing and diving flight, and \(o\) is the gravity center of the aircraft corresponding to Fig. 1. Then, \(G_y\) and \(G_z\) can be obtained as follows

$$\begin{aligned} G_y= & {} m\omega _\mathrm{m} v=Gmg, \end{aligned}$$
(2a)
$$\begin{aligned} G_z= & {} 0, \end{aligned}$$
(2b)

where the \(G\) value represents how many times larger than the gravity acceleration.

Fig. 2
figure 2

Climbing–diving flight model

Full size image

2.3 Breathing crack model

The cross section of the cracked shaft is shown in Fig. 3, where it is supposed that the initial orientation of the crack coincides with y-axis. \(F_y\) and \(F_z\) can be denoted by [7, 16]

$$\begin{aligned} F_y= & {} f\left( {\omega t} \right) \Delta k\left( {y\cos ^{2}\omega t+z\sin \omega t\cos \omega t} \right) \!,\end{aligned}$$
(3a)
$$\begin{aligned} F_z= & {} f\left( {\omega t} \right) \Delta k\left( y\sin \omega t\cos \omega t+z\sin ^{2}\omega t \right) \!, \end{aligned}$$
(3b)

where \(\Delta k\) is the crack stiffness that represents the effect of the crack depth on the stiffness of the shaft, \(f\left( {\omega t} \right) \) reflects the breathing of the crack. Supposing that the breathing of the crack depends on the direction of the maneuver load, then we have

$$\begin{aligned} f\left( {\omega t} \right) =\frac{1+\cos \omega t}{2}\!. \end{aligned}$$
(4)
Fig. 3
figure 3

Schematic diagram of the cross section of the cracked shaft

Full size image

2.4 Equations of motion

Substituting (2) and (3) into (1), noting (4), the equations of motion of the system are obtained as follows

$$\begin{aligned}&\!\!\!m\ddot{y}+c\dot{y}+ky \nonumber \\&\!\!\!\qquad -\,\frac{\Delta k}{2}\left( {1+\cos \omega t} \right) \left( {y\cos ^{2}\omega t+z\sin \omega t\cos \omega t} \right) \nonumber \\&\!\!\!\qquad +\,\alpha y^{3}=me\omega ^{2}\cos \omega t+Gmg, \end{aligned}$$
(5a)
$$\begin{aligned}&\!\!\! m\ddot{z}+c\dot{z}+kz\nonumber \\&\!\!\!\qquad -\,\frac{\Delta k}{2}\left( {1+\cos \omega t} \right) \left( {y\sin \omega t\cos \omega t+z\sin ^{2}\omega t} \right) \nonumber \\&\!\!\!\qquad +\,\alpha z^{3}=me\omega ^{2}\sin \omega t. \end{aligned}$$
(5b)

Letting \(Y=\frac{y}{\delta }\),  \(Z=\frac{z}{\delta }\),  \(\tau =\omega t\),  \(s=\frac{\omega }{\omega _{\mathrm{c0}} }\),  \(K=\frac{\Delta k}{k}\),  \(E=\frac{e}{\delta }\), where \(\delta =\frac{mg}{k}\),  \(\omega _{\mathrm{c0}} =\sqrt{\frac{k}{m}}\), the dimensionless equations of Eq. (5) can be obtained as follows

$$\begin{aligned}&\!\!\!{Y}''+2\xi {Y}'+\frac{1}{s^{2}}Y\nonumber \\&\!\!\!\qquad -\,\frac{K}{2s^{2}}\left( {1+\cos \tau } \right) \left( {Y\cos ^{2}\tau +Z\sin \tau \cos \tau } \right) \nonumber \\&\!\!\!\qquad +\,K_1 Y^{3}=E\cos \tau +\frac{G}{s^{2}},\end{aligned}$$
(6a)
$$\begin{aligned}&\!\!\! {Z}''+2\xi {Z}'+\frac{1}{s^{2}}Z\nonumber \\&\!\!\!\qquad -\,\frac{K}{2s^{2}}\left( {1+\cos \tau } \right) \left( {Y\sin \tau \cos \tau +Z\sin ^{2}\tau } \right) \nonumber \\&\!\!\!\qquad +\,K_1 Z^{3}=E\sin \tau , \end{aligned}$$
(6b)

where \(K_1 =\frac{\alpha \delta ^{2}}{m\omega ^{2}}\).

The basic system parameters are shown as follows [28, 42]

$$\begin{aligned} m= & {} 32.1\,\quad \hbox {kg},\quad k=2.5\times 10^{7}\text { N m}^{-1}, \nonumber \\&\alpha =3.8\times 10^{14}\text { N m}^{-3},\,\nonumber \\ \xi= & {} 0.02, \quad e=10 \upmu m, \quad K=0.1, \quad G=5. \end{aligned}$$
(7)

3 Response analysis

3.1 Equations transforming

Considering the condition of weak damping, shallow crack and weak support nonlinearity, letting \(q_1 =Y\),   \(q_2 =Z\),   \(\omega _1 =\frac{1}{s}\),   \(\varepsilon a_1 =2\xi \),   \(\varepsilon a_2 =\frac{K}{8s^{2}}\),   \(\varepsilon a_3 =K_1 \), \(G_1 =\frac{G}{s^{2}}\), where \(\varepsilon \) is a small parameter, then (7) can be transformed as

$$\begin{aligned} {q}''_1+ & {} \omega _{1}^{2} q_1 =-\varepsilon a_1 {q}'_1 +\varepsilon a_2 \left( \left( 2+3\cos \tau +2\cos 2\tau \right. \right. \nonumber \\+ & {} \left. \left. \cos 3\tau \right) q_1 +\left( {\sin \tau +2\sin 2\tau +\sin 3\tau } \right) q_2 \right) \nonumber \\- & {} \varepsilon a_3 q_1^3 +E\cos \tau +G_1 , \end{aligned}$$
(8a)
$$\begin{aligned} {q}''_2+ & {} \omega _1^2 q_2 =-\varepsilon a_1 {q}'_2 +\varepsilon a_2 \left( \left( 2+\cos \tau -2\cos 2\tau \right. \right. \nonumber \\- & {} \left. \left. \cos 3\tau \right) q_2 +\left( {\sin \tau +2\sin 2\tau +\sin 3\tau } \right) q_1 \right) \nonumber \\- & {} \varepsilon a_3 q_2^3 +E\sin \tau . \end{aligned}$$
(8b)

Equation (8) can be analytically solved by using the multiple scales method [43, 44] to investigate the 2:1 and 3:1 super-harmonic resonances and the corresponding local bifurcation characteristics of the system. The solving processes are given in the following two sections.

3.2 Equations solving for 2:1 super-harmonic resonance

Letting \(T_1 =\tau \) and \(T_2 =\varepsilon \tau \), supposing that the tuning parameter \(\sigma \) satisfies

$$\begin{aligned} \omega _1^2 =2^{2}-\varepsilon \sigma =4-\varepsilon \sigma . \end{aligned}$$
(9)

Supposing the solutions of Eq. (8) are as follows

$$\begin{aligned} q_1= & {} u_{11} +\varepsilon u_{12} ,\end{aligned}$$
(10a)
$$\begin{aligned} q_2= & {} u_{21} +\varepsilon u_{22}. \end{aligned}$$
(10b)

Substituting (10) into Eq. (8) and equating the coefficients of \(\varepsilon ^{0}\) and \(\varepsilon ^{1}\) to zero, it can be obtained that

$$\begin{aligned} \varepsilon ^{0}: \end{aligned}$$
$$\begin{aligned} D_{1}^{2} u_{11} +4u_{11}= & {} E\cos \tau +G_1 ,\end{aligned}$$
(11a)
$$\begin{aligned} D_{1}^{2} u_{21} +4u_{21}= & {} E\sin \tau ; \end{aligned}$$
(11b)
$$\begin{aligned}&\varepsilon ^{1}:\nonumber \\&\!\!\!D_1^2 u_{12} +2D_1 D_2 u_{11} +4u_{12} -\sigma u_{11} =-a_1 D_1 u_{11} \nonumber \\&\!\!\! \quad +\,a_2 \left( {2+3\cos \tau +2\cos 2\tau +\cos 3\tau } \right) u_{11}\nonumber \\&\!\!\! \quad +\,a_2 \left( {\sin \tau +2\sin 2\tau +\sin 3\tau } \right) u_{21} -a_3 u_{11}^3 , \end{aligned}$$
(12a)
$$\begin{aligned}&\!\!\!D_1^2 u_{22} +2D_1 D_2 u_{21} +4u_{22} -\sigma u_{21} =-a_1 D_1 u_{21} \nonumber \\&\!\!\!\ \quad +\,a_2 \left( {2+\cos \tau -2\cos 2\tau -\cos 3\tau } \right) u_{21} \nonumber \\&\!\!\!\ \quad +\,a_2 \left( {\sin \tau +2\sin 2\tau +\sin 3\tau } \right) u_{11} -a_3 u_{21}^3 , \end{aligned}$$
(12b)

where \(D_1 =\frac{\partial }{\partial T_1 }\),  \(D_2 =\frac{\partial }{\partial T_2 }\).

The general solutions of Eq. (11) are supposed to be

$$\begin{aligned} u_{11} \left( {T_1 ,T_2 } \right)= & {} A\left( {T_2 } \right) \cos \left( {2T_1 +\phi _1 \left( {T_2 } \right) } \right) \nonumber \\&+\,C_1 \cos T_1 +G_2 , \end{aligned}$$
(13a)
$$\begin{aligned} u_{21} \left( {T_1 ,T_2 } \right)= & {} B\left( {T_2 } \right) \sin \left( {2T_1 +\phi _2 \left( {T_2 } \right) } \right) \nonumber \\&+\,C_2 \sin T_1 , \end{aligned}$$
(13b)

where \(C_1 =C_2 =\frac{E}{3}\),  \(G_2 =\frac{G_1 }{4}\).

Substituting (13) into Eq. (12), then, according to the conditions of eliminating the secular terms, it can be obtained that

$$\begin{aligned} {A}'= & {} -\frac{1}{8}\left( 4a_1 A+4a_2 C_1 \sin \phi _1 \right. \nonumber \\&\quad \left. +\,4a_2 G_2 \sin \phi _1 -3a_3 C_1^2 G_2 \sin \phi _1 \right) , \end{aligned}$$
(14a)
$$\begin{aligned} A{\phi }'_1= & {} -\frac{1}{4}\sigma A+\frac{1}{16}\left( 3a_3 A^{3}+6a_3 AC_1^2 \right. \nonumber \\&\quad \left. +\,12a_3 AG_2^2 -8a_2 A-8a_2 C_1 \cos \phi _1 \right. \nonumber \\&\quad \left. -\,8a_2 G_2 \cos \phi _1 +6a_3 C_1^2 G_2 \cos \phi _1 \right) , \end{aligned}$$
(14b)
$$\begin{aligned} {B}'= & {} -\frac{1}{4}\left( 2a_1 B+a_2 C_1 \sin \phi _2 +a_2 C_2 \sin \phi _2 \right. \nonumber \\&\quad \left. +\,2a_2 G_2 \sin \phi _2 \right) , \end{aligned}$$
(14c)
$$\begin{aligned} B{\phi }'_2= & {} -\frac{1}{4}\sigma B+\frac{1}{16}\left( 3a_3 B^{3}+6a_3 C_2^2 B-8a_2 B \right. \nonumber \\&\quad \left. -\,4a_2 C_1 \cos \phi _2 -4a_2 C_2 \cos \phi _2 \right. \nonumber \\&\left. -\,8a_2 G_2 \cos \phi _2 \right) , \end{aligned}$$
(14d)

where \(\left( \right) ^{\prime }=\frac{\hbox {d}}{\hbox {d}T_2 }\left( \right) \).

Equating the right sides of Eq. (14) to zero, then eliminating \(\phi _1\) and \(\phi _2\), the bifurcation equations of the system can be obtained as follows

$$\begin{aligned}&\!\!\!\frac{16a_1^2 A^{2}}{\left( {-4a_2 C_1 -4a_2 G_2 +3a_3 C_1^2 G_2 } \right) ^{2}}\nonumber \\&\!\!\!\quad +\,\frac{A^{2}\left( {3a_3 A^{2}+6a_3 C_1^2 -8a_2 -4\sigma +12a_3 G_2^2 } \right) ^{2}}{4\left( {-4a_2 C_1 -4a_2 G_2 +3a_3 C_1^2 G_2 } \right) ^{2}}\nonumber \\&\!\!\!\quad -1=0, \end{aligned}$$
(15a)
$$\begin{aligned}&\!\!\! \frac{4a_1^2 B^{2}}{a_2^2 \left( {C_1 +C_2 +2G_2 } \right) ^{2}}\nonumber \\&\!\!\!\quad +\,\frac{B^{2}\left( {3a_3 B^{2}+6a_3 C_2^2 -8a_2 -4\sigma } \right) ^{2}}{16a_2^2 \left( {C_1 +C_2 +2G_2 } \right) ^{2}}\nonumber \\&\!\!\!\quad -1=0, \end{aligned}$$
(15b)

or

$$\begin{aligned}&\!\!\!9a_3^2 \bar{{A}}^{3}+12a_3 \left( {3a_3 C_1^2 -4a_2 -2\sigma +6a_3 G_2^2 } \right) \bar{{A}}^{2}\nonumber \\&\!\!\!\qquad +\,\left( {64a_1^2 \!+\!4\left( {3a_3 C_1^2 -4a_2 \!-\!2\sigma \!+\!6a_3 G_2^2 } \right) ^{2}} \right) \bar{{A}}\nonumber \\&\!\!\!\qquad -\,4\left( {4a_2 C_1 \!+\!4a_2 G_2 \!-\!3a_3 C_1^2 G_2 } \right) ^{2}=0, \end{aligned}$$
(16a)
$$\begin{aligned}&9a_3^2 \bar{{B}}^{3}+12a_3 \left( {3a_3 C_2^2 -4a_2 -2\sigma } \right) \bar{{B}}^{2}\nonumber \\&\!\!\!\qquad +\,\left( {64a_1^2 +4\left( {3a_3 C_2^2 -4a_2 -2\sigma } \right) ^{2}} \right) \bar{{B}}\nonumber \\&\!\!\!\qquad -\,4\left( {2a_2 \left( {C_1 +C_2 } \right) +4a_2 G_2 } \right) ^{2}=0, \end{aligned}$$
(16b)

where \(\bar{{A}}=A^{2}\),   \(\bar{{B}}=B^{2}\).

From (16), the maneuver load \(G_2\) makes significant effects on the coefficients of \(\bar{{A}}^{2}\), \(\bar{{A}}^{1}\) and \(\bar{{A}}^{0}\) due to its coupling with the nonlinear stiffness parameter \(a_3\) and its coupling with the crack parameter \(a_2\) (see 16a). Moreover, the coupling between the crack and the maneuver load also makes an effect on the coefficient of \(\bar{{B}}^{0}\) for the bifurcation equation of the horizontal direction (see 16b). Based on (16), the response characteristics as well as the bifurcation characteristics of the system for 2:1 super-harmonic resonance can be investigated analytically.

3.3 Equations solving for 3:1 super-harmonic resonance

Letting \(T_1 =\tau \) and \(T_2 =\varepsilon \tau \), supposing that the tuning parameter \(\sigma \) satisfies

$$\begin{aligned} \omega _1^2 =3^{2}-\varepsilon \sigma =9-\varepsilon \sigma . \end{aligned}$$
(17)

Supposing the solutions of Eq. (8) are as follows

$$\begin{aligned} q_1= & {} u_{11} +\varepsilon u_{12} ,\end{aligned}$$
(18a)
$$\begin{aligned} q_2= & {} u_{21} +\varepsilon u_{22}. \end{aligned}$$
(18b)

Substituting (18) into Eq. (8) and equating the coefficients of \(\varepsilon ^{0}\) and \(\varepsilon ^{1}\) to zero, it can be obtained that

$$\begin{aligned} \varepsilon ^{0}: \end{aligned}$$
$$\begin{aligned} D_1^2 u_{11} +9u_{11}= & {} E\cos \tau +G_1 , \end{aligned}$$
(19a)
$$\begin{aligned} D_1^2 u_{21} +9u_{21}= & {} E\sin \tau ; \end{aligned}$$
(19b)
$$\begin{aligned} \varepsilon ^{1}: \end{aligned}$$
$$\begin{aligned}&\!\!\!D_1^2 u_{12} +2D_1 D_2 u_{11} +9u_{12} -\sigma u_{11} =-a_1 D_1 u_{11} \nonumber \\&\!\!\!\quad +\,a_2 \left( {2+3\cos \tau +2\cos 2\tau +\cos 3\tau } \right) u_{11} \nonumber \\&\!\!\!\quad +\,a_2 \left( {\sin \tau +2\sin 2\tau +\sin 3\tau } \right) u_{21} -a_3 u_{11}^3 , \end{aligned}$$
(20a)
$$\begin{aligned}&\!\!\!D_1^2 u_{22} +2D_1 D_2 u_{21} +9u_{22} -\sigma u_{21} =-a_1 D_1 u_{21} \nonumber \\&\!\!\!\quad +\,a_2 \left( {2+\cos \tau -2\cos 2\tau -\cos 3\tau } \right) u_{21} \nonumber \\&\!\!\!\quad +\,a_2 \left( {\sin \tau +2\sin 2\tau +\sin 3\tau } \right) u_{11} -a_3 u_{21}^3 , \end{aligned}$$
(20b)

where \(D_1 =\frac{\partial }{\partial T_1 }\), \(D_2 =\frac{\partial }{\partial T_2}\).

The general solutions of Eq. (19) are supposed to be

$$\begin{aligned}&\!\!\!u_{11} \left( {T_1 ,T_2 } \right) =A\left( {T_2 } \right) \cos \left( {3T_1 +\phi _1 \left( {T_2 } \right) } \right) \nonumber \\&\!\!\!\quad +\,C_1 \cos T_1 +G_2 ,\end{aligned}$$
(21a)
$$\begin{aligned}&\!\!\!u_{21} \left( {T_1 ,T_2 } \right) =B\left( {T_2 } \right) \sin \left( {3T_1 +\phi _2 \left( {T_2 } \right) } \right) \nonumber \\&\!\!\!\quad +\,C_2 \sin T_1 , \end{aligned}$$
(21b)

where \(C_1 =C_2 =\frac{E}{8}\), \(G_2 =\frac{G_1 }{9}\).

Substituting (21) into Eq. (20), then according to the conditions of eliminating the secular terms, it can be obtained that

$$\begin{aligned} {A}'= & {} -\frac{1}{24}\Big ( 12a_1 A+4a_2 C_1 \sin \phi _1 \nonumber \\&\left. -\,4a_2 C_2 \sin \phi _1 +4a_2 G_2 \sin \phi _1 -a_3 C_1^3 \sin \phi _1 \right) ,\nonumber \\ \end{aligned}$$
(22a)
$$\begin{aligned} A{\phi }'_1= & {} -\frac{1}{6}\sigma A+\frac{1}{24}\left( 3a_3 A^{3}+6a_3 C_1^2 A+12a_3 G_2^2 A \right. \nonumber \\&\;\left. -\,8a_2 A-4a_2 C_1 \cos \phi _1 +4a_2 C_2 \cos \phi _1 \right. \nonumber \\&\;\left. -\,4a_2 G_2 \cos \phi _1 +a_3 C_1^3 \cos \phi _1 \right) , \end{aligned}$$
(22b)
$$\begin{aligned} {B}'= & {} -\frac{1}{24}\Big (12a_1 B+4a_2 C_1 \sin \phi _2 -4a_2 C_2 \sin \phi _2 \nonumber \\&\left. +\,4a_2 G_2 \sin \phi _2 +a_3 C_2^3 \sin \phi _2 \right) , \end{aligned}$$
(22c)
$$\begin{aligned} B{\phi }'_2= & {} -\frac{1}{6}\sigma B+\frac{1}{24}\left( 3a_3 B^{3}+6a_3 C_2^2 B-8a_2 B \right. \nonumber \\&\left. -\,4a_2 C_1 \cos \phi _2 +4a_2 C_2 \cos \phi _2 \right. \nonumber \\&\left. -\,4a_2 G_2 \cos \phi _2 -a_3 C_2^3 \cos \phi _2 \right) , \end{aligned}$$
(22d)

where \(( )^{\prime }=\frac{\hbox {d}}{\hbox {d}T_2 }( )\).

Equating the right sides of Eq. (22) to zero, then eliminating \(\phi _1\) and \(\phi _2\), the bifurcation equations of the system can be obtained as follows

$$\begin{aligned}&\!\!\! \frac{144a_1^2 A^{2}}{\left( {-4a_2 C_1 +4a_2 C_2 -4a_2 G_2 +a_3 C_1^3 } \right) ^{2}}\nonumber \\&\!\!\!\qquad +\,\frac{A^{2}\left( {3a_3 A^{2}+6a_3 C_1^2 -8a_2 -4\sigma +12a_3 G_2^2 } \right) ^{2}}{\left( {-4a_2 C_1 +4a_2 C_2 -4a_2 G_2 +a_3 C_1^3 } \right) ^{2}}\nonumber \\&\!\!\!\qquad -\,1=0, \end{aligned}$$
(23a)
$$\begin{aligned}&\!\!\! \frac{144a_1^2 B^{2}}{\left( {-4a_2 C_2 +4a_2 C_1 +4a_2 G_2 +a_3 C_2^3 } \right) ^{2}}\nonumber \\&\!\!\!\qquad +\,\frac{B^{2}\left( {3a_3 B^{2}+6a_3 C_2^2 -8a_2 -4\sigma } \right) ^{2}}{\left( {-4a_2 C_2 +4a_2 C_1 +4a_2 G_2 +a_3 C_2^3 } \right) ^{2}}\nonumber \\&\!\!\!\qquad -\,1=0, \end{aligned}$$
(23b)

or

$$\begin{aligned}&\!\!\!9a_3^2 \bar{{A}}^{3}+12a_3 \left( {3a_3 C_1^2 -4a_2 -2\sigma +6a_3 G_2^2 } \right) \bar{{A}}^{2}\nonumber \\&\!\!\!\quad +\left( {144a_1^2 +4\left( {3a_3 C_1^2 -4a_2 -2\sigma +6a_3 G_2^2 } \right) ^{2}} \right) \bar{{A}}\nonumber \\&\!\!\!\quad -\left( {a_3 C_1^3 -4a_2 \left( {C_1 -C_2 } \right) -4a_2 G_2 } \right) ^{2}=0,\end{aligned}$$
(24a)
$$\begin{aligned}&\!\!\! 9a_3^2 \bar{{B}}^{3}+12a_3 \left( {3a_3 C_2^2 -4a_2 -2\sigma } \right) \bar{{B}}^{2}\nonumber \\&\!\!\!\quad +\left( {144a_1^2 +4\left( {3a_3 C_2^2 -4a_2 -2\sigma } \right) ^{2}} \right) \bar{{B}}\nonumber \\&\!\!\!\quad -\left( {a_3 C_2^3 +4a_2 \left( {C_1 -C_2 } \right) +4a_2 G_2 } \right) ^{2} =0, \end{aligned}$$
(24b)

where \(\bar{{A}}=A^{2}\), \(\bar{{B}}=B^{2}\).

From (24), the maneuver load \(G_2\) makes significant effects on the coefficients of \(\bar{{A}}^{2}\), \(\bar{{A}}^{1}\) and \(\bar{{A}}^{0}\) due to its coupling with the nonlinear stiffness parameter \(a_3\) and its coupling with the crack parameter \(a_2\) (see 24a), which is similar to (16). Besides, the coupling between the crack and the maneuver load also makes an effect on the coefficient of \(\bar{{B}}^{0}\) for the bifurcation equation of the horizontal direction (see 24b). Based on (24), the response characteristics as well as the bifurcation characteristics of the system for 3:1 super-harmonic resonance can be investigated analytically.

3.4 Response analysis for 2:1 and 3:1 super-harmonic resonances

In this section, the response characteristics of the system for both 2:1 and 3:1 super-harmonic resonances affected by the crack coefficient and the maneuver load are analyzed according to the corresponded bifurcation Eqs. (16) and (24).

The 2:1 and 3:1 super-harmonic responses of the system for both \(q_1\) and \(q_2\) affected by the crack coefficient under different maneuver load magnitudes are shown in Figs. 4 and  5, which are for \(G=2\) representing a smaller maneuver load situation and for \(G=5\) representing a larger one. As shown in Fig. 4, the resonance peak amplitudes for both \(q_1\) and \(q_2\) increase, and the corresponded resonance frequencies decrease with the increase of the crack coefficient or the crack depth, which is very familiar to us from references [5, 9, 12]. But in Fig. 5, as the crack coefficient increases, it is shown that the resonance frequencies corresponding to the resonance peak amplitudes for both \(q_1\) and \(q_2\) increase, since the resonance response curves show a hard spring characteristic when the crack coefficient becomes larger. Moreover, the super-harmonic response characteristics of \(q_1\) and \(q_2\) for both 2:1 and 3:1 super-harmonic resonances are very similar to each other for both in Figs. 4 and  5.

Fig. 4
figure 4

Super-harmonic responses for \(G=2\). a For 2:1 super-harmonic resonance. b For 3:1 super-harmonic resonance

Full size image
Fig. 5
figure 5

Super-harmonic responses for \(G=5\). a For 2:1 super-harmonic resonance. b For 3:1 super-harmonic resonance

Full size image

Noted that there are some differences between the frequency responses of the system in the vertical and the horizontal directions for the same parameters, which means that the resonances frequencies in the vertical and the horizontal directions are not the same. This phenomenon is due to the asymmetry of the maneuver load, since the maneuver load is in the vertical direction only (see Eqs. 6a, 6b). The differences between the vertical and the horizontal responses affected by the maneuver load can also be found in Eqs. (16a) and (16b) for 2:1 super-harmonic resonance and in Eqs. (24a) and (24b) for 3:1 super-harmonic resonance. The larger the maneuver load is, the larger the difference becomes (see Figs. 4, 5). This asymmetry maneuver load-induced phenomenon has also been discussed in [45].

Figures 6 and  7 show the 2:1 and 3:1 super-harmonic responses of the system for both \(q_1\) and \(q_2\) affected by the maneuver load under different crack coefficient magnitudes, which are, respectively, for \(K=0.05\) representing a smaller crack depth situation and for \(K=0.1\) representing a larger one. As shown in Fig. 6, the resonance peak amplitudes for both \(q_1\) and \(q_2\) increase, and the corresponding resonance frequencies also increase with the increase of the maneuver load. In particular, for \(q_1\), the maneuver load makes an significant effect in increasing the resonance frequencies for both the 2:1 and 3:1 super-harmonic resonances. In Fig. 7, the increase of the resonance frequencies corresponding to the resonance peak amplitudes as well as a hard spring characteristic of the resonance response curve is shown for \(q_2\) when the maneuver load gets larger, but there is not an apparent hard spring characteristic shown for the resonance response curves of \(q_1\). Moreover, the effects of the maneuver load on the super-harmonic response characteristics of 2:1 and 3:1 super-harmonic resonances are very similar to each other for both \(q_1\) and \(q_2\) according to Figs. 6 and  7.

Fig. 6
figure 6

Super-harmonic responses for \(K=0.05\). a For 2:1 super-harmonic resonance. b For 3:1 super-harmonic resonance

Full size image
Fig. 7
figure 7

Super-harmonic responses for \(K=0.1\). a For 2:1 super-harmonic resonance. b For 3:1 super-harmonic resonance

Full size image

3.5 Numerical verification

In this section, we would like to carry out direct numerical computations for Eq. (8) to verify the correctness of the theoretical results obtained in the previous section. Firstly, the calculation formulas of the theoretical responses for both 2:1 and 3:1 super-harmonic resonances are given to obtain the theoretical results accordingly. Then, the fourth-order Runge–Kutta method is employed to demonstrate the numerical results of the computations. Finally, the theoretical results are compared with the numerical results in the form of diagrams for time response and frequency response, respectively.

From (13), the theoretical calculation formulas of \(q_1\) and \(q_2\) for 2:1 super-harmonic resonance are given by

$$\begin{aligned} q_1= & {} A\cos \left( {2\tau +\phi _1 } \right) +C_1 \cos \tau +G_2 \nonumber \\= & {} A\left( {\cos 2\tau \cos \phi _1 -\sin 2\tau \sin \phi _1 } \right) \nonumber \\&+\,C_1 \cos \tau +G_2 , \end{aligned}$$
(25a)
$$\begin{aligned} q_2= & {} B\sin \left( {2\tau +\phi _2 } \right) +C_2 \sin \tau \nonumber \\= & {} B\left( {\sin 2\tau \cos \phi _2 +\cos 2\tau \sin \phi _2} \right) \nonumber \\&+\,C_2 \sin \tau , \end{aligned}$$
(25b)

where \(C_1 =C_2 =\frac{E}{3}\),  \(G_2 =\frac{G_1 }{4}\), and

$$\begin{aligned} \sin \phi _1= & {} \frac{4a_1 A}{-4a_2 C_1 -4a_2 G_2 +3a_3 C_1^2 G_2 }, \quad \nonumber \\ \cos \phi _1= & {} -\frac{A\left( {3a_3 A^{2}\!+\!6a_3 C_1^2 \!-\!8a_2 \!-\!4\sigma \!+\!12a_3 G_2^2 } \right) }{2\left( {-4a_2 C_1 -4a_2 G_2 +3a_3 C_1^2 G_2 } \right) } ;\nonumber \\ \end{aligned}$$
(26a)
$$\begin{aligned} \sin \phi _2= & {} -\frac{2a_1 B}{a_2 \left( {C_1 +C_2 +2G_2 } \right) }, \quad \nonumber \\ \cos \phi _2= & {} \frac{B\left( {3a_3 B^{2}+6a_3 C_2^2 -8a_2 -4\sigma } \right) }{4a_2 \left( {C_1 +C_2 +2G_2 } \right) }. \end{aligned}$$
(26b)

And from (21), the theoretical calculation formulas of \(q_1\) and \(q_2\) for 3:1 super-harmonic resonance are given by

$$\begin{aligned} q_1= & {} A\cos \left( {3\tau +\phi _1 } \right) +C_1 \cos \tau +G_2 \nonumber \\= & {} A\left( {\cos 3\tau \cos \phi _1 -\sin 3\tau \sin \phi _1 } \right) \nonumber \\&+\,C_1 \cos \tau +G_2 ,\end{aligned}$$
(27a)
$$\begin{aligned} q_2= & {} B\sin \left( {3\tau +\phi _2 } \right) +C_2 \sin \tau \nonumber \\= & {} B\left( {\sin 3\tau \cos \phi _2 +\cos 3\tau \sin \phi _2} \right) \nonumber \\&+\,C_2 \sin \tau , \end{aligned}$$
(27b)

where \(C_1 =C_2 =\frac{E}{8}\),  \(G_2 =\frac{G_1 }{9}\), and

$$\begin{aligned} \sin \phi _1= & {} \frac{12a_1 A}{-4a_2 C_1 +4a_2 C_2 -4a_2 G_2 +a_3 C_1^3 }, \nonumber \\ \cos \phi _1= & {} -\frac{A\left( {3a_3 A^{2}\!+\!6a_3 C_1^2 \!-\!8a_2 -4\sigma \!+\!12a_3 G_2^2 } \right) }{\!-\!4a_2 C_1 \!+\!4a_2 C_2 \!-\!4a_2 G_2 \!+\!a_3 C_1^3 };\nonumber \\ \end{aligned}$$
(28a)
$$\begin{aligned} \sin \phi _2= & {} -\frac{12a_1 B}{-4a_2 C_2 \!+\!4a_2 C_1 \!+\!4a_2 G_2 \!+\!a_3 C_2^3 }, \quad \nonumber \\ \cos \phi _2= & {} \frac{B\left( {3a_3 B^{2}+6a_3 C_2^2 -8a_2 -4\sigma } \right) }{-4a_2 C_2 +4a_2 C_1 +4a_2 G_2 +a_3 C_2^3 }. \end{aligned}$$
(28b)

Then, according to (25) and (27), the theoretical responses of \(q_1\) and \(q_2\) for both 2:1 and 3:1 super-harmonic resonances can be obtained.

Figure 8 shows the comparisons of the time responses of \(q_1\) and \(q_2\) between theoretical and numerical results for \(G=5\) and \(K=0.1\) under different rotation speeds. Figure 8a, b are, respectively, for 2:1 and 3:1 super-harmonic resonances of \(q_1\). Figure 8c, d are, respectively, for the double solutions of \(q_2\) in the hysteresis region of rotation speed for 2:1 super-harmonic resonance, and Fig. 8e, f are for that of 3:1 super-harmonic resonance. It shows a small phase difference between the theoretical and the numerical results in Fig. 8a, b, c, e, while in Fig. 8d, f, the phase difference is not apparent, but the amplitude difference takes the main part.

Fig. 8
figure 8

Comparisons of the time responses between theoretical and numerical results for \(G=5\) and \(K=0.1\). a For \(\omega =472\,\hbox {rad/s}\). b For \(\omega =314\,\hbox {rad/s}\). c, d For \(\omega =448\,\hbox {rad/s}\). e, f For \(\omega =296\,\hbox {rad/s}\)

Full size image

The frequency responses of theoretical and numerical results are also compared in Fig. 8 to give an insight into the global error of the theoretical response of the system with respect to the numerical one for the same parameters. The corresponding results for 2:1 and 3:1 super-harmonic resonances are shown in Fig. 9, where the responses are represented by the effective value, denoted as

$$\begin{aligned} E(q_n )=\frac{1}{T}\int \limits _0^T {q_n (t)\mathrm{d}t}. \end{aligned}$$
(29)

Figure 9a shows the comparisons of the frequency responses of \(q_1\) and \(q_2\) between theoretical and numerical results for 2:1 super-harmonic resonance, and Fig. 9b shows that for 3:1 super-harmonic resonance. Throughout the two subfigures, some differences between the theoretical results and the corresponding numerical results can be observed especially for the resonance peak values and the corresponded rotation speeds. And the differences for \(q_1\) are more apparent than that for \(q_2\) for both 2:1 and 3:1 super-harmonic resonances. But from the overall point of view, the theoretical results of the frequency response curves reach a good agreement with the numerical results qualitatively.

Fig. 9
figure 9

Comparisons of the frequency responses between theoretical and numerical results for \(G=5\) and \(K=0.1\). a For 2:1 super-harmonic resonance. b For 3:1 super-harmonic resonance

Full size image

4 Bifurcation analysis

In this section, we investigate the local bifurcation characteristics of the system for both 2:1 and 3:1 super-harmonic resonances due to the variation of the maneuver load as well as the effect of the crack depth. The two-state variable singularity method [46–48] is employed in an engineering way to demonstrate different bifurcation modes of the discussed rotor system. Herein, we take an unfolding directly from the bifurcation equations. The unfolding is not an universal unfolding, but a so-called engineering unfolding. Actually, this approach is not so rigorous in the mathematical sense, but it has a great significance for engineering applications. Moreover, we take the maneuver load and the crack coefficient directly as the unfolding parameters and take the rotation speed directly as the bifurcation parameter. So that the bifurcation characteristics of the system affected by the parameters we care most in engineering designs can be reflected directly and exactly.

4.1 Bifurcation analysis for 2:1 super-harmonic resonance

By substituting \(\sigma =4-\frac{k}{m\omega ^{2}}\),  \(a_1 =2\xi \),  \(a_2 =\frac{k}{8m\omega ^{2}}K\),  \(a_3 =\frac{\alpha \delta ^{2}}{m\omega ^{2}}\),  \(G_2 =\frac{k}{4m\omega ^{2}}G\) into Eq. (16) and taking \(\lambda =\omega ^{2}\),  \(\alpha _1 =\frac{k}{m}\),  \(\alpha _2 =\frac{k}{8m}\),  \(\alpha _3 =\frac{\alpha \delta ^{2}}{m}\),  \(\alpha _4 =\frac{k}{4m}\),  \(\varepsilon _1 =\alpha _2 K\),  \(\varepsilon _2 =\alpha _4 G\),  \(\beta =4\lambda -\alpha _1\), the following equations can be obtained

$$\begin{aligned}&9\alpha _3^2 \lambda ^{4}\bar{{A}}^{3}+12\alpha _3 \left( \left( {3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}\right. \nonumber \\&\qquad \left. +\,6\alpha _3 \varepsilon _2^2 \right) \lambda ^{2}\bar{{A}}^{2}\!+\!\left( 256\xi ^{2}\lambda ^{6}\!+\!4\left( \left( 3C_1^2 \alpha _3 -4\varepsilon _1 \right. \right. \right. \nonumber \\&\qquad \left. -\,2\beta \Big )\lambda ^{2}+6\alpha _3 \varepsilon _2^2 \right) ^{2} \Big )\bar{{A}} -4\Big (4C_1 \varepsilon _1 -4\varepsilon _1 \varepsilon _2 \nonumber \\&\qquad \left. +\,3C_1^2 \alpha _3 \varepsilon _2 \right) ^{2}\lambda ^{4}=0, \end{aligned}$$
(30a)
$$\begin{aligned}&\!\!\! 9\alpha _3^2 \bar{{B}}^{3}+12\alpha _3 \left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \bar{{B}}^{2}\nonumber \\&\!\!\!\qquad +\,\left( {256\xi ^{2}\lambda ^{2}+4\left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) ^{2}} \right) \bar{{B}}\nonumber \\&\!\!\!\qquad -\,16\left( {\left( {C_1 +C_2 } \right) \varepsilon _1 -2\varepsilon _1 \varepsilon _2 } \right) ^{2}=0. \end{aligned}$$
(30b)

Taking \(\lambda \) as the bifurcation parameter and taking \(\varepsilon _1\) and \(\varepsilon _2\) as the unfolding parameters, the left side of Eq. (30) can be viewed as an engineering unfolding of the discussed bifurcation system, which is denoted as

$$\begin{aligned} F_1= & {} 9\alpha _3^2 \lambda ^{4}\bar{{A}}^{3}+12\alpha _3 \left( \left( {3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}\right. \nonumber \\&\left. \quad +\,6\alpha _3 \varepsilon _2^2 \right) \lambda ^{2}\bar{{A}}^{2}+\bigg ( 256\xi ^{2}\lambda ^{6}+4\Big ( \Big ( 3C_1^2 \alpha _3\nonumber \\&\quad -\,4\varepsilon _1 -2\beta \Big )\lambda ^{2}+6\alpha _3 \varepsilon _2^2 \Big )^{2} \bigg )\bar{{A}} -4\Big ( 4C_1 \varepsilon _1 \nonumber \\&\quad -\,4\varepsilon _1 \varepsilon _2 +3C_1^2 \alpha _3 \varepsilon _2 \Big )^{2}\lambda ^{4},\end{aligned}$$
(31a)
$$\begin{aligned} F_2= & {} 9\alpha _3^2 \bar{{B}}^{3}+12\alpha _3 \left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \bar{{B}}^{2}\nonumber \\&\quad +\,\left( {256\xi ^{2}\lambda ^{2}+4\left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) ^{2}} \right) \bar{{B}}\nonumber \\&\quad -\,16\left( {\left( {C_1 +C_2 } \right) \varepsilon _1 -2\varepsilon _1 \varepsilon _2 } \right) ^{2}. \end{aligned}$$
(31b)

Furthermore, the derivatives of \(F_1\) and \(F_2\) can be obtained as follows

$$\begin{aligned}&F_{1\bar{{A}}} =27\alpha _3^2 \lambda ^{4}\bar{{A}}^{2}+24\alpha _3 \left( \left( {3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}\right. \nonumber \\&\qquad \left. \ \ +\,6\alpha _3 \varepsilon _2^2 \right) \lambda ^{2}\bar{{A}}+256\xi ^{2}\lambda ^{6}\nonumber \\&\qquad \ \ +\,4\left( {\left( {3C_1^2 \alpha _3 -4\varepsilon _1 \!-\!2\beta } \right) \lambda ^{2}\!+\!6\alpha _3 \varepsilon _2^2 } \right) ^{2},\nonumber \\ \end{aligned}$$
(32a)
$$\begin{aligned}&F_{1\bar{{A}}\bar{{A}}} =54\alpha _3^2 \lambda ^{4}\bar{{A}}+24\alpha _3 \left( \left( {3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}\right. \nonumber \\&\qquad \left. \ \ \ +\,6\alpha _3 \varepsilon _2^2 \right) \lambda ^{2},\end{aligned}$$
(32b)
$$\begin{aligned}&F_{2\bar{{B}}} =27\alpha _3^2 \bar{{B}}^{2}+24\alpha _3 \left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \bar{{B}}\nonumber \\&\qquad \ \ +\,256\xi ^{2}\lambda ^{2}+4\left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) ^{2},\end{aligned}$$
(32c)
$$\begin{aligned}&F_{2\bar{{B}}\bar{{B}}} =54\alpha _3^2 \bar{{B}}+24\alpha _3 \left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) ,\end{aligned}$$
(32d)
$$\begin{aligned}&F_{1\lambda } =36\alpha _3^2 \lambda ^{3}\bar{{A}}^{3}+48\alpha _3 \left( \left( {3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}\right. \nonumber \\&\qquad \left. \ \ -\,2\lambda ^{3}+3\alpha _3 \varepsilon _2^2 \right) \lambda \bar{{A}}^{2} +8\left( 192\xi ^{2}\lambda ^{4}\right. \nonumber \\&\qquad \left. \ \ +\,\left( \left( 3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta \right) \lambda ^{2}\right. \right. \nonumber \\&\qquad \left. \left. \ \ +\,6\alpha _3 \varepsilon _{2}^{2} \right) \left( \left( {3C_1^2 \alpha _3 -4\varepsilon _1 -8} \right) \lambda \right. \right. \nonumber \\&\qquad \left. \left. \ \ +\,2\left( 3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta \right) \right) \right) \lambda \bar{{A}} -16\left( 4C_1 \varepsilon _1 \right. \nonumber \\&\qquad \left. \ \ -\,4\varepsilon _1 \varepsilon _2 +3C_1^2 \alpha _3 \varepsilon _2 \right) ^{2}\lambda ^{3}, \end{aligned}$$
(32e)
$$\begin{aligned}&F_{2\lambda } =-96\alpha _3 \bar{{B}}^{2}\nonumber \\&\qquad \ \ \ +\,\left( {512\xi ^{2}\lambda ^{2}-64\left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) } \right) \bar{{B}},\nonumber \\ \end{aligned}$$
(32f)
$$\begin{aligned}&F_{1\bar{{B}}} =F_{2\bar{{A}}} =F_{1\bar{{A}}\bar{{B}}} =F_{2\bar{{A}}\bar{{B}}} =0. \end{aligned}$$
(32g)

According to the two-state variable singularity method [46], the calculation formulas of the transition sets for Eq. (30) are as follows:

Bifurcation set:

$$\begin{aligned}&\!\!\!B\!=\!\Big \{ \left( {\varepsilon _1 ,\varepsilon _2 } \right) \in R^{2}: \exists \left( {\bar{{A}},\bar{{B}}, \lambda } \right) \hbox { s.t.} F_1 \!=\!0,\nonumber \\&\!\!\!\quad \qquad F_2 =0, F_{1\bar{{A}}} F_{2\bar{{B}}} -F_{1\bar{{B}}} F_{2\bar{{A}}} =0, F_{1\bar{{A}}} F_{2\lambda } \nonumber \\&\!\!\!\quad \qquad -F_{1\lambda } F_{2\bar{{A}}} =0 \Big \}. \end{aligned}$$
(33)

Hysteresis set:

$$\begin{aligned}&\!\!\!H=\left\{ \left( {\varepsilon _1 , \varepsilon _2 } \right) \in R^{2}: \exists \left( {\bar{{A}}, \bar{{B}}, \lambda } \right) \hbox { s.t. }F_1 =0, F_2 =0, \right. \nonumber \\&\!\!\!\qquad \quad \left. F_{1\bar{{A}}} F_{2\bar{{B}}} -F_{1\bar{{B}}} F_{2\bar{{A}}} =0, F_{1\bar{{A}}} {\bar{{A}}}'-F_{1\bar{{B}}} {\bar{{B}}}'=0, \right. \nonumber \\&\!\!\!\qquad \quad \left. F_{1\bar{{A}}} f_2 -F_{2\bar{{A}}} f_1 =0, {Z}'\ne 0, {Z}'=\left( {{\bar{{A}}}', {\bar{{B}}}'} \right) , \right. \nonumber \\&\!\!\!\qquad \quad \left. f_1 =\left( {F_{1\bar{{A}}\bar{{A}}} {\bar{{A}}}'^{2}+2F_{1\bar{{A}}\bar{{B}}} {\bar{{A}}}'{\bar{{B}}}'+F_{1\bar{{B}}\bar{{B}}} {\bar{{B}}}'^{2}} \right) , \right. \nonumber \\&\!\!\!\qquad \quad \left. f_2 =\left( {F_{2\bar{{A}}\bar{{A}}} {\bar{{A}}}'^{2}+2F_{2\bar{{A}}\bar{{B}}} {\bar{{A}}}'{\bar{{B}}}'+F_{2\bar{{B}}\bar{{B}}} {\bar{{B}}}'^{2}} \right) \right\} . \end{aligned}$$
(34)

Double limit set:

$$\begin{aligned}&\mathrm{DL}=\left\{ \left( {\varepsilon _1 , \varepsilon _2 } \right) \in R^{2}: \exists \left( {Z_1 , Z_2 , \lambda } \right) \hbox { s.t. }F_1 =0, \right. \nonumber \\&\qquad \qquad \left. F_2 =0, F_{1\bar{{A}}} F_{2\bar{{B}}} -F_{1\bar{{B}}} F_{2\bar{{A}}} =0, Z_1 \ne Z_2 , \right. \nonumber \\&\qquad \qquad Z=\left( {\bar{{A}}, \bar{{B}}} \right) \Big \}. \end{aligned}$$
(35)

Accordingly, the transition sets for 2:1 super-harmonic resonance can be obtained by numerical calculations. Two curves of hysteresis set in \(K-G\) parameter plane are demonstrated and shown in Fig. 10, by which, the parameter plane is divided into three regions. It indicates that different parameter combinations from different regions make different bifurcation characteristics for the frequency response of the system. Different bifurcation modes for different parameter combinations from the three regions and the two curves are shown in Fig. 11. In Fig. 11a, both of the frequency response curves for \(q_1 \) and \(q_2\) have a hysteresis characteristic. In Fig. 11c, however, only the frequency response curve for \(q_2\) has a hysteresis characteristic, but that for \(q_1\) has no hysteresis characteristic. In Fig. 11e, however, both of the frequency response curves for \(q_1\) and \(q_2\) do not show hysteresis characteristic. Figure 11b, d show the critical cases of the hysteresis phenomena for the frequency responses of \(q_1\) and \(q_2\), respectively.

Fig. 10
figure 10

Transition sets in \(K-G\) parameter plane (two hysteresis sets)

Full size image
Fig. 11
figure 11

Different bifurcation modes for parameter combinations from different regions or curves in Fig. 10. a For \(K=0.14\) and \(G=4\) from region I. b For \(K=0.104\) and \(G=5\) from curve H1. c For \(K=0.08\) and \(G=6\) from region II. d For \(K=0.053\) and \(G=7\) from curve H2. e For \(K=0.04\) and \(G=8\) from region III

Full size image

4.2 Bifurcation analysis for 3:1 super-harmonic resonance

By substituting \(\sigma =9-\frac{k}{m\omega ^{2}}\), \(a_1 =2\xi \), \(a_2 =\frac{k}{8m\omega ^{2}}K\), \(a_3 =\frac{\alpha \delta ^{2}}{m\omega ^{2}}\), \(G_2 =\frac{k}{9m\omega ^{2}}G\) into Eq. (24) and taking \(\lambda =\omega ^{2}\), \(\alpha _1 =\frac{k}{m}\), \(\alpha _2 =\frac{k}{8m}\), \(\alpha _3 =\frac{\alpha \delta ^{2}}{m}\), \(\alpha _4 =\frac{k}{9m}\), \(\varepsilon _1 =\alpha _2 K\), \(\varepsilon _2 =\alpha _4 G\), \(\beta =9\lambda -\alpha _1\), the following equations can be obtained

$$\begin{aligned}&\!\!\!9\alpha _3^2 \lambda ^{4}\bar{{A}}^{3}+12\alpha _3 \left( \left( {3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}\right. \nonumber \\&\!\!\!\left. \quad +\,6\alpha _3 G_2^2 \right) \lambda ^{2}\bar{{A}}^{2}+\left( 576\xi ^{2}\lambda ^{6}\right. \nonumber \\&\!\!\!\left. \quad +\,4\left( {\left( {3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}+6\alpha _3 \varepsilon _2^2 } \right) ^{2} \right) \bar{{A}}\nonumber \\&\!\!\!\quad -\,\left( {C_1^3 \alpha _3 -4\left( {C_1 -C_2 } \right) \varepsilon _1 +4\varepsilon _1 \varepsilon _2 } \right) ^{2}\lambda ^{4}=0,\nonumber \\ \end{aligned}$$
(36a)
$$\begin{aligned}&\!\!\! 9\alpha _3^2 \bar{{B}}^{3}+12\alpha _3 \left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \bar{{B}}^{2}\nonumber \\&\!\!\!\quad +\,\left( {576\xi ^{2}\lambda ^{2}+4\left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) ^{2}} \right) \bar{{B}}\nonumber \\&\!\!\!\quad -\left( {C_2^3 \alpha _3 +4\left( {C_1 -C_2 } \right) \varepsilon _1 -4\varepsilon _1 \varepsilon _2 } \right) ^{2}=0. \end{aligned}$$
(36b)

Taking \(\lambda \) as the bifurcation parameter and taking \(\varepsilon _1\) and \(\varepsilon _2\) as the unfolding parameters, the left side of Eq. (36) can be viewed as an engineering unfolding of the discussed bifurcation system, which is denoted as

$$\begin{aligned} F_1= & {} 9\alpha _3^2 \lambda ^{4}\bar{{A}}^{3}+12\alpha _3 \left( \left( {3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}\right. \nonumber \\&\quad \left. +\,6\alpha _3 G_2^2 \right) \lambda ^{2}\bar{{A}}^{2}+\left( 576\xi ^{2}\lambda ^{6}+4\left( \left( 3C_1^2 \alpha _3 \right. \right. \right. \nonumber \\&\quad \left. -\,\left. \left. 4\varepsilon _1 -2\beta \right) \lambda ^{2}+6\alpha _3 \varepsilon _2^2 \right) ^{2} \right) \bar{{A}} \nonumber \\&\quad -\,\left( \left( {C_1^3 \alpha _3 -4\left( {C_1 -C_2 } \right) \varepsilon _1 } \right) \lambda +4\varepsilon _1 \varepsilon _2 \right) ^{2}\lambda ^{2},\nonumber \\ \end{aligned}$$
(37a)
$$\begin{aligned} F_2= & {} 9\alpha _3^2 \lambda ^{2}\bar{{B}}^{3}+12\alpha _3 \left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}\bar{{B}}^{2}\nonumber \\&\quad +\,\left( {576\xi ^{2}\lambda ^{2}+4\left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) ^{2}} \right) \lambda ^{2}\bar{{B}}\nonumber \\&\quad -\,\left( {\left( {C_2^3 \alpha _3 +4\left( {C_1 -C_2 } \right) \varepsilon _1 } \right) \lambda -4\varepsilon _1 \varepsilon _2 } \right) ^{2}.\nonumber \\ \end{aligned}$$
(37b)

Furthermore, the derivatives of \(F_1\) and \(F_2\) can be obtained as follows

$$\begin{aligned} F_{1\bar{{A}}}= & {} 27\alpha _3^2 \lambda ^{4}\bar{{A}}^{2}+24\alpha _3 \left( \left( {3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}\right. \nonumber \\&\left. +\,6\alpha _3 \varepsilon _2^2 \right) \lambda ^{2}\bar{{A}}+576\xi ^{2}\lambda ^{6}\nonumber \\&+\,4\left( \! {\left( \! {3C_1^2 \alpha _3 {-}4\varepsilon _1 -2\beta } \right) \lambda ^{2}{+}6\alpha _3 \varepsilon _2^2 }\! \right) ^{2}, \end{aligned}$$
(38a)
$$\begin{aligned} F_{1\bar{{A}}\bar{{A}}}= & {} 54\alpha _3^2 \lambda ^{4}\bar{{A}}+24\alpha _3 \left( \left( {3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}\right. \nonumber \\&\left. +\,6\alpha _3 \varepsilon _2^2 \right) \lambda ^{2}, \end{aligned}$$
(38b)
$$\begin{aligned}&\!\!\! F_{2\bar{{B}}} =27\alpha _3^2 \lambda ^{2}\bar{{B}}^{2}+24\alpha _3 \left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}\bar{{B}}\nonumber \\&\!\!\!\quad +\left( 576\xi ^{2}\lambda ^{2}+4\left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) ^{2} \right) \lambda ^{2},\end{aligned}$$
(38c)
$$\begin{aligned}&\!\!\! F_{2\bar{{B}}\bar{{B}}} =54\alpha _3^2 \lambda ^{2}\bar{{B}}+24\alpha _3 \left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2},\nonumber \\ \end{aligned}$$
(38d)
$$\begin{aligned}&\!\!\! F_{1\lambda } =36\alpha _3^2 \lambda ^{3}\bar{{A}}^{3}+48\alpha _3 \left( \left( {3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}\right. \nonumber \\&\!\!\!\qquad \quad \left. -\,2\lambda ^{3}+3\alpha _3 \varepsilon _2^2 \right) \lambda \bar{{A}}^{2} \nonumber \\&\!\!\!\qquad \quad +\,8\left( 432\xi ^{2}\lambda ^{4}+\left( \left( {3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda ^{2}\right. \right. \nonumber \\&\!\!\!\qquad \quad +\left. 6\left. \alpha _3 \varepsilon _2^2 \right) \left( \left( 3C_1^2 \alpha _3 -4\varepsilon _1 -8 \right) \lambda \right. \right. \nonumber \\&\!\!\!\qquad \quad +\left. \left. 2\left( 3C_1^2 \alpha _3 -4\varepsilon _1 -2\beta \right) \right) \right) \lambda \bar{{A}}\nonumber \\&\!\!\!\qquad \quad -\,2\left( \left( {C_1^3 \alpha _3 -4\left( {C_1 -C_2 } \right) \varepsilon _1 } \right) \lambda +4\varepsilon _1 \varepsilon _2 \right) ^{2}\lambda \nonumber \\&\!\!\!\qquad \quad +\,8\left( {C_1 -C_2 } \right) \varepsilon _1 \lambda ^{2},\end{aligned}$$
(38e)
$$\begin{aligned}&\!\!\! F_{2\lambda } =18\alpha _3^2 \lambda \bar{{B}}^{3}+24\alpha _3 \left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) \lambda \bar{{B}}^{2}\nonumber \\&\!\!\!\qquad \quad +\,2\left( {576\xi ^{2}\lambda ^{2}+4\left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) ^{2}} \right) \lambda \bar{{B}} \nonumber \\&\!\!\!\qquad \quad +\,\left( {1152\xi ^{2}\lambda -144\left( {3C_2^2 \alpha _3 -4\varepsilon _1 -2\beta } \right) } \right) \lambda ^{2}\bar{{B}}\nonumber \\&\!\!\!\qquad \quad -\,2\left( {C_2^3 \alpha _3 +4\left( {C_1 -C_2 } \right) \varepsilon _1 } \right) \left( \left( C_2^3 \alpha _3 \right. \right. \nonumber \\&\!\!\!\quad \qquad +\left. 4\left. \left( {C_1 -C_2 } \right) \varepsilon _1 \right) \lambda -4\varepsilon _1 \varepsilon _2 \right) .\end{aligned}$$
(38f)
$$\begin{aligned}&\!\!\! F_{1\bar{{B}}} =F_{2\bar{{A}}} =F_{1\bar{{A}}\bar{{B}}} =F_{2\bar{{A}}\bar{{B}}} =0. \end{aligned}$$
(38g)

Similar to the analysis for 2:1 super-harmonic resonance in the previous section, the transition sets for 3:1 super-harmonic resonance can be obtained by numerical calculations according to the calculation formulas (33)–(35). As shown in Fig. 12, two curves of hysteresis set in \(K-G\) parameter plane are demonstrated, by which, the parameter plane is divided into three regions. Accordingly, different parameter combinations from different regions makes different bifurcation characteristics for the frequency response of the system. Different bifurcation modes for different parameter combinations from the three regions and the two curves are shown in Fig. 13. In Fig. 13a, both of the frequency response curves for \(q_1\) and \(q_2\) have a hysteresis characteristic. In Fig. 13c, however, only the frequency response curve for \(q_2\) has a hysteresis characteristic, while that for \(q_1\) has no hysteresis characteristic. In Fig. 13e, both of the frequency response curves for \(q_1\) and \(q_2\) do not show hysteresis characteristic. Figure 13b, d show the critical cases of hysteresis phenomenon for the frequency responses of \(q_1\) and \(q_2\), respectively. These results are very similar to that for 2:1 super-harmonic resonance in the previous section.

Fig. 12
figure 12

Transition sets in \(K-G\) parameter plane (two hysteresis sets)

Full size image
Fig. 13
figure 13

Different bifurcation modes for parameter combinations from different regions or curves in Fig. 12. a For \(K=0.14\) and \(G=4\) from region I. b For \(K=0.105\) and \(G=5\) from curve H1. c For \(K=0.08\) and \(G=6\) from region II. d For \(K=0.055\) and \(G=7\) from curve H2. e For \(K=0.04\) and \(G=8\) from region III

Full size image

5 Conclusions

In this paper, the response characteristics as well as the local bifurcation characteristics of an aircraft cracked rotor system for the 2:1 and 3:1 super-harmonic resonances have been investigated analytically. The equations of motion of the system have been formulated considering not only the nonlinear stiffness of Duffing type and the breathing of a transverse crack on the shaft, but also the maneuver load induced by the climbing and diving flight of the aircraft. By means of solving the motion equations by using the multiple scales method, the bifurcation equations for both 2:1 and 3:1 super-harmonic resonances have been obtained, respectively. Accordingly, the responded response characteristics and local bifurcation characteristics of the system affected by the crack coefficient and the maneuver load have been analyzed.

In the case of smaller maneuver load, it has been shown that the resonance peak amplitudes for both vertical and horizontal responses increase, and the corresponded resonance frequencies decrease with the increase of the crack coefficient, which is the basic property of general rotor systems with crack faults [5, 9, 12]. In the case of larger maneuver load, however, the resonance response curves show a hard spring characteristic when the crack coefficient becomes larger, and as a result, the corresponded resonance frequencies increase with the increase of the crack coefficient. This phenomenon has not been reported in the previous studies. Moreover, for a certain crack coefficient, the effect of the maneuver load on increasing the super-harmonic resonance frequencies of the responses in the vertical direction is much more dramatic than that in the horizontal direction, while that effect on the hysteresis characteristic in the horizontal direction is more significant than that in the vertical direction. In addition, these theoretical results have been verified through numerical computations.

Furthermore, the two-state variable singularity method has been employed for the bifurcation analysis, through which, it has been demonstrated that two hysteresis set curves dividing \(K-G\) parameter plane into three regions for each case of the two super-harmonic resonances. Accordingly, different parameter combinations from different regions make different bifurcation characteristics for the frequency response of the system. The approach in this paper will provide an effective and convenient way to analyze the bifurcation characteristics of dynamical systems, and the results will contribute to a better understanding of the effect of the maneuver load on the response and bifurcation characteristics of aircraft cracked rotor systems.