Design criteria of bistable nonlinear energy sink in steady-state dynamics of beams and plates

Abstract

A bistable nonlinear energy sink (BNES) conceived for the passive vibration control of beam and plate structures under harmonic excitation is investigated. By applying an Incremental Harmonic Balance (IHB) method together with an adjusted arc-length continuation technique, the frequency and amplitude responses are obtained, and their respective trends are discussed in detail from three aspects. The simplest single-mode dynamics is first considered with a special focus on the coupled effect of the cubic nonlinear stiffness and the negative linear stiffness, where an analytical treatment using complex-averaging method is also applied to obtain the slow invariant manifold for understanding the underlying dynamics. Then the multi-mode dynamics of the beam are discussed in variation of each parameter. As a result, a simple step-by-step design rule for the BNES is summarized. Finally, the obtained results and design criteria of the BNES in the beam case are extended to a 2D plate, realizing a broadband control for multi-mode plate vibration. It is found that compared to a traditional cubic one, a BNES can have a better performance both on the frequency and amplitude point of view.

1 Introduction

Passive vibration control is a subject of special concern in many fields of engineering. In this realm, one of the classical methods is a tuned mass damper (TMD) [1, 2], whose effectiveness has been discussed in various systems under different excitations [3,4,5]. A common drawback for such a linear TMD is that: it is only effective in the vicinity of a single resonant frequency. To overcome this, the idea of using nonlinear phenomena to design broadband vibration absorbers has thus emerged, leading to the development of the so-called nonlinear energy sink (NES) [6, 7].

The general implementation of an NES consists in a lightweight localized nonlinear device attached to the primary system with strongly nonlinear couplings for passive energy localization into itself. Unlike the linear TMD, the essential nonlinearities in the NES make it possible to generate rich dynamical regimes that are incapable in linear or weakly nonlinear systems. More precisely, beyond a certain energy level, a one-way irreversible nonlinear energy transfer phenomenon, termed as targeted energy transfer (TET) is activated [8, 9], providing a highly efficient mechanism for broadband vibration suppression. Analytical and numerical studies for NES to take advantage of the TET phenomenon, and hence to achieve vibration suppression in a broadband manner, were demonstrated in [10,11,12,13,14]. Experimental verifications for the effectiveness of NES with TET are also numerous [15,16,17]. The applications of NES for efficient broadband vibration mitigation could be found in many engineering fields, from nonlinear beams and plates [18,19,20], to buildings [21] and aerospace systems [22, 23]. On the other hand, by TET, NESs are also successfully applied in the field of energy harvesting in some recent investigations [24,25,26,27].

Many types of NES have been developed to obtain optimum performance. Depending on the type of the nonlinearity, the simplest and also the most studied one is an oscillating attachment with essentially cubic nonlinear stiffness [28, 29], while other kinds of designs could be found based on piece-wise nonlinearity [30, 31], vibro-impact dynamics [32,33,34], rotational element [35, 36], nonlinear membrane [37], and magnet [38, 39]. Along the same lines, another new extension to the NES, referred to as the Bistable Nonlinear Energy Sink (BNES), is proposed in some recent studies [40,41,42]. In this configuration, a bistable potential function is realized by adding a negative linear stiffness into the classical cubic NES. It has been shown that compared to the aforementioned NESs, a BNES can reduce the minimal energy that is required to activate the targeted energy transfer.

The transient dynamical regimes of a BNES coupled to a linear oscillator are investigated in [40, 41], analytically and numerically. With the limiting phase trajectories (LPTs), it was then demonstrated that depending on the initial energy induced to the system, the BNES can be able to achieve different dynamical mechanisms for strong energy transfer: for high energy inputs, the dynamics are governed by 1:1 and 1:3 resonances, and strongly modulated regime is observed; at low energy levels, periodic intra-well or chaotic cross-well responses are activated for the energy exchange between the linear oscillator and the nonlinear attachment. The optimal tuning of the BNES in a 2-dof linear primary system under impulse is considered [42], and compared with the classical TMD and NES. Experiments are also conducted in [43, 44], showing that this BNES can realize TET for various impacts, and has a better frequency performance than existing passive devices. Recently, the forced dynamics of the BNES coupled to a linear oscillator under periodic excitation is discussed in [45], where the efficiency of each response regime and its corresponding threshold is derived and examined, it is proved that for the periodic excitation, the intra-well oscillation and the 1:1 resonance play the most important role for effective suppression, in the low and high excitation level, respectively.

Although these studies have revealed that a properly designed BNES may be more effective than the other types of NES enumerated above, most of them still focus on transient dynamics and consider discrete oscillators. The forced dynamics for such a BNES in more complex structures such as beams and plates is still not well understood, so its corresponding design criteria are uncertain. On the other hand, in recent researches, the advances of NESs are developing toward applications in continuous and complex structures. Some existing studies [19, 46,47,48] on the classical cubic NES have shown that in continuous systems, NES may exhibit much richer dynamics and stronger parameter sensitivity, which is quite different from what was observed in discrete systems. Therefore, the dynamics of BNES in these systems need to be further addressed. In light of these facts, the main purpose of this paper is thus to study the steady dynamics of BNES in continuous beam and plate structures, and to establish the design guidelines for broadband suppression of vibrations involving multiple modes.

This paper is organized as follows: The equation of motion is introduced in Sect. 2, and an IHB method is applied for calculating the forced responses of the system. Then, a validation test on the IHB method is presented in Sect. 3. Sections 4 and 5 are respectively the dynamics and parametric design of the bistable NES in beam and plate systems. Finally, the conclusions and discussions are presented in Sect. 6.

2 Model description

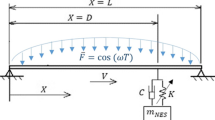
Figure. 1 depicts the schematic of the considered system, it consists of a simply supported, linear Euler-Bernoulli beam coupled to a lightweight nonlinear attachment. The beam is considered to be of length L, and subjected to a harmonic excitation induced at $x=x_F$ with temporal part $F(t)=F \cos \omega t$. The attachment is located at the position $x=x_c$, with a total mass m that is assumed to be small as compared to the beam mass. Finally, it is noted that the restoring force of the nonlinear oscillator is contributed by two parts: a cubic nonlinear component $k_n$ and a negative linear stiffness $k_l$, thus acting as a bistable nonlinear energy sink (BNES) in the literature [40, 41].

Fig. 1

A linear beam coupled to a bistable nonlinear energy sink

Let $u=u(x,t)$ and $v=v(t)$ denote respectively the displacement of the beam and that of the attached BNES, then the governing equations for such a system shown in Fig. 1 are given by

$$\begin{aligned}&\rho _s {u_{tt}} + {C_1}{u_t} + EI{u_{xxxx}} + f\delta (x-{x_c}) \nonumber \\&\quad = F(x, t), \end{aligned}$$

(1a)

$$\begin{aligned}&m{\ddot{v}} = f, \end{aligned}$$

(1b)

$$\begin{aligned}&f = {k_l}w + {k_n}{w^3} + {C_2}{\dot{w}}, \end{aligned}$$

(1c)

$$\begin{aligned}&w = u\left( {{x_c},\;t} \right) - v, \end{aligned}$$

(1d)

where $\rho _s$, E, and I are the mass per unit length, Young’s Modulus, and inertia moment of the beam. $C_1$ and $C_2$ account for the damping of the beam and the BNES. f is the interaction between the beam and the BNES, characterized as a function of the relative displacement w and relative velocity ${\dot{w}}$.

Define $\varepsilon = m/\rho _s L$ as the ratio between the mass of the BNES and the total mass of the beam, it is convenient to have a dimensionless form for Eq. (1) by introducing

$$\begin{aligned} \begin{aligned} {\bar{x}}&= \frac{x}{L},{\bar{u}} = \frac{u}{L},{\bar{v}} = \frac{v}{L},{\bar{w}} = \frac{w}{L},{\bar{t}} = \sqrt{\frac{{EI}}{{\rho _s {L^4}}}} t,\\ {{{\bar{k}}}_l}&= \frac{{{L^3}{k_l}}}{{EI}},{{{\bar{k}}}_n} = \frac{{{L^5}{k_n}}}{{EI}}, \sigma = \frac{{{C_1}{L^2}}}{{2\sqrt{\rho _s EI} }},\\ \xi&= \frac{{{C_2}L}}{{2\sqrt{\rho _s EI} }}, {\bar{F}} = \frac{{{L^2}F}}{{EI}},{\bar{\omega }} = \omega {L^2}\sqrt{\frac{{\rho _s}}{{EI}}}. \end{aligned} \end{aligned}$$

(2)

Substituting these variables into Eq. (1) and dropping for simplicity the overbars in the obtained equations yields

$$\begin{aligned}&{u_{tt}} + 2\sigma {u_t} + {u_{xxxx}} + f\delta \left( {x - {x_c}} \right) = F(x, t), \end{aligned}$$

(3a)

$$\begin{aligned}&\varepsilon {\ddot{v}} = f, \end{aligned}$$

(3b)

$$\begin{aligned}&f = {k_l}w + {k_n}{w^3} + 2\xi {\dot{w}}, \end{aligned}$$

(3c)

$$\begin{aligned}&w = u\left( {{x_c},\;t} \right) - v. \end{aligned}$$

(3d)

A modal expansion is applied to discretize the system, the displacement $u=u(x,t)$ is thus written in terms of

$$\begin{aligned} u(x,t) = \sum \limits _{i = 1}^{N_m} {{\phi _i}(x){q_i}(t)} \end{aligned}$$

(4)

with ${\phi _i}(x)$ the mode function for each $i=1, 2, \cdots , N_m$, and ${q_i}(t)$ the associated modal coordinate. For simply supported boundary condition, the mode functions together with the eigenfrequencies are computed via

$$\begin{aligned} {\phi _i}(x) = {{\sqrt{{2}} }}\sin \left( {i\pi x} \right) ,\;\;{{\varOmega }_i} = {i^2}{\pi ^2},\;i = 1,2, \cdots \end{aligned}$$

(5)

Denoting ${\mathbf{q}}=[q_1, q_2, \cdots , q_{N_m}]^T$ as a vector of the modal coordinates, $\varvec{\Omega }$ as a diagonal matrix such that $\varvec{\Omega }= diag({\varOmega }_i)$, and introducing $\mathbf{S }_c = {[{\phi _1}({x_c}), \cdots ,}{{\phi _{{N_m}}}({x_c})]}$, $\mathbf{S }_F = {[{\phi _1}({x_F}), \cdots ,{\phi _{{N_m}}}({x_F})]}$ be the matrices that containing all the first $N_m$ modes at the point $x_c$ and $x_F$. Implying the above expressions together with Eq. (4) into system (3), one can easily obtain

$$\begin{aligned}&\ddot{\mathbf{q }} + 2\sigma \dot{\mathbf{q }} + \varvec{\Omega }^2{\mathbf{q }} + {\mathbf{S }}_c^T f = {\mathbf{S }}_F^T F \cos \omega t, \end{aligned}$$

(6a)

$$\begin{aligned}&\varepsilon {\ddot{v}} = f, \end{aligned}$$

(6b)

$$\begin{aligned}&f = {k_l}w + {k_n}{w^3} + 2\xi {\dot{w}}, \end{aligned}$$

(6c)

$$\begin{aligned}&w = {\mathbf{S }}_{\mathbf{c }}{\mathbf{q }} - v. \end{aligned}$$

(6d)

Let ${\mathbf{X }} = {[{\mathbf{q }}^T,v]^T}$, and rescale the time variable as $\tau = \omega t$, Eq. (6) can finally be rewritten as

$$\begin{aligned}&\omega ^2 {\bar{\mathbf{M }}} \ddot{\mathbf{X }} + \omega {\bar{\mathbf{C }}}\dot{\mathbf{X }} + {\bar{\mathbf{K }}}{\mathbf{X } + {\bar{\mathbf{K }}}_n }({\mathbf{S }}{\mathbf{X }})^2{\mathbf{X }} = {\bar{\mathbf{F }}} \cos \tau \end{aligned}$$

(7)

where

$$\begin{aligned} {\bar{\mathbf{M }}}= & {} \left[ {\begin{array}{*{20}{c}} {\mathbf{I }}_{\mathbf{n }}&{}{}\\ {}&{}{ \varepsilon } \end{array}} \right] ,\; {\bar{\mathbf{C }}} = 2\sigma \left[ {\begin{array}{*{20}{c}} {\mathbf{I }}_{\mathbf{n }}&{}{}\\ {}&{}0 \end{array}} \right] + 2\xi \mathbf{S }^T \mathbf{S }, \nonumber \\ {\bar{\mathbf{K }}}= & {} \left[ {\begin{array}{*{20}{c}} {\varvec{\Omega }^2}&{}{}\\ {}&{}0 \end{array}} \right] + {k_l}\mathbf{S }^T \mathbf{S },\;{\bar{\mathbf{K }}}_n = {k_n}\mathbf{S }^T \mathbf{S }, \nonumber \\ {\bar{\mathbf{F }}}= & {} \left[ {\begin{array}{*{20}{c}} {\mathbf{S }_F^T}\\ { 0} \end{array}} \right] F,\;\mathbf{S } = \left[ {\begin{array}{*{20}{c}} {\mathbf{S }_c}, {-1} \end{array}} \right] . \end{aligned}$$

(8)

Eqution (7) shows that how the problem is transferred to a standard form of multi-degree-of-freedom vibration system. It is emphasized that although Eq. (7) is derived from a simply supported beam in Fig. 1. It is also valid for other boundary conditions or for a plate, by modifying only the characteristic matrices presented in Eq. (8), which will then be specified later.

In order to calculate the periodic solutions for the system described by Eq. (7), an Incremental Harmonic Balance (IHB) method [49,50,51] is employed due to its simplicity in handling multi-degree-of-freedom nonlinear systems, and advantages in analyzing the frequency and amplitude response. Other alternatives, such as the shooting method [52, 53], the collocation method [54], the invariant manifold method [55], or a recently proposed integral-equation approach [56], will also be applicable for readers of particular interests.

Let $\mathbf{X }_0,{\bar{\mathbf{F }}}_0,{\omega _0}$ be a set of solution for Eq. (7), and introduce a small increment in each of the three parameters according to

$$\begin{aligned} \mathbf{X } = \mathbf{X }_0 + {\varDelta } \mathbf{X },\omega = {\omega _0} + {\varDelta } \omega ,{\bar{\mathbf{F }}} = {\bar{\mathbf{F }}}_0 + {\varDelta } \mathbf{F }, \end{aligned}$$

(9)

Eq. (7) can first be rewritten with respect to the increments and then using the harmonic balance process, the solutions of system (7) are expressed in terms of

$$\begin{aligned} {X_k}= & {} {a_0} + \sum \limits _{i = 1}^n {\left( {{a_{ki}}\cos i\tau + {b_{ki}}\sin i\tau } \right) }, \nonumber \\ {\varDelta } {X_k}= & {} {\varDelta } {a_0} + \sum \limits _{i = 1}^n {\left( {{\varDelta } {a_{ki}}\cos i\tau + \;{\varDelta } {b_{ki}}\sin i\tau } \right) }, \end{aligned}$$

(10)

and finally, one obtains

$$\begin{aligned} {{\mathbf{K }}_{mc}}{\varDelta } {\mathbf{N }} = {\mathbf{R }} + {{\mathbf{R }}_{mc}}{\varDelta } \omega + {{\mathbf{R }}_f}{\varDelta } {\mathbf{F }}, \end{aligned}$$

(11)

where the matrices are specified in “Appendix A”.

The periodic solution ${\mathbf{N }}$ is thus described in terms of the excitation amplitude F and frequency $\omega$. For interest of studying the frequency response of the system, one may fix the amplitude of the external excitation, i.e., assuming ${\varDelta } {\mathbf{F }} = 0$ in Eq. (11), and likewise, for amplitude response, one set ${\varDelta } {\omega } = 0$ in Eq. (11). In the general implementation of the IHB method, a continuation scheme is usually coupled for the path-following solution. Particular continuation techniques include Gauss-Newton algorithms, piecewise linear, and Pseudo-arc-length, to name just a few. In this work, a two-point tracing algorithm [49] that improved from the traditional Pseudo-arc-length continuation method is applied. Finally, The stabilities of the periodic solutions can be analyzed by means of the Floquet theory, in which the transition matrix is calculated using a precise Hsu’s method following [49, 57], see for details in Appendix B.

3 Validation Test

A convergence study is first realized in order to select appropriately the number of modes used in the calculation, one such example is performed in Fig. 2. With $N_m=1$, a linear resonance peak occurs at $\omega =9$ near the first natural frequency ${\varOmega }_1$, and two nonlinear resonances can be observed respectively in $\omega \in [1, 6.5]$ and $\omega \in [15, 29]$. When the second mode of the beam is taken into account, the nonlinear resonances behave quite differently, especially in the higher frequencies. Corresponding to what was identified in $\omega \in [15, 29]$ for $N_m=1$, this nonlinear resonance now shows a more complete structure in a wider frequency range $\omega \in [16, 36]$ and with a sharp peak occurs at $\omega =36$. In addition, as frequency increases, another new nonlinear resonance around the second natural frequency ${\varOmega }_2$ is observed in $\omega \in [38, 47]$. For further larger number of modes, the system behaves the same as with $N_m=2$, only slight differences are indicated on the response curves. To conclude, at least two modes are required to ensure the convergence in the interested frequency range $\omega \in [0, 50]$. In later analysis related to the beam case, $N_m=5$ will then be selected for our calculations.

Generally, the forced vibrations satisfy the 1:1 resonance condition, which is characterized by the first order harmonics $\cos \tau$ and $\sin \tau$. Higher order harmonics can provide better approximations for describing the super-harmonic and sub-harmonic resonances under some special conditions, however, they also complicate a lot the analysis. Since our main purpose is to seek for simple guidelines to design the BNES for effective reductions of resonant peaks at each mode of a beam or a plate, the 1:1 resonance condition is assumed, i.e., the first order harmonics are the most significant to characterize the dynamics of the system, while the higher order of the harmonics, as compared to the first order ones, could be eliminated, see in [49, 51]. In the simulations hereafter, we keep only the terms 1, $\cos \tau$, and $\sin \tau$ in the IHB approximation.

Fig. 2

Convergence of the frequency response curve as $N_m$ increases from 1 to 10, for $k_n=10000$, $k_l=-20$, $\xi =0.1$, $\sigma =0.1$, $\varepsilon =0.1$, $x_c=0.7$, $x_F=0.3$, $F=5$. Solid and dashed lines: stable and unstable branches on the response curve. Stars are the results reported by the $4^{th}$ Rouge-Kutta method with $N_m=5$, the point at $\omega =20$ is simulated under initial condition $[\mathbf{X }(0); {{\dot{\mathbf{X }}}}(0)]=[-0.018, 0.006, 0, 0, 0, -0.0086, 0.0085, 0.0016, 0, 0, 0, -0.026]^T$, the two points at $\omega =30$ are simulated under $[\mathbf{X(0) }; {\dot{\mathbf{X }}}(0)]=[0.014, 0.04, 0, 0, 0, -0.162, 0.23, 0.34, 0, 0, 0, -1.8]^T$ for the solution $|u_c|=0.04$, and under $[\mathbf{X(0) }; {\dot{\mathbf{X }}}(0)]=[-0.007, 0.01, 0, 0, 0, -0.0036, 0.006, 0.01, 0, 0, 0, -0.03]^T$ for the solution $|u_c|=0.022$, other points are simulated uner zero initial conditions

The converged IHB solutions are also compared to the simulations using a $4^{th}$ Rouge-Kutta method at some frequencies with a single stable solution to examine their accuracy. As it is clear, a good agreement could be observed. At the other frequencies, the frequency response curve may undergo several Saddle-Node (SN) bifurcations and Neimark-Sacker (NS) bifurcations, bringing unstable branches or multiple states. Depending on the initial conditions, the response regimes at these frequencies may converge to a stable periodic orbit predicted by the IHB, or to other possible quasi-periodic or chaotic attractors. The complete identification of the dependence of the system response on the initial condition is, however, out of the scope of this paper. Our concentration will be on the parametric effect of the structures of response curves. The practical implication here is that such bifurcations provide richer dynamics, and by adjusting the characteristic parameters of the BNES, one is able to control their affecting frequency bands and amplitude levels to activate response regimes that are more effective than the usual periodic response in a given interval to reduce the linear resonance peak and achieve better damping performance. Motivated by this, we would like to restrict our analysis to the most used case of zero initial conditions, and the responses of the beam and the BNES at four different frequencies are then shown in Fig. 3(a–d). Several distinct regimes could thus be identified: at $\omega =5$, where there are three periodic solutions with very close values, a small amplitude periodic intra-well response is observed, the BNES enters in one of its potential wells, and oscillates about the stable equilibrium that characterized by the dashed line $w=\sqrt{ - {k_l}/{k_n}}=0.0447$. For $\omega =31$, the BNES exhibits a chaotic cross-well dynamics, in this case, the BNES oscillates between its two equilibrium and the amplitude is slightly larger than the stable equilibrium. At $\omega =38$, a usual stable periodic response is shown and the amplitude of the BNES is symmetrical. Finally for $\omega =43$, the vibration amplitudes of the beam and the BNES show strong modulation, and consequently, the response regime is the well-known strongly modulated response (SMR) as referred to in the literature.

Among these four regimes, the intra-well and cross-well dynamics result from the special potential well of the BNES, and hence are not able to be observed in a classical cubic NES. While the SMR and the usual periodic response could be found in almost all the existing types of NES. For a classical NES, its efficacy is mainly due to the SMR, and the general tuning is to activate such SMR at the interested frequencies that one wants to control according to the level of vibrations, so as to avoid as much as possible the sharp periodic resonance peaks. However, the SMR can exist only in a certain amplitude range, the classical cubic NES becomes inefficient when the vibration amplitude is low. On the contrary, a BNES, by taking advantage of its special potential well, provides intra-well or cross-well dynamics in the low vibration level, the former, has been recognized as another effective regime other than the SMR for vibration suppression. Our design will thus be mainly devoted to operating the SMR and intra-well dynamics to realize broad control over a wide range of forcing amplitudes and frequencies.

Fig. 3

Response regimes on the frequency response curve for four different values of excitation frequency, with system parameters the same as in Fig. 2

Finally in this section, by fixing the excitation frequency at $\omega =42$, e.g., in the vicinity of the second resonance frequency, and changing the excitation amplitude, the amplitude responses of the beam and the BNES are illustrated in Fig. 4. At low excitation level, a stable branch 1 characterized by a straight line is identified, representing a linear behavior. An unstable branch 2 then occurs in $F \in [2, 20]$, the BNES becomes effective by taking advantage of its nonlinearity. More precisely, the response curve no longer shows a linear growth but flattened. It first stretches horizontally to the left, after reaching the folding point B, it then bends to the right-down direction and finally connected to another stable branch 3 at position C. Throughout the whole unstable branch, and at the beginning of the high-amplitude stable branch with $F<30$ (point D), the response amplitude of the beam keeps decreasing as the excitation level increases, an effective vibration suppression mechanism is thus achieved. Concerning the response regimes on the amplitude response curve, the intra-well response lies on the first stable branch 1 with relatively low forcing amplitudes, while the SMR generally exists at higher forcing amplitudes on the unstable branch 2 and the other stable branch 3. As such, in the discussions hereafter, we will also refer to the response at the forcing level corresponding to branch 1 as the low-amplitude response, while the response at branches 2 and 3 will be termed as the high-amplitude response.

Fig. 4

Amplitude response for $\omega =42$, with excitation amplitude increases from $F=0.5$ to $F=100$, the other parameters are the same as in Fig. 2

Up to now, we have obtained the frequency and amplitude responses of the system, based on which the typical dynamical behaviors of the BNES are briefly discussed. In the next section, a detailed analysis will be carried out concerning the parametric trends of the frequency and amplitude responses, so as to finally figure out practical but simple criteria that guiding the design of the BNES in complex structures.

4 Response and design in beam system

The tuning of a BNES in continuous systems such as beams and plates is of course not an easy issue, which requires special insights into their complicated dynamics that are affected by various parameters. To carry out the analysis, it is hence convenient and necessary to start from the simplest case of single-mode dynamics, as it allows one to find some simple guidelines as well as analytical demonstrations. Focusing on the single-mode dynamics in the beam system, in this section a detailed parametric analysis on the frequency and amplitude response will first be performed in Sect. 4.1, and then an analytical treatment based on the so-called Slow Invariant Manifold (SIM) will be given in Sect. 4.2. Finally, the conclusions found will be extended to the multi-mode dynamics in Sect. 4.3 and Sect. 4.4 for more general designs.

4.1 Single-mode dynamics around ${\varOmega }_1$

Considering the first mode resonant vibration, the excitation frequency $\omega$ is hence assumed to be in the vicinity of the first natural frequency such that the vibrations of the other modes can be eliminated. Particular interests are paid to the effects of the two parameters: the nonlinear stiffness $k_n$ and the negative stiffness $k_l$.

Figure 5 compares the frequency responses of the system with different values of nonlinear stiffness $k_n$. At $k_n=2$, there is a single stable branch with a resonance peak that occurs at $\omega =10$, the BNES behaves linearly. The dynamics changes dramatically when $k_n=10$, as bifurcations appear, strong nonlinearity begins to be excited in the vicinity of the resonance frequency. As a result, the response regime also changes from periodic to strongly modulated, leading to a remarkable reduction on the resonance peak. With increasing $k_n$, the overall performance improves and suppression bandwidth increases, an effective mechanism for broadband vibration control is thus realized. Judging from the relative motion, one can also find that as $k_n$ increases, the frequency response curve bends to the right, hence a hardening phenomenon is addressed. Finally, for an inappropriately too large stiffness such as $k_n=40$, an undesired periodic response peak arises on the left hand of the resonance frequency at $\omega =9$, the performance deteriorates again.

Fig. 5

Effect of nonlinear stiffness $k_n$ on the frequency response. (a): $u_c$, beam response at the attached point, and (b): w, relative motion between the NES and the beam. $k_l=0$, $\xi =\sigma =0.1$, $\varepsilon =0.1$, $x_c=0.7$, $x_F=0.3$, $F=5$

Varying the negative stiffness $k_l$, the results are illustrated in Fig. 6. It is noted that an addition of a negative stiffness $k_l$ at a small modulus can eliminate the undesired response at the left hand of the main resonance frequency. However, increasing the modulus of $k_l$ causes detrimental effects with continuously narrowed effective frequency bands and increased resonance peaks. Indeed, this is the opposite of the $k_n$ behavior shown in Fig. 5, i.e., increasing $|k_l|$ shows an equivalent trend with that brought by decreasing $k_n$. It should be emphasized that, the above discussions and conclusions are restricted to the special case in which the strongly modulated regime is excited in the resonant vibration. For other situations, the conclusions might change, in fact, as one will find later in this section that, at the low amplitude vibration level, the bistability induced by the negative stiffness can improve the effectiveness of the NES. But anyhow, the equivalent effect between $k_l$ and $k_n$ is highlighted to be of special significance, since in the research hereafter, the readers will see how a BNES can be optimized by controlling simultaneously the value of both $k_l$ and $k_n$, so that to improve the low-amplitude performance without affecting a lot the high-amplitude behavior.

Fig. 6

Effect of negative stiffness $k_l$ on the frequency response. a: $u_c$, beam response at the attached point, and b: w, relative motion between the BNES and the beam. $k_n=40$, $\xi =\sigma =0.1$, $\varepsilon =0.1$, $x_c=0.7$, $x_F=0.3$, $F=5$

Another set of investigation is then carried out for an exhaustive justification of the BNES performance at different forcing amplitude. To do this, the normalized amplitude responses, i.e., the responses of $\left| {{u_c}} \right|$ and $\left| w \right|$ divided by the forcing amplitude F, are hence investigated. Figure 7 plots the response curves at $\omega =10$ for three different values of $k_n$. As it is apparent, the BNES is particularly effective at a certain range of ’moderate’ excitation level, within which a strongly nonlinear behavior is activated and the beam response decreases largely along an unstable branch until reaching its minimal. While for excitation level either too high or too low, it might behave inefficiently and linearly. Increasing the nonlinear stiffness $k_n$ does not change the overall shape of the amplitude response curve but brings a left shift, the BNES is thus tuned to be effective towards a lower excitation level, and vise versa.

Fig. 7

Effect of $k_n$ on the amplitude response. a: $u_c$, beam response at the attached point, and b: w, relative motion between the BNES and the beam. $k_l=-10$, $\xi =\sigma =0.1$, $\varepsilon =0.1$, $x_c=0.7$, $x_F=0.3$, and $\omega =10$

On the contrary, Fig. 8 shows that, increasing the modulus of the negative stiffness $k_l$ leads to an inverse right shift effect on the amplitude response, with the optimal performance of the BNES tuned towards the higher amplitude. As such, the trade-off between $k_n$ and $k_l$ that has previously been pointed out in the frequency response, also exists in the amplitude response. On the other hand, however more importantly, Fig. 8 also illustrates that by introducing a negative stiffness for a bistable configuration, the low-amplitude performance shows an evident improvement. This improvement, as further interpreted by the comparison in Fig. 9, is obviously brought by the specific advantage that in low excitation levels, the BNES can exhibit intra-well dynamics, with which the amplitude of $u(x_c,t)$ decreases significantly from around 0.1 (BNES with $k_l=-20$) to 0.03 (classical cubic NES) at $F=0.4$.

Fig. 8

Effect $k_l$ on the amplitude response. a: $u_c$, beam response at the attached point, and b: w, relative motion between the BNES and the beam. $k_n=100$, $\xi =\sigma =0.1$, $\varepsilon =0.1$, $x_c=0.7$, $x_F=0.3$, and $\omega =10$

Fig. 9

Response comparison of a classical cubic NES to a BNES at low excitation level $F=0.4$ for the cases shown in Fig. 8. a: a classical cubic NES with $k_n$=100, b: a BNES with $k_n$=100 and $k_l$=-20

4.2 Analytical treatment

The observations in Sect. 4.1 show that the trade-off between $k_l$ and $k_n$ plays an important role in operating the response regimes of the system to improve the performance of the BNES. In this section, a simple analytical treatment is thus proposed to derive a closed-form relationship of this trade-off between $k_l$ and $k_n$ when the BNES is working at the optimal SMR, so as to guide the design of the BNES for suppressing the resonant vibration of the beam at an arbitrary mode. The analysis relies on the so called concept Slow Invariant Manifold (SIM), which has been widely demonstrated to be a very successful analytical tool for approximating the dynamics [42, 45, 58, 59]. Although such a SIM is generally not solvable in continuous systems with many degrees of freedom, in the special case of single mode dynamics, the system can be reduced to a 2-dof equivalent system that consists of a single beam mode and the BNES, allowing one to calculate the SIM structure and analyze the dynamics. The aim of this section is to derive the SIM for the first mode resonant vibrations of the beam, hence to provide an analytical perspective. To do this, a complex averaging method [45, 58] is employed to Eq. (7) by introducing the following variable change

$$\begin{aligned} {\psi }{e^{j\tau }} = {\dot{\mathbf{X }}} + j\mathbf{X }, \end{aligned}$$

(12)

with j the unit imaginary. Then, the displacements and their derivatives can be rewritten in terms of the complex variables as

$$\begin{aligned} \mathbf{X }= & {} \dfrac{{{\psi }{e^{j\tau }} - {\psi }^*{e^{ - j\tau }}}}{{2j}},\; {{\dot{\mathbf{X }}}} = \dfrac{{{\psi }{e^{j\tau }} + {\psi }^*{e^{ - j\tau }}}}{2}, \nonumber \\ {{\ddot{\mathbf{X }}}}= & {} {{\dot{\psi }}}{e^{j\tau }} + j \dfrac{{{\psi }{e^{j\tau }} - {\psi }^*{e^{ - j\tau }}}}{2}, \end{aligned}$$

(13)

where $\psi ^*$ is the complex conjugate of $\psi$. Substituting Eq (13) into Eq. (7) and averaging the fast terms leads to

$$\begin{aligned}&2{\omega ^2}{\bar{\mathbf{M }}}{\dot{\psi }} + \omega {\bar{\mathbf{C }}}\psi - j \left( {\bar{\mathbf{K }}} - {\omega ^2{\bar{\mathbf{M }}} + \frac{{3{{\left| {\mathbf{S }\psi } \right| }^2}}{{\bar{\mathbf{K }}}_n}}{4}} \right) \psi \nonumber \\&\quad = {\bar{\mathbf{F }}}. \end{aligned}$$

(14)

Eq. (14) is called the slowly modulated equation that approximates the initial system described by Eq. (7). It can be demonstrated that under the 1:1 resonance condition, Eq. (14) gives identical solutions to that of the IHB method with only the first order harmonic.

For resonant vibrations near the first mode, $\omega \approx {\varOmega }_1$ is satisfied and the contributions of the other modes could thus be neglected. In this way, one has $\mathbf{X }=[q_1,v]^T$, and $\psi =[\psi _1, \psi _v]^T$. Introducing ${\psi _c} = {\phi _1}\left( {{x_c}} \right) {\psi _1}$ and ${\psi _w} = {\phi _1}\left( {{x_c}} \right) {\psi _1} - {\psi _v}$ to retrieve for sake of convenience the complex amplitude of the beam motion $u(x_c, t)$ and the relative motion w, and injecting these relationships to Eq. (14) gives the following

$$\begin{aligned} \begin{aligned}&{{\dot{\psi }}_c} + \frac{\epsilon {{\tilde{\sigma }} }}{2}{\psi _c} + \epsilon {\tilde{f}} = \frac{\epsilon {{\tilde{F}}}}{2},\\&{{{\dot{\psi }} }_w} + \frac{j}{2}\left( {{\psi _w} - {\psi _c}} \right) + \frac{{\epsilon {\tilde{\sigma }} }}{2}{\psi _c} + \left( {1 + \epsilon } \right) {\tilde{f}} = \frac{{\epsilon {\tilde{F}}}}{2},\\ \end{aligned} \end{aligned}$$

(15)

with

$$\begin{aligned} \begin{aligned}&{\tilde{f}} = \frac{{{\tilde{\xi }} }}{2}{\psi _w} - \frac{{j{{{\tilde{k}}}_l}}}{2}{\psi _w} - \frac{{3j{{{\tilde{k}}}_n}}}{8}{\left| {{\psi _w}} \right| ^2}{\psi _w},{\tilde{F}} = \frac{F}{{{\varOmega }_1^2\varepsilon }},\\&{\tilde{\xi }} = \frac{{2\xi }}{{{{\varOmega }_1}\varepsilon }},{{{\tilde{k}}}_l} = \frac{{{k_l}}}{{{\varOmega }_1^2\varepsilon }},{{{\tilde{k}}}_n} = \frac{{{k_n}}}{{{\varOmega }_1^2\varepsilon }}, \epsilon = \varepsilon \phi _1^2\left( {{x_c}} \right) , \\&{\tilde{\sigma }} = \frac{{2\sigma }}{{{{\varOmega }_1}\epsilon }}. \end{aligned} \end{aligned}$$

Then, taking into account that the mass ratio between the nonlinear attachment and the beam is small, a multi-scale method with respect to the small parameter $\epsilon$ is introduced for the analysis of Eq. (15). Let $\psi = \psi \left( {{\tau _0},\;{\tau _1}, \cdots } \right)$, ${\tau _k} = {\epsilon ^k}\tau$, $k = 0,\;1, \cdots$, and rewrite the time derivative as

$$\begin{aligned} \frac{d}{{d\tau }} = \frac{\partial }{{\partial {\tau _0}}} + \epsilon \frac{\partial }{{\partial {\tau _1}}} + \cdots \end{aligned}$$

(16)

The equation can be expanded according to the orders of $\epsilon$, for which the $\epsilon ^0$ order system is

$$\begin{aligned} \begin{aligned} \frac{{\partial {\psi _c}}}{{\partial {\tau _0}}}&= 0,\;\; \frac{{\partial {\psi _w}}}{{\partial {\tau _0}}}&+ \frac{j}{2}\left( {{\psi _w} - {\psi _c}} \right) + {\tilde{f}} = 0, \end{aligned} \end{aligned}$$

(17)

and set the derivative with respect to $\tau _0$ to zero yields

$$\begin{aligned} \begin{aligned} \left| {{\psi _c}} \right| ^2&= {4{\varOmega }_1^2{\xi ^2}\left| {{\psi _w}} \right| ^2} + {\left( {{k_l} - {\varOmega }_1^2\varepsilon } \right) ^2}\left| {{\psi _w}} \right| ^2\\&\quad - \frac{{3{k_n}\left( {{k_l} - {\varOmega }_1^2\varepsilon } \right) }}{2}\left| {{\psi _w}} \right| ^4 + \frac{{9k_n^2}}{{16}}\left| {{\psi _w}} \right| ^6. \end{aligned} \end{aligned}$$

(18)

Equation (18) defines the SIM structure for the first mode vibration of the system. As it can be recognized that, the SIM depends both on the nonlinear stiffness $k_n$ and the negative stiffness $k_l$. An illustration of the SIM structure in relationship of these two parameters is given in Fig. 10a–b. Increasing $k_n$, the topology of the SIM becomes smaller, and the unstable branch shifts towards the left down direction. The same conclusion could also be drawn by decreasing $|k_l|$. Hence, the nonlinear stiffness $k_n$ and negative stiffness $k_l$ play a similar role on the shape of the SIM structure. This explains the previous counterbalance between $k_l$ and $k_n$ as observed in the frequency and amplitude response curves in the last section.

Fig. 10

SIM structure in dependence of a: nonlinear stiffness $k_n$, b: negative stiffness $k_l$; and c: sketch for the state of the system moving along the SIM

As depicted in Fig. 10c, the SIM shows an ’S’ shape with two folding points $P_1$ and $P_2$, at which the moving trend and stability changes. As the state of the system can move only along the SIM, when the system is vibrating at a relatively small amplitude level, its state will be on the lower stable branch 1 and produces only stable periodic response. This corresponds to the behavior of a small $k_n$ in the frequency response ($k_n=2$ in Fig. 6) or the low-amplitude case in the amplitude response. If the vibration of the system is strong enough to reach the folding point $P_1$, then since branch 2 is unstable, the state of the system may jump from $P_1$ to $P_u$ that is of the same hight on the other stable branch 3, in the same way, another similar jump may also occur between $P_2$ and $P_d$. This is the fundamental mechanism of SMR, with which the BNES can be most effective for vibration suppression, the SMR can be found from the unstable regions of the frequency or amplitude responses. Finally, if the amplitude is too large, the BNES will finally work only on branch 3 and stable periodic response appears again, as represented by the undesired response in the frequency response ($k_n=40$ in Fig. 6) or the high-amplitude stable branch in the amplitude response.

Following the prescriptions given in the literature that related to discrete oscillators, see e.g. [42, 45, 58], the design of the BNES for SMR needs to adjust the BNES parameters so that the system is working in the vicinity of the second folding point $P_2$ to excite the Strongly Modulated Regime (SMR) for the most efficient suppression. This critical value of $k_n$ at the folding point $P_2$ could be found by introducing $Z = {\left| {{\psi _w}} \right| ^2}$ in Eq. (18) and setting its derivative with respect to Z to zero, and is expressed as

$$\begin{aligned} \frac{{{k_n}}}{{{\varOmega }_1^2}} = \frac{{8\left( {\varepsilon - \frac{{{k_l}}}{{{\varOmega }_1^2}}} \right) \pm 4\sqrt{{{\left( {\varepsilon - \frac{{{k_l}}}{{{\varOmega }_1^2}}} \right) }^2} - \frac{{12{\xi ^2}}}{{{\varOmega }_1^2}}} }}{{9{{\left| {{\psi _w}} \right| }^2}}}, \end{aligned}$$

(19)

for the exists of a pair of bifurcations, the negative stiffness must satisfies ${k_l} < {\varOmega }_1^2\varepsilon - 2\sqrt{3} \xi {{\varOmega }_1}$. Eq. (19) thus gives the explict trade-off $k_l$ and $k_n$ of for the optimal SMR in the BNES as a function of the vibration amplitude ${\left| {{\psi _w}} \right| }$.

Once the SMR is optimized by the trade-off relationship in Eq. (19), one could then take advantage of the bistability of the BNES to improve its low-amplitude performance by operating on the intra-well response regime, an example for such operation is illustrated in Fig. 11. In Fig. 11, by calculating at first the trade-off relationship in Eq. (19) at the amplitude level of ${\left| {{\psi _w}} \right| }=0.65$, four different pairs of the $k_l$ and $k_n$ are obtained and marked in the enlarged figure with circles, including $k_l=0, k_n=30$ (black) as a classical cubic NES and $k_l=-3, k_n=40$ (brown), $k_l=-6, k_n=50$ (red), $k_l=-10, k_n=62$ (blue) as another three BNESs, then the amplitude response curves computed using the IHB for the four configurations are compared in the main figure, one can see that by balancing $k_l$ and $k_n$ in the BNES according to the trade-off, the low-amplitude performance (the stable branches at the low forcing amplitude level) of the BNES could be gradually improved without affecting too much the high-amplitude behavior (the unstable branches and the stable branches at the high amplitude level) on the amplitude response curve.

Fig. 11

Adjusting simultaneously the value of both $k_l$ and $k_n$ to improve the low-amplitude performance without affecting a lot the high-amplitude behavior, Each curve in the main figure is obtained with a pair of $k_l$ and $k_n$ depicted in the sub-figure with the circle at the same color

It is worthwhile to mention that although Eq. (18) and Eq. (19) are derived for the first mode resonant vibration, one can easily obtain similar expressions of the SIM for the kth mode by simply replacing the subscript “1” by “k”. All the conclusions that are valid here and in the previous Sect. 4.1 that related to the 1st mode can also be equivalently drawn for an arbitrary kth mode, we just skip these for conciseness.

4.3 Multi-mode dynamics

We now consider further the multi-mode dynamics, the first parameter to be investigated is the nonlinear stiffness $k_n$, its effect on the frequency response is depicted in Fig. 12. For a small value of $k_n=10$, the responses at both modes show a single periodic resonance peak, the nonlinearity is not strong enough to bend the response curve and the damping performance is thus mainly due to the linear part of the system. Compared to the peaks shown without an absorber, one can observe that the gain is limited at mode 1 but considerable at mode 2. As $k_n$ increases in the range [10, 120], the frequency response changes dramatically in the vicinity of the first natural frequency. More precisely, a set of SN and NS bifurcations occur, as a result, the resonance curve near mode 1 does not go up to a single linear stable peak but crosses the resonant region through a curved unstable branch. By creating a dent in this region, the peak response is remarkably reduced. Moreover, the corresponding response regime in the vicinity of the first mode changes also from periodic to SMR, the damping performance of the BNES improves continuously with a lower and lower resonance peak. On the other hand, at mode 2, neither the response regime nor the performance shows an observable difference for $k_n$ varies in this range. Continue to increase $k_n$ in the range of [120, 1e4], another set of bifurcations occur near the first mode, resulting in an undesired periodic resonance with peak value as high as the one without an absorber, the BNES thus loses its effectiveness at mode 1. Along with the occurrence of the undesired periodic response, the bifurcations also generate two new branches, stretching respectively toward the left and right hand of the first natural frequency. While the left one is then degenerated, the stretching of the right one eventually creates a significant nonlinear resonance peak (the blue ellipse) between the first and second natural frequency. With $k_n$ increases up to around 1500, the right-hand nonlinear resonance approaches the resonant frequency range of mode 2, and the SMR begins to be activated at mode 2. After that, by increasing further the value of $k_n$, the performance at the second mode could be much more improved with the sharp resonance peaks flattened and reduced. However, unfortunately, for all these designs with higher values of $k_n$, their performances at the first mode are particularly poor, almost no damping effect could be addressed.

Fig. 12

Frequency responses for nonlinear stiffness $k_n$ varies. $u_c$: the amplitude of the beam at checking point $x=0.7$. Other parameters are selected as $k_l=-20$, $\xi =0.1$,$\varepsilon =0.1$, $\sigma =0.1$, $x_c=0.7$, $x_F=0.3$, $F=5$. The magenta curve is the beam response without an absorber, working as a reference case. The boxes with arrows at some interested positions indicate the steady-state responses of the beam simulated under zero initial condition

One can note that, for controlling the vibrations, the nonlinear stiffness should also be arranged consistently to the targeted modes. An effective reduction of vibrations at a higher mode requires correspondingly a higher value of $k_n$, which is logical but generally prevents the possibility for simply selecting a $k_n$ that can be simultaneously optimal for all the modes. Hence, the appropriate tuning of a BNES for multi-mode vibrations over a wide frequency range resides in a balanced performance at each interested mode. With this in mind, a critical working point at around $k_n=120$ is recommend according to the examples shown in Fig. 12, for which the BNES produces SMR in the first mode and with intra-well responses in the second mode. It must be noted that, such a critical working point represents an intrinsic limitation of the BNES design. For robust concerns, special cares shall be taken to ensure $k_n$ is not beyond this critical point, or equivalently, the applied forcing is not above the designed value here. There is also an instruction that tuning the stiffness to activate SMR at the first mode outperforms that activated at the second one, as verified by the fact that the former provides also an acceptable performance at the second mode, whereas the latter loses the first mode damping effect. This criterion will then be further demonstrated in the coming discussions that, a BNES with $k_n$ pre-tuned to a lower mode allows the possibility to adjust other counting parameters to improve higher mode performances, while the opposite is not true.

Fig. 13

Frequency responses of $u_c$ for damping $k_l$ varies, a: with nonlinear stiffness $k_n=50$, the BNES pre-tuned to have SMR near the first mode, b: with $k_n=4000$, with SMR pre-tuned tuned to the second mode. Other parameters are selected as $\xi =0.1$,$\varepsilon =0.1$, $\sigma =0.1$, $x_c=0.7$, $x_F=0.3$, $F=5$

Figure. 13 summarizes then the effect of the negative stiffness $k_l$. In consideration of the fact that the existence of SMR at mode 1 and mode 2 require very different values of $k_n$, two special cases are thus performed. In Fig. 13a, a relative small value of $k_n=50$, with SMR activated at mode 1, is presented. One can see that a possible balanced control could then be found at around $k_l=-4$, where the peaks at both modes are considerably reduced. While in Fig. 13b, a parallel case with $k_n=4000$ for SMR activated around mode 2 is shown, the picture becomes much different: varying $k_l$ now only brings sensitive difference near the second mode, but does not lead to any peak reduction at the first one. Even for $|k_l|$ increases up to 250, with losing the performance at mode 2, the sharp peak at mode 1 remains unchanged, the BNES become very badly designed with both peaks the same hight as the ones without an absorber.

The key conclusion could be drawn from Fig. 12 Fig. 13 is that the nonlinear stiffness $k_n$ dominates the negative stiffness $k_l$ in the resonant dynamics in the following two aspects: first, if the nonlinear stiffness is appropriately designed near one of the resonance modes, the effect of varying $k_l$ is then similar to the nonlinear stiffness. Second, when the nonlinear stiffness is inappropriately chosen that acts ineffective at one of the resonant modes, then changing the negative stiffness can not improve the performance of the BNES. Hence, to design the BNES, the nonlinear stiffness should be carefully arranged, otherwise, the tuning of other parameters would be meaningless.

To support this statement, the effect of the damping coefficient is then investigated under two different situations. The first situation with $k_n=50$ and for SMR targeting mode 1 is shown in Fig. 14a. On increasing $\xi$, the response regime near the first natural frequency changes from SMR to periodic, and generally a weak damping is enough once the stiffness is well designed, increasing properly the damping $\xi =0.04$ can reduce the dynamical instability and eliminate the additional nonlinear resonance peak at around $\omega =30$ to bring considerable improvement on the overall performance. For $\xi >0.04$, the SMR at the first mode reduces and eventually degenerates to periodic response with peak value increases continuously, leads to a deterioration of the performance. At mode 2, the bifurcations vanish at a very low damping level and the response is periodic intra-well regime at most of the damping values, the performance improves at first for $\xi <1$ and decreases at $\xi >1$. In the case of $k_n=50$, one can find that the damping ratio has significant effects on both modes, for whatever SMR or intra-well response. At mode 1, a smaller $\xi$ is recommended for the BNES to take advantage of its strong nonlinearity to achieve SMR in this frequency range for suppression, while for mode 2 with intra-well dynamics, a linear characteristic is shown and requires a larger $\xi$ to ensure the reduction performance. As a balanced reduction for mode 1 and 2, $\xi =0.2$ could be observed with the peak of mode 1 and 2 at a similar hight. A second situation for $k_n=4000$, tuning to the second mode is depicted in Fig. 14b, varying the damping now has quite a different effect. Although the damping effect is remarkable for the second mode, this is not the case near the first one: whatever the damping varies, the sharp resonance peaks always exist and the BNES remains ineffective.

Fig. 14

Frequency responses of $u_c$ for damping $\xi$ varies, a: with nonlinear stiffness $k_n=50$ and negative stiffness $k_l=-5$, the BNES pre-tuned to have SMR near the first mode, b: with $k_n=4000$ and $k_l=-20$, SMR pre-tuned to the second mode. Other parameters are selected as $\varepsilon =0.1$, $\sigma =0.1$, $x_c=0.7$, $x_F=0.3$, $F=5$

The next parameter considered in this section is $x_c$, the location of the BNES on the beam. Fig. 15a and b show the dependence of the response curves on different $x_c$, for $k_n$ tuned targeting respectively mode 2 and mode 1. The result confirms again the rule that, when the nonlinear stiffness $k_n$ is pre-tuned to mode 2, the subsequent influence of $x_c$ is observable only around mode 2, while for $k_n$ tuned to the first mode, $x_c$ affects significantly the performance at both mode 1 and mode 2. A clear grasp related to the underlying mode shape functions can be revealed. More precisely, for the peak reduction of mode 2, an optimal location $x_c=0.75$ together with a worst location $x_c=0.5$ can be respectively addressed, with clear correspondence to the local maximum ($x_c=0.75$) and node ($x_c=0.5$) of the shape function of mode 2. Along with that for mode 1, an optimal location at $x_c=0.5$ is also observed. This is to say that, the tuning of the location $x_c$ is to put the BNES in the local maximum of the mode functions, whose combined effect between mode 1 and mode 2 resulting in the value $x_c=0.7$ for a balanced overall performance. Always keep in mind that the nonlinear stiffness should be appropriately chosen at first, otherwise there would be no effects by changing the location.

Fig. 15

Effect of the position $x_c$ to $u_c$, amplitude of the beam at checking point $x=0.7$, a: with nonlinear stiffness $k_n=50$ and negative stiffness $k_l=-5$, the BNES pre-tuned to have SMR near the first mode, b: with $k_n=4000$ and $k_l=-20$, SMR pre-tuned to the second mode. Other parameters are selected as $\varepsilon =0.1$, $\sigma =0.1$, $\xi =0.2$, $x_F=0.3$, $F=5$

The effect of the mass ratio $\varepsilon$ is shown in Fig. 15, it is also clear that when the SMR is targeted near mode 1, effective peak reduction could be observable around both modes by selecting an appropriate $\varepsilon$. There exists a critical value of $\varepsilon =0.1$, around which the SMR is activated. Beyond this critical value, increasing $\varepsilon$ causes a slight performance decrease, hence $\varepsilon =0.1$ is recommended. With $k_n=4000$ and the BNES pre-tuned to mode 2, the variation of $\varepsilon$ only has effects near mode 2 and now a smaller critical value $\varepsilon =0.02$ is observed, while the performance at mode 1 remains ineffective, there is no evident peak reduction as compared to the case without an absorber.

Fig. 16

Effect of the mass ratio $\varepsilon$ to $u_c$, amplitude of the beam at checking point $x=0.7$, a: with nonlinear stiffness $k_n=50$ and negative stiffness $k_l=-5$, the BNES pre-tuned to have SMR near the first mode, b: with $k_n=4000$ and $k_l=-20$, SMR pre-tuned to the second mode. Other parameters are selected as $x_c=0.7$, $\sigma =0.1$, $\xi =0.2$, $x_F=0.3$, $F=5$

4.4 Appropriate design procedure of BNES

As the parameters affecting the steady-state response of the beam have been investigated, the appropriate design of the BNES could now be possible. We are aiming at proposing some simple criteria in order to take advantage of its strong nonlinearity and bi-stability to flat the response curves and reduce the resonance peaks over an interested frequency range that cover multi-mode vibrations. As such, the effectiveness of the BNES is represented by the gains on peak reductions at each beam mode, as compared to the case without an absorber.

There are five parameters to be designed in the BNES: the nonlinear stiffness $k_n$, the negative linear stiffness $k_l$, the damping ratio $\xi$, the location $x_c$, and the mass ratio $\varepsilon$. Among these, the effect of $x_c$ and $\varepsilon$ are obvious and direct. The selection of $x_c$ relies on the insight of the mode shape functions of the considered modes, which, as illustrated in Fig. 15, results in the arrangement of $x_c=0.7$ as a balance between mode 1 and mode 2. And for $\varepsilon$, one only needs to reach a critical threshold for activating the SMR. Following an idea of suppressing the vibration using a mass as small as possible, $\varepsilon =0.1$ is selected as a result of Fig. 16. Having these at hand, it is therefore natural to fix $x_c=0.7$ and $\varepsilon =0.1$ during the tuning procedures, for the remaining parameters $k_n$, $k_l$ and $\xi$, the following rules could be summarized:

• The nonlinear stiffness $k_n$ should be highlighted at first as it is crucial for the nonlinearity and dominates the other parameters. The trick here is to adjust $k_n$ near the critical working point as shown in Fig. 12 to maximize the effect of SMR at the lowest natural frequency to flat the resonance curve. This rule is important from the following: first, if $k_n$ is too small as compared than this critical value, then the SMR is not exhibited and the resonance peak is not flattened enough; second, if $k_n$ is above this critical value, a set of bifurcations will appear in the resonant frequency and leads to undesired periodic responses with peaks as high as the one without an absorber; third, if the $k_n$ is not tuned targeting the lowest natural frequency but the higher modes or other frequencies, then, there exists either nonlinear resonance peaks at some frequency region (see the ellipse in Fig. 12) or undesired periodic responses at the lowest mode, in either case, the performance deteriorates.

• Adjusting the negative stiffness $k_l$ provides a set of trade-offs (in Eq. (19)) with minimal effects on the performance at the critical working point. This trade-off effect provides us with further adjustments on the low-amplitude intra-well response regimes for improving the robustness of the BNES. Obviously, this trade-off adjustment is special only for a BNES, but not achievable in a classical cubic NES where $k_l=0$ is restricted.

• Third, tuning the damping $\xi$ to increase the bandwidth and improve the performance at other modes, the proper values could be quite straightforward from the frequency response curve and balancing the resonance peaks.

Once the above procedures are down, one could be able to obtain several candidates of appropriately designed BNESs with trade-offs between $k_l$ and $k_n$, for effective reduction over the frequency range with multi-mode beam vibrations, under an arbitrarily selected forcing amplitude F, see in Fig. 17a. As such, a further adjustment based on the trade-offs is to turn the attention to the performance at lower forcing amplitude level to play on the intra-well dynamics. As an example, we consider the BNES we optimized at $F=5$, and now check the performance at a much lower forcing amplitude $F=0.2$ and to see how the parameters affect the performance, as in this case the vibration is too small to activate the nonlinear behavior, the effect of $k_n$ is thus neglected and the system could be approximated to be linear with dynamics depends only on the linear stiffness $k_l$ and the linear damping $\xi$. Fig. 17b shows the frequency response of the BNES for different values of $\xi$ at this excitation level and it is apparent that a linear characteristic is observed: there exist two fixed points P and Q on the response curves that are independent of the damping. The tuning procedure could mimic the famous tuning of Den-Hartog on TMD, by adjusting at first the stiffness $k_l$ to make P and Q in the same hight and then modifying the damping to make the frequency curve cross the P and Q horizontally, one obtains $k_l=-3.8$ and $\xi =0.2$.

Fig. 17

Special design procedures of BNES, a: trade-offs of $k_n$ and $k_l$ at four different forcing amplitudes for $\xi =0.2$, b: tuning of intra-well dynamics at a low forcing amplitude $F=0.2$, with BNES parameters assigned as $k_l=-3.8$, $k_n=53$, and for three different values of damping $\xi =0.05$, $\xi =0.2$, and $\xi =1$

With these design criteria step by step, we finally have the the parameters for an appropriately tuned BNES with $k_n=53$, $k_l=-3.8$, $x_c=0.7$, $\xi =0.2$, and $\epsilon =0.1$, as well as a tuned classical cubic NES as $k_n=35$, $x_c=0.7$, $\xi =0.2$, and $\epsilon =0.1$. This NES and BNES are both well designed for the balanced vibration suppression over the frequency range $\omega \in [0, 50]$, targeting the forcing condition $x_F=0.3$, $F=5$. In order to compare their performance, the frequency response curves of the designed BNES and the classical NES are then plotted at three different forcing amplitude levels in Fig. 18. It can be seen that at the designed forcing amplitude $F=5$, the BNES and the NES are almost identical and are both effective with clear reductions of resonance peaks at both modes. However, at the excitation level either higher or lower than the designed forcing amplitude, the BNES outperforms the classical NES, especially in the low-amplitude case, by taking advantage of the intra-well response, the BNES shows a much lower peak at mode 1 than the classical cubic NES.

Fig. 18

Frequency response of the beam at three different forcing amplitudes, compared among black: the designed BNES, and red: the designed classical NES, and magenta: no absorber. a: the designed working amplitude $F=5$, b: a low amplitude $F=0.2$, c: a high amplitude $F=100$

Fig. 19

A thin rectangle plate with an attached bistable nonlinear energy sink

Fig. 20

Response of a four-edge simply supported rectangular plate coupled to a BNES, where $u_c$: plate response at checking point $(x, y)=(0.7,0.5)$, and w: relative motion between the BNES and the plate. Other parameters are selected as $\eta =0.8$, $\varepsilon =0.1$, $k_n=2e5$, $k_l=-10$, $\xi =\sigma =0.1$, $(x_c, y_c)=(0.7,0.5)$, $(x_F, y_F)=(0.3, 0.2)$, $F=1$. $N_m=10$

Fig. 21

Amplitude response for plate showing that controlling both the nonlinear and negative stiffness, the large amplitude response do not change, but the low amplitude response improves. black: $k_n=1e4$, brown: $k_n=1.2e4$, $k_l=-10$, red: $k_n=1.4e4$, $k_l=-20$, blue: $k_n=2e4$, $k_l=-50$, magenta: $k_n=3e4$, $k_l=-100$. Other parameters are selected as $k_n=2e5$, $k_l=-10$, $\xi =\sigma =0.1$, $x_c=(0.7,0.5)$, $x_F=(0.3, 0.2)$, and $\omega =25$ at the first resonance frequency

5 Application in a rectangular plate

As mentioned earlier, one of the specific advantages of the framework developed in Sect. 2 is that it not only valid for the afore discussed beam system, but can also be applied to plate structures by simply changing the corresponding matrices $\mathbf{S }_c$, $\mathbf{S }_F$, and ${\varvec{\Omega }}$. In this section, the methods and discussions are parallelized to the 2D case of a thin rectangular plate coupled to a BNES, so that to gain the insights necessary for the design. As depicted in Fig. 19, the system investigated now consists of a linear thin rectangular plate with an attached BNES at $(x_c, y_c)$, and subjected to a harmonic excitation $F(t)=F \cos \omega t$ induced at $(x_F, y_F)$. Without loss of generality, the governing equations can be written in the dimensionless form as

$$\begin{aligned}&{u_{tt}} + 2\sigma {u_t} + {\varDelta }^2 u + {f}\delta \left( {x - {x_c},\;y - {y_c}} \right) \nonumber \\&\quad = F \left( x, y, t \right) \end{aligned}$$

(20a)

$$\begin{aligned}&\varepsilon {\ddot{v}} = f \end{aligned}$$

(20b)

$$\begin{aligned}&f = {k_l}w + {k_n}{w^3} + 2\xi {\dot{w}} \end{aligned}$$

(20c)

$$\begin{aligned}&w = u\left( {{x_c},\;{y_c},\;t} \right) - v \end{aligned}$$

(20d)

where ${\varDelta }$ is the 2D Laplace operator, and the other definitions are just the same as in the beam ones.

Assuming four-edge simply supported boundary condition, the eigenmodes and the eigenfrequencies of the plate can then be expressed as follows,

$$\begin{aligned} \begin{aligned}&{\phi _{ij}}\left( {x,y} \right) = \frac{2}{{\sqrt{\eta } }}\sin \left( {i\pi x} \right) \sin \left( {\frac{{j\pi y}}{\eta }} \right) ,\;\\&{{\varOmega }_{ij}} = {\pi ^2}\left( {{i^2} + \frac{{{j^2}}}{{{\eta ^2}}}} \right) ,\;\;i,j = 1,2... \end{aligned} \end{aligned}$$

(21)

where $\eta$ accounts for the aspect ratio of the plate, ${\varOmega }_{ij}$ is the circular frequency of the mode, and $\phi _{ij}$ is the eigenfunction. Using these expressions to derive the corresponding $\mathbf{S }_c$, $\mathbf{S }_F$, and ${\varvec{\Omega }}$ that serves the matrix equation Eq. (7), the frequency and amplitude response curves can then be calculated similarly to the beam case.

The frequency response curves for different values of $k_n$ are shown in Fig. 20. Contrary to the common expectations in the previous beam case, the system reveals that the strong nonlinear effects can now be able to be activated simultaneously near all the linear resonant modes for effective reductions on their peak responses, as verified by the fact that as $k_n$ increases up to a critical value of $k_n>1e4$, the response curves bend to the right and flattened at all the resonance modes. Thus, a broadband suppression is realized.

The main effect of the negative stiffness could also be found to be significant on the amplitude responses illustrated in Fig. 21. Clearly enough, by balancing the negative stiffness $k_l$ and the cubic nonlinear stiffness $k_n$, the BNES is able to improve its low amplitude performance without affecting its high amplitude effectiveness, hence provides a more robust solution with respect to the forcing amplitude than the classical cubic NES.

6 Conclusion

The forced dynamics of a bistable nonlinear energy sink (BNES) attached to the beam and plate structures under harmonic excitation, is discussed. By studying the frequency and amplitude responses together with their respective trends, the criteria for the parametric design of a BNES in such continuous systems for broadband vibration suppression are given.

For vibrations around a certain mode, the theoretical results evidenced that, the negative stiffness $k_l$ and nonlinear stiffness $k_n$ have a quite similar effect on the frequency and amplitude responses, as well as on the underlying slow invariant manifold. Realizing this and by taking advantage of the bistability, a balanced control between $k_l$ and $k_n$ could be found to improve the low-amplitude performance of the BNES without affecting too much the high-amplitude dynamics.

Extending the analysis to the multi-mode beam dynamics, we found that whether shown a bistable configuration or not, the nonlinear stiffness appears to be the most important parameter that characterizes the behavior of the system. As such, a simple but effective tuning procedure of highlighting at first to tune the nonlinear stiffness $k_n$ targeting the lowest mode to activate SMR around it, is proposed. Then the following steps reside in adjusting the damping to improve the performance for higher modes and balancing $k_l$ and $k_n$ to improve the low-amplitude performance. Finally, by varying the location of the BNES, it is found that the BNES achieves impressive peak reduction at a given mode when it is located at the local maximum of the corresponding shape function, hence the recommended location for multi-mode vibrations results from a combined effect of the mode functions. A properly designed BNES following such procedure is then compared to the classical cubic NES at three different forcing amplitudes, and it is found that the BNES outperforms the classical NES at both below and above the designed forcing amplitude, showing a better robustness.

Moreover, the key results and design criteria obtained in the beam case are applied to the 2D case of a thin rectangular plate. And it is found that the proposed guidelines can also be well applied to multi-mode plate vibrations to achieve its broadband suppression.

All our results have confirmed the effectiveness of a BNES to achieve broadband vibration suppression in continuous structures such as beams and plates.

Appendices

Appendix A: Matrices in Eq. (11)

The matrices in Eq. (11) are calculated as

$$\begin{aligned} \begin{aligned}&{\mathbf {N}} = {\left[ {\begin{array}{*{20}{c}} {{\mathbf {N}}_1^T,\;{\mathbf {N}}_2^T,\; \cdots ,\;{\mathbf {N}}_{{N_m}}^T} \end{array}} \right] ^T}, \\&{{\mathbf {N}}_k} = \left[ {{a_0},{a_{k1}},{a_{k2}} \cdots ,{a_{kn}},{b_{k1}},{b_{k2}}, \cdots {b_{kn}}} \right] , \\&{{\mathbf {K}}_{mc}} = \omega _0^2{\mathbf {M}} + {\omega _0}{\mathbf {C}} + {\mathbf {K}} + 3{{\mathbf {K}}_{n0}}, \\&{\mathbf {R}} = {\mathbf {F}} - \left( {\omega _0^2{\mathbf {M}} + {\omega _0}{{\mathbf {C}}_{n0}} + {\mathbf {K}} + {{\mathbf {K}}_{n0}}} \right) {\mathbf {N}}, \\&{{\mathbf {R}}_{mc}} = - \left( {2{\omega _0}{\mathbf {M}} + {\mathbf {C}}} \right) {\mathbf {N}}, \\&{\mathbf {M}} = \int _0^{2\pi } {{{\varvec{\Lambda }}^T}{{\bar{\mathbf {M}}\ddot{{\varLambda }} }}} d\tau , {\mathbf {K}} = \int _0^{2\pi } {{{\varvec{\Lambda }}^T}{{\bar{\mathbf {K}}{\varLambda } }}} d\tau , \\&{{\mathbf {K}}_{n0}} = \int _0^{2\pi } {{{\varvec{\Lambda }}^T}{{{{\bar{\mathbf {K}}}}}_{n0}}{\varvec{\Lambda }}} d\tau , {\mathbf {C}} = \int _0^{2\pi } {{{\varvec{\Lambda }}^T}{{\bar{\mathbf {C}}{\dot{{\varLambda }}} }}} d\tau , \\&{{\mathbf {R}}_f} = \int _0^{2\pi } {{{\varvec{\Lambda }}^T}\cos \tau } d\tau , {\mathbf {F}} = \int _0^{2\pi } {{{\varvec{\Lambda }}^T}{{{{\bar{\mathbf {F}}}}}_0}\cos \tau } d\tau . \\&{\varvec{\Lambda }} = diag\left[ {{\mathbf {D}},{\mathbf {D}}, \cdots {\mathbf {D}}} \right] , \\&{\mathbf {D}} = \left( {1,\cos \tau ,\cos 2\tau , \cdots ,\sin \tau ,sin2\tau , \cdots } \right) \end{aligned} \end{aligned}$$

(A.1)

Appendix B: Stability analysis using Floquet theory

The stabilities of the periodic solutions can be analyzed by means of the Floquet theory. Let ${\mathbf{X }} = {{\mathbf{X }}_0} + {\varDelta } {\mathbf{X }}$ and consider the perturbation motion of Eq. (7) near the fixed point ${{\mathbf{X }}_0}$ yields

$$\begin{aligned} {\omega ^2}{\bar{\mathbf{M }}}{\varDelta } {{\ddot{\varvec{X}}}} + \omega {{\bar{\mathbf{C }}}}{\varDelta } {\dot{\mathbf{X }}} + \left( {{\bar{\mathbf{K }}} + 3{{{\bar{\mathbf{K }}}}_{n0}}} \right) {\varDelta } {\mathbf{X }} = 0, \end{aligned}$$

(B.2)

or equivalently,

$$\begin{aligned} {\dot{\mathbf{Y }}} = {\mathbf{Q }}\left( \tau \right) {\mathbf{Y }}, \end{aligned}$$

(B.3)

with

$$\begin{aligned}&{\mathbf{Q }}\left( \tau \right) = \left[ {\begin{array}{*{20}{c}} 0&{}{\mathbf{I }}_n\\ { - \frac{{{\bar{\mathbf{M }}}}^{ - 1}}{{{\omega ^2}}}\left( {{\bar{\mathbf{K }}} + 3{{{\bar{\mathbf{K }}}}_{n0}}} \right) }&{}{ - \frac{{{\bar{\mathbf{M }}}}^{ - 1}}{\omega }{{{\bar{\mathbf{C }}}}}} \end{array}} \right] ,\\&{\mathbf{Y }} = \left[ {\begin{array}{*{20}{c}} {{\varDelta } {\mathbf{X }}}\\ {{\varDelta } {\dot{\mathbf{X }}}} \end{array}} \right] . \end{aligned}$$

Since the solution $\mathbf{X }_0$ is periodic with period $T = 2\pi$, the associated matrix ${\mathbf{Q }}\left( \tau \right)$ must also have the same property, which in turn implies ${\mathbf{Q }}\left( {\tau + T} \right) = {\mathbf{Q }}\left( \tau \right)$ and ${\mathbf{Y }}\left( {\tau + T} \right)$ solves Eq. (B.3) as well. The relationship between ${\mathbf{Y }}\left( {\tau + T} \right)$ and ${\mathbf{Y }}\left( {\tau } \right)$ can be expressed as

$$\begin{aligned} {\mathbf{Y }}\left( {\tau + T} \right) = {\mathbf{P }}{\mathbf{Y }}\left( \tau \right) , \end{aligned}$$

(B.4)

where ${\mathbf{P }}$ is usually termed as the transition matrix in the literature. Many researches have been devoted to evaluate the transition matrix ${\mathbf{P }}$. In this paper a precise Hsu’s method is applied following [49, 57], in which the period T is divided equally into n intervals with time step h, such that for the kth interval $[{\tau _k},{\tau _{k + 1}}]$, ${\mathbf{Q }}\left( \tau \right) ={{\mathbf{Q }}_k}$ is assumed to be constant, then the local transition matrix ${{\mathbf{P }}_k}$ from ${\tau _k}$ to ${\tau _{k+1}}$ writes,

$$\begin{aligned} {{\mathbf{P }}_k} = {e^{h{{\mathbf{Q }}_k}}} = {\mathbf{I }} + \sum \limits _{j = 1}^n {\frac{{{{\left( {h{{\mathbf{Q }}_k}} \right) }^j}}}{{j!}}}, \end{aligned}$$

(B.5)

thus the transition matrix P can be approximated by multiplying all the local matrices ${{\mathbf{P }}_k}$ together as

$$\begin{aligned} {\mathbf{P }} = \mathop {\varPi }\limits _{i = 1}^n {{\mathbf{P }}_k}. \end{aligned}$$

(B.6)

In the framework of the Floquet theory, the stability of the periodic response is then determined by checking the eigenvalues of P. If the spectral radius of P is less than 1, then the periodic solution is asymptotic stable, otherwise, it is unstable.