1 Introduction

Tuned mass damper (TMD) is an energy reduction device with a mass connected to a main system by a linear spring firstly conceived by Frahm [1]. This device has been extensively studied and proved that it is simple and efficient but limited in the vicinity of a single frequency [2]. In contrast, nonlinear vibration absorber is proved effective to broaden the suppression bandwidth [3]. In the past approximately fifteen years, the phenomenon of targeted energy transfer (TET) existing in a series of nonlinear vibration absorber called nonlinear energy sink (NES) is considerably studied [4, 5]. Many kinds of NES with different couple nonlinearities are developed and investigated: cubic NES [6–9], rotational NES [10, 11], piece-wise NES [12], NES by nonlinear membrane [13, 14] and vibro-impact (VI) NES [15, 16], in which special orbits for the occurrence of TET are observed by studying the underlying Hamiltonian system and the energy of the main system can be irreversibly transferred into attached VI NES and dissipated effectively during transient resonance captures. Actually, the main damping mechanism of VI NES is that the energy of main system is transferred and dissipated at the same moments of impact.

VI NES is also referred as impact damper, and its dynamics has been extensively studied [17, 18] since the initial study about an acceleration damper (an early name of the impact damper) by Lieber [19]. The principle is to transfer the energy of the main system to a small attached mass and to dissipate the energy by their mutual impact interactions. Although there exist different types of impact models [20], it has been proven that there is a similarity of several important vibro-impact systems under certain specific limits or constraints [21].

The research of impact damper has been around two main themes. The first one is about its dynamics: response regimes and their stability by analytical study in [22] and with experimental validation in [23, 24], bifurcation and chaos by numerical study with the combination use of time series, phase trajectories, bifurcation diagrams [25], Poincare maps [26] and Lyapunov exponent [27]. Similar study has been carried out for the impact oscillator by Pekerta [28]. Based on the above-mentioned work, the first point of view on the relationship between parameters and dynamics is established.

Another topic of research is concentrated on the efficiency of energy dissipation for free or forced vibration [29, 30]. The influence of system parameters (e.g., mass ratio, clearance and coefficient of restitution) is considerably investigated. The finite experimental results are concentrated on response regimes by measuring the acceleration of main system [29] or displacement of impact damper directly [31]. To evaluate the efficiency of TET, the second point of view about the relationship between parameters and the energy (e.g., amplitude) of main system is constructed.

Inspired by the extensive study in the domain of TET, an asymptotic analytical method originally used for cubic NES [32] is improved to explain the transient TET process for linear oscillator coupled with VI NES under free excitation [33], i.e., inconstant amplitude and frequency spectrum. The study of VI NES was extended under periodic excitation [34, 35] and for quenching chatter instability [36].

Slow invariant manifold (SIM) which can describe all possible fixed points and possible variation routes is obtained through the above analytical method in the first order of the timescale, and fixed points are obtained by combining equations in the first and second orders. The condition of 1:1 resonance between main system and VI NES (i.e., two impacts per cycle) required for the application of this method is relaxed to cover some more general cases (i.e., non 1:1 resonance) [37]. Actually, this asymptotic approach describes the impact system from another point of view. However, the recent research about the impact damper as NES with this new approach is limited to study the topological structure of SIM and possible response regimes. Other aspects of its dynamics (e.g., bifurcation, chaos and optimization) should be studied further, and the past work about impact damper should be understood with new horizons. Therefore, study of the dynamics from this new point of view will be the first objective of this paper.

Another goal will be concentrated on the efficiency of TET. It is observed that resonance is the essence for all NES from the perspective of TET and the type of resonance decides its efficiency [5]. The 1:1 resonance regime is claimed and proved to be the most efficient. Considering two impacts per cycle for VI NES, it may be an ideal candidate to illustrate the 1:1 resonance and the variation of efficiency of TET with more clear and direct evidences.

The system composed of a linear oscillator (LO) and a VI NES will be studied in this paper. In Sect. 2, modeling and the analytical treatments are developed. In Sect. 3, the influence of parameters on dynamics and energy reduction is analyzed by analytical and numerical results. In Sect. 4, the experimental results are presented. Finally, the conclusion is addressed.

Fig. 1
figure 1

Schema of a LO coupled with a VI NES under periodic excitation

Full size image

2 Modeling and analytical treatment

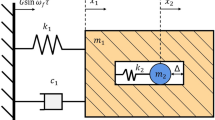
System of harmonically forced LO attached with a VI NES is presented in Fig. 1 and described by the following equation:

$$\begin{aligned} \begin{aligned}&{\ddot{x}}+\varepsilon \lambda _1{\dot{x}}+x=\varepsilon G\sin \varOmega \tau +\varepsilon ^2 \lambda _1 G\varOmega \cos \varOmega \tau \\&\varepsilon {\ddot{y}}=0\\&\forall \left| x-y\right| < b \end{aligned} \end{aligned}$$
(1)

The corresponding physical parameters are expressed as follows:

$$\begin{aligned} \begin{array}{l} \varepsilon ={\dfrac{m_{{2}}}{m_{{1}}}}, \quad {\omega _{{0}}}^{2}={\dfrac{k_{{1}}}{m_{{1}}}},\quad \tau =\omega _{{0}}t,\\ \lambda _1={\dfrac{c_{{1}}}{m_{{2}}\omega _{{0}}}},\quad \varOmega ={\dfrac{\omega }{\omega _{{0}}}}, \quad G=\dfrac{F}{\varepsilon } \end{array} \end{aligned}$$

where x, \(m_1\), \(c_1\) and \(k_1\) are the displacement, mass, damping and stiffness of the LO, respectively. y and \(m_2\) are displacement and mass of VI NES. The dots denote differentiation with respect to dimensionless time \(\tau \). b represents the clearance. \(x_{{e}} \left( t \right) =F\sin \left( \varOmega \,t \right) \) is the displacement imposed on the base.

When \(|x-y|=b\), an impact occurs. The state of the system after impact is obtained using the simplified shock theory and the condition of total momentum conservation:

$$\begin{aligned} \begin{aligned}&x^+=x^-,\quad y^+=y^-\\&{\dot{x}}^++\varepsilon {\dot{y}}^+={\dot{x}}^-+\varepsilon {\dot{y}}^-,\\&\quad {\dot{x}}^+-{\dot{y}}^+=-r\left( {\dot{x}}^--{\dot{y}}^-\right) ,\\&\text {for } |x-y|=b \end{aligned} \end{aligned}$$
(2)

where r is the restitution coefficient and the superscripts \(+\) and − denote time immediately after and before impact. New variables representing the displacement of the center of mass and the internal displacement of the VI NES are introduced as follows:

$$\begin{aligned} v=x+\varepsilon y,\quad w=x-y \end{aligned}$$
(3)

Substituting Eq. (3) into Eqs. (1) and (2), the equation between impacts in barycentric coordinate is given as:

$$\begin{aligned} \begin{aligned}&{\ddot{v}}+\varepsilon \lambda _1\dfrac{{\dot{v}}+\varepsilon {\dot{w}}}{1+\varepsilon }+\dfrac{v+\varepsilon w}{1+\varepsilon }\\&=\varepsilon G\sin \varOmega \tau +\varepsilon ^2\lambda _1 G\varOmega \cos \varOmega \tau \\&{\ddot{w}}+\varepsilon \lambda _1\dfrac{{\dot{v}}+\varepsilon {\dot{w}}}{1+\varepsilon }+\dfrac{v+\varepsilon w}{1+\varepsilon }\\&=\varepsilon G\sin \varOmega \tau +\varepsilon ^2\lambda _1 G\varOmega \cos \varOmega \tau \\&\forall |w|<b \end{aligned} \end{aligned}$$
(4)

and the impact condition (2) is rewritten as:

$$\begin{aligned} \begin{aligned}&v^+=v^-,\quad w^+=w^-,\\&{\dot{v}}^+={\dot{v}}^-,\quad {\dot{w}}^+=-r{\dot{w}}^-,\quad \text {for } |w|=b \end{aligned} \end{aligned}$$
(5)

Multiple scales are introduced in the following form:

$$\begin{aligned} \begin{aligned}&v(\tau ;\varepsilon )=v_0(\tau _0,\tau _1,\ldots )+\varepsilon v_1(\tau _0,\tau _1,\ldots )+\ldots \\&w(\tau ;\varepsilon )=w_0(\tau _0,\tau _1,\ldots )+\varepsilon w_1(\tau _0,\tau _1,\ldots )+\ldots \\&\tau _k=\varepsilon ^k \tau ,\quad k=0,1,\ldots \end{aligned} \end{aligned}$$
(6)

A detuning parameter (\(\sigma \)) representing the nearness of the forcing frequency \(\varOmega \) to the reduced natural frequency of the LO is introduced:

$$\begin{aligned} \varOmega =1+\varepsilon \sigma \end{aligned}$$
(7)

Substituting Eqs. (6) and (7) into Eqs. (4) and  (5), then equating coefficients of like power of \(\varepsilon \) gives:

Order \(\varepsilon ^0\):

$$\begin{aligned}&D_0^2v_0+v_0=0 \nonumber \\&D_0^2w_0+v_0=0,\quad \forall |w_0|<b \end{aligned}$$
(8)
$$\begin{aligned}&v_0^+ = v_0^-,\quad w_0^+=w_0^-,\nonumber \\&D_0v_0^+ = D_0v_0^-,\quad D_0w_0^+=-rD_0w_0^-,\nonumber \\&\text {for } |w_0|=b \end{aligned}$$
(9)

Order \(\varepsilon ^1\):

$$\begin{aligned} \begin{array}{c} D_0^2v_1+v_1=-2D_0D_1v_0-\lambda _1 D_0v_0-w_0+v_0\\ +\,G\sin \left( \tau _0+\sigma \tau _1\right) \end{array} \end{aligned}$$
(10)

Here, the SIM will be obtained through the first order and the fixed points will be obtained by combining the first order and the second order, as have been done in [34].

For \(v_0\), Eqs. 8 and 9 simply represent an undamped harmonic oscillator case and its solution can be expressed as follows:

$$\begin{aligned} v_0=C(\tau _1)\sin \left( \tau _0+\theta (\tau _1)\right) \end{aligned}$$
(11)

For \(w_0\), Eqs. 8 and 9 represent a harmonically forced impact oscillator with symmetric barrier. Under the assumption of 1:1 resonance (i.e., motion with two symmetric impact per cycle), its solution can be searched in the following form:

$$\begin{aligned} w_0= & {} C(\tau _1)\sin \left( \tau _0+\theta (\tau _1)\right) \nonumber \\&+\,\frac{2}{\pi }B(\tau _1)\varPi \left( \tau _0+\eta (\tau _1)\right) \end{aligned}$$
(12)

where \(\varPi (z)\) is a nonsmooth saw-tooth function [38, 39]. This folded function and its derivative are depicted in Fig. 2 and are expressed as follows:

$$\begin{aligned}&\varPi (z)=\arcsin (\sin z),\nonumber \\&M(z)=\frac{\mathrm{d}\varPi }{\mathrm{d}z}=sgn(\cos z) \end{aligned}$$
(13)

According to Eqs. (12) and (13), impact occurs at \(T_0=\pi /2-\eta +j\pi \) with \(j=0,1,2,\ldots \) The impact condition \(|w_0|=b \) is rewritten with Eq. (12) as:

$$\begin{aligned} C\cos \left( \eta -\theta \right) =b-B \end{aligned}$$
(14)
Fig. 2
figure 2

Representation of the nonsmooth functions \(\varPi (z)\) and M(z)

Full size image

Rewriting now the inelastic impact condition (9) yields:

$$\begin{aligned} C\left( 1+r\right) \sin \left( \eta -\theta \right) =\frac{2}{\pi }B\left( 1-r\right) \end{aligned}$$
(15)

Combining Eqs. (14) and (15), a relation between B and C is obtained as follows:

$$\begin{aligned} C^2=\left( 1+\frac{4\left( 1-r\right) ^2}{\pi ^2\left( 1+r\right) ^2}\right) B^2-2b B+b^2 \end{aligned}$$
(16)

An example of the SIM with \(b=1\) and \(r=0.6\) is presented in Fig. 3. The stability of SIM is analyzed by the approach used in [22], in which the stable branch is defined by the condition that the modulus of all the eigenvalues of a certain matrix relating conditions after each of two consecutive impacts is less than unity. And it also can be evaluated by direct numerical integration of Eq. (8).

Fig. 3
figure 3

SIM of VI NES: one stable branch in blue thick line and two unstable branches in red fine line . (Color figure online)

Full size image

In order to obtain the fixed points or study the evolution of motion of system on the SIM for strongly modulated response (SMR), Eq. (10) at the next order of approximation is analyzed. To identify terms that produce secular terms, the function of \(w_0\) is expanded in Fourier series in the following form:

$$\begin{aligned} \begin{aligned} w_{{0}}=&C(\tau _1)\sin \left( \tau _0+\theta (\tau _1)\right) + E\left( \tau _1\right) \\ {}&\sin \left( \tau _{{0}}+\zeta \left( T_{{1}} \right) \right) +RFC \\ \end{aligned} \end{aligned}$$
(17)

where RFC represents the rest frequency components compared to the first two terms. \(E\left( \tau _1\right) \) is decided by the motion of VI NES. Equation (17) is a more general and relaxed analytical description with respect to the motion of VI NES compared to the case of just 1:1 resonance (i.e., two symmetric impacts per cycle). If the case of 1:1 resonance exists, the fixed points can be analytically obtained. However, only partial duration of the whole process is in resonance for response regimes like free vibration and SMR. In these two cases, the above-relaxed equation is useful and efficient to explain the underlying mechanism.

Table 1 Parameters of the experiment
Full size table

Substituting Eqs. (11), (12) and (17) into Eq. (10) and eliminating terms that produce secular terms gives:

$$\begin{aligned} \begin{aligned}&D_1C=-\frac{1}{2}\lambda _1 C-\frac{1}{2}E\sin \left( \varTheta \right) +\frac{1}{2}G\sin \left( \eta \right) \\&D_1{\eta }=\frac{1}{2}\,{ G \cos \left( \eta \right) /C}-\frac{1}{2}\,{E\cos \left( \varTheta \right) /C}+\sigma \end{aligned} \end{aligned}$$
(18)

where

$$\begin{aligned} \begin{aligned}&\varTheta =\zeta -\theta \\&\eta =\sigma \tau _1-\theta \end{aligned} \end{aligned}$$
(19)

\( \varTheta \) represents the phase difference related to that between LO and VI NES. \(\eta \) represents the phase difference related to that between LO and outside excitation.

3 Analytical and numerical results

3.1 Response regimes

The experimental identified parameters of the system in Table 1 (see Sect. 4) will be used. The regime is labeled by the quantity \(z=p/n\), where p is the number of impacts and n is the number of excitation periods T during the considered time [25]. Five different response regimes exist with the variation of clearance under outside excitation with the frequency of 8.5 Hz, and they are categorized by the value of z as shown in Fig. 4. The first, second and third columns represent the displacement of LO, relative displacement and projection of motion (i.e., yellow lines) into SIM, respectively. z can be observed from the second column combined with the first column, i.e., the total occurrence times of extreme relative displacement value (i.e., b or \(-b\)) during one period of LO. Figure 4a is chosen as the representation for all case with \(z>2\), in which \(z=3\) and \(z=4\) coexist. In this case, the time difference between impacts is not equally distributed as showed in the middle subfigure and the stable projected motion is located at the right unstable branch of SIM and it is far from the stable blue branch as showed in the right subfigure. Moreover, the number of impacts increases with the decrease of clearance, but the impulse strength decreases. Figure 4b represents two asymmetric impacts per cycle with \(z =2\). The time difference between two impacts is not the same, and the projected motion is closer to the stable blue thick branch. Figure 4c represents two symmetric impacts per cycle with \(z =2\). It is seen in the right subfigure that the steady projected motion can be represented by a point in the stable branch of SIM except the transient process at the beginning. A SMR is presented in Fig. 4d, and the alternative appearance of \(z=2\) and \(z<2\) can be seen in the middle and right subfigures. For the part \(z=2\), the case with two impacts per cycle occurs and its variance is governed by the blue stable branch. For the part \(z<2\), the case with sparse impacts occurs, and its variation law is not known. This irregularity is also demonstrated by the variation of amplitude of LO in the left subfigure, which reveals the chaotic characteristic of SMR. Figure 4e demonstrates loose impact case with \(z<2\), in which transient 1:1 resonance with continuous two impacts per cycle does not exist. In this area, the response is chaos. From the variation of impact number and displacement amplitude of LO in Fig. 4, it is seen that the average value of z with long time duration decreases and the average value of amplitude of displacement (x) decreases at the first place and then increases.

Fig. 4
figure 4

Displacement of LO in the first column, relative displacement in the second column and motion of system projected into SIM in the third column for different response regimes: a \( z >2\); b \(z =2\) and asymmetric; c \(z =2\) and symmetric; d \(z =2\) and \(z <2\) for SMR; e \(z <2\)

Full size image

3.2 Areas of SIM

From the third column of Fig. 4, it is seen that the relative position of motion projected into SIM varies with clearance. According to the value of \(C^2\), 4 areas can exist. This law of variation by numerical study can also be analytically obtained, and the result is shown in Fig. 5a. With the increase of clearance, one of the fixed point represented by red circle will move along the SIM from area Z1 with \(z >2\) to \(z =2\) through a series of grazing bifurcation. In area Z2, the regime with two asymmetric impacts per cycle persists until the critical point between stable blue branch and the right unstable red branch, in which the double period bifurcation occurs. Then the regime with two symmetric impacts per cycle occurs. If the above process is continued, there exist two routes entering into chaos. The first case is shown in Fig. 5b, and the two unstable points will approach each other and then disappear. The response regime is SMR demonstrated in Fig. 4d, and the duration time of transient 1:1 resonance part will decrease with the increase of clearance, which is numerically observed by an outside excitation frequency 8.5 Hz. Another case is demonstrated in Fig. 5c with an outside excitation frequency 8 Hz. Two fixed points exist in the stable branch and then disappear by collision with each other. During the evolution of this case, there exist two possible solutions, i.e., two symmetric impacts per cycle and SMR. The regime chaos in area 4 will appear after the collision of fixed points at the end of the above two cases with further increase of clearance. The above analysis process for the variation of regimes can be applied to other parameters, although the specific variation route will depend on the specific parameters. In return, different bifurcations and routes to chaos can be explained with the above analysis approach.

Fig. 5
figure 5

Areas of SIM: a 4 typical areas; b a first case in Z3; c a second case in Z3

Full size image

3.3 Transition phenomena and optimization criteria

From the above analysis, there exist two possible transition routes to chaos with two different transition regions, which are, respectively, defined as hysteresis region and beat motion region. The former corresponds to Fig. 5c in which the response regime is ambiguous (1:1 resonance or SMR). The latter corresponds to Fig. 5b characterized by the SMR of main system [28]. Two boundaries can be analytically obtained by two bifurcation conditions (i.e., the bifurcation shown in Fig. 6a and the bifurcation demonstrated in Fig. 6b). The first one is defined by the contact point between the left unstable red branch and the stable blue branch, and the other condition is obtained by the collision of the two fixed points. For a frequency bandwidth, the above two transition regions are obtained and shown in Fig. 6c. A1 represents the hysteresis region, which is numerically validated by coexistence of SMR and 1:1 resonance, which has been experimentally observed in [24]. A2 represents the beat motion region. The point P1 represents the singular point in which the continuous transition without SMR (i.e., no intermittency) exists. From the variation of displacement amplitude of LO in Fig. 4, it is reasonable to assume that the optimal energy dissipation exists at the point where 1:1 resonance disappears, which is represented by the red cross in Fig. 6c. Different response regimes in different areas (i.e., Z1, Z2, Z3 and Z4) are also validated by numerical results, and they are represented by the squares, circle and star.

Fig. 6
figure 6

Transition phenomenon: a saddle-node bifurcation boundary; b Hopf bifurcation boundary; c transition regions

Full size image

3.4 Influence of frequency

With the variation of relative value between the amplitude of outside force and clearance (i.e., G / b), the relative position of frequency response function (FRF) of the main system will vary and it will result in the location change of the projected motion in the SIM. This phenomenon has been experimentally observed in [34]. For a fixed G, this relative location will change from area Z1 to Z4 (i.e., from black thick dotted curve to blue thin curve) with the increase of b as shown in Fig. 7. For any relative location, just some interval of frequency can situate in area Z3 (e.g., red fine dotted curve and green thick curve), in which the most efficient energy reduction by TET is possible, no matter in the form of resonance capture by the 1:1 resonance regimes or just one part of the process in resonance capture by SMR. This is the reason why one optimal designed parameter will not still be optimal for another frequency. The fact is that the 1:1 resonance regime for all range of frequency is not possible. Another phenomenon is about possible types of bifurcations and routes to chaos during sweep experiments (e.g., observed in [27]). All possible cases can be explained clearly. For the case of fine blue line in Fig. 7b, there will not exist any route to chaos. However, there will be two possible routes for the case represented by the thick black dotted line, i.e., the first route can go up along the line as follows: two symmetric impacts, then two asymmetric impacts, then increase the number of impacts until total chaos. The second route can go down along the line in the following way: two symmetric impacts, then SMR, then decrease of the duration time for the 1:1 resonance part of SMR until total chaos. The typical cases with fine red dotted line and thick green line can be a little different but can be explained in the same way. For the past researches about parameter optimization for a frequency range around resonant frequency, different cases have been observed and explained. However, the study is incomplete and the goal is not clear. From Fig. 7, the optimization criterion is clear and is just to make the objected bandwidth of frequency located in the area Z3 as more as possible. Normally, the objective bandwidth of frequency is around the natural frequency of LO; therefore, the case with fine red fine dotted line is the better.

Fig. 7
figure 7

Influence of frequency on the dynamics around SIM: a SIM; b relative position of FRF

Full size image

3.5 Influence of mass ratio and damping

The SMR projected in SIM is shown in Fig. 8a. More information about the variation mechanism of the displacement of LO and intern displacement is shown in Fig. 4d. In the stable branch with thick blue curve, the good prediction with a high correlation between theoretical blue curve and numerical green curve is seen and enlarged in Fig. 8c, which cannot be obtained by the traditional analytical approach comprehensively summarized in [17]. For the analytical method firstly developed in [33], its objective is to analyze the transient resonance capture (two impacts per cycle) during free vibration and it is also applied to periodically forced vibration. Its application requires small magnitude of mass ratio and damping. For the transition part between non 1:1 resonance and 1:1 resonance shown in Fig. 8b and the stable part shown in Fig. 8c, the vertical value difference of every vertical yellow line is decided by the energy dissipation of impact related to mass ratio and restitution coefficient (the influence of restitution will be explained later) and that of every horizontal yellow line is decided by the energy dissipation related to the damping of LO. Large energy reduction resulted from large mass ratio and damping will result in the failure of this approach, i.e., the prediction of SIM to projected motions, although it may increase the efficiency of energy reduction. From Fig. 4d, it is seen that the response is strongly modulated and the local maxima changes every time, which is defined as chaotic SMR in [35]. To explain its variation trend, the non 1:1 resonance motion of VI NES should be considered and its average action force on the LO should be developed in Fourier series. Its small amplitude in Eq. (17) reveals the cause for the increase of the amplitude of main system. This way of treatment is also fairly convenient to understand experimental results which will be explained in the experimental part. In addition, a method applying limiting phase trajectories by studying the underlying Hamiltonian system is used to explain the formation of SMR in a duffing system under biharmonic excitation [40]. Actually, it is expected that the optimal point obtained by this method could be closely related to the limit point entering into SMR from two impacts per cycle for the system with VI NES. Here, the interaction force of the impact moment is stressed here to explain the formation process.

Fig. 8
figure 8

SMR projected into SIM: a motion projected in green lines; b an enlarged view of transition part; c an enlarged view of 1:1 resonance part. (Color figure online)

Full size image

3.6 Influence of restitution coefficient

From Eq. (16) and Fig. 3, there exists a minimal value for the occurrence of 1:1 resonance. When the restitution of coefficient is varied with the amplitude of LO (black dotted line) and other parameters fixed, the relative position of SIM will vary as shown in Fig. 9a. When \(r=1\) showed in red fine curve, it will locate in area Z1, in which the impact number is large but with low impact impulse strength. As a result, the energy dissipation is not high. With the decrease of r, the transition will follow along the black arrow in Fig. 9b. When \(r=0.2\) showed in black thick dotted curve, the impact number will be low and impact pulse may be large. Globally, it will result in low efficiency. Therefore, an intermediate value will be optimal and lead to a maximal value of E in Eq. (17).

Fig. 9
figure 9

Influence of restitution coefficient: a SIMs with different r; b relative position for different r

Full size image
Fig. 10
figure 10

Experimental setup: a global configuration; b a detailed view of VI NES

Full size image

4 Experimental results

The experimental setup is presented in Fig. 10a. It consists of a LO, with an embedded VI NES. The whole system is embedded on 10 kN electrodynamic shaker. The displacement of the LO and the imposed displacement of the shaker are measured using contact-less laser displacement sensors. The acceleration of the LO is measured by a accelerometer. A detailed view of the VI NES is presented in Fig. 10b. It simply consists of a closed cavity of length \(d+2b\), where d is the diameter of the ball and b can be adjusted by a cylinder in the cavity. The cylinder and the other side cover are made of hardened steel. The parameters of the system have been identified by performing modal analysis and are summarized in Table 1. The excitation frequency is fixed to 8 Hz.

4.1 Route to chaos

The route to chaos can be judged in different ways such as those showed by the variation of response in different columns of Fig. 4, but they require the displacement and velocity of VI NES to be known as a prerequisite, which is not allowed and limited by available measure device. Another way is to use a return map of time difference between every two consecutive impacts [41]. For a limited time of data acquisition with the excitation period given, the time of impact \({t_i}\) can be measured as showed by red stars in right subfigures of Fig. 11a–f. The acceleration of LO (blue curve) will change abruptly, and then the time difference between these moments \(\delta t_i\) can be calculated. Two neighboring time difference \(\delta t_i\) and \(\delta t_{(i+1)}\) can form one point \((\delta t_i , \delta t_{(i +1)})\), and every two points can constitute a vector with the first point \((\delta t_i , \delta t_{(i +1)})\) and the second point \((\delta t_{(i+1) }, \delta t_{(i +2)})\).

Fig. 11
figure 11

Route of the variation of regimes: a \(b=0.3\) mm, chaos and \(z>3\); b \(b=2.5\) mm and \(z=3\); c \(b=4\) mm, asymmetric resonance and \(z=2\); d \(b=7.5\) mm, symmetric resonance with \(z=2\); e \(b=11.5\) mm, SMR and partially with \(z=2\) ; f \(b=20\) mm, chaos and \(z<2\); g location of different regimes in SIM

Full size image

With the variation of b, different response regimes have been observed. All left subfigures in Fig. 11a, f represent the time difference return map, and the yellow dotted triangle can be expressed by L1: \( \delta t_x + \delta t_{y}=T \) (1/8 s) , L2: \( \delta t_x = T (1/8 \,s) \) and L3 \( \delta t_{y}=T\) (1/8  s). The black dotted line can be expressed by L4: \( \delta t_x = \delta t_y \). All right subfigures in Fig. 11a, f represent a typical sample of the acceleration of LO, in which the red stars denote the time of impact and the value of acceleration. Figure 11g demonstrates the relative position of every regime in SIM. For \(b=0.3\) mm, the results are shown in Fig. 11a, there exist more than 3 impacts during one period, and the distribution of impact time is also irregular, which is judged as chaos. For \(b=2.5\) mm shown in Fig. 11b, there exist three impacts every period and the impact time distribution is not equal but stable which is illustrated by the fact that all vector form in a triangle; meanwhile, all points are inside L1. For \(b=4\)  mm in Fig. 11c, the vector is located at the L1, which means that it just exist two impacts every period. However, the absolute value of acceleration is not equal. For \(b=7.5\) mm in Fig. 11d, there also exist two impacts per cycle, but this time the absolute value of acceleration is almost equal. For \(b=11.5\) mm in Fig. 11e, the case of two impact per cycle and no impact appears alternatively and the duration time of 1:1 resonance is short and irregular. For \(b=20\) mm in Fig. 11f, all points are in the right and up side of L1, and it means that two impacts per cycle do not exist during the whole process, i.e., transient resonance captures do not exist.

In summary, the relative position in the SIM moves with the increase of clearance as observed by the study in the last section. The value of acceleration (i.e., impulse strength) is small although with many impacts during one period for small clearance. Then it augments with the two impacts per cycle, and the efficiency of TET is the largest. A further increase of clearance, instantaneous large value (i.e., strong impulse strength) can exist, but it cannot persist during the whole process. From analytical analysis, the number and strength of impact impulse can decide the value of E in Eq. (17) directly and it will then decide the efficiency of TET, which is validated by experimental results here.

Fig. 12
figure 12

TET during SMR: a acceleration of LO; b return map of time difference; c superposition of acceleration (blue curve) and displacement of LO (red curve) and displacement of shaker (black curve); d–f enlarged views of c. (Color figure online)

Full size image

4.2 TET during SMR

A SMR with \(b=15\)  mm is demonstrated in Fig. 12, which is characterized by the intermittency of 1:1 resonance (i.e., two impacts per cycle) and the chaotic strongly modulated amplitude of LO. In Fig. 12a, the acceleration of LO with the duration 5 s is demonstrated by the blue curve and meanwhile the points of the impact moments represented by red stars illustrate the time and acceleration value of impact moments. The intermittent and chaotic characteristic is demonstrated by the irregular occurrence and duration time of 1:1 resonance as showed by the distribution of impact points in Fig. 12a and also by transient escape in the return map of time difference shown in Fig. 12b. In Fig. 12c, the black curve and red curve represent the displacement (mm) of shaker and LO, respectively, which is superimposed with the acceleration of LO. Here, the influence of the amplitude and frequency of impact to the energy reduction is showed by the variation of the amplitude of LO. The transient resonance captures are seen by two impacts per cycle, in which TET is possible. In the first equation of Eq. (18), the amplitude variation of main system at the slow timescale is decided only by the amplitude (i.e., E) which is obtained by Fourier transfer and has the same frequency as that of LO, provided that the damping of LO and outside excitation are fixed. For the decreasing period of the amplitude of LO, two impacts per cycle and large value of impact impulse strength are required to guarantee the condition of 1:1 resonance and large impact damping as shown in Fig. 12e. Otherwise, it will increase for not enough dense impacts illustrated in Fig. 12f or not big enough impact impulse even with two impacts per cycle as shown in Fig. 12d. Therefore, although 1:1 resonance (two impacts per cycle) is necessary for TET, their efficiency is different for different 1:1 resonance regimes as is showed by the difference of acceleration value for the same 1:1 resonance regime from the above experimental results and is also analytically represented by different points at the stable blue branch in Fig. 3. Or it is reasonable to suppose that the most efficient case is the one with not only 1:1 resonance but also the largest impact impulse strength in impact moments as may be presented by the optimal curve proposed in Fig. 6, which is out the scope of this paper and need to be studied further.

If we look closely, there exist small peaks of the acceleration during the period defined by no impacts period as has been used in the analysis, which is showed for the time around \(t=2.7\) s in Fig. 12f. This phenomenon is probably caused by the small inclination of the LO which results in the location of the ball in one side rather than in the middle [42]. Another problem is that the time difference is not equal for two consecutive impacts per cycle as has not been predicted by analytical results, which is possibly caused by the friction between LO and VI NES, the inclination of LO and the difference of the restitution coefficient at each side [24]. Although the above two phenomena have not been considered in the analytical study, they do not influence the above-obtained conclusion.

5 Conclusion

An asymptotic analytical approach is developed for vibrating system with VI NES. All response regimes are analyzed and organized around the SIM analytically obtained, which represents all possible 1:1 resonance points and establishes the relationship between motion of main system and VI NES. The influence of system parameters and initial conditions on the dynamics and efficiency of energy reduction is demonstrated with analytical and numerical results. Experimental results prove the existence of different regimes and different routes to chaos. TET during SMR is also experimentally demonstrated.

The general equation (i.e., Eq. (18)) can not only be used to solve fixed points but also explain the amplitude variation of the 1:1 resonance regimes for free and forced vibration. In addition, it can explain the complicated variation of amplitude from experimental results. Considering that the impact system (e.g., impact oscillator and impact damper) is similar from the viewpoint of main systems with the help of interacting force presented in the form of Fourier series, the analytical method can be popularized.

That all regimes are organized around SIM provides another point of view compared to the combination of parameters and regimes for the study of dynamics or that of parameters and amplitude for the study of energy reduction efficiency used by researchers like Peterka [25]. Specifically, the influence of different parameters on the appearance of different response regimes can be investigated by the same criteria with the SIM as an intermediate. The optimal design parameter is decided by whether the 1:1 resonance occurs.

Another interesting phenomenon is about the SMR from experimental results. It demonstrates different efficiency of TET for different regimes with short duration. It can be imagined that it is related to the transient process if the outside excitation is interrupted abruptly and set to zero. Therefore, it can provide some proof for the optimization for free vibration system with transient TET. The complicated experimental SMR characterized by strongly modulation and chaotic impacts proves the convenient application of the extended analytical method.