1 Introduction

In the study of aircraft with an axially speed, many models are initially treated as static free beams, and the effect of axial motion is not considered. However, when the aircraft flies at a high speed, it produces a high temperature of thousands of degrees Celsius. Aerodynamic heating can affect the dynamic environment; in particular, induced vibration caused by sudden temperature changes with thermal shock in the structure.

Gilat et al. [1] considered the dynamic responses of the metal matrix-reinforcing laminated composite plates under thermomechanical coupling effect and solved the problem by Runge–Kutta methods. Ghayesh et al. [2] investigated the nonlinear dynamics of an axially moving beam with time-dependent axial speed, including numerical results for the nonlinear resonant response of the system in the subcritical speed regime and global dynamical behavior. Chen and Yang [3] used the method of multiple scales to study the nonlinear free transverse vibration of an axially moving beam. Ghayesh et al. [4] investigated the nonlinear forced dynamics of an axially moving viscoelastic beam in the supercritical speed regime, when the system is beyond the first instability.

Hein et al. [5] conducted a thermal shock analysis of functionally graded and layered materials using a numerical method. Ghayesh et al. [6] investigated the thermomechanical nonlinear dynamics of a buckled axially moving beam numerically with special consideration to the case with a three-to-one internal resonance between the first two modes. Yao Zhang and Jing-rui Zhang [7] investigated the combined control of fast attitude maneuver and stabilization for large complex spacecraft. Ding and Chen [8] applied the fast Fourier transform to explore the natural frequencies of nonlinear vibrations of axially moving beams. Ghayesh et al. [9] investigated numerically the coupled longitudinal–transverse nonlinear dynamics of an axially accelerating beam, and this problem is classified as a parametrically excited gyroscopic system. Shi-rong Li et al. [10] put forward the transient dynamic responses of an isotropic beam subjected to thermal shock with the use the differential quadrature method. Burak Özhan and Pakdemirli [11] applied steady-state solutions based on a model with arbitrary linear and cubic operators to study an axially moving Euler–Bernoulli beam and an axially moving viscoelastic beam. Ghayesh et al. [12] investigated the nonlinear coupled longitudinal–transverse vibrations and stability of an axially moving beam subjected to a distributed harmonic external force, which is supported by an intermediate spring. Rostam et al. [13] proposed six different vibration control strategies to suppress both the flexural and torsional vibrations of a curved beam traversed by off-center moving loads. Ghayesh et al. [14] investigated an axially moving beam with coupled longitudinal and transverse displacements by considering a case with a three-to-one internal resonance.

To suppress the transverse vibration caused by thermal shock, several researchers have used active control methods, including boundary control method and distributed control method to design the controller and actuator. However, these methodologies are more complex than their passive counterparts. Several researchers have studied how to improve the performance of nonlinear energy sink to dissipate the primary system oscillatory energy [15–17]. Different points of view are considered for a comprehensive review of previous studies associated with the current work. A nonlinear energy sink (NES) is a dynamic system that composed of a small mass, a damper, and a nonlinear stiffness spring. In such a system, vibration energy can be “pumped” from the linear part to the nonlinear part [18–21], and the NES can perform over low-frequency and high-frequency ranges and transfer and dissipate significant vibration energy.

Angelo and Daniele [22] presented the use of nonlinear energy sink as a passive control device is extended here to a nonlinear elastic string, in internal resonance conditions, excited by an external harmonic force. Zhang et al. [23] analyzed the effectiveness of an NES connected to an axially moving string and proved that the NES can effectively suppress the vibration of the axially moving string with transverse wind loadings. Yang et al. [24] conducted a numerical study on a pipe NES system and found that the system can efficiently transfer and dissipate the vibration energy caused by the fluid movement in the pipe. Kani et al. [25] investigated the vibration control of a nonlinear simply supported beam with an essentially nonlinear attachment and optimized the NES parameters with the use of both sensitivity analysis and particle swarm optimization method. Ahmadabadi and Khadem [26] investigated grounded and ungrounded configurations of NES attached to a cantilever beam and found that the latter effectively dissipates vibration energy. Georgiades and Vakakis [27] utilized numerical methods to prove that input shock energy is locally dissipated and rapidly transferred from a linear, flexible simply supported beam to the attached NES. Masoumeh Parseh et al. [28] investigated steady-state dynamic of the beam by two different theories of Euler–Bernoulli and Timoshenko. Complex averaging method combined with arc length continuation is used to achieve an approximate solution for the steady-state vibrations of the system based on 1:1 resonance condition.

Previous studies on the thermal shocks in beams used cantilever beams or simply supported beams, instead of moving beams, as models. Thus, in this study, the suppression of thermal shock-induced vibration of an axially moving beam with an NES is examined. The equation for the transverse vibration of the beam is established using Hamilton’s principle, and the equation for the beam with an NES was approximated by the Galerkin method. The primary system can be well controlled by choosing proper parameters of the NES on the premise of the best system performance. The results of the numerical algorithm used to obtain the displacement responses of the beams with NES and without NES attached under the thermal shock show that the control effect of NES and the NES efficiency are good and could help to reduce the axially moving beam oscillations rapidly.

Fig. 1
figure 1

Axially moving beam with nonlinear energy sink

Full size image

2 Dynamical model

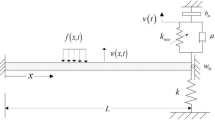
The target system, as depicted in Fig. 1, consists of an axially moving beam with simply supported ends on which a NES is attached and thermal shock is imposed on it. Compared their equations of motion with Ref. [23], the main emphasis is to study the impact of thermal shock, but NES is connected between the string and the ground in Ref. [23].

The length of the beam is l, the flexural rigidity is EI, the density per unit length is \(\rho \), the movement speed of the beam in the axial direction of the rigid body is V, I is the moment of inertia, \(\eta \) is the viscosity coefficient of the beam material, the nonlinear (cubic) spring stiffness is K, the NES dissipation is D, and the NES mass is \(m_\mathrm{NES}\). The transverse displacements of the beam and the NES relative to the horizontal X-axis are represented by Y(X, T) and U(X, T). The governing equation of motion can be obtained using Hamilton’s principle, as shown in the following equation [29]:

$$\begin{aligned}&\rho \left( \frac{\partial ^{2}Y(X,T)}{\partial T^{2}}+2V\frac{\partial ^{2}Y(X,T)}{\partial X\partial T}+V^{2}\frac{\partial ^{2}Y(X,T)}{\partial X^{2}}\right) \nonumber \\&\quad -\left( {P}^{\prime }\frac{\partial Y(X,T)}{\partial X} +P\frac{\partial ^{2}Y(X,T)}{\partial X^{2}}\right) \nonumber \\&\quad +EI\frac{\partial ^{4}Y(X,T)}{\partial X^{4}}+\eta I\frac{\partial ^{5}Y(X,T)}{\partial X^{4}\partial T}+\frac{{\hbox {d}}M(X)}{{\hbox {d}}X}\nonumber \\&\quad +\,\Bigg \{K\left[ Y(x_d ,T)-U(x_d ,T)\right] ^{3}\nonumber \\&\quad \left. +\,D\left( \frac{\partial Y(x_d,T)}{\partial T}-\frac{\partial U(x_d ,T)}{\partial T}\right) \right\} \nonumber \\&\delta (X-x_d )=0 \end{aligned}$$
(1)
$$\begin{aligned}&\quad m_\mathrm{NES} \frac{\partial ^{2}U(x_d ,T)}{\partial T^{2}}+K\left[ U(x_d ,T)-Y(x_d ,T)\right] ^{3}\nonumber \\&\quad +\,D\left[ \frac{\partial U(x_d ,T)}{\partial T}-\frac{\partial Y(x_d ,T)}{\partial T}\right] =0 \end{aligned}$$
(2)

where

$$\begin{aligned} P(x)= & {} -\int _x^l {\rho v_t } \mathrm{d}x+N(x) \end{aligned}$$
(3)
$$\begin{aligned} N(x)= & {} \int _0^h {Ew\alpha \Delta \bar{{T}}(x,z,t)\mathrm{d}z} \end{aligned}$$
(4)
$$\begin{aligned} M(x)= & {} \int _0^h {Ew\alpha \Delta \bar{{T}}(x,z,t)z\mathrm{d}z} \end{aligned}$$
(5)

where P is the axial force, N is the thermal axial force, M is the thermal bending moment, h is the height of the beam cross section, z is the coordinate in the direction of thickness, w is the width of the beam cross section, \(\alpha \) is the linear expansion coefficient, \(\bar{{T}}\) is the temperature field under thermal shock, and \(x_d \) is the NES position on the beam.

The following is non-dimensional quantities

$$\begin{aligned} x= & {} \frac{X}{L},y=\frac{Y}{L},t=\frac{T}{L^{2}}\sqrt{\frac{{\hbox {EI}}}{\rho }},\nonumber \\ v= & {} {\hbox {VL}}\sqrt{\frac{\rho }{{\hbox {EI}}}},{p}^{\prime }=\frac{{P}^{\prime }L^{3}}{{\hbox {EI}}}p=\frac{{\hbox {PL}}^{2}}{{\hbox {EI}}}, \nonumber \\ \alpha _1= & {} \frac{\eta }{L^{2}}\sqrt{\frac{I}{\rho E}},{m}^{\prime }=\frac{{\hbox {d}}M}{{\hbox {d}}X}\frac{L^{3}}{{\hbox {EI}}},k=\frac{{\hbox {KL}}^{6}}{{\hbox {EI}}},\nonumber \\ \sigma= & {} \frac{{\hbox {DL}}^{2}}{\sqrt{\rho {\hbox {EI}}}},\varepsilon =\frac{m_{{\hbox {NES}}} }{\rho } \end{aligned}$$
(6)

Substituting Eq. (6) into Eqs. (1) to (2) yields the following dimensionless form

$$\begin{aligned}&\frac{\partial ^{2}y(x,t)}{\partial t^{2}}+2v\frac{\partial ^{2}y(x,t)}{\partial x\partial t}+v^{2}\frac{\partial ^{2}y(x,t)}{\partial x^{2}}\nonumber \\&\quad -\left( {p}^{\prime }\frac{\partial y(x,t)}{\partial x}+p\frac{\partial ^{2}y(x,t)}{\partial x^{2}}\right) \nonumber \\&\quad +\,\frac{\partial ^{4}y(x,t)}{\partial x^{4}}+\alpha _1 \frac{\partial ^{5}y(x,t)}{\partial x^{4}\partial t}+{m}^{\prime }(x)\nonumber \\&\quad +\,\left\{ k\left[ y(x_d ,t)-u(x_d ,t)\right] ^{3}\right. \nonumber \\&\quad \left. +\,\sigma \left( \frac{\partial y(x_d ,t)}{\partial t} -\frac{\partial u(x_d ,t)}{\partial t}\right) \right\} \delta (x-x_d )=0 \nonumber \\ \end{aligned}$$
(7)
$$\begin{aligned}&\varepsilon \frac{\partial ^{2}u(x_d ,t)}{\partial t^{2}}+k\left[ u(x_d ,t)-y(x_d ,t)\right] ^{3}\nonumber \\&\quad +\,\sigma \left[ \frac{\partial u(x_d ,t)}{\partial t}-\frac{\partial y(x_d ,t)}{\partial t}\right] =0 \end{aligned}$$
(8)

3 Galerkin method

Based on the Galerkin method, the lateral vibration displacement can be expressed by the superposition of the intrinsic mode function of the beam at a certain moment. The displacement expansion is assumed to be

$$\begin{aligned} y(x,t)=\sum _{j=1}^N {q_j } (t)\Phi _j (x) \end{aligned}$$
(9)

where \(q_j (t)\) are the generalized coordinates of the discretized system. The beam is supported by pinned ends, so we designate \(\Phi _j (x)=\sqrt{2}\sin \lambda _j x,\lambda _j =j\pi \), where the \(\sqrt{2}\) factor is for ensuring orthonormality.

Fig. 2
figure 2

Comparison of the transient response of the moving beam with NES and without NES with zero velocity at different positions. a \(x_d = 0.9\), b \(x_d = 0.7\), c \(x_d = 0.6\), d \(x_d = 0.55\)

Full size image

Substituting Eq. (9) into Eqs. (7) and (8) yields

$$\begin{aligned}&\sum _{j=1}^N \left[ \phi _j (x)\ddot{q}_j (t)+2v{\phi }^{\prime }_j (x)\dot{q}_j (t)+v^{2}{\phi }^{\prime \prime }_j (x)q_j (t)\right. \nonumber \\&\quad \left. -({p}^{\prime }{\phi }^{\prime }_j (x)q_j (t)+p{\phi }^{\prime \prime }_j (x)q_j (t)) \right. \nonumber \\&\quad \left. +\,\phi _j ^{(4)}(x)q_j (t)+\alpha _1 \phi _j ^{(4)}(x)\dot{q}_j (t)\right] \nonumber \\&\quad +\,{m}^{\prime }(x)+\left\{ k\left[ \sum _{j=1}^N {\phi _j } (x_d )q_j (t)-u(x_d ,t)\right] ^{3}\right. \nonumber \\&\quad \left. +\,\sigma \left( \sum _{j=1}^N {\phi _j } (x_d )\dot{q}_j (t)-\frac{\partial u(x_d ,t)}{\partial t}\right) \right\} \delta (x-x_d )=0\nonumber \\ \end{aligned}$$
(10)
$$\begin{aligned}&\varepsilon \frac{\partial ^{2}u(x_d ,t)}{\partial t^{2}}+k(u(x_d ,t)-\sum _{j=1}^N {\phi _j } (x_d )q_j (t))^{3}\nonumber \\&\quad +\,\sigma \left( \frac{\partial u(x_d ,t)}{\partial t} -\sum _{j=1}^N {\phi _j } (x_d )\dot{q}_j (t)\right) =0 \end{aligned}$$
(11)

Multiplying Eq. (10) by \(\phi _{i}(x)\) and integrating over the domain [0, l] yield.

$$\begin{aligned}&\delta _{jj} \ddot{q}_j (t)+(2va_{jj} +\alpha _1 e_{jj} )\dot{q}_j (t)+(v^{2}b_{jj} \nonumber \\&\quad -\,c_{jj} -d_{jj} +e_{jj} )q_j (t)+{m}^{\prime }(x)\nonumber \\&\quad +\left\{ k\left[ \sum _{j=1}^N {\phi _j } (x_d )q_j (t)-u(x_d ,t)\right] ^{3}\right. \nonumber \\&\quad \left. +\,\sigma \left( \sum _{j=1}^N {\phi _j } (x_d )\dot{q}_j (t)-\frac{\partial u(x_d ,t)}{\partial t}\right) \right\} \phi _j (x_d ) \nonumber \\&=0 \end{aligned}$$
(12)
$$\begin{aligned}&\quad \varepsilon \frac{\partial ^{2}u(x_d ,t)}{\partial t^{2}}+k(u(x_d ,t)\nonumber \\&\quad -\sum _{j=1}^N {\phi _j } (x_d )q_j (t))^{3}\nonumber \\&\quad +\,\sigma \left( \frac{\partial u(x_d ,t)}{\partial t}-\sum _{j=1}^N {\phi _j } (x_d )\dot{q}_j (t)\right) =0 \end{aligned}$$
(13)

where

$$\begin{aligned} \delta _{jj}= & {} \int _0^l {\phi _j ^{2}} (x)\mathrm{d}x, \quad a_{jj} =\int _0^l {\phi _j } (x){\phi }^{\prime }_j (x)\mathrm{d}x, \nonumber \\ b_{jj}= & {} \int _0^l {\phi _j (x){\phi }^{\prime \prime }_j } (x)\mathrm{d}x\\ c_{jj}= & {} \!\int _0^l {{p}^{\prime }} \phi _j (x){\phi }^{\prime }_j (x)\mathrm{d}x, d_{jj} {=}\!\int _0^l {p\phi _j } (x){\phi }^{\prime \prime }_j (x)\mathrm{d}x, \nonumber \\ e_{jj}= & {} \int _0^l {\phi _j } (x)\phi _j ^{(4)}(x)\mathrm{d}x \end{aligned}$$

Equations (12) and (13) show a multi-degree-of-freedom nonlinear system. The NES is applicable to all modes of the beam and can extract the vibration energy from each beam mode.

4 Transient temperature field

Assuming that the initial temperature of the system is \(\bar{T}_0\), the upper surface of the beam is suddenly subjected to a temperature increase in \(\bar{T}_1 =\bar{T}_u -\bar{T}_0\) and the lower surface of the beam is subjected to a temperature increment of \(\bar{{T}}_2 =\bar{{T}}_e -\bar{T}_0\) [29], where \(\bar{{T}}_u\) [30] and \(\bar{T}_e\) are the temperatures of the upper and lower surfaces of the beam after thermal shock, respectively. The equations for the heat transfer process and the initial and boundary conditions are described as follows:

$$\begin{aligned}&c\rho \frac{\partial \bar{{T}}}{\partial t}=K_1 \frac{\partial ^{2}\bar{{T}}}{\partial z^{2}} \end{aligned}$$
(14)
$$\begin{aligned}&\left\{ {\begin{array}{l} \bar{{T}}(z,0)=\bar{{T}}_0 =20 \\ \bar{{T}}(h,t)=\bar{{T}}_u =10^{\wedge } 6\cdot (1-t/0.01)\cdot \sin (\pi x) \\ \bar{{T}}(0,t)=\bar{{T}}_e =10^{\wedge } 5\cdot (1-t/0.01)\cdot \sin (\pi x) \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(15)

where c is the specific heat capacity, \(K_{1}\) is the thermal conductivity coefficient, and h is the beam thickness. The solution of the equation can be obtained using the variable separation approach.

$$\begin{aligned} \bar{{T}}(z,t)= & {} \sum _{n=1}^{2k} {\frac{2}{n\pi }} (\bar{{T}}_u -\bar{{T}}_e )\exp \left\{ -\left( \frac{an\pi }{h}\right) ^{2}t\right\} \nonumber \\&\sin \left( \frac{n\pi z}{h}\right) +\frac{\bar{{T}}_u -\bar{{T}}_e }{h}z+\bar{{T}}_e \nonumber \\&+\sum _{n=1}^{2k-1} \left[ -\frac{2}{n\pi } (\bar{{T}}_u -\bar{{T}}_e )+\frac{1.2732}{h}(\bar{{T}}_0 -\bar{{T}}_e )\right] \nonumber \\&\times \exp \left\{ -\left( \frac{an\pi }{h}\right) ^{2}t\right\} \sin \left( \frac{n\pi z}{h}\right) \end{aligned}$$
(16)

where

$$\begin{aligned} a^{2}=\frac{K_1 }{c\rho } \end{aligned}$$

Equation (16) is used to obtain the temperature difference in the thickness of the beam. Equations (4) and (5) are used to obtain the thermal axial load and the thermal bending moment, respectively. The obtained results are plugged into Eq. (13) to solve the vibration of the model.

Fig. 3
figure 3

Comparison of the transient response of the moving beam with NES and without NES with the velocity of 2 at different positions. a \(x_d = 0.9\), b \(x_d = 0.7\), c \(x_d = 0.6\), d \(x_d = 0.55\)

Full size image
Fig. 4
figure 4

Comparison of the transient response of the moving beam with NES and without NES with the velocity of 2 at different positions. a \(x_d = 0.9\), b \(x_d = 0.7\), c \(x_d = 0.6\), d \(x_d = 0.55\)

Full size image

5 Effectiveness of nonlinear energy sink

After the transient temperature field has been determined and the parameters of the model equation have been calculated, the calculation results are plugged into the equation. The numerical algorithm is then used to solve the equation. In the Galerkin discretization process, the transverse displacement is approximated by \(N = 2\). The initial vibration of the moving model is induced by the initial speed. Accordingly, the following initial distributed velocity is imposed:

$$\begin{aligned} \dot{q}_2 (0){\,=\,}X, q_1 (0){\,=\,}q_2 (0){\,=\,}\dot{q}_1 (0){\,=\,}u(0){\,=\,}\dot{u}(0){\,=\,}0\nonumber \\ \end{aligned}$$
(17)

where X is a constant. First, we take a set of system parameters: \(K=8000\), \(m_\mathrm{NES} =1, l=1, D=1000,\eta =0.1, x_d =0.7, v=5\) and \(X=0.2, and x_a\) is the position of the thermal bending moment. The NES efficiency is calculated by the expression

$$\begin{aligned} E_\mathrm{NES} =\frac{\int _0^t \sigma \left[ \dot{u}(x_d ,t)-\mathop {\sum }\nolimits _{j=1}^N \phi _j (x_d )\dot{q}_j (t)\right] ^{2}\mathrm{d}\tau }{0.01\cdot f\cdot X}\nonumber \\ \end{aligned}$$
(18)

where

$$\begin{aligned} f=\int _0^l {[m_x } \phi _1 (x_a )]\mathrm{d}x \end{aligned}$$

Equation (18) indicates the percentage of the entire vibration energy absorbed by the NES up to time t, given that the time of the thermal shock is 0.01.

Fig. 5
figure 5

NES efficiency versus its location (other parameters of the NES are \(K=8000\), \(D=1000\), \(m_\mathrm{NES} =1\))

Full size image
Fig. 6
figure 6

Effect of the nonlinear mass on the NES performance (other parameters of the NES: a \(K=8000\), \(D=1000, x_d =0.7\); b \(K=8000\), \(D=1200, x_d =0.7\))

Full size image

In Fig. 2, the transient responses of the moving beams with and without NES fitted at different positions (The model is symmetrical, so the latter half of the model is studied and four locations are selected roughly.) under thermal shock are compared with zero velocity. The beam without NES exhibited sustained oscillations under thermal shock. By contrast, the transient displacement responses of the beam with an NES converge over time. Different positions of the beam are then selected to examine the effect of the NES on a vibration. The results clearly show the convergence of the oscillation responses. The transient responses of the moving beams with and without NES fitted at different positions under thermal shock are compared with the velocity of 2 in Fig. 3. In Fig. 4, the transient responses of the moving beams with and without NES fitted at different positions under thermal shock are compared with the velocity of 5. The comparison of these three graphs can be drawn that when the axial velocity varies from 0 to 5, the speed of convergence of the vibration is different and the convergence effect is good while the location of the NES is in the vicinity of 0.7.

In Fig. 5, the NES efficiency versus its location is demonstrated, the NES efficiency of is maximum, while the location of the NES is in the vicinity of 0.25 and 0.78. The position of the most powerful beam vibration must be determined to suppress the vibration of the beam effectively. Installing the NES at this position can effectively improve the NES efficiency. The results are consistent with the results obtained from the above figures.

Fig. 7
figure 7

Effect of the NES mass on its efficiency (other parameters of the NES are \(K=8000\), \(x_d =0.7, m_\mathrm{NES} =1\))

Full size image

The effect of the mass parameter of the NES on its efficiency is shown in Fig. 6. As it can be seen that the mass parameter is 0.4, the NES efficiency is maximum. Comparison of (a) and (b) can also be showed that increasing the damping parameter tends to increase the NES efficiency. The effect of the damping parameter of the NES on its efficiency is shown in Fig. 7. With the increase in damping, the NES efficiency also increased, but the desired amplification of the damping parameter provides some practical restrictions, and it will be considered equal to 1000 by all aspects of consideration.

6 Conclusions

In this study, an axially moving beam subjected to a thermal shock that induces a transverse vibration is investigated. The transverse vibration equation and boundary conditions are formulated using Hamilton’s principle. The approximate equation for the system response is obtained by the Galerkin method. The transient vibration displacement response of the beam and the NES efficiency at different locations are obtained by solving the equation. Based on the numerical results, the NES can irreversibly transfer and dissipate vibrational energy, it is in the vicinity of 0.25 and 0.78, and the control effect of the model is the best, where the thermal shock is imposed on. As it can be seen, increasing the damping parameter tends to increase the NES efficiency; however, the mass parameter is suitable just in a limited range. The primary system can be well controlled by choosing proper parameters of the NES on the premise of the best system performance and help to reduce the axially moving beam oscillations rapidly.