Time delay improves beneficial performance of a novel hybrid energy harvester

Abstract

The performances of an energy harvester are usually limited. To improve these, the time-delayed feedback control is used in a novel nonlinear hybrid energy harvester for different types of external excitation. Based on the generalized harmonic transformation, the equivalent uncoupled equation, the vibration response, the harvested power and stochastic resonance of the hybrid energy harvester with time-delayed control are analyzed to obtain the standards for appropriate values of different control parameters. The response under harmonic excitation exhibits that time-delayed feedback control technique can stabilize unstable periodic orbits of the attractor to enhance the output power of electromechanical systems. For harmonic excitation or stochastic excitation, the value of the averaging harvested power of the system without time-delayed feedback control is lower than that of the control system, which plays a great realistic significance in the choose of the control parameters for improving the performance of the hybrid energy harvester. In case of combined harmonic and stochastic excitations, the time-delayed feedback control also can enhance stochastic resonance phenomenon, which can lead to a large response and give out a high output power.

1 Introduction

Over the past few decades, efficient applications of nonlinear mechanical oscillators with the wide resonance frequency band for energy harvesting (EH) have drawn increasing attention [1,2,3,4]. The wideband nonlinear mechanical oscillators outperform the linear counterpart in some aspects due to the fact that they have the ability of widen the usable bandwidth of effective operation [5, 6]. A common method to design the wideband nonlinear mechanical oscillator is to combine a snap-through mechanism, which could cause large amplitude motion and dramatically increase power generation. Ramlan et al. [7] showed that more power is harvested by the nonlinear bistable snap-through system, especially for frequencies lower than the resonant frequency. Chirp and band-limited noise excitations are used to confirm the wideband characteristic of a piezoelectric snap-through EH [8]. Chen et al. [9, 10] revealed snap-through EHs outperform the linear under Gaussian white noise excitation. Yang et al. [11] investigated the efficiency of electromagnetic vibration EH of the snap-through mechanism that considered the gravity subjected to harmonic and stochastic excitations. Meanwhile, multiple transduction techniques used in a single device are another method for harvesting wideband power [12,13,14]. These important studies have provided many valuable insights, yet little work has been directed toward multiple transduction techniques in the context of snap-through EH.

Owing to the drawback of the snap-through EH, a new model of hybrid energy harvester (HEH) combining piezoelectric and electromagnetic transduction techniques is proposed in this paper. The proposed HEH consists of a smooth and discontinuous oscillator, a lumped mass, a piezoelectric ceramics and two ring permanent magnets. The smooth and discontinuous oscillator is created by the pair of oblique springs based on the snap-through mechanism and a vertical linear spring [15, 16]. Although the snap-through mechanism can achieve vibration strengthening over a broad frequency band, complex dynamic phenomena including bifurcation phenomenon and unstable periodic orbits embedded within a chaotic attractor could be induced if the nonlinear mechanical systems are not designed or controlled properly [17]. Hence, different control devices are introduced to enhance the stability and improve EH effectiveness. In particular, the effect of time-delayed control must be designed and utilized to make the controller as effective as possible [18, 19]. It is significant to reveal the regularity of existence of complex dynamic behaviors for HEH with time-delayed feedback control.

Due to the benefits of vibration control performance, time-delayed control has become very popular among researchers focusing on feedback control [20,21,22,23]. If time delay is actively used, then the structure can return to stability at a much faster rate [24, 25]. Hu et al. [26] studied the primary resonance and subharmonic resonance of a harmonically forced Duffing oscillator with weak nonlinearity and weak delay feedback. Nayfeh and Baumann [27] showed that time-delayed feedback controller undergoes a supercritical bifurcation for practical operating ranges and has a significant advantage in container cranes applications. Xu et al. [28, 29] studied the optimum value of time delay of active control used in a nonlinear isolation system to improve the system robustness and transmissibility performance. Yang and Cao [30, 31] presented analytical studies of nonlinear transition dynamics and resonances of a stiffness nonlinearities oscillator under displacement and velocity time-delayed feedback control. Recently, Karami and Inman [32] have established a unified approximation method to illustrate the effect of electromechanical coupling on the performance of HEHs, and the influence of time-delayed parameters on the power output of the class systems is studied in [33]. The authors in [33] explored the advantages of time-delayed parameters in vibration EH under harmonic excitation. In our analysis, this paper performs a detailed study of time-delayed feedback for control of the novel HEH.

The rest of the paper is organized as follows. In Sect. 2, we present the model with time-delayed feedback control of HEH combining piezoelectric and electromagnetic transduction. Section 3 derives the harvested power and equivalent equation of the HEH. The nonlinear dynamic characteristics and broadband EH characteristics of such a HEH under different types of external excitation are briefly analyzed in Sect. 4. Finally, some conclusions are drawn in Sect. 5.

Fig. 1

Schematic of the piezoelectric and electromagnetic HEH. (Color online)

Fig. 2

a Representative mechanical schematic of the HEH with time-delayed feedback control. b Equivalent coupled circuit for piezoelectric element. c Equivalent circuit for electromagnetic element. (Color online)

2 Hybrid energy harvester with time delay

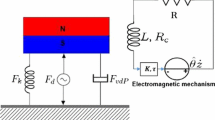
The proposed HEH is illustrated in Fig. 1 depending on the designed of snap-through mechanism. It consists of a smooth and discontinuous oscillator, a lumped mass M, a piezoelectric ceramics and two ring permanent magnets. The smooth and discontinuous oscillator is created by the pair of oblique springs and a vertical linear spring. The deformation of the springs induced the electrical field across the piezoelectric ceramics. The ring permanent magnets produce a radial magnetic field $B_e$, and a cylindrical coil connected to the rigid housing moves up and down to cut the magnetic induction lines. The energy harvester generates power from piezoelectric and electromagnetic transducers, which is referred to as a HEH. The piezoelectric and electromagnetic transducers are connected to separate external resistors, R and $R_v$, respectively.

Using the Newton’s law and Kirchhoff’s law, the coupled equations governing the system mechanical states, the electric current and electric voltage are written as

$$\begin{aligned}&M\ddot{x}+C\dot{x}+\frac{\text {d}U(x)}{\text {d}x} +B_e\bar{I}L_c+\kappa \bar{V}\nonumber \\&\quad =-\,M\ddot{y}+F(x_\delta ,\dot{x}_\delta ), \end{aligned}$$

(1a)

$$\begin{aligned}&B_eL_c\dot{x}=L_i\dot{\bar{I}}+(R+R_c)\bar{I}, \end{aligned}$$

(1b)

$$\begin{aligned}&\kappa \dot{x}=C_{p}\dot{\bar{V}}+\frac{\bar{V}}{R_{v}}, \end{aligned}$$

(1c)

where C means the coefficient of viscous damping; x, $L_c$ and $\bar{I}$ are the displacement, the length of the coil and the current that flows in the coil, respectively; $L_i$ and $R_c$ are the inductance and resistance of the coil, and $\kappa$ is a linear electromechanical coupling coefficient; $\bar{V}$ is the voltage measured across $R_v$; $C_{p}$ is the piezoelectric capacitance; $\ddot{y}$ is the input base excitation.

The control signal, in Fig. 2a, is set as $F(x_\delta ,\dot{x}_\delta )=\varLambda _1x(T-\delta )+\varLambda _2\dot{x}(T-\delta )$, where $\varLambda _1$ and $\varLambda _2$ are displacement and velocity feedback intensities and $\delta$ is the feedback time delay. The restoring force potential of the mechanical oscillator can be expressed as

$$\begin{aligned} U(x)=\frac{1}{2}(K_v+2K_h)x^2-2K_hL\sqrt{x^2+l^2} , \end{aligned}$$

(2)

where $K_h$ and $K_v$ are the stiffness of the springs; L is the free length of oblique springs; l is the length of the oblique spring compressed in the horizontal direction.

The non-dimensional form of Eq. (1) can be derived as

$$\begin{aligned}&\ddot{q}+c\dot{q}+q+r q \left( 1-\frac{1}{\sqrt{q^2+\alpha ^2}}\right) +\theta I+\rho V\nonumber \\&\quad =\ddot{z}+g_1q(t-\tau )+g_2\dot{q}(t-\tau ),\end{aligned}$$

(3a)

$$\begin{aligned}&\nu \dot{q}=\dot{I}+\mu I, \end{aligned}$$

(3b)

$$\begin{aligned}&\gamma \dot{q}=\dot{V}+\lambda V, \end{aligned}$$

(3c)

by letting $q=x/L, z=-y/L, \alpha =l/L, r=\omega _2^2/\omega _1^2, t=\omega _1T, \omega _1^2=K_v/M, \omega _2^2=2K_h/M, c={C}/{(M\omega _1)}, I={\bar{I}}/{L}, \theta ={B_eL_c}/{(M\omega _1^2)}, \mu ={(R+R_c)}/{L_i}, \nu ={B_eL_c\omega _1}/{L_i}, V={\bar{V}}/{L}, \rho ={\kappa }/{(M\omega _1^2)}, \lambda ={1}/{(C_{p}R_{v}\omega _1)}, \gamma ={\kappa }/{C_{p}}$, $g_1=\varLambda _1/(M\omega _1^2), g_2=\varLambda _2/(M\omega _1), \tau =\omega _1\delta$. Here, $\omega _1$ represents the natural frequency of the associated linear mechanical system, c is the non-dimensional damping coefficient, r is the non-dimensional nonlinear stiffness coefficient, $\alpha$ is the non-dimensional geometric coefficient, $\rho$ and $\theta$ are the linear dimensionless electromechanical coupling coefficients, and $\mu$ is the ratio between the resistance and inductance constants of the harvester. $\nu$ is the electromagnetic coupling term in the electrical equation, $\lambda$ is the reciprocal of the time constant of the resistive–capacitive circuit, $\gamma$ is the piezoelectric coupling term in the electrical equation, $g_1$ and $g_2$ are non-dimensional displacement and velocity feedback intensities, $\tau$ is the non-dimensional feedback time delay, and $\ddot{z}$ is the input base excitation. The symbols of geometric and physical parameters are presented in Table 1. The parameters are set as $r=1$, $c=0.15$, $\theta =0.9$, $\rho =0.8$, $\mu =0.5$, $\nu =0.4$, $\lambda =0.5$, $\gamma =0.6$, unless otherwise stated.

Table 1 Parameters and symbols of the HEH

3 The harvested power and equivalent system

This section is devoted to derive the harvested power and equivalent equation of the HEH with time-delayed feedback control. The total harvested power P(t) is one of the most important features of the HEH. Based on the magnetic and piezoelectric circuits, the non-dimensional harvested powers can be derived as $P_c(t)=\mu \theta I^2(t)$ and $P_v(t)=\lambda \rho V^2(t)$. In order to derive the harvested power and equivalent equation, the impact of the magnetic and piezoelectric circuits on the mechanical system should be firstly determined, i.e., establishing the explicit expressions of the electric current and voltage to the mechanical states.

Compared to the system states, the displacement amplitude Q, frequency $\omega$, mechanical energy H and initial phase $\varTheta (t)$ are all slow-varying processes. Using the generalized harmonic transformation [34, 35], the system displacement and velocity can be expressed as:

$$\begin{aligned}&q(t)=Q(t)\cos \phi (t), \end{aligned}$$

(4a)

$$\begin{aligned}&\dot{q}(t)=-Q(t)\omega (Q, \phi ) \sin \phi (t), \end{aligned}$$

(4b)

$$\begin{aligned}&\phi (t)=\psi (t)+\varTheta (t), \end{aligned}$$

(4c)

$$\begin{aligned}&\omega (Q, \phi )=\text {d}\psi (t)/\text {d}t. \end{aligned}$$

(4d)

After harmonic transformation, the motions with time delay take the form

$$\begin{aligned} q(t-{\tau })&= Q\cos [\omega (Q, \phi )(t-{\tau })+\varTheta (t)]\nonumber \\&=q(t)\cos [\omega (Q, \phi )\tau ]-\dot{q}(t)\frac{\sin [\omega (Q, \phi )\tau ]}{\omega (Q, \phi )}, \end{aligned}$$

(5a)

$$\begin{aligned} \dot{q}(t-{\tau })&=-Q\omega (Q, \phi ) \sin [\omega (Q, \phi ) (t-{\tau })+\varTheta (t)]\nonumber \\&=q(t)\omega (Q, \phi )\sin [\omega (Q, \phi )\tau ]\nonumber \\&\qquad +\dot{q}(t)\cos [\omega (Q, \phi )\tau ]. \end{aligned}$$

(5b)

Integrating Eqs. (3b) and (3c) yields the following explicit expressions of the electric current and voltage

$$\begin{aligned} I(t)= & {} A_1e^{-\lambda _1 t}+\int _0^t e^{-\lambda _1 t}\dot{q}(t_s)\text {d}t_s, ~~~V(t)=A_2e^{-\lambda _2 t}\nonumber \\&+\int _0^t e^{-\lambda _2 t}\dot{q}(t_s)\text {d}t_s, \end{aligned}$$

(6)

where the general solutions $A_1e^{-\lambda _1 t}$ and $A_2e^{-\lambda _2 t}$ are unknown functions and have negligible influence on the stationary response due to the exponential decay nature. Through the integration by parts and the variable transformation $s=t-t_s$, Eq. (6) can be approximated by

Fig. 3

The equivalent restoring force potential U(q) as a function of displacement q for different values of geometric coefficient $\alpha$ and time delay $\tau$. The parameters are a$g_1=0, g_2=0, \tau =0$, b$g_1=-0.3, g_2=0.1, \alpha =0.2$. (Color online)

Fig. 4

Phase trajectories of the HEH for different control parameters $g_1$, $g_2$ and $\tau$. The parameters are $\alpha =0.2$, $a=0.2$, $\omega =1.1,$a–c$g_2=0.1, \tau =1$, d–f$g_1=-0.3, \tau =1$, g–i$g_1=-0.3, g_2=0.1$. (Color online)

$$\begin{aligned} I(t)\approx \int _0^t e^{-\lambda _1 t} \dot{q}(t-s)\text {d}s,~~~V(t)\approx \int _0^t e^{-\lambda _2 t}\dot{q}(t-s)\text {d}s. \end{aligned}$$

(7)

Through the relation in Eq. (5b), $\dot{q}(t-s)$ can be approximated as:

$$\begin{aligned}&\dot{q}(t-s)=q(t)\omega (Q, \phi )\sin [\omega (Q, \phi )s]\nonumber \\&\quad +\,\dot{q}(t)\cos [\omega (Q, \phi )s]. \end{aligned}$$

(8)

Substituting Eq. (8) into Eq. (7) and vanishing the exponential decay terms, one obtains

$$\begin{aligned} I(t) \approx&\frac{\nu \omega ^2(Q, \phi )}{\mu ^2+\omega ^2}q(t)+\frac{\nu \mu }{\mu ^2+\omega ^2(Q, \phi )}\dot{q}(t) \nonumber \\ =&\frac{Q(t)\nu \omega (Q, \phi )}{\mu ^2 +\omega ^2(Q, \phi )}[\omega (Q, \phi )\cos \phi (t)-\mu \sin \phi (t)], \end{aligned}$$

(9a)

$$\begin{aligned} V(t) \approx&\frac{\gamma \omega ^2(Q, \phi )}{\lambda ^2+\omega ^2}q(t)+\frac{\gamma \lambda }{\lambda ^2+\omega ^2(Q, \phi )}\dot{q}(t) \nonumber \\ =&\frac{Q(t)\gamma \omega (Q, \phi )}{\lambda ^2 +\omega ^2(Q, \phi )}[\omega (Q, \phi )\cos \phi (t)-\lambda \sin \phi (t)]. \end{aligned}$$

(9b)

Owing to

$$\begin{aligned}&\omega (Q, \phi )\cos \phi (t)-\mu \sin \phi (t)\nonumber \\&\quad =\sqrt{\mu ^2+\omega ^2(Q, \phi )}\cos \left[ \phi (t) +\tan ^{-1}\frac{\mu }{\omega (Q, \phi )}\right] , \end{aligned}$$

(10)

the relationship between the displacement amplitude Q(t), steady-state current amplitude $Q_{c}(t)$ and electric voltage amplitude $Q_{v}(t)$ can be written as

$$\begin{aligned} Q_{c}(t)&=\frac{\nu \omega (Q, \phi )}{\sqrt{\mu ^2+\omega ^2(Q, \phi )}}Q(t), \nonumber \\ Q_{v}(t)&=\frac{\gamma \omega (Q, \phi )}{\sqrt{\lambda ^2+\omega ^2(Q, \phi )}}Q(t). \end{aligned}$$

(11)

Therefore, the total harvested power P(t) can be expressed as

$$\begin{aligned} P(t)= & {} \mu \theta I^2(t)+\lambda \rho V^2(t)\nonumber \\= & {} \mu \theta \left[ \frac{\nu \omega (Q, \phi )}{\sqrt{\mu ^2+\omega ^2(Q, \phi )}}Q(t)\right] ^2\nonumber \\&+\,\lambda \rho \left[ \frac{\gamma \omega (Q, \phi )}{\sqrt{\lambda ^2+\omega ^2(Q, \phi )}} Q(t) \right] ^2. \end{aligned}$$

(12)

Substituting Eqs. (5) and (9) into the mechanical Eq. (3a) leads to the following equivalent uncoupled mechanical equation

$$\begin{aligned}&\ddot{q}+(c+\varepsilon +\zeta )\dot{q}+(1+\eta +\beta )q\nonumber \\&\quad +\,r q\left( 1-\frac{1}{\sqrt{q^2+\alpha ^2} }\right) =\ddot{z}, \end{aligned}$$

(13)

where

$$\begin{aligned}&\varepsilon =\frac{\theta \nu \mu }{\mu ^2+\omega ^2(Q, \phi )}+\frac{\rho \gamma \lambda }{\lambda ^2+\omega ^2(Q, \phi )}, \end{aligned}$$

(14a)

$$\begin{aligned}&\eta =\frac{\theta \nu \omega ^2(Q, \phi )}{\mu ^2+\omega ^2(Q, \phi )}+\frac{\rho \gamma \omega ^2(Q, \phi )}{\lambda ^2+\omega ^2(Q, \phi )}, \end{aligned}$$

(14b)

$$\begin{aligned}&\zeta =g_1\frac{\sin [\omega (Q, \phi )\tau ]}{\omega (Q, \phi )}-g_2\cos [\omega (Q, \phi )\tau ], \end{aligned}$$

(14c)

$$\begin{aligned}&\beta =-\,g_1\cos [\omega (Q, \phi )\tau ]-g_2\omega (Q, \phi )\sin [\omega (Q, \phi )\tau ]. \end{aligned}$$

(14d)

It is obvious that the impacts of the external circuits and time-delayed feedback control on the mechanical system are equivalent to damping with $\varepsilon$, $\zeta$, and stiffness with $\eta$, $\beta$. The equivalent damping coefficient with time delay is $c+\varepsilon +\zeta$, while the equivalent restoring force potential with time delay can be expressed as

$$\begin{aligned} U(q)=\frac{1}{2}(1+\eta +\beta +r)(q^2 +\alpha ^2)-r\sqrt{q^2+\alpha ^2}. \end{aligned}$$

(15)

As shown in Fig. 3a, HEHs can now be classified into three major categories based on the shape of their potential energy function. The hybrid harvester is linear mono-stable when $r=0$, nonlinear mono-stable when $\alpha \ge 0.5$ and $r=1$, and nonlinear bistable when $\alpha <0.5$ and $r=1$. Figure 3b shows the impact of time delay $\tau$ on the potential energy.

The equivalent uncoupled mechanical Eq. (13) can be rewritten in the following form as a two-variable dynamical system

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}=\varpi , \\ \dot{\varpi }=-\left( c+\varepsilon +\zeta \right) \varpi -\left( 1+\eta +\beta \right) q\\ \quad -\,rq\left( 1-\frac{1}{\sqrt{q^2+\alpha ^2}}\right) +\ddot{z}. \end{array}\right. \end{aligned}$$

(16)

Without excitations and damping, the equilibria of the system (16) can be written as

$$\begin{aligned}&q_{1,2}=\pm \sqrt{r^2\left( 1+\eta +\beta +r\right) ^{-2}-\alpha ^2} ~~~\text {(stable)},\nonumber \\&\quad q_{u}=0 ~~~\text {(unstable)}. \end{aligned}$$

(17)

By linearizing Eq. (16) at the three singular points $Q_{s1}(q_{1}, 0)$, $Q_{s2}(q_{2}, 0)$ and $Q_{u}(q_{u}, 0)$, we have the eigenvalues of the characteristic equation:

$$\begin{aligned} \left\{ \begin{array}{l} \iota _{1,2}=\pm \sqrt{-\left( 1+\eta +\beta +r\right) +\left( 1+\eta +\beta +r\right) ^3 \frac{\alpha ^2}{r^2}}, \\ \sigma _{1,2}=\pm \sqrt{-\left( 1+\eta +\beta +r\right) +\frac{r}{\alpha }}. \end{array}\right. \end{aligned}$$

(18)

The effects of time-delayed feedback on EH dynamics of the HEH are discussed in the following sections for different types of external excitation.

4 Role of time-delayed feedback control on EH dynamics

Fig. 5

Harvested voltage histories (left column) and phase trajectories (right column) of the HEH for different displacement feedback control intensity $g_1$. Purple lines from the uncontrolled system. The parameters are $\alpha =0.2$, $a=0.2$, $\omega =1.0$, $g_2=0.1$, $\tau =1$. (Color online)

Fig. 6

Harvested voltage histories (left column) and phase trajectories (right column) of the HEH for different velocity feedback control intensity $g_2$. Purple lines from the uncontrolled system. The parameters are $\alpha =0.2$, $a=0.2$, $\omega =1.0$, $g_1=-0.3$, $\tau =1$. (Color online)

Fig. 7

Harvested voltage histories (left column) and phase trajectories (right column) of the HEH for different time delay $\tau$. Purple lines from the uncontrolled system. The parameters are $\alpha =0.2$, $a=0.2$, $\omega =1.0$, $g_1=-0.3$, $g_2=0.1$. (Color online)

Fig. 8

Amplitude–frequency responses of the HEH for different control parameters $g_1$, $g_2$ and $\tau$. The parameters are $\alpha =0.4$, $a=0.2$, a$g_2=0.1, \tau =1$, b$g_1=-0.3, \tau =1$, c$g_1=-0.3, g_2=0.1$. (Color online)

Fig. 9

Harvested voltage–frequency response of the HEH for different control parameters $g_1$, $g_2$ and $\tau$. The parameters are $\alpha =0.4$, $a=0.2$, a$g_2=0.1, \tau =1$, b$g_1=-0.3, \tau =1$, c$g_1=-0.3, g_2=0.1$. (Color online)

Fig. 10

Harvested power–frequency response of the HEH for different control parameters $g_1$, $g_2$ and $\tau$. The parameters are $\alpha =0.4$, $a=0.2$, a$g_2=0.1, \tau =1$, b$g_1=-0.3, \tau =1$, c$g_1=-0.3, g_2=0.1$. (Color online)

Fig. 11

Harvested power–frequency response of the HEH for different control parameters $g_1$, $g_2$ and $\tau$. The parameters are $r=1$, $\alpha =0.4$ for nonlinear system, $r=0$ for linear system, $a=0.2$, a$g_2=0.1, \tau =2$, b$g_1=-0.1, \tau =2$, c$g_1=-0.1, g_2=0.1$. (Color online)

4.1 The case of harmonic excitation

In this part, we consider a harmonic excitation $\ddot{z}=a\cos (\omega t)$, where a and $\omega$ denote the amplitude and frequency of the harmonic excitation force, respectively. Numerical simulation and theoretical analysis are carried out to investigate the dynamical responses of the HEH under base excitation. For numerical analysis, the governing equations (3) are solved by the Runge–Kutta method, and the geometric and physical parameters used are listed in Table 1.

4.1.1 Analysis in the time domain

The phase trajectories of the HEH for different control parameters $g_1$, $g_2$ and $\tau$ are presented in Fig. 4 with $\alpha =0.2$, $a=0.2$, $\omega =1.1$. The response is at period-1 for $g_1=-0.3$, $g_2=0.1, 0.2, 0.3$ and $\tau =1$ [see Fig. 4c–g]. Then, the response turns to be unstable periodic attractors for $g_1=-0.1, -0.2$ and $\tau =1.5, 2$ [see Fig. 4a, b, h and i], under which electromechanical system produces a lower power output.

With the geometric and physical parameters listed in Table 1 and $\alpha =0.2$, $a=0.2$, $\omega =1.1$, we can obtain the harvested voltage histories and phase trajectories of the HEH for different control parameters $g_1$, $g_2$ and $\tau$. As shown in Figs. 5, 6 and 7, when the uncontrolled HEH is driven by harmonic excitation force, the system exhibits two unstable periodic attractors between the two potential wells and yields the unstable periodic voltage histories, and unstable periodic displacement and velocity. This leads to two low-energy intrawell motions and small harvesting output voltage and current, displacement, and velocity. EH system exhibits unstable periodic attractor has been observed, and experimental validation is carried out to compare and analyze the efficiencies of energy generation [36]. For the controlled HEH, the system oscillates exhibits a high-energy interwell motion with large amplitude periodic oscillation, leading to significant increases in the displacement, velocity and harvested voltage, as shown in Figs. 5, 6 and 7 for different control parameters $g_1$, $g_2$ and $\tau$. The results from Figs. 5, 6 and 7 also indicate the time-delayed feedback control technique that allows one to stabilize unstable periodic orbits of the attractor. Stabilizing unstable periodic orbits of dynamical systems using time-delayed feedback control has been shown in different nonlinear systems [37,38,39,40,41]; however. here stabilization effects of time delay on the unstable periodic attractors will effectively enhance the output power of electromechanical systems.

4.1.2 Analysis in the frequency domain

In this subsection, the amplitude–frequency response characteristics will be derived by the averaging method. Based on the generalized harmonic transformation in equations (4), the HEH (3) will be transformed into the following equations:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{Q}(t)=-\frac{1}{\omega }\varLambda (Q, \varTheta )\sin (\omega t+\varTheta ), \\ \dot{\varTheta }(t)=-\frac{1}{Q\omega }\varLambda (Q, \varTheta ) \cos (\omega t+\varTheta ), \end{array}\right. \end{aligned}$$

(19)

where

$$\begin{aligned} \varLambda (Q, \varTheta )= & {} Q\omega ^2\cos (\omega t+\varTheta )\nonumber \\&+\,\left( c+\varepsilon +\zeta \right) Q \omega \sin (\omega t+\varTheta )\nonumber \\&-\,(1+\eta +\beta +r)b\cos (\omega t+\varTheta )\nonumber \\&+\,\frac{r Q\cos (\omega t+\varTheta )}{\sqrt{Q^2\cos ^2(\omega t+\varTheta )+\alpha ^2}} +a\cos (\omega t).\nonumber \\ \end{aligned}$$

(20)

Over a period of oscillations from 0 to $2\pi$, we obtain the following averaging equations for the amplitude Q and phase $\varTheta$

$$\begin{aligned} \left\{ \begin{array}{l} \dot{Q}=-\,\frac{1}{2\omega }\left[ Q\omega (c+\varepsilon +\zeta )+a\sin \varTheta \right] , \\ \dot{\varTheta }=-\,\frac{1}{2Q\omega }\left[ -Q(1+\eta +\beta +r)\right. \\ \qquad \left. +\,Q\omega ^2+a\cos \varTheta +\frac{Qr}{\pi }\varGamma (Q)\right] . \end{array}\right. \end{aligned}$$

(21)

where

$$\begin{aligned} \varGamma (Q)= & {} \int ^{2\pi }_{0}\frac{\cos ^2(\omega t+\varTheta )}{\sqrt{Q^2\cos ^2(\omega t+\varTheta )+\alpha ^2}}\text {d}(\omega t+\varTheta )\nonumber \\= & {} \frac{4}{Q^2}\left[ \sqrt{Q^2+\alpha ^2}\text {EllipticE} \left( \sqrt{\frac{Q^2}{Q^2+\alpha ^2}} \right) \right. \nonumber \\&\left. -\,\frac{\alpha ^2}{\sqrt{Q^2+\alpha ^2}}\text {EllipticK} \left( \sqrt{\frac{Q^2}{Q^2+\alpha ^2}} \right) \right] .\nonumber \\ \end{aligned}$$

(22)

EllipticK($*$) and EllipticE($*$) denote the complete elliptic integral of the first kind and the second kind with their elliptic modulus $*$, respectively.

Let $\dot{Q}=0$ and $\dot{\varTheta }=0$, and the terms of $\sin \varTheta$ and $\cos \varTheta$ can be solved. With $\sin ^2\varTheta +\cos ^2\varTheta =1$, the averaging amplitude–frequency response relationship under different time-delayed feedback parameters is derived as the following formula:

$$\begin{aligned}&{[}Q\omega (c+\varepsilon +\zeta )]^2\nonumber \\&\quad +\left[ -Q(1+\eta +\beta +r)+Q\omega ^2 +\frac{Qr}{\pi }\varGamma (Q) \right] ^2=a^2.\nonumber \\ \end{aligned}$$

(23)

With the constraints of Eq. (12), the dimensionless total averaging harvested power can then be obtained as

$$\begin{aligned} P_{\mathrm{ave}}= & {} \mu \theta I^2_{\mathrm{ave}}+\lambda \rho V^2_{\mathrm{ave}}=\mu \theta \left( \frac{\nu \omega }{\sqrt{\mu ^2+\omega ^2}}Q_{\mathrm{ave}}\right) ^2\nonumber \\&+\,\lambda \rho \left( \frac{\gamma \omega }{\sqrt{\lambda ^2+\omega ^2}}Q_{\mathrm{ave}} \right) ^2, \end{aligned}$$

(24)

where $Q_{\mathrm{ave}}$ is the amplitude of Q(t) solved from Eq. (23).

With the geometric and physical parameters listed in Table 1 and $\alpha =0.4, a=0.2$ , the effects of different control parameters $g_1$, $g_2$ and $\tau$ on frequency responses of the HEH have been investigated as shown in Figs. 8 and 11, respectively.

Figure 8 shows a typical amplitude–frequency response curve for the nonlinear bistable EH system. $\varOmega _1$ and $\varOmega _2$ represent the jump-up and jump-down frequencies. The maximum amplitude response is depicted by $Q_m$, and the frequency when the maximum amplitude response occurs is given by $\varOmega _m$. When the displacement feedback intensity $g_1$ increases, the maximum amplitude $Q_m$ in resonant regime increases, the primary resonance phenomenon is enhanced, and the frequency of the maximum amplitude response shifts toward higher frequency [see Fig. 8a]. The effect of velocity feedback intensity $g_2$ and time delay $\tau$ on amplitude–frequency is plotted in Fig. 8b, c. The maximum amplitude $Q_m$ in resonant regime decreases and the frequency of the maximum amplitude response shifts toward lower frequency, the primary resonance phenomenon is weakened when $g_2$ and $\tau$ increase.

Figure 8 also shows that the maximum response amplitudes in resonant regime are increased compared to that of the uncontrolled HEH. We note that the maximal harvested power depends on the amplitude, and the corresponding amplitude of the displacement is proportional to the amplitude. Namely, increasing the control parameters is advantageous to strengthen the vibrations in resonant regime, where vibrational EH is needed.

Similarly, the variations of the total averaging harvested voltage of the nonlinear bistable HEH versus the excitation frequency are presented in Fig. 9 for different control parameters $g_1$, $g_2$ and $\tau$. The results show that the performance of the nonlinear bistable HEH is also improved in the presence of time-delayed feedback control.

We calculated the total averaging harvested power of the nonlinear bistable HEH for different control parameters $g_1$, $g_2$ and $\tau$, as shown in Fig. 10. The maximum amplitude $Q_m$ increases with increase in $g_1$ and decreases with increase in $g_2$ and $\tau$ as shown in Fig. 8, and the maximum total averaging harvested power is almost same for all cases of amplitude response. The maximum total averaging harvested power of the system without time-delayed feedback control is lower than that of the control system. We can also observe that more power is harvested by the HEH, especially for frequencies lower than the resonant frequency.

Finally, the variations of the total averaging harvested power of the nonlinear bistable HEH for different control parameters compared to the case of linear mono-stable HEH are shown in Fig. 11. It can be seen that the maximum total averaging harvested power at the resonant frequency for the nonlinear system is larger than that of the linear system for different control parameters. In other words, the nonlinear bistable HEH can outperform the linear mono-stable harvester. Meanwhile, the time-delayed feedback control is also effective for improving the EH performance of linear system.

Fig. 12

The stationary probability density $p_{\mathrm{st}}( Q)$ of amplitude Q for different control parameters $g_1$, $g_2$, $\tau$ and noise intensity D. The parameters are $\omega =1.0$, a$g_2=0.1, \tau =1, D=0.1$, b$g_1=-0.3, \tau =1, D=0.1$, c$g_1=-0.3, g_2=0.1, D=0.1$, d$g_1=-0.3, g_2=0.1, \tau =1$. (Color online)

Fig. 13

The stationary averaging amplitude $e_{\mathrm{st}}[ Q]$ as a function of noise intensity D for different control parameters $g_1$, $g_2$ and $\tau$. The parameters are $\omega =1.0$, a$g_2=0.1, \tau =1.5$, b$g_1=-0.3, \tau =1.5$, c$g_1=-0.3, g_2=0.1$. (Color online)

Fig. 14

The averaging harvested power $e_{\mathrm{st}}[P]$ as a function of noise intensity D for different control parameters $g_1$, $g_2$ and $\tau$. The parameters are $\omega =1.0$, a$g_2=0.1, \tau =1.5$, b$g_1=-0.3, \tau =1.5$, c$g_1=-0.3, g_2=0.1$. (Color online)

4.2 The case of stochastic excitation

A comprehensive analysis of a real HEH must take account of environmental fluctuations, which always affect the system by changing its dynamic regime. Thus, the deterministic HEH (3) must be modified by considering the presence of stochastic excitation, i.e., $\ddot{z}$ = $\xi (t)$, which can be modeled by a Gaussian white noise process with a very small correlation time. The stochastic excitation $\xi (t)$ is therefore characterized by the well-known statistical properties, such as $\left\langle \xi (t)\right\rangle =0$, $\left\langle \xi (t)\xi (t')\right\rangle =2D\delta (t-t')$, where $\left\langle *\right\rangle$ denotes the expected value, D is the intensity of Gaussian white noise, and $\delta$ is the Dirac-delta function.

4.2.1 Steady-state response

When the excitation is set as $\ddot{z}$ = $\xi (t)$, the solutions of the HEH (3) with time-delayed feedback control for different parameters are solved by the stochastic averaging method [34, 35]. After dimensionless transfer as Eq. (4), the equivalent uncoupled Eq. (13) can be written as

$$\begin{aligned} \dot{Q}(t)= & {} \varPi _1(Q, \phi , t)+\varsigma _{1}(Q, \phi , t)\xi (t), \end{aligned}$$

(25)

$$\begin{aligned} \dot{\varTheta }(t)= & {} \varPi _2(Q, \phi , t)+\varsigma _{2}(Q, \phi , t)\xi (t), \end{aligned}$$

(26)

where $\varPi _{1,2}$ and $\varsigma _{1,2}$ are given by

$$\begin{aligned} \varPi _1(Q, \phi , t)= & {} \frac{1}{\omega }\left[ \left( c+\varepsilon +\zeta \right) Q \omega \sin ^2\phi \right. \nonumber \\&-\,(1+\eta +\beta +r)b\cos \phi \sin \phi \nonumber \\&\left. +\,\frac{r Q\cos \phi \sin \phi }{\sqrt{Q^2\cos ^2\phi +\alpha ^2}}\right] , \end{aligned}$$

(27)

$$\begin{aligned} \varPi _2(Q, \phi , t)= & {} \frac{1}{Q\omega }\left[ \left( c+\varepsilon +\zeta \right) Q \omega \sin \phi \cos \phi \right. \nonumber \\&-\,(1+\eta +\beta +r)b\cos ^2\phi \nonumber \\&\left. +\,\frac{r Q\cos ^2\phi }{\sqrt{Q^2\cos ^2\phi +\alpha ^2}}\right] , \end{aligned}$$

(28)

$$\begin{aligned} \varsigma _{1}(Q, \phi , t)= & {} -\frac{\sin \phi }{\omega }, \end{aligned}$$

(29)

$$\begin{aligned} \varsigma _{2}(Q, \phi , t)= & {} -\frac{\cos \phi }{Q\omega }. \end{aligned}$$

(30)

Based on the theorem proposed by Khasminskii [42], $(Q, \varTheta )$ can be considered as two-dimensional diffusive Markov processes approximately. Then, the Itô stochastic differential equations of (25) and (26) are in the form

$$\begin{aligned} \text {d} Q(t)= & {} a_1(Q, \phi , t)+b_{1}(Q, \phi , t)\text {d}W(t), \end{aligned}$$

(31)

$$\begin{aligned} \text {d} \varTheta= & {} a_2(Q, \phi , t)+b_{2}(Q, \phi , t)\text {d}W(t), \end{aligned}$$

(32)

where

$$\begin{aligned} a_1(Q, \phi , t)&=\varPi _1(Q, \phi , t)+\frac{1}{2}b_{1}\frac{\partial b_{1}}{\partial Q} +\frac{1}{2}b_{2}\frac{\partial b_{1}}{\partial \phi },\\ a_2(Q, \phi , t)&=\varPi _2(Q, \phi , t)+\frac{1}{2}b_{1}\frac{\partial b_{2}}{\partial Q} +\frac{1}{2}b_{2}\frac{\partial b_{2}}{\partial \phi },\\ b_{1}(Q, \phi , t)&=\sqrt{2D\varsigma ^2_{1}(Q, \phi , t)},\\ b_{2}(Q, \phi , t)&=\sqrt{2D\varsigma ^2_{2}(Q, \phi , t)}, \end{aligned}$$

and the standard Wiener process W(t) is the diffusion process with a null drift coefficient and a unit diffusion coefficient.

By applying the stochastic averaging method to Eqs. (31) and (32), we can obtain the following stochastic equations:

$$\begin{aligned} \bar{a}_1(Q)&=\frac{1}{2\pi }\int _0^{2\pi }a_1(Q, \phi , t)\text {d}\phi ,\\ \bar{a}_2(Q)&=\frac{1}{2\pi }\int _0^{2\pi }a_2(Q, \phi , t)\text {d}\phi ,\\ \bar{b}_{1}(Q)&=\sqrt{\frac{1}{2\pi }\int _0^{2\pi }b^2_1(Q, \phi , t)\text {d}\phi },\\ \bar{b}_{2}(Q)&=\sqrt{\frac{1}{2\pi }\int _0^{2\pi }b^2_2(Q, \phi , t)\text {d}\phi }. \end{aligned}$$

Then, the Fokker–Planck–Kolmogorov equation of the amplitude Q corresponding to Eq. (31) can be given by [43]

$$\begin{aligned} \frac{\partial p(Q,t)}{\partial t}= & {} -\frac{\partial }{\partial Q}\left[ \bar{a}_1(Q)\right] p(Q,t)\nonumber \\&+\frac{1}{2}\frac{\partial ^2}{\partial Q^2}\left[ \bar{b}_1^2(Q)p(Q,t)\right] , \end{aligned}$$

(33)

where p(Q, t) is the transition probability density function of displacement amplitude Q, $\bar{a}_1(Q)=\frac{\left( c +\varepsilon +\zeta \right) }{2}Q-\frac{D}{2Q}$, $\bar{b}_1^2(Q)=D$. The initial condition of Eq. (33) is taken as $p=\delta (a-a_0), t=0$. Thus, the stationary solution of Eq. (33) for HEH (3) considering the presence of stochastic excitation is the following form:

$$\begin{aligned} p_{\mathrm{st}}(Q)=N\exp \left[ -\left( c+\varepsilon +\zeta \right) \frac{Q^2}{2D} +\frac{1}{2}\ln Q\right] . \end{aligned}$$

(34)

where $p_{\mathrm{st}}(Q)$ is the stationary probability density function of displacement amplitude Q and N is a normalization constant. Then, the stationary averaging amplitude $e_{\mathrm{st}}[ Q]$ can be obtained as follows:

$$\begin{aligned} e_{\mathrm{st}}[ Q]=\int ^{+\infty }_{0}Qp_{\mathrm{st}}(Q)\text {d}Q. \end{aligned}$$

(35)

With the geometric and physical parameters listed in Table 1, the effects of different control parameters $g_1$, $g_2$, $\tau$ and noise intensity D on the stationary probability density $p_{\mathrm{st}}(Q)$ of the displacement amplitude Q can be seen in Fig. 12 through Eq. (34), respectively. It is observed from Fig. 12 that the stationary probability density as a function of displacement amplitude Q exhibits one peak. In all cases in Fig. 12, the peak of the probability distribution of the system without time-delayed feedback control is higher than that of the control system. When the noise intensity D is fixed to 0.1, with increase in the values of $g_1$ and $g_2$, the peak becomes lower and the position of the peak shifts to a larger value of displacement amplitude Q [see Fig. 12a, b]. On the contrary, the peak becomes higher and the position of the peak shifts to a smaller value of displacement amplitude Q with increasing time delay $\tau$, as shown in Fig. 12c. When the control parameters $g_1$, $g_2$ and $\tau$ are fixed, the peak becomes lower and the position of the peak shifts to a larger value of displacement amplitude Q with increasing noise intensity D.

In order to get a deep understanding of the observed dynamics and the influences of different control parameters $g_1$, $g_2$, $\tau$ and noise intensity D, we can compute the stationary averaging amplitude $e_{\mathrm{st}}[ Q]$. In all cases in Fig. 13, the stationary averaging amplitude $e_{\mathrm{st}}[ Q]$ increases with increasing noise intensity D, leading to the higher response of the system, which is very beneficial to the improvement of EH performance. In Fig. 13a, b, the stationary averaging amplitude $e_{\mathrm{st}}[ Q]$ increases as the values of $g_1$ and $g_2$ increase. However, the stationary averaging amplitude $e_{\mathrm{st}}[ Q]$ decreases as the values of $\tau$ increase.

4.2.2 Averaging harvested power

Through the relation in Eq. (11), the averaging square values of the electric current and voltage take the following general from:

$$\begin{aligned} e_{\mathrm{st}}[I^2]= & {} e_{\mathrm{st}}[Q_{c}^2]=\frac{\nu ^2}{\mu ^2+1}e_{\mathrm{st}}[Q^2]\nonumber \\= & {} \frac{\nu ^2}{\mu ^2+1}\int ^{+\infty }_{0}Q^2p_{\mathrm{st}}(Q)\text {d}Q, \end{aligned}$$

(36)

$$\begin{aligned} e_{\mathrm{st}}[V^2]= & {} e_{\mathrm{st}}[Q_{v}^2]=\frac{\gamma ^2}{\lambda ^2+1}e_{\mathrm{st}}[Q^2]\nonumber \\= & {} \frac{\gamma ^2}{\lambda ^2+1}\int ^{+\infty }_{0}Q^2p_{\mathrm{st}}(Q)\text {d}Q. \end{aligned}$$

(37)

Thus, the total stationary averaging harvested power can be expression as

$$\begin{aligned} e_{\mathrm{st}}[P]=e_{\mathrm{st}}[P_c]+e_{\mathrm{st}}[P_v]=\mu \theta e_{\mathrm{st}}[I^2] +\lambda \rho e_{\mathrm{st}}[V^2] . \end{aligned}$$

(38)

To measure the averaging harvested power obtained in (38), the effects of different control parameters $g_1$, $g_2$, $\tau$ and noise intensity D on the performance of the HEH are illustrated in Fig. 14. In all cases in Fig. 14, it is seen that the averaging harvested power $e_{\mathrm{st}}[P]$ increases with the increase in noise intensity D. The increase in averaging harvested power present in Fig. 14 has been observed in other different types of energy harvester under stochastic excitation [9,10,11, 44, 45]. Meanwhile, the value of the averaging harvested power $e_{\mathrm{st}}[P]$ of the system without time-delayed feedback control is lower than that of the control system, which plays a great realistic significance in the choose of the control parameters for improving the performance of the HEH. In Fig. 14a, b, the averaging harvested power $e_{\mathrm{st}}[P]$ increases as the values of $g_1$ and $g_2$ increase. However, the averaging harvested power $e_{\mathrm{st}}[P]$ decreases as the values of $\tau$ increase. The above results also indicate that the time-delayed feedback control is effective for improving the performance of the HEH under stochastic excitation.

4.3 The case of combined harmonic and stochastic excitations

In the above study, the HEH is a nonlinear bistable system driven by a harvestable harmonic or stochastic excitation. In addition, to analyze in more detail the effect of the excitations on the performance of HEH, we will consider the simultaneous action of harmonic and stochastic excitations, i.e., $\ddot{z}=a\cos (\omega t)+\xi (t)$, for the HEH located in certain zone. Therefore, three basic ingredients are simultaneously satisfied: (i) nonlinear bistable system with a double potential, (ii) a weak periodic signal $a\cos (\omega t)$ and (iii) an inherent noise $\xi (t)$. Stochastic resonance is a major physical phenomenon for meeting these conditions, which should be sought for the application to improve vibrational EH.

4.3.1 Stochastic resonance for EH strategy

To quantitatively characterize the stochastic resonance for EH, one can calculate the signal-to-noise ratio (SNR) using the output power spectra of the signal $S_1(\bar{\omega }_d)$ and the output power spectra of noise $S_2(\bar{\omega }_d)$ [46]. To do so, the output SNR of the HEH can be defined as the ratio of the output power spectra:

$$\begin{aligned} \text {SNR}=\frac{\int ^\infty _0S_1(\bar{\omega }_d)\text {d} \bar{\omega }_d}{S_2(\bar{\omega }_d={\omega })}. \end{aligned}$$

(39)

In order to get the expression of the SNR, one can firstly calculate the mean escape time ($MET_{1,2}$) of the process q(t) to reach the state $q_{1,2}$ with initial condition $q_{2,1}$. Applying the steepest descent method [47], the $MET_{1,2}$ is given by the Kramers-like formula

$$\begin{aligned} MET_{1,2}= & {} MET_{q_{2,1}\rightarrow q_{1,2}}\nonumber \\= & {} \frac{2\pi }{\sqrt{\iota _1\iota _2}} \sqrt{-\frac{\sigma _2}{\sigma _1}} \exp \left[ U_{e}(q_u,t)-U_{e}(q_{1,2},t)\right] ,\nonumber \\ \end{aligned}$$

(40)

where $U_{e}(q,t)$ is the effective potential energy function and $\iota _{1,2}$ and $\sigma _{1,2}$ are given by Eq. (18), respectively. When the HEH (3) is under the simultaneous action of harmonic and stochastic excitations, the effective potential energy $U_{e}(q,t)$ can be solved as

$$\begin{aligned} U_{e}(q,t)= & {} \frac{1}{D}\left( c+\varepsilon +\zeta \right) \nonumber \\&\left[ \frac{1}{2}\varpi ^{2}+\frac{1}{2} \left( 1+\eta +\beta +r\right) q^2 \right. \nonumber \\&\left. -\,r\sqrt{q^2+\alpha ^2}-qa\cos ({\omega }t)\right] . \end{aligned}$$

(41)

In addition, the mean escape time $MET_{1,2}$ ultimately leads to the escape rate $ER_{1,2}$ for $ER_{1,2}=1/MET_{1,2}$. Substituting Eq. (41) into Eq. (40), the escape rate $ER_{1,2}$ can be further obtained as:

$$\begin{aligned} ER_{1,2}= & {} \frac{\sqrt{\iota _1\iota _2}}{2\pi }\sqrt{-\frac{\sigma _1}{\sigma _2}}\nonumber \\&\exp \left[ \varUpsilon _1\left( \varUpsilon _2q^2_{1,2} -r\sqrt{q_{1,2}^2+\alpha ^2}\right. \right. \nonumber \\&\left. \left. -\,q_{1,2} a\cos ({\omega } t)-r\alpha \right) \right] , \end{aligned}$$

(42)

with

$$\begin{aligned} \varUpsilon _1=\frac{1}{D}\left( c+\varepsilon +\zeta \right) ,~~~\varUpsilon _2 =\frac{1}{2}\left( 1+\eta +\beta +r\right) . \end{aligned}$$

(43)

Equation (42) can be expanded using a Taylor series as:

$$\begin{aligned} ER_{1,2}=ER_{0}\left[ 1\mp q_{1,2}a\cos ({\omega } t) +\frac{1}{2}q^2_{1,2}a^2\cos ^2({\omega } t)\pm \cdots \right] , \end{aligned}$$

(44)

where

$$\begin{aligned} ER_{0}= & {} \frac{\sqrt{\iota _1\iota _2}}{2\pi }\sqrt{-\frac{\sigma _1}{\sigma _2}}\nonumber \\&\exp \left[ \varUpsilon _1\left( \varUpsilon _2|q_{1,2}|^2 -r\sqrt{|q_{1,2}|^2+\alpha ^2} -r\alpha \right) \right] .\nonumber \\ \end{aligned}$$

(45)

Fig. 15

The output SNR as a function of noise intensity D for different control parameters $g_1$, $g_2$ and $\tau$. The parameters are $a=0.2$, $\omega =1.0$, a$g_2=0.2, \tau =1.5$, b$g_1=-0.3, \tau =1.5$, c$g_1=-0.3, g_2=0.2$. (Color online)

Fig. 16

The output SNR as a function of noise intensity D for different harmonic excitation parameters a and $\omega$. The parameters are $\alpha =0.3$, $g_1=-0.2, g_2=0.2, \tau =1.5$. (Color online)

Subsequently, the output spectrum of system can be expressed as $S(\bar{\omega }_d)=S_1(\bar{\omega }_d)+S_2(\bar{\omega }_d)$. One defines $ER_1\varXi =ER_0\varUpsilon _1|x_{1,2}|a$. Then, $S_1(\bar{\omega }_d)$ and $S_2(\bar{\omega }_d)$ can be written as

$$\begin{aligned} \left\{ \begin{array}{l} S_1(\bar{\omega }_d)=\frac{\pi q_{1,2}^2(ER_1\varXi )^2}{2(ER_0^2 +{\omega }^2)}[\delta (\bar{\omega }_d-{\omega })+\delta (\bar{\omega }_d+{\omega })],\\ S_2(\bar{\omega }_d)=\left[ 1-\frac{(ER_1\varXi )^2}{2(ER_0^2+{\omega }^2)}\right] \frac{2q_{1,2}^2ER_0}{ER_0^2+\bar{\omega }_d^2}. \end{array}\right. \end{aligned}$$

(46)

Thus, the output SNR can be finally obtained as:

$$\begin{aligned} \text {SNR}=\frac{\pi (ER_0\varUpsilon _1|q_{1,2}|a)^2(ER_0^2+{\omega }^2)}{4 ER_0(ER_0^2+{\omega }^2)-2ER_0D^2(ER_0\varUpsilon _1|q_{1,2}|a)^2}. \end{aligned}$$

(47)

The occurrence of the stochastic resonance is defined as the ratio of the peak height of the power spectral intensity to the height of the noisy background at the same frequency. Given its nature, stochastic resonance appears very suitable for the current application as random and periodic vibrations often exist simultaneously in HEHs.

4.3.2 Delay-enhanced stochastic resonance strategy

For the HEH proposed in this paper, the snap-through mechanism creates the double-well potential necessary for stochastic resonance. When excited by harmonic and stochastic excitation, the lumped mass will undergo large amplitude vibration due to stochastic resonance with transitions between the two potential wells. For improving the performance of energy harvester, the phenomena of stochastic resonance have been used efficiently [48,49,50], but the development of practical methods for the precise control of stochastic resonance is a further challenge to overcome. To overcome this, we propose a novel EH strategy that particularly suits bistable or multistable energy harvester, which takes advantage of stochastic resonance by using time-delayed feedback control.

By virtue of the expressions of the output SNR (47), the resulting dependence of the output SNR on noise intensity D is presented in Fig. 15 for different control parameters $g_1$, $g_2$, $\tau$. There exhibits a maximum in the output SNR, which is the so-called stochastic resonance phenomenon [46, 51, 52]. In Fig. 15a, the maximum of the output SNR decreases as the value of $g_1$ increases. However, the maximum of the output SNR increases as the value of $g_2$ or $\tau$ increases, as shown in Fig. 15b, c. That is, time-delayed feedback control can enhance stochastic resonance phenomenon, which is beneficial for improving the performance of HEH.

For the control parameters that are fixed, Fig. 16 shows the output SNR as a function of noise intensity D for different harmonic excitation parameters a and $\omega$. From Fig. 16, it can be seen that the stochastic resonance phenomenon of the system without time-delayed feedback control is weaker than that of the control system, in three different cases of harmonic excitation parameters a and $\omega$. Consequently, the control is beneficial for increasing amplitude, which has significant applications in many fields of EH. The phenomena of delay-enhanced stochastic resonance have been shown in other nonlinear systems; however, here the delay-enhanced stochastic resonance strategy exists in the HEH. It should be noted that experiments have validated that active power can be increased at stochastic resonance [53, 54], showing that the response can indeed be amplified, and indicate that the available power generated under stochastic resonance is noticeably higher than the power that can be collected under other harvesting conditions [55, 56]. It is believed that delay-enhanced stochastic resonance EH strategy may be significant in practice and will be pursued through further analytical and experimental investigation.

5 Conclusions

This paper investigated the influence of time-delayed feedback control on nonlinear HEH for different types of excitation, and its electromechanical equations are derived and solved. The nonlinear dynamic characteristics and broadband EH characteristics including vibration responses for harmonic excitation and steady-state response for stochastic excitation are considered as the optimization standards. Based on these properties, this research provides the guidance for designing the time-delayed feedback control parameters and the optimization standards for different types of external excitation to improve the performance of HEH. The time-delayed feedback control technique allows one to stabilize unstable periodic orbits of the attractor, which will effectively enhance the output power of electromechanical systems. The maximum total averaging harvested power of the system without time-delayed feedback control is lower than that of the control system; that is, the control strategy is effective for improving the EH performance of the HEH under harmonic excitation. In case of stochastic excitation, the stationary averaging amplitude increases with increasing noise intensity, leading to the higher response of the system, which is very beneficial to the improvement of EH performance. The stationary averaging amplitude increases as the values of $g_1$ and $g_2$ increase, and decreases as the values of $\tau$ increase. Meanwhile, the value of the averaging harvested power of the system without time-delayed feedback control is lower than that of the control system, which plays a great realistic significance in the choose of the control parameters for improving the performance of the HEH. In case of combined harmonic and stochastic excitations, the time-delayed feedback control also can enhance stochastic resonance phenomenon, which can lead to a large response and give out a high output power. The stochastic resonance phenomenon of the system without time-delayed feedback control is weaker than that of the control system.

The biggest challenge of time-delay feedback control of EH is the automatic supply of electrical energy to the control system. The power consumed by the control system should be less than the actual increase, so that the control of the EH has practical significance. In the future, the control parameters can be optimized according to the required power. In addition, the time-delay feedback control requires current input, and the control strategy can be introduced to tune the current online, thus reducing the energy consumption and improving the beneficial performance.