Dynamical properties of a forced vibration isolation system with real-power nonlinearities in restoring and damping forces

Abstract

In this paper, the time-delayed cubic velocity feedback and the real-power form of restoring and damping forces are combined to improve the performance of vibration isolation. The primary resonance, dynamic stability and transmissibility are studied for a forced vibration isolation system with real-power exponents in restoring and damping force terms under base excitation. Based on the method of multiple scales, the equivalent damping is first proposed to interpret the effect of feedback control on the dynamic behavior of the real-power isolation system, such as the frequency island phenomenon. In this regard, the isolation system indicates the softening behavior for under-linear restoring force and hardening behavior for over-linear restoring force. And multi-valued responses, especially five-valued responses, are found under under-linear restoring force. To verify this result, the stability boundaries are characterized and presented excellent agreement with the responses. Then, for avoiding the jump phenomenon, an analytical criterion is derived and confirmed by the numerical simulation. Furthermore, with the purpose of suppressing the amplitude peak and governing the resonance stability, appropriate feedback gains and time delays are derived. Finally, the effects of the system parameters on the energy transmissibility is investigated. Results show that the strategy proposed in this paper is practicable and feedback parameters are significant factors to improve the isolation effectiveness for the real-power isolation system.

1 Introduction

Elastic properties of many mechanical and engineering systems obey the Hooke’s law. This law is an approximation that states the force needed to deform a spring is proportional to its deflection [1, 2]. However, this force, which is equal to the restoring force induced in the spring, decreases or increases more rapidly than the deflection, i.e., it depends nonlinearly on the deflection, implying softening and hardening behaviors. Therefore, this type of the force–deflection relationship is usually expressed in a polynomial form with a linear term and a quadratic or cubic nonlinear term.

However, there are many materials whose elastic deformations cannot be exactly described by Hooke’s law [2], which leads to the force–deflection relationship with non-polynomial form [2–6]. Specifically, the nonlinear materials of Ramberg–Osgood type, in which the exponent of the restoring force is a fraction higher than 1, have been applied to depict the elastic properties of the aircraft materials such as aluminum and titanium [2, 3]. Another type of materials, in which the exponent of the restoring force is a rational number, has been used in copper alloys called Ludwick type [4, 5]. Additionally, based on the study of impulse propagation, the interaction of the elastic beads with dissipative contacts was also characterized by the fractional-order potential with the exponent between 2.5 and 3 [6].

Actually, the studies of dynamical behaviors of these materials have been received much attention. For example, in a vibration isolation system with positive real-power restoring and damping forces, the response and transmissibility have been examined by Mallik [7]. In recent years, Kovacic [1, 8, 9] obtained abundant research results about this kind of systems. In Ref. [8], the expression of the energy–displacement function of a system with a nonnegative real-power restoring force has been expressed in terms of incomplete Gamma functions. The relative and absolute displacement transmissibility with a $n$th power damper has been discussed in Ref. [9]. But limited analytical results on the dynamics under active control were reported in the present researches of the real-power vibration isolation systems.

It is well known that active control technique with time delays has been widely used in mechanical and structural vibrations for sensing structural vibrations and delivering appropriate control forces to counteract structural motions. The reason is that during the process of sensing and calculating the necessary control forces, especially in the limited bandwidth of actuators, time delay can be existed and unavoidable. Actually, over the past decades, great attention has been paid to the stability analysis of delay controlled systems [10–18]. Famous examples are presented by Hu [10, 11]. From the concept of the equivalent damping ratio, they proposed an appropriate choice of feedback gains and time delays to enhance the control performance. Nayfeh and Baumann [17] applied a time-delay position feedback controller to reduce the sway of container cranes. To our knowledge, previous works only focused on the systems in which the force–deflection relationship is the polynomial form.

In this paper, we concentrate on gaining an insight into the dynamics of a vibration isolation system with non-polynomial form of restoring force and real-power exponent of fractional damping under time-delayed cubic velocity feedback control. A brief description of the mathematical model for a forced oscillator with real-power exponents of the restoring and damping forces under time-delayed feedback control is presented in Sect. 2. By the method of multiple scales, primary resonances and stability conditions are derived in Sect. 3. And then in Sects. 4–6, the effects of system parameters on the dynamical behaviors are revealed and the classification of the steady-state solutions is discussed. In Sect. 7, the transmissibility indices have been plotted for relevant parameters to study the performance characteristics. Finally, Sect. 8 summarizes main results.

2 The mechanical model and multi-scale analysis

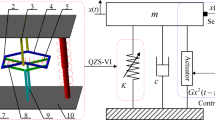
The system investigated in this paper is shown in Fig. 1. It comprises an isolated mass $M$ and a base vibrating harmonically with an active vibration controller. The motion of the base is given by $y=Y\cos (\varOmega _e t)$. The isolator placed between the mass and the base is modeled by linear-plus-nonlinear springs and a nonlinear damper [9].

Fig. 1

Mechanical model of the vibration isolation system with an active vibration controller

The equation of motion of the mass is given by

$$\begin{aligned}&M\ddot{X}+C_1\, \hbox {sgn}(\dot{X})\left| {\dot{X}} \right| ^{\alpha }+K_1 X+K_2\,\hbox {sgn}(X)\left| X \right| ^{\beta }\nonumber \\&\quad +\,C_2 \dot{X}^{3}(t-\delta )=FY\cos (\varOmega _e t), \end{aligned}$$

(1)

where $X$ is the relative displacement $X=z-y$, dots indicate derivative with respect to time $t$. $\alpha$ is an arbitrary positive real number, and the coefficient $C_1$ stands for the corresponding damping coefficient. $K_1$ is the coefficient of the linear stiffness. $\beta$ is an arbitrary nonnegative real number, and the coefficient $K_2$ stands for the corresponding stiffness coefficient. $\hbox {sgn}(x)$ and $\hbox {sgn}(\dot{x})$ are the sign functions.

By introducing the following dimensionless parameters,

$$\begin{aligned}&x=\frac{X}{Y},\quad \tau =\omega _0 t,\quad \varOmega =\frac{\varOmega _e }{\omega _0 },\quad 2\zeta _1 =\frac{C_1 Y^{\alpha -1} }{M\omega _0^{2-\alpha }},\\&\omega ^{2}=\frac{K_1 }{M\omega _0^2 }, \quad k=\frac{K_2 Y^{\alpha -1} }{M\omega _0^2 },\quad \zeta _2 =\frac{C_2 \omega _0 Y^2}{M}, \\&\tau _0 =\omega _0 \delta ,\quad f=\frac{F}{M\omega _0^2 }. \end{aligned}$$

The following dimensionless equation of motion is derived

$$\begin{aligned}&\ddot{x}+2\zeta _1\, \hbox {sgn}(\dot{x})\left| {\dot{x}} \right| ^{\alpha }+\omega ^{2}x+k\,\hbox {sgn}(x)\left| x \right| ^{\beta }\nonumber \\&\quad +\,\zeta _2 \dot{x}^{3}(\tau -\tau _0 )=f\cos (\varOmega \tau ), \end{aligned}$$

(2)

where dots denote differentiation with respect to dimensionless time $\tau$.

For the necessity of the multiple-scale method, we may denote

$$\begin{aligned} \zeta _1 =\varepsilon \hat{{\zeta }}_1 ,\quad k=\varepsilon \hat{{k}},\quad \zeta _2 =\varepsilon \hat{{\zeta }}_{2}\quad \hbox {and}\quad f=\varepsilon \hat{{f}}. \end{aligned}$$

Then, Eq. (2) can be rewritten as

$$\begin{aligned} \ddot{x}+\omega ^{2}x= & {} \varepsilon (-2\hat{{\zeta }}_1\, \hbox {sgn}(\dot{x})\left| {\dot{x}} \right| ^{\alpha }-\hat{{k}}\,\hbox {sgn}(x)\left| x \right| ^{\beta }\nonumber \\&-\,\hat{{\zeta }}_2 \dot{x}^{3}(\tau -\tau _0 )+\hat{{f}}\cos (\varOmega \tau )). \end{aligned}$$

(3)

In this paper, we will extend the method of multiple scales to investigate the responses and its stability of system (2). The uniformly approximate solution of Eq. (3) is supposed in the form by the multiple-scale method

$$\begin{aligned} x(\tau ,\varepsilon )=x_0 (T_0 ,T_1 )+\varepsilon x_1 (T_0 ,T_1 )+\cdots , \end{aligned}$$

(4)

where $T_0 =\tau$ is a fast time scale and $T_1 =\varepsilon \tau$ is a slow time scale. By denoting the differential operators $D_0 =\partial /{\partial T_0 }$ and $D_1 =\partial /{\partial T_1 }$, we get

$$\begin{aligned} \frac{\partial }{\partial t}=D_0 +\varepsilon D_1 +\cdots ,\quad \frac{\partial ^{2}}{\partial t^{2}}=D_0^2 +2\varepsilon D_0 D_1 +\cdots . \end{aligned}$$

(5)

Substituting Eqs. (4) and (5) into Eq. (3) and comparing coefficients of $\varepsilon$ with the same powers, we obtain the following equations

$$\begin{aligned}&D_0^2 x_0 (T_0 ,T_1 )+\omega ^{2}x_0 (T_0 ,T_1 )=0, \nonumber \\&D_0^2 x_1 (T_0 ,T_1 )+\omega ^{2}x_1 (T_0 ,T_1 )=-2D_0 D_1 x_0 (T_0 ,T_1 )\nonumber \\&\quad -\,2\hat{{\zeta }}_1\, \hbox {sgn}(D_0 x_0 )\left| {D_0 x_0 } \right| ^{\alpha }-\hat{{k}}\,\hbox {sgn}(x_0 )\left| {x_0 } \right| ^{\beta }\nonumber \\&\quad -\,\hat{{\zeta }}_2 D_0^3 x_0 (T_0 -\tau _0 ,T_1 )+\hat{{f}}\cos (\varOmega T_0 ). \end{aligned}$$

(6)

Considering the first linear equation in Eq. (6), the general solution can be expressed as

$$\begin{aligned} x_0 (T_0 ,T_1 )=A(T_1 )\cos (\omega T_0 +\varphi (T_1 )), \end{aligned}$$

(7)

where $A=A(T_1)$ and $\varphi =\varphi (T_1 )$ are functions of the slow time scale $T_1$.

$\hbox {sgn}(D_0 x_0 )\left| {D_0 x_0 } \right| ^{\alpha }$ and $\hbox {sgn}(x_0 )\left| {x_0 } \right| ^{\beta }$ can be expanded into the Fourier series [1]:

$$\begin{aligned} \hbox {sgn}(D_0 x_0 )\left| {D_0 x_0 } \right| ^{\alpha }= & {} \hbox {sgn}(-\omega A\sin (\omega T_0 +\varphi ))\nonumber \\&\times \left| {\omega A\sin (\omega T_0 +\varphi )} \right| ^{\alpha }\nonumber \\= & {} \left| {\omega A} \right| ^{\alpha }(-b_{1\alpha } \sin (\omega T_0 +\varphi )\nonumber \\&+\,b_{3\alpha } \sin (3\omega T_0 +3\varphi ))+\cdots ,\end{aligned}$$

(8)

$$\begin{aligned} \hbox {sgn}(x_0 )\left| {x_0 } \right| ^{\beta }= & {} \hbox {sgn}(A\cos (\omega T_0 +\varphi ))\nonumber \\&\times \left| {A\cos (\omega T_0 +\varphi )} \right| ^{\beta }\nonumber \\= & {} \left| A \right| ^{\beta }(b_{1\beta } \cos (\omega T_0 +\varphi )\nonumber \\&+\,b_{3\beta } \cos (3\omega T_0 +3\varphi ))+\cdots ,\nonumber \\ \end{aligned}$$

(9)

with the coefficients $b_{1\alpha }$ and $b_{3\alpha }$ being

$$\begin{aligned} b_{1\alpha } =\frac{2}{\sqrt{\pi }}\frac{\Gamma \left( {1+\frac{\alpha }{2}} \right) }{\Gamma \left( {\frac{3\,+\,\alpha }{2}} \right) },\quad b_{3\alpha } =\frac{\alpha -1}{\sqrt{\pi }}\frac{\Gamma \left( {1+\frac{\alpha }{2}} \right) }{\Gamma \left( {\frac{5\,+\,\alpha }{2}} \right) }, \end{aligned}$$

(10)

where $\Gamma$ is the Euler Gamma function. And $b_{1\beta }$ and $b_{3\beta }$ being defined by Eq. (10), but with the symbol $\alpha$ replaced by $\beta$. More details about the Fourier series expansion can be found in [1].

In order to investigate the primary resonance of system (2), the detuning parameter $\sigma$ is introduced, and then, the excitation frequency can be written as $\varOmega =\omega +\varepsilon \sigma$, and so, $\varOmega T_0 =\omega T_0 +\sigma T_1$. Meanwhile, introducing new variable $\Phi (T_1 )=\sigma T_1 -\varphi (T_1 )$ and substituting Eqs. (7), (8), and (9) on the second equation of Eq. (6), we can obtain

$$\begin{aligned}&D_0^2 x_1 (T_0 ,T_1 )+\omega ^{2}x_1 (T_0 ,T_1 )\nonumber \\&\quad =2{A}'(T_1 )\omega \sin (\omega T_0 +\varphi )\nonumber \\&\qquad +\,2\omega \sigma A(T_1 )\cos (\omega T_0 +\varphi )\nonumber \\&\qquad -\,2\omega A(T_1 ){\Phi }'(T_1 )\hbox {cos}(\omega T_0 +\varphi )\nonumber \\&\qquad +\,2\hat{{\zeta }}_1 \omega ^{\alpha }b_{1\alpha } A^{\alpha }(T_1 )\sin (\omega T_0 +\varphi )\nonumber \\&\qquad -\,\hat{{k}}b_{1\beta } A^{\beta }(T_1 )\cos (\omega T_0 +\varphi )\nonumber \\&\qquad +\,\frac{3}{4}\hat{{\zeta }}_2 A^{3}(T_1 )\omega ^{3}\cos (\omega \tau _0 )\sin (\omega T_0 +\varphi )\nonumber \\&\qquad -\,\frac{3}{4}\hat{{\zeta }}_2 A^{3}(T_1 )\omega ^{3}\sin (\omega \tau _0 )\cos (\omega T_0 +\varphi )\nonumber \\&\qquad +\,\hat{{f}}\cos \Phi \cos (\omega T_0 +\varphi )-\hat{{f}}\sin \Phi \sin (\omega T_0 +\varphi ).\nonumber \\ \end{aligned}$$

(11)

Eliminating the secular term in Eq. (11), it can be derived

$$\begin{aligned}&{A}'(T_1 )=-\hat{{\zeta }}_1 \omega ^{\alpha -1}b_{1\alpha } A^{\alpha }(T_1 )-\frac{3}{8}\hat{{\zeta }}_2 A^{3}(T_1 )\omega ^{2}\nonumber \\&\qquad \times \cos (\omega \tau _0 )+\frac{\hat{{f}}}{2\omega }\sin \Phi , \nonumber \\&A(T_1 ){\Phi }'(T_1) = A(T_1 )\sigma -\frac{\hat{{k}}}{2\omega }b_{1\beta } A^{\beta }(T_1 ) \nonumber \\&\qquad -\frac{3}{8}\hat{{\zeta }}_2 A^{3}(T_1 )\omega ^{2}\sin (\omega \tau _0 )+\frac{\hat{{f}}}{2\omega }\cos \Phi . \end{aligned}$$

(12)

The steady-state solutions of system (2) are denoted as $A_0$ and $\Phi _0$ with conditions ${A}'=0$ and ${\Phi }'=0$ satisfied, which leads to the following results

$$\begin{aligned}&\hat{{\zeta }}_1 \omega ^{\alpha -1}b_{1\alpha } A_0^\alpha +\frac{3}{8}\hat{{\zeta }}_2 \omega ^{2}\cos (\omega \tau _0 )A_0^3 =\frac{\hat{{f}}}{2\omega }\sin \Phi _0 , \nonumber \\&-\sigma A_0 +\frac{\hat{{k}}}{2\omega }b_{1\beta } A_0^\beta +\frac{3}{8}\hat{{\zeta }}_2 \omega ^{2}\sin (\omega \tau _0 )A_0^3 =\frac{\hat{{f}}}{2\omega }\cos \Phi _0.\nonumber \\ \end{aligned}$$

(13)

Therefore, the frequency response equation can be expressed as

$$\begin{aligned}&\left( \hat{{\zeta }}_1 \omega ^{\alpha -1}b_{1\alpha } A_0^\alpha +\frac{3}{8}\hat{{\zeta }}_2 \omega ^{2}\cos (\omega \tau _0 )A_0^3 \right) ^{2}\nonumber \\&\qquad +\left( \frac{\hat{{k}}}{2\omega }b_{1\beta } A_0^\beta +\frac{3}{8}\hat{{\zeta }}_2 \omega ^{2}\sin (\omega \tau _0 )A_0^3 -\sigma A_0 \right) ^{2}\nonumber \\&\quad =\frac{\hat{{f}}^{2}}{4\omega ^{2}}. \end{aligned}$$

(14)

Now, we examine the stability of the steady-state response by introducing the perturbation terms as

$$\begin{aligned} A=A_0 +A_1 , \quad \Phi =\Phi _0 +\Phi _1 \end{aligned}$$

(15)

where $A_0$ and $\Phi _0$ are governed by Eq. (13), $A_1$ and $\Phi _1$ are perturbation terms.

Substituting Eq. (15) into Eq. (12) and neglecting the nonlinear terms, we can obtain the linearization modulation of Eq. (11) at $A_0$ and $\Phi _0$,

$$\begin{aligned}&{A}'_1 =\left( -\hat{{\zeta }}_1 \omega ^{\alpha -1}b_{1\alpha } \alpha A_0^{\alpha -1} -\frac{9}{8}\hat{{\zeta }}_2 \omega ^{2}A_0^2 \cos (\omega \tau _0 )\right) A_1 \nonumber \\&\qquad \qquad +\,\frac{\hat{{f}}}{2\omega }\cos \Phi _0 \Phi _1 ,\nonumber \\&A_0 {\Phi }'_1 =\left( \sigma -\frac{\hat{{k}}}{2\omega }b_{1\beta } \beta A_0^\beta -\frac{9}{8}\hat{{\zeta }}_2 \omega ^{2}\sin (\omega \tau _0 )A_0^3 \right) A_1\nonumber \\&\qquad \qquad -\,\frac{\hat{{f}}}{2\omega }\sin \Phi _0 \Phi _1. \end{aligned}$$

(16)

The characteristic equation of the coefficient matrix of Eq. (16) is

$$\begin{aligned} \lambda ^{2}-(C_1 +C_4 )\lambda +C_1 C_4 -C_2 C_3 =0, \end{aligned}$$

(17)

where $\lambda$ denotes eigenvalues of coefficient matrix and

$$\begin{aligned} C_1= & {} -\hat{{\zeta }}_1 \omega ^{\alpha -1}b_{1\alpha } \alpha A_0^{\alpha -1} -\frac{9}{8}\hat{{\zeta }}_2 \omega ^{2}A_0^2 \cos (\omega \tau _0 ),\\ C_2= & {} \frac{\sigma }{A_0 }-\frac{\hat{{k}}}{2\omega }b_{1\beta } \beta A_0^{\beta -1} -\frac{9}{8}\hat{{\zeta }}_2 \omega ^{2}\sin (\omega \tau _0 )A_0^2 ,\\ C_3= & {} \frac{\hat{{f}}}{2\omega }\cos \Phi _0 , \quad C_4 =-\frac{\hat{{f}}}{2\omega A_0 }\sin \Phi _0 . \end{aligned}$$

According to the Routh–Hurwitz criterion [19], the steady-state solutions of Eq. (11) are asymptotically stable if the following two inequalities hold simultaneously

$$\begin{aligned} \varSigma _1= & {} C_1 +C_4 <0,\end{aligned}$$

(18)

$$\begin{aligned} \varSigma _2= & {} C_1 C_4 -C_2 C_3 >0. \end{aligned}$$

(19)

In fact, if $\varSigma _2$ is negative, the corresponding steady-state solutions in Eq. (13) lose stability via a saddle-node bifurcation, which means that the jump phenomenon could happen. Since the discriminant of Eq. (17) is $\varSigma _1^2 -4\varSigma _2$, the steady-state solutions associated with $\varSigma _1^2 -4\varSigma _2 <0$ are foci, while those associated with $\varSigma _1^2 -4\varSigma _2 >0$ are nodes. These points are stable (unstable) when $\varSigma _1 <0(\varSigma _1 >0)$. Actually, the stability boundary $\varSigma _1$ indicates the critical condition that the sign of real parts of both roots of the characteristic equation changes. A change from negative real parts to positive real parts indicates the presence of Hopf bifurcation. Therefore, the nontrivial solutions are stable if and only if the conditions $\varSigma _1 <0$ and $\varSigma _2 >0$ are satisfied.

3 Effects of real-power exponents on the system response and stability

To verify the effectiveness of the multiple-scale method, the steady-state response is constructed by using the fourth-order Runge–Kutta algorithm. The parameters of isolation system are set as $\omega =1.0,\varepsilon =0.1,k=0.2,\alpha =3/2,\beta =4/3,f=0.1, \zeta _1 =0.05,\zeta _2 =0.03,\tau _0 =3\pi /4$, unless otherwise stated.

3.1 Effects of real-power exponent $\beta$ of restoring force term

Firstly, we consider the effects of the real-power exponent $\beta$ of restoring force term on the steady-state response of the system. The variations of the steady-state response $A_0$ with detuning parameter $\sigma$ are shown in Fig. 2 for different values of $\beta$. As a comparison, approximate analytical results derived by Eq. (14) are depicted by solid lines and the numerical results are given by circles. Excellent agreements can be found between them.

Fig. 2

Steady-state responses of system (2) versus detuning parameter: a $\beta =1/9$; b $\beta =1/5$; c $\beta =1/3$; d $\beta =4/3$; e $\beta =5/2$; f $\beta =9/2$; g, h the local amplification of $\beta =1/9$; i the local amplification of $\beta =1/3$ (solid lines analytical results, circles numerical results; dashed lines stability boundaries)

It is obvious that the steady-state response curves are bent to the left-hand side for $\beta <1$ indicating the softening stiffness property (see, for example, Fig. 2a–c) and to the right side for $\beta >1$ indicating the hardening stiffness property (see, for example, Fig. 2d–f), which are consistent with the results shown in [1].

Furthermore, note that the frequency island phenomenon always exists in spite of different values of $\beta$. Actually, this also leads to the occurrence of the multi-valued responses. Table 1 describes the multi-valued response characteristic shown in Fig. 2. We take $\beta =1/9$ (in Fig. 2a) as an example, and to make this clear, the amplification of two parts of the response curve is shown in Fig. 2g, h. In the interval of $\sigma \in \left[ {0.0,0.0983} \right]$, the response is single-valued; as $\sigma$ increases, the triple-valued solution occurs in a narrow region $\sigma \in \left[ {0.0983,0.1009} \right]$; then, in the island region $\sigma \in [0.1009,0.1465]$, the system has five steady-state solutions corresponding to every value of $\sigma$; further, with larger $\sigma$, in the interval of $\sigma \in \left[ {0.1465,2.7685} \right]$, the response keeps the triple-valued case; subsequently, for certain value of $\sigma$, only one steady-state solution remains. We can denote this kind of response characteristic as 1S-3S-5S-3S-1S (in this paper, $n$S presents that the numbers of steady-state solutions are $n$).

Table 1 The multi-valued response characteristic of the system with different real-power exponent $\beta$

From Table 1, it can be found that with the increase in real-power exponent $\beta$, the system response can be very different. With larger $\beta$, as shown in Fig. 2f, the island part is very close to one continuous curve rather than a closed loop and almost lies on the boundary of the saddle-node points. This kind of response property is also verified when $\beta >9/2$, only the response curve of the island part lies in a larger interval of $\sigma$.

Next, according to Eqs. (18) and (19), the stability of the steady-state solutions is discussed. It is clear that numerical simulation could not obtain the corresponding data of the closed loops in Fig. 2, which is determined by the stability of the steady-state solutions. Particularly, as indicated in Fig. 2, the stability boundaries are plotted by the dash lines, that is to say, in the shaded regions $(\varSigma _2 <0)$, and above the dash line $(\varSigma _1 =0)$, the steady-state solutions are unstable. Hence, in the closed loop, the steady-state solutions are unattainable. Moreover, the response characteristic of the branch on the lower amplitude part is the same with the traditional frequency response curve with jump, where the middle of the three solutions is unstable and the smallest and largest ones are stable. Thus, for five-valued response, only two steady-state solutions which lie in the lower amplitude branch (in Fig. 2a, b) are attainable.

Furthermore, it is clear that with the increase in $\beta$, the unstable region $(\varSigma _2 <0)$ from two independent parts becomes only one part which lies in the high amplitude part (Fig. 2e, f). Actually, due to $\beta >1$ the response characteristic of the system indicates the hardening stiffness property, meanwhile the minimum value of the unstable region $\varSigma _2 <0$ in the high amplitude part decreases; therefore, the unstable solutions of the response curves can be covered by this region, as shown in Fig. 2e, f.

3.2 Effects of real-power exponent $\alpha$ of damping term

In this section, the effects of the real-power exponent $\alpha$ of damping term on the steady-state response of the system are studied.

As indicated in Fig. 3, for smaller value of $\alpha \;(\alpha =1/2)$, the steady-state response curve is continuous with the apparent maximum. As increasing $\alpha$, the left and right branches become closer to each other, and lastly, the response curve is separated into two parts as plotted for the cases of $\alpha =3/2$ and $\alpha =2$, which are also referred to as the frequency islands. Further, increasing $\alpha$ shows a gradual shift from multi-valued response behavior to single unique response, i.e., the closed loop disappears and only the low frequency branch remains $(\alpha =3)$. Moreover, as presented in Fig. 3a for $f$, there is a narrow region in which the numerical response could not gain, which is verified by the stability analysis.

Fig. 3

Steady-state responses of system (2) versus detuning parameter: a $\alpha =1/2$; b $\alpha =3/2$; c $\alpha =2$; d $\alpha =3$ (solid lines analytical results, circles numerical results, dash lines stability boundaries, dashed-dotted lines nodes boundaries)

3.3 Analysis of the classification of the steady-state solutions in Sects. 3.1 and 3.2

As discussed in previous sections, the responses have distinct for different real-power exponents $\alpha$ or $\beta$; therefore, the stability classification of the steady-state solutions is also very different. In the following part, it can be analyzed specifically according to the stability classification discussed at the end of Sect. 2.

It is evident in Fig. 4a–c, when $\beta$ is fixed $(\beta =4/3)$ under smaller value of $\alpha \;(\alpha =1/2$ in Fig. 4a), the saddle points lie in one uniform region $(\varSigma _2 <0)$, and outside this region, the remaining points are nodes and foci. The division line for nodes and foci is the boundary $\varSigma _1^2 -4\varSigma _2 =0$, and the dash line $\varSigma _1 =0$ is the boundary for the stable and unstable nodes and foci. Therefore, only the steady-stable solutions below the dash line $\varSigma _1 =0$ and outside the shaded region $\varSigma _2 <0$ are attainable.

Fig. 4

The classification of the steady-state solutions: a $\alpha =1/2, \beta =4/3$; b $\alpha =3/2,\beta =4/3$; c $\alpha =3,\beta =4/3$; d $\alpha =3/2,\beta =1/9$; e $\alpha =3/2,\beta =5/2$; f The local amplification of b

With the increase of $\alpha$, the distribution of the steady-state solutions is also different. As $\alpha$ is greater than 1 ($\alpha =3/2$ and $\alpha =3$), the regions of saddle points from one uniform region become two separate parts: One lies in the high amplitude part and the other one lies in the lower amplitude part. With larger $\alpha$, the size of the saddle-point regions reduces, and outside the saddle regions, the steady-state solutions are stable everywhere (Fig. 4c). Meanwhile, the size of the node region increases obviously, and the nodes are all stable in the $\varOmega$–$A_0$ plane.

Next, by comparing Fig. 4b–e, the effects of the real-power exponent $\beta$ can be presented. With smaller $\beta$, as shown in Fig. 4d $(\beta =1/9)$, the saddle points lie in two regions, that is to say, the saddle-node bifurcation can occur in the lower amplitude part or the higher amplitude part. As increasing $\beta$ ($\beta =4/3$ in Fig. 4b), the area in the lower amplitude part reduces obviously, and Fig. 4f is the amplification in the rectangular region of Fig. 4b; then, the smaller saddle-point region disappears ($\beta =5/2$ in Fig. 4e), and only the high amplitude part remains.

As can be seen that the real-power exponents of restoring and damping forces have a significant influence on the stability classification of the steady-state solutions of the real-power isolation system.

3.4 Jump avoidance

In previous sections, the saddle-node bifurcation results in the existence of the jump phenomenon. A jump will occur as long as there are two points on the steady-state response curve with a vertical slope, corresponding to ${\hbox {d}\sigma }/{\hbox {d}A_{0} }=0$. Because of the undesirable and destructive effects of the jump in practical situations, to find the condition required to avoid jump is important. The jump can be avoided if it can be ensured that the frequency response of the system is unique [20, 21]. According to Eq. (14), we have

$$\begin{aligned} \sigma ^{2}-2C_5 \sigma +C_5^2 -C_6 =0 \end{aligned}$$

where $C_5 =\frac{\hat{{k}}}{2\omega }b_{1\beta } A_0^{\beta -1} +\frac{3}{8}\hat{{\zeta }}_2 \omega ^{2}\sin (\omega \tau _0 )A_0^2$, $C_6 =\frac{\hat{{f}}^{2}}{4\omega ^{2}A_0^2 }-C_4^2$.

Then, the detuning parameter can be derived as follows

$$\begin{aligned} \sigma =C_5 \pm \sqrt{C_6 }, \end{aligned}$$

(20)

Differentiating both sides of Eq. (20) with respect to $A_0$ and substituting ${\hbox {d}\sigma }/{\hbox {d}A_{0} }=0$ yield

$$\begin{aligned} C_8 \pm \frac{1}{2\sqrt{C_6 }}\left( {-\frac{\hat{{f}}^{2}}{2\omega ^{2}A_0^3 }-2C_4 C_7 } \right) =0, \end{aligned}$$

(21)

where

$$\begin{aligned} C_7= & {} -\hat{{\zeta }}_1 \omega ^{\alpha -1}(\alpha \!-\!1)b_{1\alpha } A_0^{\alpha -2} \!-\!\frac{3}{4}\hat{{\zeta }}_2 \omega ^{2}\cos (\omega \tau _0 )A_0 ,\\ C_8= & {} \frac{\hat{{k}}}{2\omega }b_{1\beta } (\beta -1)A_0^{\beta -2} +\frac{3}{4}\hat{{\zeta }}_2 \omega ^{2}\sin (\omega \tau _0 )A_0 . \end{aligned}$$

According to Eq. (21), Fig. 5 depicts the critical amplitude $A_0$ as a function of real-power exponent $\alpha$. As shown in Fig. 5, there are more than one point satisfying ${\hbox {d}\varOmega }/{\hbox {d}A_{0} }=0$ when $\alpha$ is smaller than 2.554, indicating the existence of the jump. Hence, $\alpha =2.554$ is the minimum and acceptable value of $\alpha$ in practical design to avoid the jump for given system parameters. This result also confirms the steady-state responses presented in Fig. 3, and the island area will shrink gradually when $\alpha$ is greater than 2, and thus, the vertical tangents in the island area are almost coincidence. For $\alpha$ is greater than 2.554, the island area disappears, and thus, there is no jump, such as $\alpha =3$ shown in Fig. 3d.

Fig. 5

No-jump region indicating maximum acceptable value of $\alpha$

4 Equivalent damping of the system

In order to define the equivalent damping, multiplying both sides of Eq. (14) with $\varepsilon ^{2}$ and then Eq. (14) can be rewritten as

$$\begin{aligned}&\left[ \left( 2\zeta _1 \omega ^{\alpha -1}b_{1\alpha } A_0^{\alpha -1} +\frac{3}{4}\zeta _2 \omega ^{2}\cos (\omega \tau _0 )A_0^2 \right) ^{2}\right. \nonumber \\&\quad +\,\left( \frac{k}{\omega }b_{1\beta } A_0^{\beta -1} +\frac{3}{4}\zeta _2 \omega ^{2}\sin (\omega \tau _0 )A_0^2\right. \nonumber \\&\left. \left. \quad -\,2\varepsilon \sigma \right) ^{2}\right] \omega ^{2}A_0^2 =f^{2}. \end{aligned}$$

(22)

Therefore, the equivalent damping can be defined as [10]

$$\begin{aligned} \zeta _\mathrm{eq} =\zeta _1 \omega ^{\alpha -1}b_{1\alpha } A_0^{\alpha -1} +\frac{3}{8}\zeta _2 \omega ^{2}\cos (\omega \tau _0 )A_0^2 , \end{aligned}$$

(23)

Only the positive velocity feedback is considered, letting ${\mathrm{d}\zeta _\mathrm{eq} }/{\mathrm{d}\tau _0 }=0$, it is easy to obtain an infinite number of time delays $\tau _0 ={n\pi }/\omega$, $n=0,1,2,\ldots$, at which $\zeta _\mathrm{eq}$ goes to the extreme values

$$\begin{aligned}&\zeta _{\min } =\zeta _1 \omega ^{\alpha -1}b_{1\alpha } A_0^{\alpha -1} -\frac{3}{8}\zeta _2 \omega ^{2}A_0^2 , \nonumber \\&\zeta _{\max } =\zeta _1 \omega ^{\alpha -1}b_{1\alpha } A_0^{\alpha -1} +\frac{3}{8}\zeta _2 \omega ^{2}A_0^2 . \end{aligned}$$

(24)

Obviously, $\zeta _{\max }$ is the equivalent damping of controlled system without time delay $(\tau =0)$; therefore, time delay would weaken the damping effectiveness of velocity feedback and the peak amplitude could rise, which can be confirmed by Fig. 6.

Fig. 6

Comparison of steady-state response of controlled system and uncontrolled system (solid lines controlled system, dashed lines uncontrolled system)

In this paper, only the case of $\omega =1.0$ is considered; hence, as $\tau _0$ lies in $\left[ {0,\pi /2} \right]$ and $\left[ {{3\pi }/2,2\pi } \right]$, the following inequality is satisfied

$$\begin{aligned} \zeta _1 b_{1\alpha } A_0^{\alpha -1} \le \zeta _\mathrm{eq} \le \zeta _1 b_{1\alpha } A_0^{\alpha -1} +\frac{3}{8}\zeta _2 A_0^2 . \end{aligned}$$

Note that $\zeta _1 b_{1\alpha } A_0^{\alpha -1}$ is the equivalent damping ratio of uncontrolled system and $\zeta _1 b_{1\alpha } A_0^{\alpha -1} +{3\zeta _2 A_0^2 }/8$ is the equivalent damping ratio of controlled system without time delay. It means that, compared with the uncontrolled system, the velocity feedback with nonzero time delay has the function of increasing the equivalent damping value and decreasing the response amplitude, but less efficient than without time delay, which can be verified by Fig. 6a–c, g–i.

When $\tau _0$ lies in $\left[ {\pi /2,{3\pi }/2} \right]$, it has

$$\begin{aligned} \zeta _1 b_{1\alpha } A_0^{\alpha -1} -\frac{3}{8}\zeta _2 A_0^2 \le \zeta _\mathrm{eq} \le \zeta _1 b_{1\alpha } A_0^{\alpha -1} . \end{aligned}$$

As a result, the value of the equivalent damping is even smaller than the equivalent damping of the uncontrolled system, and thus, such feedback control fails to suppress the response amplitude in the resonance region.

Figure 6 shows the effects of time delay on the response amplitude according to Eq. (14), which coincides with the variation of equivalent damping $\zeta _\mathrm{eq}$ discussed in above analysis.

5 Effects of feedback parameters on the system response

In this section, the effects of time delay and feedback gain on the steady-state responses are analyzed. Meanwhile, stability analysis and the classification of the steady-state solutions are also discussed. The excitation frequency $\varOmega$ is selected as $\varOmega =1.05$.

5.1 The effects of time delay and feedback gain

Here, two different cases of real-power exponent $\beta$ are considered: small $(\beta =1/3)$ and larger than unity $(\beta =4/3)$; meanwhile, three values of feedback gain $\zeta _2$ ($\zeta _2 =0.03,0.05$ and $0.1$) are chosen to analyze the effects of feedback parameters in each case, as shown in Figs. 7 and 8.

Fig. 7

The effects of time delays on the steady-state response and stability boundaries for $\beta =1/3$, a1 $\zeta _2 =0.03$; b1 $\zeta _2 =0.05$; c1 $\zeta _2 =0.1$ (solid lines steady-state response curves, dashed lines unstable boundaries, dotted lines nodes boundaries)

Fig. 8

The effects of time delays on the steady-state response and stability boundaries for $\beta =4/3$, a2 $\zeta _2 =0.03$; b2 $\zeta _2 =0.05$; c2 $\zeta _2 =0.1$ (solid lines steady-state response curves, dashed lines unstable boundaries, dotted lines nodes boundaries)

The steady-state response curves for the cases of $f=0.1$ and $f=0.2$, respectively, are plotted by the solid lines. And the shaded regions surrounded by the dash lines present the unstable regions. Steady-state solutions, which lie in the unstable region II, are saddle points, the corresponding boundary points are saddle node bifurcation points, the steady-state solutions interior the node region are nodes, and outside this region, they are foci. And the boundaries of the unstable region I are the division lines for stable and unstable nodes and foci. Moreover, the points on the boundaries of the unstable region I are Hopf bifurcation points, which result in the quasi-periodic motion in the original system.

Note that as given by Eq. (14), the response amplitude is a periodic function with period ${2\pi }/\omega$, implying that the dynamical behavior shown in Figs. 7 and 8 presents periodically. By comparing Fig. 7 with Fig. 8, as $\beta <1$ with increasing feedback gain $\zeta _2$, the peak amplitude of the response $A_0$ can be suppressed; meanwhile, the size of unstable region I increases gradually, and the shape of the unstable region II is also different; as $\beta >1$, the distribution of steady-state solutions is quite distinct. As can be seen, the size of the saddle-point regions (Unstable region II) reduces apparently, i.e., the saddle points only lie in the smaller closed loops; meanwhile, the size of the unstable region I is almost unchanged. Thus, the area in which the steady-state solutions are stable on the $\tau$–$A_0$ plane is larger than the case of $\beta <1$. In addition, it is also found that the node regions from one uniform region $(\beta <1)$ becomes to two separate regions which lie in the high amplitude part and lower amplitude part, respectively (Fig. 8a2, b2).

The results in this section indicate that the size, shape and location of stable and unstable regions depend on the system parameters and the feedback control gains. An appropriate choice of the time delay and the feedback gain can suppress the response amplitude and perform an efficient vibration control.

5.2 Selecting feedback parameters for suppressing peak amplitude

It is evident that unavoidable time delays in controllers give rise to complicated dynamics and can produce instability in controlled systems. In this part, we aim to find suitable feedback parameters which can give stable steady-state response and reduce the amplitude peak of the resonance.

Taking the peak amplitude $A_0 =1$ as an example, Fig. 9 shows the relation of time delay $\tau _0$ with feedback gain $\zeta _2$, which are derived by Eq. (14) and depicted by solid lines. In Fig. 9a for the case of $f=0.1$, the critical parameter pairs are closed loops in every period ${2\pi }/\omega$, outside these loops, where the optional parameters regions corresponding to the peak amplitude are smaller than 1. However, not the whole parameter pairs are satisfied the stability conditions outside the loops. According to the stability conditions (18–19), the stable boundaries which are depicted by dash lines can be derived, just outside the shaded regions the pairs are available for stable responses. As a comparison, for the case of $f=0.2$, it is depicted in Fig. 9b, the critical parameter pairs are one continuous curve, which is similar to the results in [18]. And above this curve, where the optional parameters regions corresponding to the peak amplitude smaller than 1 and stable parameter pairs also lie outside the shaded regions.

Fig. 9

Design control parameter pairs (time delay and feedback gain) for suppressing the maximum amplitude and the shaded regions represent the unstable parameter regions

The results obtained in this section suggest that the time delay and feedback gain may be used as a control switch to control the peak amplitude and stability of the steady-state response.

6 Effects of excitation amplitude on the system response

According to the analysis discussed in the previous sections, it is clear that the excitation amplitude $f$ plays a very important role in the response of the system, and thus, it is meaningful to study the effects of $f$ on the response of the system.

The real-power exponent $\beta =1/3$ is taken as an example. From Fig. 10, it is easily found that the amplitude response characteristic can be quite distinct with different values of $f$. For larger $f(f=0.2)$, the steady-state response curve is continuous. As decreasing $f$, the continuous curve is separated into two parts, and it is accompanied with the appearance of the frequency island phenomenon.

Fig. 10

The steady-state response with different excitation amplitudes $f$ for $\beta =1/3$

In order to confirm the response characteristic, the steady-state response as a function of excitation amplitude $f$ is presented in Fig. 11, and $\sigma =0.05,\sigma =0.13, \sigma =0.2$ and $\sigma =0.3$ are taken as examples. When the detuning parameter $\sigma$ is smaller ($\sigma =0.05$ in Fig. 11a), with the increase in $f$, the response amplitude $A_0$ keeps increasing perpetually. However, with larger $\sigma$, the multi-valued response can be observed. Actually, it also includes two kinds of cases: the five-valued response and the triple-valued response. For the case of $\sigma =0.13$, it is a little complicated. In the interval of $f\in [0.02315,0.05641]$, the response is triple-valued; when $f\in [0.05641, \quad 0.08475]$, the characteristic of five-valued response is observed; then, when $f\in [0.08475, 0.16628]$, it occurs triple-valued case again; subsequently, it keeps the single-valued case. For the case of $\sigma =0.2$, as shown in Fig. 11c, only in the interval $f\in [0.02595,0.06798]$ the triple-valued response is observed, which is agreement with the results shown in Fig. 10. For the case of $\sigma =0.3$, as displayed in Fig. 11d, there exist two intervals in which the responses are triple-valued. On one hand, the lower amplitude branch exists jump with smaller $f$ (as shown in Fig. 10 for $f=0.05$); on the other hand, with larger $f$, the steady-state response curve is hardening stiffness property and bends toward right; therefore, it also exists jump phenomenon.

Fig. 11

The steady-state response as a function of excitation amplitude $f$ for $\beta =1/3$. a $\sigma = 0.05$, b $\sigma =0.13$, c $\sigma =0.2$, d $\sigma =0.3$

7 Energy transmissibility of the isolation system with time-delay feedback

For a linear vibration isolation system, the force transmissibility is used to evaluate the effectiveness of the vibration isolator. Note that in a nonlinear isolator, the transmitted signal may contain subharmonic, superharmonic and sometimes chaotic behavior. Thus, the transmissibility defined by the linear theory of vibration isolation should be redefined by using a suitable performance index. Energy transmissibility [22–25] is introduced and defined in [24, 25] as

$$\begin{aligned} T_r (\varOmega )=20\log _{10} \sqrt{\frac{P_R }{P_e }}, \end{aligned}$$

(25)

in which $P_R$ and $P_e$ denote the power of the transmission force and excitation force, respectively. And they can be expressed as

$$\begin{aligned} P_R= & {} \frac{\varOmega }{2\pi }\int _0^{\frac{2\pi }{\varOmega }} {(F_R )^{2}\mathrm{d}t} ,\nonumber \\ P_e= & {} \frac{\varOmega }{2\pi }\int _0^{\frac{2\pi }{\varOmega }} {(F_e )^{2}\mathrm{d}t} . \end{aligned}$$

(26)

where $F_R$ is the restoring force of the isolation system and can be written as

$$\begin{aligned} F_R= & {} 2\zeta _1\, \hbox {sgn}(\dot{x})\left| {\dot{x}} \right| ^{\alpha }+\omega ^{2}x+k\,\hbox {sgn}(x)\left| x \right| ^{\beta }\nonumber \\&+\,\zeta _2 \dot{x}^{3}(\tau -\tau _0 ), \end{aligned}$$

(27)

and the excitation force is assumed as $F_e =f\cos (\varOmega \tau )$. The Runge–Kutta algorithm is employed to estimate energy transmissibility. According to the definition of the energy transmissibility, the smaller of $T_r$, the better the performance of the system.

Figure 12 shows the comparison of the transmissibility with different damping coefficients $\zeta _1$ for uncontrolled system. As increasing $\zeta _1$, the maximum of this transmissibility decreases, moving toward lower frequencies. However, as described in [22], the increase in $\zeta _1$ is detrimental for vibration isolation in frequency band where isolation is required.

Fig. 12

Transmissibility curves with different damping coefficients $\zeta _1$ for uncontrolled system

Furthermore, the real-power exponent $\alpha$ of damping term is found to play an important role in determining the characteristic of power transmission. Figure 13 shows how the energy transmissibility changes with excitation frequency $\varOmega$ for various values of damping exponent $\alpha$. A nonlinear isolator with hardening stiffness property but damping exponent $\alpha \le 2$, in the lower frequency range the transmissibility is positive and the maximum of this transmissibility reduces as increasing $\alpha$. Roughly, the frequency band with negative energy transmissibility appears at the same point. However, it should be noted that the transmissibility for damping exponent $\alpha >2$ illustrated in Fig. 13b is qualitatively different the one appearing in Fig. 13a $(\alpha \le 2)$. The maximum of this transmissibility is almost the same in spite of different value of $\alpha$. Moreover, the transmissibility has a local minimum, the existence of which was also observed by Ruzicka and Derby [26]. Figure 13b additionally shows that this local minimum shifts toward higher frequencies as damping index $\alpha$ is decreased.

Fig. 13

Transmissibility curves with different real-power exponents $\alpha$ for uncontrolled system. a $k =0.2, \zeta _1=0.05$

Additionally, as indicated in Figs. 12 and 13, the critical point with negative energy transmissibility appears at the same point $(\varOmega \approx 1.5492)$, but in Ref. [24], the critical point should be $\sqrt{2}$. The reason for the difference is that the existence of the nonlinear stiffness term $k\,\hbox {sgn}(x)\left| x \right| ^{\beta }$. An example is taken to verify this conclusion. As shown in Fig. 14 for the case of $k=0.0$, by comparing with Fig. 13, it can be seen that the critical point $\varOmega$ is approximate $\sqrt{2}$ rather than 1.5492, which is consistent with Ref. [24]. And the critical point $\varOmega$ for the appearance of the maximum transmissibility also shifts to left and is equal to 1.0 for the case of $k=0.0$.

Fig. 14

Transmissibility curves with different real-power exponents $\alpha$ for $k=0$

Then, for the controlled system without time delay, Fig. 15 compares the effects of the feedback gain $\zeta _2$ on the energy transmissibility. It is seen that with the increase of the feedback, the transmissibility can be suppressed in the resonance region, while it is almost the same in the lower or higher frequency range. Therefore, cubic velocity feedback breaks through the barrier existing in the passive vibration isolation system.

Fig. 15

Transmissibility curves with different feedback gains $\zeta _2$ for controlled system without time delay

For the controlled system with different time delays, Fig. 16 shows the variation of energy transmissibility under feedback gain $\zeta _2 =0.5$. As time delay increases, the maximum of the transmissibility increases and also shifts toward higher frequencies. Meanwhile, the jump will occur when time delay $\tau _0 ={3\pi }/8$. The increase in time delay produces adverse influences on the energy transmissibility as shown in Fig. 16, and thus, the control scheme with very small time delay is preferable to control vibration.

Fig. 16

Transmissibility curves with different time delays for controlled system

8 Conclusions

This paper has been concerned with the time-delayed cubic velocity feedback and base-excited vibration isolators whose elastic properties are modeled by a certain real-power restoring force and a damping force. Based on the method of multiple scales, the steady-state responses and their dynamical stability have been analyzed. The isolation system indicates the softening behavior for under-linear restoring force and hardening behavior for over-linear restoring force, and thus, multi-valued responses with frequency island phenomenon are induced. Particularly, five-valued responses in which two of them are stable have been observed for under-linear restoring force. This result is confirmed by the direct numerical simulation and stability analysis. Meanwhile, the classification of the steady-state solutions is also discussed, and interesting dynamic characteristics are found. In order to avoid the appearance of the jump phenomenon, a design criterion is also derived.

To illustrate the effect of feedback parameters on the system response, the concept of the equivalent damping is proposed. The size, shape and location of stable and unstable regions depend on the system parameters and the feedback control gains. In addition, to control the resonance level under a specified value, the feedback parameters are determined by the frequency response together with stability boundaries which must be utilized to exclude the unstable parameter combinations. Finally, the energy transmissibility of the controlled system is studied. The feedback gain can suppress the maximum of the transmissibility in the resonance region and keep unchanged in the high frequency range where vibration isolation is needed.