1 Introduction

Recent advances in miniaturized and self-contained electronics [1,2,3,4] have led to the fabrication of new batteries, which have a long life span and can work independently. In light of such challenges, vibration-based energy harvesting, notably the piezoelectric energy harvesting, has flourished as a major thrust area of micro power generation. By exploiting the ability of the piezoelectric materials, various devices have been developed to transform mechanical motions directly into electricity in response to mechanical stimuli and external vibrations [5,6,7,8].

The traditional linear energy harvesters [9,10,11,12] were the first adopted design of vibration energy harvesters. The linear energy harvesters have a very narrow effective frequency bandwidth, which limits the applicability and usefulness of VEHs. To resolve this problem, nonlinearity was introduced to extend the bandwidth of the energy harvester [13,14,15,16,17,18]. Erturk et al. [13] proposed a non-resonant piezomagnetoelastic energy harvester to overcome the narrow bandwidth restriction of conventional resonant cantilever configuration. Cottone et al. [14] found numerically and experimentally that the nonlinear oscillators could outperform the linear ones under stochastic excitation. Daqaq [15] illustrated that the stiffness nonlinearity caused the spectral amplitude to decrease and shifted the peaks toward large frequencies. Stanton et al. [16] constructed a nonlinear unimodal energy harvester, which expanded the effective frequency bandwidth in specific conditions by adjusting the force between the magnets and making the energy harvester present soft or hard characteristics. Gammaitoni et al. [17] revealed that the bistable energy harvester is superior to the linear ones under stochastic excitation via numerical simulation and experiment. Erturk et al. [18] studied the bistable piezoelectric energy harvester and proved that the system can produce a drastic periodic or chaotic motion under harmonic excitation with a wide low-frequency range based on theoretical analysis and experiments.

In practice, numerous dynamical systems are associated with the random fluctuating environment or noise excitation [19,20,21,22,23]. It is necessary to consider the influence of random environment excitation on the performance of nonlinear energy harvester. To evaluate the performance of the VEHs under noise, it is important to develop analytical approaches for solving the mean output power. Recently, some analytical techniques have been proposed to study the response of nonlinear energy harvester under Gaussian white noise excitation [24,25,26,27,28,29,30,31]. For example, Daqaq [24] presented the voltage response statistics by using the method of moment and demonstrated that the time constant ratio of the energy harvester plays a key role in developing the performance of VEHs under Gaussian white noise. Jiang and Chen [25,26,27] developed some random vibration methods, such as the equivalent linearization technique, the stochastic averaging method and the Fokker–Planck–Kolmogorov (FPK) equation, to analyze the nonlinear piezoelectric energy harvesters under Gaussian white noise. They demonstrated that quadratic nonlinearity only and quadratic combined with properly cubic nonlinearities can increase the mean-square output. He et al. [28] employed the statistical linearization techniques and a finite element method of FPK equation to investigate the mean steady-state output of the energy harvester. Kumar et al. [29] used the finite element method to solve the FPK equation of the associated bistable energy harvester and analyzed the effects of the system parameters on the mean-square output voltage and power. Jin et al. [30, 31] introduced the generalized harmonic transformation to decouple the electromechanical equations and applied the approximate analytical technique to derive a semi-analytical solution of the corresponding nonlinear VEHs subjected to Gaussian white noise excitation. However, the above-mentioned papers only consider the effects of the additive Gaussian white noise on nonlinear VEHs. To the knowledge of authors, there are no studies investigating the nonlinear VEHs under correlated additive and multiplicative noise excitations.

The aim of this study is to analyze the response and the performance of the nonlinear VEHs subjected to correlated additive and multiplicative Gaussian white noise excitations. In Sect. 2, the governing equations of the nonlinear VEHs under correlated noise excitations are established. In Sect. 3, the generalized harmonic transformation is adopted to simplify the analysis of the coupled equations. From the modified second-order differential equation, an equivalent nonlinear equation for the joint stationary probability density (SPD) of system mechanical states is derived. The \(\hbox {It}\hat{{\hbox {o}}}\) stochastic differential equation of the equivalent nonlinear system is derived through the stochastic averaging method. The approximate expressions of the joint SPD and the mean-square displacement are directly obtained in Sect. 4. In Sect. 5, the effects of system parameters and correlated noise on the performance of the VEHs are discussed based on theoretical analysis and numerical simulation. Meanwhile, the numerical results are presented to validate the effectiveness of the proposed technique. Finally, some conclusions are drawn in Sect. 6.

2 Nonlinear VEHs under correlated noise

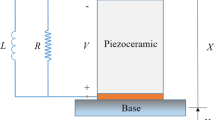
In order to explore the effects of correlated noise on the nonlinear VEHs, we consider a tunable axially loaded energy harvester consisting of a mechanical oscillator coupled to an electric circuit through an electromechanical coupling conversion mechanism [24]. The basic model is shown in Fig. 1. The axial preload P serves to tune the natural frequency of the beam and to introduce a cubic nonlinearity proportional to the magnitude of the axial load.

Fig. 1
figure 1

Schematics of nonlinear energy harvester

Full size image

The coupled equations governing the system mechanical states and the electric voltage are written as

$$\begin{aligned}&m\ddot{{\bar{x}}}+c\dot{{\bar{x}}}+\frac{\hbox {d}{\bar{U}} ({\bar{x}})}{\hbox {d}{\bar{x}}}+\theta {\bar{v}}=-m\ddot{x}_\mathrm{b} , \end{aligned}$$
(1a)
$$\begin{aligned}&C_p \ddot{{\bar{v}}}+\frac{{\bar{v}}}{R}=\theta {\bar{v}}. \end{aligned}$$
(1b)

where \({\bar{x}}\) represents the displacement of the mass m, \({\bar{v}}\) is the voltage measured across the equivalent resistive load R, c is a linear viscous damping coefficient. \(\theta \) is the linear electromechanical coupling coefficient, and \(C_p\) is the effective capacitance of the piezoelectric element. \(\ddot{x}_\mathrm{b}\) is the base acceleration, and the dots represent the derivative with respect to time \(\tau \). The potential function of the mechanical subsystem \({\bar{U}}({\bar{x}})\) takes the following general form:

$$\begin{aligned} {\bar{U}}({\bar{x}})=\frac{1}{2}k_1 (1-r){\bar{x}}^{2}+\frac{1}{4}k_2 {\bar{x}}^{4}. \end{aligned}$$
(2)

where \(k_1\) and \(k_2\) are the linear and nonlinear stiffness coefficients. r is introduced to permit tuning of the linear stiffness around its nominal value. To nondimensionalize Eq. (1), the transformations are introduced as follows

$$\begin{aligned} x=\frac{{\bar{x}}}{l_c }, \quad t=\tau \omega _n , \quad v=\frac{C_p }{\theta l_c }{\bar{v}}. \end{aligned}$$
(3)

in which \(l_c \) is a length scale as the ratio of the area of the equivalent piezoelectric capacitor to the distance between the parallel plates and \(\omega _n =\sqrt{{k_1 }/m}\) is the short-circuit natural frequency of the harvester. Using the above transformations (3), Eq. (1) is rewritten as

$$\begin{aligned}&\ddot{x}+2\xi \dot{x}+\frac{\mathrm{d}U\left( x \right) }{\hbox {d}x}+\kappa ^{2}v = \ddot{x}_\mathrm{b} , \end{aligned}$$
(4a)
$$\begin{aligned}&\dot{v}+av=\dot{x} \end{aligned}$$
(4b)

with

$$\begin{aligned} U(x)=\frac{1}{2}(1-r)x^{2}+\frac{1}{4}\delta x^{4}. \end{aligned}$$
(5)

and

$$\begin{aligned} \xi= & {} \frac{c}{2\sqrt{k_1 m}}, \quad \kappa ^{2}=\frac{\theta ^{2}}{k_1 C_p }, \nonumber \\ \alpha= & {} \frac{1}{RC_P \omega _n }, \quad \delta =\frac{k_2 l_c^{2}}{k_1 }. \end{aligned}$$
(6)

where \(\xi \) is the mechanical damping ratio, \(\kappa \) is the linear dimensionless electromechanical coupling coefficient, \(\alpha \) is the ratio between the mechanical and electrical time constants of the harvester. Moreover, \(\delta \) is the coefficient of cubic nonlinearity. Based on the shape of the potential energy function, the energy harvesters can be classified into two major categories, as shown in Fig. 2. When \(r>1\) and \(\delta >0\), the potential function U(x) is bistable with three equilibrium points. If \(r\le 1\) and \(\delta >0\), the potential function U(x) is nonlinear monostable and has only one equilibrium point.

Fig. 2
figure 2

Plot of potential U(x) for different values of r and \(\delta \)

Full size image

It is known that the output power \(\bar{{P}}={{\bar{v}}^{2}}/R\) is an important quantity in energy harvesting. To get the non-dimensional expression of the output power, we introduce the transformation \(P=\bar{{P}}/(k_1 \omega _n l_c^{2})\) and obtain

$$\begin{aligned} P=\alpha \kappa ^{2}v^{2}. \end{aligned}$$
(7)

In Eq. (4a), \(\ddot{x}_\mathrm{b} =x^{2}\varepsilon _1 (t)+\varepsilon _2 (t)\) is selected as a combination of correlated multiplicative and additive Gaussian white noise, which satisfies the following statistical properties:

$$\begin{aligned} \left\langle {\varepsilon _1 (t)\varepsilon _1 ({t}')} \right\rangle= & {} 2D\delta (t-{t}'),\nonumber \\ \left\langle {\varepsilon _2 (t)\varepsilon _2 ({t}')} \right\rangle= & {} 2Q\delta (t-{t}'),\nonumber \\ \left\langle {\varepsilon _1 (t)\varepsilon _2 ({t}')} \right\rangle= & {} \left\langle {\varepsilon _1 ({t}')\varepsilon _2 (t)} \right\rangle =2\lambda \sqrt{DQ}\delta (t-{t}'). \end{aligned}$$
(8)

where D and Q are the multiplicative and additive noise intensity, respectively. \(\lambda \) is the cross-correlation between the multiplicative and additive noise.

3 The equivalent nonlinear system

To decouple Eq. (4), we integrate Eq. (4b) and give the following explicit expression of the voltage

$$\begin{aligned} v(t)=C_1 e^{-\alpha t}+\int \limits _0^t {e^{-\alpha (t-\tau )}} \dot{x}(\tau )d\tau , \end{aligned}$$
(9)

where the general solution \(C_1 e^{-\alpha t}\) in Eq. (9) has negligible influence on the stationary response. Then, using the transformation \(s=t-\tau \), Eq. (9) can be approximated by

$$\begin{aligned} v(t)\approx \int \limits _0^t {e^{-\alpha s}} \dot{x}(t-s){\hbox {d}}s. \end{aligned}$$
(10)

Using the generalized harmonic function [31], the system states of Eq. (4) are written as

$$\begin{aligned} x(t)= & {} A(t)\cos \phi (t), \end{aligned}$$
(11a)
$$\begin{aligned} \dot{x}(t)= & {} -A(t)\omega (A,\phi )\sin \phi (t), \end{aligned}$$
(11b)
$$\begin{aligned} \phi (t)= & {} \psi (t)+\Theta (t). \end{aligned}$$
(11c)
$$\begin{aligned} \omega (A,\phi )={\hbox {d}}\psi (t)/{\hbox {d}}t . \end{aligned}$$
(12)

where A, B, \(\phi \), \(\psi \) and \(\Theta \) are random processes, and A are related to the mechanical energy H(t). Compared to the system states, the amplitude A, frequency \(\omega \), mechanical energy H and initial phase \(\Theta (t)\) are all slow-varying random processes. Thus, for small s, \(\dot{x}(t-s)\) can be approximated as:

$$\begin{aligned} \dot{x}(t-s)\approx -A(t)\omega (A,\phi )\sin [\omega (A,\phi )(t-s)+\Theta (t)]. \end{aligned}$$
(13)

Expanding the sinusoidal function and substituting Eqs. (11a)–(11b) into Eq. (13) yields:

$$\begin{aligned} \dot{x}(t-s)\approx & {} -\dot{x}(t)\cos [\omega (A,\phi )s]\nonumber \\&+\,x(t)\omega (A,\phi )\sin [\omega (A,\phi )s]. \end{aligned}$$
(14)

Substituting Eq. (14) into Eq. (10) and vanishing the exponential decay terms, one obtains:

$$\begin{aligned} v(t)\approx & {} \frac{\omega ^2 (A,\phi )}{\alpha ^{2}+\omega ^{2} (A,\phi )}x(t)\nonumber \\&+\frac{\alpha }{\alpha ^{2}+\omega ^2 (A,\phi )}\dot{x}(t). \end{aligned}$$
(15)

Then, one can obtain the equivalent uncoupled mechanical equation by substituting Eq. (15) into Eq. (4a)

$$\begin{aligned} \ddot{x}+\zeta \dot{x}+f(x)=x^{2}\varepsilon _1 (t)+\varepsilon _2 (t). \end{aligned}$$
(16)

where

$$\begin{aligned}&\zeta =2\xi +\frac{\kappa ^{2}\alpha }{\alpha ^{2}+\omega ^{2}(A,\phi )},\nonumber \\&f(x)=\frac{\omega ^{2}(A,\phi )\kappa ^{2}}{\alpha ^{2}+\omega ^{2}(A,\phi )}+\frac{\mathrm{d}U(x)}{\hbox {d}x}. \end{aligned}$$

The frequency function can be obtained through the equivalent potential energy

$$\begin{aligned} \omega (A,\phi )=\frac{{\hbox {d}}\psi }{{\hbox {d}}t}=\sqrt{\frac{2\left[ {U^{*}(A)-U^{*}(A\cos \phi )} \right] }{A^{2}\sin ^{2}\phi }}. \end{aligned}$$
(17)

where the equivalent potential energy is given by

$$\begin{aligned} U^{*}=\int \limits _0^{x}f(u){\hbox {d}}u \end{aligned}$$
(18)

According to Eq. (17), the frequency function can be obtained,

$$\begin{aligned} \omega (A,\phi )=\sqrt{\frac{\Lambda _1 +\sqrt{\Lambda _1^2 +4\Lambda _0 }}{2}}. \end{aligned}$$
(19)

where

$$\begin{aligned} \Lambda _1= & {} \kappa ^{2}-\alpha ^{2}+1-r+\delta A^{2}(3+\cos 2\phi )/4,\\ \Lambda _0= & {} \left[ {1-r+\delta A^{2}(3+\cos 2\phi )/4} \right] \alpha ^{2}. \end{aligned}$$

Further integrating Eq. (19) with respect to \(\phi \) from 0 to \(2\pi \) leads to the averaged frequency

$$\begin{aligned} \omega (A)=\omega _0 (A)=\sqrt{1-r+\kappa ^{2}+\delta A^{2}}. \end{aligned}$$
(20)

4 Steady-state response

The equivalent nonlinear system (16) can be solved by stochastic averaging method for light damping and weak random excitation. Equation (11) can be regarded as a set of random van der Pol transformations from \(x,\dot{x}\) to \(A,\Phi \). Substituting Eq. (11) into Eq. (16) yields

$$\begin{aligned} \frac{{\hbox {d}}A(t)}{{\hbox {d}}t}= & {} m_1 (A,\phi ,t)+\sigma _{11} (A,\phi ,t)\varepsilon _1 (t)\nonumber \\&+\,\sigma _{12} (A,\phi ,t)\varepsilon _2 (t), \nonumber \\ \frac{{\hbox {d}}\phi (t)}{{\hbox {d}}t}= & {} m_2 (A,\phi ,t)+\sigma _{21} (A,\phi ,t)\varepsilon _1 (t)\nonumber \\&+\,\sigma _{21} (A,\phi ,t)\varepsilon _2 (t); \end{aligned}$$
(21)

where

$$\begin{aligned} m_1 (A,\phi ,t)= & {} -\frac{\zeta A^{2}\omega ^{2}(A,\phi )}{f(A)}\sin ^2\phi ,\\ m_2(A,\phi ,t)= & {} -\frac{\zeta A\omega { }^2(A,\phi )}{f(A)}\sin \phi \cos \phi .\\ \sigma _{11} (A,\phi ,t)= & {} -\frac{A^{3}}{f(A)}\omega (A,\phi )\cos ^{2}\phi \sin \phi ,\\ \sigma _{12} (A,\phi ,t)= & {} -\frac{A}{f(A)}\omega (A,\phi )\sin \phi .\\ \sigma _{21} (A,\phi ,t)= & {} -\frac{A^{2}}{f(A)}\omega (A,\phi )\cos ^{3}\phi ,\\ \sigma _{22} (A,\phi ,t)= & {} -\frac{1}{f(A)}\omega (A,\phi )\cos \phi . \end{aligned}$$

Based on the theorem proposed by Khasminskii [33], the \((A,\phi )\) can be considered as two-dimensional diffusive Markov processes approximately. Then, the \(\hbox {It}\hat{{\hbox {o}}}\) stochastic differential equations of Eq. (21) are derived as:

$$\begin{aligned} {\hbox {d}}A(t)= & {} a_1 (A,\phi ,t){\hbox {d}}t+b_1 (A,\phi ,t){\hbox {d}}W(t), \end{aligned}$$
(22a)
$$\begin{aligned} {\hbox {d}}\phi (t)= & {} a_2 (A,\phi ,t){\hbox {d}}t+b_2 (A,\phi ,t){\hbox {d}}W(t). \end{aligned}$$
(22b)

where

$$\begin{aligned} a_1 (A,\phi ,t)= & {} m_1 (A,\phi ,t)+\frac{1}{2}b_1 \frac{\partial b_1}{\partial A}+\frac{1}{2}b_2 \frac{\partial b_1 }{\partial \phi },\\ a_2 (A,\phi ,t)= & {} m_2 (A,\phi ,t)+\frac{1}{2}b_1 \frac{\partial b_2 }{\partial A}+\frac{1}{2}b_2 \frac{\partial b_2 }{\partial \phi }, \\ b_1 (A,\phi ,t)= & {} \sqrt{2D\sigma _{11}^2 (A,\phi ,t)+4\lambda \sqrt{QD}\sigma _{11} (A,\phi ,t)\sigma _{12} (A,\phi ,t)+2Q\sigma _{12}^2 (A,\phi ,t)}, \\ b_2 (A,\phi ,t)= & {} \sqrt{2D\sigma _{21}^2 (A,\phi ,t)+4\lambda \sqrt{QD}\sigma _{21} (A,\phi ,t)\sigma _{22} (A,\phi ,t)+2Q\sigma _{22}^2 (A,\phi ,t)}. \end{aligned}$$

and the standard Wiener process \(W\left( t \right) \) is the diffusion process with a null drift coefficient and a unit diffusion coefficient.

Applying the stochastic averaging method to Eq. (22) yields the following expression

$$\begin{aligned} \bar{{a}}_1 (A)= & {} \frac{1}{2\pi }\int \limits _0^{2\pi } {a_1 } (A,\phi ,t){\hbox {d}}\phi ,\nonumber \\ \bar{{a}}_2 (A)= & {} \frac{1}{2\pi }\int \limits _0^{2\pi } {a_2 } (A,\phi ,t){\hbox {d}}\phi , \nonumber \\ \bar{{b}}_1 (A)= & {} \sqrt{\frac{1}{2\pi }\int \limits _0^{2\pi } {b_1^2 } (A,\phi ,t){\hbox {d}}\phi },\nonumber \\ \bar{{b}}_2 (A)= & {} \sqrt{\frac{1}{2\pi }\int \limits _0^{2\pi } {b_2^2 } (A,\phi ,t){\hbox {d}}\phi }. \end{aligned}$$
(23)
Fig. 3
figure 3

Mesh surface of \(E(x^{2})\) and E(P): a \(E(x^{2})-(D,\lambda )\); b \(E(P)-(D,\lambda )\); c \(E(x^{2})-(\delta ,r)\); d \(E(P)-(\delta ,r)\)

Full size image
Fig. 4
figure 4

Mesh surface of \(E(x^{2})\) and E(P): a \(E(x^{2})-(\alpha ,\xi )\); b \(E(P)-(\alpha ,\xi )\); c \(E(x^{2})-(\kappa ,\xi )\); d \(E(P)-(\kappa ,\xi )\)

Full size image
Fig. 5
figure 5

a The joint SPD \(p\left( {x,\dot{x}} \right) \) obtained by using MCS; b the joint SPD \(p\left( {x,\dot{x}} \right) \) obtained from analytical solution (28); c theoretical and simulated results of SPD p(x); d theoretical and simulated results of SPD \(p(\dot{x})\). Symbol “–” denotes the analytical result, and symbol “\(\hbox {o}\)” denotes the MCS result

Full size image
Fig. 6
figure 6

The mean-square displacement \(E(x^{2})\) as a function of: a the ratio of time constant \(\alpha \); b the electromechanical coupling coefficient \(\kappa \); c the mechanical damping ratio \(\xi \); d the cubic nonlinearity \(\delta \); e the tuning parameter of linear stiffness r

Full size image
Fig. 7
figure 7

a PSD of x(t) with different \(\delta \); b PSD of x(t) with different r; c the E(P) versus \(\delta \); d the E(P) versus r

Full size image
Fig. 8
figure 8

a PSD of x(t) with different D and Q; b PSD of x(t) with different \(\lambda \); c the E(P) versus \(\delta \); d the E(P) versus r; e the E(P) versus \(\lambda \)

Full size image
Fig. 9
figure 9

a The E(P) versus \(\alpha \); b The E(P) versus \(\kappa \); c The E(P) versus \(\xi \)

Full size image

Then, the FPK equation associated with Eq. (22a) is of the form

$$\begin{aligned} \frac{\partial p}{\partial t}=-\frac{\partial }{\partial A}\left[ {\bar{{a}}_1 (a)p} \right] +\frac{1}{2}\frac{\partial ^{2}}{\partial A^{2}}\left[ {\bar{{b}}_1^2 (a)p} \right] . \end{aligned}$$
(24)

where \(p=p(a,t\left| {a_0 ,0} \right. )\) is the transition probability density of displacement amplitude, \(\bar{{a}}_1 (a)=\left. {\bar{{a}}_1 (A)} \right| _{A=a} \) and \(b_1^2 (a)=\left. {b_1^2 (A)} \right| _{A=a} \). The initial condition of Eq. (24) is taken as

$$\begin{aligned} p=\delta (a-a_0 ),\;t=0. \end{aligned}$$
(25)

The stationary solution of Eq. (24) for system (16) is of the form:

$$\begin{aligned} p(a)=&\frac{c}{\bar{{b}}_1^2 }\exp \left[ {\int \limits _0^a {\frac{2\bar{{a}}_1 (u)}{\bar{{b}}_1^2 (u)}{\hbox {d}}u} } \right] \nonumber \\ =\,&c(k_1 a+\delta a^{3})({Da^{2}}/{4+Q})^{\zeta _2 }\nonumber \\&\times \left( {\frac{a^{2}+4Q/D}{a^{2}+1-r+\kappa /\delta }} \right) ^{1/2}\exp \left( -\frac{2\sigma \zeta _1 a^{2}}{D}\right) . \end{aligned}$$
(26)

where c is a normalization constant and \(k_1 ={\kappa ^{2}}/(\alpha ^{2}+1)+1-r\), \(\zeta _1 =2\xi +{\kappa ^{2}\alpha }/{(\alpha ^{2}+1)}\), \(\zeta _2 =\zeta _1 {(8\delta Q-2k_1 D)}/{D^{2}}-1\).

From Eq. (26), the SPD of total energy or energy envelop can be obtained as follows:

$$\begin{aligned} p(H)=p(a)\left| {\frac{{\hbox {d}}a}{{\hbox {d}}H}} \right| =\left. {\frac{p(a)}{f(a)}} \right| _{a=U^{*-1}(H)} . \end{aligned}$$
(27)

where \(a=U^{*-1}(H)\) is the inverse function of \(H=U^{*}(a)\). The SPD of displacement and velocity can be further obtained from p(H) as follows:

$$\begin{aligned} p(x,\dot{x})=\left. {\frac{p(H)}{T(H)}} \right| _{{H=y^{2}}/{2+U^{*}(x)}} . \end{aligned}$$
(28)

where T(H) can be obtained from T(a) by the transformation \(H=U^{*}(a)\).

Thus, the mean-square displacement reads:

$$\begin{aligned} E(x^{2})=\int \limits _{-\infty }^{+\infty } {\int \limits _{-\infty }^{+\infty } {x^{2}p(x,\dot{x})dxd\dot{x}} } . \end{aligned}$$
(29)

From Eq. (15), the mean-square value of the electric voltage is given by

$$\begin{aligned} E(v^{2})= & {} E\left[ {\left( {\frac{\omega (A,\phi )}{\alpha ^{2}+\omega (A,\phi )}} \right) } \right] \nonumber \\&+\,E\left[ {\left( {\frac{\alpha \dot{x}}{\alpha ^{2}+\omega (A,\phi )^{2}}} \right) } \right] \nonumber \\&+\,2E\left[ {\frac{\alpha \omega (A,\phi )}{(\alpha ^{2}+\omega (A,\phi ))^{2}}} \right] . \end{aligned}$$
(30)

Then, the mean output power reads:

$$\begin{aligned} E(P)=\alpha \kappa ^{2}E(v^{2}). \end{aligned}$$
(31)

where \(E[\cdot ]\) denotes the mathematical expectation.

5 Results and discussion

To understand the above theoretical results, one can turn to a case study, where the parameters are chosen as \(\xi =0.01\), \(\kappa =0.75\), \(r=0\), \(\delta =0.5\), \(\alpha =0.05\), \(D=0.005\), \(Q=0.005\) and \(\lambda =0.5\). The effects of the correlated noise and the system parameters on the mean-square displacement and the mean output power are explored theoretically and numerically. Moreover, the Monte Carlo simulations (MCS) of the original system (4) are performed to verify the approximate analytical results obtained in Sect. 4.

5.1 Stochastic response analysis

The mean-square displacement \(E(x^{2})\) and the mean output power E(P) are important for the miniaturization of device and the energy harvesting. To understand the above theoretical results (29) and (31), we study the \(E(x^{2})\) and E(P) for different noise intensities and system parameters in Figs. 3 and 4. Figure 3 shows the \(E(x^{2})\) and E(P) increase as the multiplicative noise intensity D increases. However, the cross-correlation \(\lambda \) has no obvious influence on the \(E(x^{2})\) and E(P) (see Figs. 3a, b). It is seen that the \(E(x^{2})\)and E(P) decrease with an increase of \(\delta \). The \(\delta \) degrades the performance of the energy harvester under correlated Gaussian white noise. The \(E(x^{2})\) and E(P) increase with the increase of r in Figs. 3c, d. As the tuning parameter becomes larger, the restoring becomes weaker and the displacement becomes larger.

In Fig. 4, the influences of the system parameters on the performance of the energy harvester are illustrated. It is seen that the \(E(x^{2})\) and E(P) dramatically decrease with the increase of the viscous damping coefficient \(\xi \). When the ratio of time constant \(\alpha \) increases, the \(E(x^{2})\) monotonically decreases. While the E(P) first increases, reaches a maximum and then decreases. In other words, there is an optimal \(\alpha \) to get the maximal E(P), which plays a great realistic significance in the choose of the proper parameters for improving the performance of piezoelectric VEHs. In Fig. 4c, d, as the electromechanical coupling coefficient \(\kappa \) increases, the \(E(x^{2})\) decreases dramatically, while the E(P) first increases and then begins to level off.

5.2 Monte Carlo simulation

The Monte Carlo simulations of system (4) are performed so as to verify the accuracy of the proposed technique and the effectiveness of the analytical results. Figure 5a shows the joint SPD \(p(x,\dot{x})\) obtained from the original system (4) by using the fourth-order Runge–Kutta method, while the result shown in Fig. 5b is calculated by the analytical solution (28). The \(p(x,\dot{x})\) displays an unimodal structure corresponding to the nonlinear monostable potential function. Figure 5c, d, respectively, shows the variances of the SPD p(x) and \(p(\dot{x})\) with different \(\kappa \). It is seen that the height of the single peak is increased with increasing \(\kappa \). Meanwhile, the numerical result of Eq. (4) basically coincides with that of analytical solution (28), which validates the effectiveness and the precision of the proposed technique.

Based on the analytical solution (29) and the MCS results, the effects of the system parameters on the mean-square displacement of piezoelectric VEHs are shown in Fig. 6. It is seen that the approximate analytical results in Eq. (29) well coincide with the numerical solutions of Eq. (4).

In the following, the PSD and the output power of piezoelectric VEHs are calculated numerically as shown in Figs. 7, 8 and 9. In Fig. 7a, the spectral amplitudes decrease and the peaks shift toward large frequency as the \(\delta \) increases. That is, the \(\delta \) expands the spectral response. Figure 7c shows that the E(P) decreases with an increase of \(\delta \). The influences of the r on the PSD and the E(P) are shown in Fig. 7b, d. The peaks of the PSD shift toward small frequency with the increase of r as shown in Fig. 7c. However, the r does not broaden the spectral response. The E(P) increases with the increase of r.

The effects of the correlated multiplicative and additive noise on the PSD of displacement and the E(P) are shown in Fig. 8. Figure 8a, b depicts the dependence of the PSD on the correlated noise. In Fig. 8a, the spectral amplitudes increase and the peaks shift toward large frequency as the multiplicative noise intensity D increases. The PSD is changed from one peak to two peaks with the increase of additive noise intensity Q. Figure 8b shows that the cross-correlation \(\lambda \) has no obvious effect on the PSD of displacement. In Fig. 8c, e the E(P) increases slightly as the D and \(\lambda \) increase. While the E(P) increases remarkably as the Q increases. That is, the additive noise intensity Q plays an active role in improving the E(P). Figure 9a demonstrates that the E(P) shows a resonance-like structure with the increase of \(\alpha \). In Fig. 9b, the E(P) first increases and then begins to level off as the \(\kappa \) increases. The E(P) decreases with the increase of the \(\xi \) as shown in Fig. 9c. Obviously, the MCS results shown in Figs. 6, 7, 8 and 9 well coincide with the analytical results shown in Figs. 3 and 4.

6 Conclusions

In this paper, a stochastic averaging technique combined with the generalized harmonic transformation is applied to analyze the response of the nonlinear VEHs under the correlated Gaussian white noises. Using the generalized harmonic transformation, the equivalent nonlinear system is derived according to the modified nonlinear system. The averaged \(\hbox {It}\hat{{\hbox {o}}}\) stochastic differential equation for the equivalent nonlinear system is established through the stochastic averaging method. Then, the joint SPD of system is obtained by solving the corresponding FPK equation. The influences of the system parameters on the mean-square displacement and the mean output power are discussed in detail. It is shown that the stiffness-type nonlinearities can broaden the harvester’s bandwidth, but have almost no influence on the mean-square displacement and hardly enhance the expected value of the mean output power. Furthermore, the mean output power increases with the increase of the noise intensities and the cross-correlation between noises. That is, the correlated noise plays an active role in improving the performance of the nonlinear VEHs. The curve of the mean output power first increases with increasing the ratio of time constant, reaches a maximum and then decreases. In other words, the mean output power can get the maximum at an optimal ratio of time constant. This phenomenon is of great significance to energy harvesting because the ratio of time constant is important to characterize performance of nonlinear vibration energy harvester under random excitations [34]. Finally, numerical results demonstrate the accuracy of the proposed technique and the effectiveness of the analytical solution.