1 Introduction

Pipe are extensively applied in oil and chemical industries, power hydraulics systems, mechanical engineering and biological engineering, and nuclear industry. The flow-induced vibration and noise are inevitable due to strong fluid–pipe interaction [1,2,3,4,5,6,7,8,9,10]. In this context, conventional linear vibration isolators, such as tuned mass dampers (TMD), were applied to suppress the unwanted vibration and noise. However, the inherent narrow band performance limits their application. Moreover, the nature frequency of the pipe is highly dependent on the flow speed, which commonly changes in practice. Therefore, the passive and adaptive vibration suppression is a challenge to date.

Nonlinear energy sink (NES) has recently attracted a great deal of interest due to their ability to provide essentially nonlinear stiffness, leading to exciting applications in robust vibration suppression, energy harvesting, and advanced control. Therefore, increasing interest has been paid to NES, for example, Vakakis group [11,12,13] realized the targeted energy transfer (TET) in beams, plates, and rods. Zulli and Luongo [14] successfully reduced the transverse vibration of a nonlinear elastic string. Chen et al. [15] implemented a NES in the truss core of a sandwich plate; they showed that the shock-induced large amplitude can be reduced. Luongo and Zulli [16] presented a mixed multiple scale/harmonic balance algorithm to analyze a multi-degree-of-freedom system subjected to external excitation. Yan et al. [17] realized partial and complete vibration suppression of supersonic flutter. Blanchard et al. [18] completely suppressed the transverse vortex-induced vibration of a linearly sprung circular cylinder immersed in an incompressible flow by using a rotational NES. Zhang et al. [19, 20] utilized a NES to stabilize the transverse vibration of an axially moving string and a beam. Yang et al. [21] used a NES to suppress the excessive vibration of a satellite during launching. In our previous work [22], we applied a NES to absorb the vibration energy of a pipe conveying fluid. We realized the robust vibration suppression when the flow speed of the fluid changed from low to high. Lee [23, 24] numerically and experimentally demonstrated the vibration suppression of aeroelastic instability by using the concept of broadband passive TET. On the other hand, the general concept of NES was extended to the field of energy harvesting in the past few years, which enables non-ideal structures maintain at a stable periodic orbit and achieve maximized harvesting efficiency [25,26,27,28,29].

However, the conventional NES has a limitation, that is, the inherent input energy threshold. The TET happens only if the input energy (initial condition) exceeds a certain value, otherwise, the energy absorbing efficiency of the NES is relative low. For example, in our previous work [22], we have achieved a maximum efficiency 87% when the initial impulse of the pipe is 0.2. If the threshold is not succeeded, the efficiency drops to \(\sim 40\%\). Therefore, some researchers devoted to modify the NES for achieving a lower threshold or higher efficiency. For example, Gendelman et al. integrated two conventional NESs and found that the threshold value of the combined NES is greatly minimized [30]. Kong et al. [31] adopted a modified NES with nonlinear damping to improve the vibration reduction performance. Wei et al. [32] presented a novel targeted energy transfer mechanism; they took NES as an actuator to keep the system vibrating on the optimal state. As a result, their optimized NES completely removed the threshold, absorbing most vibration energy for extremely wide range of initial impulse. AL-Shudeifat [33] designed a highly efficient nonlinear energy sink by using an asymmetric magnet configuration. In their work, considerable enhancement of the energy dissipation was achieved. Al-Shudeifat [34] designed a highly efficient nonlinear sink by integrating a negative and essentially a nonlinear stiffness component.

The above-mentioned research has suggested that it is possible to further enhance the performance of adaptive vibration suppression of a pipe conveying fluid by using a novel NES. The pipes are the idea test platform to verify the robustness of the enhanced NES, as the flow speed is inherent variable. In this paper, we aim to seek a modified NES with a lower threshold, high energy dissipation efficiency, and robustness.

Fig. 1
figure 1

Schematic of a fluid-conveying pipe with an enhanced nonlinear energy sink

Full size image

2 Equation of motion

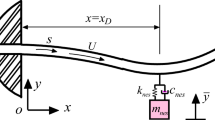
A simple supported pipe made of viscoelastic materials is shown in Fig. 1; an enhanced NES system is implement on the pipe. In this configuration, two side springs are initially compressed at the horizontal position, and therefore, some potential energy can be pre-stored. At the upstairs and downstairs stable equilibrium positions, the springs are unloaded, which means there is no stretched or compressed deformation. This configuration produces a linear negative stiffness and nonlinear stiffness. The detailed derivation for the nonlinear stiffness can be found in Ref. [34]. The governing equation of the pipe–NES system takes the following form:

$$\begin{aligned}&\eta \hbox {EI}\frac{\partial ^{5}W(X,T)}{\partial X^{4}\partial T}+\hbox {EI}\frac{\partial ^{4}W(X,T)}{\partial X^{4}}\nonumber \\&\quad +\,M_\mathrm{f} V^{2}\frac{\partial ^{2}W(X,T)}{\partial X^{2}} \nonumber \\&\quad +\,2M_\mathrm{f} V\frac{\partial ^{2}W(X,T)}{\partial X\partial T}+(M_\mathrm{f} +m_\mathrm{p} )\frac{\partial ^{2}W(X,T)}{\partial T^{2}} \nonumber \\&\quad +\,\left\{ K_{\mathrm{NL}} (Z-Z_\mathrm{c} )^{3}-K_\mathrm{a} (Z-Z_\mathrm{c} )\right. \nonumber \\&\left. \quad +\,C\left[ \frac{\partial W(d,T)}{\partial T}-\frac{\partial Y(T)}{\partial T}\right] \right\} \delta (X-D)=0 \end{aligned}$$
(1a)
$$\begin{aligned}&m_\mathrm{NES} \frac{\partial ^{2}Y}{\partial T^{2}}-K_{\mathrm{NL}} (Z-Z_\mathrm{c} )^{3}+K_\mathrm{a} (Z-Z_\mathrm{c} )\nonumber \\&\quad +\,C\left( \frac{\partial Y}{\partial T}-\frac{\partial W}{\partial T}\right) =0, \end{aligned}$$
(1b)

where W(X, T) and Y(X, T) are the oscillating transverse displacement of the pipe and the enhanced NES, respectively. \(Z=W-Y\), \(L{=}\sqrt{L_0^2 \hbox {+}Z_\mathrm{c}^2 }\). EI and \(\eta \) are the bending stiffness and the viscoelastic coefficient. \(M_\mathrm{f}\), \(m_\mathrm{p}\), and \(m_\mathrm{NES} \) are the masses of the fluid, pipe, and the nonlinear energy sink, respectively. V is the flow speed and C is the NES dissipation. \(K_{\mathrm{NL}}\) and \(K_{\mathrm{a}}\) are the nonlinear and negative stiffness. D is the NES position. It is noted that system (1) is significantly different from our previous work [22], in which we utilized only one conventional NES with essential nonlinearity (in this paper, we call it type I NES). In contrast, we integrate negative and nonlinear stiffness for improving vibration isolation performance. The net nonlinear force of the two springs can be expressed as [34]:

$$\begin{aligned} F_{\mathrm{net}}\approx & {} -2k(Z-Z_\mathrm{c} )\left[ {1-\frac{L}{\sqrt{\left( L_0^2 +(Z-Z_\mathrm{c} )^{{2}}\right) }}} \right] \\\approx & {} K_\mathrm{a} (Z-Z_\mathrm{c} )-K_{\mathrm{NL}} (Z-Z_\mathrm{c} )^{3}, \end{aligned}$$

where \(K_\mathrm{a} {=}2k\left( \frac{L}{L_{0} }-{1}\right) \), \(K_{\mathrm{NL}} =\frac{kL}{L_0^3 }\).

Introduce the following non-dimensional quantities:

$$\begin{aligned}&w = \frac{W}{L},\quad {x = \frac{X}{L}}\quad {y = }\frac{Y}{L}\nonumber \\&{t = \frac{T}{{{L^2}}}}\quad \sqrt{\frac{{\hbox {EI}}}{{{M_\mathrm{f}} + {M_\mathrm{p}}}}} ,\quad {\beta = }\frac{{{M_\mathrm{f}}}}{{{M_\mathrm{f}} + {m_\mathrm{p}}}}\nonumber \\&\alpha = \frac{\eta }{{{L^2}}}\sqrt{\frac{{\hbox {EI}}}{{{M_\mathrm{f}} + {m_\mathrm{p}}}}} ,\nonumber \\&\varepsilon = \frac{{{m_\mathrm{NES}}{L^2}}}{{\sqrt{{\hbox {EI}}({M_\mathrm{f}} + {M_\mathrm{p}})} }},\quad {v = {\hbox {VL}}\sqrt{\frac{M}{{\hbox {EI}}}} },\nonumber \\&{{k_{\mathrm{NL}}} = \frac{{{K_{\mathrm{NL}}}{L^6}}}{{\hbox {EI}}}}\nonumber \\&\lambda = \frac{{{L^2}C}}{{\sqrt{{\hbox {EI}}({M_\mathrm{f}} + {M_\mathrm{p}})} }},\quad {{k_\mathrm{a}} = \frac{{{K_\mathrm{a}}{L^4}}}{{\hbox {EI}}}} ,\nonumber \\&{{z_\mathrm{c}}} = \frac{{{Z_\mathrm{c}}}}{L},\quad {d = \frac{D}{L}}. \end{aligned}$$
(2)

Substituting Eq. (2) into Eq. (1) yields the following dimensionless form:

$$\begin{aligned}&\alpha \frac{\partial ^{5}w(x,t)}{\partial x^{4}\partial t}+\frac{\partial ^{4}w(x,t)}{\partial x^{4}}+v^{2}\frac{\partial ^{2}w(x,t)}{\partial x^{2}}\nonumber \\&\quad +\,2\sqrt{\beta }v\frac{\partial ^{2}w(x,t)}{\partial x\partial t}+\frac{\partial ^{2}w(x,t)}{\partial t^{2}} \nonumber \\&\quad +\,\left\{ k_{\mathrm{NL}} [z(d,t)-z_\mathrm{c} (t)]^{3}-k_\mathrm{a} [z(d,t)-z_\mathrm{c} (t)]\right. \nonumber \\&\left. \quad +\,\lambda \left[ \frac{\partial w(d,t)}{\partial t}-\frac{\partial \bar{{y}}(t)}{\partial t}\right] \right\} \delta (x-d)=0. \nonumber \\&\varepsilon \frac{\partial ^{2}\bar{{y}}(t)}{\partial t^{2}}-k_{\mathrm{NL}} [z(d,t)-z_\mathrm{c} (t)]^{3}+k_\mathrm{a} [z(d,t)-z_\mathrm{c} (t)]\nonumber \\&\quad +\,\lambda \left[ \frac{\partial \bar{{y}}(t)}{\partial t}-\frac{\partial y(d,t)}{\partial t}\right] =0. \end{aligned}$$
(3)

3 The Galerkin method

The standard Galerkin method is taken to approximate discrete the system (3); thus, the displacement expansion is assumed as [35, 36]

$$\begin{aligned} w(x,t)=\sum _{r=1}^N {\phi _r (x)q_r (t)} , \end{aligned}$$
(4)

where \(\phi _r (x)\) are the mode function for the free undamped vibrations of the pipe, which satisfies the associated boundary conditions. \(q_{r}\) (t) are the generalized coordinates. Substituting Eq. (4) into Eq. (3) yields

$$\begin{aligned}&\sum _{r=1}^N \left[ \lambda _r^4 \alpha \phi _r (x)\dot{q}_r (t)+\lambda _r^4 \phi _r (x)q_r (t)+v^{2}{\phi }''_r (x)q_r (t)\right. \nonumber \\&\left. \quad +\,2v\sqrt{\beta }{\phi }'_r (x)\dot{q}_r (t)+\phi _r (x)\ddot{q}_r (t)\right] \nonumber \\&\quad +\,\left\{ k_{\mathrm{NL}} \left[ \sum _{r=1}^N {\phi _r (d)q_r (t)-\bar{{y}}(t)} \right] ^{3}\right. \nonumber \\&\left. \quad -\,k_\mathrm{a} \left( \sum _{r=1}^N {\phi _r (d)q_r (t)-} \bar{{y}}(t)-z_\mathrm{c} \right) \right. \nonumber \\&\left. \quad +\,\lambda \left[ \sum _{r=1}^N {\phi _r (d)\dot{q}_r (t)-} \dot{\bar{{y}}}(t)\right] \right\} \delta (x-d)=0 \end{aligned}$$
(5a)
$$\begin{aligned}&\varepsilon \ddot{\bar{{y}}}(t)+k_{\mathrm{NL}} \left[ \bar{{y}}(t)-\sum _{r=1}^N {\phi _r (d)q_r (t)} \right] ^{3}\nonumber \\&\quad +\,k_\mathrm{a}\left( \sum _{r=1}^N {\phi _r (d)q_r (t)-} \bar{{y}}(t)-z_\mathrm{c}\right) \nonumber \\&\quad +\,\lambda \left[ \dot{\bar{{y}}}(t)-\sum _{r=1}^N {\phi _r (d)\dot{q}_r (t)} \right] =0, \end{aligned}$$
(5b)

where \(\phi _r =\sqrt{2}\sin \lambda _r x\), \(\lambda _r =r\pi \) if a pipe is simply supported. The factor \(\sqrt{2}\) is used for ensuring orthonormality. Multiply Eq. (6) by \(\phi _s (x)\) and integrate over the domain [0, 1] results in

$$\begin{aligned}&\delta _{sr} \ddot{q}_r (t)\hbox {+}\lambda _r^4 \alpha \delta _{sr} \dot{q}_r (t)+\lambda _r^4 \delta _{sr} q_r (t)\nonumber \\&\quad +\,v^{2}c_{sr} q_r (t)+2v\sqrt{\beta }b_{sr} \dot{q}_r (t) \nonumber \\&\quad +\,\left\{ k_{\mathrm{NL}} \left[ \sum _{r=1}^N {\phi _r (d)q_r (t)-} \bar{{y}}(t)\right] ^{3}\right. \nonumber \\&\left. \quad -\,k_\mathrm{a} \left[ \sum _{r=1}^N {\phi _r (d)q_r (t)-} \bar{{y}}(t)\right] , \right. \nonumber \\&\left. \quad +\,\lambda \left[ \sum _{r=1}^N {\phi _r (d)\dot{q}_r (t)-} \dot{\bar{{y}}}(t)\right] \right\} \phi _r (d)=0 \end{aligned}$$
(6a)
$$\begin{aligned}&\varepsilon \ddot{\bar{{y}}}(t)+k_{\mathrm{NL}} \left[ \bar{{y}}(t)-\sum _{r=1}^N {\phi _r (d)q_r (t)} \right] ^{3}\nonumber \\&\quad +\,k_\mathrm{a} \left[ \sum _{r=1}^N {\phi _r (d)q_r (t)-} \bar{{y}}(t)\right] \nonumber \\&\quad +\,\lambda \left[ \dot{\bar{{y}}}(t)-\sum _{r=1}^N {\phi _r (d)\dot{q}_r (t)} \right] =0, \end{aligned}$$
(6b)

where

$$\begin{aligned}&\delta _{sr} =\int _0^1 {\phi _s } (x)\phi _r (x)\mathrm{d}x\quad {b_{sr} =\int _0^1 {\phi _s } (x){\phi }'_r (x)\mathrm{d}x} \nonumber \\&c_{sr} =\int _0^1 {\phi _s } (x){\phi }''_r (x)\mathrm{d}x. \end{aligned}$$
(7)

\(\delta _{sr}\) is the Kronecker’s delta and \(\lambda _{r}\) is the \(r\hbox {th}\) eigenvalues for the free undamped vibrations of the pipe. Equation (6) can be written as a compact form:

$$\begin{aligned}&\mathrm{M}\ddot{q}_r (t)+\mathbf{C}\dot{q}_r (t)+\mathbf{K}q_r (t) \nonumber \\&\quad +\left\{ k_{\mathrm{NL}} \left[ \sum _{r=1}^N {\phi _r (d)q_r (t)-} \bar{{y}}(t)\right] ^{3}\right. \nonumber \\&\left. \quad -\,k_\mathrm{a} \left[ \sum _{r=1}^N {\phi _r (d)q_r (t)-} \bar{{y}}(t)\right] \right. \nonumber \\&\left. \quad +\,\lambda \left[ \sum _{r=1}^N {\phi _r (d)\dot{q}_r (t)-} \dot{\bar{{y}}}(t)\right] \right\} \phi _r (d)=0 \end{aligned}$$
(8a)
$$\begin{aligned}&\varepsilon \ddot{\bar{{y}}}(t)+k_{\mathrm{NL}} \left[ \bar{{y}}(t)-\sum _{r=1}^N {\phi _r (d)q_r (t)} \right] ^{3}\nonumber \\&\quad +\,k_\mathrm{a} \left[ \sum _{r=1}^N {\phi _r (d)q_r (t)-} \bar{{y}}(t)\right] \nonumber \\&\quad +\,\lambda \left[ \dot{\bar{{y}}}(t)-\sum _{r=1}^N {\phi _r (d)\dot{q}_r (t)}\right] =0, \end{aligned}$$
(8b)

where

$$\begin{aligned}&\mathbf{\mathrm{M}}=\delta _{sr} ,\quad {\mathbf{C}=} 2v\sqrt{\beta }b_{sr} +\lambda _r^4 \alpha \delta _{sr} ,\nonumber \\&{\mathbf{K}=} \lambda _r^4 \delta _{sr} +v^{2}c_{sr} =\omega _r^2, \end{aligned}$$
(9)

where M, C, and K are the mass, damping, and stiffness matrices, and \(\omega _{r}\) is the \(r\hbox {th}\) natural frequency of the pipe. It is noted from matrix K that the natural frequency of the pipes is dependent on the flow velocity.

In our previous work, we concluded that the type I NES with an essential nonlinearity can lock in multiple natural frequencies for varying flow velocities. By using NES, we have achieved a high efficiency (\(\sim 87\%\)) vibration isolation performance. However, there are two limitations of the research; first, the type I NES has an energy threshold (initial impact velocity \({X}>0.14\)) that means type I NES is functional for a sufficient large initial impact. Second, the energy dissipation efficiency is not high. In this paper, we integrate both the negative and essentially nonlinear stiffness to overcome these limitations.

Fig. 2
figure 2

a Time history of the pipe’s response with typical NES, enhanced NES, and without NES. b Wavelet spectrum for the enhanced NES. c Wavelet spectrum for type I NES

Full size image

4 Effectiveness of NES

In this section, we will examine the effectiveness of our enhanced NES for stabilizing the pipe. It is obvious that Eq. (8) cannot be solved by using analytical methods. Here, we use numerical methods to simulate Eq. (8). In this section, an initial impact is imposed to initiate the oscillation:

$$\begin{aligned} \dot{q}_1 (0)=X, q_r (0)=\dot{q}_2 (0)=\cdots =\dot{q}_r =\bar{{y}}(0)=\dot{\bar{{y}}}(0)=0. \end{aligned}$$

In the following simulation, we take the system parameters as \(k_\mathrm{a} =3.36\), \(k_{\mathrm{NL}} =22.56\), \(d=0.4,\alpha =0\), \(\lambda =0.1\), \(v=1\), \(\beta =0.4\). It is shown in Fig. 1 that our enhanced NES is ungrounded; as discussed in [37], the smaller mass ratio \(\varepsilon \) is more effective for triggering TET; therefore, we choose a smaller value \(\varepsilon =0.1\). This makes the enhanced NES as an excellent candidate as a lightweight vibration absorber. We note that the mass effect was also discussed in acoustic diode system [38], in which the one-way energy transfer takes place from large to small oscillator. Therefore, the enhanced NES is assumed to be lightweight, which means that \(m_\mathrm{NES} /(M_\mathrm{f} +m_\mathrm{p} )<<1\). Moreover, it is well known that the NES is activated only when the magnitude of the input energy exceeds a threshold, which limits the practical application for the primary structure subjects to low and intermediate impact velocities. For comparison, we utilize a smaller value \(X=0.1\), comparing with our previous work using classical NES [22].

Figure 2 shows the time history of the pipe’s response with and without NES. The blue line denotes the pipe without NES; the black dotted line denotes the response of the pipe with a type I NES (classical NES). The red line denotes the response of the pipe with an enhanced NES. It is shown in Fig. 2a that a significant reduction in the vibration amplitude of the pipe conveying flowing fluid is achieved by both type I NES and the present enhanced NES. Moreover, it is obvious that the enhanced NES can dissipate vibration energy with a higher efficiency. To confirm this observation, we use the wavelet transform (WT) to examine the enhancement. As shown in Fig. 2b, the WT spectra identify the transient dominant frequency components. The transient frequency is 9.86, which is corresponding to the first linear frequency obtained from Eq. (10), \(\omega _1 =\sqrt{\pi ^{4}-v^{2}\pi ^{2}}\). It is clear that both the type I NES and enhanced NES engage in 1:1 resonance from the initial stage of the transient dynamics. Specially, it is shown in Fig. 2c that the enhanced NES has a shorter and stronger resonance process, suggesting a considerable enhanced efficiency. In contrast, the type I NES takes more time to stabilize the system.

To further demonstrate the vibration suppression performance, we change the flow velocities as \(v=0.5\) and 1.5. As shown in Fig. 3, the enhanced NES can reduce the vibration amplitude of the pipe significantly, suggesting the adaptive and robust effect. We next introduce the energy dissipation as

$$\begin{aligned} E_\mathrm{NES} (t)=\frac{\lambda \int _0^t {\left[ \dot{\bar{{y}}}(\tau )-\sum \limits _{i=1}^N {\Phi _i (d)\dot{q}_i (t)} \right] ^{2}\mathrm{d}\tau } }{(X^{2}/2)}. \end{aligned}$$
(10)

Figure 4 depicts the dependence of the vibrational energy portion absorbed by the NES as a function of the dimensionless stiffness \(k_{\mathrm{a}}\). It is shown that when the stiffness increases, the energy efficiency first increases and then decreases after reaching the maximum value 98.19% at \(k_{\mathrm{a}}=21.5\). This value is higher than our previous work, in which we achieved a maximum value 87% [21]. This demonstrates that the combination of the negative stiffness and nonlinearity enables the NES that engages resonance in a lower and broader frequency range. Therefore, a faster transient energy transfer takes place.

Figure 5 shows the effect of mass ratio \(\beta \) on the energy dissipation. As the mass ratio \(\beta \) increases, the fluid mass contained in pipe increases. It is seen that the energy dissipation portion slightly decreases from 95.8 to 93.8% for any possible value \(0<\beta <1\). That implies that the mass ratio is not sensitive to the enhanced NES performance.

Figure 6 presents the optimal position for the NES implementation. It is shown that the energy dissipated by the enhanced NES is highly dependent on d. We note a region with much higher values when the enhanced NES is placed near center of the pipe. In contrast, significantly lower values are observed when the enhanced NES is placed near the boundaries of the pipe where all modes possess zero displacements. This result suggests that an enhanced NES must be optimized implemented at an optimized position, where a major portion of the energy can be absorbed.

Fig. 3
figure 3

Robustness of the enhanced NES for different flow speed

Full size image
Fig. 4
figure 4

Dependence of the portion of vibration energy absorbed and dissipated by the enhanced NES as a function of the NES stiffness k

Full size image
Fig. 5
figure 5

Dependence of the portion of vibration energy absorbed and dissipated by the enhanced NES as a function of the mass ratio \(\beta \)

Full size image
Fig. 6
figure 6

Dependence of the portion of vibration energy absorbed and dissipated by the enhanced NES as a function of implemented position d

Full size image

5 Conclusions

We presented an enhanced nonlinear energy sink for vibration suppression of a pipe conveying fluid. The enhanced NES is designed by a special configuration with geometric nonlinearity. As a result, it is found that such a device can be treated as a bi-stable energy sink with linear and nonlinear negative stiffness components. We show that an excellent, robust performance is achieved for suppressing the pipe vibration. This is due to the combining role of the negative and cubic stiffness that enables the cascaded strong resonance capture. Our enhanced NES can further reduce the threshold of the input energy and absorb the vibration in a faster way. In the optimization, we realized a maximum energy absorb efficiency 98.19%, which is much higher than our previous work.