1 Introduction

1.1 Application background and literature review

A clear understanding of the dynamics of miniaturized beams is important for the design of microelectromechanical systems (MEMS) (Younis 2011; Park and Gao 2006; Sedighi and Shirazi 2015; Ebrahimi and Hosseini 2017; Dai et al. 2015b), resonators (Nayfeh and Younis 2005), sensors (Lun et al. 2006; McFarland and Colton 2005), microswitches (Ghayesh et al. 2013; Rahaeifard and Ahmadian 2015; Hu et al. 2004; Younis et al. 2003; Nayfeh et al. 2005), microfluidic devices (Yin et al. 2011; Sparks et al. 2009; Zhang et al. 2016b; Kural and Özkaya 2015; Hu et al. 2016), energy harvester (Hu et al. 2011) and so on.

Due to the recent development in microengineering and micromechanics, microbeams coupled with various multi-field actuations have received considerable attention from researchers around the world. One typical example of microstructures interacted with fluid field is the system of microbeams containing internal fluid flow, which becomes the key components in many microstructures and microsystems and has widespread applications, including fluid storage, drug delivery, microfluidic devices, micromachined fountain pen, biomolecular and nanoparticle detection and so forth (Wang et al. 2016; Sparks et al. 2009; Kural and Özkaya 2015; Lee et al. 2010; Olcum et al. 2015; Hanay et al. 2012; Burg et al. 2007). Since the performance of the fluid-loaded microbeam is directly related to its dynamical behavior, it is not surprising that many studies have focused on the dynamics of the system of microbeams containing internal fluid flow.

The investigations of the static and dynamic behaviors of microbeams conveying fluid are based on either classical or non-classical size-dependent models. There exist a few studies utilizing the theories of conventional (classical) continuum mechanics to predict the vibration characteristics and stability of microbeams/micropipes conveying fluid. For instance, Rinaldi et al. (2010) conducted a theoretical analysis of microscale resonators containing internal fluid flow and investigated the effects of flow velocity on damping, stability and frequency shift of the system. Zhong et al. (2016) analyzed the thermoelastic damping in a fluid-conveying microbeams for designing microresonators with high quality factor. Zhang et al. (2016a) studied the stability, frequency shift and energy dissipation of suspended microchannel resonators conveying fluid with opposite directions. Guo et al. (2010) considered the non-uniformity of the flow velocity distribution in fluid-conveying micropipes caused by the viscosity of internal fluid.

The first investigation of the size-dependent microbeams conveying fluid based on non-classical continuum mechanics was carried out in 2010. Some of the remarkable contributions in this area were made by Yang et al. (2014), Mashrouteh et al. (2016), Hosseini et al. (2016), Dehrouyeh-Semnani et al. (2016), Li et al. (2016), Setoodeh and Afrahim (2014), Arani et al. (2014), Wang and his co-workers (Wang et al. 2013; Wang 2010; Xia and Wang 2010). The dynamics of microbeams with supported or clamped-free ends, linear, nonlinear and chaotic dynamics, microbeams with straight or curved configuration, and size-dependent properties are some aspects of the considered issues.

In some cases, microbeams conveying fluid are piezoelectrically (Abbasnejad et al. 2015), electromagnetically (Rhoads et al. 2013), electrochemically and/or electrostatically actuated (Kim et al. 2016) in engineering applications. Several investigations have been carried out regarding the dynamic characteristics of microbeams coupling fluid flow and other field forces. For instance, Abbasnejad et al. (2015) presented the stability analysis of a fluid-conveying microbeam, which is axially loaded with a pair of piezoelectric layers locating at its top and bottom surfaces; they found that imposing voltage on the piezoelectric layers can significantly suppress the effect of fluid flow on the vibration characteristics of the system. Kim et al. (2016) modeled electrostatically actuated hollow microtube resonators as one kind of microbeams conveying fluid. Amiri et al. (2016) proposed a theoretical approach to investigate the stability of smart microbeams conveying fluid based on the magneto-thermo-electro-elasticity theory; they showed that the stability of microbeams can be controlled by varying magnetoelectric potential. In addition, Dai et al. (2015a) and Yan et al. (2016) recently studied the dynamical characteristics of fluid-conveying microbeams actuated by electrostatic force, showing that both pull-in and flow-induced instabilities can occur in such dynamical system. Among these valuable studies, only few were devoted to the topic of dynamical behavior of electrostatically actuated microbeams conveying fluid. If any, they mainly explored the stability rather than the dynamic oscillations of the microbeam, because they either neglect the geometric nonlinearities associated with the cantilever’s deformation or approximate the electrostatic force via Taylor series expansion which leads to insufficient results especially in the case of large deflections.

Indeed, the prediction of dynamic responses of electrostatically actuated microbeams is also important for MEMS applications. For instance, if the microbeam is subjected to a time-varying voltage, the system may undergo dynamic pull-in instability rather than static pull-in instability (see, e.g., Nayfeh and Younis 2005; Younis 2011). In such case, the displacements of the microbeam are generally time dependent and the dynamic oscillations need to be considered.

In this study, the system under consideration is an electrostatically actuated microbeam conveying fluid with clamped-free boundary conditions. The lateral motion of the microbeam is coupled with the internal fluid flow. Thus, this is a typical nonlinear fluid–structure interaction system. For a cantilevered microbeam conveying fluid, the system is nonconservative, and hence, flutter instability is possible, which is known as a dynamic form of instability. When the microbeam is undergoing flutter, the displacement of the microbeam is time dependent, and hence, the analysis of dynamic responses of the system is necessary.

1.2 Contributions of the present work

In the present study, for the first time, the fully nonlinear coupled equations of motion are proposed for exploring the instability mechanism and dynamic oscillations of a cantilevered microbeam conveying fluid under electrostatic actuation. The geometric nonlinearities associated with the possible large-amplitude motions of the microbeam are essentially included in the mathematical model. These geometric nonlinearities have not been accounted for in previous studies on dynamical behaviors of electrostatically actuated microbeams conveying fluid. To ensure accurate and converged results, a high-dimensional discretized model will be constructed while keeping the highly nonlinear electrostatic load term intact.

In addition, it will be shown that the internal fluid flow has a significant effect on the stability and dynamic responses of the microbeam under electrostatic actuation. Thus, the knowledge gained from this multi-field-coupled system can be potentially applied in controlling the electromechanical behaviors of microbeam-based MEMS via changing the fluidic parameters (e.g., flow velocity).

2 Analytical model

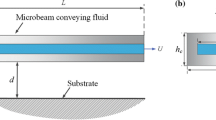
The dynamical system diagrammatically shown in Fig. 1 is comprised of a cantilevered microbeam of length L, subjected to internal fluid flow with a steady velocity U. In the derivation of the equation of motion of the coupled system, the internal fluid flow is characterized by a plug-flow regime first. Then, the obtained equation of motion will be extended to perform an analysis for microbeams containing laminar fluid flow.

Fig. 1
figure 1

a Schematic of an electrostatically actuated microbeam containing internal fluid flow; b cross-section view of the fluid-loaded microbeam

Full size image

In particular, a biased voltage V is applied to the microbeam, causing an electrostatic attraction between the microbeam and the substrate. Thus, the microbeam can be actuated by the electrostatic interaction between the microbeam and the substrate underneath. Generally, the value of the electrostatic force is associated with the deflection of the microbeam.

To model the dynamics of the microbeam, a Hamiltonian derivation of the equation of motion is briefly presented here. According to the discussion by Paidoussis (1998) and Benjamin (1961), the Hamilton’s principle for this dynamical system can be written as

$$\delta \int\nolimits_{{t_{1} }}^{{t_{2} }} {L_{0} {\text{d}}t} = \int\nolimits_{{t_{1} }}^{{t_{2} }} {\left\{ {MU\left[ {\left( {\frac{{\partial \varvec{r}_{L} }}{\partial t}} \right) + U\varvec{\tau}_{L} } \right] \cdot \delta \varvec{r}_{L} } \right\}} {\text{d}}t$$
(1)

where δ is the variational symbol; L 0 is the Lagrangian of the system (L 0 = T b  + T f −V b −V e , T b and V b being the kinetic and potential energies associated with the microbeam, T f the kinetic energy of the enclosed fluid and V e the electric energy); r L and τ L represent, respectively, the position vector and the tangential unit vector at the tip end of the microbeam; M is the mass of fluid per unit length; and t is the time.

The kinetic energy of the microbeam and the fluid may be, respectively, evaluated by (Paidoussis 1998)

$$T_{b} = \frac{1}{2}m\int\nolimits_{0}^{L} {\left( {\dot{x}^{2} + \dot{W}^{2} } \right)} \;{\text{d}}s,\quad T_{f} = \frac{1}{2}M\int\nolimits_{0}^{L} {\left[ {\left( {\dot{x} + Ux^{\prime } } \right)^{2} + \left( {\dot{W} + UW^{\prime } } \right)^{2} } \right]} \;{\text{d}}s$$
(2)

where ( )· and ( )′ denote the derivative with respect to time, t, and the curvilinear coordinate along the centerline of the deformed microbeam, s, respectively; x is the axial coordinate in the sense of Eulerian description; m is the mass of the microbeam per unit length; and W(s, t) is the lateral deflection of the microbeam.

The potential energy of the system consists of two components: the strain energy V b and the electric energy V e ; they are given by (Paidoussis 1998; Yan et al. 2016)

$$V_{b} = \frac{1}{2}\int\nolimits_{0}^{L} {EI\kappa^{2} } {\text{d}}s,\;\;V_{e} = \frac{{\varepsilon V^{2} }}{2}\int\nolimits_{0}^{L} {\frac{{b_{0} }}{d - W}} {\text{d}}s$$
(3)

where EI is the flexural rigidity of the microbeam, κ is the curvature of the microbeam and can be expressed as \(\kappa = \frac{{W^{\prime \prime } }}{{\sqrt {1 - W^{\prime 2} } }}\) according to the inextensible condition, ε is the dielectric constant of the gap medium, d is the gap distance between the microbeam and the substrate and b 0 is the outside cross-section width of the microbeam.

Finally, recalling that \(\dot{x} \sim 0\), and \(x^{\prime } \simeq 1 - \frac{1}{2}W^{\prime 2}\), substituting Eqs. (2) and (3) into (1) and making use of the standard variational techniques and the boundary conditions for a cantilever, after some manipulation, the nonlinear equation of motion is found to be

$$\begin{aligned} & (m + M)\ddot{W} + 2MU\dot{W}^{\prime } \left( {1 + W^{\prime 2} } \right) + MU^{2} \left( {1 + W^{\prime 2} } \right)W^{\prime \prime } + c\dot{W} \\ & \quad + \,EI\left[ {W^{ \prime\prime\prime\prime } \left( {1 + W^{\prime 2} } \right) + 4W^{\prime } W^{\prime \prime } W^{ \prime\prime\prime } + W^{\prime \prime 3} } \right] + W^{\prime } \int\nolimits_{0}^{s} {(m + M)\left( {\dot{W}^{\prime 2} + W^{\prime } \ddot{W}^{\prime \prime } } \right){\text{d}}s} \\ & \quad - \,W^{\prime \prime } \left[ {\int\nolimits_{s}^{L} {\int\nolimits_{0}^{s} {(m + M)\left( {\dot{W}^{\prime } + W^{\prime } \ddot{W}^{\prime \prime } } \right){\text{d}}s{\text{d}}s} + \int\nolimits_{s}^{L} {\left( {2MUW^{\prime } \dot{W}^{\prime } + MU^{2} W^{\prime } W^{\prime \prime } } \right){\text{d}}s} } } \right] + q(W) = 0 \\ \end{aligned}$$
(4)

where q(W) is the electric force due to the applied voltage. In Eq. (4), the viscous damping effect has been included and c is the viscous damping coefficient. The nonlinear force q(W) exerted on the deformable microbeam is given by

$$q\left( W \right) = - \frac{{\varepsilon b_{0} V^{2} }}{{2\left( {d - W} \right)^{2} }}$$
(5)

Defining the following quantities

$$\xi = \frac{s}{L},\;w = \frac{W}{d},\;\tau = \left( {\frac{EI}{m + M}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \frac{t}{{L^{2} }},\;u = \left( {\frac{M}{EI}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} UL,\;\beta = \frac{M}{M + m},\;\sigma = \frac{{cL^{2} }}{{\left[ {(m + M)EI} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }},\;\alpha = \frac{{\varepsilon b_{0}^{{}} L^{4} }}{{2EId^{3} }},\;\phi = \left( {\frac{d}{L}} \right)^{2}$$
(6)

Equation (4) may be written in the following dimensionless form

$$\begin{aligned} w^{\prime \prime \prime \prime} + u^{2} w^{\prime \prime } + 2u\sqrt \beta \dot{w}^{\prime } + \sigma \dot{w} + \ddot{w} \hfill \\ + \phi \left\{ {\left( {w^{{^{ \prime\prime\prime\prime } }} w^{\prime 2} + 4w^{\prime } w^{\prime \prime } w^{ \prime\prime\prime } + \eta^{\prime \prime 3} } \right) + u^{2} w^{\prime 2} w^{\prime \prime } + 2u\sqrt \beta \dot{w}^{\prime } w^{\prime 2} + w^{\prime } \int\nolimits_{0}^{\xi } {\left( {\dot{w}^{\prime 2} + w^{\prime } \ddot{w}^{\prime } } \right){\text{d}}\xi } } \right. \hfill \\ \left. { - w^{\prime\prime } \left[ {\int\nolimits_{\xi }^{1} {\int\nolimits_{0}^{\xi } {\left( {\dot{w}^{\prime 2} + w^{\prime } \ddot{w}^{\prime } } \right){\text{d}}\xi } {\text{d}}\xi + \int\nolimits_{\xi }^{1} {\left( {2u\sqrt \beta w^{\prime } \dot{w}^{\prime } + u^{2} w^{\prime } w^{\prime \prime } } \right){\text{d}}\xi } } } \right]} \right\} - \frac{{\alpha V^{2} }}{{\left( {1 - w} \right)^{2} }} = 0 \hfill \\ \end{aligned}$$
(7)

in which ( )· and ()′ are now derivatives with respect to non-dimensional τ and ξ.

As discussed by Guo et al. (2010), for laminar internal fluid flow, either the mean flow velocity u or the mass ratio β in Eq. (7) should be viewed as the ‘equivalent’ value. The concepts of ‘equivalent mean flow velocity’ and ‘equivalent mass ratio’ were introduced firstly by Guo et al. (2010). The relationship between the equivalent parameters (\(\tilde{u}\) and \(\tilde{\beta }\)) and the usually used parameters (u and β) was defined by \(\tilde{u} = \sqrt {\alpha^{*} } u\) and \(\tilde{\beta } = \beta /\alpha^{*}\)(Guo et al. 2010), with α * being a coefficient related to the flow velocity profile representing the size effect of microflow. For laminar flows in a circular micropipe, the value of α * can be exactly calculated and was found to be 4/3 (Guo et al. 2010). By using the concepts of equivalent mean flow velocity and equivalent mass ratio, Eq. (7) is also valid for the system of a microbeam conveying viscous (laminar) fluid flow.

It should be pointed out that several nonlinear inertial terms appear in Eq. (7). However, these nonlinear inertial terms can be converted to equivalent stiffness and velocity-dependent terms via a perturbation technique (Paidoussis 1998). In this way, Eq. (7) can be further written as

$$w^{\prime \prime \prime \prime} + u^{2} w^{\prime \prime } + \sigma \dot{w} + 2u\sqrt \beta \dot{w}^{\prime } + \ddot{w} + N_{1} (w) + N_{2} (w) = 0$$
(8)

where the nonlinear terms \(N_{1} (w)\) and \(N_{2} (w)\) are given by

$$N_{1} (w) = - \frac{{\alpha V^{2} }}{{\left( {1 - w} \right)^{2} }}$$

and

$$\begin{aligned} N_{2} (w) = \phi \left\{ {2u\sqrt \beta \dot{w}^{\prime } w^{\prime 2} + u^{2} w^{\prime \prime } w^{\prime 2} + 3w^{\prime } w^{\prime \prime } w^{ \prime\prime\prime } + w^{\prime \prime 3} } \right. \hfill \\ + w^{\prime } \int\nolimits_{0}^{\xi } {\left( {\dot{w}^{\prime 2} - 2u\sqrt \beta w^{\prime } \dot{w}^{\prime \prime } - u^{2} w^{\prime } w^{ \prime\prime\prime } + w^{\prime \prime } w^{ \prime\prime\prime\prime } } \right){\text{d}}\xi } \hfill \\ - w^{\prime \prime } \int\nolimits_{\xi }^{1} {\int\nolimits_{0}^{\xi } {\left( {\dot{w}^{\prime 2} - 2u\sqrt \beta w^{\prime } \dot{w}^{\prime \prime } - u^{2} w^{\prime } w^{ \prime\prime\prime } + w^{\prime \prime } w^{ \prime\prime\prime\prime } } \right){\text{d}}\xi } {\text{d}}\xi } \hfill \\ \left. { - w^{\prime \prime } \int\nolimits_{\xi }^{1} {\left( {2u\sqrt \beta w^{\prime } \dot{w}^{\prime } + u^{2} w^{\prime } w^{\prime \prime } + w^{\prime \prime } w^{ \prime\prime\prime } } \right){\text{d}}\xi } } \right\} \hfill \\ \end{aligned}$$
(9)

If we compare Eq. (8) to those given by Dai et al. (2015b) or Yan et al. (2016), it is clear that the former has accounted for geometric nonlinearities associated with the deformation of the microbeam. In order to discretize the infinite-dimensional system, the Galerkin’s method is introduced; thus, we have

$$w\left( {\xi ,\tau } \right) = \sum\limits_{r = 1}^{\infty } {\varphi_{r} \left( \xi \right)q_{r} \left( \tau \right)}$$
(10)

where q r (τ) are the rth generalized coordinates and φ r (ξ) are the corresponding dimensionless eigenfunctions of a cantilevered beam. It is noted that the series in Eq. (10) may be truncated at a suitably large value of r = N. Upon substituting Eqs. (10) into (8), multiplying by φ s (ξ) and integrating over the domain [0, 1], one obtains

$${\mathbf{\ddot{q} + C\dot{q} + Kq + f(q,\dot{q}) = 0}}$$
(11)

where q is the generalized displacement vector and the elements of all coefficient matrices may be computed from the integrals of the eigenfunctions φ i (ξ) and their derivatives. Once q has been calculated from Eq. (11), the lateral deflection of the microbeam [w(ξ,τ)] can be expressed using Eq. (10).

3 Results

It has been reported that when N = 4 is taken, it is capable of obtaining convergent results for nonlinear oscillations of cantilevered beams\pipes conveying fluid (Paidoussis 1998). Therefore, in the following analysis, we will truncate the series of Eq. (10) at N = 4. In all cases, the maximum flow velocity considered is below u = 10; unless otherwise stated, several key system parameters were fixed to be: α = 3.9, σ = 0.0239 (Farokhi and Ghayesh 2016), ϕ = 0.25, and β = 0.2. Moreover, by converting Eq. (11) into the first-order form, the transformed state equation can be solved by using a fourth-order Runge–Kutta integration algorithm. In all calculations, q 1(0) is the only nonzero value of initial conditions.

To demonstrate the reliability of the theoretical model and the calculation procedure, some typical results are compared with the measured data given by Hu et al. (2004) and the numerical results provided by Dai et al. (2015a). Then, a set of calculations will be made to explore the nonlinear dynamics of the electrostatically actuated microbeam conveying fluid, as described in the rest of this section.

3.1 Validation of the present results

To validate the reliability of the present model and calculation procedure, we firstly predict the static tip-end deflections of the electrostatically actuated microbeam without internal fluid flow. A set of experimental parameters were selected, which are given in Table 1. Based on these data, Hu et al. (2004) have experimentally examined the static defections of the microbeam.

Table 1 The experimental parameters of a microbeam (Hu et al. 2004)
Full size table

As shown in Fig. 2a, the dashed line represents the result obtained using the full nonlinear model governed by Eq. (11) with N = 4 and q 1(0) = −0.2, and the center symbols + represent the experimental results provided by Hu et al. (2004). It is observed that the results predicted by the present model agree well with the experimental data.

Fig. 2
figure 2

a Comparison between theoretical and experimental results for an electrostatically actuated microbeam defined by Hu et al. (2004); the nonzero term of initial conditions is selected to be q 1(0) = − 0.2. b Instability region in the (u, α 1/2 V) plane for an electrostatically actuated microbeam conveying fluid with α = 1.3119: comparison between the present results and Dai et al.’s GDQR results (2015a); the zero initial conditions were selected for calculations

Full size image

As another example, a microbeam system in the presence of internal fluid flow is considered. The microbeam under consideration is conveying fluid in the laminar flow regime. The same problem has been analyzed by Dai et al. (2015a) and by Yan et al. (2016). Some calculations were done with varying u and α 0.5 V, while keeping other system parameters in accordance with those utilized by Dai et al. (2015a). The results using zero initial conditions are plotted in Fig. 2b, showing the system to be stable below the instability boundaries, unless u or α 0.5 V is large enough to give rise to instability. Agreement between the present results and the GDQR (generalized differential quadrature rule) results (Dai et al. 2015a) is achieved.

3.2 Instability mechanism of electrostatically actuated microbeams conveying fluid

Although the mechanism of pull-in and flow-induced instabilities of an electrostatically actuated microcantilever conveying fluid has been recently studied by Dai et al. (2015a) and Yan et al. (2016), a few words here will nevertheless be useful.

Based on Eq. (11), the critical voltage, V cr, as a function of u is calculated and shown in Fig. 3, for q 1(0) = 0. It is clear that V cr strongly depends on u. Furthermore, the V cr curve (instability boundary) displays an inverted V shape. In the range of 0 ≤ u ≤ 4.58, the expected form of instability of the microbeam is the well-known ‘pull-in’ instability, which has been widely reported in the studies of electrostatically actuated microbeams. In the range of 5.27 ≤ u ≤ 5.6, however, the preferred form of instability is flutter, which is a type of flow-induced instability. It should be stressed that, at u = 5.6, the flutter could occur even for zero voltage. It is then of interest to find that, in the range of 4.58 ≤ u ≤ 5.27, the pull-in and flutter instability would concurrently occur. Thus, in the region just above the dashed line shown in Fig. 3, one might have expected that the dynamic response of the microbeam may be interesting, as will be discussed in the later subsections.

Fig. 3
figure 3

The critical voltage for pull-in and/or flutter instabilities, V cr, of a cantilevered microbeam conveying fluid, as a function of flow velocity u, for q 1(0) = 0

Full size image

Accordingly, the instability of the microbeam is related to both the electric force and the internal fluid flow. As shown in Fig. 3, the presence of applied voltage can destabilize the system of microbeams conveying fluid, while the occurrence of internal fluid with low flow velocity would stabilize the system of electrostatically actuated microbeams. It should be mentioned that pull-in and flow-induced instabilities could concurrently occur in a certain range of flow velocity, which has not been pointed out in previous studies.

3.3 Effect of initial conditions on the instability boundaries

It is noted that for the electrostatically actuated microbeam conveying fluid, two types of instability are possible, as discussed in the above subsection. The results shown in Fig. 3 correspond to the microbeam system with q 1(0) = 0. It is of interest to examine the effect of initial conditions on the instability boundaries of the microbeam system in this subsection.

The various instability boundaries for four different initial conditions, namely q 1(0) = −0.2, 0, 0.1 and 0.2, are plotted in Fig. 4. It is observed that the initial conditions have no obvious effect on the instability boundaries for two ranges of flow velocity (e.g., 2 ≤ u ≤ 4.7 and 5.3 ≤ u ≤ 5.6). As shown in Fig. 4b, however, in the range of 0 ≤ u ≤ 2 approximately, the initial conditions with negative value of q 1(0) can increase the critical voltage, while those with positive value of q 1(0) would decrease V cr, comparing to that under initial condition of q 1(0) = 0. Interestingly, as the flow velocity is successively increased in the range of 0 ≤ u ≤ 2, the difference among the results based on these four initial conditions becomes weak. Thus, the internal fluid flow seems to be able to eliminate the effect of initial conditions on the pull-in instability boundaries to some extent.

Fig. 4
figure 4

The critical voltage for pull-in and/or flutter instabilities, V cr, of a cantilevered microbeam conveying fluid, as a function of flow velocity u, for various initial conditions: a for a range of 0 ≤ u ≤6, b for a range of 0 ≤ u ≤2 and c for another range of 4.6 ≤ u ≤5.3

Full size image

In another range of 4.7 < u < 5.3 approximately, it is observed from Fig. 4c that the initial conditions have a slight effect on the critical voltage. It is noted that, again, the initial conditions with negative q 1(0) can increase the critical voltage, while those with positive q 1(0) would decrease V cr.

Therefore, within the flow velocity range of 0 ≤ u ≤ 2 or 4.7 < u < 5.3, an initial perturbation of displacement may change the instability boundary. In other words, an originally stable (unstable) system may become unstable (stable) due to initial perturbations. This finding can enhance one’s understanding of the stability mechanism of electrostatically actuated microbeams conveying fluid.

3.4 Dynamic responses near the instability boundaries

The motivation for investigating the dynamic responses in the vicinity of the instability boundaries comes from two reasons. The first is to obtain theoretical results for comparing the dynamical behavior of a stable system to that of an unstable system in the region just beyond instability threshold. The second is provided by the findings shown in Fig. 3 for electrostatically actuated microbeam conveying fluid: The cantilevered system may lose stability via flutter and pull-in instabilities as well as the combination of both. Hence, it is of interest to discover the distinct of dynamic responses near the onset of instability for these three types of instability. Since the initial conditions do not qualitatively affect the instability mechanism of the system (see Fig. 4), in this subsection, the nonzero term of initial conditions is defined by q 1(0) = 0.2. Typical results are presented in the form of phase portraits and time trace diagrams in Figs. 5, 6, 7 and 8.

Fig. 5
figure 5

Phase portraits and time trace diagrams near the pull-in instability boundary, for u = 0: a V = 0.47 and b V = 0.473

Full size image
Fig. 6
figure 6

Phase portraits and time trace diagrams near the pull-in instability boundary, for u = 1.5: a V = 0.699 and b V = 0.700

Full size image
Fig. 7
figure 7

Phase portraits and time trace diagrams near the boundary associated with both flutter and pull-in instabilities, for u = 5.1: a V = 1.765 and b V = 1.766

Full size image
Fig. 8
figure 8

Phase portraits and time trace diagrams near the flutter instability boundary, for V = 0.6: a u = 5.5 and b u = 5.62

Full size image

The dynamic response of the system near the pull-in instability boundary for u = 0 is illustrated in Fig. 5. For V = 0.47, at which the microbeam system is stable, it is seen from Fig. 5a that the oscillation of the microbeam is slowly damped with time going on. It may be foreseen that the microbeam would become motionless after a long time. For V = 0.473, which is slightly larger than the critical voltage, the phase portrait and time trace diagram (see Fig. 5b) show that the microbeam occurs pull-in during a short time; the dimensionless tip-end displacement of the microbeam is one eventually.

Figure 6a, b shows examples of the dynamic responses of the microbeam system subjected to a low flow velocity (u = 1.5), for two slightly different values of applied voltage. Clearly, the microbeam is stable when V = 0.699 (see Fig. 6a) and unstable when V = 0.7 (see Fig. 6b). Comparing the results shown in Fig. 6a with that in Fig. 5a, it is immediately found that the oscillation of the former is damped more quickly and the microbeam is finally deflected at a static configuration. The quickly damped oscillation is attributed to the fact that, for u = 1.5, the internal fluid flow induces positive damping in all modes of the system, which accelerates the decay of the oscillation.

Similar results for u = 5.1 are illustrated in Fig. 7a, b, for V = 1.765 and 1.766, respectively. By referring to Figs. 3 and 4, in the case of u = 5.1, the microbeam would be concurrently subjected to flutter and pull-in instabilities at a critical voltage. When V = 1.765, the system is stable, as shown in Fig. 7a. For a slightly larger voltage, i.e., V = 1.766, the system becomes unstable (see Fig. 7b). The dynamic response of the microbeam shown in Fig. 7b is interesting. The microbeam experiences a periodic-like motion around a nonzero position during the transient response. This transient periodic-like motion, however, is amplified quickly and the pull-in behavior takes place thereafter.

The results for V = 0.6 and two different higher flow velocities are shown in Fig. 8, where u = 5.5 corresponds a stable system, while u = 5.62 is for a microbeam subjected to flutter instability. The phase portrait and time trace diagram shown in Fig. 8b indicate that the oscillation of the microbeam is periodic (limit cycle motion), which is not amplified with time going on. This dynamic feature is clearly different from that shown in Fig. 7b.

3.5 Global dynamics of electrostatically actuated microbeams conveying fluid

In Sect. 3.4, the dynamical behavior of the microbeam near the instability boundaries has been discussed. In the following, it is of interest to explore the global dynamics of the electrostatically actuated microbeam conveying fluid, by examining the possible responses of the microbeam for several typical values of applied voltage and a wide range of flow velocity. For that purpose, we select q 1(0) = 0 as the initial condition. Three different values of V will be chosen for calculations for the nonlinear equation of (11).

One of the efficient ways to understand the global dynamics of the microbeam system is by looking at the bifurcation diagrams, consisting of successive amplitudes of the oscillations. Such diagrams are shown in Figs. 9, 10 for the problem at hand, to clarify the essential behavior of the microbeam. The variable parameter is u, while the output utilized to display bifurcations is the tip-end displacement of the microbeam.

Fig. 9
figure 9

Bifurcation diagram of the dimensionless tip-end displacement versus u for V = 0.5

Full size image
Fig. 10
figure 10

Bifurcation diagram of the dimensionless tip-end displacement versus u for V = 1.2

Full size image

3.5.1 Nonlinear dynamics of microbeams conveying fluid with small voltage

The nonlinear dynamics of the electrostatically actuated microbeam conveying fluid will be examined first for small voltages. It is noted from the stability boundaries given in Fig. 3, for small voltages (e.g., V = 0.5), as the flow velocity increases, the system undergoes a Hopf bifurcation at a critical value, shown at the right side of Fig. 3.

The bifurcation diagram for V = 0.5 with various flow velocities is plotted in Fig. 9. It is seen that when the flow velocity is lower than 5.8, the microbeam is stable. Thus, it has a static deflection due to the presence of electric force. The static deflection of the microbeam decreases with increasing flow velocity, up to u = 5.8, indicating that the internal fluid flow has a stabilization effect on the system in this range of flow velocities. At u = 5.8, the occurrence of Hopf bifurcation yields a limit cycle motion, which is asymmetric due to the biased electric force.

With the increase in flow velocity beyond the Hopf bifurcation, interestingly, the size of the limit cycle motion is amplified first and then decreased. The decrease trend of the oscillation amplitudes with increasing flow velocity can be related to the oscillation frequencies of the dynamic system: A higher oscillation frequency is always accompanied with a smaller amplitude. For instance, the oscillation frequency for u = 10 is about 1.67 times that for u = 8; however, the former size of limit cycle motion is much smaller than the latter one.

3.5.2 Nonlinear dynamics of microbeams conveying fluid with moderate voltage

A bifurcation diagram for V = 1.2 is shown in Fig. 10. It is noted that for such moderate value of V, there is an instability–restabilization–instability sequence as the flow velocity increases from 0 to 10 (see Fig. 3). Indeed, the results shown in Fig. 10 indicate that the microbeam is subjected to a pull-in instability with a final displacement of w(1,τ) = 1 in the range of 0 ≤ u ≤ 4. In the range of 4 ≤ u ≤ 5.47, the microbeam is stable with a static deflection, and the value of this deflection decreases with increasing flow velocity. At about u = 5.47, the Hopf bifurcation occurs and an asymmetric limit cycle motion is generated. Similarly, it is observed that the size of the limit cycle motion is decreased when the flow velocity is gradually increased in the range of 8 ≤ u ≤ 10.

3.5.3 Nonlinear dynamics of microbeams conveying fluid with large voltage

More interesting dynamical behavior is obtained if the applied voltage is fairly large (e.g., V = 1.8). In this case, the microbeam is unstable for all flow velocities, as shown in Fig. 3.

A bifurcation diagram for V = 1.8 is shown in Fig. 11, where the amplitudes of steady displacement versus flow velocity are plotted. It is seen that in the range of 0 ≤ u ≤ 9.15 approximately, the microbeam is pulled in, and hence, the tip-end displacement is equal to 1 eventually. With increasing flow velocity (u) to 9.16, the asymmetric limit cycle motion (period-1 motion) occurs. At this bifurcation point, however, the size of the limit cycle motion is not zero but suddenly amplified. This is significantly different from that shown in Figs. 9 and 10, where the size of the limit cycle motion is close to zero at the Hopf bifurcation point.

Fig. 11
figure 11

Bifurcation diagram of the dimensionless tip-end displacement versus u for V = 1.8

Full size image

Lastly, it is instructive to look at the phase portrait and time trace diagram in the vicinity of u = 9.15 and V = 1.8. Typical results for u = 9.15 and V = 1.8 are plotted in Fig. 12. From this figure, it is noted that the microbeam would be subjected to a transient motion of chaos. That is to say, the motion is chaotic-like for a time, but eventually become a divergent motion. Here, this transient chaos is termed as ‘chaotic divergence.’

Fig. 12
figure 12

Phase portraits and time trace diagram for u = 9.15 and V = 1.8, showing a chaotic divergence motion

Full size image

4 Conclusions

In this paper, the theoretical modeling and nonlinear dynamics of an electrostatically actuated microbeam conveying fluid have been presented. The nonlinear governing equation of the cantilevered microbeam is derived with consideration of the nonlinearities associated with both large-amplitude oscillations and nonlinear electrostatic force. Due to the concurrent presence of internal fluid flow and electric field, either pull-in or flow-induced instability is possible. The dynamic responses near and away from the instability boundaries are analyzed based on extensive calculations.

Compared with previous studies, several new dynamical features of this system have been found. The first new feature is that the combination of both pull-in and flow-induced instabilities can occur in this dynamical system for moderate flow velocities. The second new feature is associated with the effect of initial conditions on the instability boundaries. Results show that the instability boundaries can be affected by initial conditions for low and moderate flow velocities. The third new feature displayed is that various motions may occur beyond the instability boundaries. It is found that the microbeam may be pulled in beyond the static pull-in instability boundaries. When the flow velocity is higher than the threshold of flutter instability, however, limit cycle motions would occur. Of particular interest is that the microbeam may undergo transient periodic-like and chaotic divergence motions when the flow velocity and applied voltage fall in the unstable parameter region, which is beyond the combined boundary of the pull-in and flutter instabilities.

Consequently, it is shown that the internal fluid flow plays an important role in such microfluidic system coupling with electrostatic force, which demonstrates that the electromechanical behavior of the microbeam is sensitive to the internal fluid flow. Therefore, the knowledge gained from this study is also expected to offer potential applications in controlling the electromechanical behaviors of microbeam-based MEMS via changing the fluidic parameters (e.g., flow velocity).