Vibration control of a pipe conveying fluid under external periodic excitation using a nonlinear energy sink

Abstract

This paper investigates the effects of a smooth nonlinear energy sink (NES) on the vibration suppression of a fixed-fixed pipe conveying fluid under excitation of an external harmonic load. Pipe is modeled using the Euler–Bernoulli beam theory, and the NES has an essentially nonlinear stiffness and a linear damping. The required conditions that allow for saddle-node bifurcation, Hopf bifurcation and strongly modulated responses (SMRs) in the system are studied. The SMR phenomenon in the system response is considered as the most efficient regime of response for vibration mitigation. In addition, the effects of damping value of the NES, location of the NES on the pipe, magnitude of the external force and the fluid velocity on the dynamical behavior of the system are investigated. The Runge–Kutta and complexification-averaging methods are employed for numerical and analytical solutions, respectively. Finally, the efficiency of an optimal NES in the energy reduction of the primary system is compared to that of an optimal linear absorber. It can be seen that reducing the distance between the NES and the pipe supports decreases the probability of occurrence of the SMR and weak modulated response; moreover, it provides suitable conditions for occurrence of the saddle-node bifurcation. Furthermore, increasing the fluid velocity decreases the amplitude of steady-state response of the system and extends the unstable region of the response. The results show that the middle of the pipe is the best position for connecting the NES to a fixed-fixed pipe conveying fluid under the external periodic excitation.

1 Introduction

Mathematical modeling and vibration mitigation of a pipe conveying fluid have been the subject of a great number of scientific investigations over years. Indeed, the results of the conducted researches can be applied to a wide range of engineering fields, such as oil transportation facilities, municipal water supply systems, risers, nuclear steam supply systems and heat exchangers. Starting with the linear equations of motion for pipes [1], several refined models have been presented leading to highly nonlinear models of pipes [2]. In order to get a broad overview, one can consider [3–5]. Generally, the principal reason for a pipe vibration that causes instability of the dynamic response and large deformations is interactions of pipe conveying fluid with external excitation. Extensive researches have been carried out in the literature to address this subject [6, 7]. The majority of researches proposed the active vibration control of pipe conveying fluid for vibration suppression and preventing system failure due to fatigue. The active controllers make a closed loop system and detect the variations of parameters employing different sensors [8, 9].

Passive vibration control of pipe conveying fluid has not been well studied, although it may yield interesting results. It should be noted that active controllers need sensors, equipment and external energy supplies. Thus, it is clear that these methodologies are more complex than passive ones. Moreover, the passive strategies are simple to be designed and inherently stable. Therefore, they are more suitable for usage in the field of engineering, especially for pipe conveying oil and gas at the bottom of the oceans. The results of employing passive vibration control techniques to reduce the vibration of pipes in engineering fields reveal that variations in the frequency of the excitation force can adversely affect the effectiveness of these techniques. As a result, their efficiency would be a narrow band such as the classical linear tuned mass dampers (TMDs) [10, 11].

In recent years, nonlinear energy sinks have been widely taken into consideration instead of TMDs or weakly nonlinear absorbers to mitigate the transient and steady-state vibrations of discrete and continuous systems based on numerical and analytical approaches [12–14].

Fig. 1

A schematic view of the fluid transfer system with nonlinear energy sink under harmonic external load

Ahmadabadi and Khadem [15] investigated the attenuation of a drill string self-excited oscillations using a nonlinear energy sink. They studied various positions of the drill string and different types of NESs for vibration mitigation. Xiong et al. [16] studied vibration reduction of a nonlinear mechanical system coupled to a NES under the impact of the narrow band stochastic excitations. They compared the NES efficiency to that of a linear absorber based on the complexification-averaging method and integration method; moreover, the results were verified using a numerical approach. Kani et al. [17] surveyed design and efficiency of a nonlinear energy sink attached to a beam with different support conditions. Starosvetsky and Gendelman [18] analyzed the vibration suppression of a two-degree-of-freedom linear system using a nonlinear energy sink. Moreover, they compared the efficiency of the NES to that of a best-tuned linear absorber. Ahmadabadi and Khadem [19] investigated annihilation of high-amplitude periodic responses of a forced two-degree-of-freedom oscillatory system using a nonlinear energy sink. Kani et al. [20] investigated vibration control of a nonlinear beam employing a nonlinear energy sink. The NES parameters were optimized based on maximizing the targeted energy transfer (TET) from nonlinear continuous system to NES. Bab et al. [21] investigated the performance of a number of smooth nonlinear energy sinks on the vibration attenuation of a rotor system under excitation of a mass eccentricity force. They used multiple-scale harmonic balance method to show that when the external force reaches its medium magnitude, the range of happening of SMR in the area of the system parameters is extended. Ahmadabadi and Khadem [22] investigated a coupled nonlinear energy sink and a piezoelectric-based vibration energy harvester positioned on a free-free beam under a shock excitation. The efficiency of the NES and the harvester for two configurations was studied; then, the optimal parameters of the system for the maximum dissipated energy in the NES and the highest harvested energy by the piezoelectric element were extracted. Luongo and Zulli [23] investigated the use of a nonlinear energy sink to control vibrations of a nonlinear structure under the effects of a bi-frequency harmonic excitation. Yang et al. [24] analyzed the targeted energy transfer in pipe conveying fluid with NES. They showed that the NES could robustly absorb and dissipate a major portion of the vibrational energy of the pipe. Bab et al. [25] investigated the efficiency of a number of smooth NESs on the vibration attenuation of a rotor system under excitation of a mass eccentricity force. They showed that when the external force reaches its medium magnitude, the area of the occurrence of the SMR in the domain of the system parameters would be larger and the collection of the NESs performs impressively. Ahmadabadi and Khadem [26] reviewed the influence of grounded and ungrounded NESs attached to a cantilever beam on the energy mitigation of the coupled system under excitation of an external shock. They investigated the effects of the nonlinear normal modes of the system on the occurrence of the one-way irreversible energy pumping. Gendelman [27] investigated TET in a two-degree-of-freedom system consisting of a primary linear oscillator and NES with non-polynomial potential. Bab et al. [28] analyzed the performance of a smooth nonlinear energy sink to mitigate vibrations of a rotating beam under an external force. They showed that the best range for the parameters of the NES is the one in which SMR and WMR occur simultaneously.

According to the above-mentioned researches, in order to simulate the oil transmission systems under the ocean, one may investigate the effects of the smooth NES on vibration control of a pipe conveying fluid under external harmonic load. In the current paper the Euler–Bernoulli beam theory is used for modeling the pipe conveying fluid. It is assumed that a distributed external periodic load is applied to the entire pipe. In this context, a small mass NES is used to reduce the pipe vibrations. Also, the damping and the stiffness of the NES is assumed linear and nonlinear, respectively. In order to detect the maximum efficiency of the absorber, various points of the pipe are examined for the attachment of the NES. Furthermore, the existence of the saddle-node, WMR and SMR in the space of magnitude of external force, the damping of NES and the position of NES on the pipe are investigated. In addition, the frequency response curves and phase portraits of the system are depicted.

2 Mathematical model of the considered system

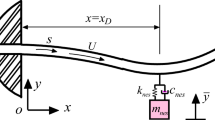
In this paper, the Hamiltonian approach is used to derive the equations of motion. A cylindrical pipe with fixed-fixed ends (two fixed supports), density $\rho _\mathrm{p}$, length L, diameter D [in oil transmission systems used in oceans the ratio of pipes length to their diameter is assumed to be large ($L/D\gg 1$)] with thickness t, conveying fluid is considered (see Fig. 1). X and Z are the spatial coordinates, and w(x, t) is transverse displacement of the pipe at position x. Let us denote time with t, derivatives with respect to the spatial variable with ($_ x$)and derivatives with respect to time with ($_ t$). $E_\mathrm{p}I_\mathrm{p}$ is the flexural rigidity of the pipe; $c_\mathrm{p}$ is damping of pipe, and $A_{f}$ and $A_\mathrm{p}$ are the cross-sectional areas of the pipe and flow, respectively, and they are all assumed to be constant. Fluid velocity $U_{f}$ is constant, and $\rho _{f}$ is fluid density. Fluid transfer system is under the excitation of a sinusoidal force $f\left( t \right) =F_0 \hbox {sin}(\Omega t)$, where $F_{0}$ and $\Omega$ are the magnitude and angular frequency of the external force, respectively. For vibration reduction, a nonlinear energy sink is used with nonlinear cubic spring, $K\theta ^{3}$, damping, $C\dot{\theta }$, and mass m. Absolute displacement of the NES is u and d is the distance of connecting point of the NES to the pipe, measured from the left pipe support (as shown in Fig. 1).

The fluid velocity in the reference coordinates system can be obtained using the Euler–Bernoulli beam theory as [3]:

$$\begin{aligned} v_\mathrm{fl} =U_f \mathop i\limits ^\wedge +\left[ {\frac{\partial w(x,t)}{\partial t}+U_f \frac{\partial w(x,t)}{\partial s}} \right] \mathop k\limits ^\wedge \end{aligned}$$

(1)

In the above equation, s is a curvilinear coordinate $s \in$ [0, L]. Total kinetic energy of the system ($T_\mathrm{tot}$) is the sum of the kinetic energy of the pipe ($T_\mathrm{p}$), the fluid ($T_\mathrm{fl}$) and the NES ($T_\mathrm{NES}$) as shown in Eqs. (2)–(5):

$$\begin{aligned} T_\mathrm{tot}= & {} T_\mathrm{P} +T_\mathrm{fl} +T_\mathrm{NES} \end{aligned}$$

(2)

$$\begin{aligned} T_P= & {} \frac{1}{2}\rho _p A_p \int _0^L {(w_t^2 (x,t))\hbox {d}x} \end{aligned}$$

(3)

$$\begin{aligned} T_\mathrm{fl}= & {} \frac{1}{2}\rho _\mathrm{fl} A_{f} \int _0^L [(w_t (x,t) \nonumber \\&+\,U_f w_x (x,t))^{2}+U_f^2 ]\hbox {d}x \end{aligned}$$

(4)

$$\begin{aligned} T_\mathrm{NES}= & {} \frac{1}{2}m_\mathrm{NES} u_t^2 (t) \end{aligned}$$

(5)

The potential energy of the system ($V_\mathrm{tot}$) is sum of the elastic potential energy of the pipe ($V_\mathrm{p}$) and NES ($V_\mathrm{NES}$) relative to the equilibrium position of the system. The corresponding equations can be written according to Eqs. (6)–(8):

$$\begin{aligned} V_\mathrm{tot}= & {} V_P +V_\mathrm{NES} \end{aligned}$$

(6)

$$\begin{aligned} V_\mathrm{p}= & {} \frac{1}{2}\rho _p A_p \left[ \int _0^L {E_p I_p w_{xx}^2 (x,t))^{2}\hbox {d}x} \right] \end{aligned}$$

(7)

$$\begin{aligned} V_\mathrm{NES}= & {} \frac{1}{4}K[u(t)-w(x,t)\times \delta (x-d)]^{4} \end{aligned}$$

(8)

where $\delta (x)$ is the Dirac delta function.

Total work done by non-conservative forces ($W_\mathrm{nc}$) because of the external harmonic load, damping of NES and damping of pipe is given by:

$$\begin{aligned} W_\mathrm{nc}= & {} F_0 \cos (\Omega t)\times w(x,t)-\frac{1}{2}C\times [u_t (t)-w_t (x,t)\nonumber \\&\times \, \delta (x-d)]^{2}-\frac{1}{2}c_p \times w_t^2 (x,t)^{2} \end{aligned}$$

(9)

Based on the Hamilton principle, one has:

$$\begin{aligned} \int _{t_1 }^{t_2 } {(\delta T_\mathrm{tot} -\delta V_\mathrm{tot} +\delta } W_\mathrm{nc} )\hbox {d}t=0 \end{aligned}$$

(10)

Substituting Eqs. (2)–(9) in Eq. (10) and applying the variational techniques, the governing partial differential equation can be derived as:

$$\begin{aligned}&E_p I_p w_{xxxx} (x,t)+c_p w_t (x,t)+\rho _f A_f [U_f^2 w_{xx} (x,t)\nonumber \\&\quad +\,2U_f w_{tx} (x,t)]+[\rho _f A_f +\rho _p A_p ]w_{tt} (x,t) \nonumber \\&\quad +\left\{ K[w(x,t)\times \delta (x-d)-u(t)]^{3}\right. \nonumber \\&\quad \left. +C[w_t (x,t)\times \delta (x-d)-u_t (t)] \right\} =F_0 \sin (\Omega t) \nonumber \\&\quad mu_{tt} (t)+C[w_t (x,t) \nonumber \\&\quad \times \, \delta (x-d)-u_t (t)]+K[w(x,t) \nonumber \\&\quad \times \, \delta (x-d)-u(t)]^{3}=0 \end{aligned}$$

(11)

In the above equations, the first one is the partial differential equation of the pipe and the second one is the ordinary differential equation of the nonlinear energy sink. In Eq. (11), $E_p I_p w_{xxxx}$ and $c_p w_t$ present the flexural restoring force and the damping force of the pipe, respectively. The expression $\rho _f A_f [U_f^2 w_{xx} (x,t)+2U_f w_{tx} (x,t)]$ represents the flow-related centrifugal force (associated with pipe curvature) and flow-related Coriolis force [1, 3]. The expression $[\rho _f A_f +\rho _p A_p ]w_{tt}$ is acting force on the pipe because of the inertia of the pipe and the fluid that flows through it. The term $\left\{ {K[w\times \delta (x-d)-u]^{3}+C[w_t \times \delta (x-d)-u_t ]} \right\}$ represents the force component acting on the pipe at ($x=d)$ that comes from nonlinear energy sink stiffness and damping. Finally, $F_0 \sin (\Omega t)$ represents the external harmonic load that excites the system.

The shape functions of a fixed-fixed beam are considered for pipe conveying fluid according to Eq. (8) to apply the Galerkin method. Thus, one has [29]:

$$\begin{aligned} \phi _i (x)= & {} \cosh (\lambda _i x)-\cos (\lambda _i x)-\frac{\sin (\lambda _i {l}')+\sinh (\lambda _i {l}')}{\cos (\lambda _i {l}')+\cosh (\lambda _i {l}')}.\nonumber \\&\{\sinh (\lambda _i x)-\sin (\lambda _i x)\} \end{aligned}$$

(12)

The values of $\lambda _j {l}'$ for different modes are $\lambda _1 {l}'=4.73,\lambda _2 {l}'=7.53,\lambda _3 {l}'=10.99,\ldots$ which are obtained by solving frequency equation of the fixed-fixed beam ($\cosh (x)\cos (x)=1$) [29].

Starosvetsky and Gendelman studied the efficiency of a nonlinear energy sink in vibration reduction of a two-degree-of-freedom system [18]. They proved that in the system under the periodic or narrow band excitation, when the frequencies of the primary system are well separated, it can be considered as a two-degree-of-freedom system, which includes the desired mode of the primary system and NES. In this case, separated values of $\lambda _j {l}'$ show that the system frequencies are sufficiently separated. Thus, the coupled pipe and NES system can be considered as a two-degree-of-freedom system, which includes the first (and the most important) vibration mode of the pipe and NES. With the aim of transforming the above equations to dimensionless ones, the following variables are considered:

$$\begin{aligned} \bar{{w}}= & {} \frac{w}{L},\bar{{x}}=\frac{x}{L}, \bar{{u}}=\frac{u}{L}, \bar{{t}}=\frac{t}{a},\bar{{d}}=\frac{d}{L},\nonumber \\ \bar{{U}}_f= & {} \sqrt{ \frac{\rho _f (\rho _f A_f +\rho _p A_p )A_f L^{3}}{\lambda _1 ^{4}mE_p I_p }} U_f ,\bar{{\gamma }}=\frac{\rho _f A_f L}{m} \nonumber \\ \beta= & {} \frac{KL^{6}(\rho _f A_f +\rho _p A_p )}{\lambda _1 ^{4}mE_p I_p },\nonumber \\ \bar{{\alpha }}= & {} \frac{CL^{2}\sqrt{(\rho _f A_f +\rho _p A_p )}}{\lambda _1 ^{2}m\sqrt{E_p I_p }},\nonumber \\ a= & {} \frac{L^{2}}{\lambda _1 ^{2}} \sqrt{\frac{\rho _f A_f +\rho _p A_p }{E_p I_p }},\bar{{\Omega }}=\Omega a \nonumber \\ \bar{{F}}= & {} \frac{F_0 L^{4}(\rho _f A_f +\rho _p A_p )}{\lambda _1 ^{4} mE_p I_p },\nonumber \\ \bar{{c}}_p= & {} \frac{c_p L^{3}\sqrt{(\rho _f A_f +\rho _p A_p )}}{m\lambda _1 ^{2}\sqrt{E_p I_p }},\nonumber \\ \varepsilon= & {} \frac{m}{(\rho _f A_f +\rho _p A_p )L} \end{aligned}$$

(13)

Considering dimensionless parameters in Eq. (13), the corresponding dimensionless equations are obtained as follows:

$$\begin{aligned}&\bar{{w}}_{\bar{{x}}\bar{{x}}\bar{{x}}\bar{{x}}} (\bar{{x}},\bar{{t}}) +\varepsilon \bar{{c}}_p \bar{{w}}_{\bar{{t}}} (\bar{{x}},\bar{{t}}) +\varepsilon \bar{{U}}_f^2 \bar{{w}}_{\bar{{x}}\bar{{x}}} (\bar{{x}},\bar{{t}})\nonumber \\&\quad +\,2\varepsilon \sqrt{\bar{{\gamma }}}\bar{{U}}_f \bar{{w}}_{\bar{{t}}\bar{{x}}} (\bar{{x}},\bar{{t}})+\bar{{w}}_{\bar{{t}}\bar{{t}}} (\bar{{x}},\bar{{t}}) \nonumber \\&\quad +\,\varepsilon \left\{ \bar{{\beta }}[\bar{{w}}(\bar{{x}},\bar{{t}})\times \delta (\bar{{x}}-\bar{{d}})-\bar{{u}}(\bar{{t}})]^{3} \right. \nonumber \\&\quad +\,\left. \bar{{\alpha }}[\bar{{w}}_{\bar{{t}}} (\bar{{x}},\bar{{t}})\times \delta (\bar{{x}}- \bar{{d}})-\bar{{u}}_{\bar{{t}}} (\bar{{t}})] \right\} = \varepsilon \bar{{F}}\cos (\bar{{\Omega }}\bar{{t}}) \nonumber \\&\varepsilon \bar{{u}}_{tt} (\bar{{t}})+\varepsilon \bar{{\alpha }} \times [\bar{{u}}_t (\bar{{t}})-\bar{{w}}_t (\bar{{x}},\bar{{t}}) \times \delta (\bar{{x}}-\bar{{d}})]\nonumber \\&\quad +\,\varepsilon \bar{{\beta }} [\bar{{u}}(\bar{{t}})\times \delta (\bar{{x}}-\bar{{d}})-\bar{{w}} (\bar{{x}},\bar{{t}})]^{3}=0 \end{aligned}$$

(14)

The coupled partial differential equations of the system are transformed to ordinary differential equations using the Galerkin method. For this purpose, it is assumed that the response of the pipe is as follows:

$$\begin{aligned} \bar{{w}}(\bar{{x}},\bar{{t}})=\sum _{i=1}^n {\phi _i (\bar{{x}}} )q_i (\bar{{t}}) \end{aligned}$$

(15)

With regard to the properties of Dirac delta function and the first mode of the pipe and using the Galerkin method, the equations governing the pipe and NES are obtained as coupled ordinary differential equations, and integrating over the domain [0, 1] yields:

$$\begin{aligned}&m_{11} (q_1 (\bar{{t}}))_{tt} +k_{11} q_1 (\bar{{t}}) +\varepsilon \mu q_1 (\bar{{t}})+\varepsilon \xi (q_1 (\bar{{t}}))_t \nonumber \\&\quad + \varepsilon \bar{{\alpha }}\phi _1 (\bar{{d}}) \{\phi _1 (\bar{{d}})(q_1 (\bar{{t}}))_t -(\bar{{u}}(\bar{{t}}))_t \}\nonumber \\&\quad +\,\varepsilon \bar{{\beta }}\phi _1 (\bar{{d}})\{\phi _1 (\bar{{d}}) q_1 (\bar{{t}})-\bar{{u}}(\bar{{t}})\}^{3}=\varepsilon \bar{{F}}\cos (\bar{{\Omega }}\bar{{t}}) \nonumber \\&\quad \varepsilon \bar{{u}}(\bar{{t}})_{tt} +\varepsilon \alpha [(\bar{{u}}(\bar{{t}}))_t -\phi _1 (\bar{{d}})(q_1 (\bar{{t}}))_t ]\nonumber \\&\quad +\,\varepsilon \beta [\bar{{u}} (\bar{{t}})-\phi _1 (\bar{{d}})q_1 (\bar{{t}})]^{3}=0 \end{aligned}$$

(16)

The coefficients of this equation are presented in “Appendix 1.” In Eq. (16), asymmetry of the coupled equations causes complexity. Therefore, for obtaining symmetric equations, a new coordinate transformation is used. For this purpose, $q_1 (\bar{{t}})$ and ${q}'_1 (\bar{{t}})$ are considered as the first mode displacement and the displacement of the pipe at the location of the NES. In addition, considering ${q}'_1 (\bar{{t}})=\phi _1 (\bar{{d}})\times q_1 (\bar{{t}})$, Eq. (16) can be written as Eq. (17):

$$\begin{aligned}&\frac{m_{11} }{\phi _{_{1d} }^2 }({q}'_1 (\bar{{t}}))_{tt} +\frac{k_{11} }{\phi _{_{1d} }^2 }{q}'_1 (\bar{{t}})+\varepsilon \frac{\mu }{\phi _{1d} }{q}'_1 (\bar{{t}})\nonumber \\&\quad +\,\varepsilon \frac{\xi }{\phi _{1d} } ({q}'_1 (\bar{{t}}))_t +\varepsilon \alpha \{({q}'_1 (\bar{{t}}))_t -(\bar{{u}}(\bar{{t}}))_t \}\nonumber \\&\quad +\varepsilon \beta \{{q}'_1 (\bar{{t}})-\bar{{u}}(\bar{{t}})\}^{3} =\varepsilon \frac{\bar{{F}}}{\phi _{1d} }\cos (\bar{{\Omega }}\bar{{t}} +\phi ) \nonumber \\&\varepsilon \bar{{u}}(\bar{{t}})_{tt} +\varepsilon \alpha [(\bar{{u}}(\bar{{t}}))_t -({q}'_1 (\bar{{t}}))_t ]\nonumber \\&+\,\varepsilon \beta [\bar{{u}}(\bar{{t}})-{q}'_1 (\bar{{t}})]^{3}=0 \end{aligned}$$

(17)

Considering ${m}'_{11} =m_{11} /\phi _{_{1d} }^2 ,{k}'_{11} =k_{11} /\phi _{_{1d} }^2 ,\phi _1 (\bar{{d}})=\phi _{1d}$, Eq. (17) can be written as follows:

$$\begin{aligned}&{m}'_{11} ({q}'_1 (\bar{{t}}))_{tt} +{k}'_{11} {q}'_1 (\bar{{t}}) +\varepsilon \frac{\mu }{\phi _{1d} }{q}'_1 (\bar{{t}}) +\varepsilon \frac{\xi }{\phi _{1d} }({q}'_1 (\bar{{t}}))_t \nonumber \\&\qquad +\,\varepsilon \alpha \{({q}'_1 (\bar{{t}}))_t -(\bar{{u}}(\bar{{t}}))_t \} +\varepsilon \beta \{{q}'_1 (\bar{{t}})-\bar{{u}}(\bar{{t}})\}^{3} \nonumber \\&\quad =\varepsilon \frac{\bar{{F}}}{\phi _{1d} }\cos (\bar{{\Omega }}\bar{{t}} +\phi ) \nonumber \\&\quad \varepsilon \bar{{u}}_{tt} (\bar{{t}})+\varepsilon \alpha [(\bar{{u}}(\bar{{t}}))_t -({q}'_1 (\bar{{t}}))_t ] \nonumber \\&\qquad +\,\varepsilon \beta [\bar{{u}}(\bar{{t}})-{q}'_1 (\bar{{t}})]^{3}=0 \end{aligned}$$

(18)

For the sake of simplicity, the parameters are given without index and bar in the following sections.

3 Analytical treatments

3.1 Complexification-averaging method and stability analysis

The complexification-averaging method is used to achieve the steady-state response of the coupled systems of pipe and absorber Eq. (18). This method was developed by Manevitch for extraction of the transient and steady-state response of systems with NES [30]. Both the slow-varying and the fast-varying parts of the motion can be separated using this method. Fast and slow parts are related to natural frequency and the amplitude of vibration, respectively. Considering the fact that the system behavior is investigated around the first natural frequency, a detuning parameter $\sigma$ is defined that represents the nearness of the excitation frequency to the natural frequency of the main system [31]. It can be formulated as $k_{11} =m_{11} (\Omega ^{2}+\varepsilon \sigma )$. Finally, assuming $q_1 (\bar{{t}})=x_1 (t)$ and $\bar{{u}}(\bar{{t}})=x_2 (t)$, Eq. (18) will be:

$$\begin{aligned}&m_{11} (x_1 (t))_{tt} +m_{11} (\Omega ^{2}+\varepsilon \sigma )x_1 (t) \nonumber \\&\qquad +\,\varepsilon \frac{\zeta }{\phi _{1d} }(x_1 (t))_t +\varepsilon \frac{\mu }{\phi _{1d} }x_1 (t) \nonumber \\&\qquad +\,\varepsilon \alpha \{(x_1 (t))_t -(x_2 (t))_t \} +\varepsilon \beta \{x_1 (t)-x_2 (t)\}^{3}\nonumber \\&\quad =\varepsilon \frac{F}{\phi _{1d} } \cos (\Omega t) \nonumber \\&\varepsilon (x_2 (t))_{tt} +\varepsilon \alpha [(x_2 (t))_t -(x_1 (t))_t ]\nonumber \\&\qquad +\,\varepsilon \beta [x_2 (t)-x_1 (t)]^{3}=0 \end{aligned}$$

(19)

In Eq. (19), the $\xi$ is the non-dimensional damping of the system; $\mu$ is the non-dimensional fluid velocity, and $\alpha$ and $\beta$ are stiffness and damping of NES, respectively.

As well, it is common in the literature that ratio of nonlinear energy sink mass to the main system (pipe) mass is assumed to be small; moreover, it is assumed that the stiffness of the nonlinear energy sink is nonlinear. The coordinate transformation of Eq. (20) transfers ($x_{1}$) and ($x_{2}$) to the coordinates of the mass center (v(t)) and relative displacement (w(t)). This transformation is employed to investigate the efficiency of NES. The relative displacement is important, and this transformation indicates a better transmission of energy from the pipe to the NES and ultimately the energy dissipation:

$$\begin{aligned} v(t)= & {} x_1 (t)+\varepsilon x_2 (t) \nonumber \\ w(t)= & {} x_1 (t)-x_2 (t) \end{aligned}$$

(20)

In the complexification-averaging method, the response of the system is obtained using the sum of the responses of dominant frequencies. Here, for the pipe and absorber movements, it can be assumed that the system has a dominant frequency; thus, it can be written as $v(t)=v_1 (t), w(t)=w_1 (t)$. In complexification-averaging method, the following parameters are defined with complex parameters $(i=\sqrt{-1})$:

$$\begin{aligned} \psi _1 (t)= & {} (v_1 (t))+i\Omega v_1 (t) \end{aligned}$$

(21)

$$\begin{aligned} \psi _2 (t)= & {} (w_1 (t))+i\Omega w_1 (t) \end{aligned}$$

(22)

The displacements of the system components using the defined complex parameters are as follows:

$$\begin{aligned}&v_1 (t)=\frac{1}{2i\Omega }\left( {\psi _1 (t)-\psi _1^*(t)} \right) , \nonumber \\&w_1 (t)=\frac{1}{2i\Omega }\left( {\psi _2 (t)-\psi _2^*(t)} \right) \nonumber \\&(v_1 (t))_t =\frac{1}{2}(\psi _1 (t)+\psi _1^*(t)), \nonumber \\&(w_1 (t))_t =\frac{1}{2}(\psi _2 (t)+\psi _2^*(t)) \nonumber \\&(v_1 (t))_{tt} =(\psi _1 (t))_t -\frac{i\Omega }{2}\left( {\psi _1 (t) +\psi _1^*(t)} \right) , \nonumber \\&(w_1 (t))_{tt} =(\psi _2 (t))_t -\frac{i\Omega }{2}\left( {\psi _2 (t) +\psi _2^*(t)} \right) \end{aligned}$$

(23)

In Eq. (23), star indicates conjugate of the corresponding parameters. Defining the following equations, the fast and slow vibration behavior of the system can be separated as:

$$\begin{aligned} \psi _1 (t)= & {} \phi _1 (t)\hbox {e}^{i\Omega t},\quad \psi _1^*\left( t \right) =\phi _{_1 }^*(t)\hbox {e}^{-i\Omega t} \nonumber \\ \psi _2 (t)= & {} \phi _2 (t)\hbox {e}^{i\Omega t},\quad \psi _2^*(t)=\phi _{_2 }^*(t)\hbox {e}^{-i\Omega t} \end{aligned}$$

(24)

In this relation, ($\hbox {e}^{i\Omega t}$) is related to fast-varying part of motion and the natural frequency of the system; $\phi _1 \left( t \right)$ and $\phi _2 \left( t \right)$ indicate the complex amplitude modulations of center of mass and the motion of the pipe relative to the NES (the vibration amplitudes). Substituting Eqs. (20)–(24) in (19), the equations governing behavior of the slow-varying part of the system is obtained as follows (keeping only terms containing $\hbox {e}^{i\Omega t}$ yields the following slow modulated system):

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t}\phi _1 \left( t \right) -\frac{\varepsilon }{8\Omega ^{3} \left( {1+\varepsilon } \right) }\{4i\phi _{1d} \phi _1 \left( t \right) \mu \Omega ^{2} \nonumber \\&\quad -\,4\phi _{1d} \phi _2 \left( t \right) \varepsilon \xi \Omega ^{3}-3i\phi _2 \left( t \right) \left| {\phi _2 \left( t \right) } \right| ^{2} \beta \nonumber \\&\quad -\,4\phi _{1d} \phi _1 \left( t \right) \xi \Omega ^{3} +3i\phi _2 \left( t \right) \left| {\phi _2 \left( t \right) } \right| ^{2} \beta \varepsilon \phi _{1d}^2 \nonumber \\&\quad -\,4\phi _2 \left( t \right) \alpha \varepsilon \Omega ^{3}\phi _{1d}^2 +4 F \phi _{1d} \Omega ^{3}+4i\Omega ^{4}\phi _2 \left( t \right) \nonumber \\&\quad -\,4 \phi _2 \left( t \right) \alpha \Omega ^{3}\phi _{1d}^2 +4i\phi _1 \left( t \right) \sigma \Omega ^{2}+4\phi _2 \left( t \right) \alpha \varepsilon \Omega ^{3}\nonumber \\&\quad +\,4 F \phi _{1d} \varepsilon \Omega ^{3} -3i\phi _2 \left( t \right) \left| {\phi _2 \left( t \right) } \right| ^{2} \beta \varepsilon \nonumber \\&\quad +\,3 i\phi _2 \left( t \right) \left| {\phi _2 \left( t \right) } \right| ^{2}\beta \phi _{1d}^2 +4i\phi _2 \left( t \right) \varepsilon \sigma \Omega ^{2} \nonumber \\&\quad +\,4i\phi _{1d} \phi _2 \left( t \right) \varepsilon \mu \Omega ^{2}-4i\Omega ^{4}\phi _1 \left( t \right) \nonumber \\&\quad +\,4\phi _2 \left( t \right) \alpha \Omega ^{3}\}=0 \nonumber \\&\frac{\hbox {d}}{\hbox {d}t}\phi _2 \left( t \right) -\frac{1}{8\Omega \left( {1+\varepsilon } \right) }\{4i\phi _{1d} \phi _2 \left( t \right) \varepsilon ^{2}\mu \Omega ^{2} \nonumber \\&\quad -\,4\phi _{1d} \phi _2 \left( t \right) \varepsilon ^{2}\xi \omega _0 ^{3} +4\phi _{1d} F\varepsilon ^{2}\Omega ^{3}\nonumber \\&\quad +\,3i\phi _2 \left( t \right) \left| {\phi _2 \left( t \right) } \right| ^{2}\beta -4i\Omega ^{4}\phi _2 \left( t \right) -4\phi _2 \left( t \right) \alpha \Omega ^{3} \nonumber \\&\quad -\,4\phi _{1d} \phi _1 \left( t \right) \varepsilon \xi \Omega ^{3} +3i\phi _2 \left( t \right) \left| {\phi _2 \left( t \right) } \right| ^{2}\beta \varepsilon \phi _{1d}^2 \nonumber \\&\quad -\,4\phi _2 \left( t \right) \alpha \varepsilon ^{2}\Omega ^{3}\phi _{1d}^2 +4F\phi _{1d} \varepsilon y\Omega ^{3}\nonumber \\&\quad -\,4\phi _2 \left( t \right) \alpha \varepsilon \Omega ^{3}\phi _{1d} ^{2}+4i\Omega ^{4}\phi _1 \left( t \right) \nonumber \\&\quad +\,3i\phi _2 \left( t \right) \left| {\phi _2 \left( t \right) } \right| ^{2} \beta \varepsilon +4i\phi _2 \left( t \right) \varepsilon ^{2}\sigma y \Omega ^{2} \nonumber \\&\quad +\,3i\phi _2 \left( t \right) \left| {\phi _2 \left( t \right) } \right| ^{2}\beta \varepsilon ^{2}\phi _{1d}^2 +4i\phi _{1d} y\phi _1 \left( t \right) \varepsilon \mu \Omega ^{2}\nonumber \\&\quad +\,4i\phi _1 \left( t \right) \varepsilon \sigma \Omega ^{2} -4\phi _2 \left( t \right) \alpha y\varepsilon \Omega ^{3}\}=0 \end{aligned}$$

(25)

To commence, the stationary points of the equation are obtained. This analysis is physically important because it represent the steady oscillatory motion of the system according to Eq. (19). To obtain the stationary points of Eq. (25), all time derivatives are set equal to zero and by performing some manipulations (extracting $\phi _1$ from the first relation of Eq. (25), and substituting it in the second relation), a simpler equation is obtained as:

$$\begin{aligned}&[9\beta ^{2}\left( \phi _{1d} ^{4}\Omega ^{4}-2\phi _{1d} ^{3}\mu \Omega ^{2}+\phi _{1d} ^{2}\xi ^{2}\Omega ^{2}-2\phi _{1d} ^{2} \sigma \Omega ^{2}\right. \nonumber \\&\quad \left. +\,\phi _{1d} ^{2}\mu ^{2}+2\phi _{1d} \mu \sigma +\sigma ^{2} \right) ]\left| {\phi _{2f} } \right| ^{6} \nonumber \\&\quad +\,[24\beta \Omega ^{4}\left( \phi _{1d} ^{3}\mu \Omega ^{2}- \phi _{1d} ^{2}\xi ^{2}\Omega ^{2}+\phi _{1d} ^{2}\sigma \Omega ^{2}\right. \nonumber \\&\quad \left. - \phi _{1d} ^{2}\mu ^{2}-2\phi _{1d} \mu \sigma -\sigma ^{2} \right) ] \left| {\varphi _{2f} } \right| ^{4} \nonumber \\&\quad +\,[16\Omega ^{6}(\phi _{1d} ^{4}\alpha ^{2}\Omega ^{4}+2\phi _{1d} ^{3} \alpha \xi \Omega ^{4}\nonumber \\&\quad -\,2\phi _{1d} ^{3}\alpha ^{2}\mu \Omega ^{2}+ \phi _{1d} ^{2}\alpha ^{2}\xi ^{2}\Omega ^{2}+\phi _{1d} ^{2}\xi ^{2} \Omega ^{4}\nonumber \\&\quad -\,2\phi _{1d} ^{2}\alpha ^{2}\sigma \Omega ^{2}+\phi _{1d} ^{2} \alpha ^{2}\mu ^{2} \nonumber \\&\quad +\,\phi _{1d} ^{2}\mu ^{2}\Omega ^{2}+2\phi _{1d} \alpha ^{2}\mu \sigma +2\phi _{1d} \mu \sigma \Omega ^{2}\nonumber \\&\quad +\,\alpha ^{2}\sigma ^{2} +\sigma ^{2}\Omega ^{2})]\left| {\varphi _{2f} } \right| ^{2}-16\phi _{1d} ^{2} F^{2}\Omega ^{10}=0 \end{aligned}$$

(26)

In Eq. (26), $\varphi _{1f}$ and $\varphi _{2f}$ are the steady-state magnitude of functions $\phi _1 \left( t \right)$ and $\phi _2 \left( t \right)$. Also, $\varphi _{2f}$ is a proper approximation of w(t).The absorption efficiency is evaluated by considering changes in $\left| {\varphi _{2f} } \right|$. The higher and lower values of $\left| {\varphi _{2f} } \right|$ and $\left| {\varphi _{1f} } \right|$, respectively, would improve the absorbent performance. Assuming $S=\left| {\varphi _{2f} } \right| ^{2}$, Eq. (26) is simplified to:

$$\begin{aligned} \alpha _3 S^{3}+\alpha _2 S^{2}+\alpha _1 S+\alpha _4 =0 \end{aligned}$$

(27)

The coefficients of Eq. (27) are presented in “Appendix 2.” Equation (27) can have one or three responses depending on different magnitude of parameters in the system. For this reason and continuity of response, various bifurcation points such as saddle node are probable in the system response. In order to determine the saddle-node bifurcation points, in addition to establishing Eq. (27), derivative of this relation should be equal to zero [32]:

$$\begin{aligned} 3\alpha _3 S^{2}+2\alpha _2 S+\alpha _1 =0 \end{aligned}$$

(28)

Equation (28) is a necessary condition for occurrence of the saddle-node bifurcations. The boundary of occurrence of the saddle-node bifurcations as a function of the system parameters can be obtained by eliminating S from Eqs. (27) and (28).

Furthermore, in order to determine Hopf bifurcation, around the stationary points, one may define small complex perturbations $\delta _1 (t)$ and $\delta _2 (t)$. Reintroducing the slow-varying modulations as [14, 33, 34]:

$$\begin{aligned} \phi _1 (t)=\phi _{1f} +\delta _1 (t), \phi _2 (t)=\phi _{2f} +\delta _2 (t) \end{aligned}$$

(29)

Substituting Eq. (29) in (25) and ignoring the nonlinear perturbation terms and keeping only linear terms with respect to $\delta _i$ ($i= 1\ldots 2$), four coupled ordinary differential equations governing the behavior of the system around the equilibrium points are obtained as follows:

$$\begin{aligned}&\dot{\delta }_1 =\frac{\delta _1 \varepsilon \left( {-\phi _{1d} \xi \Omega +i\phi _{1d} \mu -i\Omega ^{2}+i\sigma } \right) }{2\Omega \left( {1+\varepsilon } \right) }+\frac{3i\delta _2^*\left( {\phi _{1d}^2 -1} \right) \beta \varepsilon \phi _{2f}^2 }{8\Omega ^{3}}+\frac{\varepsilon i\delta _2 }{4\left( {1+\varepsilon } \right) \Omega ^{3}}\{2\varepsilon \mu \phi _{1d} \Omega ^{2}\nonumber \\&\quad -\,2i\Omega ^{3}\alpha +3\phi _{1d}^2 \left| {\phi _{2f} } \right| ^{2}\beta \varepsilon +2i\phi _{1d} \Omega ^{3}\varepsilon \xi +2i\phi _{1d}^2 \Omega ^{3}\alpha \varepsilon +3\phi _{1d}^2 \left| {\phi _{2f} } \right| ^{2}\beta +2i\phi _{1d}^2 \Omega ^{3}\alpha -3\left| {\phi _{2f} } \right| ^{2}\beta \varepsilon +2\Omega ^{4}\nonumber \\&\quad +2\varepsilon \sigma \Omega ^{2} -2i\Omega ^{3}\alpha \varepsilon -3\left| {\phi _{2f} } \right| ^{2}\beta \}\nonumber \\&\dot{\delta }_2 =\frac{i\delta _1 \left( {\phi _{1d} \varepsilon \mu +i\phi _{1d} \varepsilon \xi \Omega +\varepsilon \sigma +\Omega ^{2}} \right) }{2\Omega \left( {1+\varepsilon } \right) }+\frac{3i\delta _2^*\left( {\varepsilon \phi _{1d}^2 +1} \right) \beta \phi _{2f}^2 }{8\Omega ^{3}} \nonumber \\&\quad +\,\delta _2 \left\{ \frac{i\left( {i\phi _{1d} \varepsilon ^{2}\xi \Omega +i\phi _{1d}^2 \alpha \varepsilon ^{2}\Omega +\varepsilon ^{2}\mu \phi _{1d} +i\phi _{1d}^2 \alpha \varepsilon \Omega +i\alpha \Omega (\varepsilon +1)+\varepsilon ^{2}\sigma -\Omega ^{2}} \right) }{2\Omega \left( {1+\varepsilon } \right) }+\frac{3i\left( {\varepsilon \phi _{1d}^2 +1} \right) \beta \left| {\phi _{2f} } \right| ^{2}}{4\Omega ^{3}}\right\} \nonumber \\ \end{aligned}$$

(30)

The characteristic polynomial equation of the above coupled equations is obtained as [33]:

$$\begin{aligned} \mu ^{4}+\eta _1 \mu ^{3}+\eta _2 \mu ^{2}+\eta _3 \mu +\eta _4 =0 \end{aligned}$$

(31)

The coefficients of Eq. (31) are presented in “Appendix 3.” Hopf bifurcation is a region that slow-varying part of the system behavior is transferred from a static state to a dynamic one. Hopf bifurcation occurs when Eq. (31) has a pair of pure complex-conjugate roots as $\mu =\pm j\omega _H$ [33].

In fact, $\omega _H$ is the characteristic frequency of periodic orbits in the system and is generated from the bifurcation of the fixed points (in Hopf bifurcations, fixed points are transformed into orbits in state space of parameters). If one of the roots of Eq. (31) has a positive real part, the fixed point will be unstable. On the other hand, if all roots of Eq. (31) have negative real parts, the system will be stable. Separating the real and imaginary parts of Eq. (31), can obtain the following relations:

$$\begin{aligned}&\eta _3^2 -\eta _2 \eta _3 \eta _1 +\eta _4 \eta _1^2 =0 \end{aligned}$$

(32)

$$\begin{aligned}&\omega _H^2 =\frac{\eta _3 }{\eta _1 }\Rightarrow \omega _H =\pm \left\{ \frac{\varepsilon }{64\Omega ^{6}(\phi _{1d}^2 \alpha \varepsilon +\phi _{1d} \varepsilon \xi +\alpha )}\right. \nonumber \\&\left. \quad \times \, (16\phi _{1d}^3 \alpha ^{2} \varepsilon \xi \Omega ^{6}+16\phi _{1d}^2 \alpha \varepsilon \xi ^{2}\Omega ^{6}\right. \nonumber \\&\left. \quad +\,27\phi _{1d}^3 \beta ^{2}\varepsilon \xi \phi _{2f}{ }^{4} +16\phi _{1d}^2 \alpha \Omega ^{8}+16\phi _{1d}^2 \alpha \varepsilon \mu ^{2} \Omega ^{4}\right. \nonumber \\&\left. \quad +\,16\phi _{1d} \alpha ^{2}\xi \Omega ^{6}+16\phi _{1d} \xi \Omega ^{8} +32\phi _{1d} \alpha \varepsilon \mu \sigma \Omega ^{4} \right. \nonumber \\&\quad -\,48\phi _{1d} \beta \xi \Omega ^{4}\phi _{2f}{ }^{2}+27 \phi _{1d} \beta ^{2}\xi \phi _{2f}{ }^{4}\nonumber \\&\left. \quad +\,16\alpha \varepsilon \sigma ^{2}\Omega ^{4})\right\} ^{\frac{1}{2}} \end{aligned}$$

(33)

Equation (32) is the condition of existence of Hopf bifurcation, and Eq. (33) is the natural frequency of the periodic vibration generated by the Hopf bifurcation. Simplifying Eq. (32) and assuming that $S=\left| {\varphi _{2f} } \right| ^{2}$, it can be rewritten to a fourth-order equation in terms of the S that may have even four roots Eq. (35).

$$\begin{aligned} v_1 S^{4}+v_2 S^{3}+v_3 S^{2}+v_4 S+v_5 =0 \end{aligned}$$

(34)

The coefficients of this equation are presented in “Appendix 4.” Solving and eliminating S from two coupled Eqs. (27) and (34), conditions of Hopf bifurcation occurrence can be obtained as a function of the system parameters.

3.2 Analysis of the SMR (relaxation oscillations of the averaged flow)

One of the important notes in the analytical solution of nonlinear systems is that the system response is dependent on initial conditions. If the initial conditions are close enough to a stationary point of the system (steady-state response), they will be absorbed in them; otherwise, they may be absorbed in other dynamic regimes that exist in the system. Therefore, it can be said that the analysis of the previous section is local; hence, they are established where the initial conditions of the system are close to these steady-state responses. The SMR phenomenon was analyzed in [33]. In general, the existence of strong modulated responses demonstrates the efficiency of NES under excitation of a harmonic force [35]. For strong modulated response analysis, one may use the first-order coupled equation of (25) related to slow-varying part of the motion. For this purpose, one obtains $\phi _1 \left( t \right)$ in terms of $\phi _2 \left( t \right)$ and its time derivatives by performing an algebraic on the second relation. Then, substituting it in the first relation, a second-order differential equation in terms of $\phi _2 \left( t \right)$ is obtained that shows vibration behavior of the system, where its final form is as follows:

$$\begin{aligned}&\frac{\hbox {d}^{2}\varphi _2 }{\hbox {d}t^{2}}-\frac{3i\beta (\varepsilon \phi _{1d}^2 +1)}{8\Omega ^{3}}\frac{\hbox {d}}{\hbox {d}t}\{\varphi _2 \left| {\varphi _2 } \right| ^{2}\}\nonumber \\&\quad +\,\left\{ \frac{3i\varepsilon \zeta \beta \phi _{1d} }{16\Omega ^{3}} -\frac{3\varepsilon \mu \beta }{16\Omega ^{4}} -\frac{3\varepsilon \sigma \beta }{16\Omega ^{4}} +\frac{3\phi _{1d} \varepsilon \beta }{16\Omega ^{2}}\right\} \nonumber \\&\varphi _2 \left| {\varphi _2 } \right| ^{2} \nonumber \\&\quad +\,\left\{ \frac{\alpha (\varepsilon \phi _{1d}^2 +1)}{2} -\frac{i\varepsilon (\sigma +\phi _{1d} \mu )}{2\Omega }\right. \nonumber \\&\left. \quad +\,\frac{\zeta \varepsilon \phi _{1d} }{2}+\frac{i\Omega }{2}\right\} \frac{\hbox {d}\varphi _2 }{\hbox {d}t} \nonumber \\&\quad +\,\left\{ \frac{i\Omega \varepsilon \alpha \phi _{1d}^2 }{4} -\frac{i\varepsilon \sigma \alpha }{4\Omega } -\frac{i\varepsilon \phi _{1d} \mu \alpha }{4\Omega }\right. \nonumber \\&\left. \quad +\,\frac{i\Omega \varepsilon \zeta \phi _{1d} }{4} +\frac{\phi _{1d} \varepsilon \zeta \alpha }{4} +\frac{\varepsilon \sigma }{4} +\frac{\varepsilon \mu \phi _{1d} }{4}\right\} \varphi _2\nonumber \\&\quad -\,\frac{i\Omega \varepsilon \phi _{1d} F}{4}=0 \end{aligned}$$

(35)

The method of multiple scales is used to analyze Eq. (35). With this aim, the following time scales are introduced $\tau _j =\varepsilon ^{j}t, j=0, 1,\ldots$. The first scale $\tau _0$ is a fast-order time scale and $\tau _1$ is a slow one defined using a small parameter $(\varepsilon )$. In this case, the relations of derivatives of these time scales are:

$$\begin{aligned} \varphi _j= & {} \varphi _j (\tau _0 ,\tau _1 ,\ldots ) \nonumber \\ \frac{\hbox {d}}{\hbox {d}t}= & {} \frac{\partial }{\partial \tau _0 } +\varepsilon \frac{\partial }{\partial \tau _1 }+\cdots =D_0 +\varepsilon D_1 \nonumber \\ \frac{\hbox {d}^{2}}{\hbox {d}t^{2}}= & {} \frac{\partial ^{2}}{\partial \tau _0^2 } +2\varepsilon \frac{\partial ^{2}}{\partial \tau _0 \partial \tau _1 }+\cdots =D_0^2\nonumber \\&+2\varepsilon D_0 D_1 +\cdots \end{aligned}$$

(36)

Substituting Eqs. (36) in (35) and considering the terms with the same power of $\varepsilon$, different time scales are obtained as follows:

$$\begin{aligned}&O(\varepsilon ^{0}): \frac{\partial ^{2}\varphi _2 }{\partial \tau _0^2 } +\left[ \frac{i\Omega +\alpha }{2}\right] \frac{\partial \varphi _2 }{\partial \tau _0 } -\frac{3i\beta }{8\Omega ^{3}}\frac{\partial }{\partial \tau _0 }\nonumber \\&\quad \left[ \varphi _2 \left| {\varphi _2 } \right| ^{2}\right] =0 \nonumber \\&O(\varepsilon ^{1}): 2\frac{\partial ^{2}\varphi _2 }{\partial \tau _0 \partial \tau _1 }-\left[ \frac{i(\phi _{1d} \mu +\sigma )}{2\Omega } -\frac{\phi _{1d} (\alpha \phi _{1d} +\zeta )}{2}\right] \nonumber \\&\frac{\partial \varphi _2 }{\partial \tau _0 }-\frac{3i}{8\Omega ^{3}} \frac{\partial }{\partial \tau _0 }\left[ \varphi _2 \left| {\varphi _2 } \right| ^{2}\right] -\frac{3i\beta \phi _{1d}^2 }{8\Omega ^{3}} \frac{\partial }{\partial \tau _1 }\left[ \varphi _2 \left| {\varphi _2 } \right| ^{2}\right] \nonumber \\&\quad +\,\left[ \frac{i\Omega }{2}+\frac{\alpha }{2}\right] \frac{\partial \varphi _2 }{\partial \tau _1 } +\left[ \frac{i\Omega \phi _{1d} (\zeta +\alpha \phi _{1d} )}{4}+\frac{\phi _{1d} \alpha \zeta }{4}\right. \nonumber \\&\quad \left. -\frac{i(\sigma +\phi _{1d} \mu )\alpha }{4\Omega }+\frac{(\sigma +\phi _{1d} \mu )}{4}\right] \varphi _2 \nonumber \\&\quad +\,\left[ \frac{3\beta \phi _{1d} }{16\Omega ^{2}}-\frac{3(\sigma +\zeta \Omega \phi _{1d} +\mu )\beta }{16\Omega ^{4}}\right] \nonumber \\&\quad \varphi _2 \left| {\varphi _2 } \right| ^{2}-\frac{i\Omega \phi _{1d} F}{4}=0 \nonumber \\&O(\varepsilon ^{2}):\ldots \end{aligned}$$

(37)

The first relation of Eq. (37), taking the limit $\varepsilon \rightarrow 0$ in Eq. (36), is related to the fastest time scale. This expression can be integrated and presented in the following form:

$$\begin{aligned}&D_0 \varphi _2 +\left\{ \frac{i\Omega +\alpha }{2}\right\} \varphi _2 -\frac{3i\beta }{8\Omega ^{3}}\varphi _2 \left| {\varphi _2 } \right| ^{2}\nonumber \\&\quad =C(\tau _1 ,\tau _2 ,\ldots ) \end{aligned}$$

(38)

By limiting the system responses to the time scale $\tau _0$ and $\tau _1$, when $\tau _0 \rightarrow \infty$, parameters in $\tau _0$ order remains invariant, and $\varphi _2$ reaches an asymptotic equilibrium where $\varphi _2 =\varphi _2 (\tau _1 )$ and $(\tau _0 \rightarrow \infty :\frac{\partial \varphi _2 }{\partial \tau _\partial }=0)$. Accordingly, the equilibrium response (38) is calculated as follows:

$$\begin{aligned} \left\{ \frac{i\Omega +\alpha }{2}\right\} \varphi (\tau _1 )-\frac{3i\beta }{8\Omega ^{3}}\varphi (\tau _1 )\left| {\varphi (\tau _1 )} \right| ^{2}=C(\tau _1 ) \end{aligned}$$

(39)

Rewriting the above equation in a polar form $(\varphi (\tau _1 )=N(\tau _1 )e^{i\theta (\tau _1 )})$, it is obtained as follows:

$$\begin{aligned}&\frac{\alpha N(\tau _1 )}{2}e^{i\theta (\tau _1 )}+\left[ \frac{\Omega N(\tau _1 )}{2}-\frac{3\beta N(\tau _1 )^{3}}{8\Omega ^{3}}\right] ie^{i\theta (\tau _1 )}\nonumber \\&\quad =\left| {C(\tau _1 )} \right| e^{i\arg (C(\tau _1 ))} \end{aligned}$$

(40)

Fig. 2

Slow invariant manifold diagram of the system (the jump phenomenon and the saddle-node bifurcations) for $\Omega =1, \beta =1, \alpha =0.4$

The parameter magnitudes are obtained using the above equation as:

$$\begin{aligned} \left[ \frac{\alpha N(\tau _1 )}{2}\right] ^{2}+\left[ \frac{\Omega N(\tau _1 )}{2}-\frac{3\beta N(\tau _1 )^{3}}{8\Omega ^{3}}\right] ^{2}=\left| {C(\tau _1 )} \right| ^{2}\nonumber \\ \end{aligned}$$

(41)

Assuming $S(\tau _1 )=N^{2}(\tau _1 )$ Eq. (41) is obtained as follows:

$$\begin{aligned} \left[ \frac{\alpha }{2}\right] ^{2}S(\tau _1 )+\left[ \frac{\Omega }{2}-\frac{3\beta S(\tau _1 )}{8\Omega ^{3}}\right] ^{2}S(\tau _1 )=\left| {C(\tau _1 )} \right| ^{2}\nonumber \\ \end{aligned}$$

(42)

From Eq. (40), the relation between the angles is obtained from the following equation:

$$\begin{aligned} \theta (\tau _1 )=\arg (\left| {C(\tau _1 )} \right| )+\tan ^{-1}\left( \frac{3\beta S(\tau _1 )-4\Omega ^{4}}{4\alpha \Omega ^{3}}\right) \nonumber \\ \end{aligned}$$

(43)

The number of roots of Eq. (42) depends on the magnitudes of $\left| {C(\tau _1 )} \right|$, $\Omega$, $\beta$ and $\alpha$. The homogeneous Eq. (42), in accordance with the properties of cubic functions, is strictly a monotonic function (ascending or descending) or a non-monotonic function (with the maximum and minimum). In the monotonic case, independent of $\left| {C(\tau _1 )} \right|$, the equation has only one root, but in the non-monotonic case, depending on the magnitude of $\left| {C(\tau _1 )} \right|$, it has one or three roots, and parameter variations lead to generation of the saddle-node bifurcation; as a result, a set of stable and unstable branches are created. If the derivative of homogeneous part of Eq. (42) has real solution, non-monotonic case will occur; otherwise, system is strictly monotonic. The extrema of Eq. (42) can be obtained as follows:

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}S}\left\{ \left[ \frac{\alpha }{2}\right] ^{2}S(\tau _1 )+\left[ \frac{\Omega }{2}-\frac{3\beta S(\tau _1 )}{8\Omega ^{3}}\right] ^{2}S(\tau _1 )\right\} =0\nonumber \\&\quad \Rightarrow N_{1,2} =\sqrt{S_{1,2} }=\sqrt{\frac{4\Omega ^{3}}{3\beta }\left[ \frac{2\Omega }{3}\pm \frac{\sqrt{\Omega ^{2}-3\alpha ^{2}}}{3}\right] }\nonumber \\ \end{aligned}$$

(44)

Equation (44) demonstrates that for $\alpha <\Omega \sqrt{3}$ (relatively low damping) system has a pair of roots and the saddle-node bifurcations occur. Also, for $\alpha >\Omega \sqrt{3}$ it has a root, and saddle-node bifurcations do not occur at all [36]. At order $\tau _0$, if the system has a root, it will be stable, but if there are three roots, two of them will be stable and the other one will be unstable. In addition, the system ultimately is absorbed in one of the nodes at this order of time. Slow invariant manifold diagram of the system for parameters $\Omega =1$, $\beta =1$ and $\alpha =0.4$ is shown in Fig. 2. This concept was used based on [14, 37, 38]. This figure shows that there is a possibility for jump phenomenon between the regions because there are two stable response regions. This phenomenon causes relaxation oscillation on the behavior of the system [33]. This event occurs if the dynamic behavior of the system is absorbed in one of these stable branches; otherwise, it is possible that system absorbed in other regimes.

With the aim of investigating the occurrence of jump phenomenon, the behavior of the system around the stable slow invariant manifold, in the time order $\tau _1$ when $\tau _0 \rightarrow \infty$, should be studied. When $\tau _0 \rightarrow \infty$ it can be said that the parameters in $\tau _0$ order do not change at this time order, and if A is a temporal parameters in the system, one will have $\frac{\partial A}{\partial \tau _0 }=0$; however, these parameters still vary the order of $\tau _1$ because time $\tau _1$ is slower than $\tau _0$. Consequently, assuming $\Phi (\tau _1 )=\lim _{\tau _0 \rightarrow \infty } \varphi _2 (\tau _0 ,\tau _1 )$, the order $\upvarepsilon ^{1}$ of Eq. (37) becomes:

$$\begin{aligned}&\left[ \frac{i\Omega }{2}+\frac{\alpha }{2}\right] \frac{\partial \Phi }{\partial \tau _1 }-\frac{3i\beta }{8\Omega ^{3}}\frac{\partial }{\partial \tau _1 }\left[ \Phi \left| \Phi \right| ^{2}\right] \nonumber \\&\quad +\,\left[ \frac{3\beta \phi _{1d} }{16\Omega ^{2}}-\frac{3(\sigma +\zeta \Omega \phi _{1d} +\mu )\beta }{16\Omega ^{4}}\right] \Phi \left| \Phi \right| ^{2} \nonumber \\&\quad +\,\left[ \frac{i\Omega \phi _{1d} (\zeta +\alpha \phi _{1d} )}{4}+\frac{\phi _{1d} \alpha \zeta }{4}-\frac{i(\sigma +\phi _{1d} \mu )\alpha }{4\Omega }\right. \nonumber \\&\quad \left. +\frac{(\sigma +\phi _{1d} \mu )}{4}\right] \Phi -\frac{i\Omega \phi _{1d} F}{4}=0 \end{aligned}$$

(45)

Using complex numbers, one has:

$$\begin{aligned}&\left[ \frac{i\Omega +\alpha }{2}-\frac{3i\beta }{4\Omega ^{3}}\left| \Phi \right| ^{2}\right] \frac{\partial \Phi }{\partial \tau _1 }-\frac{3i\beta \left| \Phi \right| ^{2}}{8\Omega ^{3}}\frac{\partial \Phi ^{*}}{\partial \tau _1 }=G\rightarrow \nonumber \\&\quad G=-\left[ \frac{i\Omega \phi _{1d} (\zeta +\alpha \phi _{1d} )}{4}+\frac{\phi _{1d} \alpha \zeta }{4}\right. \nonumber \\&\quad \left. -\frac{i(\sigma +\phi _{1d} \mu )\alpha }{4\Omega }+\frac{(\sigma +\phi _{1d} \mu )}{4}\right] \Phi \nonumber \\&\quad +\,\left[ \frac{3\beta \phi _{1d} }{16\Omega ^{2}}-\frac{3(\sigma +\zeta \Omega \phi _{1d} +\mu )\beta }{16\Omega ^{4}}\right] \Phi \left| \Phi \right| ^{2}\nonumber \\&\quad +\,\frac{i\Omega \phi _{1d} F}{4} \end{aligned}$$

(46)

In order to obtain the expression of $\left( \frac{\partial \Phi }{\partial \tau _1 }\right)$, which indicates variation of slow dynamics of the system around the slow invariant manifold, and performing an algebraic manipulation, it is obtained as follows:

$$\begin{aligned}&\frac{\partial \Phi }{\partial \tau _1 }\nonumber \\&\quad =\frac{8\Omega ^{3}[[4\alpha \Omega ^{3}-4i\Omega ^{4}+6i\beta \left| \Phi \right| ^{2}]G+3i\beta \Phi ^{2}G^{*}]}{16\alpha ^{2}\Omega ^{6}+16\Omega ^{8}-48\Omega ^{4}\beta \left| \Phi \right| ^{2}+27\beta ^{2}\left| \Phi \right| ^{4}}\nonumber \\ \end{aligned}$$

(47)

Assuming $(\Phi (\tau _1 )=N(\tau _1 )e^{i\theta (\tau _1 )})$ and substituting in Eq. (46), one may obtain [14]:

$$\begin{aligned}&\left[ \frac{i\Omega +\alpha }{2}-\frac{3i\beta }{4\Omega ^{3}}N\left( \tau _1 \right) ^{2}\right] \left[ \left( \frac{\partial N\left( \tau _1 \right) }{\partial \tau _1 }\right. \right. \nonumber \\&\quad \left. \left. +iN\left( \tau _1 \right) \frac{\partial \theta \left( \tau _1 \right) }{\partial \tau _1 }\right) e^{i\theta \left( \tau _1 \right) }\right] -\frac{3i\beta N\left( \tau _1 \right) ^{2}}{8\Omega ^{3}}\nonumber \\&\quad \left[ \left( \frac{\partial N\left( \tau _1 \right) }{\partial \tau _1 }-iN\left( \tau _1 \right) \frac{\partial \theta \left( \tau _1 \right) }{\partial \tau _1 }\right) e^{-i\theta \left( \tau _1 \right) }\right] \nonumber \\&\quad =\left[ \frac{3\beta \phi _{1d} }{16\Omega ^{2}}-\frac{3\left( \sigma +\zeta \Omega \phi _{1d} +\mu \right) \beta }{16\Omega ^{4}}\right] N\left( \tau _1 \right) ^{3}e^{i\theta \left( \tau _1 \right) }\nonumber \\&\quad -\,\left[ \frac{i\Omega \phi _{1d} \left( \zeta +\alpha \phi _{1d} \right) }{4}+\frac{\phi _{1d} \alpha \zeta }{4}\right. \nonumber \\&\quad \left. -\frac{i\left( \sigma +\phi _{1d} \mu \right) \alpha }{4\Omega }+\frac{\left( \sigma +\phi _{1d} \mu \right) }{4}\right] N\left( \tau _1 \right) e^{i\theta \left( \tau _1 \right) }\nonumber \\&\quad +\,\frac{i\Omega \phi _{1d} F}{4} \end{aligned}$$

(48)

Each of the real and imaginary parts of this complex algebraic equation is an ordinary first-order equation. $\frac{\partial N(\tau _1 )}{\partial \tau _1 }$ and $\frac{\partial \theta (\tau _1 )}{\partial \tau _1 }$ can be obtained by solving these coupled differential equations as follows [14]:

$$\begin{aligned}&\frac{\partial N\left( \tau _1 \right) }{\partial \tau _1 }=-\phi _{1d} \left[ 16\phi _{1d} N\left( \tau _1 \right) \alpha \Omega ^{8}-16F\cos \left( \theta \right) \Omega ^{8}\right. \nonumber \\&\quad -\,16F\sin \left( \theta \right) \alpha \Omega ^{7}+16N\left( \tau _1 \right) \alpha ^{2}\xi \Omega ^{6}\nonumber \\&\quad +\,16N\left( \tau _1 \right) \xi \Omega ^{8}+9N\left( \tau _1 \right) ^{5}\beta ^{2}\xi \nonumber \\&\quad \left. +12F\cos \left( \theta \right) N\left( \tau _1 \right) ^{2}\beta \Omega ^{4}-24N\left( \tau _1 \right) ^{3}\beta \xi \Omega ^{4}\right] \nonumber \\&\quad /\{32\alpha ^{2}\Omega ^{6}+32\Omega ^{8}-96N\left( \tau _1 \right) ^{2}\beta \Omega ^{4}+54N\left( \tau _1 \right) ^{4}\beta ^{2}\} \nonumber \\&\frac{\partial \theta \left( \tau _1 \right) }{\partial \tau _1 }=-\left[ 16\phi _{1d} F\sin \left( \theta \right) \Omega ^{9}-16N\left( \tau _1 \right) \sigma \Omega ^{8}\right. \nonumber \\&\quad -\,27N\left( \tau _1 \right) ^{5}\beta ^{2}\sigma -36\phi _{1d} F\sin \left( \theta \right) N\left( \tau \right) ^{2}\beta \Omega ^{5}\nonumber \\&\quad -\,16\phi _{1d} F\cos \left( \theta \right) \alpha \Omega ^{8} +48N\left( \tau _1 \right) ^{3}\beta \sigma \Omega ^{4}\nonumber \\&\quad -\,16\phi _{1d} N\left( \tau _1 \right) \alpha ^{2}\mu \Omega ^{6}+48\phi _{1d} N\left( \tau _1 \right) ^{3}\beta \mu \Omega ^{4}\nonumber \\&\quad +\,16\phi _{1d} ^{2}N\left( \tau _1 \right) \alpha ^{2}\Omega ^{8}-16\phi _{1d} N\left( \tau _1 \right) \mu \Omega ^{8} \nonumber \\&\quad -\,12\phi _{1d} ^{2}N\left( \tau _1 \right) ^{3}\beta \Omega ^{6}+27\phi _{1d} ^{2}N\left( \tau _1 \right) ^{5}\beta ^{2}\Omega ^{2}\nonumber \\&\quad -\,27\phi _{1d} N\left( \tau _1 \right) ^{5}\beta ^{2}\mu -16N\left( \tau _1 \right) \alpha ^{2}\sigma \Omega ^{6}\nonumber \\&\quad \left. +24\phi _{1d} N\left( \tau _1 \right) ^{3}\alpha \beta \xi \Omega ^{4}\right] \nonumber \\&\quad \bigg /\left\{ 2N\left( \tau _1 \right) \Omega \left( 16\alpha ^{2}\Omega ^{6}+16\Omega ^{8}-48N\left( \tau _1 \right) ^{2}\beta \Omega ^{4}\right. \right. \nonumber \\&\quad \left. \left. +27N\left( \tau _1 \right) ^{4}\beta ^{2}\right) \right\} \end{aligned}$$

(49)

The possibility of occurrence of relaxation oscillation phenomenon can be investigated by plotting the phase plane of Eq. (49). These coupled equations give information about dynamics of the system at slow time scale. Equilibrium points are those which give numerators = 0 and denominator $\ne 0$. On the other hand, fold singularities which can generate SMR are those which satisfy both numerators = 0 and denominator = 0. In addition, denominator = 0 generates, fold lines in the system [14, 39, 40]. If the system is not under external load, it is clear that the amplitude of the system will be close to zero due to damping. In fact, in Fig. 2 jump from the high amplitude to the low amplitudes of stable slow invariant manifold is evident, but the system should be able to jump from low amplitudes to high amplitudes for occurrence of the SMR. This phenomenon occurs when the saddle-node bifurcation takes place in the phase plane $N(\tau _1 )-\theta (\tau _1 )$ at the low critical amplitudes equivalent to the amplitude of the system $SN_{1 }$ in Fig. 2. This means that in the lower branch direction, dynamic flows are changed upward in the lower branch and the probability of occurrence of the jump phenomenon from the low stable manifold to the high one and the SMR would exist. To calculate the magnitude of the external critical force (necessary condition of relaxation oscillation phenomenon) that occurs in the amplitude $SN_{1}$ (saddle-node bifurcation occurs), the numerator of Eq. (47) should be equal to zero [14, 30, 35]:

$$\begin{aligned}&27i\Phi \left| \Phi \right| ^{4}\beta ^{2}\phi _{1d}^2 \Omega ^{2}+24i\Phi \left| \Phi \right| ^{2}\alpha \beta \xi \phi _{1d} \Omega ^{4}\nonumber \\&\quad -\,12i\Phi \left| \Phi \right| ^{2}\beta \phi _{1d} ^{2}\Omega ^{6}-16i\alpha ^{2}\Phi \sigma \Omega ^{6} \nonumber \nonumber \\&\quad +\,48i\Phi \left| \Phi \right| ^{2}\beta \mu \phi _{1d} \Omega ^{4}-27i\Phi \left| \Phi \right| ^{4}\beta ^{2}\mu \phi _{1d} \nonumber \\&\quad +\,16\Omega ^{9}\phi _{1d} ^{2}\alpha \Phi -27i\Phi \left| \Phi \right| ^{4}\beta ^{2}\sigma \nonumber \nonumber \\&\quad +\,16\phi _{1d} \alpha ^{2}\Phi \xi \Omega ^{7}+16\Omega ^{9}\phi _{1d} \Phi \xi -16\Omega ^{9}\phi _{1d} F\nonumber \\&\quad -\,16i\Phi \sigma \Omega ^{8}-24\Phi \left| \Phi \right| ^{2}\beta \phi _{1d} \xi \Omega ^{5} \nonumber \\&\quad -\,16i\phi _{1d} F\alpha \Omega ^{8}+48i\Phi \left| \Phi \right| ^{2}\beta \sigma \Omega ^{4}\nonumber \\&\quad +\,24\phi _{1d} F\left| \Phi \right| ^{2}\beta \Omega ^{5}-12\phi _{1d} F\beta \Phi ^{2}\Omega ^{5} \nonumber \\&\quad -\,16i\phi _{1d} \mu \Phi \Omega ^{8}+9\phi _{1d} \Phi \left| \Phi \right| ^{4}\beta ^{2}\xi \Omega \nonumber \\&\quad +\,16i\phi _{1d}^2 \alpha ^{2}\Phi \Omega ^{8}-16i\phi _{1d} \alpha ^{2}\mu \Phi \Omega ^{6}=0 \end{aligned}$$

(50)

Assuming polar relation $(\Phi =N(\tau _1 )e^{i\theta (\tau _1 )})$ and trigonometric simplification, complex Eq. (50) is separated into two real equations:

$$\begin{aligned}&12{ FN}\left( \tau \right) ^{2}\beta \Omega ^{5}\cos \left( \theta \right) -16\cos \left( \theta \right) \Omega ^{9}F\nonumber \\&\quad -\,16\sin \left( \theta \right) F\alpha \omega _0 ^{8}+16\Omega ^{9}\phi _{1d} \alpha N\left( \tau \right) \nonumber \\&\quad +\,16\alpha ^{2}N\left( \tau \right) \xi \Omega ^{7} +16\Omega ^{9}N\left( \tau \right) \xi \nonumber \\&\quad -\,24N\left( \tau \right) ^{3}\beta \xi \Omega ^{5}+9N\left( \tau \right) ^{5}\beta ^{2}\xi \omega _0 =0 \nonumber \\&\quad 16\phi _{1d} F\sin \left( \theta \right) \Omega ^{9}-16N\left( \tau \right) \sigma \Omega ^{8}\nonumber \\&\quad -\,27N\left( \tau \right) ^{5}\beta ^{2}\sigma -36\phi _{1d} F\sin \left( \theta \right) N\left( \tau \right) ^{2}\beta \Omega ^{5}\nonumber \\&\quad -\,16\phi _{1d} F\cos \left( \theta \right) \alpha \Omega ^{8} +48N\left( \tau \right) ^{3}\beta \sigma \Omega ^{4}\nonumber \\&\quad -\,16\phi _{1d} N\left( \tau \right) \alpha ^{2}\mu \Omega ^{6}+48\phi _{1d} N\left( \tau \right) ^{3}\beta \mu \Omega ^{4}\nonumber \\&\quad +16\phi _{_{1d} }^2 N\left( \tau \right) \alpha ^{2}\Omega ^{8}-12\phi _{_{1d} }^2 N\left( \tau \right) ^{3}\beta \Omega _0 ^{6} \nonumber \\&\quad -\,16\phi _{1d} N\left( \tau \right) \mu \Omega ^{8}+27\phi _{_{1d} }^2 N\left( \tau \right) ^{5}\beta ^{2}\Omega ^{2}\nonumber \\&\quad -\,27\phi _{1d} N\left( \tau \right) ^{5}\beta ^{2}\mu -16N\left( \tau \right) \alpha ^{2}\sigma \Omega ^{6}\nonumber \\&\quad +\,24\phi _{1d} N\left( \tau \right) ^{3}\alpha \beta \xi \Omega ^{4}=0 \end{aligned}$$

(51)

Two unknowns $\sin (\theta (\tau ))$ and $\cos (\theta (\tau ))$ are calculated by solving these equations as follows [39]:

$$\begin{aligned}&\cos (\theta (\tau ))=\frac{\left( {4\alpha \phi _{_{1d} }^2 \Omega ^{4}+4\zeta \phi _{1d} \Omega ^{4}-3\phi _{_{1d} }^2 N\left( \tau \right) ^{2}\beta \zeta -4\alpha \phi _{_{1d} }^2 \mu \Omega ^{2}-4\alpha \sigma \Omega ^{2}} \right) N\left( \tau \right) }{4\phi _{1d} F\Omega ^{4}}\nonumber \\&\sin \left( {\theta (\tau )} \right) =\frac{\left( {4\alpha \zeta \phi _{1d} \Omega ^{4}+3\phi _{_{1d} }^2 N\left( \tau \right) ^{2}\beta \Omega ^{2}+4\mu \phi _{1d} \Omega ^{4}+4\sigma \Omega ^{4}-3\phi _{1d} N\left( \tau \right) ^{2}\beta \mu -3N\left( \tau \right) ^{2}\beta \sigma } \right) N\left( \tau \right) }{4\phi _{1d} F\Omega ^{5}} \end{aligned}$$

(52)

Finally, the angle $\theta$ can be obtained as:

$$\begin{aligned} \theta _{[i]}= & {} \sin ^{-1}\left( \frac{4\alpha \Omega ^{3}}{\sqrt{16\alpha ^{2}\Omega ^{6}+16\Omega ^{8}-24N_{[i]} (\tau )^{2}\beta \Omega ^{4}+9N_{[i]} \left( \tau \right) ^{4}\beta ^{2}}}\right) \nonumber \\&\quad \pm \cos ^{-1}\left( \frac{N_{[i]} (\tau )\phi _{1d} \left( {16\phi _{1d} \alpha ^{2}\zeta \Omega ^{6}+16\Omega ^{8}\alpha +16\Omega ^{8}\zeta -24N_{[i]} (\tau )^{2}\beta \zeta \Omega ^{4}+9N_{[i]} (\tau )^{4}\beta ^{2}\zeta } \right) }{4\Omega ^{4}\phi _{1d} F\sqrt{\left( {16\alpha ^{2}\Omega ^{6}+16\Omega ^{8}-24N_{[i]} (\tau )^{2}\beta \Omega ^{4}+9N_{[i]} (\tau )^{4}\beta ^{2}} \right) }}\right) \end{aligned}$$

(53)

Substituting each of the two critical amplitudes $N_{1}$ and $N_{2}$ in Eq. (44), into the above equation, gives angles at which saddle-node bifurcations occur in the low and high critical amplitudes, respectively. The critical magnitude of the external forces $F_{\mathrm{critical}[i]} (i=1\ldots 2)$ for occurrence of the saddle-node bifurcations is obtained from Eq. (53), when the absolute value of the argument of $\cos ^{-1}$ is equal to unity:

$$\begin{aligned}&F_{critical[i]} \nonumber \\&\quad =\frac{N_i \left( {16\phi _{1d} \alpha \Omega ^{8}+16\alpha ^{2}\xi \Omega ^{6}+16\xi \Omega ^{8}-24N_i ^{2}\beta \xi \Omega ^{4}+9N_i ^{4}\beta ^{2}\xi } \right) }{4\Omega ^{4}\sqrt{16\alpha ^{2}\Omega ^{6}+16\Omega ^{8}-24N_i ^{2}\beta \Omega ^{4}+9N_i ^{4}\beta ^{2}}} \end{aligned}$$

(54)

When the magnitude of external load is smaller than the first critical amplitude, all trajectories are finally attracted to fixed points which are below the unstable region (as shown in Figs. 11, 23). If the magnitude of the external force is greater than the first critical amplitude and smaller than the second critical amplitude $(F_\mathrm{critical[2]}>F>F_\mathrm{critical[1]} )$, the saddle-node bifurcations will occur in the lower critical amplitude, and the node will disappear in lower stable regions (as shown in Fig. 12). If the magnitude of the external force is greater than the second critical amplitude, the saddle-node bifurcation will occur in the upper critical amplitude, and the node will appear in high amplitudes (as shown in Fig. 21). Consequently, it can be inferred that the necessary condition for the occurrence of the SMR in the system and jumping from the low amplitude to the high amplitude, is that the magnitude of the external excitation should be greater than the first critical amplitude $(F>F_\mathrm{critical[1]} )$.

To check that whether the system jumps repetitively from the high amplitude to the low one and vice versa along with the slow invariant manifold of system and the SMR occurrence, a map is considered. This map illustrates that whether a dynamic flow that starts from a point with lower critical amplitude $N_{1}$ and angle between $\theta _1$ and $\theta _2$, after a double jump (rapid flow dynamics) and a double slow dynamic flow where a closed loop is formed, finally returns to this region or not (according to Figs. 13, 20). These four parts of the motion can be seen in the closed loop in Fig. 14. This is achieved by examining the dynamic flow angle $\theta (\tau )$ over time. If the dynamic flow returns to the first region (between $\theta _1$ and $\theta _2$), the SMR will occur in the system surely [33]. In other words, it is the sufficient condition for the existence of the SMR behavior. This map is called the sustained jumping map. After periods of time, may be the system be absorbed in other regimes in the system response, where no relaxation oscillation phenomenon can be seen. For example, it may be attracted to a node, which represents a simple oscillatory response with a constant amplitude and frequency (as shown in Fig. 29).

Since jump phenomenon occurs rapidly, it can be said that the energy $\left| C \right|$ in the system remains constant during its occurrence; moreover, according to Eq. (41), when the system jumps from a point with amplitude $N_{1}$ to a point with amplitude $N_{u}$ (see Fig. 2), one has from the balance of energy [14]:

$$\begin{aligned}&\left[ \frac{\alpha }{2}\right] ^{2}S_1 (\tau _1 )+\left[ \frac{\Omega }{2}-\frac{3\beta S_1 (\tau _1 )}{8\Omega ^{3}}\right] ^{2}S_1 (\tau _1 )\nonumber \\&\quad =\left| {C(\tau _1 )} \right| ^{2}=\left[ \frac{\alpha }{2}\right] ^{2}S_u (\tau _1 )\nonumber \\&\qquad +\,\left[ \frac{\Omega }{2}-\frac{3\beta S_u (\tau _1 )}{8\Omega ^{3}}\right] ^{2}S_u (\tau _1 )\Rightarrow \nonumber \\&\quad \left[ \frac{\alpha }{2}\right] ^{2}S_u +\left[ \frac{\Omega }{2}-\frac{3\beta S_u }{8\Omega ^{3}}\right] ^{2}S_u \nonumber \\&\quad =\frac{2\Omega ^{3}(\sqrt{\Omega ^{2}-3\alpha ^{2}}-2\Omega )(3\alpha ^{2}+\Omega ^{3}+\Omega \sqrt{\Omega ^{2}-3\alpha ^{2}})}{81\beta }\nonumber \\&\quad \Rightarrow S_u =\left| {N_u } \right| ^{2}=\frac{8\Omega ^{3}}{9\beta }\left[ \Omega +\sqrt{\Omega ^{2}-3\alpha ^{2}}\right] \end{aligned}$$

(55)

Similarly, from the balance of energy between the points, the end of the jump with lower amplitude $(N_d )$ and the point with the amplitude $(N_2 )$, the amplitude $(N_d )$ value can be obtained by some mathematical manipulations as follows [14]:

$$\begin{aligned} S_d =\left| {N_d } \right| ^{2}=\frac{8\Omega ^{3}}{9\beta }[\Omega -\sqrt{\Omega ^{2}-3\alpha ^{2}}] \end{aligned}$$

(56)

To determine the changes of angle value in the jump, it can be noticed that the magnitude of $C(\tau _1 )$ [which is actually a sign of energy in the system, Eq. (39)] is constant. Using $\varphi (\tau _1 )=N(\tau _1 )e^{i\theta (\tau _1 )}$, it will be:

$$\begin{aligned}&\left[ \frac{\alpha N_1 }{2}+i\left[ \frac{\Omega N_1 }{2}-\frac{3\beta N_1^3 }{8\Omega ^{3}}\right] \right] e^{i\theta _1 }\nonumber \\&\quad =\left[ \frac{\alpha N_u }{2}+i\left[ \frac{\Omega N_u }{2}-\frac{3\beta N_u^3 }{8\Omega ^{3}}\right] \right] e^{i\theta _u }\nonumber \\&\Rightarrow \sqrt{\left( \frac{\alpha N_1 }{2}\right) ^{2}+\left( \frac{\Omega N_1 }{2}-\frac{3\beta N_1^3 }{8\Omega ^{3}}\right) ^{2}}e^{i\theta _1}\nonumber \\&e^{i\tan ^{-1}\left( \frac{{4\Omega }^{4}-3N_1^2 \beta }{4\alpha \Omega ^{3}}\right) }\nonumber \\&\quad =\sqrt{\left( \frac{\alpha N_u }{2}\right) ^{2}+\left( \frac{\Omega N_u }{2}-\frac{3\beta N_u^3 }{8\Omega ^{3}}\right) ^{2}}e^{i\theta _u }\nonumber \\&e^{i\tan ^{-1}\left( \frac{{4\Omega }^{4}-3N_u^2 \beta }{4\alpha \Omega ^{3}}\right) } \end{aligned}$$

(57)

The equality of magnitudes was expressed in Eq. (55). Based on the equality of angles in Eq. (57), one can write:

$$\begin{aligned}&\theta _1 +\tan ^{-1}\left( \frac{{4\Omega }^{4}-3N_1^2 \beta }{4\alpha \Omega ^{3}}\right) =\theta _u \nonumber \\&\quad +\,\tan ^{-1}\left( \frac{{4\Omega }^{4}-3N_u^2 \beta }{4\alpha \Omega ^{3}}\right) \Rightarrow \theta _u =\theta _1 \nonumber \\&\quad +\,\tan ^{-1}\left( \frac{{4\Omega }^{4}-3N_1^2 \beta }{4\alpha \Omega ^{3}}\right) -\tan ^{-1}\left( \frac{{4\Omega }^{4}-3N_u^2 \beta }{4\alpha \Omega ^{3}}\right) \nonumber \\ \end{aligned}$$

(58)

Fig. 3

Existence of the saddle-node bifurcations in the parameter space of $F, \alpha$ and d for $\sigma =1$, $\mu =-1$

Using trigonometric relations, it will be:

$$\begin{aligned} \theta _u =\theta _1 +\tan ^{-1}\left( \frac{9\alpha \sqrt{\Omega ^{2}-3\alpha ^{2}}}{15\alpha ^{2}-\Omega \sqrt{\Omega ^{2}-3\alpha ^{2}}-\Omega ^{2}}\right) \nonumber \\ \end{aligned}$$

(59)

Change of the angle between two points with the amplitude $N_{2}$ and $N_{d}$ in the second jump which is similar to the above can be obtained as follows:

$$\begin{aligned} \theta _d =\theta _2 -\tan ^{-1}\left( \frac{9\alpha \sqrt{\Omega ^{2}-3\alpha ^{2}}}{15\alpha ^{2}+\Omega \sqrt{\Omega ^{2}-3\alpha ^{2}}-\Omega ^{2}}\right) \nonumber \\ \end{aligned}$$

(60)

4 Numerical methods

The coupled equations of the pipe conveying fluid and nonlinear energy sink, Eq. (19), are transferred into the state-space equations using the Galerkin method for n modes of pipe. The equations are solved numerically using Ode45 in MATLAB.

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t}q_j =q_{j+1} \nonumber \\&\frac{\hbox {d}}{\hbox {d}t}q_{j+1} =\left[ \varepsilon \frac{F}{\phi _{1d} }\cos (\Omega t)-m_{jj} (\Omega ^{2}+\varepsilon \sigma )\sum _{i=1}^n {\phi _i } q_i\right. \nonumber \\&\left. \quad -\,\varepsilon \frac{\zeta }{\phi _{1d} }\sum _{i=1}^n {\phi _i } q_{i+1} -\varepsilon \frac{\mu }{\phi _{1d} }\sum _{i=1}^n {\phi _i } q_i\right. \nonumber \\&\left. \quad -\,\varepsilon \alpha \left\{ \sum _{i=1}^n {\phi _i } q_{i+1} -q_{n+2} \right\} \right. \nonumber \\&\left. \quad -\,\varepsilon \beta \left\{ \sum _{i=1}^n {\phi _i } q_i -q_{n+1} \right\} ^{3}\right] \Bigg /m_{jj} \nonumber \\&\frac{\hbox {d}}{\hbox {d}t}q_{n+1} =q_{n+2} \nonumber \\&\frac{\hbox {d}}{\hbox {d}t}q_{n+2} =-\alpha \left\{ q_{n+2} -\sum _{i=1}^n {\phi _i } q_{i+1} \right\} -\beta \left\{ q_{n+1}\right. \nonumber \\&\quad \left. -\sum _{i=1}^n {\phi _i } q_i \right\} ^{3} \end{aligned}$$

(61)

5 Results of analytical and numerical solutions

In this section, the numerical examples are illustrated. To check the method of solution, the case of a straight clamped-clamped pipe conveying fluid with circular cross section is investigated. The geometrical parameters of the system are defined as $D=1$m, $L=10$m, $t=0.02$.

The material properties and working conditions are chosen for steel and oil; thus, $\rho _\mathrm{p}=140$ kg/m, $E_\mathrm{p}=207$ Gpa, $\rho _{f}$ =680 kg/m, $c_\mathrm{p}=30$ N s m$^{-2}$, $U_{f} =5$ m/s. From Eqs. (13) and (16) the resonant frequency of the first mode of primary system would be $\omega _1 =\sqrt{k_{11} /m_{11} }=1$. After performing some algebraic calculations, one gets the following dimensionless quantities $\zeta =0.01,\mu =-1$.

Fig. 4

Existence of the saddle-node bifurcations in the parameter space of F, $\alpha$ and d for $\sigma =1$, $\mu =-2$

In order to investigate optimal parameters for NES on pipe, one may study the saddle-node and Hopf bifurcations and magnitude of external force for occurrence of the relaxation oscillation phenomenon. Diagram of saddle-node bifurcations for $\sigma =1$, $\xi =0.01$, $\mu =-1$ is shown in Fig. 3.

This graph is in the parameter space of F, $\alpha$ and d which are the non-dimensional damping of the NES, non-dimensional amplitude of the external load and non-dimensional distance of the NES location from the pipe supports, respectively. It can be seen that, in this space, the saddle-node bifurcations would occur for $0<d<0.2$, $0.8<d<1$ and a small region for $0.3<d<0.7$. This means that locating the NES close to the middle of the pipe leads to occurrence of the saddle-node bifurcations only for small regions. In addition, the amplitudes of the external force in which the saddle-node bifurcations happen will decrease. On the other hand, the saddle-node bifurcations will occur for large regions by locating the NES close to the pipe supports. Also, the amplitudes of external force in which the saddle-node bifurcations happen will increase by approaching the location of NES to the pipe supports. It is obvious because the vibration amplitude is smaller where the NES is close to the pipe supports; hence, greater forces are needed for excitation.

Also, the saddle node occurs for smaller NES damping values close to the pipe supports. The saddle-node bifurcations are heavily dependent on the detuning parameter. For example, for $\sigma =3$, the saddle-node bifurcations occur in the whole length of the pipe. Also occurrence of the saddle-node bifurcations is dependent on the fluid velocity and damping of the pipe. The probability of occurrence of saddle-node bifurcation increases slightly, i.e., instability increases, by increasing the fluid velocity and decreasing the system damping (see Fig. 4).

Fig. 5

Space of the saddle-node bifurcations for positive and negative values of detuning parameter ($\mu =-1$, $d=0.2$)

In additional projection of the solutions of Eqs. (27) and (28), the three-dimensional space of parameters (F, $\alpha$, $\sigma$) and the saddle-node bifurcations boundary for various positive and negative detuning values $\sigma$ are presented in Fig. 5.

Hopf bifurcation diagram in parameter space (F, $\alpha$, $\sigma$) is depicted in Fig. 6. For $\sigma =1$, with the installation of NES, in the entire length of the pipe, Hopf bifurcation occurs ($0<d<1$). Similar to the saddle-node bifurcation diagram, the amplitudes of the external load decrease by increasing distance of NES from the pipe supports. Studies have shown that unlike the saddle-node bifurcations, Hopf bifurcation occurrence is not highly dependent on changes of detuning parameter ($\sigma$). In addition, it can be inferred that if the fluid velocity increases (increasing $\mu$), surface of Fig. 6 will be shifted upward slightly (increasing critical force amplitude).

Fig. 6

Existence of the Hopf bifurcations in the parameter space of F, $\alpha$ and d for $\sigma =1$, $\mu =-1$

Fig. 7

Amplitudes of the external force for occurrence of the SMR in the parameter space of F, $\alpha$ and d

Fig. 8

Occurrence of Hopf and saddle-node bifurcations and critical amplitudes of external force for $d=0.5$, $\sigma =1$, $\mu =-1$

Fig. 9

Force response diagram of the system for $d=0.5$, $\alpha =0.4$, $\sigma =1$, $\mu =-1$

Fig. 10

Force response diagram of the system for $d=0.5$, $\alpha =0.4$, $\sigma =1$, $\mu =-3$

Fig. 11

Phase plane of the slow motion of the system for $d=0.5$, $\alpha =0.4$, $F=0.3$, $\sigma =1$, $\mu =-1$ (point 1 in Fig. 8)

Fig. 12

Phase plane of the slow motion of the system for $d=0.5$, $\alpha =0.4$, $F=1.2$, $\sigma =1$, $\mu =-1$ (point 2 in Fig. 8)

Fig. 13

Sustained jumping map (occurrence of the SMR) for $d=0.5$, $\alpha =0.4$, $F=1.2$, $\sigma =1$, $\mu =-1$ (point 2 in Fig. 8)

Fig. 14

Trajectory of the slow motion of the system in the phase plane for $d=0.5$, $\alpha =0.4$, $F=1.2$, $\sigma =1$, $\mu =-1$ (point 2 in Fig. 8)

Fig. 15

Frequency response diagram of the system for $d=0.5$, $\alpha =0.4$, $F=1.2$, $\mu =-1$ (point 2 in Fig. 8)

Fig. 16

Time history of the system (the existence of the SMR) for $d=0.5$, $\alpha =0.4$, $F=1.2$, $\sigma =-2$, $\mu =-1$ (point 2 in Fig. 8)

Fig. 17

Poincare map of the relative displacement $d=0.5$, $\alpha =0.4$, $F=1.2$, $\sigma =1$, $\mu =-1$ (point 2 in Fig. 8)

Fig. 18

Frequency spectrum for the relative displacement $d=0.5$, $\alpha =0.4$, $F=1.2$, $\mu =-1$ (point 2 in Fig. 8) and $\sigma =0$

Fig. 19

Frequency response curve of the system for $d=0.5$, $\alpha =0.4$, $F=1.9$, $\mu =-1$ (point 3 in Fig. 8)

Figure 7 shows the magnitude of critical external force for the occurrence of SMR in the parameter space of F, $\alpha$ and d. Studies show that these critical values are not dependent on the detuning parameter value ($\sigma$). Unlike the saddle-node and Hopf bifurcations, in this case, amplitude of critical external force increases by approaching the NES location at the middle of the pipe. In addition, it can be seen that changing the position of the NES does not affect the range of NES damping in which the SMR occurs. This range would be $0<\alpha <\Omega /\sqrt{3}$ that can be obtained from Eq. (44). Furthermore, amplitude of critical external force has a direct relation with the value of pipe damping and is not sensitive to the fluid velocity changes.

The above discussions show that the dynamic behavior of the coupled pipe conveying fluid and the NES performance are quietly dependent on the location of the NES on the pipe (d). For this reason and symmetry in boundary conditions of the pipe, four sections on the pipe ($d=0.5$, $d=0.35$, $d=0.19$ and $d=0.1$) are selected to investigate the optimal parameters of NES. The system can show various dynamic behaviors, depending on the parameters of the system located at each zone of the F-$\alpha$ space [33]. The first selected section for NES position is at the middle of the pipe. When the NES is positioned on the middle of the pipe, spatial parameter of the system is $\phi _{1d} =1.5581$; hence, the required calculations are performed for $\sigma =1$. For this case, Fig. 8 shows Hopf and saddle-node bifurcation diagrams and critical amplitudes of external force (necessary condition for the occurrence of SMR phenomenon) for $\sigma =1$. If NES is in the middle of the pipe, the saddle-node bifurcation region will be very small. Therefore, the dynamic behavior of the system in three points 1, 2 and 3 in Fig. 8 is studied. For these points, the phase plane of slow motion Eq. (49), the sustained jumping map and the frequency response curve are analyzed for different parameters. According to Figs. 4, 6 and 7, if the fluid velocity increases (increasing $\mu$), Fig. 8 will change slightly. Hopf bifurcation area will be extended and will be shifted upward slightly. Also, the saddle-node regions will be extended slightly and critical force borders will not move. Generally, there is no basic change in the nature of Fig. 8.

To understand what was said about the bifurcation analyses, a single plot of Fig. 9 is presented where the amplitude of the steady-state periodic solution $\left| {\varphi _{2f} } \right|$ is depicted as a function of the amplitude of the external harmonic load for ($\sigma =1$, $\mu =-1$, $\alpha =0.4$). In Fig. 8 for $\alpha =0.4$, increasing the external force value leads to cutting the boundaries of Hopf bifurcation in two points $H_{1}$ and $H_{2}$, and the instability will appear between these two points. Due to motion in this path, one does not cut the saddle-node bifurcation borders; therefore, there is no jump phenomenon in Fig. 9. Boundary of instability in Fig. 8 is consistent with Fig. 9.

Also, as expected, the amplitude of steady state of relative displacement of the pipe and NES increases smoothly by increasing the external excitation value. Furthermore, the schematic of Fig. 9 with formation of a turning point changes slowly to the schematic of Fig. 10 by increasing the fluid velocity. As a result, amplitude of the steady-state response decreases slowly and the required force magnitude for occurrence of the WMR increases. Also, the unstable region (Hopf bifurcation) is extended slightly.

In Fig. 11, the phase plane of the slow motion of point 1 is illustrated ($d=0.5$, $\alpha =0.4$, $\sigma =1$, $\mu =-1$, $F=0.3$). As shown in Fig. 11, there is only one node in the phase plane of this point because the excitation force magnitude of point 1 is smaller than the critical value. As it was shown, all trajectories in this diagram approach a node with amplitude value of 0.3 which represents a periodic motion of the system based on the complexification-averaging method. In this case the external force on the system is smaller than the critical value ($F<F_\mathrm{critical [1]})$; thus, it does not satisfy the necessary condition of the SMR; hence, there is no need to check the sufficient condition of the SMR (sustained jumping map).

Amplitude of excitation force at point 2 is in the region of Hopf bifurcation and above the critical force (regarding the necessary condition for the SMR). This phenomenon is a probable reason for the SMR occurrence; therefore, the necessary condition for jumping between the lower and upper amplitudes will be met in this position. The phase plane of this case is drawn in Fig. 12 which shows that the node has been disappeared. Also, it can be seen that jumping from the low amplitude to the high amplitude can happen due to the bifurcation in the lower amplitudes. In order to determine when the SMR definitely occurs, one should check sufficient conditions for existence and continuation of the jump phenomenon. The expected diagram is shown in Fig. 13 (sustained jumping map).

As it can be seen, after a high number of oscillations (each oscillation includes two jumps and two slow parts of the slow-varying response), all of the closed paths, which indicate that the presence of the SMR, would reach to a unit angle $(\theta =-0.12\, \hbox {radian})$. This fact proves that if the dynamic flow starts from all points of the region between the angles $\theta _1$ and $\theta _2$ on the amplitude N$_{1}$, it will reach the first region (between the angles $\theta _1 -\theta _2 )$.

In order to show this issue schematically, the trajectory of the system is drawn in Fig. 14, which ultimately would be attracted to the four-part motion and form a closed loop.

Considering the motion with the amplitude $\hbox {N}_{1}$, it can be seen that the system is transferred with a rapid move (jump) to a point with the amplitude $N_{u}$; then, the flow can be transmitted to a point with amplitude $N_{2}$ via the slow dynamic motion. Here, with a jump back to the stable region with low amplitude, it turns and reaches to a point with amplitude $N_{d}$. Then, it moves through a slow flow to a point with amplitude $N_{1}$. As it stands from Fig. 14, system is abandoned at position $\theta =1$ and $N=N_{1}$; then, after twice oscillations, it swings to the left side and forms a stable closed loop, which is the sign of the occurrence of SMR.

According to Eq. (26), the frequency response curve with aforesaid system parameters at point 1 is studied. The system has only one stable response. In this case, the SMR and WMR (which is due to the general Hopf bifurcation) do not occur. For the parameters at point 2, as it can be seen in Fig. 15, the saddle-node and Hopf bifurcations occur. Also, for some values of detuning parameter, there are three types of responses. It should be noted that for $-10.1<\sigma <12.8$ and $-2.8<\sigma <5.3$, the SMR and the WMR occur, respectively. For $4.2<\sigma <8.1$, a high amplitude periodic motion exists. The frequency response curves are not highly sensitive to changes of the fluid velocity. In general, the amplitude of response decreases and the range of the Hopf bifurcations are extended slightly by increasing the fluid velocity. Furthermore, it can be seen that, for $\sigma =7$, the system can have three different solutions that are high-amplitude periodic motion, low-amplitude periodic motion and SMR. The numerical results demonstrate that only the low-amplitude periodic motion occurs for $\sigma =7$. Also, for $\sigma =-2$, regarding the analytical results, two different responses exist that are the WMR and the SMR, but the numerical results for an arbitrary initial condition illustrate that only the SMR exists for $\sigma =-2$. In this case, due to the existence of the SMR, the dynamic behavior of the system does not approach the WMR (Fig. 16).

In order to evaluate the behavior of the system for these values of the parameters, time response, Poincare map and frequency spectrum are obtained using the numerical methods Eq. (61). As it is expected, by studying the pipe and NES coupled systems for parameters of point 2 in Fig. 8, only the SMR occurs for any initial conditions. In fact, the SMR does not let the behavior of the system approach WMR

Additionally, the time histories of the system with one, two and three Galerkin modes are depicted in Fig. 16. It is obvious that the steady-state response with one, two or three Galerkin modes are similar. Indeed, this figure proves that the higher Galerkin modes are effective only for the transient behavior. Consequently, as it was mentioned before, since the system is excited periodically, Galerkin approximation with the first mode is sufficient to analyze the steady-state dynamic’ behavior.

As expected, the Poincare map and frequency spectrum, related to pipe and NES vibrations for point 2 in Fig. 8, are consistent with the time history diagram. Figure 17 shows the Poincare map of the steady-state response of the system in the form of a continuous closed loop constituted by a large number of points which indicates the existence of a quasi-periodic motion.

Three peaks at main harmonics $\Omega$, 3$\Omega$ and 5$\Omega$ are evidenced in the frequency spectrum of the response of the system (Fig. 18). The results show that $\Omega$ is the strongest component in the response, and 3$\Omega$ and 5$\Omega$ are the other components in the frequency spectrum of the pipe response. These results are consistent with those of [41].

The frequency response curve for the system parameters at point 3 is drawn in Fig. 19. The system has stable response with the high amplitude for $4.2<\sigma <9.8$. In this case, the SMR occurs for $-13.7<\sigma <2.2$, and the WMR can be seen for $-4.5<\sigma <-0.9$ and $6.2<\sigma <6.9$ and saddle node occurs for two ranges $4.2<\sigma <4.7$ and $6.2<\sigma <9.8$.

Fig. 20

Sustained jumping map (the absence of the SMR) for $d=0.5$, $\alpha =0.4$, $F=1.2$, $\mu =-1$ (point 2 in Fig. 8) and $\sigma =5$

Fig. 21

Phase plane of the slow motion for $d=0.5$, $\alpha =0.4$, $F=2$, $\sigma =1$, $\mu =-1$ (point 5 in Fig. 8)

Fig. 22

Occurrence of Hopf and saddle-node bifurcations and critical magnitude of external force for $d=0.35$, $\sigma =1$, $\mu =-1$

Fig. 23

Phase plane of the slow motion of the system for $d=0.35$, $\alpha =0.4$, $F=0.4$, $\sigma =1$, $\mu =-1$ (point 4 in Fig. 22)

Fig. 24

Monte Carlo simulations of steady-state attractors of the dynamics for randomly varying initial conditions $d=0.35$, $\alpha =0.4$, $F=1$, $\sigma =1$, $\mu =-1$ (point 5 in Fig. 22)

Fig. 25

Occurrence of Hopf and saddle-node bifurcations and critical magnitude of external force for $d=0.19$, $\sigma =1$, $\mu =-1$

Fig. 26

Force response diagram of the system for $d=0.19$, $\alpha =0.4$, $\sigma =1$, $\mu =-1$

Fig. 27

Frequency response curve of the system for $d=0.19$, $\alpha =0.4$, $F=0.4$, $\sigma =1$, $\mu =-1$ (point 8 in Fig. 25)

Fig. 28

Phase plane of the slow motion for $d=0.19$, $\alpha =0.4$, $F=0.4$, $\sigma =1$, $\mu =-1$ (point 8 in Fig. 25)

In order to examine the SMR occurrence for $\sigma =5$, at point 2 (Fig. 8), it is required to check sufficient conditions for existence and ongoing of the jump phenomenon from the high amplitude to the low amplitude and vice versa (sustained jumping map). The investigation shows that after thousands of oscillations, all the trajectories reach to an angle $\theta =-7.3\,\hbox {radian}$ (Fig. 20).

The other difference between the dynamical behavior of point 2 and that of point 3 is the existence of a node in the slow-motion phase plane of point 3 within the high-amplitude range. (In other words, one can say that at point 2, the node is in the unstable region, between critical amplitudes $N_{1}$ and $N_{2}$.) The phase portrait of the slow motion of the system for parameters of point 3 is demonstrated in Fig. 21. For the loads higher than value of point 3, this node gets away from the critical amplitude $N_2$ and its absorption region gets larger.

The next location of the NES position is $d=0.35$. In this case, the spatial parameter of the system is $\phi _{1d} =1.2987$. Figure 22 shows the occurrence of Hopf and saddle-node bifurcations and the amplitudes of the critical external force for occurrence of SMR in the F-$\alpha$ space. In this section, for points 4, 5 and 6 in Fig. 22, the dynamic behaviors of the system are studied.

In this parameter space, the saddle-node bifurcation region is very small in the system as it was in Fig. 8. The schematic of variations of the steady-state response versus excitation force amplitude in Fig. 22 is similar to Fig. 9.

As discussed in the preceding case, like point 1 in Fig. 8, since amplitude of excitation force at point 4 in Fig. 22 is under the first critical excitation, $F>F_{critical[1]}$ and below the Hopf bifurcation (see Fig. 23), the phase plane shows only one node which is closer to the lower critical amplitude $N_{1}$ in comparison with the point 1 in Fig. 8. It is worthy to mention that the absorption area of this node is smaller than that of the phase plane diagram of point 1 which shows that the numerical results are in accordance with the analytical ones, and the system is attracted to a periodic motion with the amplitude of 0.61 for any arbitrary initial conditions. This point is under the curve of critical force; hence, there the necessary condition for the SMR is not met. In addition, the frequency response curve of the system for point 4 is similar to that of point 1. The dynamical behavior of the system at point 5 is identical to that of point 2; thus, the SMR happens in this case. The only difference between the dynamical behaviors of point 5 and point 4 is the existence of the node in the slow-motion phase plane of point 4. Since, the parameters of the system are located inside the Hopf bifurcation area at point 5, the node does not exist in the slow-motion phase plane. The range of existence of the SMR, WMR and high-amplitude periodic motion would be $-5.2<\sigma <7.7$, $-1.3<\sigma <3.5$ and $3.2<\sigma <5$, respectively.

It can be seen that for $\sigma =-1$, the low-amplitude periodic motion and SMR exist in the system. In order to illustrate this point, one may perform Monte Carlo simulations of the steady-state dynamics for different values of randomly picked initial conditions. Figure 24 shows dependency of the types of the system response to various initial conditions within $-1<q_1 ,\dot{q}_1 ,q_2 <1$ and $\dot{q}_2 =0$. It is shown that both types of motions occur. In the range of initial conditions, for 80–90 % of cases the SMR occurs, and for 10–20 % of them the low-amplitude motion happens. Obviously, in the most cases, the SMR occurs in the range of the above-mentioned initial conditions. It is clear that the SMR would be less likely to occur for the lower values of initial conditions.

Also, for the parameters of point 6, the SMR occurs. Point 6 is outside the critical external force region, so there is a node in the slow-motion phase plane for high-amplitude region. For point 6, the range of existence of the SMR and WMR, saddle-node region and high-amplitude periodic motion is $-8.2<\sigma <11.2$, $-2.3<\sigma <4.4$ and $3.1<\sigma <6.1$, respectively.

The third location for the NES position is $d=0.19$. In this case, the spatial parameter of the system is $\phi _{1d} =0.5712$. Figure 25 shows the occurrence of Hopf and saddle-node bifurcations and the amplitudes of the external force for occurrence of SMR in the $F- \alpha$ space. It can be seen that unlike the previous cases, the saddle-node bifurcations in this condition occurs for $\sigma =1$. In this section, for points 7, 8, 9, 10, 11 and 12 of Fig. 25, the dynamic behavior of the system is studied. In addition, in this figure for $\alpha =0.4$ points $S_{1}$ and $S_{2}$ are the limits of occurrence of the saddle-node bifurcations, and points $H_{3}$ and $H_{4}$ are the limits of occurrence of Hopf bifurcations.

Figure 26 shows the variations of the steady-state response of the system versus excitation force amplitude corresponding to Fig. 25. For $\alpha =0.4$ (in Fig. 25), increasing the external force magnitude results in crossing the boundaries of Hopf and saddle-node bifurcations at four points $H_{3}$, $H_{4}$ and $S_{1}$, $S_{2,}$, respectively, and they are consonant with homonymous points of Fig. 26. It can be inferred that different external force magnitudes lead to different solutions. As it can be seen in Fig. 26, for $0.25<F<0.68$ (the saddle-node bifurcations occur), there are three solutions, but the system has only one non-trivial stable solution outside this region, which increases monotonically as external force increases. In this region the high- and low-amplitude periodic motion regions are stable, but the saddle-node bifurcation and WMR regions ($0.51<F<0.66$) are unstable. As the external force increases, the amplitude of solution increases along the lower branch to the saddle-node bifurcation point $S_{1}$, and when F increases further, a sudden jump occurs from point $S_{1}$ to the upper stable branch. By reversing this procedure, the relative displacement decreases slowly along the upper stable branch as it reaches the saddle-node bifurcation point $S_{2}$, where it experiences a jump down to the lower stable branch. As indicated in Fig. 26, sweeping the force leads to the jump phenomenon and hysteresis in the response. Generally, it can be said that the system has three periodic solutions in the saddle-node region, but it has one solution out of this region. Also, boundary of Hopf and saddle-node bifurcations in Fig. 25 is consistent with Fig. 26. Furthermore, it is shown that the saddle-node bifurcation region gets smaller by decreasing the fluid velocity; therefore, the schematic of Fig. 26, after formation of a turning point close to the point $S_{1}$, changes slowly to the schematic of Fig. 10 by decreasing the fluid velocity. As a result, the possibility of the jump phenomenon decreases.

Fig. 29

Trajectory of the slow motion in the phase plane for $d=0.19$, $\alpha =0.4$, $F=0.4$, $\sigma =1$, $\mu =-1$ (point 8 in Fig. 25)

As previously discussed, excitation force magnitude of point 7 in Fig. 25 is smaller than the critical value of points 1 and 6. As a result, there is only one node in the phase plane of this point which represents system absorption to a periodic motion with the amplitude value equal to 0.15 for any initial conditions. The numerical results demonstrate that the transient response has a longer time in comparison with the previous case. The possibility of occurrence of SMR is proved by studying the phase plane of the slow motion of the system related to points 12 and 13. For point 12, the WMR does not occur at all and the SMR occurs for $-1<\sigma <0.3$. The frequency response curve of the system for point 8 is depicted in Fig. 27. This point is above the first critical excitation and below the Hopf bifurcation area; therefore, the saddle-node bifurcations (the high-amplitude region) are very small in the frequency response curve.

As it is visible in Figs. 15, 19 and 27, increasing the magnitude of the external force leads to increasing the input energy of the system; in addition, the occurrence possibility of a high-amplitude motion increases and the island-like zone of high amplitudes is extended and moves closer to the low-amplitude zone. Furthermore, it can be seen that the SMR and WMR regions shift slightly to the positive values of detuning parameter by increasing the fluid velocity.

Since the system parameters corresponding to point 8 are inside the saddle-node bifurcation area and above the first critical external load amplitude, two nodes exist for lower and higher amplitudes in the slow-motion phase plane (Fig. 28); therefore, the SMR does not occur at this point. The trajectory of the slow motion of point 8 (in Fig. 25) in the phase plane is plotted in Fig. 29. As it can be seen, the system dynamic trajectory after several motions in the closed loop (indicating the SMR) is absorbed in a node (indicating the low-amplitude periodic motion for $N=0.36,\theta =1.65)$.

The frequency response curve of the system for points 9 and 10 is similar to Fig. 15. For point 9, system has a stable response with high amplitude and saddle node ($1<\sigma <1.1$ and $1<\sigma <1.1)$. In this case, the SMR occurs for $-1.8<\sigma <1.3$, and the WMR occurs for $0.3<\sigma <0.7$. For point 10, system has a stable response with high amplitude and saddle node ($0.8<\sigma <1.2$ and $0.9<\sigma <1.1)$. In this case, the SMR occurs for $-2<\sigma <1.5$, and the WMR occurs for $0.3<\sigma <0.7$. The dynamic behavior of the system at point 9 is identical to that of point 10; therefore, the SMR occurs. The frequency response curve of the system for points 11 and 12 is similar to Fig. 19, and the island-like zone of high amplitudes joins to the low-amplitude regions. For point 11, system has a stable response with high amplitude and saddle node ($0.9<\sigma <1.5)$. In this case, the SMR occurs for $-1.6<\sigma <2.4$ and the WMR occurs for $0<\sigma <1.1$. For point 12, system has stable response with high amplitude for $1<\sigma <1.7$. In this case, the SMR occurs for $-0.9<\sigma <0.4$ and the WMR and saddle node occur at two regions ($-0.3<\sigma <0.1$ and $1.3<\sigma <1.4)$ and ($1<\sigma <1.1$ and $1.3<\sigma <1.7)$, respectively. The accuracy of the non-occurrence of SMR is approved by investigating the sustained jumping map for points 11 and 12.

Fig. 30

Occurrence of Hopf and saddle-node bifurcations and critical magnitude of external force for $d=0.1$, $\sigma =1$, $\mu =-1$

Fig. 31

Trajectory of the slow motion of the system in the phase plane for $d=0.1$, $\alpha =0.4$, $F=0.75$, $\sigma =1$, $\mu =-1$ (point 14 in Fig. 30)

The last position of NES position is $d=0.1$, which is close to the pipe support. In this case, spatial parameter of the system is $\phi _{1d} =0.2246$. Figure 30 demonstrates the existence of Hopf and saddle-node bifurcations and amplitudes of the external force for the occurrence of the SMR in the $F- \alpha$ space for $\sigma =1$. Also, the dynamic behavior of the system is evaluated for parameters of the points 13, 14, 15 and 16 in Fig. 30.

The schematic of variation of the steady-state response of the system versus excitation amplitude force corresponding to Fig. 30 is similar to Fig. 26. In Fig. 30, for $\alpha =0.4$, increasing the external force magnitude leads to crossing the boundaries of Hopf and the saddle-node bifurcations at the same points ($S_{1}-H_{3}$, $S_{2}-H_{4}$ in Fig. 29); therefore, the length of Hopf and the saddle-node bifurcation regions are equal in this diagram. The system with parameters of point 13 in Fig. 30 has a periodic motion similar to points 1, 4 and 7. The range of the occurrence of the WMR for point 13 is $0.37<\sigma <0.4$. Since this point is under critical force, the SMR does not happen.

The amplitude of force excitation for point 14 is greater than the critical force ($F>F_\mathrm{critical [1]})$, so, the jump phenomenon would happen. The trajectory of the slow motion of the system in the phase plane for parameters of point 14 is demonstrated in Fig. 31. It can be seen that the system ultimately is attracted to the low-amplitude node. This is the sign of the longer transient response in this case. It can be explained that when NES is connected close to the pipe supports, the vibration amplitude of the pipe is smaller at this position; therefore, the absorber needs a longer time to transfer the system to a desired motion regime.

The range of existence of the SMR and WMR for parameters of point 14 is $0.1<\sigma <0.2$ and $0.44<\sigma <0.5$, respectively. For parameters of the points 15 and 16, the SMR does not occur, at all. It can be seen that the SMR (sign of the absorber performance) is limited and often does not occur at this NES location.

Finally, the efficiency of the optimal NES (corresponding to point 2 parameters in Fig. 8) is compared to that of an optimal linear absorber. The parameters related to point 4 (Fig. 8), and around it, are selected as the optimal parameters for the NES on account of the fact that the range of the existence of the SMR in detuning parameter region [in the frequency response curve) is the greatest at this point than that of other points of the system ($-12.3<\sigma <15.9)$. Den Hartog relation [42] is used to obtain the optimal linear absorber parameters (Eq. (62)).

Fig. 32

Total system energy frequency responses without any absorber, with the optimal linear absorber and with NES (with parameters of point 2 in Fig. 8)

To compare these two cases in Eqs. (19) and (20), damping and masses of absorber have the same value. The absorbers stiffness is obtained based on tuning of the parameters for optimal absorbers Eqs. (63) and (64). In addition, the values of the external forces for two cases have the same magnitude.

$$\begin{aligned}&m_{11} \ddot{x}_1 (t)+m_{11} (\Omega ^{2}+\varepsilon \sigma )x_1 (t)+\varepsilon \frac{\zeta }{\phi _{1d} }\dot{x}_1 (t)\nonumber \\&\quad +\,\varepsilon \frac{\mu }{\phi _{1d} }x_1 (t) \nonumber \\&\quad +\,\varepsilon c_{lin} \{\dot{x}_1 (t)-\dot{x}_2 (t)\}+\varepsilon k_{lin} \{x_1 (t)-x_2 (t)\}\nonumber \\&\quad =\varepsilon \frac{F}{\phi _{1d} }\cos (\Omega t) \nonumber \\&\varepsilon \ddot{x}_2 (t)+\varepsilon \alpha [\dot{x}_2 (t)-\dot{x}_1 (t)]\nonumber \\&\quad +\,\varepsilon \beta [x_2 (t)-x_1 (t)]=0 \end{aligned}$$

(62)

$$\begin{aligned}&\frac{\omega _\mathrm{absorber} }{\omega _\mathrm{primary-mass} }=\frac{1}{1+\frac{\varepsilon }{m_{jj} }} \end{aligned}$$

(63)

$$\begin{aligned}&\frac{\varepsilon c_{lin} }{2m_{jj} \omega _n }=\sqrt{\frac{3\frac{\varepsilon }{m_{jj} }}{8\left( 1+\frac{\varepsilon }{m_{jj} }\right) }} \end{aligned}$$

(64)

With the aim of comparing the efficiency of the linear absorber to that of the NES in the vibration control of a pipe conveying fluid, the total energy of system in two cases (with NES and with linear absorber) for different values of the external force, angular frequency and around the resonance frequency is calculated Eq. (65)

$$\begin{aligned} E_\mathrm{totNES}= & {} \frac{1}{2}m_{jj} \sum _{i=1}^n {\phi _i } ({{x}})\dot{q}^{2}_i ({{t}})+\frac{1}{2}\varepsilon \dot{q}^{2}_{n+1} ({{t}})\nonumber \\&+\,\frac{1}{2}(\varepsilon \mu +k_{jj} )\sum _{i=1}^n {\phi _i } ({{x}})q_i^2 ({{t}})\nonumber \\&+\frac{1}{2}\varepsilon \beta \left\{ \sum _{i=1}^n {\phi _i } ({{x}})q_i ({{t}})-q_{n+1} ({{t}})\right\} ^{4} \nonumber \\ E_\mathrm{totlinear}= & {} \frac{1}{2}m_{11} \phi _1 ({{x}})\dot{q}^{2}_1 ({{t}})\nonumber \\&+\frac{1}{2}\varepsilon \dot{q}^{2}_{n+1} ({{t}})+\frac{1}{2}(\varepsilon \mu +k_{11} )\phi _1 ({{x}})q_1^2 ({{t}})\nonumber \\&+\frac{1}{2}\varepsilon k_{lin} \{\phi _1 ({{x}})q_1 ({{t}})-q_3 ({{t}})\} \end{aligned}$$

(65)

Figure 32 shows that the total energy of the pipe conveying fluid without any absorber, with attached optimal NES (with one, two and three modes of the pipe), and the attached optimal linear absorber under external force for different angular frequencies.

The linear optimal absorber is more efficient than the NES right on and near the resonance frequency. It can be seen that the resonance frequency of the system is divided into two frequencies around itself which is in accordance with the classical features of the linear absorbers. For these frequencies, the pipe has large amplitude which is the feature of the linear absorbers. The analytical solution indicates that the SMR takes place in this region. In general, right on and near the resonance frequency, the optimal linear absorber is more efficient than the NES. However, the NES is more efficient than the optimal linear absorber in a large frequency range around the resonance frequency. When a system has a variable natural frequency or is under a variable external excitation frequency, this feature of the NES becomes important. For example, a pipe conveying fluid in the ocean may have a variant natural frequency due to the different wave velocity of the ocean, erosion over time and the lack of precision in manufacturing process.

6 Conclusions

The performance of a smooth NES on vibration of a pipe conveying fluid under harmonic external load has been investigated in this paper. The Euler–Bernoulli beam theory has been used to model the pipe. Linear damping and an essentially nonlinear stiffness have been considered for nonlinear energy sink. The required conditions for existence of the Hopf and saddle-node bifurcations and the occurrence of the SMR have been discussed. The influences of the location of the NES on the pipe, the damping of the NES, the magnitude of external force and the fluid velocity on the dynamical behavior of pipe conveying fluid have been investigated.

The results show that the range of the parameters in which the SMR and the Hopf bifurcations occur simultaneously is the best case for vibration control, and the existence of the saddle-node bifurcation does not affect the desirable behavior of the system noticeably. The system is usually attracted to the SMR that is an appropriate dynamic regime for the performance of an NES. Also, when low-amplitude periodic motions, high-amplitude periodic motions and SMR and WMR occur simultaneously, the system is usually attracted to the SMR.

The NES position affects the range of magnitude of external force that allows for the occurrence of SMR. This is one of the advantages of using NES in comparison with the linear absorber.

Increasing the fluid velocity leads to decreasing the amplitude of motion, and extending the unstable region (saddle-node and Hopf bifurcation). Also, it has been proved that the occurrence possibility of the SMR and WMR phenomena increases for positive values of the detuning parameter by increasing the fluid velocity.

The NES is more desirable in the large frequency range around the resonance frequency, but the optimal linear absorber is more efficient than the NES, right on and near the resonance frequency.

Probability of saddle-node and the SMR occurrence increases and decreases, respectively, by approaching the pipe supports. Also, the transient response lasts longer. When the NES location is near the pipe supports, for the best parameters of that section, the range of the existence of SMR in the frequency response curve is smaller. Also, when the NES is placed at the middle section of the pipe, the range of the existence of the SMR in the frequency response curve is greater and the transient response lasts shorter. Based on these discussions, the best range of the NES parameters for achieving an efficient vibration control corresponds to point 2 in Fig. 8.

Appendices

Appendix 1

$$\begin{aligned} m_{11}= & {} \int _0^1 {\phi _1^2 (\bar{{x}})\hbox {d}\bar{{x}},\mu =\int _0^1 \bar{{U}}_f ^{2}\phi _1 (\bar{{x}})\left[ \frac{\hbox {d}^{2}\phi _1 (\bar{{x}})}{\hbox {d}\bar{{x}}^{2}}\right] \hbox {d}\bar{{x}}} ,k_{11}\\= & {} \int _0^1 {\phi _1 (\bar{{x}})\left[ \frac{\hbox {d}^{4}\phi _1 (\bar{{x}})}{\hbox {d}\bar{{x}}^{4}}\right] } \hbox {d}\bar{{x}}, \xi =\int _0^1 {\bar{{c}}_p \phi _1 ^{2}(\bar{{x}})} \hbox {d}\bar{{x}},\bar{{F}}\\= & {} \int _0^1 {\bar{{F}}\phi _1 (\bar{{x}})\hbox {d}\bar{{x}}} \end{aligned}$$

Appendix 2

$$\begin{aligned} \alpha _1= & {} 16\Omega ^{6}\left( {\begin{array}{l} \phi _{1d}^4 \alpha ^{2}\Omega ^{4}+2\phi _{1d}^3 \alpha \xi \Omega ^{4}-2\phi _{1d}^3 \alpha ^{2}\mu \Omega ^{2}\\ \quad +\phi _{1d}^2 \alpha ^{2}\xi ^{2}\Omega ^{2}+\phi _{1d}^2 \xi ^{2}\Omega ^{4}+\alpha ^{2}\sigma ^{2} \\ -2\phi _{1d}^2 \alpha ^{2}\sigma \Omega ^{2}+\phi _{1d}^2 \alpha ^{2}\mu ^{2} +\phi _{1d}^2 \mu ^{2}\Omega ^{2}\\ \quad +2\phi _{1d} \alpha ^{2}\mu \sigma +2\phi _{1d} \mu \sigma \Omega ^{2}+\sigma ^{2}\Omega ^{2} \\ \end{array}} \right) \\ \alpha _2= & {} 24\beta \Omega ^{4}\left( \phi _{1d}^3 \mu \Omega ^{2}-\phi _{1d}^2 \xi ^{2}\Omega ^{2}+\phi _{1d}^2 \sigma \Omega ^{2}\right. \\&\quad \left. -\,\phi _{1d}^2 \mu ^{2}-2\phi _{1d} \mu \sigma -\sigma ^{2} \right) \\ \alpha _3= & {} 9\beta ^{2}\left( \phi _{1d}^4 \Omega ^{4}-2\phi _{1d}^3 \mu \Omega ^{2}+\phi _{1d}^2 \xi ^{2}\Omega ^{2}\right. \\&\quad \left. -\,2\phi _{1d}^2 \sigma \Omega ^{2}+\phi _{1d}^2 \mu ^{2}+2\phi _{1d} \mu \sigma +\sigma ^{2} \right) \\ \alpha _4= & {} -16\phi _{1d}^2 F^{2}\Omega ^{10} \end{aligned}$$

Appendix 3

$$\begin{aligned} \eta _1= & {} \phi _{1d}^2 \alpha \varepsilon +\phi _{1d} \varepsilon \xi +\alpha \\ \eta _2= & {} \frac{1}{64\Omega ^{6}}(16\phi _{1d}^4 \alpha ^{2}\varepsilon ^{2}\Omega ^{6}+32\phi _{1d}^3 \alpha \varepsilon ^{2}\xi \Omega ^{6}\\&+\,27\phi _{1d}^4 \beta ^{2}\varepsilon ^{2}\phi _{2f}{}^{4}+16\phi _{1d}^2 \varepsilon ^{2}\xi ^{2}\Omega ^{6}\\&+\,48\phi _{1d}^3 \beta \varepsilon ^{2}\mu \Omega \phi _{2f}{}^{2} +32\phi _{1d}^2 \alpha ^{2}\varepsilon \Omega ^{6}\\&+\,48\phi _{1d}^2 \beta \varepsilon ^{2}\sigma \Omega ^{2}\phi _{2f}{} ^{2}+16\phi _{1d}^2 \varepsilon ^{2}\mu ^{2}\Omega ^{4}\\&+\,64\phi _{1d} \alpha \varepsilon \xi \Omega ^{6}+54\phi _{1d}^2 \beta ^{2}\varepsilon \phi _{2f}{} ^{4} \\&+\,32\phi _{1d} \varepsilon ^{2}\mu \sigma \Omega ^{4}+16\alpha ^{2}\Omega ^{6}+16\varepsilon ^{2}\sigma ^{2}\Omega ^{4}\\&+\,16\Omega ^{8}-48\beta \Omega ^{4}\phi _{2f}{} ^{2}+27\beta ^{2}\phi _{2f}{} ^{4}) \\ \eta _3= & {} \frac{\varepsilon }{64\Omega ^{6}}(16\phi _{1d}^3 \alpha ^{2}\varepsilon \xi \Omega ^{6}+16\phi _{1d}^2 \alpha \varepsilon \xi ^{2}\Omega ^{6}\\&+\,27\phi _{1d}^3 \beta ^{2}\varepsilon \xi \phi _{2f}{} ^{4}+16\phi _{1d}^2 \alpha \Omega ^{8}\\&+\,16\phi _{1d}^2 \alpha \varepsilon \mu ^{2}\Omega ^{4} +16\phi _{1d} \alpha ^{2}\xi \Omega ^{6}+16\phi _{1d} \xi \Omega ^{8}\\&+\,32\phi _{1d} \alpha \varepsilon \mu \sigma \Omega ^{4}-48\phi _{1d} \beta \xi \Omega ^{4}\phi _{2f}{} ^{2}\\&+27\phi _{1d} \beta ^{2}\xi \phi _{2f}{} ^{4}+16\alpha \varepsilon \sigma ^{2}\Omega ^{4}) \\ \eta _4= & {} \frac{\varepsilon ^{2}}{256\Omega ^{8}}(16\phi _{1d}^4 \alpha ^{2}\Omega ^{10}+32\phi _{1d}^3 \alpha \xi \Omega ^{10}\\&+\,27\phi _{1d}^4 \beta ^{2}\Omega ^{4}\phi _{2f}{} ^{4}-32\phi _{1d}^3 \alpha ^{2}\mu \Omega ^{8}\\&-\,48\beta \sigma ^{2}\Omega ^{4}\phi _{2f}{} ^{2} +16\phi _{1d}^2 \alpha ^{2}\xi ^{2}\Omega ^{8}\\&+\,16\phi _{1d}^2 \xi ^{2}\Omega ^{10}+48\phi _{1d}^3 \beta \mu \Omega ^{6}\phi _{2f}{} ^{2}\\&-\,32\phi _{1d}^2 \alpha ^{2}\sigma \Omega ^{8}-48\phi _{1d}^2 \beta \xi ^{2}\Omega ^{6}\phi _{2f}{} ^{2} \\&-\,54\phi _{1d}^3 \beta ^{2}\mu \Omega ^{2}\phi _{2f}{} ^{4}+16\phi _{1d}^2 \alpha ^{2}\mu ^{2}\Omega ^{6}\\&+\,27\phi _{1d}^2 \beta ^{2}\xi ^{2}\Omega ^{2}\phi _{2f}{} ^{4}+48\phi _{1d}^2 \beta \sigma \Omega ^{6}\phi _{2f}{} ^{2}\\&+\,27\beta ^{2}\sigma ^{2}\phi _{2f}{} ^{4} +16\phi _{1d}^2 \mu ^{2}\Omega ^{8}\\&-54\phi _{1d}^2 \beta ^{2}\sigma \Omega ^{2}\phi _{2f}{} ^{4}-48\phi _{1d}^2 \beta \mu ^{2}\Omega ^{4}\phi _{2f}{} ^{2}\\&+\,32\phi _{1d} \alpha ^{2}\mu \sigma \Omega ^{6}+32\phi _{1d}^ \mu \sigma \Omega ^{8} \\&+\,27\phi _{1d}^2 \beta ^{2}\mu ^{2}\phi _{2f}{} ^{4}-96\phi _{1d} \beta \mu \sigma \Omega ^{4}\phi _{2f}{} ^{2}\\&+\,16\alpha ^{2}\sigma ^{2}\Omega ^{6}+16\sigma ^{2}\Omega ^{8}+54\phi _{1d} \beta ^{2}\mu \sigma \phi _{2f}{} ^{4}) \end{aligned}$$

Appendix 4

$$\begin{aligned} v_1= & {} -\frac{729}{4096}\frac{\varepsilon \phi _{1d} \beta ^{4}\xi \left( {\phi _{1d}^2 \varepsilon +1} \right) ^{2}\left( {\phi _{1d}^4 \alpha \varepsilon ^{2}+\phi _{1d}^3 \varepsilon ^{2}\xi +2\phi _{1d}^2 \alpha \varepsilon +\alpha } \right) }{\Omega ^{12}}\\ v_2= & {} -\frac{81\varepsilon \phi _{1d} \beta ^{3}\xi \left( {\phi _{1d}^2 \varepsilon +1} \right) }{256\Omega ^{10}}\\&(\phi _{1d}^5 \alpha \varepsilon ^{3}\mu +\phi _{1d}^4 \alpha \varepsilon ^{3}\sigma -\phi _{1d}^4 \alpha \varepsilon ^{2}\Omega ^{2}\\&+\,\phi _{1d}^4 \varepsilon ^{3}\mu \xi +\phi _{1d}^3 \varepsilon ^{3}\sigma \xi \\&-\,\phi _{1d}^3 \varepsilon ^{2}\xi \Omega ^{2}+\phi _{1d}^3 \alpha \varepsilon ^{2}\mu +\phi _{1d}^2 \alpha \varepsilon ^{2}\sigma \\&-\,3\phi _{1d}^2 \alpha \varepsilon \Omega ^{2}-2\alpha \Omega ^{2}) \\ v_3= & {} -\frac{9\varepsilon \phi _{1d} \beta ^{2}}{256\Omega ^{8}}\{6\phi _{1d} ^{8}\alpha ^{3}\varepsilon ^{4}\xi \Omega ^{2}+15\phi _{1d} ^{7}\alpha ^{2}\varepsilon ^{4}\xi ^{2}\Omega ^{2}\\&+\,12\phi _{1d} ^{6}\alpha \varepsilon ^{4}\xi ^{3}\Omega ^{2}+22\alpha \xi \Omega ^{4}+3\phi _{1d} ^{7}\alpha ^{2}\varepsilon ^{4}\mu ^{2}\\&+\,24\phi _{1d} ^{6}\alpha ^{3}\varepsilon ^{3}\xi \Omega ^{2} +3\phi _{1d} ^{5}\varepsilon ^{4}\xi ^{4}\Omega ^{2}+6\phi _{1d} ^{6}\alpha ^{2}\varepsilon ^{4}\mu \sigma \\&+\,6\phi _{1d} ^{6}\alpha ^{2}\varepsilon ^{3}\mu \Omega ^{2}+6\phi _{1d} ^{6}\alpha \varepsilon ^{4}\mu ^{2}\xi \\&+\,6\alpha ^{3}\xi \Omega ^{2}-12\phi _{1d} \alpha \varepsilon ^{2}\mu \sigma \xi +3\phi _{1d} \alpha ^{2}\Omega ^{4} \\&+\,42\phi _{1d} ^{5}\alpha ^{2}\varepsilon ^{3}\xi ^{2}\Omega ^{2}+3\phi _{1d} ^{5}\alpha ^{2}\varepsilon ^{4}\sigma ^{2}\\&+\,6\phi _{1d} ^{5}\alpha ^{2}\varepsilon ^{3}\sigma \Omega ^{2}+3\phi _{1d} ^{5}\alpha ^{2}\varepsilon ^{2}\Omega ^{4}\\&+\,18\phi _{1d} ^{4}\alpha \varepsilon ^{3}\xi ^{3}\Omega ^{2}+6\phi _{1d} ^{5}\alpha ^{2}\varepsilon ^{3}\mu ^{2}\\&-\,6\alpha \varepsilon ^{2}\sigma ^{2}\xi +12\phi _{1d} ^{5}\alpha \varepsilon ^{4}\mu \sigma \xi -4\phi _{1d} ^{5}\alpha \varepsilon ^{3}\mu \xi \Omega ^{2}\\&+\,3\phi _{1d} ^{5}\varepsilon ^{4}\mu ^{2}\xi ^{2}-4\phi _{1d} ^{4}\alpha \varepsilon ^{3}\sigma \xi \Omega ^{2}\\&+\,6\phi _{1d} ^{4}\alpha \varepsilon ^{2}\xi \Omega ^{4}+6\phi _{1d} ^{4}\varepsilon ^{4}\mu \sigma \xi ^{2} \\&+\,36\phi _{1d} ^{4}\alpha ^{3}\varepsilon ^{2}\xi \Omega ^{2}+6\phi _{1d} ^{4}\alpha \varepsilon ^{4}\sigma ^{2}\xi \\&-\,10\phi _{1d}^4 \varepsilon ^{3}\mu \xi ^{2}\Omega ^{2}+12\phi _{1d} ^{4}\alpha ^{2}\varepsilon ^{3}\mu \sigma \\&+\,12\phi _{1d} ^{4}\alpha ^{2}\varepsilon ^{2}\mu \Omega ^{2}+39\phi _{1d} ^{3}\alpha ^{2}\varepsilon ^{2}\xi ^{2}\Omega ^{2} \\&+\,3\phi _{1d}^3 \varepsilon ^{4}\sigma ^{2}\xi ^{2}10\phi _{1d} ^{3}\varepsilon ^{3}\sigma \xi ^{2}\Omega ^{2}\\&+\,3\phi _{1d} ^{3}\varepsilon ^{2}\xi ^{2}\Omega ^{4}+6\phi _{1d} ^{3}\alpha ^{2}\varepsilon ^{3}\sigma ^{2}\\&+\,12\phi _{1d} ^{3}\alpha ^{2}\varepsilon ^{2}\sigma \Omega ^{2}+6\phi _{1d} ^{3}\alpha ^{2}\varepsilon \Omega ^{4}\\&+\,3\phi _{1d} \alpha ^{2}\varepsilon ^{2}\sigma ^{2} \\&-\,4\phi _{1d} ^{3}\alpha \varepsilon ^{2}\mu \xi \Omega ^{2}+6\phi _{1d} ^{2}\alpha \varepsilon ^{2}\xi ^{3}\Omega ^{2}\\&+\,3\phi _{1d} ^{3}\alpha ^{2}\varepsilon ^{2}\mu ^{2}+24\phi _{1d} ^{2}\alpha ^{3}\varepsilon \xi \Omega ^{2} -4\phi _{1d} ^{2}\alpha \varepsilon ^{2}\sigma \xi \Omega ^{2}\\&+\,28\phi _{1d} ^{2}\alpha \varepsilon \xi \Omega ^{4} +6\phi _{1d} ^{2}\alpha ^{2}\varepsilon \mu \Omega ^{2}-6\phi _{1d} ^{2}\alpha \varepsilon ^{2}\mu ^{2}\xi \\&+\,12\phi _{1d} \alpha ^{2}\varepsilon \xi ^{2}\Omega ^{2}+6\phi _{1d} \alpha ^{2}\varepsilon \sigma \Omega ^{2} +6\phi _{1d} ^{2}\alpha ^{2}\varepsilon ^{2}\mu \sigma \} \\ \end{aligned}$$

$$\begin{aligned} v_4= & {} -\frac{3\varepsilon \phi _{1d} \alpha \beta }{16\Omega ^{6}}\{\phi _{1d} ^{7}\alpha ^{2}\varepsilon ^{4}\mu \xi \Omega ^{2}\\&+\,\phi _{1d} ^{6}\alpha ^{2}\varepsilon ^{4}\sigma \xi \Omega ^{2}-\phi _{1d} ^{6}\alpha ^{2}\varepsilon ^{3}\xi \Omega ^{4}\\&+\,2\phi _{1d} ^{6}\alpha \varepsilon ^{4}\mu \xi ^{2}\Omega ^{2}+2\varepsilon ^{2}\sigma ^{2}\xi \Omega ^{2} \\&-\,2\phi _{1d} ^{5}\alpha \varepsilon ^{3}\xi ^{2}\Omega ^{4}+\phi _{1d} ^{5}\varepsilon ^{4}\mu \xi ^{3}\Omega ^{2}\\&+\,\phi _{1d} ^{6}\alpha \varepsilon ^{4}\mu ^{3}+2\phi _{1d} ^{5}\alpha ^{2}\varepsilon ^{3}\mu \xi \Omega ^{2}\\&+\,\phi _{1d} ^{4}\varepsilon ^{4}\sigma \xi ^{3}\Omega ^{2}-\phi _{1d} ^{4}\varepsilon ^{3}\xi ^{3}\Omega ^{4} \\&+\,3\phi _{1d} ^{5}\alpha \varepsilon ^{4}\mu ^{2}\sigma +\phi _{1d} ^{5}\alpha \varepsilon \mu \Omega ^{2}\\&+\,\phi _{1d} ^{5}\varepsilon ^{4}\mu ^{3}\xi +2\phi _{1d} ^{4}\alpha ^{2}\varepsilon ^{3}\sigma \xi \Omega ^{2}\\&-\,4\phi _{1d} ^{4}\alpha ^{2}\varepsilon ^{2}\xi \Omega ^{4}+2\phi _{1d} ^{4}\alpha \varepsilon ^{3}\mu \xi ^{2}\Omega ^{2} \\&+\,3\phi _{1d} ^{4}\alpha \varepsilon ^{4}\mu \sigma ^{2}+2\phi _{1d} ^{4}\alpha \varepsilon ^{3}\mu \sigma \Omega ^{2}\\&-\,\phi _{1d} ^{4}\alpha \varepsilon ^{2}\mu \Omega ^{4}+3\phi _{1d} ^{4}\varepsilon \epsilon ^{4}\mu ^{2}\sigma \xi \\&+\,\phi _{1d} ^{4}\varepsilon ^{3}\mu ^{2}\xi \Omega ^{2}+2\phi _{1d} ^{3}\alpha \varepsilon ^{3}\sigma \xi ^{2}\Omega ^{2} \\&-\,6\phi _{1d} ^{3}\alpha \varepsilon ^{2}\xi ^{2}\Omega ^{4}+\phi _{1d} ^{4}\alpha \varepsilon ^{3}\mu ^{3}\\&+\,\phi _{1d} ^{3}\alpha ^{2}\varepsilon ^{2}\mu \xi \Omega ^{2}+\phi _{1d} ^{3}\alpha \varepsilon ^{4}\sigma ^{3}\\&+\,\phi _{1d} ^{3}\alpha \varepsilon ^{3}\sigma ^{2}\Omega ^{2}-\phi _{1d} ^{3}\alpha \varepsilon ^{2}\sigma \Omega ^{4}-2\xi \Omega ^{6} \\&-\,\phi _{1d} ^{3}\alpha \varepsilon \Omega ^{6}+3\phi _{1d} ^{3}\varepsilon ^{4}\mu \sigma ^{2}\xi +2\phi _{1d} ^{3}\varepsilon ^{3}\mu \sigma \xi \Omega ^{2}\\&-\,\phi _{1d} ^{3}\varepsilon ^{2}\mu \xi \Omega ^{4}-2\phi _{1d} ^{2}\varepsilon ^{2}\xi ^{3}\Omega ^{4}+3\phi _{1d} ^{3}\alpha \varepsilon ^{3}\mu ^{2}\sigma \\&+\,\phi _{1d} ^{3}\alpha \varepsilon ^{2}\mu ^{2}\Omega ^{2}+\phi _{1d} ^{2}\alpha ^{2}\varepsilon ^{2}\sigma \xi \Omega ^{2}-5\phi _{1d} ^{2}\alpha ^{2}\varepsilon \xi \Omega ^{4}\\&+\,\phi _{1d} ^{2}\varepsilon ^{4}\sigma ^{3}\xi +\phi _{1d} ^{2}\varepsilon ^{3}\sigma ^{2}\xi \Omega ^{2}-\phi _{1d} ^{2}\varepsilon ^{2}\sigma \xi \Omega ^{4} \\&-\,\phi _{1d} ^{2}\varepsilon \xi \Omega ^{6}+3\phi _{1d} ^{2}\alpha \varepsilon ^{3}\mu \sigma ^{2}+2\phi _{1d} ^{2}\alpha \varepsilon ^{2}\mu \sigma \Omega ^{2}\\&-\,\phi _{1d} ^{2}\alpha \varepsilon \mu \Omega ^{4}+2\phi _{1d} ^{2}\varepsilon ^{2}\mu ^{2}\xi \Omega ^{2}-4\phi _{1d} \alpha \varepsilon \xi ^{2}\Omega ^{4} \\&+\,\phi _{1d} \alpha \varepsilon ^{3}\sigma ^{3}+\phi _{1d} \alpha \varepsilon ^{2}\sigma ^{2}\Omega ^{2}-\phi _{1d} \alpha \varepsilon \sigma \Omega ^{4}\\&-\,\phi _{1d} \alpha \Omega ^{6}+4\phi _{1d} \varepsilon ^{2}\mu \sigma \xi \Omega ^{2}-2\alpha ^{2}\xi \Omega ^{4}\\&+\,2\phi _{1d}^5 \alpha \varepsilon ^{4}\sigma \xi ^{2}\Omega ^{2}\} \\ v_5= & {} -\frac{\varepsilon \phi _{1d} \alpha }{16\Omega ^{4}}\phi _{1d} ^{4}\alpha ^{2}\varepsilon ^{2}\xi \Omega ^{2}+2\phi _{1d} ^{3}\alpha \varepsilon ^{2}\xi ^{2}\Omega ^{2}\\&+\,\phi _{1d}^2 \varepsilon ^{2}\xi ^{3}\Omega ^{2}+\phi _{1d} ^{3}\alpha \varepsilon ^{2}\mu ^{2}+2\phi _{1d}^2 \alpha ^{2}\varepsilon \xi \Omega ^{2} \\&+\,2\phi _{1d}^2 \alpha \varepsilon ^{2}\mu \sigma +2\phi _{1d} ^{2}\alpha \varepsilon \mu \Omega ^{2}+\phi _{1d} ^{2}\varepsilon ^{2}\mu ^{2}\xi \\&+\,2\phi _{1d} \alpha \varepsilon \xi ^{2}\Omega ^{2}+\phi _{1d} \alpha \varepsilon ^{2}\sigma ^{2}\\&+\,2\phi _{1d} \alpha \varepsilon \sigma \Omega ^{2}+\phi _{1d} \alpha \Omega ^{4}+2\phi _{1d} \varepsilon ^{2}\mu \sigma \xi \\&+\,\alpha ^{2}\xi \Omega ^{2}+\varepsilon ^{2}\sigma ^{2}\xi +2\varepsilon \sigma \xi \Omega ^{2}\\&+\,2\phi _{1d} \varepsilon \mu \xi \Omega ^{2}\}\times \{\phi _{1d} ^{4}\alpha ^{2}\varepsilon ^{2}\Omega ^{2}+2\phi _{1d} ^{3}\alpha \varepsilon ^{2}\xi \Omega ^{2} \\&+\,\phi _{1d} ^{2}\varepsilon ^{2}\xi ^{2}\Omega ^{2}+\varepsilon ^{2}\sigma ^{2}+\phi _{1d} ^{2}\varepsilon ^{2}\mu ^{2}+2\phi _{1d} \alpha \varepsilon \xi \Omega ^{2}a \\&+\,2\phi _{1d} \varepsilon ^{2}\mu \sigma +2\phi _{1d} ^{2}\alpha ^{2}\varepsilon \Omega ^{2}-2\phi _{1d} \varepsilon \mu \Omega ^{2}+\alpha ^{2}\Omega ^{2}\\&-\,2\varepsilon \sigma \Omega ^{2}+\xi \Omega ^{4}+\Omega ^{4}\} \end{aligned}$$