Dynamics of 1-dof and 2-dof energy sink with geometrically nonlinear damping: application to vibration suppression

Abstract

Nonlinear energy sink (NES) refers to a lightweight nonlinear device that is attached to a primary linear or weakly nonlinear system for passive energy localization into itself. In this paper, the dynamics of 1-dof and 2-dof NES with geometrically nonlinear damping is investigated. For 1-dof NES, an analytical treatment for the bifurcations is developed by presenting a slow/fast decomposition leading to slow flows, where a truncation damping and failure frequency are reported. Existence of strongly modulated response (SMR) is also determined. The procedures are then partly paralleled to the investigation of 2-dof NES for the bifurcation analysis, with particular attention paid to the effect of mass distribution between the NES. To study the frequency response for 2-dof NES, the periodic solutions and their stability are obtained by incremental harmonic balance method and Floquet theory, respectively. Poincare map and energy spectrum are specially introduced for numerical analysis of the systems in the neighborhood of resonance frequency, which in turn are used to compare the efficiency of the NESs to the application of vibration suppression. It is demonstrated that a 2-dof NES can generate extra SMR by adjusting its mass distribution and hence to a great extent reduces the undesired periodic responses and provides with a more effective vibration absorber.

1 Introduction

Effective suppression of unwanted vibrational energy from disturbances into a main system is an important concern in various engineering applications. One of the popular solutions for this problem is a tuned vibration absorber (TVA) from Frahm [1], which generally refers to a lightweight attachment that is coupled to the main system via viscous damping and a linear spring. The classical TVA has been widely studied in the literature [2,3,4,5], and it is proved to be simple and efficient, but also has a major drawback: Namely, it can only be effective in the neighborhood of a single frequency. There is thus a consideration of employing a nonlinear system for TVA, such as the nonlinear energy sink (NES) [6, 7]. In fact, most of the studies show that, depending on the application, NESs can be far more effective in vibration suppression than linear absorbers [8,9,10,11].

As described in [6], an NES refers to a relatively small and spatially localized nonlinear attachment, which is attached to a primary linear or weakly nonlinear system for passive energy localization into itself. Although looks very similar to the linear TVA, addition of an NES leads to essential changes in the dynamics of the entire system. Mainly discussed from a vibration mitigation point of view, it was demonstrated that systems with strongly nonlinear elements are able to achieve dynamical regimes that are unavailable in common weakly nonlinear systems, and the attached NES can react efficiently for broadband suppression unlike the linear TVA. The conceptually new phenomenon of targeted energy transfer (energy pumping) [12, 13], where a specific amount of energy was injected to the main structure is transiently transferred to the NES in a one-way irreversible fashion, was intensively demonstrated and studied in Refs. [14,15,16,17,18,19], both analytically and numerically. Experimental treatments of NES are also numerous [20,21,22]. The effectiveness of NES can be found in the applications to nonlinear beams [23, 24], buildings [25], space structures [26], and aeroelastic system [27]. Moreover, given the phenomenon of targeted energy transfer that NESs have shown, some issues of using NESs for energy harvesting were also discussed in recent investigations [28,29,30].

Recent studies concerned with the effect of a NES on nonlinear coupled systems subject to harmonic excitations were performed by Gendelman et al. [31,32,33]. They revealed an unusual response regime exists in the vicinity of exact 1:1 resonance as a strongly modulated regime (SMR), which can be interpreted as a jump between the stable branches on the slow invariant manifold. For the existence of SMR, the system must be essentially nonlinear and the mass of the NES must be much less than the mass of the primary system. In their further study [34], an optimization of nonlinear vibration absorber was presented numerically, through which they demonstrated that a strongly modulated regime (SMR) can provide more efficient energy suppression than steady-state response. The SMR is then broadly studied in various dynamical systems and in recent literatures [35,36,37,38]. Based on its superiority in vibration mitigation, SMR provides a new idea and mechanism for optimal design of NESs [39, 40].

Despite the fruitful achievements obtained in the previous studies, most of them considered only the nonlinear stiffness in the coupling between the primary structure and the NES, and the effect of damping has not received enough attention. However, by taking into consideration of nonlinear damping with piecewise quadratic characteristics [41] in a system comprised of a linear oscillator subject to harmonic excitation, Starosvetsky and Gendelman found that the nonlinearity of damping provides a new and feasible solution to eliminate the undesired periodic regimes near the main resonance frequency of the system. On the other hand, according to Andersen’s research, the presence of geometrically nonlinear damping can lead to dynamical instability [42]. Similar studies on nonlinear damping could also be found in [43] and [44], where the energy exchange and amplitudes decay are discussed. These studies have confirmed without exception that the nonlinearity of damping, which is generally neglected in most of the literature, plays a important role in these coupled vibrating systems with an attached NES. Nevertheless, their research leaves a lot of questions about the insights for the effects of nonlinear damping on the dynamics of coupled nonlinear systems, and more importantly, they only considered the case of 1-dof NES.

In light of the previous achievements and existing drawbacks, it is therefore only natural that this paper will mainly be devoted to the dynamical behavior of coupled systems with both nonlinear damping and stiffness coupling elements, including the bifurcations and strongly modulated regimes, in order to show the effects of nonlinear damping. Particular interests will be paid to the effect of a 2-dof NES on the response regimes and performance of vibration suppression. The structure of this paper is as follows: The dynamics of a linear oscillator with a 1-dof NES is studied analytically in Sect. 2, with special focus on its bifurcations and the existence SMR responses. Section 3 on the one hand parallels for 2-dof NES the bifurcation analysis in Sect. 2, while the response regimes near the resonance frequency are investigated by the IHB method, mainly considered the effect of mass distribution in the 2-dof NES. Then, the applications of the proposed 1-dof and 2-dof NES to vibration suppression are presented in Sect. 4. Section 5 is devoted to concluding remarks and discussions.

2 Dynamics of a linear oscillator with a 1-dof NES

2.1 Problem formulation

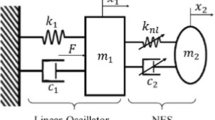
Consider a harmonically forced linear oscillator with an attached 1-dof NES depicted in Fig. 1. According to Fig. 1, $F={F_0}\cos \left( {\omega t} \right)$ stands for the external force, and ${m_1}$ and ${m_2}$ are the mass of the linear oscillator and the NES, respectively. The linear oscillator possesses a linear stiffness ${k_1}$ and viscous damping ${c_1}$, while the NES is induced by a cubic nonlinear stiffness ${k_2}$ and a geometrical nonlinear damping ${c_2}$.

Fig. 1

System with a linear oscillator and an NES

Set ${c_1}=0$, and let ${x_1}$ and ${x_2}$ denote the displacement of linear oscillator and NES, and then, the equation of the system writes

$$\begin{aligned}&{m_1}{{\ddot{x}}_1} + {k_1}{x_1} + {c_2}{({x_1} - {x_2})^2}({{\dot{x}}_1} - {{\dot{x}}_2})\nonumber \\&\quad +\,{k_2}{({x_1} - {x_2})^3} = F\cos \left( {\omega t} \right) \nonumber \\&{m_2}{{\ddot{x}}_2} + {c_2}{({x_2} - {x_1})^2}({{\dot{x}}_2} - {{\dot{x}}_1}) + {k_2}{({x_2} - {x_1})^3} = 0\nonumber \\ \end{aligned}$$

(1)

The geometrically nonlinear damping with the specific form ${c_2}{({x_1} - {x_2})^2}({{\dot{x}}_1} - {{\dot{x}}_2})$ in Eq. (1) was also referred in Refs. [42,43,44]. Reference [42] provided a detailed realization of this type of nonlinear damping by two linear dampers, and for sake of convenience, its main ideas are also presented in “Appendix A”. Without loss of generality, it is convenient to recast Eq. (1) into a dimensionless form of order (1); letting $\varepsilon = \frac{{{m_2}}}{{{m_1}}}$ and defining the following variables

$$\begin{aligned} \tau = \sqrt{\frac{{{k_1}}}{{{m_1}}}} t,\frac{{{k_2}}}{{{k_1}}} = \varepsilon k,\varepsilon \lambda = {c_2}\sqrt{\frac{1}{{{k_1}{m_1}}}} ,\frac{{{F_0}}}{{{m_1}}} = \varepsilon A \end{aligned}$$

one has

$$\begin{aligned}&{{\ddot{x}}_1} + {x_1} + \varepsilon {\lambda _1}{{\dot{x}}_1} + \varepsilon {\lambda _2}{({x_1} - {x_2})^2}({{\dot{x}}_1} - {{\dot{x}}_2})\nonumber \\&\quad +\, \varepsilon k{({x_1} - {x_2})^3} = \varepsilon A\cos \omega \tau \nonumber \\&\varepsilon {{\ddot{x}}_2} + \varepsilon {\lambda _2}{({x_2} - {x_1})^2}({{\dot{x}}_2} - {{\dot{x}}_1}) + \varepsilon k{({x_2} - {x_1})^3} = 0\nonumber \\ \end{aligned}$$

(2)

Two assumptions in Eq. (2) should be emphasized here. Firstly, it is assumed in this system that $0 < \varepsilon \ll 1$, which means the NES is lightweight compared to the linear oscillator. Secondly, as matter of 1:1 resonance condition, the frequency of the harmonic excitation is assumed to be at the near neighborhood of the eigenfrequency of the linear oscillator in the order of ${\varepsilon ^1}$,

$$\begin{aligned} \omega = 1 + \varepsilon \delta \end{aligned}$$

(3)

and make the following variable changes

$$\begin{aligned} u = {x_1} + \varepsilon {x_2}, v = {x_1} - {x_2} \end{aligned}$$

(4)

Owing to its definition, u represents the mass center motion and v represents the relative motion of between the linear and nonlinear oscillators; hence, Eq. (2) becomes

$$\begin{aligned}&\ddot{u} + \frac{{u + \varepsilon v}}{{1 + \varepsilon }} = \varepsilon A\cos \left( {1 + \varepsilon \delta } \right) \tau \nonumber \\&\ddot{v} + \left( {1 + \varepsilon } \right) \lambda {v^2}\dot{v} + \frac{{u + \varepsilon v}}{{1 + \varepsilon }}\nonumber \\&\quad +\,\left( {1 + \varepsilon } \right) k{v^3} = \varepsilon A\cos \left( {1 + \varepsilon \delta } \right) \tau \end{aligned}$$

(5)

It is awkward to investigate directly Eq. (5); in order to study the system analytically, we therefore need to approximating the dynamics. A complex averaging method is applied here, based on the work of Starosvetsky and Gendelman [32, 35, 41], by making the following change of variables according to

$$\begin{aligned} {\varphi _1}{e^{it}}= & {} \dot{u} + iu,{\varphi _2}{e^{it}} = \dot{v} + iv\nonumber \\ {\psi _1}= & {} {\varphi _1}{e^{ - i\varepsilon \delta t}},{\psi _2} = {\varphi _2}{e^{ - i\varepsilon \delta t}} \end{aligned}$$

(6)

and omitting the fast terms from the resulting set of equations, one can obtain the slow flow of the previous system as

$$\begin{aligned}&{{\dot{\psi } }_1} + i\varepsilon \delta {\psi _1} + \frac{{i\varepsilon }}{{2\left( {1 + \varepsilon } \right) }}\left( {{\psi _1} - {\psi _2}} \right) = \frac{{\varepsilon A}}{2}\nonumber \\&{{\dot{\psi } }_2} + i\varepsilon \delta {\psi _2} + \frac{i}{{2\left( {1 + \varepsilon } \right) }}\left( {{\psi _2} - {\psi _1}} \right) \nonumber \\&\quad +\,\frac{{\left( {1 + \varepsilon } \right) \lambda }}{8}{\left| {{\psi _2}} \right| ^2}{\psi _2} - \frac{{3i\left( {1 + \varepsilon } \right) k}}{8}{\left| {{\psi _2}} \right| ^2}{\psi _2} = \frac{{\varepsilon A}}{2}\nonumber \\ \end{aligned}$$

(7)

This equation is called the averaged flow of the system, and the later analysis of this section will be focused on Eq. (7).

2.2 Bifurcation analysis

Let the time derivatives of Eq. (7) to zero lead to

$$\begin{aligned}&i\varepsilon \delta {\psi _1} + \frac{{i\varepsilon }}{{2\left( {1 + \varepsilon } \right) }}\left( {{\psi _1} - {\psi _2}} \right) = \frac{{\varepsilon A}}{2}\nonumber \\&i\varepsilon \delta {\psi _2} + \frac{i}{{2\left( {1 + \varepsilon } \right) }}\left( {{\psi _2} - {\psi _1}} \right) \nonumber \\&\quad +\,\frac{{\left( {1 + \varepsilon } \right) \lambda }}{8}{\left| {{\psi _2}} \right| ^2}{\psi _2} - \frac{{3i\left( {1 + \varepsilon } \right) k}}{8}{\left| {{\psi _2}} \right| ^2}{\psi _2} = \frac{{\varepsilon A}}{2}\nonumber \\ \end{aligned}$$

(8)

where ${\psi _1}$ and ${\psi _1}$ represent the fixed points of the system and the solution of Eq. (8) can be expressed as

$$\begin{aligned}&{\psi _1} = \frac{{{\psi _2} - i\left( {1 + \varepsilon } \right) A}}{{2\varepsilon \delta + 2\delta + 1}}\nonumber \\&\frac{{9{k^2} +{\lambda ^2}}}{{16}}{\left| {{\psi _2}} \right| ^6} - 3kM\delta {\left| {{\psi _2}} \right| ^4} \nonumber \\&+\,4{M^2}{\delta ^2}{\left| {{\psi _2}} \right| ^2} = {M^2}{A^2} \end{aligned}$$

(9)

with

$$\begin{aligned} M = \frac{{2\varepsilon \delta + 1}}{{2\varepsilon \delta + 2\delta + 1}} \end{aligned}$$

The second part of Eq. (9) can be simplified as

$$\begin{aligned} {\alpha _1}Z + {\alpha _2}{Z^2} + {\alpha _3}{Z^3} = {A^2} \end{aligned}$$

(10)

where

$$\begin{aligned} Z = {\left| {{\psi _2}} \right| ^2},{\alpha _1} = 4{\delta ^2},{\alpha _2} = - \frac{{3k\delta }}{M},{\alpha _3} = \frac{{9{k^2} + {\lambda ^2}}}{{16{M^2}}} \end{aligned}$$

and therefore, taking the derivative of Eq. (10) with respect to Z results to

$$\begin{aligned} 3{\alpha _3}{Z^2} + 2{\alpha _2}Z + {\alpha _1} = 0 \end{aligned}$$

(11)

which upon substituting into Eq. (10) and eliminating Z give an equation of the form $A = f\left( {\lambda ,\delta } \right)$.

According to the expression given by $A = f\left( {\lambda ,\delta } \right)$, the boundary of the saddle-node bifurcation on the $\left[ {\lambda ,A} \right]$ plane is plotted in Fig. 2, where the whole plane is separated into regions of one periodic solution and regions of three periodic solutions by the red line of $A = f\left( {\lambda ,\delta } \right)$. In Fig. 2, the parameters are assigned as $\varepsilon = 0.1, k = 4/3,\delta = 3$. Figure 3 is generated by varying the value of $\delta$ , with $\delta > 0$ for plots in Fig. 3 and $\delta < 0$ for plots in Fig. 3b.

Fig. 2

Plot of saddle-node bifurcation on the $\left[ {\lambda ,A} \right]$ plane

Fig. 3

Saddle-node bifurcation with $\delta$ varies, a $\delta > 0$ and b $\delta < 0$

On the $\left[ {\lambda ,A} \right]$ plane, the saddle-node bifurcation appears to be an ’triangle’ inside in which the system has three fixed points. Look at the solutions that are shown in Fig. 2 as a spot-check of the different regions. For $\lambda =1, A=2$, there are three real fixed points. However, for any parameter outside of this region,$\lambda =1, A=0.5$ or $\lambda =1, A=3.5$, only one of the three periodic solutions is real.

From inspection of Fig. 3, it is obvious that the saddle-node bifurcations for the system all have the same shape as $\delta$ varies; while the upper boundary of the ’triangles’ is rather flat, the lower boundary could be quite steep for some values of $\delta$. At $\delta =0$, the saddle-node bifurcation vanishes. For $\delta >0$, with the increase of $\delta$ the area of the ’triangle’ also increases, as a consequence, the regions of three fixed points for a relatively wider range of excitation amplitude A for a certain value of $\lambda$. Similar conclusions are drawn in Fig. 3b for $\delta <0$. It should be noted from Fig. 3a, b, that there is a threshold for the value of damping $\lambda = \sqrt{3} k=2.31$, beyond which the saddle-node bifurcation vanished, and only one real fixed point exists. We called this value as truncation damping.

Now that the fixed points are calculated in Eq. (8), and their stability can consequently be determined. To do this, we need to study the perturbation motion near the fixed points; letting

$$\begin{aligned} {\psi _1} = {\psi _{10}} + {\varDelta _1},\mathop {}\limits _{} {\psi _2} = {\psi _{20}} + {\varDelta _2} \end{aligned}$$

(12)

and inserting these variables into Eq. (7), one have

$$\begin{aligned} {{\dot{\varDelta } }_1}= & {} - \,i\varepsilon \delta {\varDelta _1} - \frac{{i\varepsilon }}{{2\left( {1 + \varepsilon } \right) }}\left( {{\varDelta _1} - {\varDelta _2}} \right) \nonumber \\ \dot{\varDelta } _1^*= & {} i\varepsilon \delta \varDelta _1^* + \frac{{i\varepsilon }}{{2\left( {1 + \varepsilon } \right) }}\left( {\varDelta _1^* - \varDelta _2^*} \right) \nonumber \\ {{\dot{\varDelta } }_2}= & {} -\, i\varepsilon \delta {\varDelta _2} + \frac{i}{{2\left( {1 + \varepsilon } \right) }}\left( {{\varDelta _1} - {\varDelta _2}} \right) \nonumber \\&+\,\frac{{3i\left( {1 + \varepsilon } \right) k}}{4}{\left| {{\psi _{20}}} \right| ^2}{\varDelta _2} + \frac{{3i\left( {1 + \varepsilon } \right) k}}{8}\psi _{20}^2\varDelta _2^*\nonumber \\&-\,\frac{{\lambda \left( {1 + \varepsilon } \right) }}{4}{\left| {{\psi _{20}}} \right| ^2}{\varDelta _2} - \frac{{\lambda \left( {1 + \varepsilon } \right) }}{8}\psi _{20}^2\varDelta _2^*\nonumber \\ \dot{\varDelta } _2^*= & {} i\varepsilon \delta \varDelta _2^* - \frac{i}{{2\left( {1 + \varepsilon } \right) }}\left( {\varDelta _1^* - \varDelta _2^*} \right) \nonumber \\&-\,\frac{{3i\left( {1 + \varepsilon } \right) k}}{4}{\left| {{\psi _{20}}} \right| ^2}\varDelta _2^* - \frac{{3i\left( {1 + \varepsilon } \right) k}}{8}\psi _{20}^{*2}{\varDelta _2}\nonumber \\&-\,\frac{{\lambda \left( {1 + \varepsilon } \right) }}{4}{\left| {{\psi _{20}}} \right| ^2}\varDelta _2^* - \frac{{\lambda \left( {1 + \varepsilon } \right) }}{8}\psi _{20}^{*2}{\varDelta _2} \end{aligned}$$

(13)

Apparently, the characteristic polynomial of Eq. (13) has the following form

$$\begin{aligned} {\mu ^4} + {\gamma _1}{\mu ^3} + {\gamma _2}{\mu ^2} + {\gamma _3}\mu + {\gamma _4} = 0 \end{aligned}$$

(14)

where ${\mu }$ is the eigenvalues whose coefficients can be calculated by MATLAB, and

$$\begin{aligned} \gamma _1= & {} \frac{\lambda \left( 1 + \varepsilon \right) }{2}\nonumber \\ \gamma _2= & {} \frac{3\left( 9k^2 + \lambda ^2 \right) \left( 1 + \varepsilon \right) ^2}{64}{Z}^2- \frac{3k\left( 1 + 2\delta \varepsilon + 2\delta \varepsilon ^2\right) }{4}Z\nonumber \\&+\,\frac{{8{\varepsilon ^2}{\delta ^2} + 4\varepsilon \delta + 1}}{4}\nonumber \\ \gamma _3= & {} \frac{\varepsilon \lambda }{8}\left( 4\varepsilon ^2\delta ^2 + 4\varepsilon \delta ^2 + 4\varepsilon \delta + 1 \right) Z\nonumber \\ {\gamma _4}= & {} \frac{3\varepsilon ^2\left( 9k^2 + \lambda ^2\right) \left( 2\varepsilon \delta + 2\delta + 1 \right) ^2}{256}Z^2\nonumber \\&-\,\frac{{3{\varepsilon ^2}k\delta \left( {2\varepsilon \delta + 1}\right) \left( {2\varepsilon \delta + 2\delta + 1} \right) }}{8}Z\nonumber \\&+\,\frac{{{\varepsilon ^2}{\delta ^2}}}{4}{{\left( {2\varepsilon \delta + 1} \right) }^2} \end{aligned}$$

(15)

where $Z = {\left| {{\psi _{20}}} \right| ^2}$.

The occurence of Hopf bifurcation implies

$$\begin{aligned} \mu = \pm \,i\varOmega \end{aligned}$$

(16)

Employing Eqs. (14), (16) and separating the results into real and imaginary parts lead to

$$\begin{aligned} {\varOmega ^4} - {\gamma _2}{\varOmega ^2} + {\gamma _4} = 0,\varOmega \left( {{\gamma _1}{\varOmega ^2} - {\gamma _3}} \right) = 0 \end{aligned}$$

(17)

and then eliminating ${\varOmega }$ in the above equation, we deduce

$$\begin{aligned} \gamma _3^2 - {\gamma _2}{\gamma _1}{\gamma _3} + {\gamma _4}\gamma _1^2 = 0 \end{aligned}$$

(18)

In view of Eq. (15), MATLAB was then applied to transform Eq. (18) into the following polynomial form with respect to Z in accordance with its power decrease, and determine each coefficients ${v_i}$, for

$$\begin{aligned} {v_1}{Z^2} + {v_2}Z + {v_3} = 0 \end{aligned}$$

(19)

and solving for z in this equation leads to

$$\begin{aligned} {Z_{1,2}} = \frac{{ -\, {v_2} \pm \sqrt{v_2^2 - 4{v_1}{v_3}} }}{{2{v_1}}} \end{aligned}$$

(20)

and plugging solutions Eq. (20) into Eq. (10), the boundaries of stability are finally given by

$$\begin{aligned} {\alpha _1}{Z_i} \,+\, {\alpha _2}Z_i^2 \,+\, {\alpha _3}Z_i^3 \,+\, {\alpha _4} = 0,i = 1,2 \Rightarrow A = f\left( \lambda \right) \end{aligned}$$

(21)

Figure 4 depicts the bifurcation diagram for $\varepsilon = 0.1,k = 4/3,\delta = 0.5$. The Hopf Bifurcation is characterized as the solid curve that separates the stable regions from unstable ones on the $\left[ {\lambda ,A} \right]$ plane. In certain regions, the coexistence of Hopf and saddle-node bifurcation could also be observed.

Fig. 4

Bifurcations for $\varepsilon = 0.1,k = 4/3,\delta = 0.5$, solid line: Hopf bifurcation, dashed line: saddle-node bifurcation

The amplitude response of the system is shown in Fig. 5, with $\lambda = 2.25$ for the plots in Fig. 5a and $\lambda = 0.5$ in Fig. 5b, respectively. The stability of solutions along the curves is spot-checked for their chosen parameters and the unstable ones are marked as stars. One can naturally find that in Fig. 5a, there is only Hopf bifurcation, while in Fig. 5b, both of the Hopf and saddle-node bifurcations exist.

Fig. 5

Amplitude response. a $\lambda = 2.25$, b $\lambda = 0.5$, ${N_{20}}$ stands for the value of $\left| {{\psi _{20}}} \right|$

Fig. 6

Frequency response, $\varepsilon = 0.1,k = 4/3,\lambda = 0.5,A = 1$

Figure 6 illustrates the frequency response for the system in which the parameters are assigned as $\varepsilon = 0.1,k = 4/3,\lambda = 0.5,A = 1$. Near the resonance frequency, the coexistence of Hopf and saddle-node bifurcations could be observed. More importantly, some of the solutions with large amplitudes become unstable; from this sense, the vibrational response of the system is reduced by the instabilities of these solutions. However, on the left hand of the main resonance frequency, for some values of $\delta$, the system has only one stable periodic solution. Obviously, these periodic solutions can lead to the failure of vibration suppression for the system and should be avoided as much as possible. To emphasize this phenomenon, we may called a solution in this case as undesired solution and $\delta$ the failure frequency, and in Fig. 6, for example, the interval of the failure frequency is $\delta \in \left[ -\,0.75,\;-\,0.45 \right]$.

2.3 Strongly modulated response

The combination of essential nonlinearity together with the rich bifurcation phenomenon brings about a possibility of response regimes referred to Starosvetsky and Gendelman as strongly modulated response (SMR), which is qualitatively different from steady-state and weakly modulated responses existing in the vicinities of averaged flow equations in conditions of 1:1 resonance. The goal of this section is to determine the frequency range for the existence of the SMR.

The two first-order equations in system (7) can be rewritten to a second-order ODE with respect to the single variable ${\psi _2}$. Without confusion, we hereafter drop the subscript of ${\psi _2}$ for simplicity

$$\begin{aligned}&\ddot{\psi }+ \frac{\mathrm{d}}{{\mathrm{d}t}}\left[ {\frac{{i\left( {1 + 4\varepsilon \delta } \right) }}{2}\psi + \frac{{\left( {\lambda - 3ik} \right) \left( {1 + \varepsilon } \right) }}{8}{{\left| \psi \right| }^2}\psi } \right] \nonumber \\&\qquad -\, \frac{\varepsilon }{2}\left[ {\delta \left( {1 + 2\varepsilon \delta } \right) - \frac{{\left( {3k + i\lambda } \right) \left( {1 + 2\delta + 2\varepsilon \delta } \right) }}{8}{{\left| \psi \right| }^2}} \right] \psi \nonumber \\&\quad = \frac{{i\varepsilon \left( {1 + 2\varepsilon \delta } \right) A}}{4} \end{aligned}$$

(22)

As mentioned by the assumption that $0 < \varepsilon \ll 1$, it is therefore convenient to expand Eq. (22) by means of multiple scales approach with respect to $\varepsilon$ according to the substitution; hence, one have

$$\begin{aligned}&{\varepsilon ^0}:D_0^2\psi + {D_0}\left( {\frac{i}{2}\psi + \frac{{\lambda - 3ik}}{8}{{\left| \psi \right| }^2}\psi } \right) = 0\nonumber \\&{{\varepsilon ^1}:2{D_0}{D_1}\psi + {D_0}\left( {2i\delta \psi + \frac{{\lambda - 3ik}}{8}{{\left| \psi \right| }^2}\psi } \right) }\nonumber \\&\quad +\,{D_1}\left( {\frac{i}{2}\psi + \frac{{\lambda - 3ik}}{8}{{\left| \psi \right| }^2}\psi } \right) \nonumber \\&\quad -\, \frac{\delta }{2}\psi + \frac{{\left( {i\lambda + 3k} \right) \left( {1 + 2\delta } \right) }}{{16}}{{\left| \psi \right| }^2}\psi = \frac{{iA}}{4} \end{aligned}$$

(23)

Considering first the order ${\varepsilon ^0}$ of Eq. (23), a trivial integration gives

$$\begin{aligned} {D_0}\psi + \frac{i}{2}\psi + \frac{{\lambda - 3ik}}{8}{\left| \psi \right| ^2}\psi = C\left( {{\tau _1}, \cdots } \right) \end{aligned}$$

(24)

whose fixed points are written as

$$\begin{aligned} \frac{i}{2}\psi + \frac{{\lambda - 3ik}}{8}{\left| \psi \right| ^2}\psi = C \end{aligned}$$

(25)

or equivalently

$$\begin{aligned} \frac{{9{k^2} + {\lambda ^2}}}{{16}}{Z^3} - \frac{{3k}}{2}{Z^2} + Z = 4{C^2} \end{aligned}$$

(26)

where $Z = {N^2} = {\left| \psi \right| ^2}$. Taking the derivative of the each side with respect to Z, then

$$\begin{aligned} \frac{3}{{16}}\left( {9{k^2} + {\lambda ^2}} \right) {Z^2} - 3kZ + 1= 0 \end{aligned}$$

(27)

with the following roots being

$$\begin{aligned} {Z_{1,2}}= & {} \frac{1}{{9{k^2} + {\lambda ^2}}}\left( {8k \mp 4\sqrt{{k^2} - \frac{{{\lambda ^2}}}{3}} } \right) \nonumber \\\Rightarrow & {} {N_{1,2}} = \sqrt{\frac{1}{{9{k^2} + {\lambda ^2}}}\left( {8k \mp 4\sqrt{{k^2} - \frac{{{\lambda ^2}}}{3}} } \right) }\nonumber \\ \end{aligned}$$

(28)

Equation (26) was used to generate the slow invariant manifold (SIM) projection on the $[N,4{C^2}]$ plane shown in Fig. 7. $N_1$ and $N_2$ in Eq. (32) were used to plot the fold lines of the SIM, and they define the fold lines that correspond to the locations on the SIM at which the trajectories of the SIM may jump between stable branches. Note that in the triple-valued region, the left and right are stable and the middle branch is unstable. The SIM could be considered to be the space in which the system response occurs on the slow time scale, and the state of the system can move only on the SIM. When a state moves up along the left stable branch to $N_1$, since the instability of the middle branch, the state may jump to the point $N_u$ on the right branch with the same value of C. Similarly, a state that approaches to $N_2$ may also jump to $N_d$. The jump on the SIM between its stable branches gives a fundamental mechanism of SMR.

Fig. 7

SIM projection, solid line: stable branch, dashed line: unstable branch, arrow: jump between the stable branches

Now, let’s study the ${\varepsilon ^1}$ order equation of Eq. (23); assuming ${\tau _0} \rightarrow +\,\infty$, the ${\varepsilon ^1}$ equation can be simplified to

$$\begin{aligned}&{D_1}\left( {\frac{i}{2}\psi + \frac{{\lambda - 3ik}}{8}{{\left| \psi \right| }^2}\psi } \right) - \frac{\delta }{2}\psi \nonumber \\&\quad +\,\frac{{\left( {i\lambda + 3k} \right) \left( {1 + 2\delta } \right) }}{{16}}{\left| \psi \right| ^2}\psi = \frac{{iA}}{4} \end{aligned}$$

(29)

letting

$$\begin{aligned} \varGamma = \frac{\delta }{2}\psi + \frac{{iA}}{4} - \frac{{\left( {i\lambda + 3k} \right) \left( {1 + 2\delta } \right) }}{{16}}{\left| \psi \right| ^2}\psi \end{aligned}$$

the equation becomes

$$\begin{aligned} \left( {\frac{i}{2} + \frac{{\lambda - 3ik}}{4}{{\left| \psi \right| }^2}} \right) \frac{{\partial \psi }}{{\partial {\tau _1}}} + \frac{{\lambda - 3ik}}{8}{\psi ^2}\frac{{\partial {\psi ^*}}}{{\partial {\tau _1}}} = \varGamma \end{aligned}$$

(30)

and taking the complex conjugate of Eq. (30) and substituting to Eq. (30), one can derive

$$\begin{aligned} \frac{{\partial \psi }}{{\partial {\tau _1}}} = \frac{{2\varGamma \left( {\frac{{\lambda + 3ik}}{2}{{\left| \psi \right| }^2} - i} \right) - \frac{{\lambda - 3ik}}{2}{\psi ^2}{\varGamma ^*}}}{{\frac{3}{{16}}\left( {9{k^2} + {\lambda ^2}} \right) {{\left| \psi \right| }^4} - 3k{{\left| \psi \right| }^2} + 1}} \end{aligned}$$

(31)

Considering $\psi = N{e^{i\theta }}$, the equation can then be written as

$$\begin{aligned} 2g\left( {N} \right) \frac{{\partial N}}{{\partial {\tau _1}}}= & {} - \frac{\lambda }{4}{N^3} - \frac{{3k}}{4}{N^2}A\cos \theta \nonumber \\&+ \,\frac{\lambda }{4}{N^2}A\sin \theta + A\cos \theta \nonumber \\ 2g\left( {N} \right) \frac{{\partial \theta }}{{\partial {\tau _1}}}= & {} - \frac{{27{k^2} + 3{\lambda ^2}}}{{16}}\left( {1 + 2\delta } \right) {N^4}\nonumber \\&+\, \frac{{3k}}{4}\left( {1 + 8\delta } \right) {N^2} + \frac{{9kNA\sin \theta }}{4}\nonumber \\&+\, \frac{{3\lambda NA\cos \theta }}{4} - 2\delta - \frac{{A\sin \theta }}{N} \end{aligned}$$

(32)

where

$$\begin{aligned} g\left( {N} \right) = \frac{3}{{16}}\left( {9{k^2} + {\lambda ^2}} \right) {N^4} - 3k{N^2} + 1 \end{aligned}$$

For sake of convenience, let ${f_1}\left( {N,\theta } \right)$ and ${f_2}\left( {N,\theta } \right)$ represent the right hands of the first and second equation for system (32). As the fold lines occur when $g\left( N \right) =0$, the equations are therefore can be rescaled time by the function $g\left( N \right)$ to the following flow without singularities

$$\begin{aligned} N'= & {} {f_1}\left( {N,\theta } \right) \nonumber \\ \theta '= & {} {f_2}\left( {N,\theta } \right) \end{aligned}$$

(33)

The phase portraits for system with different parameters are shown Fig. 8 where the arrows denote the direction of the trajectories with time increase. On the lower fold line, the two folded singularities corresponding to the value of $\theta$ at which $\theta ' =0$ are denoted by ${\Theta _1}$ and ${\Theta _2}$ in each figure. The phase portraits only show stable trajectories on the SIM.

Fig. 8

Phase portraits with $\delta$ varying, a $\delta =0$, b $\delta =-2$, c $\delta =2.5$. Rest parameters are $\varepsilon = 0.1,k = 4/3,\lambda = 0.5,A = 1$

In Fig. 8a, we can see that there is an interval of $\theta$ bounded by the folded singularities for which all phase trajectories can arrive to and jump from ${N_1}$. See also Fig. 8b, c where an attractor exists in the lower or the upper branch, not every trajectory that starts from the lower fold of the SIM could reach the initial interval $[{\Theta _1},{\Theta _2}]$; according to Ref. [41] this interval is called the jump interval J. For those points mapped into J, the phase trajectory jumps from a point of J to the upper branch of the SIM, then it moves along the line of the super-slow flow to the upper fold line, and then it jumps back to the lower branch and moves to the lower fold line, commencing on one of the points of the interval R in order to enable the next jump. This fact suggests the possible existence of SMR, and to simplify this procedure, a 1D map from J to itself can be conducted to determine the parametric zones of existence of the SMR.

Taking into account that C is constant, Eq. (30) can be rewritten as

$$\begin{aligned}&\frac{{9{k^2} + {\lambda ^2}}}{{16}}Z_{1,2}^3 - \frac{{3k}}{2}Z_{1,2}^2 + {Z_{1,2}}\nonumber \\&\quad = \frac{{9{k^2} + {\lambda ^2}}}{{16}}Z_{u,d}^3 - \frac{{3k}}{2}Z_{u,d}^2 + {Z_{u,d}} \end{aligned}$$

(34)

and thus, solving the equation gives

$$\begin{aligned} {N_u}= & {} \sqrt{\frac{8}{{9{k^2} + {\lambda ^2}}}\left( {k + \sqrt{{k^2} - \frac{{{\lambda ^2}}}{3}} } \right) }\nonumber \\ {N_d}= & {} \sqrt{\frac{8}{{9{k^2} + {\lambda ^2}}}\left( {k - \sqrt{{k^2} - \frac{{{\lambda ^2}}}{3}} } \right) } \end{aligned}$$

(35)

In addition, according to Eq. (25), the phase angle of the fixed point can be calculated

$$\begin{aligned} \theta + {\tan ^{ - 1}}\left[ {\frac{{4 - 3kZ}}{{\lambda Z}}} \right] = \arg C \end{aligned}$$

(36)

and then, manipulations between Eqs. (35) and (36) yield the phase angle at ${N_u}$ on the upper stable branch from the jump at ${N_1}$, together with ${N_d}$ on the lower stable branch from the jump at ${N_2}$, let

$$\begin{aligned} {P_i} = \frac{{4 - 3k{Z_i}}}{{\lambda {Z_i}}},i = 1,2,u,d \end{aligned}$$

and the relations then write

$$\begin{aligned} {\theta _{u,d}} = {\theta _{1,2}} + {\tan ^{ - 1}}\left[ {\frac{{{P_{1,2}} - {P_{u,d}}}}{{1 + {P_{1,2}}{P_{u,d}}}}} \right] \end{aligned}$$

(37)

The 1D map is shown in Fig. 9. Furthermore, by varying values of $\delta$, Fig. 10 is generated.

Fig. 9

1D mapping for $\delta =0$

Fig. 10

1D mapping by varying $\delta$ from − 5.85 to 2.68. a $\delta =-\,5.85$, b $\delta =-\,2$, c $\delta =2.5$, d $\delta =2.68$

From varying $\delta$ and observing when trajectories from the ${\Theta _1}$ and ${\Theta _1}$ interval no longer returned, the SMR could be found to exist in the intervals of $\delta \in [ -\, 5.85,2.68]$. Let $\delta =0$, an example of the SMR regime is plotted in Fig. 11, and for the effectiveness of SMR considered from vibration suppression point of view will be discussed in Sect. 4.

Fig. 11

Poincare section and time response of the linear oscillator for $\delta =0$, existence of SMR regime

3 Dynamics of a linear oscillator with a 2-dof NES

This section parallels for 2-dof NES the development in Sect. 2 but is far more complicated in its dynamics. Considering first the particular condition of $\omega = 1$ (the frequency of excitation equals to the natural frequency of linear oscillator), the bifurcations of the system are studied similar to that we have done in the case of 1-dof NES. Instead of analytical treatment, an IHB method is used for its simplicity to understand the frequency response of the system.

3.1 Model description

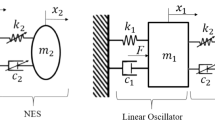
The system considered in this section is depicted in Fig. 12.

Fig. 12

System of a linear oscillator and an attached 2-dof NES

According to Fig. 12, the relations among the mass of these oscillators could be expressed as

$$\begin{aligned} {m_2} + {m_3} = \varepsilon {m_1},{m_2} = \alpha \varepsilon {m_1},{m_3} = \left( {1 - \alpha } \right) \varepsilon {m_1} \end{aligned}$$

(38)

and here $\varepsilon$ is the ratio between the total mass of the NES and the mass of the linear oscillator and $\alpha$ stands for the mass distribution of the 2-dof NES.

Taking similarly the procedure carried in Sect. 2, one can immediately write the dimensionless form equation as follows

$$\begin{aligned}&{{\ddot{x}}_1} + {x_1} + \varepsilon {k_1}{\left( {{x_1} - {x_2}} \right) ^3}\nonumber \\&\quad +\,\varepsilon {\lambda _1}{\left( {{x_1} - {x_2}} \right) ^2}\left( {{{\dot{x}}_1} - {{\dot{x}}_2}} \right) = \varepsilon A\cos \left( {\omega \tau } \right) \nonumber \\&\alpha {{\ddot{x}}_2} + {k_1}{\left( {{x_2} - {x_1}} \right) ^3} + {k_2}{\left( {{x_2} - {x_3}} \right) ^3}\nonumber \\&\quad +\,\,{\lambda _1}{\left( {{x_2} - {x_1}} \right) ^2}\left( {{{\dot{x}}_2} - {{\dot{x}}_1}} \right) \nonumber \\&\quad +\,\,{\lambda _{2\,}}{\left( {{x_2} - {x_3}} \right) ^2}\left( {{{\dot{x}}_2} - {{\dot{x}}_3}} \right) = 0\nonumber \\&\left( {1 - \alpha } \right) {{\ddot{x}}_3} + {k_2}{\left( {{x_3} - {x_2}} \right) ^3}\nonumber \\&\quad +\,\,{\lambda _{2\,}}{\left( {{x_3} - {x_2}} \right) ^2}\left( {{{\dot{x}}_3} - {{\dot{x}}_2}} \right) = 0 \end{aligned}$$

(39)

3.2 Analytical treatment at $\omega = 1$

Setting $\omega = 1$ and utilizing the variable change ${\dot{x}_i} + i{x_i} = {\varphi _i}{e^{i\tau }},i = 1,2,3$, one consequently has the slow dynamical flow of the system

$$\begin{aligned}&{{\dot{\varphi } }_1} + \frac{{\varepsilon {p_1}}}{8}{\left| {{\varphi _u}} \right| ^2}{\varphi _u} = \frac{{\varepsilon A}}{2}\nonumber \\&{{\dot{\varphi } }_u} - \frac{i}{2}\left( {{\varphi _1} - {\varphi _u}} \right) + \frac{{1 + \alpha \varepsilon }}{{8\alpha }}{p_1}{\left| {{\varphi _u}} \right| ^2}{\varphi _u}\nonumber \\&\quad - \,\,\frac{{{p_2}}}{{8\alpha }}{\left| {{\varphi _v}} \right| ^2}{\varphi _v} = \frac{{\varepsilon A}}{2}\nonumber \\&{{\dot{\varphi } }_v} + \frac{i}{2}{\varphi _v} - \frac{{{p_1}}}{{8\alpha }}{\left| {{\varphi _u}} \right| ^2}{\varphi _u} + \frac{{{p_2}}}{{8\alpha \left( {1 - \alpha } \right) }}{\left| {{\varphi _v}} \right| ^2}{\varphi _v} = 0\nonumber \\ \end{aligned}$$

(40)

where

$$\begin{aligned} {p_i} = {\lambda _i} - 3i{k_i},i = 1,2,{\varphi _u} = {\varphi _1} - {\varphi _2},{\varphi _v} = {\varphi _2} - {\varphi _3} \end{aligned}$$

Considering first the fixed points of system (40) and letting the time derivative of Eq. (40) to zero yield

$$\begin{aligned}&\frac{{\varepsilon A}}{2} - \frac{{\varepsilon {p_1}}}{8}{\left| {{\varphi _u}} \right| ^2}{\varphi _u} = 0\nonumber \\&\frac{{1 + \alpha \varepsilon }}{{8\alpha }}{p_1}{\left| {{\varphi _u}} \right| ^2}{\varphi _u} - \frac{i}{2}\left( {{\varphi _1} - {\varphi _u}} \right) - \frac{{{p_2}}}{{8\alpha }}{\left| {{\varphi _v}} \right| ^2}{\varphi _v} = \frac{{\varepsilon A}}{2}\nonumber \\&\frac{i}{2}{\varphi _v} - \frac{{{p_1}}}{{8\alpha }}{\left| {{\varphi _u}} \right| ^2}{\varphi _u} + \frac{{{p_2}}}{{8\alpha \left( {1 - \alpha } \right) }}{\left| {{\varphi _v}} \right| ^2}{\varphi _v} = 0 \end{aligned}$$

(41)

which finally implies the following decoupled form

$$\begin{aligned}&{\left| {{\varphi _u}} \right| ^2}{\varphi _u} = \frac{{4A}}{{{p_1}}}\nonumber \\&\left( {\frac{{{p_2}{{\left| {{\varphi _v}} \right| }^2}}}{{4\left( {1 - \alpha } \right) }} + i\alpha } \right) {\varphi _v} = A\nonumber \\&{\varphi _1} = {\varphi _u} + \left( {1 - \alpha } \right) {\varphi _v} - iA \end{aligned}$$

(42)

It can be noted that for the first equation in (42), regardless of the parameters change, there exists only one solution for ${\varphi _u}$. In addition, according to the third equation in (42), once the value of ${\varphi _u}$ and ${\varphi _v}$ is uniquely given, the value of ${\varphi _1}$ is then also uniquely determined. Therefore, the numbers of fixed points depend on the numbers of roots in the second equation of (42). Rewriting the second equation of (42) gives

$$\begin{aligned} \frac{{\lambda _2^2 + 9k_2^2}}{{16{{\left( {1 - \alpha } \right) }^2}}}{\left| {{\varphi _v}} \right| ^6} - \frac{{3\alpha {k_2}}}{{2\left( {1 - \alpha } \right) }}{\left| {{\varphi _v}} \right| ^4} + {\alpha ^2}{\left| {{\varphi _v}} \right| ^2} - {A^2} =0 \end{aligned}$$

(43)

It is not difficult to observe from Eq. (43) that the number of solutions is only related to the second part of the nonlinear coupling ${\lambda _2}$ and ${k _2}$, the mass distribution of the NES $\alpha$ and the amplitude of excitation A; in other words, the saddle-node bifurcation will also related only to these parameters. The equation has the form

$$\begin{aligned} {\eta _1}Z + {\eta _2}{Z^2} + {\eta _3}{Z^3} + {\eta _4}\mathrm{{ = }}0 \end{aligned}$$

(44)

with $Z = {\left| {{\varphi _v}} \right| ^2}$, and to determine the numbers of roots, the Cardano discriminant $\varDelta$ of Eq. (44) can be written as

$$\begin{aligned} \varDelta = {\left( {\frac{{\eta _2^3}}{{27\eta _3^3}} - \frac{{{\eta _1}{\eta _2}}}{{6\eta _3^2}} + \frac{{{\eta _4}}}{{{\eta _3}}}} \right) ^2} + {\left( {\frac{{{\eta _1}}}{{3{\eta _3}}} - \frac{{\eta _2^2}}{{9\eta _3^2}}} \right) ^3} \end{aligned}$$

(45)

and owing to the values of the discriminant: When $\varDelta >0$, Eq. (44) has only one real root, when $\varDelta =0$, Eq. (44) has three real roots and at least two of them are equal, and when $\varDelta <0$, Eq.(44) has three unequal real roots. In this way, saddle-node bifurcation could be found by setting $\varDelta =0$.

Figure 13 shows the values of the discriminant as function of external excitation and mass distribution of the NES, respectively. Either the change of the mass distribution $\alpha$ or the amplitude A can lead to saddle-node bifurcation. This is totally different from the case of single dof NES where there is no saddle-node bifurcation at $\omega = 1$.

Fig. 13

Values of the Cardano discriminant, as function of a the amplitude of excitation A and b mass distribution of the NES

The saddle-node bifurcation on the $[{\lambda _2},A]$ and plane is depicted in Fig. 14. The plots shows a quite similar shape to the case of single dof NES as a ’triangle’ bounded by which there are three fixed points, and the critical value of damping ${\lambda _2} = \sqrt{3} k$ could also be found for the vanish of saddle-node bifurcation. An interesting phenomenon is that with the increase of $\alpha$ , the ’triangle’ moves up on the plane and then turns back down after reaching the peak at $\alpha =0.7$.

Fig. 14

Saddle-node bifurcation on the $[{\lambda _2},A]$ plane

Studying more precisely the effect of $\alpha$ on the saddle-node bifurcation of the system, Fig. 15 shows the bifurcation diagram on the $[{\lambda _2},\alpha ]$ plane. For the regions bounded by the curve, there are three fixed points and the bifurcation diagram turns out to be more complicated than the one on the $[{\lambda _2},A]$. The symmetric relation for the dependence of saddle-node bifurcation on the mass distribution $\alpha$ can be immediately found. On the other hand, the whole plane can be divided into three main regions (see the area 1, area 2 and area 3 in Fig. 15) by the two vertical line of ${\lambda _2}=1.41$ and ${\lambda _2}=2.31$, and by varying the values of $\alpha$, the saddle-node bifurcation appears two times in area 1, four times in area 2 and vanishes in area 3.

Fig. 15

Saddle-node bifurcation on the $[{\lambda _2},\alpha ]$ plane

Observing the perturbation motion near the fixed points, letting

$$\begin{aligned} {\varphi _1} = {\varphi _{10}} + {\varDelta _1},{\varphi _u} = {\varphi _{u0}} + {\varDelta _u},{\varphi _v} = {\varphi _{v0}} + {\varDelta _v} \end{aligned}$$

(46)

and applying these relations to Eq. (40), one have

$$\begin{aligned} \dot{\varDelta }_1= & {} - \,\frac{\varepsilon p_1}{8}\left( 2\left| \varphi _{u0} \right| ^2\varDelta _u + \varphi _{u0}^2\varDelta _u^* \right) \nonumber \\ \dot{\varDelta }_1^*= & {} -\, \frac{\varepsilon p_1^*}{8}\left( 2\left| \varphi _{u0} \right| ^2\varDelta _u^* + \varphi _{u0}^*2\varDelta _u \right) \nonumber \\ \dot{\varDelta }_u= & {} \frac{p_2}{8\alpha } \left( 2\left| \varphi _{v0} \right| ^2\varDelta _v + \varphi _{v0}^2\varDelta _v^* \right) + \frac{i}{2}\left( \varDelta _1 - \varDelta _u \right) \nonumber \\&- \,\frac{1 + \alpha \varepsilon }{8\alpha } p_1\left( 2\left| \varphi _{u0} \right| ^2\varDelta _u + \varphi _{u0}^2\varDelta _u^* \right) \nonumber \\ \dot{\varDelta }_u^*= & {} \frac{p_2^*}{8\alpha } \left( 2\left| \varphi _{v0} \right| ^2\varDelta _v^* + \varphi _{v0}^*2\varDelta _v \right) - \frac{i}{2}\left( \varDelta _1^* - \varDelta _u^* \right) \nonumber \\&- \,\frac{1 + \alpha \varepsilon }{8\alpha } p_1^*\left( 2\left| \varphi _{u0} \right| ^2\varDelta _u^* + \varphi _{u0}^*2\varDelta _u \right) \nonumber \\ \dot{\varDelta }_v= & {} - \frac{i}{2}\varDelta _v - \frac{p_1}{8\alpha } \left( 2\left| \varphi _{u0} \right| ^2\varDelta _u + \varphi _{u0}^2\varDelta _u^* \right) \nonumber \\&- \, \frac{p_2}{{8\alpha } \left( 1 - \alpha \right) }\left( 2\left| \varphi _{v0} \right| ^2\varDelta _v + \varphi _{v0}^2\varDelta _v^* \right) \nonumber \\ \dot{\varDelta }_v^*= & {} \frac{i}{2}\varDelta _v - \frac{p_1^*}{8\alpha } \left( 2\left| \varphi _{u0} \right| ^2\varDelta _u^* + \varphi _{u0}^*2\varDelta _u \right) \nonumber \\&- \, \frac{p_2^*}{{8\alpha } \left( 1 - \alpha \right) }\left( 2\left| \varphi _{v0} \right| ^2\varDelta _v^* + \varphi _{v0}^*2\varDelta _v \right) \end{aligned}$$

(47)

and the characteristic polynomial of the above linear system has the form

$$\begin{aligned} {\mu ^6} + {\gamma _1}{\mu ^5} + {\gamma _2}{\mu ^4} + {\gamma _3}{\mu ^3} + {\gamma _4}{\mu ^2} + {\gamma _5}\mu + {\gamma _6} =0\nonumber \\ \end{aligned}$$

(48)

where ${\mu }$ is the eigenvalues whose coefficients can be calculated by MATLAB.

The bifurcation diagram is depicted in Fig. 16, where the Hopf bifurcation that separates stable areas ${W^s}$ from unstable areas ${W^u}$ is represented by the dot line, and the saddle-node bifurcation for this particular parameter is plotted by the solid line. Instead of the simple curve that has shown in the case of 1-dof NES , the Hopf bifurcation (see from the dot line) becomes rather intricate now. The two main branches, corresponding to high amplitude and low amplitude, can now be found in the diagram, and the coexistence of Hopf and saddle-node bifurcation could be found at low-amplitude area. When the excitation amplitude increases, the system may have several bifurcations even if there is only one fixed point. To specify this, Fig. 17 shows two example of the amplitude response for $\alpha = 0.6,\varepsilon = 0.1,{k_1} = {k_2} = 1.33,{\lambda _1} = 0.5$. In Fig. 17a, ${\lambda _2} = 2.5$, there is only one fixed point through A variation, while in Fig. 17b ${\lambda _2} = 0.5$, there could be three fixed points for some values of A. However, in both cases, the system can occur several times of Hopf bifurcation.

Fig. 16

Bifurcation diagrams, dot line: Hopf bifurcation, solid line: saddle-node bifurcation

Fig. 17

Amplitude response for $\alpha = 0.6,\varepsilon = 0.1,{k_1} = {k_2} = 1.33,{\lambda _1} = 0.5$, a ${\lambda _2} = 2.5$, b ${\lambda _2} = 0.5$, ${N_{v0}}$ stands for the value of $\left| {{\phi _{v0}}} \right|$

Finally, we plot the response of the system as a function of $\alpha$ in Fig. 18. Adjusting the mass distribution $\alpha$ of the NES brings about rich response regimes, together with a huge influence on their amplitude. With the effect of saddle-node and Hopf bifurcation, the number and stability of solutions change; consequently, that is, the interval for three fixed points is $\alpha \in \left[ {0.509\;0.651} \right] \cup \left[ {0.834\;0.916} \right]$, while the instability of these solutions occurs for $\alpha \in \left[ {0.389\;0.741} \right] \cup \left[ {0.834\;0.916} \right]$. Note also that the response curve bends from both sides to the middle and creates a dent in the middle area. This dent, if considered from a vibration suppression point of view, provides a effective reduction for the system response.

Fig. 18

Response of the system as a function of $\alpha$

3.3 Response analysis using incremental harmonic balance method

The previous analytical treatment is carried out based on the particular condition $\omega = 1$; when the frequency of excitation changes, the dynamics of the system becomes rather more complicated, which in turn brings difficulties for the analytical study of system (39). Take this into consideration, an incremental harmonic balance (IHB) method [45,46,47] is applied mainly in this section for its simplicity in the analysis of multi-dof oscillating system.

Making a change of variables according to $\tau \mathrm{{ = }}\omega t$, the system becomes

$$\begin{aligned} {\omega ^2}\bar{M}\ddot{X} + \omega {\bar{C}_n}\dot{X} + \left( {\bar{K} + {{\bar{K}}_n}} \right) X = \bar{F}\cos \tau \end{aligned}$$

(49)

where

$$\begin{aligned} \bar{M} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{\varepsilon }}&{}{}&{}{}\\ {}&{}\alpha &{}{}\\ {}&{}{}&{}{1 - \alpha } \end{array}} \right] ,\bar{K} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{\varepsilon }}&{}{}&{}{}\\ {}&{}0&{}{}\\ {}&{}{}&{}0 \end{array}} \right] ,\bar{F} = \left[ {\begin{array}{*{20}{c}} A\\ 0\\ 0 \end{array}} \right] \end{aligned}$$

Let ${X_0},{F_0},{\omega _0}$ be a set of solution for Eq. (49), then the first step of IHB is the incremental process, consider an increment in the vicinity of ${X_0},{F_0},{\omega _0}$ of the following form

$$\begin{aligned} X = {X_0} + \varDelta X,\omega = {\omega _0} + \varDelta \omega ,\bar{F} = {\bar{F}_0} + \varDelta F \end{aligned}$$

(50)

inserting Eq. (50) into (49) and omitting the high-order terms yield

$$\begin{aligned}&\omega _0^2{{\bar{\mathbf{M}}}}\varDelta {{\ddot{\mathbf{X}}}} + {\omega _0}{{{{\bar{\mathbf{C}}}}}_{n0}}\varDelta {{\dot{\mathbf{X}}}}\nonumber \\&\qquad + \left( {{{\bar{\mathbf{K}}}} + 2{{{{\bar{\mathbf{C}}}}}_{k0}}{\omega _0} + 3{{{{\bar{\mathbf{K}}}}}_{n0}}} \right) \varDelta \mathbf{{X}}\nonumber \\&\quad = {{\bar{\mathbf{R}}}} - \left( {2{\omega _0}{{\bar{\mathbf{M}}}}{{{{\ddot{\mathbf{X}}}}}_0} + {{{{\bar{\mathbf{C}}}}}_{n0}}{{{{\dot{\mathbf{X}}}}}_0}} \right) \varDelta \omega + \varDelta \mathbf{{F}}\cos \tau \end{aligned}$$

(51)

with

$$\begin{aligned} {{{{\bar{\mathbf{C}}}}}_{k0}}= & {} {{{{\bar{\mathbf{C}}}}}_k}\left( {{\mathbf{{X}}_0}} \right) = \left[ {\begin{array}{*{20}{c}} {{\lambda _1}{C_1}}&{}{ -\, {\lambda _1}{C_1}}&{}0\\ { -\, {\lambda _1}{C_1}}&{}{{\lambda _1}{C_1} + {\lambda _2}{C_2}}&{}{ - \,{\lambda _2}{C_2}}\\ 0&{}{ -\, {\lambda _2}{C_2}}&{}{{\lambda _2}{C_2}} \end{array}} \right] \\ {C_1}= & {} \left( {{x_1} - {x_2}} \right) \left( {{{\dot{x}}_1} - {{\dot{x}}_2}} \right) ,{C_2} = \left( {{x_2} - {x_3}} \right) \left( {{{\dot{x}}_2} - {{\dot{x}}_3}} \right) \end{aligned}$$

and here ${{\bar{\mathbf{R}}}}$ is called error vector, if ${X_0},{F_0},{\omega _0}$ is the precise solution of Eq. (49), and one has ${{\bar{\mathbf{R}}}} = 0$. Particularly, the expression of ${{\bar{\mathbf{R}}}}$ is expressed as

$$\begin{aligned} {{\bar{\mathbf{R}}}} = {{{{\bar{\mathbf{F}}}}}_0}\cos \tau - \omega _0^2{{\bar{\mathbf{M}}}}{{{{\ddot{\mathbf{X}}}}}_0} - {\omega _0}{{{{\bar{\mathbf{C}}}}}_{n0}}{{{{\dot{\mathbf{X}}}}}_0} - \left( {{{\bar{\mathbf{K}}}} + {{{{\bar{\mathbf{K}}}}}_{n0}}} \right) {\mathbf{{X}}_0} \end{aligned}$$

(52)

The next step of IHB is the harmonic balance process, and assume the solutions of system (49) can be expressed in the form of trigonometric series

$$\begin{aligned} {x_k}= & {} \sum \limits _{i = 1}^n {{a_{ki}}} \cos \left( {2i - 1} \right) \tau \nonumber \\&+\sum \limits _{i = 1}^n {{b_{ki}}} \sin \left( {2i - 1} \right) \tau = \mathbf{{D}}{\mathbf{{N}}_k}\nonumber \\ \varDelta {x_k}= & {} \sum \limits _{i = 1}^n {\varDelta {a_{ki}}} \cos \left( {2i - 1} \right) \tau \nonumber \\&+\sum \limits _{i = 1}^n {\varDelta {b_{ki}}} \sin \left( {2i - 1} \right) \tau = \mathbf{{D}}\varDelta {\mathbf{{N}}_k} \end{aligned}$$

(53)

where

$$\begin{aligned} \mathbf{{N}}_k= & {} \left[ a_{k1},a_{k2} \cdots ,a_{kn},b_{k1},b_{k2}, \cdots b_{kn} \right] \\ \varDelta \mathbf{{N}}_k= & {} \left[ \varDelta a_{k1}, \ldots ,\varDelta a_{kn},\varDelta b_{k1}, \ldots \varDelta b_{kn} \right] \\ \mathbf{{D}}= & {} \left( \cos \tau ,\cos 3\tau , \ldots ,\sin \tau ,sin3\tau , \ldots \right) \end{aligned}$$

rewriting Eq. (53) in matrix form to have

$$\begin{aligned} {\mathbf{{X}}_0} = \mathbf{{SN}},\varDelta \mathbf{{X}} = \mathbf{{S}}\varDelta \mathbf{{N}} \end{aligned}$$

(54)

with

$$\begin{aligned} \mathbf{{N}}= & {} {\left[ {\begin{array}{*{20}{c}} {\mathbf{{N}}_1^T}&{\mathbf{{N}}_2^T}&{\mathbf{{N}}_3^T} \end{array}} \right] ^T}\\ \varDelta \mathbf{{N}}= & {} {\left[ {\begin{array}{*{20}{c}} {\varDelta \mathbf{{N}}_1^T}&{\varDelta \mathbf{{N}}_2^T}&{\varDelta \mathbf{{N}}_3^T} \end{array}} \right] ^T}\\ \mathbf{{S}}= & {} \mathrm{dia}\left[ {\mathbf{{D}},\mathbf{{D}}, \ldots \mathbf{{D}}} \right] \end{aligned}$$

Substituting Eq. (54) into Eq. (51) and employing the following relation

$$\begin{aligned}&\int _0^{2\pi } {\delta {{\left( {\varDelta \mathbf{{X}}} \right) }^T}} [\omega _0^2{{\ddot{\mathbf{M}}}}\varDelta {{\ddot{\mathbf{X}}}} + {\omega _0}{{{{\bar{\mathbf{C}}}}}_{n0}}\varDelta {{\ddot{\mathbf{X}}}}\nonumber \\&\qquad +\, ({{\bar{\mathbf{K}}}} + 2{{{{\bar{\mathbf{C}}}}}_{k0}}{\omega _0} + 3{{{{\bar{\mathbf{K}}}}}_{n0}})\varDelta \mathbf{{X}}]\mathrm{d}\tau \nonumber \\&\quad = \int _0^{2\pi } {\delta {{\left( {\varDelta \mathbf{{X}}} \right) }^T}} [{{\bar{\mathbf{R}}}} - (2{\omega _0}{{\ddot{\mathbf{M}}}}{{{{\ddot{\mathbf{X}}}}}_0}\nonumber \\&\qquad +\, {{{{\bar{\mathbf{C}}}}}_{n0}}{{{{\ddot{\mathbf{X}}}}}_0})\varDelta \omega + \varDelta \mathbf{{F}}\cos \tau ]\mathrm{d}\tau \end{aligned}$$

(55)

one finally obtains the algebraic equation

$$\begin{aligned} {\mathbf{{K}}_{\mathrm{mc}}}\varDelta \mathbf{{N}} = \mathbf{{R}} + {\mathbf{{R}}_{\mathrm{mc}}}\varDelta \omega + {\mathbf{{R}}_f}\varDelta \mathbf{{F}} \end{aligned}$$

(56)

where

$$\begin{aligned} {\mathbf{{K}}_{\mathrm{mc}}}= & {} \omega _0^2\mathbf{{M}} + {\omega _0}{\mathbf{{C}}_{n0}} + \mathbf{{K}} + 2{\omega _0}{\mathbf{{C}}_{k0}} + 3{\mathbf{{K}}_{n0}}\\ {\mathbf{{R}}_f}= & {} \int _0^{2\pi } {{\mathbf{{S}}^T}\cos \tau } \mathrm{d}\tau \\ \mathbf{{R}}= & {} \mathbf{{F}} - \left( {\omega _0^2\mathbf{{M}} + {\omega _0}{\mathbf{{C}}_{n0}} + \mathbf{{K}} + {\mathbf{{K}}_{n0}}} \right) \mathbf{{N}}\\ {\mathbf{{R}}_{\mathrm{mc}}}= & {} - \left( {2{\omega _0}{} \mathbf{{M}} + {\mathbf{{C}}_{n0}}} \right) \mathbf{{N}},\\ \mathbf{{M}}= & {} \int _0^{2\pi } \mathbf{{S}}^T{\bar{\mathbf{M}}}{\ddot{\mathbf{S}}} \mathrm{d}\tau \\ \mathbf{{K}}= & {} \int _0^{2\pi } {{\mathbf{{S}}^T}{} \mathbf{{KS}}} d\tau \\ {\mathbf{{K}}_{n0}}= & {} \int _0^{2\pi } {{\mathbf{{S}}^T}{{{{\bar{\mathbf{K}}}}}_{n0}}{} \mathbf{{S}}} \mathrm{d}\tau \\ {\mathbf{{C}}_{n0}}= & {} \int _0^{2\pi } {{\mathbf{{S}}^T}{{{{\bar{\mathbf{C}}}}}_{n0}}{{\dot{\mathbf{S}}}}} \mathrm{d}\tau \\ {\mathbf{{C}}_{k0}}= & {} \int _0^{2\pi } {{\mathbf{{S}}^T}{{{{\bar{\mathbf{C}}}}}_{k0}}{} \mathbf{{S}}} \mathrm{d}\tau \\ \mathbf{{F}}= & {} \int _0^{2\pi } {{\mathbf{{S}}^T}{{{{\bar{\mathbf{F}}}}}_0}\cos \tau } \mathrm{d}\tau \end{aligned}$$

In order to study the frequency response of system (39), one may fix the amplitude of the external excitation. Thus, let $\varDelta \mathbf{{F}} = 0$ in Eq. (56), and then, Eq. (56) can be simplified as

$$\begin{aligned} {\mathbf{{K}}_{\mathrm{mc}}}\varDelta \mathbf{{N}} = \mathbf{{R}} + {\mathbf{{R}}_{\mathrm{mc}}}\varDelta \omega \end{aligned}$$

(57)

Figure 19 shows an example for the frequency response of the system. One may first notice the complex saddle-node bifurcation here, under whose influence there can simultaneously exist up to five periodic solutions. The curves bend to the right as the amplitude increases and hence show a harden-type nonlinearity. Note also that the bending phenomenon acts extremely noticeable for the curve of the linear structure; as a result, the amplitude of the linear structure near the main resonance frequency is also significantly reduced. To this extent, the effectiveness of the 2-dof NES for vibration reduction could be found in the vicinity of the main resonance frequency.

Fig. 19

Frequency response of the system, ${N_1}$ : amplitude of the linear structure, ${N_{21}}$: amplitude for the relative motion of first-order NES to the linear structure, ${N_{32}}$: amplitude for the relative motion of second-order NES to the first-order NES

Once the periodic solutions are obtained, their stability can consequently be studied by applying Floquet theory to the perturbation motion that is defined by

$$\begin{aligned} \mathbf{{X}} = {\mathbf{{X}}_0} + \varDelta \mathbf{{X}} \end{aligned}$$

(58)

which upon employing Eq. (49) leads to

$$\begin{aligned} {\omega ^2}{{\ddot{\mathbf{M}}}}\varDelta {{\ddot{\mathbf{X}}}} + \omega {{{\bar{\mathbf{C}}}}_{n0}}\varDelta {{\ddot{\mathbf{X}}}} + \left( {{{\bar{\mathbf{K}}}} + 2{{{{\bar{\mathbf{C}}}}}_{k0}}\omega + 3{{{{\bar{\mathbf{K}}}}}_{n0}}} \right) \varDelta \mathbf{{X}} = 0 \end{aligned}$$

(59)

According to Floquet theory, the above system can be rewritten as

$$\begin{aligned} {{\dot{\mathbf{Y}}}} = \mathbf{{Q}}\left( \tau \right) \mathbf{{Y}} \end{aligned}$$

(60)

where

$$\begin{aligned} \mathbf{{Q}}\left( \tau \right)= & {} \left[ {\begin{array}{*{20}{c}}0&{}\mathbf{{I}}\\ {-\frac{1}{{{\omega ^2}}}{{{{\ddot{\mathbf{M}}}}}^{ - 1}}\left( {{{\bar{\mathbf{K}}}} + 2\omega {{{{\bar{\mathbf{C}}}}}_{k0}} + 3{{{{\bar{\mathbf{K}}}}}_{n0}}} \right) }&{}{ - \frac{1}{\omega }{{{{\ddot{\mathbf{M}}}}}^{ - 1}}{{{{\bar{\mathbf{C}}}}}_{n0}}} \end{array}} \right] \\ \mathbf{{Y}}= & {} \left[ {\begin{array}{*{20}{c}} {\varDelta \mathbf{{X}}}\\ {\varDelta {{\ddot{\mathbf{X}}}}} \end{array}} \right] \end{aligned}$$

In light of the periodicity of the solution ${X_0}$, with the period $T = 2\pi$, the related matrix $Q\left( \tau \right)$ must also be periodic, with period the same as ${X_0}$. Suppose a certain solution of Eq. (60) to be

$$\begin{aligned} \mathbf{{y}} = \left[ {{\mathbf{{Y}}_1},{\mathbf{{Y}}_2} \ldots {\mathbf{{Y}}_n}} \right] = \left[ {\begin{array}{*{20}{c}} {{y_{11}}}&{} \ldots &{}{{y_{1n}}}\\ \vdots &{} \ddots &{} \vdots \\ {{y_{n1}}}&{} \cdots &{}{{y_{nn}}} \end{array}} \right] \end{aligned}$$

(61)

Since $\mathbf{{Q}}\left( {\tau + T} \right) = \mathbf{{Q}}\left( \tau \right)$, $y\left( {\tau + T} \right)$ solves Eq. (61) as well. Furthermore, the two solutions have the relationship,

$$\begin{aligned} y\left( {\tau + T} \right) = \mathbf{{P}}y\left( \tau \right) \end{aligned}$$

(62)

where P is called the transition matrix between the solutions

For Eq. (62), Floquet theory claims that if the spectral radius of P less than 1, then the periodic solutions of the system are asymptotic stable, and vise versa. Hence, the problem now is to calculate the spectral radius of P for given solutions.

The transition matrix P can be calculated by means of the following approximate method. First of all, let the period of the system be discretized equally into n intervals, for the kth interval $[{\tau _k},{\tau _{k + 1}}]$, and the value of $\mathbf{{Q}}\left( \tau \right)$ is approximated by the constant matrix. Let ${\mathbf{{Q}}_k} = \mathbf{{Q}}\left( {{\tau _k}} \right)$, the local transition matrix ${\mathbf{{P}}_k}$ from ${\tau _k}$ to ${\tau _k+1}$ writes

$$\begin{aligned} {\mathbf{{P}}_k} = {e^{h{\mathbf{{Q}}_k}}} = \mathbf{{I}} + \sum \limits _{j = 1}^n {\frac{{{{\left( {h{\mathbf{{Q}}_k}} \right) }^j}}}{{j!}}} \end{aligned}$$

(63)

and multiplying the local transition matrix together from $k=1$ to n leads to the value of P

$$\begin{aligned} \mathbf{{P}} = \mathop \varPi \limits _{i = 1}^n {\mathbf{{P}}_k} \end{aligned}$$

(64)

Fig. 20

Floquet analysis for the frequency response, solid line: stable solutions, star: unstable solutions

Fig. 21

Floquet analysis for the frequency response with undesired periodic response eliminated, solid line: stable solutions, star: unstable solutions

Fig. 22

Poincare section for the system with red area represents the steady state, ${x_1},{v_1}$: the displacement and velocity of the linear oscillator, x, v: the displacement and velocity of the center of mass of the NES

Now the transition matrix P is calculated by Eq. (64), and its eigenvalues can be checked. In this way, the stability of the periodic solutions can finally be investigated. Taking into consideration the frequency response of the linear oscillator depicted in Fig. 19, the main results of its stability analysis are shown in Fig. 20. There are two regions of unstable solutions near natural frequency of the linear oscillator, stable periodic solutions which exist in the small frequency range between the two regions, or over the intervals which deviate from the natural frequency. Although the stable periodic solutions on the left hand of the main resonance frequency still exist, their amplitudes are much more desirable than those in the case of system with 1-dof NES. Figure 21 illustrates that, by appropriately designing the parameters of the 2-dof NES, the periodic solutions become unstable; hence, the undesired response on the left hand of the main resonance frequency could be eliminated.

Studying the response regimes near the main resonance frequency, the Poincare sections are generated in Fig. 22 for system with different parameters of $\delta \mathrm{{\,=\, -\,0}}\mathrm{{.5,-\,0}}\mathrm{{.3,0,0}}\mathrm{{.3,0}}\mathrm{{.5}}$ (with corresponding excitation frequencies determined by $\omega \mathrm{{\,=\,}}1 + \varepsilon \delta$). Figure 22 shows that when $\delta \mathrm{{\,=\, -\,0}}\mathrm{{.5}}$, $\delta \mathrm{{\,=\,0}}$ and $\delta \mathrm{{\,=\,0}}\mathrm{{.5}}$, the system possesses periodic response. When $\delta \mathrm{{\,=\, -\,0}}\mathrm{{.3}}$, the response of the linear oscillator is periodic, whereas the response of the NES now becomes chaotic. When $\delta \mathrm{{\,=\,0}}\mathrm{{.3}}$, both the response of the linear oscillator and the NES are chaotic. One major conclusion that can be drawn from the plots as shown in Fig. 22 is that the response regimes between the linear oscillator and the NES are not always consistent, which is significantly different from the case in a system with a 1-dof NES.

3.4 SMR in the system with a 2-dof NES

Obviously, the rich dynamics in the coupled system with a 2-dof NES brings a possibility for the existence of SMR. This subsection aims at studying the SMR in the case of 2-dof NES. In general, such a challenging problem is hardly possible to be treated analytically similar to the procedures we have outlined in the 1-dof case, since the slow invariant manifold is not solvable. However, we can still perform direct numeric simulation to find some useful conclusions. For the sake of numeric simulation, the value $\varepsilon = 0.1$ and zero initial conditions have been chosen for all the examples, and the other parameters will be reported case by case.

At first, one may naturally come up with the following question: Since a 2-dof NES can produce much richer dynamics than the 1-dof one, can it also generate extra SMR in the system? This question can be answered by comparing the responses of the linear oscillator in 1-dof and 2-dof NES systems with similar parameters. To establish reasonable comparisons, we make arrangements for the parameters of the systems according to the following principle: Given the parameters of the 2-dof NES system, the parameters of the compared 1-dof NES system will be obtained by setting the mass distribution $\alpha = 1$ in the 2-dof NES system. Based on this setting, we adjust the value of ${\lambda _2}$, ${k_2}$, and $\alpha$ for a 2-dof NES to see if there exists extra SMR when the response regime is not SMR in the compared 1-dof NES system.

Fig. 23

Time response for system of 1-dof and 2-dof NES, ${x_1}$: the displacement of the linear oscillator. The parameters of the 2-dof NES system: a $A = 1$, $\delta = - 1$, ${\lambda _1} = 0.5$, ${k_1} = 1.33$, ${\lambda _2} = 0.2$, ${k_2} = 0.5$, $\alpha = 0.6$, b $A = 0.3$, $\delta = 0.5$, ${\lambda _1} = 1$, ${k_1} = 1$, ${\lambda _2} = 0.1$, ${k_2} = 1$, $\alpha = 0.6$

Figure 23a, b presents two examples of the comparison. As shown in Fig. 23a, the response regimes of the 1-dof and 2-dof NES system are simple periodic (no modulation) and strongly modulated, respectively. Similar results are found from Fig. 23b; for the response regime of the 1-dof NES system is weakly modulated and in 2-dof NES system is strongly modulated. Hence, a 2-dof NES can generate extra SMR in the system by adjusting its parameters ${\lambda _2}$, ${k_2}$, and $\alpha$. Given the generated extra SMR in the system, one can also see that the average amplitude and vibrational energy of the linear oscillator can be reduced significantly. The creation of the extra SMR in 2-dof NES can be explained as follows: On the one hand, the existence of SMR is closely related to the dynamical instability of the system. On the other hand, as it was indicated in our previous analysis, a 2-dof NES can to a large extent enhance this instability near the main resonance frequency of the system, which as a result provides more possibilities for the emergence of SMR.

Table 1 Response regimes for different external excitation in system with 1-dof and 2-dof NES, and the response regimes are divided into the following three classes, S strongly modulated, W weakly modulated, P simple periodic (no modulation)

Fig. 24

Time response for system with a 2-dof NES as mass distribution $\alpha$ varies, system parameter: $A = 0.1$, $\delta = 0$, ${\lambda _1} = 0.5$, ${k_1} = 1.33$, ${\lambda _2} = 1.5$, ${k_2} = 1.33$, ${x_1}, {x_2},{x_3}$: the displacement of the linear oscillator, the first and second mass of the NES

Further information of the comparisons is summarized in Table 1, where the response regimes of 1-dof and 2-dof NES systems are reported under different external excitation conditions. The other parameters in table are chosen as ${\lambda _1} = 1$, ${k_1} = 1$, ${\lambda _2} = 0.1$, ${k_2} = 1$. Clearly enough, the introduction of a 2-dof NES brings extra SMR to the system. In most cases, the response regimes in these systems are consistent, which to a certain extent also implies the similarity on the basic mechanisms that govern each response regime in these systems. Hence, one should always keep in mind that in order to gain the extra SMR, the parameters of the 2-dof NES should also be appropriately chosen.

Another set of numeric simulation was performed to reveal the dependence of the response regime on the value of the mass distribution $\alpha$ of the 2-dof NES. The results are illustrated in Fig. 24. As one can see, the variation of $\alpha$ in the NES can bring about significant change in the response of the linear oscillator and the NES. In addition, the linear oscillator and the NES can share quite different responses, as verified by the either of the cases that have shown for $\alpha = 0.6$ or $\alpha = 0.7$, and the response regime is weakly modulated in the linear oscillator, but strongly modulated in each mass of the NES.

The following points should be emphasized: First of all, an appropriately designed 2-dof NES can generate extra SMR for the coupled system. Second, the mass distribution $\alpha$ of the 2-dof NES plays an important role in the dynamics of the system. Third, the consistence breaking could occur in the response regimes between the linear oscillator and the 2-dof NES. These conclusions are generally useful and helpful in the problem of vibration suppression that we are going to solve in the next section.

4 Application to vibration suppression

Motivated by the previous study, this section concerned with the above development about 1-dof and 2-dof NES to the application of vibration suppression. The goal of this section is to develop an one-parametric tuning procedure of strongly nonlinear vibration absorber of the previous described dynamical system for 1-dof and 2-dof NES, with numerical verification of the effectiveness of 2-dof NESs on the 1-dof ones.

Due to the rich response regimes (periodic, quasiperiodic or chaotic) that exist in the vicinity of the main resonance frequency, the amplitude of the system response could also be time dependent. Thus, we will use the energy spectrum instead of the amplitude to assess the efficiency of the nonlinear absorbers. The energy spectrum is obtained by calculating the average energies of the linear oscillator over period of time exceeding the period of modulation by at least an order of magnitude. That is,

$$\begin{aligned} E = {\left\langle {\frac{1}{2}\dot{x}_1^2 + \frac{1}{2}x_1^2} \right\rangle _t} \end{aligned}$$

(65)

and from this sense, the main purpose of the optimization of an absorber is reducing the energy of the linear oscillator expressed in Eq. (65). On the other hand, the trick here is to set the parameters to obtain nonperiodic solutions.

Before we embark on tuning process performance, it is necessary and convenient to let some of the system parameters be fixed when the rest varies. For simulations hereafter in this section, we set the fixed parameters as $\varepsilon = 0.1, A = 0.3$, the response of the systems is obtained by direct numerical integration, and then, the value of E defined in Eq. (65) for each system is calculated by taking their average values over the time interval $t \in [2000,3000]$.

Fig. 25

Energy spectrum for the main structure through $\lambda$ variation in the vicinity of the main resonance frequency

Let us first consider the case of 1-dof NES, and to evaluate the importance of damping, let $k=1$, the energy spectrum for system with $\lambda =1.8$ and $\lambda =0.2$ is generated in Fig. 25, respectively. As the truncation damping can be calculated as $\lambda =1.73$, hence for $\lambda =1.8$, there is no bifurcation in the system and the system possesses steady-state response in the vicinity of the resonance frequency, whereas for $\lambda =0.2$ the system can provide strongly modulated response (Fig. 26). The main conclusion from these two figures is that the vibrational energy is largely reduced when the system has strongly modulated response, as verified by the drastic reduction on the overall level of the energy spectrum for $\lambda =0.2$.

Fig. 26

Poincare section and time response for the system, ${y_1},{v_1}$: the displacement and velocity of the linear oscillator

Fig. 27

Energy spectrum for the main structure through k variation in the vicinity of the main resonance frequency

Figure 27 further reveals the effect of stiffness variation on the system energy spectrum, with the response for different values of k being point-checked by the Poincare section in Fig. 28. The obtained results illustrate that, by varying k in an interval of modulated response, total system energy and kinetic energy of the primary mass can be monotonically reduced (in average). However, when the value of k continues to enlarge as $k=4.3$, an undesired periodic response occurred in the left side of the resonance frequency. We call this the failure of efficiency, and it should be avoided when designing the vibration absorbers.

Fig. 28

Poincare section for the system with red area represents the steady state, ${y_1},{v_1}$: the displacement and velocity of the linear oscillator, ${y_2},{v_2}$: the displacement and velocity of the NES

A parametric optimization can be carried out by simply varying the value of damping $\lambda$ and stiffness k and checking the energy spectrum of the system, and the optimal value for this special case is finally obtained as $\lambda =1.7, k=4.5$. To show the effectiveness of the nonlinear absorber with nonlinear damping, the energy spectrum is also compared with the optimal performance of the NES with linear damping in Ref. [34], the results are shown in Fig. 29, and it could be found that the NES with nonlinear damping can have a better performance on the suppression of vibrational energy induced to the linear oscillator.

Fig. 29

Comparison of energy spectrum of the best tuned NES with linear and nonlinear damping

In terms of 2-dof NES, the influence of mass distribution $\alpha$ on the performance of the 2-dof NES as vibration absorber is studied of special consideration. As indicated in Fig. 30, by varying the value of $\alpha$ with the other parameter fixed, the undesired periodic response occurred in the 1-dof NES can be effectively eliminated. Moreover, the elimination of the undesired response to a great extent liberated the parameter limitation of NES as effective vibration absorber in the 1-dof case and hence can be of great significance to the optimization of 2-dof NES for vibration suppression.

Fig. 30

Energy spectrum for the main structure through parameter variation for the elimination of undesired periodic response

The optimization of the 2-dof NES is rather subtle and sometimes meaningless. However, based on the energy spectrum for the best tuned 1-dof NES, the parameters of the 2-dof can also be appropriately designed. For example, one satisfactory parameters for the 2-dof NES could be assigned as ${\lambda _1} = 1.7,{\lambda _2} = 0.2,{k_1} = 7.5,{k_2} = 0.2,\alpha = 0.9$; the energy spectrum of system with 2-dof is plotted and compared with the best tuned 1-dof NES in Fig. 31. One can conclude that the 2-dof NES has a much better performance than the 1-dof NES, and the vibration energy at the both sides of the main resonance frequency is significantly reduced. Therefore, the 2-dof NES can provide with a better vibration absorber.

Fig. 31

Energy spectrum of 1-dof NES with best tuned parameters and 2-dof NES with chosen parameter as ${\lambda _1} = 1.7,{\lambda _2} = 0.2,{k_1} = 7.5,{k_2} = 0.2,\alpha = 0.9$

5 Conclusion

The obtained results on the dynamics of energy sink with geometrically nonlinear damping demonstrate that the nonlinear damping can bring about rich bifurcations and response regimes. A truncation damping of value $\lambda = \sqrt{3} k$ can be observed for the vanishing of saddle-node and Hopf bifurcations; for the frequency response, the interval of the failure frequency should be noted. The truncation damping and failure frequency range combined with the SMR provide a important description of the formation and dynamic behavior in the system under consideration.

For 2-dof NES, the mass distribution of the NES plays an important role in the dynamics of the system, which is far from being purely parametric and introduces new dynamics when compared to the corresponding systems 1-dof NES. In addition, the dynamics of the system depends more on the second dof of the 2-dof NES.

We have also found that for a NES induced by nonlinear damping can provide (for some specific system parameters values) better total energy suppression of the main structure than does a linear one. It should be emphasized that a 2-dof NES can generate extra strongly modulated response (SMR) by adjusting its mass distribution, which in turn eliminates the undesired periodic response occurred in the case of 1-dof NES. Moreover, the elimination of the undesired response also to a great extent liberated the parameter limitation of NES as effective vibration absorber in the 1-dof case. Therefore, the 2-dof NES can provide with a better vibration absorber.

Appendix A: Realization of geometrically nonlinear damping

This appendix is devoted to the realization of geometrically nonlinear damping, and one may also refer to Ref. [42,43,44] for its main ideas. The trick here is to use two linear dampers described in Fig. 32, and the dampers are aligned horizontally with one end pinned and the other free to translate vertically a distance x.

Fig. 32

Realization of geometrically nonlinear damping by means of two linear dampers

Let the displacement along each damper be $\delta$, and then, the force in each damper can be computed as

$$\begin{aligned} {F_i} = c\dot{\delta } ,\;\;\;i = 1,2 \end{aligned}$$

(A.1)

one thus have the total vertical force

$$\begin{aligned} F = 2c\dot{\delta } \sin \theta \end{aligned}$$

(A.2)

from geometry, one has the following relationship

$$\begin{aligned} \delta = \sqrt{{l^2} + {x^2}} - l,\;\;\;\;\sin \theta = \frac{x}{{\sqrt{{l^2} + {x^2}} }} \end{aligned}$$

(A.3)

and hence, the time derivative of $\delta$ is

$$\begin{aligned} \dot{\delta } = \frac{{x\dot{x}}}{{\sqrt{{l^2} + {x^2}} }} = \dot{x}\sin \theta \end{aligned}$$

(A.4)

Substituting Eqs. (A.3) and (A.4) into Eq. (A.2) leads to

$$\begin{aligned} F = 2c\dot{x}{\sin ^2}\theta \end{aligned}$$

(A.5)

assuming small angles

$$\begin{aligned} \sin \theta \approx \theta \approx \tan \theta = \frac{x}{l} \end{aligned}$$

(A.6)

one finally have the equation for total force

$$\begin{aligned} F = \frac{{2c}}{{{l^2}}}{x^2}\dot{x} \propto {x^2}\dot{x} \end{aligned}$$

(A.7)

Thus, we have the nonlinear damping. The validity of the small angle approximation can be preserved by selecting a suitably long distance l in the physical setting.