Limit cycles bifurcating from a zero–Hopf singularity in arbitrary dimension

Abstract

For a $C^{m+1}$ differential system on $\mathbb {R}^n$, we study the limit cycles that can bifurcate from a zero–Hopf singularity, i.e., from a singularity with eigenvalues $\pm ~bi$ and $n-2$ zeros for $n\ge 3$. If the singularity is at the origin and the Taylor expansion of the differential system (without taking into account the linear terms) starts with terms of order m, then $\ell$ limit cycles can bifurcate from the origin with $\ell \in \{0,1,\ldots , 2^{n-3}\}$ for $m=2$ [see Llibre and Zhang (Pac J Math 240:321–341, 2009)], with $\ell \in \{ 0,1,\ldots ,3^{n-2}\}$ for $m=3$, with $\ell \le 6^{n-2}$ for $m=4$, and with $\ell \le 4\cdot 5^{n-2}$ for $m=5$. Moreover, $\ell \in \{0,1,2\}$ for $m=4$ and $n=3$, and $\ell \in \{0,1,2,3,4,5\}$ for $m=5$ and $n=3$. In particular, the maximum number of limit cycles bifurcating from the zero–Hopf singularity grows up exponentially with n for $m=2,3$.

1 Introduction and statement of the main results

We recall that a zero–Hopf singularity is an isolated equilibrium point of an n-dimensional autonomous system with $n\ge 3$ with linear part having $n-2$ zero eigenvalues and a pair of purely imaginary eigenvalues. It turns out that its unfolding has a rich dynamics in a neighborhood of the singularity (see for example Guckenheimer and Holmes [4, 5], Scheurle and Marsden [12], Kuznetsov [6] and the references therein). Moreover, a zero–Hopf bifurcation may lead to a local birth of “chaos.” More precisely, it was shown that some invariant sets of the unfolding can be obtained from the bifurcation from the singularity under appropriate conditions (cf. [3, 12]).

In this paper, we use the first-order averaging theory to study the zero–Hopf bifurcation of $C^{m+1}$ differential systems on $\mathbb {R}^n$ with $n \ge 3$ and $m\le 5$. We assume that these systems have a singularity at the origin with linear part with eigenvalues $\varepsilon a \pm b i$ and $\varepsilon c_k$ for $k=3,\ldots ,n$, where $\varepsilon$ is a small parameter. Each of these systems can be written in the form

$$\begin{aligned} \dot{x}= & {} \varepsilon a x - b y\nonumber \\&+~\sum _{i_1+\cdots +i_n= m} a_{i_1\cdots i_n} x^{i_1} y^{i_2} z_3^{i_3} \cdots z_n^{i_n} + P, \nonumber \\ \dot{y}= & {} b x + \varepsilon a y\nonumber \\&+~\sum _{i_1+\cdots +i_n= m} b_{i_1\cdots i_n} x^{i_1} y^{i_2} z_3^{i_3} \cdots z_n^{i_n} + Q, \nonumber \\ \dot{z}_ k= & {} \varepsilon c_k z_k\nonumber \\&+~\sum _{i_1+\cdots +i_n= m} c_{i_1\cdots i_n,k} x^{i_1} y^{i_2} z_3^{i_3} \cdots z_n^{i_n} + R_k,\nonumber \\&\quad k=3,\ldots , n, \end{aligned}$$

(1)

where the constants $a_{i_1\cdots i_n}$, $b_{i_1\cdots i_n}$, $c_{i_1\cdots i_n,k}$, a, b and $c_k$ are real, $ab \ne 0$ and P, Q and $R_k$ are the remainder terms in the Taylor series. We refer the reader to [1, 2, 10, 11, 14] and the references therein for details on the study of limit cycles and averaging theory.

Our main result concerns the number of limit cycles that can bifurcate from the origin in a zero–Hopf bifurcation. We show that the number of bifurcated limit cycles can grow exponentially with the dimension of the system.

Theorem 1

For $m=3$, there exist $C^4$ differential systems of the form (1) for which $\ell$ limit cycles, with $\ell \in \{0,1,\ldots ,3^{n-2}\}$, bifurcate from the origin at $\varepsilon =0$. In other words, for $\varepsilon >0$ sufficiently small there are systems having exactly $\ell$ limit cycles in a neighborhood of the origin and these tend to the origin when $\varepsilon \searrow 0$.

Theorem 1 is proved in Sect. 3. For $n=3$, this results was established in [7] also with the description of the type of stability of the limit cycles. For $m=2$, a corresponding result was established earlier in [8] showing that there exist $C^3$ differential systems of the form (1) for which $\ell$ limit cycles, with $\ell \in \{0,1,\ldots ,2^{n-3}\}$, bifurcate from the origin at $\varepsilon =0$.

Now we consider the cases $m=4$ and $m=5$.

Theorem 2

For $m=4$ and $\varepsilon >0$ sufficiently small, any $C^5$ differential system of the form (1) can have at most $6^{n-2}$ limit cycles in a neighborhood of the origin, and these tend to the origin when $\varepsilon \searrow 0$. When $n=3$, the maximum number of limit cycles that can bifurcate from the origin is 2 and this bound is attained.

The proof of Theorem 2 is given in Sect. 4.

Theorem 3

For $m=5$ and $\varepsilon >0$ sufficiently small, any $C^6$ differential system of the form (1) can have at most $4 \cdot 5^{n-2}$ limit cycles in a neighborhood of the origin, and these tend to the origin when $\varepsilon \searrow 0$. When $n=3$, the maximum number of limit cycles which can bifurcate from the origin is 5 and this bound is attained.

The proof of Theorem 3 is given in Sect. 5.

2 First-order averaging method for periodic orbits

In this section, we describe briefly the first-order averaging method via the Brouwer degree obtained in [1] (see [11] for the general theory). Roughly speaking, the method relates the solutions of a non-autonomous periodic differential system to the singularities of its averaged differential system. The conditions for the existence of a simple isolated zero of the averaged function are expressed in terms of the Brouwer degree. We emphasize that the vector field need not be differentiable.

Consider the system

$$\begin{aligned} \dot{x}(t)=\varepsilon f(t,x) + \varepsilon ^2 g(t,x, \varepsilon ), \end{aligned}$$

(2)

where $f :\mathbb {R}\times D\rightarrow \mathbb {R}^n$ and $g :\mathbb {R}\times D \times (-\delta ,\delta ) \rightarrow \mathbb {R}^n$ are continuous functions, T-periodic in the first variable, and D is a bounded open subset of $\mathbb {R}^n$. We define a function $f^0 :D \rightarrow \mathbb {R}^n$ by

$$\begin{aligned} f^0(x)=\frac{1}{T} \int _0^T f(s,x)\hbox {d}s. \end{aligned}$$

Finally, we denote by $d_B(f^0,V, v)$ the Brouwer degree of $f^0$ in a neighborhood V of v.

Theorem 4

Assume that:

• (i) f and g are locally Lipschitz with respect to x;

• (ii) for $v \in D$ with $f^0(v)=0$, there exists a neighborhood V of v such that $f^0(z) \ne 0$ for $z \in \overline{V} {\setminus } \{v\}$ and $d_B (f^0, V, v) \ne 0$.

Then for $|\varepsilon |> 0$ sufficiently small, there exists an isolated T-periodic solution $x(t,\varepsilon )$ of system (2) such that $x(0,\varepsilon ) \rightarrow v$ when $\varepsilon \rightarrow 0$. Moreover, if f is $C^2$ and g is $C^1$ in a neighborhood of a simple zero v of $f^0$, the stability of the limit cycle $x(t,\varepsilon )$ is given by the stability of the singularity v of the averaged system $\dot{z} =\varepsilon f^0(z)$.

We recall that if $f^0$ is of class $C^1$ and the determinant of the Jacobian matrix at a zero v is nonzero, then $d_B(f^0,V,v) \ne 0$, and the zeros are called simple zeros of $f^0$ (see [9]).

3 Proof of Theorem 1

Making the change of variables

$$\begin{aligned} x=r \cos \theta ,\quad y=r \sin \theta ,\quad z_i=z_i, \quad i=3,\ldots ,n \end{aligned}$$

(3)

with $r > 0$, system (1) becomes

$$\begin{aligned} \dot{r}= & {} \varepsilon a r +\sum \left( a_{i_1\cdots i_n} \cos \theta +b_{i_1\cdots i_n} \sin \theta \right) (r \cos \theta )^{i_1}\nonumber \\&(r \sin \theta )^{i_2}z_3^{i_3} \cdots z_n^{i_n} + O_4, \nonumber \\ \dot{\theta }= & {} \frac{1}{r} \left( b r + \sum \left( b_{i_1\cdots i_n} \cos \theta - a_{i_1\cdots i_n} \sin \theta \right) (r \cos \theta )^{i_1}\right. \nonumber \\&\left. (r \sin \theta )^{i_2} z_3^{i_3} \cdots z_n^{i_n} + O_4\right) , \nonumber \\ \dot{z}_k= & {} \varepsilon c_k z_k + \sum c_{i_1\cdots i_n,k} (r \cos \theta )^{i_1}\nonumber \\&(r \sin \theta )^{i_2} z_3^{i_3} \cdots z_n^{i_n} + O_4, \quad k=3,\ldots ,n, \end{aligned}$$

(4)

where $O_4=O_4(r,z_3,\ldots ,z_n)$ and with the sums going over $i_1+\cdots +i_n=3$. Taking $a_{00e_{ij}}=b_{00e_{ij}}=0$, where $e_{ij} \in \mathbb {Z}_+^{n-2}$ has the sum of the entries equal to 3, one can easily verify that in some neighborhood of $(r,z_3,\ldots ,z_n)=(0,0,\ldots ,0)$ with $r>0$ we have $\dot{\theta }\ne 0$ since $b \ne 0$ ($\mathbb {Z}_+$ denotes the set of all nonnegative integers). Taking $\theta$ as the new independent variable, in a neighborhood of $(r,z_3,\ldots ,z_n)=(0,0,\ldots , 0)$ with $r > 0$, system (4) becomes

$$\begin{aligned} \frac{\hbox {d}r}{\hbox {d} \theta }= & {} \frac{r \left( \varepsilon a r + \sum \left( a_{i_1\cdots i_n} \cos \theta + b_{i_1\cdots i_n} \sin \theta \right) (r \cos \theta )^{i_1} (r \sin \theta )^{i_2} z_3^{i_3} \cdots z_n^{i_n} + O_4\right) }{br + \sum \left( b_{i_1\cdots i_n} \cos \theta -a_{i_1\cdots i_n} \sin \theta \right) (r \cos \theta )^{i_1} (r \sin \theta )^{i_2} z_3^{i_3} \cdots z_n^{i_n} + O_4}, \nonumber \\ \frac{\hbox {d} z_k}{\hbox {d} \theta }= & {} \frac{r \left( \varepsilon c_k z_k+ \sum c_{i_1\cdots i_n,k} (r \cos \theta )^{i_1} (r \sin \theta )^{i_2} z_3^{i_3} \cdots z_n^{i_n} + O_4\right) }{br + \sum \left( b_{i_1\cdots i_n} \cos \theta -a_{i_1\cdots i_n} \sin \theta \right) (r \cos \theta )^{i_1} (r \sin \theta )^{i_2} z_3^{i_3} \cdots z_n^{i_n} + O_4}, \end{aligned}$$

(5)

for $k=3,\ldots ,n$, with the sums going over $i_1+\cdots + i_n=3$. Note that this system is $2 \pi$-periodic in $\theta$.

In order to apply the averaging theory, we rescale the variables by setting

$$\begin{aligned} (r,z_3,\ldots ,z_n)=\left( \varepsilon ^{1/2} \sigma , \varepsilon ^{1/2} \tau _3,\ldots , \varepsilon ^{1/2} \tau _n\right) . \end{aligned}$$

(6)

Then system (1) becomes

$$\begin{aligned} \frac{\hbox {d} \sigma }{\hbox {d} \theta }= & {} \varepsilon f_1 (\theta ,\sigma ,\tau _3,\ldots ,\tau _n) + \varepsilon ^2 g_1(\theta ,\sigma , \tau _3,\ldots ,\tau _n), \nonumber \\ \frac{\hbox {d} \tau _k}{\hbox {d} \theta }= & {} \varepsilon f_k (\theta ,\sigma ,\tau _3,\ldots ,\tau _n) + \varepsilon ^2 g_k(\theta ,\sigma , \tau _3,\ldots ,\tau _n),\nonumber \\ \end{aligned}$$

(7)

for $k=3,\ldots ,n$, where

Now system (7) has the normal form (2) for applying the averaging theory with $x=(\sigma ,\tau _3,\ldots ,\tau _n)$, $t =\theta$, $T=2 \pi$, and

$$\begin{aligned}&f(\theta ,\sigma ,\tau _3,\ldots ,\tau _n)=(f_1(\theta ,\sigma ,\tau _3,\ldots ,\tau _n),\nonumber \\&\quad f_3(\theta ,\sigma ,\tau _3,\ldots ,\tau _n), \ldots , f_n(\theta ,\sigma ,\tau _3,\ldots ,\tau _n)). \end{aligned}$$

(8)

The averaged system of system (7) is given by

$$\begin{aligned} \dot{y} =\varepsilon f^0(y), \quad y=(\sigma ,\tau _3,\ldots ,\tau _n) \in \Omega , \end{aligned}$$

(9)

where $\Omega$ is some neighborhood of the origin $(\sigma ,\tau _3,\ldots ,\tau _n)=(0,0,\ldots ,0)$, with $\sigma > 0$ and

$$\begin{aligned} f^0(y)=\left( f_1^0(y),f_3^0(y),\ldots ,f_n^0(y)\right) , \end{aligned}$$

(10)

where

$$\begin{aligned} f_i^0(y)=\frac{1}{2 \pi } \int _0^{2 \pi } f_i(\theta ,\sigma ,\tau _3,\ldots ,\tau _n) \hbox {d} \theta ,\quad i=1,3,\ldots ,n. \end{aligned}$$

One can show after some calculations that

(11)

for $k=3,\ldots ,n$, where $e_j \in \mathbb {Z}_+^{n-2}$ is the unit vector with the jth entry equal to 1, and $e_{ij} \in \mathbb {Z}_+^{n-2}$ has the sum of the ith and jth entries equal to 2 and the other equal to 0 (note that i can be equal to j), $e_{ijl} \in \mathbb {Z}_+^{n-2}$ has the sum of the ith, jth and lth entries equal to 3 and the other equal to zero (again, i, j and l can be equal).

Now we apply Theorem 4 to obtain limit cycles of system (7). After applying the rescaling (6), these limits become infinitesimal limit cycles for system (5) that tend to the origin when $\varepsilon \searrow 0$. Consequently they will be limit cycles bifurcating from the zero–Hopf bifurcation of (1) at the origin.

We first compute the simple singularities of system (9). Since the transformation from the Cartesian coordinates $(x,y,z_3,\ldots ,z_n)$ to the cylindrical coordinates $(r,\theta ,z_3,\ldots ,z_n)$ is not a diffeomorphism at $r=0$, we consider the zeros of the averaged function $f^0$ of (11) with $\sigma > 0$. So we need to compute the zeros of the equations

$$\begin{aligned}&8 a + \left( a_{12\mathbf{0}_{n-2}}+ b_{21\mathbf{0}_{n-2}} + 3\left( a_{30\mathbf{0}_{n-2}}+ b_{03\mathbf{0}_{n-2}}\right) \right) \sigma ^2 \nonumber \\&\quad +~4\sum _{3 \le i \le j \le n}^n \left( a_{10e_{ij}} + b_{01e_{ij}}\right) \tau _i \tau _j=0, \nonumber \\&2 c_k \tau _k + \sum _{j=3}^n \left( c_{20e_j,k}+ c_{02e_j,k}\right) \sigma ^2 \tau _j\nonumber \\&\quad +~2 \sum _{3 \le i \le j \le l \le n} c_{00e_{ijl},k} \tau _i \tau _j \tau _l=0, \end{aligned}$$

(12)

for $k=3,\ldots ,n$. Since the coefficients of this equation are arbitrary, one can simplify the notation by writing it in the form

$$\begin{aligned}&a + a_1 \sigma ^2 + \sum _{3 \le i \le j \le n}^n a_{ij} \tau _i \tau _j =0, \nonumber \\&c_k \tau _k + \sum _{j=3}^n c_{j,k} \sigma ^2 \tau _j + \sum _{3 \le i \le j \le l \le n} c_{ijl,k} \tau _i \tau _j \tau _l =0,\nonumber \\ \end{aligned}$$

(13)

for $k=3,\ldots ,n$, where $a_1, a_{ij}, c_{j,k}$ and $c_{ijl,k}$ are arbitrary constants.

Let $\mathcal {C}$ be the set of all algebraic systems of the form in (13). We claim that there is a system in $\mathcal {C}$ with exactly $3^{n-2}$ simple zeros. An example is

$$\begin{aligned}&a+ a_1 \sigma ^2=0,\end{aligned}$$

(14)

$$\begin{aligned}&c_k \tau _k + \sum _{j=3}^k c_{j,k} \sigma ^2 \tau _j\nonumber \\&\quad + \sum _{3 \le i \le j \le l \le k} c_{ijl,k} \tau _i \tau _j \tau _l =0, \quad k=3,\ldots ,n, \end{aligned}$$

(15)

with all the coefficients nonzero. Equation (14) is linear in $\sigma ^2$, and Eq. (15) is a cubic algebraic equation in the $\tau _j$’s. Substituting the unique positive solution $\sigma _{0}$ of (14) into (15) with $k=3$, we find that this last equation has exactly three different real solutions $\tau _{30}$, $\tau _{31}$ and $\tau _{32}$ choosing appropriately the coefficients $c_{3,3}$ and $c_{333,3}$. Introducing one of the four solutions $(\sigma _{0}, \tau _{3i})$, $i=0,1,2$, into (15) with $k=4$, and choosing appropriately the values of the coefficients of (15) with $k=4$, we obtain three different solutions $\tau ^i_{40}$, $\tau ^i_{41}$ and $\tau ^i_{42}$ of $\tau _4$. Moreover, one can choose the coefficients so that the nine solutions $(\tau _{3i},\tau ^i_{40},\tau ^i_{41}, \tau ^i_{42})$ for $i=0,1,2$ are distinct. Repeating this process, one can show that for an appropriate choice of the coefficients in (14) and (15), these equations have $3^{n-2}$ different zeros. Since $3^{n-2}$ solutions of (14) and (15) is the maximum number that equations (13) can have by Bezout theorem (see [13]), we conclude that every solution is simple, and so the determinant of the Jacobian of the system evaluated at the solutions $(\tau _{3i},\tau ^i_{40},\tau ^i_{41}, \tau ^i_{42})$ is nonzero. This establishes the claim.

Using similar arguments, one can also choose the coefficients of the former system so that it has $\ell$ simple real solutions with $\ell \in \{0,1,\ldots ,3^{n-2}\}$. Taking the averaged system (9) with $f^0$ having the coefficients as in (14)–(15), the averaged system (9) has exactly $\ell \in \{0,1,\ldots ,3^{n-2}\}$ singularities with $\sigma > 0$. Moreover, the determinants of the Jacobian matrix $\partial f^0/\partial y$ at these singularities do not vanish, because all the singularities are simple. By Theorem 4, we conclude that there are systems (1) with a number $\ell \in \{0,1,\ldots ,3^{n-2}\}$ of limit cycles bifurcating from the origin. This completes the proof of Theorem 1.

4 Proof of Theorem 2

Making the cylindrical change of variables in (3) in the region $r > 0$, system (1) becomes system (4), now with the sum over $i_1+\cdots + i_n=4$. Taking $a_{00e_{ij}}=b_{00e_{ij}}=0$, where $e_{ij} \in \mathbb {Z}_+^{n-2}$ has the sum of its entries equal to 4, it is easy to show that in an appropriate neighborhood of $(r,z_3,\ldots ,z_n)=(0,0,\ldots ,0)$ we have $\dot{\theta }\ne 0$. Choosing $\theta$ as the new independent variable, in a neighborhood of $(r,z_3,\ldots ,z_n)=(0,0,\ldots , 0)$ system (4) becomes system (5), again with the sum running over $i_1+\cdots + i_n=4$. Note that this system is $2 \pi$-periodic in $\theta$.

To apply the averaging theory in the proof of Theorem 2, we rescale the variables, setting

$$\begin{aligned} (r,z_3,\ldots ,z_n)=\left( \varepsilon ^{1/3} \sigma , \varepsilon ^{1/3} \tau _3,\ldots , \varepsilon ^{1/3} \tau _n\right) . \end{aligned}$$

Then system (5) becomes system (7) with

Now (7) has the normal form (2) of the averaging theory with $x=(\sigma ,\tau _3,\ldots ,\sigma _n)$, $t =\theta$, $T=2 \pi$, and f as in (8). The averaged system of system (7) with the previous functions $f_1$ and $f_k$ can be written as system (9), where $\Omega$ is an appropriate neighborhood of the origin $(\sigma ,\tau _3,\ldots ,\sigma _n)=(0,0,\ldots ,0)$ with $\sigma > 0$ and $f^0(y)$ given by (10). After some computations, we obtain

$$\begin{aligned} f_1^0= & {} \frac{1}{8 b} \sigma \left( 8 a + \sum _{j=3}^{n} (a_{12e_j}+ b_{21e_j}\right. \\&\left. +~3(a_{30e_j}+ b_{03e_j})) \sigma ^2 \tau _j \right. \\&\left. +~4 \sum _{3 \le i \le j \le l \le n}^n (a_{10e_{ijl}} + b_{01e_{ijl}}) \tau _i \tau _j \tau _l\right) , \\ f_k^0= & {} \frac{1}{8 b} \left( 8 c_k \tau _k + 3 \sum _{j=3}^n (c_{04\mathbf{0}_{n-2},k}\right. \\&\left. +~c_{22\mathbf{0}_{n-2}k}+ c_{40\mathbf{0}_{n-2},k})\sigma ^4 \right. \\&\left. +~4 \sum _{3 \le i \le j \le n} ( c_{20e_{ij},k} + c_{02e_{ij},k}) \sigma ^2 \tau _i \tau _j\right. \\&\left. +~8 \sum _{3 \le i \le j \le l \le u \le n} c_{00e_{ijlu},k} \tau _i \tau _j \tau _l \tau _u \right) \end{aligned}$$

for $k=3,\ldots ,n$, where $e_{ijlu} \in \mathbb {Z}_+^{n-2}$ has the sum of the ith, jth, lth and uth entries equal to 4 and the others equal to 0 (these entries can coincide).

Now we apply Theorem 4 to obtain the limit cycles of system (7) (with the sum running over $i_1+\cdots + i_n=4$). After the rescaling (6), these limits will become infinitesimal limit cycles for system (5), which tend to the origin when $\varepsilon \searrow 0$. Consequently they will be limit cycles bifurcating from the origin of the zero–Hopf bifurcation of system (1).

Using Theorem 4 to study the limit cycles of system (7), we only need to compute the simple zeros of system (9) (with the sum running over $i_1+\cdots + i_n=4$). So we need to compute the zeros of the equations

$$\begin{aligned}&8 a + \sum _{j=3}^{n} \left( a_{12e_j}+ b_{21e_j} + 3(a_{30e_j}+ b_{03e_j})\right) \sigma ^2 \tau _j\nonumber \\&\quad +~4 \sum _{3 \le i \le j \le l \le n}^n (a_{10e_{ijl}} + b_{01e_{ijl}}) \tau _i \tau _j \tau _l=0, \nonumber \\&8 c_k \tau _k + 3 \sum _{j=3}^n \left( c_{04\mathbf{0}_{n-2},k}+c_{22\mathbf{0}_{n-2},k}+ c_{40\mathbf{0}_{n-2},k}\right) \sigma ^4 \nonumber \\&\quad +~4 \sum _{3 \le i \le j \le n} \left( c_{20e_{ij},k} + c_{02e_{ij},k}\right) \sigma ^2 \tau _i \tau _j\nonumber \\&\quad +~8 \sum _{3 \le i \le j \le l \le u \le n} c_{00e_{ijlu},k} \tau _i \tau _j \tau _l \tau _u =0, \end{aligned}$$

(16)

for $k=3,\ldots ,n$.

Isolating $\sigma$ from the first equation in (16), taking into account that $\sigma > 0$ and substituting it in the other equations of (16), the numerator becomes a polynomial equation of degree 6. By Bezout theorem, the maximum number of solution that system (16) can have is $6^{n-2}$. We do not know whether the bound is reached because in the first equation of (16) it appears $\sigma ^2 \tau _j$ instead of $\sigma ^2$ as in the first equation of (12). So we cannot apply the same arguments as in the proof of Theorem 1, and thus, we cannot show that the bounds are reached.

Now we consider the particular case of $\mathbb {R}^3$. In this case, we have

$$\begin{aligned} f_1^0= & {} \frac{ \sigma }{8 b} \left( 8 a + (a_{121} +b_{211} +3(a_{301} +b_{031})) \sigma ^2 \tau _3\right. \\&\left. +~4 (a_{103} +b_{013})\tau _3^3\right) , \\ f_2^{0}= & {} \frac{1}{8 b} \left( 8 c_3\tau _3 + (3 c_{040,3} + c_{220,3} +3 c_{400,3}) \sigma ^4\right. \\&\left. +~4 (c_{022,3} +c_{202,3}) \sigma ^2 \tau _3^2 + 8 c_{004,3} \tau _3^4 \right) . \end{aligned}$$

We need to compute the zeros of

$$\begin{aligned}&8 a + (a_{121} +b_{211} +3(a_{301} +b_{031})) \sigma ^2 \tau _3\\&\quad +~4 (a_{103} +b_{013})\tau _3^3=0, \\&8 c_3\tau _3 + \left( 3 c_{040,3} + c_{220,3} +3 c_{400,3}\right) \sigma ^4\\&\quad +~4\left( c_{022,3} +c_{202,3}\right) \sigma ^2 \tau _3^2 + 8 c_{004,3} \tau _3^4=0. \end{aligned}$$

Setting $\sigma ^2 =R$, from the first equation we get

$$\begin{aligned} R= -\frac{4 (2 a +(a_{103} +b_{013})\tau _3^3)}{\tau _3 (a_{121} +3 a_{301} +3 b_{031} +b_{211})}. \end{aligned}$$

Substituting $\sigma ^2$ into the second equation and looking at the numerator, we get a polynomial of degree two in the variable $\tau _3^3$. It has two solutions. Note that there is only one real solution for the cubic equation $x^3=A$ for A real and so the second equation has at most two solutions. We claim that $\sigma$ can be chosen to be positive for these two real solutions and that these solutions are simple. The claim can be verified using the example

$$\begin{aligned} \begin{array}{l} \dot{x} =\varepsilon a x -b y + 2 x y^2 z, \\ \dot{y} = b x +\varepsilon a y, \\ \dot{z} = \varepsilon z + a x^2 y^2 +\dfrac{3 z^4}{32 a^3}. \end{array} \end{aligned}$$

The averaged function for this system is

$$\begin{aligned} \left( f_1^0,f_2^0\right) = \left( \frac{\sigma \left( 8 a+2 \sigma ^2 \tau \right) }{8 b}, \frac{1}{8 b}\left( \frac{3 \tau ^4}{4 a^3}+a \sigma ^4+8 \tau \right) \right) . \end{aligned}$$

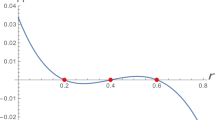
It has only two zeros with $\sigma >0$, which give the two periodic solutions

$$\begin{aligned} (x_i(t,\varepsilon ),y_i(t,\varepsilon ),z_i(t,\varepsilon )) \end{aligned}$$

for $i=1,2$ such that

$$\begin{aligned} (x_1(0,\varepsilon ),y_1(0,\varepsilon ), z_1(0,\varepsilon )) \rightarrow (\sqrt{2},0,-2 a) \end{aligned}$$

and

$$\begin{aligned} (x_2(0,\varepsilon ),y_2(0,\varepsilon ),z_2(0,\varepsilon )) \rightarrow (\sqrt{2} \cdot 3^{1/6},0,-2 a/3^{1/3}) \end{aligned}$$

when $\varepsilon \rightarrow 0$. This completes the proof of Theorem 2.

5 Proof of Theorem 3

Making the cylindrical change of variables in (3) in the region $r > 0$, system (1) becomes system (4), with the sum running over $i_1+\cdots + i_n=5$. Proceeding as in the proofs of Theorems 1 and 2, in a neighborhood of $(r,z_3,\ldots ,z_n)=(0,0,\ldots , 0)$ with $r > 0$ system (4) becomes system (5), again with the sum running over $i_1+\cdots + i_n=5$. We note that this system $2 \pi$-periodic in $\theta$.

To apply the averaging theory, we rescale the variables, setting

$$\begin{aligned} (r,z_3,\ldots ,z_n)=(\varepsilon ^{1/4} \sigma , \varepsilon ^{1/4} \tau _3,\ldots , \varepsilon ^{1/4} \tau _n). \end{aligned}$$

Then system (1) becomes system (7), with $i_1+\cdots +i_n=5$. Note that system (7) has the form (2) of the averaging theory. Proceeding as in the proofs of Theorems 1 and 2, we obtain

for $k=3,\ldots ,n$, where $e_{ijluv} \in \mathbb {Z}_+^{n-2}$ has the sum of the ith, jth, lth, uth and vth entries equal to 5 and the other entries equal to zero (these entries can coincide).

We need to compute the zeros of the equations

$$\begin{aligned}&16 a + \left( a_{14\mathbf{0}_{n-2}} +a_{32\mathbf{0}_{n-2}} +a_{50\mathbf{0}_{n-2}} + b_{41\mathbf{0}_{n-2}}\right. \\&\left. \quad +~b_{23\mathbf{0}_{n-2}} +b_{05\mathbf{0}_{n-2}} \right) \sigma ^4 \\&\quad +~\sum _{j=3}^k 2\left( a_{12e_{ij}}+b_{21e_{ij}} + 3(a_{30e_{ij}}+b_{03e_{ij}})\right) \sigma ^2 \tau _i \tau _j\\&\quad +~8\sum _{3 \le i \le j \le l \le u \le n} ( a_{10e_{ijlu}}+b_{01e_{ijlu}}) \tau _i \tau _j \tau _l \tau _u=0, \\&8 c_k\tau _k + \sum _{j=3}^n \left( 3 c_{04e_{j},k} + 3 c_{40e_{j},k} + c_{22e_{j},k} \right) \sigma ^4 \tau _j\\&\quad +~4 \sum _{3 \le i \le j \le l \le n} \left( c_{02e_{ijl},k}+c_{20e_{ijl},k}\right) \sigma ^2 \tau _i \tau _j \tau _l \\&\quad +~8 \sum _{3 \le i \le j \le l \le u \le v \le n} c_{00e_{ijluv},k} \tau _i \tau _j \tau _l \tau _u \tau _v=0, \end{aligned}$$

for $k=3,\ldots ,n$. By Bezout theorem, the maximum number of solutions that we can have is $4 \cdot 5^{n-2}$. As in the proof of Theorem 2, in general this upper bound is not reached, as we will verify in dimension three.

Now consider the particular case of $\mathbb {R}^3$. In this case, we have

$$\begin{aligned}&f_1^0 = \frac{\sigma }{16 b} \left( 16 a + A\sigma ^4 + B\sigma ^2 \tau _3^2 + C\tau _3^4 \right) , \\&f_2^0 = \frac{\tau _3}{8 b} \left( 8 c_3 + D \sigma ^4 + F \sigma ^2 \tau _3^2 + G \tau _3^4\right) , \end{aligned}$$

where

$$\begin{aligned} A= & {} a_{140} +a_{320} +5 a_{500} + b_{410} +b_{230} +5b_{050}, \\ B= & {} 2(a_{122} + b_{212} + 3 (a_{302} +b_{032})), \\ C= & {} 8(a_{104}+b_{014}), \\ D= & {} 3 (c_{041} +c_{401}) +c_{221}, \\ F= & {} 4(c_{023}+c_{203}), \\ G= & {} 8 c_{005}. \end{aligned}$$

We need to compute the zeros of the system

$$\begin{aligned}&16 a + A\sigma ^4 + B\sigma ^2 \tau _3^2 + C\tau _3^4 =0, \\&\tau _3\left( 8 c_3 + D \sigma ^4 + F \sigma ^2 \tau _3^2 + G \tau _3^4\right) =0. \end{aligned}$$

If $\tau _3=0$, then $f_1^0=0$ has a unique real positive solution $\sigma$ that we write as $(\sigma _0,0)$. Now we consider the case $\tau _3 \ne 0$. Let

$$\begin{aligned} \begin{array}{l} W_1= 2 \sqrt{\dfrac{\alpha -\beta }{\delta }}, \\ R_1= \dfrac{W_1 \left( -~D B^2+A F B+2 a D F B-2 a A F^2+\beta \right) }{2 (2 a D-A) (B D-A F)}, \\ W_3= 2 \sqrt{\dfrac{\alpha +\beta }{\delta }}, \\ R_3= \dfrac{W_3 \left( -~D B^2+A F B+2 a D F B-2 a A F^2-\beta \right) }{2 (2 a D-A) (B D-A F)}, \end{array} \end{aligned}$$

where

$$\begin{aligned} \alpha= & {} 2 A C D + A B F -B^2 D- 2 A^2 G - 4 C D^2 a +2 B D F a -2 A F^2 a + 4 A D G a, \\ \beta= & {} \sqrt{(B D - A F)^2 (B^2 - 4 B F a - 4 A (C - 2 G a) + 4 a (2 C D + F^2 a - 4 D G a))}, \\ \delta= & {} C^2 D^2 + G (B^2 D - A B F + A^2 G)+C (-~B D F + A (F^2 - 2 D G)). \end{aligned}$$

Setting $(f_1^0,f_2^0)=0$ in $R=\sigma ^2$ and $W=\tau _3^2$, we get four solutions, say

$$\begin{aligned} (R_1,W_1),\quad (-~R_1,-~W_1),\quad (R_3,W_3),\quad (-~R_3,-~W_3). \end{aligned}$$

Since $R=\sigma ^2$ must be positive, we conclude that only two of them are possible. Then we can have five simple solutions $(\sigma _0,0), (\sqrt{R_1}, \pm ~\sqrt{W_1})$ and $(\sqrt{R_3}, \pm ~ \sqrt{W_3})$ as illustrated by the system

$$\begin{aligned} \dot{x}= & {} -\dfrac{\varepsilon }{35} x -b y +\dfrac{16}{35} x y^4 + \dfrac{34}{35} x y^2 z^2, \\ \dot{y}= & {} b x -\dfrac{\varepsilon }{35} y,\\ \dot{z}= & {} \varepsilon z + \dfrac{y^4 z}{4}. \end{aligned}$$

The averaged function $(f_1^0,f_2^0)$ for this system is

$$\begin{aligned}&\left( \frac{\sigma }{16 b} \left( \frac{16 \sigma ^4}{35}+\frac{68 \sigma ^2 \tau _3^2}{35}+\frac{64 \tau _3^4}{35}-\frac{16}{35}\right) ,\right. \\&\left. \quad \frac{\tau _3}{4 b} \left( \frac{3 \sigma ^4}{4}+\sigma ^2 \tau _3^2-\frac{23 \tau _3^4}{4}+8\right) \right) . \end{aligned}$$

This function has five zeros with $\sigma >0$, which provide five periodic solutions $(x_i(t,\varepsilon ), y_i(t,\varepsilon ), z_i(t,\varepsilon ))$ for $i=0,\ldots ,4$ such that

$$\begin{aligned} (x_0(0,\varepsilon ),y_0(0,\varepsilon ),z_0(0,\varepsilon ))\rightarrow & {} (1,0,0),\\ (x_1(0,\varepsilon ),y_1(0,\varepsilon ),z_1(0,\varepsilon ))\rightarrow & {} \left( \sqrt{2}/3^{1/4}, 0, \sqrt{2}/3^{1/4}\right) , \\ (x_2(0,\varepsilon ),y_2(0,\varepsilon ),z_2(0,\varepsilon ))\rightarrow & {} \left( \sqrt{2}/3^{1/4}, 0, -~\sqrt{2}/3^{1/4}\right) \!, \\ (x_3(0,\varepsilon ),y_3(0,\varepsilon ),z_3(0,\varepsilon ))\rightarrow & {} (\sqrt{6},0,\sqrt{2}), \end{aligned}$$

and

$$\begin{aligned} (x_4(0,\varepsilon ),y_4(0,\varepsilon ),z_4(0,\varepsilon )) \rightarrow (\sqrt{6},0,-\sqrt{2}), \end{aligned}$$

when $\varepsilon \rightarrow 0$. This completes the proof of Theorem 3.