1 Introduction

In [4] Genesio and Tesi, inspired by the problem of determining conditions under which a nonlinear dynamical system presents chaotic behavior, introduced the following third-order ordinary differential Eq.

$$\begin{aligned} {\dddot{x}} + a {\ddot{x}} + b {\dot{x}} + c x - x^2 = 0, \end{aligned}$$
(1)

where a, b and c are parameters and the dot indicates derivative with respect to the time t. If we define \(y=\dot{x}\) and \(z={\dot{y}}\) the differential Eq. (1) becomes the first-order differential system

$$\begin{aligned} \begin{array}{l} {\dot{x}} = y, \\ {\dot{y}} = z, \\ {\dot{z}} = -c x - b y - a z + x^2, \end{array} \end{aligned}$$
(2)

which is commonly known as the Genesio system. Based on the harmonic balance principle the authors of [4] presented two practical methods for predicting the existence and the location of chaotic motions. For instance, system (2) exhibits chaotic dynamical behaviors when \(a = 1.2\), \(b = 2.92\) and \(c = 6\).

We can find in the literature several articles concerning system (2). For instance, issues on synchronization of Genesio chaotic system have been studied in the articles [3, 9, 10, 15]. Already in [16] the authors studied the Hopf bifurcation and the existence of Silnikov homoclinic orbit for this system. Stability analysis and Hopf bifurcation of the Genesio system with distributed delay feedback have been studied in [5].

In this paper we have two main objectives. The first one is to show that system (2) exhibits a transcritical bifurcation, i.e., there is an exchange of stability that takes place at some equilibrium point of this system for certain bifurcation values of the parameters of the system. The analysis of transcritical bifurcation occurring in the Genesio system will be carried out with respect to the parameter c.

The second objective is to study the existence of the zero-Hopf equilibria and of the zero-Hopf bifurcations in the Genesio system (2). We recall that a zero-Hopf equilibrium of a three-dimensional autonomous differential system is an isolated equilibrium point of the system such that the linear part at this equilibrium has a zero eigenvalue and a pair of purely imaginary eigenvalues.

Usually the main tool for studying a zero-Hopf bifurcation is to pass the system to the normal form of a zero-Hopf bifurcation. However, our analysis of the zero-Hopf bifurcation occurring in the Genesio system will use the averaging theory, a summary of the results of this theory that we need here is given in Sect. 2. The averaging theory has already been used to study Hopf and zero-Hopf bifurcations in some others differential systems, see for instance [1, 2, 7, 8].

As far as we know nobody has studied the existence or nonexistence of transcritical bifurcations, zero-Hopf equilibria, and zero-Hopf bifurcations in the Genesio system (2).

Our main results are the following ones.

Theorem 1

Consider the Genesio system (2) and assume that the parameters a and b vary in the set K given by

$$\begin{aligned} K = \{(a,b) \in \mathbb {R}^2 : b \ne 0\} \setminus \{(0,b) \in \mathbb {R}^2 : b > 0\}. \end{aligned}$$

Then, system (2) exhibits a transcritical bifurcation at the equilibrium point located at the origin of coordinates when \(c=0\).

Next proposition characterizes when the equilibrium points of system (2) are zero-Hopf equilibria.

Proposition 1

The Genesio system (2) has a unique zero-Hopf equilibrium localized at the origin of coordinates when \(a = c = 0\) and \(b > 0\).

In what follows we shall study when the Genesio system (2) having a zero-Hopf equilibrium point at the origin of coordinates have a zero-Hopf bifurcation producing some periodic orbit. For doing this we consider \(\varepsilon \)–perturbations of the values of the parameters for which system (2) has a zero-Hopf equilibrium. The small parameter \(\varepsilon \) is necessary in order to apply the averaging theory, and the analysis of the zero-Hopf bifurcation will be carried out with respect to it.

Fig. 1
figure 1

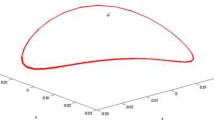
The periodic orbit (3) for the values \(\alpha =\omega =1\), \(\beta =0\), \(\gamma =2\) and \(\varepsilon =1/100\)

Full size image

Theorem 2

Consider the Genesio system (2) with the parameters \(a = \varepsilon \alpha \), \(b = \omega ^{2} + \varepsilon \beta \) and \(c = \varepsilon \gamma \), with \(\omega > 0\) and \(\varepsilon \) a sufficiently small parameter. Then, this system exhibits a zero-Hopf bifurcation at the equilibrium point located at the origin of coordinates when \(\varepsilon = 0\) if \(\gamma ^{2} -\alpha ^2\omega ^4 > 0\). Moreover, the periodic orbit \((x(t,\varepsilon ),y(t,\varepsilon ),z(t,\varepsilon ))\) bifurcating from this equilibrium point satisfies that \((x(0,\varepsilon ),y(0,\varepsilon ),z(0,\varepsilon ))\) is

$$\begin{aligned}&\varepsilon \bigg (\dfrac{\gamma - \alpha \omega ^2}{2} - \dfrac{\sqrt{\gamma ^2 - \alpha ^2 \omega ^4}}{\sqrt{2}}, 0, \dfrac{\omega ^2\sqrt{\gamma ^2 - \alpha ^2 \omega ^4}}{\sqrt{2}} \bigg ) \nonumber \\&\quad +\,\mathcal {O}(\varepsilon ^2), \end{aligned}$$
(3)

if \(\varepsilon > 0\) is sufficiently small, see Fig. 1. If \( \lambda _{\pm }=(-\alpha \omega ^2 \pm \sqrt{3\alpha ^2 \omega ^4 - 2\gamma ^2})/\) \((2\omega ^3)\), then this periodic orbit is stable when \(\text {Re}(\lambda _{\pm }) < 0\), and unstable if \(\text {Re}(\lambda _{+}) > 0\) or \(\text {Re}(\lambda _{-}) > 0\).

Theorem 1 is proved in Sect. 3, and Proposition 1 and Theorem 2 are proved in Sect. 4. The rest of the article is organized as follows. In Sect. 2, we present the basic definitions and results necessary for proving Theorems 1 and 2.

2 Preliminaries

2.1 Transcritical bifurcation

Consider the following differential equation in \(\mathbb {R}^n\)

$$\begin{aligned} {{\dot{\mathbf {x}}}} = f(\mathbf {x},\mu ) \end{aligned}$$
(4)

depending on a parameter \(\mu \in \mathbb {R}\). We assume that f is enough differentiable. The following theorem (see [13]) states the necessary conditions in order that system (4) exhibits a transcritical bifurcation. See also [6] page 149, or [11] page 338. We will use Theorem 3 for proving Theorem 1.

In the theorem below we use the notation \(D_\mathbf {x} f\) to denote the Jacobian matrix of the function f. We also use the notation \((\partial f/\partial \mu ) \) to indicate the vector of partial derivatives of the components of f with respect to \(\mu \in \mathbb {R}\). \(A^T\) will denote the transpose of the matrix A.

Theorem 3

Consider the one-parameter family (4) and assume that there is \(\mathbf {x}_0 \in \mathbb {R}^n\) such that \(f(\mathbf {x}_0,\mu ) = 0\) for all \(\mu \), i.e., \(\mathbf {x}_0\) is an equilibrium point of system (4) for all parameter values. Furthermore, when \(\mu = \mu _0\) suppose that the following hypotheses hold.

(H1):

The Jacobian matrix \(M = D_\mathbf {x} f(\mathbf {x}_0,\mu _0)\) has a simple eigenvalue \(\lambda = 0\) with eigenvector v, and \(M^T\) has an eigenvector w corresponding to the eigenvalue \(\lambda = 0\).

(H2):

M has k eigenvalues with negative real parts, and \(n-k-1\) eigenvalues with positive real parts.

(H3):

\(w^T \big ( (\partial f/\partial \mu ) (\mathbf {x}_0,\mu _0) \big ) = 0\).

(H4):

\(w^T \big ( D_\mathbf {x} (\partial f/\partial \mu ) (\mathbf {x}_0,\mu _0) v \big ) \ne 0\).

(H5):

\(w^T \big ( D^2_\mathbf {x} f (\mathbf {x}_0,\mu _0) (v,v) \big ) \ne 0\).

Then, system (4) exhibits a transcritical bifurcation at the equilibrium point \(\mathbf {x}_0\) at the bifurcation value \(\mu = \mu _0\).

2.2 Averaging theory

In this subsection we present some basic results on the averaging theory, which will be used in the proof of Theorem 2. For a general introduction to the averaging theory see for instance the book of Sanders, Verhulst and Murdock [12].

Consider the following initial value problem

$$\begin{aligned} {\dot{\mathbf {x}}}=\varepsilon F(t,\mathbf {x})+\varepsilon ^2 G(t,\mathbf {x},\varepsilon ), \quad \mathbf {x}(0)=\mathbf {x}_0, \end{aligned}$$
(5)

and the averaged differential equation

$$\begin{aligned} {\dot{\mathbf {y}}}=\varepsilon f({{\mathbf {y}}}), \quad \mathbf {y}(0)=\mathbf {x}_0. \end{aligned}$$
(6)

In Eqs. (5) and (6), \(\mathbf {x}, \mathbf {y} \in D\), where \(D \subset \mathbb {R}^n\) is an open set, \(t\in [0,\infty )\) and \(\varepsilon \) is a small positive parameter. The functions \(F : [0,\infty ) \times D \rightarrow \mathbb {R}^n\) and \(G : [0,\infty ) \times D \times (0,\varepsilon _0] \rightarrow \mathbb {R}^n\) are assumed to be periodic of period T in the variable t, and \(f: D \rightarrow \mathbb {R}^n\) is given by

$$\begin{aligned} f(\mathbf {y})=\dfrac{1}{T}\int _{0}^{T}F(t,\mathbf {y})dt. \end{aligned}$$
(7)

The next theorem establishes that, under certain conditions, the equilibrium points of the averaged Eq. (6) correspond to T–periodic solutions of system (5). See [14] for a proof.

Theorem 4

Consider the initial value problems (5) and (6) and suppose that F, its Jacobian \(D_{\mathbf {x}} F\), its Hessian \(D_{\mathbf {xx}} F\), G and its Jacobian \(D_{\mathbf {x}} G\) are continuous and bounded by a constant independent of \(\varepsilon \) in \([0,\infty ) \times D\) and \(\varepsilon \in (0,\varepsilon _0]\). Further we assume that F and G are T–periodic in t, with T independent of \(\varepsilon \). Then, the following statements hold.

  1. (a)

    For \(t \in [0,1/\varepsilon ]\) we have \(\mathbf {x}(t)- \mathbf {y}(t) = \mathcal {O}(\varepsilon )\) as \(\varepsilon \rightarrow 0\).

  2. (b)

    If p is an equilibrium point of system (6) such that

    $$\begin{aligned} \det D_{\mathbf {y}} f (p) \ne 0, \end{aligned}$$
    (8)

    then there exists a periodic solution \(\mathbf {x}(t,\varepsilon )\) of period T of system (5) such that \(\mathbf {x}(0,\varepsilon )-p= \mathcal {O}(\varepsilon )\) as \(\varepsilon \rightarrow 0\).

  3. (c)

    If all the real parts of the eigenvalues of the matrix \(D_{\mathbf {y}} f (p)\) are negative, then the periodic solution \(\mathbf {x}(t, \varepsilon )\) is stable. If some real part of the eigenvalues is positive, then the periodic solution \(\mathbf {x}(t, \varepsilon )\) is unstable.

3 Proof of Theorem 1

We recall that the analysis of transcritical bifurcation occurring in the Genesio system will be carried out with respect to the parameter c. So using the notation of Sect. 2.1, we have \(\mu = c\) and the vector field f associated with the Genesio system (2) is given by

$$\begin{aligned} f(\mathbf {x},c) = (y,z,-c x-by-az+x^2), \end{aligned}$$

where \(\mathbf {x} = (x,y,z) \in \mathbb {R}^3\). Note that, in order to simplify the notation, we are using (x, y, z) instead of \((x_1,x_2,x_3)\).

The vector field f has two equilibrium points \(\mathbf {x}_0 = (0,0,0)\) and \(\mathbf {x}_c = (c,0,0)\) which collide at the origin when \(c = 0\). Moreover, when \(c=0\) we have that the matrix

$$\begin{aligned} M = D_\mathbf {x} f(\mathbf {x}_0,0) = \left( \begin{array}{ccc} 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad -b &{}\quad -a \end{array} \right) \end{aligned}$$

has a simple eigenvalue \(\lambda = 0\). In fact, the characteristic polynomial of M is given by

$$\begin{aligned} p(\lambda ) = -\lambda ^3 - a\lambda ^2 - b\lambda , \end{aligned}$$

whose roots are

$$\begin{aligned} \lambda = 0, \quad \lambda _{\pm } = \dfrac{-a \pm \sqrt{a^2 - 4b}}{2}. \end{aligned}$$

Since by hypothesis the parameters a and b belong to the set \(K = \{(a,b) \in \mathbb {R}^2 : b \ne 0\} \setminus \{(0,b) \in \mathbb {R}^2 : b > 0\}\), then both eigenvalues \(\lambda _{\pm }\) have nonzero real part.

The transcritical bifurcation is characterized by the exchange of stability of the equilibrium point \(\mathbf {x}_c = (c,0,0)\) when the parameter c passes through the bifurcation value \(c=0\). Note that it is a difficult task to study the stability of the equilibrium point \(\mathbf {x}_c\), for \(c \ne 0\), by analyzing the roots of the characteristic polynomial of the matrix \(D_\mathbf {x} f(\mathbf {x}_c,c)\), that is the polynomial \(q(\lambda ) = -\lambda ^3 - a\lambda ^2 - b\lambda + c\). Thus, we will use Theorem 3 to show that the system (2) exhibits a transcritical bifurcation.

Note that the vectors \(v = (1,0,0)\) and \(w = (b,a,1)\) are eigenvectors of the matrices M and \(M^T\), respectively, corresponding to the eigenvalue \(\lambda = 0\). Furthermore, we have that

$$\begin{aligned} w^T \big ( (\partial f/\partial c) (\mathbf {x}_0,0) \big )= & {} \left( \begin{array}{ccc} b &{} a &{} 1 \\ \end{array} \right) \left( \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right) = 0,\\ w^T \big ( D_\mathbf {x} (\partial f/\partial c) (\mathbf {x}_0,0) v \big )= & {} \left( \begin{array}{ccc} b &{} a &{} 1 \\ \end{array} \right) \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ -1 &{}\quad 0 &{}\quad 0 \end{array} \right) \\ \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right)= & {} -1 \ne 0,\\ w^T \big ( D^2_\mathbf {x} f (\mathbf {x}_0,0) (v,v) \big )= & {} \left( \begin{array}{ccc} b &{} a &{} 1 \\ \end{array} \right) \left( \begin{array}{c} 0 \\ 0 \\ 2 \end{array} \right) = 2 \ne 0. \end{aligned}$$

Thus, all the hypotheses of Theorem 3 are satisfied. Therefore, the system (2) exhibits a transcritical bifurcation at the equilibrium point at the origin at the bifurcation value \(c = 0\). This completes the proof of Theorem 1.

4 Proof of Proposition 1 and Theorem 2

Proof of Proposition 1

We saw that the characteristic polynomial of the linear part of system (2) at the equilibrium point \(\mathbf {x}_c = (c,0,0)\) is \(q(\lambda ) = -\lambda ^3 - a\lambda ^2 - b\lambda + c\). We want to find the parameter values for which the polynomial q has a zero eigenvalue and a pair of purely imaginary eigenvalues, that is the parameter values for which q is of the form \(-\lambda (\lambda ^2 + B)\) with \(B > 0\). In order to simplify the expressions, we will put \(B = \omega ^2\), with \(\omega > 0\). Thus, imposing the condition \(q(\lambda ) = -\lambda (\lambda ^2 + \omega ^2)\), we obtain that \(a = c = 0\) and \(b = \omega ^2\). Hence, when \(a = c = 0\) and \(b>0\) there is a unique zero-Hopf equilibrium point at the origin of coordinates. Moreover, if we put \(b = \omega ^2\), with \(\omega > 0\), then the eigenvalues are 0 and \(\pm i \omega \). This completes the proof of Proposition 1. \(\square \)

Proof of Theorem 2

We shall use the averaging theory of first order described in Sect. 2.2 (see Theorem 4) in order to study if from the zero-Hopf equilibrium point located at the origin of coordinates, it bifurcates some periodic orbit by moving the parameters a, b and c of system (2). Thus, let the parameters a, b and c of system (2) be given by \(a = \varepsilon \alpha \), \(b = \omega ^{2} + \varepsilon \beta \) and \(c = \varepsilon \gamma \), with \(\varepsilon > 0\) a sufficiently small parameter. Then, the Genesio system (2) becomes

$$\begin{aligned} {\dot{x}}= & {} y, \nonumber \\ {\dot{y}}= & {} z,\\ {\dot{z}}= & {} -\varepsilon \gamma x - (\omega ^{2} + \varepsilon \beta ) y - \varepsilon \alpha z + x^2.\nonumber \end{aligned}$$
(9)

The first step in order to write our differential system (9) in the normal form for applying the averaging theory is to write the linear part at the origin of system (9) when \(\varepsilon = 0\) into its real Jordan normal form, that is into the form

$$\begin{aligned} \left( \begin{array}{ccc} 0 &{}\quad -\omega &{}\quad 0 \\ \omega &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{array} \right) . \end{aligned}$$

To do this, we apply the linear change of variables \((x,y,z) \rightarrow (X,Y,Z)\), where

$$\begin{aligned} x = \dfrac{Z - \omega X}{\omega ^2}, \quad y = Y, \quad z = \omega X. \end{aligned}$$
(10)

In the new variables (X, Y, Z), system (9) becomes

$$\begin{aligned} {\dot{X}}= & {} \dfrac{Z^2 - 2\omega XZ + \omega ^2 X^2 - \omega ^6 Y}{\omega ^5} \nonumber \\&+\, \varepsilon \dfrac{(\gamma - \alpha \omega ^2)\omega X - \beta \omega ^2 Y - \gamma Z}{\omega ^3}, \nonumber \\ {\dot{Y}}= & {} \omega X,\nonumber \\ {\dot{Z}}= & {} \dfrac{(\omega X - Z)^2}{\omega ^4} + \varepsilon \dfrac{(\gamma - \alpha \omega ^2) \omega X - \beta \omega ^2 Y - \gamma Z}{\omega ^2} .\nonumber \\ \end{aligned}$$
(11)

Now we re-scale the variables (X, Y, Z) as follows \((X,Y,Z) \rightarrow (\varepsilon u, \varepsilon v, \varepsilon w)\). Then, system (11) becomes

$$\begin{aligned} {\dot{u}}= & {} -\omega v \nonumber \\&+\, \varepsilon \dfrac{(\gamma - \alpha \omega ^2)\omega ^3 u - \beta \omega ^4 v - \gamma \omega ^2 w+ \omega ^2 u^2 -2\omega u w + w^2 }{\omega ^5},\nonumber \\ {\dot{v}}= & {} \omega u, \nonumber \\ {\dot{w}}= & {} \varepsilon \dfrac{(\gamma - \alpha \omega ^2)\omega ^3 u - \beta \omega ^4 v - \gamma \omega ^2 w + \omega ^2 u^2 - 2\omega u w + w^2 }{\omega ^4}.\nonumber \\ \end{aligned}$$
(12)

Now we pass the differential system (12) to cylindrical coordinates \((r,\theta ,w)\) defined by \(u = r \cos \theta \) and \(v = r \sin \theta \), and we obtain

$$\begin{aligned} {\dot{r}}= & {} \dfrac{\varepsilon }{\omega ^5} \Big [ (w - \gamma \omega ^2)w - \omega r (2w - \gamma \omega ^2 + \alpha \omega ^4) \cos \theta \nonumber \\&+ \, \omega ^2 r^2 \cos ^2 \theta - \beta \omega ^4 r \sin \theta \Big ]\cos \theta , \nonumber \\ {\dot{\theta }}= & {} \omega + \dfrac{\varepsilon }{\omega ^5 r} \Big [ (\gamma \omega ^2 - w)w \nonumber \\&+ \omega r (2w - \gamma \omega ^2 + \alpha \omega ^4) \cos \theta \nonumber \\&- \, \omega ^2 r^2 \cos ^2 \theta + \beta \omega ^4 r \sin \theta \Big ]\sin \theta , \nonumber \\ {\dot{w}}= & {} \dfrac{\varepsilon }{\omega ^4} \Big [ (w \!- \!\gamma \omega ^2)w \!-\! \omega r (2w \!-\! \gamma \omega ^2 \!+\! \alpha \omega ^4) \cos \theta \nonumber \\&+ \, \omega ^2 r^2 \cos ^2 \theta - \beta \omega ^4 r \sin \theta \Big ]. \end{aligned}$$
(13)

In system (13) we take \(\theta \) as the new independent variable, and we get

$$\begin{aligned} \dfrac{dr}{d\theta }= & {} \varepsilon F_1(\theta ,r,w) + O(\varepsilon ^2), \nonumber \\ \dfrac{dw}{d\theta }= & {} \varepsilon F_2(\theta ,r,w) + O(\varepsilon ^2), \end{aligned}$$
(14)

where

$$\begin{aligned} \begin{aligned}&F_1(\theta ,r,w) = \dfrac{1}{\omega ^6} \Big [ (w - \gamma \omega ^2)w \\&\quad - \omega r (2w - \gamma \omega ^2 + \alpha \omega ^4)\cos \theta \\&\quad + \omega ^2 r^2 \cos ^2 \theta - \beta \omega ^4 r \sin \theta \Big ]\cos \theta , \\&F_2(\theta ,r,w) = \dfrac{1}{\omega ^5} \Big [ (w - \gamma \omega ^2)w \\&\quad - \omega r (2w - \gamma \omega ^2 + \alpha \omega ^4) \cos \theta + \omega ^2 r^2 \cos ^2 \theta \\&\quad - \beta \omega ^4 r \sin \theta \Big ]. \end{aligned} \end{aligned}$$

Using the notation of Sect. 2.2, we have \(t = \theta \), \(T = 2\pi \), \(\mathbf {x} = (r,w)^T\) and

$$\begin{aligned}&F(\theta ,r,w) = \left( \begin{array}{c} F_1(\theta ,r,w) \\ F_2(\theta ,r,w) \end{array}\right) \quad \text {and} \quad \\&\quad f(r,w) = \left( \begin{array}{c} f_1(r,w) \\ f_2(r,w) \end{array}\right) . \end{aligned}$$

It is immediate to check that system (14) satisfies all the assumptions of Theorem 4.

Now we compute the integrals (7). We obtain that

$$\begin{aligned} \begin{aligned} f_1(r,w) =&\,\,\dfrac{1}{2\pi }\int _0^{2\pi } F_1(\theta ,r,w) \ d\theta \\ =&\, \dfrac{ r (\gamma \omega ^2 - \alpha \omega ^4 - 2w)}{2\omega ^5}, \\ f_2(r,w) =&\,\, \dfrac{1}{2\pi } \int _0^{2\pi } F_2(\theta ,r,w) \ d\theta \\ =&\,\dfrac{ 2w^2 - 2\gamma \omega ^2 w + \omega ^2 r^2}{2\omega ^5}. \end{aligned} \end{aligned}$$

The system \(f_1(r,w) = f_2(r,w) = 0\) has a unique solution \((r^*,w^*)\) with \(r^* > 0\), namely

$$\begin{aligned} r^* = \dfrac{\omega \sqrt{\gamma ^2 - \alpha ^2 \omega ^4}}{\sqrt{2}}, \qquad w^* = \dfrac{\omega ^2 (\gamma - \alpha \omega ^2)}{2}. \end{aligned}$$

The Jacobian (8) at \((r^*,w^*)\) takes the value

$$\begin{aligned} \det \dfrac{\partial (f_1,f_2)}{\partial (r,w)} \bigg |_{(r,w)=(r^*,w^*)} = \dfrac{\gamma ^2 - \alpha ^2 \omega ^4}{2\omega ^6}, \end{aligned}$$

which is nonzero by hypothesis. Moreover, the eigenvalues of the Jacobian matrix

$$\begin{aligned} \dfrac{\partial (f_1,f_2)}{\partial (r,w)} \bigg |_{(r,w)=(r^*,w^*)} \end{aligned}$$

are given by

$$\begin{aligned} \dfrac{-\alpha \omega ^2 \pm \sqrt{3\alpha ^2 \omega ^4 - 2\gamma ^2}}{2\omega ^3}. \end{aligned}$$

The rest of the proof of Theorem 2 follows immediately from Theorem 4 if we show that the periodic solution corresponding to \((r^*,w^*)\) provides a periodic orbit bifurcating from the origin of coordinates of the differential system (9) at \(\varepsilon = 0\).

Theorem 4 guarantees for \(\varepsilon > 0\) sufficiently small the existence of a periodic solution \((r(\theta ,\varepsilon ),w(\theta ,\varepsilon ))\) of system (14) such that

$$\begin{aligned}&(r(0,\varepsilon ),w(0,\varepsilon ))\\&\rightarrow \bigg ( \dfrac{\omega \sqrt{\gamma ^2 - \alpha ^2 \omega ^4}}{\sqrt{2}}, \dfrac{\omega ^2 (\gamma - \alpha \omega ^2)}{2} \bigg ), \end{aligned}$$

when \(\varepsilon \rightarrow 0\). From the second equation of system (13) we obtain that \(\theta (t,\varepsilon ) = \omega t + O(\varepsilon )\). Moreover, we have that \((r(t,\varepsilon ),\theta (t,\varepsilon ),w(t,\varepsilon ))\) is a periodic solution of system (13) such that

$$\begin{aligned}&(r(0,\varepsilon ),\theta (0,\varepsilon ),w(0,\varepsilon )) \\&\rightarrow \bigg ( \dfrac{\omega \sqrt{\gamma ^2 - \alpha ^2 \omega ^4}}{\sqrt{2}}, 0, \dfrac{\omega ^2 (\gamma - \alpha \omega ^2)}{2} \bigg ), \end{aligned}$$

when \(\varepsilon \rightarrow 0\). So for \(\varepsilon > 0\) sufficiently small system (12) has the periodic solution

$$\begin{aligned}&(u(t,\varepsilon ),v(t,\varepsilon ),w(t,\varepsilon )) = (r(t,\varepsilon )\cos \theta (t,\varepsilon ),\\&r(t,\varepsilon )\sin \theta (t,\varepsilon ),w(t,\varepsilon )), \end{aligned}$$

such that

$$\begin{aligned}&(u(0,\varepsilon ),v(0,\varepsilon ),w(0,\varepsilon )) \\&\rightarrow \bigg ( \dfrac{\omega \sqrt{\gamma ^2 - \alpha ^2 \omega ^4}}{\sqrt{2}}, 0, \dfrac{\omega ^2 (\gamma - \alpha \omega ^2)}{2} \bigg ), \end{aligned}$$

when \(\varepsilon \rightarrow 0\). This periodic solution in the differential system (11) writes as \((X(t,\varepsilon )\), \(Y(t,\varepsilon ),Z(t,\varepsilon )) = (\varepsilon u(t,\varepsilon ),\varepsilon v(t,\varepsilon ),\varepsilon w(t,\varepsilon ))\), and it satisfies that

$$\begin{aligned}&(X(0,\varepsilon ),Y(0,\varepsilon ),Z(0,\varepsilon )) \\&\rightarrow \bigg ( \dfrac{\varepsilon \omega \sqrt{\gamma ^2 - \alpha ^2 \omega ^4}}{\sqrt{2}}, 0, \dfrac{\varepsilon \omega ^2 (\gamma - \alpha \omega ^2)}{2} \bigg ), \end{aligned}$$

when \(\varepsilon \rightarrow 0\). Finally, we have that system (9) has the periodic solution \((x(t,\varepsilon )\), \(y(t,\varepsilon ),z(t,\varepsilon ))\) obtained from solution \((X(t,\varepsilon ),Y(t,\varepsilon ),Z(t,\varepsilon ))\) through the change of variables (10). It satisfies that \((x(0,\varepsilon ),y(0,\varepsilon ),z(0,\varepsilon ))\) is

$$\begin{aligned}&\varepsilon \bigg (\dfrac{\gamma - \alpha \omega ^2}{2} - \dfrac{\sqrt{\gamma ^2 - \alpha ^2 \omega ^4}}{\sqrt{2}}, 0, \dfrac{\omega ^2\sqrt{\gamma ^2 - \alpha ^2 \omega ^4}}{\sqrt{2}} \bigg ) \\&+\, \mathcal {O}(\varepsilon ^2), \end{aligned}$$

if \(\varepsilon \) is sufficiently small. Thus, \((x(0,\varepsilon ),y(0,\varepsilon ),z(0,\varepsilon )) \rightarrow (0,0,0)\) when \(\varepsilon \rightarrow 0\). Therefore, it is a periodic solution starting at the zero-Hopf equilibrium point located at the origin of coordinates when \(\varepsilon = 0\). This completes the proof of Theorem 2. \(\square \)