Bifurcation of Limit Cycles for a Kind of Piecewise Smooth Differential Systems with an Elementary Center of Focus-Focus Type

Abstract

In this paper, we study the number of limit cycles H(n) bifurcating from the piecewise smooth system formed by the quadratic reversible system (r22) for $y\ge 0$ and the cubic system ${\dot{x}} =y\bigl (1+{{\bar{x}}}^2+y^2\bigr )$, ${\dot{y}} =-{\bar{x}}\bigl (1+{{\bar{x}}}^2+y^2\bigr )$ for $y<0$ under the perturbations of polynomials with degree n, where ${{\bar{x}}}=x-1$. By using the first-order Melnikov function, it is proved that $2n+3\le H(n)\le 2n+ 7$ for $n\ge 3$ and the results are sharp for $n=0,1,2$.

1 Introduction and the Main Results

It is well known that the determination of the number and location of limit cycles for the planar polynomial systems

$$\begin{aligned} {\dot{x}}=X(x,y), ~~~~{\dot{y}}=Y(x,y) \end{aligned}$$

(1.1)

is a significant problem in the qualitative theory of planar differential systems, where $(x,y)\in {\mathbb {R}}^2$, X(x, y) and Y(x, y) are polynomials of x, y of degree n with real coefficients. An isolated closed orbit of (1.1) is called a limit cycle.

We can study limit cycles by perturbing a period annulus. Consider the system

$$\begin{aligned} \begin{aligned} {\dot{x}}={\mu ^{-1}(x,y)}{H_{y}(x,y)}+\varepsilon \, f(x,y),\quad {\dot{y}}=-{\mu ^{-1}(x,y)}{H_{x}(x,y)}+\varepsilon \, g(x,y), \end{aligned} \end{aligned}$$

(1.2)

where $\varepsilon$ ($0 < |\varepsilon |\ll 1$) is a real parameter, ${\mu ^{-1}(x,y)}{H_x(x,y)}$, ${\mu ^{-1}(x,y)} {H_y(x,y)}$, f(x, y), and g(x, y) are all polynomials of x and y. We suppose that the system (1.2)$_{\varepsilon =0}$ has at least one center. The function H(x, y) is a first integral, and $\mu (x,y)$ is an integrating factor. Hence, we can define a continuous family of periodic orbits $\Gamma _h\subset \{(x,y)\in {\mathbb {R}}^2~|~ H(x,y)=h, h \in (h_1,h_2)\}$, which is called a period annulus. For $0<|\varepsilon |\ll 1$ and $h\in (h_1, h_2)$, one can define the Poincaré map of the system (1.2) and the bifurcation function $\textbf{F}(h,\varepsilon )=\varepsilon \, \textbf{M}(h)+o( \varepsilon )$. The isolated zeroes of $\textbf{F}(h,\varepsilon )$ correspond to the limit cycles of (1.2)$_{|\varepsilon |>0}$. The study of bifurcation of limit cycles from the period annulus $\cup _{h\in (h_1,h_2)}\Gamma _h$ is called the Poincaré bifurcation, and the number of limit cycles bifurcating from the period annulus $\{ \Gamma _h ~|~ h\in (h_1,h_2) \}$ is called the Poincaré cyclicity. This is the weak Hilbert’s 16th problem proposed by V. I. Arnold [1]. There are many works on the study of the weak Hilbert’s 16th problem. One can see [14, 16, 18] and search many papers by internet.

In the last a few of years, stimulated by non-smooth phenomena in the real world such as control systems, impact and friction mechanics, and non-linear oscillations, the theory of limit cycles for piecewise smooth differential systems has been developed. In [13], the piecewise smooth planar systems are given by

$$\begin{aligned} \left( \begin{array}{c} {\dot{x}}, \ {\dot{y}}\\ \end{array}\right) =\left\{ \begin{aligned} \left( \begin{array}{c} ~f^{+}(x,y), ~ g^{+}(x,y) \\ \end{array}\right) ,\ (x,y)\in \Sigma ^{+},\\ \left( \begin{array}{c} ~ f^{-}(x,y), ~ g^{-}(x,y) \\ \end{array}\right) ,\ (x,y)\in \Sigma ^{-}, \end{aligned}\right. \end{aligned}$$

(1.3)

where $f^{\pm }(x,y)$ and $g^{\pm }(x,y)$ are $C^{\infty }$ functions, and the discontinuity boundary $\Sigma$ separating the two regions $\Sigma ^{\pm }$ is defined as $\Sigma :=\{(x,y)\in {\mathbb {R}}^2 |~S(x,y)=0\}$ with S(x, y) being a smooth function with non-vanishing gradient $\nabla S(x,y)$ on $\Sigma$, and

$$\begin{aligned}\Sigma ^{+}:=\{(x,y)\in {\mathbb {R}}^2 |~S(x,y)>0\}, \quad \Sigma ^{-}:=\{(x,y)\in {\mathbb {R}}^2 |~S(x,y)<0\}.\end{aligned}$$

The crossing set is defined as

$$\begin{aligned}\Sigma _{c}:=\{(x,y)\in \Sigma ~|~\langle \nabla S, (P^{+},Q^{+})\rangle \cdot \langle \nabla S, (P^{-},Q^{-})\rangle >0\},\end{aligned}$$

where $\langle \cdot ,\cdot \rangle$ denotes the standard scalar product. By definition, at any point $p\in \Sigma _{c}$, the orbit $\varphi (t,p)$ of the system (1.3) crosses $\Sigma$.

Many scholars are interested in the study of the crossing limit cycles of the system:

$$\begin{aligned} \left( \begin{array}{c} {\dot{x}}\\ {\dot{y}}\\ \end{array}\right) =\left\{ \begin{aligned} \left( \begin{array}{c} ~~H_{y}^{+}(x,y)/\mu ^+(x,y)+\varepsilon \, f^+(x,y) \\ -H_{x}^{+}(x,y)/\mu ^+(x,y)+\varepsilon \, g^+(x,y) \\ \end{array}\right) ,\ y\ge 0,\\ \left( \begin{array}{c} ~~ H_{y}^{-}(x,y)/\mu ^-(x,y)+\varepsilon \, f^-(x,y) \\ -H_{x}^{-}(x,y)/\mu ^-(x,y)+\varepsilon \, g^-(x,y) \\ \end{array}\right) ,\ y< 0, \end{aligned}\right. \end{aligned}$$

(1.4)

where $0 <|\varepsilon |\ll 1$, $H^{\pm }(x,y)$, $H_{y}^{\pm }(x,y)$, $H_{x}^{\pm }(x,y)$, and $\mu ^{\pm }(x,y)$ are $C^{\infty }$ functions with $\mu ^{\pm }(0,0)\ne 0$, and $f^{\pm }(x,y)$ and $g^{\pm }(x,y)$ are polynomials with degree n.

There are two main tools to solve the bifurcation of limit cycles for the system (1.4), one is the Melnikov function method developed in [10, 11, 17, 20], and the other is the averaging method established in [21]. We will introduce the Melnikov function method in the following.

The system (1.4)$_{\varepsilon }$ has two sub-systems:

$$\begin{aligned} \left\{ {\begin{aligned} {\dot{x}}&=~~{H_{y}^{+}(x,y)}/{\mu ^+(x,y)}+\varepsilon \, f^+(x,y),\\ {\dot{y}}&=-{H_{x}^{+}(x,y)}/{\mu ^+(x,y)}+\varepsilon \, g^+(x,y), \end{aligned}}~~~~~~y\ge 0,\right. \end{aligned}$$

(1.5)

and

$$\begin{aligned} \left\{ {\begin{aligned} {\dot{x}}&=~~ {H_{y}^{-}(x,y)}/{\mu ^-(x,y)}+\varepsilon \, f^-(x,y),\\ {\dot{y}}&=-{H_{x}^{-}(x,y)}/{\mu ^-(x,y)}+\varepsilon \, g^-(x,y), \end{aligned}}~~~~~~y<0.\right. \end{aligned}$$

(1.6)

We make the following assumptions as in [20].

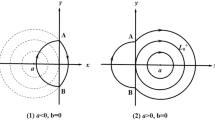
$\mathbf (A_1)$. For the system (1.4)$_{\varepsilon =0}$, there exists a nonempty open interval $(h_1, h_2)$ such that for each $h\in (h_1, h_2)$, there are two points A and B on the curve $y=0$ with

$$\begin{aligned} A:=A(h)=(a(h),0), ~B:=B(h)=(b(h),0),~~a(h)<b(h) \end{aligned}$$

(1.7)

satisfying

$$\begin{aligned}H^{+}(A(h))=H^{+}(B(h))=h,~~H^{-}(A(h))=H^{-}(B(h)).\end{aligned}$$

$\mathbf (A_2)$. For every $h\in (h_1, h_2)$, the subsystem (1.5)$_{\varepsilon =0}$ has an orbital arc $L_{h}^{+}$ starting from A(h) and ending at B(h) defined by $H^{+}(x,y)=h$ ($y\ge 0$), and the subsystem (1.6)$_{\varepsilon =0}$ has an orbital arc $L_{h}^{-}$ starting from B(h) and ending at A(h) defined by $H^{-}(x,y)={\tilde{h}}~ (:=H^-(A(h)))$ ($y<0$).

Under the assumptions $\mathbf (A_1)-\mathbf (A_2)$, the system (1.4)$|_{\varepsilon =0}$ has a family of closed orbits $L_{h}=L_{h}^{+}\cup L_{h}^{-}$ $(h\in (h_1, h_2))$. For definiteness, we assume that the orbits $L_{h}$ for $h\in (h_1, h_2)$ orientate clockwise. For $0<|\varepsilon |\ll 1$, the authors of [20] defined its bifurcation function $F(h,\varepsilon )=\varepsilon \,M(h)+o( \varepsilon )$. The authors of [10, 11, 17] obtained the following results.

Lemma 1.1

Under the assumptions $({\textbf{A}}_1)$ and $({\textbf{A}}_2)$, we have

• (i) [10] If M(h) has j zeros for $h\in \Sigma$ with each having an odd multiplicity, then (1.4)$_{\varepsilon }$ has at least j limit cycles bifurcating from the period annulus for $\varepsilon$ small;

• (ii) [11] If M(h) has at most j zeros for $h\in \Sigma$, taking into account the multiplicity, then there exist at most j limit cycles of (1.4)$_{\varepsilon }$ bifurcating from the period annulus;

• (iii) [17] The first-order Melnikov function M(h) of the system (1.4)$_{\varepsilon }$ has the following form

  $$\begin{aligned}\begin{aligned} M(h)&=\frac{H_{x}^{+}(A)}{H_{x}^{-}(A)}\left[ \frac{H_{x}^{-}(B)}{H_{x}^{+}(B)} \int _{L_{h}^{+}}\mu ^+g^{+}dx-\mu ^+f^{+}dy+\int _{L_{h}^{-}}\mu ^-g^{-}dx-\mu ^-f^{-}dy\right] , \end{aligned} \end{aligned}$$

  where A and B are defined by (1.7).

There are a lot of works on the study the limit cycle bifurcation of the system (1.4). For

$$\begin{aligned} H^{\pm }(x,y)=x^{-3}\left( \frac{1}{2}y^2 -2x^2+x\right) , ~\mu ^{\pm }(x,y)=x^{-4}, \end{aligned}$$

(1.8)

the author of [23] studied the upper bound of the number of limit cycles for $n\in {\mathbb {N}}$, and the authors of [26] obtained the exact number of limit cycles bifurcating from the center (1, 0) for $n=2,3,4$. For

$$\begin{aligned} H^{\pm }(x,y)=x^{-4}\left( \frac{1}{2}y^2 -\frac{9}{256}x^2+\frac{9}{512}\right) , ~~\mu ^{\pm }(x,y)=x^{-5}, \end{aligned}$$

(1.9)

the authors of [25] obtained the number of limit cycles bifurcating from the centers ($\pm 1$, 0). For

$$\begin{aligned}H^+(x,y)=\frac{1}{2}\left( (y-1)^2-x^2\right) ,~~H^-(x,y)=-\frac{1}{2}\left( x^2+y^2\right) ,~~\mu ^{\pm }(x,y)=1,\end{aligned}$$

the authors of [2, 19] investigated the exact number of limit cycles. For

$$\begin{aligned}H^{\pm }(x,y)=x^2+y^2, ~\mu ^+(x,y)=(1+ax)^m, ~\mu ^-(x,y)=(1+bx)^m, \end{aligned}$$

the authors of [8] investigated the number of limit cycles when $a^2+b^2\ne 0$ and $m\in {\mathbb {N}}_+$ by the averaging method.

Motivated by [3, 8, 12, 23, 24], in this paper, we will consider the bifurcation of limit cycles for the system (1.4) with

$$\begin{aligned} \begin{aligned} H^+(x,y)=\frac{1}{2}y^2+\frac{1}{2^5}x^2-\frac{1}{2^4}x, ~~ H^-(x,y)=\frac{1}{2}y^2+\frac{1}{2}{{\bar{x}}}^2, \end{aligned}\end{aligned}$$

(1.10)

and

$$\begin{aligned}\mu ^+(x,y)=x^{-1},~~ \mu ^-(x,y)=\left[ 1+{{\bar{x}}}^2+y^2\right] ^{-1},\end{aligned}$$

where ${{\bar{x}}}=x-1$. More specifically, we shall study the system

$$\begin{aligned} \begin{aligned} \left( \begin{array}{c} {\dot{x}} \\ {\dot{y}} \\ \end{array} \right) =\left\{ \begin{aligned} \left( \begin{array}{c} ~~~~~~~~~xy~~~~~+\varepsilon f^+(x,y) \\ -\frac{1}{2^4}x^2+\frac{1}{2^4}x+\varepsilon g^+(x,y) \\ \end{array} \right) ,\ y\ge 0,\\ \left( \begin{array}{c} ~~~y\bigl (1+{{\bar{x}}}^2+y^2\bigr )+\varepsilon f^-(x,y) \\ -{{\bar{x}}}\bigl (1+{{\bar{x}}}^2+y^2\bigr )+\varepsilon g^-(x,y) \\ \end{array} \right) ,\ y<0.\\ \end{aligned} \right. \end{aligned}\end{aligned}$$

(1.11)

The system (1.11)$|_{\varepsilon =0}$ has a family of periodic orbits $L_h=L^{+}_h\bigcup L^{-}_h$, where

$$\begin{aligned} & L^{+}_h=\left\{ (x,y)\in {\mathbb {R}}^2 ~|~H^+(x,y)=h,~~ h\in \left( -\frac{1}{2^5},0\right) , ~~y\ge 0 \right\} ,\\ & L^{-}_h=\left\{ (x,y)\in {\mathbb {R}}^2 ~|~H^-(x,y)={\tilde{h}}, ~~ {\tilde{h}}=\frac{1}{2}\left( 1+2^5h\right) , ~~y<0\right\} . \end{aligned}$$

For $h\in \left( -\frac{1}{2^5},0\right)$, the system (1.11)$_{\varepsilon =0}$ has a period annulus around the center (1, 0). Let H(n) denote the maximum number of limit cycles bifurcating from $h\in \left( -\frac{1}{2^5},0\right)$. The main results are the following.

Theorem 1.2

For the system (1.11), we have the following results by using the first-order Melnikov function:

• (i) $2n+3\le H(n)\le 2n+7$ for $n\ge 3$;

• (ii) $H(n)=2n+3$ for $n=0,1,2$.

Remark 1.3

• (i)  In [7], the authors classified the quadratic reversible systems

  $$\begin{aligned} \left( \begin{array}{c} {\dot{x}} \\ {\dot{y}} \end{array} \right) = \left( \begin{array}{c} xy \\ \frac{\bar{a}+\bar{b}+2}{2(\bar{a}-\bar{b})}y^2-\frac{\bar{a}+\bar{b}-2}{8(\bar{a}-\bar{b})^3}x^2 +\frac{\bar{b}-1}{2(\bar{a}-\bar{b})^3}x +\frac{\bar{a}-3\bar{b}+2}{8(\bar{a}-\bar{b})^3} \end{array} \right) , ~~\bar{a}, \bar{b}\in {{\mathbb {R}}}, ~ \bar{a}\ne \bar{b}, \nonumber \\ \end{aligned}$$

  (1.12)

  with elliptic integral curves into 18 types (denoted by (r1)–(r18)), and they also identified the 4 types with conic integral curves (denoted by (r19)–(r22)). The system (1.12) can also be found in [12]. The system (r5) is obtained by $\bar{a}=\frac{5{\bar{b}}}{3}+\frac{2}{3}$ and ${\bar{b}}\ne -1$ in (1.12). Setting ${\bar{b}}=1$ in (r5), we can obtain $H^{\pm }(x,y)$ and $\mu ^{\pm }(x,y)$ given in (1.9).

• (ii)   The authors of [12] studied the Poincaré bifurcation of the system (r22), which is defined by setting ${\bar{a}}=-2$ and ${\bar{b}}=0$ in (1.12).

• (iii)   It is known that the first-order Melnikov function M(h) of the system (1.2) is analytic for $h\in [h_1, h_2)$ if ${\mu ^{-1}(x,y)}{H_x(x,y)}$, ${\mu ^{-1}(x,y)} {H_y(x,y)}$, f(x, y), and g(x, y) are all polynomials of x and y, where we assume $H(x,y)=h_1$ corresponds to the elementary center. However, the first-order Melnikov function M(h) of the system (1.4) may not be analytic at $h=h_1$, where we suppose $h=h_1$ corresponds to the center of the system (1.4), even if ${H^{\pm }_x(x,y)}/{\mu ^{\pm }(x,y)}$, ${H^{\pm }_y(x,y)}/{\mu ^{\pm }(x,y)}$, $f^{\pm }(x,y)$, and $g^{\pm }(x,y)$ are all polynomials of x and y.

  For the system (1.11), which has the same first integral and integrating factor with the system (r22) for $y\ge 0$, the first-order Melnikov function M(h) is not analytic at the point $h=-\frac{1}{2^5}$ (see the expressions of $I_{1,0}(h)$ and $I_{0,0}(h)$ in Lemma 3.1). To obtain the lower bound of limit cycles bifurcating from the period annulus, we will extend $I_{1,0}(h)$ and $I_{0,0}(h)$ analytically to the complex domain and then prove that the generators of M(h) are linearly independent such that we can use Lemma 2.3 and obtain Lemma 3.7.

  This paper is organized as follows. In Sect. 2, we will give some helpful results on determining the number of isolated zeros of a function. In Sect. 3, we will obtain the expression of the first-order Melnikov function of the system (1.11), and then prove Theorem 1.2.

2 Preliminaries

In this section, we shall introduce some results on the estimation of the number of isolated zeros of the Melnikov functions.

Definition 2.1

[9] Let $f_0(x),f_1(x),\ldots ,f_{n-1}(x)$ be analytic functions on an open interval $U\subset {\mathbb {R}}$. The ordered set ${\mathcal {F}}:=\left[ f_0(x),f_1(x),\ldots ,f_{n-1}(x)\right]$ is said to be an extended complete Chebyshev system (for short, an ECT-system) on U if, for all $k=1,2,\ldots ,n$, any nontrivial linear combination

$$\begin{aligned}c_0f_0(x)+c_1f_1(x)+\cdots +c_{k-1}f_{k-1}(x)\end{aligned}$$

has at most $k-1$ isolated zeros on U counted with multiplicities.

Lemma 2.2

• (i) [9] The ordered set ${\mathcal {F}}:=[f_0(x),f_1(x),\ldots ,f_{n-1}(x)]$ is an ECT-system on U if and only if, for each $k=1,2,\ldots ,n$,

  $$\begin{aligned} W\left[ f_0, f_1,\ldots ,f_{k-1}\right] (x)\ne 0,~~for~all~x\in U,\end{aligned}$$

  where $W\left[ f_0, f_1,\ldots , f_{k-1}\right] (x)$ is the Wronskian of the functions $f_0(x),f_1(x),\ldots ,f_{k-1}(x)$.

• (ii) [22] The ordered set ${\mathcal {F}}:=\left[ f_0(x),f_1(x),\ldots ,f_{n-1}(x)\right]$ is an ECT-system with accuracy 1 on U if all the Wronskians are non-vanishing except $W\left[ f_0, f_1,\ldots ,f_{n-1}\right] (x)$, which has exactly one zero on U and this zero is simple. Then, any nontrivial linear combination

  $$\begin{aligned}c_0f_0(x)+c_1f_1(x)+\cdots +c_{n-1}f_{n-1}(x)\end{aligned}$$

  has at most n isolated zeros on U. Moreover, for any configuration of $m\le n$ zeros there exists n constants $c_{i}$, $i=0,1,\ldots ,n-1$, such that $f(x)=\sum \limits _{i=0}^{n-1}c_{i}f_{i}(x)$ realizing it.

Lemma 2.3

[5] Consider $p+1$ linearly independent analytical functions $f_i:U\rightarrow {\mathbb {R}}, i=0,1,\ldots ,p$, where $U \subset {\mathbb {R}}$ is an open interval. Suppose that there exists $j \in \{0,1,\ldots ,p\}$ such that $f_{j}|_U$ has a constant sign. Then there exist $p+1$ constants $C_{i}$, $i=0,1,\ldots ,p$, such that $f(x):=\sum \limits _{i=0}^{p}C_{i}f_{i}(x)$ has at least p simple zeros in U.

From the Lemma 4.5 in [8], we have the following equivalent conclusion in Lemma 2.4.

Lemma 2.4

[8] Denote by $F_k(v)$ a polynomial of degree k and $g^{(k)}(v)$ the kth-order derivative of a function g(v). We have the following conclusions.

• (i) Suppose $H_1(v):=\sum \limits ^{n}_{i=0}B_{i}v^i\ln \frac{1+b\sqrt{v}}{1-b\sqrt{v}}$ with $v=u^2$, $n\in {\mathbb {N}}$ and $B_i$, $i=0,1,\ldots , n$ are constants. Then, for $k\ge 2n+1$,

  $$\begin{aligned} \frac{d^k}{du^k}H_1(v)=\left\{ \begin{aligned} \frac{\sqrt{v}F_{\frac{k-2}{2}}(v)}{\left( 1-b^2v\right) ^k}, ~~&\text {{ k}} ~\text {is}~ \text {even}, \\ \frac{F_{\frac{k-1}{2}}(v)}{\left( 1-b^2v\right) ^k}, ~~~&\text {{ k}}~ \text {is} ~\text {odd}. \end{aligned}\right. \end{aligned}$$

• (ii) Suppose $H_2(v):=\sum \limits ^{n}_{i=0}A_{i}v^i\frac{1}{\left( 1-b^2v\right) ^{m-\frac{1}{2}}}$ with $v=u^2$, $2\le m\in {\mathbb {N}}^+$, $n\in {\mathbb {N}}$ and $A_i$, $i=0,1,\ldots , n$ are constants. Then, for all $k\in {\mathbb {N}}^+$,

  $$\begin{aligned} \frac{d^k}{du^k}H_2(v)=\left\{ \begin{aligned} \frac{F_{n^*}(v)}{(1-b^2v)^{k+m-\frac{1}{2}}}, ~~&k\, \text {is}\, \text {even}, \\ \frac{\sqrt{v}F_{n^*}(v)}{(1-b^2v)^{k+m-\frac{1}{2}}}, ~~~&k\text { is odd}, \end{aligned}\right. \end{aligned}$$

  where

  $$\begin{aligned} n^*=\left\{ \begin{aligned} m-1+\left[ \frac{k}{2}\right] , ~~&{m-1\le n\le \left[ \frac{k}{2}\right] +m-1}, \\ n+\left[ \frac{k}{2}\right] , \qquad ~~&0\le n \le m-2\text { or }n\ge \left[ \frac{k}{2}\right] +m. \end{aligned}\right. \end{aligned}$$

For a real sequence $\{c_0,\ c_1,\ldots ,\ c_n\}$ we denote by

$$\begin{aligned} \begin{aligned} N\{c_0,\ c_1,\ldots ,\ c_n\} \end{aligned} \end{aligned}$$

(2.1)

the number of changes in sign in this sequence (skip zero(s), if it appears in this sequence). To find the number of real roots of a polynomial f(x) for $x \in (a, b)$, the following two criteria are well known.

Lemma 2.5

[15] Suppose that f(x) is a polynomial of degree n with real coefficients, $a<b$ are two real numbers, $f (a)\ne 0$, $f (b)\ne 0$, and the derivatives of f(x) are

$$\begin{aligned}f (x),\ f ^{'}(x),\ f ^{''}(x), \ldots ,\ f ^{(n)}(x). \end{aligned}$$

• (i) Fourier-Budan Theorem. If

  $$\begin{aligned} & N\left\{ f (a),\ f ^{'}(a),\ f ^{''}(a), \ldots ,\ f ^{(n)}(a)\right\} =p,\\ & N\{f (b),\ f ^{'}(b),\ f ^{''}(b), \ldots ,\ f ^{(n)}(b)\}=q, \end{aligned}$$

  then $p \ge q$, and the number of real roots (counting the multiplicity) of f(x) for $x \in (a, b)$ is equal to either $p-q$ or $p-q-r$, where r is a positive even integer. In particular, if $p = q$ (resp. $p = q + 1$), then f(x) has no (resp. has a unique) real root in (a, b).

• (ii) Sturm Theorem. Assume that f(x) has no multiple root in (a, b), and we construct the sequence $\{f_0(x),\ f_1(x),\ f_2(x), \ldots , f_s(x)\}$ as follows: $f_0(x) = f (x),\ f_1(x) = f^{'}(x)$. Divide $f_0(x)$ by $f_1(x)$, and take the remainder with negative sign as $f_2(x)$, then divide $f_1(x)$ by $f_2(x)$, and take the remainder with negative sign as $f_3(x)$, ..., the last remainder with negative sign (a non-zero number) is $f_s(x)$. If

  $$\begin{aligned} & N\{f_0 (a),\ f _1(a),\ f _2(a),\ldots ,\ f _s(a)\}=p,\\ & N\{f_0 (b),\ f _1(b),\ f _2(b), \ldots ,\ f _s(b)\}=q,\end{aligned}$$

  then $p \ge q$ and the number of real roots of f(x) for $x \in (a, b)$ is equal to $p-q$.

3 Proof of Theorem 1.2

We shall first obtain the algebraic structure of M(h) of the system (1.11). Without loss of generality, we can assume that

$$\begin{aligned} \begin{aligned} f^{+}(x,y)=\,&\sum _{i+j=0}^n a_{i,j}^{+} x^i y^j, \quad f^{-}(x,y)=\,\sum _{i+j=0}^n a_{i,j}^{-} (x-1)^i y^j,\\ g^{+}(x,y)=\,&\sum _{i+j=0}^n b_{i,j}^{+} x^i y^j,\quad g^{-}(x,y)=\sum _{i+j=0}^n b_{i,j}^{-} (x-1)^i y^j. \end{aligned} \end{aligned}$$

(3.1)

The point (1, 0) is an elementary center of focus-focus type (see [4] for the definition) corresponding to $h=-\frac{1}{2^5}$. For $h\in \left( -\frac{1}{2^5},0\right)$, denote

$$\begin{aligned} \begin{aligned} u(h):=\sqrt{1+2^5h}, \quad I_{i,j}(h):=\int _{L^+_h}x^{i-1}y^jdx. \end{aligned}\end{aligned}$$

(3.2)

It is easily seen that the semi orbit $L^{+}_h$ intersects the x-axis at points A(a(h), 0) and B(b(h), 0)), where

$$\begin{aligned} \begin{aligned} a(h)=1-u(h),~~~b(h)=1+u(h). \end{aligned}\end{aligned}$$

(3.3)

Lemma 3.1

For $h\in \left( -\frac{1}{2^5},0\right)$, we have

$$\begin{aligned} \begin{aligned} I_{1,1}(h)=\,&\frac{\pi }{8}\left( 1+2^5h\right) , \qquad I_{0,1}(h)=\frac{\pi }{4}\left( 1-4\sqrt{-2h}\right) , \\ I_{1,0}(h)=\,&2\sqrt{1+2^5h}, \qquad I_{0,0}(h)=\ln \frac{1+\sqrt{1+2^5h}}{1-\sqrt{1+2^5h}}. \\ \end{aligned} \end{aligned}$$

Proof

For $j\ge 1$, by direct calculation, we have $I_{i,j}\left( -\frac{1}{2^5}\right) =0$ and

$$\begin{aligned}\begin{aligned} I^{'}_{i,j}(h)=&\int ^{b(h)}_{a(h)}jx^{i-1}y^{j-1}\frac{\partial y}{\partial h}dx+b^{i-1}(h)y^{j}(b(h),h)\frac{d (b(h))}{d h}\\&-a^{i-1}(h)y^{j}(a(h),h)\frac{d( a(h))}{d h}.\\ \end{aligned}\end{aligned}$$

From (3.3), we have

$$\begin{aligned}\frac{d (b(h))}{d h}=-\frac{d( a(h))}{d h}=\frac{2^4}{\sqrt{1+2^5h}}\ne \infty , \ h\in \left( -\frac{1}{2^5},0\right) .\end{aligned}$$

Hence, by $y(b(h),h)=y(a(h),h)=0$, we have

$$\begin{aligned}\begin{aligned} I^{'}_{i,j}(h)=&\int ^{b(h)}_{a(h)}jx^{i-1}y^{j-1}\frac{\partial y}{\partial h}dx. \end{aligned}\end{aligned}$$

By $H^{+}(x,y(x,h))=h$ in (1.10), we have $\frac{\partial y}{\partial h}=\frac{1}{y}$, which yields $I^{'}_{i,j}(h)=jI_{i,j-2}(h).$ Therefore,

$$\begin{aligned} \begin{aligned} hI^{'}_{i,j}(h)=\,&j\int ^{b(h)}_{a(h)}\left( \frac{1}{2}y^2+\frac{1}{2^5}x^2 -\frac{1}{2^4}x\right) x^{i-1}y^{j-2}dx \\ =\,&\frac{j}{2}I_{i,j}(h)+\frac{j}{2^5}I_{i+2,j-2}(h) -\frac{j}{2^4}I_{i+1,j-2}(h). \end{aligned}\end{aligned}$$

(3.4)

Also, we have

$$\begin{aligned} \begin{aligned} I_{1,-1}(h)=\,&4\int ^{b(h)}_{a(h)}\frac{dx}{\sqrt{(b(h)-x)(x-a(h))}} \\ =\,&4\int ^{1}_{-1}\frac{ds}{\sqrt{1-s^2}}=4\pi ,\\ I_{2,-1}(h)=\,&4u(h)\int ^{1}_{-1}\frac{sds}{\sqrt{1-s^2}} +4\int ^{1}_{-1}\frac{ds}{\sqrt{1-s^2}} =4\pi ,\\ I_{3,-1}(h)=\,&4\int ^{1}_{-1}\frac{(u(h)s+1)^2ds}{\sqrt{1-s^2}} =4\pi \left( 16h+\frac{3}{2}\right) . \end{aligned}\end{aligned}$$

(3.5)

According to (3.4) and (3.5), we get

$$\begin{aligned} \begin{aligned} hI^{'}_{0,1}(h) =\,&\frac{1}{2}I_{0,1}(h)-\frac{1}{8}\pi , \quad I_{0,1}\left( -\frac{1}{2^5}\right) =0. \end{aligned}\end{aligned}$$

(3.6)

By solving the differential equation (3.6), we can get $I_{0,1}(h)=\frac{\pi }{4}\left( 1-4\sqrt{-2h}\right)$. Similarly, we can get the expressions of $I_{1,1}(h)$, $I_{1,0}(h)$ and $I_{0,0}(h)$. This ends the proof. $\square$

Lemma 3.2

We have the following results:

• (i) We have $I_{-1,1}(h)=\frac{1}{16h}\left[ \frac{1}{2}I_{0,1}(h)-I_{1,1}(h)\right]$.

• (ii) For $i\ge 1$, we have

  $$\begin{aligned}I_{i,1}(h)={\hat{\alpha }}_{i,1}(h)I_{1,1}(h),~~ I_{i,0}(h)={\hat{\alpha }}_{i,0}(h)I_{1,0}(h),\end{aligned}$$

  where ${\hat{\alpha }}_{i,1}(h)$, ${{\hat{\alpha }}_{i,0}}(h)$ are polynomials of h with degree $\left[ \frac{i-1}{2}\right]$.

• (iii) If $j\ge 2$, then

  $$\begin{aligned} I_{1,j}(h)=\left\{ \begin{aligned} \delta _{\left[ \frac{j}{2}\right] ,0}(h)I_{1,0}(h), ~~&\text {if } j\text { is even}, \\ \delta _{\left[ \frac{j}{2}\right] ,1}(h)I_{1,1}(h), ~~&\text {if }j\text { is odd}, \end{aligned}\right. \end{aligned}$$

  where $\delta _{0,1}(h)=1$, and

  $$\begin{aligned} \begin{aligned} \delta _{k,0}(h)=\,&\frac{(2k)!!}{(2k+1)!!}\left( 2h+\frac{1}{2^4}\right) ^k, \ k\ge 0,\\ \delta _{k,1}(h)=\,&\frac{(2k+1)!!}{(2k+2)!!}\left( 2h+\frac{1}{2^4}\right) ^k, \ k\ge 1. \\ \end{aligned}\end{aligned}$$

  (3.7)

• (iv) If $j\ge 2$, then

  $$\begin{aligned} I_{0,j}(h)=\left\{ \begin{aligned} \gamma _{[\frac{j}{2}],0}(h)I_{0,0}(h)+\gamma _{\left[ \frac{j}{2}\right] ,1}(h)I_{1,0}(h), ~~&\text {if }j\text { is even}, \\ \gamma _{[\frac{j}{2}],0}(h)I_{0,1}(h)+\gamma _{\left[ \frac{j}{2}\right] ,2}(h)I_{1,1}(h), ~~&\text {if }j\text { is odd}, \end{aligned}\right. \end{aligned}$$

  where

  $$\begin{aligned} \begin{aligned} \gamma _{k,0}(h)=\,&(2h)^k, \\ \gamma _{k,1}(h)=\,&\frac{1}{2^4}\left[ (2h)^{k-1}+(2h)^{k-2}\delta _{1,0}(h) +\cdots + \delta _{k-1,0}(h)\right] , \\ \gamma _{k,2}(h)=\,&\frac{1}{2^4}\left[ (2h)^{k-1}+(2h)^{k-2}\delta _{1,1}(h) +\cdots + \delta _{k-1,1}(h)\right] . \\ \end{aligned}\end{aligned}$$

  (3.8)

Proof

Let $D^+_h$ be the interior of $L^+_h\cup \overrightarrow{BA}$. Then, by the Green’s formula, we have

$$\begin{aligned}\begin{aligned} \int _{L^+_h}x^{i-1}y^{j}dy=\,&\left( \int _{L^+_h\cup \overrightarrow{BA}}- \int _{\overrightarrow{BA}}\right) x^{i-1}y^{j}dy =-(i-1)\int \int _{D^+_h}x^{i-2}y^{j}dxdy \end{aligned}\end{aligned}$$

and

$$\begin{aligned}\begin{aligned} \int _{L^+_h}x^{i-2}y^{j+1}dx=\,&\left( \int _{L^+_h\cup \overrightarrow{BA}}- \int _{\overrightarrow{BA}}\right) x^{i-2}y^{j+1}dx =(j+1)\int \int _{D^+_h}x^{i-2}y^{j}dxdy. \end{aligned}\end{aligned}$$

Thus, we have

$$\begin{aligned} \begin{aligned} \int _{L^+_h}x^{i-1}y^{j}dy=&-\frac{i-1}{j+1}I_{i-1,j+1}(h). \end{aligned}\end{aligned}$$

(3.9)

(1)  We first claim that

$$\begin{aligned} \left\{ \begin{aligned} I_{-1,1}(h)=\,&\frac{1}{2^4h}\left[ \frac{1}{2}I_{0,1}(h)-I_{1,1}(h)\right] , \\ I_{2,0}(h)=\,&I_{1,0}(h), \\ I_{2,1}(h)=\,&I_{1,1}(h),\\ I_{3,0}(h)=\,&\frac{4}{3}(8h+1)I_{1,0}(h). \\ \end{aligned}\right. \end{aligned}$$

(3.10)

In fact, from $H^{+}(x,y(x,h))=h$ in (1.10), we can get

$$\begin{aligned} \begin{aligned} y\frac{\partial y}{\partial x}+\frac{1}{2^4}x-\frac{1}{2^4}=0. \end{aligned}\end{aligned}$$

(3.11)

Multiplying $H^{+}(x,y(x,h))=h$ in (1.10) and (3.11) by $x^{i-1}y^{j-2}dx$ and $x^{i-2}y^jdx$, respectively, and integrating over $L^{+}_h$, combined with (3.9), we have

$$\begin{aligned} \begin{aligned} I_{i,j}(h)=2hI_{i,j-2}(h)+\frac{1}{2^3}I_{i+1,j-2}(h) -\frac{1}{2^4}I_{i+2,j-2}(h), \ j\ge 2, \end{aligned}\end{aligned}$$

(3.12)

$$\begin{aligned} \begin{aligned} I_{i,j}(h)=I_{i-1,j}(h)+\frac{2^4(i-2)}{j+2}I_{i-2,j+2}(h). \end{aligned}\end{aligned}$$

(3.13)

Combining (3.12) and (3.13), we have

$$\begin{aligned} & I_{i,j}(h)=\frac{j}{i+j}\left[ 2hI_{i,j-2}(h) +\frac{1}{2^4}I_{i+1,j-2}(h)\right] , \ j\ge 2, \end{aligned}$$

(3.14)

$$\begin{aligned} & 2^4iI_{i,j}(h)=j[I_{i+2,j-2}(h)-I_{i+1,j-2}(h)], \ j\ge 2. \end{aligned}$$

(3.15)

Taking $(i,j)=(2,0),(2,1),(3,0)$ in (3.13), and $(i,j)=(-1,3)$ in (3.15), respectively, we have

$$\begin{aligned} \begin{aligned} I_{2,0}(h)=\,&I_{1,0}(h), ~~\quad \quad \qquad \quad I_{2,1}(h)=I_{1,1}(h),\\ I_{3,0}(h)=\,&I_{2,0}(h)+2^3I_{1,2}(h), ~~ I_{-1,3}(h)=\,\frac{3}{2^4}[I_{0,1}(h)-I_{1,1}(h)]. \end{aligned}\end{aligned}$$

(3.16)

Hence, we obtain the second and third formulas in (3.10). Taking $(i,j)=(-1,3)$ and (1, 2) in (3.14), we have

$$\begin{aligned} \begin{aligned} I_{-1,3}(h)=\,&3hI_{-1,1}(h)+\frac{3}{2^5}I_{0,1}(h), \\ I_{1,2}(h)=\,&\frac{2}{3}\left[ 2hI_{1,0}(h)+\frac{1}{2^4}I_{2,0}(h)\right] . \\ \end{aligned}\end{aligned}$$

(3.17)

Combining (3.16) and (3.17), we get the first and fourth formulas in (3.10).

(2)  Next, we will prove the results of (ii) by induction. In fact, by (3.10), it is easy to check that the results hold for $i=1,2,3$. Suppose that the results hold for $1\le i\le k-1 (k\ge 4)$. Then for $i=k$, it follows from (3.13) and (3.14) that

$$\begin{aligned} \begin{aligned} I_{i,j}(h)=\,&\frac{2i+j-2}{i+j}I_{i-1,j}(h) +\frac{2^5(i-2)}{i+j}hI_{i-2,j}(h),\ j\ge 0. \end{aligned}\end{aligned}$$

(3.18)

For $j=0,1$, by induction assumption, we get

$$\begin{aligned} \begin{aligned} I_{i,j}(h)=\,&\left[ \frac{2i+j-2}{i+j}{\hat{\alpha }}_{i-1,j}(h) +\frac{2^5(i-2)}{i+j}h{\hat{\alpha }}_{i-2,j}(h)\right] I_{1,j}(h)\\:=\,&{\hat{\alpha }}_{i,j}(h)I_{1,j}(h), \end{aligned}\end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \deg {\hat{\alpha }}_{i,j}(h)=&\max \left\{ \left[ \frac{i-2}{2}\right] , \left[ \frac{i-3}{2}\right] +1\right\} =\left[ \frac{i-1}{2}\right] .\\ \end{aligned}\end{aligned}$$

(3)  Finally, we will give the proofs of (iii) and (iv). Let $i=2$ in (3.13) and $i=1$ in (3.14), then

$$\begin{aligned} \begin{aligned} I_{1,j}(h)=\frac{j}{1+j}\left( 2h+\frac{1}{2^4}\right) I_{1,j-2}(h), \quad j\ge 2, \end{aligned}\end{aligned}$$

(3.19)

which implies the results of (iii). Taking $i=0$ in (3.14), we have

$$\begin{aligned} \begin{aligned} I_{0,j}(h)=2hI_{0,j-2}(h)+\frac{1}{2^4}I_{1,j-2}(h), \quad j\ge 2. \end{aligned}\end{aligned}$$

(3.20)

Suppose $j=2k$, it is easily obtained that

$$\begin{aligned} \begin{aligned} I_{0,2k}(h)=(2h)^kI_{0,0}(h)+\frac{1}{2^4}\sum _{i=0}^{k-1}(2h)^{k-1-i} I_{1,2i}(h). \end{aligned}\end{aligned}$$

(3.21)

Substituting the first formula of (iii) into (3.21), we can obtain the first formula of (iv). By similar arguments, we can get the second formula of (iv). This ends the proof. $\diamondsuit$

By Lemma 1.1, (3.1) and (3.9), we have $M(h)=M^+(h)+M^-(h)$, where

$$\begin{aligned} \begin{aligned} M^+(h)=&\sum _{i+j=0}^{n}\int _{L_{h}^{+}}\left( b_{i,j}^+x^{i-1}y^j +\frac{i-1}{j+1}a_{i,j}^+x^{i-2}y^{j+1}\right) dx =\sum _{i+j=0, i\ge -1}^{n}\rho _{i,j} I_{i,j}(h), \\ M^-(h)=\,&\frac{H_{x}^{+}(A)}{H_{x}^{-}(A)} \sum _{i+j=0}^{n}\int _{L_{h}^{-}}\frac{b_{i,j}^-(x-1)^{i}y^jdx -a_{i,j}^-(x-1)^{i}y^{j}dy}{1+(x-1)^2+y^2} =\,\sum _{k=1}^{n+1}\frac{\tau _{k-1}u^{k}(h)}{1+u^2(h)}, \end{aligned}\nonumber \\ \end{aligned}$$

(3.22)

and

$$\begin{aligned} \left\{ \begin{aligned} \rho _{i,0}=\,&b_{i,0}^+, \quad i\ge 0, \qquad \rho _{-1,j+1}=\frac{-1}{j+1}a_{0,j}^+, \quad j\ge 0, \\ \rho _{i,j}=\,&b_{i,j}^++\frac{i}{j}a_{i+1,j-1}^+, \quad i\ge 0, ~~ j\ge 1. \\ \tau _k=\,&\frac{1}{16}\sum _{i+j=k}(-1)^{j+1}\left( b_{i,j} ^{-}\kappa _{1,i,j}-a_{i,j}^{-}\kappa _{2,i,j}\right) , ~ 0\le k\le n, \\ \kappa _{1,i,j}=\,&\int ^{\pi }_{0}\cos ^{i}\theta \sin ^{j+1}\theta ~ d\theta ,\\ \kappa _{2,i,j}=\,&\int ^{\pi }_{0}\cos ^{i+1}\theta \sin ^j\theta ~ d\theta . \end{aligned}\right. \end{aligned}$$

(3.23)

Let

$$\begin{aligned} a_j:=\left\{ \begin{aligned}&\rho _{0,j}+\frac{j+2}{2^{4}}\rho _{-1,j+2}, ~~ 0\le j\le n-1, \\&~~~~~~~\rho _{0,n},\qquad \qquad ~~~~~~~~ j=n, \end{aligned}\right. \end{aligned}$$

(3.24)

$$\begin{aligned} b_j:=\left\{ \begin{aligned}&\rho _{1,0}-2^{-3}\rho _{-1,2},\qquad \qquad ~ \ j=0, \\&\rho _{1,1}-3\cdot 2^{-4}\rho _{-1,3},\qquad ~~~~ \ j=1, \\&-2^{-4}(j+2)\rho _{-1,j+2},~~ 2\le j\le n-1, \end{aligned}\right. \end{aligned}$$

(3.25)

$$\begin{aligned} \left\{ \begin{aligned} c_j:=\,&\rho _{j,0}+\sum _{i+k=3, i\ge 1,k\ge 2}^{n}c_{i,k,j}~\rho _{i,k}, \ 2\le j\le n, \\ d_j:=\,&\rho _{j,1}+\sum _{i+k=3, i\ge 1,k\ge 2}^{n}d_{i,k,j}~\rho _{i,k},\ 2\le j\le n-1; \end{aligned}\right. \end{aligned}$$

(3.26)

where $c_{i,k,j}$ and $d_{i,k,j}$ are constants, and

$$\begin{aligned} \begin{aligned} \alpha _1(h):=\,&\sum _{k=0}^{\left[ \frac{n}{2}\right] }a_{2k}\gamma _{k,0}(h), \qquad \beta _1(h):=\,\sum _{k=0}^{\left[ \frac{n-1}{2}\right] }a_{2k+1}\gamma _{k,0}(h), \\ \alpha _2(h):=\,&\sum _{k=1}^{\left[ \frac{n}{2}\right] }a_{2k}\gamma _{k,1}(h) +\sum _{k=0}^{\left[ \frac{n-1}{2}\right] }b_{2k}\delta _{k,0}(h) +\sum _{i=2}^{n}c_{i}{\hat{\alpha }}_{i,0}(h), \\ \beta _2(h):=\,&\sum _{k=1}^{\left[ \frac{n-1}{2}\right] }a_{2k+1}\gamma _{k,2}(h) +\sum _{k=0}^{\left[ \frac{n-2}{2}\right] }b_{2k+1}\delta _{k,1}(h) +\sum _{i=2}^{n-1}d_{i}{\hat{\alpha }}_{i,1}(h). \end{aligned}\end{aligned}$$

(3.27)

According to Lemma 3.2 (ii)–(iv), we can easily obtain that $\alpha _{1}(h)$, $\alpha _{2}(h)$, $\beta _1(h)$ and $\beta _2(h)$ are polynomials of h with $\deg \alpha _1(h)\le \left[ \frac{n}{2}\right]$, $\deg \alpha _2(h), \deg \beta _1(h)\le \left[ \frac{n-1}{2}\right]$ and $\deg \beta _2(h)\le \left[ \frac{n-2}{2}\right]$ for $n\ge 3$. $\square$

Lemma 3.3

For $h\in \left( -\frac{1}{2^5},0\right)$, and $n\ge 3$, we have

• (i) The first-order Melnikov function of the system (1.11) can be expressed as

  $$\begin{aligned} \begin{aligned} M(h)=\,&\alpha _1(h)I_{0,0}(h)+\alpha _2(h)I_{1,0}(h) +\beta _1(h)I_{0,1}(h)\\&+\beta _2(h)I_{1,1}(h) +\frac{{\rho _{-1,1}}}{16h}\left[ \frac{1}{2}I_{0,1}(h)-I_{1,1}(h)\right] +\sum _{k=1}^{n+1}\frac{\tau _{k-1}u^{k}(h)}{1+u^2(h)}. \end{aligned}\end{aligned}$$

• (ii) There exist the parameters $a_{i,j}^{+}$ and $b_{i,j}^{+}$ such that

  $$\begin{aligned}\begin{aligned} \alpha _{1}(h)=\,&\sum _{k=0}^{\left[ \frac{n}{2}\right] }A_{k}h^k,~~~ \alpha _{2}(h)=\sum _{k=0}^{\left[ \frac{n-1}{2}\right] }C_{k}h^k, \\ \beta _{1}(h)=\,&\sum _{k=0}^{\left[ \frac{n-1}{2}\right] }B_{k}h^k,~~ \beta _{2}(h)=\sum _{k=0}^{\left[ \frac{n-2}{2}\right] }D_{k}h^k, \end{aligned}\end{aligned}$$

  where the coefficients $A_{k}$, $B_{k}$, $C_{k}$ and $D_{k}$ are the linear functions of $a_{i,j}^{+}$ and $b_{i,j}^{+}$ given by (3.1) and they are independent.

Proof

(1)  Let $L(f_i(x), \ 0\le i \le n)$ be a linear combination of the functions $f_0(x), f_1(x), \ldots$, $f_n(x)$. For $i\ge 1, k\ge 1, j\ge 2$, we have

$$\begin{aligned} \begin{aligned} I_{i,2k}(h)=\,&L(I_{i+2k-k_1,0}(h), \ 0\le k_1 \le k), \\ I_{i,2k+1}(h)=\,&L(I_{i+2k-k_1,1}(h), \ 0\le k_1 \le k), \\ I_{-1,j}(h)=\,&-2^{-4}j\left[ I_{1,j-2}(h)-I_{0,j-2}(h)\right] . \end{aligned}\end{aligned}$$

(3.28)

We will prove the results in (3.28) by induction. In fact, by (3.15), we have

$$\begin{aligned} \begin{aligned} I_{i,j}(h)=\frac{j}{2^4i}\left[ I_{i+2,j-2}(h)-I_{i+1,j-2}(h)\right] , \\ \end{aligned}\end{aligned}$$

(3.29)

which yields the first formula in (3.28) holds for $i\ge 1$ and $k=1$. Suppose that the first formula in (3.28) holds for $i\ge 1$, $k=1,2,\ldots ,m$. Then for $i\ge 1$, $k=m+1$, by (3.29), we have

$$\begin{aligned} \begin{aligned} I_{i,2m+2}(h)=\,&\frac{2m+2}{2^4i}\left[ I_{i+2,2m}(h)-I_{i+1,2m}(h)\right] , \\ =\,&L\bigl (I_{i+2m+2-k_1,0}(h), \ 0\le k_1 \le m\bigr )\\&+L\bigl (I_{i+2m+1-k_1,0}(h), \ 0\le k_1 \le m\bigr )\\ =\,&L\bigl (I_{i+2m+2-k_1,0}(h), \ 0\le k_1 \le m+1\bigr ). \end{aligned}\end{aligned}$$

(3.30)

By the same method, we obtain the second formula in (3.28), and the third formula follows from (3.15) with $i=-1$ and $j\ge 2$. For $n\ge 3$, according to (3.22) and (3.28), we have

$$\begin{aligned} \begin{aligned} M^+(h)=\,&\sum _{j=0}^{n}\rho _{0,j} I_{0,j}(h)+\sum _{i=1}^{n}\rho _{i,0} I_{i,0}(h)+\sum _{i=1}^{n-1}\rho _{i,1} I_{i,1}(h)\\ \,&+\sum _{j=2}^{n+1}\rho _{-1,j} I_{-1,j}(h)+\sum _{j=2 }^{n-1}\sum _{i=1}^{n-j}\rho _{i,j} I_{i,j}(h)+\rho _{-1,1} I_{-1,1}(h) \\ =\,&\sum _{j=0}^{n}a_{j} I_{0,j}(h)+\sum _{j=0}^{n-1}b_{j} I_{1,j}(h)\\ \,&+\sum _{i=2}^{n}c_{i} I_{i,0}(h)+\sum _{i=2}^{n-1}d_{i} I_{i,1}(h)+\rho _{-1,1} I_{-1,1}(h).\\ \end{aligned}\end{aligned}$$

(3.31)

By using Lemma 3.2, after a simple simplification, we can obtain the expression of $M^+(h)$ for $n\ge 3$. According to (3.22), we obtain the expression of M(h).

(2)  Next, we will prove the result of (ii). According to (3.27), we only need to prove that there exist the coefficients $a_i, b_i, c_i$, and $d_i$ defined in (3.24–3.26) such that $A_i, B_i, C_i$, and $D_i$ are independent. Suppose $c_i=0$ $(i=2,3, \ldots ,n)$ and $d_i=0$ $(i=2,3, \ldots ,n-1)$. Denote

$$\begin{aligned} \begin{aligned} A_{k,j}:=\,&\frac{(2k)!!}{(2k+1)!!}\left( \begin{array}{c} k \\ j \\ \end{array} \right) 2^{5j-4k},\quad B_{k,i,j}:=2^{j-4}A_{k-1-j,i}, \\ {\overline{A}}_{k,j}:=\,&\frac{(2k+1)!!}{(2k+2)!!}\left( \begin{array}{c} k \\ j \\ \end{array} \right) 2^{5j-4k},\quad {\overline{B}}_{k,i,j}:=2^{j-4}{\overline{A}}_{k-1-j,i}. \end{aligned}\end{aligned}$$

Then we have

$$\begin{aligned} \begin{aligned} \delta _{k,0}(h)=\,&\sum _{j=0}^{k}A_{k,j}h^{j},\quad \delta _{k,1}(h)=\sum _{j=0}^{k}{\overline{A}}_{k,j}h^{j}, \quad \gamma _{k,0}(h)=2^kh^k, \\ \gamma _{k,1}(h)=\,&\sum _{i=0}^{k-1}\sum _{j=0}^{k-1-i}B_{k,i,j} h^{i+j}, \quad \gamma _{k,2}(h)=\sum _{i=0}^{k-1}\sum _{j=0}^{k-1-i}{\overline{B}}_{k,i,j} h^{i+j}. \end{aligned}\end{aligned}$$

(3.32)

Suppose that n is even. Substituting (3.32) into (3.27), we obtain that

$$\begin{aligned} \begin{aligned} \alpha _{1}(h)=\,&\sum _{k=0}^{\frac{n}{2}}A_{k}h^k,~~~ \alpha _{2}(h)=\sum _{k_1=0}^{\frac{n-2}{2}}C_{\frac{n-2}{2}-k_1} h^{\frac{n-2}{2}-k_1}, \\ \beta _{1}(h)=\,&\sum _{k=0}^{\frac{n-2}{2}}B_{k}h^k,~~~ \beta _{2}(h)=\sum _{k_1=0}^{\frac{n-2}{2}}D_{\frac{n-2}{2}-k_1} h^{\frac{n-2}{2}-k_1}, \end{aligned}\end{aligned}$$

(3.33)

where $A_{k}=2^ka_{2k}$, $B_{k}=2^ka_{2k+1}$, and

$$\begin{aligned} \begin{aligned} C_{\frac{n-2}{2}-k_1}=\,&\sum _{k=\frac{n}{2}-k_1}^{\frac{n}{2}} \alpha _{2,k,\frac{n-2}{2}-k_1}, \quad D_{\frac{n-2}{2}}=b_{n-1} {\overline{A}}_{\frac{n-2}{2},\frac{n-2}{2}}, \\ D_{\frac{n-2}{2}-k_1}=&\sum _{k=\frac{n}{2}-k_1}^{\frac{n-2}{2}} \beta _{2,k,\frac{n-2}{2}-k_1}+b_{n-1-2k_1} {\overline{A}}_{\frac{n-2}{2}-k_1,\frac{n-2}{2}-k_1},~~ k_1=1,2,\cdots ,\frac{n-2}{2},\\ \alpha _{2,k,j}=\,&a_{2k}\sum _{i=0}^{j}B_{k,i,j-i}+b_{2k-2} A_{k-1,j},\\ \beta _{2,k,j}=\,&a_{2k+1}\sum _{i=0}^{j}{\overline{B}}_{k,i,j-i}+b_{2k+1} {\overline{A}}_{k,j}. \end{aligned}\end{aligned}$$

Denote

$$\begin{aligned} \begin{aligned} \overrightarrow{\xi }_1:=&\left( A_{0},A_{1},\cdots ,A_{\frac{n}{2}}\right) ,\quad \overrightarrow{\xi }_2:=\left( B_{0},B_{1},\cdots ,B_{\frac{n-2}{2}}\right) ,\\ \overrightarrow{\xi }_3:=&\left( C_{0},C_{1},\cdots ,C_{\frac{n-2}{2}}\right) ,~ \overrightarrow{\xi }_4:=\left( D_{0},D_{1},\cdots ,D_{\frac{n-2}{2}}\right) ,\\ \overrightarrow{\eta }_1:=&\left( a_{0},a_{2},\cdots ,a_{n}\right) ,\qquad \overrightarrow{\eta }_2:=\left( a_{1},a_{3},\cdots ,a_{n-1}\right) ,\\ \overrightarrow{\eta }_3:=&\left( b_{0},b_{2},\cdots ,b_{n-2}\right) ,~~~~ \overrightarrow{\eta }_4:=\left( b_{1},b_{3},\cdots ,b_{n-1}\right) .\\ \end{aligned}\end{aligned}$$

Then we have that

$$\begin{aligned} \begin{aligned} \frac{\partial (\overrightarrow{\xi }_1,\overrightarrow{\xi }_2,\overrightarrow{\xi }_3,\overrightarrow{\xi }_4)}{\partial (\overrightarrow{\eta }_1,\overrightarrow{\eta }_2,\overrightarrow{\eta }_3,\overrightarrow{\eta }_4)} =&\begin{pmatrix} \frac{\partial \left( \overrightarrow{\xi }_1,\overrightarrow{\xi }_2\right) }{\partial \left( \overrightarrow{\eta }_1,\overrightarrow{\eta }_2\right) }& 0_{(n+1)\times n}\\ \frac{\partial \left( \overrightarrow{\xi }_3,\overrightarrow{\xi }_4\right) }{\partial \left( \overrightarrow{\eta }_1,\overrightarrow{\eta }_2\right) }& \frac{\partial \left( \overrightarrow{\xi }_3,\overrightarrow{\xi }_4\right) }{\partial \left( \overrightarrow{\eta }_3,\overrightarrow{\eta }_4\right) }\\ \end{pmatrix}, \end{aligned} \\ \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \frac{\partial \left( \overrightarrow{\xi }_3,\overrightarrow{\xi }_4\right) }{\partial \left( \overrightarrow{\eta }_3,\overrightarrow{\eta }_4\right) } = \begin{pmatrix} A_{0,0}& A_{1,0}& \ldots & A_{\frac{n-2}{2},0}& 0& 0& \ldots & 0\\ 0& A_{1,1}& \ldots & A_{\frac{n-2}{2},1}& 0& 0& \ldots & 0\\ \vdots & \vdots & \ddots & \vdots & 0& 0& \ldots & 0\\ 0& 0& 0& A_{\frac{n-2}{2},\frac{n-2}{2}}& 0& 0& \ldots & 0\\ 0& 0& 0& 0& {\overline{A}}_{0,0}& {\overline{A}}_{1,0}& \ldots & {\overline{A}}_{\frac{n-2}{2},0}\\ 0& 0& 0& 0& 0& {\overline{A}}_{1,1}& \ldots & {\overline{A}}_{\frac{n-2}{2},1} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & 0 \\ 0& 0& 0& 0& 0& 0& \ldots & {\overline{A}}_{\frac{n-2}{2},\frac{n-2}{2}}\\ \end{pmatrix}, \end{aligned} \\ \end{aligned}$$

and $0_{(n+1)\times n}$ is the $(n+1)\times n$ null matrix. Hence, we have $\det \frac{\partial \left( \overrightarrow{\xi }_1,\overrightarrow{\xi }_2\right) }{\partial \left( \overrightarrow{\eta }_1,\overrightarrow{\eta }_2\right) } =2^{\frac{n}{2}}\prod _{k=0}^{\frac{n-2}{2}}2^{2k}$, and

$$\begin{aligned} \begin{aligned} \det \frac{\partial \left( \overrightarrow{\xi }_1,\overrightarrow{\xi }_2,\overrightarrow{\xi }_3,\overrightarrow{\xi }_4\right) }{\partial \left( \overrightarrow{\eta }_1,\overrightarrow{\eta }_2,\overrightarrow{\eta }_3,\overrightarrow{\eta }_4\right) } =&\det \frac{\partial \left( \overrightarrow{\xi }_1,\overrightarrow{\xi }_2\right) }{\partial \left( \overrightarrow{\eta }_1,\overrightarrow{\eta }_2\right) } \cdot \det \frac{\partial \left( \overrightarrow{\xi }_3,\overrightarrow{\xi }_4\right) }{\partial \left( \overrightarrow{\eta }_3,\overrightarrow{\eta }_4\right) }\\ =&2^{\frac{n}{2}}\prod _{k=0}^{\frac{n-2}{2}}2^{2k}A_{k,k}{\overline{A}}_{k,k}\ne 0, \end{aligned} \end{aligned}$$

which implies that the coefficients $A_i, B_i, C_i$, and $D_i$ are independent. The case that n is odd can be analyzed similarly. This ends the proof. $\square$

Denote by $h(u):=\left( u^2-1\right) /2^5$ the inverse function of u(h), $u\in (0,1)$. To use Lemmas 2.3 and 2.4, we rewrite the M(h) as in following Remark 3.4.

Remark 3.4

From Lemma 3.3, we have the following results:

• (i) For $u\in (0,1)$, $M(h(u))=M_1(u)+M_2(u)+M_3(u)$, where

  $$\begin{aligned} \begin{aligned} M_1(u)=\,&\alpha _1(h(u))\ln \frac{1+u}{1-u}, \\ M_2(u)=\,&\frac{\pi }{4}\beta _1(h(u))\left( 1-\sqrt{1 - u^2}\right) +\frac{{\rho _{-1,1}}\pi }{4}\left( \frac{1}{\sqrt{1 - u^2}}-1\right) ,\\ M_3(u)=\,&2\alpha _2(h(u))u+\frac{\pi }{8}\beta _2(h(u))u^2 +\sum _{k=1}^{n+1}\frac{\tau _{k-1}u^{k}}{1+u^2}. \end{aligned}\end{aligned}$$

• (ii) There exist the parameters $a_{i,j}^{\pm }$ and $b_{i,j}^{\pm }$ such that

  $$\begin{aligned} \begin{aligned} M(h(u))=\,&\sum _{k=0}^{\left[ \frac{n}{2}\right] }{\widetilde{A}}_{k}u^{2k}\ln \frac{1+u}{1-u} +\sum _{k=0}^{\left[ \frac{n-1}{2}\right] }{\widetilde{B}}_{k}u^{2k}\left( 1-\sqrt{1 - u^2}\right) \\&+\frac{u}{1+u^2}\sum _{k=0}^{n+1}{\widetilde{C}}_{k}u^{k} +\frac{{\rho _{-1,1}}\pi }{4}\left( \frac{1}{\sqrt{1 - u^2}}-1\right) , \end{aligned}\end{aligned}$$

  where

  $$\begin{aligned} \begin{aligned} {\widetilde{A}}_k:=\,&\sum _{j=k}^{\left[ \frac{n}{2}\right] }(-1)^{j-k}A_{j}\left( \begin{array}{c} j \\ k \\ \end{array} \right) 2^{-5j},\quad {\widetilde{B}}_k:=\sum _{j=k}^{\left[ \frac{n-1}{2}\right] }(-1)^{j-k}B_j\left( \begin{array}{c} j \\ k \\ \end{array} \right) 2^{-5j}, \end{aligned}\end{aligned}$$

  and the coefficients ${\widetilde{C}}_k$ are the linear functions of $C_{i}, D_{i},$ and $\tau _{i}$ given by Lemma 3.3(ii) and they are independent.

Lemma 3.5

For the system (1.11), we have $H(n)\le 2n+7$ for $n\ge 3$.

Proof

Suppose $n\ge 3$. Let $v=u^2$, ${\widetilde{M}}(v)=(1+v)M(h(\sqrt{v}))$, then ${\widetilde{M}}(v)$ and $M(h(\sqrt{v}))$ have the same number of zeros on (0, 1). According to (3.27), we know that $\deg \alpha _1(h)\le \left[ \frac{n}{2}\right]$, $\deg \alpha _2(h)\le \left[ \frac{n-1}{2}\right]$, $\deg \beta _1(h)\le \left[ \frac{n-1}{2}\right]$, and $\deg \beta _2(h)\le \left[ \frac{n-2}{2}\right]$. We use the notations $F^{\alpha _1}_{\left[ \frac{n}{2}\right] }(v)$, $F^{\alpha _2}_{\left[ \frac{n-1}{2}\right] }(u^{2})$, $F^{\beta _1}_{\left[ \frac{n-1}{2}\right] }(v)$, $F^{\beta _2}_{\left[ \frac{n-2}{2}\right] }(u^{2})$, and $F^{\tau }_{n+1}(u)$ for $\alpha _1(h(u))$, $\alpha _2(h(u))$, $\beta _1(h(u))$, $\beta _2(h(u))$, and $\sum \limits _{k=0}^{n}\tau _{k}u^{k+1}$, respectively. By Lemma 3.3 and Remark 3.4 (i), we have

$$\begin{aligned} \begin{aligned} {\widetilde{M}}(v)=\,&{\widetilde{M}}_1(v) +{\widetilde{M}}_2(v)+{\widetilde{M}}_3(u),\\ \end{aligned}\end{aligned}$$

where

$$\begin{aligned} \begin{aligned} {\widetilde{M}}_1(v)=\,&(1+v)F^{\alpha _1}_{\left[ \frac{n}{2}\right] }(v)\ln \frac{1+\sqrt{v}}{1-\sqrt{v}}, \quad \\ {\widetilde{M}}_2(v)=\,&\frac{\pi }{4}\frac{1-v^2}{(1-v)^{\frac{3}{2}}} \left( \rho _{-1,1}-F^{\beta _1}_{\left[ \frac{n-1}{2}\right] }(v)(1-v)\right) ,\\ {\widetilde{M}}_3(u)=\,&uF^{\tau }_{n+1}(u)+\left( 1+u^2\right) \left( \frac{\pi }{4}F^{\beta _1}_{\left[ \frac{n-1}{2}\right] }\left( u^{2}\right) +2uF^{\alpha _2}_{\left[ \frac{n-1}{2}\right] }\left( u^{2}\right) \right. \\&\left. +\frac{\pi }{8}F^{\beta _2}_{\left[ \frac{n-2}{2}\right] }\left( u^{2}\right) u^{2}-\frac{{\rho _{-1,1}}\pi }{4}\right) . \end{aligned}\end{aligned}$$

Then, by Lemma 2.4, we have

$$\begin{aligned} \begin{aligned} \frac{d^{n+3}}{du^{n+3}}{\widetilde{M}}(v)=\,&\frac{\sqrt{v}F_{\frac{n+1}{2}}(v)}{(1-v)^{n+3}} +\frac{F_{\frac{n+3}{2}+1}(v)}{(1-v)^{n+3+\frac{3}{2}}}\\ =\,&\frac{1}{(1-v)^{n+3+\frac{3}{2}}}\left( F_{\frac{n+3}{2}+1}(v)+\sqrt{v}(1-v)^{\frac{3}{2}}F_{\frac{n+1}{2}}(v)\right) \end{aligned}\end{aligned}$$

for n odd and

$$\begin{aligned} \begin{aligned} \frac{d^{n+3}}{du^{n+3}}{\widetilde{M}}(v)=\,&\frac{F_{\frac{n+2}{2}}(v)}{(1-v)^{n+3}} +\frac{\sqrt{v}F_{\frac{n+2}{2}+1}(v)}{(1-v)^{n+3+\frac{3}{2}}}\\ =\,&\frac{1}{(1-v)^{n+3+\frac{3}{2}}}\left( \sqrt{v}F_{\frac{n+2}{2}+1}(v)+(1-v)^{\frac{3}{2}}F_{\frac{n+2}{2}}(v)\right) \end{aligned}\end{aligned}$$

for n even, where $F_k(x)$ is the polynomial of x with degree k. Let $\frac{d^{n+3}}{du^{n+3}}{\widetilde{M}}(v)=0$, that is

$$\begin{aligned} \left\{ \begin{aligned}&F_{\frac{n+3}{2}+1}(v)=-\sqrt{v}(1-v)^{\frac{3}{2}}F_{\frac{n+1}{2}}(v),\quad ~ \text { { n} is odd}, \\&\sqrt{v}F_{\frac{n+2}{2}+1}(v)=-(1-v)^{\frac{3}{2}}F_{\frac{n+2}{2}}(v),\quad ~ \text { { n} is even}. \\ \end{aligned}\right. \end{aligned}$$

By squaring the above equations, we obtain that $\frac{d^{n+3}}{du^{n+3}}{\widetilde{M}}(v)$ has at most $n+5$ zeros, multiplicity taken into account. According to Rolle’s theorem and $M(h(0))=0$, M(h(u)) has at most $2n+7$ zeros on (0, 1) counted with multiplicities. This ends the proof. $\square$

For $u\in (0,1)$, denote

$$\begin{aligned}\begin{aligned} I_{1}(u):=1-\sqrt{1 - u^2},\qquad I_{2}(u):=\ln \frac{1+u}{1-u}, \end{aligned}\end{aligned}$$

then

$$\begin{aligned} \begin{aligned} I_{1}(u)=\frac{4}{\pi }(I_{0,1}(h(u))),\quad I_{2}(u)=I_{0,0}(h(u)). \end{aligned}\end{aligned}$$

(3.34)

Consider the complex domain $D:={\mathbb {C}}{\setminus } \{u\in {\mathbb {R}}\mid u\le -1~ \text {or} ~u\ge 1\}$. When $u\in \{u\in {\mathbb {R}}\mid u\le -1 ~ \text {or} ~ u\ge 1\}$, we denote by $I^{\pm }_{1}(u)$ and $I^{\pm }_{2}(u)$ the analytic continuations of $I_{1}(u)$ and $I_{2}(u)$ along an arc such that $Im (u)>0$ ($Im (u)<0$), respectively. For example, $I^{\pm }_{1}(u)$ are the analytic continuations of $I_{1}(u)$ in the region $D\cap \{u\in {\mathbb {C}} ~|~Im (u)>0 ~ (Im (u)<0)\}$, respectively. To determine the arguments of $I^{\pm }_{1}(u)$ in the region $\{u\in {\mathbb {R}}\mid u\le -1~ \text {or} ~u\ge 1\}$, we need to make an arc starting from the region $\{u\in {\mathbb {R}}\mid 0<u<1\}$ along the upper (lower) half complex plane to the region $\{u\in {\mathbb {R}}\mid u\le -1~ \text {or} ~u\ge 1\}$. Then we get the following conclusions of $I_{1}(u)$, $I_{2}(u)$, $I^{\pm }_{1}(u)$ and $I^{\pm }_{2}(u)$.

Lemma 3.6

For $I_{1}(u)$ and $I_{2}(u)$, we have the following results.

• (i) The functions $I_{1}(u)$ and $I_{2}(u)$ can be analytically extended to the complex domain $D={\mathbb {C}}{\setminus } \{u\in {\mathbb {R}}\mid u\le -1~ \text {or} ~u\ge 1\}$.

• (ii) The functions $I^{\pm }_{1}(u)$ satisfy

  $$\begin{aligned} I^{+}_{1}(u)-I^{-}_{1}(u)=\left\{ \begin{aligned} 2i\sqrt{ u^2-1}, ~~&\text {for }u\in (1,+\infty ), \\ -2i\sqrt{ u^2-1}, ~&\text {for }u\in (-\infty ,-1). \end{aligned}\right. \end{aligned}$$

• (iii) The functions $I^{\pm }_{2}(u)$ satisfy $~ I^{+}_{2}(u)-I^{-}_{2}(u)=2\pi i ~$ for $u\in (-\infty ,-1)\cup (1,+\infty )$.

Proof

Note that $I^{\pm }_{1}(u)$ are both analytic continuation of $I_{1}(u)$. When $u\in (1, +\infty )$, $I^{\pm }_{1}(u)$ are not analytic at $u=1$, then we have

$$\begin{aligned}\begin{aligned} I^{+}_{1}(u)-I^{-}_{1}(u)=\,&-\sqrt{1 + u}|1 - u|^{\frac{1}{2}}e^{-i\frac{\pi }{2}}+\sqrt{1 + u}|1 - u|^{\frac{1}{2}}e^{i\frac{\pi }{2}}\\ =\,&2i\sqrt{ u^2-1}. \end{aligned}\end{aligned}$$

By the same method, when $u\in (-\infty , -1)$, $I^{\pm }_{1}(u)$ are not analytic at $u=-1$, then we have

$$\begin{aligned}\begin{aligned} I^{+}_{1}(u)-I^{-}_{1}(u)=\,&-\sqrt{1 - u}|1 + u|^{\frac{1}{2}}e^{i\frac{\pi }{2}}+\sqrt{1 - u}|1 + u|^{\frac{1}{2}}e^{-i\frac{\pi }{2}}\\ =\,&-2i\sqrt{ u^2-1}. \end{aligned}\end{aligned}$$

When $u\in (1, +\infty )$, we have

$$\begin{aligned}\begin{aligned} I^{+}_{2}(u)-I^{-}_{2}(u)=\,&(\ln (1+u)-\ln |1-u|+i\pi )\\ \,&-(\ln (1+u)-\ln |1-u|-i\pi )=2\pi i. \end{aligned}\end{aligned}$$

When $u\in (-\infty ,-1)$, we have

$$\begin{aligned}\begin{aligned} I^{+}_{2}(u)-I^{-}_{2}(u)=\,&(\ln |1+u|+i\pi -\ln (1-u))\\ \,&-(\ln |1+u|-i\pi -\ln (1-u))=2\pi i. \end{aligned}\end{aligned}$$

This ends the proof. $\square$

To get a lower bound for the number of zeros of M(h), we let

$$\begin{aligned}\begin{aligned} {\overline{M}}(u):=M(h(u))\varphi (u), \quad \varphi (u):=1-u^4, \quad \psi (u):=u(1-u^2), \end{aligned}\end{aligned}$$

then M(h(u)) and ${\overline{M}}(u)$ have the same number of zeros for $u\in (0,1)$.

Lemma 3.7

For $n\ge 3$, the generating functions of ${\overline{M}}(u)$ are the following $2n+4$ linearly independent functions for $u\in (0,1)$:

$$\begin{aligned} \begin{aligned}&I_{1}(u)\varphi (u), ~ u^2I_{1}(u)\varphi (u), ~ u^4I_{1}(u)\varphi (u), \ldots ,~ u^{2\left[ \frac{n-1}{2}\right] }I_{1}(u)\varphi (u), \\&I_{2}(u)\varphi (u), ~ u^2I_{2}(u)\varphi (u), ~ u^4I_{2}(u)\varphi (u), \ldots ,~ u^{2\left[ \frac{n}{2}\right] }I_{2}(u)\varphi (u), \\&\left( u^2-I_{1}(u)\right) \left( 1+u^2\right) , \quad \psi (u), ~ u\psi (u), ~ u^2\psi (u), \ldots ,~ u^{n+1}\psi (u). \\ \end{aligned}\end{aligned}$$

(3.35)

Moreover, there exists the system (1.11) such that its M(h(u)) has at least $2n+3$ simple zeros for $u\in (0,1)$, namely, $H(n)\ge 2n+3$.

Proof

Suppose that G(u) is a linear combination of the generating functions in (3.35), and

$$\begin{aligned} \begin{aligned} G(u):=\,&\sum _{k=0}^{\left[ \frac{n-1}{2}\right] }\bar{A}_{k}u^{2k}I_{1}(u)\varphi (u) +\sum _{k=0}^{\left[ \frac{n}{2}\right] }\bar{B}_{k}u^{2k}I_{2}(u)\varphi (u)\\&+\sum _{k=0}^{n+1}\bar{C}_{k}u^{k}\psi (u) +{\bar{\rho }}_{0}\left( u^2-I_{1}(u)\right) \left( 1+u^2\right) \equiv 0. ~~ \end{aligned}\end{aligned}$$

(3.36)

By Lemma 3.6, G(u) can be analytically extended to the complex domain D. When $u>1$, we have

$$\begin{aligned}\begin{aligned} G^{+}(u)-G^{-}(u)=\,&2i\sqrt{ u^2-1}\left( \sum _{k=0}^{\left[ \frac{n-1}{2}\right] }\bar{A}_{k}u^{2k}\varphi (u) -{\bar{\rho }}_0(1+u^2)\right) \\&+2\pi i \sum _{k=0}^{\left[ \frac{n}{2}\right] }\bar{B}_{k}u^{2k}\varphi (u)\equiv 0,~~ \end{aligned}\end{aligned}$$

which implies ${\bar{\rho }}_0=0$, $\bar{A}_{k}=0$ $\left( k=0,1, \ldots ,\left[ \frac{n-1}{2}\right] \right)$ and $\bar{B}_{k}=0$ $\left( k=0,1, \ldots ,\left[ \frac{n}{2}\right] \right)$. Hence, $G(u)\equiv 0$ becomes

$$\begin{aligned}\sum _{k=0}^{n+1}\bar{C}_{k}u^{k}\psi (u)\equiv 0,\end{aligned}$$

which yields $\bar{C}_{k}=0$ $(k=0,1,\ldots , n+1)$. Therefore, the generating functions of ${\overline{M}}(u)$ are linearly independent.

By Lemma 2.3 and Remark 3.4 (ii), there exists the system (1.11) such that its M(h(u)) has at least $2n+3$ simple zeros for $u\in (0,1)$. The result $H(n)\ge 2n+3$ follows from Lemma 1.1. This ends the proof. $\square$

Lemma 3.8

For $n=0,1,2$, we have $H(n)= 2n+3$.

Proof

By the same method as Lemma 3.3 (i), for $n=2$, we have $hM(h)=\sum \limits _{i=1}^8{\tilde{a}}_ig_{i}(h)$, where

$$\begin{aligned} \begin{aligned} g_{1}(h)=\,&{hu(h)}/\left( {1+u^2(h)}\right) ,~~~~ g_{2}(h)=u(h)g_{1}(h), ~~~~ g_{4}(h)= \frac{1}{2}I_{0,1}(h)-I_{1,1}(h),\\ \bigl (g_{3}(h),&g_{5}(h), g_{6}(h),g_{7}(h), g_{8}(h)\bigr )=\bigl (hI_{1,1}, hI_{0,1},hI_{1,0},h^2I_{0,0}, hI_{0,0}\bigr ), \end{aligned}\end{aligned}$$

and

$$\begin{aligned} \begin{aligned} {\tilde{a}}_1=\,&\tau _{0}-\tau _{2},~~~ {\tilde{a}}_2=\tau _{1},~~~ {\tilde{a}}_3=\rho _{1,1}-\frac{3}{16}\rho _{-1,3},~~~ {\tilde{a}}_4=\frac{\rho _{-1,1}}{16},~~ {\tilde{a}}_5=\rho _{0,1}+\frac{3}{16}\rho _{-1,3}, ~~ \\ {\tilde{a}}_6=\,&\rho _{1,0}+\frac{\rho _{0,2}}{2^4}+\rho _{2,0} -\frac{1}{8}\rho _{-1,2}+\frac{1}{2}\tau _{2},~~ {\tilde{a}}_7=2\rho _{0,2}, ~~~ {\tilde{a}}_8=\rho _{0,0} +\frac{1}{8}\rho _{-1,2}. \end{aligned}\end{aligned}$$

(3.37)

We have $hM(h)\in \textrm{Span} ({\mathcal {F}}_{3-n})$, $n=0,1,2$, where

$$\begin{aligned}\begin{aligned} {\mathcal {F}}_1=\left[ g_{1},g_{2},\ldots ,g_{8}\right] (h),~~ {\mathcal {F}}_2=[ g_{1},g_{2},g_{4},g_{5},g_{6},g_{8}](h),~~ {\mathcal {F}}_3=[ g_{4}, g_{8}, g_{1}](h). \end{aligned}\end{aligned}$$

We shall prove that ${\mathcal {F}}_1$ is an ECT-system on $\left( -\frac{1}{2^5},0\right)$. Let $x=\sqrt{-h}\in \left( 0, 2^{-\frac{5}{2}}\right)$ and $W_{i}(h)=W[ g_{1},g_{2},\ldots ,g_{i}](h) (i=1,2,\ldots ,8)$. By calculations, we see that each of $W_{i}(h)$ is non-vanishing on $\left( -\frac{1}{2^5},0\right)$ for $i=1,2,3$.

For $i=4,\ldots ,8$, we get $W_{i}(h)=\xi _{i}(h)\Phi _i(x(h))$, where $\xi _{i}(h)$ for $i=4,5,6$ is non-vanishing, and $\xi _{i}(h)= m_i(h)\Phi _{i1}(h)$ with $m_i(h)$ non-vanishing for $i=7,8$, and

$$\begin{aligned} \Phi _4(x)=\,&-15 - 180 \sqrt{2} x - 1392 x^2 - 1344 \sqrt{2} x^3 + 4096 x^4, \\ \Phi _5(x)=\,&-15 - 240 \sqrt{2} x - 3040 x^2 - 10240 \sqrt{2} x^3 - 68352 x^4 \\&- 151552 \sqrt{2} x^5 - 229376 x^6 + 262144 \sqrt{2} x^7, \\ \Phi _6(x)=\,&5 + 80 \sqrt{2} x + 864 x^2 + 1024 \sqrt{2} x^3 - 11008 x^4 - 12288 \sqrt{2} x^5 \\&+ 131072 x^6 + 131072 \sqrt{2} x^7, \\ \Phi _7(h)=\,&\frac{\Phi _{72}(h)}{\Phi _{71}(h)} +\ln \frac{1 + u(h)}{1 - u(h)}, \qquad \Phi _8(h)=\frac{\Phi _{82}(h)}{\Phi _{81}(h)} +\ln \frac{1 + u(h)}{1 - u(h)},\\ \Phi _{71}(h)=\,&61440 h^3 u(h) \left( 21 + 1152 h + 19712 h^2 + 139264 h^3\right) , \\ \Phi _{72}(h)=\,&5 + 944 h + 89088 h^2 + 4096 \left( 143 + 3456 \sqrt{-2h}\right) h^3\\&+ 65536 \left( -1603 + 12032 \sqrt{-2h}\right) h^4, \\&+16777216 \left( -155 + 872 \sqrt{-2h}\right) h^5 + 67108864 \left( -255 + 1472 \sqrt{-2h}\right) h^6,\\ \Phi _{81}(h)=\,&245760 h^3 \left( 21 + 3036 h + 168192 h^2 + 4918272 h^3 + 79200256 h^4 + 530579456 h^5\right) , \\ \Phi _{82}(h)=\,&u(h) \left( 5 + 1152 h + 149504 h^2 + 12288 (-817 + 9216 \sqrt{-2h} \right) h^3 +\\&65536 \left( -21445 + 152576 \sqrt{-2h} \right) h^4 + 1048576 \left( -51923 + 343296 \sqrt{-2h} \right) h^5 \\&+ 167772160 \left( -6239 + 40064 \sqrt{-2h} \right) h^6 \\&+ 6442450944 \left( -1265 + 7872 \sqrt{-2h} \right) h^7\bigg ). \\ \end{aligned}$$

For $i=4,5,6$, by calculations, we know the resultant of $\Phi _i(x)$ and $\Phi ^{'}_i(x)$ is non-vanishing, which implies $\Phi _i(x)$ has no multiple zeros. By analysis the Sturm’s sequence of $\Phi _i(x)$, we know $\Phi _i(x)$ has no zero on $\left( 0, 2^{-\frac{5}{2}}\right)$ by Lemma 2.5. For $i=7$, since $\lim _{h\rightarrow -\frac{1}{2^5}+}\Phi _7(h)=0$ and

$$\begin{aligned}\Phi ^{'}_7(h)= \frac{301 x \left( -63 - 3600 h - 95488 h^2 - 929792 h^3\right) \left( x-2^{-\frac{5}{2}}\right) ^4}{15360 (-h)^{9/2} \left( 1 + 2^5 h\right) ^{5/2} \left( 21 + 480 h + 4352 h^2\right) ^2 }\Phi _6(x)<0, \end{aligned}$$

we obtain that $\Phi _7(h)$ is strictly decreasing and has no zero for $h\in \left( -\frac{1}{2^5},0\right)$.

Next, we will prove that $W_{8}(h)$ is non-vanishing on $\left( -\frac{1}{2^5},0\right)$. With the aid of Mathematica, we find that $\Phi _{81}(h)$ has a unique zero at $h_0\approx -0.0159034\in \left( -\frac{1}{2^5},0\right)$, and $W_8(h_0)=-9.31821\times 10^{36}<0$. We claim that $\Phi _8(h)$ is non-vanishing on $\left( -\frac{1}{2^5},h_0\right) \cup (h_0,0)$. In fact, we have

$$\begin{aligned}\begin{aligned} \Phi ^{'}_8(h)=\,&\frac{- \left( x-2^{-\frac{5}{2}}\right) ^4{\overline{\Phi }}_{81}(h){\overline{\Phi }}_{82}(x)}{240 x^8 \left( 1 + 2^5 h\right) ^{\frac{3}{2}} {\overline{\Phi }}_{83}^2(h)}, \\ \end{aligned}\end{aligned}$$

where

$$\begin{aligned} {\overline{\Phi }}_{81}(h)=\,&63 + 5760 h + 269376 h^2 + 6125568 h^3 + 54280192 h^4,\\ {\overline{\Phi }}_{82}(x)=\,&5 + 80 \sqrt{2} x + 352 x^2 - 7168 \sqrt{2} x^3 - 81664 x^4 + 167936 \sqrt{2} x^5 + 2670592 x^6 \\&- 5111808 \sqrt{2} x^7-62914560 x^8 + 20971520 \sqrt{2} x^9 + 536870912 x^{10} \\&+536870912 \sqrt{2} x^{11},\\ {\overline{\Phi }}_{83}(h)=\,&21 + 2364 h + 92544 h^2 + 1956864 h^3 + 16580608 h^4.\\ \end{aligned}$$

By calculation the Sturm’s sequence of ${\overline{\Phi }}_{81}(h)$ and ${\overline{\Phi }}_{82}(x(h))$, we know that they have 0,1 zeros on $\left( -\frac{1}{2^{5}},0\right)$, respectively. With the aid of Mathematica, ${\overline{\Phi }}_{82}(x(h))$ has a unique zero $h_*\approx -0.0134724\in (h_0,0)$, and $\Phi _8(h)$ has a negative local maximum at $h=h_*$, which implies $\Phi _8(h)$ is non-vanishing on $(h_0,0)$. Since $\Phi _8(h)$ is strictly increasing on $\left( -\frac{1}{2^{5}},h_0\right)$ and $\lim _{h\rightarrow -\frac{1}{2^5}+}\Phi _8(h)=0$, $\Phi _8(h)$ is also non-vanishing on $\left( -\frac{1}{2^{5}},h_0\right)$. Thus, we obtain $H(2)=7$.

We can similarly prove that the ordered set ${\mathcal {F}}_2$ is an ECT-system on $\left( -\frac{1}{2^{5}},0\right)$, and ${\mathcal {F}}_3$ is an ECT-system with accuracy 1 on $\left( -\frac{1}{2^{5}},0\right)$. This ends the proof. $\square$

Theorem 1.2. follows from Lemmas 3.5, 3.7, and 3.8.