1 Introduction

Deformable elements such as microbeams, microplates, and microshells are the essential components of microelectromechanical systems (MEMS) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Their widespread applications, for instance in microactuators, microswitches, microresonators, and microgyroscopes, have motivated a great deal of investigations [17,18,19,20,21,22,23,24]. The mechanical components of MEMS devices, i.e. microbeams [25, 26], microplates [27, 28], or microshells, usually undergo large deformations and exhibit strongly nonlinear behaviours. Hence, it is of significant importance to examine the nonlinear static and dynamic characteristics of these micromechanical elements as an initial step for developing accurate models for MEMS. Apart from their nonlinear behaviour, microelements display size-dependent behaviour, as reported experimentally [29,30,31]. Such behaviour can only be captured through use of higher-order continuum mechanics theories [18, 32,33,34,35,36,37,38]; the present study employs the modified couple stress theory (MCST) [39,40,41] to capture the size effects.

Fig. 1
figure 1

Schematic representation of a doubly curved microshell in an orthogonal curvilinear coordinate

Full size image

There are not many studies in the literature on the static and dynamic characteristics of microshells. For instance, the size-dependent dynamical stability of shear deformable functionally graded cylindrical microshells was examined by Sahmani et al. [42]. In another study, Lou et al. [43] investigated the buckling behaviour of an axially and radially loaded simply supported functionally graded microshell, while accounting for size effects based on the MCST. Beni et al. [44] contributed to the field by deriving the equations of motion of a functionally graded cylindrical shell making use of the MCST and studying the free vibrational characteristics of the system of simply supported boundary conditions. Mehralian and Beni [45] studied the torsional size-dependent buckling of cylindrical shells made of functionally graded materials employing the MCST; in particular, they studied the torsional buckling of clamped and simply supported cylindrical shells utilising the generalised differential quadrature method. Fadaee and co-investigators [46, 47] obtained the exact solution for the free vibration of moderately thick functionally graded doubly curved shallow shell panels.

All the aforementioned valuable studies examined either the linear free vibration or the buckling behaviour of cylindrical shells. The current study is the first to perform a nonlinear forced dynamic analysis on doubly curved microshells. More specifically, a reliable analytical model of the microshell is developed while accounting for geometric nonlinearities and size effects. The model, consisting of three coupled nonlinear partial differential equations (PDEs), is discretised into a high-dimensional set of ordinary differential equations (ODEs) and solved numerically via a continuation technique. Various bifurcation points in the resonant response are detected, and the effects of modal interactions and internal resonances are highlighted.

2 Model development for doubly curved microshells

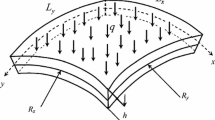
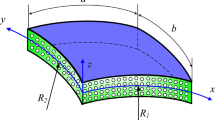
The doubly curved microshell under consideration, with a rectangular base, is depicted in Fig. 1. The motion of the microshell is defined within an orthogonal curvilinear coordinate system of \(x=R_x \psi _x \), \(y=R_y \psi _y \), and z, with \(\psi _x \) and \(\psi _y \) being the angular curvilinear coordinates and \(R_{x}\) and \(R_{y}\) being the principal curvature radii. w, u, and v denote the displacements of the microshell mid-plane in the z, x, and y directions, respectively. The microshell dimensions are denoted by h, i.e. the thickness of the microshell in the z direction, and a and b, i.e. the curvilinear sizes in the x and y directions, respectively. \(\psi _a \) and \(\psi _b \) denote the curvilinear angles and are equal to \(a/{R_x }\) and \(b/{R_y }\), respectively.

In the following, the kinetic and potential energies of the doubly curved microshell in are formulated utilising the MCST [39] and Donnell’s nonlinear shell theory [48]. To this end, first the displacement field of the shallow microshell, based on Donnell’s theory, is formulated as

$$\begin{aligned} U_x =-\frac{z}{R_x }\frac{\partial w}{\partial \psi _x }+u,\quad U_y =-\frac{z}{R_y }\frac{\partial w}{\partial \psi _y }+v,\quad U_z =w. \end{aligned}$$
(1)

The variation of the kinetic energy of the doubly curved microshell, with the mass density \(\rho \), can be formulated based on Donnell’s theory as

$$\begin{aligned} \delta K_\mathrm{E}= & {} \int _0^{\psi _a } \int _0^{\psi _b } \rho h\left[ \frac{\partial w}{\partial t}\delta \left( {\frac{\partial w}{\partial t}} \right) +\frac{\partial u}{\partial t}\delta \left( {\frac{\partial u}{\partial t}} \right) \right. \nonumber \\&\left. +\,\frac{\partial v}{\partial t}\delta \left( {\frac{\partial v}{\partial t}} \right) \right] R_x R_y \mathrm{d}\psi _x \mathrm{d}\psi _y . \end{aligned}$$
(2)

The virtual work of the damping can be written as

$$\begin{aligned} \delta W_\mathrm{D}= & {} -c\int _0^{\psi _a } {\int _0^{\psi _b } {\left( {\frac{\partial w}{\partial t}\delta w+\frac{\partial u}{\partial t}\delta u+\frac{\partial v}{\partial t}\delta v} \right) } } \nonumber \\&R_x R_y \mathrm{d}\psi _x \mathrm{d}\psi _y . \end{aligned}$$
(3)

The virtual work of time-dependent harmonic distributed pressure applied to the doubly curved microshell in the positive z direction can be expressed as

$$\begin{aligned} \delta W_\mathrm{P} =\int _0^{\psi _a } {\int _0^{\psi _b } {\left( {p_1 \cos \left( {\omega t} \right) \delta w} \right) R_x R_y \mathrm{d}\psi _x \mathrm{d}\psi _y } } . \end{aligned}$$
(4)

Based on the MCST [39], the strain energy of the system consists of classical terms, i.e. the stress and strain tensors denoted by \({\varvec{\sigma }}\) and \({\varvec{\varepsilon }}\), respectively, as well as non-classical higher-order terms, i.e. the deviatoric part of the symmetric couple stress tensor and the symmetric rotation gradient tensor shown by m and \({\varvec{\chi }}\), respectively. It is worth mentioning that for the sake of consistency with Donnell’s shell theory, the assumptions (\(1+z/R_{y})\approx 1\) and (\(1+z/R_{x})\,\,\,\ \approx 1\) are utilised in the final expressions for the strain and symmetric rotation gradient tensors.

In order to derive the components of \({\varvec{\chi }}\) in an orthogonal curvilinear coordinate, the transformation rules from Cartesian coordinate to curvilinear coordinates, as defined by Eringen [49], are utilised. Following the steps defined by Eringen [49], one can obtain the components of \({\varvec{\chi }}\) as

$$\begin{aligned} \chi _{xx}= & {} \frac{\partial ^{2}w}{R_x R_y \partial \psi _x \partial \psi _y }-\frac{1}{2R_x }\frac{\partial u}{R_y \partial \psi _y } \nonumber \\&\quad +\,\frac{1}{2}\left( {\frac{1}{R_x }-\frac{1}{R_y }} \right) \frac{\partial v}{R_x \partial \psi _x }, \nonumber \\ \chi _{yy}= & {} -\frac{\partial ^{2}w}{R_x R_y \partial \psi _x \partial \psi _y }+\frac{1}{2R_y }\frac{\partial v}{R_x \partial \psi _x } \nonumber \\&\quad +\,\frac{1}{2}\left( {\frac{1}{R_x }-\frac{1}{R_y }} \right) \frac{\partial u}{R_y \partial \psi _y }, \nonumber \\ \chi _{zz}= & {} \frac{1}{2R_y }\frac{\partial u}{R_y \partial \psi _y }-\frac{1}{2R_x }\frac{\partial v}{R_x \partial \psi _x }, \nonumber \\ \chi _{xy}= & {} \frac{1}{2}\left( {\frac{1}{2R_x }\frac{\partial u}{R_x \partial \psi _x }-\frac{\partial ^{2}w}{R_x^2 \partial \psi _x^2 }} \right) \nonumber \\&\quad -\,\frac{1}{2}\left( {\frac{1}{2R_y }\frac{\partial v}{R_y \partial \psi _y }-\frac{\partial ^{2}w}{R_y^2 \partial \psi _y^2 }} \right) , \nonumber \\ \chi _{xz}= & {} -\frac{1}{4}\left( {\frac{\partial ^{2}u}{R_x R_y \partial \psi _x \partial \psi _y }-\frac{\partial ^{2}v}{R_x^2 \partial \psi _x^2 }} \right) \nonumber \\&\quad +\,\frac{1}{4}\left( {\frac{1}{R_x }+\frac{1}{R_y }} \right) \frac{v}{R_y }-\frac{1}{2R_x }\frac{\partial w}{R_y \partial \psi _y }, \nonumber \\ \chi _{yz}= & {} -\frac{1}{4}\left( {\frac{\partial ^{2}u}{R_y^2 \partial \psi _y^2 }-\frac{\partial ^{2}v}{R_x R_y \partial \psi _x \partial \psi _y }} \right) \nonumber \\&\quad -\, \frac{1}{4}\left( {\frac{1}{R_x }+\frac{1}{R_y }} \right) \frac{u}{R_x }+\frac{1}{2R_y }\frac{\partial w}{R_x \partial \psi _x }, \end{aligned}$$
(5)

in which the assumptions (\(1+z/R_{y})\approx 1\) and (\(1+z/R_{x}) \quad \approx 1\) are made in the final expressions.

Having obtained the components of \({\varvec{\chi }}\), those of m can be derived as

$$\begin{aligned}&\left[ {m_{xx} ,m_{yy} ,m_{zz} ,m_{xy} ,m_{xz} ,m_{yz} } \right] =\frac{El^{2}}{1+\nu }\nonumber \\&\quad \left[ {\chi _{xx} ,\chi _{yy} ,\chi _{zz} ,\chi _{xy} ,\chi _{xz} ,\chi _{yz} } \right] , \end{aligned}$$
(6)

in which l is the material length-scale parameter, E is the Young’s modulus, and \(\nu \) is the Poisson’s ratio.

On the basis of Donnell’s nonlinear theory of shallow shells, the strain tensor components are given by

$$\begin{aligned} \begin{array}{l} \varepsilon _{xx} =\frac{w}{R_x }+\frac{\partial u}{R_x \partial \psi _x }+\frac{1}{2}\left( {\frac{\partial w}{R_x \partial \psi _x }} \right) ^{2}-z\frac{\partial ^{2}w}{R_x^2 \partial \psi _x^2 }, \\ \varepsilon _{yy} =\frac{w}{R_y }+\frac{\partial v}{R_y \partial \psi _y }+\frac{1}{2}\left( {\frac{\partial w}{R_y \partial \psi _y }} \right) ^{2}-z\frac{\partial ^{2}w}{R_y^2 \partial \psi _y^2 }, \\ \varepsilon _{xy} =\frac{1}{2}\left( {\frac{\partial v}{R_x \partial \psi _x }+\frac{\partial u}{R_y \partial \psi _y }} \right) +\frac{1}{2}\left( {\frac{\partial w}{R_y \partial \psi _y }\frac{\partial w}{R_x \partial \psi _x }} \right) \\ \qquad \quad -\,z\frac{\partial ^{2}w}{R_x R_y \partial \psi _x \partial \psi _y }. \\ \end{array} \end{aligned}$$
(7)

The corresponding stress tensor components can be obtained as

$$\begin{aligned} \left[ {\sigma _{xx} ,\sigma _{yy} ,\sigma _{xy} } \right]= & {} \frac{E}{1-\nu ^{2}}\left[ \left( {\varepsilon _{xx} +\nu \varepsilon _{yy} } \right) ,\right. \nonumber \\&\left. \left( {\varepsilon _{yy} +\nu \varepsilon _{xx} } \right) ,\left( {1-\nu } \right) \varepsilon _{xy} \right] , \end{aligned}$$
(8)

in which the plane stress condition is assumed.

Having obtained the components of \({\varvec{\sigma }}\), \({\varvec{\varepsilon }}\), m, and \({\varvec{\chi }}\), the strain energy of the microshell can be constructed employing the MCST [39]. In particular, based on Donnell’s shallow shell theory [48] and assuming (\(1+z/R_{y})\) and (\(1+z/R_{x}) \quad \approx 1\), the strain energy can be formulated as

$$\begin{aligned} \delta \varPi _\mathrm{E}= & {} \int _0^{\psi _a } \int _0^{\psi _b } \int _{-h/2}^{h/2} \Big [ m_{xx} \delta \chi _{xx} +m_{yy} \delta \chi _{yy}\nonumber \\&+\,m_{zz} \delta \chi _{zz} +2m_{xy} \delta \chi _{xy} +2m_{xz} \delta \chi _{xz} \nonumber \\&+\,2m_{yz} \delta \chi _{yz}+ \sigma _{xx} \delta \varepsilon _{xx} +\sigma _{yy} \delta \varepsilon _{yy} \nonumber \\&+\,2\sigma _{xy} \delta \varepsilon _{xy} \Big ] R_x R_y \mathrm{d}\psi _x \mathrm{d}\psi _y \mathrm{d}z. \end{aligned}$$
(9)

Employing generalised Hamilton’s principle, and utilising the following stress resultants

$$\begin{aligned} \begin{array}{l} \left[ {N_x ,N_y ,N_{xy} } \right] =\displaystyle \int \limits _{-\frac{h}{2}}^{\frac{h}{2}} {\left[ {\sigma _{xx} ,\sigma _{yy} ,\sigma _{xy} } \right] \mathrm{d}z} , \\ \left[ {M_x ,M_y ,M_{xy} } \right] =\displaystyle \int \limits _{-\frac{h}{2}}^{\frac{h}{2}} {\left[ {\sigma _{xx} ,\sigma _{yy} ,\sigma _{xy} } \right] z \mathrm{d}z} ,\\ \left[ {Y_x ,Y_y ,Y_z ,Y_{xy} ,Y_{xz} ,Y_{yz} } \right] \\ =\displaystyle \int \limits _{-\frac{h}{2}}^{\frac{h}{2}} {\left[ {m_{xx} ,m_{yy} ,m_{zz} ,m_{xy} ,m_{xz} ,m_{yz} } \right] \mathrm{d}z} , \\ \end{array} \end{aligned}$$
(10)

the doubly curved microshell equations of motion are derived as

$$\begin{aligned}&\rho h\frac{\partial ^{2}u}{\partial t^{2}}+c\frac{\partial u}{\partial t}-\frac{\partial N_x }{R_x \partial \psi _x }-\frac{\partial N_{xy} }{R_y \partial \psi _y } \nonumber \\&+\,\frac{1}{2R_x }\left( {\frac{\partial Y_x }{R_y \partial \psi _y }-\frac{\partial Y_{xy} }{R_x \partial \psi _x }} \right) -\frac{1}{2}\left( {\frac{1}{R_x }-\frac{1}{R_y }} \right) \nonumber \\&\times \frac{\partial Y_y }{R_y \partial \psi _y } -\frac{1}{2R_y }\frac{\partial Y_z }{R_y \partial \psi _y }-\,\frac{1}{2R_x }\left( {\frac{1}{R_x }+\frac{1}{R_y }} \right) Y_{yz} \nonumber \\&-\frac{1}{2}\frac{\partial }{R_y \partial \psi _y }\left( {\frac{\partial Y_{xz} }{R_x \partial \psi _x }+\frac{\partial Y_{yz} }{R_y \partial \psi _y }} \right) =0, \end{aligned}$$
(11)
$$\begin{aligned}&\rho h\frac{\partial ^{2}v}{\partial t^{2}}+c\frac{\partial v}{\partial t}-\frac{\partial N_{xy} }{R_x \partial \psi _x }-\frac{\partial N_y }{R_y \partial \psi _y } \nonumber \\&-\,\frac{1}{2R_y }\left( {\frac{\partial Y_y }{R_x \partial \psi _x }-\frac{\partial Y_{xy} }{R_y \partial \psi _y }} \right) -\frac{1}{2}\left( {\frac{1}{R_x }-\frac{1}{R_y }} \right) \nonumber \\&\times \frac{\partial Y_x }{R_x \partial \psi _x } +\frac{1}{2R_x }\frac{\partial Y_z }{R_x \partial \psi _x }+\,\frac{1}{2R_y }\left( {\frac{1}{R_x }+\frac{1}{R_y }} \right) Y_{xz} \nonumber \\&+\frac{1}{2}\frac{\partial }{R_x \partial \psi _x }\left( {\frac{\partial Y_{xz} }{R_x \partial \psi _x }+\frac{\partial Y_{yz} }{R_y \partial \psi _y }} \right) =0, \end{aligned}$$
(12)
$$\begin{aligned}&\rho h\frac{\partial ^{2}w}{\partial t^{2}}+c\frac{\partial w}{\partial t}+\frac{N_x }{R_x }+\frac{N_y }{R_y } \nonumber \\&-\left( {\frac{\partial ^{2}M_x }{R_x^2 \partial \psi _x^2 }+2\frac{\partial ^{2}M_{xy} }{R_x R_y \partial \psi _x \partial \psi _y }+\frac{\partial ^{2}M_y }{R_y^2 \partial \psi _y^2 }} \right) \nonumber \\&-\,p_1 \cos \left( {\omega t} \right) -\frac{\partial }{R_x \partial \psi _x }\left( {N_{xy} \frac{\partial w}{R_y \partial \psi _y }+N_x \frac{\partial w}{R_x \partial \psi _x }} \right) \nonumber \\&-\,\frac{\partial }{R_y \partial \psi _y }\left( {N_y \frac{\partial w}{R_y \partial \psi _y }+N_{xy} \frac{\partial w}{R_x \partial \psi _x }} \right) \nonumber \\&-\,\frac{\partial }{R_x \partial \psi _x }\left( {\frac{\partial Y_{xy} }{R_x \partial \psi _x }+\frac{\partial Y_y }{R_y \partial \psi _y }} \right) \nonumber \\&+\,\frac{\partial }{R_y \partial \psi _y }\left( {\frac{\partial Y_{xy} }{R_y \partial \psi _y }+\frac{\partial Y_x }{R_x \partial \psi _x }} \right) \nonumber \\&+\,\frac{1}{R_x }\frac{\partial Y_{xz} }{R_y \partial \psi _y }-\frac{1}{R_y }\frac{\partial Y_{yz} }{R_x \partial \psi _x }=0. \end{aligned}$$
(13)

Writing the stress resultants in Eqs. (11)–(13) in terms of the middle surface displacements, and utilising the notation \(x=R_x \psi _x \), \(y=R_y \psi _y \) for brevity, the expanded form of the equations of motion of the microshell is obtained as

$$\begin{aligned}&\rho h\frac{\partial ^{2}u}{\partial t^{2}}+c\frac{\partial u}{\partial t}-\frac{Eh}{1-\nu ^{2}} \left( \frac{\partial ^{2}u}{\partial x^{2}}+\frac{1}{R_x }\frac{\partial w}{\partial x}+\frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial w}{\partial x}\right. \nonumber \\&\quad \left. +\,\nu \frac{\partial ^{2}v}{\partial x\partial y}+\frac{\nu }{R_y }\frac{\partial w}{\partial x}+\nu \frac{\partial ^{2}w}{\partial x\partial y}\frac{\partial w}{\partial y} \right) -\frac{1}{2}\frac{Eh}{1+\nu }\nonumber \\&\quad \times \left( {\frac{\partial ^{2}u}{\partial y^{2}}+\frac{\partial ^{2}v}{\partial x\partial y}+\frac{\partial ^{2}w}{\partial y^{2}}\frac{\partial w}{\partial x}+\frac{\partial ^{2}w}{\partial x\partial y}\frac{\partial w}{\partial y}} \right) \nonumber \\&\quad +\,\frac{1}{8}\frac{Ehl^{2}}{1+\nu }\left[ {\left( {\frac{\partial ^{4}u}{\partial x^{2}\partial y^{2}}+\frac{\partial ^{4}u}{\partial y^{4}}-\frac{\partial ^{4}v}{\partial x^{3}\partial y}-\frac{\partial ^{4}v}{\partial x\partial y^{3}}} \right) } \right. \nonumber \\&\quad -\,\frac{1}{R_x^2 }\frac{\partial ^{2}u}{\partial x^{2}}+\left( {\frac{1}{R_x^2 }-\frac{3}{R_x R_y }+\frac{1}{R_y^2 }} \right) \frac{\partial ^{2}v}{\partial x\partial y}\nonumber \\&\quad -\left( {\frac{2}{R_x^2 }-\frac{6}{R_x R_y }+\frac{4}{R_y^2 }} \right) \frac{\partial ^{2}u}{\partial y^{2}}+\left( {\frac{1}{R_x^2 }+\frac{2}{R_x R_y }+\frac{1}{R_y^2 }} \right) \nonumber \\&\quad \left. \times \frac{u}{R_x^2 } \right] -\frac{1}{4}\frac{Ehl^{2}}{1+\nu }\left[ \frac{1}{R_x R_y }\left( {\frac{1}{R_x }+\frac{1}{R_y }} \right) \frac{\partial w}{\partial x}\right. \nonumber \\&\quad \left. -\,\frac{1}{R_x}\frac{\partial ^{3}w}{\partial x^{3}}-\left( {\frac{4}{R_x }-\frac{3}{R_y }} \right) \frac{\partial ^{3}w}{\partial x\partial y^{2}} \right] =0, \end{aligned}$$
(14)
$$\begin{aligned}&\rho h\frac{\partial ^{2}v}{\partial t^{2}}+c\frac{\partial v}{\partial t}-\frac{Eh}{1-\nu ^{2}} \left( \frac{\partial ^{2}v}{\partial y^{2}}+\frac{1}{R_y }\frac{\partial w}{\partial y}+\frac{\partial ^{2}w}{\partial y^{2}}\frac{\partial w}{\partial y}\right. \nonumber \\&\quad \left. +\,\nu \frac{\partial ^{2}u}{\partial x\partial y}+\frac{\nu }{R_x }\frac{\partial w}{\partial y}+\nu \frac{\partial ^{2}w}{\partial x\partial y}\frac{\partial w}{\partial x}\right) -\frac{1}{2}\frac{Eh}{1+\nu }\nonumber \\&\quad \times \left( {\frac{\partial ^{2}v}{\partial x^{2}}+\frac{\partial ^{2}u}{\partial x\partial y}+\frac{\partial ^{2}w}{\partial x\partial y}\frac{\partial w}{\partial x}+\frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial w}{\partial y}} \right) \nonumber \\&\quad +\,\frac{1}{8}\frac{Ehl^{2}}{1+\nu }\left[ \left( {\frac{\partial ^{4}v}{\partial x^{4}}+\frac{\partial ^{4}v}{\partial x^{2}\partial y^{2}}-\frac{\partial ^{4}u}{\partial x^{3}\partial y}-\frac{\partial ^{4}u}{\partial x\partial y^{3}}} \right) \right. \nonumber \\&\quad \left. -\,\frac{1}{R_y^2 }\frac{\partial ^{2}v}{\partial y^{2}}+\left( {\frac{1}{R_x^2 }-\frac{3}{R_x R_y }+\frac{1}{R_y^2 }} \right) \frac{\partial ^{2}u}{\partial x\partial y} \right. \nonumber \\&\quad -\,\left( {\frac{4}{R_x^2 }-\frac{6}{R_x R_y }+\frac{2}{R_y^2 }} \right) \frac{\partial ^{2}v}{\partial x^{2}}+\left( {\frac{1}{R_x^2 }+\frac{2}{R_x R_y }+\frac{1}{R_y^2 }} \right) \nonumber \\&\quad \left. \times \frac{v}{R_y^2 } \right] -\frac{1}{4}\frac{Ehl^{2}}{1+\nu }\left[ \frac{1}{R_x R_y }\left( {\frac{1}{R_x }+\frac{1}{R_y }} \right) \frac{\partial w}{\partial y}\right. \nonumber \\&\quad \left. -\,\frac{1}{R_y }\frac{\partial ^{3}w}{\partial y^{3}}-\left( {\frac{4}{R_y }-\frac{3}{R_x }} \right) \frac{\partial ^{3}w}{\partial x^{2}\partial y} \right] =0 \end{aligned}$$
(15)
$$\begin{aligned}&\rho h\frac{{{\partial ^2}w}}{{\partial {t^2}}} + c\frac{{\partial w}}{{\partial t}} - {p_1}\cos \left( {\omega t} \right) + \left( {\frac{1}{{12}}\frac{{E{h^3}}}{{1 - {\nu ^2}}} + \frac{1}{2}\frac{{Eh{l^2}}}{{1 + \nu }}} \right) \nonumber \\&\quad \times \left( {\frac{{{\partial ^4}w}}{{\partial {x^4}}} + 2\frac{{{\partial ^4}w}}{{\partial {x^2}\partial {y^2}}} + \frac{{{\partial ^4}w}}{{\partial {y^4}}}} \right) \nonumber \\&\quad +\, \frac{{Eh}}{{1 - {\nu ^2}}}\left[ \left( {\frac{1}{{R_x^2}} + \frac{{2\nu }}{{{R_x}{R_y}}} + \frac{1}{{R_y^2}}} \right) w\right. \nonumber \\&\quad +\, \left( {\frac{1}{{{R_x}}} + \frac{\nu }{{{R_y}}}} \right) \frac{{\partial u}}{{\partial x}} + \left( {\frac{1}{{{R_y}}} + \frac{\nu }{{{R_x}}}} \right) \frac{{\partial v}}{{\partial y}} \nonumber \\&\quad \left. -\, \frac{1}{2}\left( {\frac{1}{{{R_x}}} + \frac{\nu }{{{R_y}}}} \right) {\left( {\frac{{\partial w}}{{\partial x}}} \right) ^2}- \,\frac{1}{2}\left( {\frac{\nu }{{{R_x}}} + \frac{1}{{{R_y}}}} \right) {\left( {\frac{{\partial w}}{{\partial y}}} \right) ^2} \right] \nonumber \\&\quad -\, \frac{{Eh}}{{1 - {\nu ^2}}}\left[ {\frac{{{\partial ^2}w}}{{\partial {x^2}}}\frac{{\partial u}}{{\partial x}} + \nu \frac{{{\partial ^2}w}}{{\partial {x^2}}}\frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial x}}\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \nu \frac{{\partial w}}{{\partial x}}\frac{{{\partial ^2}v}}{{\partial x\partial y}}} \right. \nonumber \\&\quad +\, \frac{{{\partial ^2}w}}{{\partial {y^2}}}\frac{{\partial v}}{{\partial y}} + \nu \frac{{{\partial ^2}w}}{{\partial {y^2}}}\frac{{\partial u}}{{\partial x}}+ \frac{{\partial w}}{{\partial y}}\frac{{{\partial ^2}v}}{{\partial {y^2}}} + \nu \frac{{\partial w}}{{\partial y}}\frac{{{\partial ^2}u}}{{\partial x\partial y}}\nonumber \\&\quad +\, w\frac{{{\partial ^2}w}}{{\partial {x^2}}}\left( {\frac{1}{{{R_x}}} + \frac{\nu }{{{R_y}}}} \right) + w\frac{{{\partial ^2}w}}{{\partial {y^2}}}\left( {\frac{\nu }{{{R_x}}} + \frac{1}{{{R_y}}}} \right) \nonumber \\&\quad +\, \frac{3}{2}\frac{{{\partial ^2}w}}{{\partial {x^2}}}{\left( {\frac{{\partial w}}{{\partial x}}} \right) ^2} + \frac{3}{2}\frac{{{\partial ^2}w}}{{\partial {y^2}}}{\left( {\frac{{\partial w}}{{\partial y}}} \right) ^2} + \frac{\nu }{2}\frac{{{\partial ^2}w}}{{\partial {x^2}}}{\left( {\frac{{\partial w}}{{\partial y}}} \right) ^2}\nonumber \\&\quad \left. + \,\frac{\nu }{2}\frac{{{\partial ^2}w}}{{\partial {y^2}}}{\left( {\frac{{\partial w}}{{\partial x}}} \right) ^2} + 2\nu \frac{{\partial w}}{{\partial x}}\frac{{{\partial ^2}w}}{{\partial x\partial y}}\frac{{\partial w}}{{\partial y}} \right] \nonumber \\&\quad - \,\frac{{Eh}}{{1 + \nu }}\left[ \frac{{\partial u}}{{\partial y}}\frac{{{\partial ^2}w}}{{\partial x\partial y}} + \frac{1}{2}\frac{{\partial w}}{{\partial x}}\frac{{{\partial ^2}u}}{{\partial {y^2}}} + \frac{1}{2}\frac{{{\partial ^2}u}}{{\partial x\partial y}}\frac{{\partial w}}{{\partial y}}\right. \nonumber \\&\quad +\, \frac{1}{2}\frac{{{\partial ^2}v}}{{\partial x\partial y}}\frac{{\partial w}}{{\partial x}} + \frac{{\partial v}}{{\partial x}}\frac{{{\partial ^2}w}}{{\partial x\partial y}} + \frac{1}{2}\frac{{{\partial ^2}v}}{{\partial {x^2}}}\frac{{\partial w}}{{\partial y}}\nonumber \\&\quad \left. {+ \frac{1}{2}\frac{{{\partial ^2}w}}{{\partial {x^2}}}{{\left( {\frac{{\partial w}}{{\partial y}}} \right) }^2} + \frac{1}{2}\frac{{{\partial ^2}w}}{{\partial {y^2}}}{{\left( {\frac{{\partial w}}{{\partial x}}} \right) }^2} + 2\frac{{{\partial ^2}w}}{{\partial x\partial y}}\frac{{\partial w}}{{\partial x}}\frac{{\partial w}}{{\partial y}}} \right] \nonumber \\&\quad - \,\frac{{Eh{l^2}}}{{1 + \nu }}\left[ \left( {\frac{1}{{{R_x}}} - \frac{3}{{4{R_y}}}} \right) \frac{{{\partial ^3}u}}{{\partial x\partial {y^2}}} - \left( {\frac{3}{{4{R_x}}} - \frac{1}{{{R_y}}}} \right) \frac{{{\partial ^3}v}}{{\partial {x^2}\partial y}}\right. \nonumber \\&\quad +\, \frac{1}{4}\left( {\frac{1}{{{R_x}}}\frac{{{\partial ^3}u}}{{\partial {x^3}}} + \frac{1}{{{R_y}}}\frac{{{\partial ^3}v}}{{\partial {y^3}}}} \right) + \frac{1}{2}\left( {\frac{1}{{R_x^2}}\frac{{{\partial ^2}w}}{{\partial {y^2}}} + \frac{1}{{R_y^2}}\frac{{{\partial ^2}w}}{{\partial {x^2}}}} \right) \nonumber \\&\quad \left. -\,\frac{1}{{4{R_x}{R_y}}}\left( {\frac{1}{{{R_x}}} + \frac{1}{{{R_y}}}} \right) \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right) \right] = 0. \end{aligned}$$
(16)

In order to be able to solve these highly nonlinear PDEs, they need to be discretised into a set of nonlinear ODEs via a Galerkin method [50, 51]. To this end, the middle surface displacements of the microshell are written as series expansions, consisting of spatial functions and time-dependent ones. In particular, for the microshell under consideration in the present study, i.e. a fully clamped one with immovable edges, the displacements are defined as

$$\begin{aligned} \begin{array}{l} u(x,y,t)=\sum \limits _{i=1}^{S_u } {\sum \limits _{j=1}^{T_u } {\phi _i \left( {\frac{x}{a}} \right) \phi _j \left( {\frac{y}{b}} \right) } } u_{i,j} (t), \\ v(x,y,t)=\sum \limits _{i=1}^{S_v } {\sum \limits _{j=1}^{T_v } {\phi _i \left( {\frac{x}{a}} \right) \phi _j \left( {\frac{y}{b}} \right) } } v_{i,j} (t), \\ w(x,y,t)=\sum \limits _{i=1}^{S_w } {\sum \limits _{j=1}^{T_w } {\Psi _i \left( {\frac{x}{a}} \right) \Psi _j \left( {\frac{y}{b}} \right) w_{i,j} (t)} } , \\ \end{array} \end{aligned}$$
(17)

in which \(u_{i,j} (t)\), \(v_{i,j} (t)\), and \(w_{i,j} (t)\) are unknown time-dependent generalised coordinates \(\varphi _i \) and \(\Psi _i \) are given by

$$\begin{aligned} \phi _i \left( {\frac{x}{a}} \right)= & {} \sin \left( {\frac{i\pi x}{a}} \right) , \end{aligned}$$
(18)
$$\begin{aligned} \Psi _i \left( {\frac{x}{a}} \right)= & {} \cosh \left( {\frac{\theta _i x}{a}} \right) -\cos \left( {\frac{\theta _i x}{a}} \right) \nonumber \\&\quad -\,\alpha _i \left[ {\sinh \left( {\frac{\theta _i x}{a}} \right) -\sin \left( {\theta _i \frac{x}{a}} \right) } \right] , \end{aligned}$$
(19)

in which \(\alpha _i ={\left( {\cos \theta _i -\cosh \theta _i } \right) }/{\left( {\sin \theta _i -\sinh \theta _i } \right) }\) and \(\theta _i \) denotes the ith root of the frequency equation for a clamped-clamped beam; \(\phi _j \left( {y/b} \right) \) and \(\Psi _j \left( {y/b} \right) \) can be formulated in a similar fashion. The assumed spatial trial functions are consistent with the following boundary conditions of a fully clamped microshell with immovable edges

$$\begin{aligned} \begin{array}{l} u=v=w=0\, \hbox {at }x= 0, a\hbox { and }y=0, b \\ {\partial w}/{\partial x}=0,\, \hbox {at }x= 0, a, {\partial w}/{\partial y}=0, \, \hbox {at }y=0, b. \\ \end{array} \end{aligned}$$
(20)

Inserting the assumed displacements in Eq. (17) into the nonlinear equations of motion, i.e. Eqs. (14)–(16), and applying the two-dimensional Galerkin technique results in a set of nonlinear ODEs. This set of ODEs is solved utilising a continuation technique [52,53,54,55].

Fig. 2
figure 2

Nonlinear frequency–amplitude diagrams of the doubly curved microshell: the maximum amplitude of the generalised coordinates a \(w_{1,1}\), b \(w_{3,1}\), c \(w_{3,3}\), and d \(w_{5,1}\). \(R_{x}/a = 25.0\) and \(P_{1} =30.0\)

Full size image

3 Nonlinear resonant response

A nonlinear forced dynamic analysis is conducted in this section so as to construct the resonant frequency–amplitude diagrams of the system and to investigate the existence of any modal interactions. In order to ensure reliable results, a 38-degree-of-freedom (DOF) discretised model is examined by retaining 10 symmetric modes for the out-of-plane motion, i.e. \(w_{1,1}\), \(w_{3,1}\), \(w_{1,3}\), \(w_{5,1}\), \(w_{1,5}\), \(w_{3,3}\),\( w_{7,1}\), \(w_{1,7}\), \(w_{5,3}\), and\( w_{3,5}\), and 14 modes for each of the in-plane motions, i.e. \(u_{2,1}\),\( u_{2,3}\),\( u_{4,1}\), \(u_{2,5}\), \(u_{4,3}\), \(u_{6,1}\),\( u_{2,7}\), \(u_{4,5}\),\( u_{6,3}\), \(u_{8,1}\), \(u_{4,7}\),\( u_{6,5}\),\( u_{8,3}\), and\( u_{10,1}\) for the motion in the x direction and \(v_{1,2}\),\( v_{3,2}\), \(v_{1,4}\),\( v_{5,2}\), \(v_{3,4}\),\( v_{1,6}\), \(v_{7,2} \quad v_{5,4}\), \(v_{3,6}\), \(v_{1,8}\), \(v_{7,4}\), \(v_{5,6}\), \(v_{3,8}\), and \(v_{1,10}\) for the motion in the y direction. As we shall see in the numerical results, due to presence of strong modal interactions, it is essential to retain such a large number of modes in order to ensure reliable numerical results. Furthermore, the reason for retaining only the symmetric modes is the symmetric configuration of the microshell as well as the symmetric external out-of-plane harmonic pressurisation. This 38-DOF discretised model is solved numerically through use of a well-optimised continuation technique. Additionally, an eigenvalue analysis is performed in order to extract the natural frequencies of the doubly curved microshell and to determine the primary and secondary resonant regions.

Fig. 3
figure 3

Nonlinear frequency–amplitude diagrams of the doubly curved microshell: the maximum amplitude of the generalised coordinates a \(w_{1,1}\), b \(w_{3,1}\), c \(w_{3,3}\), and d \(w_{5,1}\). \(R_{x}/a = 10.0\) and \(P_{1}=55.0\)

Full size image

For the cases examined in this study, the microshell is assumed to be made of aluminium of mechanical properties: \(E=71\, \hbox {GPa}\), \(\nu =0.33\), and \(\rho =2770\, \hbox {kg/m}^{3}\). In this study, a spherical microshell is considered, i.e. of equal principal radii of curvature, and the microshell is assumed to have a square base, i.e. of equal curvilinear lengths in the x and y directions. The dimensions of the microshell are considered to be \(a= b =500\, \upmu \hbox {m}\) and \(h=3\, \upmu \hbox {m}\). According to the available experimental data for aluminium length-scale parameter [31], and the analytical formula in Ref. [56], the length scale of the aluminium, for the thickness of \(3 \,\upmu \hbox {m}\), can be calculated as \(1.0\, \upmu \hbox {m}\). For ease of computation, the following dimensionless quantities are used in the numerical simulations

$$\begin{aligned}&t^{*}=\frac{t}{a^{2}\sqrt{{\rho h}/D}}, \end{aligned}$$
(21)
$$\begin{aligned}&\Omega =\omega a^{2}\sqrt{{\rho h}/D}, \end{aligned}$$
(22)
$$\begin{aligned}&P_1 =\frac{p_1 a^{4}}{Dh} , \end{aligned}$$
(23)
$$\begin{aligned}&c_d =\frac{ca^{2}}{\sqrt{\rho hD}} , \end{aligned}$$
(24)
$$\begin{aligned}&\omega _{1,1} =\hat{{\omega }}_{1,1} a^{2}\sqrt{{\rho h}/D}, \end{aligned}$$
(25)

in which D is the microshell flexural rigidity, i.e. \({Eh^{3}}/{12(1-\nu ^{2})}\), and \(\hat{{\omega }}_{1,1} \) is the dimensional out-of-plane (1,1) natural frequency of the microshell. Additionally, in the numerical calculations, \(c_{d}\) is replaced by 2\(\zeta \omega \)\(_{1,1}\), with \(\zeta \) and \(\omega \)\(_{1,1}\) being the modal damping ratio and the dimensionless (1,1) natural frequency. \(\zeta \) is set to 0.005 for all the cases investigated in this study. Furthermore, for all the cases examined \(R_{x}= R_{y}\) since the system under consideration is a spherical microshell.

Fig. 4
figure 4

Nonlinear frequency–amplitude diagrams of the doubly curved microshell: the maximum amplitude of the generalised coordinates a \(w_{1,1}\), b \(w_{3,1}\), c \(w_{3,3}\), and d \(w_{5,1}\). \(R_{x}/a = 5.725\) and \(P_{1} =80.0\)

Full size image

The nonlinear frequency–amplitude diagrams of the doubly curved microshell are plotted in Fig. 2 when \(R_{x}/a = 25.0\) and \(P_{1}=30.0\). For this case, the fundamental natural frequency is equal to 53.19. As seen in sub-figure (a), the microshell exhibits a complex resonant response consisting of softening and hardening regions. In particular, the microshell displays four saddle-node (SD) bifurcations in the primary resonant region, while each of these bifurcations causes a jump to either a smaller-amplitude or larger-amplitude stable limit cycle. Comparison of sub-figure (a) and (b) shows that modal interactions occur between the (1,1) and (3,1) modes which causes an energy transfer in the vicinity of \(\Omega /{\omega }_{1,1}=1.02\) from the (1,1) mode to the (3,1) mode. This causes an extra peak in the response amplitude of the \(w_{3,1}\). Furthermore, a comparison of sub-figures (a) and (b) shows that the maximum amplitude of the \(w_{3,1}\) is almost 10% of that of \(w_{1,1}\).

The next figure, i.e. Fig. 3, shows the resonant frequency–amplitude response of the doubly curved microshell when \(R_{x}/a = 10.0\) and \(P_{1}=55.0\). For this case, \(\omega _{1,1}= 87.81\). Compared to the case of Fig. 2, here the principal radii of curvature are reduced and the time-dependent pressure amplitude is increased. First, it is visible that the resonant response of the microshell becomes more complicated as the principal radii of curvature are reduced, resulting in six bifurcation points in the resonant region. As seen, the microshell initially displays a strong softening-type nonlinear behaviour with two saddle-node bifurcations at points \(\hbox {SD}_{1}\) and \(\hbox {SD}_{2}\). By further increasing the excitation frequency ratio, a torus (TR) bifurcation occurs at point \(\hbox {TR}_{1}\) (\(\Omega /{\omega }_{1,1}=0.9708\)) which causes the microsystem to lose stability. The stability is regained when a secondary torus bifurcation occurs at point \(\hbox {TR}_{2}\) (\(\Omega /{\omega }_{1,1}= 0.9835\)). It is interesting to note that after the initial strong softening behaviour, another softening resonant region of smaller amplitude appears in the vicinity of \(\Omega /{\omega }_{1,1}= 1.0\). A comparison of sub-figures (a) and (b) reveals that the maximum response amplitude of the \(w_{3,1}\) is around 25% of that of \(w_{1,1}\). This shows that the due to decreased principal radii of curvature, the contribution of higher modes of oscillation becomes more significant.

Figure 4 shows the frequency–amplitude plots of the microshell of \(R_{x}/a = 5.725\) when \(P_{1}=80.0\). \(\omega \)\(_{1,1}\) for this case is calculated as 136.30. Compared to the previous cases, the new behaviour appearing here is the emergence of two new solution branches (showed by red in the magnified part) as a result of occurrence four period-doubling (PD) bifurcations. As seen, each of these solution branches bifurcate from the original solution branch at the point a period-doubling bifurcation until they reach another period-doubling bifurcation point on the original solution branch. Furthermore, each of these new branches loses stability via a torus bifurcation. Additionally, it is seen that a secondary resonant region appears in the vicinity of \(\Omega /{\omega }_{1,1} =1.45\), which is in fact the resonant region for mode (3,1). A comparison of primary resonant regions in sub-figures (a) and (b) shows that the maximum amplitude of the \(w_{3,1}\) is almost 40% of that of \(w_{1,1}\). This is more than the previous cases, which shows again that as the principal radii of curvature is reduced, the amplitudes of higher modes of vibration increase substantially. This proves the significance of employing a large number of modes in the discretised model when examining the behaviour of such systems.

Fig. 5
figure 5

Effect of principal radius of curvature on the frequency–amplitude diagrams of the doubly curved microshell: the maximum amplitude of the generalised coordinates a \(w_{1,1}\) and b \(w_{3,1}\). \(P_{1}=30.0\)

Full size image

The effect of the principal radii of curvature on the nonlinear frequency–amplitude diagrams of the microshell is illustrated in Fig. 5. As seen, due to decreased radius of curvature, the response of the system becomes of softening type. Furthermore, it is visible that the ratio max(\(w_{3,1})\)/max(\(w_{1,1})\) increases as the radius of curvature decreases.

Fig. 6
figure 6

Comparison between the resonant responses of the microshell predicted by the modified couple stress and classical theories: the maximum amplitude of the generalised coordinates (a) \(w_{1,1}\) and (b) \(w_{3,1}\). \(R_{x}/a = 25.0\) and \(P_{1} =30.0\)

Full size image

As mentioned at the beginning of this section, the length-scale parameter for the system under consideration is obtained as 1.0 \(\mu \hbox {m}\). In order to examine the effect of this parameter, a comparison is made between the frequency–amplitude diagrams of the system when this length scale is set to zero. It is worth mentioning that when the length-scale parameter is set to zero, the MCST becomes equivalent to the classical theory. Figure 6 illustrates the comparison of the resonant responses of the microshell (\(R_{x}/a = 25.0\) and \(P_{1}=30.0\)) obtained via the MCST (i.e. when \(l=1.0\, \upmu \hbox {m}\)) to that obtained based on the classical theory (i.e. when \(l=0\)). The MCST predicts \(\omega _{1,1}=53.19\), while the classical theory predicts \(\omega _{1,1}= 47.42\), i.e. with 11% difference. As a result, the classical theory predicts the resonant region at smaller excitation frequencies. Furthermore, it is seen that the classical theory predicts a much larger amplitude for \(w_{3,1}\) compared to the MCST. The comparison between the two theories for another case, i.e. when \(R_{x}/a = 10.0\) and \(P_{1}=55.0\), is depicted in Fig. 7. For this case, \(\omega _{1,1}\) predicted by MCST is 87.81, while that obtained by classical theory is 84.01, i.e. with 4% difference. Hence, this shows that due to decreased radius of curvature, the difference between the natural frequencies predicted by the two theories decreases. The comparison of frequency–amplitude curves shows that the classical theory predicts the resonant region at a slightly smaller excitation frequency. Furthermore, it is seen that the amplitude of the oscillation predicted by the MCST is more than that obtained via the classical theory.

Fig. 7
figure 7

Comparison between the resonant responses of the microshell predicted by the modified couple stress and classical theories: the maximum amplitude of the generalised coordinates a \(w_{1,1}\) and b \(w_{3,1}\). \(R_{x}/a = 10.0\) and \(P_{1} =55.0\)

Full size image

4 Conclusions

This study examined the nonlinear size-dependent dynamical characteristics of doubly curved microshells in the resonant region. The nonlinear equations of motion of the microshell nonlinear are developed in the framework of the MCST and on the basis of Donnell’s nonlinear shell theory. A high-dimensional Galerkin truncation scheme is utilised obtain the discretised form of the equations. Numerical simulations are conducted in order to obtain the nonlinear frequency–amplitude plots for various cases and to extract bifurcation points and the stability of the solution branches.

The nonlinear investigations showed that depending on the value of the principal radius of curvature, the nonlinear resonant behaviour changes significantly. In general, the following conclusions are drawn: (i) Due to decreased principal radii of curvature, the nonlinear response of the system becomes of softening type in the primary resonant region. (ii) As the principal radii of curvature are decreased, the contribution of higher modes of oscillation becomes more, and hence, the importance of employing a large-DOF discretised model becomes more significant. (iii) At smaller radii of curvature, the difference between MCST and classical theory in predicting the natural frequency becomes less significant. (iv) For the cases examined in this study, the MCST predicts larger oscillation amplitude compared to the classical theory.