1 Introduction

Microscale continuous elements can be found in a large class of electromechanical devices and engineering components. Among them, microbeams are present, for example in microactuators, biosensors, microswitches, and electrostatically excited microactuators (Azizi et al. 2013; Krylov et al. 2011; Li et al. 2008; Yu et al. 2012; Ghayesh et al. 2013c; Farokhi and Ghayesh 2015b; Ghayesh and Farokhi 2015; Gholipour et al. 2014; Farokhi and Ghayesh 2015a). The experimental investigations discovered that microbeams display size-dependent deformation behaviour; classical continuum theories cannot predict this behaviour. The necessity of taking into account size effects resulted in the advent of new continuum theories, namely the strain gradient and modified couple stress theories, so as to investigate the size-dependent deformation phenomenon.

The linear and nonlinear size-dependent motion of Euler–Bernoulli microbeams has been examined by several authors in the literature and is still of interest today (Farokhi et al. 2013a, b). Starting with the linear aspects, Kong et al. (2008) examined the size-dependent natural frequencies of an Euler–Bernoulli microbeam. Akgöz and Civalek (2011, 2013) investigated the free oscillations and buckling of a microbeam, based on both the strain gradient and modified couple stress theories, respectively. Asghari et al. (2010a) examined the size-dependent behaviour of functionally graded microbeams employing the modified couple stress theory. Şimşek (2010) analyzed the motion characteristics of an embedded microbeam under the action of a moving microparticle. These investigations were extended to nonlinear analyses, for example, by Ghayesh et al. (2013a, 2013d), who examined the size-dependent nonlinear behaviour of a microbeam on the basis of both the strain gradient and modified couple stress theories.

The literature review on the motion characteristics of Timoshenko microbeams can also be divided into linear and nonlinear models (Ghayesh et al. 2013b). Starting with the linear aspects, Ma et al. (2008) analyzed the size-dependent behaviour of a Timoshenko microbeam by means of the modified couple stress theory. Wang et al. (2010) examined the similar model based on the strain gradient elasticity theory. The bending and thermal postbuckling of a functionally graded Timoshenko microbeam were examined by Ansari et al. (2011, 2013) via the strain gradient theory. Nateghi and Salamat-talab (2013) examined the thermal effects on the size-dependent behaviour of functionally graded microbeams. These studies were extended and pursued for nonlinear models, for example, by Ramezani (2012) and Asghari et al. (2010b); they solved the equations of motion via the method of multiple scales and examined the nonlinear free oscillations of the system; these valuable studies were based on the approximate analytical techniques via a single-mode truncation.

All of the above-mentioned precious investigations studied the motion characteristics of perfectly straight microbeams. However, different internal or external imperfections in manufacturing process can cause an initial curvature (geometric imperfection) in the microbeam. Moreover, in MEMS applications, when the system is subject to parallel-plate electrostatic force, such as in a parallel-plate capacitor, an initial curvature is induced in the microbeam; moreover, in resonators, the dynamic behaviour of the system is influenced by both quadratic and cubic nonlinearities which are caused as a result of the initial curvature (electrostatic forces) and mid-plane stretching, respectively (Younis 2011); hence, taking into account an initial imperfection in the microbeam leads to a more accurate and practical model. As we shall see in this paper, this initial imperfection changes the motion characteristics of the system substantially, for some cases.

This paper, for the first time, examines the size-dependent dynamics of an initially slightly curved Timoshenko microbeam taking into account both the longitudinal and transverse motions as well as rotation. The microbeam under consideration is modelled as a high-dimensional system with 24 degrees of freedom—solving such a large model requires a huge amount of computations and hence necessitates the development of well-optimized computer codes. In particular, the pseudo-arclength continuation technique is utilized to solve the equations of motion numerically. A stability analysis is conducted via use of the Floquet theory. The frequency-response and force-response curves of the system are constructed for different cases. A comparison between the results associated with the modified couple stress and classical continuum theories is made.

2 Equations of motion and high-dimensional discretization

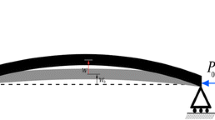
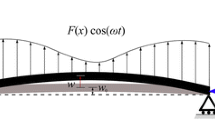
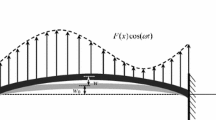
Depicted in Fig. 1 is an initially slightly curved Timoshenko microbeam. The length, cross-sectional area, and second moment of area of the microbeam are represented by L, A, and I, respectively; E and μ represent the Young’s modulus and the shear modulus, respectively. The microbeam is hinged at both ends and subjected to a distributed harmonic excitation load per unit length, \( F(x) \cos(\omega t) \), in the z direction. x and z, denotes the axial and transverse directions, respectively. The displacements in the x and z directions (i.e. the longitudinal and transverse displacements) are denoted by \( u(x,t) \) and \( w(x,t) \), respectively; \( \phi (x,t) \) is the rotation of the transverse normal.

Fig. 1
figure 1

Schematic representation of an imperfect Timoshenko microbeam subject to a transverse distributed harmonic excitation load

Full size image

The equations of motion are obtained employing the modified couple stress theory and by means of Hamilton’s principle, under the following assumptions: (1) the Timoshenko beam theory is employed taking into account the longitudinal displacement as well; (2) a uniform cross-sectional area is assumed along the entire length of the beam; (3) mid-plane stretching is the source of the geometric nonlinearity yielding the nonlinear strain–displacement relation; (4) there is a small initial curvature in the transverse direction denoted by \( w_{0} (x) \).

The strain energy of the system, based on the modified couple stress theory, is given by (Yang et al. 2002)

$$ U = \frac{1}{2}\int_{V} {\left[ {{{\varvec{\upsigma}} :\varvec{\upvarepsilon} +\mathbf{m}}:\varvec{\upchi}} \right]{\text{d}}v} {,} $$
(1)

where σ, ε, m, χ represent the stress, strain, deviatoric part of the symmetric couple stress, and the symmetric curvature tensors, respectively.

The symmetric curvature tensor χ is related to the rotation vector θ such that

$$ {\varvec{\upchi}} = \frac{1}{2}\left( {\nabla \varvec{\uptheta} + \left( {\nabla\varvec{\uptheta}}\right)^{T} } \right){,} $$
(2)

where the rotation vector θ itself is related to the displacement vector u by

$$ {\varvec{\uptheta}} = \frac{1}{2}\nabla \times {\mathbf{u}}{,} $$
(3)

with the following displacement field

$$ u_{x} = u(x,t) + z\phi (x,t),\quad u_{y} = 0,\quad u_{z}= w(x,t) + {w_0} (x), $$
(4)

where \( \phi (x,t) \) represents the rotation of the transverse normal and \( w_{0} (x) \) stands for the initial curvature of the microbeam associated with zero initial stresses.

Inserting Eq. (4) into Eq. (3), and substituting the resultant equation into Eq. (2) results in the following non-zero components of the symmetric curvature tensor

$$ {\upchi}_{xy} = {\chi}_{yx} = \frac{1}{4}\left( {\frac{\partial \phi }{\partial x} - \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right). $$
(5)

The stress tensor and the deviatoric part of the symmetric couple stress tensor can be written as

$$ {\varvec{\upsigma}} = \lambda \text{tr}({\varvec{\upvarepsilon}}){\mathbf{I}} + 2\mu {\varvec{\upvarepsilon}}, $$
(6)
$$ {\mathbf{m}} = 2 l^{2} \mu \varvec{\upchi}, $$
(7)

where λ and μ are the Lame constants, and l denotes the material length-scale parameter.

The nonlinear strain-displacement relations, associated with zero initial stresses, and the corresponding stresses for an initially slightly curved Timoshenko microbeam are given by

$$\begin{aligned} \varepsilon _{{xx}} &= \frac{{\partial u}}{{\partial x}} + \frac{{1}}{{2}}\left( {\frac{{\partial w}}{{\partial x}}} \right)^{{2}} + \frac{{\partial w}}{{\partial x}}\frac{{\text{d}}w_{{0}} }{{\text{d}}x} + z\frac{{\partial \phi }}{{\partial x}}, \\ \varepsilon _{{xz}} &= \varepsilon _{{zx}} = \frac{{1}}{{2}}\left( {\frac{{\partial w}}{{\partial x}} + \phi } \right), \end{aligned}$$
(8)
$$\begin{aligned} {\sigma _{xx}} &= E\left[ {\frac{{\partial u}}{{\partial x}} + \frac{1}{2}{{\left( {\frac{{\partial w}}{{\partial x}}} \right)}^2} + \frac{{\partial w}}{{\partial x}}\frac{{{\rm{d}}{w_0}}}{{{\rm{d}}x}} + z\frac{{\partial \phi }}{{\partial x}}} \right], \\{\sigma _{xz}} &= {\sigma _{zx}} = \mu {K_s}\left( {\frac{{\partial w}}{{\partial x}} + \phi } \right),\end{aligned}$$
(9)

where K s is the shear correction factor.

The size-dependent strain energy of the system can be obtained by substituting Eqs. (5) and (7)–(9) into Eq. (1) as follows

$$ \begin{aligned} U &= \frac{1}{2}EI\int_{0}^{L} {\left( {\frac{\partial \phi }{\partial x}} \right)}^{2} {\text{d}}x + \frac{1}{2}EA\int_{0}^{L} {\left[ {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial w}{\partial x}\frac{{\text{d}}w_{0} }{{\text{d}}x}} \right]}^{2} {\text{d}}x\\ & \quad + \frac{1}{2}\mu A\int_{0}^{L} {\left[ {K_{s} \left( {\frac{\partial w}{\partial x} + \phi } \right)^{2} + \frac{{l^{2} }}{4}\left( {\frac{\partial \phi }{\partial x} - \frac{{\partial^{2}}w}{{\partial x^{2} }}} \right)^{2} } \right]{\text{d}}x} \\ \end{aligned} $$
(10)

The kinetic energy of the system can be expressed as

$$ T = \frac{1}{2}\rho A\int_{0}^{L} {\left[ {\left( {\frac{\partial u}{\partial t}} \right)^{2} + \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right]} {\text{d}}x + \frac{1}{2}\rho I\int_{0}^{L} {\left( {\frac{\partial \phi }{\partial t}} \right)^{2} } {\text{d}}x{.} $$
(11)

The variations of the works done by the distributed harmonic excitation load and the viscous damping can be formulated as

$$ \delta W_{F} = \int_{0}^{L} {F(x)\cos (\omega t)} \delta w{\text{d}}x, $$
(12)
$$ \delta W_{D} = - c_{d} \int_{0}^{L} {\left( {\frac{\partial u}{\partial t}\delta u{ + }\frac{\partial w}{{\partial t}}{\delta w}} \right){\text{d}}x} - c_{r} \int_{0}^{L} {\left( {\frac{\partial \phi }{{\partial t}}\delta\phi } \right){\text{d}}x}{,} $$
(13)

where c d denotes the viscous damping coefficient of the longitudinal and transverse displacements and c r represents that of the rotation. Inserting Eqs. (10)–(13) into generalized Hamilton’s principle results in the following nonlinear equations of motion:

$$ \rho A\frac{{\partial^{2} u}}{{\partial t^{2} }} - EA\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} +\frac{{\text{d}}w_{0}} {{\text{d}}x}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial w}}{\partial x}\frac{{\text{d}}^{2} w_{0} }{{\text{d}}x^{2} }} \right) + c_{d} \frac{{\partial u}}{{\partial t}}{ = 0,} $$
(14)
$$ \begin{aligned} & \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} - EA\left[ {\frac{\partial u}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial x^{2} }}\frac{{\partial {\text{w}}}}{\partial x} + \frac{\partial u}{\partial x}\frac{{{\text{d}}^{2} w_{0} }}{{\text {d}x^{2} }} + \frac{{\partial^{2} u}}{{\partial x^{2} }}\frac{{{\text{d}}w_{0} }}{\text{d} x} + \frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{{{\text{d}}w_{0} }}{\text{d} x}} \right)^{2} } \right. \\ &\quad \quad \;\left. { + 2\frac{{\text{d}^{2} w_{0} }}{{\text{d} x^{2} }}\frac{{\text{d}}w_{0} }{\text{d} x}\frac{\partial w}{\partial x} + \frac{3}{2}\frac{{{\text{d}}^{2} w_{0} }}{{\text{d} x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} + 3\frac{{{\text{d}}w_{0} }}{\text{d} x}\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{\partial w}{\partial x} + \frac{3}{2}\frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right] \\ & \quad \quad \; - \mu AK_{s} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{\partial \phi }{\partial x}} \right) + \frac{{\mu Al^{2} }}{4}\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} - \frac{{\partial^{3} \phi }}{{\partial x^{3} }}} \right) - F(x)\cos(\omega t) + c_{d} \frac{\partial w}{\partial t} = 0, \\ \end{aligned} $$
(15)
$$ \rho I\frac{{\partial^{2} \phi }}{{\partial t^{2} }}-EI\frac{{\partial^{2} \phi }}{{\partial x^{2} }} + \mu AK_{s} \left( {\frac{\partial w}{\partial x} + \phi } \right) +\frac{{\mu Al^{2} }}{4}\left( {\frac{{\partial^{3} w}}{{\partial x^{3} }} - \frac{{\partial^{2} \phi }}{{\partial x^{2} }}} \right) + c_{r} \frac{\partial \phi }{\partial t} = 0, $$
(16)

with the following equations for the boundary conditions

$$ \left. {EA\left[ {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} { + }\frac{\partial w}{\partial x}\frac{{{\rm{d}}w_{0} }}{{\text{d}}x}} \right]\delta u} \right|_{0}^{L} { = 0,} $$
(17)
$$ \begin{aligned} &\left\{ {EA\left( {\frac{\partial w}{\partial x} +\frac{{\text{d}}w_{0} }{{\text{d}}x}} \right)\left[ {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial w}{\partial x}\frac{{{\text{d}}w_{0} }}{{\text{d}}x}} \right]} \right. \hfill \\ &\left. {\left. {\quad { + }\mu A\left[ {K_{s} \left( {\frac{\partial w}{\partial x} + \phi } \right) + \frac{{l}^{2} }{4}\left( {\frac{{\partial^{2} \phi }}{{\partial {x}^{2} }} - \frac{{\partial^{3} w}}{{\partial x^{3} }}} \right)} \right]} \right\}{\delta w}} \right|_{0}^{L} { = 0} \hfill \\ \end{aligned} $$
(18)
$$ \left. {\left[ {EI\frac{\partial \phi }{\partial x} + \frac{{\mu Al^{2} }}{4}\left( {\frac{\partial \phi }{\partial x} - \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} \right]\delta \phi } \right|_{0}^{L} { = 0,} $$
(19)
$$ \left. {\frac{{\mu Al^{2} }}{4}\left( {\frac{\partial \phi }{\partial x} - \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)\delta \left( {\frac{\partial w}{\partial x}} \right)} \right|_{0}^{L} = 0, $$
(20)

which can be further simplified for a hinged-hinged microbeam as

$$ \left. u \right|_{{x{ = 0}}} = \left. u \right|_{{x = L}} { = 0,} $$
(21)
$$ \left. w \right|_{{x{ = 0}}} = \left. w \right|_{{x = L}} { = 0,} $$
(22)
$$ \left. {\left\{ {EI\frac{\partial \phi }{\partial x} + \frac{{\mu A{l}^{2} }}{4}\left( {\frac{\partial \phi }{\partial x} - \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} \right\}} \right|_{x = 0,L} = 0 $$
(23)
$$ \left. {\frac{{\mu Al^{2} }}{4}\left( {\frac{\partial \phi }{\partial x} - \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} \right|_{x = 0,L} { = 0}{.} $$
(24)

Introducing the following dimensionless parameters

$$ \begin{aligned} x^{*} & = \frac{x}{L}, u^{*} = \frac{u}{L}, w^{*} = \frac{w}{L}, w_{0}^{*} = \frac{{w_{0} }}{L}, \\ \beta &= \sqrt {\frac{{EAL^{2} }}{EI}} , \alpha = \sqrt {\frac{{\mu AL^{2} }}{EI}} , t^{*} = t\sqrt {\frac{EI}{{\rho AL^{4} }}} ,\varOmega = \omega \sqrt {\frac{{\rho AL^{4} }}{EI}} , \\ c_{d}^{*} & = \frac{{c_{d} L^{4} }}{EI}\sqrt {\frac{EI}{{\rho AL^{4} }}} , c_{r}^{*} = \frac{{c_{r} AL^{4} }}{{EI^{2} }}\sqrt {\frac{EI}{{\rho AL^{4} }}} , \eta = \frac{l}{L},F^{*} = \frac{{FL^{3} }}{EI}, \hfill \\ \end{aligned} $$
(25)

substituting them into Eqs. (14)–(16), and dropping the asterisk notation for brevity gives the following nonlinear equations of motion for the longitudinal, transverse, and rotational motions, respectively

$$ \frac{{\partial^{2} u}}{{\partial t^{2} }} - \beta^{2} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} +\frac{{{\rm{d}}w_{0} }}{{\text{d}}x}\frac{{\partial^{2} w}}{{\partial x^{2} }} +\frac{\partial w}{\partial x}\frac{{{\text{d}}^{2} w_{0} }}{{\text{d}}x^{2} }} \right) + c_{d} \frac{\partial u}{\partial t}{ = 0,} $$
(26)
$$ \begin{aligned} & \frac{{\partial^{2} w}}{{\partial t^{2} }} - \beta^{2} \left[ {\frac{\partial u}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{\partial u}{\partial x}\frac{{\hbox{d}}^{2} w_{0} }{{\hbox{d}x^{2} }} + \frac{{\partial^{2} u}}{{\partial x^{2} }}\frac{\partial w}{\partial x} + \frac{{\partial^{2} u}}{{\partial x^{2} }}\frac{{\hbox{d}}w_{0} }{\hbox{d}x} + \frac{3}{2}\frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right. \\ & \quad \left. { + \frac{3}{2}\frac{{\hbox{d}}^{2} w_{0} }{{\hbox{d}x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{{\hbox{d}}w_{0} }{\hbox{d}x}} \right)^{2} + 2\frac{{\hbox{d}}^{2} {w}_{0} }{{\hbox{d}}x^{2} }\frac{{\hbox{d}}{w}_{0} }{\hbox{d}x}\frac{\partial w}{\partial x} + 3\frac{{\hbox{d}}{w}_{0} }{\hbox{d}x}\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{\partial w}{\partial x}} \right] \\ & \quad - \alpha^{2} K_{s} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{\partial \phi }{\partial x}} \right) + \frac{1}{4}\alpha^{2} \eta^{2} \left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} - \frac{{\partial^{3} \phi }}{{\partial x^{3} }}} \right) - F(x)\cos (\varOmega t) + c_{d} \frac{\partial w}{\partial t} = 0, \\ \end{aligned} $$
(27)
$$ \frac{{\partial^{2} \phi }}{{\partial t^{2} }} - \beta^{2} \frac{{\partial^{2} \phi }}{{\partial x^{2} }} + \alpha^{2} \beta^{2} K_{s} \left( {\frac{\partial w}{\partial x} + \phi } \right) + \frac{1}{4}\alpha^{2} \beta^{2} \eta^{2} \left( {\frac{{\partial^{3} w}}{{\partial x^{3} }} - \frac{{\partial^{2} \phi }}{{\partial x^{2} }}} \right) + c_{r} \frac{\partial \phi }{\partial t}{ = 0}{.} $$
(28)

A discretized model of the system is obtained by the application of the Galerkin method to the equations of motion. In other words, the nonlinear partial differential equations of motion are discretized into a set of nonlinear ordinary differential equations via the Galerkin scheme such that

$$ w(x{,}t) = \sum\limits_{{k{ = 1}}}^{M} {\varphi_{k} (x)q_{k} (t),} $$
(29)
$$ \phi (x{,}t) = \sum\limits_{{k{ = 1}}}^{N} {\psi_{k} (x)p_{k} (t),} $$
(30)
$$ u(x,t) = \sum\limits_{k = 1}^{Q} {\varphi_{k} (x)r_{k} (t),} $$
(31)

where φ k represents the kth eigenfunction for the transverse motion of a linear hinged-hinged beam and ψ k  = φ ′ k /(kπ); q k (t), p k (t), and r k (t) denote the kth generalized coordinates of the transverse, rotational, and longitudinal motions, respectively.

The application of the Galerkin scheme with F(x) = f 1 φ 1(x) and w 0(x) = A 0 φ 1(x) results in

$$ \begin{aligned} & \sum\limits_{{j{ = 1}}}^{Q} {\left( {\int_{0}^{1} {\varphi_i \varphi_j {\text{d}}x}} \right)} {\ddot{r}}_{j} - \beta^{2} \left[ {\sum\limits_{{j{ = 1}}}^{Q} {\left( {\int_{0}^{1} {\varphi_i \varphi_{j}^{{\prime \prime }} {\text{d}}x} } \right)} r_{j} + \sum\limits_{{j{ = 1}}}^{M} {\sum\limits_{{k{ = 1}}}^{M} {\left( {\int_{0}^{1} {{\varphi }_i {\varphi }_{j}^{{\prime }} {\varphi }_{k}^{{\prime \prime }} {\text{d}}x}} \right)q_{j} q_{k} } } } \right. \\ & \left. + {\sum\limits_{{j{ = 1}}}^{M} {\left( {\int_{0}^{1} {A_{0} \varphi_{1}^{{\prime }} \varphi_i {\varphi }_{j}^{{\prime \prime }} } } \right)q_{j} } + \sum\limits_{{j{ = 1}}}^{M} {\left( {\int_{0}^{1}{A_{0} {\varphi }_{1}^{{\prime \prime }} {\varphi }_i {\varphi }_{j}^{{\prime }} {\text{d}}x} } \right)q_{j} } } \right] + c_{d} \sum\limits_{{j{ = 1}}}^{Q} {\left( {\int_{0}^{1} {{\varphi }_i {\varphi }_{j} {\text{d}}x} } \right)} \dot{r}_{j} = 0,\quad i = 1, 2, \ldots, Q, \\ \end{aligned} $$
(32)
$$ \begin{aligned} & \sum\limits_{j = 1}^{M} {\left( {\int_{0}^{1} {\varphi_{i} \varphi_{j} \text{d}x} } \right)} \textit{\"{q}}_{j} - \beta^{2} \sum\limits_{j = 1}^{Q} {\sum\limits_{k = 1}^{M} {\left[ {\left( {\int_{0}^{1} {\varphi_{i} \varphi_{j}^{\prime } \varphi_{k}^{\prime \prime } {\text{d}}x} } \right) + \left( {\int_{0}^{1} {\varphi_{i} \varphi_{j}^{\prime \prime } \varphi_{k}^{\prime } {\text{d}}x} } \right)} \right]r_{j} q_{k} } } \\ & \quad - \beta^{2} \sum\limits_{j = 1}^{Q} {\left[ {\left( {\int_{0}^{1} {A_{0} \varphi_{1}^{\prime } \varphi_{i} \varphi_{j}^{\prime \prime } {\text{d}}x} } \right) + \left( {\int_{0}^{1} {A_{0} \varphi_{1}^{\prime \prime } \varphi_{i} \varphi_{j}^{\prime }{\text{d}}x} } \right)} \right]r_{j} } \\ & \quad - \beta^{2} \sum\limits_{j = 1}^{M} {\left[ {\left( {\int_{0}^{1} {\left( {A_{0} \varphi_{1}^{\prime } } \right)^{2} \varphi_{i} \varphi_{j}^{\prime \prime } {\text{d}}x} } \right) + 2\left( {\int_{0}^{1} {A_{0}^{2} \varphi_{1}^{\prime } \varphi_{1}^{\prime \prime } \varphi_{i} \varphi_{j}^{\prime }{\text{d}}x} } \right)} \right]q_{j} } \\ & \quad - \beta^{2} \sum\limits_{j = 1}^{M} {\sum\limits_{k = 1}^{M} {\left[ {\frac{3}{2}\left( {\int_{0}^{1} {A_{0} \varphi_{1}^{\prime \prime } \varphi_{i} \varphi_{j}^{\prime } \varphi_{k}^{\prime } {\text{d}}x} } \right) + 3\left( {\int_{0}^{1} {A_{0} \varphi_{1}^{\prime } \varphi_{i} \varphi_{j}^{\prime } \varphi_{k}^{\prime \prime } {\text{d}}x} } \right)} \right]q_{j} q_{k} } } \\ & \quad - \frac{3}{2}\beta^{2} \sum\limits_{j = 1}^{M} {\sum\limits_{k = 1}^{M} {\sum\limits_{l = 1}^{M} {\left( {\int_{0}^{1} {\varphi_{i} \varphi_{j}^{\prime } \varphi_{k}^{\prime } \varphi_{l}^{\prime \prime }{\text{d}}x} } \right)} q_{j} q_{k} q_{l} } } - \alpha^{2} K_{s} \sum\limits_{j = 1}^{M} {\left( {\int_{0}^{1} {\varphi_{i} \varphi_{j}^{\prime \prime }{\text{d}}x} } \right)} q_{j} \\ & \quad - \alpha^{2} K_{s} \sum\limits_{j = 1}^{N} {\left( {\int_{0}^{1} {\varphi_{i} \psi_{j}^{\prime }{\text{d}}x} } \right)} p_{j} + \frac{1}{4}\alpha^{2} \eta^{2} \left( {\sum\limits_{j = 1}^{M} {\left( {\int_{0}^{1} {\varphi_{i} \varphi_{j}^{\prime \prime \prime \prime }{\text{d}}x} } \right)} q_{j} - \sum\limits_{j = 1}^{N} {\left( {\int_{0}^{1} {\varphi_{i} \psi_{j}^{\prime \prime \prime} {\text{d}}x} } \right)} p_{j} } \right) \\ & \quad + c_{d} \sum\limits_{j = 1}^{M} {\left( {\int_{0}^{1} {\varphi_{i} \varphi_{j}{\text{d}}x} } \right)} \dot{q}_{j} - \int_{0}^{1} {f_{1} \phi_{1} \phi_{i}{\text{d}}x} \cos (\varOmega t) = 0,\quad i = 1,2,\ldots, M, \\ \end{aligned} $$
(33)
$$ \begin{aligned} & \sum\limits_{j = 1}^{N} {\left( {\int_{0}^{1} {\psi_{i} \psi_{j}{\text{d}}x} } \right)} \textit{\"{p}}_{j} - \beta^{2} \sum\limits_{j = 1}^{N} {\left( {\int_{0}^{1} {\psi_{i} \varphi_{j}^{{\prime \prime }}{\text{d}}x} } \right)} p_{j} \\ & \quad + \alpha^{2} \beta^{2} K_{s} \left( {\sum\limits_{j = 1}^{M} {\left( {\int_{0}^{1} {\psi_{i} \varphi_{j}^{{\prime }}{\text{d}}x} } \right)} q_{j} + \sum\limits_{j = 1}^{N} {\left( {\int_{0}^{1} {\psi_{i} \psi_{j}{\text{d}}x} } \right)} p_{j} } \right) \\ & \quad + \frac{1}{4}\alpha^{2} \beta^{2} \eta^{2} \left( {\sum\limits_{j = 1}^{M} {\left( {\int_{0}^{1} {\psi_{i} \varphi_{j}^{{{\prime \prime \prime }}}{\text{d}}x} } \right)} q_{j} - \sum\limits_{j = 1}^{N} {\left( {\int_{0}^{1} {\psi_{i} \psi_{j}^{{\prime \prime }}{\text{d}}x} } \right)} p_{j} } \right) \\ & \quad + c_{r} \sum\limits_{j = 1}^{N} {\left( {\int_{0}^{1} {\psi_{i} \psi_{j}{\text{d}}x} } \right)} \dot{p}_{j} = 0,\quad i = 1, 2, \ldots , N, \\ \end{aligned} $$
(34)

where the dot and prime notations represent the differentiations with respect to the dimensionless time and axial coordinate, respectively.

Equations (32)–(34) represent a set of M + N + Q second-order ordinary differential equations which are transformed into a new set of double-dimensional 2(M + N + Q) first-order nonlinear ordinary differential equations through use of a change of variables via \( x_{i} = \dot{q}_{i} \),\( y_{i} = \dot{p}_{i} \), and \( z_{i} = \dot{r}_{i} \). A high-dimensional system is selected in the present study by choosing M = N = Q = 16; due to symmetrical configuration of the system and the external forces, the dynamic response of the system is defined by only the symmetric modes (i.e. with odd subscripts for transverse and rotational motions and even subscripts for the longitudinal motion). As a result, the continuous system is truncated into a 24-degree-of-freedom system. An eigenvalue analysis (Ghayesh 2010, 2011) is conducted upon the linear terms of the discretized equations of motion to obtain the linear natural frequencies of the system. The pseudo-arclength continuation technique is employed to solve a set of 48 first-order nonlinear ordinary differential equations, consisting of both quadratic and cubic nonlinear terms, and to obtain the frequency-response and force-response curves of the system. A stability analysis is conducted via use of the Floquet theory; see Ref. (Argyris et al. 2015) for more detailed information of this theory.

3 Results

The numerical calculations are performed for an epoxy microbeam with the following mechanical properties: E = 1.44 GPa, μ = 521.7 MPa, ρ = 1220 kg/m3, and l = 17.6 μm. The shear correction factor, K s , is set to 5/6 throughout the numerical simulation (Ma et al. 2008).

The frequency-response curves under primary excitation are illustrated in Fig. 2 through a, b the maximum and minimum amplitudes of the first generalized coordinate of the transverse motion, respectively, and (c, d) those of the first generalized coordinate of the rotation, respectively. The numerical calculations are carried out for a microbeam with dimensions h = 2 l = 35.2 μm, L = 80 h, and b = 15 h, with the following dimensionless parameters: β = 277.128, α = 166.803, A 0 = 0.003, η = 0.00625, c d  = c r  = 0.05, and f 1 = 0.0075. As seen in this figure, the system displays a hardening behaviour; as shown in panel 2 (a), theoretically, the maximum amplitude of the stable periodic motion increases with increasing frequency of external excitation until point A (\( \varOmega = 1.1344\omega_{1} \)) is hit, where the stability is lost via a limit point bifurcation—the maximum amplitude of the q 1 motion at point A is equal to 0.00748. As the excitation frequency is decreased, theoretically, this now unstable solution branch decays until the next limit point bifurcation at point B (\( \varOmega = 1.0115\omega_{1} \)) is reached. Beyond that point, the amplitude of the stable response decreases with increasing excitation frequency. It is worthwhile noting that, as seen in panels (a) and (b), due to the initial curvature of the microbeam, the maximum and minimum amplitudes of the q 1 motion are not equal.

Fig. 2
figure 2

Frequency-response curves of the system: a, b the maximum and minimum amplitudes of the first generalized coordinate of the transverse motion, respectively. c, d the maximum and minimum amplitudes of the first generalized coordinate of the rotation, respectively; β = 277.128, α = 166.803, A 0 = 0.003, η = 0.00625, f 1 = 0.0075, and c d  = c r  = 0.05. Solid and dotted lines represent the stable and unstable solutions, respectively

Full size image

Selecting a higher value for the initial curvature (i.e. A 0 = 0.005) from A 0 = 0.003 in Fig. 2, a new set of frequency-response curves are obtained, shown in Fig. 3. As seen in this figure, as a result of increased amplitude of the initial curvature, the contribution of the quadratic nonlinear terms becomes dominant initially and the system displays a softening behaviour first and then tends to a hardening one. As shown in Fig. 3a, corresponding to the first generalized coordinate of the transverse motion, the maximum amplitude of q 1 motion increases until point A (\( \varOmega = 0.9890\omega_{1} \)) is reached, where the first limit point bifurcation occurs. The stability is regained at point B (\( \varOmega = 0.9799\omega_{1} \)) by means of the second limit point bifurcation. The amplitude of the stable periodic response increases with the excitation frequency until point C (\( \varOmega = 1.0138\omega_{1} \)) is hit, where the stability is lost via the third limit point bifurcation. This now unstable solution branch lasts until point D (\( \varOmega = 0.9837\omega_{1} \)) is hit, where the stability is regained once again via the forth limit point bifurcation. From comparison of Figs. 2 and 3, one can draw the conclusion that due to increased amplitude of the initial curvature, the number of limit point bifurcations increases to four and the system displays both softening and hardening behaviours.

Fig. 3
figure 3

Frequency-response curves of the system: a, b the maximum and minimum amplitudes of the first generalized coordinate of the transverse motion, respectively. c, d the maximum and minimum amplitudes of the first generalized coordinate of the rotation, respectively; β = 277.128, α = 166.803, A 0 = 0.005, η = 0.00625, f 1 = 0.0075, and c d  = c r  = 0.05. Solid and dotted lines represent the stable and unstable solutions, respectively

Full size image

Figure 4 illustrates a comparison between the results obtained via the modified couple stress and the classical continuum theories, in order to examine the effect of the length-scale parameter on the system response. As seen in this figure, as a result of taking into account the length-scale parameter both the initial softening and the latter hardening behaviours of the system decrease; the modified couple stress theory predicts a weaker nonlinear behaviour compared to the classical theory.

Fig. 4
figure 4

Comparison between the frequency-response curves of the system obtained via modified couple stress and classical continuum theories: a, b the first generalized coordinate of the transverse motion and rotation, respectively; β = 277.128, α = 166.803, A 0 = 0.004, f 1 = 0.007, and c d  = c r  = 0.05; η = 0.003125 for the modified couple stress theory and η = 0 for the classical theory. Solid and dotted lines represent the stable and unstable solutions, respectively

Full size image

Figure 5 shows the effect of the amplitude of the initial curvature, A 0, on the resonant response of the system. As seen in panel (a), due to increased amplitude of the initial curvature the initial softening behaviour becomes stronger which is due to the dominant effect of the quadratic nonlinear terms for higher A 0. As a result, the size-dependent nonlinear resonance occurs at lower excitation frequencies—for A 0 = 0.006, the nonlinear resonance occurs at an excitation frequency less than the first linear natural frequency of the transverse motion. Moreover, due to increased amplitude of the initial curvature, the maximum amplitude of the q 1 motion decreases while that of the p 1 motion increases slightly.

Fig. 5
figure 5

The effect of A 0 (the amplitude of the initial curvature) on the frequency-response curve of the system: a, b the first generalized coordinate of the transverse motion and rotation, respectively. The values of A 0 are denoted on the curves; β = 277.128, α = 166.803, η = 0.00625, f 1 = 0.0075, and c d  = c r  = 0.05. Solid and dotted lines represent the stable and unstable solutions, respectively

Full size image

The frequency-response curves of the system for various forcing amplitudes are depicted in Fig. 6. As shown in the figure, for lower forcing amplitudes, the dominant nonlinear behaviour of the system is a softening-type. However, it is seen that that for higher forcing amplitudes the initial softening behaviour is continued by a secondary hardening behaviour. Moreover, the entire response region becomes wider as a result of increased forcing amplitude.

Fig. 6
figure 6

The effect of the forcing amplitude, f 1, on the frequency-response curves of the system: a, b the first generalized coordinate of the transverse motion and rotation, respectively. The values of f 1 are denoted on the curves; β = 277.128, α = 166.803, A 0 = 0.005, η = 0.00625, and c d  = c r  = 0.05

Full size image

The force-response curves of the system are depicted in Fig. 7 through a, b the first generalized coordinate of the transverse motion and rotation, respectively. These curves are obtained by varying the forcing amplitude f 1 for a fixed excitation frequency. As seen in panel (a), the amplitude of the q 1 motion increases from zero with increasing forcing amplitude until point A (f 1 = 0.01664) is reached, where the motion becomes unstable via a limit point bifurcation. Decreasing the forcing amplitude, the amplitude of this now unstable branch increases until point B (f 1 = 0.00320) is hit where the second limit point bifurcation occurs.

Fig. 7
figure 7

Variation of the maximum amplitude of the first generalized coordinate of the transverse motion (a) and rotation (b) with increasing forcing amplitude; β = 277.128, α = 166.803, A0 = 0.003, η = 0.00625, Ω = 1.02 ω 1 , and c d  = c r  = 0.05. Solid and dotted lines represent the stable and unstable solutions, respectively

Full size image

The comparison between the force-response curves of the system obtained via the modified couple stress and the classical continuum theories is depicted in Fig. 8. It can be concluded that, the classical theory predicts the occurrence of the first limit point bifurcation at significantly higher forcing amplitude.

Fig. 8
figure 8

Comparison between the force-response curves of the system obtained via modified couple stress and classical continuum theories: a, b the first generalized coordinate of the transverse motion and rotation, respectively;β = 277.128, α = 166.803, A 0 = 0.003, Ω = 1.015 ω 1 , and c d  = c r  = 0.05; η = 0.003125 for the modified couple stress theory and η = 0 for the classical theory. Solid and dotted lines represent the stable and unstable solutions, respectively

Full size image

The force-response curves of the system for a higher value of the amplitude of the initial curvature (A 0 = 0.005) are shown in Fig. 9. As seen in this figure, the system displays more complex behaviour with four limit point bifurcations shown by A, B, C, and D, in the figure. In other words, the system displays a stable periodic response until point A (f 1 = 0.00650) is reached where the response becomes unstable; the stability is regained at point B via the second limit point bifurcation. As the forcing amplitude is increased form point B (f 1 = 0.00255) an initial stable periodic response up to point C (f 1 = 0.02696) occurs, which is continued by an unstable solution branch between points C and D. Beyond point D (f 1 = 0.00603), the amplitude of the stable periodic response increases with the forcing amplitude.

Fig. 9
figure 9

Variation of the maximum amplitude of the first generalized coordinate of the transverse motion (a) and rotation (b) with increasing forcing amplitude; β = 277.128, α = 166.803, A0 = 0.005, η = 0.00625, Ω = 0.99 ω 1 , and c d  = c r  = 0.05. Solid and dotted lines represent the stable and unstable solutions, respectively

Full size image

Figure 10 shows the force-response curves for various amplitudes of the initial curvature, A 0. It is seem that as a result of increased amplitude of the initial curvature, the entire response region becomes wider which increases the difference between the first and second limit point bifurcations. Moreover, the occurrences of the first and second limit point bifurcations are delayed to higher forcing amplitudes, due to increased A 0.

Fig. 10
figure 10

The effect of A 0 on the force-response curves of the system: (a, b) the first generalized coordinate of the transverse motion and rotation, respectively. The values of A 0 are denoted on the curves; β = 277.128, α = 166.803, η = 0.00625, Ω = 1.015 ω 1 , and c d  = c r  = 0.05. Solid and dotted lines represent the stable and unstable solutions, respectively

Full size image

4 Concluding remarks

The nonlinear motion characteristics of an imperfect Timoshenko microbeam have been examined numerically. The potential energy stored in the system was obtained on the basis of the modified couple stress theory. Hamilton’s principle was then utilized in order to obtain the nonlinear equations of motion for the longitudinal, transverse, and rotational motions. The equations of motion of the continuous system were discretized into a high-dimensional set of ordinary differential equations via the application of the Galerkin technique. The discretized equations of motion were solved by means of the pseudo-arclength continuation technique in order to obtain the resonant responses. A stability analysis was also conducted via use of the Floquet theory.

The numerical results for the frequency-response curves showed that for lower amplitudes of the initial curvature, the system displays a hardening behaviour while for higher values, the system displays both softening and hardening behaviours. Comparing the results obtained via the modified couple stress theory and classical theories showed that the modified couple stress theory predicts weaker softening and hardening nonlinear behaviours. It was shown that the secondary hardening behaviour occurs only at higher forcing amplitudes. The results for the force-response curves of the system showed that, there are two or four limit point bifurcations depending on the system parameters. It was also shown that the modified couple stress theory predicts a lower forcing amplitude for the first limit point bifurcation, compared to the classical continuum theory. Examining the effect of the amplitude of the initial imperfection on the force-response curves showed that the occurrences of both limit point bifurcations are shifted to higher forcing amplitudes as A 0 is increased.