Observer-based quantized sliding mode ${\varvec{\mathcal {H}}}_{\varvec{\infty }}$ control of Markov jump systems

Abstract

An adjustable quantized approach is adopted to treat the $\mathcal {H}_{\infty }$ sliding mode control of Markov jump systems with general transition probabilities. To solve this problem, an integral sliding mode surface is constructed by an observer with the quantized output measurement and a new bound is developed to bridge the relationship between system output and its quantization. Nonlinearities incurred by controller synthesis and general transition probabilities are handled by separation strategies. With the help of these measurements, linear matrix inequalities-based conditions are established to ensure the stochastic stability of the sliding motion and meet the required $\mathcal {H}_{\infty }$ performance level. An example of single-link robot arm system is simulated at last to demonstrate the validity.

1 Introduction

Recently, much research effort has been devoted into Markov jump systems (MJSs) due to theirs’ well prospective applications in economic systems, flight control systems and robot systems [1]. Transition probabilities (TPs) which dominate the system behavior in the jumping process, in most studies, are required to be known [2,3,4,5,6,7,8,9,10,11,12]. Unfortunately, it is impossible to get TPs precisely owing to environment factors, instrument errors and measure costs [13]. Hence, in the viewpoint of engineering, TPs allowed to be partial known are investigated in [14,15,16,17] by means of robust methodologies, Gaussian transition probability density function and Kronecker product technique, respectively.

Alternatively, sliding mode control (SMC) is an effective method to eliminate impact of uncertainty and has advantages of fast response and robustness [18, 19]. Regarding the sliding mode technique to cope with uncertain MJSs [20], proposes a linear matrix inequality solution to the existence of linear sliding surfaces. This result is extended by [21] where an integral sliding mode surface is developed for singular MJSs. In [22], a dynamic sliding surface relying on system states and inputs is developed for descriptor MJSs. Wei et al. [23] utilized a descriptor system setup to treat the sliding mode output control of semi-MJSs. Contrast to the above results with ideal TPs, [24] constructs an integral sliding mode control approach for stochastic MJSs with incomplete TPs. In this result, the sliding mode controller depends on the accessability of partly known TPs. Along this line, robust sliding mode synthesis of MJSs with time delay is addressed in [25] where TPs are known, uncertain but time varying, and unknown.

Noticeably, the above results are almost assumed that system outputs are transmitted via analog channels. To be consistent with digital channels in network environment, signal quantization is necessary [26]. Although the quantization could improve the transmission efficiency, it could cause nonlinearities which degenerate system performance or even destroy system stability [27,28,29,30,31]. Therefore, the investigation on MJSs with quantization has been conducted in [32,33,34,35]. To be specific [32], adopts the non-conservative sector bound approach to cope with the logarithmic quantized state feedback control of MJSs. Rasool and Nguang [33] treats the network delay as a finite state Markov process and utilizes a logarithmic quantization strategy to tackle the quantized robust $\mathcal {H}_\infty$ control problem. Via augmenting the quantization error into system vector [34], converts the quantized fault-tolerant control of MJSs into the sliding mode control of a description system. In contrast to above results with known TPs, quantized output $\mathcal {H}_\infty$ filtering of MJSs with known, uncertain and unknown TPs is built in [35]. While these quantized results have enriched the investigation on MJSs, the quantizer is nonuniform and requires infinite quantization levels around the equilibrium.

To propose a feasible solution, this paper is dedicated to the $\mathcal {H}_{\infty }$ sliding mode control of MJSs with adjustable quantized parameter. TPs cover known, uncertain and unknown. Based on the quantized system output, an observer-based integral sliding mode surface is developed and the relationship between system output and the quantized parameter is built by a technique lemma explicitly. Separation techniques are utilized to cope with the nonlinearities caused by controller synthesis and general TPs. A mode-dependent sliding mode controller is developed via the known TPs information to ensure the sliding reachability. Synthesis conditions for observer and controller gains with the required disturbance attenuation performance level $\gamma$ are solved in a unified framework. A single-link robot arm (SRA) system is simulated to show the validity of the proposed method.

The subsequent paper architecture is: some preliminaries are supplied in Sect. 2. In Sect. 3, an integral sliding mode surface based on the quantized system outputs and a sliding mode quantized controller are presented. Then, separation strategies are introduced to linearize the nonlinearities induced by quantization and incomplete TPs. A simulation is carried out in Sect. 4. Section 5 concludes this paper.

1.1 Notation

The transpose of H is presented by $H^{\mathrm{T}}$. The positive (negative) definite of H is shortened as $H>0 (H<0)$. $|x |$ and $|H |$ denote the 1-norm of the vector x and matrix H, respectively. Similarly, $||x ||$ and $||H ||$ denote 2-norm. $\mathcal {L}_2$ denotes the space of square integrable vector functions over $\left[ {0,\infty } \right)$ with $\varepsilon \left\{ {{{\left\| x \right\| }^2}} \right\} < \infty$. Finally, the symbol He(X) is used to represent $\left( X + X^{\mathrm{T}}\right)$.

2 Problem statement and preliminaries

Consider Markov jump systems with the following evolution

$$\begin{aligned} \begin{aligned} \dot{x}(t)&=(A(r(t))+\tilde{A}(r(t)))x(t)+B_1(r(t))(u(t))\\&\quad +B_2(r(t))\omega (t),\\ y(t)&=C(r(t))x(t),\\ z(t)&=C_d(r(t))x(t)+D(r(t))\omega (t), \end{aligned} \end{aligned}$$

(1)

where $x(t)\in \mathbb {R}^n$ is the system state vector, $\omega (t)\in \mathbb {R}^r$ is energy bounded disturbance belonging to $\mathcal {L}_2$. $u(t)\in \mathbb {R}^m$ is control input, y(t) is measured output and z(t) is the regulated output. $\tilde{A}(r(t))=M(r(t))E(t)N(r(t))$ where M(r(t)), N(r(t)) are known and $E(t)^{\mathrm{T}}E(t)\le I$. r(t) is continuous-time Markov process in a finite space $\mathcal {I}=\{1,2,\ldots ,N\}$ and satisfies

$$\begin{aligned}&Pr\{r(t+h)=j|r(t)=i\}\nonumber \\&\quad =\left\{ \begin{array}{l@{\quad }l} \lambda _{ij}h+o(h),&{}i\ne j\\ 1+\lambda _{ii}h+o(h),&{}i=j\\ \end{array} \right. \end{aligned}$$

(2)

where $h>0$, $\lambda _{ij}\geqslant 0$ for $i\ne j$ and $\lambda _{ii}=-\sum \nolimits ^{N}_{j=1,j\ne i}\lambda _{ij}$ for each mode i, $\lim \nolimits _{h\rightarrow 0}o(h)/h=0$.

Considering the fact that TPs may be known, uncertain and unknown [14, 36], the incomplete TP matrix with four operation modes is presented below

$$\begin{aligned} \varPi = \left[ {\begin{array}{*{20}{c}} {{\lambda _{11}}}&{}\quad {{\lambda _{12}}}&{}\quad ? &{}\quad ? \\ {{\lambda _{21}}}&{}\quad ? &{}\quad \bar{\lambda }_{23} &{}\quad ?\\ {{\lambda _{31}}} &{}\quad \bar{\lambda }_{32} &{}\quad \bar{\lambda }_{33} &{}\quad \bar{\lambda }_{34} \\ \bar{\lambda }_{41} &{}\quad \bar{\lambda }_{43} &{}\quad ? &{}\quad {{\lambda _{44}}} \end{array}} \right] . \end{aligned}$$

(3)

where $\bar{\lambda }_{ij}=\lambda _{ij}+\varphi _{ij}$, $\lambda _{ij}$ denotes known elements, $\varphi _{ij}\left( \varphi _{ij} \in \left[ -\,\delta _{ij},\delta _{ij}\right] \right)$ represents uncertain estimate error with known upper and lower bound and “?” is unknown. Furthermore, $\mathcal {I}_k^i$ is used to denote the set of known and uncertain TPs in ith row, while $\mathcal {I}_{uk}^i$ represents the set of unknown ones. For convenience, let $\hat{\lambda }_{ij}$ includes all possible cases (known, uncertain and unknown).

For the fluency of the derivative, some preliminaries of assumption, definition and lemma are given below:

Assumption 1

[36] $\omega (t)$ satisfies the following boundary d ($d>0$)

$$\begin{aligned} \begin{aligned} \int ^{\bar{T}}_0\omega ^{\mathrm{T}}(t)\omega (t)\hbox {d}t\leqslant d^2. \end{aligned} \end{aligned}$$

(4)

Definition 1

[2] The autonomous system (1) is stochastically stable (SS), if the following inequality holds:

$$\begin{aligned} \begin{aligned} \mathbb {E}\left\{ \int _0^\infty {\left\| x(t)\right\| ^2|x_0,r_0 }\right\} < +\infty \end{aligned} \end{aligned}$$

(5)

under initial conditions $x_0$ and $r_0$,

Definition 2

[2] Given $\gamma >0$ and $x_0=0$, the system (1) meets the required $\mathcal {H}_\infty$ level $\gamma$ if

$$\begin{aligned} \mathbb {E} {\int _{t_0}^\infty {z{{(t)}^{\mathrm{T}}}z(t)\hbox {d}t} } < {\gamma ^2}\mathbb {E} {\int _{t_0}^\infty {\omega {{(t)}^{\mathrm{T}}}\omega (t)\hbox {d}t} } \end{aligned}$$

(6)

holds for all nonzero $\omega (t) \in \mathcal {L}_2$.

Lemma 1

[37] The following inequality holds, for $F(t)^{\mathrm{T}}F(t)\le I$,

$$\begin{aligned} GF(t)H + {H^{\mathrm{T}}}{F^{\mathrm{T}}}(t){G^{\mathrm{T}}} \le {\varepsilon ^{ - 1}}G{G^{\mathrm{T}}} + \varepsilon {H^{\mathrm{T}}}H. \end{aligned}$$

where $\varepsilon >0$.

Lemma 2

[37] Let $\upsilon \in {\mathcal {R}^n}$, $\mathcal {P} = {\mathcal {P}^{\mathrm{T}}} \in {\mathcal {R}^{n \times n}}$ and $rank(\mathcal {H})=r<n$ ($\mathcal {H} \in \mathcal {R}^{m\times n}$), then equivalent statements are given below:

• 1. $\upsilon ^{\mathrm{T}}\mathcal {P}\upsilon$, for all $\upsilon \ne 0$, $\mathcal {H}\upsilon =0$;

• 2. $\mathcal {H}^{\bot T}\mathcal {P}\mathcal {H}^{\bot } < 0$;

• 3. $\exists \mathcal {X}\in \mathcal {R}^{n \times m}$ such that $\mathcal {P}+He(\mathcal {XH})<0$.

For $r(t)=i\in \mathcal {I}$, system matrices in the ith mode are simplified as $A_i$, $\tilde{A}_i$, $B_{1i}$, $B_{2i}$, $C_{i}$, $C_{di}$, $M_{i}$ and $N_{i}$.

As in [28], the dynamical uniform quantizer is given as follows:

$$\begin{aligned} {q_\mu }(\alpha ) \buildrel \varDelta \over = \mu (t) \cdot q\left( {\frac{\alpha }{\mu (t) }} \right) \end{aligned}$$

(7)

where $\mu (t)$ is the quantizer parameter.

Choosing the quantization error ${e_\mu (t) }$ as ${e_\mu (t) } = {q_\mu }(\alpha ) - \alpha$ gives

$$\begin{aligned} \left| {{e_\mu (t) }} \right| = \left| {{q_\mu }(\alpha ) - \alpha } \right| \le \Delta \mu (t) \end{aligned}$$

(8)

where $\varDelta =\frac{\sqrt{p} }{2}$ and p is the dimension of $\alpha$.

Lemma 3

For a positive constant $\beta >1$, if the quantizer parameter $\mu >0$ satisfies

$$\begin{aligned} \begin{aligned} \mu (t) \le \frac{|{y(t)}|}{(\beta +1)\varDelta } \end{aligned} \end{aligned}$$

(9)

then the following inequalities

$$\begin{aligned} \begin{aligned} |e_{\mu }(t)| \le \Delta \mu (t) \le \frac{1}{\beta +1} |y(t)| \end{aligned} \end{aligned}$$

(10)

holds.

Proof

Based on (8) and the result given in [28], the proof is completed. $\square$

Remark 1

Since the integral sliding mode surface is constructed by an observed state, the quantized parameter $\mu (t)$ is determined by system output. Although this lemma is an extension of [28], it could render a more tighter bound to $e_{\mu (t)}$.

Fig. 1

The structure of control system

3 Main results

3.1 Observer-based sliding manifold design

Consider the following integral sliding manifold

$$\begin{aligned} s(\hat{x}(t))= & {} B_{1i}^{\mathrm{T}}X_i\hat{x}(t)\nonumber \\&-\int ^{t}_0B_{1i}^{\mathrm{T}}X_i(A_i+B_{1i}K_i)\hat{x}(\tau )\hbox {d}\tau \end{aligned}$$

(11)

where $X_i$ is a matrix variable to be designed and $\hat{x}(t)$ is the observer state as below

$$\begin{aligned} \dot{\hat{x}}(t)= & {} A_i\hat{x}(t)+B_{1i} u(t)+B_{1i} L_i(q_{\mu }(y)-C_i\hat{x}(t))\nonumber \\ \end{aligned}$$

(12)

where $L_i$ is to be designed.

Remark 2

The choice of $B_{1i}L_i$ facilitates the sliding mode reachability analysis which will be shown in the following derivation. Although this form has been adopted in [38], the observer gain matrix $L_i$ should be given beforehand and no quantization has been considered.

To facilitate the controller construction in the following, Fig. 1 is given below.

For simplification, ${s}(\hat{x}(t))$ is abbreviated by s. Then the differential of ${s}_i$ is achieved from (11):

$$\begin{aligned} \dot{s}= & {} B_{1i}^{\mathrm{T}}X_iB_{1i}[(u(t)+L_i(q_{\mu }(y)-C_i\hat{x}(t))-K_i\hat{x}(t)].\nonumber \\ \end{aligned}$$

(13)

3.2 SMC design

In the following theorem, the sliding motion to the specified integral sliding surface $s=0$ is ensured in finite time by exploiting a proper controller.

Theorem 1

Consider systems (1) with the sliding mode functions (13). With the SMC law designed as (14), (15), (16), the state trajectories are driven onto $s=0$ in finite time and will keep on it.

$$\begin{aligned}&u(t)=u_1(t)+u_2(t), \end{aligned}$$

(14)

$$\begin{aligned}&u_1(t) = - \,\theta _i {s} + {K_i}\hat{x}, \end{aligned}$$

(15)

$$\begin{aligned}&u_2(t)=-\,\rho _i \mathrm{sign}({s}), \end{aligned}$$

(16)

where

$$\begin{aligned} {\rho _i}\ge & {} \left\| L_i\right\| {\left\| q_{\mu }(y)-C_{i}\hat{x}(t)\right\| } + \frac{1}{2}\left\| \varTheta \right\| \left\| s\right\| , \\ \varTheta= & {} \left\{ {\begin{aligned}&{\sum \limits _{j \in {\mathcal{I}_k^i}}^N {{{\lambda } _{ij}}\left( {{\bar{X}_j} - {\bar{X}_l} } \right) }+\varTheta _1, i \in {\mathcal{I}_k^i},l \in {\mathcal{I}_{uk}^i}}\\&{\sum \limits _{j \in {\mathcal{I}_k^i}}^N {{{\lambda } _{ij}}\left( { {\bar{X}_j} - {\bar{X}_i} } \right) + \varTheta _2, i \in {\mathcal{I}_{uk}^i}} }, \end{aligned}} \right. \\ \varTheta _1= & {} \sum \limits _{j \in \mathcal {I}_k^i,j \ne i}^N\left\{ { \frac{\delta _{ij}^2}{4}\eta _{ij} + \left( {\bar{X}_j} - {\bar{X}_i} - {\bar{X}_l} \right) \eta _{ij}^{-1}}\right. \\&\left. \times \left( {\bar{X}_j} - {\bar{X}_i} - {\bar{X}_l} \right) \right\} + \frac{\delta _{ii}^2}{4}\eta _{ii} +{\bar{X}_l} \eta _{ii}^{-1} {\bar{X}_l}, \\ \varTheta _2= & {} \sum \limits _{j \in \mathcal {I}_k^i}^N \left\{ {\frac{\delta _{ij}^2}{4}\eta _{ij} + \left( {\bar{X}_j} - {\bar{X}_i} \right) \eta _{ij}^{-1}}\right. \\&\left. \times \left( {\bar{X}_j} - {\bar{X}_i} \right) \right\} ,\quad (\eta _{ij}>0). \end{aligned}$$

Proof

Choose the candidate Lyapunov functional as

$$\begin{aligned} \begin{aligned} V_{1i}({s})=\frac{1}{2}{s}^{\mathrm{T}} \bar{X}_i{s} \end{aligned} \end{aligned}$$

(17)

where $\bar{X}_i=\left( B_{1i}^{\mathrm{T}}X_iB_{1i}\right) ^{-1}$.

Calculating the differential of (17) with (13) yields

$$\begin{aligned} \mathbb {E} \mathop {{V_{1i}}}\limits ^.= & {} s^{\mathrm{T}}{\bar{X}_i}\bar{X}_i^{ - 1}\left[ u(t) + {L_i}(q_{\mu }(y) - {C_i}\hat{x}(t))\right. \nonumber \\&- \left. {K_i}\hat{x}(t)\right] + s^{\mathrm{T}}\frac{1}{2} \sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}}} {\bar{X}_j}{s}. \end{aligned}$$

(18)

Taking the controller (14)–(16) into (18) gives

$$\begin{aligned} \begin{aligned} \mathbb {E} \dot{V}_{1i} =&s^{\mathrm{T}}\Big \{ - \theta _i {s} - {\rho _i}\mathrm{sign}(s)\\&+ {L_i}\left[ q_{\mu }(y) - {C_i}\hat{x} \right] \Big \} + s^{\mathrm{T}}\frac{1}{2}\sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}}} {{\bar{X}}_j}{{ s}} \\ =&-\theta _i s^{\mathrm{T}} s - \rho _i |s| + s^{\mathrm{T}} L_{i}\left( q_{\mu }(y)-C_{i}\hat{x}\right) \\&+ s^{\mathrm{T}}\frac{1}{2}\sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}}} {{\bar{X}}_j}{{s}}. \end{aligned} \end{aligned}$$

(19)

Since ${\hat{\lambda } _{ij}}$ is incomplete, according to the accessibility of diagonal elements, two cases are discussed as below to ensure the negative definiteness of $\dot{V}_{1i}$.

Case I $\left( i\in \mathcal {I}_{k}^i\right)$:

Use the property $\sum \nolimits _{l \in {I_{uk}^i}}^N {{\hat{\lambda } _{il}}} \mathrm{{ + }}\sum \nolimits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}} = 0$, one has the following fact

$$\begin{aligned} \begin{aligned} \sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}} {{{\bar{X}}_j}} } = \sum \limits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}} {{{\bar{X}}_j}} } + \sum \limits _{l \in {I_{uk}^i}}^N {{\hat{\lambda } _{il}} {{{\bar{X}}_l}} }. \end{aligned} \end{aligned}$$

(20)

Resorting to $\frac{{\sum \nolimits _{l \in {I_{uk}^i}}^N {{\hat{\lambda } _{il}}} }}{{ - \sum \nolimits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}} }}=1$, one further has

$$\begin{aligned}&\sum \nolimits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}} {{{\bar{X}}_j}} } + \sum \nolimits _{l \in {I_{uk}^i}}^N {{\hat{\lambda } _{il}} {{{\bar{X}}_j}} } \nonumber \\&\quad = \frac{{\sum \nolimits _{l \in {I_{uk}^i}}^N {{\hat{\lambda } _{il}}} }}{{ - \sum \nolimits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}} }}\left( {\sum \nolimits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}} {{{\bar{X}}_j}} } } \right) + \sum \nolimits _{l \in {I_{uk}^i}}^N {{\hat{\lambda } _{il}} {{{\bar{X}}_l}} } \nonumber \\&\quad = \frac{{\sum \nolimits _{l \in {I_{uk}^i}}^N {{\hat{\lambda } _{il}}} }}{{ - \sum \nolimits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}} }}\left( {\sum \nolimits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}\left( { {{{\bar{X}}_j}} - {{{\bar{X}}_l}} } \right) } } \right) . \end{aligned}$$

(21)

Consequently, taking (21) into (19) supplies

$$\begin{aligned} \begin{aligned} \mathbb {E} \dot{V}_{1i} =&\frac{{\sum \nolimits _{l \in {I_{uk}^i}}^N {{\hat{\lambda } _{il}}} }}{{ - \sum \nolimits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}} }} \Bigl [ s^{\mathrm{T}}\frac{1}{2}{\sum \nolimits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}\left( { {{{\bar{X}}_j}} - {{{\bar{X}}_l}} } \right) } }s \\&+ s^{\mathrm{T}} L_{i}\left( q_{\mu }(y)-C_{i}\hat{x}\right) -\theta _i s^{\mathrm{T}} s - \rho _i |s| \Bigr ]. \end{aligned} \end{aligned}$$

(22)

To get $\dot{V}_{1i}<0$, a direct way is to ensure the following terms from (22) satisfying

$$\begin{aligned} \begin{aligned}&-\rho _i |s| + s^{\mathrm{T}} L_{i}\left( q_{\mu }(y)-C_{i}\hat{x}\right) \\&\quad + s^{\mathrm{T}}\frac{1}{2}{\sum \limits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}\left( { {{{\bar{X}}_j}} - {{{\bar{X}}_l}} } \right) } }s \le 0. \end{aligned} \end{aligned}$$

(23)

Resorting to norm calculation, the left-hand side of (23) is scaled as

$$\begin{aligned}&-\rho _i |s|+ s^{\mathrm{T}} L_{i}\left( q_{\mu }(y)-C_{i}\hat{x}\right) \nonumber \\&\qquad + s^{\mathrm{T}}\frac{1}{2}{\sum \limits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}\left( { {{{\bar{X}}_j}} - {{{\bar{X}}_l}} } \right) } }s\nonumber \\&\quad \le \left\| {s}^{\mathrm{T}}{L_i} {\left( q_{\mu }(y)-C_{i}\hat{x}\right) }\right\| - \rho _i |s|\nonumber \\&\quad \quad + \frac{1}{2}\left\| {s}^{\mathrm{T}}\right\| \left\| {\sum \limits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}\left( { {{{\bar{X}}_j}} - {{{\bar{X}}_l}} } \right) } }\right\| \left\| {s}\right\| \nonumber \\&\quad \le \left\| {s}\right\| \left[ \left\| {L_i}\right\| \left( \left\| {q_{\mu }(y)-C_{i}\hat{x}}\right\| \right) \right. \nonumber \\&\quad \quad \left. + \frac{1}{2}\left\| {s}\right\| \left\| {\sum \limits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}\left( { {{{\bar{X}}_j}} - {{{\bar{X}}_l}} } \right) } } \right\| \right] -\rho _i |s|. \end{aligned}$$

(24)

Applying the fact that $\left| {s} \right| \ge \left\| {s} \right\|$, (23) holds when $\rho _i$ satisfies

$$\begin{aligned} \begin{aligned} \rho _i \ge&\left\| {L_i}\right\| \left( \left\| {q_{\mu }(y)-C_{i}\hat{x}}\right\| \right) \\&+ \frac{1}{2}\left\| {s}\right\| \left\| {\sum \limits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}} \left( { {{{\bar{X}}_j}} - {{{\bar{X}}_l}} } \right) } } \right\| . \end{aligned} \end{aligned}$$

(25)

Since ${\sum \nolimits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}\left( { {{{\bar{X}}_j}} - {{{\bar{X}}_l}} } \right) } }$ include uncertain TPs $\bar{\lambda }_{ij}$, with the help of Lemma 1, it is disposed as below

$$\begin{aligned} \begin{aligned}&\sum \limits _{j \in \mathcal {I}_k^i}^N{\bar{\lambda }_{ij}\left( {{{\bar{X}}_j}} - {{{\bar{X}}_l}} \right) } \le \sum \limits _{j \in \mathcal {I}_k^i}^N{\lambda _{ij}\left( {{{\bar{X}}_j}} - {{{\bar{X}}_l}} \right) } \\&\quad + \sum \limits _{j \in \mathcal {I}_k^i}^N{\frac{\delta _{ij}^2}{4}\eta _{ij}} + {{\bar{X}}_l}^{\mathrm{T}} \eta _{ii}^{-1} {{\bar{X}}_l}\\&\quad + \sum \limits _{j \in \mathcal {I}_k^i,j\ne i}^N { \left( {{{\bar{X}}_j}} - {{{\bar{X}}_i}} - {{{\bar{X}}_l}} \right) ^{\mathrm{T}} \eta _{ij}^{-1}}\\&\quad \times \left( {{{\bar{X}}_j}} - {{{\bar{X}}_i}} - {{{\bar{X}}_l}} \right) .\\ \end{aligned} \end{aligned}$$

(26)

Substituting (26) into (25) produces

$$\begin{aligned}&\left\| {L_i}\right\| \left( \left\| {q_{\mu }(y)-C_{i}\hat{x}}\right\| \right) + \frac{1}{2}\left\| {s}\right\| \left\| {\sum \limits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}\left( { {{{\bar{X}}_j}} - {{{\bar{X}}_l}} } \right) } } \right\| \nonumber \\&\quad \le \left\| {L_i}\right\| \left( \left\| {q_{\mu }(y)-C_{i}\hat{x}}\right\| \right) \nonumber \\&\quad \quad + \frac{1}{2}\left\| {s}\right\| \left\| { { \sum \limits _{j \in {\mathcal{I}_k^i}}^N {{{\lambda } _{ij}} \left( {{\bar{X}_j} - {\bar{X}_l} } \right) }+\varTheta _1 } }\right\| . \end{aligned}$$

(27)

As a result, in this case, ${\rho _i}$ should meet

$$\begin{aligned} \begin{aligned} {\rho _i} \ge&\left\| L_i\right\| \left( \left\| q_{\mu }(y)-C_{i}\hat{x}\right\| \right) \\&+ \frac{1}{2}\left\| s\right\| \left\| { { \sum \limits _{j \in {\mathcal{I}_k^i}}^N {{{\lambda } _{ij}}\left( {{\bar{X}_j} - {\bar{X}_l} } \right) }+\varTheta _1 } }\right\| \end{aligned} \end{aligned}$$

(28)

which is the condition in (14)–(16).

Case II ($i\in \mathcal {I}_{uk}^i$):

Utilizing the property (2) as ${\hat{\lambda }_{ii}}$ $= - \sum \nolimits _{j \in {I_k^i}}^N {{\hat{\lambda }_{ij}}} - \sum \nolimits _{l \in {I_{uk}^i}}^N {{\hat{\lambda }_{il}}}$ and taking it into (21) gives

$$\begin{aligned} \begin{aligned} \sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}} {{{\bar{X}}_j}} } =&\sum \limits _{j \in {I_k^i}}^N {{\hat{\lambda } _{ij}}\left( { {{{\bar{X}}_j}} - {{{\bar{X}}_i}} } \right) } \\&+ \sum \limits _{l \in {I_{uk}^i},l \ne i}^N {{\hat{\lambda } _{il}}\left( { {{{\bar{X}}_l}} - {{{\bar{X}}_i}} } \right) }. \end{aligned} \end{aligned}$$

(29)

Let $\bar{X}_j$, $\bar{X}_l$ satisfy ${{{\bar{X}}_l}} < {{{\bar{X}}_j}}$, then it leads to:

$$\begin{aligned} \begin{aligned} \sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}} {{{\bar{X}}_j}} } \le \sum \limits _{j \ in {I_k^i}}^N {{\hat{\lambda } _{ij}}\left( { {{{\bar{X}}_j}} - {{{\bar{X}}_i}} } \right) }. \end{aligned} \end{aligned}$$

With respect to uncertain TPs, $\sum \nolimits _{j=1}^N{\bar{\lambda }_{ij} {\bar{X}_j} }$ has the property as follows.

$$\begin{aligned} \begin{aligned} \sum \limits _{j=1}^N {\bar{\lambda }_{ij} {\bar{X}_j} } \le&\sum \limits _{j \in \mathcal {I}_{k}^i}^N{\bar{\lambda }_{ij}\left( \bar{X}_j - \bar{X}_i \right) } \\ \le&\sum \limits _{j \in \mathcal {I}_{k}^i}^N{{\lambda }_{ij}\left( \bar{X}_j - \bar{X}_i \right) } + \sum \limits _{j \in \mathcal {I}_{k}^i}^N{\frac{\delta _{ij}^2}{4}\eta _{ij}} \\&+ \sum \limits _{j \in \mathcal {I}_{k}^i}^N\left( \bar{X}_j - \bar{X}_i \right) ^{\mathrm{T}}\eta _{ij}^{-1} \left( \bar{X}_j - \bar{X}_i \right) . \end{aligned} \end{aligned}$$

(30)

In a similar way, $\sum \nolimits _{j = 1}^N {{\hat{\lambda } _{ij}} {{{\bar{X}}_j}} }$ is substituted by (30) and $\rho _i$ is required to satisfy

$$\begin{aligned} \begin{aligned} {\rho _i} \ge&\left\| L_i\right\| \left( \left\| q_{\mu }(y)-C_{i}\hat{x}\right\| \right) \\&+ \frac{1}{2}\left\| s\right\| \left\| { { \sum \limits _{j \in {\mathcal{I}_k^i}}^N {{{\lambda } _{ij}}\left( {{\bar{X}_j} - {\bar{X}_l} } \right) }+\varTheta _2 } }\right\| \end{aligned} \end{aligned}$$

(31)

which is presented in (14)–(16). $\square$

Remark 3

Due to the sign function, the sliding mode controller could render the chattering problem. To avoid this phenomenon, $-\rho _i \mathrm{sign}(s)$ is substituted by $-\rho \frac{s}{\left\| {s}\right\| +\iota }$, $(\iota >0)$ in the simulation part.

Remark 4

In [39], system states are premised to be available and the integral sliding mode surface is quantized. However, in this paper, the surface is built on the quantized system output at controller side. Moreover, the distinction of this paper and [38] is that the incomplete TPs in the former cover the cases in the latter.

3.3 Adjustment policy for $\mu (t)$

In this section, similar to [31], an adjustment policy of parameter $\mu (t)$ in the quantizer is proposed as follows.

Initialization:

Choose $\mu (t_0)$ as an arbitrary positive constant and set $\mu (t)=\mu (t_0)$;

Adjustment steps:

If $|y(t)|\ge 1$, $\mu (t)$ is taken as $\mu (t)=\frac{\lfloor |y(t)| \rfloor }{(\beta +1)\varDelta }$, where the notation $\lfloor y\rfloor$ denotes the function $\hbox {floor}(\cdot )$ which rounds the elements of y(t) to the nearest integers less than or equal to y(t).

If $0<|y(t)|<1$, take $\alpha (0<\alpha <1)$ as a fixed positive constant, there always exists a positive integer i such that $\alpha ^i \le |y(t)| < \alpha ^(i-1)$; then, we take $\mu (t)=\frac{\alpha ^i}{(\beta +1)\varDelta }$.

If $|y(t)|=0$, which means the sliding surface is arrived, then we take $\mu (t)=0$.

3.4 Stability analysis

The subsequent work pays attention to the stability of the closed-loop systems with the controller composed of (14)–(16). Since the designed sliding mode surface is proved to be accessible, a sliding motion is happened on the surface in a finite time. Then, the system stability is analyzed through $\hat{x}(t)$ and e(t).

Taking into account $s=0,\dot{s}=0$, the equivalent control law is given as follows:

$$\begin{aligned} u_{eq}(t)=K_i\hat{x}(t)-L_i\left( q_{\mu }(y)-C_i\hat{x}(t)\right) . \end{aligned}$$

(32)

Subsequently, the state trajectory under (32) is described as

$$\begin{aligned} \dot{\hat{x}}(t)=(A_i+B_{1i}K_i)\hat{x}(t). \end{aligned}$$

(33)

Setting $e(t)={x}(t)-\hat{x}(t)$ yields

$$\begin{aligned} \dot{e}\left( t\right)= & {} \left( A_i+\tilde{A}\left( t\right) \right) {x} + B_{1i}K_{i}\hat{x}+B_{2i}\omega \left( t\right) \nonumber \\&-\,B_{1i}L_{i}\left( q_{\mu }\left( y\right) -C_{i}\hat{x}\right) -A_{i}\hat{x} - B_{1i}K_{i}\hat{x} \nonumber \\= & {} \left( A_i+\tilde{A}_i\left( t\right) -B_{1i}L_iC_i\right) e\left( t\right) \nonumber \\&+\,\tilde{A}_i\left( t\right) \hat{x}\left( t\right) +B_{2i}w\left( t\right) - B_{1i}L_{i}e_{\mu }\left( t\right) . \end{aligned}$$

(34)

To get the controller and observer gains, sufficient conditions for SS with the required $\mathcal {H}_\infty$ performance are established Theorem 2.

Theorem 2

For given scalars $\tau _{1i}$,$\tau _{2i}$,$\upsilon _{1i}$,$\upsilon _{2i}$,$\upsilon _{3i}$, $\upsilon _{4i}$, if there exist symmetrical matrices $X_i,{T}_{ij}>0$ and matrices $U_{i},V_{i},W_{i},Y_{i}$ and positive scalars $\varepsilon _{1i},\varepsilon _{2i} (i \in \mathbf {I})$ such that the following inequalities hold:

$$\begin{aligned}&\left[ {\begin{array}{*{20}{c}} \varGamma _{11} &{}\quad 0 &{}\quad \varGamma _{13} &{}\quad \varGamma _{14} &{}\quad 0\\ * &{}\quad \varGamma _{22} &{}\quad \varGamma _{23} &{}\quad \varGamma _{24} &{}\quad \varGamma _{25}\\ * &{}\quad * &{}\quad \varGamma _{33} &{}\quad \varGamma _{34} &{}\quad 0\\ * &{}\quad * &{}\quad * &{}\quad \varGamma _{44} &{}\quad 0\\ * &{}\quad * &{}\quad * &{}\quad * &{}\quad \varGamma _{55}\end{array}} \right] <0,\end{aligned}$$

(35)

$$\begin{aligned}&X_l \le X_i \quad l \ne i \quad i \in {\mathcal{I}_{uk}^i},l \in {\mathcal{I}_{uk}^i}, \end{aligned}$$

(36)

where

$$\begin{aligned}&\varGamma _{11}=He({X_i}{A_i} + {\tau _{1i}}{B_{1i}}{W_{i}}) + {\varepsilon _{2i}}{N_i^{\mathrm{T}}}N_i + \bar{\varTheta },\\&\varGamma _{13}=\left[ {\begin{array}{*{20}{c}} 0&0&0&C^{\mathrm{T}}_{di}&C_i^{\mathrm{T}}&0\end{array}}\right] ,\\&\varGamma _{14}= \left\{ \begin{aligned}&\left[ {\begin{array}{*{20}{c}}\tilde{X}_{j1}&\ldots&\tilde{X}_{jm}&X_{l}&\hat{\varGamma }_{14}&0\end{array}}\right] , i \in \mathcal {I}_k^i,j \ne i,\\&\left[ {\begin{array}{*{20}{c}}X_{j1}-X_{i}&\ldots&X_{jm}-X_{i}&\hat{\varGamma }_{14}&0\end{array}}\right] , i \in \mathcal {I}_{uk}^i, \end{aligned}\right. \\&{{\hat{\varGamma }}_{14}} = {X_i}{B_{1i}} - {\tau _{1i}}{B_{1i}}{U_{i}} + {\tau _{2i}}W_{i}^{\mathrm{T}}, \\&\varGamma _{22}=He({X_i}{A_i} - {\upsilon _{1i}}{B_{1i}}{Y_{i}}{C_{i}}) + {\varepsilon _{1i}}{N_i^{\mathrm{T}}}N_i + \bar{\varTheta } , \\&\varGamma _{23}=\left[ \begin{array}{*{20}{c}} X_{i}M_{i}&X_{i}M_{i}&X_{i}B_{2i}&0&C_i^{\mathrm{T}}&\upsilon _{3i}B_{1i}Y_i \end{array}\right] ,\\&\varGamma _{24}=\left[ {\begin{array}{*{20}{c}} 0&\ldots&0&X_iB_{1i}-\upsilon _{3i}B_{1i}V_i\end{array}} \right] ,\\&\varGamma _{25}=\left\{ \begin{aligned}&\left[ {\begin{array}{*{20}{c}}\tilde{X}_{j1}&\ldots&\tilde{X}_{jm}&X_{l}&\hat{\varGamma }_{25}\end{array}}\right] ,i \in \mathcal {I}_k^i,j\ne i,\\&\left[ {\begin{array}{*{20}{c}}X_{j1}-X_{i}&\ldots&X_{jm}-X_{i}&\hat{\varGamma }_{25}\end{array}}\right] , i \in \mathcal {I}_{uk}^i, \end{aligned}\right. \\&\tilde{X}_{jk}=X_{jk}-X_{i}-X_{l},k \in \{1,\ldots ,m\},\\&{{\hat{\varGamma }}_{25}} = {X_i}{B_{1i}} - {\upsilon _{1i}}{B_{1i}}{V_{i}} + {\upsilon _{2i}}C_{i}^{\mathrm{T}}Y_{i}^{\mathrm{T}} ,\\&\varGamma _{33}=-\,\mathrm{diag}\{\varepsilon _{1i}I,\varepsilon _{2i}I,\mathcal {D}_i,{(\beta +1)^2}I,I\}, \\&\mathcal {D}_i=\left[ \begin{array}{*{20}{c}}\gamma ^{2}I&{}-D^{\mathrm{T}}_{i}\\ 0 &{} I\end{array}\right] ,\quad \varGamma _{34}=\left[ \begin{array}{*{20}{c}} 0 &{}\quad \ldots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \ldots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \ldots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \ldots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \ldots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \ldots &{}\quad 0 &{}\quad \upsilon _{4i}Y_i^{\mathrm{T}}\\ \end{array}\right] ,\\ \end{aligned}$$

$$\begin{aligned} \varGamma _{44}&=\left\{ \begin{aligned} -\, \mathrm{diag}&\{T_{ij1},\ldots ,T_{ijm}, T_{ii},He( {\tau _{2i}}{U_{i}}),\\&{He( {\upsilon _{4i}}{V_i})}\}\quad i,j \in \mathcal {I}_k^i,j \ne i,\\ -\, \mathrm{diag}&\{T_{ij1},\ldots ,T_{ijm},He( {\tau _{2i}}{U_{i}}),\\&{He( {\upsilon _{4i}}{V_i})}\}\quad i \in \mathcal {I}_{uk}^i , \end{aligned}\right. \\ \varGamma _{55}&=\left\{ \begin{aligned} -\, \mathrm{diag}&\{T_{ij1},\ldots ,T_{ijm}, T_{ii},\\&He( {\upsilon _{2i}}{V_{i}})\}\quad i,j \in \mathcal {I}_k^i,j \ne i,\\ -\, \mathrm{diag}&\{T_{ij1},\ldots ,T_{ijm},He( {\upsilon _{2i}}{V_{i}})\}, i \in \mathcal {I}_{uk}^i , \end{aligned}\right. \\ \bar{\varTheta }&=\left\{ \begin{aligned}&\sum _{j\in \mathcal {I}_k^i}^N\left\{ \lambda _{ij}(X_j-X_l)+\frac{\delta _{ij}^2}{4}T_{ij} \right\} \\&l \in \mathcal {I}_{uk}^i,i \in \mathcal {I}_k^i\\&\sum _{j\in \mathcal {I}_k^i}^N\left\{ \lambda _{ij}(X_j-X_i)+\frac{\delta _{ij}^2}{4}T_{ij} \right\} \\&i \in \mathcal {I}_{uk}^i\end{aligned}\right. \\ \end{aligned}$$

the controller (14) renders the system (1) to be SS with the $\mathcal {H}_{\infty }$ index $\gamma$. Moreover, $K_i =U_i^{ - 1}{W_i}$ and $L_i =-\,V_i^{ - 1}Y_i$.

Proof

The candidate Lyapunov function is chosen as:

$$\begin{aligned} V_{2i}=\hat{x}^{\mathrm{T}}(t)X_i\hat{x}(t)+{e}^{\mathrm{T}}(t)X_i{e}(t) \end{aligned}$$

(37)

where $X_i>0$. Calculating $\dot{V}_{2i}$ yields

$$\begin{aligned} \begin{aligned} \mathbb {E} {{\dot{V}}_{2i}}&= {{\dot{\hat{x}}}^{\mathrm{T}}}(t){X_i}\hat{x}(t) + \hat{x}^{\mathrm{T}}{(t)}{X_i}\dot{\hat{x}}(t) \\&\quad + {{\dot{e}}^{\mathrm{T}}}(t){X_i}e(t) + {e^{\mathrm{T}}}(t){X_i}\dot{e}(t)\\&\quad + {{\hat{x}}^{\mathrm{T}}}(t)\sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}}{X_j}} \hat{x}(t) \\&\quad + {e^{\mathrm{T}}}(t)\sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}}{X_j}} e(t). \end{aligned} \end{aligned}$$

(38)

Substituting (33)–(38) renders

$$\begin{aligned} \mathbb {E} {{\dot{V}}_{2i}}= & {} 2{{\hat{x}}^{\mathrm{T}}}(t){X_i}({A_i} + {B_{1i}}{K_i})\hat{\mathrm{x}}(t)\nonumber \\&+ \,2{e^{\mathrm{T}}}(t){X_i}({A_i} + {{\tilde{A}}_i}(t) - {B_{1i}}{L_i}{C_i})e(t)\nonumber \\&+ \,2{e^{\mathrm{T}}}(t){X_i}{{\tilde{A}}_i}(t)\hat{x}(t) + {{\hat{x}}^{\mathrm{T}}}(t)\sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}}{X_j}} \hat{x}(t)\nonumber \\&+ \,{e^{\mathrm{T}}}(t)\sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}}{X_j}} e(t) +2{e^{\mathrm{T}}}(t){X_i}{B_{2i}}w(t)\nonumber \\&- \,2{e^{\mathrm{T}}}(t){X_i}{B_{1i}}{L_i}e_{\mu }(t). \end{aligned}$$

(39)

Utilizing Lemma 1, the following inequality holds from (39):

$$\begin{aligned} \begin{aligned} \mathbb {E} {\dot{V}_{2i}}&\le {\hat{x}^{\mathrm{T}}}(t) \left[ He\left( {X_i}\left( {A_i} + {B_{1i}}{K_i}\right) \right) \right. \\&\quad \left. + {\varepsilon _{2i}}{N_i}^{\mathrm{T}}{N_i} + \sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}}{X_j}} \right] \hat{x}(t)\\&\quad + {e^{\mathrm{T}}}(t)\Big [He\left( {X_i}\left( {A_i} - {B_{1i}}{L_i}{C_i}\right) \right) \\&\quad + \left( {\varepsilon _{1i}}^{ - 1} + {\varepsilon _{2i}}^{ - 1}\right) {X_i}{M_i}M_i^{\mathrm{T}}{X_i} \\&\quad + {\varepsilon _{1i}}{N_i}^{\mathrm{T}}{N_i} + \sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}}{X_j}}\Big ]e(t)\\&\quad +2{e^{\mathrm{T}}}(t){X_i}{B_{2i}}w(t)\\&\quad - 2{e^{\mathrm{T}}}(t){X_i}{B_{1i}}{L_i}e_{\mu }(t). \end{aligned} \end{aligned}$$

(40)

Integrating $z^{\mathrm{T}}(t)z(t) - \gamma ^2w^{\mathrm{T}}(t)w(t)$ into (40), one has the inequality (41).

$$\begin{aligned}&\mathbb {E} {{{\dot{V}}_{2i}} + {z^{\mathrm{T}}}(t)z(t) - {\gamma ^2}{w^{\mathrm{T}}}(t)w(t)}\nonumber \\&\quad \le {{\hat{x}}^{\mathrm{T}}}(t) \left[ He\left( {X_i}\left( {A_i} + {B_{1i}}{K_i}\right) \right) + {\varepsilon _{2i}}{N_i}^{\mathrm{T}}{N_i}\right. \nonumber \\&\qquad +\,\left. \sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}}{X_j}} \right] \hat{x}(t) \nonumber \\&\qquad +\, {e^{\mathrm{T}}}(t)\left[ {\varepsilon _{1i}}{N_i}^{\mathrm{T}}{N_i} + \left( {\varepsilon _{1i}}^{ - 1} + {\varepsilon _{2i}}^{ - 1}\right) {X_i}{M_i}M_i^{\mathrm{T}}{X_i}\right. \nonumber \\&\qquad + \,\left. He\left( {X_i}\left( {A_i} - {B_{1i}}{L_i}{C_i}\right) \right) + \sum \limits _{j = 1}^N {{\hat{\lambda }_{ij}}{X_j}} \right] e(t)\nonumber \\&\qquad +\, 2{e^{\mathrm{T}}}(t){X_i}{B_{2i}}w(t) - 2{e^{\mathrm{T}}}(t){X_i}{B_{1i}}{L_i}e_{\mu }(t)\nonumber \\&\qquad + \,{w^{\mathrm{T}}}(t)\left( D_i^{\mathrm{T}}{D_i} - {\gamma ^2}I\right) w(t) + 2{{\hat{x}}^{\mathrm{T}}}(t)C_{di}^{\mathrm{T}}{D_i}w(t)\nonumber \\ \end{aligned}$$

(41)

To deal with $2{e^{\mathrm{T}}}(t){X_i}{B_{1i}}{L_i}e_{\mu }(t)$, applying Lemma 3 gives

$$\begin{aligned}&2{e^{\mathrm{T}}}(t){X_i}{B_{1i}}{L_i}e_{\mu }(t)\nonumber \\&\quad \le e^{\mathrm{T}}(t)(X_iB_{1i}L_i)(X_iB_{1i}L_i)^{\mathrm{T}} e(t)\nonumber \\&\qquad + e_{\mu }(t)^{\mathrm{T}}e_{\mu }(t) \nonumber \\&\quad \le e^{\mathrm{T}}(t)(X_iB_{1i}L_i)(X_iB_{1i}L_i)^{\mathrm{T}} e(t)\nonumber \\&\qquad + \frac{1}{(\beta +1)^2}y^{\mathrm{T}}(t)y(t)\nonumber \\&\quad = e^{\mathrm{T}}(t)(X_iB_{1i}L_i)(X_iB_{1i}L_i)^{\mathrm{T}} e(t)\nonumber \\&\qquad + \frac{1}{(\beta +1)^2}x^{\mathrm{T}}(t)(C_i)^{\mathrm{T}}(C_i)x(t)\nonumber \\&\quad = e^{\mathrm{T}}(t)(X_iB_{1i}L_i)(X_iB_{1i}L_i)^{\mathrm{T}} e(t) \nonumber \\&\qquad + \frac{1}{(\beta +1)^2}(\hat{x}+e)^{\mathrm{T}}C_i^{\mathrm{T}}C_i(\hat{x}+e). \end{aligned}$$

(42)

Substituting (42) into (41) yields

$$\begin{aligned}&\mathbb {E} {{{\dot{V}}_{2i}} + {z^{\mathrm{T}}}(t)z(t) - {\gamma ^2}{w^{\mathrm{T}}}(t)w(t)} \le \alpha ^{\mathrm{T}}(t)\varXi _i\alpha (t)\nonumber \\ \end{aligned}$$

(43)

where

$$\begin{aligned} \alpha (t)&= {\left[ {\begin{array}{*{20}{c}} {{{\hat{x}}^{\mathrm{T}}(t)}}&{{e^{\mathrm{T}}(t)}}&{{w^{\mathrm{T}}(t)}} \end{array}} \right] ^{\mathrm{T}}},\nonumber \\ {\varXi _{i}}&= \left[ {\begin{array}{*{20}{c}} {\varLambda _{11}} &{}\quad 0&{}\quad {C_{di}^{\mathrm{T}}{D_i}}\\ \mathrm{{*}}&{}\quad {{\varLambda _{22}} } &{}\quad X_iB_{2i}\\ \mathrm{{*}}&{}\quad \mathrm{{*}}&{}\quad {{\varLambda _{33}}}\\ \end{array}} \right] ,\nonumber \\ {\varLambda _{11}}&= He({X_i}({A_i} + {B_{1i}}{K_i})) + {\varepsilon _{2i}}N_i^{\mathrm{T}}{N_i} + C_{di}^{\mathrm{T}}{C_{di}}\nonumber \\&\quad + \sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}}{X_j}} + \frac{1}{(\beta +1)^2}C_i^{\mathrm{T}}C_i,\nonumber \\ {\varLambda _{22}}&= He({X_i}({A_i} - {B_{1i}}{L_i}{C_i})) + {\varepsilon _{1i}}N_i^{\mathrm{T}}{N_i} \nonumber \\&\quad + \sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}}{X_j}} + (\varepsilon _{1i}^{ - 1} + \varepsilon _{2i}^{ - 1}){X_i}{M_i}M_i^{\mathrm{T}}{X_i}\nonumber \\&\quad +\frac{1}{(\beta +1)^2}C_i^{\mathrm{T}}C_i+ (X_iB_{1i}L_i)(X_iB_{1i}L_i)^{\mathrm{T}},\nonumber \\ \varLambda _{33}&= D_i^{\mathrm{T}}{D_i} - {\gamma ^2}I. \end{aligned}$$

(44)

To ensure the stochastic stability with the required $\mathcal {H}_\infty$ performance, one just needs to prove ${\varXi _{i}}<0$. With the help of Schur complement to $\varXi _{i}$, one obtains

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{\bar{\varLambda } _{11}}}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {C_{di}^{\mathrm{T}}}&{}\quad C_i^{\mathrm{T}} &{}\quad 0\\ *&{}\quad {{\bar{\varLambda } _{22}}}&{}\quad {{X_i}{M_i}}&{}\quad {{X_i}{M_i}}&{}\quad {{X_i}{B_{2i}}}&{}\quad 0&{}\quad C_i^{\mathrm{T}}&{}\quad X_iB_{1i}L_i\\ *&{}\quad *&{}\quad { - {\varepsilon _{1i}}I}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad { - {\varepsilon _{2i}}I}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad { - {\gamma ^2}I}&{}\quad {D_i^{\mathrm{T}}}&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad { - I}&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad \bar{\varLambda } _{77}&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad -I \end{array}} \right] < 0 \end{aligned}$$

where $\bar{\varLambda }_{11} = He({X_i}({A_i} + {B_{1i}}{K_i})) + {\varepsilon _{2i}}N_i^{\mathrm{T}}{N_i}+ \sum \nolimits _{j = 1}^N {{\hat{\lambda }_{ij}}{X_j}}$, $\bar{\varLambda }_{22} = He({X_i}({A_i} - {B_{1i}}{L_i}{C_i})) + {\varepsilon _{1i}}N_i^{\mathrm{T}}{N_i}+ \sum \nolimits _{j = 1}^N {{\hat{\lambda }_{ij}}{X_j}}$, and $\bar{\varLambda }_{77} = -{(\beta +1)^2}I$.

To linearize $X_iB_{1i}K_i$ and $X_iB_{1i}L_iC_i$, by setting $K_i =U_i^{ - 1}{W_i}$, $L_i =-\,V_i^{ - 1}Y_i$, a separated approach in [36] is utilized as below

$$\begin{aligned} {X_i}{B_{1i}}{K_i}= & {} {X_i}{B_{1i}}U_i^{ - 1}{W_i} \nonumber \\= & {} ({X_i}{B_{1i}} - {B_{1i}}U)U_i^{ - 1}{W_i} + {B_{1i}}{W_i} \end{aligned}$$

(45)

$$\begin{aligned} - {X_i}{B_{1i}}{L_i}= & {} {X_i}{B_{1i}}V_i^{ - 1}{Y_i}\nonumber \\= & {} ({X_i}{B_{1i}} - {B_{1i}}V)V_i^{ - 1}{Y_i} + {B_{1i}}{Y_i}. \end{aligned}$$

(46)

Alternatively, $\varXi _i$ is equivalent to

$$\begin{aligned} \varXi _i={\mathcal {H}^ \bot }^{\mathrm{T}}\mathcal {P}{\mathcal {H}^ \bot } \end{aligned}$$

(47)

where

$$\begin{aligned} \mathcal {P}&=\left[ {\begin{array}{*{20}{c}} {{\bar{\varLambda } _{11}}}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {C_{di}^{\mathrm{T}}}&{}\quad C_i^{\mathrm{T}}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad {{\bar{\varLambda } _{22}}}&{}\quad {{X_i}{M_i}}&{}\quad {{X_i}{M_i}}&{}\quad {{X_i}{B_{2i}}}&{}\quad 0&{}\quad C_i^{\mathrm{T}}&{}\quad X_iB_{1i}L_i&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad { - {\varepsilon _{1i}}I}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad { - {\varepsilon _{2i}}I}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad { - {\gamma ^2}I}&{}\quad {D_i^{\mathrm{T}}}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad { - I}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad {\bar{\varLambda } _{77}}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad -I&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad 0 \end{array}} \right] , {\mathcal {H}^ \bot }&= \left[ {\begin{array}{*{20}{c}} I\\ \tilde{H}^\bot \end{array}} \right] . \end{aligned}$$

Calculating the kernel space of ${\mathcal {H}^ \bot }$ gives

$$\begin{aligned} \tilde{H}^\bot =\left[ {\begin{array}{*{25}{c}}{{K_i}}&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}{ - \,{L_i}{C_i}}&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}L_i \end{array}} \right] . \end{aligned}$$

Combining (45), (46) and Lemma 2 , $\varXi _i$ is rewritten as (48).

$$\begin{aligned}&\mathcal {P} + He(\mathcal {X}\mathcal {H}) \nonumber \\&\quad = \left[ {\begin{array}{*{20}{c}} {{{\hat{\varLambda } }_{11}}}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {C_{di}^{\mathrm{T}}}&{}\quad C_i^{\mathrm{T}}&{}\quad 0&{}\quad {{{\hat{\varLambda }}_{19}}}&{}\quad 0&{}\quad 0\\ *&{}\quad {{{\hat{\varLambda }}_{22}}}&{}\quad {{X_i}{M_i}}&{}\quad {{X_i}{M_i}}&{}\quad {{X_i}{B_{2i}}}&{}\quad 0&{}\quad C_i^{\mathrm{T}}&{}\quad \upsilon _{3i}B_{1i}Y_i&{}\quad 0&{}\quad {{{\hat{\varLambda }}_{210}}}&{}\quad X_iB_{1i}-\upsilon _{3i}B_{1i}V_i\\ *&{}\quad *&{}\quad { - {\varepsilon _{1i}}I}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad { - {\varepsilon _{2i}}I}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad { - {\gamma ^2}I}&{}\quad {D_i^{\mathrm{T}}}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad { - I}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad -{(\beta +1)^2}I&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad -I&{}\quad 0&{}\quad 0&{}\quad \upsilon _{4i}Y_i^{\mathrm{T}}\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad {{\hat{\varLambda }}_{99}} &{}\quad 0&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad {{\hat{\varLambda }}_{1010}}&{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad {He( - {\upsilon _{4i}}{V_i})} \end{array}} \right] \nonumber \\&\quad < 0 \end{aligned}$$

(48)

where

$$\begin{aligned} \mathcal {X}= & {} {\left[ {\begin{array}{*{20}{c}} \tilde{\mathcal {X}}_1\\ \tilde{\mathcal {X}}_2 \end{array}} \right] } , \tilde{\mathcal {X}}_1={\left[ {\begin{array}{*{20}{c}} ({{\tau _{1i}}{B_{1i}}{U_{i}} - {X_i}{B_{1i}}})^{\mathrm{T}}&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}({{\upsilon _{1i}}{B_{1i}}{V_{i}} - {X_i}{B_{1i}}})^{\mathrm{T}}&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}(\upsilon _{3i}B_{1i}V_i-X_iB_{1i})^{\mathrm{T}}&{}0&{}0&{}0&{}0&{}0&{}0\end{array}} \right] }^{\mathrm{T}}\\ \tilde{\mathcal {X}}_2= & {} \mathrm{diag}\{{{\tau _{2i}}{U_{i}}},{{\upsilon _{2i}}{V_{i}}},\upsilon _{4i}V_{i}\},\\ \mathcal {H}= & {} \left[ {\begin{array}{*{20}{c}} {K_i}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -I&{}\quad 0&{}\quad 0\\ 0&{}\quad -L_iC_i&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -I&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad L_i&{}\quad 0&{}\quad 0&{}\quad -I \end{array} }\right] ,\\ {{\hat{\varLambda } }_{11}}= & {} He({X_i}{A_i} + {\tau _{1i}}{B_{1i}}{W_{i}}) + {\varepsilon _{2i}}{N_i^{\mathrm{T}}}{N_i} + \sum \limits _{j = 1}^N {{\hat{\lambda } _{ij}}{X_j}},\hat{\varLambda }_{19}={X_i}{B_{1i}} - {\tau _{1i}}{B_{1i}}{U_{i}} + {\tau _{2i}}{W_{i}}^{\mathrm{T}},{{\hat{\varLambda }}_{1010}}={He( - {\upsilon _{2i}}{V_i})}, \\ {{\hat{\varLambda }}_{22}}= & {} He({X_i}{A_i} - {\upsilon _{1i}}{B_{1i}}{Y_{i}}{C_{i}}) + {\varepsilon _{1i}}{N_i^{\mathrm{T}}}{N_i} + \sum \limits _{j = 1}^N {{\hat{\lambda }_{ij}}{X_j}},{{\hat{\varLambda }}_{99}}= {He( - {\tau _{2i}}{U_i})},{{\hat{\varLambda }}_{210}} = {X_i}{B_{1i}} - {\upsilon _{1i}}{B_{1i}}{V_{i}} - {\upsilon _{2i}}{C_{i}}^{\mathrm{T}}{Y_{i}}^{\mathrm{T}}.\\ \end{aligned}$$

Along the similar line as Theorem 1 to handle general TPs, one gets that $\sum \nolimits _{j = 1}^N {{\hat{\lambda } _{ij}}{X_j}}$ satisfies the following inequalities

Case I ($i\in \mathcal {I}_{k}^i$):

$$\begin{aligned} \begin{aligned}&\sum \limits _{j = 1}^N {{{\hat{\lambda }} _{ij}}{X_j}} \le \sum \limits _{j \in \mathcal {I}_k^i,j \ne i}^N \Big \{ (X_j - X_i - X_l)^{\mathrm{T}} \\&\quad \times T_{ij}^{-1}(X_j - X_i - X_l)\Big \}+ X_l T_{ii}^{-1} X_l \\&\quad \times \sum \limits _{j \in {\mathcal{I}_k^i}}^N {\left( {{\lambda } _{ij}}\left( {X_j - X_l} \right) + \frac{\delta _{ij}^2}{4} T_{ij}\right) }\\ \end{aligned} \end{aligned}$$

(49)

Case II ($i\in \mathcal {I}_{uk}^i$):

$$\begin{aligned} \begin{aligned}&\sum \limits _{j = 1}^N {{{\hat{\lambda }} _{ij}}{X_j}} \le \sum \limits _{j \in {\mathcal{I}_k^i}}^N {{{\lambda } _{ij}}\left( {X_j - X_i} \right) } \\&\quad + \sum \limits _{j \in \mathcal {I}_k^i}^N{\left\{ \frac{\delta _{ij}^2}{4} T_{ij} + (X_j - X_i)^{\mathrm{T}} T_{ij} ^{-1}(X_j - X_i)\right\} .} \end{aligned} \end{aligned}$$

(50)

Taking (49) and (50) into (48) produces the fact $\varXi _i<0$, respectively. $\square$ $\square$

Remark 5

In the course of derivation, to make the obtained controller and observer synthesis conditions be solvable, Lemma 3 is utilized to deal with the nonlinear term $e^{\mathrm{T}}_{\mu }(t)e_{\mu }(t)$. As a result, the established synthesis conditions are formulated by means of linear matrix inequalities.

4 Numerical simulation

The simulation is developed on a SRA system appeared in [40] to verify the proposed method.

The evolutionary of SRA system dynamic is

$$\begin{aligned} \begin{aligned} \ddot{\theta }(t)=&-\frac{\mathcal {M} g \mathcal {L}}{J} \sin (\theta (t))-\frac{\mathcal {D}(t)}{J}\dot{\theta }(t)\\&+ \frac{1}{J}u(t) + \frac{\mathcal {L}}{J}w(t) \end{aligned} \end{aligned}$$

(51)

where $\theta (t)$, $\mathcal {M}$ and $\mathcal {L}$ are the arm’s angle position, mass payload and length, respectively. u(t), w(t), J, $\mathcal {D}(t)$ and g are the control input, external disturbance, inertia moment, the uncertain viscous friction coefficient and gravity acceleration. Moreover, $g= 9.81$, $\mathcal {L}=0.8$, and $\mathcal {D}(t)=2$. As [40], linearizing (51) gives, for $\mathcal {M}$ and J with four modes,

$$\begin{aligned} \left\{ \begin{aligned} \dot{x}(t) =&\left( {\left[ {\begin{array}{*{20}{c}}0 &{} 1\\ -\,\mathcal {L}g &{} -\frac{\mathcal {D}}{J(r(t))}\\ \end{array}}\right] + \tilde{A}(r(t),t)}\right) x(t)\\&+ \left[ {\begin{array}{*{20}{c}} 0 \\ \frac{1}{J(r(t))} \end{array}}\right] u(t) + \left[ {\begin{array}{*{20}{c}} 0 \\ \frac{\mathcal {L}}{J(r(t))} \end{array}}\right] w(t)\\ y(t)=&\left[ {\begin{array}{*{20}{c}} 1&1 \end{array}}\right] x(t)\\ z(t)=&\left[ {\begin{array}{*{20}{c}} 1&1 \end{array}}\right] x(t) + D(r(t))w(t) \end{aligned}\right. \end{aligned}$$

(52)

where $x(t)=\left[ {\begin{array}{*{20}{c}}x_1(t)&x_2(t) \end{array}}\right] ^{\mathrm{T}}$, $r(t)=\{1,2,3,4\}$, $\tilde{A}(r(t),t)=M(r(t))E(t)N(r(t))$,${D(1)} = -\, 0.1$, ${D(2)} = 0.3$,${D(3)} = 0.5$,${D(4)} = 0.2$, $\mathcal {M}(r(t))$ and J(r(t)) change depending on the jump mode. $J(1)=0.82$, $J(2)=0.74$, $J(3)=0.93$ and $J(4)=0.89$ $(\mathcal {M}(r(t))=J(r(t)))$.

The matrices of parameter perturbation and disturbance are given as:

$$\begin{aligned} \begin{aligned}&E(t)=0.2\sin (t),\\&{M_1} = {\left[ {\begin{array}{*{20}{c}} {0.1}\\ {0.2} \end{array}} \right] },\quad {N_1} = \left[ {\begin{array}{*{20}{c}} {0.3}&{0.2} \end{array}} \right] ,\\&{M_2} = {\left[ {\begin{array}{*{20}{c}} {0.2}\\ {0.1} \end{array}} \right] },\quad {N_2} = \left[ {\begin{array}{*{20}{c}} {0.2}&{0.2} \end{array}} \right] ,\\&{M_3} = {\left[ {\begin{array}{*{20}{c}} {0.1}\\ {0.1} \end{array}} \right] },\quad {N_3} = \left[ {\begin{array}{*{20}{c}} {0.2}&{0.1} \end{array}} \right] ,\\&{M_4} = {\left[ {\begin{array}{*{20}{c}} {0.2}\\ {0.2} \end{array}} \right] },\quad {N_4} = \left[ {\begin{array}{*{20}{c}} {0.1}&{0.1} \end{array}} \right] . \end{aligned} \end{aligned}$$

For initialization, the real and estimated state vectors are given as $x = {\left[ {\begin{array}{*{20}{c}} 4&5 \end{array}} \right] ^{\mathrm{T}}}$, $\hat{x} = {\left[ {\begin{array}{*{20}{c}} 0&0 \end{array}} \right] ^{\mathrm{T}}}$. Other parameters are selected as follows $\theta =0.01;\iota =0.01;\tau _{1i}=1;\tau _{2i}=1; \upsilon _{1i}=1; \upsilon _{2i}=1 ; \upsilon _{3i}=1 ;\upsilon _{4i}=1; \eta _{ij}=1(i\in \{1,2,3,4\})$ and the parameters in quantizer $\beta =4;\alpha =0.5$.

The general TP matrix is

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} { - 1.2}+\varphi _{11}&{}\quad 0.3 &{}\quad ? &{}\quad ?\\ ? &{}\quad ? &{}\quad {0.6} &{}\quad 0.3\\ {0.8} &{}\quad ? &{}\quad { - 1.5}+\varphi _{33} &{}\quad ?\\ 0.2 &{}\quad ? &{}\quad ? &{}\quad ? \end{array}} \right] \end{aligned}$$

(53)

where $\varphi _{11}=\varphi _{33}=[-\,0.1,0.1]$.

Solving conditions (35) and (36) in Theorem 2 yields

$$\begin{aligned} \begin{aligned} {X_1}&= \left[ {\begin{array}{*{20}{c}} 2.1973 &{}\quad 0.2643\\ 0.2643 &{}\quad 0.3889 \end{array}} \right] ,\quad {X_2} = \left[ {\begin{array}{*{20}{c}} 2.1973 &{}\quad 0.2643\\ 0.2643 &{}\quad 0.3889 \end{array}} \right] ,\\ {X_3}&= \left[ {\begin{array}{*{20}{c}} 1.3832 &{}\quad 0.1750\\ 0.1750 &{}\quad 0.2536 \end{array}} \right] ,\quad {X_4} = \left[ {\begin{array}{*{20}{c}} 2.2948 &{}\quad 0.2269\\ 0.2269 &{}\quad 0.4032 \end{array}} \right] ,\\ {K_1}&= \left[ {\begin{array}{*{20}{c}} 0&\quad -\,1.2195 \end{array}} \right] ,\quad {L_1} = 1.1712,\\ {K_2}&= \left[ {\begin{array}{*{20}{c}} 0&\quad -\,1.3514 \end{array}} \right] ,\quad {L_2} = 1.8885,\\ {K_3}&= \left[ {\begin{array}{*{20}{c}} 0&\quad -\,1.0753 \end{array}} \right] ,\quad {L_3} = 1.3759,\\ {K_4}&= \left[ {\begin{array}{*{20}{c}} 0&\quad -\,1.1236 \end{array}} \right] ,\quad {L_4} = 0.8016. \end{aligned} \end{aligned}$$

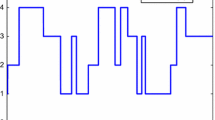
Applying the proposed sliding mode controller, the response curves of system states, quantizer parameters, input, quantized output and measured output are given in Figs. 2, 3 and 4, respectively.

Fig. 2

The curves of system states $x_1(t),x_2(t)$

Fig. 3

The curve of u(t)

Fig. 4

The curve of output $q_{\mu }(y)$

Fig. 5

The response of the quantization parameter $\mu$

It is seen that system state trajectories are stochastically stable in Fig. 2. Figure 3 shows the variation of the mode-dependent sliding mode control input with the possible mode evolution. The system output y(t) and its corresponding quantized case are depicted in Fig. 4. Figure 5 tells the quantized range varied by the proposed quantization adjustable steps.

In summary, the validity of the proposed sliding mode control approach are shown in these figures.

5 Conclusions

The quantized sliding mode control of MJSs with incomplete TPs is investigated. An observer-based integral sliding mode surface is built on the quantized system output, and effective techniques are established to cope with the quantization nonlinearities, unknown and uncertain TPs. Linear matrix inequalities-based sufficient conditions are obtained to guarantee the sliding mode reachability and the required $\mathcal {H}_\infty$ performance. The SRA system is employed to verify the proposed method.